A Novel Hybrid Predictive Model for Ultra-Short-Term Wind Speed Prediction
Abstract
:1. Introduction
- (1)
- Hybrid models based on signal decomposition. Advanced signal decomposition techniques are used to decompose wind sequences into a series of regular subsequences to smooth out the non-linear parts of the data. Wang et al. [11] proposed two WSP models, the EMD-based model and the EEMD-based model, and demonstrated experimentally that the EEMD-based model outperformed the EMD-based model. To solve the noise residuals problem of EEMD, Wang et al. [19] used CEEMD for WSP and obtained more satisfactory results. Ren et al. [20] experimentally demonstrated that the CEEMDAN-based model always performs best compared to the EMD-based model. Aside from EMD and its variants [3], wavelet transform [21,22] and VMD decomposition [23] are also common signal decomposition techniques in WSP.
- (2)
- Hybrid model based on weight assignment. This hybrid model typically uses multiple models to predict wind speed and assigns appropriate weights to each model. The final predicted values are obtained from a weighted combination of the predicted values of each model. To mitigate the adverse effects of multicollinearity of hybrid models, Jiang et al. [24] used GMDH to automatically identify the weights of three nonlinear models. The experimental results show that the application of GMDH can significantly improve the predictive power compared to the widely used equal-weighting scheme. Aytaç Altan et al. [25] used the gray wolf optimization algorithm to optimize the weighting of each IMF to create the optimal prediction model. Nie et al. [26] proposed a weight combination mechanism based on a multi-objective optimization algorithm, which further improved the prediction accuracy and predictive power of the model.
- (3)
- Hybrid model based on optimization algorithms. The model introduces some heuristic optimization algorithms to optimize the hyperparameters, weights, network structure, or thresholds of the model. Liu et al. [27] used Jaya to optimize the hyperparameters of SVM, which improved the SVM regression performance and effectively improved the prediction accuracy. Tian et al. [28] used PSO to optimize the weight coefficients of each prediction model, and the experimental results proved the necessity of the weight coefficient optimization strategy. Liu et al. [29] used GA to optimize the internal parameters of LSTM, thus improving the prediction efficiency and prediction accuracy of the model. Huang et al. [30] used the modified Bayesian optimization algorithm to optimize the hyperparameters of the prediction model and obtained more satisfactory forecasting precision and computation cost. To obtain the best network structure and weights, Liu et al. [31] combined GA and PSO to optimize the CNN prediction model and effectively addressed the problem of poor prediction performance due to wind volatility.
- (4)
- Hybrid model based on error correction. Error correction is a post-processing technique for WSP, which predicts the residuals and superimposes the results on the original prediction to obtain the corrected final prediction. Duan et al. [32] used ICEEMDAN to decompose the errors, and the experimental results showed that the error decomposition correction method can significantly improve the prediction accuracy. Liu et al. [33] proposed an adaptive multiple error correction method, which makes full use of the deeper predictable components and effectively improves the reliability and accuracy of the model. Zhang et al. [34] demonstrated experimentally that the final predictions corrected by Markov chains are closer to the original wind field data, which proves the effectiveness of Markov chains.
- A novel hybrid model is proposed for ultra-short-term WSP, which quantitatively assesses the complexity of wind speed series by SE and builds different prediction models for different subseries with different complexity separately.
- The proposed ORBLS has cyclically connected enhancement nodes that can better capture the dynamic characteristics of the wind speed sequence, and the improved PSO is used to optimize the hyperparameters of ORBLS.
- The proposed BTCN adds a dilated causal convolution layer in parallel to each residual block, which alleviates the problem of massive local information loss from dilated causal convolution.
- The ICEEMDAN is introduced to smooth the nonlinear part of the wind speed data, which further improves the forecasting performance.
- Four wind speed datasets are used to comprehensively evaluate the effectiveness and robustness of the proposed model.
2. Materials and Methods
2.1. Overall Framework of the Proposed Model
2.2. ICEEMDAN Model
2.3. Sample Entropy
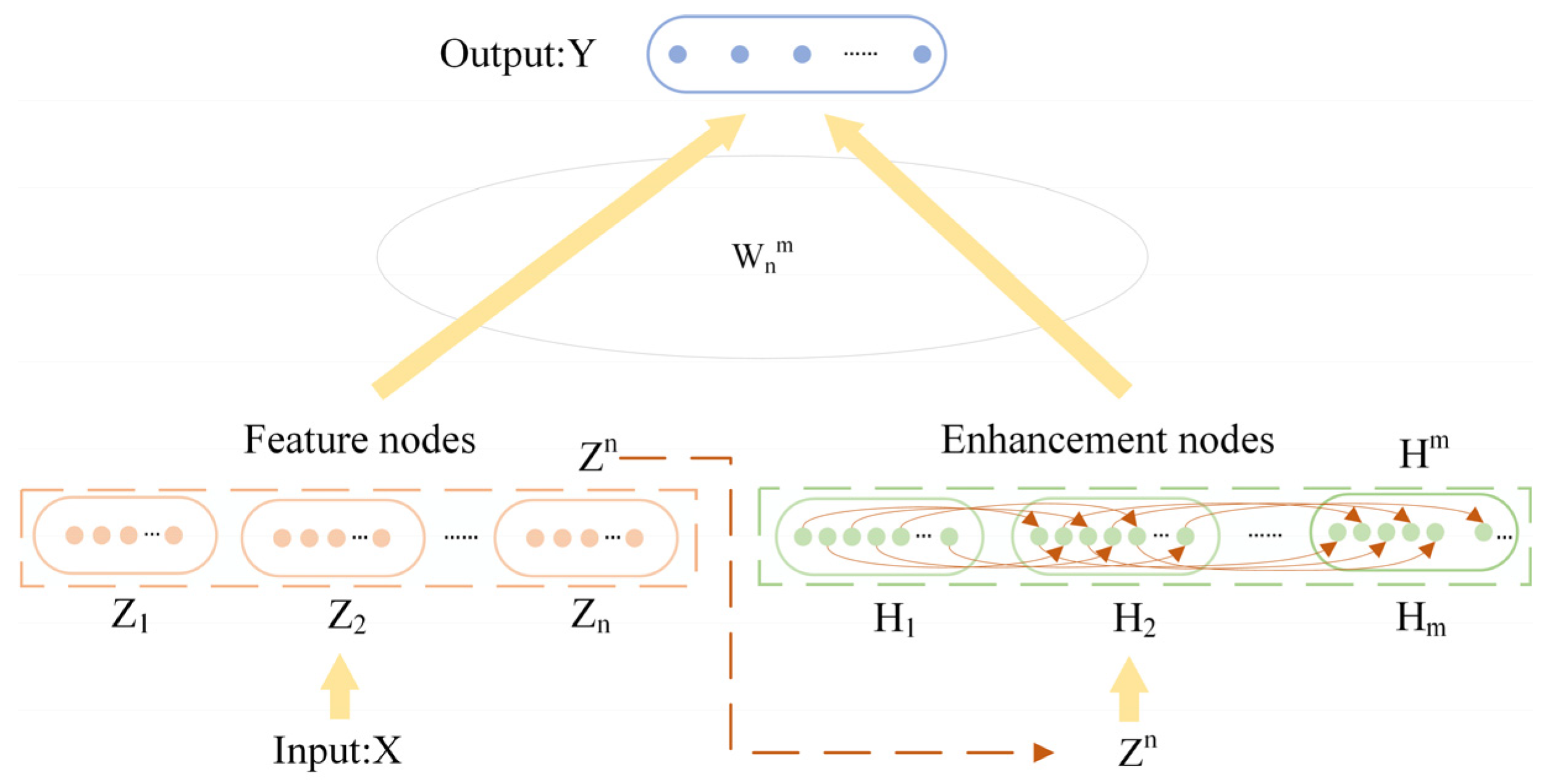
2.4. ORBLS Model
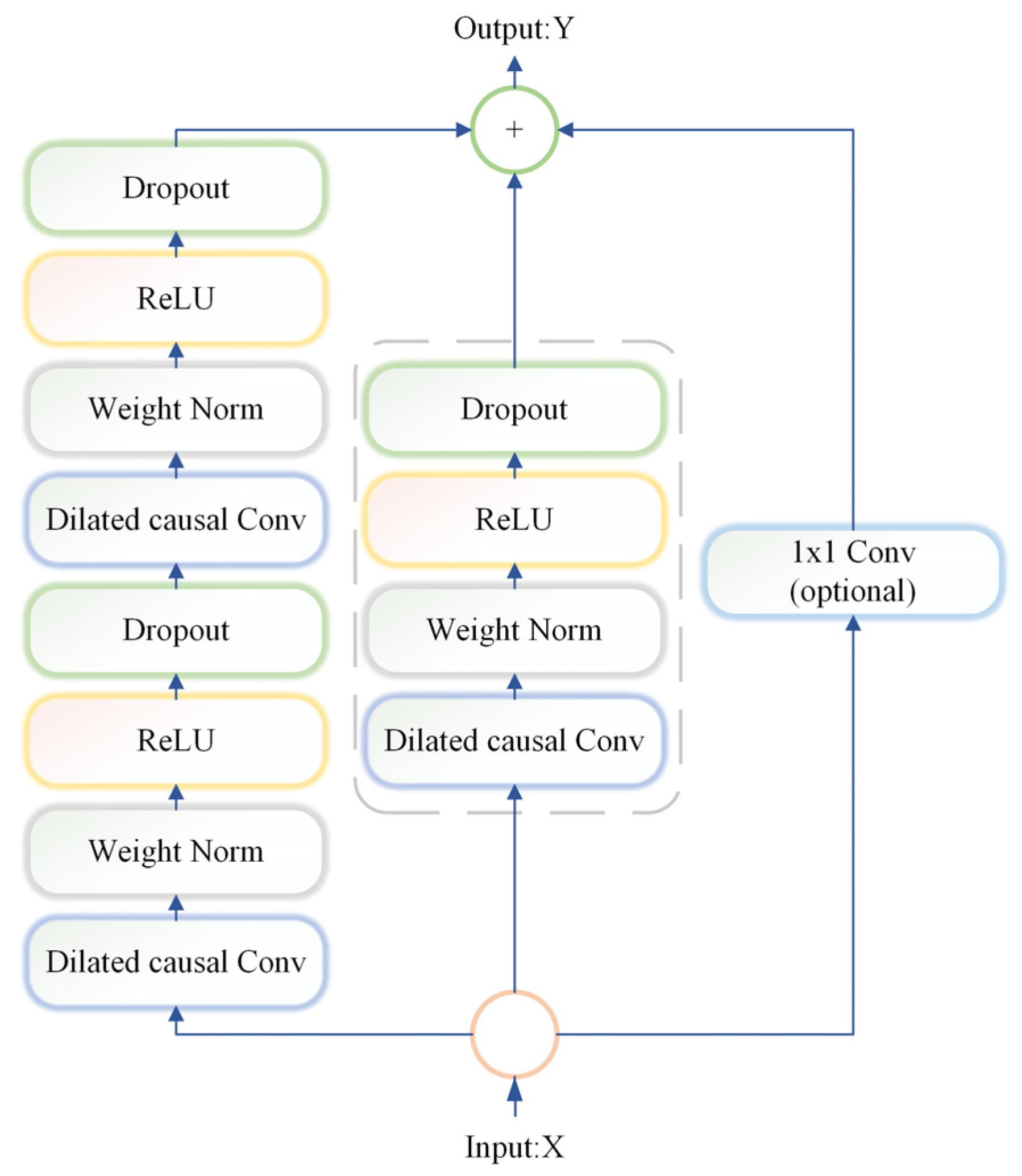
2.5. BTCN Model
2.6. The Prediction Steps
| Algorithm 1: The proposed predictive framework for WSP |
| Input: . Output: Process: 1: fork = 1: 2: get by Equation (5) 3: get by Equation (10) 4: end 5: //ORBLS algorithm main steps 6: for i = 1: do 7: Calculate 8: end 9: Obtain the final 10: for j = 1: do 11: Calculate 12: end 13: Obtain the final 14: Calculate connecting weights: 15: Obtain the 16: //BTCN algorithm main steps 17: Calculate causal convolution 18: Increase the receptive field: 19: Update the receptive field: 20: Calculate basic block |
3. Case Analysis
3.1. Data Description
3.2. Evaluation Index
3.3. Comparable Methods
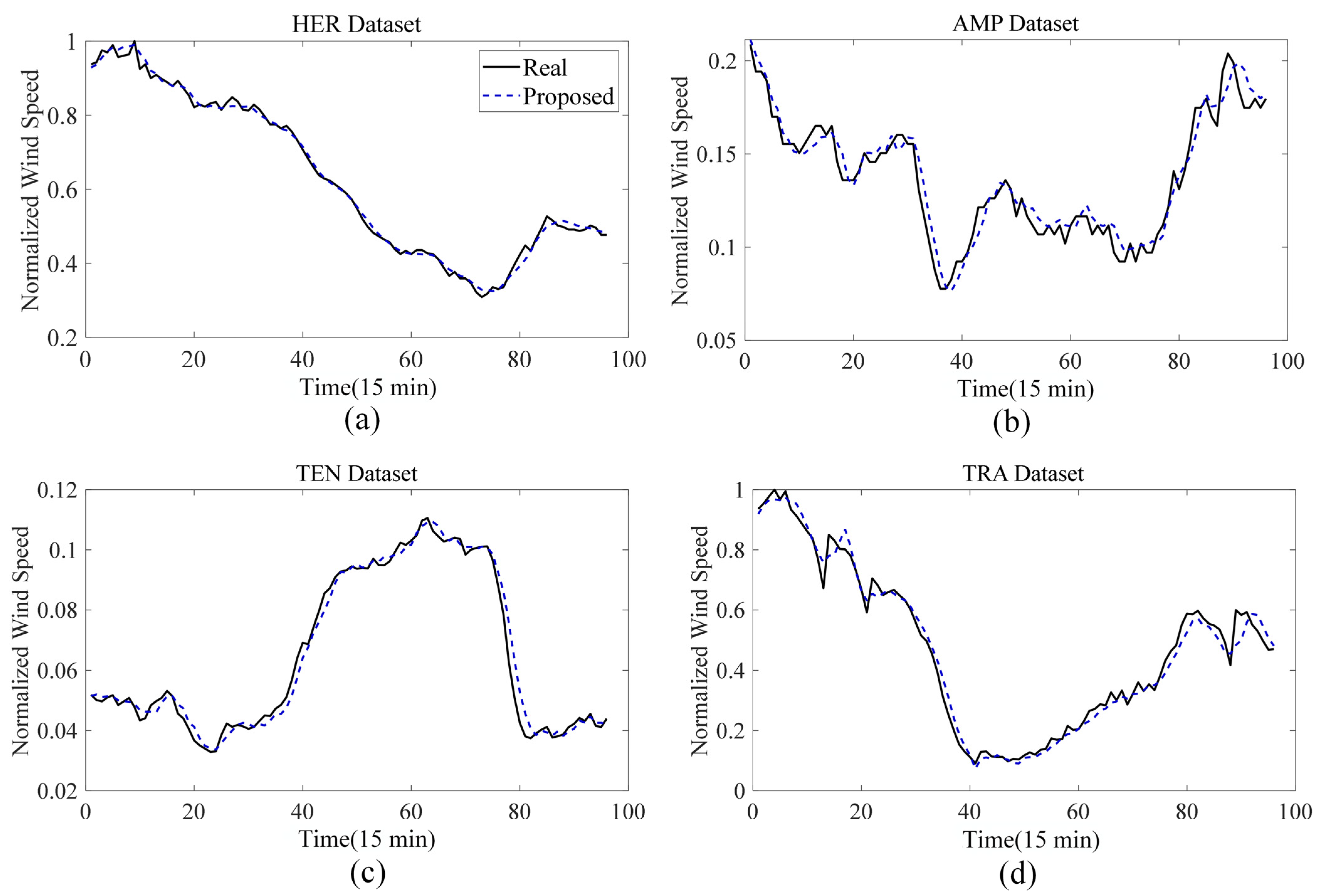
3.4. Experimental Results
3.4.1. Experiment I: Comparison between Different Forecasting Methods
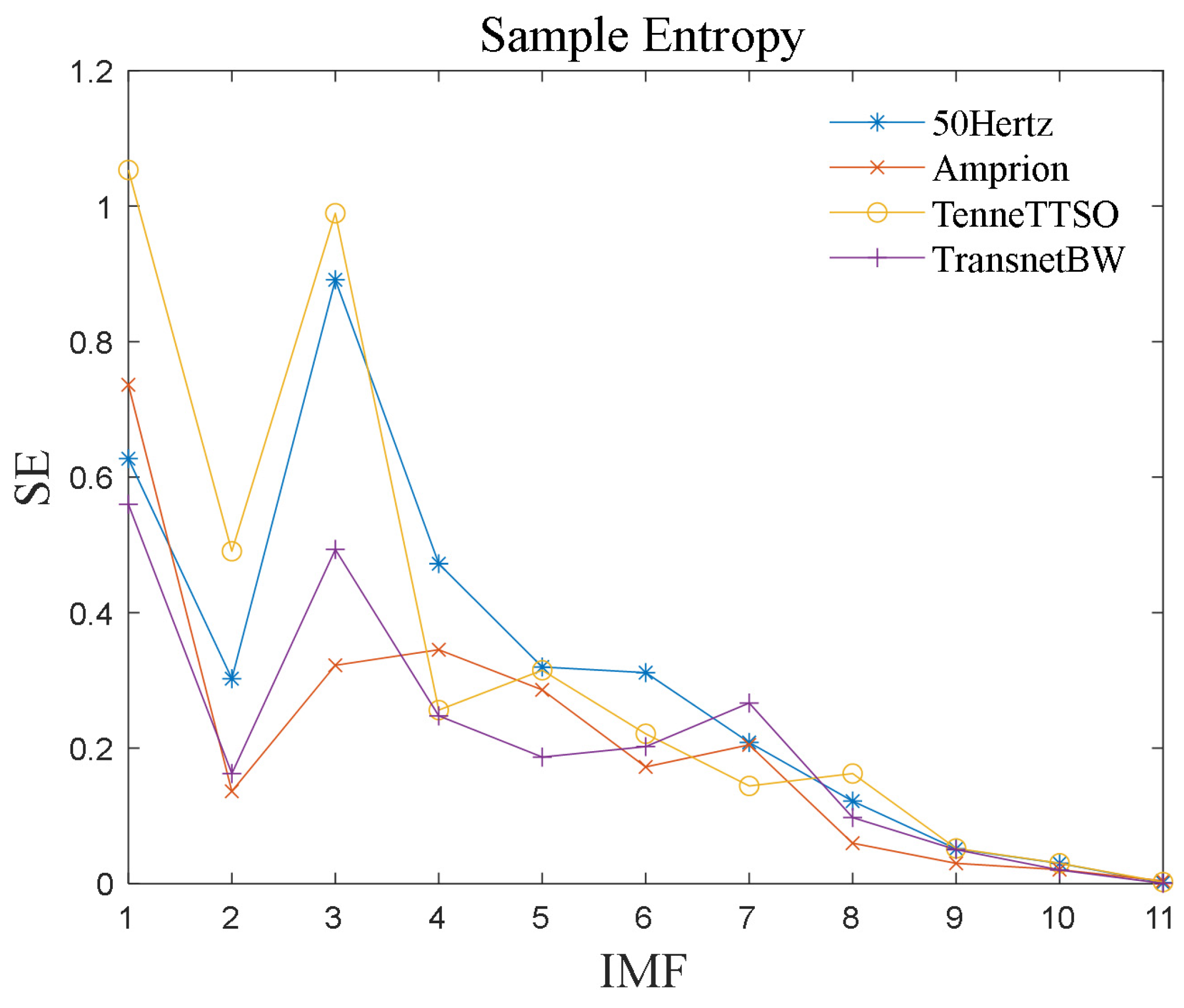
3.4.2. Experiment II: Experiments on Sample Entropy to Quantify Sequence Complexity
3.4.3. Experiment III: Ablation Experiment between Single Models and Hybrid Models
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| AI | Artificial intelligence |
| ANFIS | Adaptive-network-based fuzzy inference system |
| ARIMA | Autoregressive integrated moving average |
| BLS | Broad learning system |
| BP | Back propagation |
| BTCN | Broadened TCN |
| CEEMD | Complementary ensemble empirical mode decomposition |
| CEEMDAN | Complete ensemble empirical mode decomposition with adaptive noise |
| CNN | Convolutional neural network |
| EEMD | Ensemble empirical mode decomposition |
| EMD | Empirical mode decomposition |
| ELM | Extreme learning machine |
| GA | Genetic algorithm |
| GMDH | Group method of data handling neural network |
| GPR | Gaussian process regression |
| ICEEMDAN | Improved CEEMDAN |
| IMF | Intrinsic mode functions |
| IOWA | Induced ordered weighted averaging |
| LSTM | Long short-term memory |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
| PSO | Particle swarm optimization |
| ORBLS | Optimized recurrent BLS |
| RMSE | Root mean square error |
| SE | Sample entropy |
| SSE | Sum of squared error |
| SVM | Support vector machine |
| TCN | Temporal convolutional network |
| VMD | Variational mode decomposition |
| WSP | Wind speed prediction |
References
- Hu, J.; Wang, J.; Zeng, G. A hybrid forecasting approach applied to wind speed time series. Renew. Energy 2013, 60, 185–194. [Google Scholar] [CrossRef]
- Kavasseri, R.G.; Seetharaman, K. Day-ahead wind speed forecasting using f-ARIMA models. Renew. Energy 2009, 34, 1388–1393. [Google Scholar] [CrossRef]
- Singh, S.; Mohapatra, A. Repeated wavelet transform based ARIMA model for very short-term wind speed forecasting. Renew. Energy 2019, 136, 758–768. [Google Scholar] [CrossRef]
- Shi, J.; Liu, Y.; Li, Y.; Liu, Y.; Roux, G.; Shi, L.; Fan, X. Wind Speed Forecasts of a Mesoscale Ensemble for Large-Scale Wind Farms in Northern China: Downscaling Effect of Global Model Forecasts. Energies 2022, 15, 896. [Google Scholar] [CrossRef]
- Wang, H.; Han, S.; Liu, Y.; Yan, J.; Li, L. Sequence transfer correction algorithm for numerical weather prediction wind speed and its application in a wind power forecasting system. Appl. Energy 2019, 237, 1–10. [Google Scholar] [CrossRef]
- Hill, D.C.; McMillan, D.; Bell, K.R.W.; Infield, D. Application of Auto-Regressive Models to U.K. Wind Speed Data for Power System Impact Studies. IEEE Trans. Sustain. Energy 2011, 3, 134–141. [Google Scholar] [CrossRef]
- Do, D.-P.N.; Lee, Y.; Choi, J. Hourly Average Wind Speed Simulation and Forecast Based on ARMA Model in Jeju Island, Korea. J. Electr. Eng. Technol. 2016, 11, 1548–1555. [Google Scholar] [CrossRef] [Green Version]
- Yunus, K.; Thiringer, T.; Chen, P. ARIMA-Based Frequency-Decomposed Modeling of Wind Speed Time Series. IEEE Trans. Power Syst. 2015, 31, 2546–2556. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Srinivasan, D.; Hu, Q. Robust functional regression for wind speed forecasting based on Sparse Bayesian learning. Renew. Energy 2018, 132, 43–60. [Google Scholar] [CrossRef]
- Elsaraiti, M.; Merabet, A. A Comparative Analysis of the ARIMA and LSTM Predictive Models and Their Effectiveness for Predicting Wind Speed. Energies 2021, 14, 6782. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, N.; Wu, L.; Wang, Y. Wind speed forecasting based on the hybrid ensemble empirical mode decomposition and GA-BP neural network method. Renew. Energy 2016, 94, 629–636. [Google Scholar] [CrossRef]
- Alkesaiberi, A.; Harrou, F.; Sun, Y. Efficient Wind Power Prediction Using Machine Learning Methods: A Comparative Study. Energies 2022, 15, 2327. [Google Scholar] [CrossRef]
- Ma, X.; Jin, Y.; Dong, Q. A generalized dynamic fuzzy neural network based on singular spectrum analysis optimized by brain storm optimization for short-term wind speed forecasting. Appl. Soft Comput. 2017, 54, 296–312. [Google Scholar] [CrossRef]
- Luo, X.; Sun, J.; Wang, L.; Wang, W.; Zhao, W.; Wu, J.; Wang, J.-H.; Zhang, Z. Short-Term Wind Speed Forecasting via Stacked Extreme Learning Machine with Generalized Correntropy. IEEE Trans. Ind. Inform. 2018, 14, 4963–4971. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Wang, G.; Li, G.; Peng, J.; Liu, Y. Deep belief network based deterministic and probabilistic wind speed forecasting approach. Appl. Energy 2016, 182, 80–93. [Google Scholar] [CrossRef]
- Shang, Z.; Wen, Q.; Chen, Y.; Zhou, B.; Xu, M. Wind Speed Forecasting Using Attention-Based Causal Convolutional Network and Wind Energy Conversion. Energies 2022, 15, 2881. [Google Scholar] [CrossRef]
- Khodayar, M.; Wang, J. Spatio-Temporal Graph Deep Neural Network for Short-Term Wind Speed Forecasting. IEEE Trans. Sustain. Energy 2018, 10, 670–681. [Google Scholar] [CrossRef]
- Zhu, Q.; Chen, J.; Shi, D.; Zhu, L.; Bai, X.; Duan, X.; Liu, Y. Learning Temporal and Spatial Correlations Jointly: A Unified Framework for Wind Speed Prediction. IEEE Trans. Sustain. Energy 2019, 11, 509–523. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Z. Ultra-short-term wind speed forecasting using an optimized artificial intelligence algorithm. Renew. Energy 2021, 171, 1418–1435. [Google Scholar] [CrossRef]
- Ren, Y.; Suganthan, P.N.; Srikanth, N. A Comparative Study of Empirical Mode Decomposition-Based Short-Term Wind Speed Forecasting Methods. IEEE Trans. Sustain. Energy 2014, 6, 236–244. [Google Scholar] [CrossRef]
- Yang, Y.; Fan, C.; Xiong, H. A novel general-purpose hybrid model for time series forecasting. Appl. Intell. 2021, 52, 2212–2223. [Google Scholar] [CrossRef] [PubMed]
- Domínguez-Navarro, J.; Lopez-Garcia, T.; Valdivia-Bautista, S. Applying Wavelet Filters in Wind Forecasting Methods. Energies 2021, 14, 3181. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, G. A hybrid prediction model for forecasting wind energy resources. Environ. Sci. Pollut. Res. 2020, 27, 19428–19446. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Liu, S.; Zhao, N.; Xin, J.; Wu, B. Short-term wind speed prediction using time varying filter-based empirical mode decomposition and group method of data handling-based hybrid model. Energy Convers. Manag. 2020, 220, 113076. [Google Scholar] [CrossRef]
- Altan, A.; Karasu, S.; Zio, E. A new hybrid model for wind speed forecasting combining long short-term memory neural network, decomposition methods and grey wolf optimizer. Appl. Soft Comput. 2020, 100, 106996. [Google Scholar] [CrossRef]
- Nie, Y.; Liang, N.; Wang, J. Ultra-short-term wind-speed bi-forecasting system via artificial intelligence and a double-forecasting scheme. Appl. Energy 2021, 301, 117452. [Google Scholar] [CrossRef]
- Liu, M.; Cao, Z.; Zhang, J.; Wang, L.; Huang, C.; Luo, X. Short-term wind speed forecasting based on the Jaya-SVM model. Int. J. Electr. Power Energy Syst. 2020, 121, 106056. [Google Scholar] [CrossRef]
- Tian, Z. Modes decomposition forecasting approach for ultra-short-term wind speed. Appl. Soft Comput. 2021, 105, 107303. [Google Scholar] [CrossRef]
- Liu, Z.; Hara, R.; Kita, H. Hybrid forecasting system based on data area division and deep learning neural network for short-term wind speed forecasting. Energy Convers. Manag. 2021, 238, 114136. [Google Scholar] [CrossRef]
- Huang, H.; Jia, R.; Shi, X.; Liang, J.; Dang, J. Feature selection and hyper parameters optimization for short-term wind power forecast. Appl. Intell. 2021, 51, 6752–6770. [Google Scholar] [CrossRef]
- Liu, J.; Shi, Q.; Han, R.; Yang, J. A Hybrid GA–PSO–CNN Model for Ultra-Short-Term Wind Power Forecasting. Energies 2021, 14, 6500. [Google Scholar] [CrossRef]
- Duan, J.; Zuo, H.; Bai, Y.; Duan, J.; Chang, M.; Chen, B. Short-term wind speed forecasting using recurrent neural networks with error correction. Energy 2021, 217, 119397. [Google Scholar] [CrossRef]
- Liu, H.; Yang, R.; Wang, T.; Zhang, L. A hybrid neural network model for short-term wind speed forecasting based on decomposition, multi-learner ensemble, and adaptive multiple error corrections. Renew. Energy 2020, 165, 573–594. [Google Scholar] [CrossRef]
- Zhang, Y.; Han, J.; Pan, G.; Xu, Y.; Wang, F. A multi-stage predicting methodology based on data decomposition and error correction for ultra-short-term wind energy prediction. J. Clean. Prod. 2021, 292, 125981. [Google Scholar] [CrossRef]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E. Improved complete ensemble EMD: A suitable tool for biomedical signal processing. Biomed. Signal Process. Control 2014, 14, 19–29. [Google Scholar] [CrossRef]
- Wu, Q.; Lin, H. Daily urban air quality index forecasting based on variational mode decomposition, sample entropy and LSTM neural network. Sustain. Cities Soc. 2019, 50, 101657. [Google Scholar] [CrossRef]
- Chen, C.L.P.; Liu, Z. Broad Learning System: An Effective and Efficient Incremental Learning System Without the Need for Deep Architecture. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 10–24. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, H.; Guo, Y. Wind Power Prediction Based on PSO-SVR and Grey Combination Model. IEEE Access 2019, 7, 136254–136267. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2019, arXiv:1803.01271. [Google Scholar]
- Dokur, E.; Yuzgec, U.; Kurban, M. Performance Comparison of Hybrid Neuro-Fuzzy Models using Meta-Heuristic Algorithms for Short-Term Wind Speed Forecasting. Electrica 2021, 21, 305–321. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, G.; Chen, B.; Han, J.; Zhao, Y.; Zhang, C. Short-term wind speed prediction model based on GA-ANN improved by VMD. Renew. Energy 2020, 156, 1373–1388. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, S.; Yang, L. Wind Speed Forecasting Method Using EEMD and the Combination Forecasting Method Based on GPR and LSTM. Sustainability 2018, 10, 3693. [Google Scholar] [CrossRef] [Green Version]


| Dataset | Time-Step (min) | Mean (m/s) | Median (m/s) | Max (m/s) | Min (m/s) | Standard Deviation (m/s) |
|---|---|---|---|---|---|---|
| HER | 15 | 0.89764 | 0.65000 | 5.60000 | 0 | 0.88480 |
| AMP | 15 | 0.42297 | 0.30000 | 2.06000 | 0 | 0.38803 |
| TEN | 15 | 0.84532 | 0.59420 | 4.76590 | 0.01420 | 0.78575 |
| TRA | 15 | 0.12757 | 0.07445 | 0.86230 | 0 | 0.14548 |
| Model | Parameter Setting |
|---|---|
| PSO-ANFIS | = 300, = 40, = 1.0, = 2.0, = 4, = 4, = 52 |
| VMD-GA-BP | = 11, = 150, = 100, = 40, = 0.1, = 9 |
| EEMD-GPR-LSTM | = 11, = 200, = 100, = 100, = 50, = 20 |
| MWS-CE-ENN | = 1000, = 0.1, = 0.000001, = 40, = 5, = 6, = 1, = 100, = 0.2 |
| ICE-MOV-BFS | = 100, = 3, = 5, = 5, = 3 |
| Proposed Model | = 0.01, = 40, = 100, = 1.5, = 1.5, = 50, = 0.002, = 10−30, = 0.05, = 32, = 3, = [1, 2, 4, 8, 16] |
| Dataset | Metrics | Proposed Model | PSO-ANFIS | VMD-GA-BP | EEMD-GPR-LSTM | MWS-CE-ENN | ICE-MOV-BFS |
|---|---|---|---|---|---|---|---|
| HER | RMSE | 0.0086 | 0.0120 | 0.0137 | 0.0126 | 0.0132 | 0.0097 |
| SSE | 0.0317 | 0.0615 | 0.0806 | 0.0676 | 0.0746 | 0.0403 | |
| MAPE | 4.1366 | 5.1392 | 5.2415 | 11.7694 | 6.1941 | 4.7523 | |
| MAE | 0.0053 | 0.0077 | 0.0092 | 0.0089 | 0.0082 | 0.0069 | |
| AMP | RMSE | 0.0147 | 0.0186 | 0.0187 | 0.0296 | 0.0231 | 0.0167 |
| SSE | 0.0930 | 0.1481 | 0.1505 | 0.3743 | 0.2284 | 0.1197 | |
| MAPE | 4.1848 | 5.0249 | 6.3716 | 5.9358 | 5.8755 | 4.6723 | |
| MAE | 0.0107 | 0.0133 | 0.0146 | 0.0143 | 0.0127 | 0.0124 | |
| TEN | RMSE | 0.0087 | 0.0107 | 0.0114 | 0.0118 | 0.0129 | 0.0094 |
| SSE | 0.0324 | 0.0490 | 0.0558 | 0.0591 | 0.1601 | 0.0378 | |
| MAPE | 3.5071 | 4.1562 | 6.3884 | 5.4492 | 5.2321 | 4.8391 | |
| MAE | 0.0055 | 0.0066 | 0.0083 | 0.0073 | 0.0081 | 0.0069 | |
| TRA | RMSE | 0.0259 | 0.0369 | 0.0357 | 0.0266 | 0.0327 | 0.0264 |
| SSE | 0.2879 | 0.5829 | 0.5460 | 0.3029 | 0.4577 | 0.2983 | |
| MAPE | 5.7290 | 7.9526 | 8.8673 | 5.7345 | 6.3028 | 5.7326 | |
| MAE | 0.0183 | 0.0271 | 0.0266 | 0.0197 | 0.0244 | 0.0191 |
| Model | Subsequence Set | RMSE | SSE | MAE |
|---|---|---|---|---|
| BTCN | high subsequence set | 0.0031 | 0.0042 | 0.0016 |
| low subsequence set | 0.0085 | 0.0310 | 0.0009 | |
| ORBLS | high subsequence set | 0.0036 | 0.0056 | 0.0020 |
| low subsequence set | 0.0007 | 0.0002 | 0.0005 |
| Model | RMSE | SSE | MAPE (%) | MAE |
|---|---|---|---|---|
| TCN | 0.0175 | 0.1310 | 8.4706 | 0.0108 |
| BLS | 0.0308 | 0.4058 | 6.4823 | 0.0164 |
| BTCN | 0.0149 | 0.0952 | 5.6806 | 0.0091 |
| OBLS | 0.0122 | 0.0642 | 5.4614 | 0.0080 |
| ORBLS | 0.0117 | 0.0588 | 5.0518 | 0.0075 |
| ICEEMDAN-BTCN | 0.0146 | 0.0916 | 6.0596 | 0.0094 |
| ICEEMDAN-ORBLS | 0.0091 | 0.0356 | 4.6292 | 0.0061 |
| Proposed | 0.0086 | 0.0317 | 4.1366 | 0.0053 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, L.; Wang, Q.; Huang, J.; Chen, L.; Liang, Y.; Liu, P.X.; Li, C. A Novel Hybrid Predictive Model for Ultra-Short-Term Wind Speed Prediction. Energies 2022, 15, 4895. https://doi.org/10.3390/en15134895
Huang L, Wang Q, Huang J, Chen L, Liang Y, Liu PX, Li C. A Novel Hybrid Predictive Model for Ultra-Short-Term Wind Speed Prediction. Energies. 2022; 15(13):4895. https://doi.org/10.3390/en15134895
Chicago/Turabian StyleHuang, Longnv, Qingyuan Wang, Jiehui Huang, Limin Chen, Yin Liang, Peter X. Liu, and Chunquan Li. 2022. "A Novel Hybrid Predictive Model for Ultra-Short-Term Wind Speed Prediction" Energies 15, no. 13: 4895. https://doi.org/10.3390/en15134895
APA StyleHuang, L., Wang, Q., Huang, J., Chen, L., Liang, Y., Liu, P. X., & Li, C. (2022). A Novel Hybrid Predictive Model for Ultra-Short-Term Wind Speed Prediction. Energies, 15(13), 4895. https://doi.org/10.3390/en15134895







