Dynamic Propagation and Shear Stress Disturbance of Multiple Hydraulic Fractures: Numerical Cases Study via Multi-Well Hydrofracturing Model with Varying Adjacent Spacings

Abstract

Multi-well hydrofracturing is an important technology for forming complex fracture networks and increasing reservoir permeability. The distribution and design of horizontal wells affect fracture propagation; however, it is still unclear how the spacing between adjacent wells leads to fracture propagation, deflection and connection. In this study, the thermal-hydro-mechanical coupling effect in the hydrofracturing process is comprehensively considered and a multi-well hydrofracturing model based on the finite element–discrete element method is established. Using typical cases, the unstable propagation of hydraulic fractures in multiple horizontal wells under varying adjacent well spacings is studied. Combined with the shear stress shadow caused by in situ stress disturbed by fracture tip propagation, quantitative indexes (such as length, volume, deflection and unstable propagation behaviors of hydrofracturing fracture networks) are analyzed. The results show that the shear stress disturbance caused by multiple hydraulic fractures is a significant factor for multi-well hydrofracturing. Reducing well spacing will increase the stress shadow area and aggravate the mutual disturbance and deflection between fractures. The results of quantitative analysis show that the total length of hydraulic fractures decreases with the decrease of well spacing, and the total volume of hydraulic fractures increases with the decrease of well spacing. The results of unstable propagation and stress evolution of hydraulic fracture networks considering thermal-hydro-mechanical coupling obtained in this study can provide useful guidance for the valuation and design of hydrofracturing fracture networks in deep unconventional oil and gas reservoirs.

1. Introduction

The complexity of hydraulic fracture networks is the key to increasing unconventional oil and gas production [1]. Multi-well hydrofracturing is an important technology for forming complex fracture networks and increasing reservoir permeability. Compared with single-well hydrofracturing, the interaction between fractures in multi-well hydrofracturing is more complex. Figure 1 shows unstable dynamic propagation and deflection of multiple hydraulic fractures in multi-well hydrofracturing in tight reservoirs, in which the dynamic propagation of multiple hydraulic fractures is simultaneously affected by the adjacent perforation clusters (a: perforation cluster spacing) and adjacent wells (b: well spacing), resulting in a more complex fracture network. The hydrofracturing-induced stress field places pressure on the surrounding rock, altering the initiation pressure in the subsequent perforation, the in situ stress field and the propagation direction of hydraulic fractures [2,3,4,5,6,7,8]. The hydrofracturing-induced stress field not only can promote fracture propagation and form a more complex fracture network [9,10,11,12], but can also inhibit the growth of local fractures [6,13,14,15], which are not conducive to controlling the fracture propagation process and increasing unconventional oil and gas production [16,17,18]. It is vital to understand the relationship between the geometric distributions of multiple wells and the induced stress field and fracture propagation, so as to evaluate and optimize the hydraulic fracturing process.

The spacing of perforation clusters, fracturing sequence and well spacing are considered to be the dominant factors causing unstable propagation of parallel fractures in different extents in multi-well hydrofracturing [19,20,21,22]. When two adjacent horizontal wells are designed, the hydraulic fractures in the subsequent well propagate away from the previous well [22]. Narrow adjacent well spacing may result in intersecting stimulation reservoir volumes, causing competition behaviors between wells and affecting fracture propagation and oil and gas production [23,24]. Well spacing should be carefully selected to avoid the connection of fracture tips in adjacent horizontal wells; some studies have carried out analysis from the perspective of the hydrofracturing-induced stress field evolution. A small well spacing may create drastic stress disturbances between wells, resulting in connections of hydraulic fractures from adjacent wells in a short duration time of hydrofracturing, which inevitably reduces fracture complexity in the far field. On the other hand, if the well spacing is too large, the natural fracture between the two wells cannot be reactivated [25,26,27]. The spacing between adjacent wells can be optimized by using the variation of induced stress field evolution and disturbance in the hydrofracturing process. The simulation and evaluation results of the fracture path in the simultaneous fracturing of two horizontal wells show that when the well spacing exceeds 60 m, it can effectively alleviate the stress disturbance and improve the fracturing effects [27].

The stress shadow effect between multiple wells affects the dynamic propagation of fracture network; hence, it is critical to determine the internal mechanisms of the stress shadow effect in multi-well hydrofracturing to optimize the fracturing schemes [21,28]. The stress shadow effect depends on fracture height, mechanical properties (i.e., Young’s modulus and Poisson’s ratio), cluster spacing and well spacing [29,30,31]. When multiple horizontal wells are adjacent to each other, the stress shadows induced by perforation clusters will affect the fracture propagation patterns in each well [24]. Increasing well spacing can effectively alleviate the stress shadow effect [27,28]. However, it is still unclear how the spacings between adjacent wells lead to fracture propagation, deflection and connection, and the quantitative relationship between the induced stress field and fracture propagation is not well understood.

In order to further investigate the effect of adjacent well spacing on dynamic propagation and shear stress disturbance in multi-well hydrofracturing, the main contents of this paper are investigated as follows. Section 2 introduces the combined finite element–discrete element method considering thermal-hydro-mechanical coupling. Section 3 introduces the numerical models and cases of multiple horizontal wells, including the geometric model, finite element model, conditions and parameters setting. Section 4 introduces the results and discussions. Section 5 summarizes the conclusions of this study and prospects for future research.

2. Combined Finite Element–Discrete Element Method Considering Thermal-Hydro-Mechanical Coupling

In the hydrofracturing of the reservoir rock, the thermal field, hydraulic field and mechanical field form a mutual coupling process [32,33]. The main mechanism of the coupling process is shown in Figure 2 [34]. Through the transfer between solid stress, fluid pressure, heat and fracture networks, the thermal-hydro-mechanical coupling and fracture network mechanisms are introduced [35].

The staggered coupling scheme is adopted in this study. In hydraulic field, under the current deformation and fracture network of solid rock, the fluid pressures in the pore media of the rock matrix and fractures are computed, and the fluid pressures are transmitted to the rock matrix. In the thermal field, the heat transfer in the pore media of the rock matrix and fracture fluid are computed through the governing equation of the current time, and the heat is transmitted to the rock matrix where it induces thermal stresses. In the mechanical field, the solid deformation and stresses in the pore media of the rock matrix are computed. Furthermore, by introducing the thermal stresses, the final effective stresses can be obtained. Based on the stress states of each finite element, the fracture criterion is used to judge whether the fractures initiate or propagate. In this study, the fracture criterion considering damage evolution is used to simulate the propagation of hydraulic fractures, and the tensile strength ${\sigma }_t$ and fracture energy $G_f$ are involved, the details of which can be found in the related reference [36].

The governing equations for solid deformation, fluid flow and heat transfer are as follows:

(1)

Solid deformation

The governing equation of rock mass matrix deformation is [37]:

$$L_{}^T({\sigma }^{\prime }-\alpha m{p}_l^{})+{\rho }_B^{}g=0$$

(1)

where L is the differential operator, ${\sigma }^{\prime }$ is the effective stress tensor with ${\sigma }^{\prime }=\sigma +\alpha \mathbf{I}p$, $\alpha$ is Biot’s coefficient, $\sigma$ is the stress tensor of the rock matrix, m denotes the identity tensor, $p_l^{}$ is the pore fluid pressure of the rock mass, ${\rho }_B^{}$ is the saturated bulk density of the rock mass and g is the gravity vector. The inertia term is not concluded and the quasi-static state is considered, which is a basis for detecting the deformation and behavior of rock mass in this study.

(2)

Fluid flow

The governing equation of seepage in rock matrix is:

$$\mathrm{div}\left[\frac{k}{{\mu }_l^{}}\left(\nabla p_l^{}-{\rho }_l^{}g\right)\right]=\left(\frac{\phi }{K_l^{}}+\frac{\alpha -\phi }{K_s^{}}\right)\frac{\mathrm{d}{p}_l^{}}{\mathrm{d}t}+\alpha \frac{\mathrm{d}{\epsilon }_v^{}}{\mathrm{d}t}$$

(2)

where $k$ is the intrinsic permeability of rock mass, ${\mu }_l^{}$ is the viscosity of the pore liquid, ${\rho }_l^{}$ is the pore liquid density, $\phi$ is the porosity of porous medium, $K_l^{}$ is the pore fluid stiffness, $K_s^{}$ is the solid skeleton stiffness, ${\epsilon }_v^{}$ is the volumetric strain of rock mass pore structure and $t$ is the current moment.

The governing equation of fluid flow in the fracture is:

$$\frac{\partial }{\partial x}\left[\frac{k_{}^{fr}}{{\mu }_n^{}}\left(\nabla p_n^{}-{\rho }_{fn}^{}g\right)\right]=S_{}^{fr}\frac{\mathrm{d}{p}_n^{}}{\mathrm{d}t}+\alpha \left(\mathsf{\Delta }{\dot{e}}_{\epsilon }^{}\right)$$

(3)

where $k_{}^{fr}$ is the fracture intrinsic permeability, μ_n is the viscosity of the fracturing fluid, $p_n^{}$ is fluid pressure in the fracture, ${\rho }_{fn}^{}$ is fluid density in the fracture, $S_{}^{fr}$ is the parameter describing rock mass compressibility under fluid action and $\frac{\mathrm{d}\mathsf{\Delta }{\dot{e}}_{\epsilon }^{}}{\mathrm{d}t}$ is the strain rate. According to the plate theory of fluid, the permeability of the fluid in the fracture is:

$$k_{}^{fr}=\frac{e_{}^2}{12}$$

(4)

where $e$ is the fracture width. The fracture propagation width (aperture) can be obtained through the deformation of the rock surrounding the fracture. In the process of hydrofracturing, the fluid drives the fracture propagation, which will form the opening of the fracture width (aperture) and the fracture closure. This closure process can be obtained according to the deformation (displacement) of the surrounding rock around the fracture. The opening and closing of the fracture will lead to the change of the internal fluid storage volume, resulting in the variation of permeability and compressibility of the fluid in the hydraulic fracture, and the hydrodynamic behaviors of fluid will simultaneously change. The parameters for compressibility are expressed as:

$$S_{}^{fr}=\left(\frac{1}{e}\right)\left[\left(\frac{1}{K_n^{fr}}\right)+\left(\frac{e}{K_f^{fr}}\right)\right]$$

(5)

where $K_n^{fr}$ is the normal stiffness of the fracture and $K_f^{fr}$ is the bulk modulus of the fracturing fluid. Seepage in the rock matrix and seepage in the fracture are distinguished according to the material domains, and the corresponding governing Equations (2) and (3) are used.

(3)

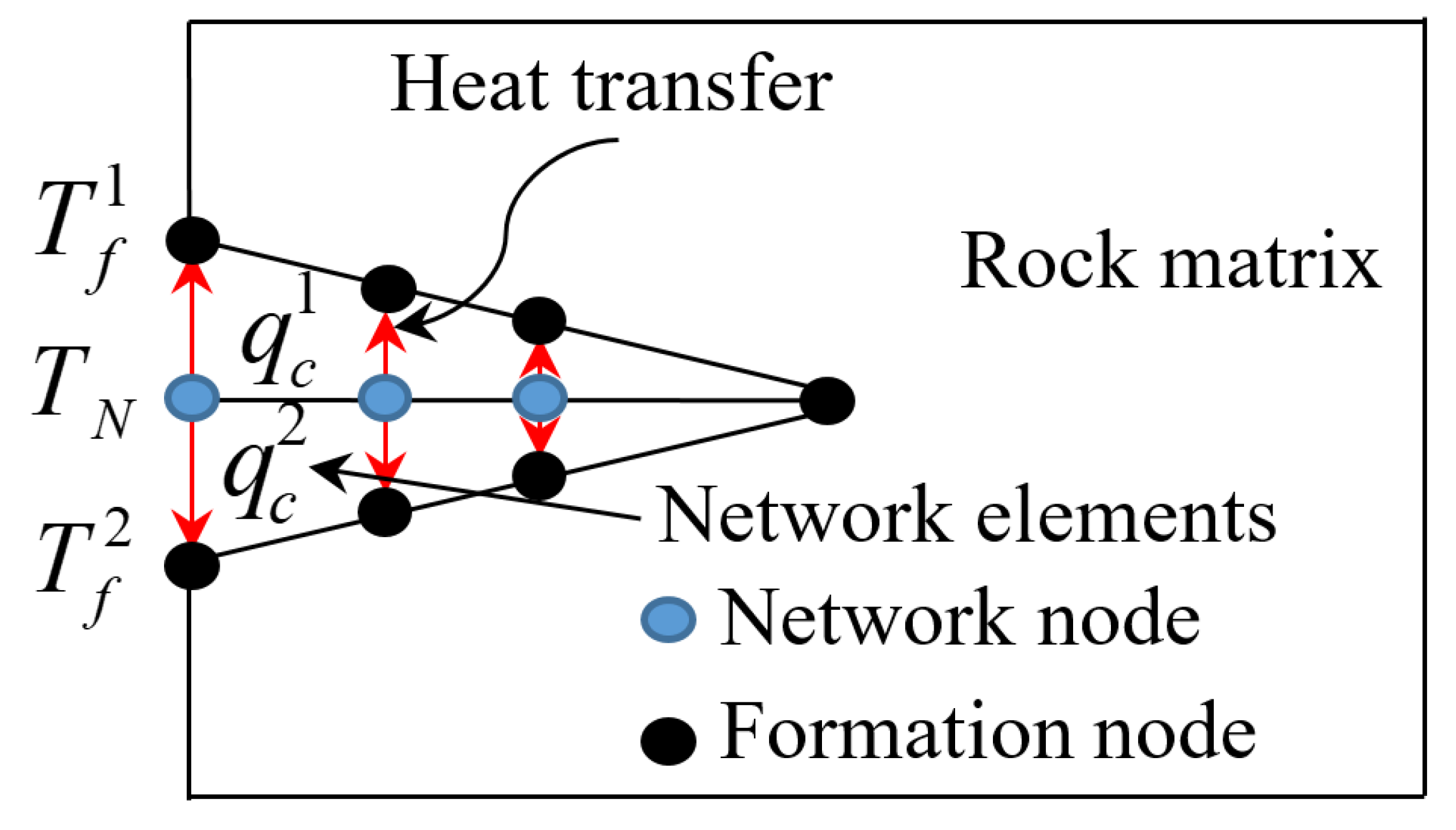
Heat transfer

The governing equation of heat transfer between the rock matrix and fracturing fluids is:

$$\mathrm{div}\left[k_b^{}\nabla T_f^{}\right]={\rho }_b^{}{c}_b^{}\frac{\partial T_f^{}}{\partial t}+{\rho }_f^{}{c}_f^{}{q}_f^{}\nabla T_f^{}$$

(6)

where $k_b$ is the thermal conductivity coefficient, $T_f$ is fluid temperature, ${\rho }_b$ is volume density, $c_b$ is the specific heat coefficient, ${\rho }_f$ is fluid density, $c_f$ is the specific heat coefficient of fluid, and ${\mathbf{q}}_f$ is Darcy fluid flux.

Heat transfer between the finite element nodes in formation and network is shown in Figure 3.

The heat transfer from the fracture network element from the fluid in the fracture zone to the rock matrix is as follows [38]:

$$q_c^1={\alpha }_c\left(T_N\right)\left(T_N-T_f^1\right)$$

(7)

$$q_c^2={\alpha }_c\left(T_N\right)\left(T_N-T_f^2\right)$$

(8)

where $q_c^1$ and $q_c^2$ are the contact heat flow between the network and formation nodes, respectively, $T_N$ is the temperature value of the node within the fracture and ${\alpha }_c$ is the contact thermal conductivity; $T_f^1$ and $T_f^2$ are the corresponding formation node temperatures.

Heat transfer through a reservoir rock can cause stress changes owing to rock shrinkage or expansion, and the volume change depends on the linear thermal coefficient of expansion:

$$\frac{\mathsf{\Delta }V}{V}={\alpha }_T\mathsf{\Delta }T$$

(9)

where $V$ is the initial volume, $\mathsf{\Delta }V$ is the incremental volume, $\mathsf{\Delta }T$ is the incremental temperature and ${\alpha }_T$ is the linear thermal expansion coefficient of the rock matrix. The variation of volume induced by temperature field may lead to the variation of stain (thermal strain) of the rock matrix. By means of the relationship between strain and stress (e.g., the constitutive relation), the temperature strain will produce the thermal stress.

In the technical aspects of the numerical solution, some detailed content, such as numerical implementation and orders of finite elements, was omitted to avoid redundancy. In this study, the combined finite element–discrete element method is used to simulate the hydraulic fracturing process. The governing equations are discretized using the finite element method. The order of the finite elements is linear. The computation accuracy of these linear elements will be insufficient compared with higher-order elements; however, the adaptive mesh refinement technology used in this study improves the solution accuracy. The nonlinear ordinary differential equations can be obtained by numerical discretization according to the finite element method. These nonlinear equations are computed by iterative methods, e.g., the Newton–Raphson iteration method.

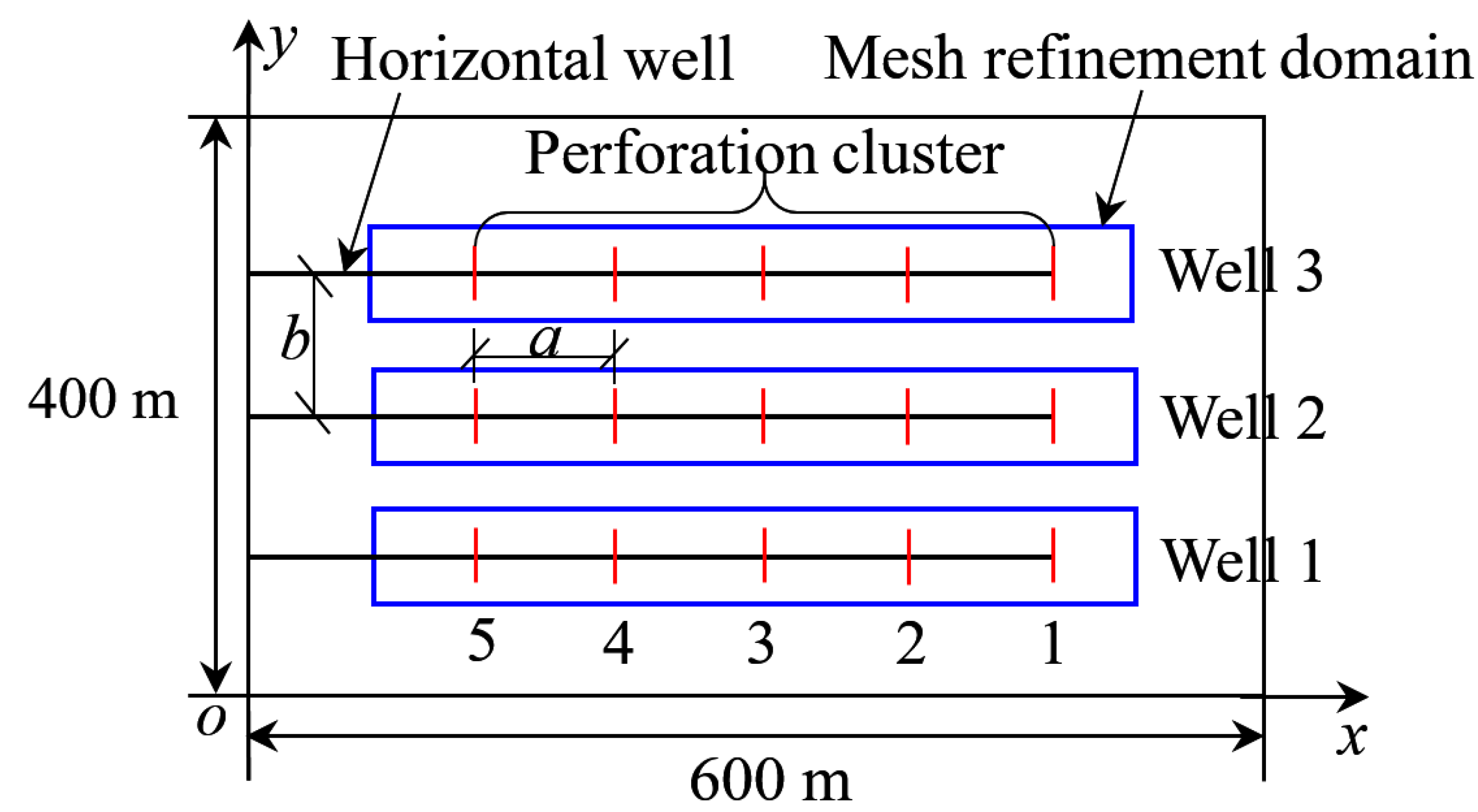
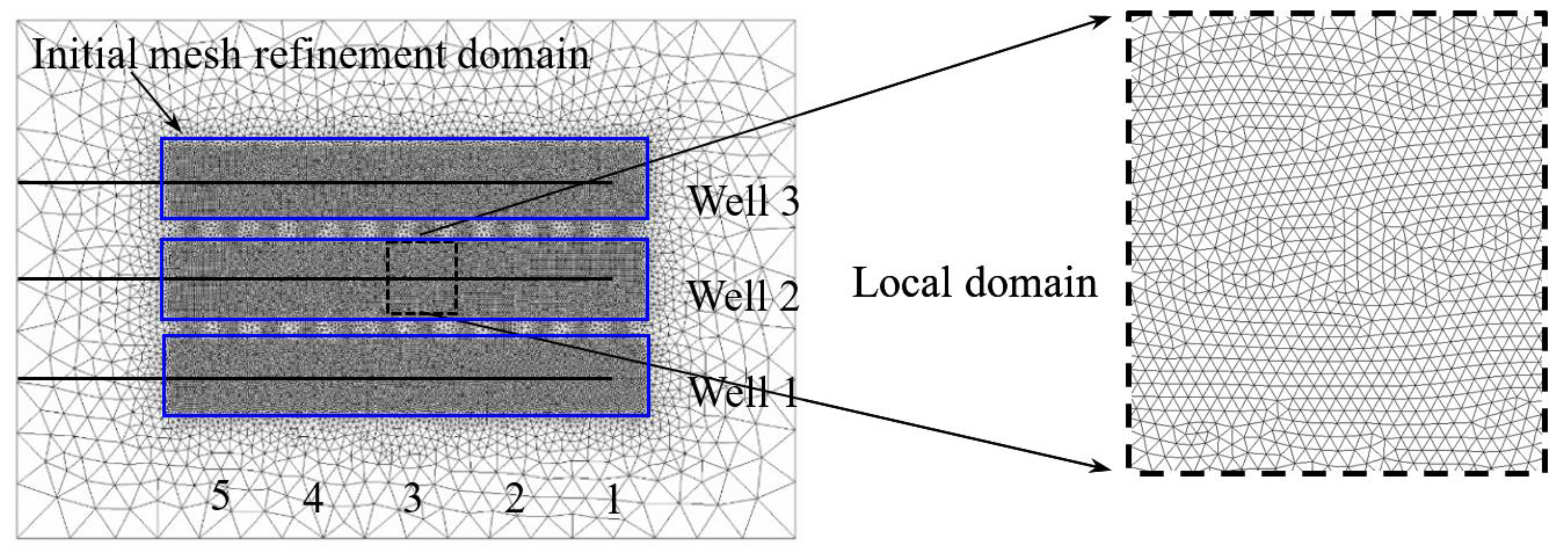
3. Numerical Models and Cases of Multiple Horizontal Wells

In this paper, a numerical model of multi-well multistage fracturing in deep tight reservoirs is established, as shown in Figure 4. Three horizontal wells (denoted as Well 1, Well 2 and Well 3) are set in this model, and five perforation clusters (numbers are 1–5 in sequence) are set for each well. There are two geometric variables in the model; a is the perforation cluster spacing and b is the well spacing. Figure 5 shows the initial mesh refinement of the finite element model; an initial dense mesh is used around local perforation domains to guarantee a reliable fracture propagation path in the initial stage. For the boundary conditions of solid field, the treatment technique of this model is to use the displacement boundary conditions (Dirichlet boundary conditions) to fix the displacements on the six surfaces of the model and impose in situ stresses at each node in the finite element model, so as to form the in situ stress field at the initial stage.

In the study of unstable propagation of fractures at different well spacing, the perforation cluster spacing a is 75 m and the well spacings b are 100 m, 75 m and 50 m. The numerical cases of different well spacings are shown in

Table 1. Numerical cases of different well spacings.

Case	a (m)	b (m)	Fracturing Fluid Temperature (°C)	Rock Matrix Temperature (°C)
I	75	100	20	60
II	75	75	20	60
III	75	50	20	60

; the perforation clusters on each well use sequential fracturing (1→2→3→4→5), the temperature of the fracturing fluid is set to 20 °C and the rock matrix temperature is set to 60 °C. The basic physical parameters of the model are set as shown in

Table 2. Basic physical parameters of the numerical model.

Parameters	Value
$\mathrm{Horizontal} \mathrm{minimum} \mathrm{in}-\mathrm{situ} \mathrm{stress} (x-\mathrm{direction}) S_h$(MPa)	40
$\mathrm{Horizontal} \mathrm{maximum} \mathrm{in}-\mathrm{situ} \mathrm{stress} (y-\mathrm{direction}) S_H$(MPa)	44
Fluid injection rate Q (m3/s)	0.5
Pore pressure $p_l^{}$ (MPa)	10
$\mathrm{Biot’s} \mathrm{coefficient} \alpha$	0.75
Elastic modulus E (GPa)	31
$\mathrm{Poisson’s} \mathrm{ratio} \nu$	0.22
Penetration k (nD)	50
$\mathrm{Porosity} \phi$	0.05
$\mathrm{Kinematic} \mathrm{viscosity} \mathrm{coefficient} {\mu }_n$$(Pa\cdot s$)	1.67 × 10−3
$\mathrm{Fracture} \mathrm{fluid} \mathrm{bulk} \mathrm{modulus} K_f^{fr}$(MPa)	2000
$\mathrm{Tensile} \mathrm{strength} {\sigma }_t$(MPa)	5.26
$\mathrm{Fracture} \mathrm{energy} G_f$$(\mathrm{N}\cdot \mathrm{m}$)	165

, which were tested on the tight rock samples in the Shengli Oilfield in Shandong Province in China.

4. Results and Discussions

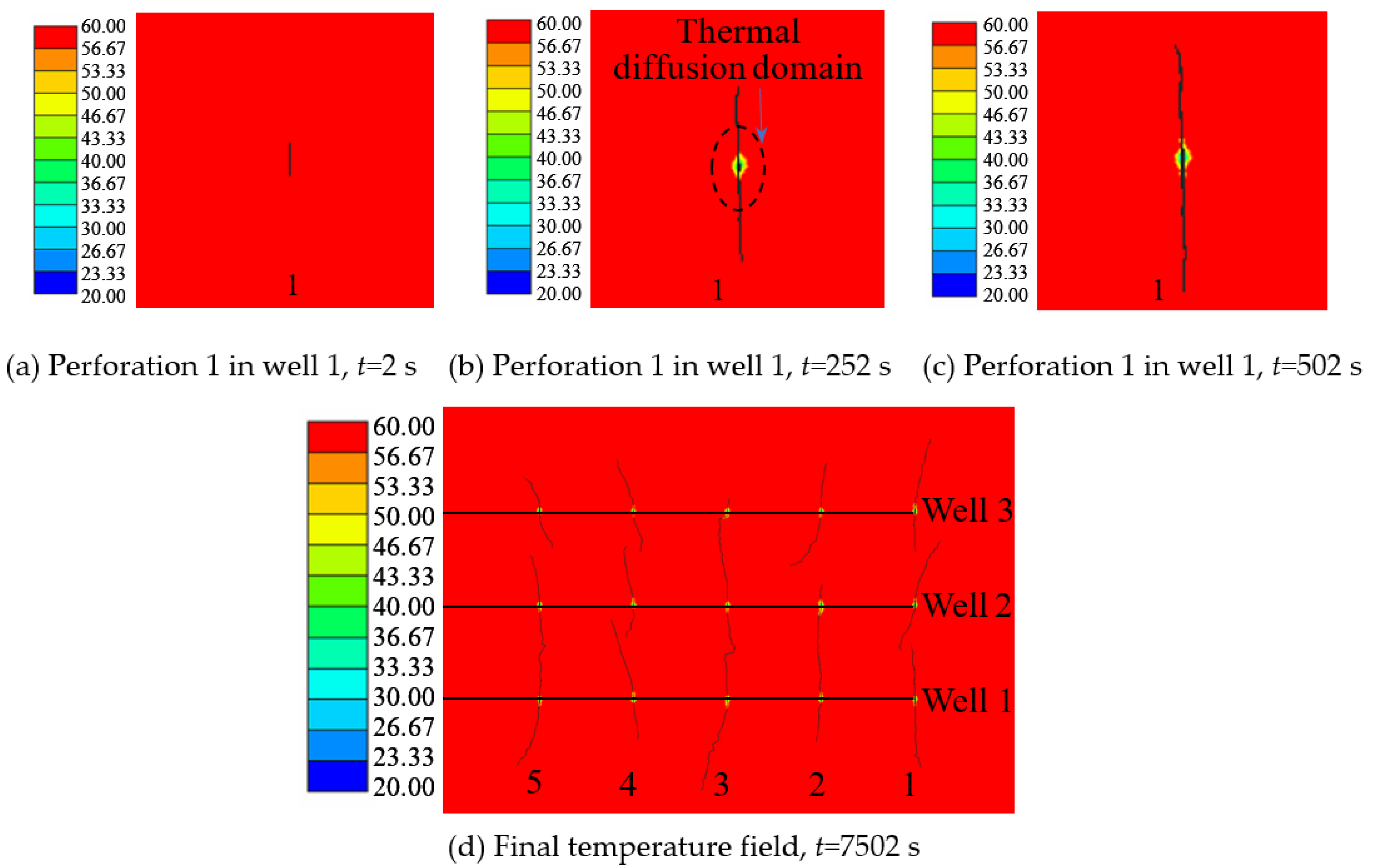
4.1. Thermal Diffusion in Fracture Propagation Process

The thermal diffusion behaviors between het rock matrix (initial temperature is 60 °C) and fracturing fluid (initial temperature is 20 °C) in the propagation process of hydrofracturing is analyzed below. Figure 6 shows the temperature evolution around hydraulic fractures in multi-well hydrofracturing. From Figure 6a–c, with the propagation of fractures in perforation 1 in Well 1, the thermal diffusion occurs between the perforation cluster and surrounding rock matrix due to the existence of a temperature gradient. The fracturing fluid gradually rises to the temperature of the formation during fracture propagation. Figure 6d is the temperature field distribution of the three wells in the final stage, and thermal diffusion occurs near each perforation; with the termination of fracturing fluid injection in the perforation cluster, the thermal diffusion between the perforation cluster and the surrounding rock matrix weakens.

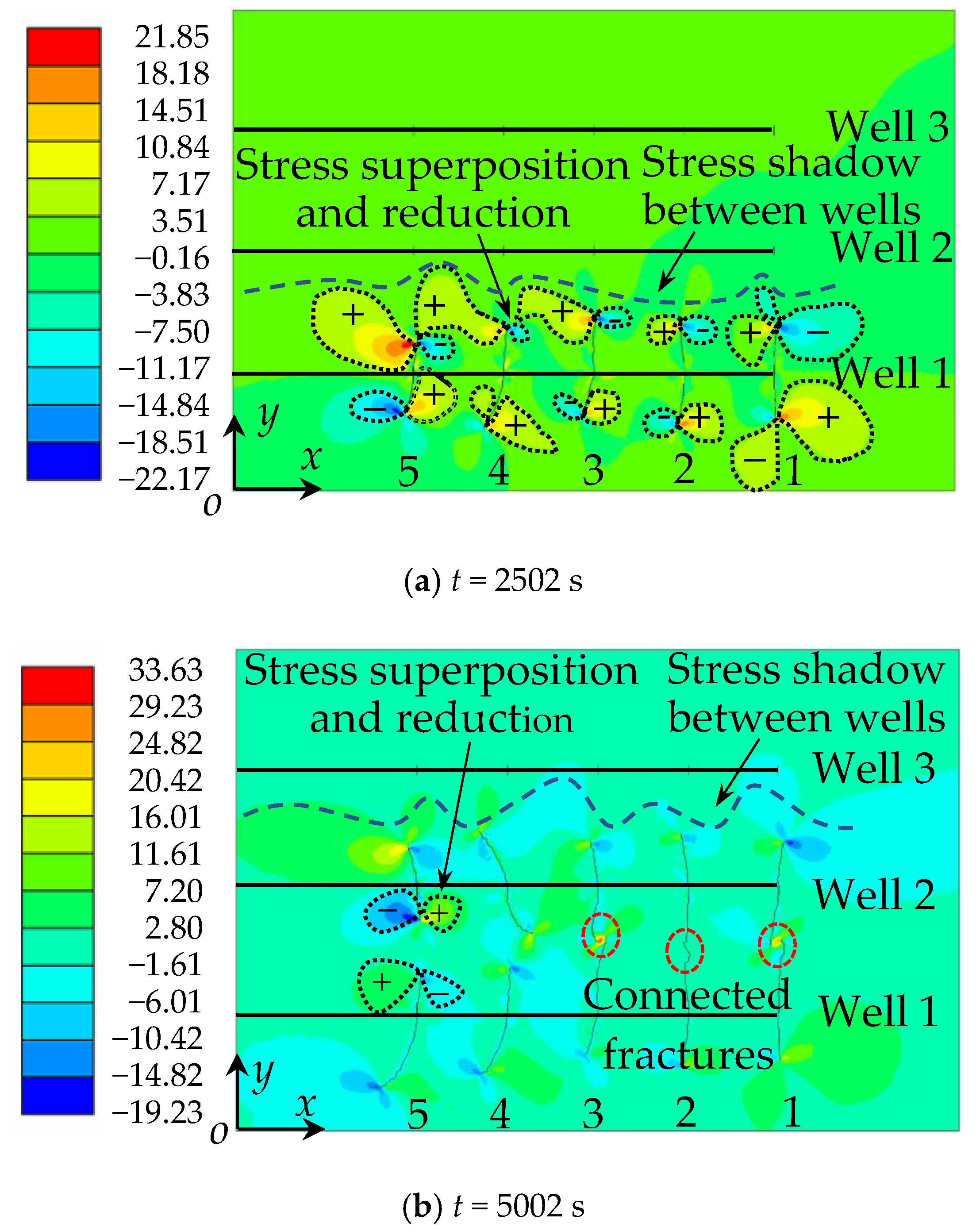
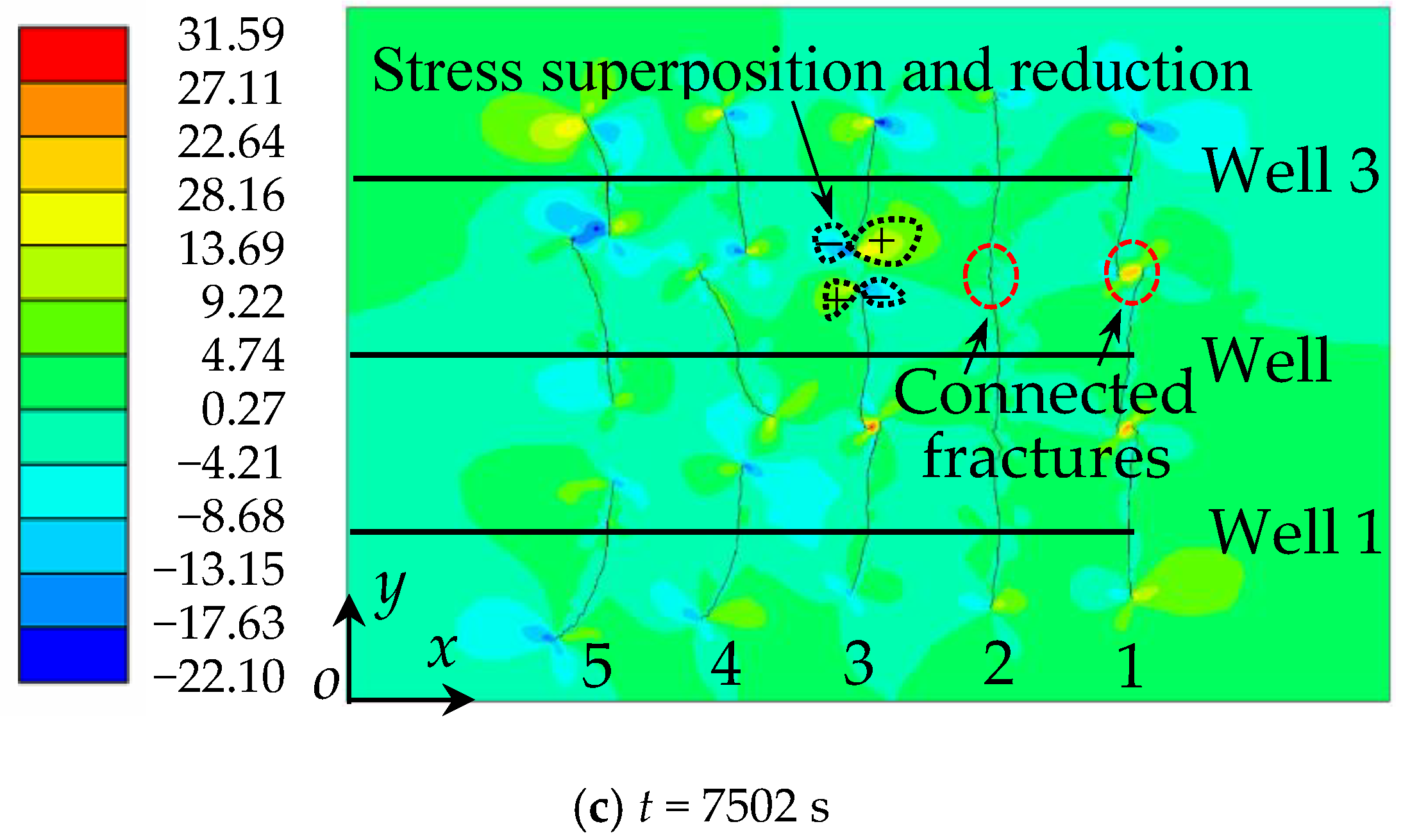
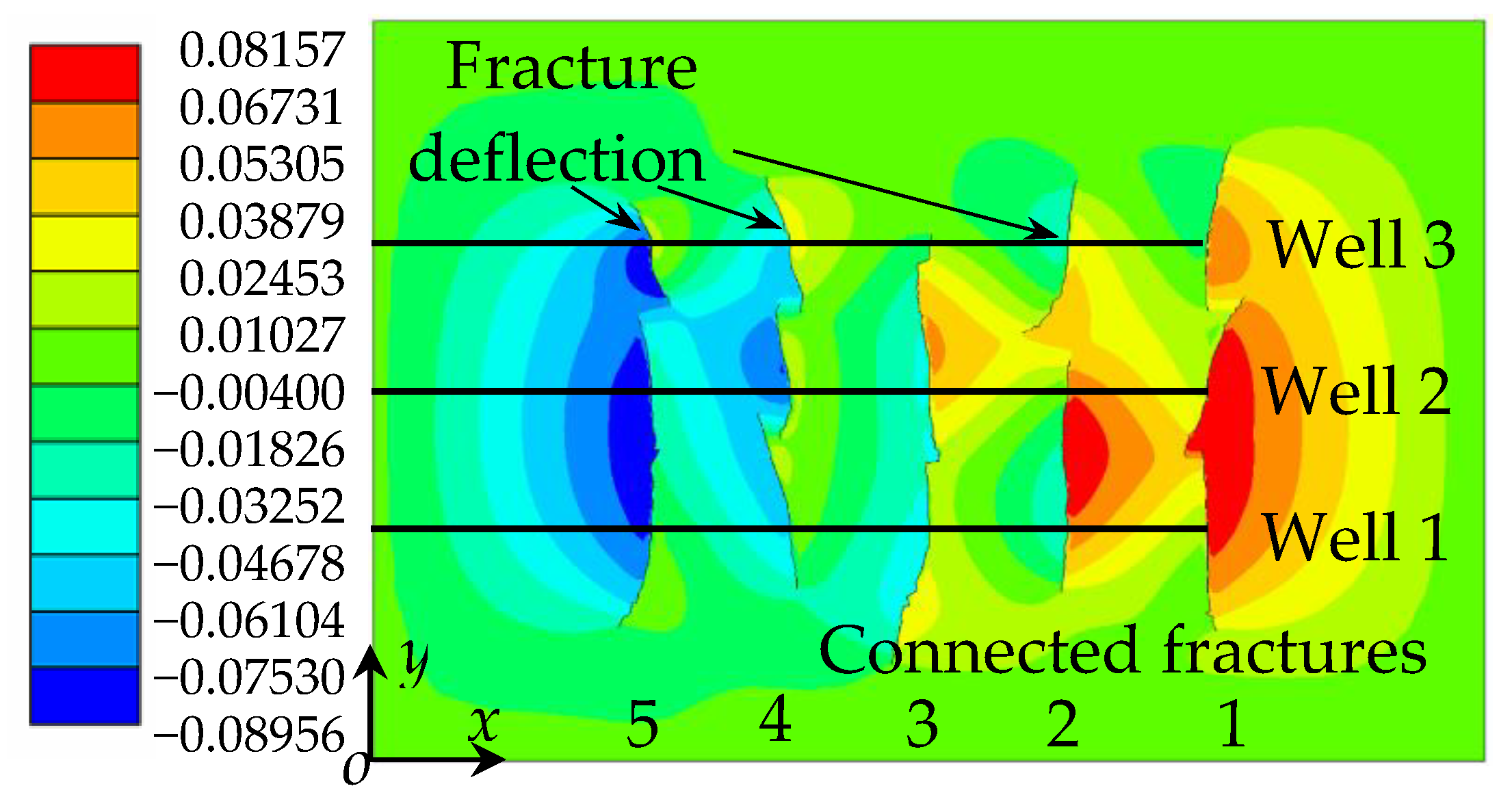
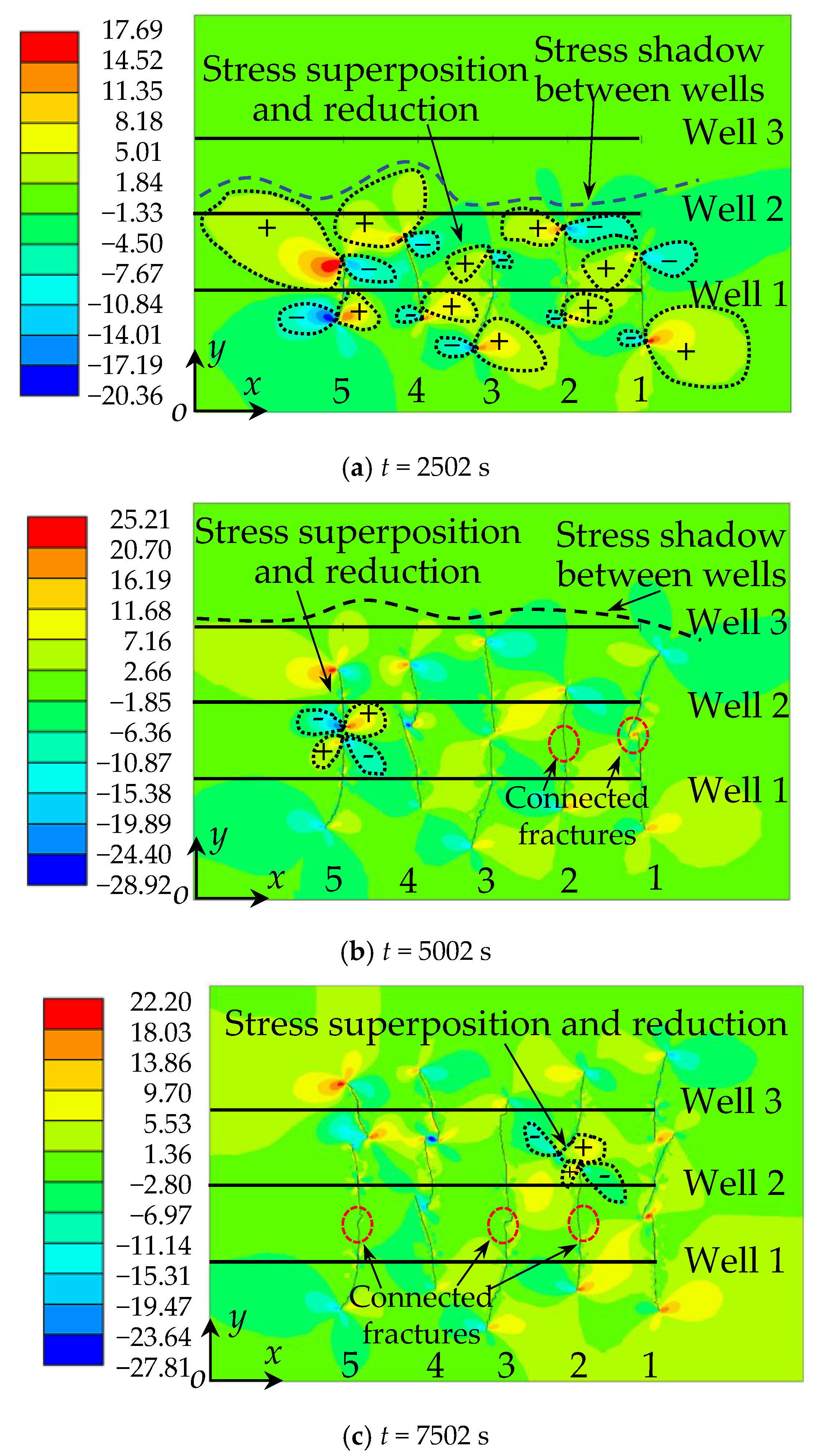
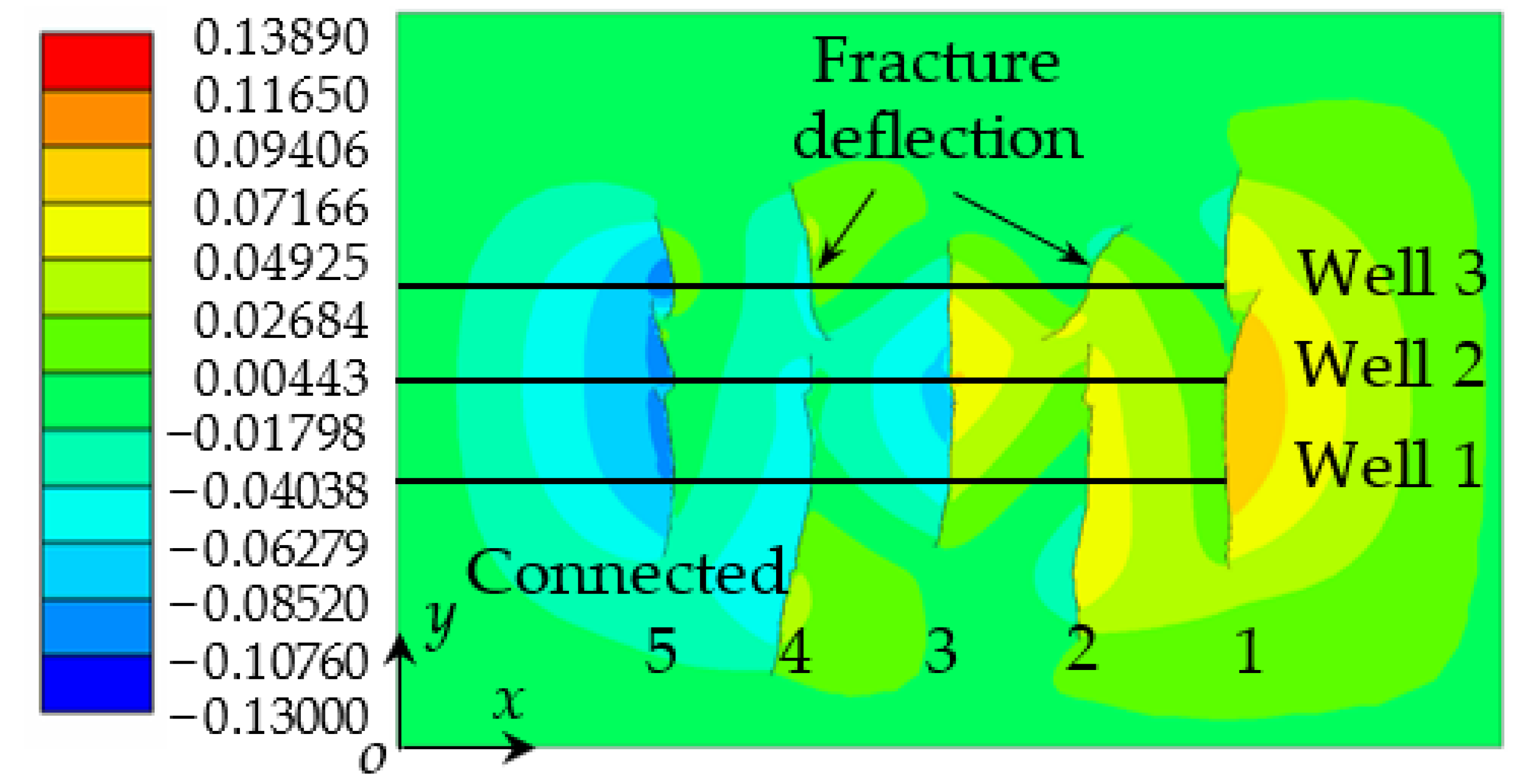
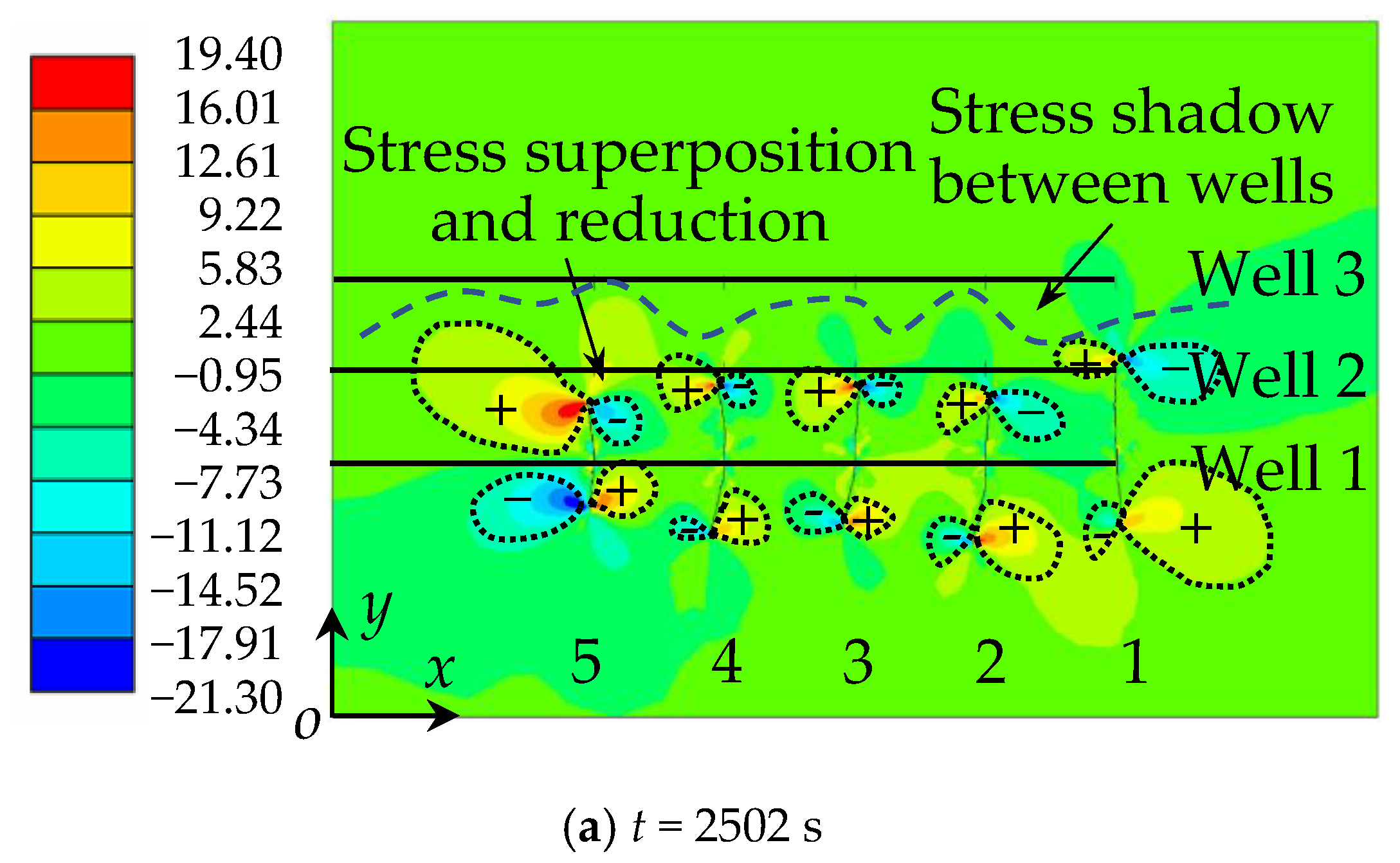
4.2. Fracture Network Propagation and Shear Stress Shadows

4.2.1. Case I: Well Spacing b = 100 m

In order to analyze the final fracture network morphology and deformation in multi-well fracturing, Figure 7 shows the distribution of hydraulic fractures when the well spacing is 100 m, and the displacement (m) in the x direction is provided to detect the deformation in the reservoir. The fractures 3, 4 and 5 of Well 1 are affected by the previous fractures 1 and 2, and deflect away from the previous fractures, which is identical to the multistage hydrofracturing in a single horizontal well [39]. Due to the influence of Well 1 on the in situ environment of the reservoir, fractures 1 and 2 of Well 2 penetrate through Well 1, and fractures 3, 4 and 5 of Well 2 deflected in different extents from Well 1; due to the influence of Well 1 and Well 2 on the in situ environment of the reservoir, fractures 1 and 2 in Well 3 are connected with Well 1, and fractures 3, 4 and 5 are deflected dramatically away from Well 2. Meanwhile, both sides of the stratum are deformed to the left and right, respectively, which is caused by fracturing fluid injected into the reservoir.

Figure 8 shows the evolution of shear stress ${\tau }_{xy}$ in sequential fracturing at 100 m well spacing, at t = 2502 s, t = 5002 s and t = 7502 s. Figure 8a shows the shear stress results of Well 1 after the sequential fracturing is completed. The superposition and reduction of positive and negative shear stress fields around fracture tips result in unequal stresses on both sides of these fracture tips, and the fracture deflects towards the high stress domain. In Figure 8b, in the local areas of the two adjacent wells, the superposition and reduction of shear stresses occur (e.g., fracture 5 in Wells 1 and 2); and these stress disturbances deflect the fractures. Meanwhile, the stress area (indicated by dashed line) of the disturbed formation in Well 2covers the positions where the fractures in Well 3 will propagate, which is the stress shadow area between multiple wells. In Figure 8c, fractures 1 and 2 in Well 3 and Well 2 are penetrated and connected, and the deflection of fractures 3, 4, and 5 occurs due to the influence of stress shadows.

4.2.2. Case II: Well Spacing b = 75 m

Figure 9 shows the final fracture network morphology and deformation in multi-well fracturing when the well spacing is 75 m. After the propagation of five fractures in Well 1, due to the influence of Well 1 on the in situ environment of the reservoir, each fracture in Well 2 is connected with Well 1 and the fractures are deflected to varying away from Well 1; the fractures in Well 3 are deflected greatly away from Well 2. Compared with the results with 100 m well spacing, smaller well spacing of 75 m makes subsequent fractures easier to deflect and adjacent fractures easier to connect together.

Figure 10 shows the evolution of shear stress ${\tau }_{xy}$ in sequential fracturing at 75 m well spacing at t = 2502 s, t = 5002 s, t = 7502 s. Figure 10a shows the shear stress results of Well 1 after the sequential fracturing is completed. The superposition and reduction of positive and negative shear stress fields around fracture tips result in unequal stresses on both sides of these fracture tips, and the fracture deflects toward the high stress domain, which is similar to Figure 8a. In Figure 10b, in the local areas of the two adjacent wells, the superposition and reduction of shear stresses occur (e.g., fracture 5 in Wells 1 and 2); and these stress disturbances deflect the fractures. Meanwhile, the stress area (indicated by dashed line) of the disturbed formation in Well 2 covers the positions where the fractures in Well 3 will propagate, which is the stress shadow area between multiple wells. In Figure 10c, fracture 3 in Well 3 and Well 2 is penetrated and connected, and the deflection of fractures 1, 2, 4, and 5 occurs due to the influence of stress shadows.

4.2.3. Case III: Well Spacing b = 50 m

Figure 11 shows the final fracture network morphology and deformation in multi-well fracturing when the well spacing is 50 m. After the propagation of five fractures in Well 1, the fractures in Wells 1 and 2 are connected, causing the narrow well spacing. In Well 3, except for fracture 3 connecting with the adjacent fracture, the other fractures are deflected to varying extents by the fractures in Well 2. Compared with the results in well spacings of 100 m and 75 m, continuing to reduce well spacing leads to more fracture connection and penetration.

Figure 12 shows the evolution of shear stress ${\tau }_{xy}$ in sequential fracturing at 50 m well spacing, at t = 2502 s, t = 5002 s and t = 7502 s. Figure 12a shows the shear stress results of Well 1 after the sequential fracturing is completed. The superposition and reduction of positive and negative shear stress fields around fracture tips result in unequal stresses on both sides of these fracture tips, and the fracture deflects toward the high stress domain. In Figure 12b, in the local areas of the two adjacent wells, the superposition and reduction of shear stresses occur (e.g., fracture 3 in Wells 1 and 2); and these stress disturbances deflect the fractures. Meanwhile, the stress area (indicated by dashed line) of the disturbed formation in Well 2 cover the positions where the fractures in Well 3 will propagate, which is the stress shadow area between multiple wells. In Figure 12c, the fractures 1, 2, 3 and 5 in Well 3 and Well 2 are penetrated and connected, and the deflection of fracture 4 occurs due to the influence of stress shadows.

Comparing the fracture network propagation and shear stress evolution of the above different well spacings, with the decrease of well spacing, the stress shadow area between adjacent wells increases, and the stress superposition and reduction increase. The fracture propagation is inhibited, the propagation length of connected fractures decreases and the deflection extent of the deflection fracture increases. The stress field disturbance generated by the fracture propagation of the previous horizontal well gradually increases the inhibitory effect on the fracture propagation of the subsequent horizontal well.

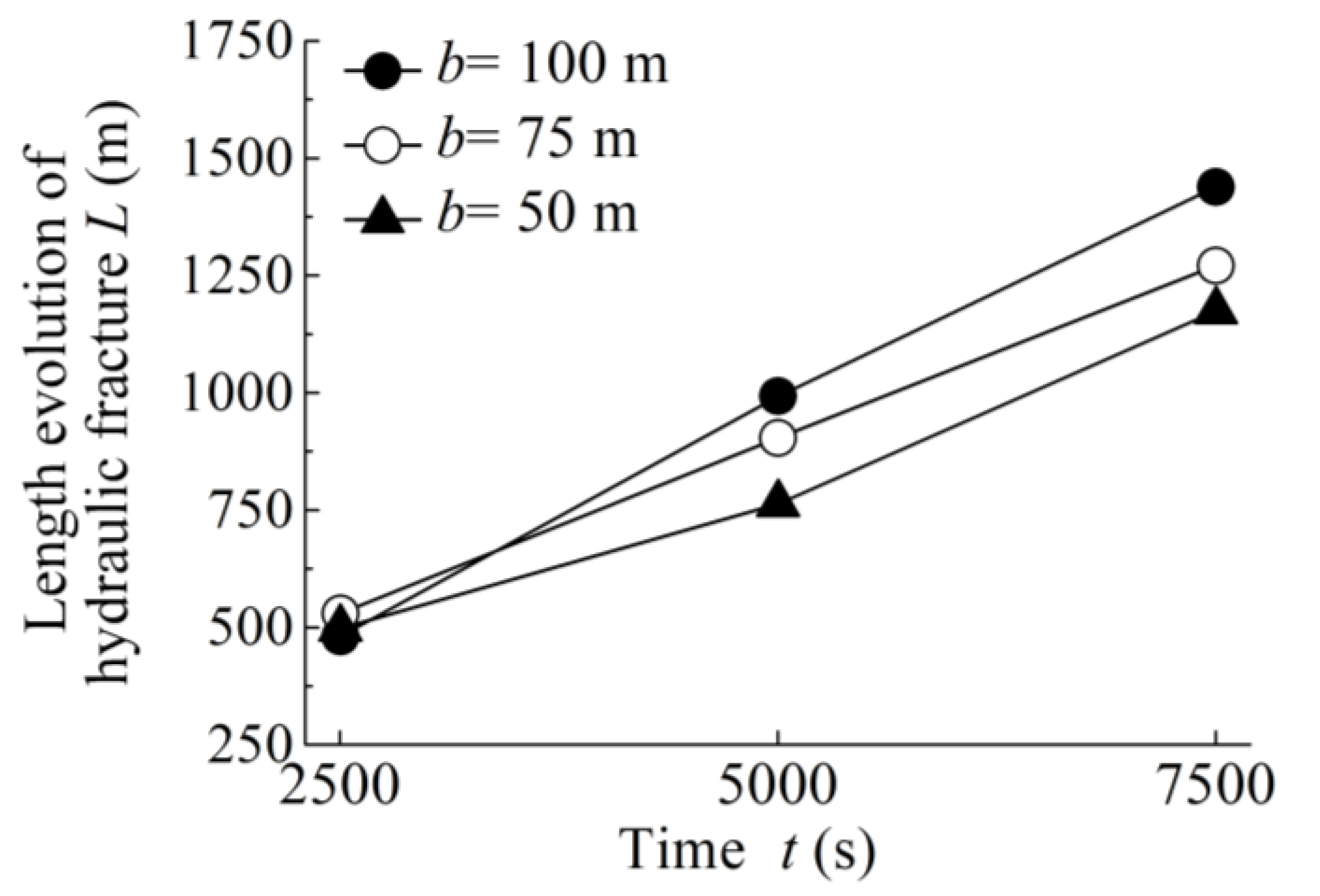
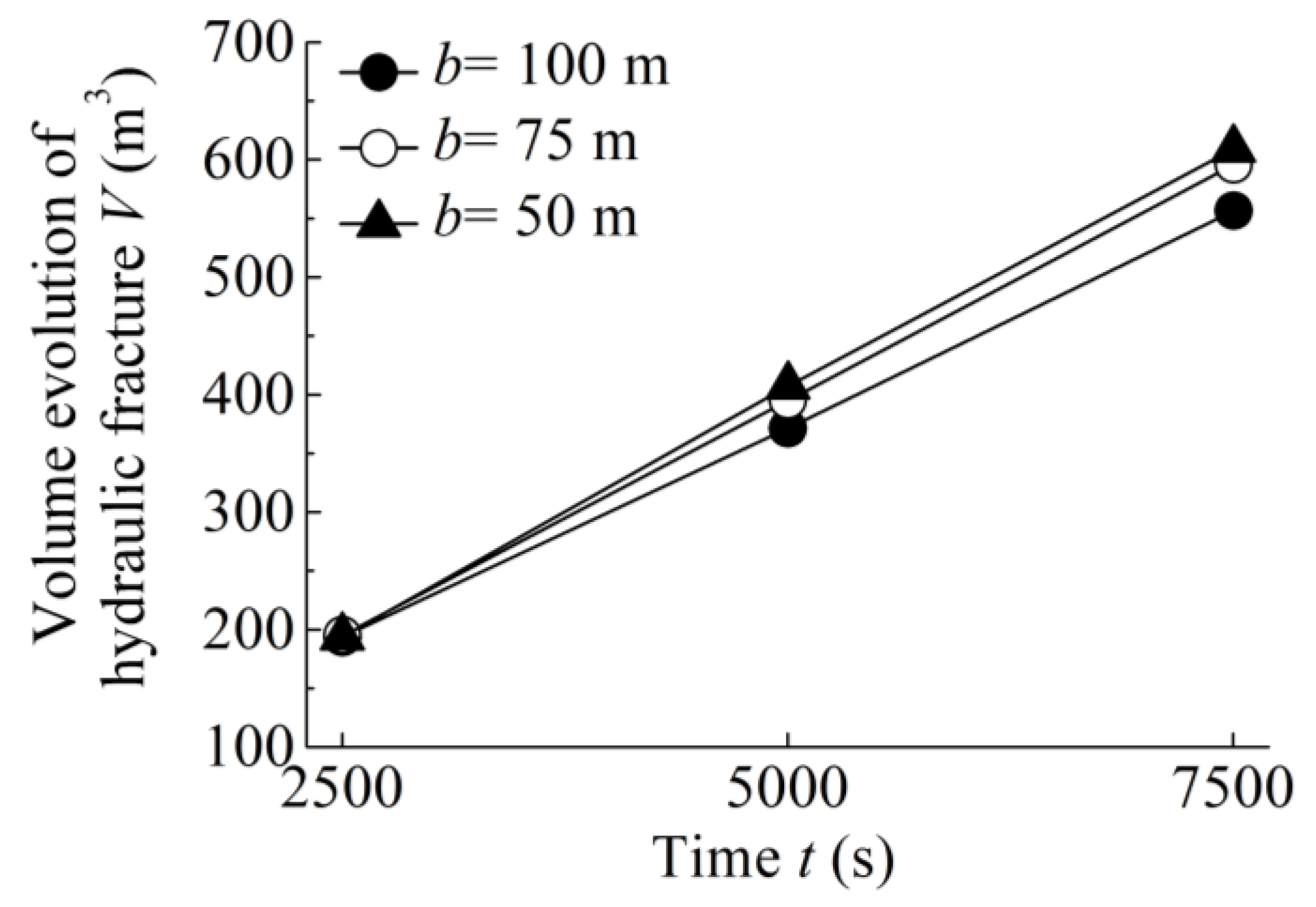
4.3. Quantitative Analysis of Fracture Length and Volume

In order to quantitatively analyze the propagation behaviors of the fracture network in the multi-well hydrofracturing model with varying adjacent spacings, the fracture length and volume of fracture network for different stages and well spacings are derived as shown in

Table 3. Fracture length and volume of fracture network for different stages and well spacings.

b (m)	Time t (s)	Fracture Length L (m)	Fracture Volume V (m3)
100	Stage 1 (t = 2502 s)	480.76	193.58
75		529.62	195.12
50		498.00	193.73
100	Stage 2 (t = 5002 s)	992.45	371.39
75		903.94	395.10
50		763.11	407.22
100	Stage 3 (t = 7502 s)	1438.69	556.38
75		1271.25	595.70
50		1174.75	608.84

. In the computation process, the discrete element method is used to analyze whether the element meets the fracture criterion to initiate and propagate. The fracture length can be found through the fracture propagation of the statistical elements. In addition, the fracture propagation width (aperture) can be obtained through the deformation of rock surrounding the fracture, and the fracture volume can be obtained by multiplying the fracture length and width (and the unit thickness of the model). With the injection of fracturing fluid, the total length and volume of the fractures increase. For the convenience of comparison and analysis, Figure 13 and Figure 14 shows the curves of the length and volume of the fracture network under different well spacings with time. The length of hydraulic fractures from the initial stage shows a decreasing trend with reduced well spacing b (b = 100 m→75 m→50 m); the reason is that the reduction of well spacing intensifies the stress shadow between fractures. On the other hand, the fracture volume from the initial stage shows an increasing trend with reduced well spacing b; the reason is that the fractures that do not easily propagate forward may hold more fracturing fluid. The final total fracture length is the largest when the well spacing is 100 m, and the final total fracture length is the smallest when the well spacing is 50 m.

The linear influence of well spacing on the propagation length and volume of the fracture network is reflected above, which can provide a reference for the evaluation of fracture networks in multi-well hydrofracturing. However, this evaluation alone is not enough; in the future, it is necessary to further investigate the influence of the smaller spacing of multiple wells (the linear relationship may no longer be valid). In addition, the impact of fracture distribution on oil and gas production should also be evaluated, because under the same fracture length and volume, different distribution forms of fracture networks will produce different oil and gas production and connect with different reservoir areas. These are some in-depth research topics to be carried out in the near future.

5. Conclusions

In this study, a multi-well hydrofracturing model is used to simulate and analyze the hydrofracturing process of multiple horizontal wells with different well spacings. The unstable propagation and stress evolution of fracture networks considering thermal-hydro-mechanical coupling are studied through the disturbed shear stress field and fracture length and volume. Some conclusions can be summarized:

• In multi-well hydrofracturing, the stress around the fracture interferes with adjacent fractures in adjacent wells. The shear stress fields around the fractures of horizontal wells are superimposed, and the fractures are deflected to the side with the larger shear stress; multi-well hydrofracturing will lead to fracture connectivity between wells;
• Varying well spacing will affect the unstable propagation of hydraulic fractures. With the decrease of well spacing, the disturbance of the stress field and the stress shadow area between wells gradually increase, the number of connected fractures also increases, the propagation length of the connected fractures gradually decreases and the unconnected fractures deflect. The degree of deflection increases and well spacing becomes an important factor affecting fracture propagation in multi-well hydrofracturing;
• In the quantitative analysis of the length and volume of fracture networks, the total length of hydraulic fractures decreases with the decrease of well spacing, and the total volume of hydraulic fractures increases with the decrease of well spacing. When the well spacing is set to 75 m under the field conditions in this study, a larger total length and volume of fracture propagation can be obtained.

In this paper, the fracture propagation and stress evolution of different well spacings in multi-well hydrofracturing are analyzed and studied. On the other hand, varying the fracturing sequence of multiple wells is actually a form of varying the well spacing. In multi-well hydrofracturing, different initiation sequences of horizontal wells may also affect unstable fracture propagation and the surrounding stress evolution. In future research, it is necessary to study the behaviors and mechanisms of unstable fracture propagation induced by varying the fracturing sequence of multiple wells.