Permeability Models of Hydrate-Bearing Sediments: A Comprehensive Review with Focus on Normalized Permeability
Abstract
1. Introduction
2. Classical Permeability Models Derived from Classical Theories
2.1. SDR Model
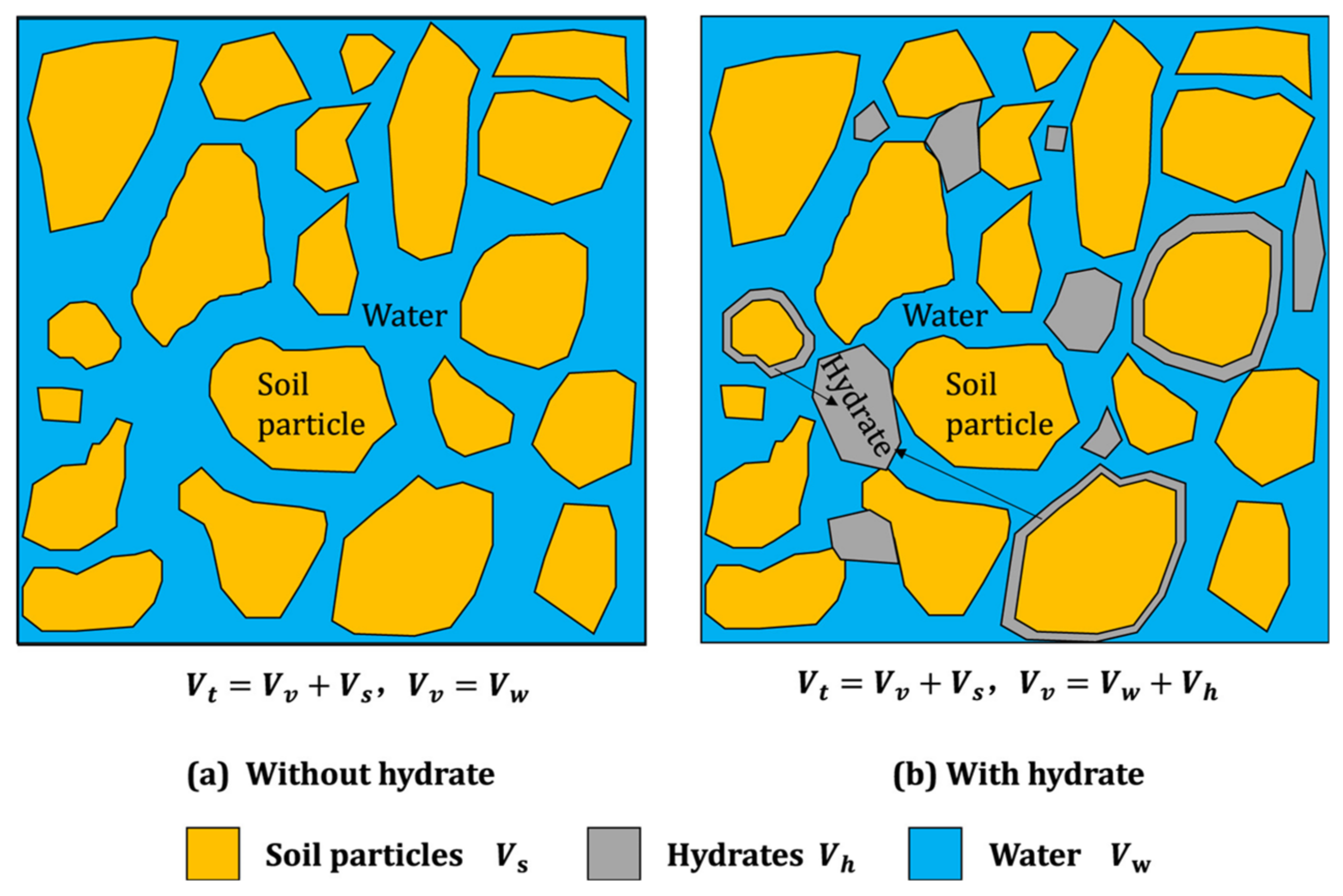
2.2. Classical Conceptual Models
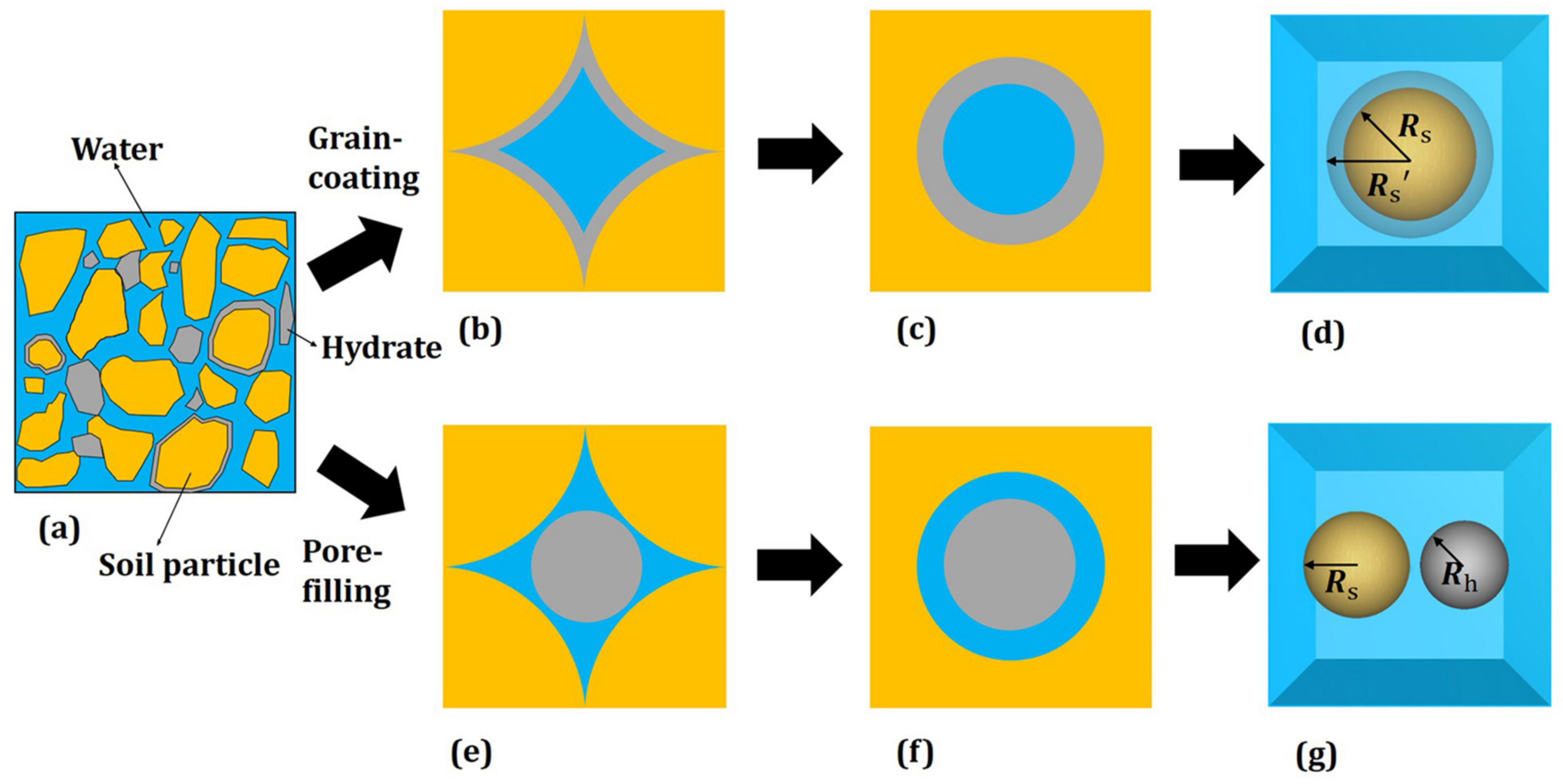
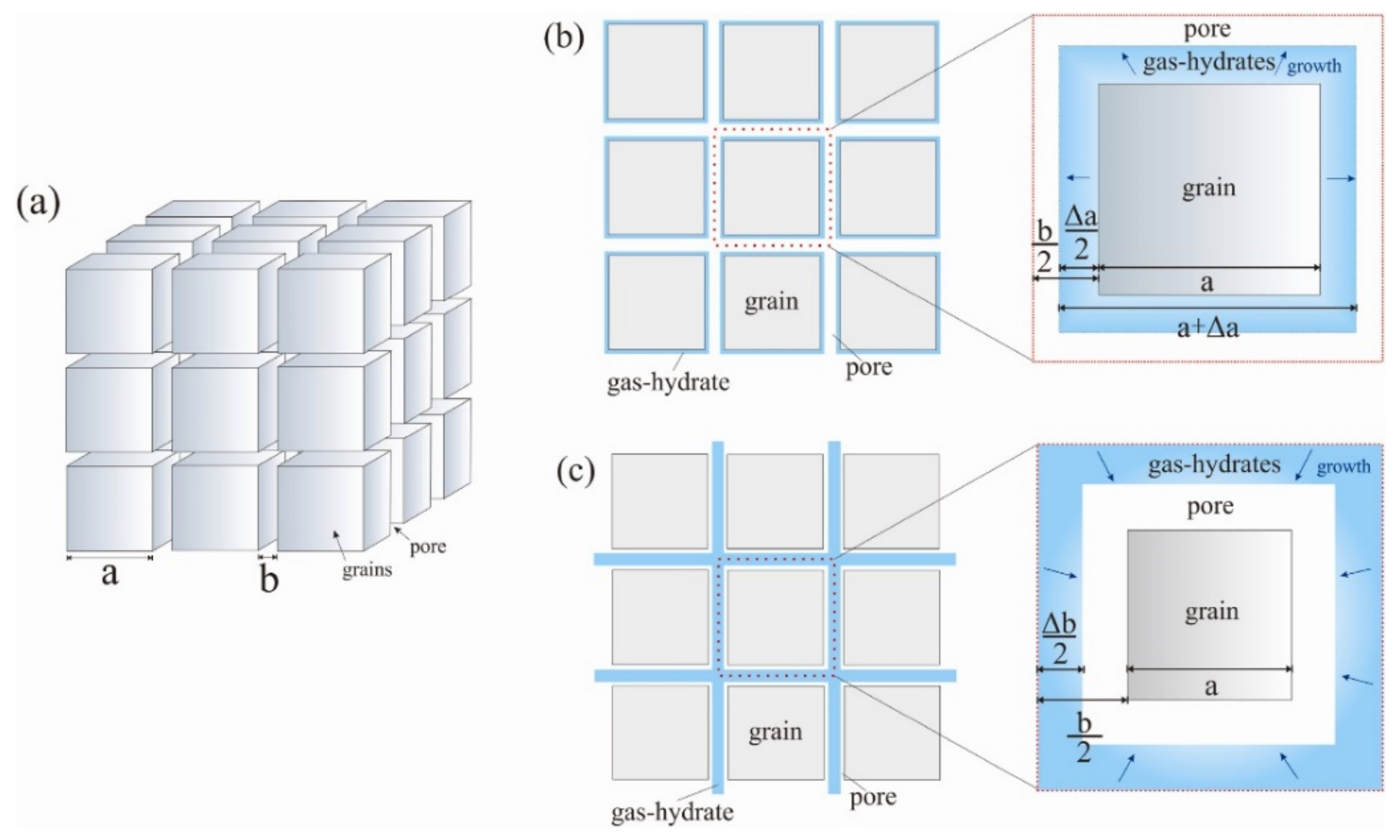
2.2.1. Parallel Capillary Tube Model
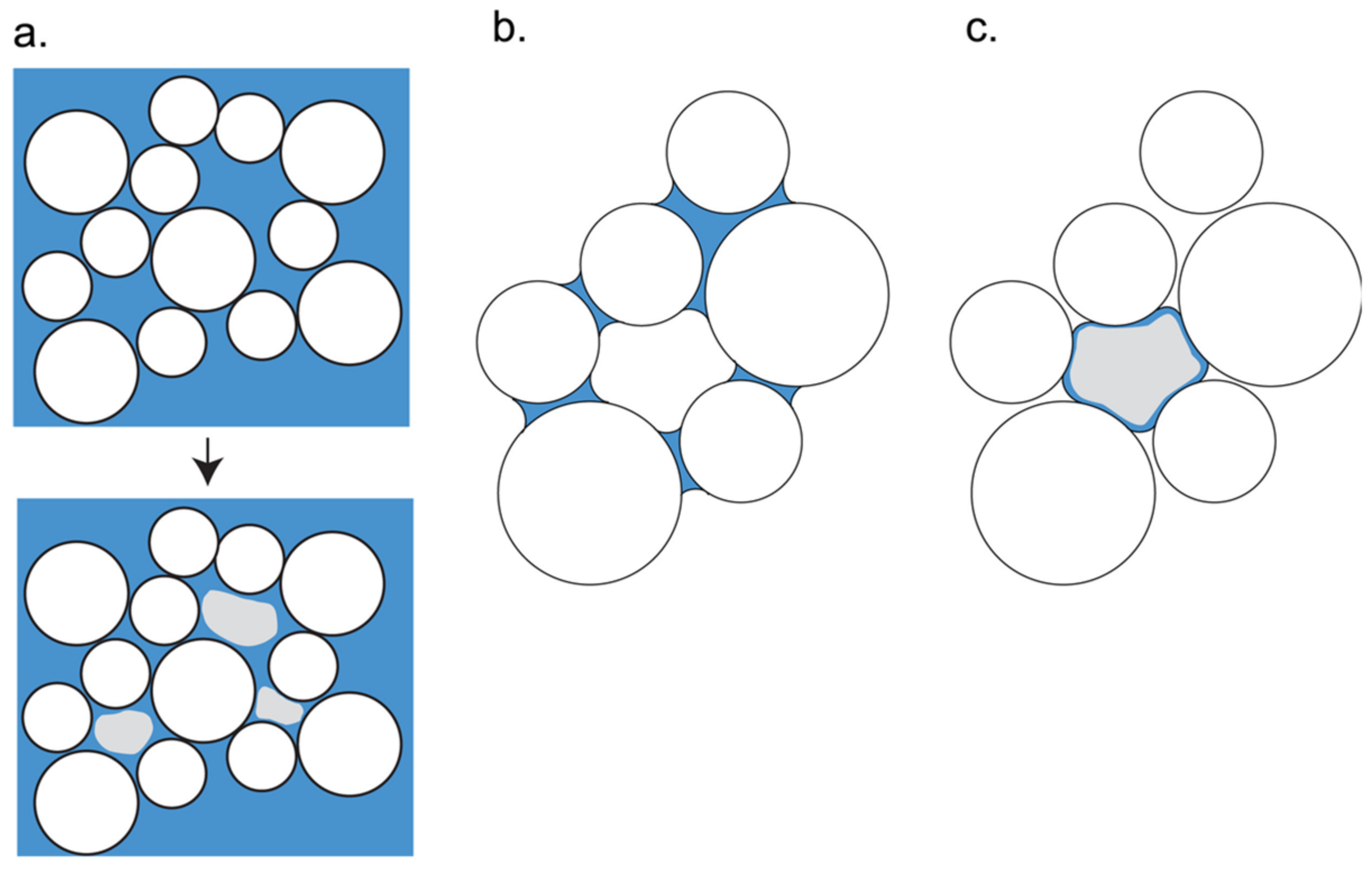
2.2.2. Kozeny Grain Model
2.3. Summary
- (1)
- The SDR model can be used for engineering applications to predict the field permeability data of hydrate reservoirs in the presence of NMR data. However, the SDR model described in this section is not well established due to the lack of consideration for the effects of hydrate formation and dissociation characteristics on the transverse surface relaxation. In addition, it is not recommended to use this model for modeling the gas production behavior of hydrate reservoirs due to the difficulty of obtaining NMR data for natural hydrate sediments.
- (2)
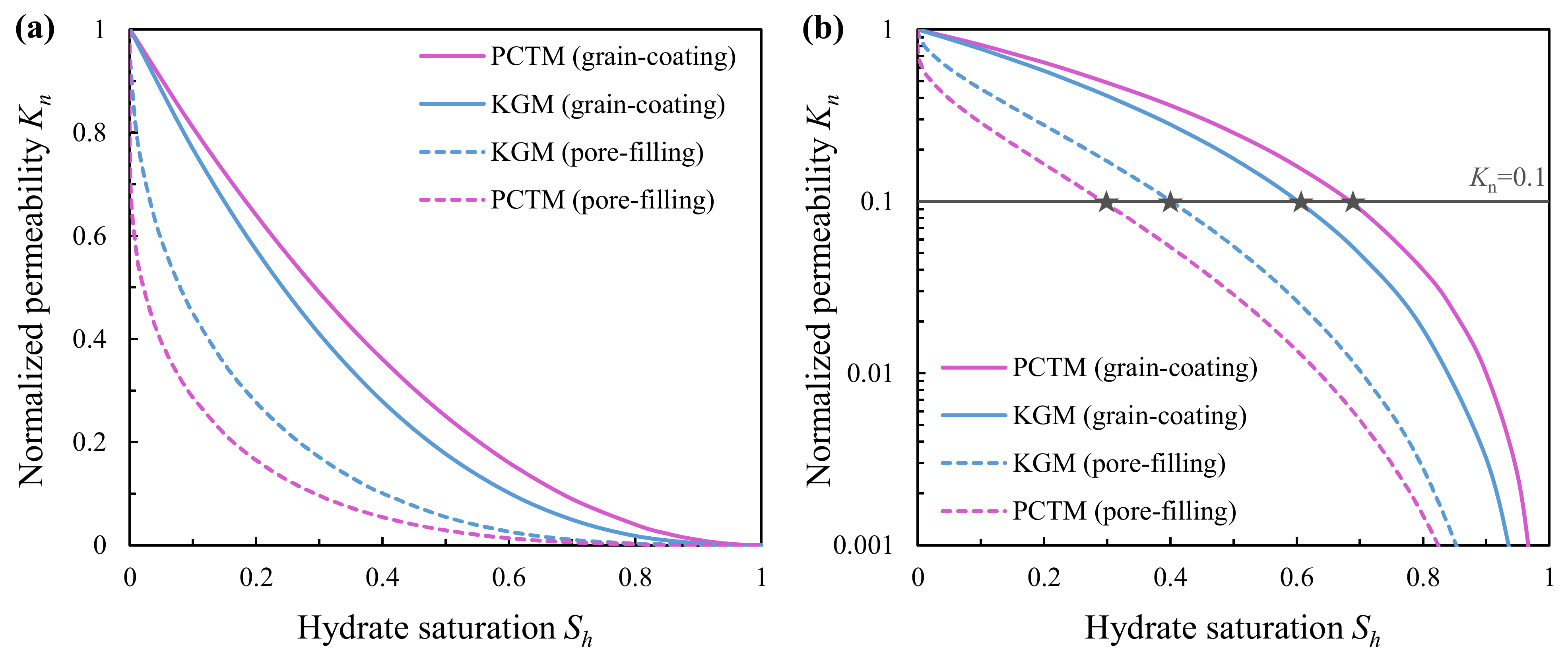
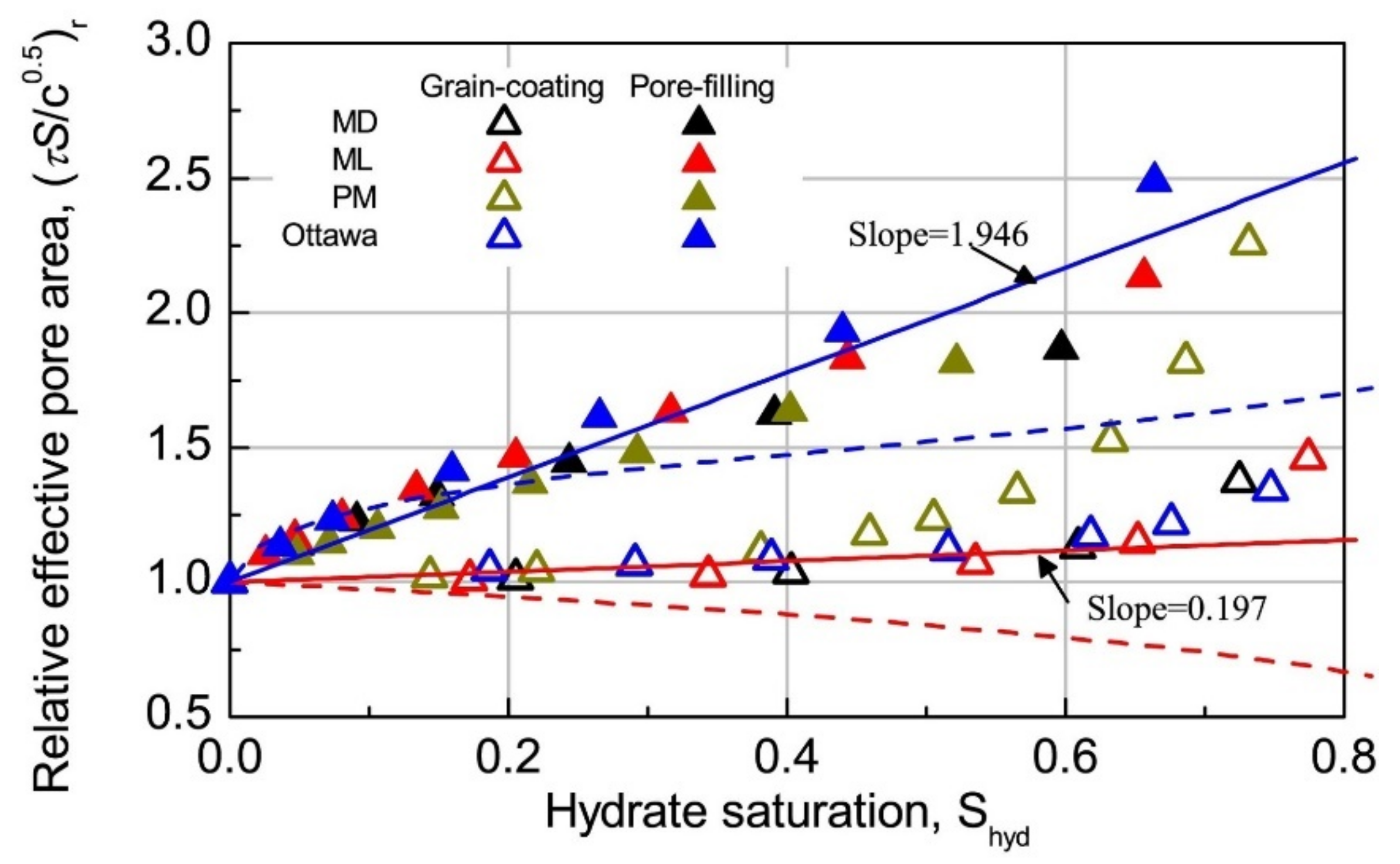
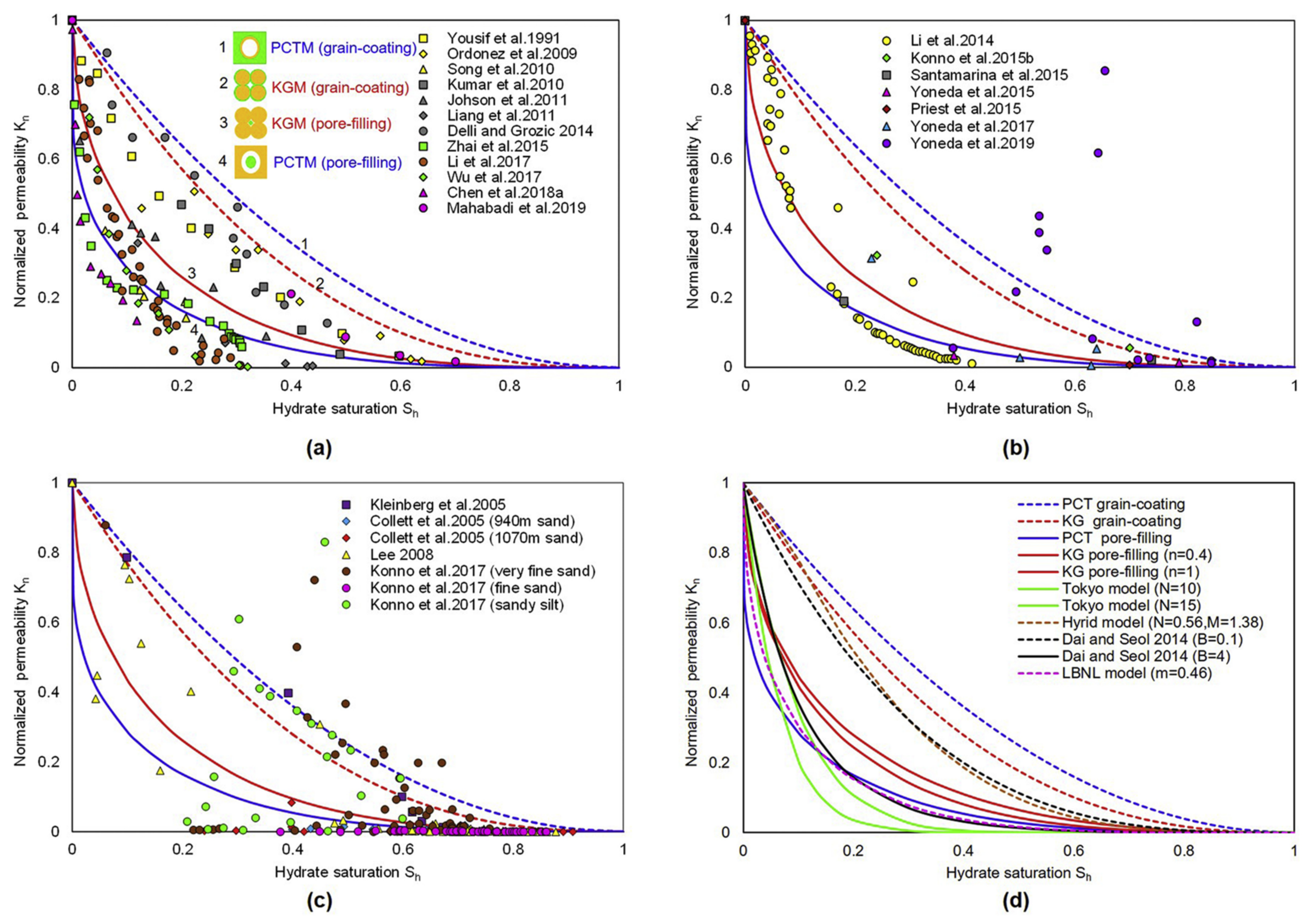
- PCTM and KGM are introduced into the study of HBS permeability, and their application to numerical modeling of gas production has been widely accepted due to their simplicity and ability to capture the main pore structure characteristic of sediments and two typical hydrate pore habits. Both models show that pore-filling hydrates decrease normalized permeability more significantly than grain-coating hydrates. They provided a theoretical fundamental basis for other permeability models considering the effect of saturation of hydrate with these two typical pore habits on permeability.
- (3)
- The prediction results of PCTM and KGM can well describe the general reduction trend of the permeability with increased hydrate saturation. However, due to the assumptions of the idealized inner structure of pore space and growth habits and morphology of hydrate, their analytical expressions are oversimplified.
- (4)
- The research methods, the advantages and limitations, the using parameters and their physical meaning of various models, and the factors that models consider are also provided. Table 1 lists the research methods, advantages, and limitations of classical models of HBSs, while Table 2 summarizes the characteristics of various classical models of HBSs.
3. Reservoir Simulator Used Models
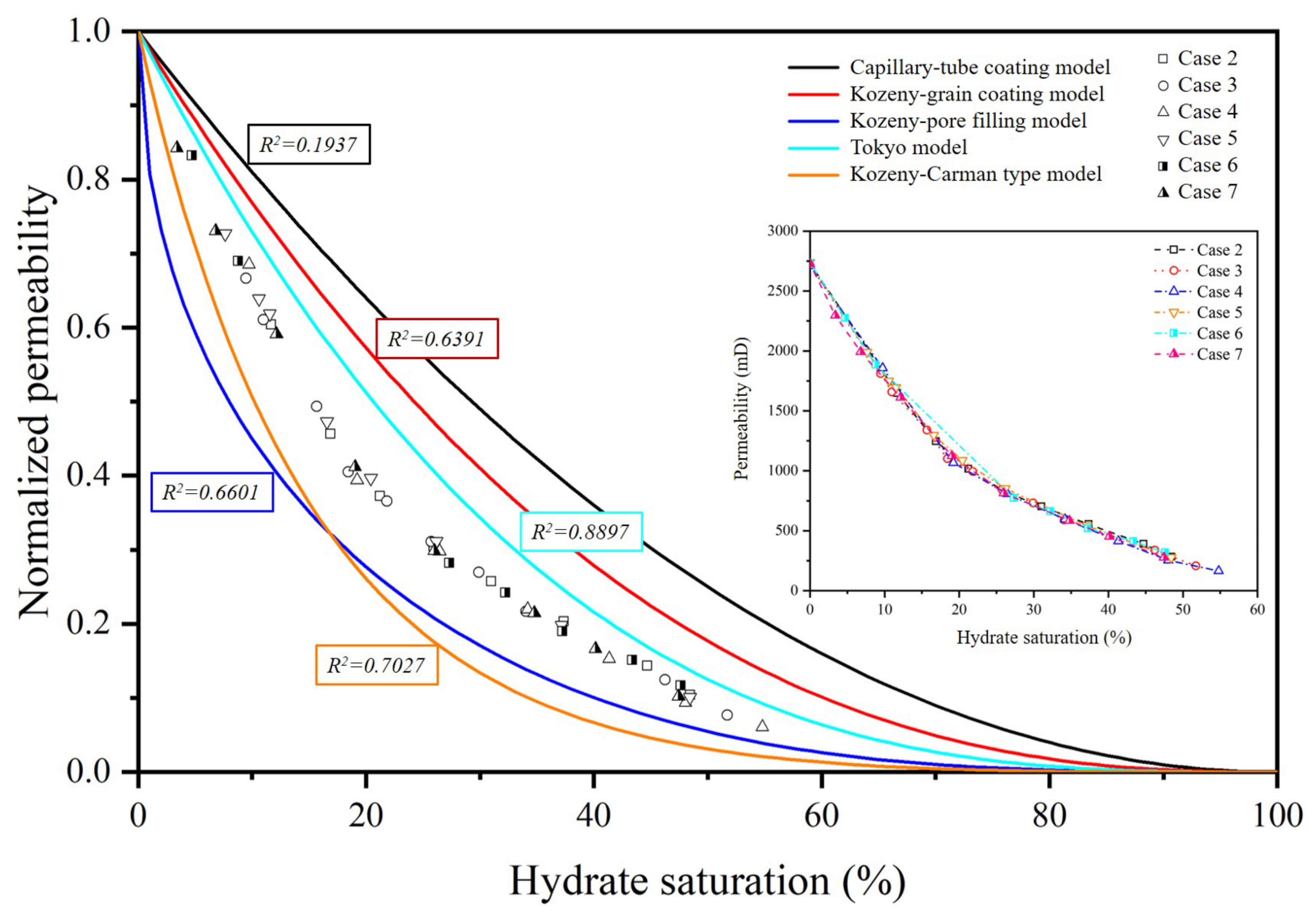
3.1. Tokyo Model
3.2. Lawrence Berkeley National Laboratory (LBNL) Model
3.3. CMG Built-In Model
3.4. Civan Model
3.5. Sakamoto et al. Model
3.6. Summary
- (1)
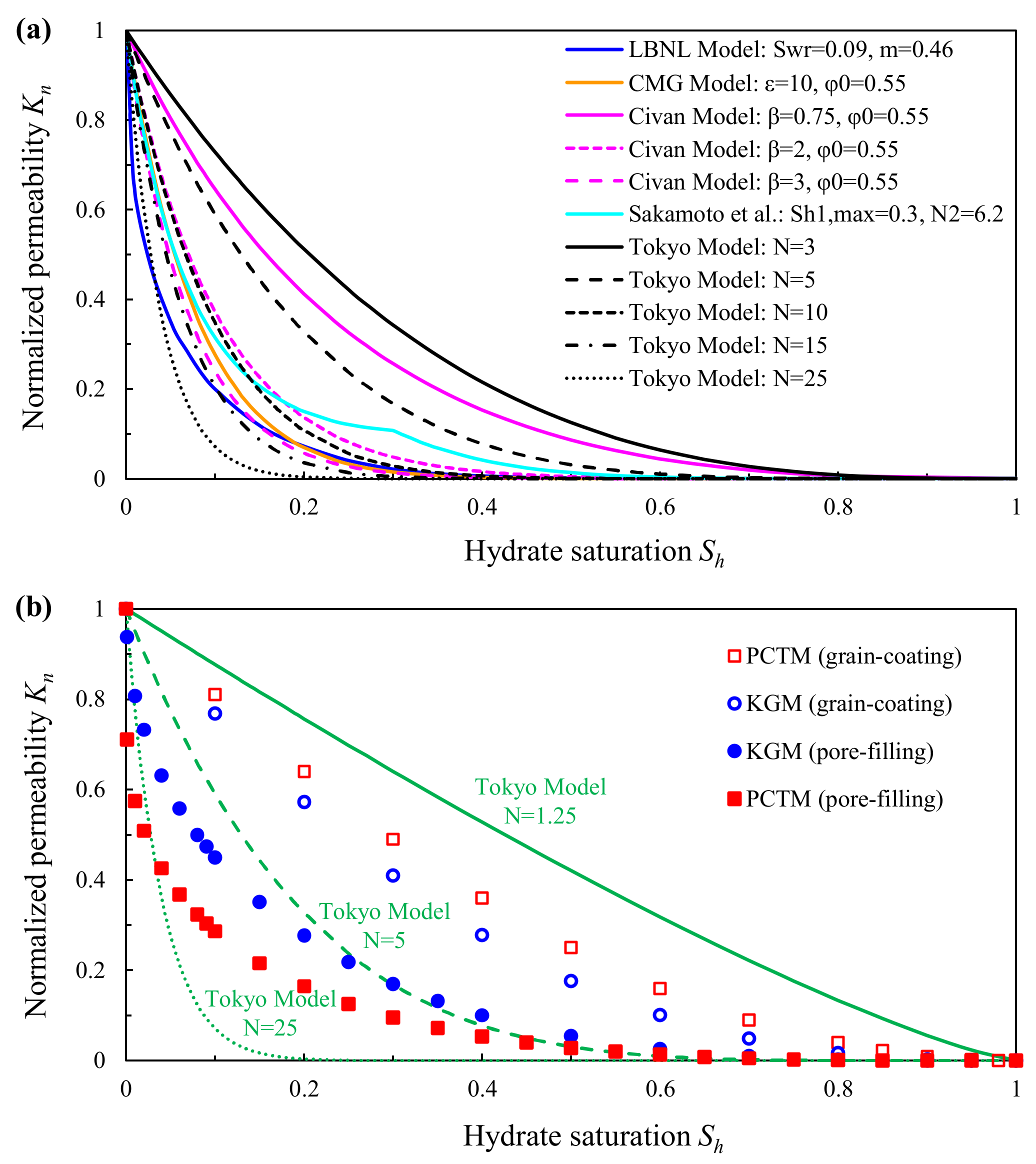
- The reservoir simulator used models for permeability prediction of HBSs directly used for the numerical study on gas production from NGH reservoirs or embedded in simulators only taking into hydrate saturation account. Moreover, the determination of empirical parameters (N, m, ε, β) lacks a reliable physical basis, and their values vary with the properties of HBSs.
- (2)
- One special parameter in the LBNL model is the irreducible water saturation Swr measured by the lab experiment and it is difficult to determine in numerical simulation, as well as Sh1,max in the Sakamoto et al. model.
- (3)
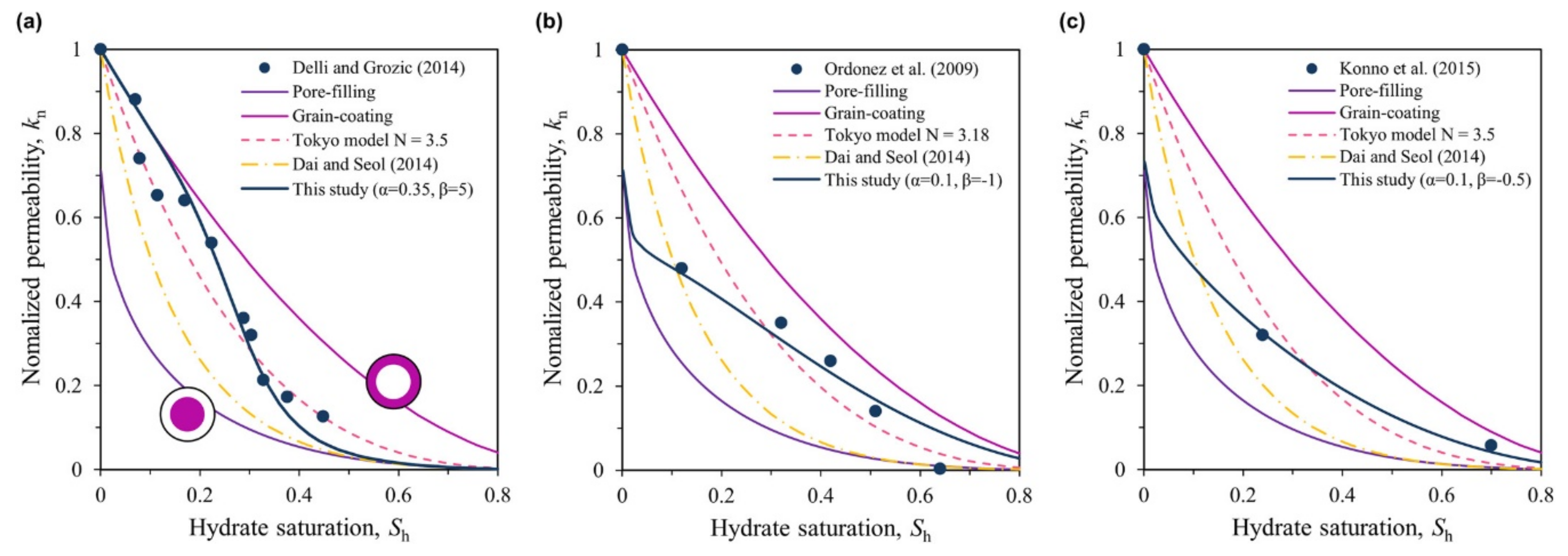
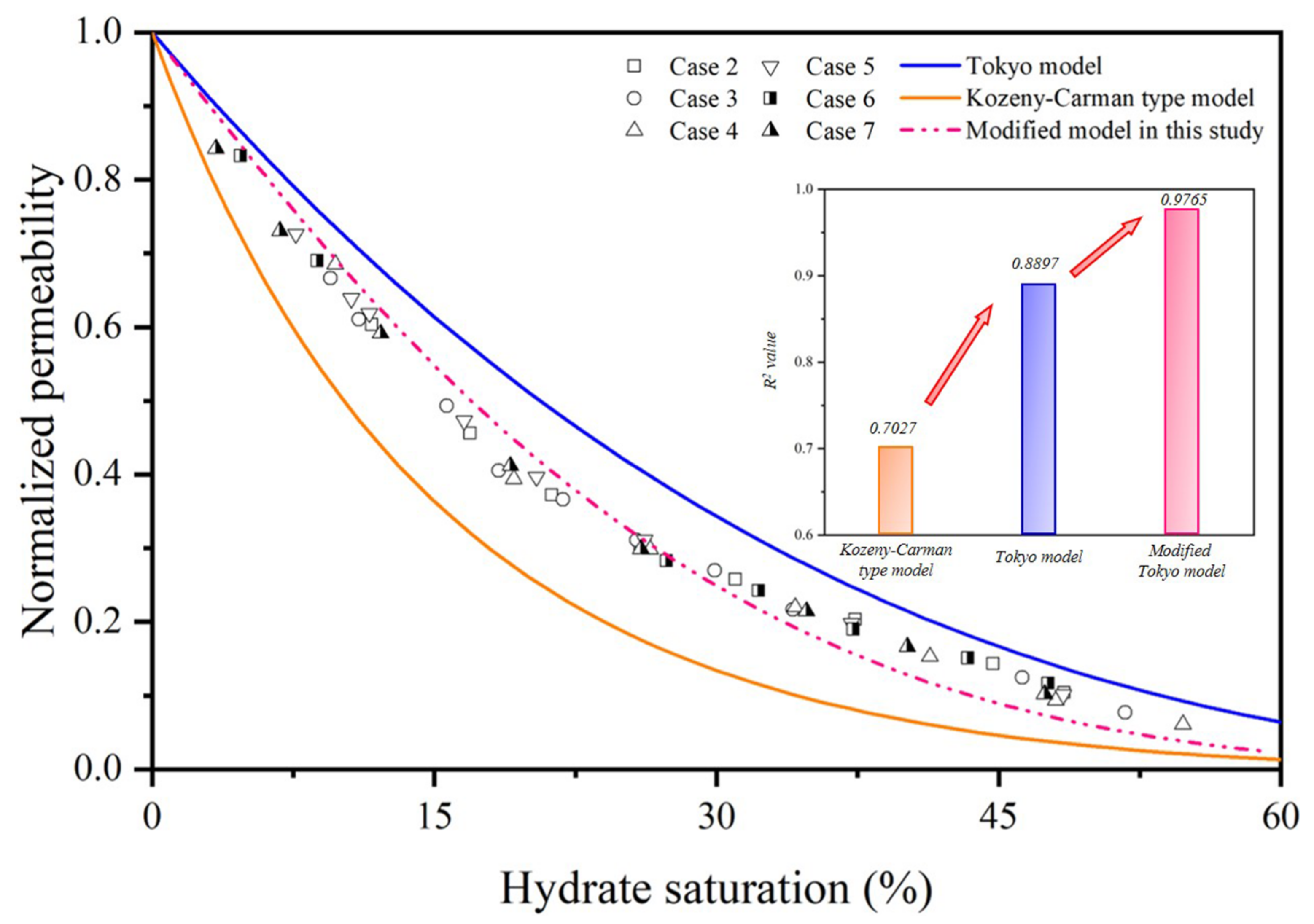
- The inherent power law fitting characteristic of the Tokyo model makes it possible to match the experimental data well by adjusting the N value. However, the determination of the N value still lacks a sound physical foundation and cannot be estimated based on lithology or other remotely detectable reservoir parameters. Since the Tokyo model is widely adopted in many modeling studies to estimate gas production from NGH reservoirs, the influence of hydrate (considering the effects of hydrate pore habits, hydrate heterogeneous distribution) and pore structure on the value of the exponent N will be a new research hotspot for the permeability model of HBSs.
- (4)
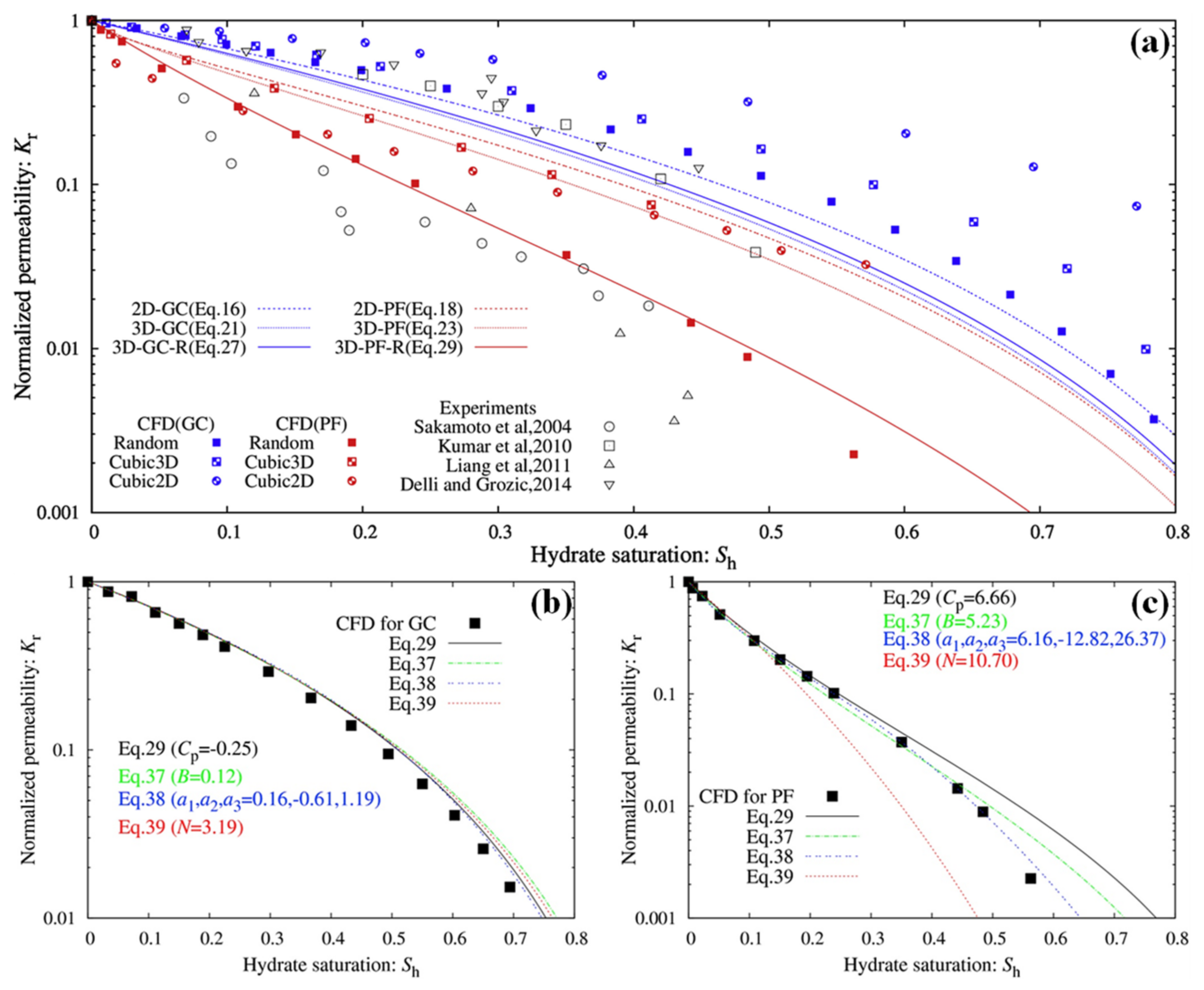
- Figure 3 shows the permeability reduction curves with varying hydrate saturation depicted by these mentioned above reservoir simulator used models. The research methods, the advantages and limitations, the using parameters and their physical meaning of various reservoir simulator used models, and the factors that models consider are also provided. Table 3 lists the methods, advantages, and limitations of these reservoir simulator used models of HBSs, while Table 4 summarizes the characteristics of these reservoir simulator used models for permeability prediction of HBSs.
4. Modified Permeability Models Based on KC Equation
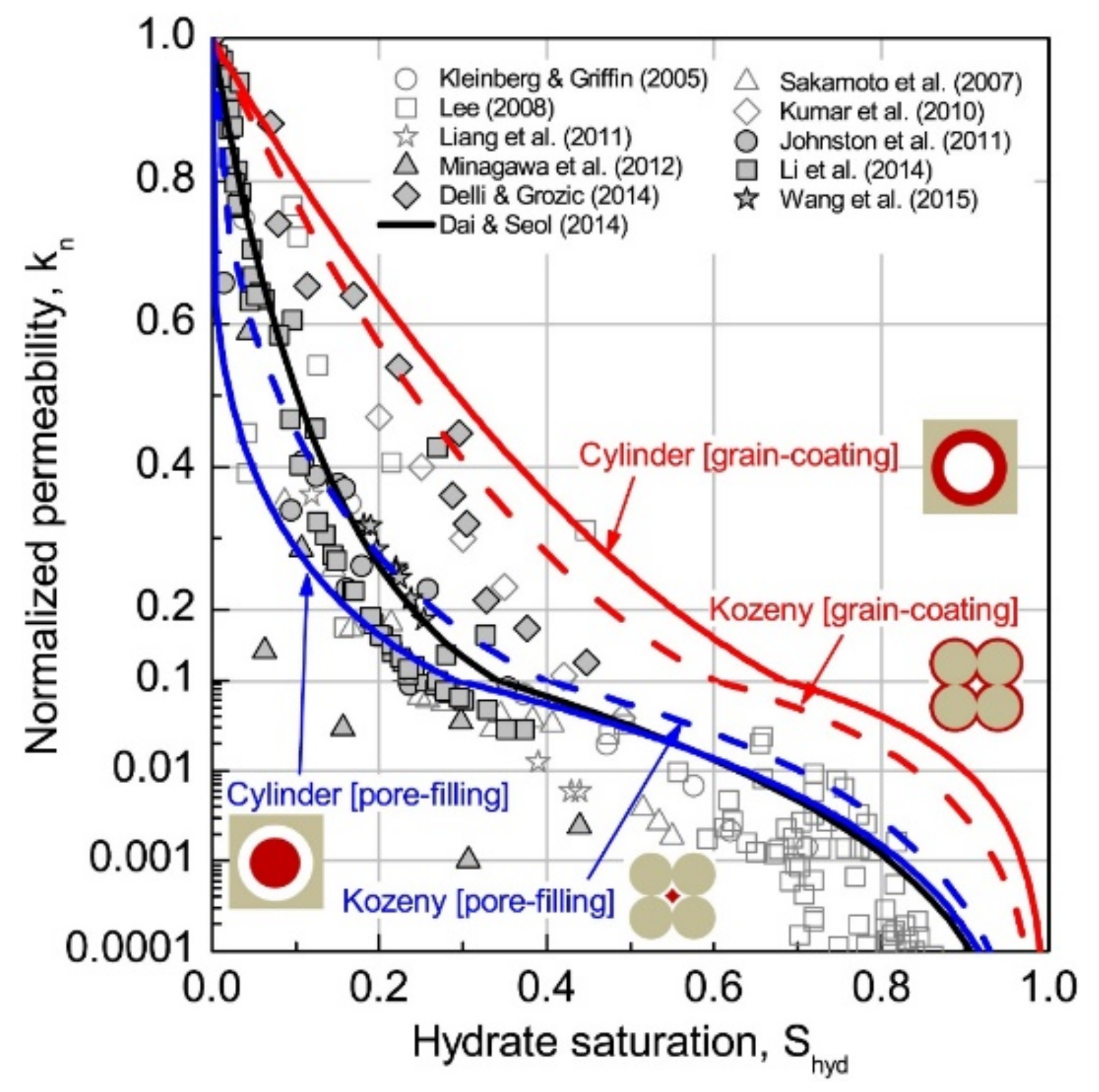
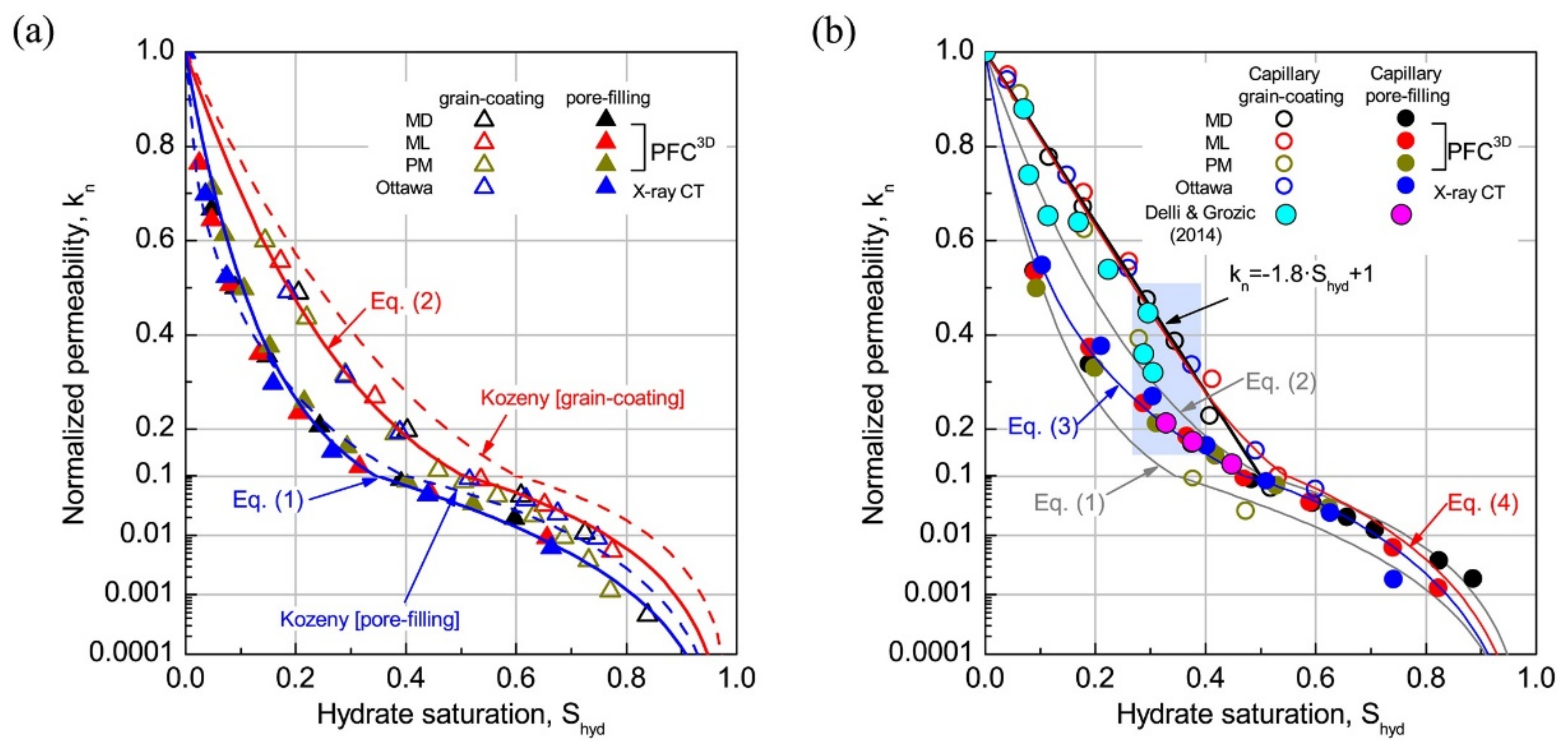
4.1. Dai and Seol Model
4.2. Kang et al. Model
4.3. Katagiri et al. Model
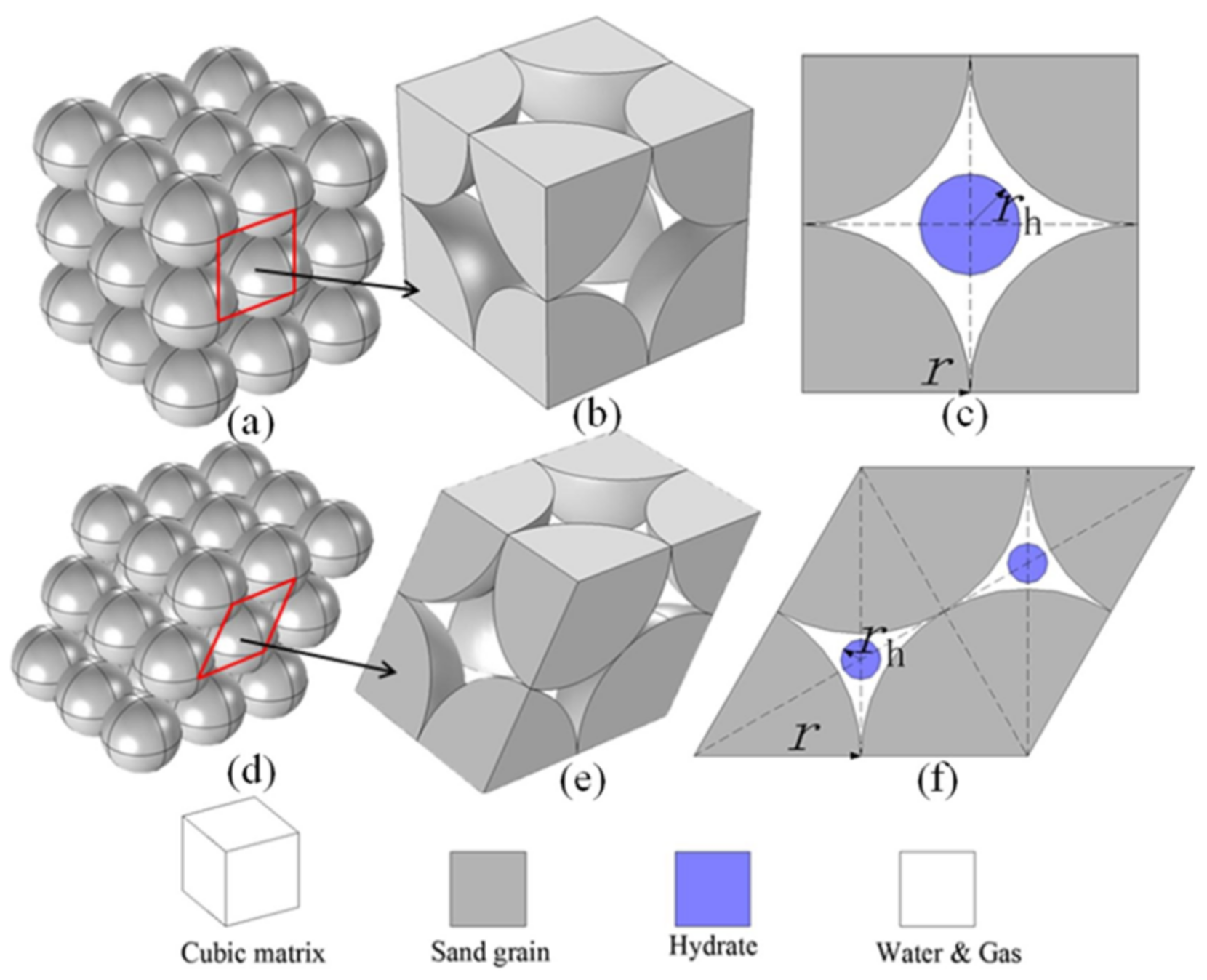
4.4. Li et al. Model
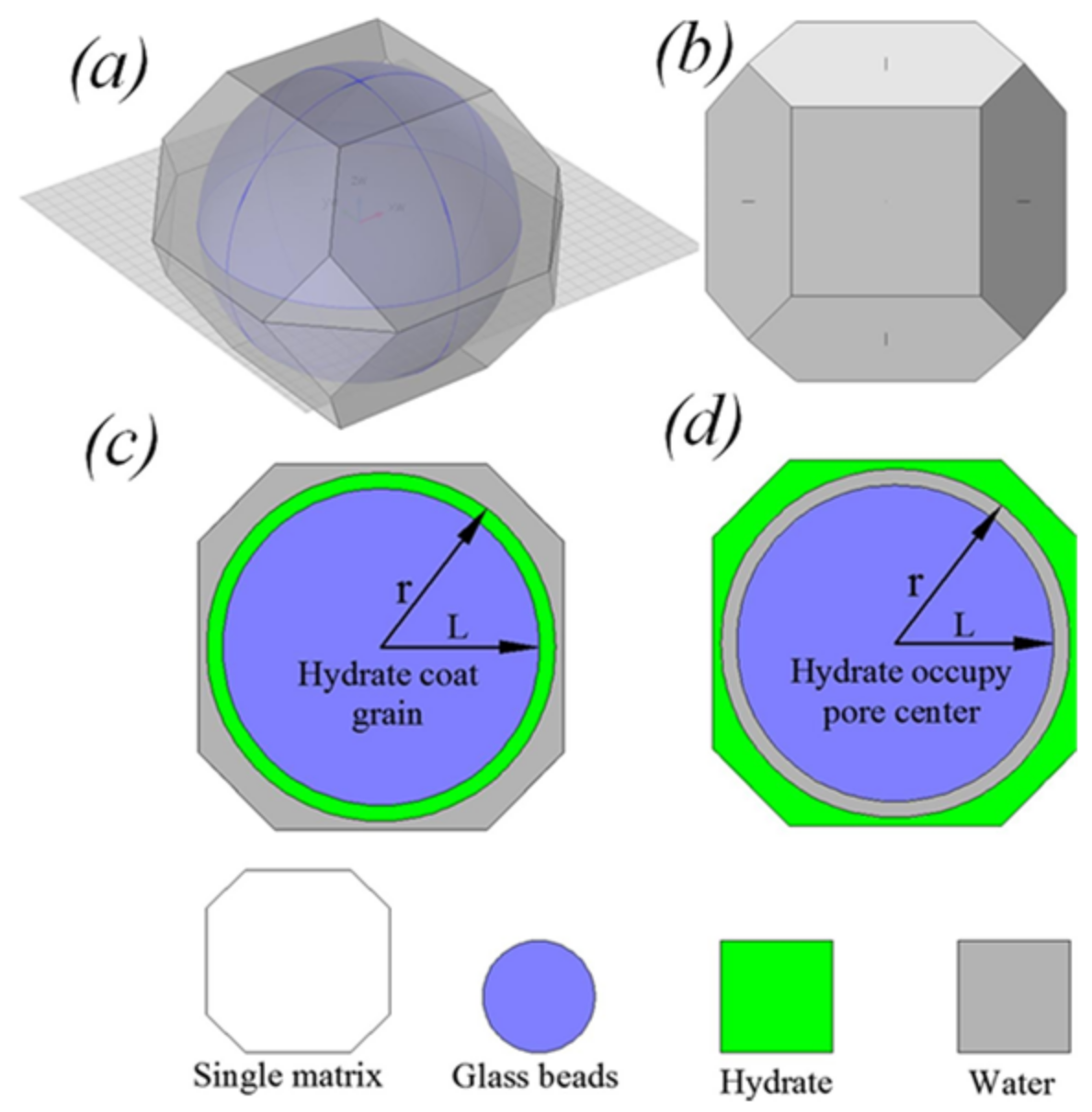
4.5. Shen et al. Model
4.6. Xiao et al. Model
4.7. Kou et al. Model
4.8. Summary
- (1)
- The modified KC model for permeability prediction of HBSs can be established by adding the fitting parameter or the polynomial, which comprehensively considers the relationship between hydrate saturation and shape factor, porosity, tortuosity, pore surface area, and pore volume based on numerical simulation results. The prediction accuracy of models could be improved by changing the value of the fitting parameters or the order of the polynomial.
- (2)
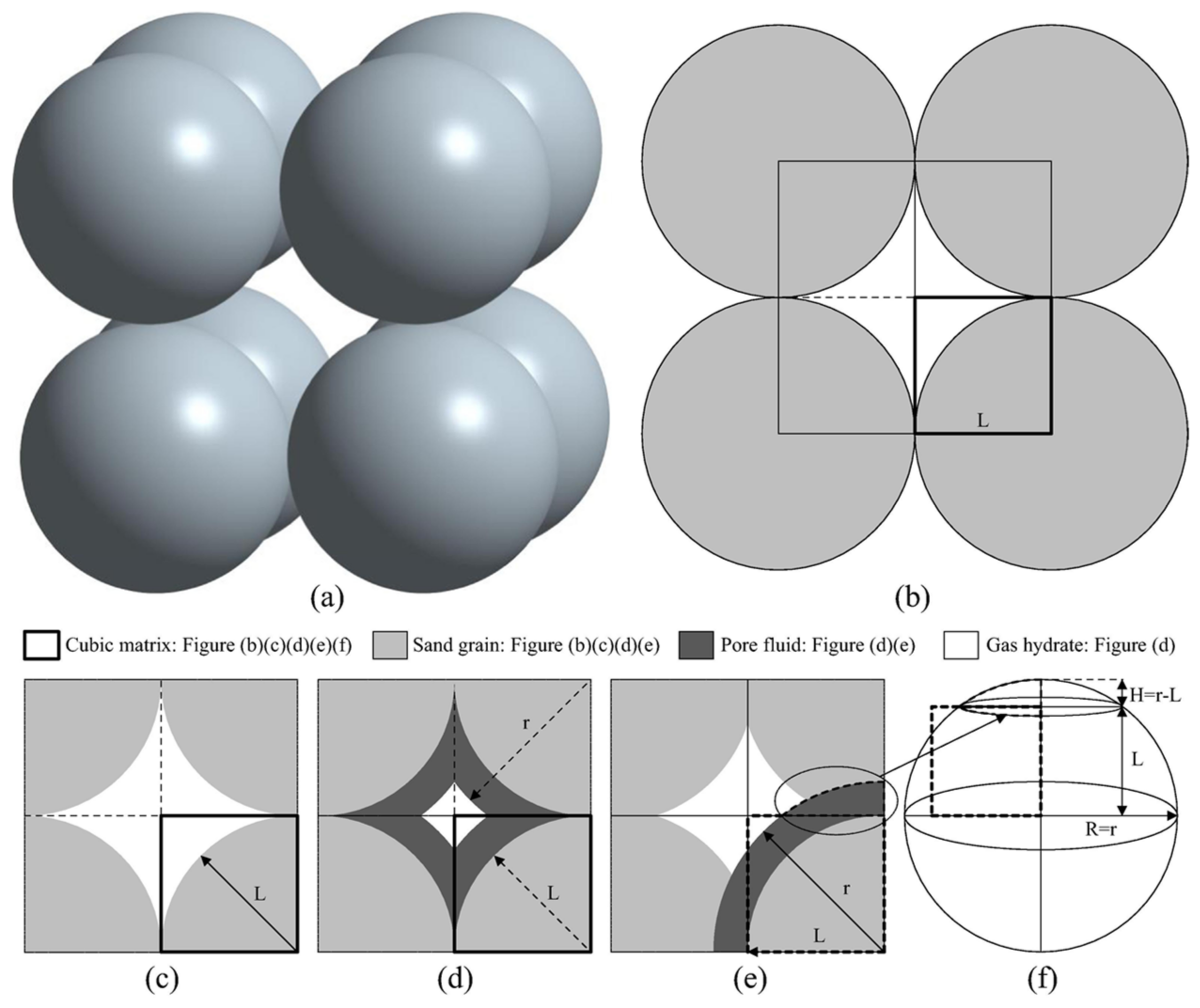
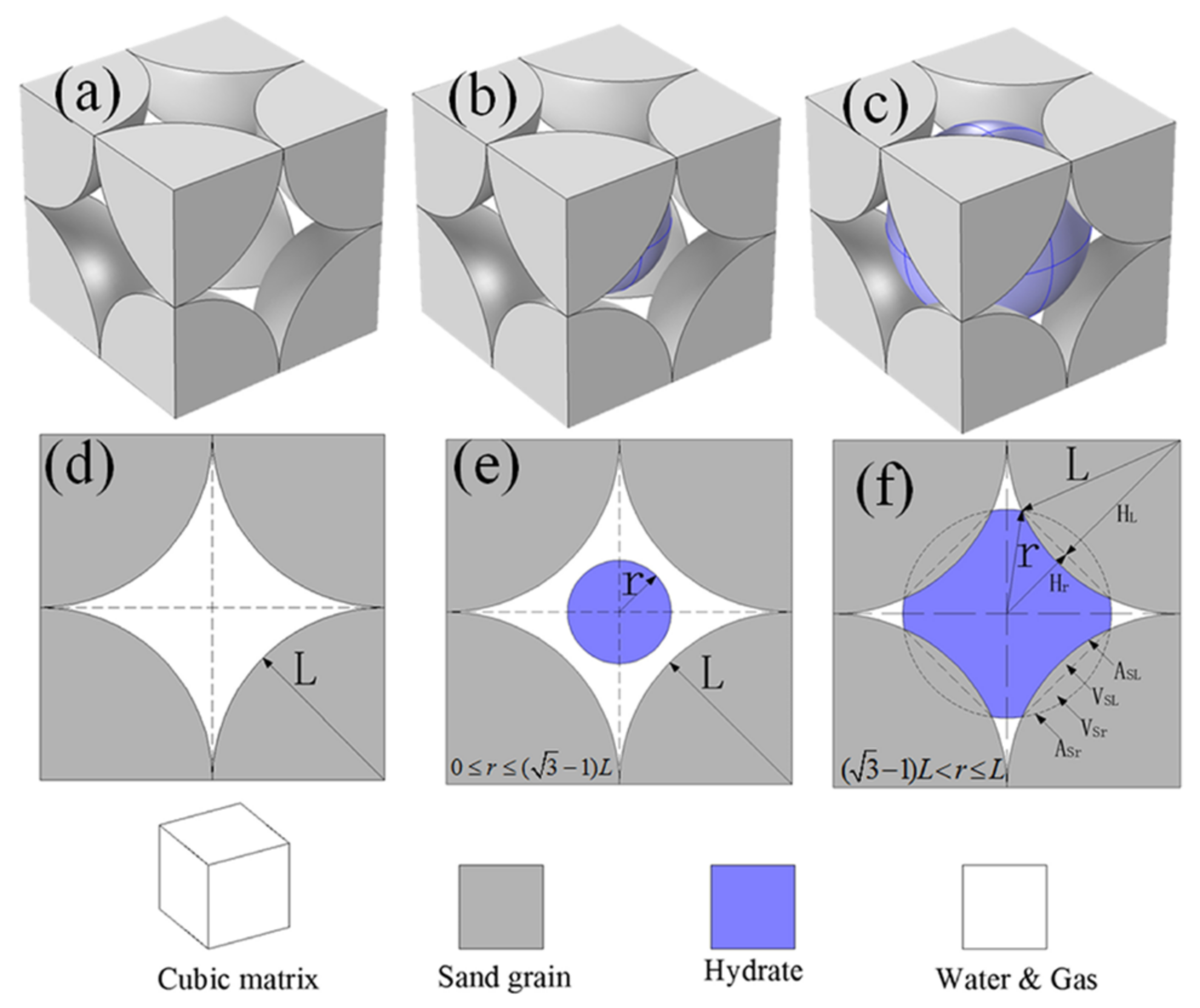
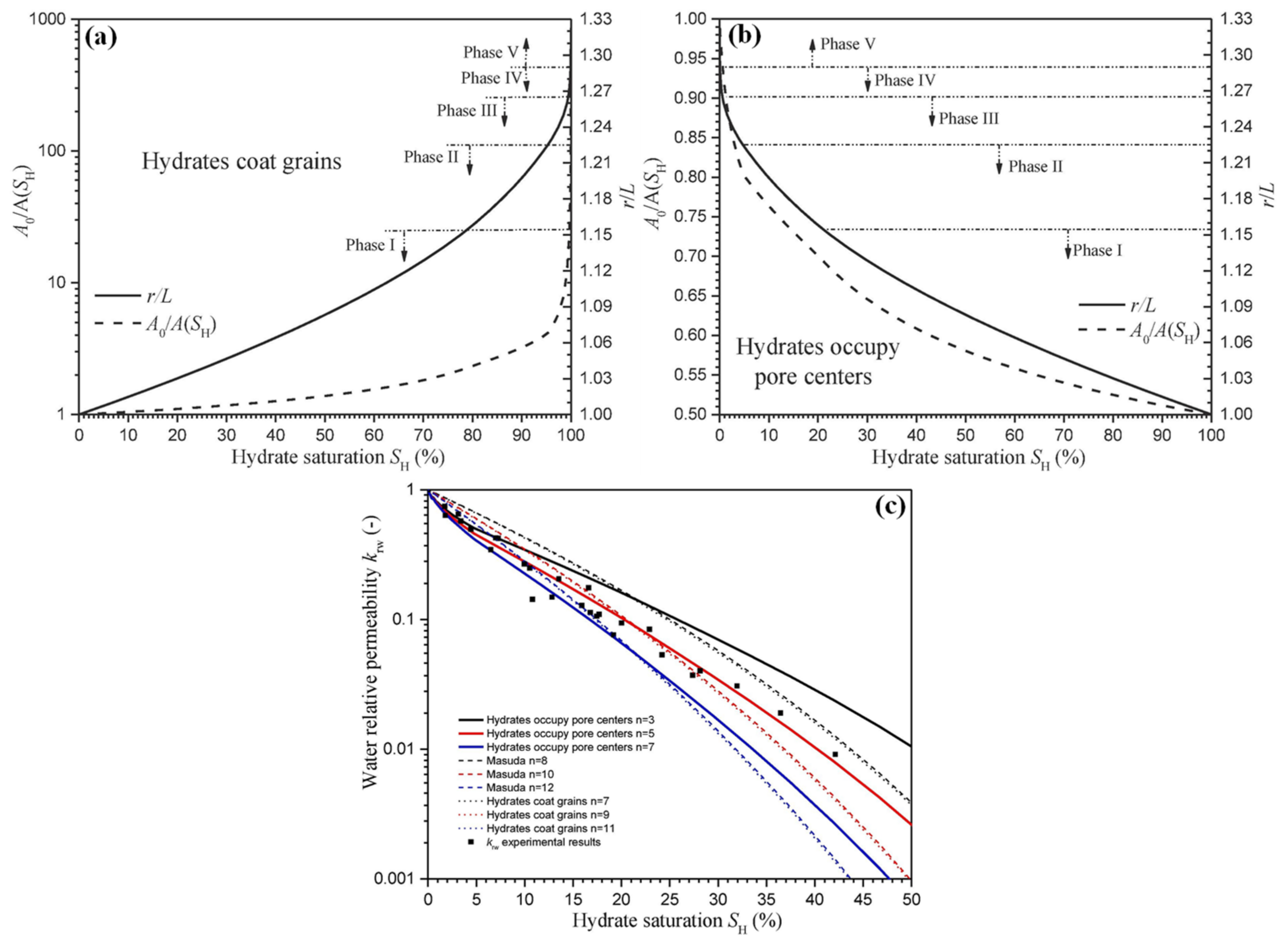
- The modified permeability model of HBSs based on the KC equation can be established by strict mathematical deduction of new expressions of Sh and the ratio of internal surface area A0/A(Sh) based on assumptions of particle stacking structures, hydrate pore habits, and 3D microscopic growth morphology. Moreover, there are only parameters in part of the modified models that represent the radius of sediment particles and hydrate to show the effect of related factors on the permeability of HBSs.
- (3)
- The KC-based modified permeability models consisted of parameters with specific physical meaning to better explain the effect of hydrate on the pore structure characteristic and permeability variation. The influences of hydrates (considering the effect factors such as the hydrate saturation and hydrate growth habits) on the pore structure characteristics (e.g., porosity, pore-throat size, tortuosity, pore connectivity) of hydrate sediments will be a new research hotspot for the permeability prediction model of HBSs.
- (4)
- The research methods, the advantages and limitations, the using parameters and their physical meaning of various modified permeability models, and the factors that models consider are also provided. Table 5 lists the methods, advantages, and limitations of these modified permeability models of HBSs, while Table 6 summarizes the characteristics of these modified permeability models for permeability prediction of HBSs.
5. Novel Permeability Models Based on New Theories and Research Methods
5.1. New SDR Model Considering the Effect of Hydrate-Related Interface Evolution
5.2. Fractal Theory-Based Permeability Prediction Model
5.2.1. Daigles Model
5.2.2. Zhang et al. Model
5.2.3. Du et al. Model
5.3. Chen et al. Model
5.4. Liu et al. Model
5.5. Hou et al. Model
5.6. Guo et al. Model
5.7. Lei et al. Model
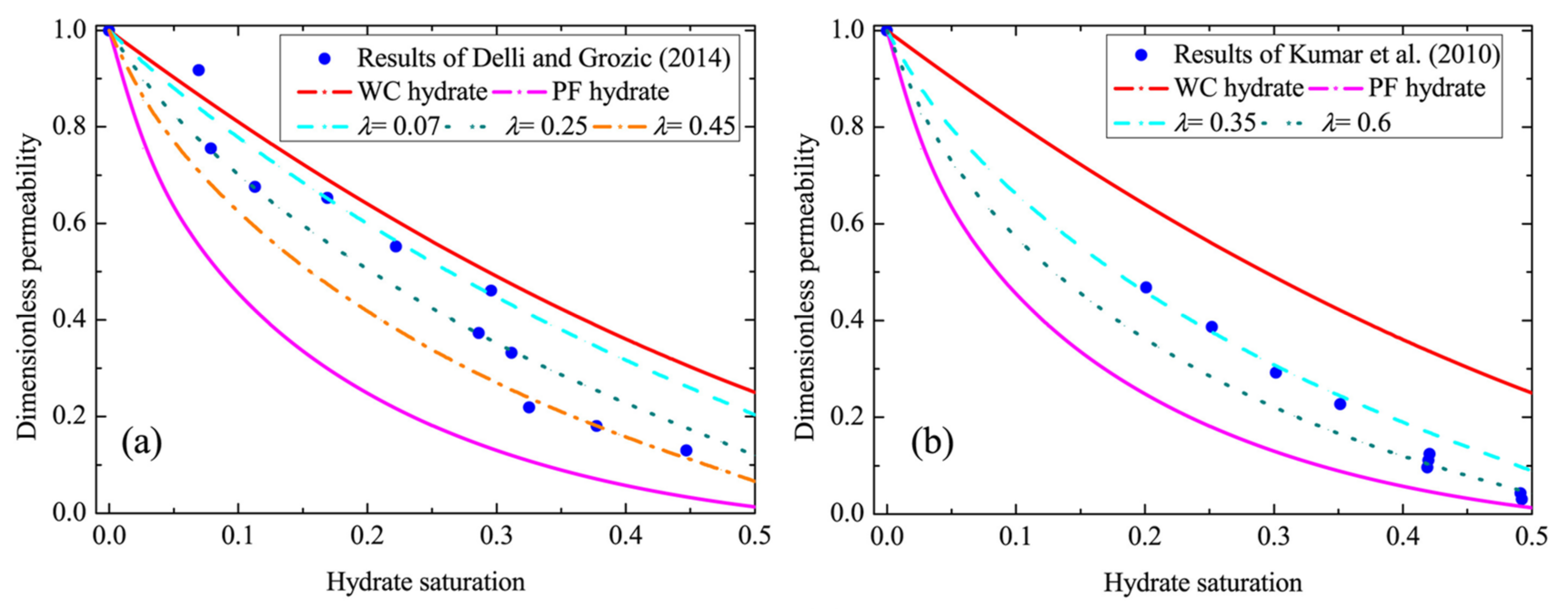
5.8. Delli and Grozic Hybrid Model
5.9. Wang et al. Hybrid Model
5.10. Lei et al. Stress-Dependent Permeability Model
5.11. Zhang et al. Stress-Dependent Permeability Model
5.12. Lv et al. Model
5.13. Summary
- (1)
- New SDR model adds one parameter to model the effect of hydrate-related interface evolution during the hydrate dissociation process on the NMR transverse surface relaxivity for closer to the actual situation and better used in engineering applications.
- (2)
- The established fractal theory-based permeability prediction models of HBSs that consider the interaction between hydrate formation/dissociation and pore structure in the host sediment enable one to well establish a quantitative relationship between pore-scale structure parameters and permeability. The most important aspect of using these models to predict HBS permeability is that microscale structure information (e.g., the maximal pore diameter and related fractal dimensions) in the porous media can be properly and precisely characterized. However, these models are all complex and many parameters cannot be accurately obtained by experiments.
- (3)
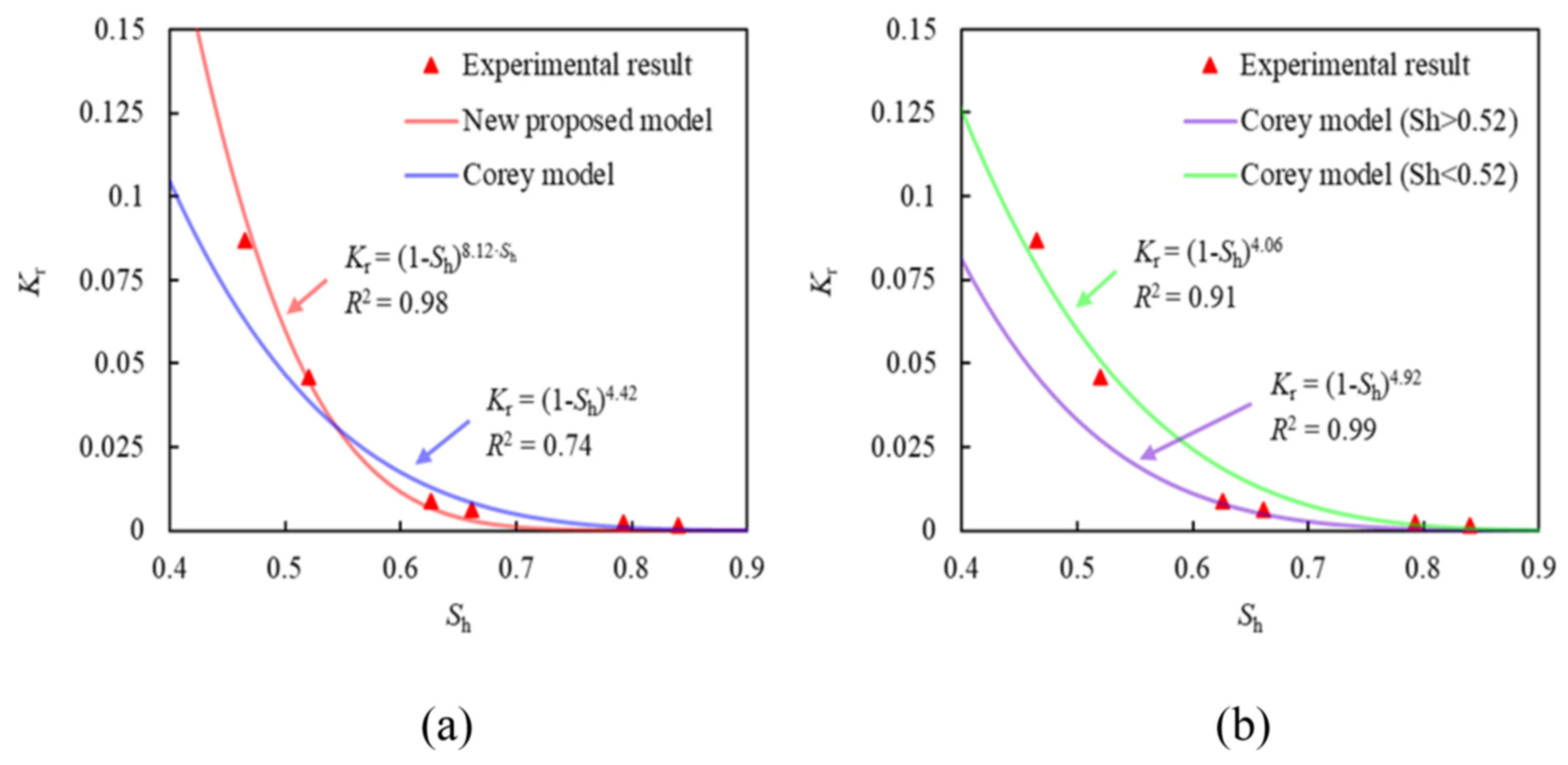
- The modified Corey models are proposed to capture the permeability variation behaviors with hydrate of HBSs using multiplying a linear Corey model with an exponential function of hydrate saturation or describing the index in a simple Corey model by a function with hydrate saturation as an independent variable. These types of models show good predictive performance due to the variability of fitting parameters. However, the fitting parameters do not have e clear physical meaning.
- (4)
- Some permeability reduction models with novel mathematic forms and physical parameters proposed by some researchers consider the pore-scale effect of hydrates on the width and tortuosity of fluid seepage channels and the size of pore space available for fluid flow. Furthermore, these models take into different hydrate pore habits within pores account and the parameters in these models have definite physical meaning and are easy to be determined. However, there are still some assumptions and simplifications in the derivation of these models. Innovatively, the permeability theoretical model that is commonly used in coalbed methane reservoirs is introduced into the gas hydrate reservoir considering the pore space characteristics and the hydrate pore morphology, which are completely different from those assumed by PCTM and KGM.
- (5)
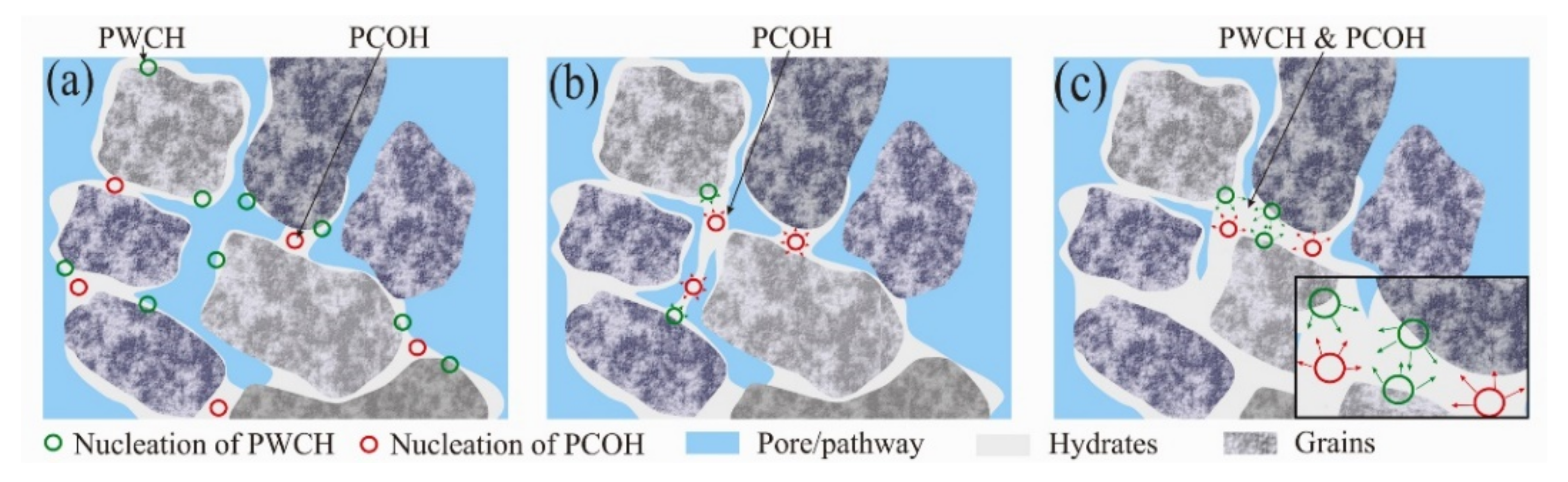
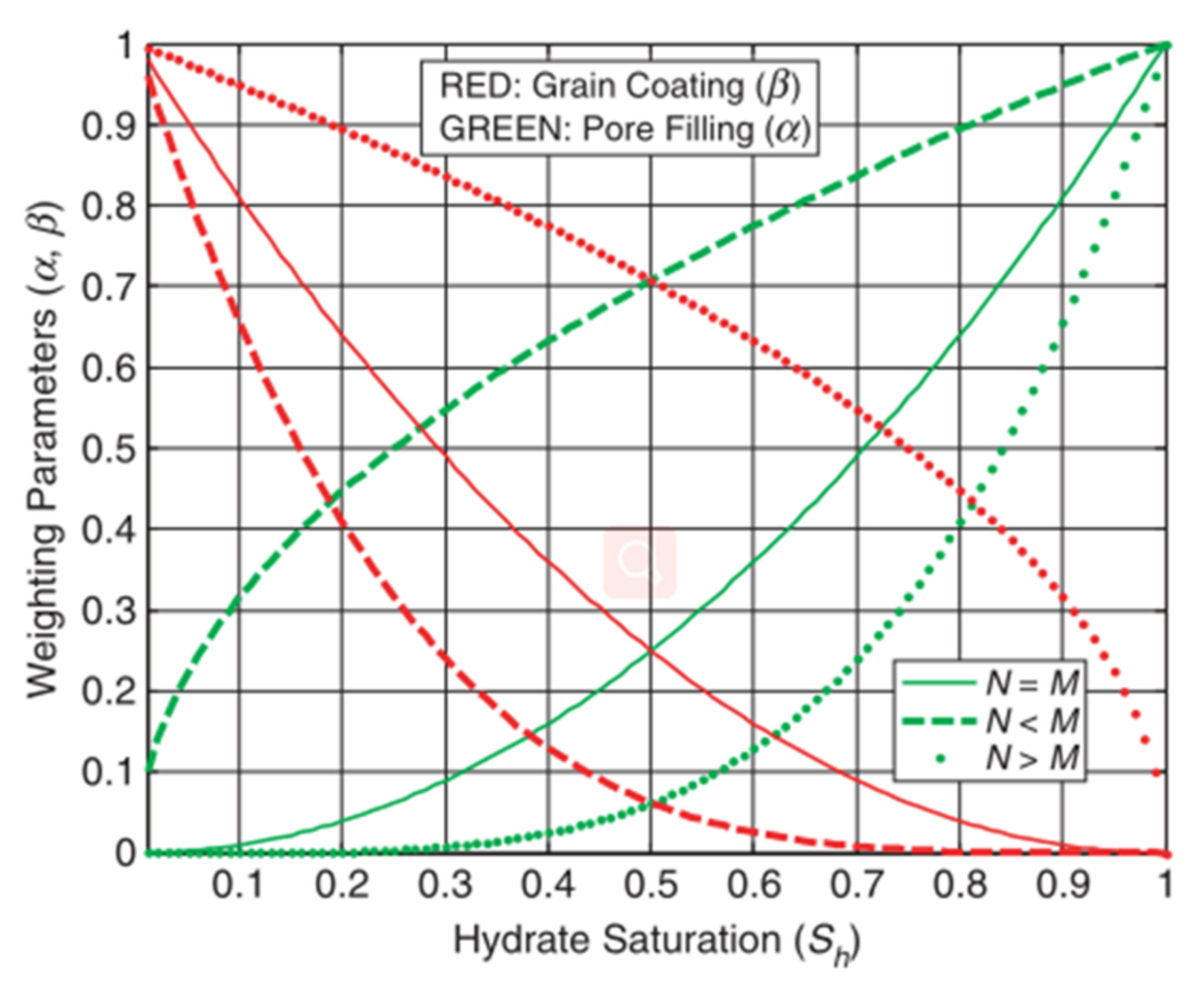
- The hybrid permeability model based on the weighted combination of existing permeability models considers the evolution of hydrate pore habits with hydrate saturation and the dominance of hydrate pore habits within pores on the permeability change. In addition, this type of model offers an elegant expression that can be easily implemented in reservoir simulators for a more accurate estimation of gas production from hydrate reservoirs.
- (6)
- The stress-dependent permeability models of HBSs capture the permeability evolution controlled by the pore structure of inner space and geomechanical behavior of hydrate reservoirs under stress conditions. However, existing models do not comprehensively consider the influence of different hydrate pore habits (e.g., grain-cementing, load-bearing hydrate, and patchy hydrates), the combined effect of particle crushing, and water-rock interactions on permeability, which are difficult to address in numerical modeling and analysis. The influence of the geomechanical behavior (considering the effects of the hydrate saturation, stress state, and hydrate pore habits) and chemical reaction between sediment and pore fluid on the permeability of fined-grained HBSs will be a new research hotspot for the permeability model of HBSs.
- (7)
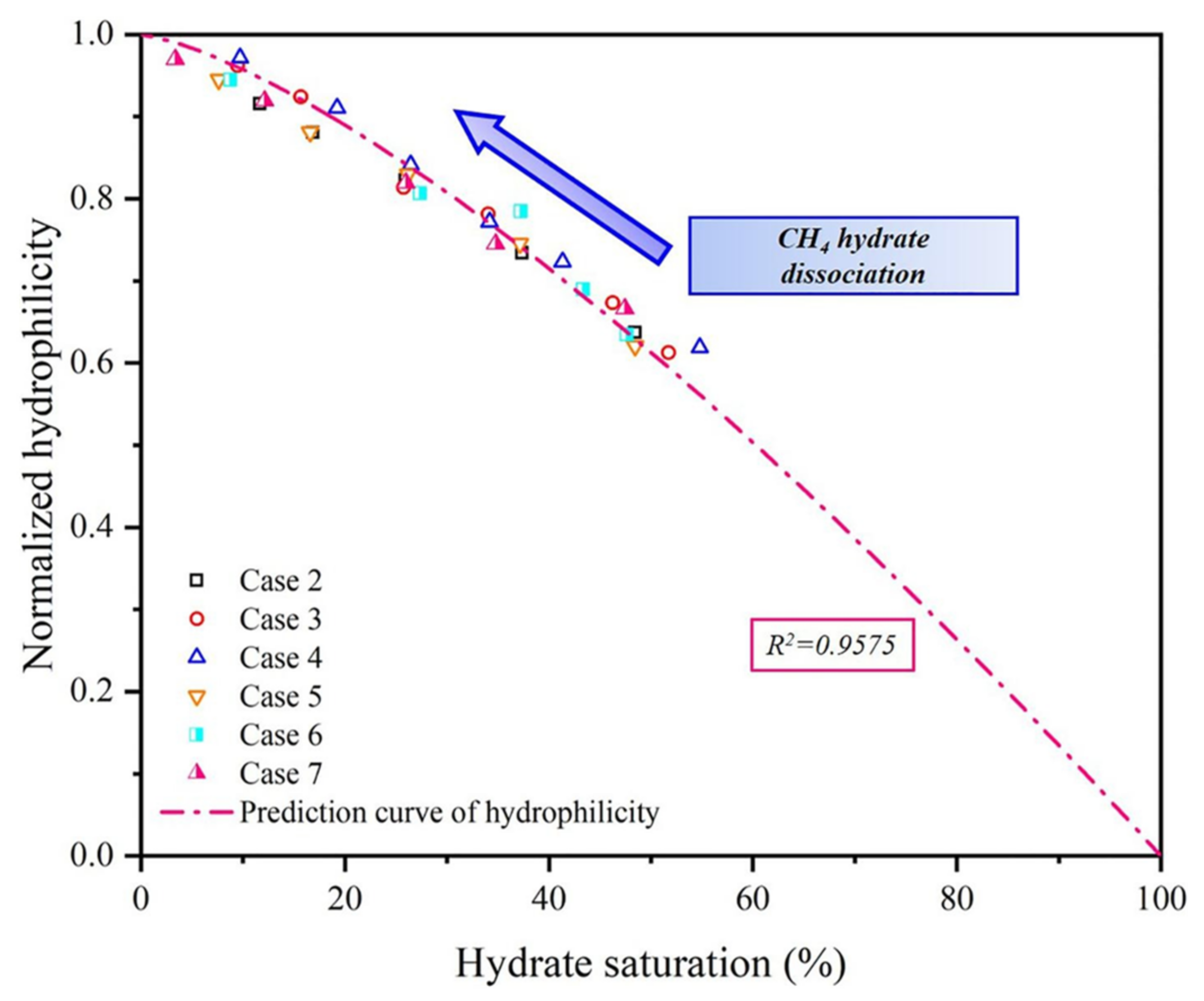
- The prediction accuracy of the modified Tokyo model considering the effect of wettability is better than reported permeability prediction models without consideration of the effect of the wettability and its evolution on the seepage characteristics. The evolution of wettability is crucial to impacting the gas–water two-phase flow in HBSs. In addition, the coupled influence mechanism of hydrate pore habits and wettability evolution on flow behavior at the pore scale in HBSs will be a new research hotspot and direction for the permeability model of HBSs.
- (8)
- The research methods, the advantages and limitations, the using parameters and their physical meaning of various novel permeability models, and the factors that models consider are also provided. Table 7 lists the methods, advantages, and limitations of these novel permeability models of HBSs, while Table 8 summarizes the characteristics of these novel permeability models that used other theories and methods for permeability prediction of HBSs.
6. Conclusions
- (1)
- The SDR model can be used for engineering applications to evaluate the permeability field data of NGH reservoirs in the presence of NMR data. PCTM and KGM were introduced into the research of HBS permeability and implemented for numerical simulations of gas production and provided a theoretical fundamental basis for other permeability models because of their simplicity and capability of capturing the main pore structure characteristic in sediments and two typical hydrate pore habits. They can well describe the general reduction trend of the permeability with increased hydrate saturation However, the analytical expressions of PCTM and KGM are oversimplified, which is too idealistic and far from actual HBSs due to the idealized inner structure of pore space and growth habits and morphology of hydrate.
- (2)
- The reservoir simulator used models took hydrate saturation into account but cannot capture the effect of hydrate pore habits on permeability. In addition, the determination of empirical parameters lacks a sound physical basis, and their values vary with the properties of HBSs. The inherent power law fitting characteristic of the Tokyo model makes good fitness by adjusting the value of parameter N. The Tokyo model is widely used in numerical modeling of gas production from hydrate reservoirs. The influence of pore structure characteristics and hydrate heterogeneous distribution on the value of the exponent N will be a new research hotspot.
- (3)
- The modified permeability models of HBSs based on the KC equation were mainly established in two ways: adding the fitting parameter or the polynomial, which comprehensively considers the relationship between hydrate saturation and pore structure properties based on numerical simulation results, or by strict mathematical deduction of new expressions of Sh and the ratio of internal surface area A0/A(Sh) based on series assumptions about sediment particles packing patterns. Some modified permeability models consisted of parameters with specific physical meaning to better explain the effect of hydrate on the characteristic of pore structure and the variation of permeability. The influences of hydrates (considering the effect factors such as the hydrate saturation, pore habits, and inhomogeneous distribution) on the pore structure characteristics (e.g., porosity, pore-throat size, tortuosity, pore connectivity) of hydrate sediments will be a new research hotspot.
- (4)
- Many novel permeability models of HBSs have been developed based on new theories and research methods investigating the effect of other hydrate- or sediment-related factors on the fluid flow and the permeability evolution. The fractal theory-based permeability model of HBSs considering the interaction between hydrate pore habits and pore structure in the host sediment enables to well establish a quantitative relationship between microstructure parameters and permeability. The modified Corey models show good predictive performance due to the variability of fitting parameters, but the fitting parameters do not have a definite physical meaning. Some permeability models with novel mathematic forms and novel physical concepts proposed by some researchers consider the effect of hydrates on the evolution of the main seepage channel and pore space size. The hybrid permeability model of HBSs considers the evolution of hydrate pore habits with hydrate saturation and the dominance of hydrate pore habits within pores on the permeability evolution.
- (5)
- The stress-dependent permeability models of HBSs capture the permeability evolution induced by the pore structure change of hydrate reservoirs under stress conditions. The influence of the geomechanical behavior and chemical reaction between sediment and pore fluid on the permeability of fined-grained HBSs will be a new research hotspot. In addition, wettability is crucial to influencing the multiphase flow in hydrate sediments. The coupled influence mechanism of hydrate pore habits and wettability evolution on seepage characteristics at the pore scale in HBSs will be a new research hotspot and direction.
7. Challenges and Suggestions of Future Research Directions
- (1)
- At present, most of the research on seepage theory in hydrate-bearing porous media still uses Darcy’s law for reference. Most of the existing permeability models contain fitting parameters or make ideal assumptions in terms of sediment pore structure and hydrate pore habits, which have great limitations in practical applications. However, there is still no universally accepted general form to reflect the permeability reduction trend in HBSs even ignoring more complex aspects (e.g., heterogeneity, actual hydrate morphology, and so on). In addition, the exponent N of the widely used Tokyo model has a large variation range and still lacks a sound physical basis, and cannot be estimated based on easily measured parameters in HBSs [44].
- (2)
- Most of the empirical parameters used in the widely used permeability models are mainly derived from experimental data fitting in the limited hydrate saturation range. These fitting parameters are only applicable to specific conditions and the permeability prediction results are usually not universally representative of their participation. Moreover, due to the lack of enough experimental data, an appropriate selection of empirical constant values in some permeability models is not available for HBSs [126].
- (3)
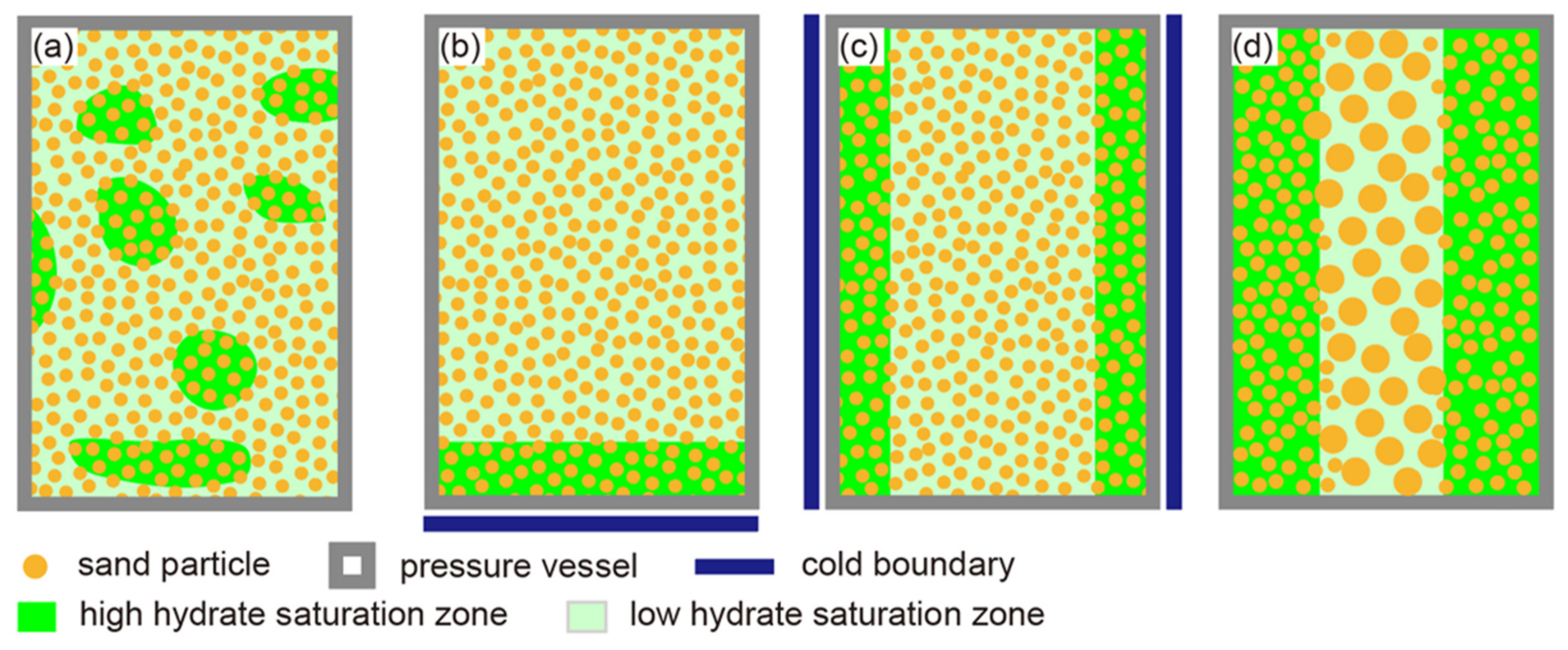
- The existing permeability models almost ignore the analysis of some pore-scale influencing factors such as pore geometries, heterogeneous distribution of hydrates and sediment particles, capillarity, wettability, and so on [53,60,63], leading to inevitable discrepancies between hypotheses in theoretical models and reality in actual sediments.
- (4)
- None of these permeability models capture the common existing issue that permeability decreases to 0 before hydrate saturation reaches 100% [60]. This is inconsistent with the concepts of percolation threshold or irreducible saturation in natural porous media. Therefore, a physically realistic permeability model should be proposed for HBSs. With the above-mentioned issue, existing models for permeability prediction could not capture the intrinsic fluid flow and transport process in the pore of the natural host sediment.
7.1. Anisotropy and Heterogeneity of HBSs
7.2. Pore Habits and Morphology of Hydrate
7.3. Pore Characteristics of Sediments
7.4. Fine-Grained Sediments
7.5. Embedded Parameters in the Model
7.6. Multi-Field Coupling Seepage Characteristics
- (1)
- Due to the decomposition of solid hydrate into liquid water and methane gas, the pore structure available for fluid flow in the sediment changes, which affects the porosity, fluid flow behavior, and permeability of the seepage field.
- (2)
- The decrease in temperature will even lead to the reformation of hydrate or the formation of ice, which will block the pores and greatly affect the seepage capacity of the reservoir.
- (3)
- The formation/decomposition of hydrate increases/decreases the cementation and support effect of hydrate on sediments, and sand migration and even formation deformation may occur, which affects the mechanical properties of the reservoir and leads to changes in pressure, porosity, and permeability of the seepage field.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sloan, E.D. Fundamental principles and applications of natural gas hydrates. Nature 2003, 426, 353–359. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Cheng, C.; Zhao, J.; Zhu, Z.; Liu, W.; Yang, M.; Xue, K. Evaluation of gas production from methane hydrates using depressurization, thermal stimulation and combined methods. Appl. Energy 2015, 145, 265–277. [Google Scholar] [CrossRef]
- Kvenvolden, K.A. Gas hydrates—geological perspective and global change. Rev. Geophys. 1993, 31, 173–187. [Google Scholar] [CrossRef]
- Yin, Z.; Linga, P. Methane hydrates: A future clean energy resource. Chin. J. Chem. Eng. 2019, 27, 2026–2036. [Google Scholar] [CrossRef]
- Makogon, Y.F.; Holditch, S.; Makogon, T.Y. Natural gas-hydrates—A potential energy source for the 21st Century. J. Pet. Sci. Eng. 2007, 56, 14–31. [Google Scholar] [CrossRef]
- Boswell, R.; Collett, T.S. Current perspectives on gas hydrate resources. Energy Environ. Sci. 2011, 4, 1206–1215. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Z.; Li, C.; Ning, F.; Liu, C.; Wu, N.; Cai, J. Hydrate growth in quartzitic sands and implication of pore fractal characteristics to hydraulic, mechanical, and electrical properties of hydrate-bearing sediments. J. Nat. Gas Sci. Eng. 2020, 75, 103109. [Google Scholar] [CrossRef]
- Wu, P.; Li, Y.; Liu, W.; Liu, Y.; Wang, D.; Song, Y. Microstructure evolution of hydrate-bearing sands during thermal dissociation and ensued impacts on the mechanical and seepage characteristics. J. Geophys. Res. Solid Earth 2020, 125, e2019JB019103. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, J.; Sun, X.; Wu, P.; Shen, S.; Liu, T.; Li, Y. Comprehensive review of geomechanical constitutive models of gas hydrate-bearing sediments. J. Nat. Gas Sci. Eng. 2021, 88, 103755. [Google Scholar] [CrossRef]
- Ren, X.; Guo, Z.; Ning, F.; Ma, S. Permeability of hydrate-bearing sediments. Earth Sci. Rev. 2020, 202, 103100. [Google Scholar] [CrossRef]
- Konno, Y.; Fujii, T.; Sato, A.; Akamine, K.; Naiki, M.; Masuda, Y.; Yamamoto, K.; Nagao, J. Key findings of the world’s first offshore methane hydrate production test off the coast of Japan: Toward future commercial production. Energy Fuels 2017, 31, 2607–2616. [Google Scholar] [CrossRef]
- Yamamoto, K.; Wang, X.-X.; Tamaki, M.; Suzuki, K. The second offshore production of methane hydrate in the Nankai Trough and gas production behavior from a heterogeneous methane hydrate reservoir. RSC Adv. 2019, 9, 25987–26013. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Feng, Y.; Okajima, J.; Komiya, A.; Maruyama, S. Production behavior and numerical analysis for 2017 methane hydrate extraction test of Shenhu, South China Sea. J. Nat. Gas Sci. Eng. 2018, 53, 55–66. [Google Scholar] [CrossRef]
- Anderson, B.J.; Kurihara, M.; White, M.D.; Moridis, G.J.; Wilson, S.J.; Pooladi-Darvish, M.; Gaddipati, M.; Masuda, Y.; Collett, T.S.; Hunter, R.B. Regional long-term production modeling from a single well test, Mount Elbert gas hydrate stratigraphic test well, Alaska North slope. Mar. Pet. Geol. 2011, 28, 493–501. [Google Scholar] [CrossRef]
- Yin, Z.; Wan, Q.-C.; Gao, Q.; Linga, P. Effect of pressure drawdown rate on the fluid production behaviour from methane hydrate-bearing sediments. Appl. Energy 2020, 271, 115195. [Google Scholar] [CrossRef]
- Li, S.; Zheng, R.; Xu, X.; Hou, J. Energy efficiency analysis of hydrate dissociation by thermal stimulation. J. Nat. Gas Sci. Eng. 2016, 30, 148–155. [Google Scholar] [CrossRef]
- Yin, Z.; Moridis, G.; Tan, H.K.; Linga, P. Numerical analysis of experimental studies of methane hydrate formation in a sandy porous medium. Appl. Energy 2018, 220, 681–704. [Google Scholar] [CrossRef]
- Yin, Z.; Moridis, G.; Chong, Z.R.; Tan, H.K.; Linga, P. Numerical analysis of experimental studies of methane hydrate dissociation induced by depressurization in a sandy porous medium. Appl. Energy 2018, 230, 444–459. [Google Scholar] [CrossRef]
- Li, S.; Wu, D.; Wang, X.; Hao, Y. Enhanced gas production from marine hydrate reservoirs by hydraulic fracturing assisted with sealing burdens. Energy 2021, 232, 120889. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, L.; Ning, F.; Liu, Z.; Sun, J.; Li, X.; Sun, J.; Hyodo, M.; Liu, C. Effect of stress on permeability of clay silty cores recovered from the Shenhu hydrate area of the South China Sea. J. Nat. Gas Sci. Eng. 2022, 99, 104421. [Google Scholar] [CrossRef]
- Hu, C.; Liu, X.; Jia, Y.; Duan, Z. Permeability anisotropy of methane hydrate-bearing sands: Insights from CT scanning and pore network modelling. Comput. Geotech. 2020, 123, 103568. [Google Scholar] [CrossRef]
- Boswell, R. Is gas hydrate energy within reach? Science 2009, 325, 957–958. [Google Scholar] [CrossRef]
- Kleinberg, R.; Flaum, C.; Griffin, D.; Brewer, P.; Malby, G.; Peltzer, E.; Yesinowski, J. Deep sea NMR: Methane hydrate growth habit in porous media and its relationship to hydraulic permeability, deposit accumulation, and submarine slope stability. J. Geophys. Res. Solid Earth 2003, 108, B10. [Google Scholar] [CrossRef]
- Delli, M.L.; Grozic, J.L. Experimental determination of permeability of porous media in the presence of gas hydrates. J. Pet. Sci. Eng. 2014, 120, 1–9. [Google Scholar] [CrossRef]
- Xu, J.; Bu, Z.; Li, H.; Li, S.; Sun, B. Pore-scale flow simulation on the permeability in hydrate-bearing sediments. Fuel 2022, 312, 122681. [Google Scholar] [CrossRef]
- Li, G.; Li, X.-S.; Lv, Q.-N.; Zhang, Y. Permeability measurements of quartz sands with methane hydrate. Chem. Eng. Sci. 2019, 193, 1–5. [Google Scholar] [CrossRef]
- Mahabadi, N.; Dai, S.; Seol, Y.; Jang, J. Impact of hydrate saturation on water permeability in hydrate-bearing sediments. J. Pet. Sci. Eng. 2019, 174, 696–703. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, J.; Zhang, Y.; Wang, D.; Li, Y.; Song, Y. Analysis of the effect of particle size on permeability in hydrate-bearing porous media using pore network models combined with CT. Fuel 2016, 163, 34–40. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, X.; Chen, D.; Yin, Z. An investigation on the permeability of hydrate-bearing sediments based on pore-scale CFD simulation. Int. J. Heat Mass Transf. 2022, 192, 122901. [Google Scholar] [CrossRef]
- Liu, W.; Wu, Z.; Li, Y.; Song, Y.; Ling, Z.; Zhao, J.; Lv, Q. Experimental study on the gas phase permeability of methane hydrate-bearing clayey sediments. J. Nat. Gas Sci. Eng. 2016, 36, 378–384. [Google Scholar] [CrossRef]
- Wu, Z.; Yang, S.; Zhang, L.; Liu, W.; Li, Y. Stress dependence of the gas permeability of montmorillonite sediments in the presence of methane hydrate. J. Pet. Sci. Eng. 2022, 208, 109697. [Google Scholar] [CrossRef]
- Yang, L.; Ai, L.; Xue, K.; Ling, Z.; Li, Y. Analyzing the effects of inhomogeneity on the permeability of porous media containing methane hydrates through pore network models combined with CT observation. Energy 2018, 163, 27–37. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Ge, K.; Zhao, J.; Song, Y. Characterizing anisotropy changes in the permeability of hydrate sediment. Energy 2020, 205, 117997. [Google Scholar] [CrossRef]
- Kou, X.; Li, X.-S.; Wang, Y.; Liu, J.-W.; Chen, Z.-Y. Heterogeneity of hydrate-bearing sediments: Definition and effects on fluid flow properties. Energy 2021, 229, 120736. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, W.; Zheng, J.; Li, Y. Effect of methane hydrate dissociation and reformation on the permeability of clayey sediments. Appl. Energy 2020, 261, 114479. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, S.; Li, H.; Li, S.; Xu, J.; Wang, X. A numerical simulation study of methane hydrate reformation during the dissociation process induced by depressurization. Fuel 2022, 313, 122983. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, J.; Zhang, Y.; Wang, D.; Li, Y.; Song, Y. Analysis of the influence of wettability on permeability in hydrate-bearing porous media using pore network models combined with computed tomography. J. Nat. Gas Sci. Eng. 2015, 26, 1372–1379. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Zhao, J.; Ai, L.; Yang, L. Variations in permeability along with interfacial tension in hydrate-bearing porous media. J. Nat. Gas Sci. Eng. 2018, 51, 141–146. [Google Scholar] [CrossRef]
- Pan, L.; Lei, L.; Seol, Y. Pore-scale influence of methane hydrate on permeability of porous media. J. Nat. Gas Sci. Eng. 2021, 87, 103758. [Google Scholar] [CrossRef]
- Dai, S.; Seol, Y. Water permeability in hydrate-bearing sediments: A pore-scale study. Geophys. Res. Lett. 2014, 41, 4176–4184. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Q.; Fan, Z.; Wei, W.; Li, M.; Wang, Y.; Huang, X.; Song, Y.; Wang, D. Equivalency and Replaceability between Different Permeability Models of Hydrate-Bearing Porous Media When Applied to Numerical Modeling of Hydrate Dissociation: Implications for Model Selection and Parameter Assignment. Energy Fuels 2021, 35, 6090–6100. [Google Scholar] [CrossRef]
- Masuda, Y.; Naganawa, S.; Ando, S.; Sato, K. Numerical calculation of gas-production performance from reservoirs containing natural gas hydrates. SPE J. 1997, 29, 201–210. [Google Scholar]
- Masuda, Y. Modeling and experimental studies on dissociation of methane gas hydrates in Berea sandstone cores. In Proceedings of the Third International Gas Hydrate Conference, Salt Lake City, UT, USA, 18–22 July 1999. [Google Scholar]
- Minagawa, H.; Ohmura, R.; Kamata, Y.; Nagao, J.; Ebinuma, T.; Narita, H.; Masuda, Y. Water permeability of porous media containing methane hydrate as controlled by the methane-hydrate growth process. AAPG Mem. 2009, 89, 734–739. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Giraldo, C.; Klump, J.; Clarke, M.; Schicks, J.M. Sensitivity analysis of parameters governing the recovery of methane from natural gas hydrate reservoirs. Energies 2014, 7, 2148–2176. [Google Scholar] [CrossRef]
- Civan, F. Scale effect on porosity and permeability: Kinetics, model, and correlation. AIChE J. 2001, 47, 271–287. [Google Scholar] [CrossRef]
- Moridis, G. EOSHYDR: A TOUGH2 module for CH4-hydrate release and flow in the subsurface. In Proceedings of the Methane Hydrates, Chiba City, Japan, 20–22 October 1998. [Google Scholar]
- Moridis, G.J. Numerical studies of gas production from methane hydrates. SPE J. 2003, 8, 359–370. [Google Scholar] [CrossRef]
- Sakamoto, Y.; Komai, T.; Miyazaki, K.; Tenma, N.; Yamaguchi, T.; Zyvoloski, G. Laboratory-scale experiments of the methane hydrate dissociation process in a porous media and numerical study for the estimation of permeability in methane hydrate reservoir. J. Thermodyn. 2010, 2010, 9879–9884. [Google Scholar] [CrossRef]
- Kozeny, J. Uber kapillare leitung der wasser in boden. R. Acad. Sci. Vienna Proc. Class I 1927, 136, 271–306. [Google Scholar]
- Carman, P.C. Fluid flow through granular beds. Trans. Inst. Chem. Eng. 1937, 15, 150–166. [Google Scholar] [CrossRef]
- Kang, D.H.; Yun, T.S.; Kim, K.Y.; Jang, J. Effect of hydrate nucleation mechanisms and capillarity on permeability reduction in granular media. Geophys. Res. Lett. 2016, 43, 9018–9025. [Google Scholar] [CrossRef]
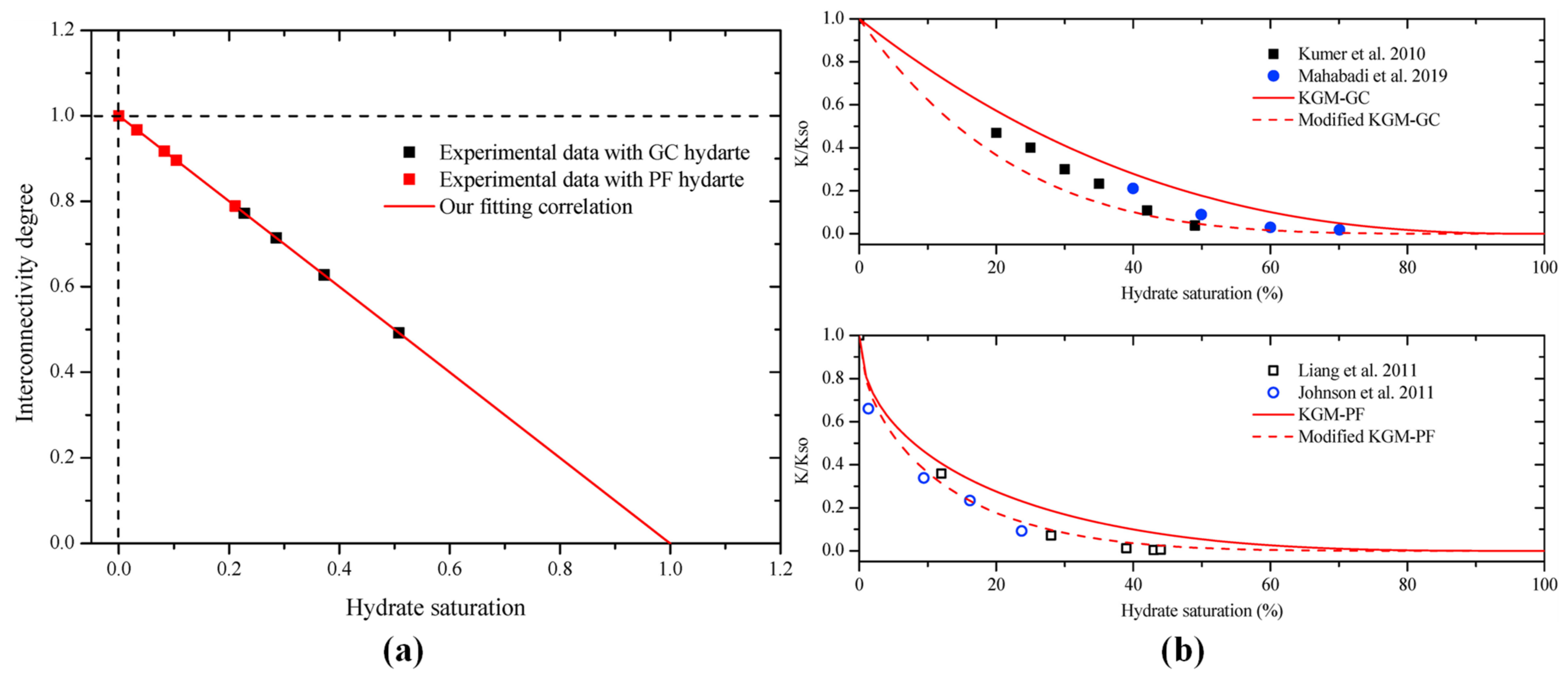
- Katagiri, J.; Konno, Y.; Yoneda, J.; Tenma, N. Pore-scale modeling of flow in particle packs containing grain-coating and pore-filling hydrates: Verification of a Kozeny–Carman-based permeability reduction model. J. Nat. Gas Sci. Eng. 2017, 45, 537–551. [Google Scholar] [CrossRef]
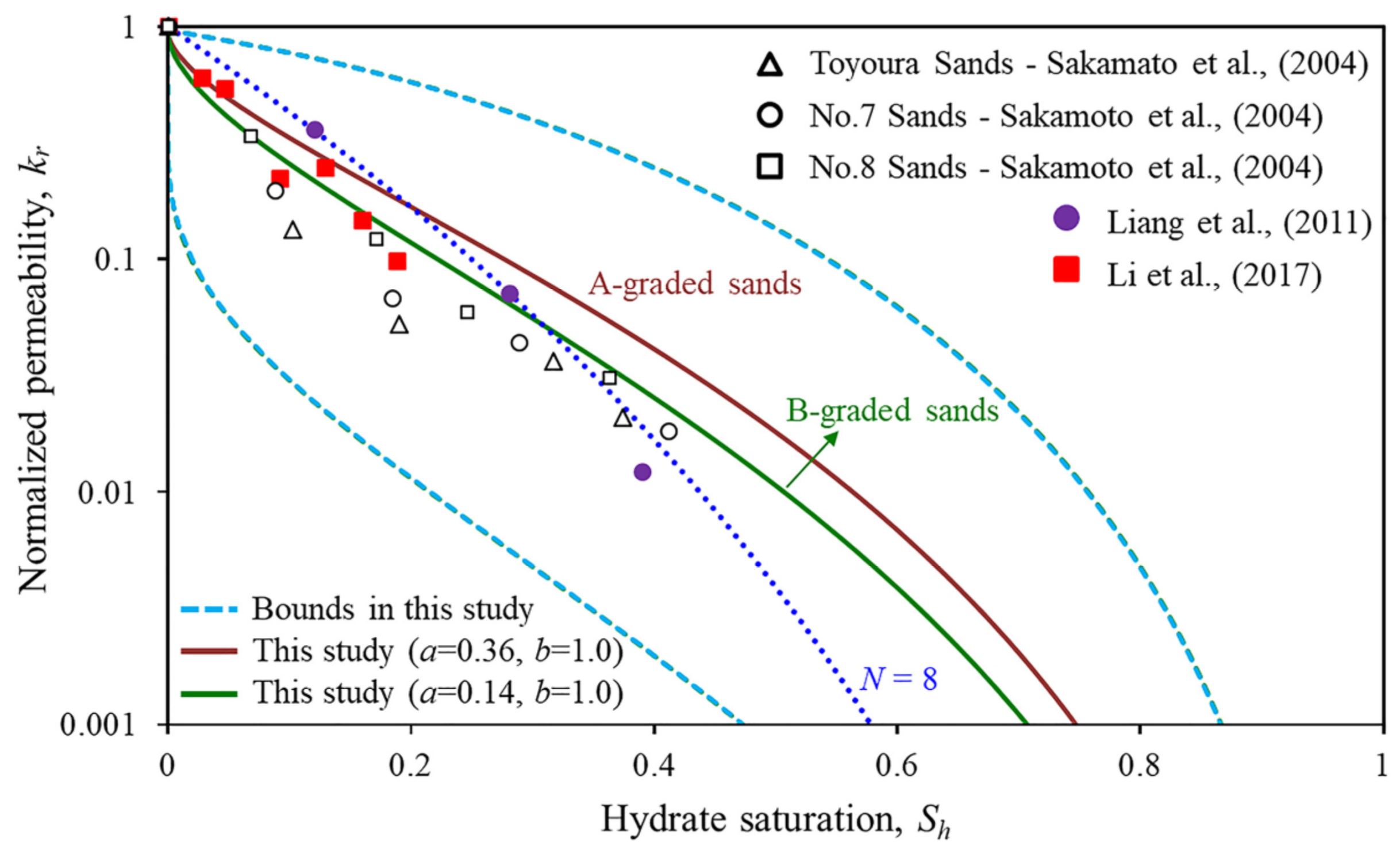
- Li, G.; Wu, D.-M.; Li, X.-S.; Lv, Q.-N.; Li, C.; Zhang, Y. Experimental measurement and mathematical model of permeability with methane hydrate in quartz sands. Appl. Energy 2017, 202, 282–292. [Google Scholar] [CrossRef]
- Shen, P.; Li, G.; Li, B.; Li, X.; Liang, Y.; Lv, Q. Permeability measurement and discovery of dissociation process of hydrate sediments. J. Nat. Gas Sci. Eng. 2020, 75, 103155. [Google Scholar] [CrossRef]
- Xiao, C.; Li, X.; Lv, Q.; Yu, Y.; Yu, J.; Li, G.; Shen, P. Experimental measurement and clustered equal diameter particle model of permeability with methane hydrate in glass beads. Fuel 2022, 320, 123924. [Google Scholar] [CrossRef]
- Guo, Z.; Fang, Q.; Nong, M.; Ren, X. A novel Kozeny-Carman-based permeability model for hydrate-bearing sediments. Energy 2021, 234, 121203. [Google Scholar] [CrossRef]
- Cai, J.; Xia, Y.; Lu, C.; Bian, H.; Zou, S. Creeping microstructure and fractal permeability model of natural gas hydrate reservoir. Mar. Pet. Geol. 2020, 115, 104282. [Google Scholar] [CrossRef]
- Daigle, H. Relative permeability to water or gas in the presence of hydrates in porous media from critical path analysis. J. Pet. Sci. Eng. 2016, 146, 526–535. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, C.; Ning, F.; Liu, L.; Cai, J.; Liu, C.; Wu, N.; Wang, D. Pore fractal characteristics of hydrate-bearing sands and implications to the saturated water permeability. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018721. [Google Scholar] [CrossRef]
- Du, P.; Zhao, C.; Peng, P.; Gao, T.; Huang, T. Fractal characterization of permeability prediction model in hydrate-bearing porous media. Chem. Eng. Sci. 2020, 218, 115576. [Google Scholar] [CrossRef]
- Hou, J.; Ji, Y.; Zhou, K.; Liu, Y.; Wei, B. Effect of hydrate on permeability in porous media: Pore-scale micro-simulation. Int. J. Heat Mass Transf. 2018, 126, 416–424. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, L.; Wang, D.; Zhang, Z.; Li, C.; Meng, Q.; Liu, C. The interface evolution during methane hydrate dissociation within quartz sands and its implications to the permeability prediction based on NMR data. Mar. Pet. Geol. 2021, 129, 105065. [Google Scholar] [CrossRef]
- Chen, X.; Verma, R.; Espinoza, D.N.; Prodanović, M. Pore-scale determination of gas relative permeability in hydrate-bearing sediments using X-ray computed micro-tomography and lattice Boltzmann method. Water Resour. Res. 2018, 54, 600–608. [Google Scholar] [CrossRef]
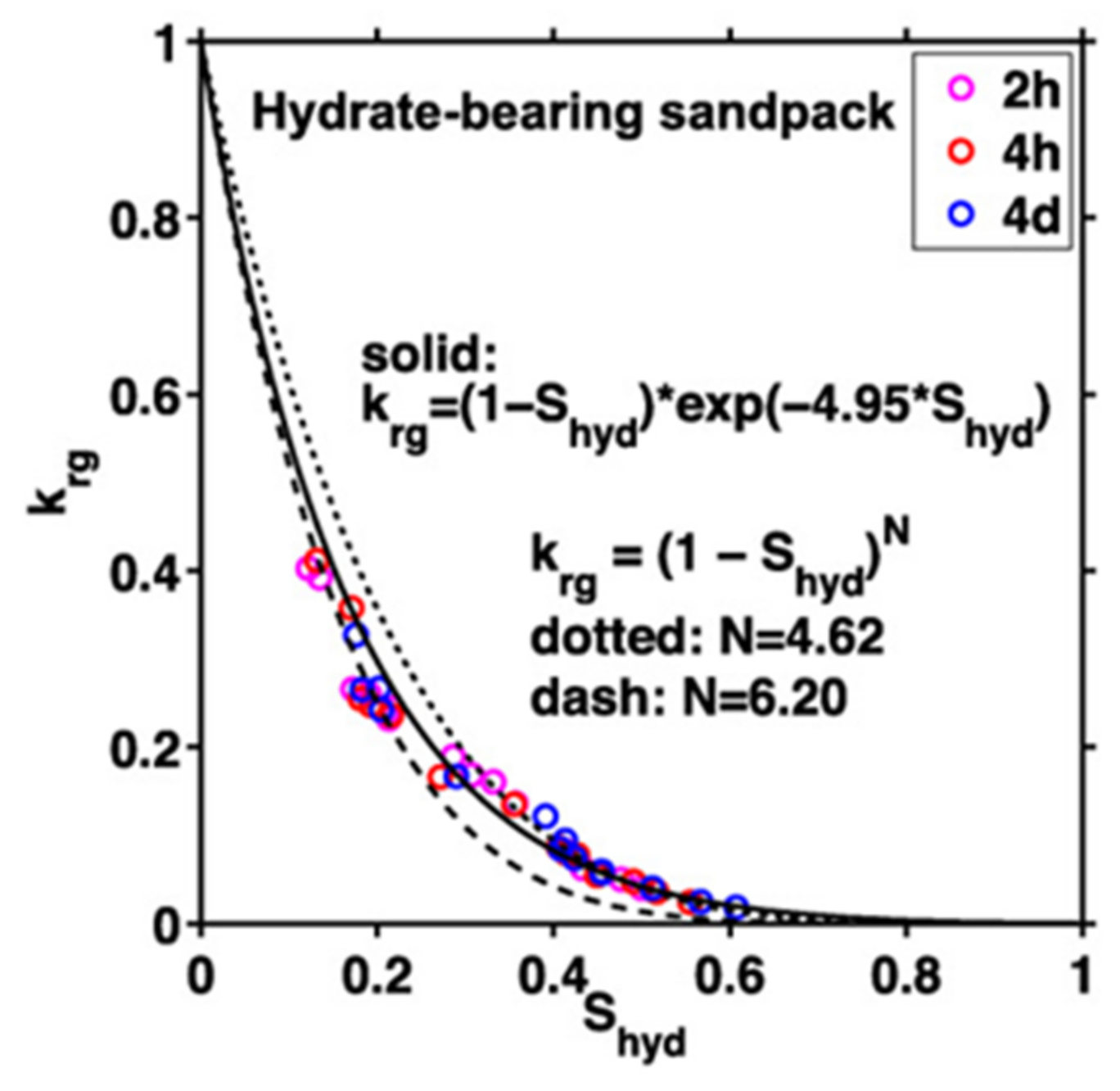
- Liu, X.; Dong, H.; Yan, W.; Arif, M.; Zhang, Y.; Golsanami, N. Influence of gas hydrate saturation and pore habits on gas relative permeability in gas hydrate-bearing sediments: Theory, experiment and case study. J. Nat. Gas Sci. Eng. 2021, 95, 104171. [Google Scholar] [CrossRef]
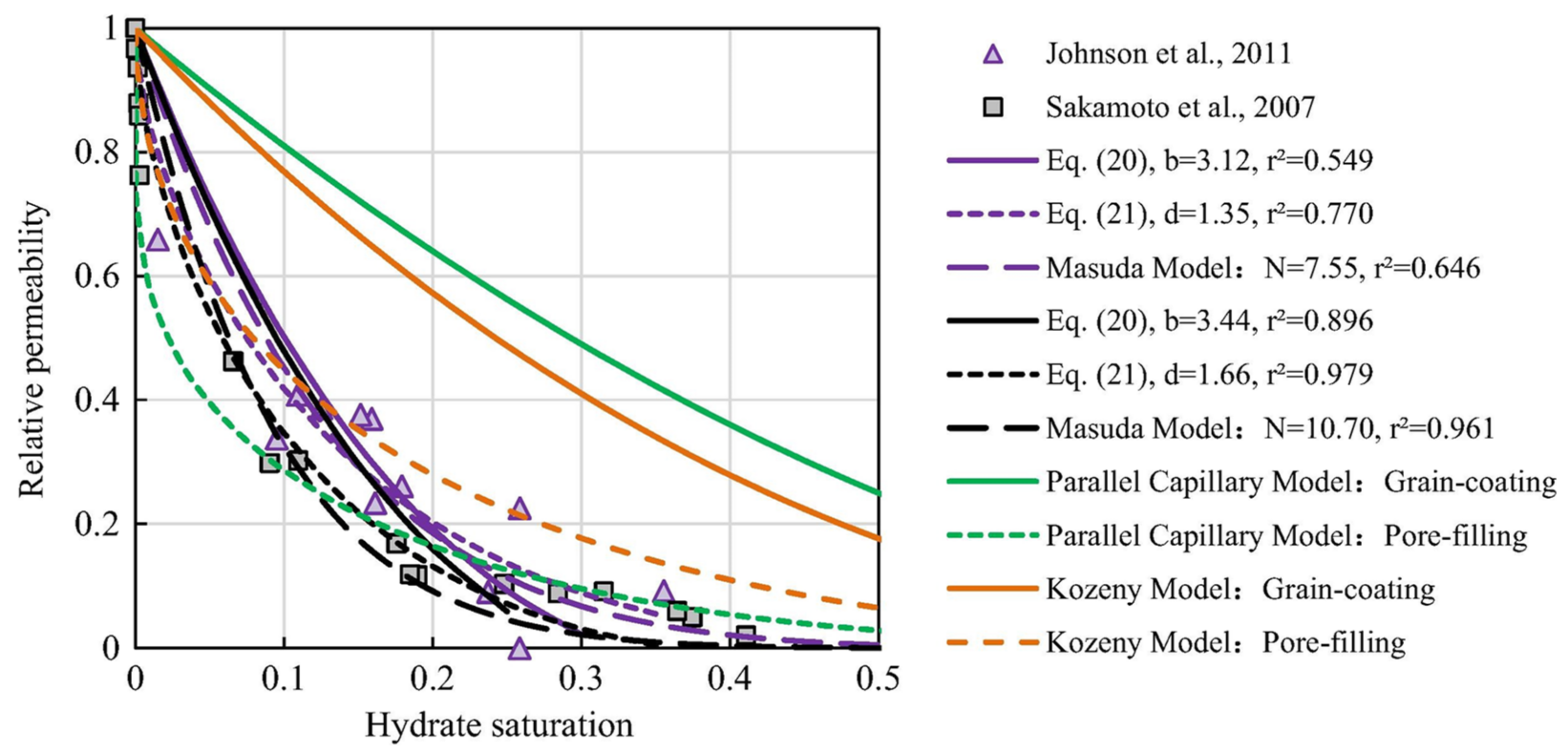
- Delli, M.L.; Grozic, J.L. Prediction performance of permeability models in gas-hydrate-bearing sands. SPE J. 2013, 18, 274–284. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, X.; Zhang, L.; Wang, Z.; Wang, D.; Dai, S. An analytical model for the permeability in hydrate-bearing sediments considering the dynamic evolution of hydrate saturation and pore morphology. Geophys. Res. Lett. 2021, 48, e2021GL093397. [Google Scholar] [CrossRef]
- Lv, J.; Xue, K.; Cheng, Z.; Wang, S.; Liu, Y.; Mu, H. New insights into gas production behavior and seepage-wettability evolution during methane hydrate dissociation in sand matrix by NMR investigation. Fuel 2022, 316, 123344. [Google Scholar] [CrossRef]
- Dai, S.; Kim, J.; Xu, Y.; Waite, W.F.; Jang, J.; Yoneda, J.; Collett, T.S.; Kumar, P. Permeability anisotropy and relative permeability in sediments from the National Gas Hydrate Program Expedition 02, offshore India. Mar. Pet. Geol. 2019, 108, 705–713. [Google Scholar] [CrossRef]
- Lei, G.; Liao, Q.; Zhang, D.; Patil, S. A mechanistic model for permeability in deformable gas hydrate-bearing sediments. J. Nat. Gas Sci. Eng. 2020, 83, 103554. [Google Scholar] [CrossRef]
- Lei, X.; Yao, Y.; Luo, W.; Wen, Z. Permeability change in hydrate bearing sediments as a function of hydrate saturation: A theoretical and experimental study. J. Pet. Sci. Eng. 2022, 208, 109449. [Google Scholar] [CrossRef]
- Gray, I. Reservoir engineering in coal seams: Part 1-The physical process of gas storage and movement in coal seams. SPE Reserv. Eng. 1987, 2, 28–34. [Google Scholar] [CrossRef]
- Kenyon, W. Nuclear magnetic resonance as a petrophysical measurement. Nucl. Geophys. 1992, 6, 153–171. [Google Scholar]
- Scheidegger, A.E. The physics of flow through porous media. In The Physics of Flow through Porous Media, 3rd ed.; University of Toronto Press: Toronto, ON, Canada, 2020. [Google Scholar]
- Röding, M.; Ma, Z.; Torquato, S. Predicting permeability via statistical learning on higher-order microstructural information. Sci. Rep. 2020, 10, 15239. [Google Scholar] [CrossRef] [PubMed]
- Hearst, J.R.; Nelson, P.H. Well Logging for Physical Properties; John Wiley & Sons, Ltd.: New York, NY, USA, 1985. [Google Scholar]
- Hearst, J.; Nelson, P.; Paillet, F. Well Logging for Physical Properties; McGraw-Hill, Ltd.: New York, NY, USA, 2000; Volume Chapter 15. [Google Scholar]
- Spangenberg, E. Modeling of the influence of gas hydrate content on the electrical properties of porous sediments. J. Geophys. Res. Solid Earth 2001, 106, 6535–6548. [Google Scholar] [CrossRef]
- Ruan, X.; Li, X.-S.; Xu, C.-G. A review of numerical research on gas production from natural gas hydrates in China. J. Nat. Gas Sci. Eng. 2021, 85, 103713. [Google Scholar] [CrossRef]
- Minagawa, H.; Ohmura, R.; Kamata, Y.; Ebinuma, T.; Narita, H.; Masuda, Y. Water permeability measurements of gas hydrate-bearing sediments. In Proceedings of the 5th International Conference on Gas Hydrates, Trondheim, Norway, 12–16 June 2005. [Google Scholar]
- Kumar, A.; Maini, B.; Bishnoi, P.; Clarke, M.; Zatsepina, O.; Srinivasan, S. Experimental determination of permeability in the presence of hydrates and its effect on the dissociation characteristics of gas hydrates in porous media. J. Pet. Sci. Eng. 2010, 70, 114–122. [Google Scholar] [CrossRef]
- Konno, Y.; Oyama, H.; Nagao, J.; Masuda, Y.; Kurihara, M. Numerical analysis of the dissociation experiment of naturally occurring gas hydrate in sediment cores obtained at the Eastern Nankai Trough, Japan. Energy Fuels 2010, 24, 6353–6358. [Google Scholar] [CrossRef]
- Konno, Y.; Jin, Y.; Uchiumi, T.; Nagao, J. Multiple-pressure-tapped core holder combined with X-ray computed tomography scanning for gas–water permeability measurements of methane-hydrate-bearing sediments. Rev. Sci. Instrum. 2013, 84, 064501. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Parker, J.; Lenhard, R.; Kuppusamy, T. A parametric model for constitutive properties governing multiphase flow in porous media. Water Resour. Res. 1987, 23, 618–624. [Google Scholar] [CrossRef]
- Phirani, J.; Pitchumani, R.; Mohanty, K.K. Transport Properties of Hydrate Bearing Formations from Pore-Scale Modeling. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 4–7 October 2009; OnePetro: Richardson, TX, USA, 2009. [Google Scholar]
- Helba, A.; Sahimi, M.; Scriven, L.; Davis, H. Percolation theory of two-phase relative permeability. SPE Reserv. Eng. 1992, 7, 123–132. [Google Scholar]
- Johnson, A.; Patil, S.; Dandekar, A. Experimental investigation of gas-water relative permeability for gas-hydrate-bearing sediments from the Mount Elbert Gas Hydrate Stratigraphic Test Well, Alaska North Slope. Mar. Pet. Geol. 2011, 28, 419–426. [Google Scholar] [CrossRef]
- Kleinberg, R.; Flaum, C.; Collett, T. Magnetic resonance log of JAPEX/JNOC/GSC et al. Mallik 5L-38 gas hydrate production research well: Gas hydrate saturation, growth habit, and relative permeability. Bull.-Geol. Surv. Can. 2005, 585, 114. [Google Scholar]
- Liang, H.; Song, Y.; Liu, Y.; Yang, M.; Huang, X. Study of the permeability characteristics of porous media with methane hydrate by pore network model. J. Nat. Gas Chem. 2010, 19, 255–260. [Google Scholar] [CrossRef]
- Kleinberg, R.; Griffin, D. NMR measurements of permafrost: Unfrozen water assay, pore-scale distribution of ice, and hydraulic permeability of sediments. Cold Reg. Sci. Technol. 2005, 42, 63–77. [Google Scholar] [CrossRef]
- Sakamoto, Y.; Komai, T.; Kawamura, T.; Minagawa, H.; Tenma, N.; Yamaguchi, T. Laboratory-scale experiment of methane hydrate dissociation by hot-water injection and numerical analysis for permeability estimation in reservoir: Part 1-Numerical study for estimation of permeability in methane hydrate reservoir. Int. J. Offshore Polar Eng. 2007, 17, ISOPE-07-17-1-047. [Google Scholar]
- Lee, M. Models for Gas Hydrate-Bearing Sediments Inferred from Hydraulic Permeability and Elastic Velocitie; Scientific Investigations Report 2008-5219; US Geological Survey: Reston, VA, USA, 2008; 14p.
- Liang, H.; Song, Y.; Chen, Y.; Liu, Y. The measurement of permeability of porous media with methane hydrate. Pet. Sci. Technol. 2011, 29, 79–87. [Google Scholar] [CrossRef]
- Minagawa, H.; Egawa, K.; Sakamoto, Y.; Komai, T.; Tenma, N.; Narita, H. Characterization of Hydraulic Permeability of Methane-Hydrate-Bearing Sediment Estimated by T2-Distribution of Proton NMR. In Proceedings of the Twenty-Second International Offshore and Polar Engineering Conference, Rhodes, Greece, 17–22 June 2012; OnePetro: Richardson, TX, USA, 2012. [Google Scholar]
- Li, C.-H.; Zhao, Q.; Xu, H.-J.; Feng, K.; Liu, X.-W. Relation between relative permeability and hydrate saturation in Shenhu area, South China Sea. Appl. Geophys. 2014, 11, 207–214. [Google Scholar] [CrossRef]
- Wang, J.-Q.; Zhao, J.-F.; Yang, M.-J.; Li, Y.-H.; Liu, W.-G.; Song, Y.-C. Permeability of laboratory-formed porous media containing methane hydrate: Observations using X-ray computed tomography and simulations with pore network models. Fuel 2015, 145, 170–179. [Google Scholar] [CrossRef]
- Sakamoto, Y.; Komai, T.; Kawabe, Y.; Tenma, N.; Yamaguchi, T. Formation and Dissociation Behavior of Methane Hydrate in Porous Media. J. MMIJ 2004, 120, 85–90. [Google Scholar] [CrossRef]
- Shen, P.; Li, G.; Li, B.; Li, X. Coupling effect of porosity and hydrate saturation on the permeability of methane hydrate-bearing sediments. Fuel 2020, 269, 117425. [Google Scholar] [CrossRef]
- Shen, P.; Li, X.; Li, Z.; Li, G. Permeability determination of hydrate sediments and a new reduction model considering hydrate growth habit. Fuel 2020, 279, 118297. [Google Scholar] [CrossRef]
- Clarke, M.; Bishnoi, P.R. Determination of the activation energy and intrinsic rate constant of methane gas hydrate decomposition. Can. J. Chem. Eng. 2001, 79, 143–147. [Google Scholar] [CrossRef]
- Kou, X.; Li, X.-S.; Wang, Y.; Wan, K.; Chen, Z.-Y. Pore-scale analysis of relations between seepage characteristics and gas hydrate growth habit in porous sediments. Energy 2021, 218, 119503. [Google Scholar] [CrossRef]
- Kleinberg, R.L. 9. Nuclear magnetic resonance. Exp. Methods Phys. Sci. 1999, 35, 337–385. [Google Scholar]
- Kvamme, B.; Graue, A.; Aspenes, E.; Kuznetsova, T.; Gránásy, L.; Tóth, G.; Pusztai, T.; Tegze, G. Towards understanding the kinetics of hydrate formation: Phase field theory of hydrate nucleation and magnetic resonance imaging. Phys. Chem. Chem. Phys. 2004, 6, 2327–2334. [Google Scholar] [CrossRef]
- Ge, X.; Liu, J.; Fan, Y.; Xing, D.; Deng, S.; Cai, J. Laboratory investigation into the formation and dissociation process of gas hydrate by low-field NMR technique. J. Geophys. Res. Solid Earth 2018, 123, 3339–3346. [Google Scholar] [CrossRef]
- Minagawa, H.; Egawa, K.; Sakamoto, Y.; Komai, T.; Tenma, N.; Narita, H. Characterization of hydraulic permeability and pore-size distribution of methane hydrate-bearing sediment using proton nuclear magnetic resonance measurement. Int. J. Offshore Polar Eng. 2012, 22, ISOPE-12-22-4-306. [Google Scholar]
- Zhang, Y.; Liu, L.; Wang, D.; Chen, P.; Zhang, Z.; Meng, Q.; Liu, C. Application of low-field nuclear magnetic resonance (LFNMR) in characterizing the dissociation of gas hydrate in a porous media. Energy Fuels 2021, 35, 2174–2182. [Google Scholar] [CrossRef]
- Liu, L.; Dai, S.; Ning, F.; Cai, J.; Liu, C.; Wu, N. Fractal characteristics of unsaturated sands—Implications to relative permeability in hydrate-bearing sediments. J. Nat. Gas Sci. Eng. 2019, 66, 11–17. [Google Scholar] [CrossRef]
- Ning, F.; Li, C.; Cai, J.; Zhang, Z.; Wang, D.; Liu, Z.; Sun, J. Study on the relative permeability of hydrate-bearing sediments by a fractal parallel capillary model. In Proceedings of the 9th International Conference on Gas Hydrates, Denver, CO, USA, 25–30 June 2017. [Google Scholar]
- Yousif, M.; Abass, H.; Selim, M.; Sloan, E. Experimental and theoretical investigation of methane-gas-hydrate dissociation in porous media. SPE Reserv. Eng. 1991, 6, 69–76. [Google Scholar]
- Ordonez, C.; Grozic, J.; Chen, W. Permeability of Ottawa sand specimens containing R-11 gas hydrates. In Proceedings of the 62nd Canadian Geotechnical Conference, Halifax, NS, Canada, 21–23 September 2009; ETDEWB. BiTech: Richmond, BC, Canada, 2009. [Google Scholar]
- Kneafsey, T.J.; Seol, Y.; Gupta, A.; Tomutsa, L. Permeability of laboratory-formed methane-hydrate-bearing sand: Measurements and observations using X-ray computed tomography. SPE J. 2011, 16, 1678–1694. [Google Scholar] [CrossRef]
- Konno, Y.; Yoneda, J.; Egawa, K.; Ito, T.; Jin, Y.; Kida, M.; Suzuki, K.; Fujii, T.; Nagao, J. Permeability of sediment cores from methane hydrate deposit in the Eastern Nankai Trough. Mar. Pet. Geol. 2015, 66, 487–495. [Google Scholar] [CrossRef]
- Chen, X.; Espinoza, D.N. Ostwald ripening changes the pore habit and spatial variability of clathrate hydrate. Fuel 2018, 214, 614–622. [Google Scholar] [CrossRef]
- Lei, L.; Seol, Y.; Choi, J.-H.; Kneafsey, T.J. Pore habit of methane hydrate and its evolution in sediment matrix–Laboratory visualization with phase-contrast micro-CT. Mar. Pet. Geol. 2019, 104, 451–467. [Google Scholar] [CrossRef]
- Tohidi, B.; Anderson, R.; Clennell, M.B.; Burgass, R.W.; Biderkab, A.B. Visual observation of gas-hydrate formation and dissociation in synthetic porous media by means of glass micromodels. Geology 2001, 29, 867–870. [Google Scholar] [CrossRef]
- O’Connell, M.; Belanger, B.; Haaland, P. Calibration and assay development using the four-parameter logistic model. Chemom. Intell. Lab. Syst. 1993, 20, 97–114. [Google Scholar] [CrossRef]
- Semenova, V.; Schiffer, J.; Steward-Clark, E.; Soroka, S.; Schmidt, D.; Brawner, M.; Lyde, F.; Thompson, R.; Brown, N.; Foster, L.; et al. Validation and long term performance characteristics of a quantitative enzyme linked immunosorbent assay (ELISA) for human anti-PA IgG. J. Immunol. Methods 2012, 376, 97–107. [Google Scholar] [CrossRef]
- Singh, H.; Myshakin, E.M.; Seol, Y. A nonempirical relative permeability model for hydrate-bearing sediments. SPE J. 2019, 24, 547–562. [Google Scholar] [CrossRef]
- Cao, S.C.; Jang, J.; Jung, J.; Waite, W.F.; Collett, T.S.; Kumar, P. 2D micromodel study of clogging behavior of fine-grained particles associated with gas hydrate production in NGHP-02 gas hydrate reservoir sediments. Mar. Pet. Geol. 2019, 108, 714–730. [Google Scholar] [CrossRef]
- Weber, D.; Mitchell, J.; McGregor, J.; Gladden, L.F. Comparing strengths of surface interactions for reactants and solvents in porous catalysts using two-dimensional NMR relaxation correlations. J. Phys. Chem. C 2009, 113, 6610–6615. [Google Scholar] [CrossRef]
- Lv, J.; Xue, K.; Zhang, Z.; Cheng, Z.; Liu, Y.; Mu, H. Pore-scale investigation of hydrate morphology evolution and seepage characteristics in hydrate bearing microfluidic chip. J. Nat. Gas Sci. Eng. 2021, 88, 103881. [Google Scholar] [CrossRef]
- Lv, J.; Cheng, Z.; Xue, K.; Liu, Y.; Mu, H. Pore-scale morphology and wettability characteristics of xenon hydrate in sand matrix-Laboratory visualization with micro-CT. Mar. Pet. Geol. 2020, 120, 104525. [Google Scholar] [CrossRef]
- Jańczuk, B.; Chibowski, E.; Białopiotrowicz, T. Interpretation of the contact angle in quartz/organic liquid film-water system. J. Colloid Interface Sci. 1984, 102, 533–538. [Google Scholar] [CrossRef]
- Mahabadi, N.; Dai, S.; Seol, Y.; Sup Yun, T.; Jang, J. The water retention curve and relative permeability for gas production from hydrate-bearing sediments: Pore-network model simulation. Geochem. Geophys. Geosyst. 2016, 17, 3099–3110. [Google Scholar] [CrossRef]
- Gaidukova, O.; Misyura, S.; Strizhak, P. Key Areas of Gas Hydrates Study. Energies 2022, 15, 1799. [Google Scholar] [CrossRef]
- Song, Y.; Huang, X.; Liu, Y.; Yang, M. Experimental study of permeability of porous medium containing methane hydrate. J. Therm. Sci. Technol. 2010, 9, 51–57. [Google Scholar]
- Zhai, C.; Sun, K.; Xin, L.; Tian, S. Experimental study of permeability of sand soil bearing sediments containing methane hydrates. J. Wuhan Univ. Technol. 2015, 37, 78–82. [Google Scholar]
- Wu, D.; Li, G.; Li, X.; Lv, X. Experimental investigation of permeability characteristics under different hydrate saturation. Chem. Ind. Eng. Prog. 2017, 36, 2916–2923. [Google Scholar]
- Chen, B.; Yang, M.; Zheng, J.-n.; Wang, D.; Song, Y. Measurement of water phase permeability in the methane hydrate dissociation process using a new method. Int. J. Heat Mass Transf. 2018, 118, 1316–1324. [Google Scholar] [CrossRef]
- Santamarina, J.C.; Dai, S.; Terzariol, M.; Jang, J.; Waite, W.F.; Winters, W.J.; Nagao, J.; Yoneda, J.; Konno, Y.; Fujii, T.; et al. Hydro-bio-geomechanical properties of hydrate-bearing sediments from Nankai Trough. Mar. Pet. Geol. 2015, 66, 434–450. [Google Scholar] [CrossRef]
- Yoneda, J.; Masui, A.; Konno, Y.; Jin, Y.; Egawa, K.; Kida, M.; Ito, T.; Nagao, J.; Tenma, N. Mechanical properties of hydrate-bearing turbidite reservoir in the first gas production test site of the Eastern Nankai Trough. Mar. Pet. Geol. 2015, 66, 471–486. [Google Scholar] [CrossRef]
- Priest, J.A.; Druce, M.; Roberts, J.; Schultheiss, P.; Nakatsuka, Y.; Suzuki, K. PCATS Triaxial: A new geotechnical apparatus for characterizing pressure cores from the Nankai Trough, Japan. Mar. Pet. Geol. 2015, 66, 460–470. [Google Scholar] [CrossRef]
- Yoneda, J.; Masui, A.; Konno, Y.; Jin, Y.; Kida, M.; Katagiri, J.; Nagao, J.; Tenma, N. Pressure-core-based reservoir characterization for geomechanics: Insights from gas hydrate drilling during 2012–2013 at the eastern Nankai Trough. Mar. Pet. Geol. 2017, 86, 1–16. [Google Scholar] [CrossRef]
- Yoneda, J.; Oshima, M.; Kida, M.; Kato, A.; Konno, Y.; Jin, Y.; Jang, J.; Waite, W.F.; Kumar, P.; Tenma, N. Permeability variation and anisotropy of gas hydrate-bearing pressure-core sediments recovered from the Krishna–Godavari Basin, offshore India. Mar. Pet. Geol. 2019, 108, 524–536. [Google Scholar] [CrossRef]
- Collett, T.S.; Lee, M.W.; Zyrianova, M.V.; Mrozewski, S.A.; Guerin, G.; Cook, A.E.; Goldberg, D.S. Gulf of Mexico Gas Hydrate Joint Industry Project Leg II log-ging-while-drilling data acquisition and analysis. Mar. Pet. Geol. 2012, 34, 41–61. [Google Scholar] [CrossRef]
- Muraoka, M.; Yamamoto, Y.; Tenma, N. Simultaneous measurement of water permeability and methane hydrate pore habit using a two-dimensional glass micromodel. J. Nat. Gas Sci. Eng. 2020, 77, 103279. [Google Scholar] [CrossRef]
- Hu, C.; Jia, Y.; Duan, Z. The influence of inhomogeneous hydrate formation on permeability anisotropy of porous media. Geo-Mar. Lett. 2021, 41, 10. [Google Scholar] [CrossRef]
- Waite, W.F.; Santamarina, J.C.; Cortes, D.D.; Dugan, B.; Espinoza, D.; Germaine, J.; Jang, J.; Jung, J.; Kneafsey, T.J.; Shin, H. Physical properties of hydrate-bearing sediments. Rev Geophys 2009, 47, 4. [Google Scholar] [CrossRef]
- Lei, L.; Santamarina, J. Laboratory strategies for hydrate formation in fine-grained sediments. J. Geophys. Res. Solid Earth 2018, 123, 2583–2596. [Google Scholar] [CrossRef]
- Moridis, G.; Collett, T.S.; Pooladi-Darvish, M.; Hancock, S.; Santamarina, C.; Boswell, R.; Kneafsey, T.; Rutqvist, J.; Kowalsky, M.B.; Reagan, M.T. Challenges, uncertainties, and issues facing gas production from gas-hydrate deposits. SPE Reserv. Eval. Eng. 2011, 14, 76–112. [Google Scholar] [CrossRef]
- Boswell, R.; Collett, T. The gas hydrates resource pyramid. Nat. Gas Oil 2006, 304, 285–4541. [Google Scholar]
- Wu, Z.; Li, Y.; Sun, X.; Wu, P.; Zheng, J. Experimental study on the effect of methane hydrate decomposition on gas phase permeability of clayey sediments. Appl. Energy 2018, 230, 1304–1310. [Google Scholar] [CrossRef]
- Wu, Z.; Yang, S.; Liu, W.; Xu, H.; Li, G.; Li, Y. Experimental Study on the Difference of Fluid Flow between Methane Hydrate-Bearing Sand and Clay Sediments. Energy Fuels 2022, 36, 2739–2750. [Google Scholar] [CrossRef]
- Wu, Z.; Yang, S.; Liu, W.; Li, Y. Permeability analysis of gas hydrate-bearing sand/clay mixed sediments using effective stress laws. J. Nat. Gas Sci. Eng. 2022, 97, 104376. [Google Scholar] [CrossRef]
- Dai, S.; Santamarina, J.C.; Waite, W.F.; Kneafsey, T.J. Hydrate morphology: Physical properties of sands with patchy hydrate saturation. J. Geophys. Res. Solid Earth 2012, 117, B11. [Google Scholar] [CrossRef]
- Bian, H.; Qin, X.; Luo, W.; Ma, C.; Zhu, J.; Lu, C.; Zhou, Y. Evolution of hydrate habit and formation properties evolution during hydrate phase transition in fractured-porous medium. Fuel 2022, 324, 124436. [Google Scholar] [CrossRef]
- Jia, B.; Xian, C.-G. Permeability measurement of the fracture-matrix system with 3D embedded discrete fracture model. Pet. Sci. 2022. [Google Scholar] [CrossRef]









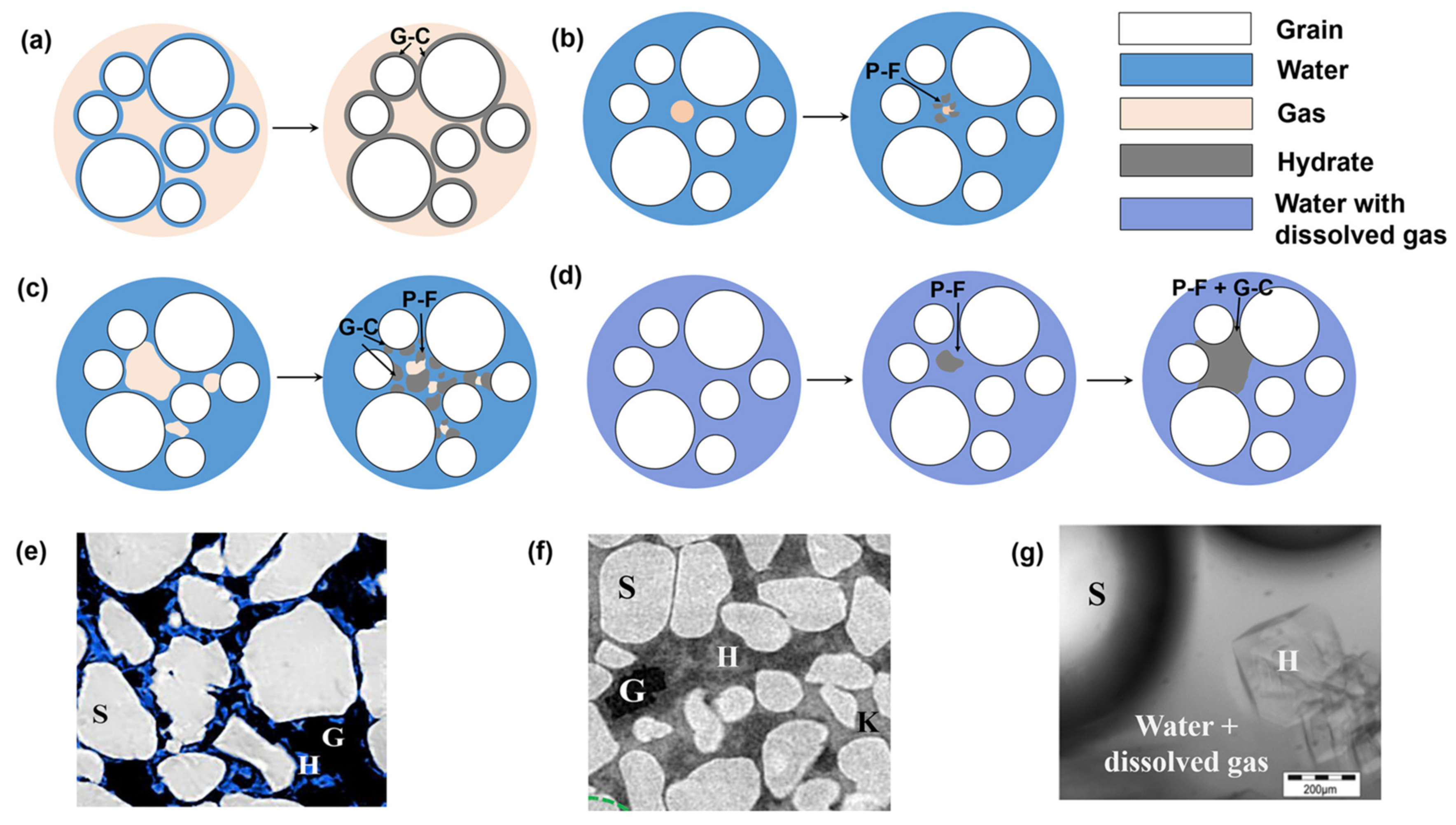




| Model | Research Methods | Advantages and Limitations |
|---|---|---|
| SDR model [23,74] | Derived based on Kenyon relationship | Simple form and generally known; but neglecting the effect of hydrate-related surface evolution on mineralogy constant C |
| PCTM [23] | Derived based on capillary tube assumption | Simple form and generally known; but a little idealistic about assumption on pore structure |
| KGM [23] | Derived based on the KC equation | Simple form and generally known; but containing empirical parameters n |
| Model | Parameters | Physical Meaning | Influencing Factors |
|---|---|---|---|
| SDR model [23,74] | T2LM | ✓ | Hydrate saturation |
| PCTM [23] | \ | \ | Hydrate saturation, pore habits, morphology, and distribution; the pore structure of sediment |
| KGM [23] | n | × | Hydrate saturation, pore habits, morphology, and distribution; the pore structure of sediment |
| Model | Research Methods | Advantages and Limitations |
|---|---|---|
| Tokyo model [42,43] | Generalized form based on PCTM | Simplest form and widely used but containing empirical parameter N |
| LBNL model [45,48,49] | Derived based on the vG model for unsaturated soils | Simple form and generally known; but containing empirical parameters m and irreducible water saturation Swr |
| CMG built-in model [46] | Derived based on KC equation | Simple form and generally known; but neglecting the effect of hydrate pore habits and pore structure and containing empirical parameter ε |
| Civan model [47] | Derived based on KC equation | Simple form and generally known; but neglecting the effect of hydrate pore habits and pore structure and containing empirical parameter β |
| Sakamoto et al. [50] | A piecewise function based on the Tokyo model | Considering two hydrate formation mechanisms; but containing empirical parameters N1 and N2 |
| Model | Parameters | Physical Meaning | Influencing Factors |
|---|---|---|---|
| Tokyo model [42,43] | N | × | Hydrate saturation and the assumed tube-wall coating hydrate; the pore structure of sediment |
| LBNL model [45,48,49] | m Sw Swr | × ✓ ✓ | Water and irreducible water saturation |
| CMG built-in model [46] | ε ϕ0 | × ✓ | Hydrate saturation; intrinsic porosity of sediment |
| Civan model [47] | β ϕ0 | × ✓ | Hydrate saturation; intrinsic porosity of sediment |
| Sakamoto et al. [50] | N1,N2 Sh1,max | × ✓ | Hydrate saturation and growth patterns; irreducible water and free water |
| Model | Research Methods | Advantages and Limitations |
|---|---|---|
| Dai and Seol [40] | Modified KC model based on PNM simulation | Simple form based on simulation results; but may not apply to all the actual sediments and containing empirical parameter B |
| Kang et al. [53] | Modified KC model based on fitting by LBM simulation | A polynomial-based model with high prediction accuracy but overfitting may arise with the increased value of the polynomial order |
| Katagiri et al. [54] | Derived based on the KC permeability model | Simple form based on geometric analyses and strict mathematical derivation but containing empirical parameter n |
| Li et al. [26,55] | Derived based on the KC permeability model | Piecewise function based on experiment results strict mathematical derivation but complicated form and based on the assumption of sediment particle and hydrate |
| Shen et al. [56,100,101] | Derived based on the KC permeability model | Analytical formula based on experimental results and strict mathematical derivation but complicated form with limited prediction range and based on the assumption of sediment particle and hydrate |
| Xiao et al. [57] | Derived based on the KC permeability model | Analytical formula based on experimental results and strict mathematical derivation but complicated form and based on the assumption of sediment particle and hydrate |
| Kou et al. [103] | Derived based on the KC permeability model and experimental results | Simple form based on pore structure analysis but aiming at specific experimental conditions and containing empirical parameters n |
| Model | Parameters | Physical Meaning | Influencing Factors |
|---|---|---|---|
| Dai and Seol [40] | B | × | Hydrate saturation and heterogeneity; tortuosity and specific surface |
| Kang et al. [53] | aiShi | × | Hydrate saturation; tortuosity, specific surface, and shape factor |
| Katagiri et al. [54] | e Cp n | ✓ ✓ × | Hydrate saturation and pore habits; 3D sediment particles packing patterns |
| Li et al. [26,55] | r1 L n | ✓ ✓ ✓ | Hydrate saturation, 3D shape, and assumed the pore-filling habit; 3D simple cubic sphere pack, the radius of pore fluid and sediment grain, shape factor |
| Shen et al. [56,100,101] | r2 L n | ✓ ✓ × | Hydrate saturation, 3D shape, and pore habits; 3D packing patterns and radius of sediment particle |
| Xiao et al. [57] | rs rh n | ✓ ✓ × | Hydrate saturation and radius of clustered hydrate particle in pore center; 3D packing patterns and radius of sediment particle |
| Kou et al. [103] | n | × | Hydrate saturation and pore habits; Pore structure and pore connectivity of sediments |
| Model | Research Methods | Advantages and Limitations |
|---|---|---|
| New SDR model [64] | Derived based on Kenyon relationship and NMR experiment data | Simple form and generally known, and considering the effect of hydrate-related interface evolution but needing NMR experiment data |
| Daigle [60] | Derived based on the pore-solid-fractal geometry with the critical path analysis method | Generally known and considering pore system properties but containing parameters that are difficult to simultaneously determine and only be suitable for disseminated hydrate within pores |
| Zhang et al. [61] | Derived based on fractal theory and experimental results | Simple form and containing parameters that quantify the evolution of pore space extracted from experimental results but containing a series of simplifications and empirical parameters, and only be suitable for coarse-grained HBSs |
| Du et al. [62] | Derived based on fractal theory and modified Hagen–Poiseuille equation | A power exponential function of structural parameters of porous media with specific physical meaning but complicated form with parameters that are difficult to determine |
| Chen et al. [65] | Modified Corey model based on fitting by LBM simulation | Simple form and generally known, an exponential function with only one fitting parameter with clear physical meaning |
| Liu et al. [66] | Modified Corey model based on fitting by LBM simulation | A simple and modified functional form effectively enhances the applicability of the simple Corey model but containing the fitting parameter without definite physical meaning and the uncertain functional relation between exponent N and hydrate saturation |
| Hou et al. [63] | Modified permeability-porosity relationship based on LBM simulation and geometrical analysis | Simple form and generally known, and considering the evolution of the control seepage channel with hydrate saturation, and containing fitting parameters related to physical phenomenon but containing empirical fitting parameters without definite physical meaning and may be restricted to two-dimensional porous media |
| Guo et al. [58] | Derived based on Poiseuille’s law and three-dimension hydraulic radius | Simple form and considering the evolution of pore size with hydrate saturation, and containing only one embedded parameter with clear physical meaning, but the accuracy may be slightly lower due to the embedded parameter assumed to be a constant parameter |
| Lei et al. [72] | Derived based on the cubic fracture-permeability model commonly used in coalbed methane reservoir | Considering the novel type assumed pore space characteristics and hydrate pore morphology but piecewise function with complicated form and relatively rough prediction accuracy |
| Delli and Grozic [24,67] | A hybrid model based on the weighted combination of the KG model with two different pore habits in sediment | Generally known and considering hybrid hydrates pore habits but containing empirical parameters and complicated calculations |
| Wang et al. [68] | A pore-morphology-weighted model based on a two-parameter logistic function and grain-coating and pore-filling PCT model | Theoretical and elegant expression with two fitting parameters with clear physical meaning, considering coexisting hydrate pore habits and their evolution with ensued hydrate crystallization but containing complicated calculations |
| Lei et al. [71] | Derived by solving the steady-state Navier–Stokes equations in a fractal capillary tube with hydrate under stress condition | Comprehensively considering the effect of radial stress and coexisting hydrate pore habits on the permeability evolution in HBSs under different hydrate saturations, but complex form with empirical parameters, and neglecting the thickness of retained water film and deformation of hydrates |
| Zhang et al. [20] | Modified KC model based on step-by-step stress loading and water permeability tests and curve fitting method | Considering the combined influence of effective stress and hydrate saturation on hydraulic properties and porosity of fined-grained HBSs but complex form and containing empirical parameters |
| Lv et al. [69] | Modified Tokyo model coupled with wettability term based on NMR measurement | Simple form and considering the influence mechanism of wettability evolution on flow behavior but containing fitting parameters and neglecting coexisting hydrate pore habits |
| Model | Parameters | Physical Meaning | Influencing Factors |
|---|---|---|---|
| New SDR model [64] | ρ2*
T2LM | ✓ ✓ | Hydrate saturation and interface evolution; the effect weight and surface proportion of quarzitic sand phase |
| Daigle [60] | β ϕ0 pc D Sx Sw | ✓ ✓ ✓ ✓ ✓ ✓ | Hydrate saturation, pore disseminated hydrates; pore structure fractal characteristics, and percolation threshold |
| Zhang et al. [61] | DT,0 λmax2* a b | ✓ ✓ × × | Hydrate saturation; pore structure fractal characteristics and maximal pore diameter |
| Du et al. [62] | ϕ0 ϕ Dt,h Dt Df,h Df DE λmax,0 λmin,0 | ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ | Hydrate saturation and coexistence of pore-filling and grain-coating hydrate; pore structure fractal characteristics, maximal pore diameter, and porosity of sediment without and with hydrates |
| Chen et al. [65] | C | ✓ | Hydrate saturation; he degree of crystal coarsening and patch size in a multiphase system |
| Liu et al. [66] | a | × | Hydrate saturation |
| Hou et al. [63] | b d | × × | Hydrate saturation, pore habits, and morphology; the intrinsic porosity of sediment and the size and tortuosity of the control seepage channel |
| Guo et al. [58] | et | ✓ | Hydrate saturation and pore habits; the change in pore volumes of sediment |
| Lei et al. [72] | ϕ0 | ✓ | Hydrate saturation, pore habits, and morphology; the pore structure and intrinsic porosity of sediment |
| Delli and Grozic [24,67] | N M | × × | Hydrate saturation and coexisting pore habits |
| Wang et al. [68] | α β | ✓ ✓ | Hydrate saturation and coexisting pore habits; hydrate formation conditions and sediments types |
| Lei et al. [71] | ν E peffr β | ✓ ✓ ✓ ✓ | Hydrate saturation and single or coexisting pore habits; retained water, effective stress, deformation of grains, and pore structure of sediment |
| Zhang et al. [20] | ϕ0 σe α0 n m | ✓ ✓ ✓ × × | Hydrate saturation; effective stress, porosity, and host sediment types |
| Lv et al. [69] | a NH b | × ✓ × | Hydrate saturation; hydrophilicity of HBSs |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Bu, Z.; Li, H.; Wang, X.; Liu, S. Permeability Models of Hydrate-Bearing Sediments: A Comprehensive Review with Focus on Normalized Permeability. Energies 2022, 15, 4524. https://doi.org/10.3390/en15134524
Xu J, Bu Z, Li H, Wang X, Liu S. Permeability Models of Hydrate-Bearing Sediments: A Comprehensive Review with Focus on Normalized Permeability. Energies. 2022; 15(13):4524. https://doi.org/10.3390/en15134524
Chicago/Turabian StyleXu, Jianchun, Ziwei Bu, Hangyu Li, Xiaopu Wang, and Shuyang Liu. 2022. "Permeability Models of Hydrate-Bearing Sediments: A Comprehensive Review with Focus on Normalized Permeability" Energies 15, no. 13: 4524. https://doi.org/10.3390/en15134524
APA StyleXu, J., Bu, Z., Li, H., Wang, X., & Liu, S. (2022). Permeability Models of Hydrate-Bearing Sediments: A Comprehensive Review with Focus on Normalized Permeability. Energies, 15(13), 4524. https://doi.org/10.3390/en15134524








