Numerical Assessment of a Tension-Leg Platform Wind Turbine in Intermediate Water Using the Smoothed Particle Hydrodynamics Method
Abstract
:1. Introduction
2. The SPH Method
2.1. Fundamentals
2.2. Governing Equations
2.3. Rigid Body Dynamics
2.4. Adopted Boundary Conditions
2.5. Coupling to MoorDyn
3. Numerical Modeling
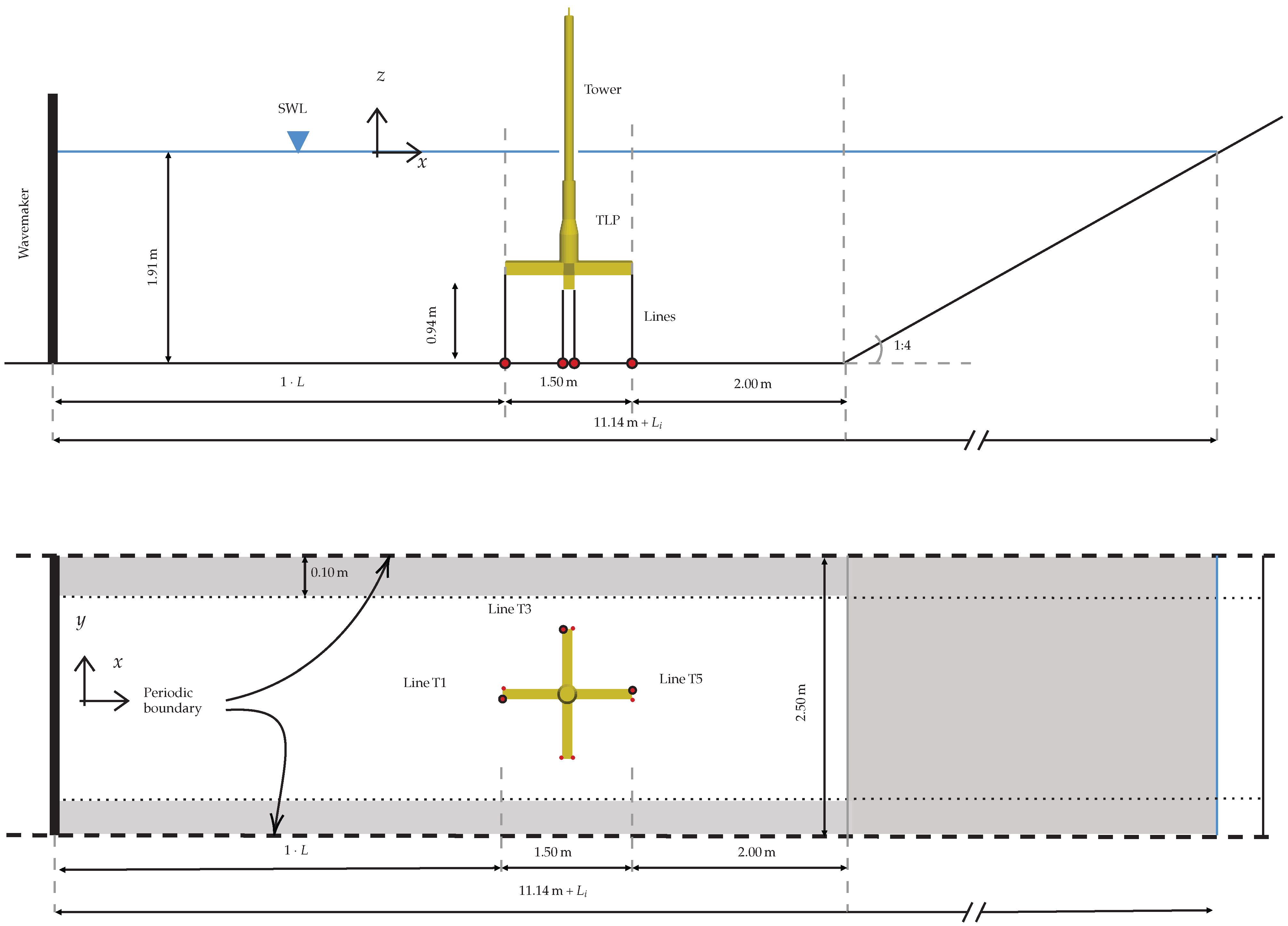
3.1. Experimental Setup
3.2. Numerical Model
3.2.1. Wave Tank Design
3.2.2. Mooring Systems
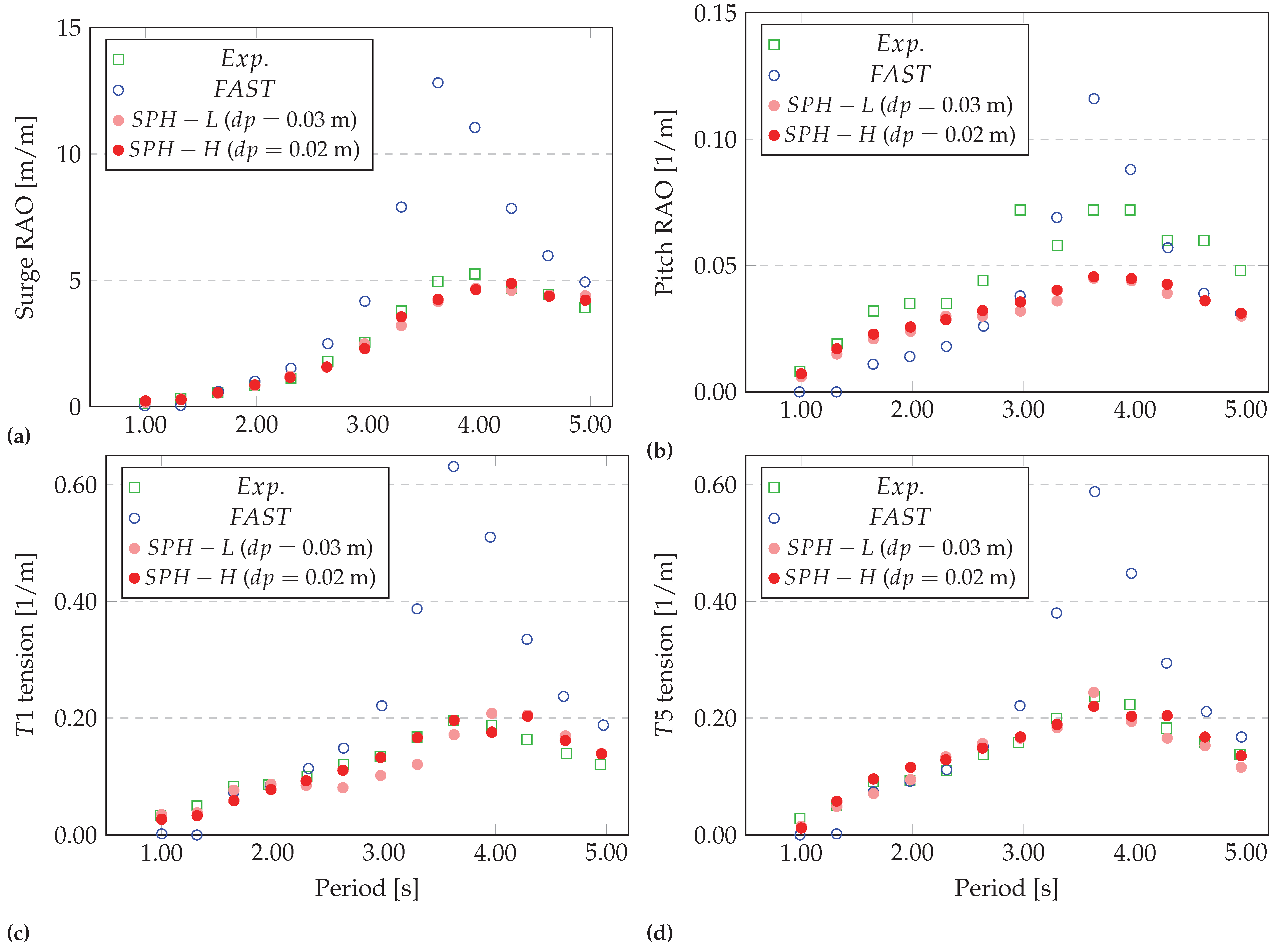
4. Validation
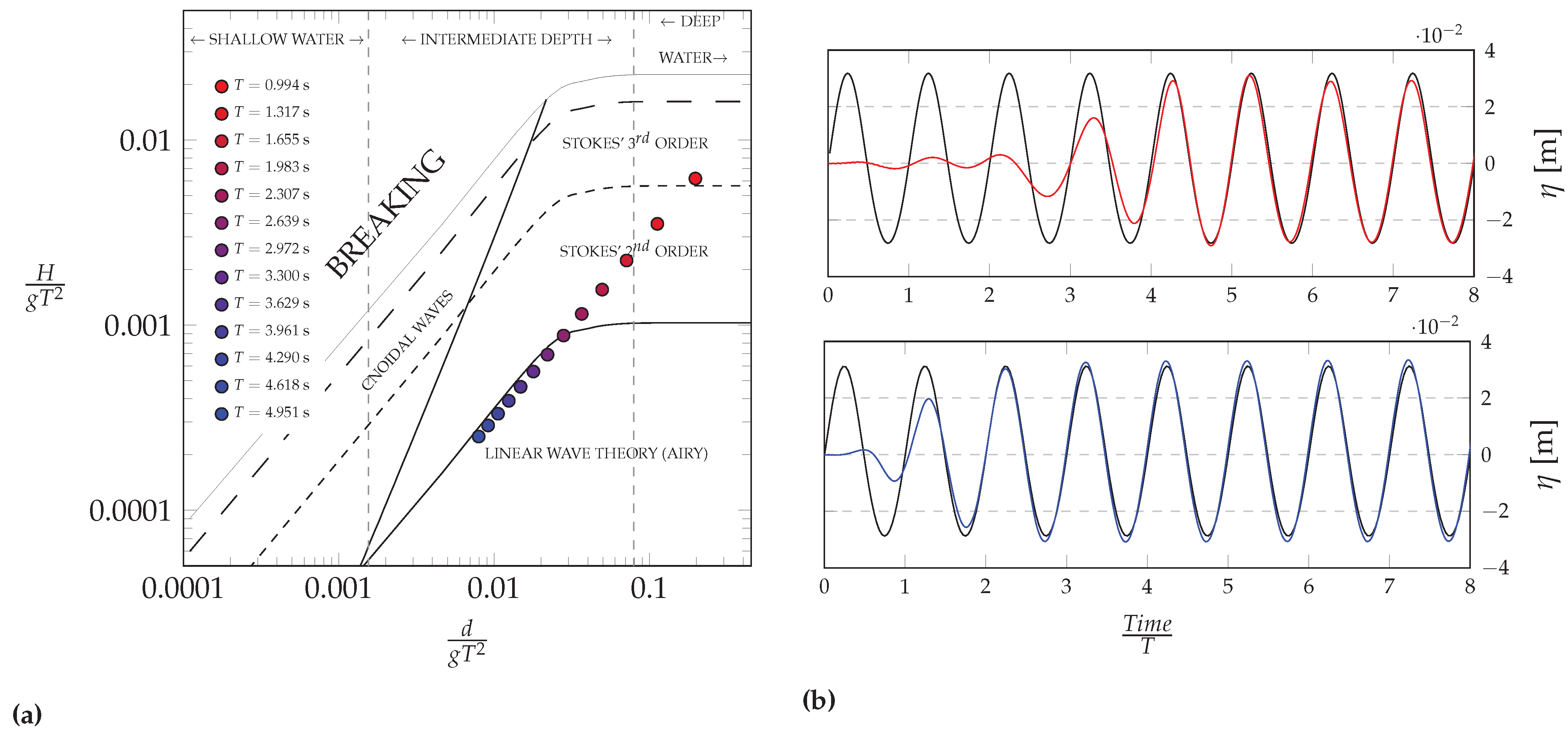
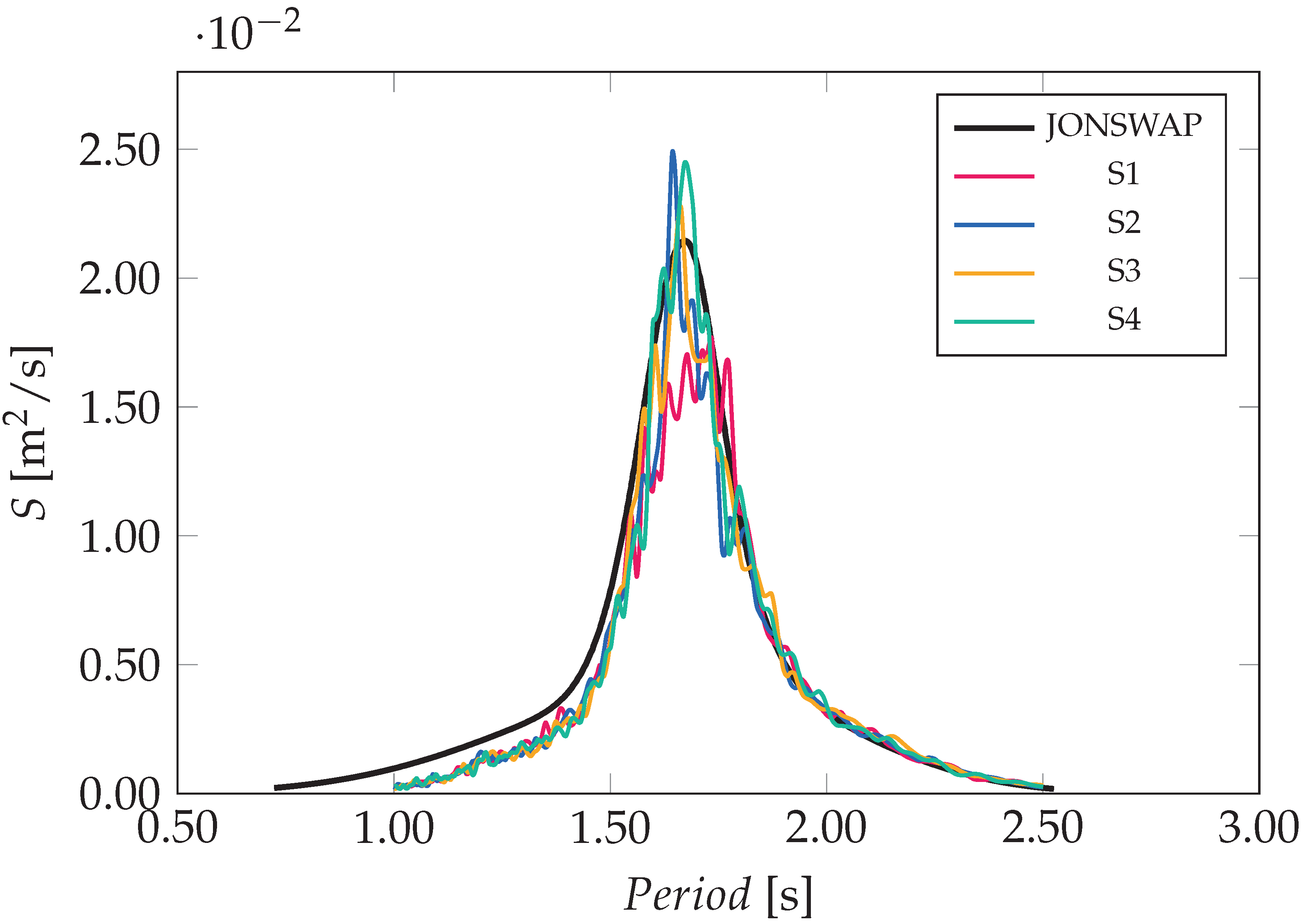
4.1. Wave Generation and Propagation
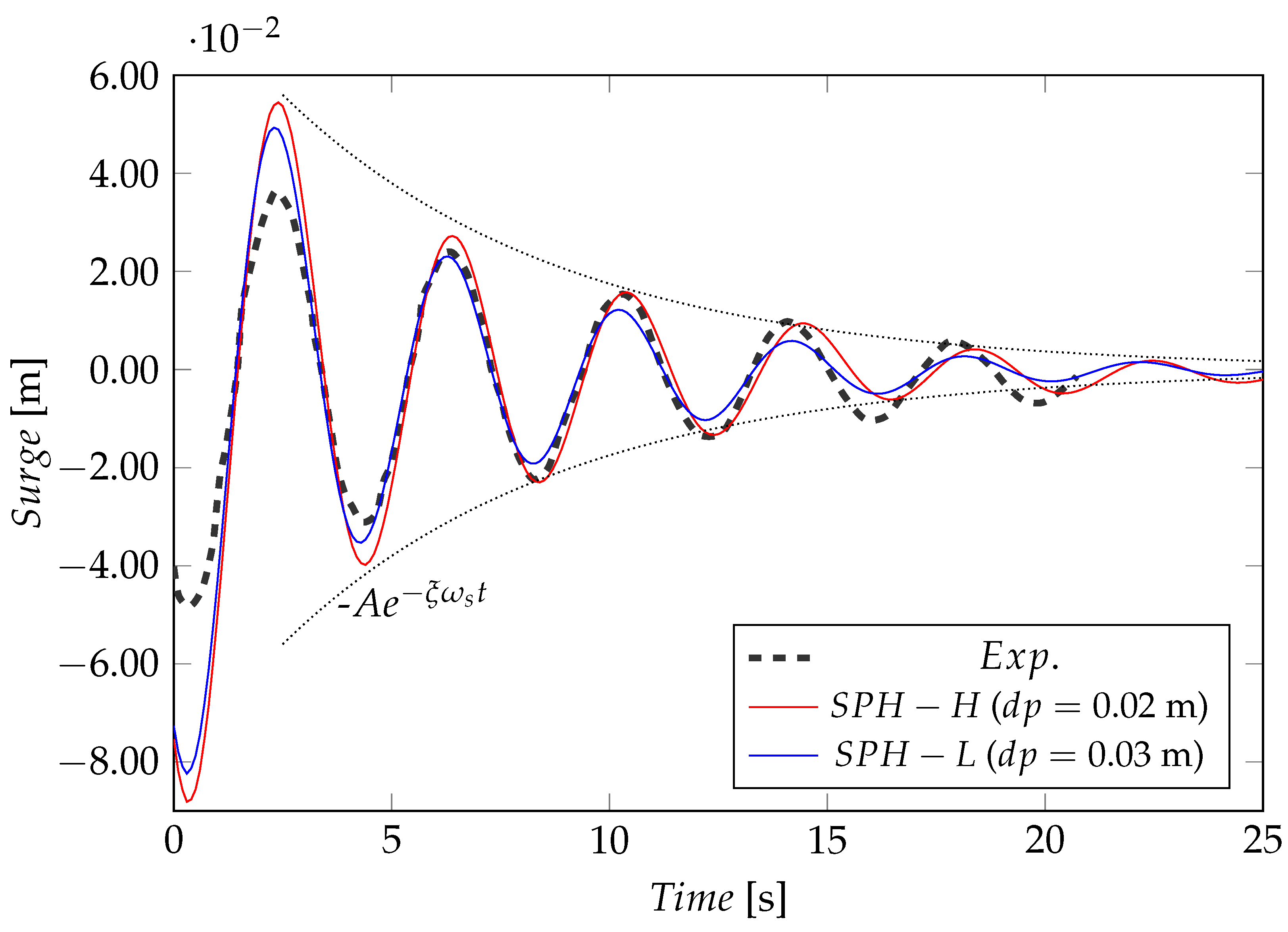
4.2. Surge Decay Test
4.3. Surge and Pitch Motion Spectra
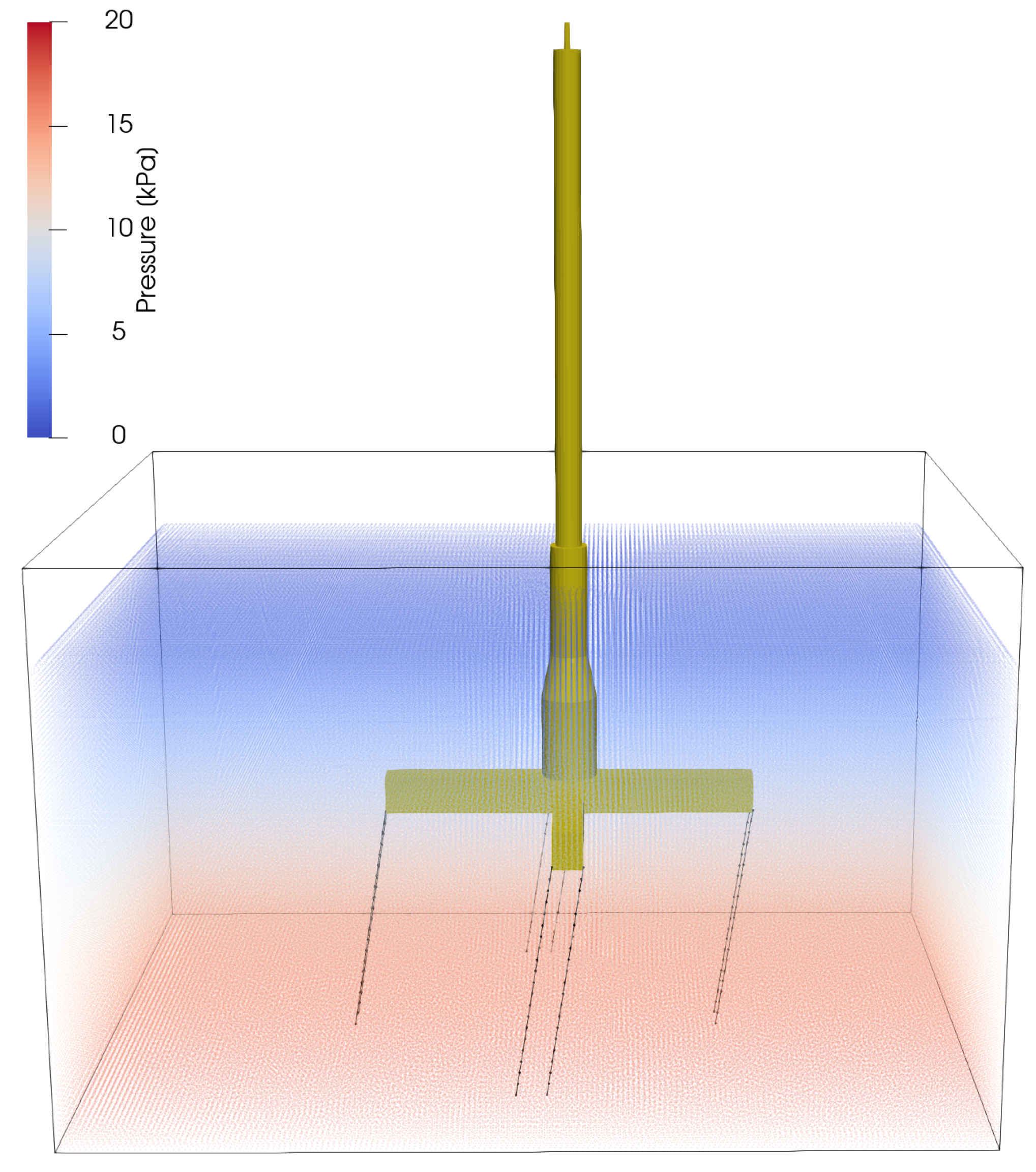
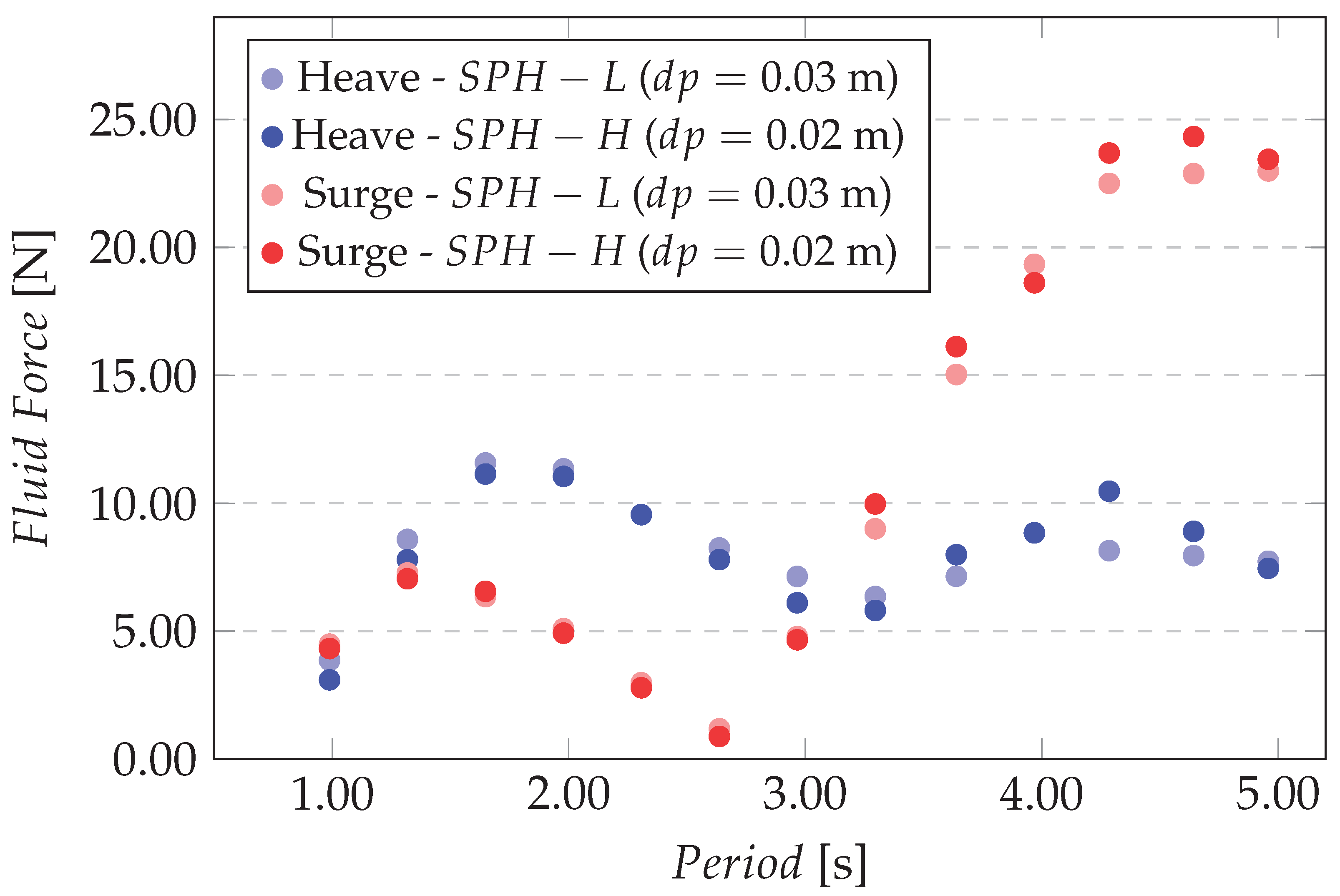
5. Numerical Investigation
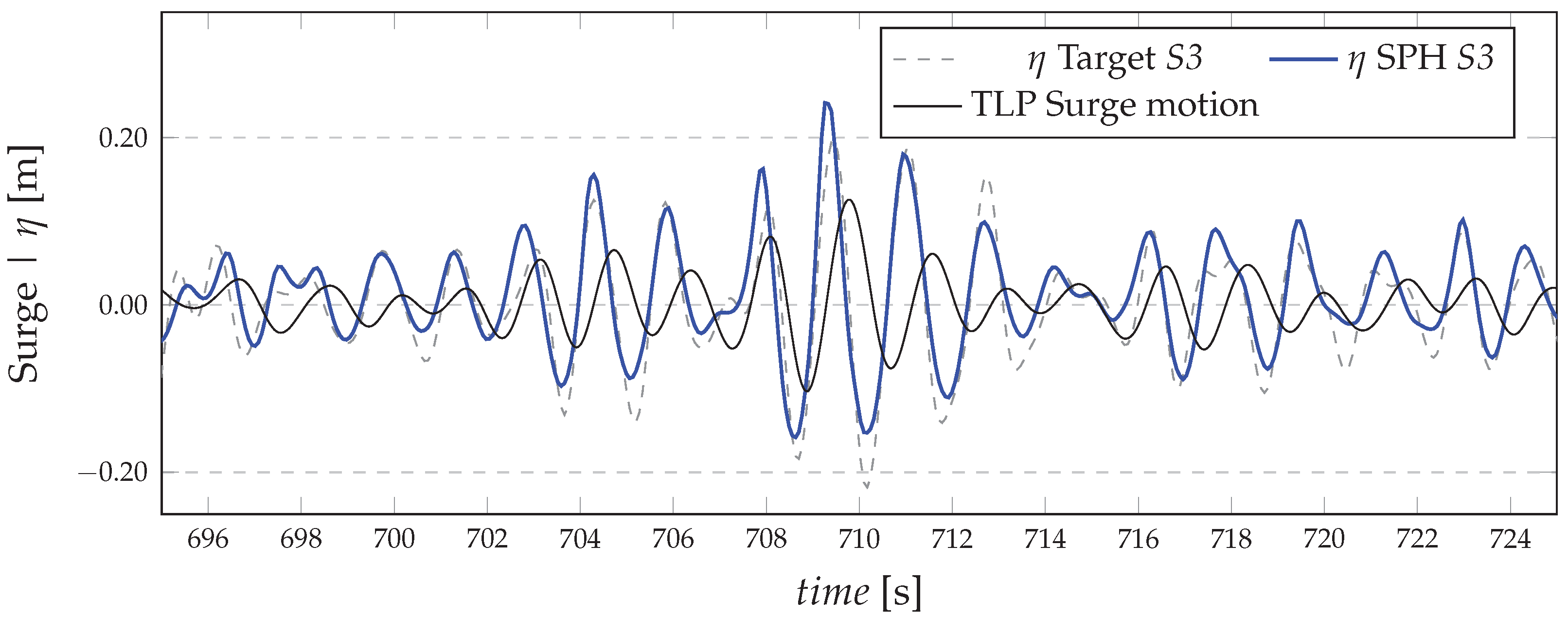
5.1. Irregular Sea States
5.2. Simulations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lange, M.; Cummins, V. Managing stakeholder perception and engagement for marine energy transitions in a decarbonising world. Renew. Sustain. Energy Rev. 2021, 152, 111740. [Google Scholar] [CrossRef]
- Myhr, A.; Bjerkseter, C.; Ågotnes, A.; Nygaard, T.A. Levelised cost of energy for offshore floating wind turbines in a life-cycle perspective. Renew. Energy 2014, 66, 714–728. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Z. Installation of offshore wind turbines: A technical review. Renew. Sustain. Energy Rev. 2021, 139, 110576. [Google Scholar] [CrossRef]
- Asim, T.; Islam, S.Z.; Hemmati, A.; Khalid, M.S.U. A Review of Recent Advancements in Offshore Wind Turbine Technology. Energies 2022, 15, 579. [Google Scholar] [CrossRef]
- Oguz, E.; Clelland, D.; Day, A.H.; Incecik, A.; López, J.A.; Sánchez, G.; Almeria, G.G. Experimental and numerical analysis of a TLP floating offshore wind turbine. Ocean. Eng. 2018, 147, 591–605. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.H.; Yang, R.Y. Study on Array Floating Platform for Wind Energy and Marine Space Optimization. Sustainability 2021, 13, 14014. [Google Scholar] [CrossRef]
- Karimirad, M.; Moan, T. Wave- and Wind-Induced Dynamic Response of a Spar-Type Offshore Wind Turbine. J. Waterw. Port Coastal Ocean. Eng. 2012, 138, 9–20. Available online: https://ascelibrary.org/doi/pdf/10.1061/%28ASCE%29WW.1943-5460.0000087 (accessed on 23 April 2022). [CrossRef] [Green Version]
- Otter, A.; Murphy, J.; Pakrashi, V.; Robertson, A.; Desmond, C. A review of modelling techniques for floating offshore wind turbines. Wind Energy 2022, 25, 831–857. Available online: https://onlinelibrary.wiley.com/doi/pdf/10.1002/we.2701 (accessed on 12 May 2022). [CrossRef]
- Bayati, I.; Jonkman, J.; Robertson, A.; Platt, A. The effects of second-order hydrodynamics on a semisubmersible floating offshore wind turbine. J. Phys. Conf. Ser. 2014, 524, 012094. [Google Scholar] [CrossRef] [Green Version]
- Karimirad, M.; Jiang, Z. 2.08—Mechanical-dynamic loads. In Comprehensive Renewable Energy, 2nd ed.; Letcher, T.M., Ed.; Elsevier: Oxford, UK, 2022; pp. 194–225. [Google Scholar] [CrossRef]
- Zhang, L.; Shi, W.; Karimirad, M.; Michailides, C.; Jiang, Z. Second-order hydrodynamic effects on the response of three semisubmersible floating offshore wind turbines. Ocean. Eng. 2020, 207, 107371. [Google Scholar] [CrossRef]
- Micallef, D.; Rezaeiha, A. Floating offshore wind turbine aerodynamics: Trends and future challenges. Renew. Sustain. Energy Rev. 2021, 152, 111696. [Google Scholar] [CrossRef]
- Robertson, A.N.; Wendt, F.; Jonkman, J.M.; Popko, W.; Dagher, H.; Gueydon, S.; Qvist, J.; Vittori, F.; Azcona, J.; Uzunoglu, E.; et al. OC5 Project Phase II: Validation of Global Loads of the DeepCwind Floating Semisubmersible Wind Turbine. Energy Procedia 2017, 137, 38–57. [Google Scholar] [CrossRef]
- Draycott, S.; Sellar, B.; Davey, T.; Noble, D.; Venugopal, V.; Ingram, D. Capture and simulation of the ocean environment for offshore renewable energy. Renew. Sustain. Energy Rev. 2019, 104, 15–29. [Google Scholar] [CrossRef]
- Robertson, A.; Wang, L. OC6 Phase Ib: Floating Wind Component Experiment for Difference-Frequency Hydrodynamic Load Validation. Energies 2021, 14, 6417. [Google Scholar] [CrossRef]
- Penalba, M.; Giorgi, G.; Ringwood, J.V. Mathematical modelling of wave energy converters: A review of nonlinear approaches. Renew. Sustain. Energy Rev. 2017, 78, 1188–1207. [Google Scholar] [CrossRef] [Green Version]
- Rakhsha, M.; Kees, C.E.; Negrut, D. Lagrangian vs. Eulerian: An Analysis of Two Solution Methods for Free-Surface Flows and Fluid Solid Interaction Problems. Fluids 2021, 6, 460. [Google Scholar] [CrossRef]
- Katsidoniotaki, E.; Göteman, M. Numerical modeling of extreme wave interaction with point-absorber using OpenFOAM. Ocean. Eng. 2022, 245, 110268. [Google Scholar] [CrossRef]
- Wang, L.; Robertson, A.; Jonkman, J.; Yu, Y.H.; Koop, A.; Borràs Nadal, A.; Li, H.; Bachynski-Polić, E.; Pinguet, R.; Shi, W.; et al. OC6 Phase Ib: Validation of the CFD predictions of difference-frequency wave excitation on a FOWT semisubmersible. Ocean. Eng. 2021, 241, 110026. [Google Scholar] [CrossRef]
- Wang, L.; Robertson, A.; Jonkman, J.; Kim, J.; Shen, Z.R.; Koop, A.; Borràs Nadal, A.; Shi, W.; Zeng, X.; Ransley, E.; et al. OC6 Phase Ia: CFD Simulations of the Free-Decay Motion of the DeepCwind Semisubmersible. Energies 2022, 15, 389. [Google Scholar] [CrossRef]
- Shadloo, M.; Oger, G.; Le Touzé, D. Smoothed particle hydrodynamics method for fluid flows, towards industrial applications: Motivations, current state, and challenges. Comput. Fluids 2016, 136, 11–34. [Google Scholar] [CrossRef]
- Gotoh, H.; Khayyer, A. On the state-of-the-art of particle methods for coastal and ocean engineering. Coast. Eng. J. 2018, 60, 79–103. [Google Scholar] [CrossRef]
- Manenti, S.; Wang, D.; Domínguez, J.; Li, S.; Amicarelli, A.; Albano, R. SPH Modeling of Water-Related Natural Hazards. Water 2019, 11, 1875. [Google Scholar] [CrossRef] [Green Version]
- Amicarelli, A.; Manenti, S.; Albano, R.; Agate, G.; Paggi, M.; Longoni, L.; Mirauda, D.; Ziane, L.; Viccione, G.; Todeschini, S.; et al. SPHERA v. 9.0.0: A Computational Fluid Dynamics research code, based on the Smoothed Particle Hydrodynamics mesh-less method. Comput. Phys. Commun. 2020, 250, 107157. [Google Scholar] [CrossRef]
- Luo, M.; Khayyer, A.; Lin, P. Particle methods in ocean and coastal engineering. Appl. Ocean. Res. 2021, 114, 102734. [Google Scholar] [CrossRef]
- Violeau, D.; Rogers, B. Smoothed particle hydrodynamics (SPH) for free-surface flows: Past, present and future. J. Hydraul. Res. 2016, 54, 1–26. [Google Scholar] [CrossRef]
- Domínguez, J.; Fourtakas, G.; Altomare, C.; Canelas, R.; Tafuni, A.; García Feal, O.; Martínez-Estévez, I.; Mokos, A.; Vacondio, R.; Crespo, A.; et al. DualSPHysics: From fluid dynamics to multiphysics problems. Comput. Part. Mech. 2021. [Google Scholar] [CrossRef]
- Tasora, A.; Serban, R.; Mazhar, H.; Pazouki, A.; Melanz, D.; Fleischmann, J.; Taylor, M.; Sugiyama, H.; Negrut, D. Chrono: An open source multi-physics dynamics engine. In Proceedings of the International Conference on High Performance Computing in Science and Engineering, Frankfurt, Germany, 19–23 June 2016; pp. 19–49. [Google Scholar] [CrossRef]
- Hall, M. MoorDyn User’s Guide. Available online: http://www.matt-hall.ca/moordyn.html (accessed on 27 December 2021).
- Tafuni, A.; Sahin, I.; Hyman, M. Numerical investigation of wave elevation and bottom pressure generated by a planing hull in finite-depth water. Appl. Ocean. Res. 2016, 58, 281–291. [Google Scholar] [CrossRef]
- Mogan, S.C.; Chen, D.; Hartwig, J.; Sahin, I.; Tafuni, A. Hydrodynamic analysis and optimization of the Titan submarine via the SPH and Finite–Volume methods. Comput. Fluids 2018, 174, 271–282. [Google Scholar] [CrossRef]
- Tagliafierro, B.; Mancini, S.; Ropero-Giralda, P.; Domínguez, J.; Crespo, A.; Viccione, G. Performance assessment of a planing hull using the smoothed particle hydrodynamics method. J. Mar. Sci. Eng. 2021, 9, 244. [Google Scholar] [CrossRef]
- Mintu, S.; Molyneux, D.; Colbourne, B. Full-scale SPH simulations of ship-wave impact generated sea spray. Ocean. Eng. 2021, 241, 110077. [Google Scholar] [CrossRef]
- Tagliafierro, B.; Ropero-Giralda, P.; Crespo, A.J.C.; Ryan, G.; Domínguez, J.; Bacelli, G.; Gómez-Gesteira, M. DualSPHysics: A numerical tool to design point-absorbing WECs. In Proceedings of the 14th European Wave and Tidal Energy Conference (EWTEC), Plymouth, UK, 5–9 September 2021. [Google Scholar]
- Crespo, A.; Altomare, C.; Domínguez, J.; González-Cao, J.; Gómez-Gesteira, M. Towards simulating floating offshore oscillating water column converters with Smoothed Particle Hydrodynamics. Coast. Eng. 2017, 126, 11–26. [Google Scholar] [CrossRef]
- Quartier, N.; Crespo, A.J.; Domínguez, J.M.; Stratigaki, V.; Troch, P. Efficient response of an onshore Oscillating Water Column Wave Energy Converter using a one-phase SPH model coupled with a multiphysics library. Appl. Ocean. Res. 2021, 115, 102856. [Google Scholar] [CrossRef]
- Brito, M.; Canelas, R.; García-Feal, O.; Domínguez, J.; Crespo, A.; Ferreira, R.; Neves, M.; Teixeira, L. A numerical tool for modelling oscillating wave surge converter with nonlinear mechanical constraints. Renew. Energy 2020, 146, 2024–2043. [Google Scholar] [CrossRef]
- Tagliafierro, B.; Montuori, R.; Vayas, I.; Ropero-Giralda, P.; Crespo, A.; Domìnguez, J.; Altomare, C.; Viccione, G.; Gòmez-Gesteira, M. A new open source solver for modelling fluid-structure interaction: Case study of a point-absorber wave energy converter with a power take-off unit. In Proceedings of the 11th International Conference on Structural Dynamics, Athens, Greece, 23–26 November 2020. [Google Scholar] [CrossRef]
- Quartier, N.; Ropero-Giralda, P.; Domínguez, J.M.; Stratigaki, V.; Troch, P. Influence of the Drag Force on the Average Absorbed Power of Heaving Wave Energy Converters Using Smoothed Particle Hydrodynamics. Water 2021, 13, 384. [Google Scholar] [CrossRef]
- Ropero-Giralda, P.; Crespo, A.J.; Tagliafierro, B.; Altomare, C.; Domínguez, J.M.; Gómez-Gesteira, M.; Viccione, G. Efficiency and survivability analysis of a point-absorber wave energy converter using DualSPHysics. Renew. Energy 2020, 162, 1763–1776. [Google Scholar] [CrossRef]
- Ropero-Giralda, P.; Crespo, A.J.C.; Coe, R.G.; Tagliafierro, B.; Domínguez, J.M.; Bacelli, G.; Gómez-Gesteira, M. Modelling a Heaving Point-Absorber with a Closed-Loop Control System Using the DualSPHysics Code. Energies 2021, 14, 760. [Google Scholar] [CrossRef]
- Tagliafierro, B.; Martínez-Estévez, I.; Domínguez, J.M.; Crespo, A.J.; Göteman, M.; Engström, J.; Gómez-Gesteira, M. A numerical study of a taut-moored point-absorber wave energy converter with a linear power take-off system under extreme wave conditions. Appl. Energy 2022, 311, 118629. [Google Scholar] [CrossRef]
- Capasso, S.; Tagliafierro, B.; Martínez-Estévez, I.; Domínguez, J.; Rahi, J.; Stratigaki, V.; Crespo, A.; Montuori, R.; Troch, P.; Gómez-Gesteira, M.; et al. On the Development of a Novel Approach for Simulating Elastic Beams in Dualsphysics with the Use of the Project Chrono Library; National Technical University of Athens: Athens, Greece, 2021; Volume 2021. [Google Scholar]
- Capasso, S.; Tagliafierro, B.; Martínez-Estévez, I.; Domínguez, J.; Crespo, A.; Viccione, G. A DEM approach for simulating flexible beam elements with the Project Chrono core module in DualSPHysics. Comput. Part. Mech. 2022. [Google Scholar] [CrossRef]
- Varghese, R.; Pakrashi, V.; Bhattacharya, S. A Compendium of Formulae for Natural Frequencies of Offshore Wind Turbine Structures. Energies 2022, 15, 2967. [Google Scholar] [CrossRef]
- Jonkman, J.M. Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine; University of Colorado at Boulder: Boulder, CO, USA, 2007. [Google Scholar]
- Tran, T.; Kim, D.; Song, J. Computational Fluid Dynamic Analysis of a Floating Offshore Wind Turbine Experiencing Platform Pitching Motion. Energies 2014, 7, 5011–5026. [Google Scholar] [CrossRef]
- Nematbakhsh, A.; Bachynski, E.E.; Gao, Z.; Moan, T. Comparison of wave load effects on a TLP wind turbine by using computational fluid dynamics and potential flow theory approaches. Appl. Ocean. Res. 2015, 53, 142–154. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Xiao, Q.; Liu, Y.; Incecik, A.; Peyrard, C.; Li, S.; Pan, G. Numerical Modelling of Dynamic Responses of a Floating Offshore Wind Turbine Subject to Focused Waves. Energies 2019, 12, 3482. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Xiao, Q.; Incecik, A.; Peyrard, C.; Wan, D. Establishing a fully coupled CFD analysis tool for floating offshore wind turbines. Renew. Energy 2017, 112, 280–301. [Google Scholar] [CrossRef] [Green Version]
- Van Rij, J.; Yu, Y.H.; Guo, Y.; Coe, R.G. A Wave Energy Converter Design Load Case Study. J. Mar. Sci. Eng. 2019, 7, 250. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.; Ren, N.; Wang, Y.; Wang, S.; Shi, W.; Zhai, G. A Comprehensive Study on the Serbuoys Offshore Wind Tension Leg Platform Coupling Dynamic Response under Typical Operational Conditions. Energies 2019, 12, 2067. [Google Scholar] [CrossRef] [Green Version]
- Monaghan, J.J. Smoothed particle hydrodynamics. Rep. Prog. Phys. 2005, 68, 1703–1759. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed Particle Hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Wendland, H. Piecewise polynomial, positive definite and compactly supported radial basis functions of minimal degree. Adv. Comput. Math. 1995, 4, 389–396. [Google Scholar] [CrossRef]
- Lo, E.; Shao, S. Simulation of near-shore solitary wave mechanics by an incompressible SPH method. Appl. Ocean. Res. 2002, 24, 275–286. [Google Scholar] [CrossRef]
- Molteni, D.; Colagrossi, A. A simple procedure to improve the pressure evaluation in hydrodynamic context using the SPH. Comput. Phys. Commun. 2009, 180, 861–872. [Google Scholar] [CrossRef]
- Antuono, M.; Colagrossi, A.; Marrone, S. Numerical diffusive terms in weakly-compressible SPH schemes. Comput. Phys. Commun. 2012, 183, 2570–2580. [Google Scholar] [CrossRef]
- Fourtakas, G.; Vacondio, R.; Domínguez, J.; Rogers, B. Improved density diffusion term for long duration wave propagation. In Proceedings of the International SPHERIC Workshop, Harbin, China, 13–16 January 2020. [Google Scholar]
- Fourtakas, G.; Dominguez, J.M.; Vacondio, R.; Rogers, B.D. Local uniform stencil (LUST) boundary condition for arbitrary 3-D boundaries in parallel smoothed particle hydrodynamics (SPH) models. Comput. Fluids 2019, 190, 346–361. [Google Scholar] [CrossRef]
- Monaghan, J.; Kos, A.; Issa, N. Fluid Motion Generated by Impact. J. Waterw. Port Coastal Ocean. Eng. 2003, 129, 250–259. [Google Scholar] [CrossRef]
- Canelas, R.B.; Domínguez, J.M.; Crespo, A.J.; Gómez-Gesteira, M.; Ferreira, R.M. A Smooth Particle Hydrodynamics discretization for the modelling of free surface flows and rigid body dynamics. Int. J. Numer. Methods Fluids 2015, 78, 581–593. [Google Scholar] [CrossRef]
- Domínguez, J.; Crespo, A.; Hall, M.; Altomare, C.; Wu, M.; Stratigaki, V.; Troch, P.; Cappietti, L.; Gómez-Gesteira, M. SPH simulation of floating structures with moorings. Coast. Eng. 2019, 153, 103560. [Google Scholar] [CrossRef]
- Ruffini, G.; Briganti, R.; De Girolamo, P.; Stolle, J.; Ghiassi, B.; Castellino, M. Numerical Modelling of Flow-Debris Interaction during Extreme Hydrodynamic Events with DualSPHysics-CHRONO. Appl. Sci. 2021, 11, 3618. [Google Scholar] [CrossRef]
- Crespo, A.; Gómez-Gesteira, M.; Dalrymple, R. Boundary conditions generated by dynamic particles in SPH methods. Comput. Mater. Contin. 2007, 5, 173–184. [Google Scholar]
- Zhang, F.; Crespo, A.; Altomare, C.; Domínguez, J.; Marzeddu, A.; Shang, S.p.; Gómez-Gesteira, M. DualSPHysics: A numerical tool to simulate real breakwaters. J. Hydrodyn. 2018, 30, 95–105. [Google Scholar] [CrossRef]
- English, A.; Domínguez, J.; Vacondio, R.; Crespo, A.; Stansby, P.; Lind, S.; Chiapponi, L.; Gómez-Gesteira, M. Modified dynamic boundary conditions (mDBC) for general purpose smoothed particle hydrodynamics (SPH): Application to tank sloshing, dam break and fish pass problems. Comput. Part. Mech. 2021. [Google Scholar] [CrossRef]
- Liu, M.; Liu, G. Restoring particle consistency in smoothed particle hydrodynamics. Appl. Numer. Math. 2006, 56, 19–36. [Google Scholar] [CrossRef]
- Capasso, S.; Tagliafierro, B.; Güzel, H.; Yilmaz, A.; Dal, K.; Kocaman, S.; Viccione, G.; Evangelista, S. A Numerical Validation of 3D Experimental Dam-Break Wave Interaction with a Sharp Obstacle Using DualSPHysics. Water 2021, 13, 2133. [Google Scholar] [CrossRef]
- Altomare, C.; Gironella, X.; Crespo, A.J. Simulation of random wave overtopping by a WCSPH model. Appl. Ocean. Res. 2021, 116, 102888. [Google Scholar] [CrossRef]
- Suzuki, T.; García-Feal, O.; Domínguez, J.M.; Altomare, C. Simulation of 3D overtopping flow–object–structure interaction with a calibration-based wave generation method with DualSPHysics and SWASH. Comput. Part. Mech. 2022. [Google Scholar] [CrossRef]
- Altomare, C.; Tagliafierro, B.; Dominguez, J.; Suzuki, T.; Viccione, G. Improved relaxation zone method in SPH-based model for coastal engineering applications. Appl. Ocean. Res. 2018, 81, 15–33. [Google Scholar] [CrossRef]
- Verbrugghe, T.; Stratigaki, V.; Altomare, C.; Domínguez, J.; Troch, P.; Kortenhaus, A. Implementation of open boundaries within a two-way coupled SPH model to simulate nonlinear wave–structure interactions. Energies 2019, 12, 697. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Estévez, I. MoorDynPlus. Available online: https://github.com/imestevez/MoorDynPlus (accessed on 27 July 2021).
- Jonkman, J. Definition of the Floating System for Phase IV of OC3; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2010. [Google Scholar]
- Altomare, C.; Domínguez, J.; Crespo, A.; González-Cao, J.; Suzuki, T.; Gómez-Gesteira, M.; Troch, P. Long-crested wave generation and absorption for SPH-based DualSPHysics model. Coast. Eng. 2017, 127, 37–54. [Google Scholar] [CrossRef]
- Gomez-Gesteira, M.; Rogers, B.; Crespo, A.; Dalrymple, R.; Narayanaswamy, M.; Dominguez, J. SPHysics—development of a free-surface fluid solver—Part 1: Theory and formulations. Comput. Geosci. 2012, 48, 289–299. [Google Scholar] [CrossRef]
- Tagliafierro, B.; Karimirad, M.; Martínez-Estévez, I.; Domínguez, J.; Crespo, A.; Gómez-Gesteira, M.; Viccione, G. Preliminary study of floating offshore wind turbines motions using the Smoothed Particle Hydrodynamics method. In Proceedings of the 41st International Conference on Offshore Mechanics and Arctic Engineering—OMAE, Hamburg, Germany, 5–10 June 2022; p. 8. [Google Scholar]
- Le Méhauté, B. An Introduction to Hydrodynamics and Water Waves; Springer Science & Business Media, Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Healy, J. Wave damping effect of beaches. In Proceedings of the Minnesota International Hydraulics Convention (IAHR); American Society of Civil Engineers: Reston, VA, USA, 1952; pp. 213–220. [Google Scholar]
- Ahn, H.; Shin, H. Experimental and Numerical Analysis of a 10 MW Floating Offshore Wind Turbine in Regular Waves. Energies 2020, 13, 2608. [Google Scholar] [CrossRef]
- Wayman, E.N.; Sclavounos, P.; Butterfield, S.; Jonkman, J.; Musial, W. Coupled dynamic modeling of floating wind turbine systems. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 1–4 May 2006. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L.; Michailides, C.; Wan, L.; Shi, W. Hydrodynamic Response of a Combined Wind-Wave Marine Energy Structure. J. Mar. Sci. Eng. 2020, 8, 253. [Google Scholar] [CrossRef] [Green Version]
- DNV-RP-C205. Recommended Practice: Environmental Conditions and Environmental Loads; DNV: Oslo, Norway, 2014. [Google Scholar]
- Hasselmann, K.; Barnett, T.; Bouws, E.; Carlson, H.; Cartwright, D.; Enke, K.; Ewing, J.; Gienapp, H.; Hasselmann, D.; Kruseman, P.; et al. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Deut. Hydrogr. Z. 1973, 8, 1–95. [Google Scholar]
- Boccotti, P. Idraulica Marittima; UTET Univertità: Milano, Italy, 2004. [Google Scholar]
- Shahroozi, Z.; Göteman, M.; Engström, J. Experimental investigation of a point-absorber wave energy converter response in different wave-type representations of extreme sea states. Ocean. Eng. 2022, 248, 110693. [Google Scholar] [CrossRef]
- Tromans, P.S.; Anaturk, A.R.; Hagemeijer, P. A new model for the kinematics of large ocean waves-application as a design wave. In Proceedings of the International Ocean and Polar Engineering Conference, ISOPE-I-91-154, Edinburgh, UK, 11–16 August 1991; Available online: https://onepetro.org/ISOPEIOPEC/proceedings-pdf/ISOPE91/All-ISOPE91/ISOPE-I-91-154/2004345/isope-i-91-154.pdf (accessed on 24 May 2022).
- Ishtiyak, M.; Sarkar, A.; Fazeres-Ferradosa, T.; Rosa-Santos, P.; Taveira-Pinto, F. Bottom-supported tension leg towers with inclined tethers for offshore wind turbines. Proc. Inst. Civ. Eng. Marit. Eng. 2021, 174, 124–133. [Google Scholar] [CrossRef]
- Barreto, D.; Karimirad, M.; Ortega, A. Effects of Simulation Length and Flexible Foundation on Long-Term Response Extrapolation of a Bottom-Fixed Offshore Wind Turbine. J. Offshore Mech. Arct. Eng. 2022, 144, 032001. [Google Scholar] [CrossRef]
- Fazeres-Ferradosa, T.; Rosa-Santos, P.; Taveira-Pinto, F.; Pavlou, D.; Gao, F.P.; Carvalho, H.; Oliveira-Pinto, S. Preface: Advanced Research on Offshore Structures and Foundation Design: Part 2. Proc. Inst. Civ. Eng. Marit. Eng. 2020, 173, 96–99. [Google Scholar] [CrossRef]
- Karimirad, M.; Rosa-Clot, M.; Armstrong, A.; Whittaker, T. Floating solar: Beyond the state of the art technology. Solar Energy 2021, 219, 1–2. [Google Scholar] [CrossRef]
- DNV-ST-0119. Floating Wind Turbine Structures; DNV: Oslo, Norway, 2021. [Google Scholar]
- Bezunartea-Barrio, A.; Fernandez-Ruano, S.; Maron-Loureiro, A.; Molinelli-Fernandez, E.; Moreno-Buron, F.; Oria-Escudero, J.; Rios-Tubio, J.; Soriano-Gomez, C.; Valea-Peces, A.; Lopez-Pavon, C.; et al. Scale Effects on Heave Plates for Semi-Submersible Floating Offshore Wind Turbines: Case Study With a Solid Plain Plate. J. Offshore Mech. Arct. Eng. 2019, 142, 31105. Available online: https://asmedigitalcollection.asme.org/offshoremechanics/article-pdf/142/3/031105/6531063/omae_142_3_031105.pdf (accessed on 24 May 2022). [CrossRef]
- Jeong, Y.J.; Park, M.S.; Kim, J.; Song, S.H. Wave Force Characteristics of Large-Sized Offshore Wind Support Structures to Sea Levels and Wave Conditions. Appl. Sci. 2019, 9, 1855. [Google Scholar] [CrossRef] [Green Version]
- Giannini, G.; Temiz, I.; Rosa-Santos, P.; roozi, Z.; Ramos, V.; Göteman, M.; Engström, J.; Day, S.; Taveira-Pinto, F. Wave Energy Converter Power Take-Off System Scaling and Physical Modelling. J. Mar. Sci. Eng. 2020, 8, 632. [Google Scholar] [CrossRef]
- Zhang, M.; Li, X.; Tong, J.; Xu, J. Load control of floating wind turbine on a Tension-Leg-Platform subject to extreme wind condition. Renew. Energy 2020, 151, 993–1007. [Google Scholar] [CrossRef]
- Awada, A.; Younes, R.; Ilinca, A. Review of Vibration Control Methods for Wind Turbines. Energies 2021, 14, 3058. [Google Scholar] [CrossRef]


| Element | Symbol | Quantity | Unit |
|---|---|---|---|
| Young’s modulus | E | 2.70 | GPa |
| Cross sectional stiffness | 30.0 | kN | |
| Nominal diameter | 4.00 | mm | |
| Density in air | 1200 | kg/m | |
| Weight in fluid | 0.02 | N | |
| Segments | N | 20 | - |
| Natural frequency (Equation (12)) | 5.21 | MHz | |
| Model time step | 19.5 × 10 | s |
| Sea State | (m) | (s) | Depth (m) | Physical Time (s) | Runtime (h/day) | |
|---|---|---|---|---|---|---|
| S | 0.224 | 1.68 | 1.91 | 5 | 2016 | 684/28 |
| V | 0.224 | 1.80 | 1.91 | 5 | 2160 | 800/32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tagliafierro, B.; Karimirad, M.; Martínez-Estévez, I.; Domínguez, J.M.; Viccione, G.; Crespo, A.J.C. Numerical Assessment of a Tension-Leg Platform Wind Turbine in Intermediate Water Using the Smoothed Particle Hydrodynamics Method. Energies 2022, 15, 3993. https://doi.org/10.3390/en15113993
Tagliafierro B, Karimirad M, Martínez-Estévez I, Domínguez JM, Viccione G, Crespo AJC. Numerical Assessment of a Tension-Leg Platform Wind Turbine in Intermediate Water Using the Smoothed Particle Hydrodynamics Method. Energies. 2022; 15(11):3993. https://doi.org/10.3390/en15113993
Chicago/Turabian StyleTagliafierro, Bonaventura, Madjid Karimirad, Iván Martínez-Estévez, José M. Domínguez, Giacomo Viccione, and Alejandro J. C. Crespo. 2022. "Numerical Assessment of a Tension-Leg Platform Wind Turbine in Intermediate Water Using the Smoothed Particle Hydrodynamics Method" Energies 15, no. 11: 3993. https://doi.org/10.3390/en15113993
APA StyleTagliafierro, B., Karimirad, M., Martínez-Estévez, I., Domínguez, J. M., Viccione, G., & Crespo, A. J. C. (2022). Numerical Assessment of a Tension-Leg Platform Wind Turbine in Intermediate Water Using the Smoothed Particle Hydrodynamics Method. Energies, 15(11), 3993. https://doi.org/10.3390/en15113993










