Comparison between Space Mapping and Direct FEA Optimizations for the Design of Halbach Array PM Motor
Abstract
:1. Introduction
2. CAD of PMSM
3. Analytical Sizing Models
3.1. Electromagnetic Torque
3.2. Full Analytical Sizing Motor Model
4. Optimization of the PMSM
4.1. Direct FEA Optimization
4.2. Space Mapping Optimization
5. Design Example
6. Optimization Problem Definition
6.1. Space Mapping Optimization
6.2. Direct FEA Optimization
7. Results
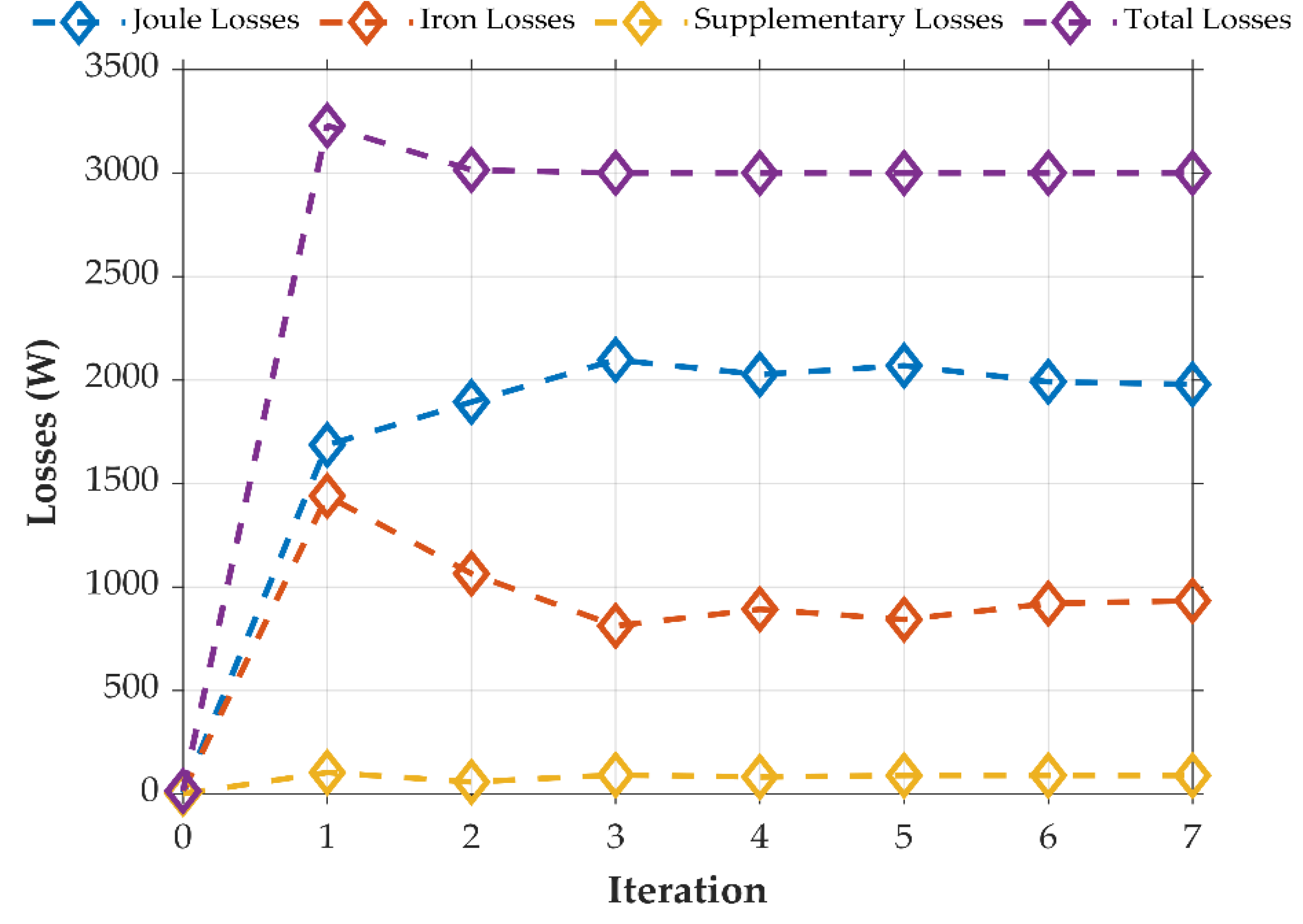
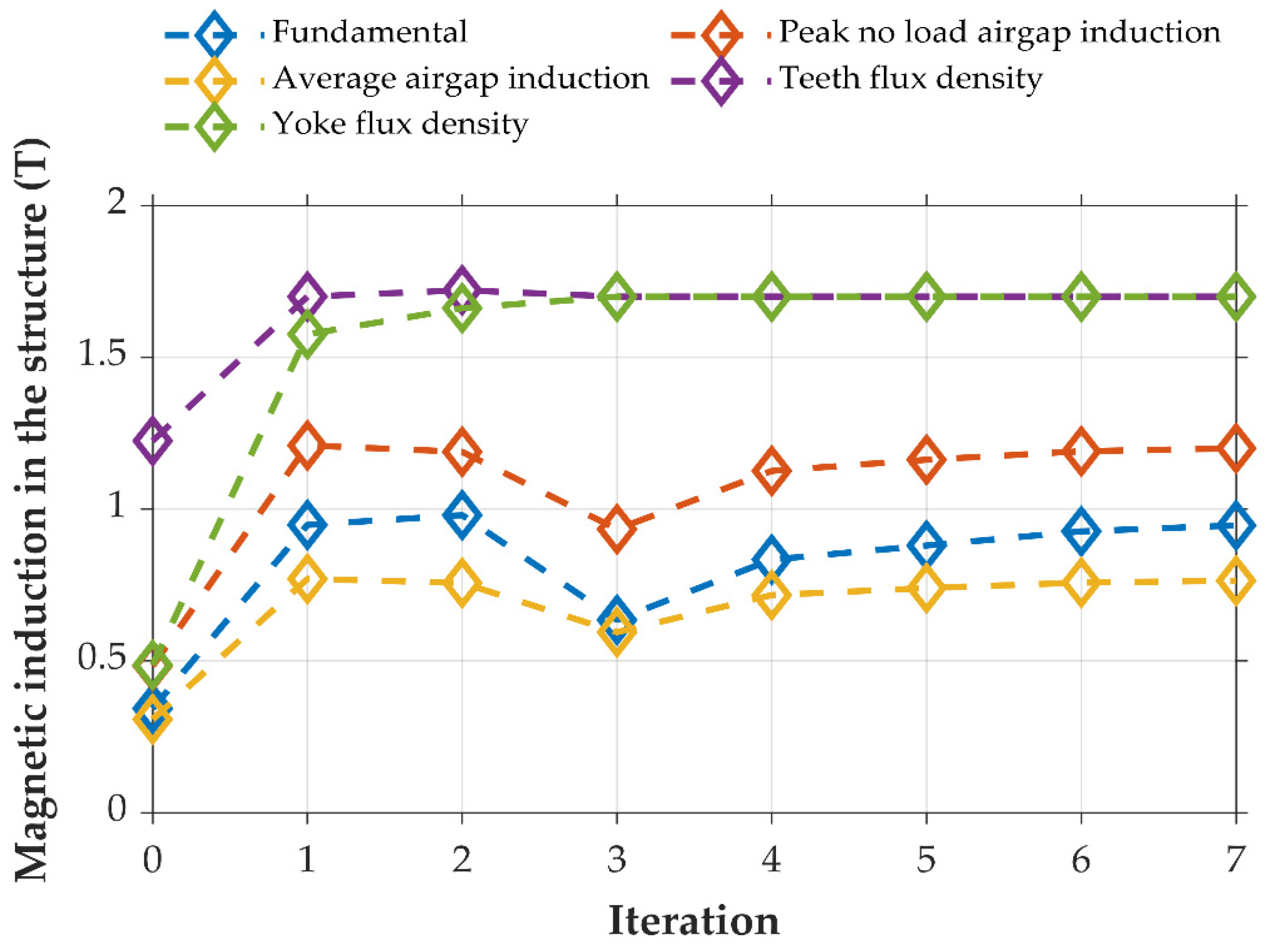
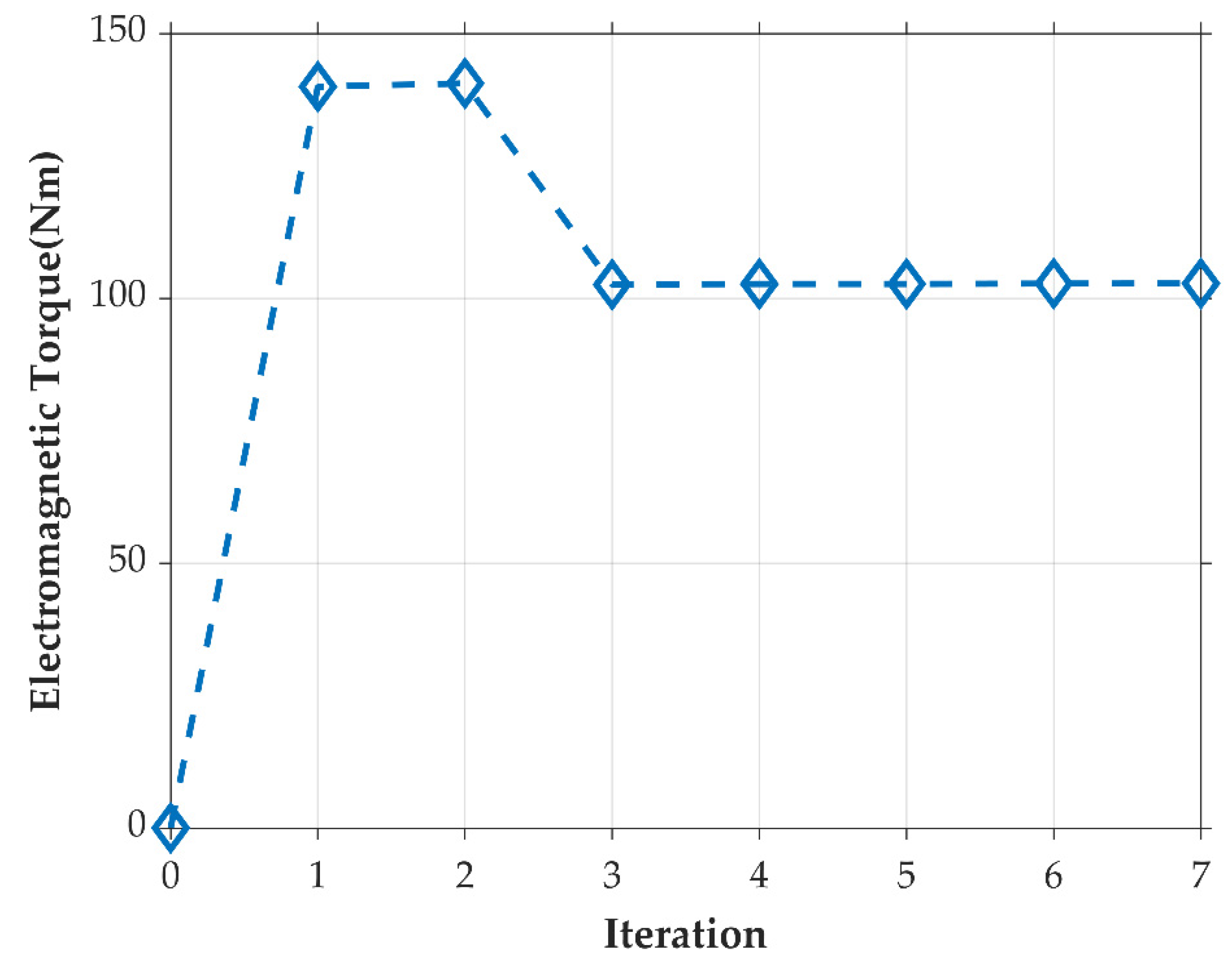
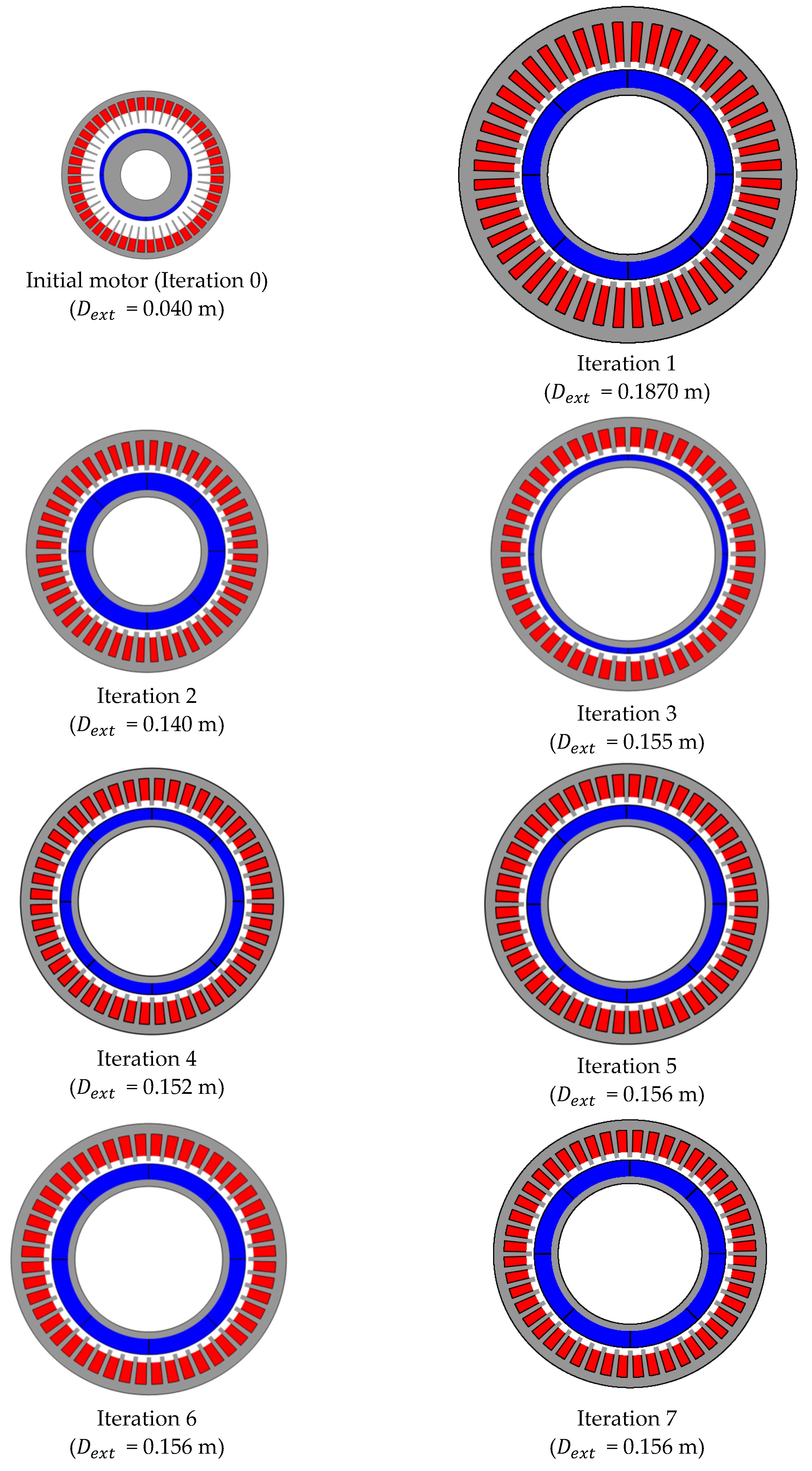
7.1. Space Mapping
7.2. FEA
8. Discussion
9. Conclusions
- -
- There is an important reduction in computing time with SM. Almost an 80% time reduction was found, considering that for direct FEA optimization, the mesh density is low and the starting point of this optimization was based on the results obtained by the SM method.
- -
- The motor geometry of the final solutions of both optimization methods is different but the motor mass difference is small (less than 3%). Power density and torque density are very similar.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Peak fundamental magnetic induction | |
| Peak no load airgap induction | |
| Average airgap induction value per pole | |
| Teeth flux density | |
| Yoke flux density | |
| Linear specific load | |
| Electrical frequency | |
| Slot number | |
| Magnet outer diameter | |
| Magnet inner diameter | |
| Stator bottom slot diameter | |
| Stator outer diameter | |
| Rotor inner diameter | |
| Slot depth | |
| Stator yoke thickness | |
| Stator slot opening factor | |
| Minimal stator length with end coil winding | |
| One turn length per coil (Concentrated winding) | |
| Number of coils per phase | |
| Coil section | |
| Motor form factor | |
| Teeth form factor | |
| Copper section | |
| Magnet volume | |
| Rotor iron volume | |
| Stator teeth iron volume | |
| Stator yoke iron volume | |
| Stator iron volume | |
| Total copper volume | |
| Joule losses in stator winding | |
| Magnetic losses in the yoke | |
| Magnetic losses in the teeth | |
| Magnetic stator losses | |
| Airgap aerodynamic losses | |
| Lateral rotor surface aerodynamic losses | |
| Total aerodynamic losses | |
| Total losses | |
| Bearing friction losses | |
| Shaft torque | |
| Electrical conductivity of electrical sheet steel at 120 °C | |
| Sheet steel mass density | |
| Fill coefficient | |
| Hysteresis coefficient | |
| Excess loss coefficient | |
| CF | Correction factor |
| Correction factor of inductance | |
| Correction factor of teeth flux density | |
| Correction factor of magnetic stator losses | |
| Correction factor of electromagnetic torque | |
| Correction factor of yoke flux density | |
| Total optimization time by space mapping technique | |
| Simulation time by the space mapping technique | |
| Simulation time by finite element for the validation of results obtained by space mapping technique | |
| Copper weight | |
| Magnets weight | |
| Iron rotor weight | |
| Iron stator weight | |
| Total active parts weight | |
| Power density | |
| Torque density | |
| Nominal RMS phase current | |
| No-load RMS phase flux | |
| Electrical phase resistance | |
| Self inductance | |
| Cyclic phase inductance | |
| Winding rated temperature | |
| Electrical resistivity at nominal temperature () | |
| Cooling effort | |
| Limit cooling effort | |
| Nominal Mechanical power | |
| Nominal Rotation speed | |
| Maximum Rotation speed | |
| DC bus voltage | |
| Inverter input voltage | |
| Maximal RMS Phase voltage (line neutral) | |
| Stator Phase number | |
| Number of turns per coil | |
| Winding factor | |
| Number of slots per pole and per phase | |
| Number of winding layers | |
| Rotor sleeve thickness | |
| Mechanical air gap thickness | |
| Stator teeth maximal induction | |
| Stator yoke maximal induction | |
| Remanent magnetization of magnet at 100 °C | |
| Stator slot fill factor | |
| Teeth tips thickness or slot wedge thickness | |
| Teeth tips width in percent of slot opening | |
| Copper density | |
| Iron (sheet) density | |
| Sleeve density | |
| Magnet density | |
| Stator electrical sheet thickness | |
| FE | Finite element |
| FEA | Finite element analysis |
| SM | Space mapping |
| Slot opening angle | |
| Motor axial length | |
| Machine control angle | |
| Magnet thickness |
References
- Zhang, R.; Fujimori, S. The role of transport electrification in global climate change mitigation scenarios. Env. Res. Lett. 2020, 15, 034019. [Google Scholar] [CrossRef]
- Varyukhin, A.N.; Zakharchenko, V.S.; Vlasov, A.V.; Gordin, M.V.; Ovdienko, M.A. Roadmap for the Technological Development of Hybrid Electric and Full-Electric Propulsion Systems of Aircrafts. In Proceedings of the—ICOECS 2019: 2019 International Conference on Electrotechnical Complexes and Systems, Ufa, Russia, 21–25 October 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Chowdhury, S.; Gurpinar, E.; Su, G.J.; Raminosoa, T.; Burress, T.A.; Ozpineci, B. Enabling Technologies for Compact Integrated Electric Drives for Automotive Traction Applications. In Proceedings of the ITEC 2019—2019 IEEE Transportation Electrification Conference and Expo, Detroit, MI, USA, 19–21 June 2019. [Google Scholar]
- Ghandriz, T.; Jacobson, B.; Islam, M.; Hellgren, J.; Laine, L. Transportation-mission-based optimization of heterogeneous heavy-vehicle fleet including electrified propulsion. Energies 2021, 14, 3221. [Google Scholar] [CrossRef]
- Pettes-Duler, M.; Roboam, X.; Sareni, B.; Lefevre, Y.; Llibre, J.F.; Fénot, M. Multidisciplinary design optimization of the actuation system of a hybrid electric aircraft powertrain. Electronics 2021, 10, 1297. [Google Scholar] [CrossRef]
- Quillet, D.; Boulanger, V.; Rancourt, D.; Freer, R.; Bertrand, P. Parallel Hybrid-Electric Powertrain Sizing on Regional Turboprop Aircraft with Consideration for Certification Performance Requirements. In Proceedings of the AIAA AVIATION 2021 FORUM, Virtual, 2–6 August 2021. [Google Scholar] [CrossRef]
- Pyrhönen, J.; Jokinen, T.; Hrabovcová, V. Design of Rotating Electrical Machines; John Wiley & Sons: Hoboken, NJ, USA, 2008; ISBN 9780470695166. [Google Scholar]
- Lei, G.; Zhu, J.; Guo, Y.; Liu, C.; Ma, B. A review of design optimization methods for electrical machines. Energies 2017, 10, 1962. [Google Scholar] [CrossRef] [Green Version]
- Bramerdorfer, G.; Tapia, J.A.; Pyrhönen, J.J.; Cavagnino, A. Modern Electrical Machine Design Optimization: Techniques, Trends, and Best Practices. IEEE Trans. Ind. Electron. 2018, 65, 7672–7684. [Google Scholar] [CrossRef]
- Abdalmagid, M.; Sayed, E.; Bakr, M.H.; Emadi, A. Geometry and Topology Optimization of Switched Reluctance Machines: A Review. IEEE Access 2022, 10, 5141–5170. [Google Scholar] [CrossRef]
- Vaschetto, S.; Tenconi, A.; Bramerdorfer, G. Sizing procedure of surface mounted PM Machines for fast analytical evaluations. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017; pp. 1–8. [Google Scholar]
- Xie, P.; Ramanathan, R.; Vakil, G.; Gerada, C. Simplified analytical machine sizing for surface mounted permanent magnet machines. In Proceedings of the 2019 IEEE International Electric Machines and Drives Conference, IEMDC 2019, San Diego, CA, USA, 12–15 May 2019; pp. 751–757. [Google Scholar]
- Moreno, Y.; Almandoz, G.; Egea, A.; Madina, P.; Escalada, A.J. Multi-physics tool for electrical machine sizing. Energies 2020, 13, 1651. [Google Scholar] [CrossRef] [Green Version]
- Vivier, S.; Friedrich, G. Comparison between Single-Model and Multimodel Optimization Methods for Multiphysical Design of Electrical Machines. IEEE Trans. Ind. Appl. 2018, 54, 1379–1389. [Google Scholar] [CrossRef]
- Grenier, J.M.; Pérez, R.; Picard, M.; Cros, J. Magnetic FEA direct optimization of high-power density, halbach array permanent magnet electric motors. Energies 2021, 14, 5939. [Google Scholar] [CrossRef]
- Krishnan, R.; Bharadwaj, A.S.; Materu, P.N. Computer-Aided Design Of Electrical Machines For Variable Speed Applications. IEEE Trans. Ind. Electron. 1988, 35, 560–571. [Google Scholar] [CrossRef]
- Ghorbanian, V.; Salimi, A.; Lowther, D.A. A computer-aided design process for optimizing the size of inverter-fed permanent magnet motors. IEEE Trans. Ind. Electron 2017, 65, 1819–1827. [Google Scholar] [CrossRef]
- Cros, J.; Viarouge, P.; Kakhki, M.T. Design and optimization of soft magnetic composite machines with finite element methods. IEEE Trans. Magn. 2011, 47, 4384–4390. [Google Scholar] [CrossRef]
- Tiegna, H.; Amara, Y.; Barakat, G. Overview of analytical models of permanent magnet electrical machines for analysis and design purposes. Math. Comput. Simul. 2013, 90, 162–177. [Google Scholar] [CrossRef]
- Rosu, M.; Zhou, P.; Lin, D.; Lonol, D.; Popescu, M.; Blaabjerg, F.; Rallabandi, V.; Staton, D. Multiphysics Simulation by Design for Electrical Machines, Power Electronics and Drives; Wiley-IEEE Press: Piscataway, NJ, USA, 2018; ISBN 9781119103448. [Google Scholar]
- Shi, T.; Qiao, Z.; Xia, C.; Li, H.; Song, Z. Modeling, analyzing, and parameter design of the magnetic field of a segmented Halbach cylinder. IEEE Trans. Magn. 2012, 48, 1890–1898. [Google Scholar] [CrossRef]
- Touhami, S.; Zeaiter, A.; Fénot, M.; Lefevre, Y.; Llibre, J. Electro-thermal Models and Design Approach for High Specific Power Electric Motor for Hybrid Aircraft. In Proceedings of the Aerospace Europe Conference, Bordeaux, France, 25–28 February 2020. [Google Scholar]
- Cheng, Q.S.; Bandler, J.W.; Koziel, S. A review of implicit space mapping optimization and modelling techniques. In Proceedings of the 2015 IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization, NEMO 2015, Ottawa, ON, Canada, 11–14 August 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 9–11. [Google Scholar]
- Bandler, J.W.; Cheng, Q.S.; Dakroury, S.A.; Mohamed, A.S.; Bakr, M.H.; Madsen, K.; Søndergaard, J. Space Mapping: The State of The Art. IEEE Trans. Microw. Theory Tech. 2004, 52, 337–361. [Google Scholar] [CrossRef]
- Bandler, J.W.; Biernacki, R.M.; Chen, S.H.; Grobelny, P.A.; Hemmers, R.H. Space Mapping Technique for Electromagnetic Optimization. IEEE Trans. Microw. Theory Tech. 1994, 42, 2536–2544. [Google Scholar] [CrossRef]
- Cros, J.; Radaorozandry, L.; Figueroa, J.; Viarouge, P. Influence of the magnetic model accuracy on the optimal design of a car alternator. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2008, 27, 196–204. [Google Scholar] [CrossRef]
- Gong, J.; Gillon, F.; Bracikowski, N. Comparison of three space mapping techniques on electromagnetic design optimization. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2018, 37, 565–580. [Google Scholar] [CrossRef]
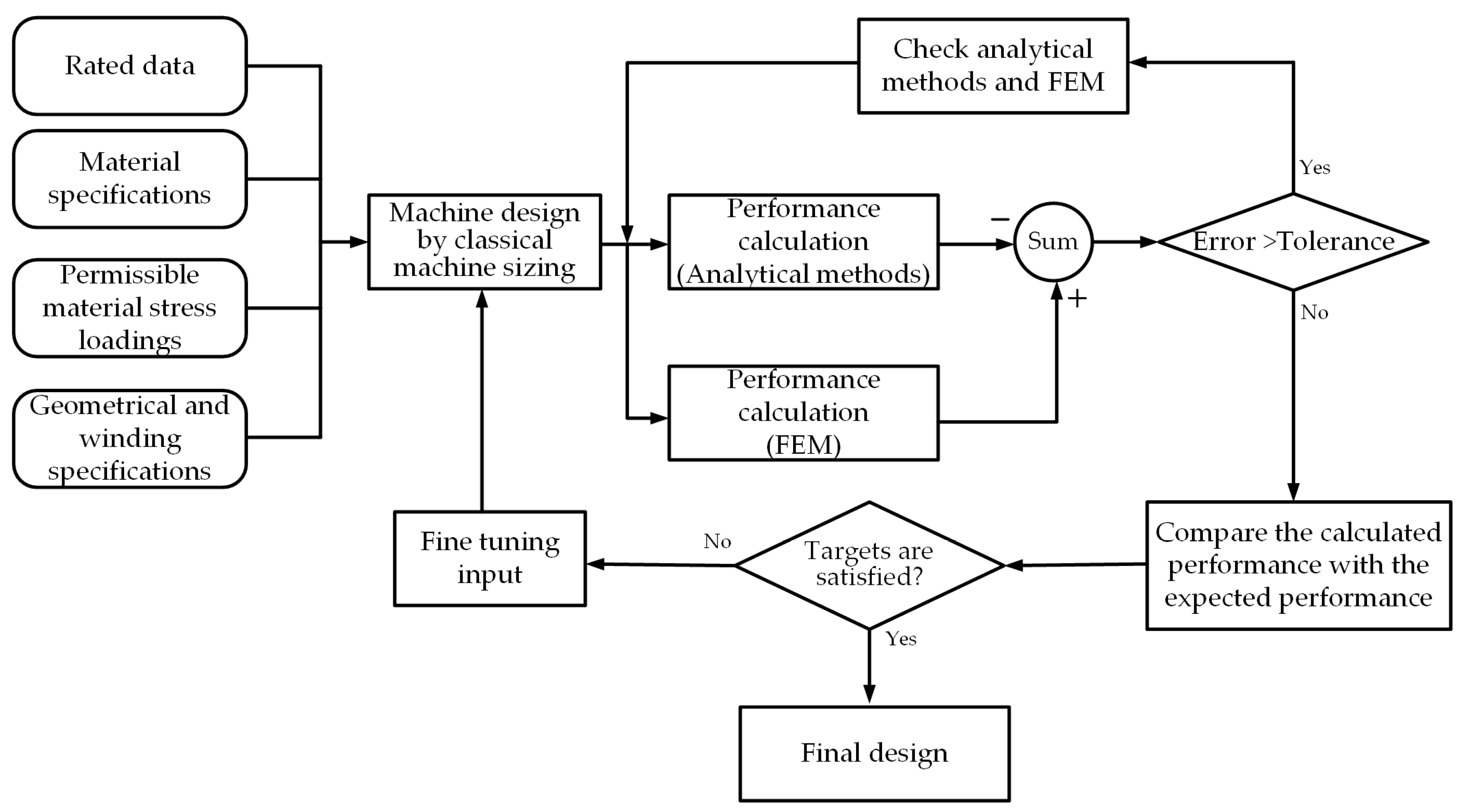
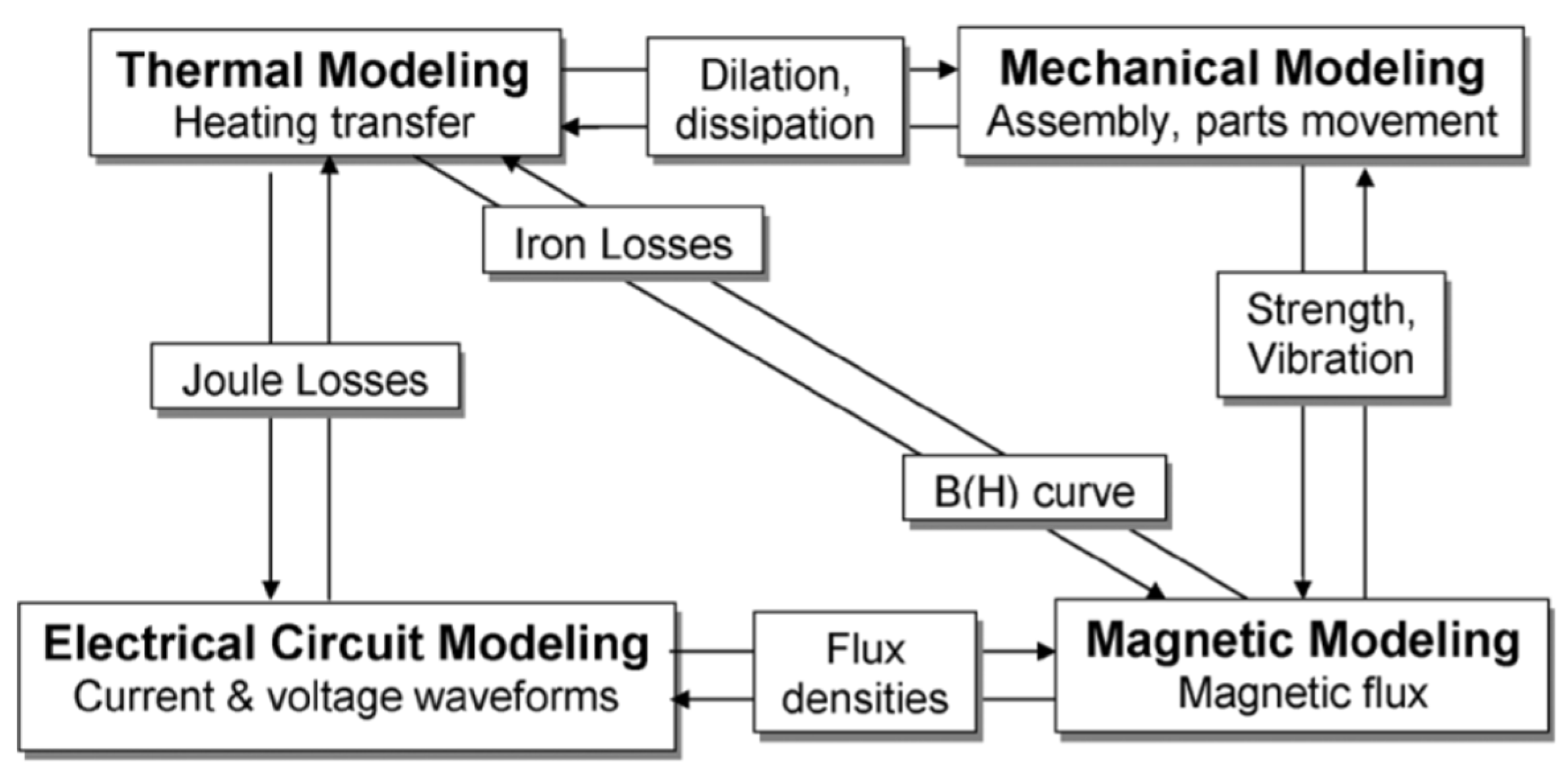
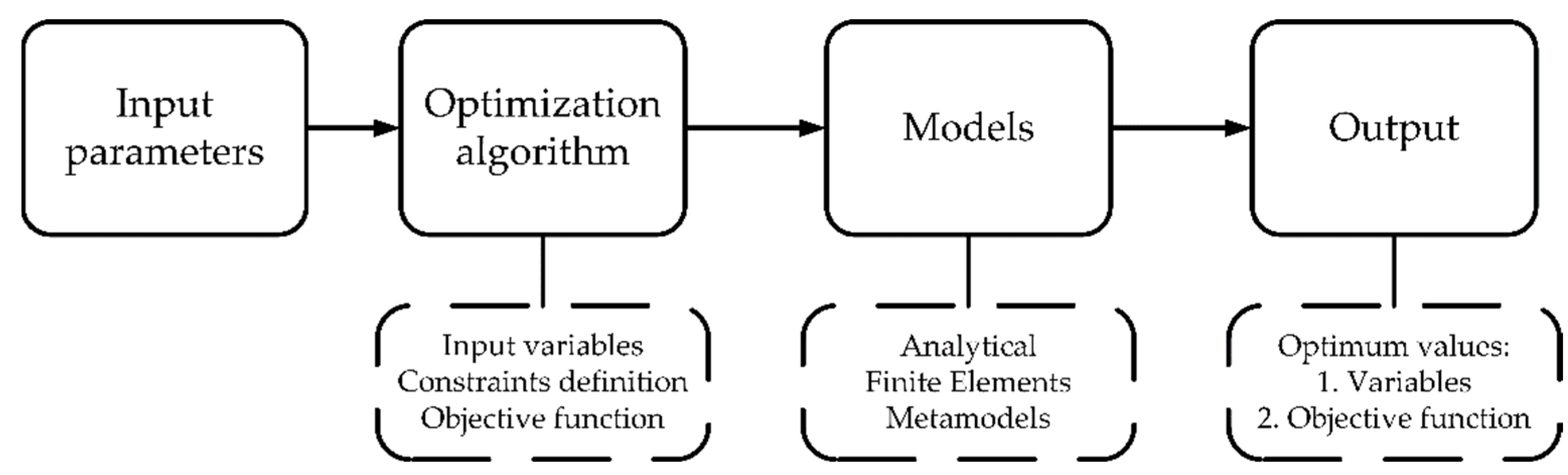


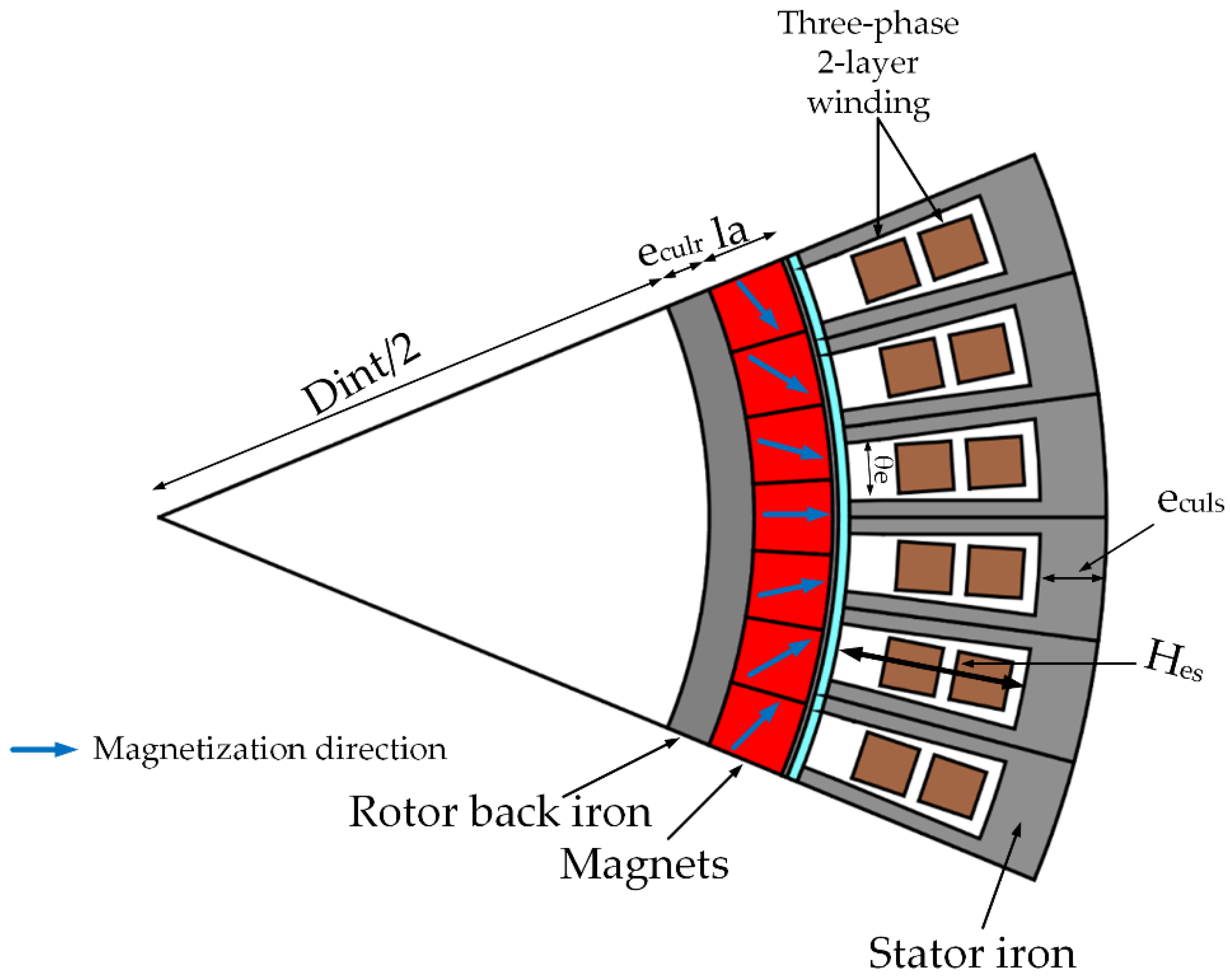


| Variable | Name | Units | Formula |
|---|---|---|---|
| Magnetic structural calculations | |||
| Peak fundamental no load airgap induction | T | Determined according to [21] | |
| Peak no load airgap induction | T | Determined according to [21] | |
| Average airgap induction value | T | ||
| Teeth flux density | T | ||
| Yoke flux density | T | ||
| Linear specific load | A/m | ||
| Electrical frequency | Hz | ||
| Slot number | - | ||
| Motor dimensional values | |||
| Magnet outer diameter | m | ||
| Magnet inner diameter | m | ||
| Stator bottom slot diameter | m | ||
| Stator outer diameter | m | ||
| Rotor inner diameter | m | ||
| Slot depth | m | ||
| Stator yoke thickness | m | ||
| Stator slot opening factor | - | ||
| Minimal stator length with end coil winding | m | ||
| One turn length per coil | m | ||
| Number of coils per phase | - | ||
| Coil section | m2 | ||
| Motor form factor | - | ||
| Teeth form factor | - | ||
| Total copper section | m2 | ||
| Material volumes | |||
| Magnet volume | m3 | ||
| Rotor iron volume | m3 | ||
| Stator teeth iron volume | m3 | ||
| Stator yoke iron volume | m3 | ||
| Stator iron volume | m3 | ||
| Total copper volume | m3 | ||
| Losses and Shaft torque | |||
| Joule losses in stator winding | W | ||
| Magnetic losses in the yoke | W | ||
| Magnetic losses in the teeth | W | ||
| Magnetic stator losses | W | ||
| Airgap aerodynamic losses | W | ||
| Lateral rotor surface aerodynamic losses | W | ||
| Total aerodynamic losses | W | ||
| Total losses | W | ||
| Bearing friction losses | W | ||
| Shaft torque | Nm | ||
| Material density and weight | |||
| Copper weight | kg | ||
| Magnets weight | kg | ||
| Iron rotor weight | kg | ||
| Iron stator weight | kg | ||
| Total active parts weight | kg | ||
| Power density | kW/kg | ||
| Torque density | Nm/kg | ||
| Electrical model | |||
| Nominal RMS phase current | A | ||
| No-load RMS phase flux | Wb | ||
| Electrical phase resistance | Ohm | ||
| Self-inductance | H | ||
| Cyclic phase inductance | H | ||
| Thermal parameters | |||
| Winding rated temperature | °C | 120 | |
| Electrical resistivity at nominal temperature () | Ohm.m | ||
| Cooling effort1 [7] | A2/m3 | ||
| Cooling effort2 [22] | W/(m3.Ohm) | ||
| Specification | Name | Units | Value |
|---|---|---|---|
| Nominal Mechanical power | W | 160,000 | |
| Nominal Rotation speed | RPM | 15,000 | |
| Shaft torque | Nm | 101.9 |
| Specification | Name | Units | Value |
|---|---|---|---|
| Input parameters | |||
| Stator Phase number | - | 3 | |
| Number of turns per coil | - | 1 | |
| Winding factor | - | 0.933 | |
| Number of slots per pole and per phase | - | 2 | |
| Number of winding layers | - | 2 | |
| Rotor sleeve thickness | m | 0.0005 | |
| Mechanical air gap thickness | m | 0.001 | |
| Stator teeth maximal induction | T | 1.7 | |
| Stator yoke maximal induction | T | 1.7 | |
| Remanent magnetization of magnet at 100 °C | T | 1.136 | |
| Stator slot fill factor | - | 0.4 | |
| Teeth tips thickness or slot wedge thickness | m | 0.003 | |
| Material mass density | |||
| Copper | kg/m3 | 8933 | |
| Iron (sheet) | kg/m3 | 7872 | |
| Carbon Sleeve | kg/m3 | 1500 | |
| Magnet | kg/m3 | 8300 | |
| Magnetic material parameters | |||
| Electrical conductivity of electrical steel (120 °C) | S/m | 2,083,333 | |
| Stator electrical sheet thickness | m | 0.000163 | |
| Sheet steel mass density | kg/m3 | 7650 | |
| Fill coefficient | - | 1 | |
| Hysteresis coefficient | - | 223 | |
| Excess loss coefficient | - | 0.524 | |
| Parameter Description | Name | Units | Constraint |
|---|---|---|---|
| Magnet thickness | m | 0.001 0.01 | |
| Magnetic circuit axial length | m | 0.02 0.5 | |
| Stator inner diameter | m | 0.03 0.5 | |
| Stator rms current density | A/m2 | 1 × 106 4 × 107 | |
| Teeth concentration factor | - | 1.1 10 | |
| Yoke concentration factor | - | 0.3 10 | |
| Total copper area in stator slots | m2 | 0.00001 0.02 |
| Parameter Description | Units | Constraint |
|---|---|---|
| Motor Form factor | - | 5 |
| Cooling effort | W/(m3Ohm) | 2 × 1012 |
| Peripheral speed | m/s | 150 |
| Yoke flux density | T | |
| Teeth flux density | T | |
| Teeth Form factor | - | 5 |
| Total losses | W | 3000 |
| Shaft torque | Nm | 101.86 |
| Parameter Description | Name | Units | Equation Modified by CF |
|---|---|---|---|
| CF inductance | - | ||
| CF teeth flux density | - | ||
| CF magnetic stator losses | - | ||
| CF electromagnetic torque | - | ||
| CF yoke flux density | - |
| Parameter Description | Name | Units | Constraint |
|---|---|---|---|
| Slot depth | m | 0.01 0.014 | |
| Rotor inner diameter | m | 0.07 0.105 | |
| Magnet thickness | m | 0.005 0.01 | |
| Slot opening angle | Rad | 0.065 0.090 | |
| Stator yoke thickness | m | 0.005 0.008 | |
| Magnetic circuit axial length | m | 0.14 0.185 | |
| Nominal RMS phase current | A | 170 250 | |
| Current control angle | Deg | −15 −5 |
| Parameter Description | Units | Constraint |
|---|---|---|
| Electromagnetic torque | Nm | 103.5 |
| Total losses | W | 3000 |
| Cooling effort | W/(m3Ohm) | 2 × 1012 |
| Yoke flux density | T | |
| Teeth flux density | T |
| Parameter Description | Units | Optimal Value | ||
|---|---|---|---|---|
| Magnet thickness | m | 0.010 | ||
| Motor axial length | m | 0.167 | ||
| Stator inner diameter | m | 0.112 | ||
| Stator rms current density | A/m2 | 1.50 × 107 | ||
| Teeth concentration factor | - | 2.984 | ||
| Yoke concentration factor | - | 3.661 | ||
| Total copper area in stator slots | m2 | 0.0014 | ||
| Calculated parameters | ||||
| Parameter Description | Units | FEA validation | SM | Error (%) |
| Electromagnetic Torque | Nm | 102.54 | 102.83 | −0.28 |
| Total active parts weight | kg | 14.79 | 14.68 | 0.74 |
| Total losses | W | 2990 | 3000 | −0.33 |
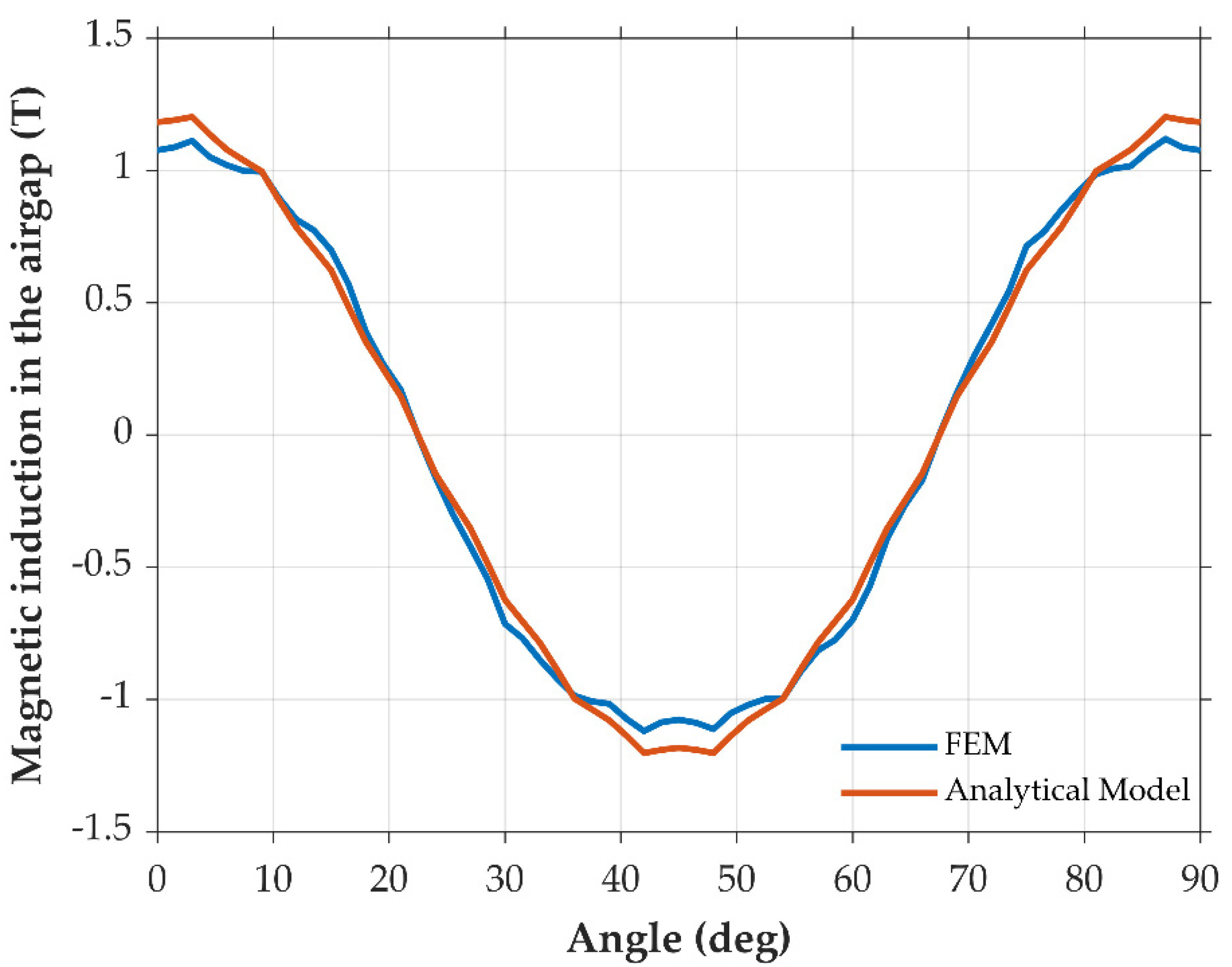
| Fundamental magnetic induction | T | 0.933 | 0.946 | −1.39 |
| Teeth flux density | T | 1.72 | 1.7 | 1.16 |
| Yoke flux density | T | 1.71 | 1.7 | 1.16 |
| Nominal phase current | Arms | 218.90 | 218.90 | 0 |
| Electrical phase resistance | Ohm | 0.0134 | 0.0137 | −2.24 |
| Cooling effort | W/(m3Ohm) | 8.46 × 1011 | 8.48 × 1011 | −0.24 |
| Magnetic stator losses | W | 941 | 933 | 0.85 |
| Parameter Description | Units | Optimal Value |
|---|---|---|
| Slot depth | m | 0.014 |
| Rotor inner diameter | m | 0.098 |
| Nominal RMS phase current | A | 242 |
| Slot opening angle | rad | 0.084 |
| Stator yoke thickness | m | 0.0059 |
| Motor axial length | m | 0.15 |
| Machine control angle | deg | −10.97 |
| Magnet thickness | m | 0.007 |
| Parameter Description | Units | Value |
|---|---|---|
| Electromagnetic Torque | Nm | 103.5 |
| Total active parts weight | kg | 14.25 |
| Total losses | W | 3000 |
| Fundamental magnetic induction | T | 0.83 |
| Teeth flux density | T | 1.7 |
| Yoke flux density | T | 1.58 |
| Nominal phase current | Arms | 242 |
| Electrical phase resistance | Ohm | 0.011 |
| Cooling effort | A2/m3 | 9.20 × 1011 |
| Parameter Description | Units | FEA | SM | Difference (%) |
|---|---|---|---|---|
| Electromagnetic Torque | Nm | 103.5 | 102.8 | +0.7 |
| Total active parts weight | kg | 14.25 | 14.68 | −3 |
| Total losses | W | 3000 | 3000 | 0.0 |
| Fundamental magnetic induction | T | 0.83 | 0.946 | −14 |
| Teeth flux density | T | 1.58 | 1.7 | −7.6 |
| Yoke flux density | T | 1.7 | 1.7 | 0.00 |
| Nominal phase current | Arms | 242 | 218.90 | +9.6 |
| Electrical phase resistance | Ohm | 0.0110 | 0.0137 | −24.6 |
| Magnetic stator losses | W | 888 | 933 | −5.1 |
| Power density | kW/kg | 11.41 | 10.90 | +4.5 |
| Simulation time | h | 5.38 | 1.2 | +77.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez, R.; Pelletier, A.; Grenier, J.-M.; Cros, J.; Rancourt, D.; Freer, R. Comparison between Space Mapping and Direct FEA Optimizations for the Design of Halbach Array PM Motor. Energies 2022, 15, 3969. https://doi.org/10.3390/en15113969
Pérez R, Pelletier A, Grenier J-M, Cros J, Rancourt D, Freer R. Comparison between Space Mapping and Direct FEA Optimizations for the Design of Halbach Array PM Motor. Energies. 2022; 15(11):3969. https://doi.org/10.3390/en15113969
Chicago/Turabian StylePérez, Ramón, Alexandre Pelletier, Jean-Michel Grenier, Jérôme Cros, David Rancourt, and Richard Freer. 2022. "Comparison between Space Mapping and Direct FEA Optimizations for the Design of Halbach Array PM Motor" Energies 15, no. 11: 3969. https://doi.org/10.3390/en15113969
APA StylePérez, R., Pelletier, A., Grenier, J.-M., Cros, J., Rancourt, D., & Freer, R. (2022). Comparison between Space Mapping and Direct FEA Optimizations for the Design of Halbach Array PM Motor. Energies, 15(11), 3969. https://doi.org/10.3390/en15113969







