An Approach for the Analysis of Energy Resource Selection Based on Attributes by Using Dombi T-Norm Based Aggregation Operators
Abstract
:1. Introduction
2. Preliminaries
- iff and .
- iff and
- .
- .
- .
- .
- .
- If , then .
- If , then .
3. IVIF Dombi Operational Laws
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
4. Dombi AOs
5. Model for MADM Using IVIF Information
5.1. Algorithm
5.2. Case Study
5.3. Example
- : Cost.
- : Quantity.
- : Reliability.
- : Sustainability.
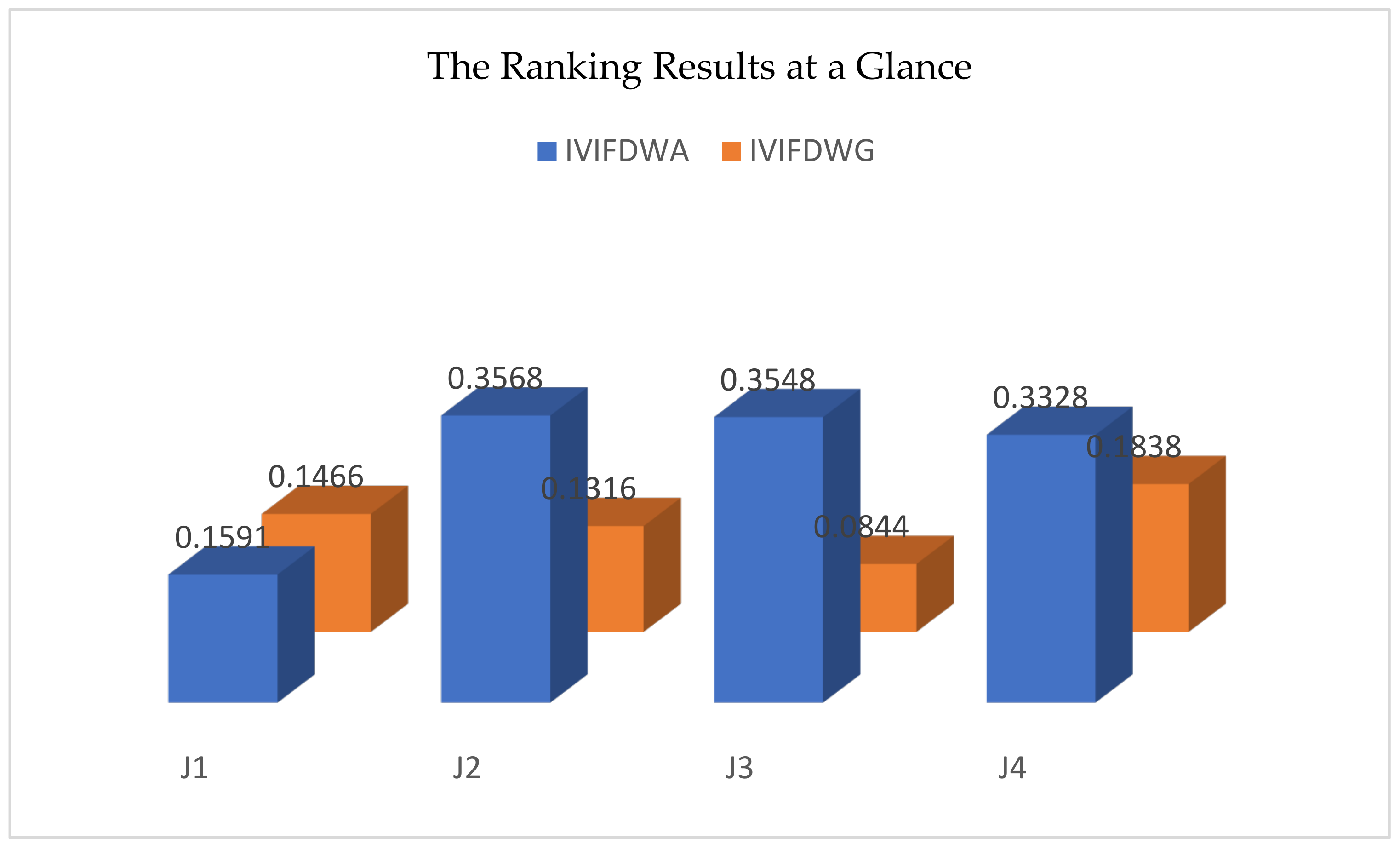
5.4. Impact of on Ranking Results
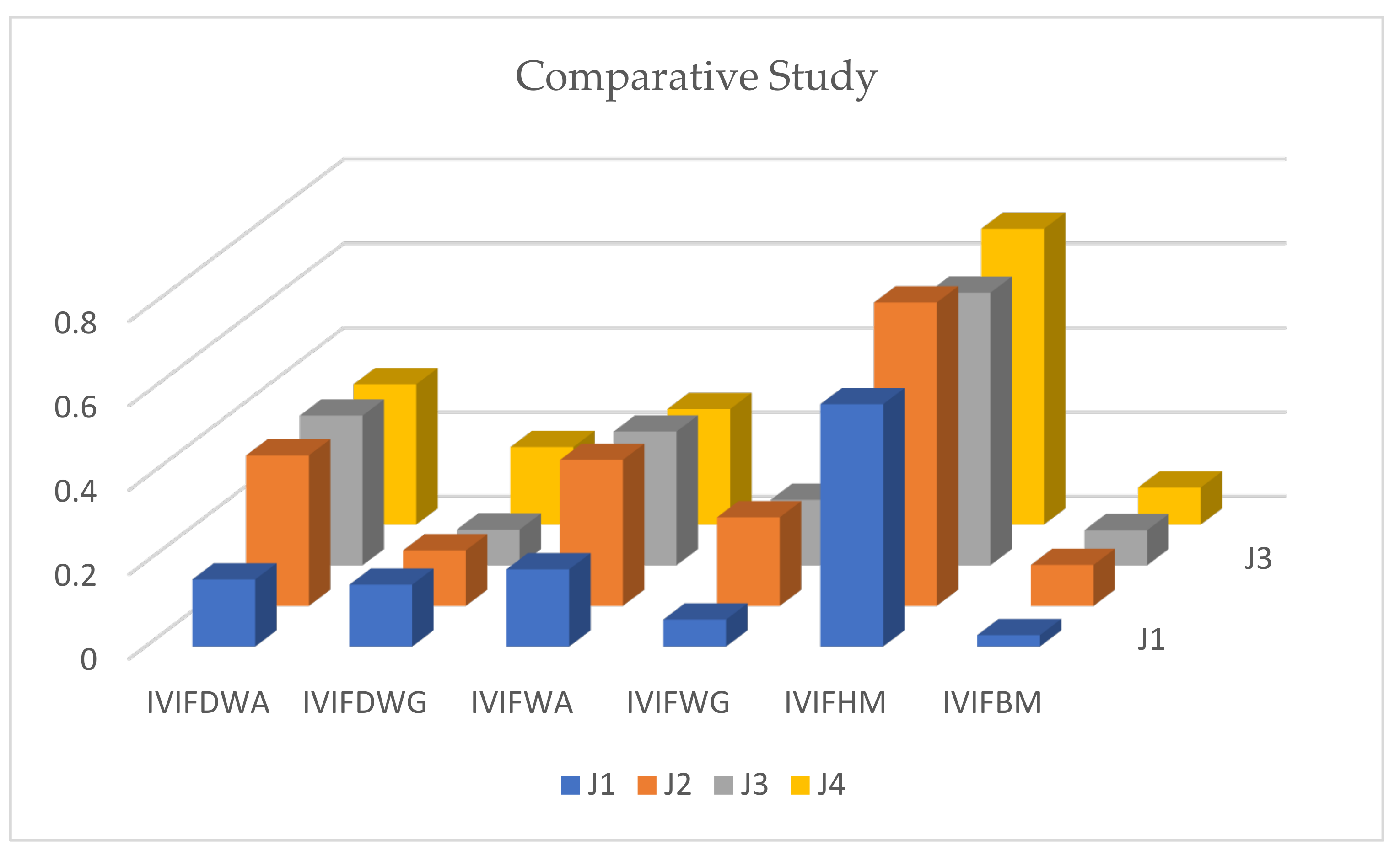
6. Comparative Study
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DTN | Dombi t-norm |
| TN | T-norm |
| TCN | T-conorm |
| MG | Membership grade |
| NMG | Non-MG |
| AO | Aggregation operator |
| IVIF | Interval-valued intuitionistic fuzzy |
| IVIFN | IVIF number |
| IVIFDWA | IVIF Dombi weighted averaging |
| IVIFDWG | IVIF Dombi weighted geometric |
| FS | Fuzzy set |
| IFS | Intuitionistic FS |
| HD | Hesitancy degree |
| MADM | Multi-attribute decision-making |
| IVIFDOWA | IVIF Dombi ordered weighted averaging |
| IVIFDHA | IVIF Dombi hybrid averaging |
| IVIFDWG | IVIF Dombi ordered weighted geometric |
| IVIFDHG | IVIF Dombi hybrid geometric |
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Kahraman, C.; Oztaysi, B.; Onar, S.C. Interval-Valued Intuitionistic Fuzzy Confidence Intervals. J. Intell. Syst. 2019, 28, 307–319. [Google Scholar] [CrossRef]
- Romaniuk, M.; Hryniewicz, O. Discrete and Smoothed Resampling Methods for Interval-Valued Fuzzy Numbers. IEEE Trans. Fuzzy Syst. 2021, 29, 599–611. [Google Scholar] [CrossRef]
- Tyagi, S.K. Reliability Analysis of a Powerloom Plant Using Interval Valued Intuitionistic Fuzzy Sets. Appl. Math. 2014, 5, 2008–2015. [Google Scholar] [CrossRef]
- Song, Y.; Fu, Q.; Wang, Y.-F.; Wang, X. Divergence-based cross entropy and uncertainty measures of Atanassov’s intuitionistic fuzzy sets with their application in decision making. Appl. Soft Comput. 2019, 84, 105703. [Google Scholar] [CrossRef]
- Wei, A.-P.; Li, D.-F.; Lin, P.-P.; Jiang, B.-Q. An information-based score function of interval-valued intuitionistic fuzzy sets and its application in multiattribute decision making. Soft Comput. 2021, 25, 1913–1923. [Google Scholar] [CrossRef]
- Xue, Y.; Deng, Y. Decision making under measure-based granular uncertainty with intuitionistic fuzzy sets. Appl. Intell. 2021, 51, 6224–6233. [Google Scholar] [CrossRef]
- Joshi, D.; Kumar, S. Improved Accuracy Function for Interval-Valued Intuitionistic Fuzzy Sets and Its Application to Multi–Attributes Group Decision Making. Cybern. Syst. 2018, 49, 64–76. [Google Scholar] [CrossRef]
- Atanassov, K.; Gargov, G. Interval valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, W. A new distance measure of interval-valued intuitionistic fuzzy sets and its application in decision making. Soft Comput. 2020, 24, 6987–7003. [Google Scholar] [CrossRef]
- Kumar, K.; Chen, S.-M. Multiattribute decision making based on interval-valued intuitionistic fuzzy values, score function of connection numbers, and the set pair analysis theory. Inf. Sci. 2021, 551, 100–112. [Google Scholar] [CrossRef]
- Liu, S.; Yu, W.; Chan, F.T.S.; Niu, B. A variable weight-based hybrid approach for multi-attribute group decision making under interval-valued intuitionistic fuzzy sets. Int. J. Intell. Syst. 2021, 36, 1015–1052. [Google Scholar] [CrossRef]
- Haiyun, C.; Zhixiong, H.; Yüksel, S.; Dinçer, H. Analysis of the innovation strategies for green supply chain management in the energy industry using the QFD-based hybrid interval valued intuitionistic fuzzy decision approach. Renew. Sustain. Energy Rev. 2021, 143, 110844. [Google Scholar] [CrossRef]
- Liu, J.; Huang, B.; Li, H.; Bu, X.; Zhou, X. Optimization-Based Three-Way Decisions with Interval-Valued Intuitionistic Fuzzy Information. IEEE Trans. Cybern. 2022, 1–15. [Google Scholar] [CrossRef]
- Xie, Y.; He, L.; Xiang, W.; Peng, Z.; Ming, X.; Goh, M. Prioritizing risk factors in sustainable supply chain using fuzzy Kano and interval-valued intuitionistic fuzzy QFD. Kybernetes 2022, in press. [CrossRef]
- Hu, X.; Yang, S.; Zhu, Y.-R. Multiple-Attribute Decision Making Based on Interval-Valued Intuitionistic Fuzzy Generalized Weighted Heronian Mean. Information 2022, 13, 138. [Google Scholar] [CrossRef]
- Jan, N.; Ullah, K.; Mahmood, T.; Garg, H.; Davvaz, B.; Saeid, A.B.; Broumi, S. Some root level modifications in interval valued fuzzy graphs and their generalizations including neutrosophic graphs. Mathematics 2019, 7, 72. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Jiang, L.; Bu, C.; Zhu, Y.; Wu, X. Interval-Valued Intuitionistic Fuzzy Decision with Graph Pattern in Big Graph. IEEE Trans. Emerg. Top. Comput. Intell. 2022, 1–11. [Google Scholar] [CrossRef]
- Liang, Z.-C.; Yang, Y.; Liao, S.-G. Interval-valued intuitionistic fuzzy two-sided matching model considering level of automation. Appl. Soft Comput. 2022, 116, 108252. [Google Scholar] [CrossRef]
- Baumann, M.; Weil, M.; Peters, J.F.; Chibeles-Martins, N.; Moniz, A.B. A review of multi-criteria decision making approaches for evaluating energy storage systems for grid applications. Renew. Sustain. Energy Rev. 2019, 107, 516–534. [Google Scholar] [CrossRef]
- Ijadi Maghsoodi, A.; Ijadi Maghsoodi, A.; Mosavi, A.; Rabczuk, T.; Zavadskas, E.K. Renewable Energy Technology Selection Problem Using Integrated H-SWARA-MULTIMOORA Approach. Sustainability 2018, 10, 4481. [Google Scholar] [CrossRef] [Green Version]
- Souzangarzadeh, H.; Rezvani, M.; Jahan, A. Selection of optimum design for conical segmented aluminum tubes as energy absorbers: Application of MULTIMOORA method. Appl. Math. Model. 2017, 51, 546–560. [Google Scholar] [CrossRef]
- Ilbahar, E.; Cebi, S.; Kahraman, C. A state-of-the-art review on multi-attribute renewable energy decision making. Energy Strategy Rev. 2019, 25, 18–33. [Google Scholar] [CrossRef]
- Taylan, O.; Kaya, D.; Demirbas, A. An integrated multi attribute decision model for energy efficiency processes in petrochemical industry applying fuzzy set theory. Energy Convers. Manag. 2016, 117, 501–512. [Google Scholar] [CrossRef]
- Xu, H.; Sze, J.Y.; Romagnoli, A.; Py, X. Selection of Phase Change Material for Thermal Energy Storage in Solar Air Conditioning Systems. Energy Procedia 2017, 105, 4281–4288. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, F.; Ullah, K. Waste Clothing Recycling Channel Selection Using a CoCoSo-D Method Based on Sine Trigonometric Interaction Operational Laws with Pythagorean Fuzzy Information. Energies 2022, 15, 2010. [Google Scholar] [CrossRef]
- Akram, M.; Ullah, K.; Pamucar, D. Performance Evaluation of Solar Energy Cells Using the Interval-Valued T-Spherical Fuzzy Bonferroni Mean Operators. Energies 2022, 15, 292. [Google Scholar] [CrossRef]
- Pamučar, D.; Badi, I.; Sanja, K.; Obradović, R. A Novel Approach for the Selection of Power-Generation Technology Using a Linguistic Neutrosophic CODAS Method: A Case Study in Libya. Energies 2018, 11, 2489. [Google Scholar] [CrossRef] [Green Version]
- Riaz, M.; Sałabun, W.; Athar Farid, H.M.; Ali, N.; Wątróbski, J. A Robust q-Rung Orthopair Fuzzy Information Aggregation Using Einstein Operations with Application to Sustainable Energy Planning Decision Management. Energies 2020, 13, 2155. [Google Scholar] [CrossRef]
- Riaz, M.; Farid, H.M.A.; Shakeel, H.M.; Aslam, M.; Mohamed, S.H. Innovative q-rung orthopair fuzzy prioritized aggregation operators based on priority degrees with application to sustainable energy planning: A case study of Gwadar. AIMS Math. 2021, 6, 12795–12831. [Google Scholar] [CrossRef]
- Ullah, K.; Mahmood, T.; Jan, N.; Ahmad, Z. Policy decision making based on some averaging aggregation operators of t-spherical fuzzy sets; a multi-attribute decision making approach. Ann. Optim. Theory Pract. 2020, 3, 69–92. [Google Scholar] [CrossRef]
- Ullah, K.; Mahmood, T.; Garg, H. Evaluation of the performance of search and rescue robots using T-spherical fuzzy hamacher aggregation operators. Int. J. Fuzzy Syst. 2020, 22, 570–582. [Google Scholar] [CrossRef]
- Ali, Z.; Mahmood, T.; Ullah, K.; Khan, Q. Einstein Geometric Aggregation Operators using a Novel Complex Interval-valued Pythagorean Fuzzy Setting with Application in Green Supplier Chain Management. Rep. Mech. Eng. 2021, 2, 105–134. [Google Scholar] [CrossRef]
- Peng, H.; Wang, J.; Cheng, P. A linguistic intuitionistic multi-criteria decision-making method based on the Frank Heronian mean operator and its application in evaluating coal mine safety. Int. J. Mach. Learn. Cybern. 2018, 9, 1053–1068. [Google Scholar] [CrossRef]
- Hussain, A.; Ullah, K.; Yang, M.-S.; Pamucar, D. Aczel-Alsina Aggregation Operators on T-Spherical Fuzzy (TSF) Information with Application to TSF Multi-Attribute Decision Making. IEEE Access 2022, 10, 26011–26023. [Google Scholar] [CrossRef]
- Dombi, J. A general class of fuzzy operators, the DeMorgan class of fuzzy operators and fuzziness measures induced by fuzzy operators. Fuzzy Sets Syst. 1982, 8, 149–163. [Google Scholar] [CrossRef]
- Seikh, M.R.; Mandal, U. Intuitionistic fuzzy Dombi aggregation operators and their application to multiple attribute decision-making. Granul. Comput. 2021, 6, 473–488. [Google Scholar] [CrossRef]
- Sinani, F.; Erceg, Z.; Vasiljević, M. An evaluation of a third-party logistics provider: The application of the rough Dombi-Hamy mean operator. Decis. Mak. Appl. Manag. Eng. 2020, 3, 92–107. [Google Scholar] [CrossRef]
- Mohanta, K.; Dey, A.; Pal, A. A study on picture Dombi fuzzy graph. Decis. Mak. Appl. Manag. Eng. 2020, 3, 119–130. [Google Scholar] [CrossRef]
- Vojinović, N.; Stević, Ž.; Tanackov, I. A Novel IMF SWARA-FDWGA-PESTEL Analysis for Assessment of Healthcare System. Oper. Res. Eng. Sci. Theory Appl. 2022, 5, 139–151. [Google Scholar] [CrossRef]
- Pamucar, D. Normalized weighted geometric Dombi Bonferroni mean operator with interval grey numbers: Application in multicriteria decision making. Rep. Mech. Eng. 2020, 1, 44–52. [Google Scholar] [CrossRef]
- UUllah, K.; Mahmood, T.; Jan, N.; Broumi, S.; Khan, Q. On bipolar-valued hesitant fuzzy sets and their applications in multi-attribute decision making. Nucleus 2018, 55, 85–93. [Google Scholar]
- Ullah, K.; Garg, H.; Gul, Z.; Mahmood, T.; Khan, Q.; Ali, Z. Interval valued T-Spherical Fuzzy Information Aggregation Based on Dombi t-norm and Dombi t-conorm for multi-attribute decision making problems. Symmetry 2021, 13, 1053. [Google Scholar] [CrossRef]
- Ye, J. Multicriteria fuzzy decision-making method based on a novel accuracy function under interval-valued intuitionistic fuzzy environment. Expert Syst. Appl. 2009, 36, 6899–6902. [Google Scholar] [CrossRef]
- Wu, L.; Wang, J.; Gao, H. Models for competiveness evaluation of tourist destination with some interval-valued intuitionistic fuzzy Hamy mean operators. J. Intell. Fuzzy Syst. 2019, 36, 5693–5709. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, Q. A multi-criteria decision making procedure based on interval-valued intuitionistic fuzzy bonferroni means. J. Syst. Sci. Syst. Eng. 2011, 20, 217–228. [Google Scholar] [CrossRef]
- Al-shami, T.M.; Ibrahim, H.Z.; Azzam, A.A.; EL-Maghrabi, A.I. SR-Fuzzy Sets and Their Weighted Aggregated Operators in Application to Decision-Making. J. Funct. Spaces 2022, 2022, 3653225. [Google Scholar] [CrossRef]
- Zulqarnain, R.M.; Siddique, I.; EI-Morsy, S. Einstein-Ordered Weighted Geometric Operator for Pythagorean Fuzzy Soft Set with Its Application to Solve MAGDM Problem. Math. Probl. Eng. 2022, 2022, 5199427. [Google Scholar] [CrossRef]
- Garg, H.; Sirbiladze, G.; Ali, Z.; Mahmood, T. Hamy mean operators based on complex q-Rung Orthopair fuzzy setting and their application in multi-attribute decision making. Mathematics 2021, 9, 2312. [Google Scholar] [CrossRef]
- Ali, Z.; Mahmood, T.; Yang, M.-S. TOPSIS Method Based on Complex Spherical Fuzzy Sets with Bonferroni Mean Operators. Mathematics 2020, 8, 1739. [Google Scholar] [CrossRef]
- Wu, L.; Wei, G.; Wu, J.; Wei, C. Some Interval-Valued Intuitionistic Fuzzy Dombi Heronian Mean Operators and their Application for Evaluating the Ecological Value of Forest Ecological Tourism Demonstration Areas. Int. J. Environ. Res. Public Health 2020, 17, 829. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ullah, K.; Hassan, N.; Mahmood, T.; Jan, N.; Hassan, M. Evaluation of Investment Policy Based on Multi-Attribute Decision-Making Using Interval Valued T-Spherical Fuzzy Aggregation Operators. Symmetry 2019, 11, 357. [Google Scholar] [CrossRef] [Green Version]
- Farahbod, F.; Eftekhari, M. Comparison of different T-norm operators in classification problems. Int. J. Fuzzy Log. Syst. 2012, 2, 33–39. [Google Scholar] [CrossRef]
- Ullah, K. Picture fuzzy maclaurin symmetric mean operators and their applications in solving multiattribute decision-making problems. Math. Probl. Eng. 2021, 2021, 1098631. [Google Scholar] [CrossRef]
- Mahmood, T. A novel approach towards bipolar soft sets and their applications. J. Math. 2020, 2020, 4690808. [Google Scholar] [CrossRef]
- Ali, Z.; Mahmood, T.; Pamucar, D.; Wei, C. Complex Interval-Valued q-Rung Orthopair Fuzzy Hamy Mean Operators and Their Application in Decision-Making Strategy. Symmetry 2022, 14, 592. [Google Scholar] [CrossRef]
- Pi, T.; Hu, H.; Lu, J.; Chen, X. The Analysis of Fintech Risks in China: Based on Fuzzy Models. Mathematics 2022, 10, 1395. [Google Scholar] [CrossRef]
- Ramakrishnan, K.R.; Chakraborty, S. A Cloud TOPSIS model for green supplier selection. Facta Univ. Ser. Mech. Eng. 2020, 18, 375–397. [Google Scholar] [CrossRef]
- Fazlollahtabar, H.; Kazemitash, N. Green supplier selection based on the information system performance evaluation using the integrated Best-Worst Method. Facta Univ. Ser. Mech. Eng. 2021, 19, 345–360. [Google Scholar] [CrossRef]
| MD | NMD | MD | NMD | MD | NMD | MD | NMD | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L | U | L | U | L | U | L | U | L | U | L | U | L | U | L | U | |
| Scores | ||
|---|---|---|
| M | Ranking Order | Optimal Alternative |
|---|---|---|
| M | Ranking Order | Optimal Alternative |
|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Waqar, M.; Ullah, K.; Pamucar, D.; Jovanov, G.; Vranješ, Ð. An Approach for the Analysis of Energy Resource Selection Based on Attributes by Using Dombi T-Norm Based Aggregation Operators. Energies 2022, 15, 3939. https://doi.org/10.3390/en15113939
Waqar M, Ullah K, Pamucar D, Jovanov G, Vranješ Ð. An Approach for the Analysis of Energy Resource Selection Based on Attributes by Using Dombi T-Norm Based Aggregation Operators. Energies. 2022; 15(11):3939. https://doi.org/10.3390/en15113939
Chicago/Turabian StyleWaqar, Mujab, Kifayat Ullah, Dragan Pamucar, Goran Jovanov, and Ðordje Vranješ. 2022. "An Approach for the Analysis of Energy Resource Selection Based on Attributes by Using Dombi T-Norm Based Aggregation Operators" Energies 15, no. 11: 3939. https://doi.org/10.3390/en15113939
APA StyleWaqar, M., Ullah, K., Pamucar, D., Jovanov, G., & Vranješ, Ð. (2022). An Approach for the Analysis of Energy Resource Selection Based on Attributes by Using Dombi T-Norm Based Aggregation Operators. Energies, 15(11), 3939. https://doi.org/10.3390/en15113939









