Abstract
During supply chain redesign processes, many environmental initiatives at facilities and their surrounding regions are affected by the closing, opening, or even broadening of facilities. These initiatives may be about the surplus renewable energies that the facility generates for its region, the renewable energy sources that are available in the area for the facility, or the ecological relationships between facilities and their surrounding regions in general. The implications of these ecological relationships for the supply chain redesign problem were considered in this study in order to minimize the negative outcomes while minimizing the process’s related expenses. Thus, to minimize the unwanted effects, an objective function is defined in addition to the cost objective, which results in a bi-objective problem. Although small cases can be solved by exact methods such as AUGMECON, for larger scales, a matheuristic algorithm needs to be developed. The efficiency of the developed algorithm was investigated through numerical instances as well as with different metrics including a Pareto analysis. The results at larger scales show a shorter runtime of the matheuristic compared to the AUGMECON algorithm. Additionally, the matheuristic method provides a wider range of decision areas for managers.
1. Introduction
Supply chain networks consist of different nodes such as suppliers, plants, warehouses, retailers, etc. Depending on the circumstances, each network has a unique set of difficulties that must be addressed in order to maximize monetary and non-monetary profits. Many of these challenges, such as transportation, storage, uncertainty of parameters, and routing and distribution, have been discussed in many studies with some details specific to certain industries [1,2,3,4,5,6]. One of the most challenging issues in this area is the supply chain network redesign problem, which will be discussed in this study.
Due to the quick changes in circumstances in today’s world, managers must analyze the situation several years after designing an ideal supply chain network to determine the degree of deviation their supply chain network exhibits from the optimal network. Supply chain network redesign is a strategic planning process for improving an existing supply chain that takes into account present locations, restrictions, and properties in order to achieve a gradual transition from the current state to the best configuration. As a result, rebuilding a supply chain is more difficult than creating a new supply chain network [7].
The number of papers that discuss supply chain network redesign is increasing, and every one of them works on different aspects of this problem to try to find the best solution. A basic paper on this problem is [8]. The decisions in this document include phase-out, merging of existing warehouses, and the establishment of new sites; the capacity could be completely transferred during unification. Furthermore, redesign decisions must be made in a way that does not jeopardize the ability to meet customer expectations. Finally, the MILP model has solved these issues by partially relaxing the allocation integer variables combined with rounding procedures.
Many studies have studied different aspects of supply chain network redesign problems. For example, [9,10,11] tried to work on the redesign problem in reverse or closed loop supply chains. Additionally, some authors, such as those of [7,12,13], consider uncertainty and deal with this uncertainty using different approaches, including stochastic or robust methods. Additionally, [14] used supply chain redesign as a way of dealing with the consequences of disruption.
During recent decades, sustainability has become one of the most important issues to be considered during the design and operation of supply chains. Sustainable supply chain management is the management of material and information flows as well as cooperation among companies along the supply chain while taking goals from all three dimensions of sustainable development (economic, environmental, and social) and stakeholder requirements into account [15].
Although sustainable supply chain practices encourage the use of sustainable energy [16] most of the time, environmental initiatives (e.g., energy sources) are often overlooked among all aspects of sustainability that should be considered throughout a sustainable redesign process. The environmental impacts are considered in some redesign papers; however, the accessibility and effect of renewable energies are not. In this paper, the effect of renewable energies and their costs and benefits for new and old warehouses of a supply chain are considered.
Unlike the great number of papers on sustainable supply chain network design problems (such as [17,18,19], etc.), there are not many papers that consider sustainable supply chain networks’ redesign. The authors of [20] worked on redesigning a sustainable reverse supply chain. They proposed a multi-objective model to minimize the cost of this process, maximizing the favorable environmental effects and the customer service level. A multi criteria programming approach algorithm to manage several objectives linked with stochastic programming to address uncertainty is developed in this investigation.
In every supply chain redesign process, there are some facilities that should be closed, some new facilities that should be built, and some that should be consolidated with each other. Depending on the region surrounding the warehouses, there are some characteristics that indicate how well this region can implement environmental initiatives such as sunlight, wind, and waves. Using such energy sources has some costs for the required energy equipment and also has some financial and non-financial benefits for the facility. In some areas, for example, the surplus energy generated can be used for other buildings, and the government may reap some financial benefits from the building that generates this energy.
We should consider several questions in order to gain a better understanding of this problem. Which environmental initiatives are available and should they be implemented? Which renewable energy sources are more accessible in which potential locations? Based on their environmental initiatives, which of the old or new potential locations for a facility can lower expenses or increase profits? How badly does a corporation want to initiate or terminate an ecological relationship in a certain region?
Additionally, there are plenty of other relevant questions that need to be addressed. The easiest way to get the best answer to all of these issues is to include this issue as one of the objectives of the mathematical model of the redesign problem in order to arrive at the optimal set of started or halted partnerships as well as the ideal cost.
The lack of papers that consider sustainability in the supply chain redesign process led us to regard this issue as one of the goals of this paper. The rest of this paper is organized as follows: in the Section 2, the problem and its assumptions are defined clearly, and a mathematical model is presented. Additionally, the mathematical model is changed based on the AUGMECON method and some problems are solved via this method. The matheuristic approach and how we used this algorithm will be described. Additionally, the same example that is solved via the AUGMECON method is then solved via the matheuristic method and the results are compared. In Section 3, some metrics are used for the comparison of the Pareto frontier results of the AUGMECON and matheuristic methods. Finally, the Section 4 summarizes the conclusions of this paper.
2. Materials and Methods
In this study, we considered a three-echelon supply chain network including manufacturing plants, warehouses, and customer zones. The main assumptions were taken from [8]. The network has some demands from different customers that need to be met. However, due to many changes to the supply chain over the years and external factors, its performance is sub-optimal. Thus, the supply chain network needs to be modified to lead the network to its new optimal or near-optimal position. During this redesign, some warehouses may be closed and some new potential warehouses may be established. Additionally, some old warehouses can be merged with some other old or even new warehouses. In this condition, we consider that the transportable capacity of the warehouse can be relocated. This capacity may include pallets, pallet racks, lift trucks, air condition tools, and so on. Most of the time, supply chain owners think that some changes such as redesigns are just absolute costs for them and they prefer to postpone this decision; however, redesigns not only advance the benefit for them in the long term but can also pay part of their own expenses by themselves. Whenever a warehouse is phased out, its capacity and equipment can be sold, and this brings revenue for the supply chain. Additionally, when a warehouse’s capacity is being relocated to another warehouse, its building can be sold and this brings revenue to the supply chain. Thus, minimizing the total cost of supply chain redesign is the objective function of this problem.
Another key issue in this area is the warehouse’s relationship with the region or the region’s components during the redesign process. The warehouse has the potential to form good ties with the surrounding neighborhood. This might be due to many different types of green collaborations; for instance, they may use electric cars in the area, which would be an environmental benefit in terms of reducing air pollution in the region. These ties may also be due to the excess amount of electricity generated by the warehouse’s renewable energy equipment (such as solar panels). The electricity authority in the region might plan for this extra energy to be utilized by other buildings in the area. As a result, when a new potential warehouse is being built or an existing warehouse is expanding due to consolidation, we will have more ecological cooperation with the region. Although there is a certain amount of expenditure associated with the installation of new equipment at these new facilities, the benefits gained through the region’s ecological collaboration are extraordinary. On the other hand, when warehouses are phased out or their capacity is transferred, their cooperation with the surrounding region will come to an end.
In a supply chain redesign process, taking into account the warehouse’s ecological relationship with the people and environment of each location is a moral concern. Warehouses are located in different regions and every region has its own circumstances. Properties in some areas may be more reliant on the electricity generated by warehouses, while in other areas, they may not. Some areas may be ideal for receiving solar energy due to their constant sunshine, while others may be gloomy and wet, making solar panels unsuitable. Therefore, during this redesign process, we should not ignore regional ecological characteristics and effects. This element is treated as a separate objective function in this paper, and it should be optimized by taking into account some weights (values) for initiating and terminating collaborations with various regions.
2.1. Mathematical Model
2.1.1. Assumptions
- A warehouse’s whole capacity is shifted when it is merged with another warehouse.
- Every existing warehouse’s entire capacity can be moved to any new or existing warehouse that is built or will be built [8].
- There is a split delivery system in place, allowing each customer’s demand to be met from various warehouses.
- There are some ecological relationships between every warehouse and its region.
- Depending on the regional situation of a warehouse (ecological features of the region and ecological effects that the warehouse can have on the area), starting or stopping collaboration will have various results.
2.1.2. Sustainable Supply Chain Network Redesign (SSCNR)
In this section, the mathematical model of the SSCNR problem is presented.
Sets and indices
| F | Set of manufacturers indexed by i,j |
| We | Set of existing warehouses indexed by i,j |
| Wn | Set of potential locations for the new warehouses indexed by i,j |
| W | ; indexed by i,j |
| K | Set of customers indexed by i,j |
| S | Set of environmental initiatives (such as electric vehicle usage, renewable electricity generation, receiving enough sunshine, etc.) indexed by s |
| i,j |
Parameters
| di | |
| capi | |
| pcij | |
| hcij | |
| rij | Total cost of merging an existing warehouse i to a new site or other existing warehouse |
| fci | |
| fmi | Fix part of the maintenance cost for warehouse i |
| fni | |
| fsi | Saved cost resulting from the phase-out of the existing warehouse i |
| fbi | |
| whis | Value (weight) of implementing environmental initiatives (cooperation with the region) type s in warehouse i |
| wfis | Value (weight) of stopping environmental initiatives type s in warehouse i |
Decision variables
| Amount of transported product from node i to node j in the first layer (plant–warehouse) | |
| Amount of transported product from node i to node j in the second layer (warehouse–customer) | |
| A binary variable equal to 1 if the capacity of warehouse i remains open () or its capacity is moved to warehouse j() or a new warehouse i is established; 0, otherwise |
The sustainable supply chain network redesign model is as follows:
Subject to:
The first objective function (1) minimizes the costs and increases revenues, including production and storage costs; transportation costs; relocation costs; and establishing, equipment, and maintenance cost. Additionally, it aims to increase the revenues derived from the phasing out and relocation of warehouses.
The second objective function (2) tries to minimize the total value of stopping environmental initiatives and maximize the total value of implementing environmental initiatives in all types of set S in different warehouses.
Constraint (3) ensures that the amount of input and output products in every open warehouse is equal. Constraint (4) ensures that the total product flows from warehouse i to the set of customers covered by this warehouse cannot be larger than the installed capacity. Constraint (5) ensures that the demands of every customer will be satisfied from every warehouse. Constraint (6) assures that existing warehouse capacity cannot be combined into an unestablished or closed warehouse. Constraint (7) limits existing warehouse j to relocate to just one other warehouse. Constraint (8) assures that new warehouse capacity cannot be moved to other warehouses. Finally, constraints (9) and (10) display types of variables.
2.2. Augmented ε-Constraint
To solve a multi-objective problem with conflicts between objectives, a multi-objective optimization method is required. Consider the general form of a multi-objective model with n objective functions where is a vector of decision variables and X is the set of feasible solutions. For and , it is said that dominates if and only if: and . The set of feasible decision vectors that are not dominated by others is called a Pareto optimal frontier. Multi-objective optimization methods search to find a vector of decision variables that belong to the Pareto optimal frontier [21].
In order to show the conflict and gain the Pareto optimal frontier of the SSCNR model, a small problem was considered and solved via the AUGMECON (augmented ε-constraint [22]) method. According to this method, one of objectives (which is the first one in the SSCNR model) is considered the objective and other objectives (the second one) are added to the constraints. In order not to lose the importance of the second objective, this constraint should be changed from inequality to equality by using a slack variable. This slack variable (SV as a free variable) should be added to the objective via an ε coefficient to consider the impact of the second objective on the main objective (Equation (11)). The mathematical model of AUGMECON for this problem is represented as follows:
Subject to:
Constraints 3–10.
In constraint (12), the right-hand side (f2) demonstrates the nadir value of the second objective. Under conditions where the second objective is ignored completely, the solved problem displays the optimal variables and through replacing these variables in the second objective, we find its nadir value, which is considered its worst value.
As mentioned above, a small size of a supply chain is considered. Its data are presented in Appendix A (Table A1 and Table A2) and all parameters are generated through GAMS 27.3.0. In this example, 20 warehouses are considered where the first 10 warehouses are existing and the other 10 are potential points for establishing new warehouses. This problem was solved in GAMS 27.3.0, CPLEX 12.2 using a computer with 6GB of RAM and Intel Core i5 2.53 GHz CPU. Its Pareto optimal frontier is illustrated in Figure 1.
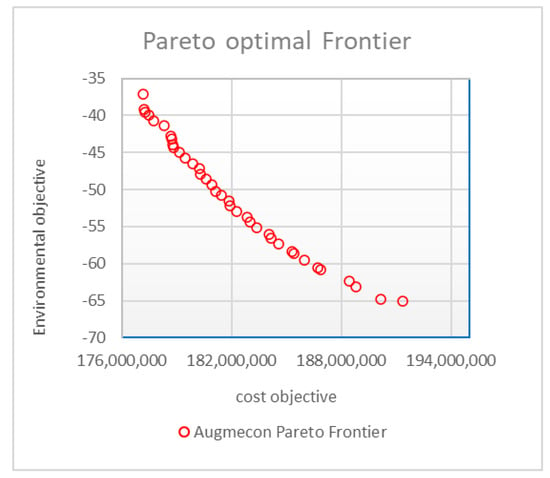
Figure 1.
Pareto optimal frontier of AUGMECON.
Figure 1 demonstrates the conflict between two objectives. Since the model is trying to minimize the total cost of the redesign process, the increase in the social object value is visible. As the model tries to minimize the ecological objective, the cost objective rises. Choosing one of the points on the frontier as the final decision depends on the preferences in the managing system of the supply chain and is up to the supply chain managers.
2.3. Matheuristic
As mentioned above, the small SSCNR model was solved in GAMS and we reached the exact solution via the AUGMECON approach, but reaching the exact solutions for bigger problems is not possible within a reasonable time. Therefore, a solution is needed for bigger scales. We have developed a matheuristic algorithm (combination of metaheuristics and mathematical modeling). Our algorithm is based on the NSGA-II method because of its popularity, its ease of use, and its capability to solve similar problems. NSGA-II was first developed by [23] based on genetic algorithms. NSGA-II was conceived as one of the famous Pareto-based multi-objective evolutionary algorithms [24].
Matheuristic in SSCNR
In the proposed algorithm, the chromosome defined for this problem is an array with a length equal to the total number of warehouses. The first group of cells demonstrates the existing warehouses while the other one represents the set of new warehouses (Figure 2). The cells regarding the existing warehouses can take a value between 0 and the total number of warehouses. This value shows the action that should be taken based on the solution. If the value is equal to 0, the warehouse must be closed, while a positive number shows the destination to which the warehouse is relocated. Note that if this value is equal to the number of the warehouse, it means that this warehouse remains open.

Figure 2.
Structure of chromosomes in the proposed algorithm for SSCNR.
The second group of cells (the new warehouses) can only take the value of 1 or 0, which shows whether the warehouse is open or not, respectively.
The value of each cell is randomly generated within the defined domain. However, all possible mistakes are revised through a correction process. In this process, on the one hand, all existing warehouses that are relocated are checked to ensure the feasibility of the decision. If the destination is not available (closed, not opened, or relocated itself), the origin warehouse cannot be transferred. As a result, in this stage of correction, the origin warehouse should be closed or remain open in its current location, or the destination warehouse should remain open/be opened. On the other hand, the total capacity is checked to ensure the feasibility of the problem. If the total capacity of the chromosome is not enough to satisfy the demands, some of the closed warehouses may be opened to add to the total capacity of the warehouse network. All chromosomes of the initial population and new offspring after each iteration will be checked through this correction process before the non-domination sorting phase.
In the first step of the algorithm (Figure 3), an initial population is generated and revised. The popsize for generating the initial population is 50. This value was determined experimentally to correspond with the quality of the solution and the time required to calculate it. In this stage, the chromosomes only contain information on whether a warehouse is open, closed, relocated, or remains unchanged. With this information, the second objective function related to the minimization of the unwanted environmental effects can be calculated for each solution. However, the first objective function is dependent on the way in which the warehouses are assigned to the factories and customers. In order to reach the optimal assignment, a two-echelon capacitated allocation problem (an MIP) is defined and solved for each chromosome. The objective value of this MIP, along with the set of allocations, are saved as the chromosome’s property. Having both objectives’ value for each chromosome, they can be ranked based on the non-domination process to form the first Pareto optimal frontier. The remaining chromosomes will be ranked via the same process to make a second frontier and so on. Then, the crowded distance between the chromosomes in each frontier is calculated by a linear distance criterion. Afterward, the chromosomes are sorted first by the frontier rank and then by descending order of crowded distance. In the next step, chromosomes generate new offspring through a crossover process. Considering the mutation chance, new offspring may have different properties in comparison with their parents. Finally, the initial population and the new generation make the new population and all steps repeated until the stop condition (maximum iteration) is met. Ultimately, the matheuristic algorithm results in a non-dominated Pareto optimal frontier.
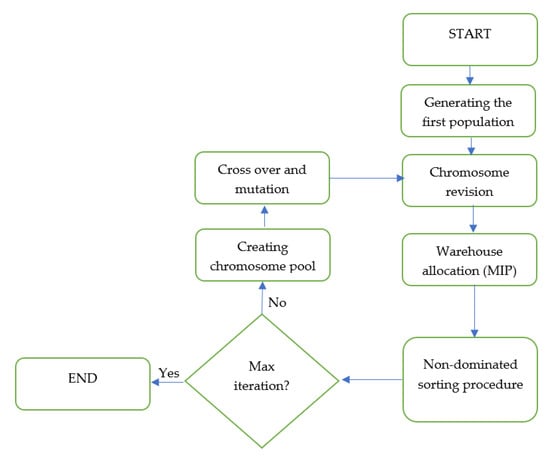
Figure 3.
The matheuristic algorithm.
Figure 4 depicts a comparison between the best Pareto frontier of the proposed matheuristic method and the Pareto optimal frontier of the AUGMECON method. As is visible in Figure 4, the proposed matheuristic method solutions (green points) are close to those of the AUGMECON method and it is acceptable for the supply chain manager, due to the good approximation of the optimal solution, to have arrived at via the exact method.
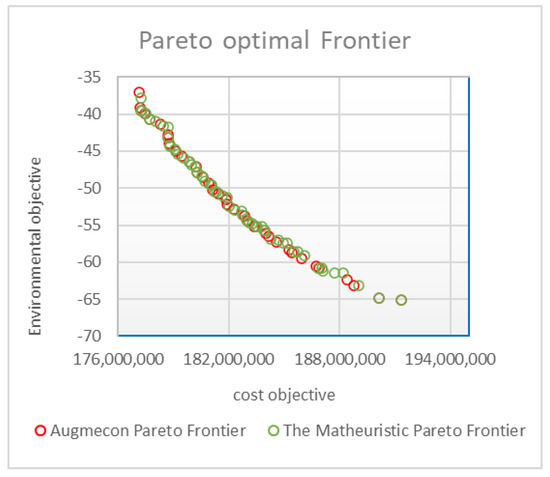
Figure 4.
Comparison between the Pareto frontier of the AUGMECON and proposed matheuristic methods.
3. Results and Discussion
In this section, two types of analysis are implemented to demonstrate how the proposed matheuristic method acts in comparison with the AUGMECON method. The first part of this analysis is an analogy of four metrics in both methods used in the previous example. The second part compares the run time of both methods on differently sized problems.
3.1. Quality Analyze
In this section, four metrics are examined in order to compare and contrast the quality of the solutions provided by both techniques. The comparison of two solution strategies in the context of a single objective problem may be used to get closer to the best solution. In multi-objective settings, however, we must compare the distinctive characteristics of solution approaches in order to evaluate them. When comparing Pareto frontier solutions, the non-dominated point ratios of each solution method, as well as their convergence, diversity, and spread, should be considered.
Metric 1. The first metric to check the quality of the solutions from the proposed matheuristic is the Pareto dominance indicator introduced by [25]. This metric measures the non-dominated points of each obtained Pareto frontier. Consider S1 and S2 sets of solutions achieved from solving the problem using the AUGMECON and the matheuristic methods, respectively; and where means that ai dominates bi. This metric measures the ratio of non-dominated points contributed by both methods (S1 and S2) to all the non-dominated points.
where NR(Sj) = 0 means that all points in Sj are dominated and where NR(Sj) = 1 indicates that all the solutions in non-dominated frontier B belong to Sj.
Metric 2. The second metric introduced by [26] is a type of distribution diversity metric.
where di is the normalized Euclidean distance between consecutive solutions and is the average of di. As is visible in the above formula, lower numbers of C(Sj) shows that the spread of points is more uniform in that Sj and that the Pareto frontier gives better decision conditions to supply chain managers.
Metric 3. The third metric was introduced by [23] and measures the spread of the solution.
where , while B* is the set of boundary solutions in B.
Metric 4. The convergence indicator introduced by [27] measures the solutions’ convergence with the original coordinates through Euclidean distance. This metric is desirable in a multi-objective solution space for minimization problems.
where fi,k determines the normalized kth objective function of the ith point of Sj. A low value of this metric shows that the Pareto frontier is closer to the original coordinates, which means better convergence.
A summary of the calculated metrics is depicted in Table 1. The example used in the previous section was solved by both methods and the runtimes of both methods were close at about 13 min. According to Table 1, in the first, second, and third metrics, the matheuristic has a better value compared to the exact method and it can be concluded that we reached more solutions over the same amount of time. The second metric reveals that the matheuristic method achieves an evenly distributed level of diversity in the Pareto frontier, and the third metric shows that this method has a wider range of solutions across the entire true front region. In the fourth metric, the exact method has a better value, but the value of this metric with the matheuristic method is not so far from that of the AUGMECON method, and according to all aspects and metrics, it is worth solving bigger problems using the matheuristic method in order to achieve a shorter runtime.

Table 1.
Performance metrics for the AUGMECON and matheuristic methods.
3.2. Solving Time Analysis
In this section, the efficiency of both algorithms at different problem scales is investigated. According to Table 2, at small and medium scales, both algorithms were able to arrive at a Pareto frontier in a relatively reasonable time. It could be inferred that the Pareto frontier obtained from the matheuristic algorithm is acceptable in four metrics compared to the AUGMECON algorithm and in some cases, it even did better than the exact algorithm in terms of the variety, spread, and distribution of the solution. At greater scales, the exact method was not able to reach the Pareto optimal frontier in a reasonable time (i.e., 100,000 s). Therefore, it makes sense to use the proposed matheuristic method to have an acceptable to near optimal Pareto frontier for a SSCNR.

Table 2.
Solving time comparison for the AUGMECON and matheuristic methods.
4. Conclusions
In this study, the ecological characteristics of the region and the ecological relationship between the warehouse and the region were considered in terms of the environmental aspects of sustainability during a supply chain network redesign. Minimizing the amount of stopped ecological collaborations and maximizing the amount of implemented environmental initiatives are regarded as objectives besides the cost objective. A matheuristic algorithm was proposed to solve problems at larger scales and the efficiency of the algorithm was shown at different problem scales and compared with those of the AUGMECON method, which is an exact algorithm. Moreover, four metrics were adopted to investigate the quality of the resulting Pareto frontier from the matheuristic algorithm. The results show that the proposed algorithm not only performs better than the AUGMECON method in terms of runtime but can provide a better distributed Pareto frontier, which provides more options for management in a SSCNR problem.
Finally, as the supply chain redesign involves stopping or starting ecological cooperation with the region, it is important to regard these activities during this process. In this paper, it was shown that this issue can be considered in models as an objective function that can affect the final decision of supply chain managers and represents an area where ecological initiatives are planned for launch. Moreover, since the proposed matheuristic approach gives an acceptable Pareto frontier that is close to the Pareto optimal frontier of the exact method (AUGMECON), it can be used to solve sustainable supply chain network redesign problems at greater scales.
Due to the high interest in ecological issues, particularly in ecological relationships between facilities and their surrounding environment, further work may incorporate new decision-making areas, such as route planning and taking into account numerous pro-ecological methods of vehicle use. Additionally, to achieve more realistic simulation conditions, researchers should consider uncertain parameters such as demands and the use of proper methodologies to solve the problem.
Some supply chain managers may prefer not to consider the other effects of their facilities on the region, but governments and environmental authorities should consider these processes as important factors in a region’s environment and economy. Therefore, they should try to encourage supply chain managers to consider these processes by providing them with motivation to do so.
Author Contributions
Conceptualization, Z.A. and P.H.; methodology, Z.A.; software, Z.A.; validation, Z.A. and P.H.; formal analysis, Z.A.; investigation, Z.A.; resources, P.H.; data curation, Z.A.; writing—original draft preparation, Z.A.; writing—review and editing, P.H.; visualization, Z.A; supervision, P.H.; project administration, P.H.; funding acquisition, P.H. All authors have read and agreed to the published version of the manuscript.
Funding
The project is financed by the Ministry of Science and Higher Education in Poland under the program “Regional Initiative of Excellence” 2019–2022 project number 015/RID/2018/19 total funding amount 10 721 040,00 PLN.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Supply chain size.
Table A1.
Supply chain size.
| Supply Chain Size | |
|---|---|
| Number of Factories | 3 |
| Number of Warehouses | 20 |
| Number of New Warehouses | 10 |
| Number of Existing Warehouses | 10 |
| Number of Customers | 200 |

Table A2.
Parameter ranges.
Table A2.
Parameter ranges.
| Parameter | Random Generation Range |
|---|---|
| di | 30,000–60,000 |
| capi | 400,000–600,000 |
| fmi | 100,000–190,000 |
| fci | 1.1–1.3 |
| fsi | 520,000–1,070,000 |
| fni | 220,000–250,000 |
| fbi | 800,000–900,000 |
| rij | 400,000–550,000 | rii = 0 |
| Pcij | 9–11.5 |
| hcij | 8.5–11.5 |
| wfis | 1–2.5 |
| whis | 1–2.5 |
References
- Gayialis, S.P.; Kechagias, E.P.; Konstantakopoulos, G.D. A city logistics system for freight transportation: Integrating information technology and operational research. Oper. Res. 2022, 22, 1–30. [Google Scholar] [CrossRef]
- Jabbar, S.; Lloyd, H.; Hammoudeh, M.; Adebisi, B.; Raza, U. Blockchain-enabled supply chain: Analysis, challenges, and future directions. Multimed. Syst. 2021, 27, 787–806. [Google Scholar] [CrossRef]
- Kechagias, E.P.; Miloulis, D.M.; Chatzistelios, G.; Gayialis, S.P.; Papadopoulos, G.A. Applying a system dynamics approach for the pharmaceutical industry: Simulation and optimization of the quality control process. WSEAS Trans. Environ. Dev. 2021, 17, 983–996. [Google Scholar] [CrossRef]
- Gayialis, S.P.; Kechagias, E.; Papadopoulos, G.A.; Konstantakopoulos, G.D. Design of a blockchain-driven system for product counterfeiting restraint in the supply chain. IFIP Int. Conf. Adv. Prod. Manag. Syst. 2019, 566, 474–481. [Google Scholar]
- Qu, S.J.; Li, Y.M.; Ji, Y. The mixed integer robust maximum expert consensus models for large-scale GDM under uncertainty circumstances. Appl. Soft Comput. J. 2021, 107, 107369. [Google Scholar] [CrossRef]
- Ji, Y.; Li, H.H.; Zhang, H.J. Risk-averse two-stage stochastic minimum cost consensus models with asymmetric adjustment cost. Group Decis. Negot. 2022, 31, 261–291. [Google Scholar] [CrossRef]
- Azadehranjbar, Z.; Bozorgi-Amiri, A.; Zandi, A. Warehouse Redesigning in a Three-Echelon Supply Chain Network with Consideration of Routing Under Uncertainty: A Light Robust Approach. RAIRO Oper. Res. 2019, 55, 147. [Google Scholar]
- Melachrinoudis, E.; Min, H. Redesigning A Warehouse Network. Eur. J. Oper. Res. 2007, 176, 210–229. [Google Scholar] [CrossRef]
- Lee, Y.J.; Baker, T.; Jayaraman, V. Redesigning an Integrated Forward–Reverse Logistics System for a Third Party Service Provider: An Empirical Study. Int. J. Prod. Res. 2012, 50, 5615–5634. [Google Scholar] [CrossRef]
- Bing, X.; Bloemhof-Ruwaard, J.; Chaabane, A.; Van Der Vorst, J. Global Reverse Supply Chain Redesign for Household Plastic Waste Under the Emission Trading Scheme. J. Clean. Prod. 2015, 103, 28–39. [Google Scholar] [CrossRef]
- Khatami, M.; Mahootchi, M.; Farahani, R.Z. Benders’ Decomposition for Concurrent Redesign of Forward and Closed-Loop Supply Chain Network with Demand and Return Uncertainties. Transp. Res. Part E Logist. Transp. Rev. 2015, 79, 1–21. [Google Scholar] [CrossRef]
- Kiya, F.; Davoudpour, H. Stochastic Programming Approach to Re-Designing a Warehouse Network Under Uncertainty. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 919–936. [Google Scholar] [CrossRef]
- Fattahi, M.; Govindan, K.; Keyvanshokooh, E. A Multi-Stage Stochastic Program for Supply Chain Network Redesign Problem with Price-Dependent Uncertain Demands. Comput. Oper. Res. 2017, 100, 314–332. [Google Scholar] [CrossRef]
- Wieteska, G. Supply Chain Redesign for Resilience—The Perspective of the Consequences of Disruption. Res. Pap. Wroc. Univ. Econ. Pract. Nauk. Uniw. Ekon. We Wroc. 2019, 547, 122–139. [Google Scholar] [CrossRef]
- Seuring, S.; Sarkis, J.; Müller, M.; Rao, P. Sustainability and Supply Chain Management—An Introduction to The Special Issue. J. Clean. Prod. 2008, 16, 1545–1551. [Google Scholar] [CrossRef]
- Manavalan, E.; Jayakrishna, K. A review of Internet of Things (IoT) embedded sustainable supply chain for industry 4.0 requirements. Comput. Ind. Eng. 2019, 127, 925–953. [Google Scholar] [CrossRef]
- Biuki, M.; Kazemi, A.; Alinezhad, A. An Integrated Location-Routing-Inventory Model for Sustainable Design of a Perishable Products Supply Chain Network. J. Clean. Prod. 2020, 260, 120842. [Google Scholar] [CrossRef]
- Abdallah, T.; Diabat, A.; Simchi-levi, D. Sustainable Supply Chain Design: A Closed-Loop Formulation and Sensitivity Analysis. Prod. Plan. Control Manag. Oper. 2012, 23, 120–133. [Google Scholar] [CrossRef]
- Bals, L.; Tate, W.L. Sustainable Supply Chain Design in Social Businesses: Advancing the Theory of Supply Chain. J. Bus. Logist. 2017, 39, 57–79. [Google Scholar] [CrossRef] [Green Version]
- Feitó-Cespón, M.; Sarache, W.; Piedra-Jimenez, F.; Cespón-Castro, R. Redesign of A Sustainable Reverse Supply Chain under Uncertaintya Case Study. J. Clean. Prod. 2017, 151, 206–217. [Google Scholar] [CrossRef]
- Hwang, C.; Masud, A.S.M. Multiple Objective Decision Making Methods And Applications: A State Of the Art Survey; Springer: Berlin/Heidelberg, Germany, 1979; Volume 164. [Google Scholar]
- Mavrotas, G. Effective Implementation of The E-Constraint Method in Multi-Objective Mathematical Programming Problems. Appl. Math. Comput. 2009, 213, 455–465. [Google Scholar] [CrossRef]
- Deb, K. A Fast and Elitist Multiobjective Genetic Algorithm. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; Feng, W.; Yuan, J. A Novel Two-Level Optimization Strategy for Multi-Debris Active Removal Mission in LEO. CMES-Comput. Modeling Eng. Sci. 2020, 122, 149–174. [Google Scholar] [CrossRef]
- Goh, C.; Tan, K.C. A Competitive-Cooperative Coevolutionary Paradigm for Dynamic Multiobjective Optimization. IEEE Trans. Evol. Comput. 2009, 13, 103–127. [Google Scholar]
- Schott, J.R. Fault Tolerant Design Using Single and Multi-Criteria Genetic Algorithms. Master’s Thesis, Department of Aeronautics and Astronautics, Massachusetts Institute of Technology, Cambridge, MA, USA, 1995. [Google Scholar]
- Mansouri, S.A.; Aktas, E.; Besikci, U. Makespan and Energy Consumption. Eur. J. Oper. Res. 2015, 248, 1–17. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).