Development of An Analytical Method for Design of Electromagnetic Energy Harvesters with Planar Magnetic Arrays
Abstract
:1. Introduction
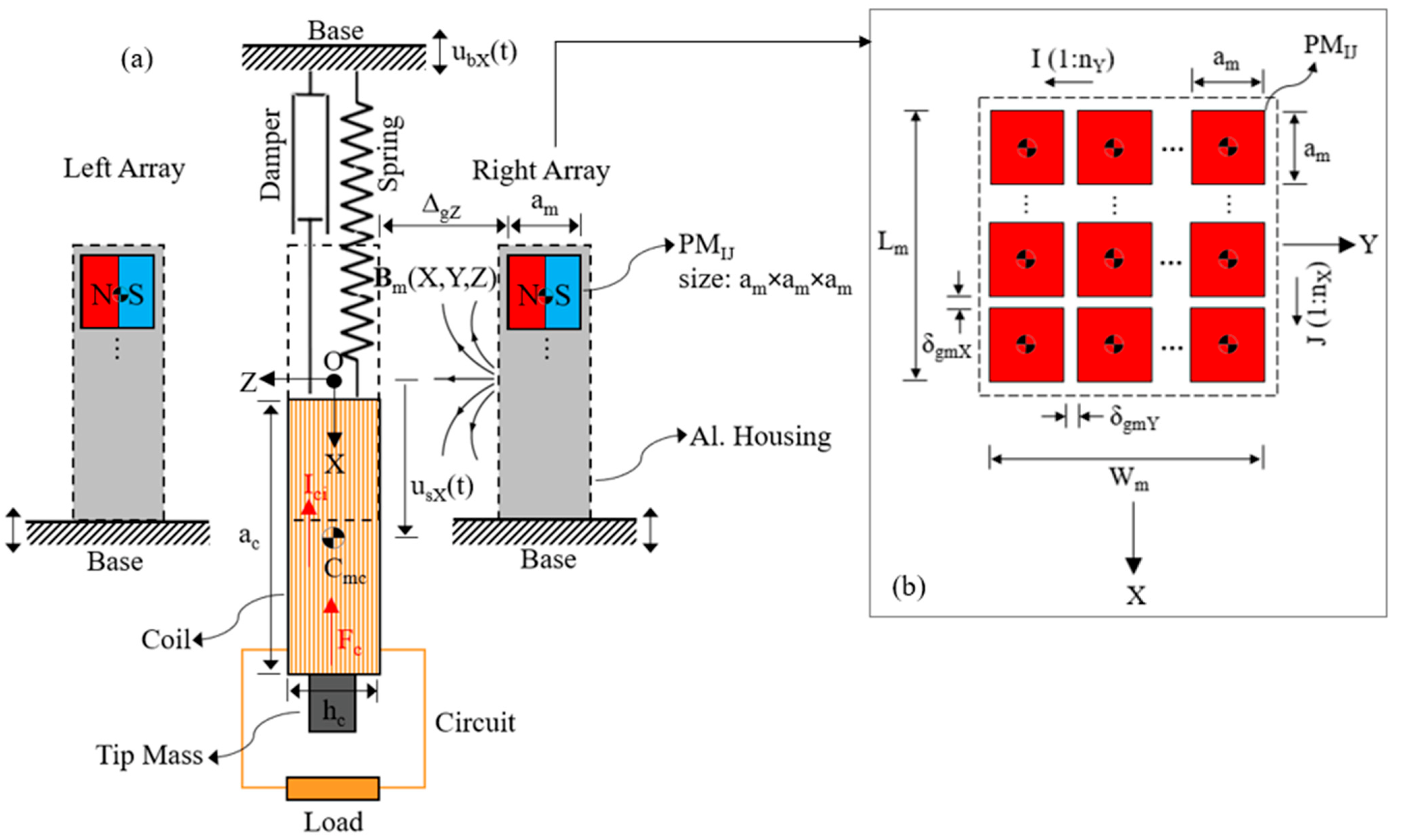
2. Mathematical Modeling of EMEHs
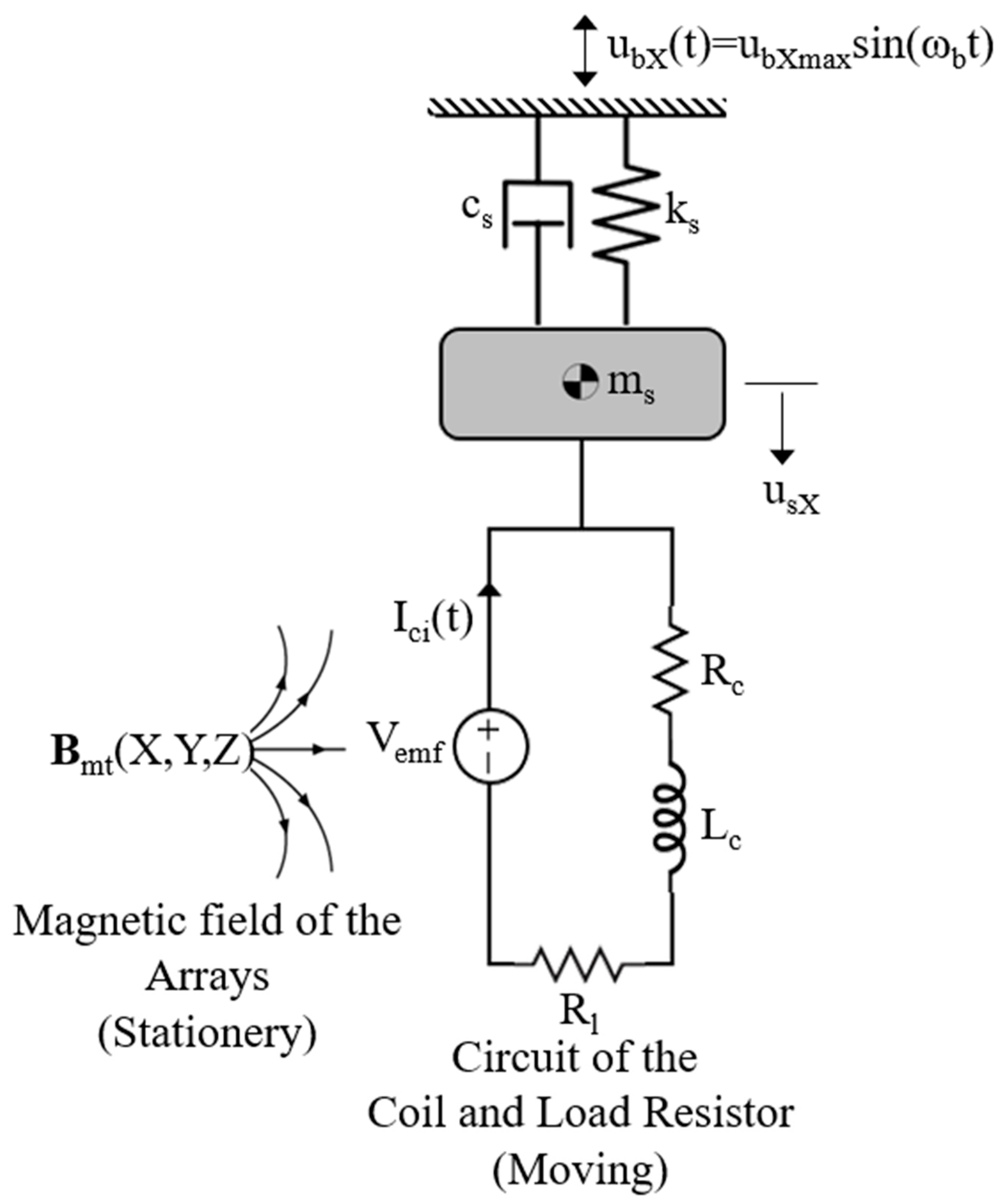
2.1. Electromechanical Model
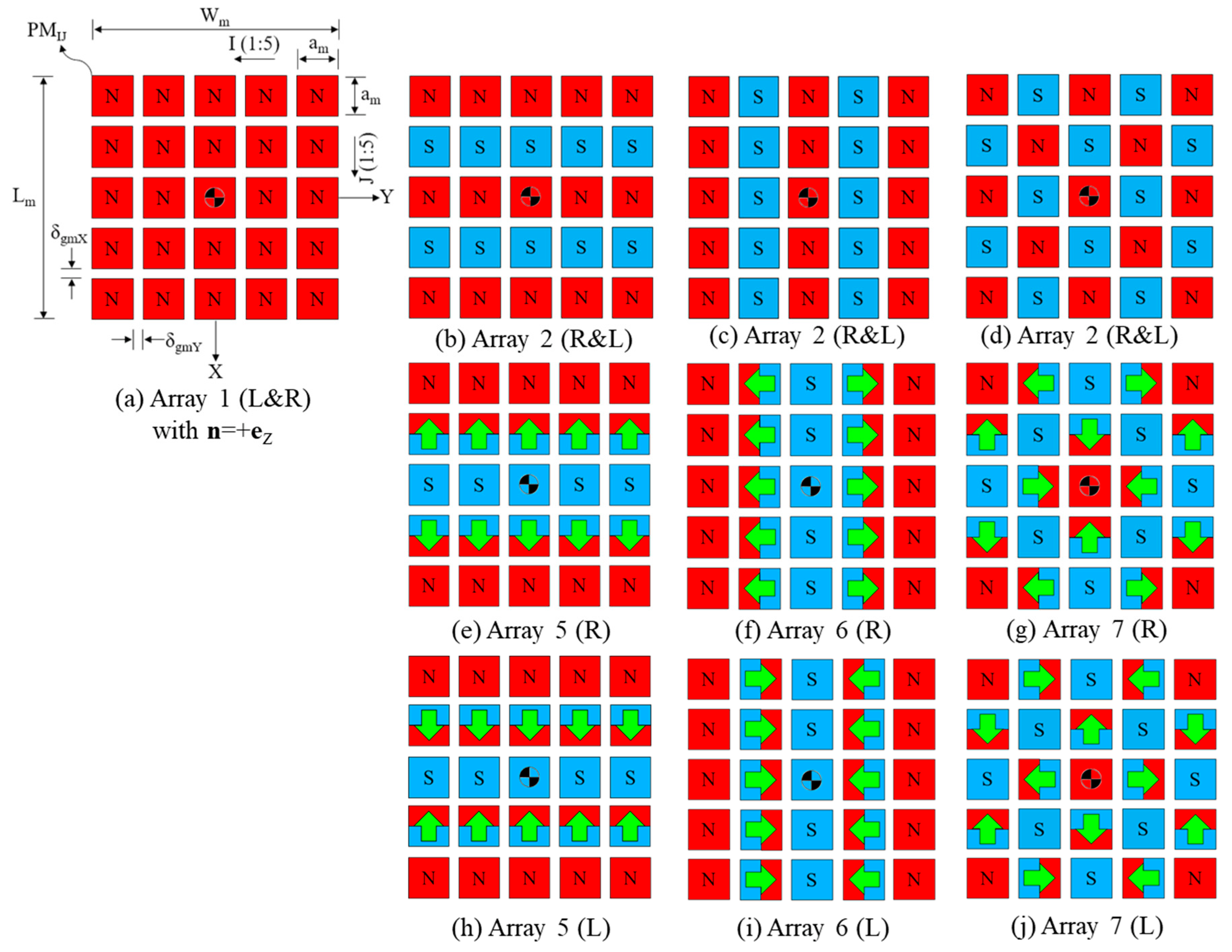
2.2. Planar Arrangement of the PMs
2.3. Thick Rectangular Coil
2.4. Magnetic Interaction of the Arrays with the Moving Coil
3. Electromechanical Equation
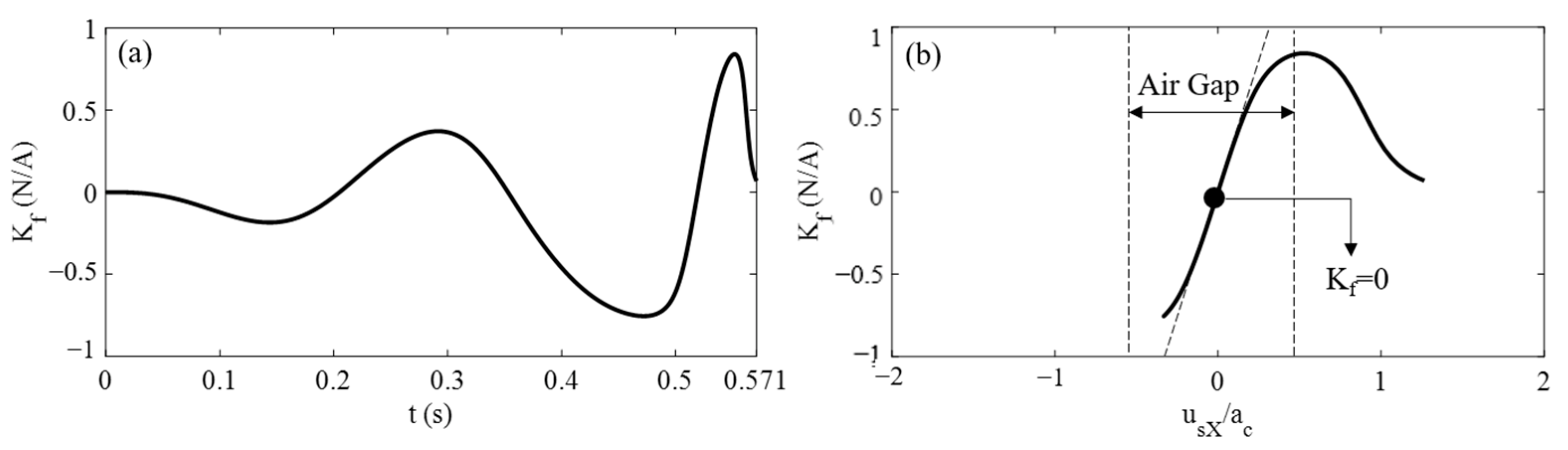
3.1. Decoupled Equation of Motion
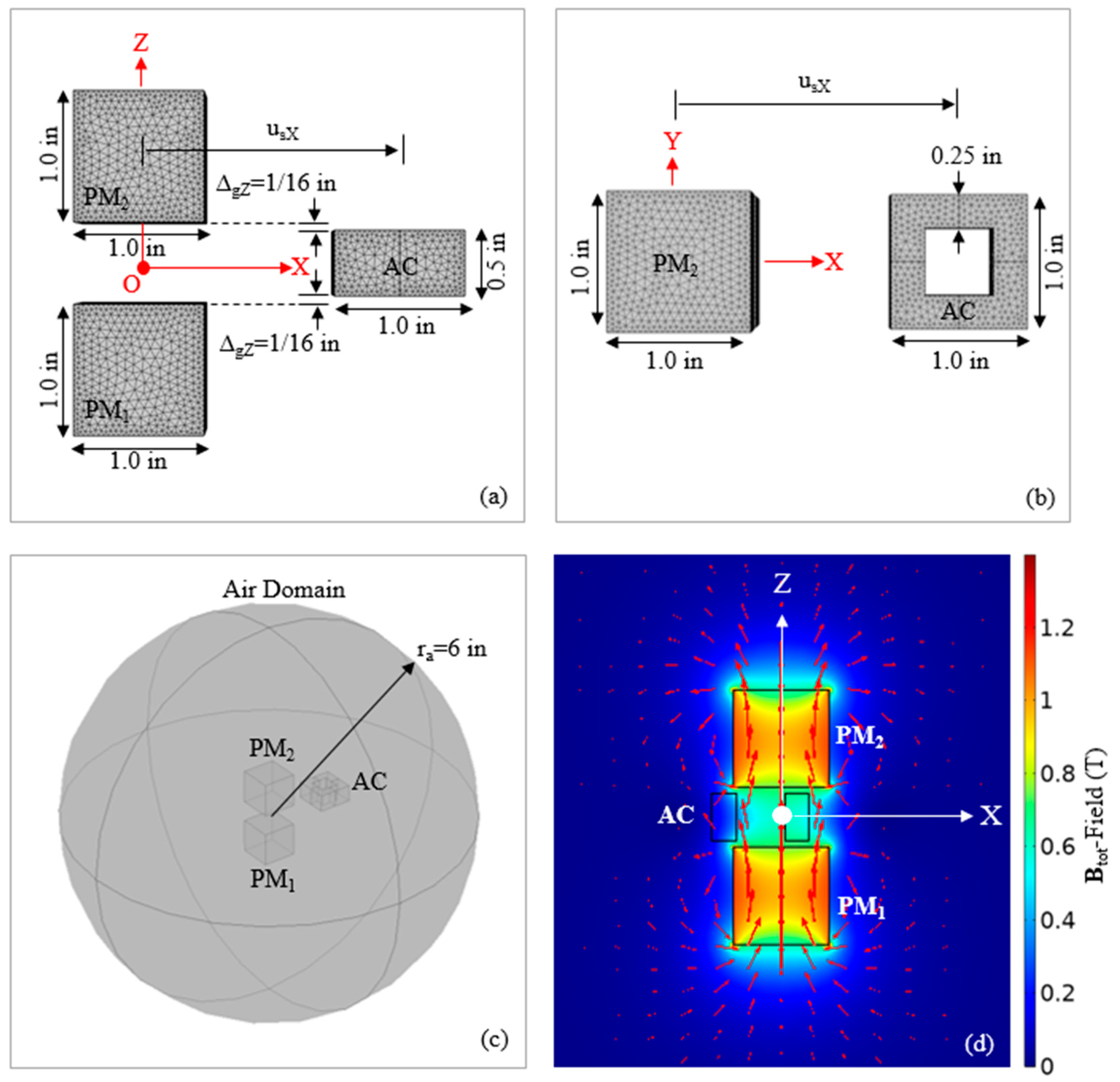
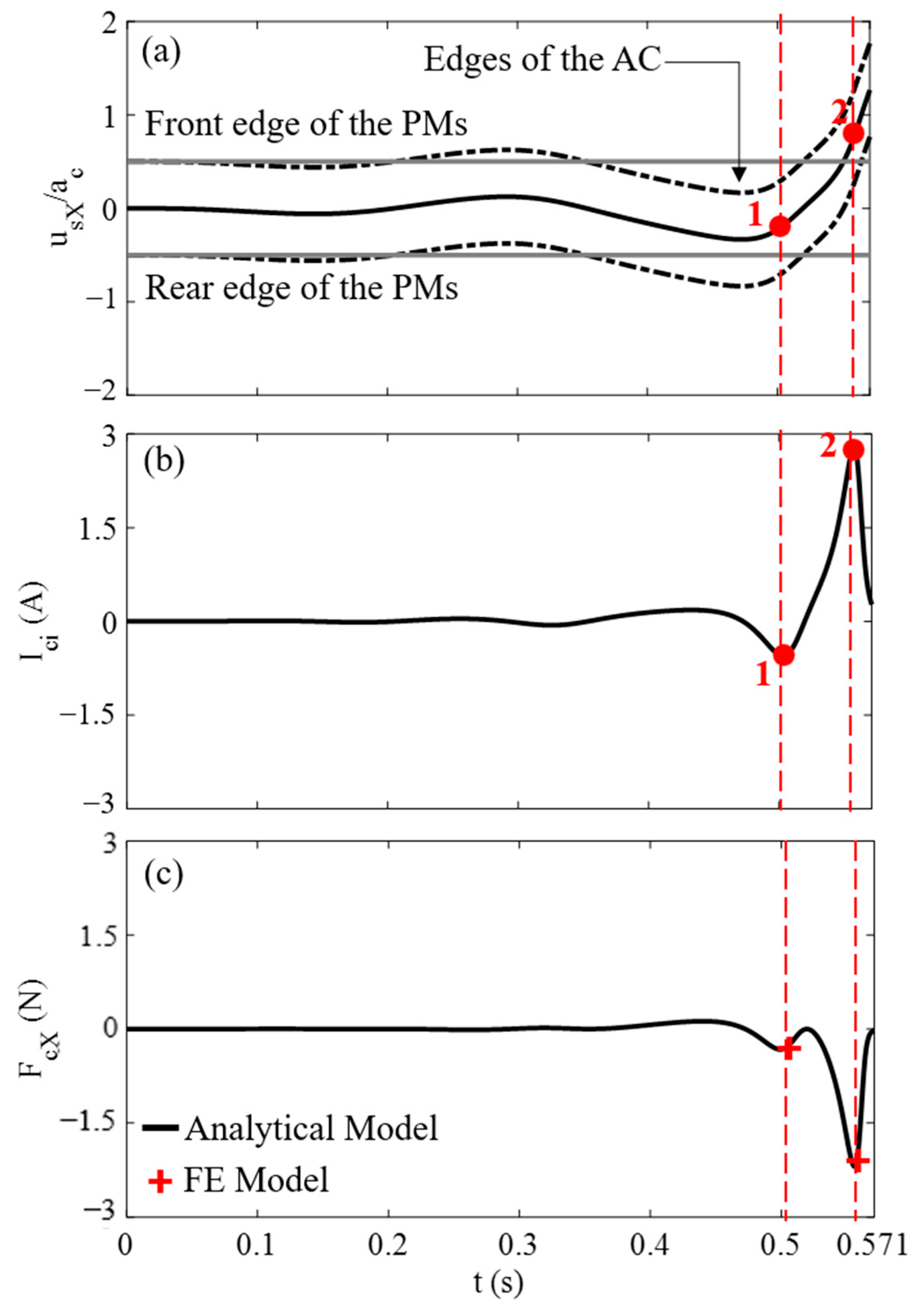
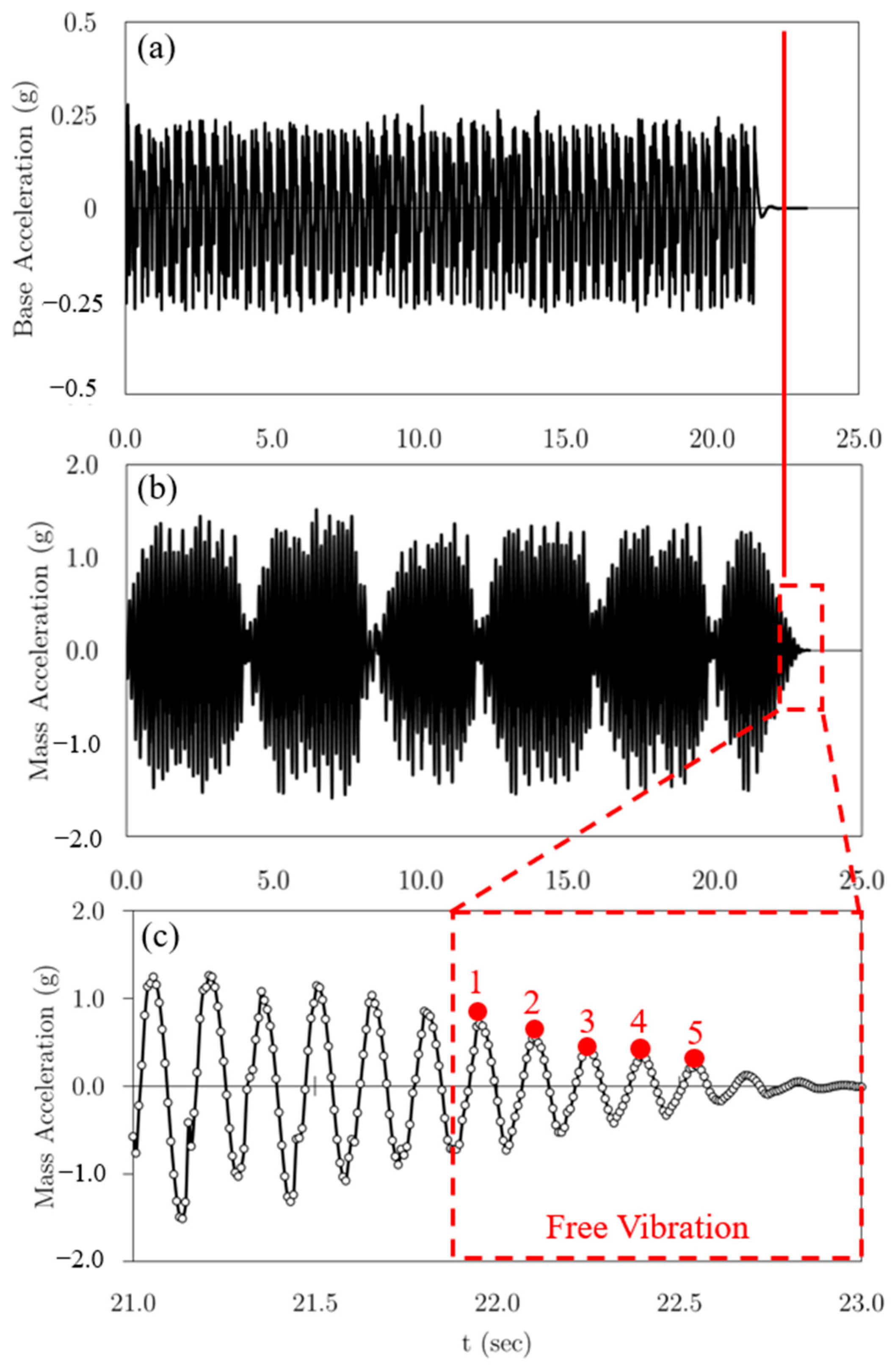
3.2. Numerical Verification
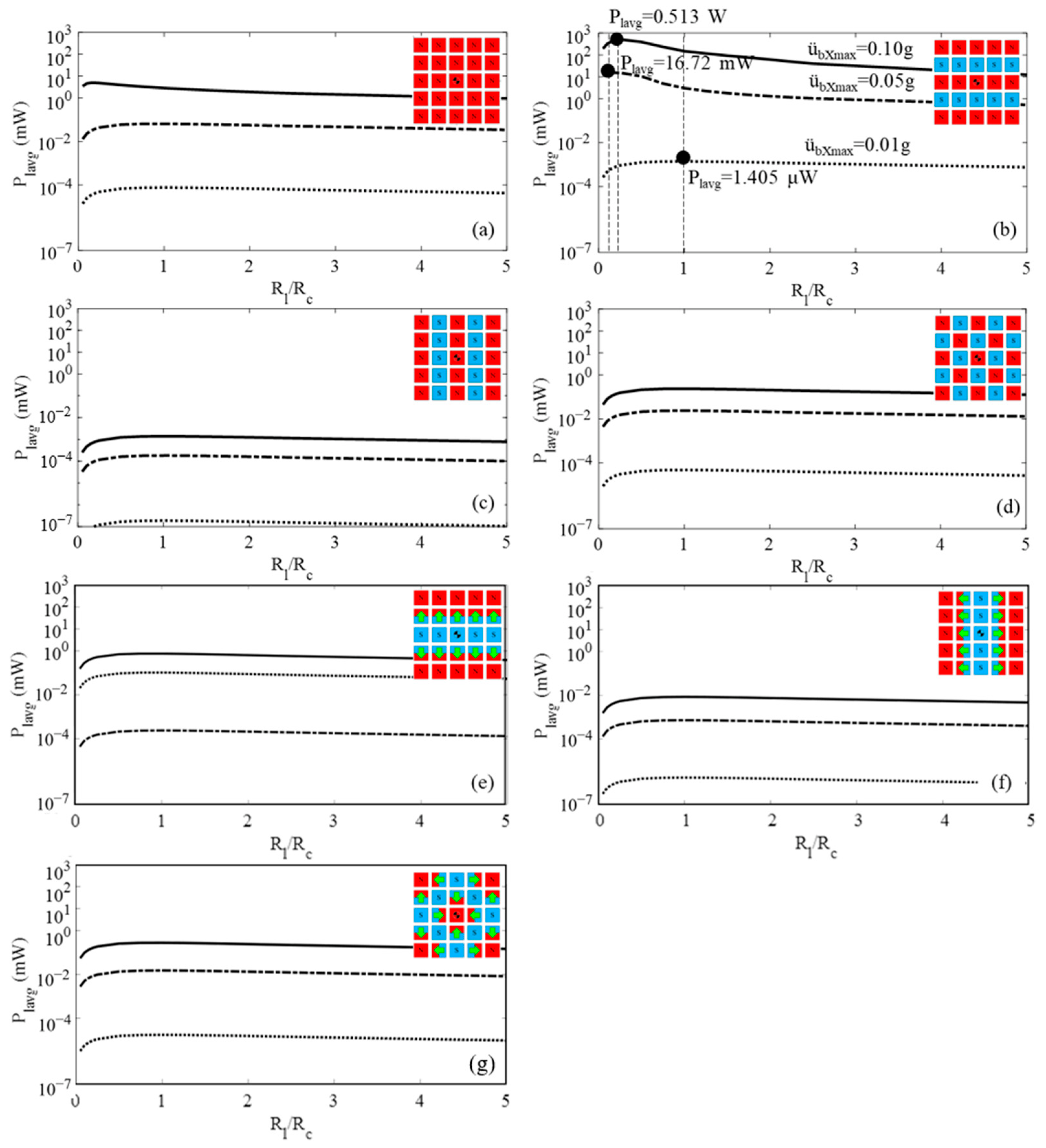
4. Parametric Study
5. Experimental Study
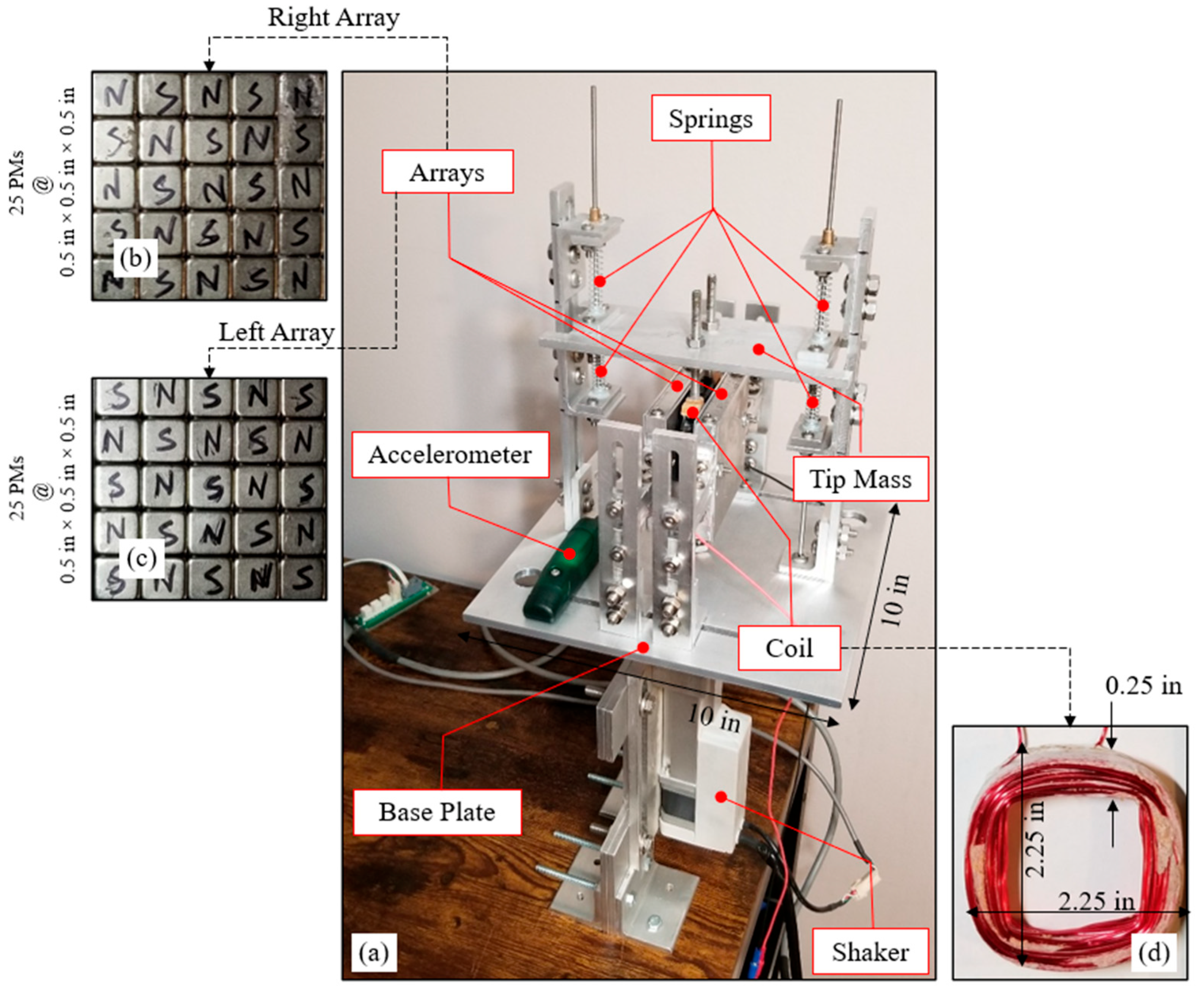
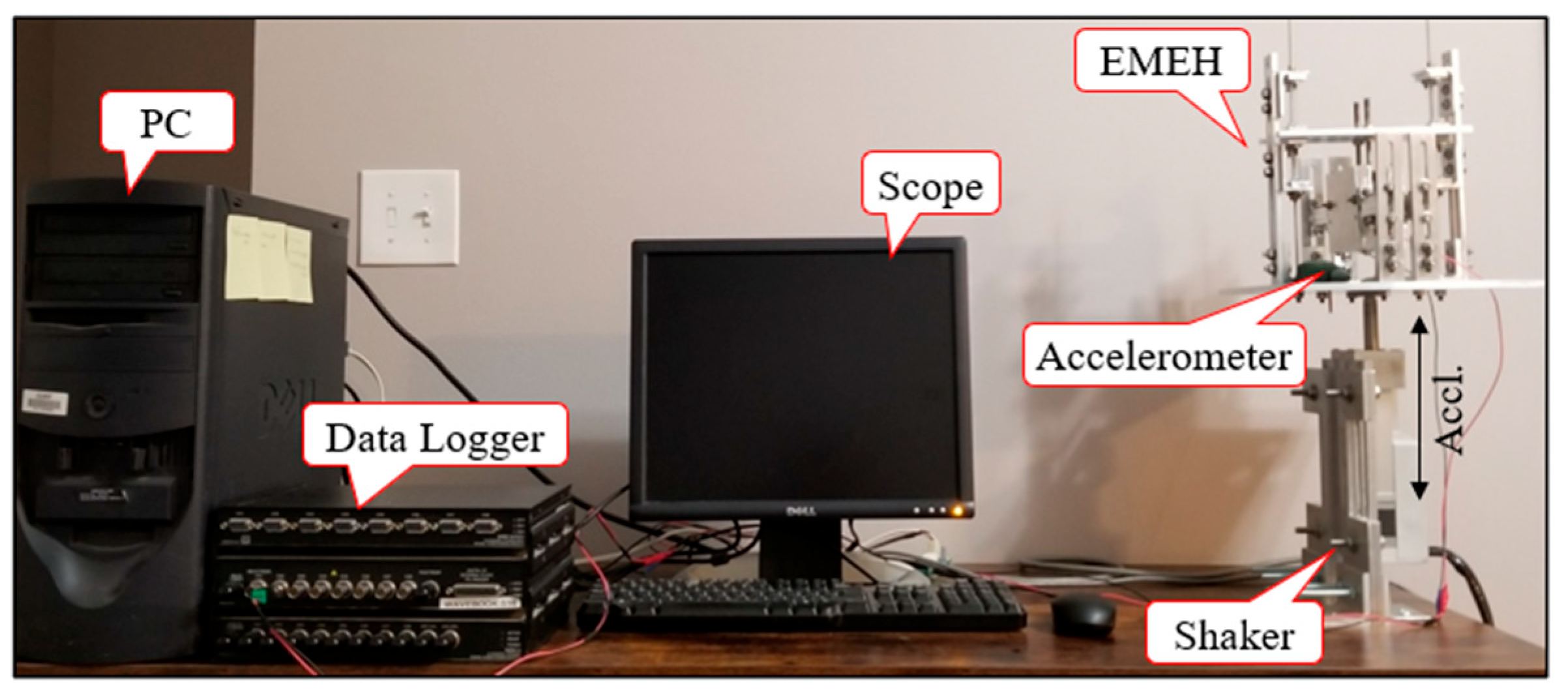
5.1. Laboratory Testing
5.2. Model Validation
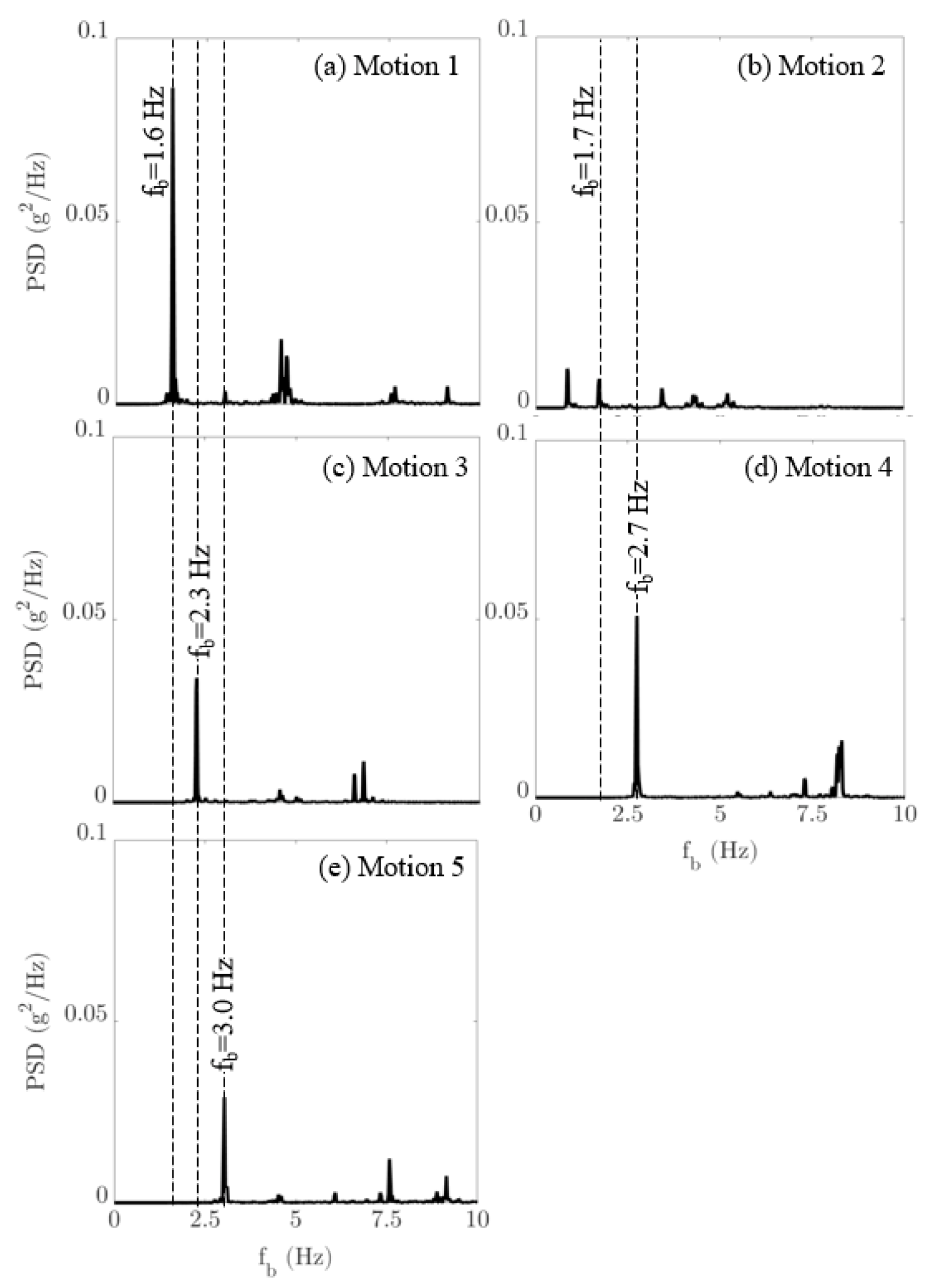
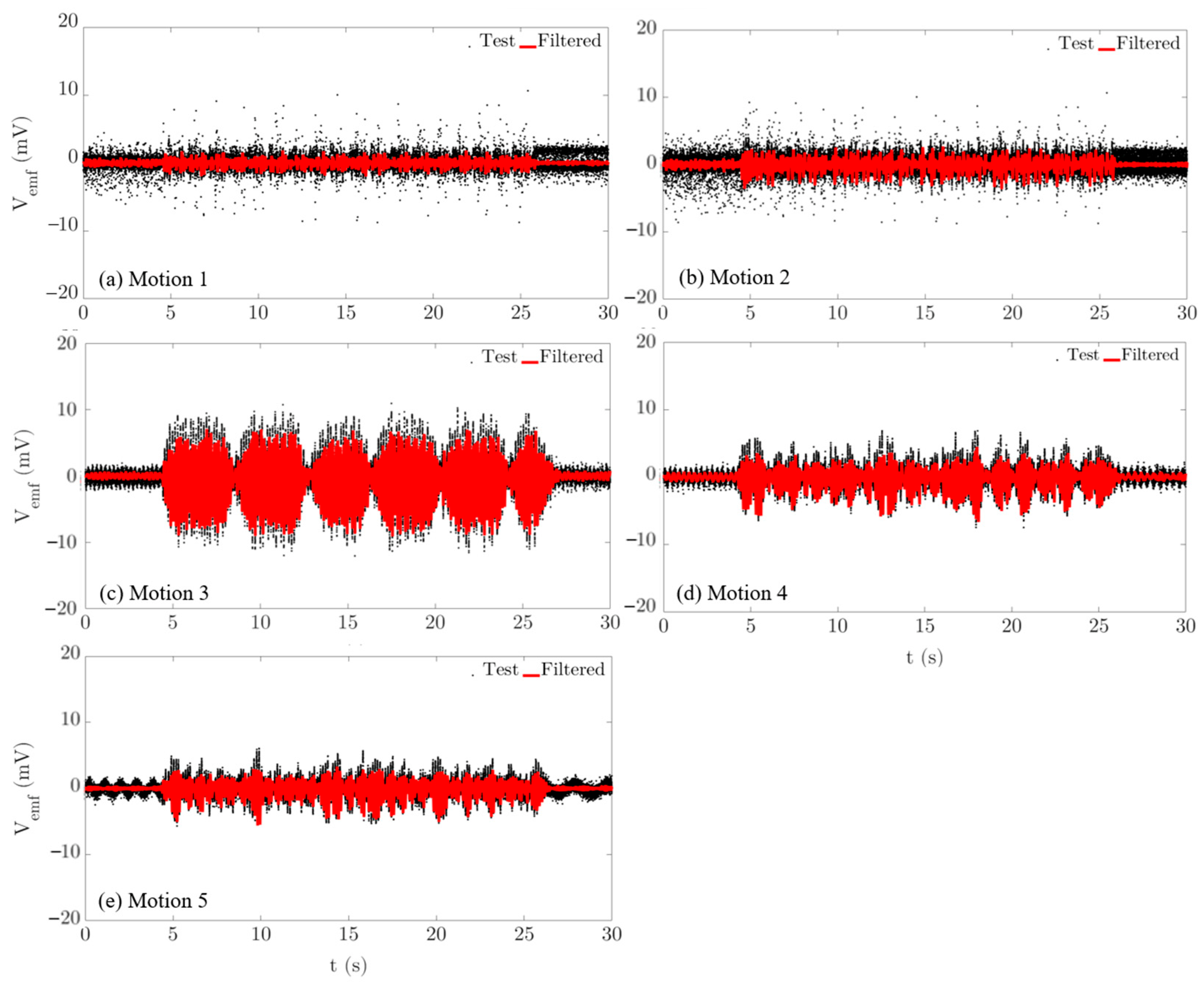
5.3. Field Testing
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Roundy, S.; Wright, P.K.; Rabaey, J.M. Energy Scavenging for Wireless Sensor Networks; Springer: New York, NY, USA, 2004. [Google Scholar]
- Williams, C.; Yates, R. Analysis of a micro-electric generator for microsystems. Sens. Actuators A Phys. 1996, 52, 8–11. [Google Scholar] [CrossRef]
- Stosiak, M. The impact of hydraulic systems on the human being and the environment. J. Theor. Appl. Mech. 2015, 53, 409–420. [Google Scholar] [CrossRef] [Green Version]
- Priya, S.; Inman, D.J. (Eds.) Energy Harvesting Technologies; Springer: New York, NY, USA, 2009; pp. 337–350. ISBN 9780387764634. [Google Scholar]
- Amjadian, M.; Agrawal, A.K. Planar arrangement of permanent magnets in design of a magneto-solid damper by finite element method. J. Intell. Mater. Syst. Struct. 2020, 31, 998–1014. [Google Scholar] [CrossRef]
- Amjadian, M.; Agrawal, A.K. A passive electromagnetic eddy current friction damper (PEMECFD): Theoretical and analytical modeling. Struct. Control Health Monit. 2017, 24, e1978. [Google Scholar] [CrossRef]
- Amjadian, M.; Agrawal, A.K. Modeling, design, and testing of a proof-of-concept prototype damper with friction and eddy current damping effects. J. Sound Vib. 2018, 413, 225–249. [Google Scholar] [CrossRef]
- Sazonov, E.; Li, H.; Curry, D.; Pillay, P. Self-Powered Sensors for Monitoring of Highway Bridges. IEEE Sens. J. 2009, 9, 1422–1429. [Google Scholar] [CrossRef] [Green Version]
- Kwon, S.-D.; Park, J.; Law, K. Electromagnetic energy harvester with repulsively stacked multilayer magnets for low frequency vibrations. Smart Mater. Struct. 2013, 22, 055007. [Google Scholar] [CrossRef] [Green Version]
- Green, P.L.; Papatheou, E.; Sims, N.D. Energy harvesting from human motion and bridge vibrations: An evaluation of current nonlinear energy harvesting solutions. J. Intell. Mater. Syst. Struct. 2013, 24, 1494–1505. [Google Scholar] [CrossRef] [Green Version]
- Pirisi, A.; Mussetta, M.; Grimaccia, F.; Zich, R.E. Novel Speed-Bump Design and Optimization for Energy Harvesting from Traffic. IEEE Trans. Intell. Transp. Syst. 2013, 14, 1983–1991. [Google Scholar] [CrossRef]
- Gatti, G.; Brennan, M.J.; Tehrani, M.G.; Thompson, D.J. Harvesting energy from the vibration of a passing train using a single-degree-of-freedom oscillator. Mech. Syst. Signal Process. 2016, 66–67, 785–792. [Google Scholar] [CrossRef] [Green Version]
- Takeya, K.; Sasaki, E.; Kobayashi, Y. Design and parametric study on energy harvesting from bridge vibration using tuned dual-mass damper systems. J. Sound Vib. 2016, 361, 50–65. [Google Scholar] [CrossRef]
- Ahmad, M.M.; Khan, F.U. Dual Resonator-Type Electromagnetic Energy Harvester for Structural Health Monitoring of Bridges. J. Bridg. Eng. 2021, 26, 04021021. [Google Scholar] [CrossRef]
- Amjadian, M.; Agrawal, A.K.; Nassif, H. Feasibility of using a high-power electromagnetic energy harvester to power structural health monitoring sensors and systems in transportation infrastructures. Proc. SPIE 2021, 2021, 115911G. [Google Scholar] [CrossRef]
- Peigney, M.; Siegert, D. Low-Frequency Electromagnetic Energy Harvesting from Highway Bridge Vibrations. J. Bridg. Eng. 2020, 25, 04020056. [Google Scholar] [CrossRef]
- El-Hami, M.; Glynne-Jones, P.; White, N.; Hill, M.; Beeby, S.; James, E.; Brown, A.; Ross, J. Design and fabrication of a new vibration-based electromechanical power generator. Sens. Actuators A Phys. 2001, 92, 335–342. [Google Scholar] [CrossRef]
- Beeby, S.P.; Torah, R.N.; Tudor, M.J.; Glynne-Jones, P.; O’Donnell, T.; Saha, C.R.; Roy, S. A micro electromagnetic generator for vibration energy harvesting. J. Micromech. Microeng. 2007, 17, 1257–1265. [Google Scholar] [CrossRef]
- Zeng, P.; Khaligh, A. A Permanent-Magnet Linear Motion Driven Kinetic Energy Harvester. IEEE Trans. Ind. Electron. 2013, 60, 5737–5746. [Google Scholar] [CrossRef]
- Elvin, N.G.; Elvin, A.A. An Experimentally Validated Electromagnetic Energy Harvester. J. Sound Vib. 2011, 330, 2314–2324. [Google Scholar] [CrossRef]
- Halim, M.A.; Cho, H.; Park, J.Y. Design and experiment of a human-limb driven, frequency up-converted electromagnetic energy harvester. Energy Convers. Manag. 2015, 106, 393–404. [Google Scholar] [CrossRef]
- Salauddin, M.; Halim, M.A.; Park, J.Y. A magnetic-spring-based, low-frequency-vibration energy harvester comprising a dual Halbach array. Smart Mater. Struct. 2016, 25, 095017. [Google Scholar] [CrossRef]
- Liu, X.; Qiu, J.; Chen, H.; Xu, X.; Wen, Y.; Li, P. Design and Optimization of an Electromagnetic Vibration Energy Harvester Using Dual Halbach Arrays. IEEE Trans. Magn. 2015, 51, 8204204. [Google Scholar] [CrossRef]
- Yang, B.; Lee, C.; Xiang, W.; Xie, J.; He, J.H.; Kotlanka, R.K.; Low, S.P.; Feng, H. Electromagnetic energy harvesting from vibrations of multiple frequencies. J. Micromech. Microeng. 2009, 19, 035001. [Google Scholar] [CrossRef]
- Foisal, A.R.M.; Hong, C.; Chung, G.-S. Multi-frequency electromagnetic energy harvester using a magnetic spring cantilever. Sens. Actuators A Phys. 2012, 182, 106–113. [Google Scholar] [CrossRef]
- Mikoshiba, K.; Manimala, J.M.; Sun, C.T. Energy harvesting using an array of multifunctional resonators. J. Intell. Mater. Syst. Struct. 2013, 24, 168–179. [Google Scholar] [CrossRef]
- Soliman, M.S.M.; Abdel-Rahman, E.; El-Saadany, E.F.; Mansour, R.R. A wideband vibration-based energy harvester. J. Micromech. Microeng. 2008, 18, 115021. [Google Scholar] [CrossRef]
- Arroyo, E.; Badel, A.; Formosa, F.; Wu, Y.; Qiu, J. Comparison of electromagnetic and piezoelectric vibration energy harvesters: Model and experiments. Sens. Actuators A Phys. 2012, 183, 148–156. [Google Scholar] [CrossRef]
- Zhu, D.; Beeby, S.; Tudor, J.; Harris, N. Vibration energy harvesting using the Halbach array. Smart Mater. Struct. 2012, 21, 075020. [Google Scholar] [CrossRef]
- Salauddin, M.; Park, J.Y. Design and experiment of human hand motion driven electromagnetic energy harvester using dual Halbach magnet array. Smart Mater. Struct. 2017, 26, 035011. [Google Scholar] [CrossRef]
- Zhu, D.; Beeby, S.; Tudor, J.; Harris, N. Increasing output power of electromagnetic vibration energy harvesters using improved Halbach arrays. Sens. Actuators A Phys. 2013, 203, 11–19. [Google Scholar] [CrossRef] [Green Version]
- Furlani, E.P. Permanent Magnet and Electromechanical Devices; Academic Press: Cambridge, MA, USA, 2001; ISBN 0122699513. [Google Scholar]
- Robertson, W.; Cazzolato, B.; Zander, A. Axial Force Between a Thick Coil and a Cylindrical Permanent Magnet: Optimizing the Geometry of an Electromagnetic Actuator. IEEE Trans. Magn. 2012, 48, 2479–2487. [Google Scholar] [CrossRef]
- Paul, C.R. Inductance; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; ISBN 9780470561232. [Google Scholar]
- Cannarella, J.; Selvaggi, J.; Salon, S.; Tichy, J.; Borca-Tasciuc, D.-A. Coupling Factor Between the Magnetic and Mechanical Energy Domains in Electromagnetic Power Harvesting Applications. IEEE Trans. Magn. 2011, 47, 2076–2080. [Google Scholar] [CrossRef]
- Mösch, M.; Fischerauer, G. A Comparison of Methods to Measure the Coupling Coefficient of Electromagnetic Vibration Energy Harvesters. Micromachines 2019, 10, 826. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Multiphysics® Modeling Software, Version 5.4; COMSOL: Burlington, MA, USA, 2018.
- Sams, H.W. Handbook of Electronics Tables and Formulas; Howard W. Sams & Co.: Carmel, IN, USA, 1986; ISBN 0672224690. [Google Scholar]
- Amjadian, M.; Agrawal, A.K. Feasibility study of using a semiactive electromagnetic friction damper for seismic response control of horizontally curved bridges. Struct. Control Health Monit. 2019, 26, e2333. [Google Scholar] [CrossRef]
- MATLAB, Version R2017b; The MathWorks Inc.: Natick, MA, USA, 2017.
- Stephen, N. On energy harvesting from ambient vibration. J. Sound Vib. 2006, 293, 409–425. [Google Scholar] [CrossRef] [Green Version]
- Zhu, S.; Shen, W.-A.; Xu, Y.-L. Linear electromagnetic devices for vibration damping and energy harvesting: Modeling and testing. Eng. Struct. 2012, 34, 198–212. [Google Scholar] [CrossRef] [Green Version]
- Zuo, L.; Cui, W. Dual-Functional Energy-Harvesting and Vibration Control: Electromagnetic Resonant Shunt Series Tuned Mass Dampers. J. Vib. Acoust. 2013, 135, 051018. [Google Scholar] [CrossRef] [Green Version]
- Shen, W.; Zhu, S.; Xu, Y.-L.; Zhu, H.-P. Energy regenerative tuned mass dampers in high-rise buildings. Struct. Control Health Monit. 2018, 25, e2072. [Google Scholar] [CrossRef]

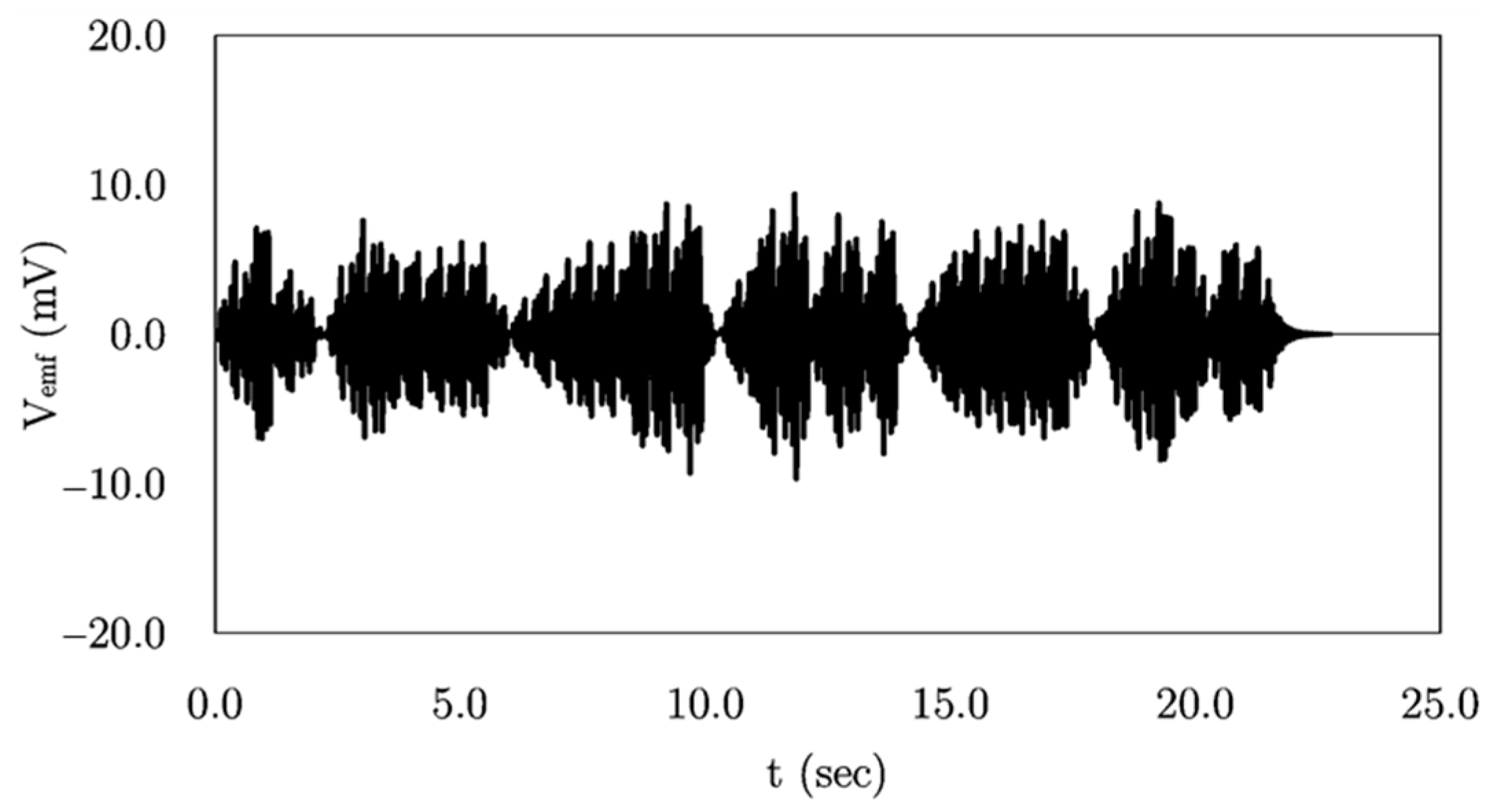

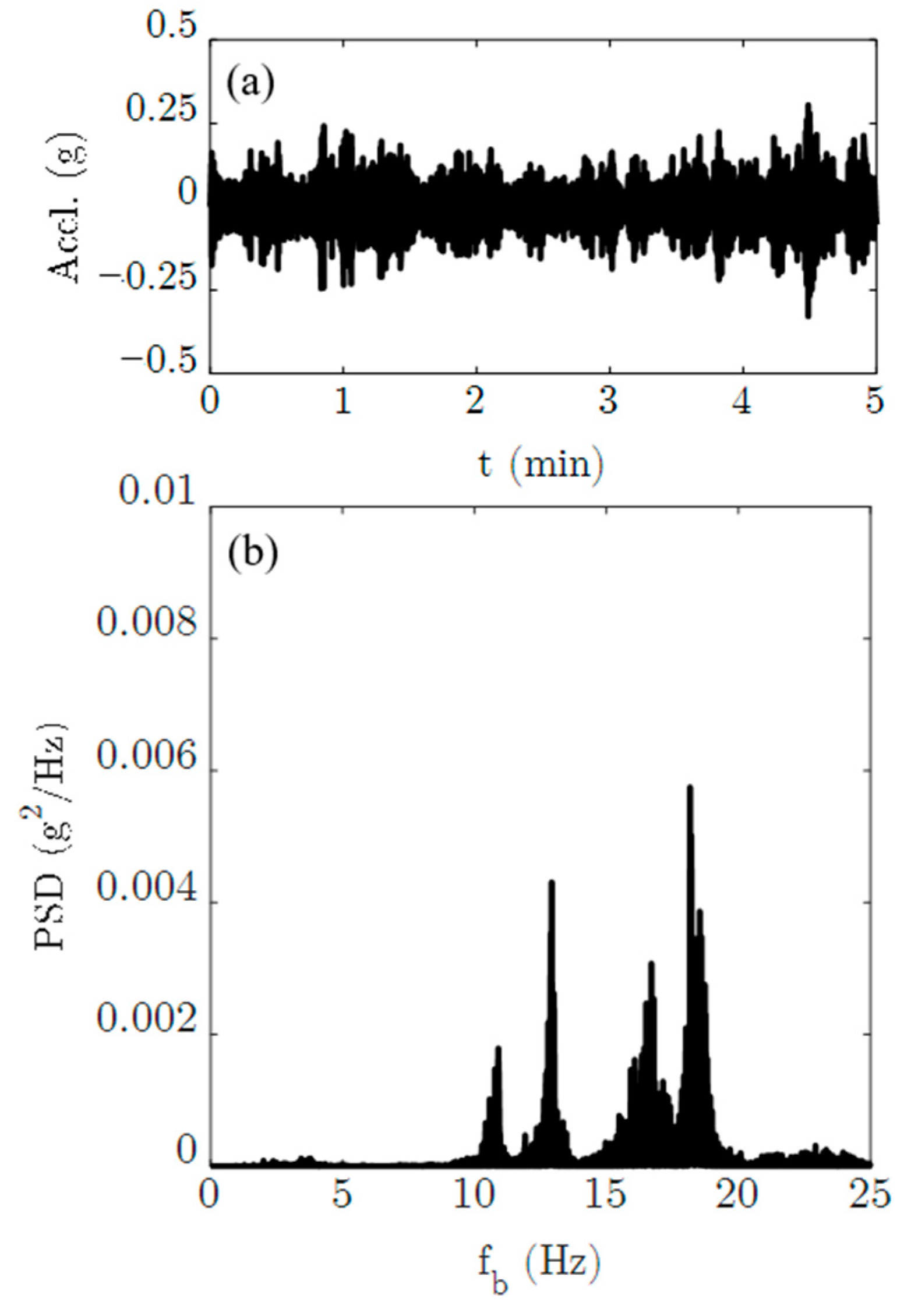
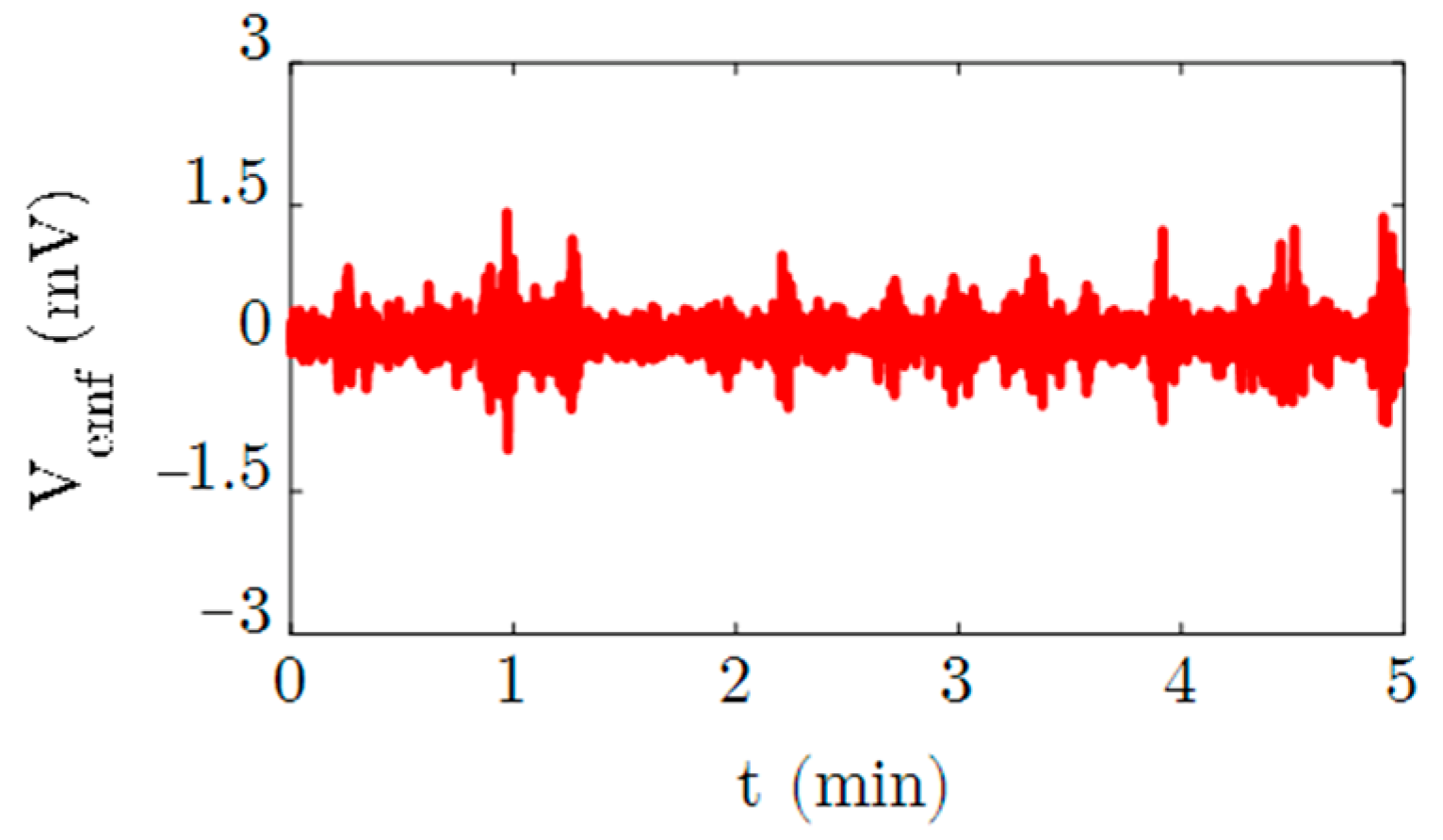
| Parameter | Value | Unit | Description |
|---|---|---|---|
| am | 1 | in | Length of the sides of the PMs |
| ac | 1 | in | Length of the sides of the coil |
| hc | 0.5 | in | Height of the coil (Nz = 13) |
| tc | 0.25 | in | Winding depth (Nt = 6) |
| dw | 1 | mm | Diameter of the copper wire (18-AWG) |
| ΔgcZ | 1/16 | in | Size of the vertical gap between the coil and the PMs |
| Brm | 1.4 | T | Magnetic remanence of the PMs (Neodymium, type N52) |
| σc | 58.58 | MS/m | Electrical conductivity of copper wire |
| Parameter | Value | Unit | Description |
|---|---|---|---|
| fb | 3.5 | Hz | Frequency of the base excitation |
| übXmax | 0.05 g | m/s2 | Maximum acceleration of the base excitation (ubXmax = übXmax/ωb2 = 15.2 cm) |
| fs | 3.5 | Hz | Frequency of the SDOF system |
| ξs | 5 | % | Critical mechanical damping ratio of the SDOF system |
| ms | 41.8 | gr | Mass of the SDOF system (ms = mw = 41.8 gr) |
| Rc | 129 | mΩ | Resistance of the coil |
| Rl | 129 | mΩ | Resistance of the electrical load (Rl/Rc = 1) |
| Parameter | Value | Unit | Description |
|---|---|---|---|
| am | 0.5 | in | Length of the sides of the PMs |
| δgmX | 1 | mm | Size of the gap between the PMs along the X-axis |
| δgmY | 1 | mm | Size of the gap between the PMs along the Y-axis |
| nX | 5 | Number of the PMs along the X-axis | |
| nY | 5 | Number of the PMs along the Y-axis | |
| ac | 2.5 | in | Length of the sides of the coil |
| hc | 0.5 | in | Height of the AC (Nz = 13) |
| tc | 0.5 | in | Winding depth (Nt = 13) |
| dw | 1 | mm | Diameter of the copper wire (18-AWG) |
| ΔgcZ | 1/16 | in | Size of the vertical gap between the coil and the PMs |
| Brm | 1.4 | T | Magnetic remanence of the PMs |
| σc | 58.58 | MS/m | Electrical conductivity of copper wire |
| fb | 3.5 | Hz | Frequency of the base excitation |
| übXmax | Var. | m/s2 | Maximum acceleration of the base excitation |
| fs | 3.5 | Hz | Frequency of the SDOF system (fs = fb) |
| ξs | 5 | % | Critical mechanical damping ratio of the SDOF system |
| ms | 241.7 | gr | Mass of the SDOF system (ms = mw) |
| Rc | 746.4 | mΩ | Resistance of the coil |
| Rl | Var. | mΩ | Resistance of the electrical load |
| i | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 0.7090 | 0.5610 | 0.4160 | 0.3410 | 0.2410 | |
| (sec) | 22.952 | 22.248 | 22.400 | 22.544 | 22.688 |
| Estimated Parameters | |||||
| (%) | 3.7 | 4.8 | 3.1 | 5.5 | |
| (Hz) | 6.6 | 6.9 | 6.6 | 6.9 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amjadian, M.; Agrawal, A.K.; Nassif, H.H. Development of An Analytical Method for Design of Electromagnetic Energy Harvesters with Planar Magnetic Arrays. Energies 2022, 15, 3540. https://doi.org/10.3390/en15103540
Amjadian M, Agrawal AK, Nassif HH. Development of An Analytical Method for Design of Electromagnetic Energy Harvesters with Planar Magnetic Arrays. Energies. 2022; 15(10):3540. https://doi.org/10.3390/en15103540
Chicago/Turabian StyleAmjadian, Mohsen, Anil. K. Agrawal, and Hani H. Nassif. 2022. "Development of An Analytical Method for Design of Electromagnetic Energy Harvesters with Planar Magnetic Arrays" Energies 15, no. 10: 3540. https://doi.org/10.3390/en15103540
APA StyleAmjadian, M., Agrawal, A. K., & Nassif, H. H. (2022). Development of An Analytical Method for Design of Electromagnetic Energy Harvesters with Planar Magnetic Arrays. Energies, 15(10), 3540. https://doi.org/10.3390/en15103540







