Energy and Conventional and Advanced Exergy Analyses of Low-Temperature Geothermal Binary-Flashing Cycle Using Zeotropic Mixtures
Abstract
:1. Introduction
2. System Description
3. System Modeling
- The system operates under steady state condition.
- The system ignores the heat loss of all components.
- The system neglects pressure losses in heat exchangers and pipelines.
- The geobrine is assumed to be pure water.
3.1. Energy Analysis
3.2. Conventional Exergy Analysis
3.3. Advanced Exergy Analysis
3.4. Flammability of the Zeotropic Mixtures
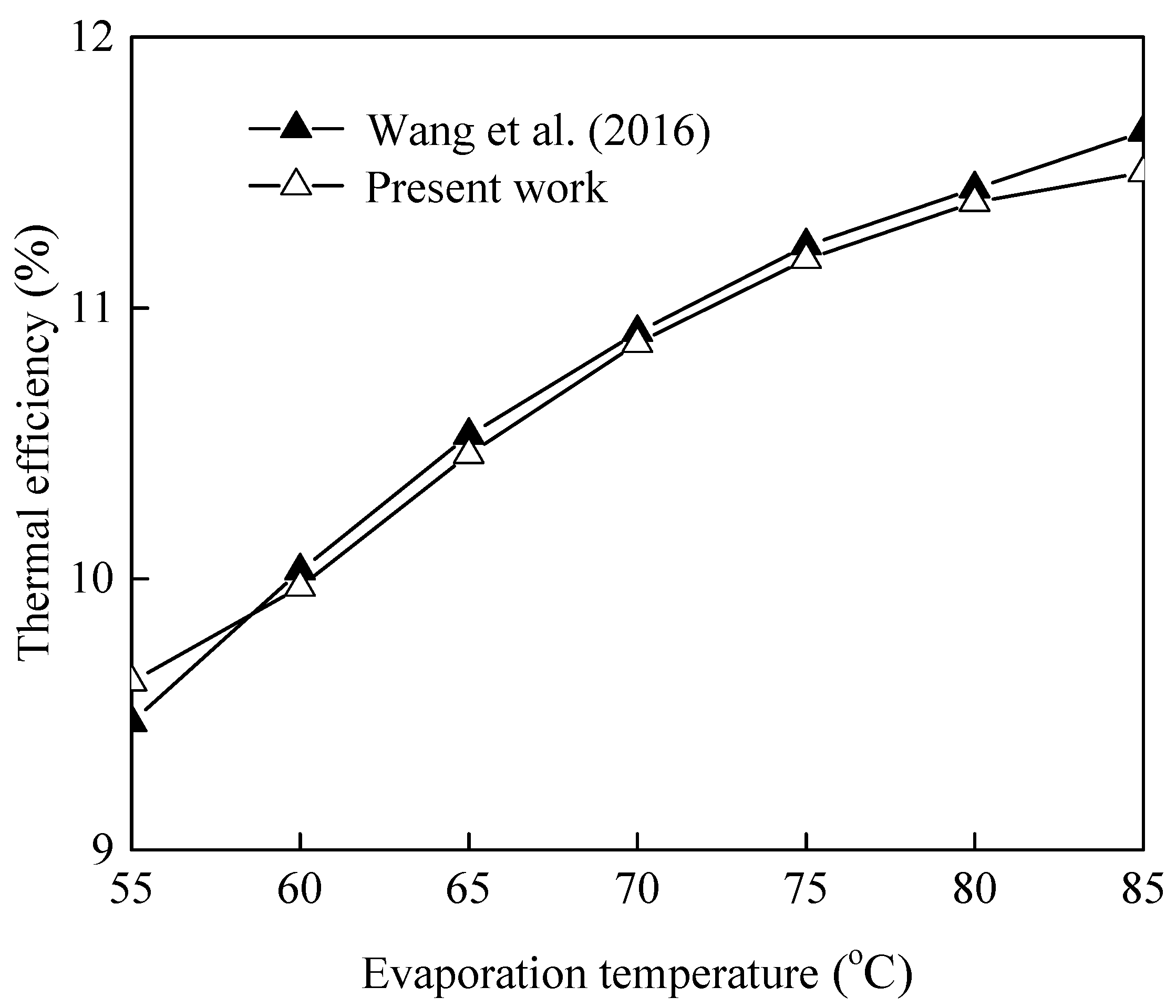
4. Model Verification
5. Results and Discussion
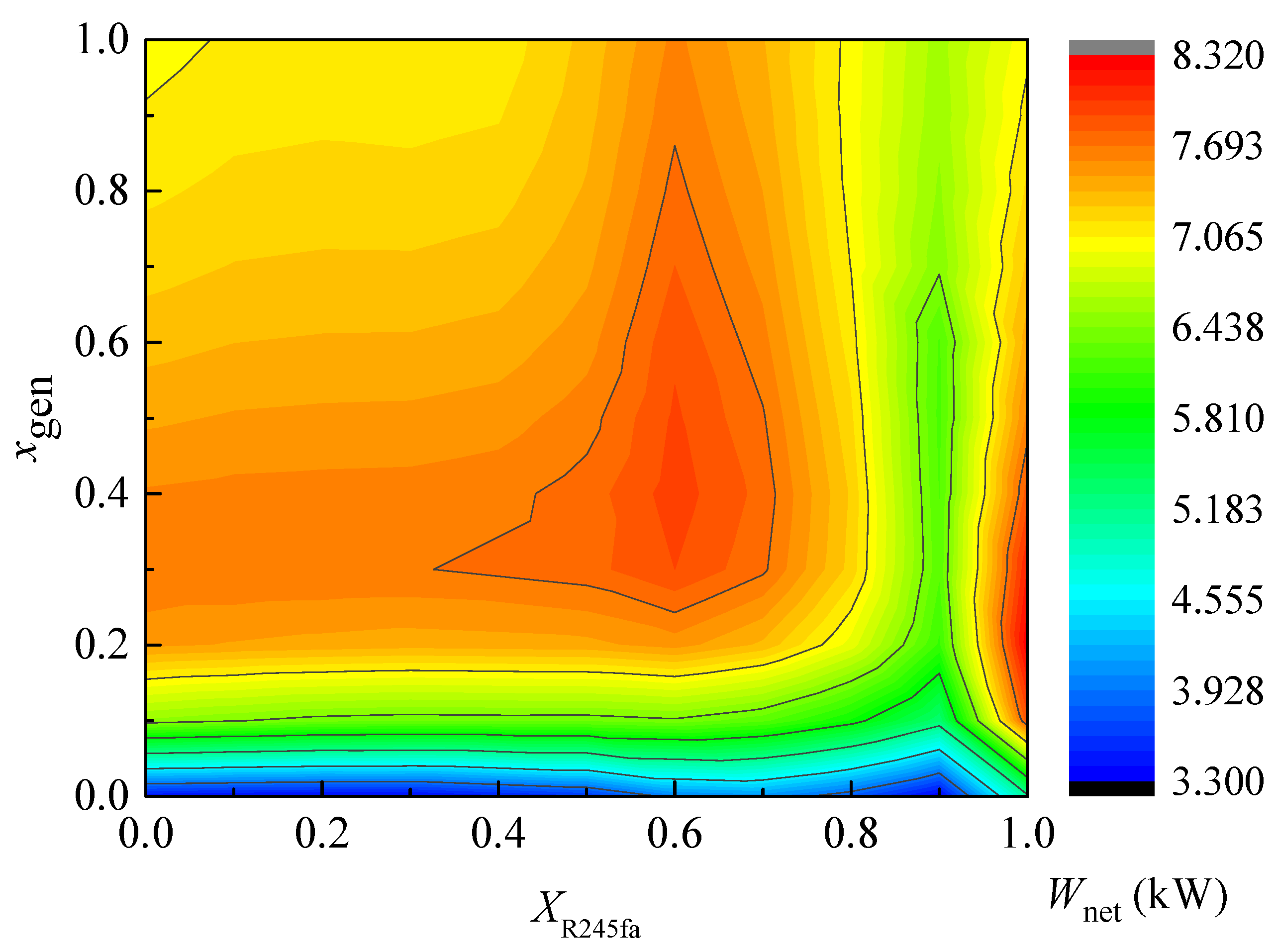
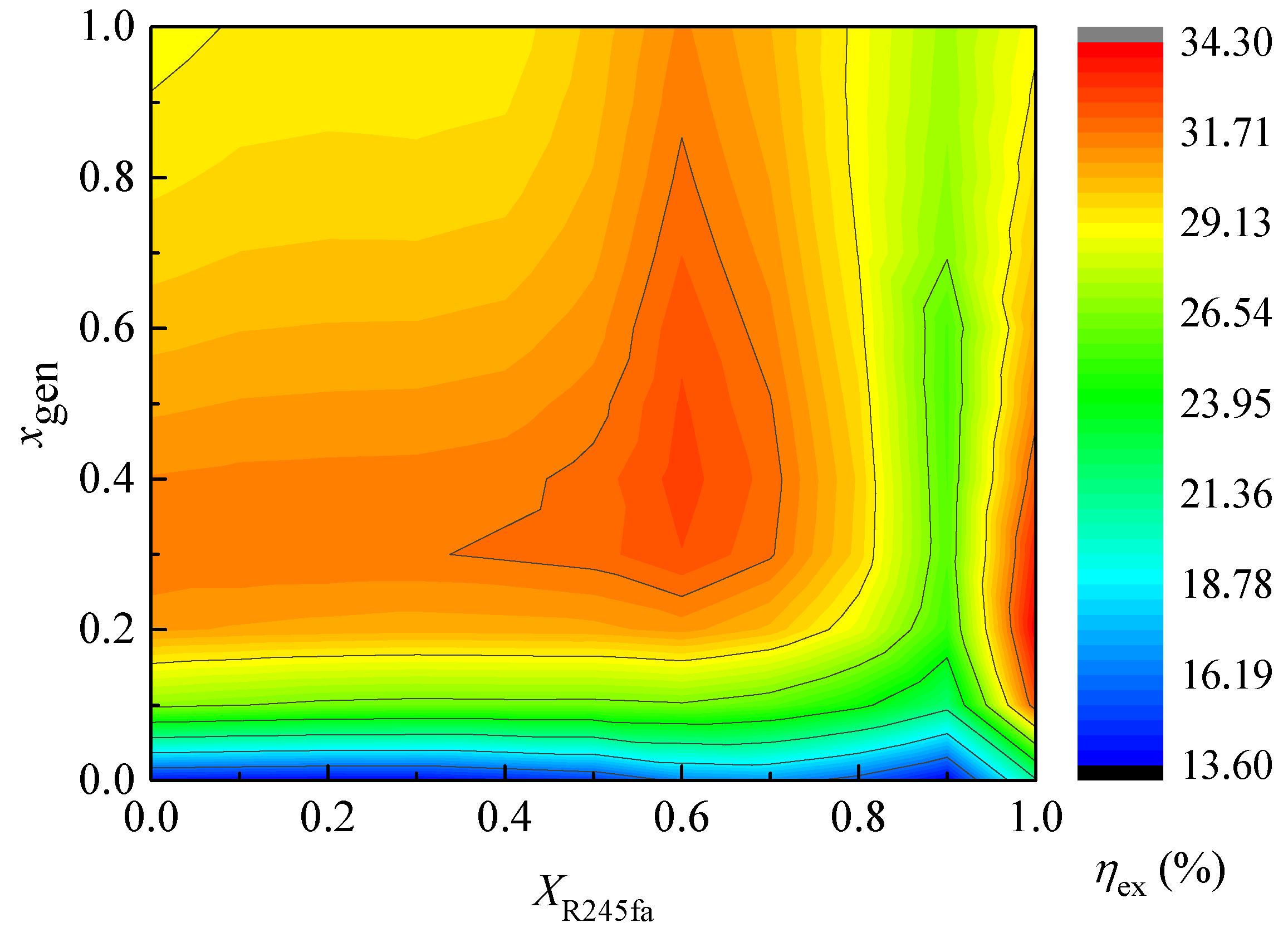
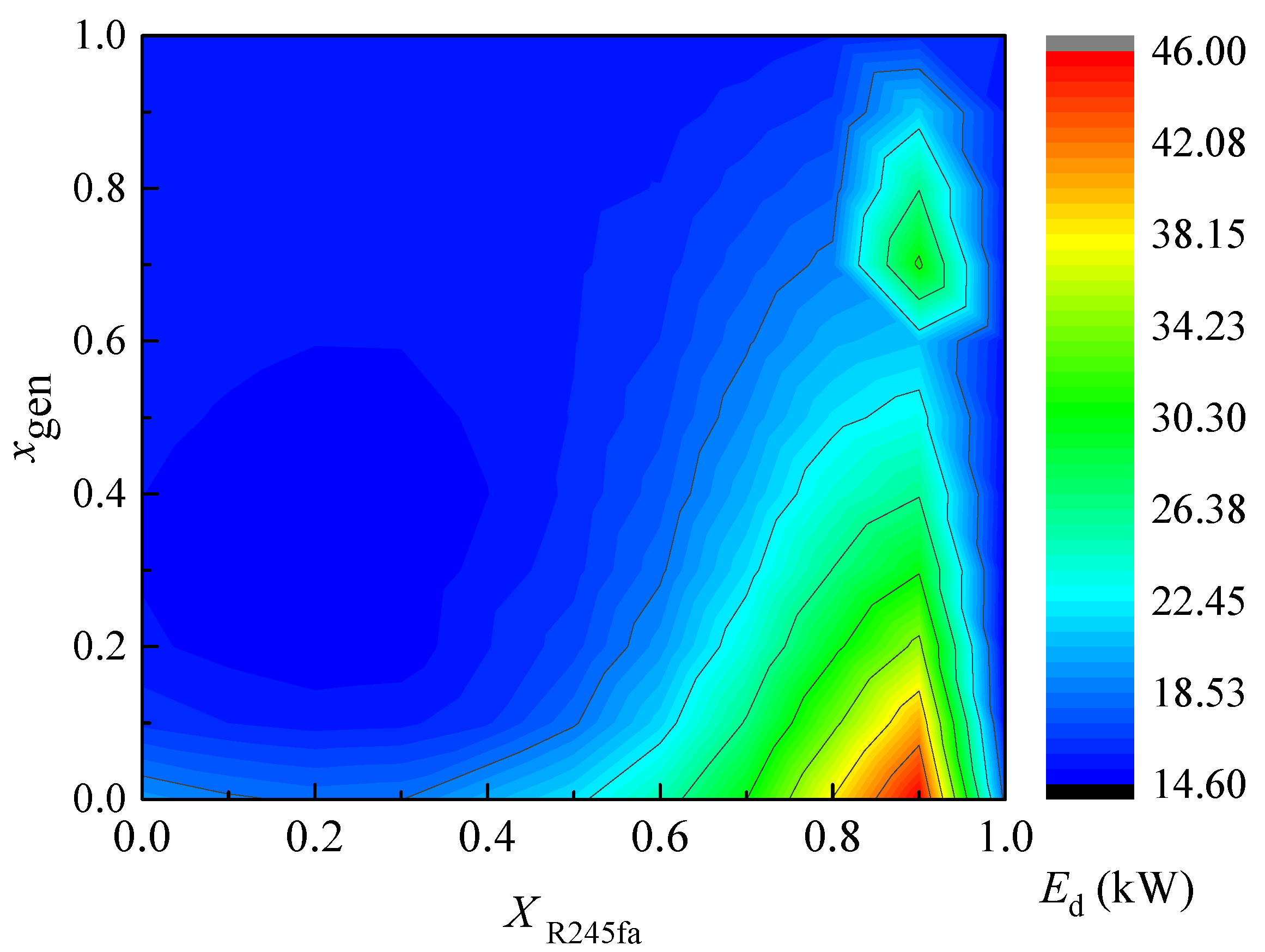
5.1. Synergy Optimization of R245fa Mass Fraction and Dryness
5.2. Conventional Exergy Analysis
5.3. Advanced Exergy Analysis
6. Conclusions
- (1)
- To suppress the flammability of the R245fa/R600a zeotropic mixtures, the R245fa mass fraction should be larger than 0.239. There exists a certain R245fa mass fraction range, at which the zeotropic mixture BFC system exhibits better performance than that of pure working fluid, with comprehensive consideration of net power output, thermal efficiency, exergy efficiency and exergy destruction. The recommended ranges of R245fa mass fraction and zeotropic mixture dryness at the evaporator outlet are 0.30~0.50 and 0.40~0.60.
- (2)
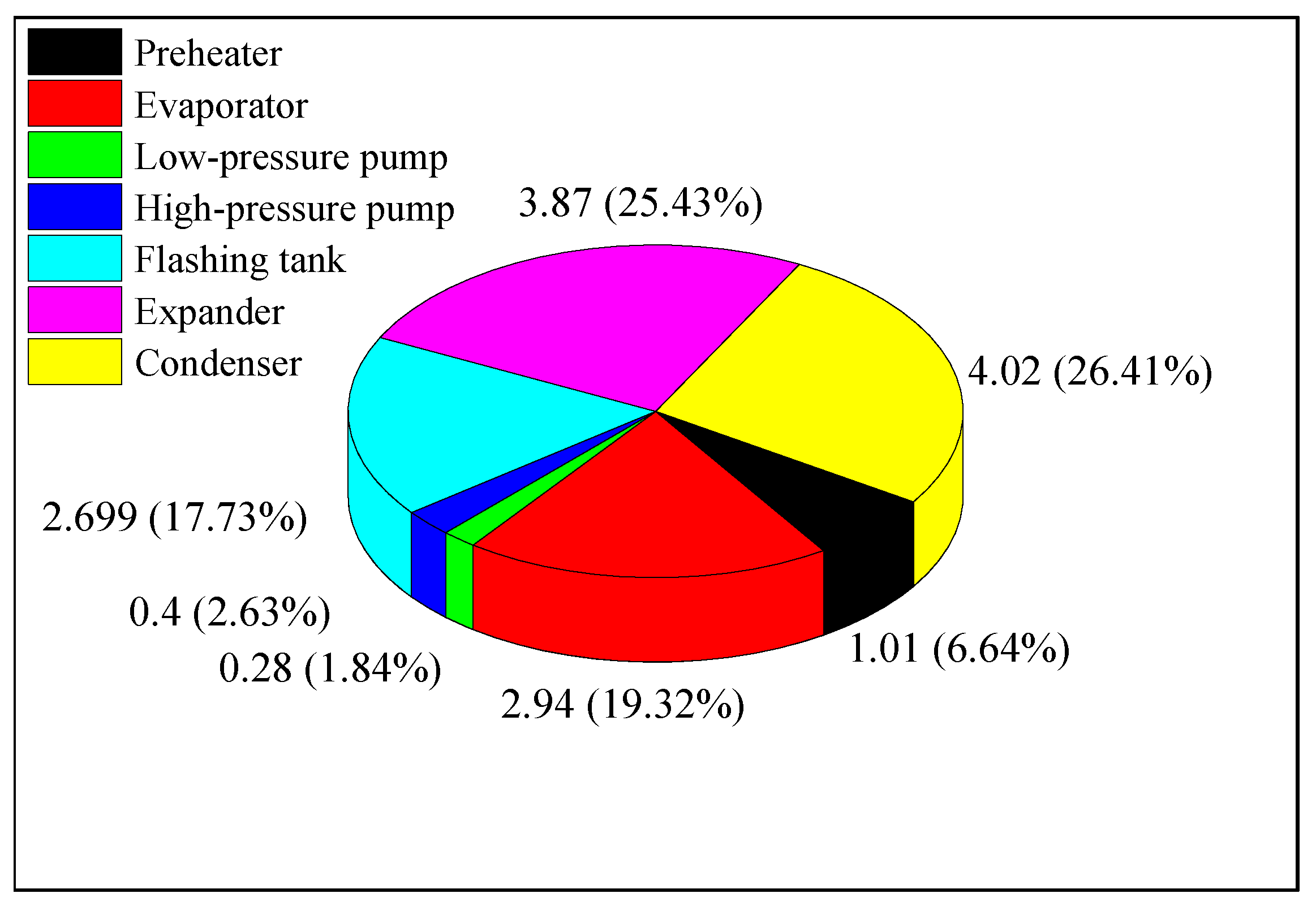
- By conventional exergy analysis, the maximum exergy destruction occurred in the condenser, followed by the expander, evaporator, flashing tank, preheater, high-pressure pump and low-pressure pump. The exergy destructions of the preheater, high-pressure pump and low-pressure pump can be ignored. The condenser should be given the first priority. The exergy destruction in the heat exchangers accounts for 52.40% of the total exergy destruction.
- (3)
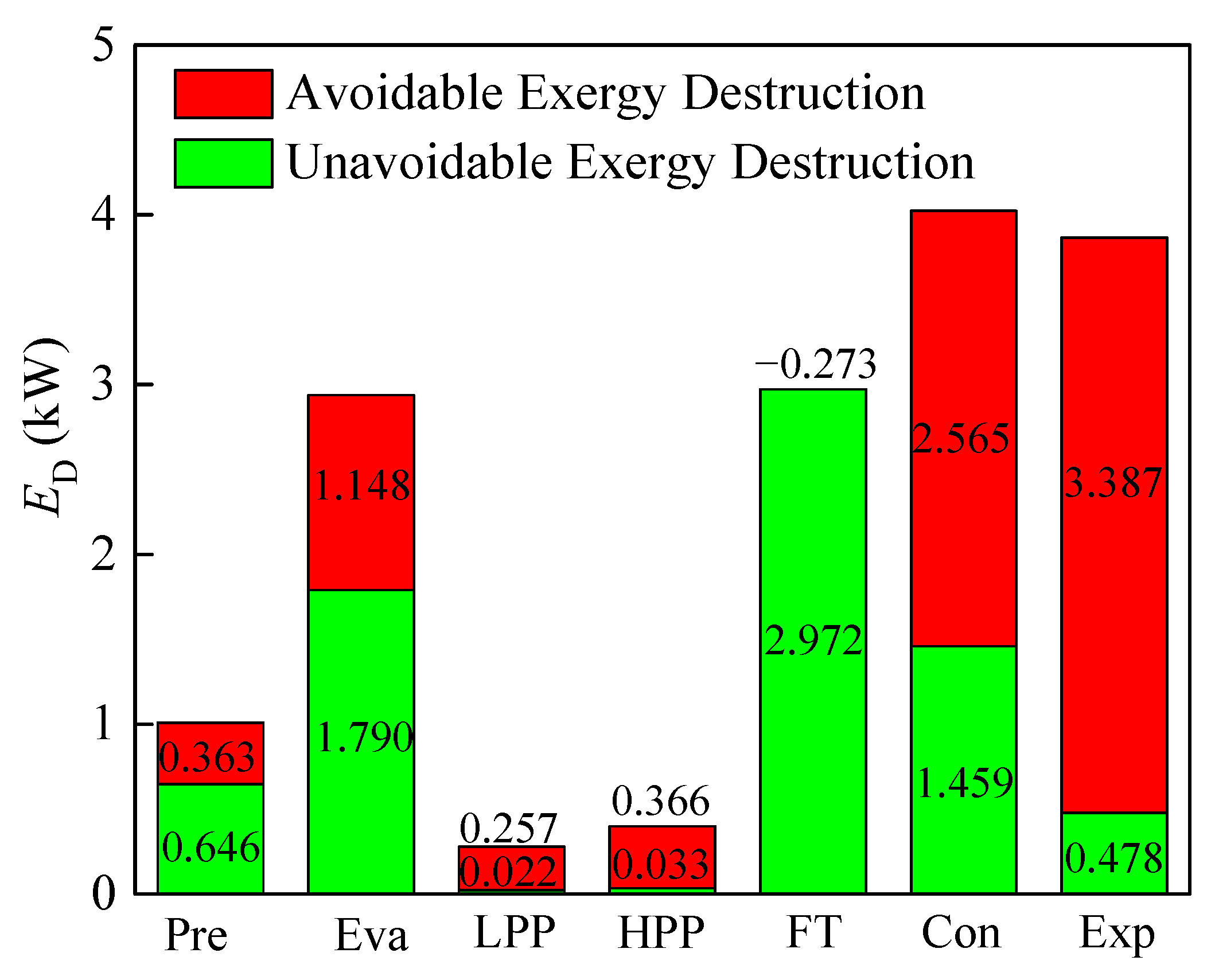
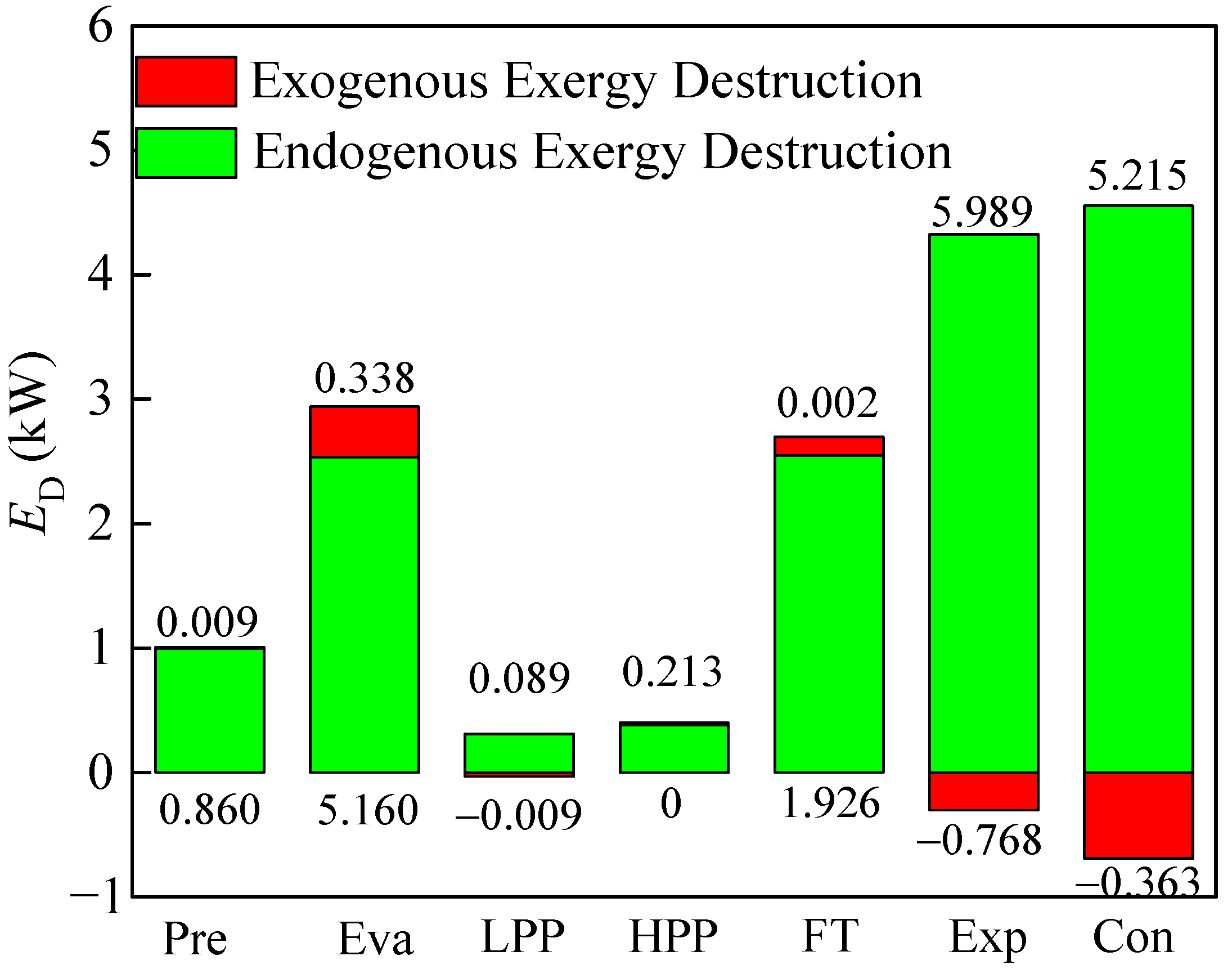
- By advanced exergy analysis, the priority should be given to the expander because of its large avoidable exergy destruction exergy destruction, followed by the condenser and evaporator. From the viewpoint of avoidability, about 48.6% of total system exergy destruction can be avoidable. The optimization sequence of BFC components deduced from the conventional and advanced methods is quite different. The interconnections among system components are not very strong, owing to small exogenous exergy destructions. Taking into account the interrelationships between components and the technical limitations of system components, the advanced exergy analysis could diagnose the detailed interactions among components of the BFC system and facilitate an exergoeconomic optimization. It clarifies the advantage of the advanced exergy analysis compared with the conventional exergy analysis.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Cmin | minimum inerting volume concentration (%) |
| cp | specific heat capacity (kJ/kg·K−1) |
| Cst | stoichiometric concentration (%) |
| e | specific exergy, (J/kg) |
| Ed | exergy destruction (W) |
| EF | input exergy (W) |
| avoidable exergy destruction (W) | |
| avoidable-endogenous exergy destruction (W) | |
| avoidable-exodogenous exergy destruction (W) | |
| endogenous exergy destruction (W) | |
| exodogenous exergy destruction (W) | |
| unavoidable exergy destruction (W) | |
| unavoidable-endogenous exergy destruction (W) | |
| unavoidable-exodogenous exergy destruction (W) | |
| Ep | output exergy (W) |
| h | specific enthalpy (kJ/kg) |
| h0 | specific enthalpy under ambient state (kJ/kg) |
| m | mass flow rate (kg/s) |
| MR245fa | molar mass of R245fa (kg/kmol) |
| MR600a | molar mass of R600a (kg/kmol) |
| Q | heat transfer rate (kW) |
| s0 | specific exergy under ambient state (kJ/kg) |
| t | temperature (°C) |
| T0 | ambient temperature (°C) |
| X | mass fraction of zeotropic mixtures (%) |
| Xmin | R245fa mass fraction of zeotropic mixtures (%) |
| x | dryness |
| v | velocity, m/s; |
| W | power/work (kW) |
| Greek | |
| η | efficiency |
| Φ | suppression coefficient |
| Subscripts | |
| 0 | ambient condition |
| 1, 2, …, | 12 state points |
| AV | avoidable |
| cf | cooling water |
| con | condenser |
| EN | endogenous |
| EX | exgenous |
| eva | evaporator |
| ex | exergy |
| exp | expander |
| FT | flash tank |
| hf | geofluid |
| HPP | high-pressure pump |
| in | inlet |
| LPP | low-pressure pump |
| max | maximum |
| net | net |
| th | thermal |
| out | outlet |
| pre | preheater |
| s | isentropic |
| UN | unavoidable |
| wf | working fluid |
| Acronyms | |
| BFC | binary-flashing cycle |
| GWP | global warming potential |
| LEC | levelized energy cost |
| ODP | ozone depletion potential |
| ORC | organic Rankine cycle |
References
- Nadimi, R.; Tokimatsu, K. Energy use analysis in the presence of quality of life, poverty, health, and carbon dioxide emissions. Energy 2018, 153, 671–684. [Google Scholar] [CrossRef]
- Huang, F.; Zheng, J.; Baleynaud, J.M.; Lu, J. Heat recovery potentials and technologies in industrial zones. J. Energy Inst. 2017, 90, 951–961. [Google Scholar] [CrossRef]
- Nguyen, K.H.; Kakinaka, M. Renewable energy consumption, carbon emissions, and development stages: Some evidence from panel cointegration analysis. Renew. Energy 2019, 132, 1049–1057. [Google Scholar] [CrossRef]
- Davidson, M.; Karplus, V.J.; Zhang, D.; Zhang, X. Policies and Institutions to Support Carbon Neutrality in China by 2060. Econ. Energy Environ. Policy 2021, 10, 7–25. [Google Scholar] [CrossRef]
- Irfan, M.; Elavarasan, R.M.; Hao, Y.; Feng, M.; Sailan, D. An assessment of consumers’ willingness to utilize solar energy in China: End-users’ perspective. J. Clean. Prod. 2021, 292, 126008. [Google Scholar] [CrossRef]
- Magazzino, C.; Mele, M.; Schneider, N. A machine learning approach on the relationship among solar and wind energy production, coal consumption, GDP, and CO2 emissions. Renew. Energy 2021, 167, 99–115. [Google Scholar] [CrossRef]
- Kong, Y.; Pang, Z.; Shao, H.; Hu, S.; Kolditz, O. Recent studies on hydrothermal systems in China: A review. Geotherm. Energy 2014, 2, 19. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.X.; Pang, M.Y.; Han, J.; Li, Y.Y.; Wang, C.B. Geothermal power in China: Development and performance evaluation. Renew. Sustain. Energy Rev. 2019, 116, 109431. [Google Scholar] [CrossRef]
- Özcan, Z.; Ekici, Ö. A novel working fluid selection and waste heat recovery by an exergoeconomic approach for a geothermally sourced ORC system. Geothermics 2021, 95, 102151. [Google Scholar] [CrossRef]
- Michaelides, E.E.; Scott, G.J. A binary-flashing geothermal power plant. Energy 1984, 9, 323–331. [Google Scholar] [CrossRef]
- Shi, H.; Michaelides, E.E. Binary dual-flashing geothermal power plants. Int. J. Energy Res. 1989, 13, 127–135. [Google Scholar] [CrossRef]
- Yuan, Z.; Michaelides, E.E. Binary-flashing geothermal power plants. J. Energy 1993, 115, 232–236. [Google Scholar] [CrossRef]
- Michaelides, E. Future directions and cycles for electricity production from geothermal resources. Energy Convers. Manag. 2016, 107, 3–9. [Google Scholar] [CrossRef]
- Wang, Y.X.; Wang, L.B.; Li, H.S.; Bu, X.B. Thermodynamic calculation and optimization of geothermal power generation in Ganzi. J. Harbin Eng. Univ. 2016, 37, 873–877. (In Chinese) [Google Scholar]
- Mosaffa, A.H.; Zareei, A. Proposal and thermoeconomic analysis of geothermal flash binary power plants utilizing different types of organic flash cycle. Geothermics 2018, 72, 47–63. [Google Scholar] [CrossRef]
- Edrisi, B.H.; Michaelides, E.E. Effect of the working fluid on the optimum work of binary-flashing geothermal power plants. Energy 2013, 50, 389–394. [Google Scholar] [CrossRef]
- Wang, L.; Bu, X.; Li, H. Investigation on geothermal binary-flashing cycle employing zeotropic mixtures as working fluids. Geothermal. Energy 2019, 7, 36. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Li, H.S.; Bu, X.B.; Wang, L.; Xie, N.; Zeng, J. Performance characteristics and working fluid selection for low-temperature binary flashing cycle. Appl. Therm. Eng. 2018, 141, 51–60. [Google Scholar] [CrossRef]
- Wang, L.; Li, H.; Bu, X. Multi-objective optimization of Binary Flashing Cycle (BFC) driven by geothermal energy. Appl. Therm. Eng. 2020, 166, 114693. [Google Scholar] [CrossRef]
- Wang, L.; Li, H.; Bu, X. Thermo-economic investigation of binary flashing cycle for enhanced geothermal system. Geothermics 2021, 89, 101951. [Google Scholar] [CrossRef]
- Tsatsaronis, G. Strengths and limitations of exergy analysis. In Thermodynamic Optimization of Complex Energy Systems; Bejan, A., Mamut, E., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999; pp. 93–100. [Google Scholar]
- Tsatsaronis, G.; Moung-Ho, P. On avoidable and unavoidable exergy destructions and investment costs in thermal systems. Energy Convers. Manag. 2002, 43, 1259–1270. [Google Scholar]
- Dai, B.; Zhu, K.; Wang, Y.; Sun, Z.; Liu, Z. Evaluation of organic Rankine cycle by using hydrocarbons as working fluids: Advanced exergy and advanced exergoeconomic analyses. Energy Convers. Manag. 2019, 197, 111876. [Google Scholar] [CrossRef]
- Nami, H.; Nemati, A.; Fard, F.J. Conventional and advanced exergy analyses of a geothermal driven dual fluid organic Rankine cycle (ORC). Appl. Therm. Eng. 2017, 122, 59–70. [Google Scholar] [CrossRef]
- Gökgedik, H.; Yürüsoy, M.; Keçebaş, A. Improvement potential of a real geothermal power plant using advanced exergy analysis. Energy 2016, 112, 254–263. [Google Scholar] [CrossRef]
- Wang, Z.; Xia, X.; Pan, H.; Zuo, Q.; Zhou, N.; Xie, B. Fluid selection and advanced exergy analysis of dual-loop ORC using zeotropic mixture. Appl. Therm. Eng. 2021, 185, 116423. [Google Scholar] [CrossRef]
- Liao, G.; Jiaqiang, E.; Zhang, F.; Chen, J.; Leng, E. Advanced exergy analysis for Organic Rankine Cycle-based layout to recover waste heat of flue gas. Appl. Energy 2020, 266, 114891. [Google Scholar] [CrossRef]
- Chen, J.; Zheng, X.; Guo, G.; Luo, X.; Chen, Y.; Yang, Z. A flexible and multi-functional organic Rankine cycle system: Preliminary experimental study and advanced exergy analysis. Energy Convers. Manag. 2019, 187, 339–355. [Google Scholar] [CrossRef]
- Montazerinejad, H.; Ahmadi, P.; Montazerinejad, Z. Advanced exergy, exergo-economic and exrgo-environmental analyses of a solar based trigeneration energy system. Appl. Therm. Eng. 2019, 152, 666–685. [Google Scholar] [CrossRef]
- Khosravi, H.; Salehi, G.R.; Azad, M.T. Design of structure and optimization of organic Rankine cycle for heat recovery from gas turbine: The use of 4E, advanced exergy and advanced exergoeconomic analysis. Appl. Therm. Eng. 2019, 147, 272–290. [Google Scholar] [CrossRef]
- Anvari, S.; Saray, R.K.; Bahlouli, K. Conventional and advanced exergetic and exergoeconomic analyses applied to a tri-generation cycle for heat, cold and power production. Energy 2015, 91, 925–939. [Google Scholar] [CrossRef]
- Ambriz-Díaz, V.M.; Rubio-Maya, C.; Ruiz-Casanova, E.; Martinez-Patino, J.; Pastor-Martínez, E. Advanced exergy and exergoeconomic analysis for a polygeneration plant operating in geothermal cascade. Energy Convers. Manag. 2020, 203, 112227. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, T.; Yang, C.; Zhang, X.; Yang, K. Advanced exergy analysis of an integrated energy storage system based on transcritical CO2 energy storage and Organic Rankine Cycle. Energy Convers. Manag. 2020, 216, 112938. [Google Scholar] [CrossRef]
- Yang, J.; Gao, L.; Ye, Z.; Hwang, Y.; Chen, J. Binary-objective optimization of latest low-GWP alternatives to R245fa for organic Rankine cycle application. Energy 2021, 217, 119336. [Google Scholar] [CrossRef]
- Feng, Y.; Hung, T.; Zhang, Y.; Li, B.; Yang, J.; Shi, Y. Performance comparison of low-grade ORCs (organic Rankine cycles) using R245fa, pentane and their mixtures based on the thermoeconomic multi-objective optimization and decision makings. Energy 2015, 93, 2018–2029. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP; Version 9.1, Standard Reference Data Program; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2013.
- Bai, T.; Yu, J.; Yan, G. Advanced exergy analysis on a modified auto-cascade freezer cycle with an ejector. Energy 2016, 113, 385–398. [Google Scholar] [CrossRef]
- Hu, Y. Advanced Exergy Analysis for a Solar Double Stage Absorption Chiller; Carnegie Mellon University: Pittsburgh, PA, USA, 2012. [Google Scholar]
- Lemort, V.; Quoilin, S.; Cuevas, C.; Lebrun, J. Testing and modeling a scroll expander integrated into an organic Rankine cycle. Appl. Therm. Eng. 2009, 29, 3094–3102. [Google Scholar] [CrossRef] [Green Version]
- Fallah, M.; Mahmoudi, S.M.S.; Yari, M.; Ghiasi, R.A. Advanced exergy analysis of the Kalina cycle applied for low temperature enhanced geothermal system. Energy Convers. Manag. 2016, 108, 190–201. [Google Scholar] [CrossRef]
- Imran, M.; Usman, M.; Park, B.S.; Kim, H.-J.; Lee, D.-H. Multi-objective optimization of evaporator of organic Rankine cycle (ORC) for low temperature geothermal heat source. Appl. Therm. Eng. 2015, 80, 1–9. [Google Scholar] [CrossRef]


| Fluid | Molecular Mass (g/mol) | Critical Temperature (°C) | ODP | GWP | Flammability a | Toxicity c |
|---|---|---|---|---|---|---|
| R245fa | 134.05 | 154.0 | 0 | 1030 | 3 | 2 |
| R600a | 58.12 | 134.7 | 0 | 3 | 3 | 1 |
| Parameters | Values |
|---|---|
| Inlet temperature of geobrine (°C) | 90 |
| Inlet temperature of cooling water (°C) | 20 |
| Degree of subcooling (°C) | 3 |
| Pinch point temperature of heat exchanger (°C) | 5 |
| Isentropic efficiency of expander (%) | 70 |
| Isentropic efficiency of pump (%) | 60 |
| Ambient temperature (°C) | 20 |
| Ambient pressure (kPa) | 101.325 |
| Component | Parameter | Real | Unavoidable | Theoretical |
|---|---|---|---|---|
| Heat exchanger | Pinch point temperature difference (°C) | 5 [37] | 0.3 [38] | 0 |
| Expander | Isentropic efficiency | 0.7 [39] | 0.95 [40] | 1 |
| Low-pressure pump | Isentropic efficiency | 0.6 [41] | 0.95 [40] | 1 |
| High-pressure pump | Isentropic efficiency | 0.6 [41] | 0.95 [40] | 1 |
| Flashing tank | Isentropic efficiency | Isenthalpic | 0.95 | 1 |
| State Point | Temperature (°C) | Pressure (kPa) | Enthalpy (kJ/kg) | Entropy (kJ/kg·K−1) | Mass Flow Rate (kg/s) | Dryness | R245fa Mass Fraction |
|---|---|---|---|---|---|---|---|
| 1 | 70.005 | 880.435 | 368.740 | 1.579 | 2.1632 | 0.141 | 0.600 |
| 2 | 70.005 | 880.435 | 546.160 | 2.097 | 0.3059 | 1 | 0.587 |
| 3 | 39.716 | 299.692 | 522.270 | 2.114 | 0.622 | 1.053 | 0.581 |
| 4 | 27.000 | 299.692 | 259.190 | 1.247 | 0.622 | 0 | 0.581 |
| 5 | 27.511 | 880.435 | 260.340 | 1.248 | 0.622 | Subcooling | 0.581 |
| 6 | 50.346 | 880.435 | 302.610 | 1.384 | 0.622 | 0 | 0.581 |
| 7 | 50.352 | 880.435 | 301.210 | 1.379 | 1.5413 | Subcooling | 0.608 |
| 8 | 50.346 | 880.435 | 301.610 | 1.380 | 2.1632 | Subcooling | 0.600 |
| 9 | 70.000 | 880.435 | 339.680 | 1.494 | 2.1632 | 0 | 0.600 |
| 10 | 70.005 | 880.435 | 339.520 | 1.494 | 1.8573 | 0 | 0.602 |
| 11 | 50.003 | 531.511 | 529.820 | 2.088 | 0.3161 | 1 | 0.576 |
| 12 | 50.003 | 531.511 | 300.490 | 1.378 | 1.5413 | 0 | 0.608 |
| Wnet = 7.876 kW; ηth = 4.590%; ηex = 32% | |||||||
| State Point | Temperature (°C) | Pressure (kPa) | Enthalpy (kJ/kg) | Entropy (kJ/kg·K−1) | Mass Flow Rate (kg/s) | Dryness | R245fa Mass Fraction |
|---|---|---|---|---|---|---|---|
| 1 | 70.007 | 880.435 | 377.840 | 1.605 | 2.163 | 0.186 | 0.600 |
| 2 | 70.007 | 880.435 | 546.040 | 2.096 | 0.402 | 1 | 0.587 |
| 3 | 36.068 | 299.646 | 516.990 | 2.097 | 0.690 | 1.032 | 0.583 |
| 4 | 27.000 | 299.646 | 259.160 | 1.247 | 0.690 | 0 | 0.583 |
| 5 | 27.276 | 880.435 | 259.880 | 1.247 | 0.690 | Subcooling | 0.583 |
| 6 | 50.207 | 880.435 | 302.270 | 1.383 | 0.690 | 0 | 0.583 |
| 7 | 50.212 | 880.435 | 300.920 | 1.378 | 1.473 | Subcooling | 0.608 |
| 8 | 50.207 | 880.435 | 301.350 | 1.379 | 2.163 | Subcooling | 0.600 |
| 9 | 70.000 | 880.435 | 339.680 | 1.494 | 2.163 | 0 | 0.600 |
| 10 | 70.007 | 880.435 | 339.460 | 1.494 | 1.761 | 0 | 0.603 |
| 11 | 50.004 | 531.495 | 529.740 | 2.088 | 0.288 | 1 | 0.576 |
| 12 | 50.004 | 531.495 | 300.460 | 1.378 | 1.473 | 0 | 0.608 |
| Wnet = 14.179 kW; ηth = 7.280%; ηex = 53.460% | |||||||
| State Point | Temperature (°C) | Pressure (kPa) | Enthalpy (kJ/kg) | Entropy (kJ/kg·K−1) | Mass Flow Rate (kg/s) | Dryness | R245fa Mass Fraction |
|---|---|---|---|---|---|---|---|
| 1 | 70.0072 | 880.4352 | 378.42 | 1.6071 | 2.1629 | 0.1886 | 0.6 |
| 2 | 70.0072 | 880.4352 | 546.03 | 2.0961 | 0.4079 | 1 | 0.587 |
| 3 | 35.2434 | 299.6433 | 515.85 | 2.0928 | 0.6944 | 1.0275 | 0.5825 |
| 4 | 27 | 299.6433 | 259.16 | 1.2465 | 0.6944 | 0 | 0.5825 |
| 5 | 27.2554 | 880.4352 | 259.85 | 1.2465 | 0.6944 | Subcooling | 0.5825 |
| 6 | 50.1945 | 880.4352 | 302.24 | 1.3825 | 0.6944 | 0 | 0.5825 |
| 7 | 50.1999 | 880.4352 | 300.89 | 1.3775 | 1.4685 | Subcooling | 0.6083 |
| 8 | 50.1945 | 880.4352 | 301.32 | 1.3791 | 2.1629 | Subcooling | 0.6 |
| 9 | 70 | 880.4352 | 339.68 | 1.4942 | 2.1629 | 0 | 0.6 |
| 10 | 70.0072 | 880.4352 | 339.46 | 1.4935 | 1.755 | 0 | 0.603 |
| 11 | 50.0036 | 531.4933 | 529.73 | 2.0881 | 0.2865 | 1 | 0.5761 |
| 12 | 50.0036 | 531.4933 | 300.46 | 1.3775 | 1.4685 | 0 | 0.6083 |
| Wnet = 15.183 kW; ηth = 7.740%; ηex = 57.010% | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Du, B.; Chen, S.; Zhao, J.; Guo, Z.; Wang, L. Energy and Conventional and Advanced Exergy Analyses of Low-Temperature Geothermal Binary-Flashing Cycle Using Zeotropic Mixtures. Energies 2022, 15, 3487. https://doi.org/10.3390/en15103487
Zhao Y, Du B, Chen S, Zhao J, Guo Z, Wang L. Energy and Conventional and Advanced Exergy Analyses of Low-Temperature Geothermal Binary-Flashing Cycle Using Zeotropic Mixtures. Energies. 2022; 15(10):3487. https://doi.org/10.3390/en15103487
Chicago/Turabian StyleZhao, Yuan, Bowen Du, Shunyi Chen, Jun Zhao, Zhipeng Guo, and Lingbao Wang. 2022. "Energy and Conventional and Advanced Exergy Analyses of Low-Temperature Geothermal Binary-Flashing Cycle Using Zeotropic Mixtures" Energies 15, no. 10: 3487. https://doi.org/10.3390/en15103487
APA StyleZhao, Y., Du, B., Chen, S., Zhao, J., Guo, Z., & Wang, L. (2022). Energy and Conventional and Advanced Exergy Analyses of Low-Temperature Geothermal Binary-Flashing Cycle Using Zeotropic Mixtures. Energies, 15(10), 3487. https://doi.org/10.3390/en15103487






