A Hybrid Feature Selection Framework Using Improved Sine Cosine Algorithm with Metaheuristic Techniques
Abstract
:1. Introduction
- (1)
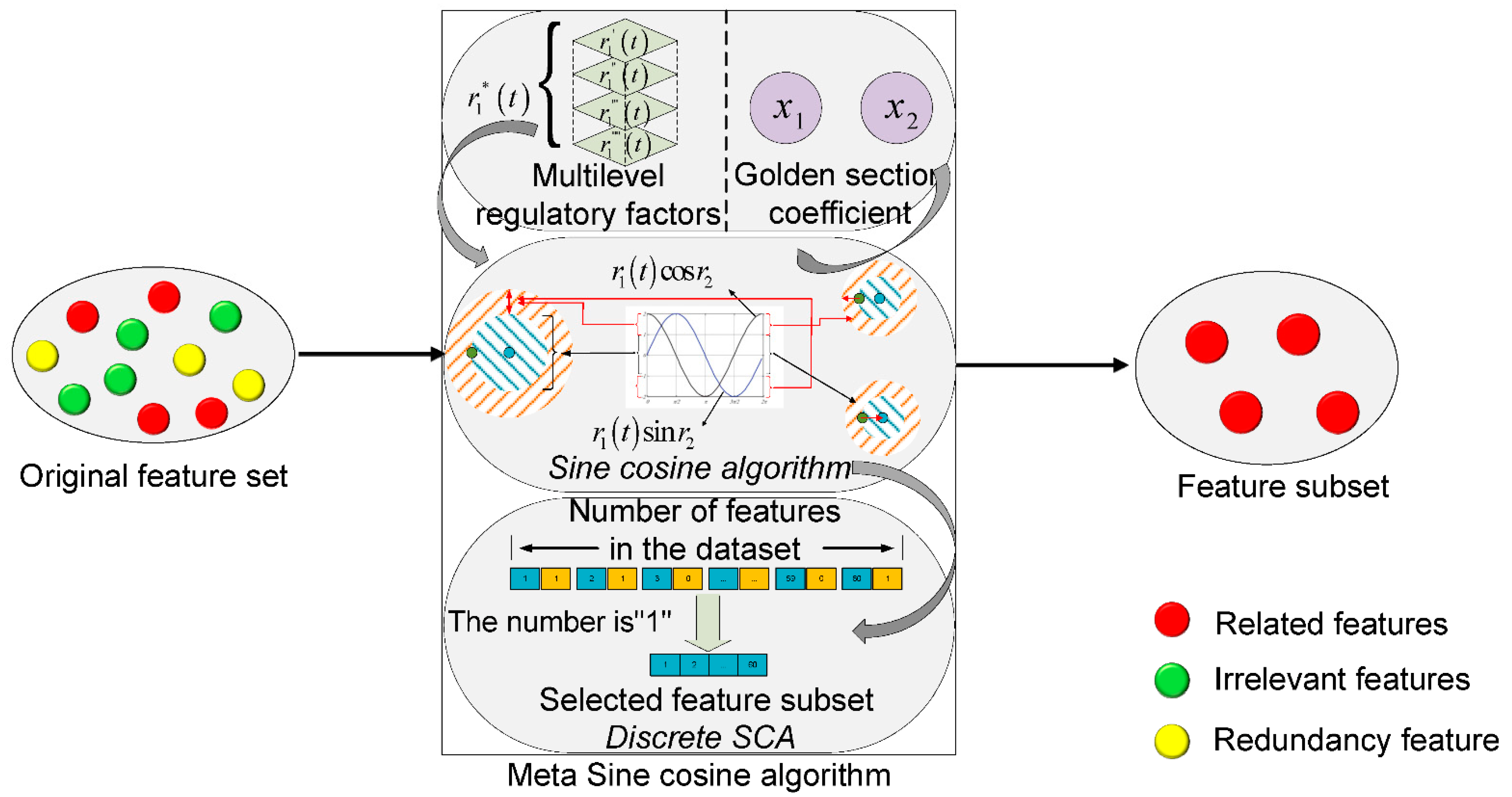
- We propose a hybrid feature selection framework, using an improved SCA with metaheuristic techniques to reduce the dimensionality of data in the face of the curse of dimensionality due to a large number of features in a dataset.
- (2)
- We analyze the optimization performance of the standard SCA algorithm and point out that the algorithm has difficulty in selecting the best feature subset during feature selection. An improved SCA (MetaSCA), based on the multilevel regulatory factor strategy and the golden section coefficient strategy, is proposed to enhance the superiority-seeking effect of the SCA and implemented for the solution of the optimal feature subset.
- (3)
- We tested the method with several datasets, to explore the performance of the method in feature selection. From the simulation results, we can see that the MetaSCA technique achieved good results in seeking the best feature subset.
2. Related Works
3. System Model and Analysis
3.1. Feature Selection Model
- Related features: Such features help to complete the classification task and improve the fit of an algorithm.
- Irrelevant features: Irrelevant features that do not help to improve the fit of an algorithm, and which are not relevant to the task at hand.
- Redundancy feature: The improvement in classification performance brought by redundant features can also be obtained from other features.
3.2. Problem Formulation
4. Hybrid Framework with Metaheuristic Techniques
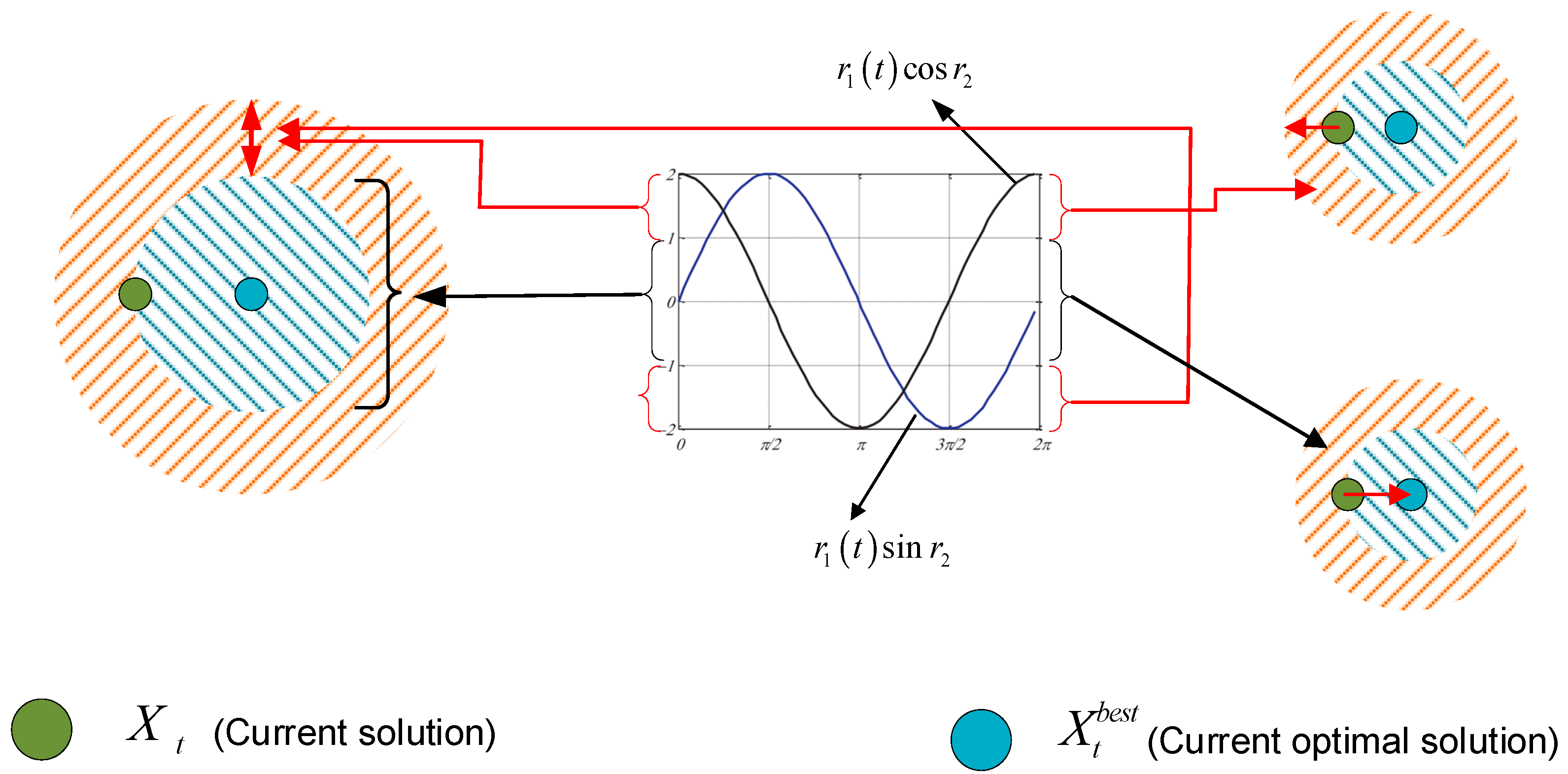
4.1. Sine Cosine Process
4.1.1. Conventional SCA Procedure
| Algorithm 1 Standard sine cosine algorithm |
| 1. Input: Number of solution , dimension of solution , maximum number of iterations , objective fitness function . |
| 2. Initialize a solution set with and quality. |
| 3. Calculate the fitness function value of each solution in the solution set according to , and find the solution with the smallest fitness value. |
| 4. Do (for each iteration) |
| 5. Update parameters ; |
| 6. Update the position of each solution in the solution set according to Formula 1; |
| 7. Calculate the fitness function value of each solution according to . |
| 8. Update current optimal solution . |
| 9. While) |
| 10. Output: Global optimal solution after iteration. |
4.1.2. Analysis of the SCA in Feature Selection
4.2. Feature Selection with Metaheuristic
4.2.1. Multilevel Regulatory Factor Strategy
4.2.2. Golden Selection Coefficient Strategy
4.2.3. Metaheuristic Process
| Algorithm 2 The MetaSCA_process for feature selection |
| 1. Input: The number of feature subsets , number of features in the training set , fitness function , maximum numbers of iterations . |
| 2. To initialize feature sets, and select the feature marked “1” from the features of each feature set to form a feature subset . |
| 3. To calculate the fitness value of each feature subset according to . Determine the minimum fitness value and the corresponding optimal feature subset . |
| 4. fordo |
| 5. for each feature subset do |
| 6. Update parameters |
| 7. if |
| 8. Update feature subset by |
| 9. else |
| 10. Update feature subset by |
| 11. end if |
| 12. Discretize according to formula 23 to obtain a new feature subset |
| 13. Calculate the fitness value of the new feature subset according to |
| 14. if |
| 15. |
| 16. |
| 17. end if |
| 18. end for |
| 19. end for |
| 20. Select the classifier and employ the best subset of features to fit the training set. |
| 21. The trained classifier is applied to classify the test set and the classification accuracy (acc) is calculated. |
| 22. Output: Optimal feature subset , Optimal fitness value , Classification accuracy acc. |
5. Performance
5.1. Datasets and Parameters
5.2. Evaluation Setup
- Average fitness. This index describes the average fitness value after running 10 experiments on each data set. Its calculation formula is shown in Equation (23).
- —illustrates the quantity of experimental runs;
- —illustrates the optimal fitness resulting from run number .
- Optimal fitness. This represents the smallest fitness in the fitness set acquired after 10 experiments on each data set. We have its selection method:
- Worst fitness. This index shows the worst fitness value in the fitness set obtained after many experiments. We have:
- Standard deviation. This shows the degree of dispersion between fitness in the fitness set obtained after many experiments. In addition, the smaller the standard deviation, the smaller the numerical difference between fitness, which means that the feature selection model is more stable. We have:
- Classification accuracy. This describes the classification accuracy of the classifier on the test set after fitting the classifier using a subset of the chosen features:
- Proportion of selected feature subset. This represents the proportion of the quantity of feature subsets selected in the total quantity of features. The smaller the proportion, the fewer the number of feature subsets. The calculation method is given as follows:
- represents the total quantity of original features in the datasets, represents the quantity of features marked as “1” in the feature subset obtained in the experiment.
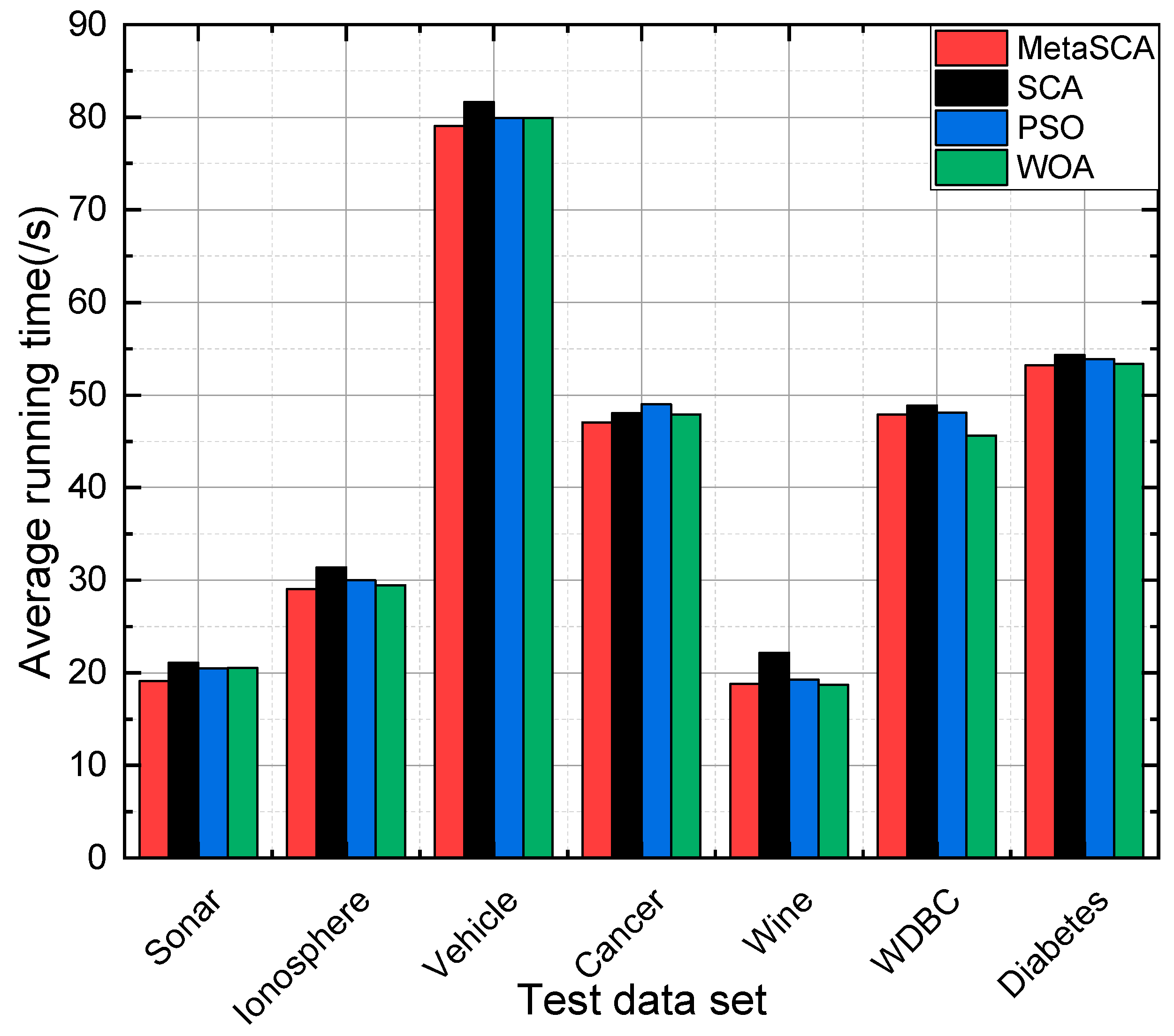
- Average running time. This represents the average time that the feature selection model runs when selecting feature subsets, which can be obtained by:
5.3. Evaluation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, X.; Zhu, X.; Wu, G.-Q.; Ding, W. Data mining with big data. IEEE Trans. Knowl. Data Eng. 2014, 26, 97–107. [Google Scholar]
- Maimon, O.; Rokach, L. (Eds.) Data Mining and Knowledge Discovery Handbook; Springer: New York, NY, USA, 2005. [Google Scholar]
- Koh, H.C.; Tan, G. Data mining applications in healthcare. J. Healthc. Inf. Manag. 2011, 19, 65. [Google Scholar]
- Grossman, R.L.; Kamath, C.; Kegelmeyer, P.; Kumar, V.; Namburu, R. (Eds.) Data Mining for Scientific and Engineering Applications; Springer Science Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Larose, D.T.; Larose, C.D. Discovering Knowledge in Data: An Introduction to Data Mining; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Zhang, S.; Zhang, C.; Yang, Q. Data preparation for data mining. Appl. Artif. Intell. 2003, 17, 375–381. [Google Scholar] [CrossRef]
- Mia, M.; Królczyk, G.; Maruda, R.; Wojciechowski, S. Intelligent optimization of hard-turning parameters using evolutionary algorithms for smart manufacturing. Materials 2019, 12, 879. [Google Scholar] [CrossRef] [Green Version]
- Glowacz, A. Thermographic Fault Diagnosis of Ventilation in BLDC Motors. Sensors 2021, 21, 7245. [Google Scholar] [CrossRef]
- Łuczak, P.; Kucharski, P.; Jaworski, T.; Perenc, I.; Ślot, K.; Kucharski, J. Boosting intelligent data analysis in smart sensors by integrating knowledge and machine learning. Sensors 2021, 21, 6168. [Google Scholar] [CrossRef]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Li, J.; Cheng, K.; Wang, S.; Morstatter, F.; Trevino, R.P.; Tang, J.; Liu, H. Feature selection: A data perspective. ACM Comput. Surv. 2017, 50, 1–45. [Google Scholar] [CrossRef]
- Kumar, V.; Minz, S. Feature selection: A literature review. SmartCR 2014, 4, 211–229. [Google Scholar] [CrossRef]
- Miao, J.; Niu, L. A survey on feature selection. Procedia Comput. Sci. 2016, 91, 919–926. [Google Scholar] [CrossRef] [Green Version]
- Jaworski, T.; Kucharski, J. An algorithm for reconstruction of temperature distribution on rotating cylinder surface from a thermal camera video stream. Prz. Elektrotechniczny Electr. Rev. 2013, 89, 91–94. [Google Scholar]
- Jun, S.; Kochan, O.; Kochan, R. Thermocouples with built-in self-testing. Int. J. Thermophys. 2016, 37, 1–9. [Google Scholar] [CrossRef]
- Glowacz, A.; Tadeusiewicz, R.; Legutko, S.; Caesarendra, W.; Irfan, M.; Liu, H.; Brumercik, F.; Gutten, M.; Sulowicz, M.; Daviu, J.A.; et al. Fault diagnosis of angle grinders and electric impact drills using acoustic signals. Appl. Acoust. 2021, 179, 108070. [Google Scholar] [CrossRef]
- Xue, B.; Zhang, M.; Browne, W.N.; Yao, X. A survey on evolutionary computation approaches to feature selection. IEEE Trans. Evol. Comput. 2015, 20, 606–626. [Google Scholar] [CrossRef] [Green Version]
- Cai, J.; Luo, J.; Wang, S.; Yang, S. Feature selection in machine learning: A new perspective. Neurocomputing 2018, 300, 70–79. [Google Scholar] [CrossRef]
- Jović, A.; Brkić, K.; Bogunović, N. A review of feature selection methods with applications. In Proceedings of the 2015 38th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 25–29 May 2015; pp. 1200–1205. [Google Scholar]
- Korobiichuk, I.; Mel’nick, V.; Shybetskyi, V.; Kostyk, S.; Kalinina, M. Optimization of Heat Exchange Plate Geometry by Modeling Physical Processes Using CAD. Energies 2022, 15, 1430. [Google Scholar] [CrossRef]
- Sánchez-Maroño, N.; Alonso-Betanzos, A.; Tombilla-Sanromán, M. Filter methods for feature selection–a comparative study. In International Conference on Intelligent Data Engineering and Automated Learning; Springer: Berlin/Heidelberg, Germany, 2007; pp. 178–187. [Google Scholar]
- Alelyani, S.; Tang, J.; Liu, H. Feature selection for clustering: A review. In Data Clustering; CRC: Boca Raton, FL, USA, 2018; pp. 29–60. [Google Scholar]
- Hancer, E.; Xue, B.; Zhang, M. Differential evolution for filter feature selection based on information theory and feature ranking. Knowl. Based Syst. 2018, 140, 103–119. [Google Scholar] [CrossRef]
- Uysal, A.K.; Gunal, S. A novel probabilistic feature selection method for text classification. Knowl. Based Syst. 2012, 36, 226–235. [Google Scholar] [CrossRef]
- Urbanowicz, R.J.; Meeker, M.; La Cava, W.; Olson, R.S.; Moore, J.H. Relief-based feature selection: Introduction and review. J. Biomed. Inform. 2018, 85, 189–203. [Google Scholar] [CrossRef]
- Fang, M.T.; Chen, Z.J.; Przystupa, K.; Li, T.; Majka, M.; Kochan, O. Examination of abnormal behavior detection based on improved YOLOv3. Electronics 2021, 10, 197. [Google Scholar] [CrossRef]
- Maldonado, S.; López, J. Dealing with high-dimensional class-imbalanced datasets: Embedded feature selection for SVM classification. Appl. Soft Comput. 2018, 67, 94–105. [Google Scholar] [CrossRef]
- Song, W.; Beshley, M.; Przystupa, K.; Beshley, H.; Kochan, O.; Pryslupskyi, A.; Pieniak, D.; Su, J. A software deep packet inspection system for network traffic analysis and anomaly detection. Sensors 2020, 20, 1637. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Panthong, R.; Srivihok, A. Wrapper feature subset selection for dimension reduction based on ensemble learning algorithm. Procedia Comput. Sci. 2015, 72, 162–169. [Google Scholar] [CrossRef] [Green Version]
- Sun, S.; Przystupa, K.; Wei, M.; Yu, H.; Ye, Z.; Kochan, O. Fast bearing fault diagnosis of rolling element using Lévy Moth-Flame optimization algorithm and Naive Bayes. Eksploat. Niezawodn. 2020, 22, 730–740. [Google Scholar] [CrossRef]
- Brezočnik, L.; Fister, I.; Podgorelec, V. Swarm intelligence algorithms for feature selection: A review. Appl. Sci. 2018, 8, 1521. [Google Scholar] [CrossRef] [Green Version]
- Fong, S.; Wong, R.; Vasilakos, A.V. Accelerated PSO Swarm Search Feature Selection for Data Stream Mining Big Data. IEEE Trans. Serv. Comput. 2015, 9, 33–45. [Google Scholar] [CrossRef]
- Jadhav, S.; He, H.; Jenkins, K. Information gain directed genetic algorithm wrapper feature selection for credit rating. Appl. Soft Comput. 2018, 69, 541–553. [Google Scholar] [CrossRef] [Green Version]
- Hafez, A.I.; Zawbaa, H.M.; Emary, E.; Hassanien, A.E. Sine cosine optimization algorithm for feature selection. In Proceedings of the 2016 International Symposium on Innovations in Intelligent Systems and Applications (INISTA), Sinaia, Romania, 2–5 August 2016; pp. 1–5. [Google Scholar]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Abd Elaziz, M.E.; Ewees, A.A.; Oliva, D.; Pengfei, D. Abd Elaziz, M.E.; Ewees, A.A.; Oliva, D.; Pengfei, D. A hybrid method of sine cosine algorithm and differential evolution for feature selection. In International Conference on Neural Information Processing; Springer: Cham, Switzerland, 2017; pp. 145–155. [Google Scholar]
- Tang, J.; Alelyani, S.; Liu, H. Feature selection for classification: A review. In Data Classification: Algorithms and Applications; CRC: Boca Raton, FL, USA, 2014; p. 37. [Google Scholar]
- Venkatesh, B.; Anuradha, J. A review of feature selection and its methods. Cybern. Inf. Technol. 2019, 19, 3–26. [Google Scholar] [CrossRef] [Green Version]
- Oreski, S.; Oreski, G. Genetic algorithm-based heuristic for feature selection in credit risk assessment. Expert Syst. Appl. 2014, 41, 2052–2064. [Google Scholar] [CrossRef]
- Mafarja, M.M.; Mirjalili, S. Hybrid whale optimization algorithm with simulated annealing for feature selection. Neurocomputing 2017, 260, 302–312. [Google Scholar] [CrossRef]
- Mafarja, M.; Mirjalili, S. Whale optimization approaches for wrapper feature selection. Appl. Soft Comput. 2018, 62, 441–453. [Google Scholar] [CrossRef]
- Tabakhi, S.; Moradi, P.; Akhlaghian, F. An unsupervised feature selection algorithm based on ant colony optimization. Eng. Appl. Artif. Intell. 2014, 32, 112–123. [Google Scholar] [CrossRef]
- Taradeh, M.; Mafarja, M.; Heidari, A.A.; Faris, H.; Aljarah, I.; Mirjalili, S.; Fujita, H. An evolutionary gravitational search-based feature selection. Inf. Sci. 2019, 497, 219–239. [Google Scholar] [CrossRef]
- Too, J.; Abdullah, A.R.; Saad, N.M.; Ali, N.M.; Tee, W. A New Competitive Binary Grey Wolf Optimizer to Solve the Feature Selection Problem in EMG Signals Classification. Computers 2018, 7, 58. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Liu, R.; Wang, X.; Chen, H.; Li, C. Boosted binary Harris hawks optimizer and feature selection. Eng. Comput. 2020, 37, 3741–3770. [Google Scholar] [CrossRef]
- Jain, I.; Jain, V.K.; Jain, R. Correlation feature selection based improved-Binary Particle Swarm Optimization for gene selection and cancer classification. Appl. Soft Comput. 2018, 62, 203–215. [Google Scholar] [CrossRef]
- Sindhu, R.; Ngadiran, R.; Yacob, Y.M.; Zahri, N.A.H.; Hariharan, M. Sine–cosine algorithm for feature selection with elitism strategy and new updating mechanism. Neural Comput. Appl. 2017, 28, 2947–2958. [Google Scholar] [CrossRef]
- Neggaz, N.; Ewees, A.A.; Elaziz, M.A.; Mafarja, M. Boosting salp swarm algorithm by sine cosine algorithm and disrupt operator for feature selection. Expert Syst. Appl. 2019, 145, 113103. [Google Scholar] [CrossRef]
- Abualigah, L.; Dulaimi, A.J. A novel feature selection method for data mining tasks using hybrid Sine Cosine Algorithm and Genetic Algorithm. Clust. Comput. 2021, 24, 2161–2176. [Google Scholar] [CrossRef]
- Kumar, L.; Bharti, K.K. A novel hybrid BPSO–SCA approach for feature selection. Nat. Comput. 2019, 20, 39–61. [Google Scholar] [CrossRef] [Green Version]
- Taghian, S.; Nadimi-Shahraki, M.H. Binary sine cosine algorithms for feature selection from medical data. arXiv 2019, arXiv:1911.07805. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A. Advances in sine cosine algorithm: A comprehensive survey. Artif. Intell. Rev. 2021, 54, 2567–2608. [Google Scholar] [CrossRef]
- Gupta, S.; Deep, K. Improved sine cosine algorithm with crossover scheme for global optimization. Knowl. Based Syst. 2019, 165, 374–406. [Google Scholar] [CrossRef]
- Gupta, S.; Deep, K.; Engelbrecht, A.P. Memory guided sine cosine algorithm for global optimization. Eng. Appl. Artif. Intell. 2020, 93, 103718. [Google Scholar] [CrossRef]
- Tanyildizi, E.; Demir, G. Golden sine algorithm: A novel math-inspired algorithm. Adv. Electr. Comput. Eng. 2017, 17, 71–78. [Google Scholar] [CrossRef]
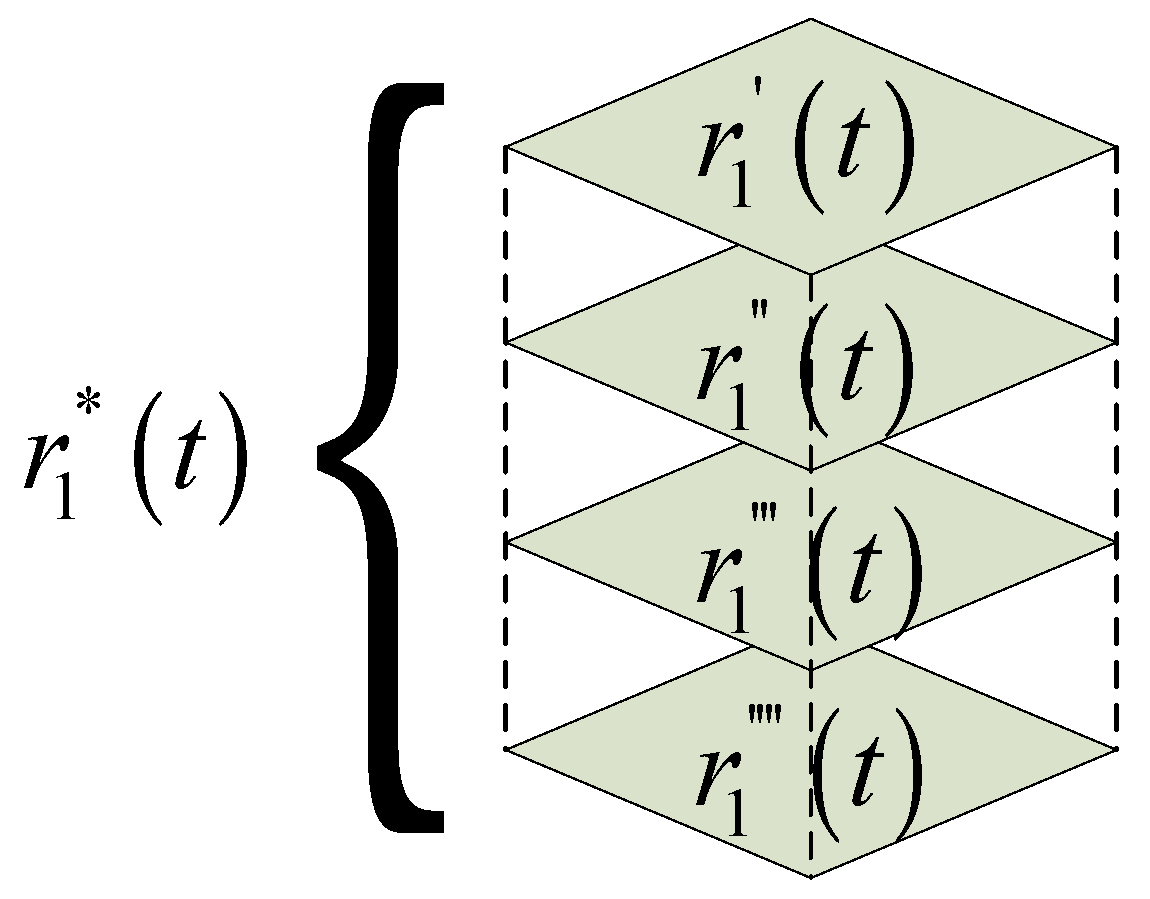
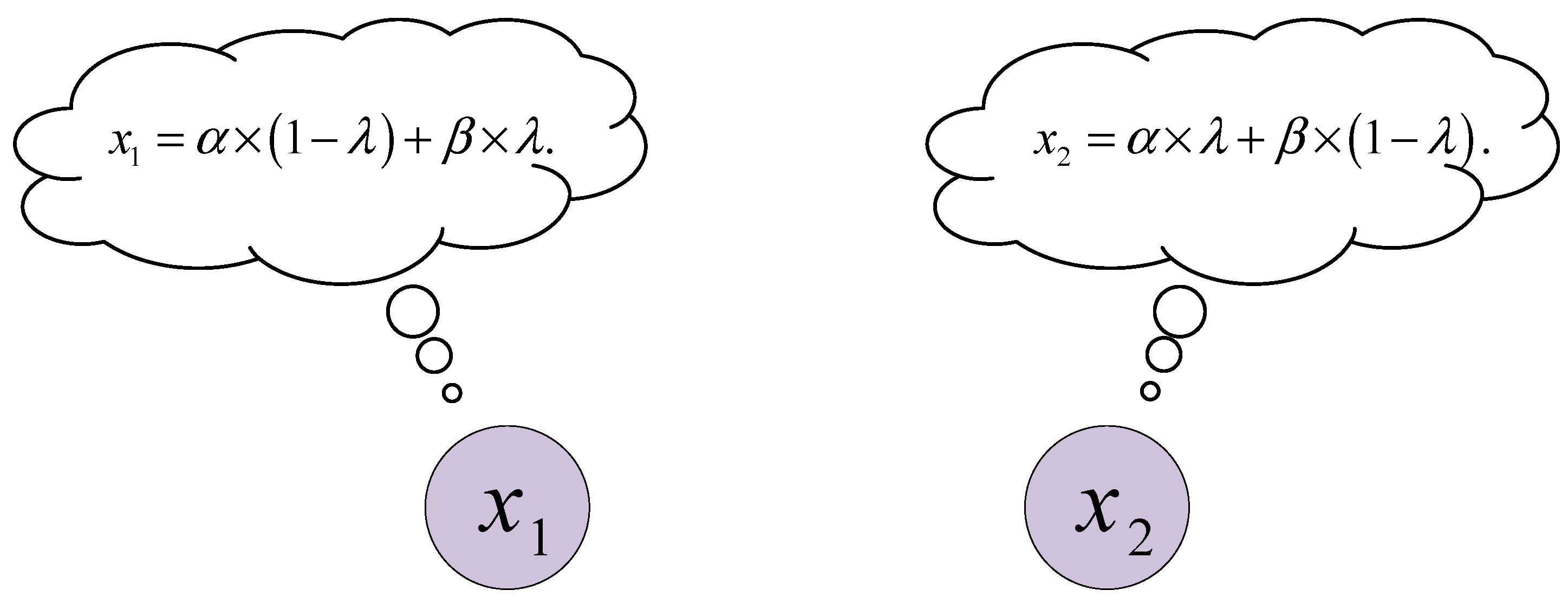





| Symbol | Definition |
|---|---|
| Position of the i-th individual in iteration t | |
| Position of the best individual in the first t iterations | |
| Multilevel regulatory factor | |
| Regulatory factor | |
| Random number with value range | |
| Feature subset of the first generation | |
| i—th feature subset in the t—th iteration | |
| Optimal feature subset in the first t iterations | |
| Mathematical expectation of feature subset | |
| D | Variance of feature subset |
| I | Diversity of feature subset |
| Number of initially generated feature subsets | |
| Number of features in the original dataset | |
| Evaluation function | |
| Maximum number of iterations | |
| Lower boundary on the value of the feature subset | |
| Upper boundary on the value of the feature subset | |
| Golden section coefficient | |
| Golden section coefficient |
| Test Data Set | Dataset Name | Characteristic Number | Number of Samples | Number of Categories |
|---|---|---|---|---|
| 1 | Sonar | 60 | 208 | 2 |
| 2 | Ionosphere | 34 | 351 | 2 |
| 3 | Vehicle | 18 | 846 | 3 |
| 4 | Cancer | 9 | 683 | 2 |
| 5 | Wine | 13 | 178 | 3 |
| 6 | WDBC | 30 | 569 | 2 |
| 7 | Diabetes | 8 | 768 | 2 |
| Parameters | Values |
|---|---|
| Number of optimization particles | 30 |
| Maximum number of iterations | 300 |
| Dimension | Number of features in the datasets |
| Number of experiments per dataset | 10 |
| Weight of classification error rate in fitness function | 0.8 |
| Dataset | Statistical Indicators | MetaSCA | SCA | PSO | WOA |
|---|---|---|---|---|---|
| Sonar | Average fitness | 0.12092 | 0.12558 | 0.15142 | 0.14263 |
| The standard fitness | 0.00566 | 0.00764 | 0.00860 | 0.01029 | |
| The optimal fitness | 0.11079 | 0.11142 | 0.13349 | 0.12142 | |
| The worst fitness | 0.12476 | 0.13412 | 0.15923 | 0.15015 | |
| Ionosphere | Average fitness | 0.07677 | 0.10978 | 0.07819 | 0.09511 |
| The standard fitness | 0.00719 | 0.00818 | 0.00654 | 0.00576 | |
| The optimal fitness | 0.06548 | 0.09400 | 0.06803 | 0.08479 | |
| The worst fitness | 0.07802 | 0.11831 | 0.08568 | 0.10410 | |
| Vehicle | Average fitness | 0.27294 | 0.27931 | 0.28440 | 0.28080 |
| The standard fitness | 0.00678 | 0.00343 | 0.00759 | 0.00611 | |
| The optimal fitness | 0.26027 | 0.27454 | 0.27139 | 0.27270 | |
| The worst fitness | 0.28083 | 0.28250 | 0.29343 | 0.28731 | |
| Cancer | Average fitness | 0.06124 | 0.06913 | 0.07176 | 0.06514 |
| The standard fitness | 0.00325 | 0.00526 | 0.00367 | 0.00385 | |
| The optimal fitness | 0.06023 | 0.06827 | 0.07102 | 0.06457 | |
| The worst fitness | 0.06174 | 0.07073 | 0.07263 | 0.06586 | |
| Wine | Average fitness | 0.05065 | 0.07578 | 0.06125 | 0.06096 |
| The standard fitness | 0.00687 | 0.00843 | 0.00284 | 0.00625 | |
| The optimal fitness | 0.04615 | 0.06547 | 0.06096 | 0.05782 | |
| The worst fitness | 0.06096 | 0.08126 | 0.06153 | 0.07154 | |
| WDBC | Average fitness | 0.06309 | 0.06391 | 0.06445 | 0.06752 |
| The standard fitness | 0.00323 | 0.00522 | 0.00536 | 0.00455 | |
| The optimal fitness | 0.05801 | 0.05403 | 0.05672 | 0.05871 | |
| The worst fitness | 0.06538 | 0.06935 | 0.07005 | 0.07274 | |
| Diabetes | Average fitness | 0.23279 | 0.24740 | 0.25432 | 0.24318 |
| The standard fitness | 0.00286 | 0.00437 | 0.00462 | 0.00326 | |
| The optimal fitness | 0.22461 | 0.24025 | 0.24663 | 0.23257 | |
| The worst fitness | 0.23865 | 0.25132 | 0.25851 | 0.24938 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Qin, H.; Przystupa, K.; Cui, Y.; Kochan, O.; Skowron, M.; Su, J. A Hybrid Feature Selection Framework Using Improved Sine Cosine Algorithm with Metaheuristic Techniques. Energies 2022, 15, 3485. https://doi.org/10.3390/en15103485
Sun L, Qin H, Przystupa K, Cui Y, Kochan O, Skowron M, Su J. A Hybrid Feature Selection Framework Using Improved Sine Cosine Algorithm with Metaheuristic Techniques. Energies. 2022; 15(10):3485. https://doi.org/10.3390/en15103485
Chicago/Turabian StyleSun, Lichao, Hang Qin, Krzysztof Przystupa, Yanrong Cui, Orest Kochan, Mikołaj Skowron, and Jun Su. 2022. "A Hybrid Feature Selection Framework Using Improved Sine Cosine Algorithm with Metaheuristic Techniques" Energies 15, no. 10: 3485. https://doi.org/10.3390/en15103485
APA StyleSun, L., Qin, H., Przystupa, K., Cui, Y., Kochan, O., Skowron, M., & Su, J. (2022). A Hybrid Feature Selection Framework Using Improved Sine Cosine Algorithm with Metaheuristic Techniques. Energies, 15(10), 3485. https://doi.org/10.3390/en15103485







