Modeling, Control System Design and Preliminary Experimental Verification of a Hybrid Power Unit Suitable for Multirotor UAVs
Abstract
1. Introduction
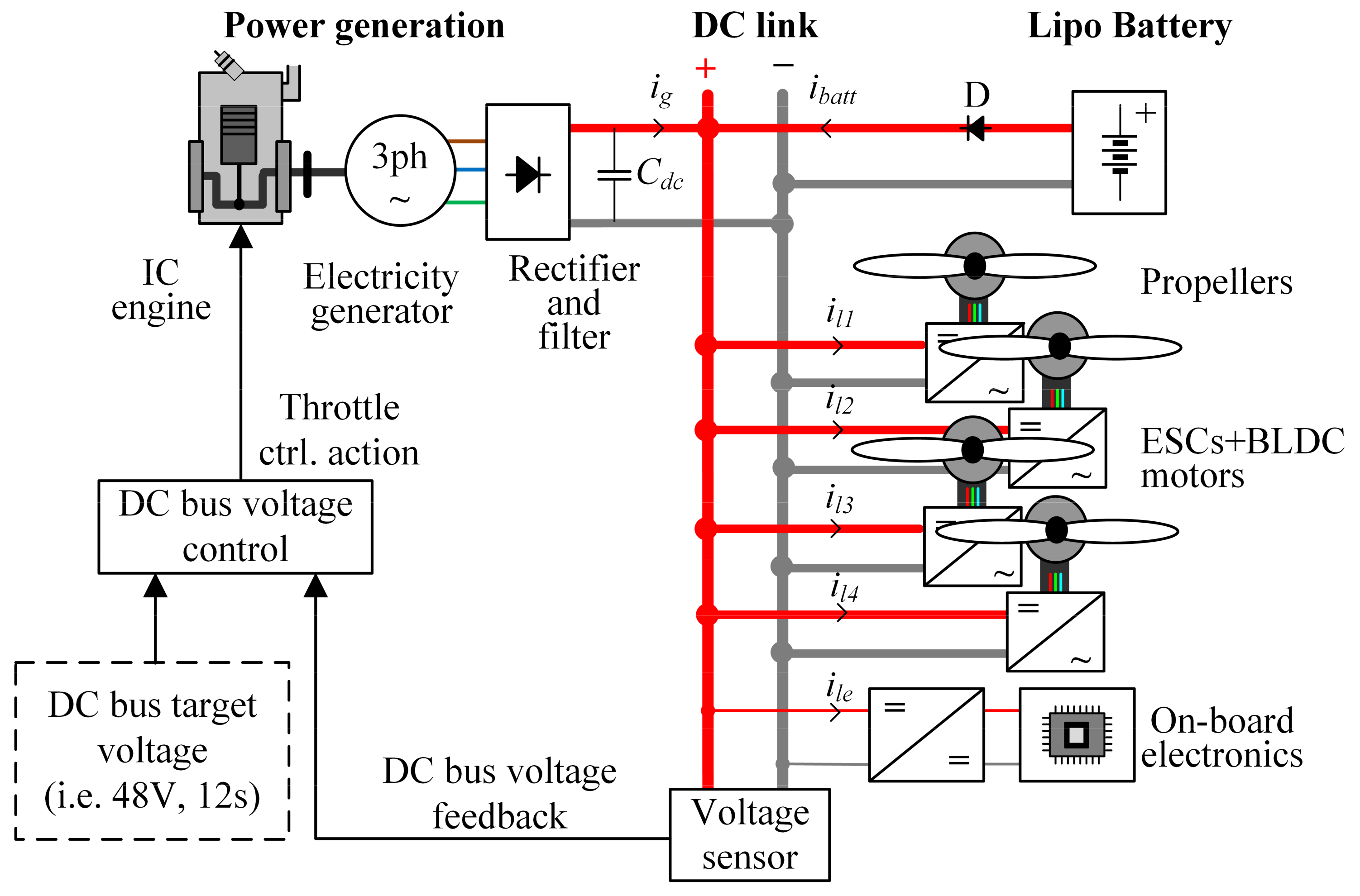
2. Hybrid Power Unit System
2.1. Overview
- ICE drives the brushless permanent magnet synchronous (BPMS) machine, used as an EG which provides for quasi-steady-state load power supply (i.e., to cover power demands needed for hovering and light maneuvering), while the battery unit is used for peak load shaving;
- The energy recovery system is not used within hybrid power unit, thus simplifying power train topology, meaning that the battery energy storage is only charged prior to the flying mission;
- ICE angular speed is controlled by a throttle servo actuator based on a small DC servomotor which positions the throttle valve according to the output of the engine-based DC bus voltage controller requiring a suitable DC bus voltage reference target and DC bus voltage measurement-based feedback.
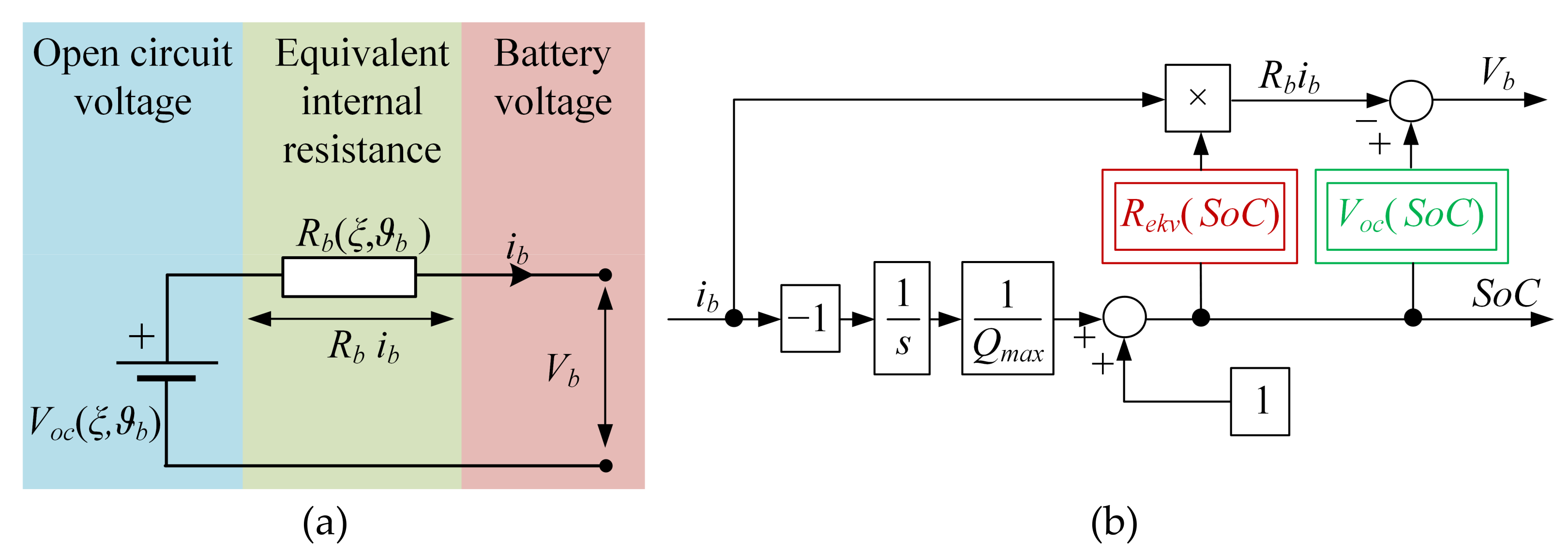
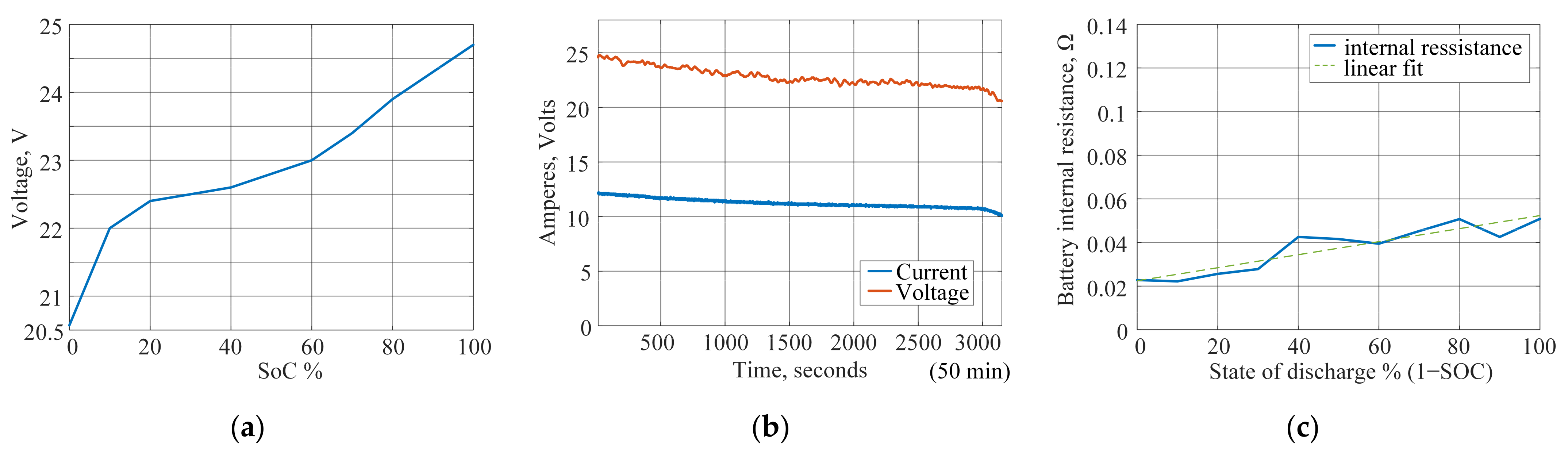
2.2. Battery Model
- Initial full charging of the battery cells to achieve 4.15 V per cell, followed by voltage stabilization (settling) to achieve electrochemical and temperature equilibrium;
- Partial battery discharging for a short period of time (i.e., 10 min);
- Allowing the battery to rest in the open–circuit condition for 3 h, in order to achieve the terminal voltage steady-state;
- Repeating the intermittent discharging steps until OCV per cell is approximately 3.4–3.5 V (which corresponds to a fully discharged battery state).
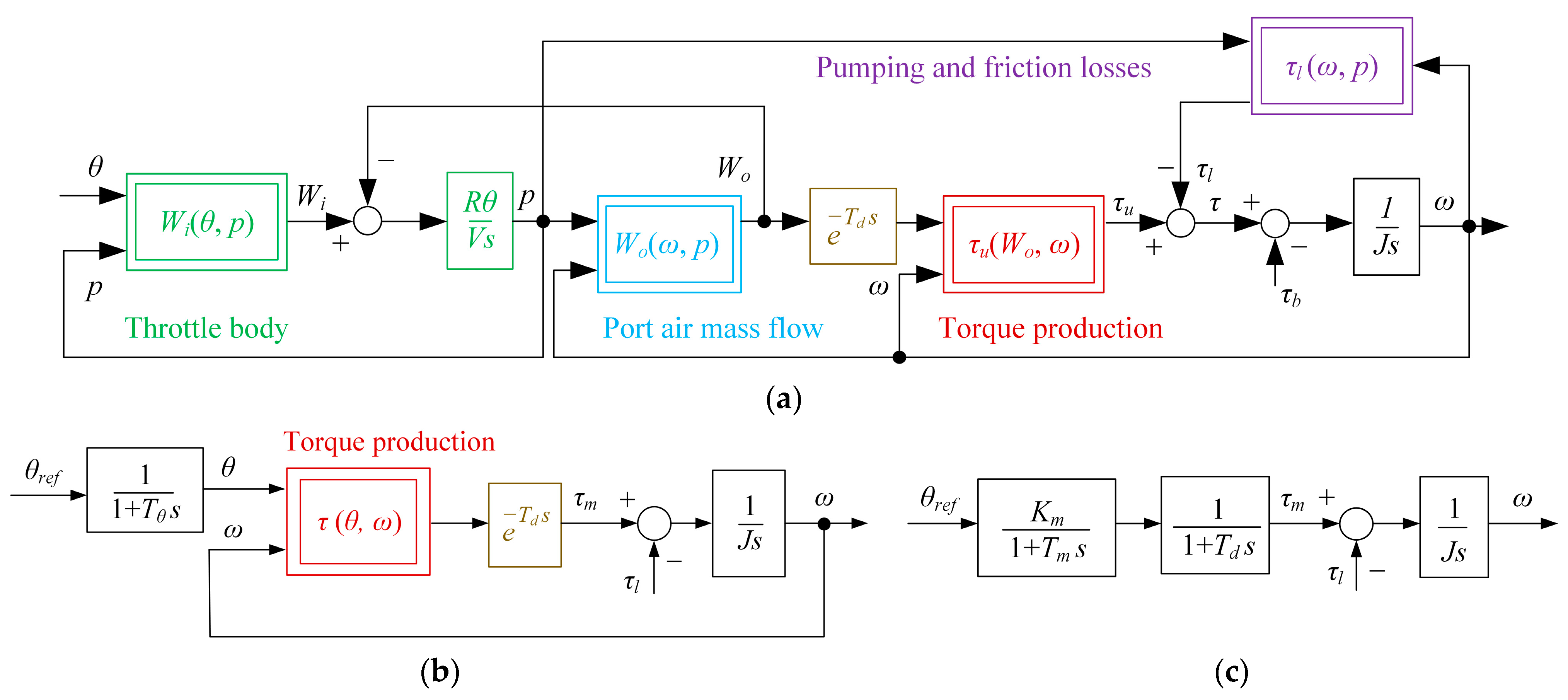
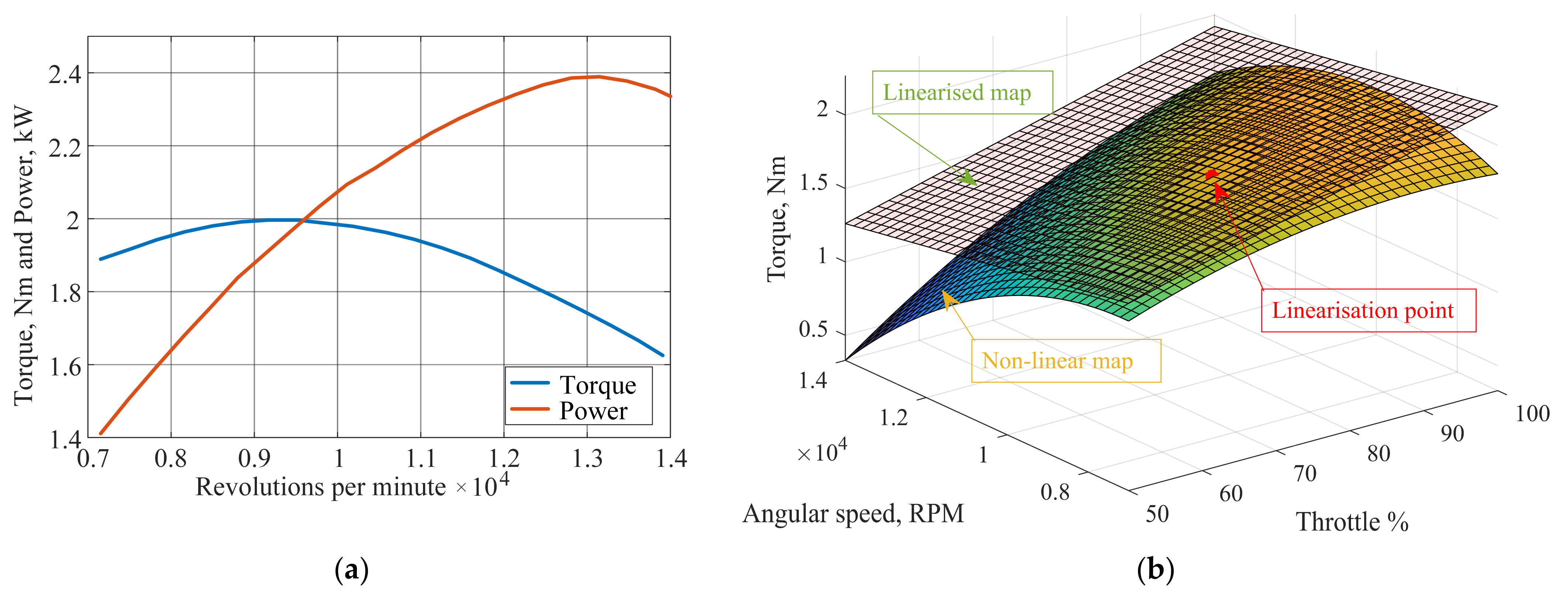
2.3. ICE Model
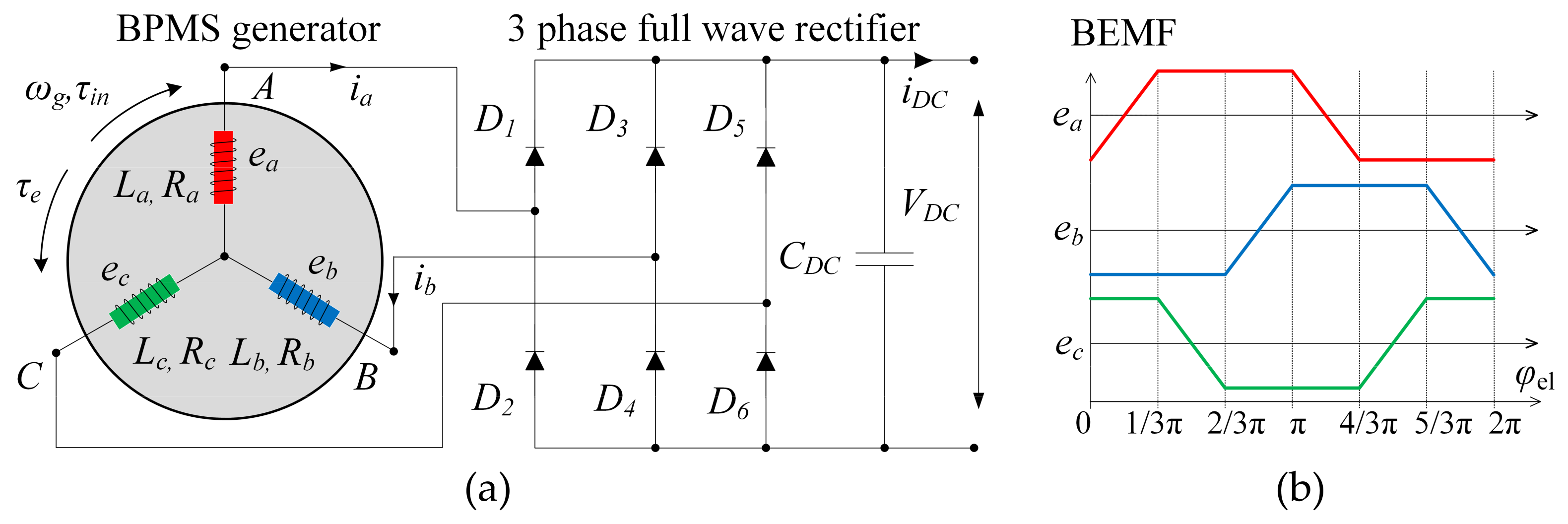
2.4. Electrical Generator and Rectifier Model
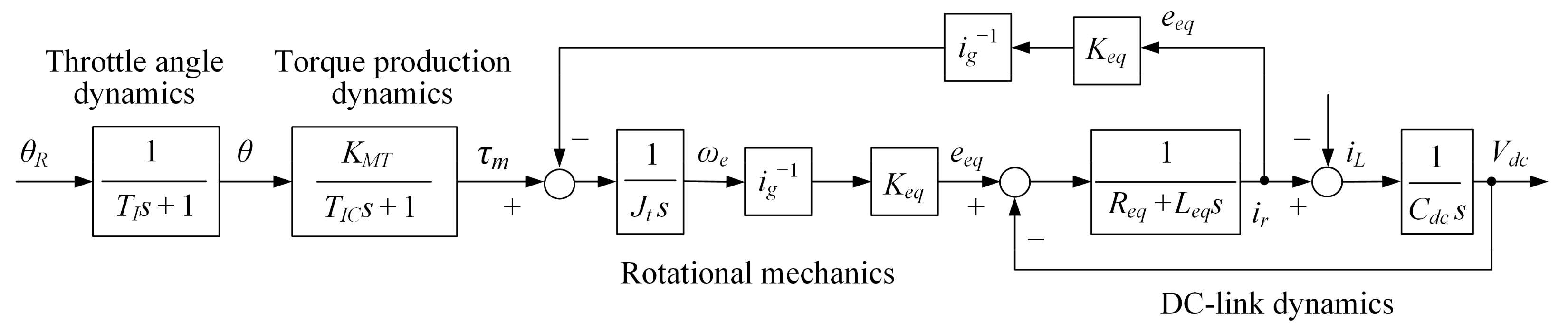
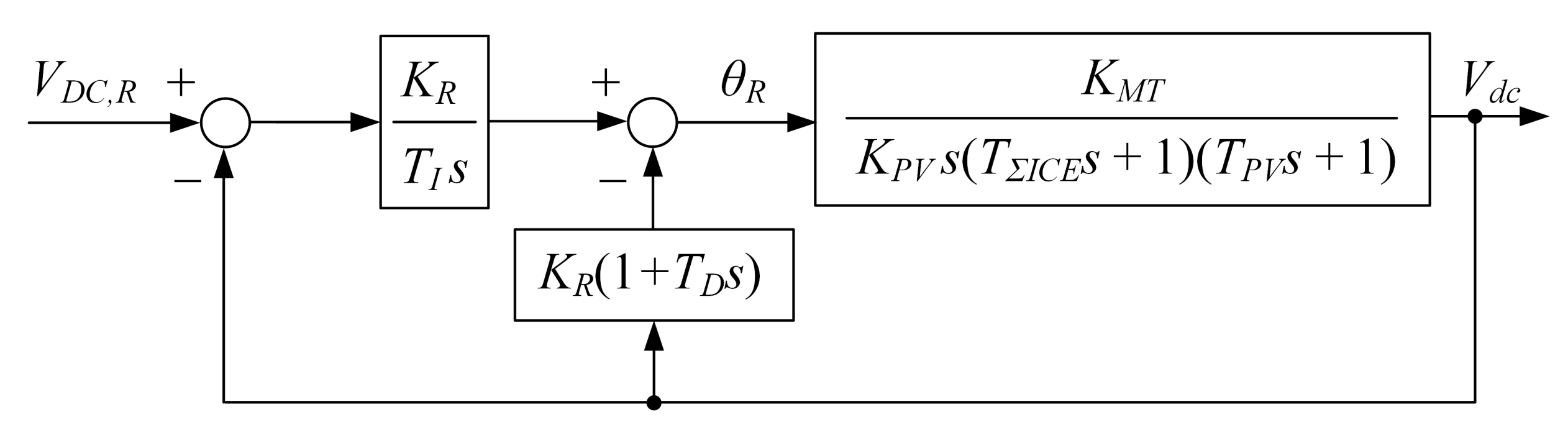
3. DC bus Voltage Feedback Control
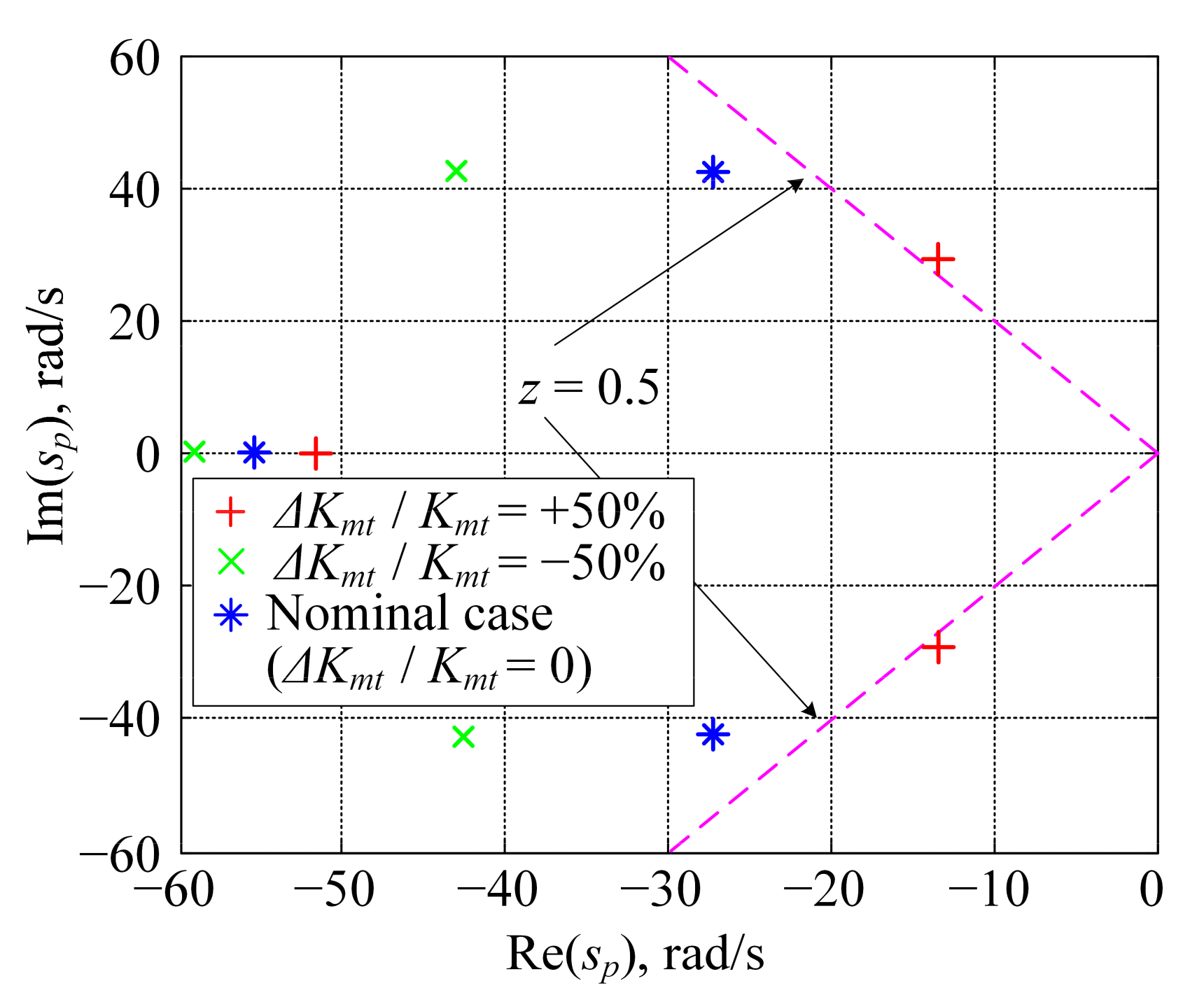
3.1. Damping Optimum Criterion
3.2. DC Bus Voltage Feedback Control through ICE Throttle Command
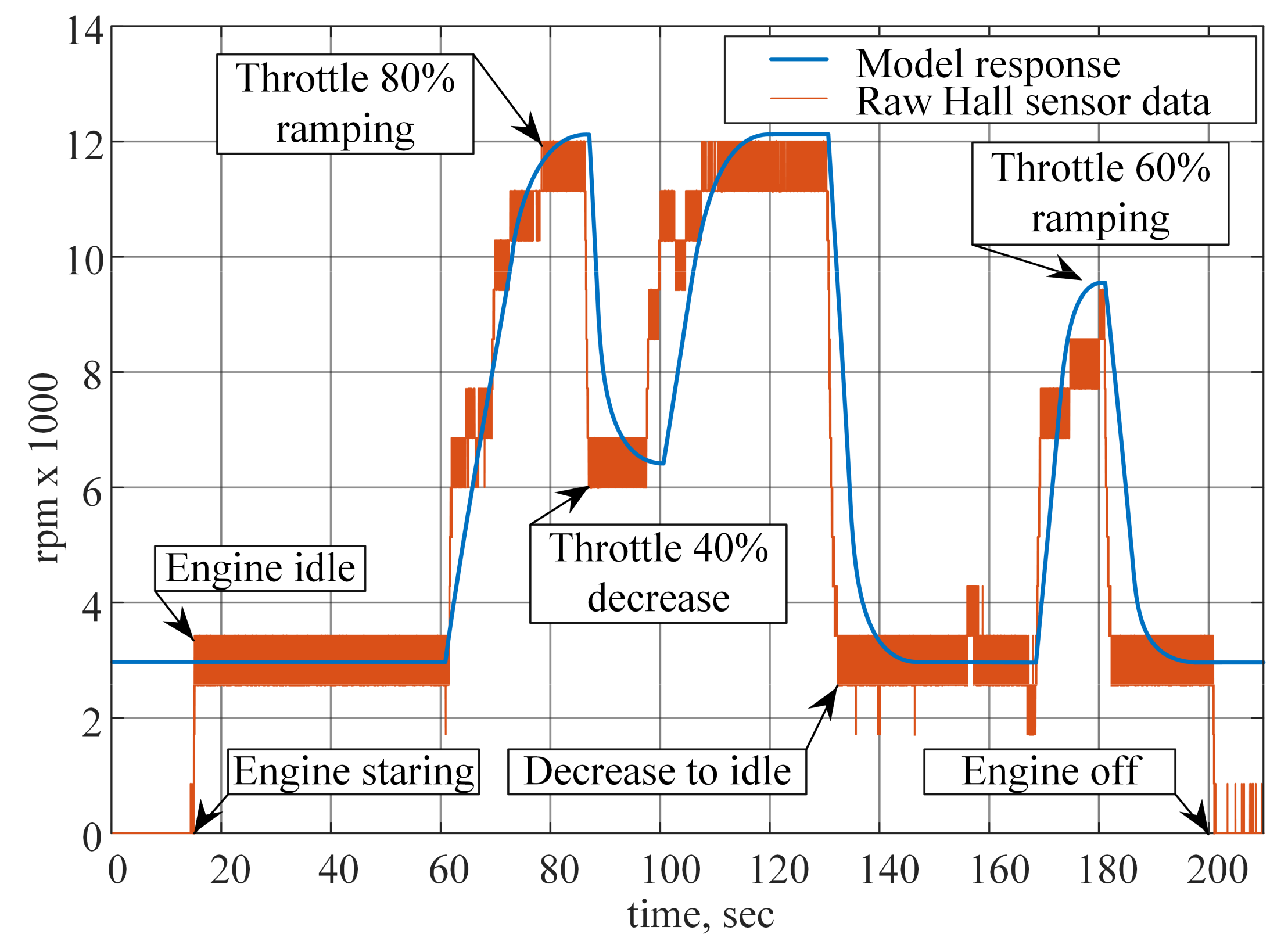
4. Experimental Verification of DC Bus Voltage Feedback Control System
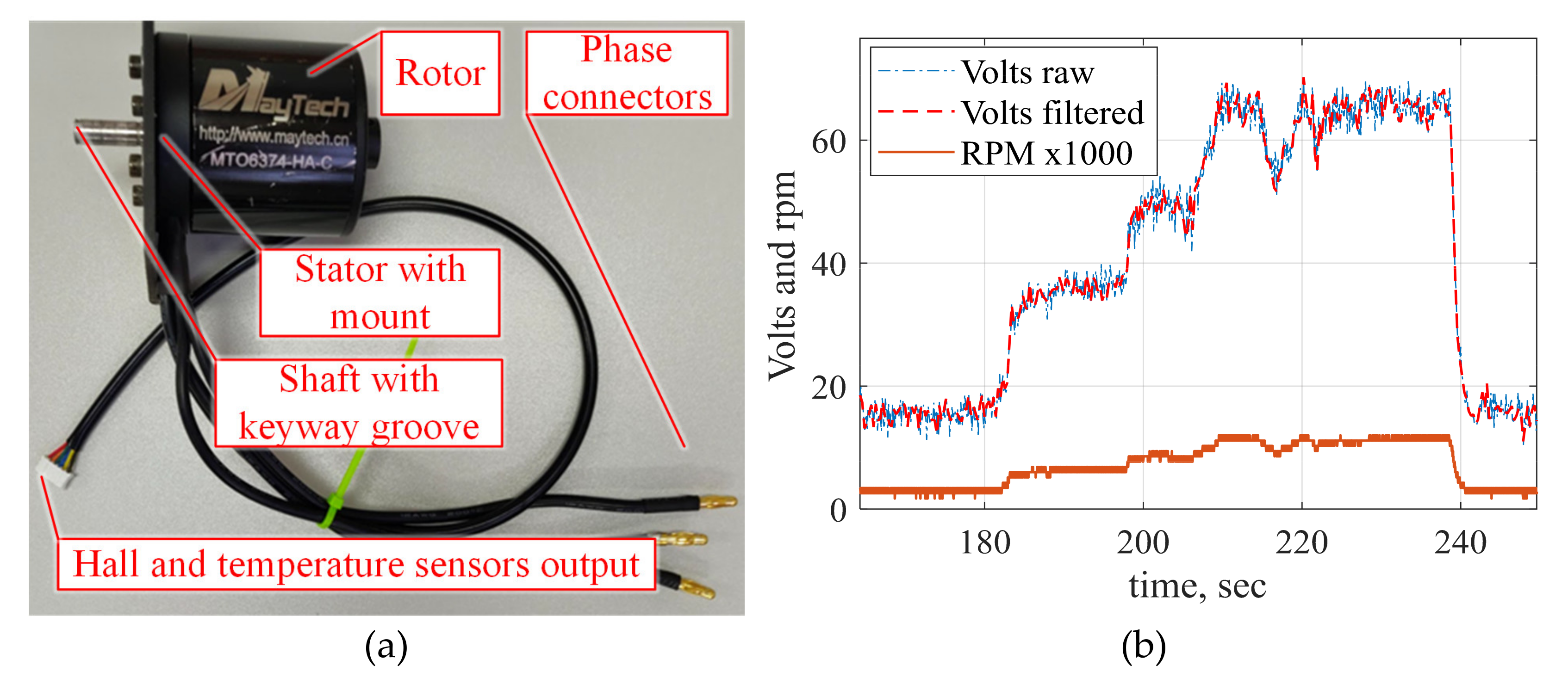
4.1. Experimental Hybrid Power Unit Realization
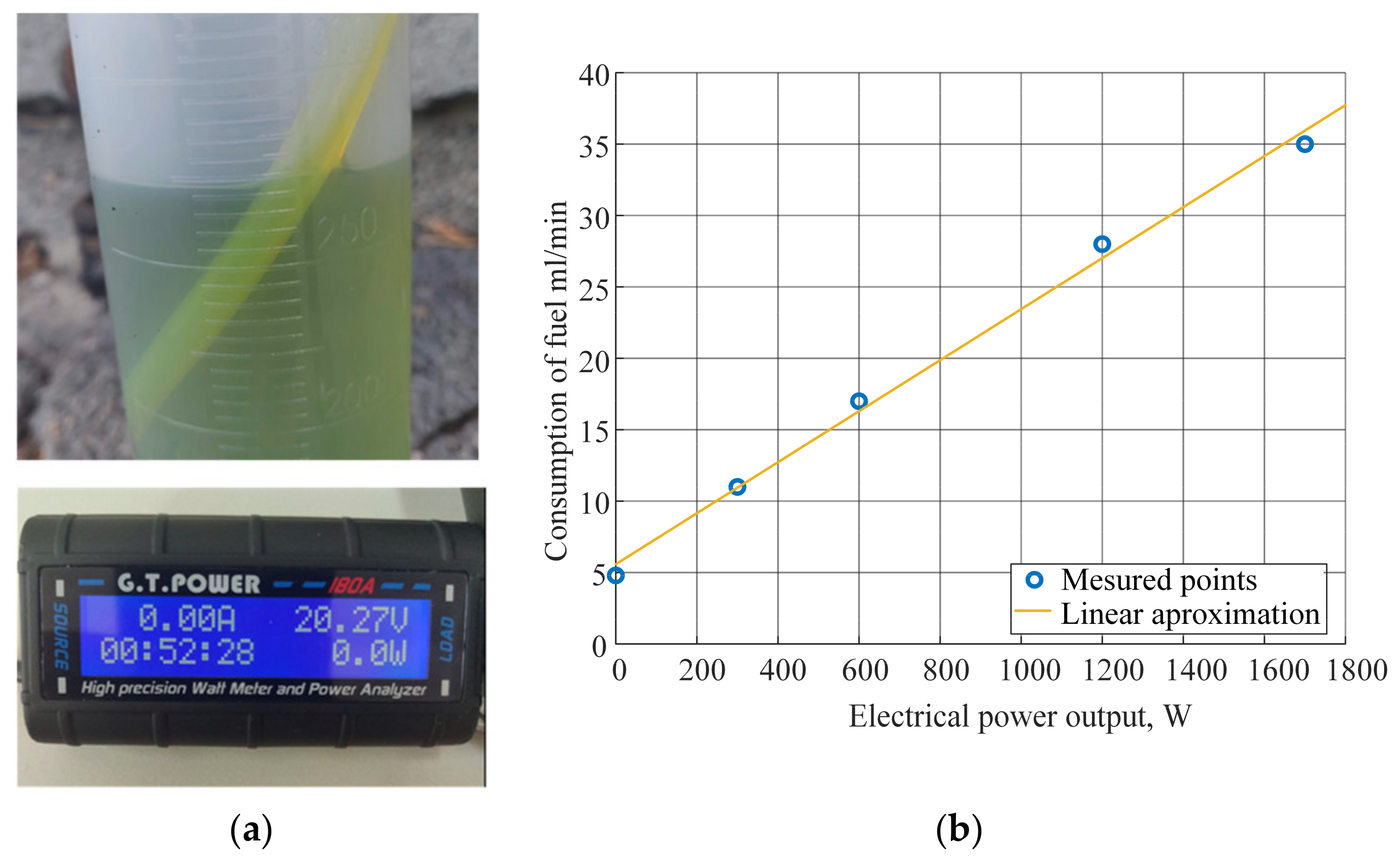
4.2. Engine Fuel Consumption
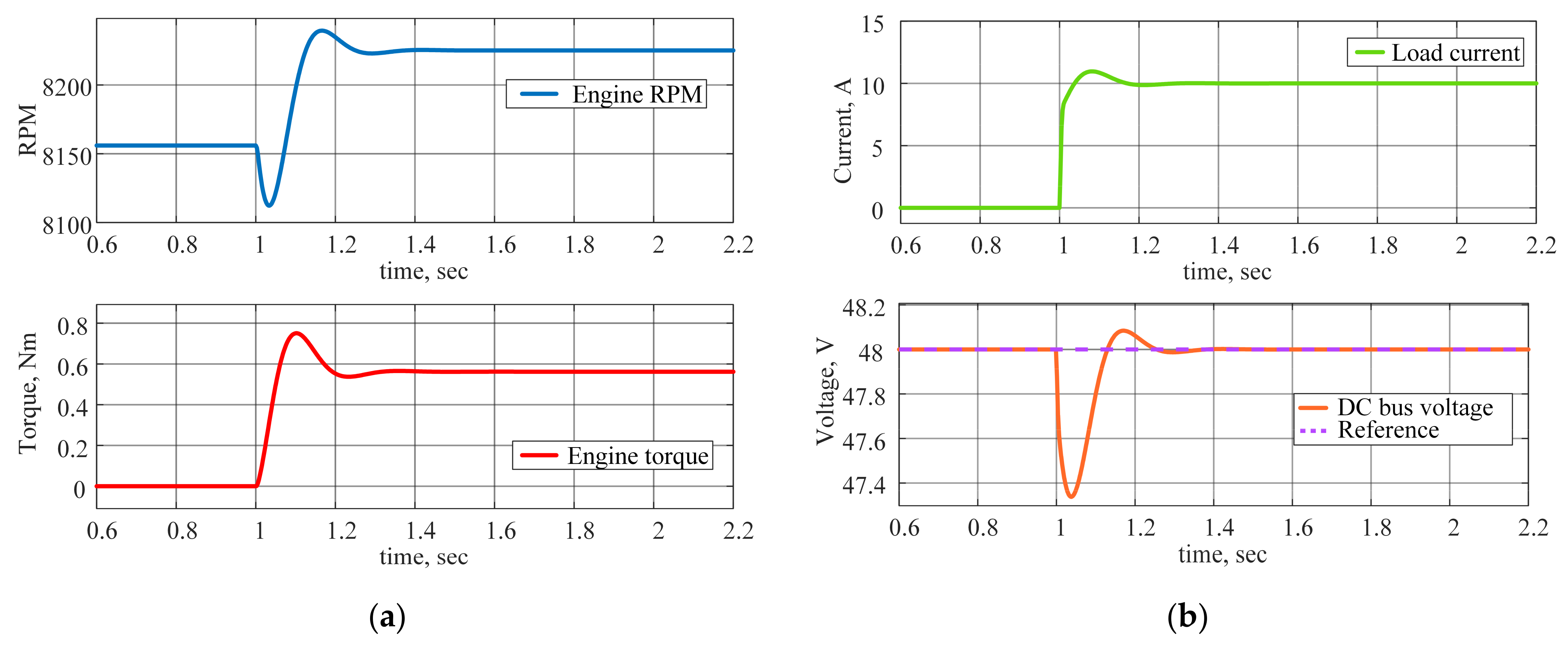
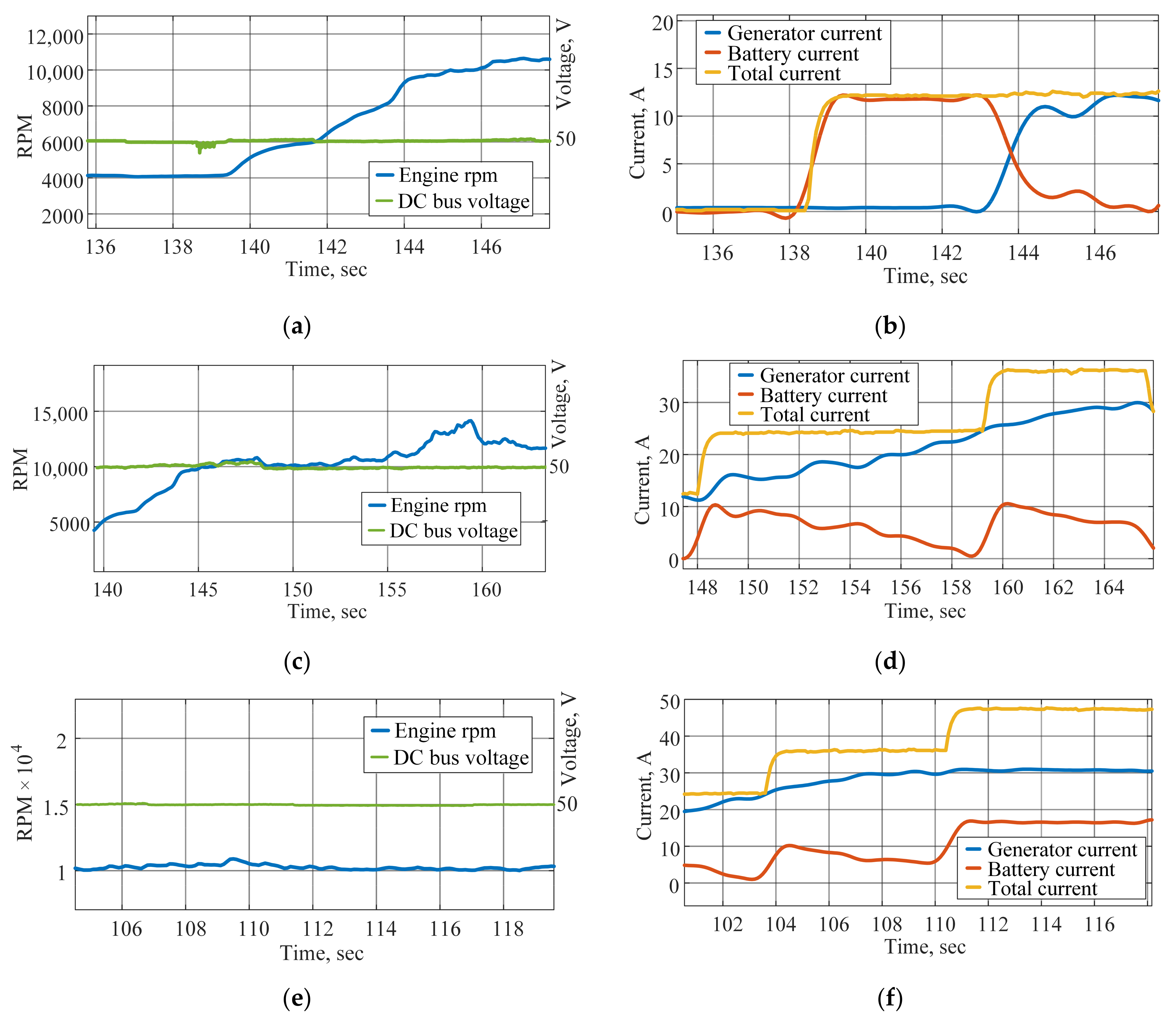
4.3. Hybrid Power Unit Measurements
- 4 Ω load (low load);
- 2 Ω load (medium load);
- 1.33 Ω load (high load);
- 1 Ω load (peak load).
5. Discussion
6. Conclusions
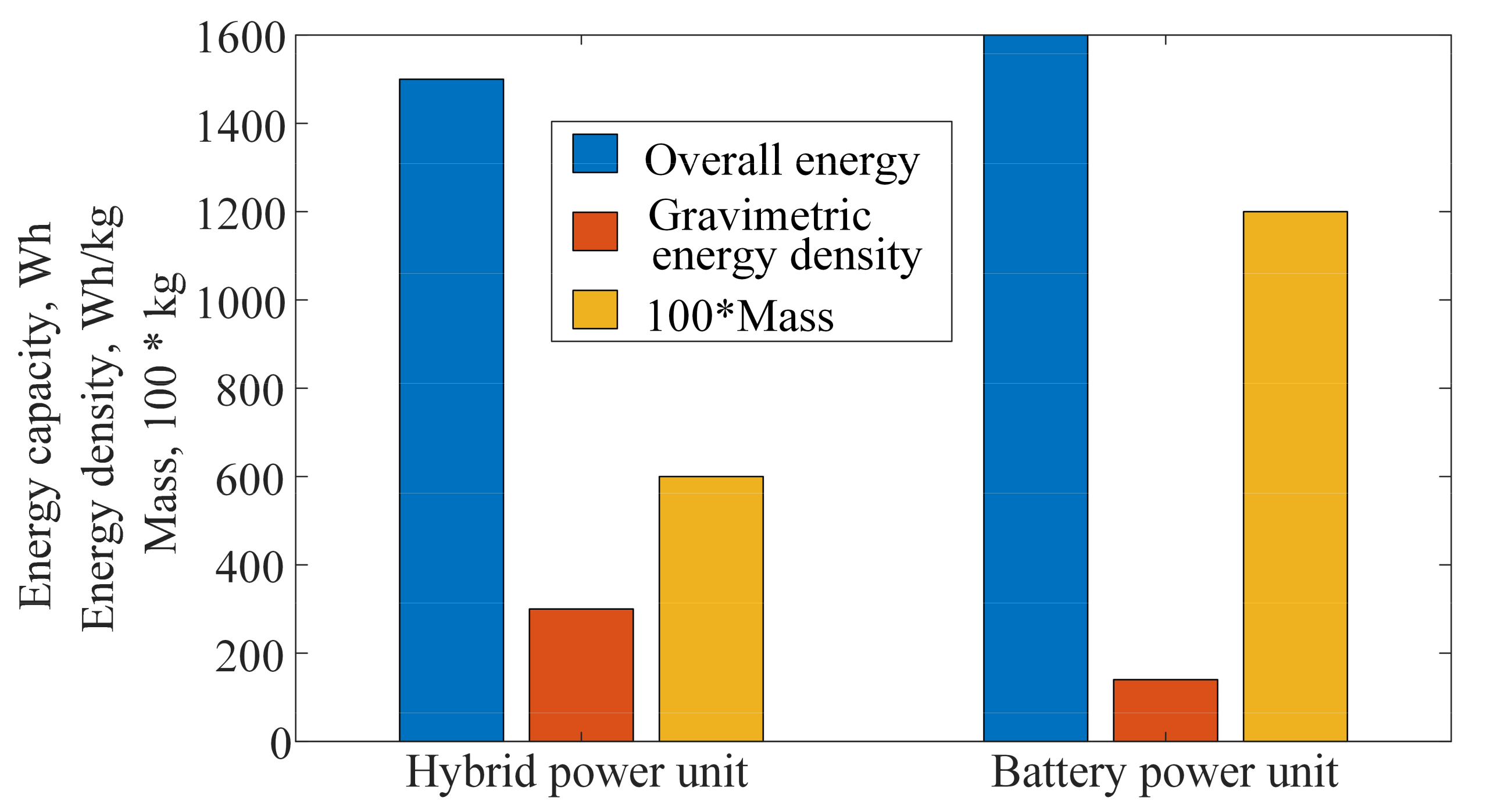
- Hybridization of the conventional ICE–EG set results in a stable power source is obtained which is characterized by the gravimetric energy density which is two times higher compared to a purely battery-based power supply;
- For the aforementioned increase in the gravimetric energy density using a hybridized ICE + EG power unit, the overall mass of the hybrid power system is two times smaller when compared to the comparable battery-based system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fischer, M.; Werber, M.; Schwartz, P.V. Batteries: Higher energy density than gasoline? Energy Policy 2009, 37, 2639–2641. [Google Scholar] [CrossRef]
- Cipek, M.; Pavković, D.; Petrić, J. A control-oriented simulation model of a power-split hybrid electric vehicle. Appl. Energy 2013, 101, 121–133. [Google Scholar] [CrossRef]
- Cipek, M.; Pavković, D.; Kljaić, Z.; Mlinarić, T. Assessment of battery-hybrid diesel-electric locomotive fuel savings and emission reduction potentials based on a realistic mountainous rail route. Energy 2019, 173, 1154–1171. [Google Scholar] [CrossRef]
- Abdul Sathar Eqbal, M.; Fernando, N.; Marino, M.; Wild, G. Hybrid propulsion systems for remotely piloted aircraft systems. Aerospace 2018, 5, 34. [Google Scholar] [CrossRef]
- Friedrich, C.; Robertson, P.A. Hybrid-electric propulsion for aircraft. J. Aircr. 2015, 52, 176–189. [Google Scholar] [CrossRef]
- Recoskie, S.; Fahim, A.; Gueaieb, W.; Lanteigne, E. Hybrid power plant design for a long-range dirigible UAV. IEEE Trans. Mechatron. 2013, 19, 606–614. [Google Scholar] [CrossRef]
- Recoskie, S.; Fahim, A.; Gueaieb, W.; Lanteigne, E. Experimental testing of a hybrid power plant for a dirigible UAV. J. Intell. Robot. Syst. 2013, 69, 69–81. [Google Scholar] [CrossRef]
- Donateo, T.; De Pascalis, C.L.; Ficarella, A. Synergy effects in electric and hybrid electric aircraft. Aerospace 2019, 6, 32. [Google Scholar] [CrossRef]
- Depcik, C.; Cassady, T.; Collicott, B.; Burugupally, S.P.; Li, X.; Alam, S.S.; Hobeck, J. Comparison of lithium ion Batteries, hydrogen fueled combustion Engines, and a hydrogen fuel cell in powering a small Unmanned Aerial Vehicle. Energy Convers. Manag. 2020, 207, 112514. [Google Scholar] [CrossRef]
- Hageman, M.D.; McLaughlin, T.E. Considerations for Pairing the IC Engine and Electric Motor in a Hybrid Power System for Small UAVs. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; p. 2132. [Google Scholar]
- McKinney, K.; Feight, J.A.; Gaeta, R.J.; Jacob, J.D. Implementation Implications of Hybrid-Electric Power Systems on Multi-Rotor UAS. In Proceedings of the 2018 AIAA Information Systems-AIAA Infotech @ Aerospace, Kissimmee, FL, USA, 8–12 January 2018; p. 986. [Google Scholar]
- Dudek, M.; Tomczyk, P.; Wygonik, P.; Korkosz, M.; Bogusz, P.; Lis, B. Hybrid fuel cell–battery system as a main power unit for small unmanned aerial vehicles (UAV). Int. J. Electrochem. Sci. 2013, 8, 8442–8463. [Google Scholar]
- Zhang, T.; Zhu, X.; Zhou, Z.; Wang, R.; Chen, R. Energy management of solar UAV level flight. In Proceedings of the IEEE International Conference on Prognostics and Health Management, Seattle, WA, USA, 11–13 June 2018. [Google Scholar]
- Panagiotou, P.; Tsavlidis, I.; Yakinthos, K. Conceptual design of a hybrid solar male UAV. Aerosp. Sci. Technol. 2016, 53, 207–219. [Google Scholar] [CrossRef]
- Phan, L.N.; Sarma, S.E.; Wojcik, C.M.; Davis, E.M.; Sena, B.A.; Lemus, J. Top Flight Technologies Inc, 2017. Micro Hybrid Generator System Drone. U.S. Patent 9,764,837, 19 September 2017. [Google Scholar]
- Jeong-Gyu, B.A.K.; Cho, J.; Kim, B.; Senghyun, Y.U.N.; Sunghong, W.O.N.; Jeong, T.C.; Sooyoung, C.H.O.; Geunho, L.E.E.; Park, K.; Juhyung, H.A.; et al. Vertical Take-Off and Landing Aircraft Using Hybrid Electric Propulsion System. U.S. Patent 9,932,118, 3 April 2018. [Google Scholar]
- Annati, R.E.; O’brien, P.L. Honeywell International Inc, 2012. Hybrid Power for Ducted Fan Unmanned Aerial Systems. U.S. Patent 8,128,019, 6 March 2012. [Google Scholar]
- Benbrook, J.A.; Hagen, C. Hybrid Powertrain Improvements for Increased Flight Duration in Multirotor Unmanned Aerial Systems. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019; p. 4306. [Google Scholar]
- Lin, C.E.; Supsukbaworn, T. Development of dual power multirotor system. Int. J. Aerosp. Eng. 2017, 2017, 9821401. [Google Scholar] [CrossRef]
- Krznar, M. Modelling and Control of Hybrid Propulsion Systems for Multirotor Unmanned Aerial Vehicles. Ph.D. Thesis, Faculty of Mechanical Engineering and Naval Architecture, University of Zagreb, Zagreb, Croatia, 2020. [Google Scholar]
- Pavkovic, D.; Deur, J.; Kolmanovsky, I. Adaptive Kalman filter-based load torque compensator for improved SI engine idle speed control. In IEEE Transactions on Control Systems Technology; IEEE: Piscataway, NJ, USA, 2008; Volume 17, pp. 98–110. [Google Scholar]
- Krznar, M.; Pavković, D.; Kozhushko, Y.; Cipek, M.; Zorc, D.; Crneković, M. Control System Design for Hybrid Power Supply of an Unmanned Aerial Vehicle Based on Linearized Averaged Process Models. In Proceedings of the IEEE International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 6 October 2020; pp. 582–587. [Google Scholar]
- Pavković, D.; Krznar, M.; Cipek, M.; Zorc, D.; Trstenjak, M. (September 2020). Internal Combustion Engine Control System Design Suitable for Hybrid Propulsion Applications. In Proceedings of the IEEE International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 6 October 2020; pp. 1614–1619. [Google Scholar]
- Lu, W.; Zhang, D.; Zhang, J.; Li, T.; Hu, T. Design and implementation of a gasoline-electric hybrid propulsion system for a micro triple tilt-rotor VTOL UAV. In Proceedings of the IEEE 6th Data Driven Control and Learning Systems (DDCLS), Chongqing, China, 16 October 2017; pp. 433–438. [Google Scholar]
- Hung, J.Y.; Gonzalez, L.F. On parallel hybrid-electric propulsion system for unmanned aerial vehicles. Prog. Aerosp. Sci. 2012, 51, 1–17. [Google Scholar] [CrossRef]
- Thurlbeck, A.P.; Cao, Y. Analysis and modeling of UAV power system architectures. In Proceedings of the 2019 IEEE Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 8 August 2019; pp. 1–8. [Google Scholar]
- Krznar, M.; Pavković, D.; Kozhushko, Y.; Cipek, M.; Zorc, D. Generator Set Control System Design for Unmanned Aerial Vehicle Hybrid Propulsion. In Proceedings of the Digital proceedings of 4th South East Europe (SEE) Sustainable Development of Energy Water and Environment Systems (SDEWES) conference, Sarajevo, Bosnia and Herzegovina, 1–5 September 2020. [Google Scholar]
- Krznar, M.; Pavković, D.; Cipek, M.; Crneković, M.; Zorc, D. Design of a low-cost DC/DC Converter Power Distribution System for a Hybrid Power Unit of the Multirotor Unamnned Aerial Vheicle. In Proceedings of the Digital proceedings of 4th South East Europe (SEE) Sustainable Development of Energy Water and Environment Systems (SDEWES) conference, Sarajevo, Bosnia and Herzegovina, 1–5 September 2020. [Google Scholar]
- Lu, B.; Yu, Q.; Fu, X.; Shi, Y.; Cai, M. Parameter matching of hybrid coaxial rotors and multi-rotor UAV’s power system. In Proceedings of the IEEE International Conference on Aircraft Utility Systems (AUS), Beijing, China, 21 November 2016; pp. 1099–1104. [Google Scholar]
- Piljek, P.; Kotarski, D.; Krznar, M. Method for Characterization of a Multirotor UAV Electric Propulsion System. Appl. Sci. 2020, 10, 8229. [Google Scholar] [CrossRef]
- Bizon, N.; Shayeghi, H.; Tabatabaei, N.M. (Eds.) Analysis, Control and Optimal Operations in Hybrid Power Systems: Advanced Techniques and Applications for Linear and Nonlinear Systems; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Hayes, J.G.; Goodarzi, G.A. Electric Powertrain: Energy Systems, Power Electronics and Drives for Hybrid, Electric and Fuel Cell Vehicles; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- He, H.; Xiong, R.; Fan, J. Evaluation of lithium-ion battery equivalent circuit models for state of charge estimation by an experimental approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
- Pavković, D.; Krznar, M.; Komljenović, A.; Hrgetić, M.; Zorc, D. Dual EKF-based state and parameter estimator for a LiFePo4 battery cell. J. Power Electron. 2017, 17, 398–410. [Google Scholar] [CrossRef]
- Deur, J.; Ivanović, V.; Pavković, D.; Jansz, M. Identification and speed control of SI engine for idle operating mode. Sae Tech. Pap. 2004. [Google Scholar] [CrossRef]
- Rajamani, R. Mean Value Modeling of SI and Diesel Engines; Springer: Boston, MA, USA, 2012. [Google Scholar]
- Cipek, M.; Petrić, J.; Pavković, D. A Novel Approach to Hydraulic Drive Sizing Methodology and Efficiency Estimation based on Willans Line. J. Sustain. Dev. Energy Water Environ. Syst. 2019, 7, 155–167. [Google Scholar] [CrossRef]
- Gamazo-Real, J.C.; Vázquez-Sánchez, E.; Gómez-Gil, J. Position and speed control of brushless DC motors using sensorless techniques and application trends. Sensors 2010, 10, 6901–6947. [Google Scholar] [CrossRef]
- Mevey, J.R. Sensorless Field-Rriented Control of Brushless Permanent Magnet Synchronous Motors. Master’s Thesis, Kansas State University, Manhattan, KS, USA, 2009. [Google Scholar]
- Hanselman, D.C. Brushless Permanent Magnet Motor Design; The Writers’ Collective: Cranston, RI, USA, 2003. [Google Scholar]
- Krznar, M.; Kotarski, D.; Pavković, D.; Piljek, P. Propeller speed estimation for unmanned aerial vehicles using Kalman filtering. Int. J. Autom. Control. 2020, 14, 284–303. [Google Scholar] [CrossRef]
- Dahbi, M.; Doubabi, S.; Rachid, A. Current Spikes Minimization Method for Three-Phase Permanent Magnet Brushless DC Motor with Real-Time Implementation. Energies 2018, 11, 3206. [Google Scholar] [CrossRef]
- Pavković, D.; Šprljan, O.; Cipek, M.; Krznar, M. Cross-axis control system design for borehole drilling based on damping optimum criterion and utilization of proportional-integral controllers. Optim. Eng. 2021, 22, 51–81. [Google Scholar] [CrossRef]
- Pavković, D.; Deur, J. Modeling and Control of Electronic Throttle Drive: A Practical Approach—From Experimental Characterization to Adaptive Control and Application; Lambert Academic Publishing: Saarbrücken, Germany, 2011. [Google Scholar]


| Description | Value |
|---|---|
| Manufacturer and model | Zenoah G320RC |
| Type | Two-stroke gasoline engine with air cooling |
| Fuel | Eurosuper 95 gasoline and synthetic 2–stroke oil mixture 25:1 |
| Bore × Stroke | 38 mm × 28 mm |
| Compression ratio | 9.1:1 |
| Maximum power output | 3.22 HP (2.4 kW) |
| Operating speed | 4000–18,000 rpm |
| Carburetor | Walbro WT–1107 |
| Ignition and spark plug | Transistor charger ignition; NGK CMR7H |
| Length, width, height | 16.7 cm, 21.5 cm, 19.6 cm |
| Mass | 2.3 kg (dry) |
| Description | Value |
|---|---|
| Model number | MTO6374–170–HA–C |
| Back emf-constant KV | 170 rpm/V |
| Maximum Current vs. Rated Current | 65 A/60 A |
| Input voltage (defined as number of LiPo Cells) | 2–12 s |
| Shaft | 8 mm with 3 mm keyway |
| Motor Weight | 830 g |
| Line resistance; line inductance (both measured) | 0.04068 Ω; 40.43 μH |
| Max. Power | 3550 W |
| Component | Description |
|---|---|
| Throttle actuator | High torque stepper motor, 5 V, separately powered |
| RPM sensor | Hall sensor, pull up logic |
| Current sensor | ACS758 Hall sensor, 100 A, 3 qty |
| Voltage sensor | Voltage divider network with ratio 22.3, 0.1% tolerance 0.5 W resistors |
| Diode | High voltage Schottky rectifier diode, Vf = 0.37 V, Imax = 250 A |
| Load switches | Logic level n–channel MOSFET, IRLZ44, Vdss = 60 V, Id = 27 A |
| Filter Capacitors | 1200 μF, electrolytic, 63 V |
| Battery | LiPo 10,000 mAh, 25 C, 12 s |
| Computer and Microcontroller | Host computer: MacBook Pro 2018 with running MATLAB/Simulink™, Microcontroller: Arduino Mega, 2 qty. |
| Load | Wirewound power resistors network, 2 Ω, 500 W, 8 qty. |
| Cooling fans for load resistors | 6–inch racing multirotor prop–motor set, 3 qty. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krznar, M.; Piljek, P.; Kotarski, D.; Pavković, D. Modeling, Control System Design and Preliminary Experimental Verification of a Hybrid Power Unit Suitable for Multirotor UAVs. Energies 2021, 14, 2669. https://doi.org/10.3390/en14092669
Krznar M, Piljek P, Kotarski D, Pavković D. Modeling, Control System Design and Preliminary Experimental Verification of a Hybrid Power Unit Suitable for Multirotor UAVs. Energies. 2021; 14(9):2669. https://doi.org/10.3390/en14092669
Chicago/Turabian StyleKrznar, Matija, Petar Piljek, Denis Kotarski, and Danijel Pavković. 2021. "Modeling, Control System Design and Preliminary Experimental Verification of a Hybrid Power Unit Suitable for Multirotor UAVs" Energies 14, no. 9: 2669. https://doi.org/10.3390/en14092669
APA StyleKrznar, M., Piljek, P., Kotarski, D., & Pavković, D. (2021). Modeling, Control System Design and Preliminary Experimental Verification of a Hybrid Power Unit Suitable for Multirotor UAVs. Energies, 14(9), 2669. https://doi.org/10.3390/en14092669








