Numerical Study of Elasto-Plastic Hydraulic Fracture Propagation in Deep Reservoirs Using a Hybrid EDFM–XFEM Method
Abstract
1. Introduction
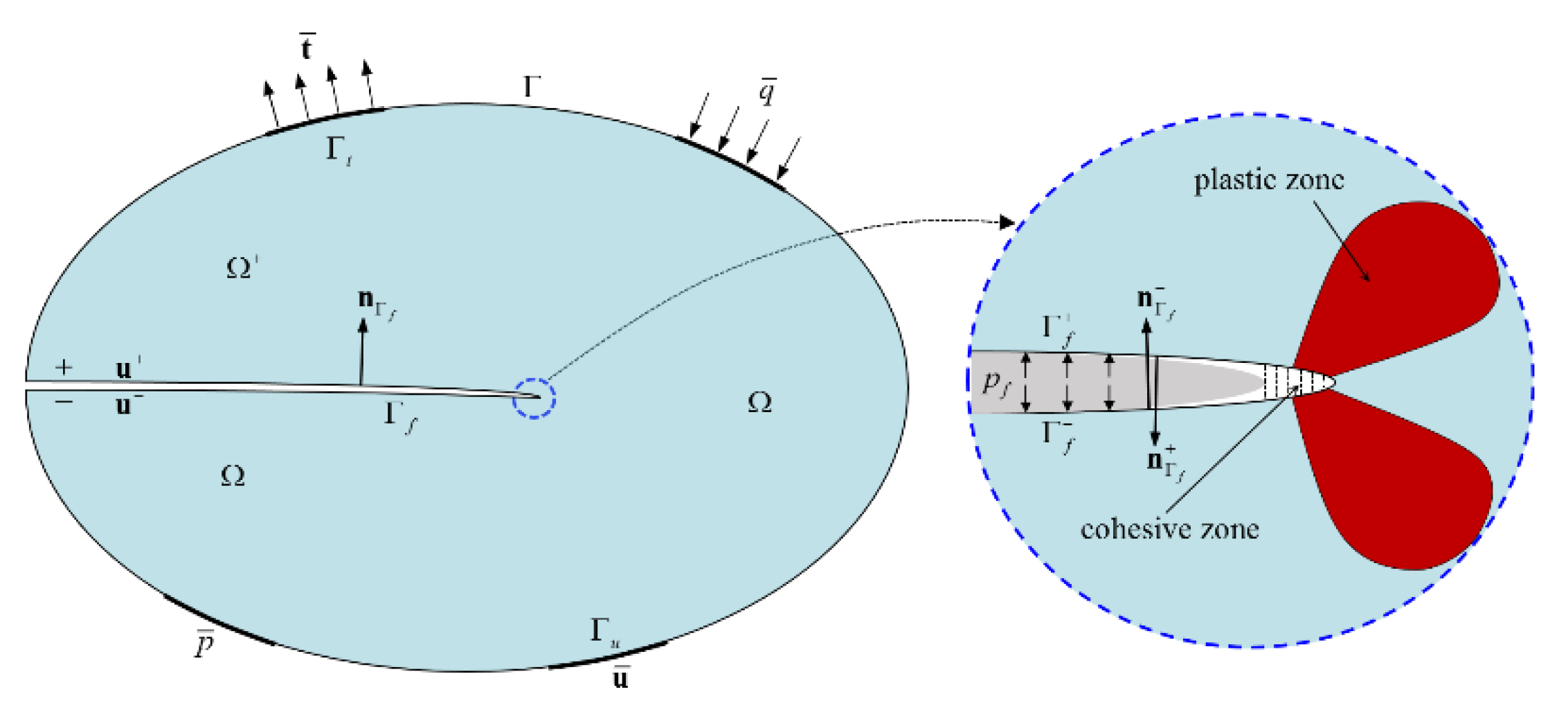
2. Mathematical Model
2.1. Rock Deformation
2.2. Fluid Flow
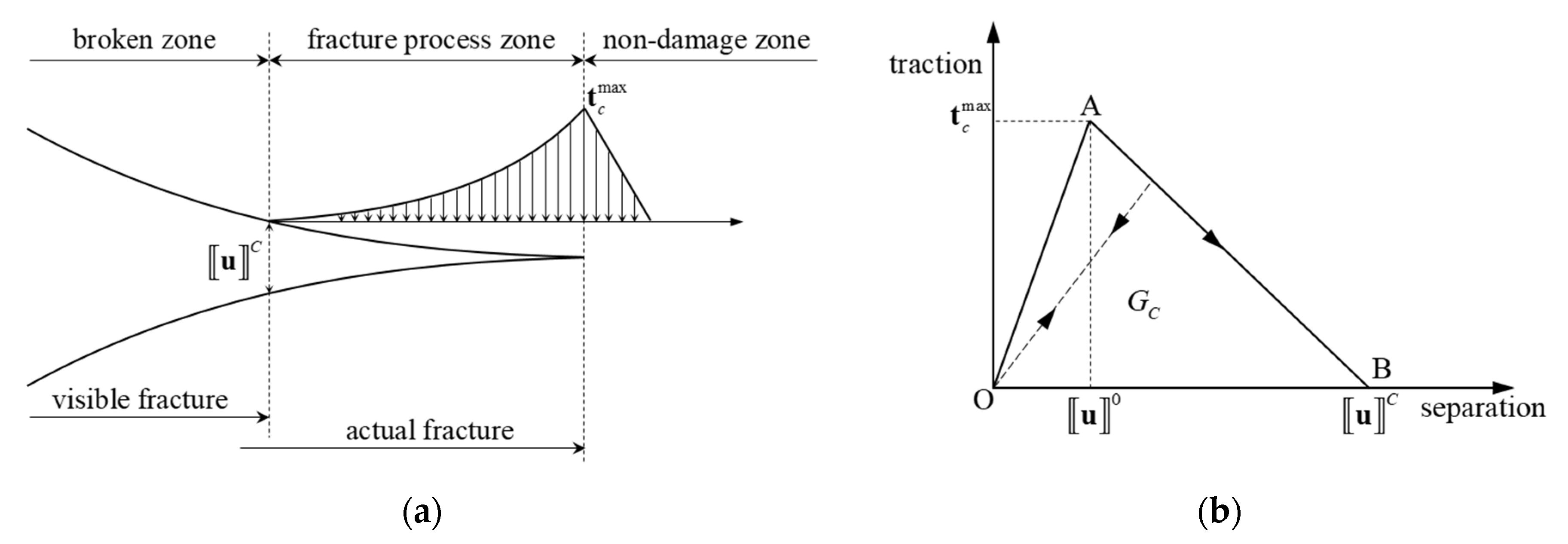
2.3. Cohesive Zone Model
3. Numerical Implementation
3.1. Displacement Field
3.2. Pressure Field
3.3. Iterative Procedure
4. Numerical Results and Discussion
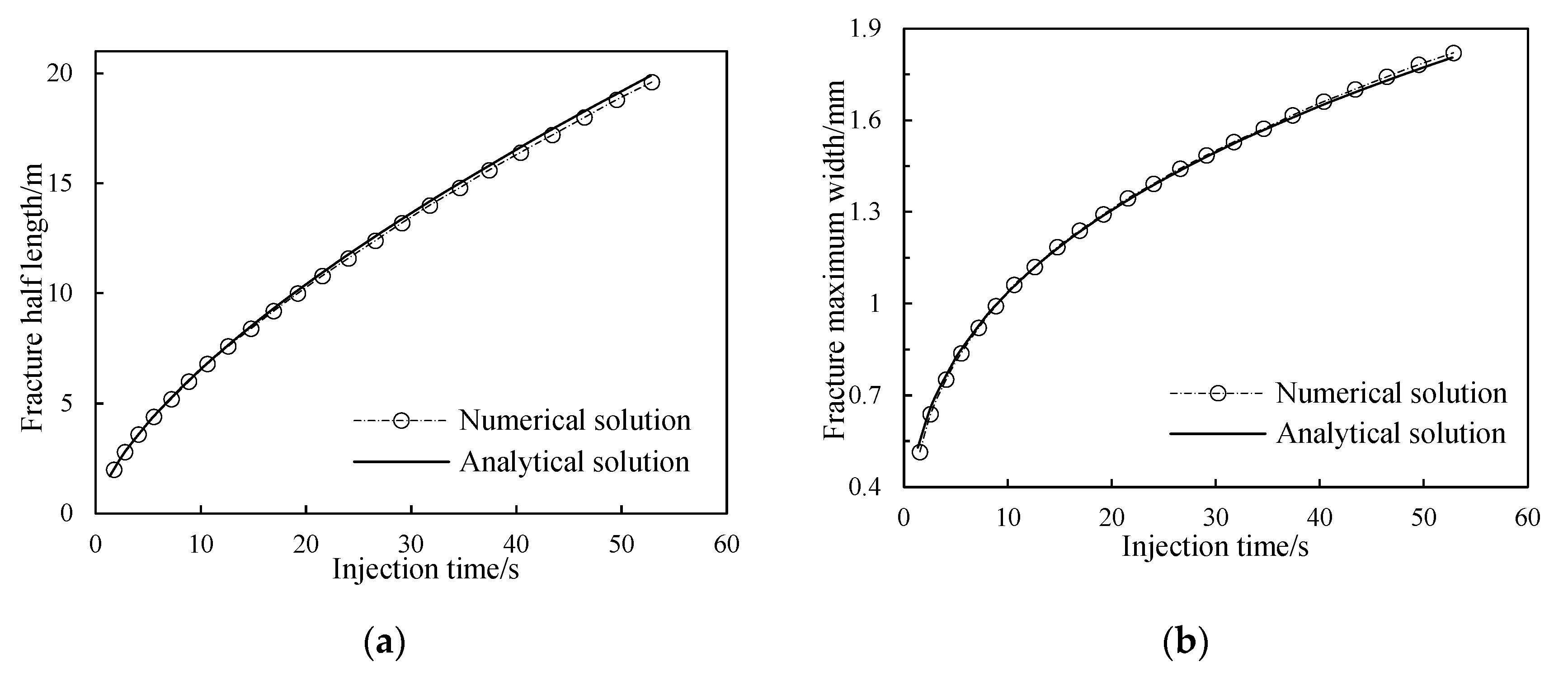
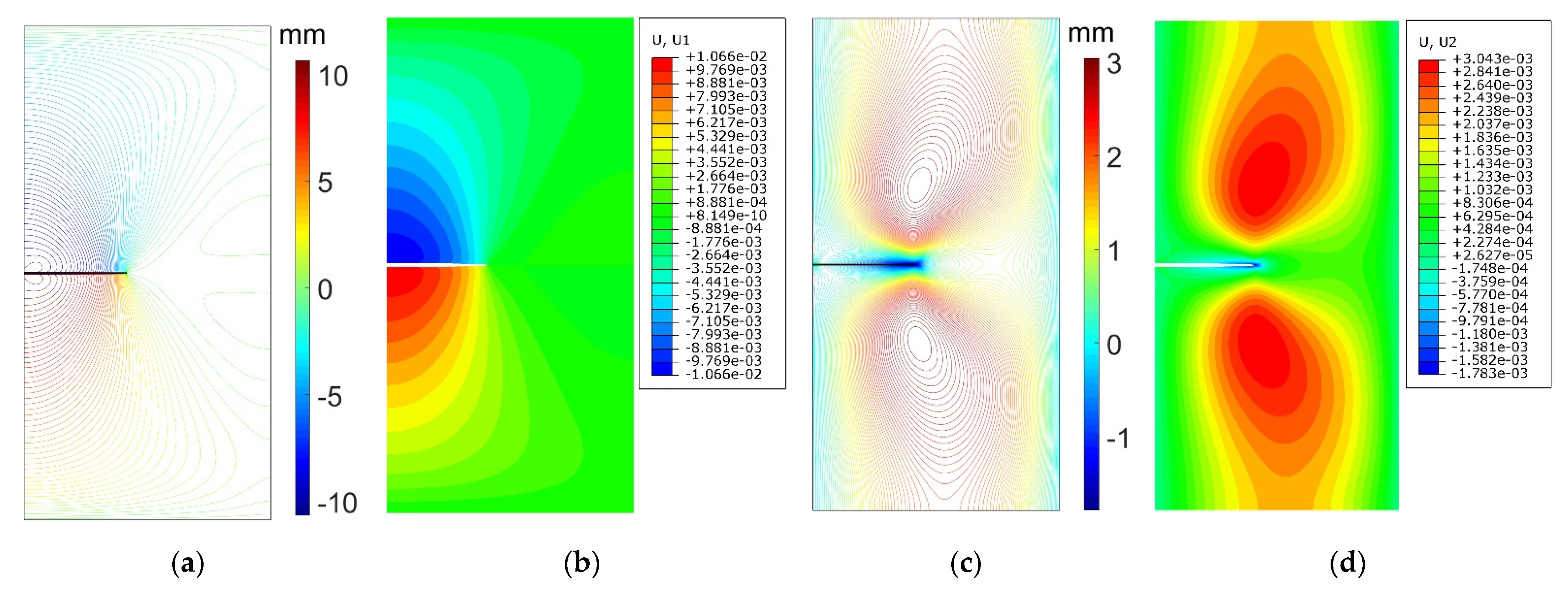
4.1. Model Verification
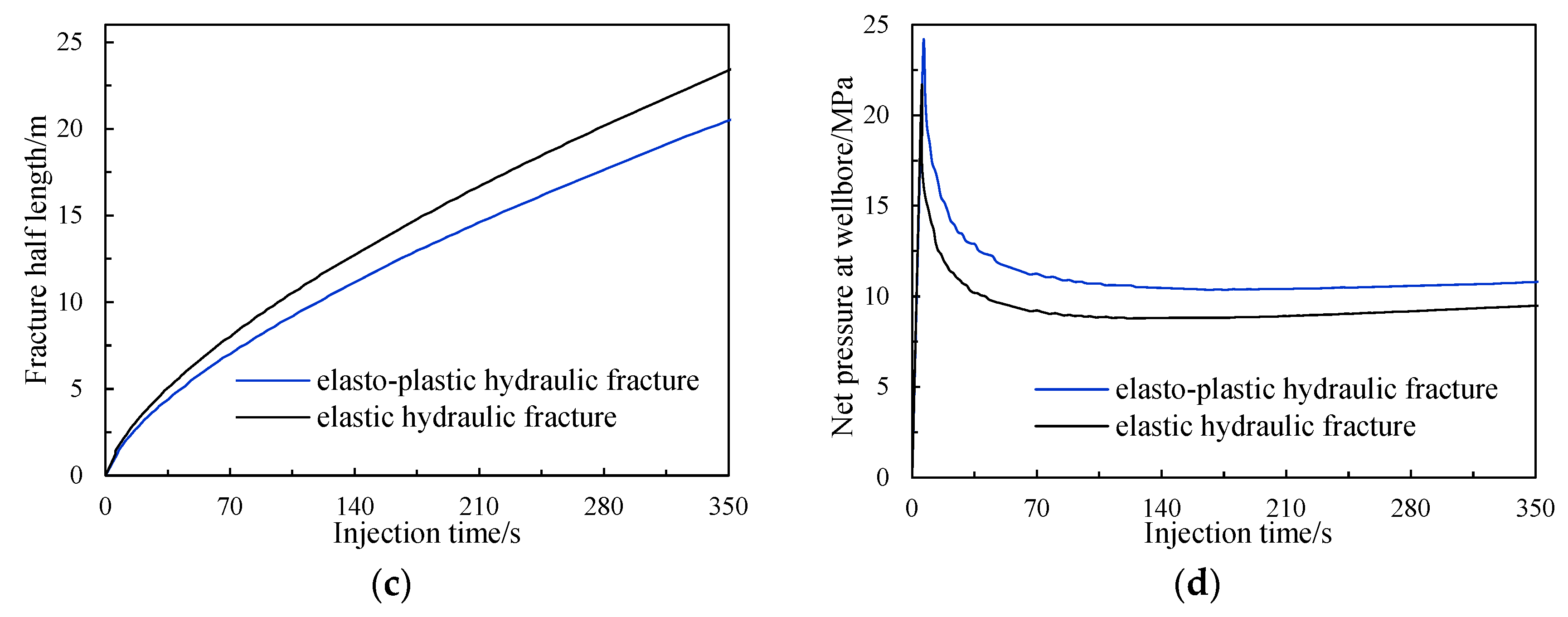
4.1.1. Fracture Propagation under Elastic Deformation
4.1.2. Fracture Propagation under Plastic Deformation
4.2. Results and Discussion
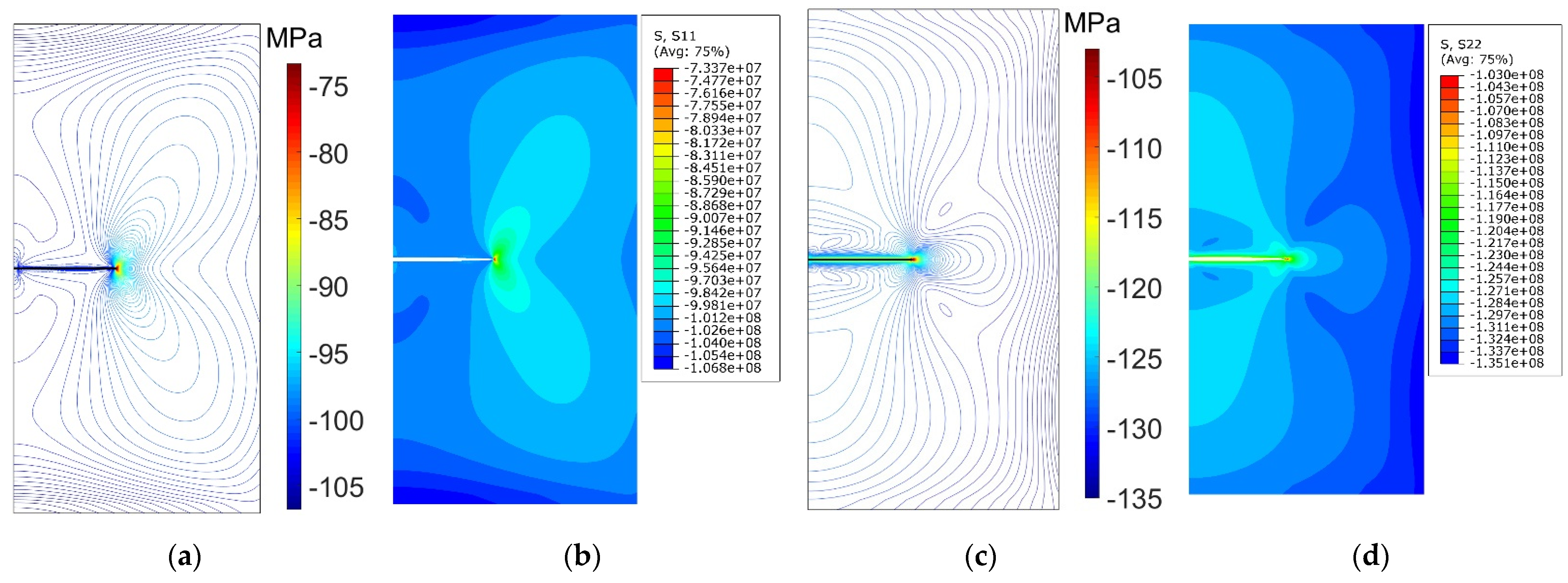
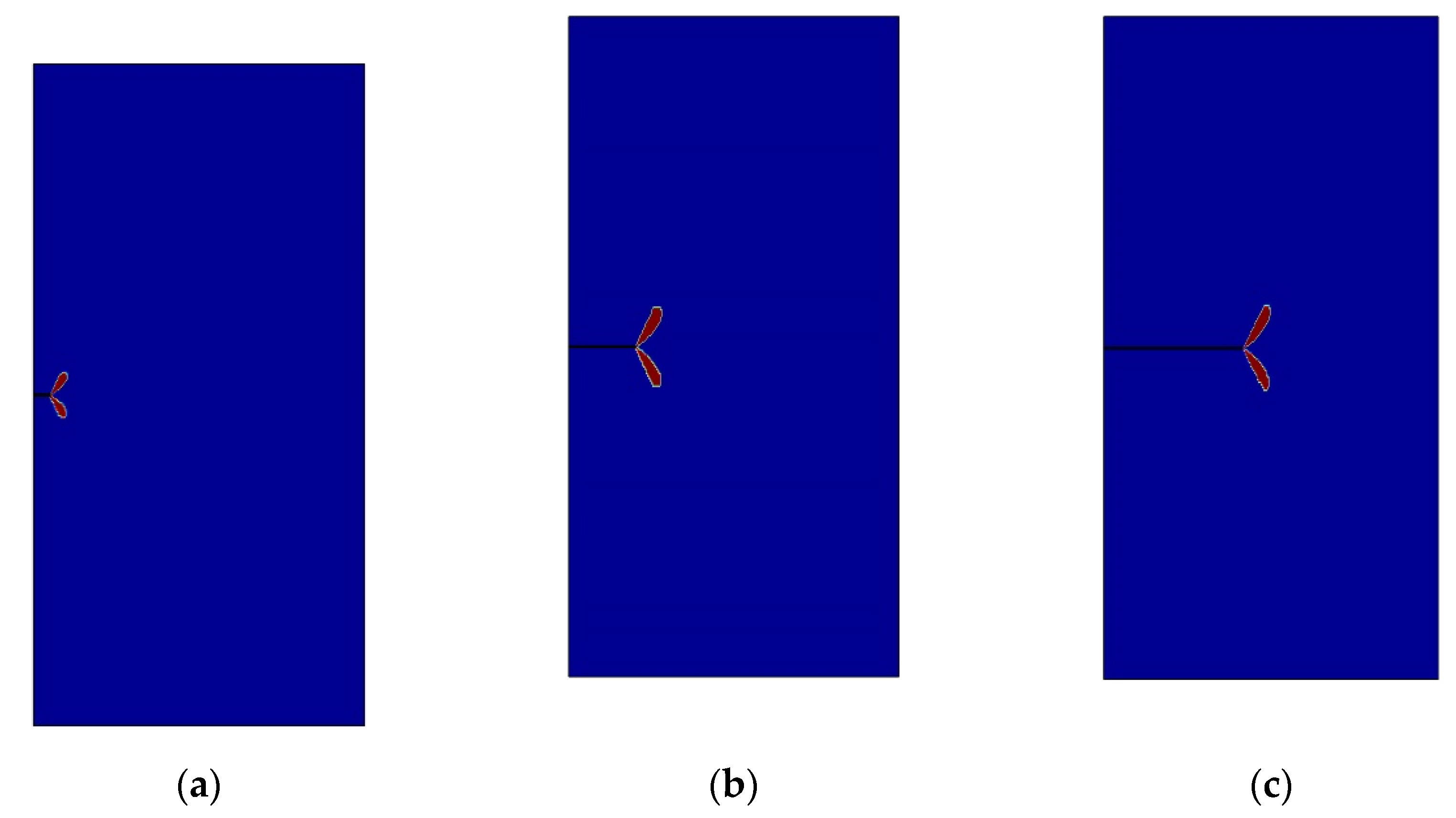
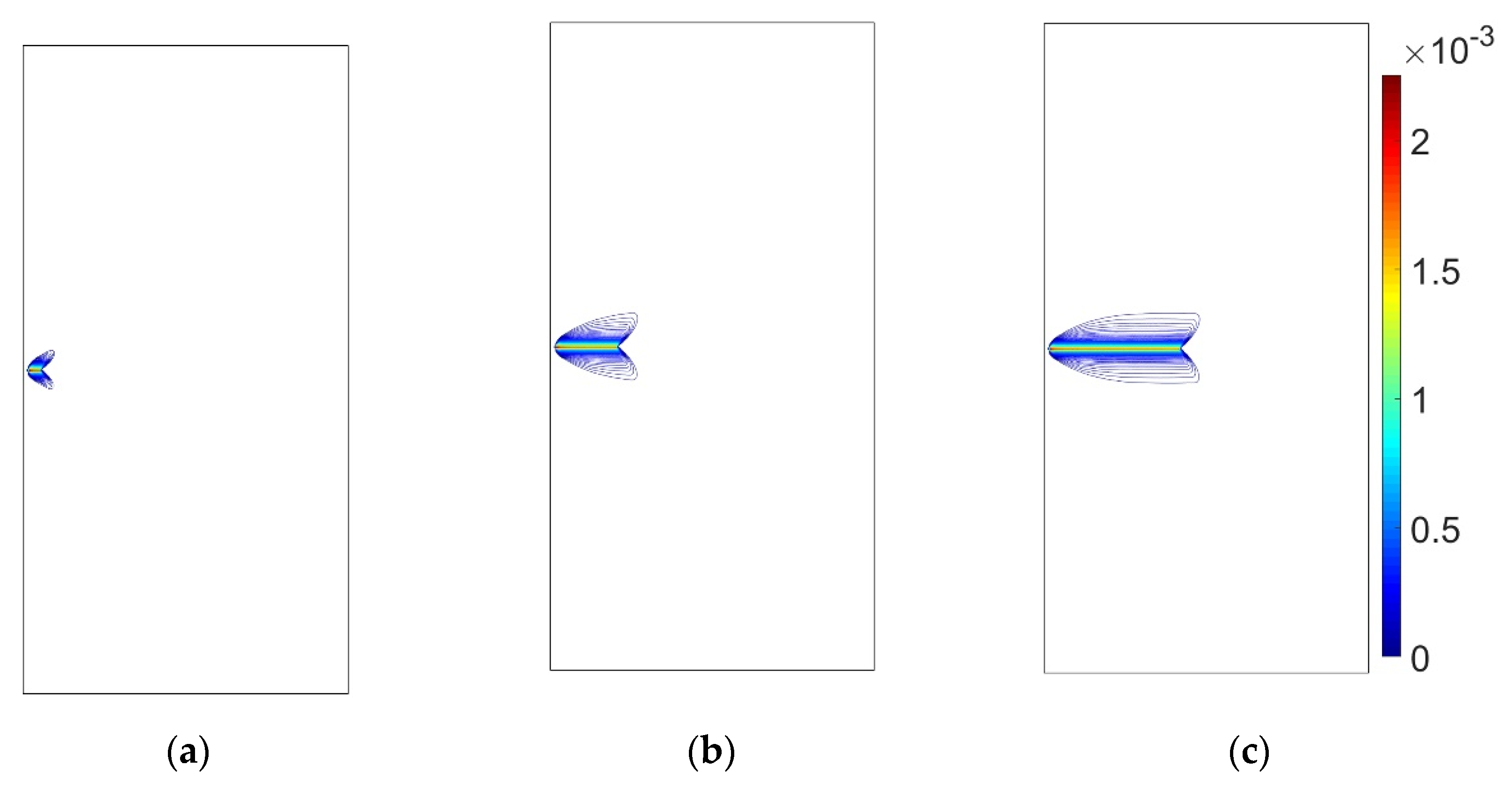
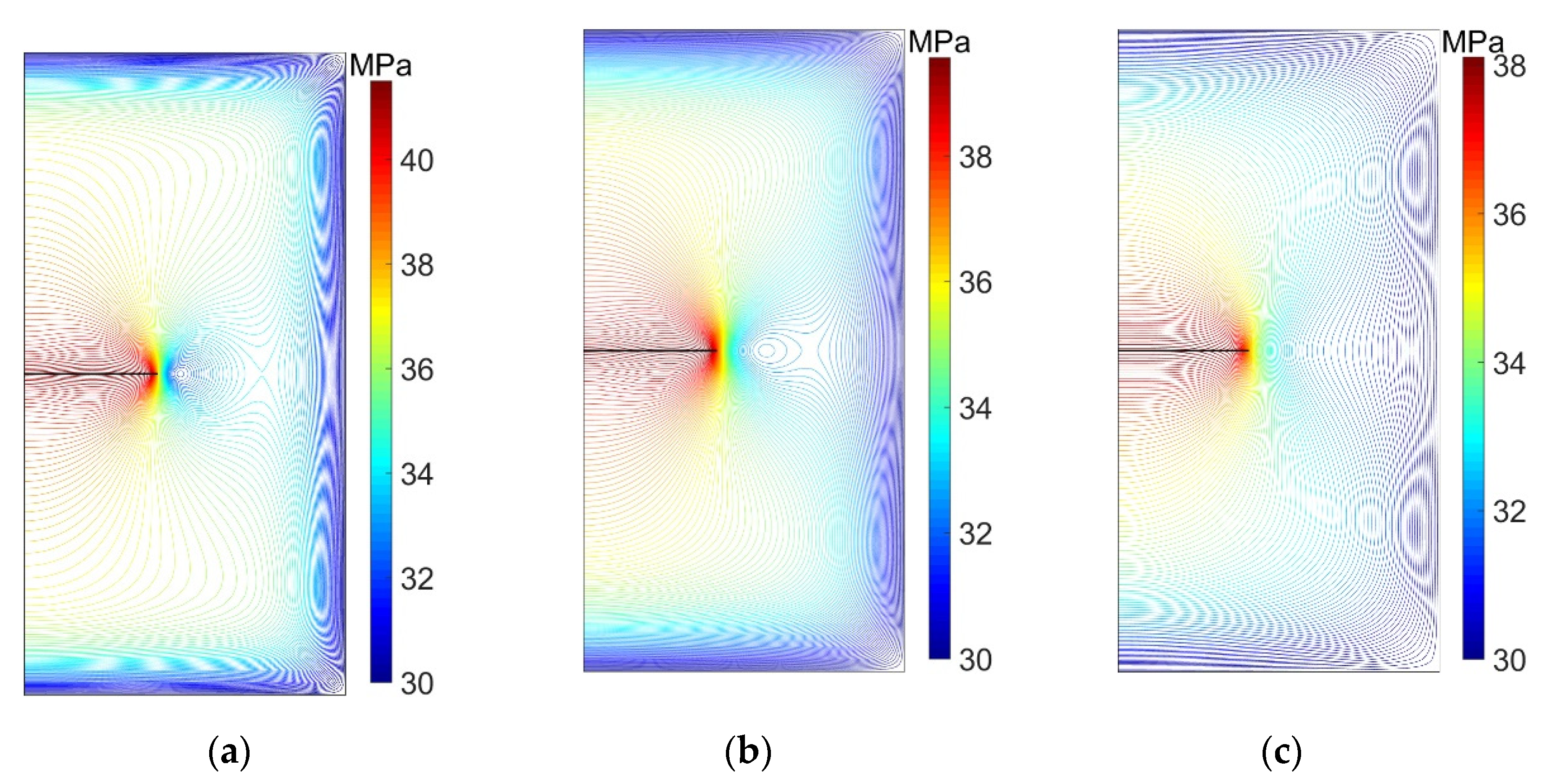
4.2.1. Evolution of Plastic Zone
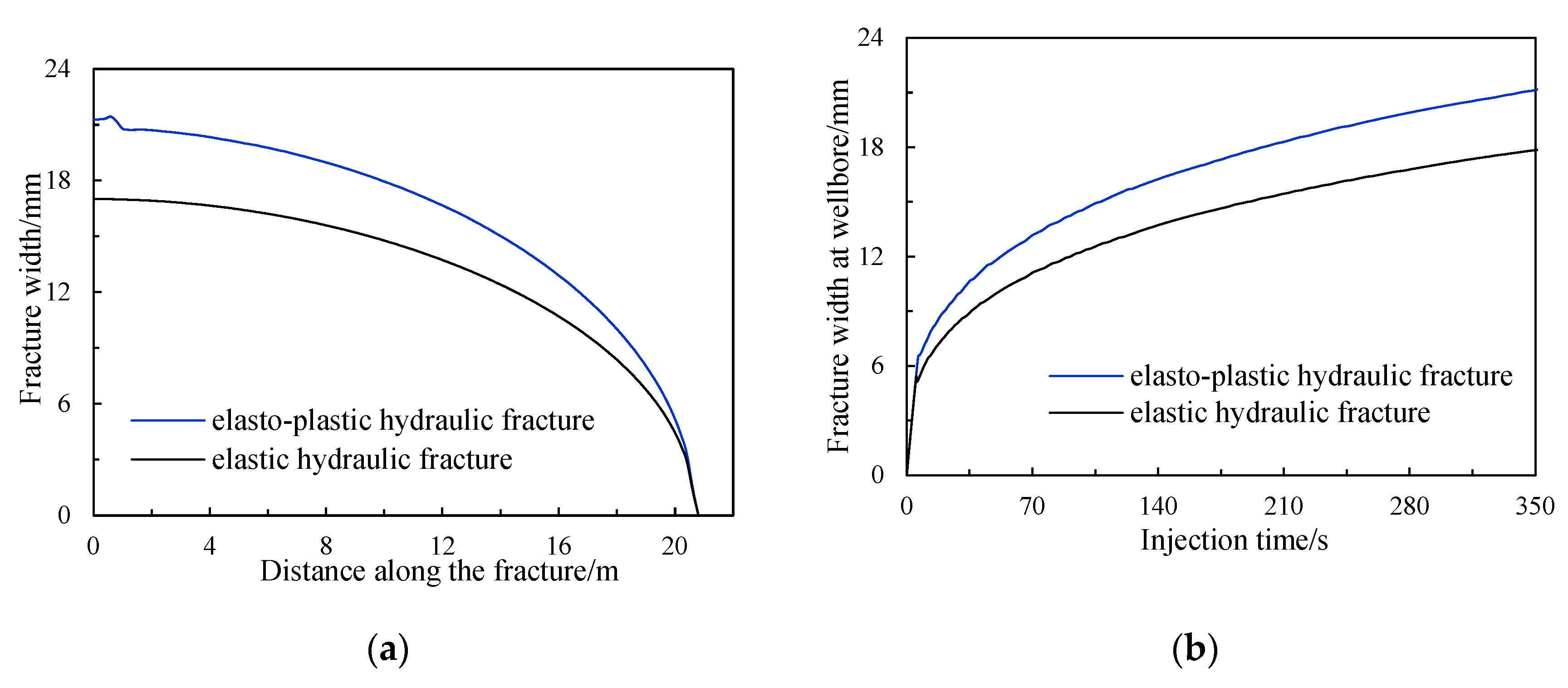
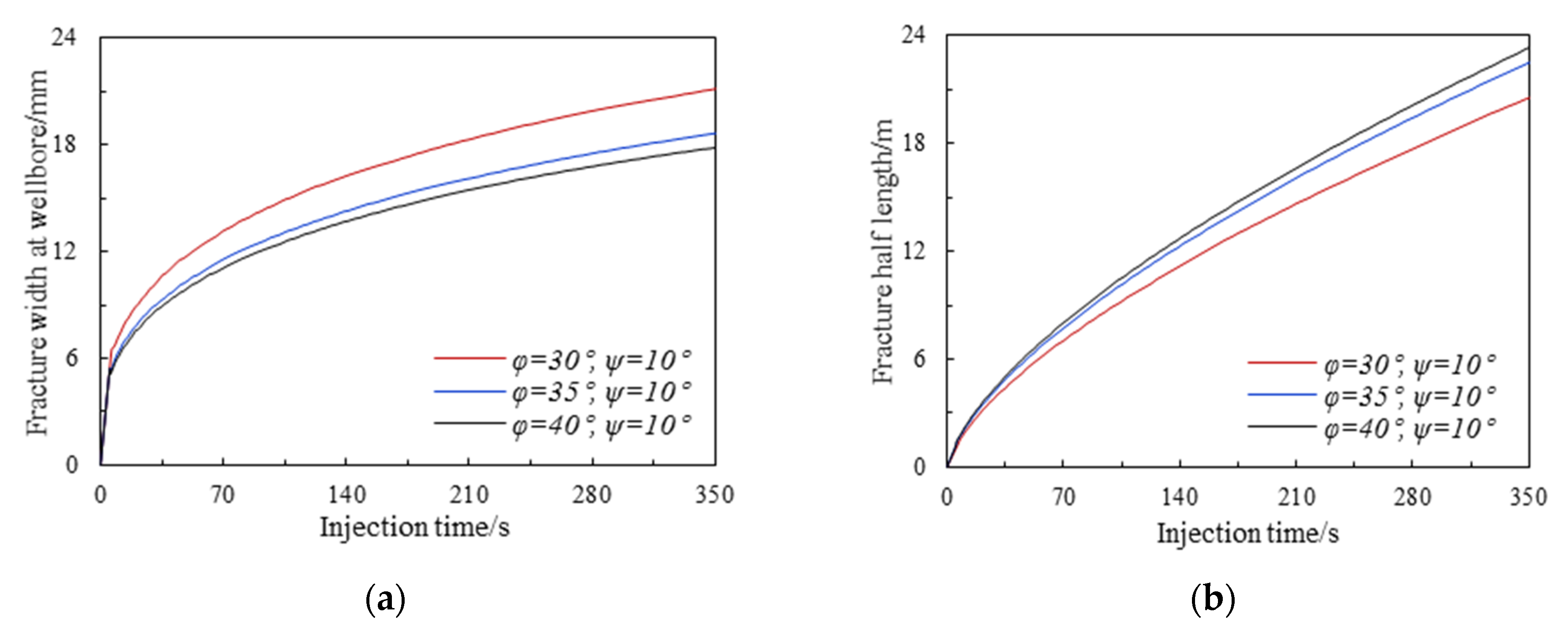
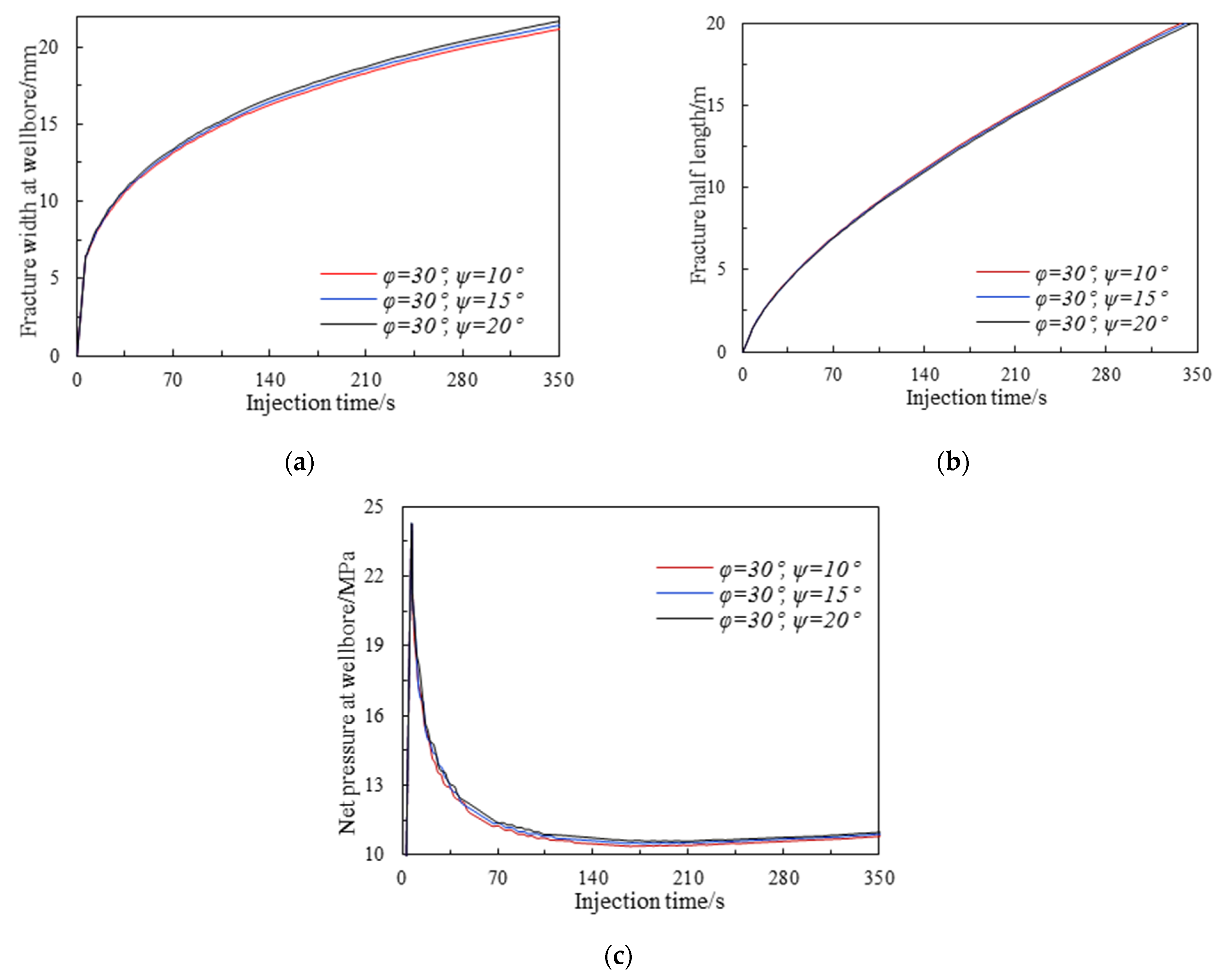
4.2.2. Effect of Plastic Deformation
4.2.3. Effect of Permeability
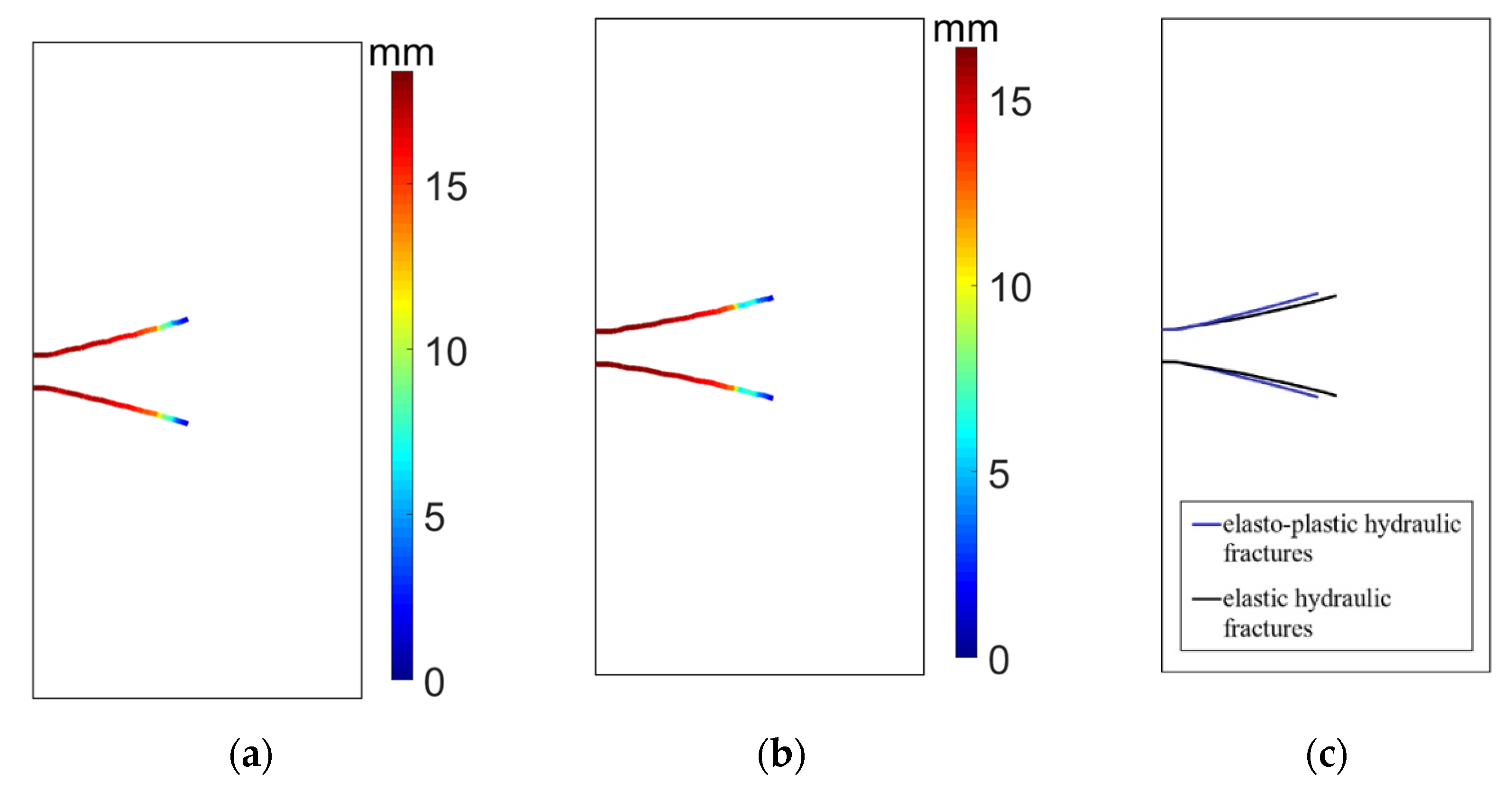
4.2.4. Extension to Multiple Hydraulic Fractures Propagation
5. Conclusions
- During hydraulic fracturing in deep reservoirs, rock plasticity results in higher energy dissipation in deep reservoirs, larger pressure is required for fracture extension, which leads to hydraulic fractures with larger openings. Therefore, larger injection volume and higher injection pressure are needed to obtain the desired fracture length;
- As the internal friction angle increases from 30° to 40°, the fracture width and injection pressure decrease while the fracture propagation velocity increases, which means the effect of plastic deformation is weakened. The effects of the dilatancy angle on hydraulic fracturing are opposite to that of the internal friction angle;
- As the matrix permeability increases from 5 mD to 20 mD, more fracturing fluid leaks into the matrix, leading to a shorter and narrower hydraulic fracture;
- For two hydraulic fracture propagations in deep reservoirs, plastic deformation can enhance the stress-shadowing effect.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pang, X.; Jia, C.; Wang, W. Petroleum geology features and research developments of hydrocarbon accumulation in deep petroliferous basins. Pet. Sci. 2015, 12, 1–53. [Google Scholar] [CrossRef]
- Yao, J.; Huang, Z.; Liu, W.; Zhang, Y.; QingDong, Z.; Yan, X. Key mechanical problems in the development of deep oil and gas reservoirs. Sci. Sin. Phys. Mech. Astron. 2018, 48, 044701. [Google Scholar]
- Olson, J. Multi-fracture propagation modeling: Applications to hydraulic fracturing in shales and tight gas sands. In Proceedings of the 42nd US Rock Mechanics Symposium (USRMS), San Francisco, CA, USA, 29 June–2 July 2008. [Google Scholar]
- Chen, M. Review of study on rock mechanics at great depth and its applications to petroleum engineering of china. Chin. J. Rock Mech. Eng. 2004, 14, 2455–2462. [Google Scholar]
- Sone, H.; Zoback, M. Visco-plastic properties of shale gas reservoir rocks. In Proceedings of the 45th US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 26–29 June 2011. [Google Scholar]
- Khristianovic, S.; Zheltov, Y. Formation of vertical fractures by means of highly viscous fluids. In Proceedings of the 4th World Petroleum Congress, Rome, Italy, 6–15 June 1955; pp. 579–586. [Google Scholar]
- Geertsma, J.; De Klerk, F. A rapid method of predicting width and extent of hydraulically induced fractures. J. Pet. Technol. 1969, 21, 571–581. [Google Scholar] [CrossRef]
- Perkins, T.; Kern, L. Widths of hydraulic fractures. J. Pet. Technol. 1961, 13, 937–949. [Google Scholar] [CrossRef]
- Nordgren, R. Propagation of a vertical hydraulic fracture. Soc. Pet. Eng. 1972, 12, 306–314. [Google Scholar] [CrossRef]
- Cleary, M.P. Comprehensive design formulae for hydraulic fracturing. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 21–24 September 1980. [Google Scholar]
- Bouteca, M. 3D analytical model for hydraulic fracturing: Theory and field test. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 17 September 1984. [Google Scholar]
- Sarris, E.; Papanastasiou, P. Modeling of hydraulic fracturing in a poroelastic cohesive formation. Int. J. Geomech. 2011, 12, 160–167. [Google Scholar] [CrossRef]
- Carrier, B.; Granet, S. Numerical modeling of hydraulic fracture problem in permeable medium using cohesive zone model. Eng. Fract. Mech. 2012, 79, 312–328. [Google Scholar] [CrossRef]
- Lecampion, B. An extended finite element method for hydraulic fracture problems. Commun. Numer. Methods Eng. 2009, 25, 121–133. [Google Scholar] [CrossRef]
- Simpson, R.; Trevelyan, J. A partition of unity enriched dual boundary element method for accurate computations in fracture mechanics. Comput. Methods Appl. Mech. Eng. 2011, 200, 1–10. [Google Scholar] [CrossRef]
- Wu, K.; Olson, J.E. Simultaneous multifracture treatments: Fully coupled fluid flow and fracture mechanics for horizontal wells. SPE J. 2015, 20, 337–346. [Google Scholar] [CrossRef]
- Torres, S.A.G.; Castaño, J.D.M. Simulation of the hydraulic fracture process in two dimensions using a discrete element method. Phys. Rev. E 2007, 75, 066109. [Google Scholar] [CrossRef]
- Damjanac, B.; Cundall, P. Application of distinct element methods to simulation of hydraulic fracturing in naturally fractured reservoirs. Comput. Geotech. 2016, 71, 283–294. [Google Scholar] [CrossRef]
- Nikolic, M.; Ibrahimbegovic, A.; Miscevic, P. Discrete element model for the analysis of fluid-saturated fractured poro-plastic medium based on sharp crack representation with embedded strong discontinuities. Comput. Methods Appl. Mech. Eng. 2016, 298, 407–427. [Google Scholar] [CrossRef]
- Nikolić, M.; Karavelić, E.; Ibrahimbegovic, A.; Miščević, P. Lattice Element Models and Their Peculiarities. Arch. Comput. Methods Eng. 2018, 25, 753–784. [Google Scholar] [CrossRef]
- Meyer, B.R.; Bazan, L.W. A discrete fracture network model for hydraulically induced fractures-theory, parametric and case studies. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 24–26 January 2011. [Google Scholar]
- Fu, P.; Johnson, S.M.; Carrigan, C.R. An explicitly coupled hydro-geomechanical model for simulating hydraulic fracturing in arbitrary discrete fracture networks. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 2278–2300. [Google Scholar] [CrossRef]
- Liu, W.; Zeng, Q.; Yao, J. Numerical simulation of elasto-plastic hydraulic fracture propagation in deep reservoir coupled with temperature field. J. Pet. Sci. Eng. 2018, 171, 115–126. [Google Scholar] [CrossRef]
- Lecampion, B.; Bunger, A.; Zhang, X. Numerical methods for hydraulic fracture propagation: A review of recent trends. J. Nat. Gas Sci. Eng. 2018, 49, 66–83. [Google Scholar] [CrossRef]
- Weng, X. Modeling of complex hydraulic fractures in naturally fractured formation. J. Unconv. Oil Gas Resour. 2015, 9, 114–135. [Google Scholar] [CrossRef]
- Papanastasiou, P. An efficient algorithm for propagating fluid-driven fractures. Comput. Mech. 1999, 24, 258–267. [Google Scholar] [CrossRef]
- Liu, F.; Gordon, P.; Meier, H.; Valiveti, D. A stabilized extended finite element framework for hydraulic fracturing simulations. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 654–681. [Google Scholar] [CrossRef]
- Zeng, Q.D.; Yao, J.; Shao, J.F. Effect of plastic deformation on hydraulic fracturing with extended element method. Acta Geotech. 2019, 14, 2083–2101. [Google Scholar] [CrossRef]
- Adachi, J.; Siebrits, E.; Peirce, A.; Desroches, J. Computer simulation of hydraulic fractures. Int. J. Rock Mech. Min. Sci. 2007, 44, 739–757. [Google Scholar] [CrossRef]
- Sarris, E.; Papanastasiou, P. Numerical modeling of fluid-driven fractures in cohesive poroelastoplastic continuum. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 1822–1846. [Google Scholar] [CrossRef]
- Wang, H.; Marongiu-Porcu, M.; Economides, M.J. Poroelastic and poroplastic modeling of hydraulic fracturing in brittle and ductile formations. SPE Prod. Oper. 2016, 31, 47–59. [Google Scholar] [CrossRef]
- Yan, X.; Huang, Z.; Yao, J.; Li, Y.; Fan, D. An efficient embedded discrete fracture model based on mimetic finite difference method. J. Pet. Sci. Eng. 2016, 145, 11–21. [Google Scholar] [CrossRef]
- Yan, X.; Huang, Z.; Yao, J.; Li, Y.; Fan, D.; Zhang, K. An efficient hydro-mechanical model for coupled multi-porosity and discrete fracture porous media. Comput. Mech. 2018, 62, 943–962. [Google Scholar] [CrossRef]
- Zeng, Q.; Liu, W.; Yao, J. Hydro-mechanical modeling of hydraulic fracture propagation based on embedded discrete fracture model and extended finite element method. J. Pet. Sci. Eng. 2018, 167, 64–77. [Google Scholar] [CrossRef]
- Zeng, Q.; Yao, J.; Shao, J. Study of hydraulic fracturing in an anisotropic poroelastic medium via a hybrid EDFM-XFEM approach. Comput. Geotech. 2019, 105, 51–68. [Google Scholar] [CrossRef]
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- De Souza Neto, E.A.; Peric, D.; Owen, D.R.J. Computational Methods for Plasticity: Theory and Applications; Wiley: Chichester, UK, 2011. [Google Scholar]
- Papanastasiou, P. The influence of plasticity in hydraulic fracturing. Int. J. Fract. 1997, 84, 61–79. [Google Scholar] [CrossRef]
- Chen, Z.; Bunger, A.; Zhang, X.; Jeffrey, R.G. Cohesive zone finite element-based modeling of hydraulic fractures. Acta Mech. Solida Sin. 2009, 22, 443–452. [Google Scholar] [CrossRef]
- Mohammadnejad, T.; Khoei, A. An extended finite element method for hydraulic fracture propagation in deformable porous media with the cohesive crack model. Finite Elem. Anal. Des. 2013, 73, 77–95. [Google Scholar] [CrossRef]
- Mohammadnejad, T.; Khoei, A. Hydro-mechanical modeling of cohesive crack propagation in multiphase porous media using the extended finite element method. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 1247–1279. [Google Scholar] [CrossRef]
- Kim, J.; Tchelepi, H.A.; Juanes, R. Stability and convergence of sequential methods for coupled flow and geomechanics: Fixed-stress and fixed-strain splits. Comput. Methods Appl. Mech. Eng. 2011, 200, 1591–1606. [Google Scholar] [CrossRef]
- Mikelić, A.; Wang, B.; Wheeler, M.F. Numerical convergence study of iterative coupling for coupled flow and geomechanics. Comput. Geosci. 2014, 18, 325–341. [Google Scholar] [CrossRef]
- Simo, J.; Taylor, R. A return mapping algorithm for plane stress elastoplasticity. Int. J. Numer. Methods Eng. 1986, 22, 649–670. [Google Scholar] [CrossRef]
- Valko, P.; Economides, M.J. Hydraulic Fracture Mechanics; Wiley: Chichester, UK, 1995; Volume 28. [Google Scholar]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Zeng, Q.; Yao, J.; Liu, Z.; Li, T.; Yan, X. Numerical Study of Elasto-Plastic Hydraulic Fracture Propagation in Deep Reservoirs Using a Hybrid EDFM–XFEM Method. Energies 2021, 14, 2610. https://doi.org/10.3390/en14092610
Liu W, Zeng Q, Yao J, Liu Z, Li T, Yan X. Numerical Study of Elasto-Plastic Hydraulic Fracture Propagation in Deep Reservoirs Using a Hybrid EDFM–XFEM Method. Energies. 2021; 14(9):2610. https://doi.org/10.3390/en14092610
Chicago/Turabian StyleLiu, Wenzheng, Qingdong Zeng, Jun Yao, Ziyou Liu, Tianliang Li, and Xia Yan. 2021. "Numerical Study of Elasto-Plastic Hydraulic Fracture Propagation in Deep Reservoirs Using a Hybrid EDFM–XFEM Method" Energies 14, no. 9: 2610. https://doi.org/10.3390/en14092610
APA StyleLiu, W., Zeng, Q., Yao, J., Liu, Z., Li, T., & Yan, X. (2021). Numerical Study of Elasto-Plastic Hydraulic Fracture Propagation in Deep Reservoirs Using a Hybrid EDFM–XFEM Method. Energies, 14(9), 2610. https://doi.org/10.3390/en14092610





