Extension of Pin-Based Point-Wise Energy Slowing-Down Method for VHTR Fuel with Double Heterogeneity

Abstract

For the resonance treatment of a very high temperature reactors (VHTR) fuel with the double heterogeneity, an extension of the pin-based pointwise energy slowing-down method (PSM) was developed and implemented into DeCART. The proposed method, PSM-double heterogeneity (DH), has an improved spherical unit cell model with an explicit tri-structural isotropic (TRISO) model, a matrix layer, and a moderator for reflecting the moderation effect. The moderator volume was analytically derived using the relation of the Dancoff factor and the mean chord length. In the first step, the pointwise homogenized cross-sections for the compact was obtained after solving the slowing down equation for the spherical unit cell. Then, the shielded cross-section for the homogenized fuel compact was generated using the original PSM. The verification calculations were performed for the fuel pins with various packing fractions, compact sizes, TRISO sizes, and fuel temperatures. Additionally, two fuel block problems with very different sizes were examined and the depletion calculation was carried out for investigating the accuracy of the proposed method. They revealed that the PSM-DH has a good performance in the VHTR problems.

1. Introduction

The Korea atomic energy research institute (KAERI) has been developing very high temperature reactors (VHTR) with various sizes for the purposes of hydrogen production application or electricity supply for remote locations. The cores consist of graphite moderator and the fuel compact which contains a graphite matrix and tri-structural isotropic (TRISO) particle fuels randomly dispersed in the matrix. It introduces a unique neutronic characteristic, the double heterogeneity (DH), which is the combination of two level of heterogeneities: one for the fuel compact and the moderator and the other for the TRISO and the matrix within the compact.

The DH effect causes considerable complexity for the resonance treatment in a lattice calculation step. The SCALE code system employed a two-step resonance treatment method [1] for the DH fuel. The method generates pointwise homogenized cross-sections for the fuel compact through pointwise slowing down calculation for a spherical unit cell model with a fuel kernel and a matrix layer. By using the homogenized cross-sections for the fuel compact, the DH problem can be transformed into a single heterogeneity problem. However, this method not only ignores the effects of coating layers and moderator but also needs excessive computation time. The verification report [2] shows that the spherical unit cell without coating layers and a moderator causes error over 300 pcm. Afterward, a new resonance treatment method [3] for DH fuel was proposed based on the equivalence theory with the intermediate resonance (IR) approximation [4,5] and the Dancoff factor [5] for the particle fuel without coating layer. Kim [6] extended the method to take the coating layer of TRISO into account using the analytical Dancoff factor for TRISO particle fuel [7]. Another approach to enhance the accuracy of the equivalence theory for the DH fuel is to estimate accurate Dancoff factor using Monte Carlo method [8].

However, recent papers [9,10] report the limitation of the equivalence theory, overestimation of 238U absorption cross-section. The pin-based pointwise energy slowing-down method (PSM) [10] was developed to overcome the limitation of the equivalence theory. It can generate problem dependent self-shielded cross-sections in the lattice calculation step and has better accuracy than the pre-generated library within reasonably acceptable calculation time.

The lattice code developed at KAERI, DeCART (Deterministic Core Analysis based on Ray Tracing) [11], uses the pre-generated multi-group library. The library is prepared using the subgroup method [12] and the direct resonance integral table method [13] which are based on the equivalence theory with the IR approximation. The library generation procedure developed for conventional light water reactor (LWR) is used for the generation of the multi-group library for VHTR with a modification for DH fuel. During the library generation procedure for VHTR, the resonance integral table is corrected by using a Monte Carlo code. However, this correction leads to the dependency of the library on the specific reactor which the correction is performed based on. In addition, for improving the inaccuracy and system-dependency of the pre-generated library of DeCART, an extension of PSM for the resonance treatment of a DH fuel, PSM-DH, was developed and implemented into DeCART [14]. For extension of the PSM to a DH fuel, it is necessary to homogenize the fuel compact region. This approach is similar to the two-step resonance treatment method of SCALE but PSM-DH has an improved spherical unit cell model with the explicit TRISO fuel and a moderator to reflect the effect of the coating layers and moderator. Additionally, it applies the PSM in place of the equivalence theory for the homogenized fuel compact.

In this work, for completing our previous work [14], a new method for increasing the calculation speed of PSM-DH was proposed and the procedure for depletion calculation was established and the verification result was presented. Additionally, the DH effect of the proposed method was examined for typical VHTR problems and the verification calculations with various compact size and TRISO radius were performed.

2. Methods

The PSM-DH is essentially based on the PSM which can generate the self-shielded cross-section for a homogenized fuel region. The method needs a pointwise homogenized cross-section for a DH fuel of VHTR prior to the resonance treatment by PSM.

In order to provide a detailed description for the PSM-DH, a simple review of the PSM is firstly stated in Section 2.1 and then the extension of the PSM to a DH region is described in the next section.

2.1. Simple Review of Pin-Based Point-Wise Slowing down Method

The PSM solves the slowing down equation [10,15] for tens of thousands of energy points within the resonance energy range in lethargy space as follows:

$${\Sigma }_{t,i}(u){\varphi }_i(u)V_i={\displaystyle \sum _{j\in F}{P}_{ji}(u)V_j{Q}_{s,j}}(u)+P_{Mi}(u)V_M{Q}_{s,M}(u),$$

(1)

where

i, j: sub-region indexes,

$u$: lethargy,

${\Sigma }_{t,i}^{}\left(u\right)$: total cross-section at sub-region i,

${\varphi }_i\left(u\right)$: the flux at sub-region i,

$P_{ji}^{}\left(u\right)$: probability that a neutron escaped from sub-region j has its first collision at sub-region i,

$V_i$: volume of a sub-region i, and

$Q_{s,j}\left(u\right)$: slowing down scattering source of a sub-region j.

Note that the subscript M is the index of the moderator region.

The collision probability (CP) tables for the given system should be known prior to solving Equation (1). The CP $P_{ij}$ can be evaluated by combining the CP table for an isolated fuel pin, $P_{ij}^{iso}$ and the shadowing effect correction factor of the fuel region, ${\eta }_F$. To evaluate $P_{ij}^{iso}$ for every energy points, it is necessary to solve the fixed source neutron transport equation, Equation (2), for an isolated pin for every energy points.

$$\mathrm{\Omega }\cdot \nabla \psi (r,\mathrm{\Omega })+{\Sigma }_t(r)\psi (r,\mathrm{\Omega })=\frac{1}{4\pi }{\delta }_i(r),$$

(2)

where

${\delta }_i(r)=\{\begin{array}{l}1\hspace{1em}\left(r\in {\mathrm{\Omega }}_i\right)\\ 0\hspace{1em}\left(r\notin {\mathrm{\Omega }}_i\right)\end{array}$ and

${\mathrm{\Omega }}_i$: sub-region i.

However, there are tens of thousands of energy points and it is time consuming to solve Equation (2) for every energy points. The computation time can be saved if the number of solution calculation of Equation (2) is reduced. Because the only input parameter of Equation (2) is the total cross-section (XS), $P_{ij}^{iso}$ is a function of fuel region total XS, ${\Sigma }_{t,F}^{}$ and it can be tabulated by solving Equation (2) for hundreds of ${\Sigma }_{t,F}^{}$ values using method of characteristics (MOC). The CP table for an isolated fuel pin can be tabulated as a function of ${\Sigma }_{t,F}^{}$ as follow:

$$P_{ij}^{iso}\left({\Sigma }_{t,F}^k\right)=\frac{{\Sigma }_{t,F}^k{\varphi }_j\left({\Sigma }_{t,F}^k\right)V_j}{V_i},$$

(3)

where ${\varphi }_j\left({\Sigma }_{t,F}^k\right)$ is the flux at the sub-region j with the k-th level total cross-section of the fuel region, ${\Sigma }_{t,F}^k$, in the isolated fuel pin problem.

The shadowing effect correction factor of the fuel region ${\eta }_F$ is defined as the ratio between the fuel escape probability in a lattice problem and the fuel escape probability in an isolated pin problem as shown in Equation (4).

$${\eta }_F\left(u\right)=\frac{P_{e,F}^{}\left(u\right)}{P_{e,F}^{iso}\left(u\right)},$$

(4)

where

$P_{e,F}^{}\left(u\right)$: fuel escape probability in a lattice problem and

$P_{e,F}^{iso}\left(u\right)$: fuel escape probability in an isolated pin problem.

The fuel escape probabilities for the two systems can be calculated from the Carlvik’s two-term rational approximation [16] with Dancoff factor. The Dancoff factor is obtained by solving the fixed source problem for the lattice problem using MOC, applying the enhanced neutron current method [17].

With the assumption that the ratio of $P_{ij}^{}$ and $P_{ij}^{iso}$ can be approximated as shown in Equation (5), $P_{ij}^{}$ is expressed in terms of the ${\eta }_F$ and $P_{ij}^{iso}$ as shown in Equation (6).

$$\frac{P_{ij}^{}}{P_{ij}^{iso}}\approx \frac{{\displaystyle \sum _{j\in F}{P}_{ij}^{}}}{{\displaystyle \sum _{j\in F}{P}_{ij}^{iso}}} \mathrm{and}$$

(5)

$$P_{ij}^{}\left(u\right)\approx P_{ij}^{iso}\left(u\right)\frac{1-P_{e,i}^{}\left(u\right)}{{\displaystyle \sum _{j\in F}{P}_{ij}^{iso}\left(u\right)}}\approx P_{ij}^{iso}\left(u\right)\frac{1-{\eta }_F\left(u\right)\left(1-{\displaystyle \sum _{j\in F}{P}_{ij}^{iso}\left(u\right)}\right)}{{\displaystyle \sum _{j\in F}{P}_{ij}^{iso}\left(u\right)}},$$

(6)

where the following relationships are used:

$${\displaystyle \sum _{j\in F}{P}_{ij}^{}\left(u\right)}=1-P_{e,i}^{}\left(u\right),$$

(7)

$$P_{e,i}^{}(u)\approx {\eta }_F(u)P_{e,i}^{iso}(u), \mathrm{and}$$

(8)

$$P_{e,i}^{iso}\left(u\right)=1-{\displaystyle \sum _{j\in F}{P}_{ij}^{iso}\left(u\right)}.$$

(9)

The CP table for an isolated fuel pin, $P_{ij}^{iso}\left(u\right)$, is evaluated as follow using the tabulated function as prepared in Equation (3):

$$P_{ij}^{iso}\left(u\right)\approx P_{ij}^{iso}\left({\Sigma }_{t,i}\left(u\right)\right).$$

(10)

Finally, the flux at an energy point of the slowing down equation, Equation (1), can be calculated with the CPs. Additionally, the effective multi-group cross-section for a resonance energy region can be simply obtained by the energy condensation as follow:

$${\sigma }_{x,i,g}^{}=\frac{{\displaystyle {\int }_{\Delta u_g}{\sigma }_{x,i}^{}{\varphi }_i(u)du}}{{\displaystyle {\int }_{\Delta u_g}{\varphi }_i(u)du}},$$

(11)

where $\Delta u_g$ is the lethargy width for an energy group g.

Detailed derivation and further information on the PSM can be found in the reference [10].

2.2. Pointwise Energy Slowing down Method for a DH Region

For a lattice problem with double heterogeneous compacts, it is necessary to obtain the pointwise homogenized cross-sections for the compact prior to the resonance treatment by the PSM. Figure 1 shows the new spherical unit cell model proposed in this work. The spherical unit cell consists of an explicit TRISO, a matrix layer, and a moderator in the outermost layer. The moderator layer is to reflect the effect of the moderator in the pin cell. It is noted that one uniform XS region including the DH region in MOC calculation has one corresponding spherical unit cell. Thus, the homogenized compact can consider the effect of the radial particle distribution.

The radii of the TRISO layers are given in the problem and the radius of the graphite matrix layer can be easily determined as follows:

$$R_m=\frac{R_T}{\sqrt[3]{F}},$$

(12)

where $F$ is the packing fraction of the TRISO particles in the compact and $R_T$ is the radius of the TRISO.

For determining the radius of the moderator layer in the unit cell, the volume of the moderator for a specific pin cell of the lattice problem can be analytically derived from the Dancoff factor and the average chord length of the moderator region. Generally, they have the following relation [4]:

$$1-D=\frac{\exp (-{\Sigma }_{t,M}\widehat{l})}{{\Sigma }_{t,M}\cdot (\overline{l}-\widehat{l})+1},$$

(13)

where D is Dancoff factor and $\overline{l}$ is the mean chord length of the moderator region. $\widehat{l}$ is the minimum distance between two compacts and ${\Sigma }_{t,M}$ is the total cross-section in the moderator. The Dancoff factor is calculated during the process of the PSM as described in Section 2.1. After replacing the mean chord length $\overline{l}$ in Equation (10) with $\frac{4V_M}{2\pi (R_p+R_c)H}$, the moderator volume for a pin cell of the lattice problem can be determined as follows:

$$V_M=\frac{\pi (R_p+R_c)H}{2}\left\{\left[\frac{\exp (-{\Sigma }_{t,M}\widehat{l})}{1-D}-1\right]\frac{1}{{\Sigma }_{t,M}}+\widehat{l}\right\},$$

(14)

where $R_c$, $R_p$, and $H$ are the radius of the compact, effective radius of the pin, and the height of the compact, respectively. Assuming that the moderator equally affects all TRISO particles in the compact, the outer radius of the moderator layer can be derived as follows:

$$R_M=\sqrt[3]{\frac{3}{4\pi N_T}\left(\pi R_c^{2}H+V_M\right)},$$

(15)

where $N_T$ is the number of the TRISO particles in a fuel compact.

The pointwise energy slowing down equation for the spherical unit cell is as follow:

$${\Sigma }_{t,l}(u){\varphi }_l(u)V_l={\displaystyle \sum _{k=1}^L{P}_{k,l}(u)V_k{Q}_{s,k}}(u),$$

(16)

where

$l$, $k$: layer indices,

$L$: total number of layers in a unit cell, and

$Q_{s,k}$: scattering source in layer $k$.

The collision probability for the layer of the unit cell, $P_{k,l}^{}$, can be straightforwardly calculated by applying Kavenoky technique [18] which is widely used for CPs of a spherical geometry. Note that the CPs should be calculated with the white boundary condition for the unit cell. Equation (16) can be rewritten using the reciprocity relation as follow:

$${\varphi }_l(u)=\frac{{\displaystyle \sum _k{Q}_{s,k}(u)\frac{P_{l,k}(u)V_l{\Sigma }_{t,l}(u)}{{\Sigma }_{t,k}(u)}}}{{\Sigma }_{t,l}(u)V_l}={\displaystyle \sum _k{Q}_{s,k}(u)\frac{P_{l,k}(u)}{{\Sigma }_{t,k}(u)}}.$$

(17)

After obtaining the pointwise energy flux for all layers from Equation (17), the pointwise homogenized cross-sections for the compact can be generated. The pointwise homogenized microscopic cross-section for a nuclide in the compact region can be obtained by the spatial homogenization as follows:

$${\sigma }_{x,c}^n(u)=\frac{{\displaystyle \sum _{k\in c}{N}_k^n{\sigma }_{x,k}^{}(u){\varphi }_k(u)V_k}}{{\displaystyle \sum _{k\in c}{N}_k^n{\varphi }_k(u)V_k}},$$

(18)

where $c$ represents the compact region which consists of the TRISO and matrix layer and $N_k^n$ is the number density of nuclide $n$ in layer $k$.

In the second step, the pointwise energy slowing down equation, Equation (1), for the homogenized fuel compact and moderator region can be readily solved by the original PSM.

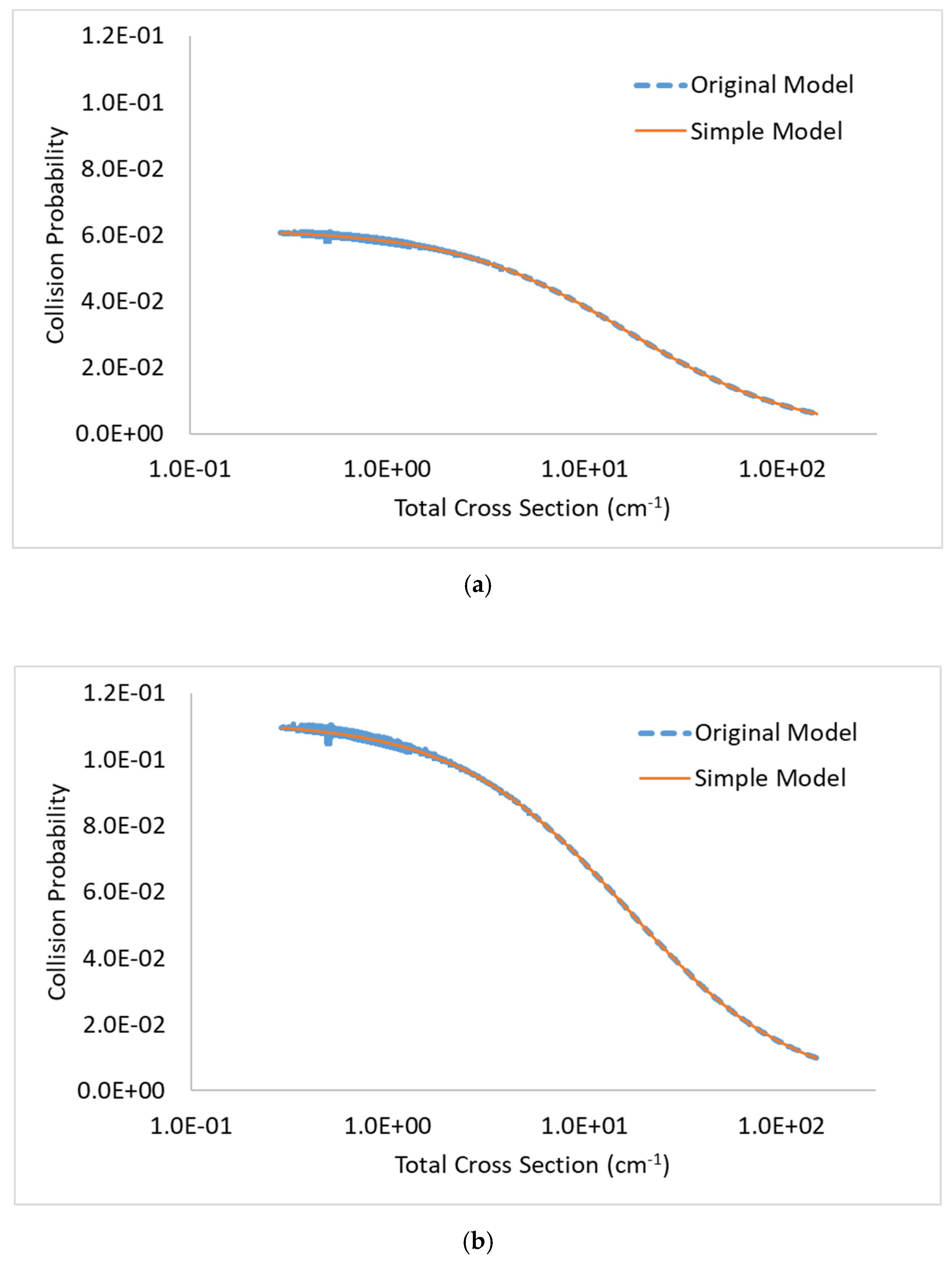
2.3. Improvement of Calculation Speed for Collision Probability of Spherical Unit Cell

In Equation (16), $P_{k,l}^{}$ should be obtained for all fuel compacts and all energy points at every burnup points in depletion calculation, which is a heavy computational burden. However, the computation time for the CP can be considerably cut down by applying the idea from the table of a CP used in the PSM.

In generating the CP table for the spherical unit cell by Kavenoky technique, it is assumed that the total cross-sections of all the layers except the fuel layer are constant in the resonance energy range and the CPs depend only on the total cross-section of the fuel kernel. Based on this assumption, the CPs are tabulated as a function of the total cross-section of the fuel kernel. This simplification can be justified by the comparison between the CPs of the original model and the simple model with the assumption. Figure 2 compares the CPs from the two models. The reference values are the CPs from the original model and were calculated with the total cross-sections for each their layer at the resonance energy region. On the contrary, the CPs from the simple model were calculated with the total cross-section of the fuel kernel at the energy point and the constant cross-sections for the other layers. The constant values for the layers were simply determined at the middle point of the resonance energy range. Except the very small oscillation in the low energy region, they are in a very good agreement. Actually, it was confirmed that the multiplication factors for pin problems obtained from two models are nearly the same.

In this work, the CPs from a layer to a layer for the spherical unit cell were calculated using Kavenoky technique for wide range of total cross-sections with 500 levels from 10⁻² to 10⁴ cm⁻¹ and were tabulated as a function of the total cross-section of the fuel kernel. In a practical problem, the CP table for the specific spherical unit cell is prepared only once prior to the resonance treatment, regardless of a pin position inside a fuel block. Therefore, this technique can significantly reduce the computation time by determining the CPs for all spherical unit cells in the whole problem domain using the linear interpolation from the CP table as below in place of Kavenoky technique:

$$P_{k,l}^{}=P_{k,l}^{table}\left({\Sigma }_{t,F}^{}\left(u\right)\right),$$

(19)

where ${\Sigma }_{t,F}^{}\left(u\right)$ is the total cross-section of the fuel layer at an energy point.

2.4. Reconstruction of Nuclide Number Densities for Depletion Calculation in a DH Region

In order to perform depletion analysis using the PSM-DH, a nuclide reconstruction process is needed for the pointwise unit cell slowing down calculation at the next burnup step. After a transport calculation using MOC, a depletion calculation for nuclide number densities at the next burnup step is performed for the homogenized compact region. The updated nuclide number densities for the homogenized compact can be simply converted to those for the fuel kernel using the reverse process of the homogenization. Afterward, the pointwise slowing down calculation for the double heterogeneous compact at the new burnup step can be performed using PSM-DH.

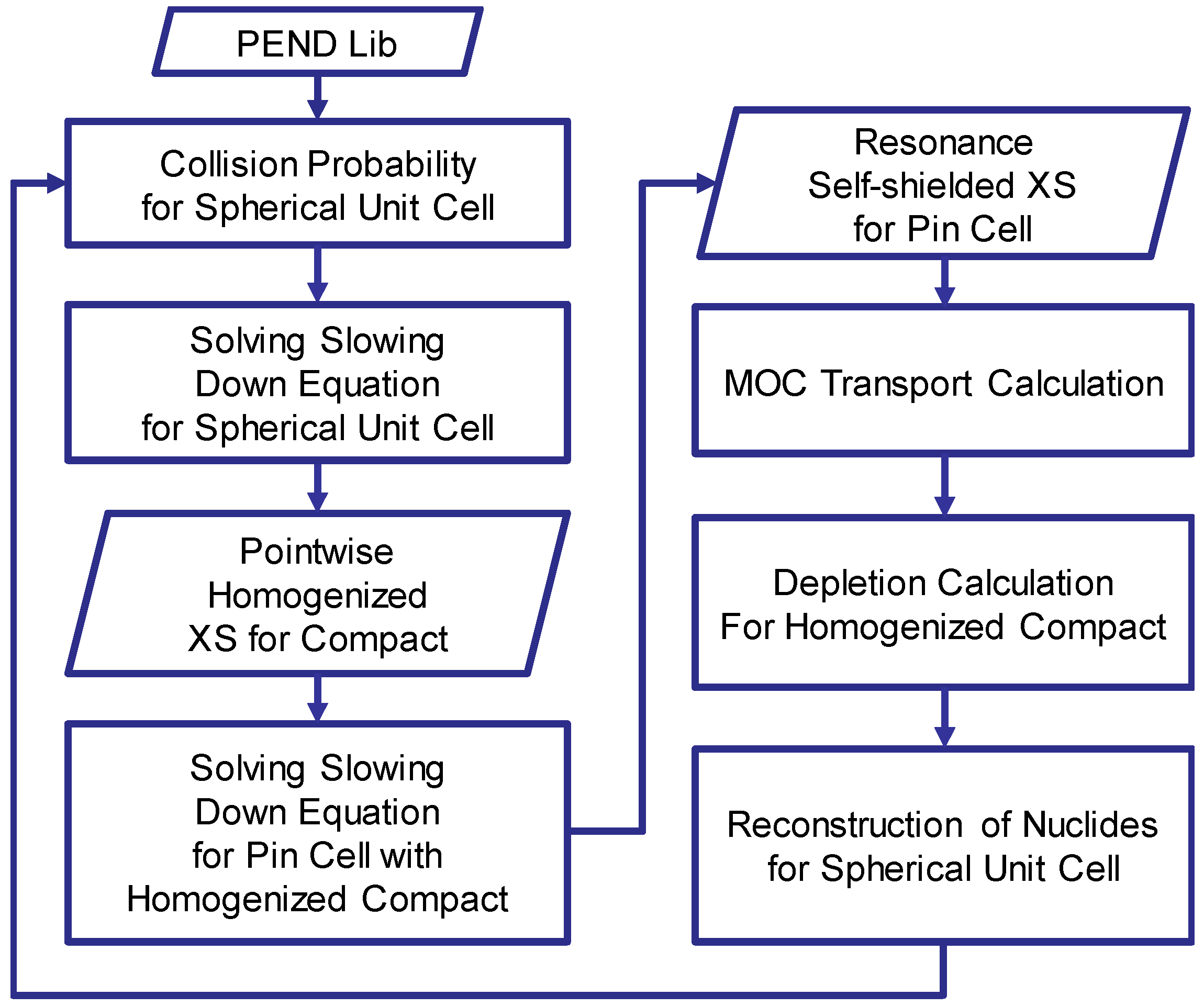
2.5. Calculation Procedure of DeCART with PSM-DH

Figure 3 shows the calculation procedure of the DeCART with PSM-DH. First, the collision probabilities for all layers of the spherical unit cell are calculated from the CP table which is priory generated using Kavenoky technique. After solving the pointwise slowing down equation for the spherical unit cell, the pointwise flux for all layers can be obtained and the pointwise homogenized cross-sections for the compact can be generated. The self-shielded multi-group cross-sections for the homogenized compact region can be then determined by applying the PSM. Finally, DeCART uses the cross-sections for a transport calculation in a DH region. In a depletion calculation, nuclide number densities of the fuel kernel of the spherical unit cell at the new burnup step should be reconstructed from the homogenized compact.

3. Numerical Results

For verifying the performance of the PSM-DH, the resonance treatment and transport calculations for various HTGR problems with DH regions based on MHTGR-350 [19] were performed and the results were compared with the reference values by McCARD [20] with ENDF/B-VII.1 library. DeCART used the multi-group cross-section based on ENDF/B-VII.1 for the fast and thermal energy range, which was processed by GROUPR of NJOY [21]. For the resonance energy groups, the PSM-DH module integrated in DeCART directly reads point-wise cross-sections processed by BROADR of NJOY and generates the self-shielded cross-sections. DeCART used the ray space of 0.02 cm, the number of polar angles of 4, and the number of azimuthal angles of 8 for the MOC calculation option.

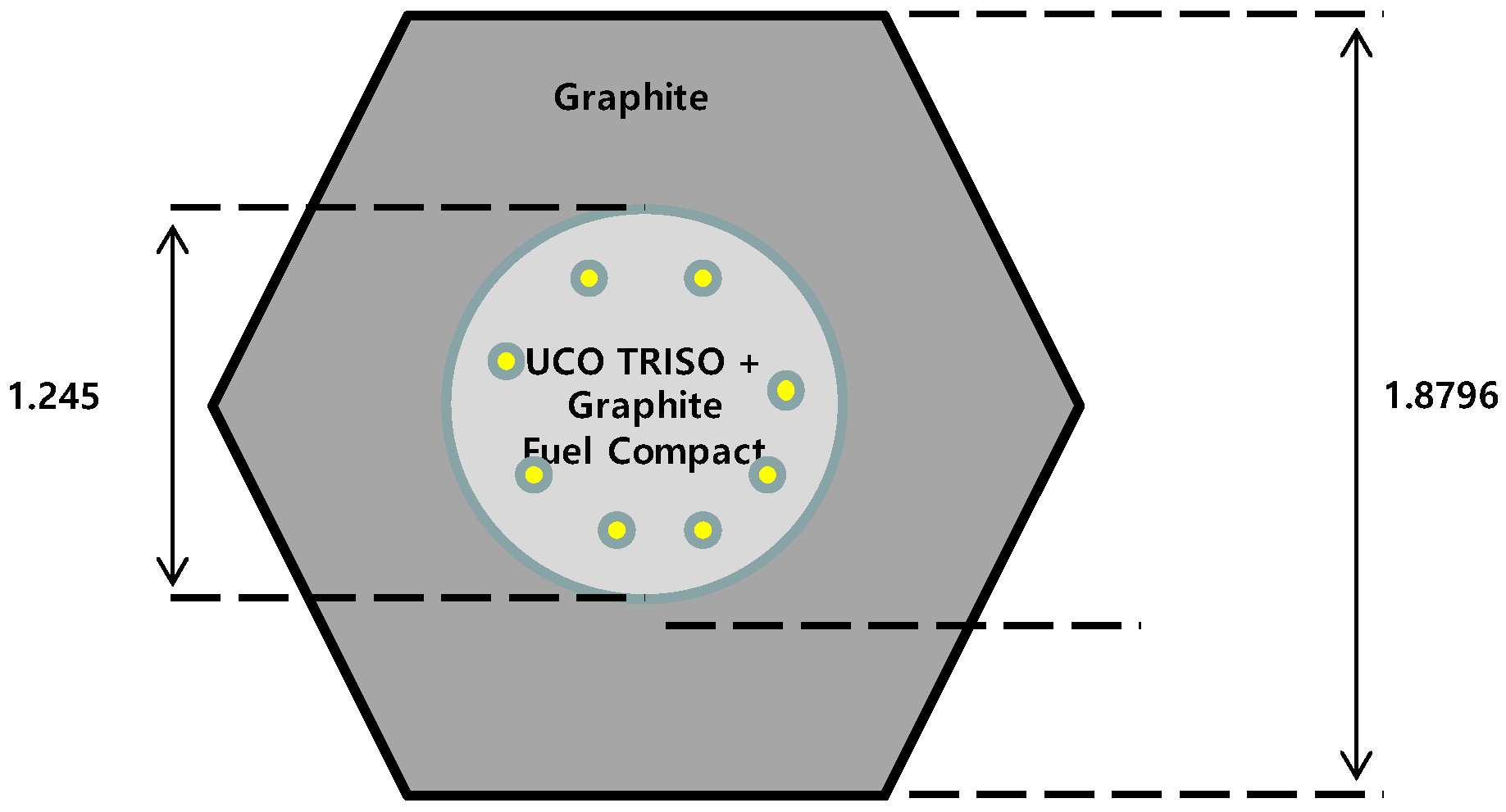
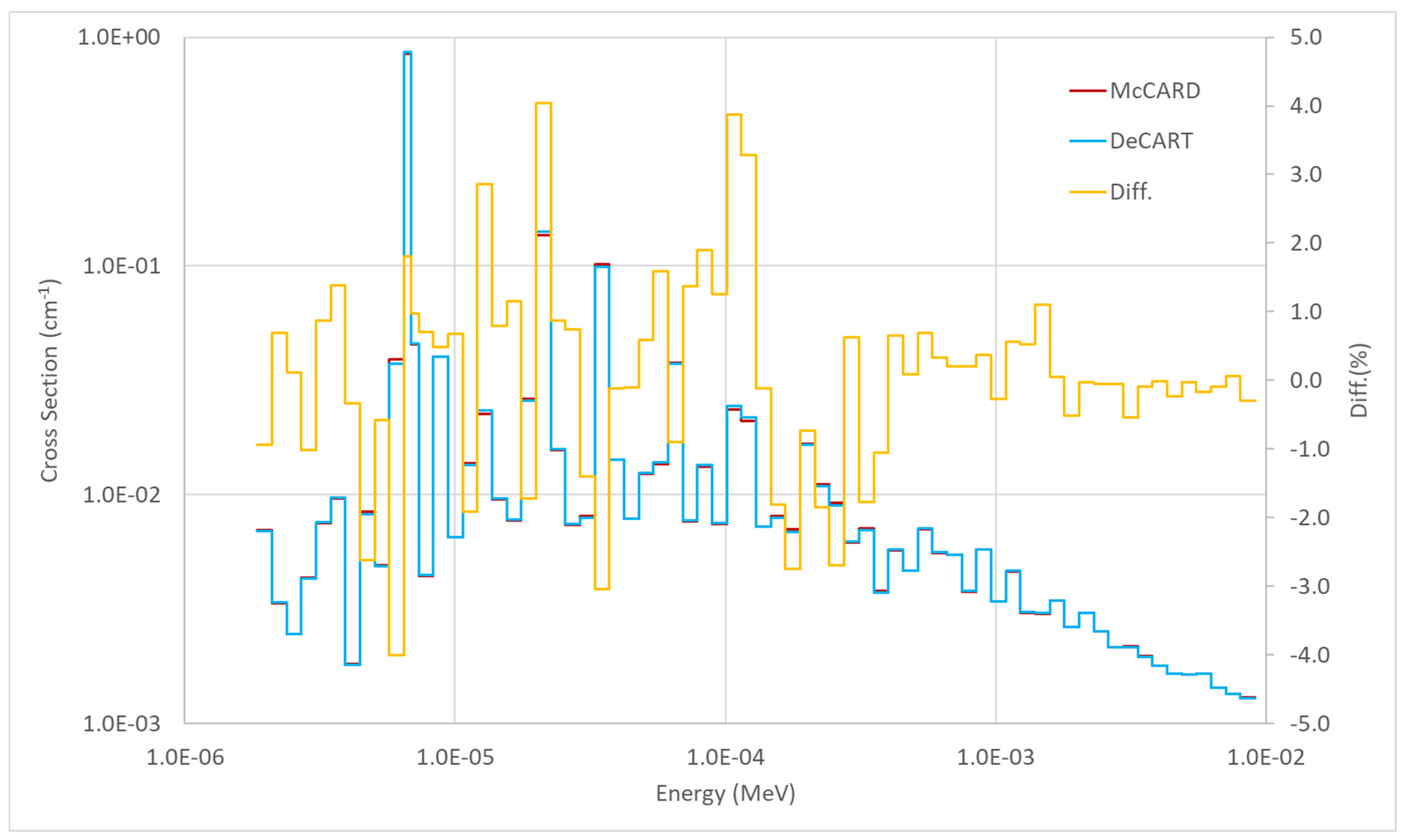
3.1. MHTGR-350 Benchmark Problems

Figure 4 shows the configuration of the DH fuel pin used in the verification calculation and

Table 1. Number density for the MHTGR pin problem.

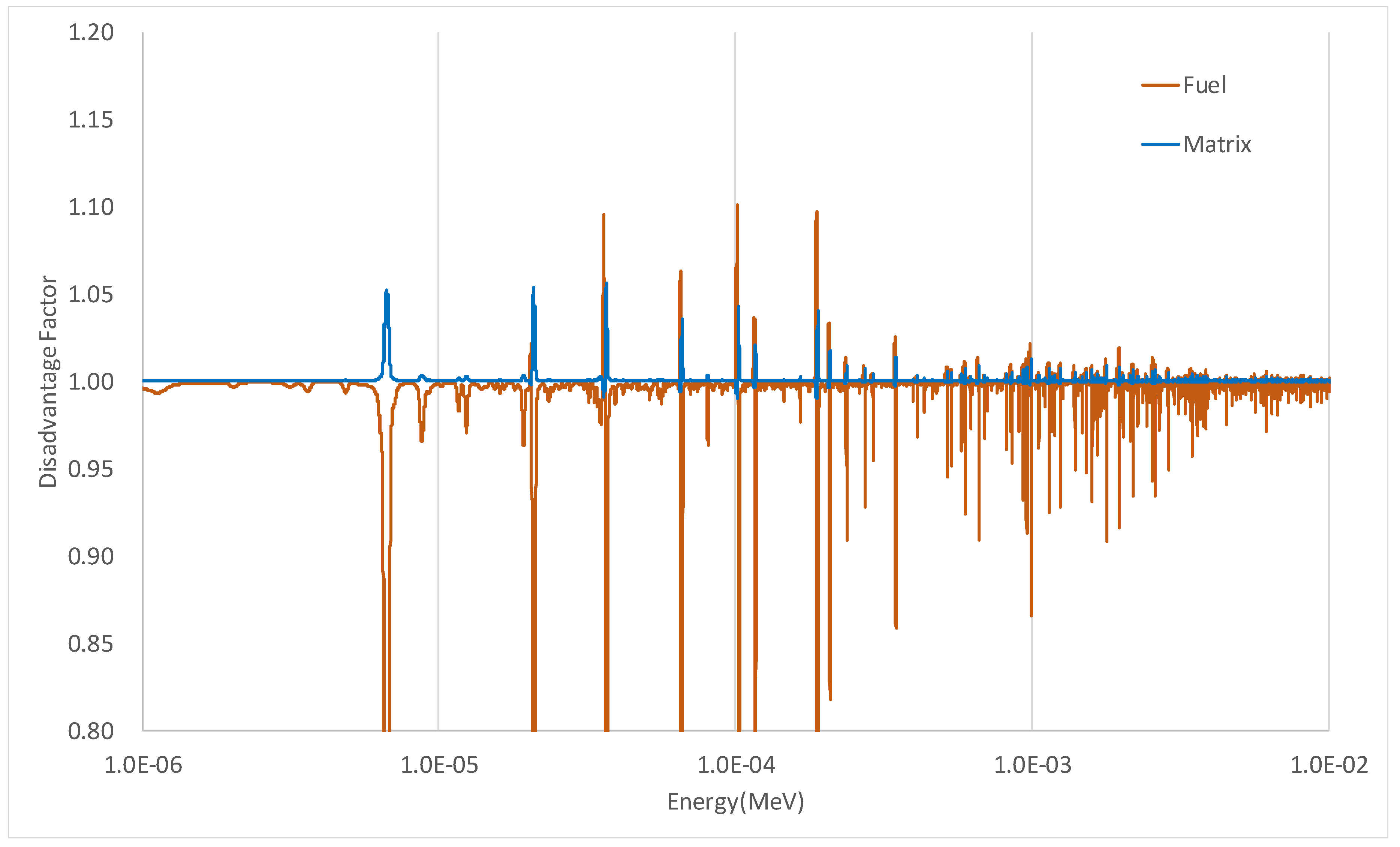
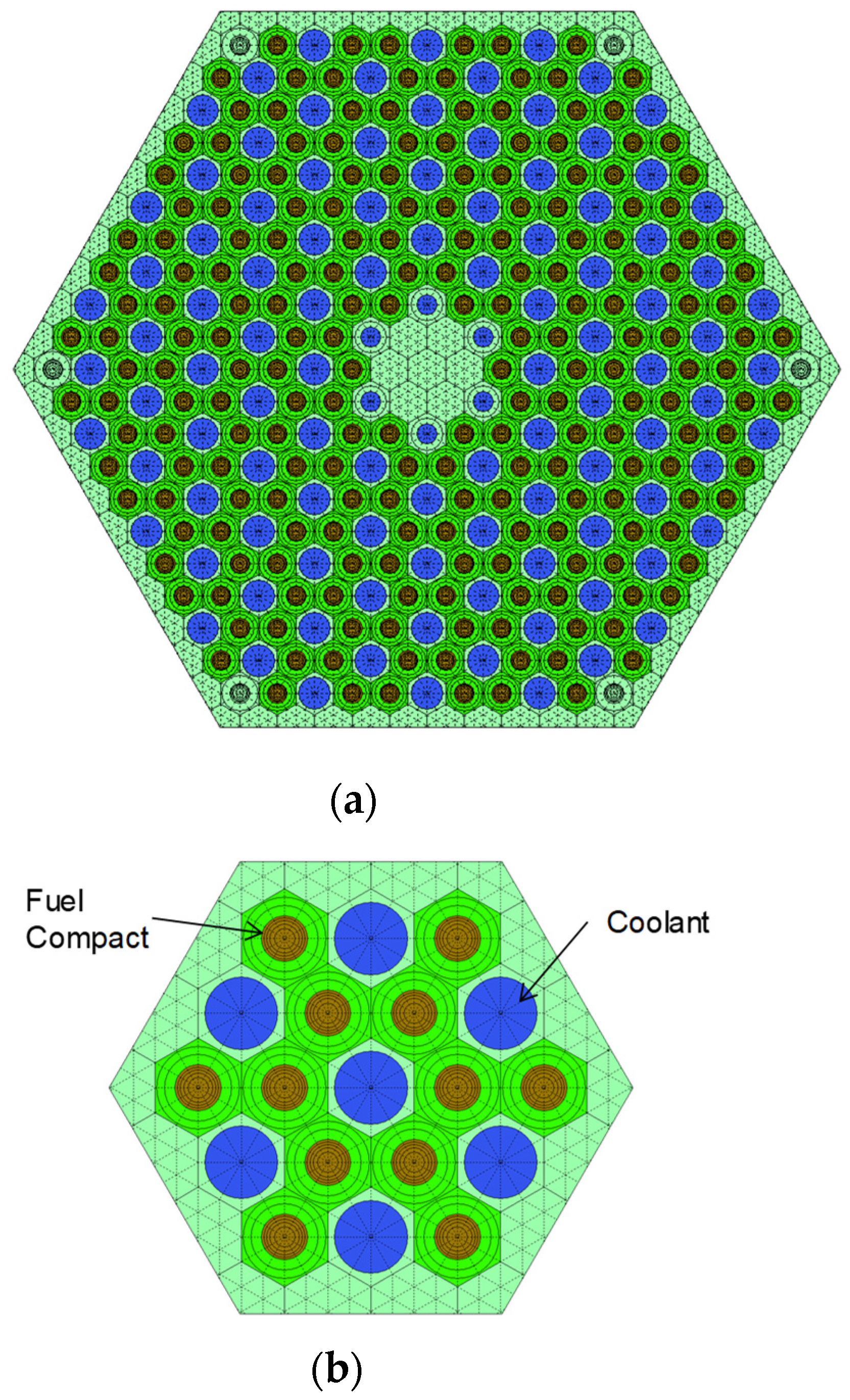
Material		Nuclide	Number Density (#/barn-cm)
TRISO Fuel Particle	Kernel	U-235	3.70 × 10−3
		U-238	1.99 × 10−2
		O-16	3.55 × 10−2
		Graphite	1.18 × 10−2
	Porous Carbon	Graphite	5.02 × 10−2
	IPyC	Graphite	9.53 × 10−2
	SiC	Si-28	4.43 × 10−2
		Si-29	2.25 × 10−3
		Si-30	1.49 × 10−3
		Graphite	4.81 × 10−2
	OPyC	Graphite	9.53 × 10−2
Compact Matrix		Graphite	8.27 × 10−2
Block Graphite		Graphite	9.28 × 10−2

lists nuclide number densities of the materials. The pin problem is taken from the OECD/NEA MHTGR-350 benchmark exercise III [19].

Table 2. k_inf and DH effect of MHTGR pin problems with various PFs at 300 K.

Packing Fraction	TEMP = 300 K
	Multiplication Factor			Double Het. Effect
	McCARD(M) (σ ≈ 14 pcm)	DeCART(D) with PSM-DH	Diff.(D-M) (pcm)	McCARD(M) (pcm)	DeCART(D) with PSM-DH (pcm)	Diff.(D-M) (pcm)
10%	1.67515	1.67490	−25	3687	3704	17
15%	1.59333	1.59231	−102	3794	3794	0
20%	1.52335	1.52155	−180	3727	3685	−42
25%	1.46397	1.46208	−189	3537	3502	−35
30%	1.41348	1.41198	−150	3297	3297	0
35%	1.37090	1.36950	−140	3084	3091	8
40%	1.33370	1.33324	−46	2839	2895	55

,

Table 3. k_inf and DH effect of MHTGR pin problems with various PFs at 600 K.

Packing Fraction	TEMP = 600 K
	Multiplication Factor			Double Het. Effect
	McCARD(M) (σ ≈ 14 pcm)	DeCART(D) with PSM-DH	Diff.(D-M) (pcm)	McCARD(M) (pcm)	DeCART(D) with PSM-DH (pcm)	Diff.(D-M) (pcm)
10%	1.63835	1.63843	8	4066	4021	−45
15%	1.55027	1.54939	−88	4310	4231	−79
20%	1.47587	1.47463	−124	4256	4165	−90
25%	1.41441	1.41284	−157	4093	3978	−115
30%	1.36300	1.36150	−150	3874	3741	−133
35%	1.31897	1.31854	−43	3577	3488	−89
40%	1.28143	1.28231	88	3259	3235	−24

,

Table 4. k_inf and DH effect of MHTGR pin problems with various PFs at 900 K.

Packing Fraction	TEMP = 900 K
	Multiplication Factor			Double Het. Effect
	McCARD(M) (σ ≈ 14 pcm)	DeCART(D) with PSM-DH	Diff.(D-M) (pcm)	McCARD(M) (pcm)	DeCART(D) with PSM-DH (pcm)	Diff.(D-M) (pcm)
10%	1.60965	1.61059	94	4244	4189	−55
15%	1.51790	1.51730	−60	4622	4508	−114
20%	1.44131	1.43984	−147	4634	4504	−130
25%	1.37792	1.37643	−149	4463	4343	−120
30%	1.32624	1.32421	−203	4256	4110	−146
35%	1.28159	1.28088	−71	3887	3846	−41
40%	1.24432	1.24464	32	3546	3575	28

and

Table 5. k_inf and DH effect of MHTGR pin problems with various PFs at 1100 K.

Packing Fraction	TEMP = 1100 K
	Multiplication Factor			Double Het. Effect
	McCARD(M) (σ ≈ 14 pcm)	DeCART(D) with PSM-DH	Diff.(D-M) (pcm)	McCARD(M) (pcm)	DeCART(D) with PSM-DH (pcm)	Diff.(D-M) (pcm)
10%	1.59459	1.59604	145	4351	4304	−47
15%	1.50021	1.50045	24	4755	4708	−47
20%	1.42191	1.42157	−35	4818	4761	−57
25%	1.35817	1.35729	−88	4668	4637	−31
30%	1.30582	1.30466	−116	4462	4431	−31
35%	1.26244	1.26117	−127	4188	4185	−4
40%	1.22552	1.22497	−55	3876	3926	50

compare the multiplication factors and the DH effect by McCARD and DeCART with PSM-DH for various packing fractions (PF) at 300 K, 600 K, 900 K, and 1100 K, respectively. The DH effect is defined with the multiplication factors of the homogeneous and double heterogeneous compact as follow:

$$f_{DH}=\frac{1}{k_{HOM}}-\frac{1}{k_{DH}},$$

(20)

The differences of the k_inf in all cases are within 203 pcm and those of the double heterogeneous effect are within 146 pcm. McCARD uses the JT algorithm [22] for the random distribution of the TRISO particles and the random distribution of the TRISO particle causes additional statistical uncertainty in multiplication factor over 100 pcm. Additionally, it is known that the PSM has error of about 100 pcm [10]. Besides that, there is another error cause. The PSM-DH can consider the DH effect only for the resonance energy range. However, it was found that the error caused by the spatial self-shielding effect of DH in the thermal energy range and fast energy range is about 30 pcm in the problem. Hence, considering the statistical uncertainty caused by the random distribution in the McCARD and the inherent error of the PSM, it is clear that they are in good agreement.

Figure 5 compares the multi-group absorption cross-sections in the resonance energy range for the homogenized compact with a packing fraction of 35% at 1100 K. There are differences of the maximum 4% between those by the two codes. Figure 6 shows the disadvantage factors of the fuel kernel and the matrix calculated by PSM-DH method.

Additionally, for verifying the accuracy of the proposed method for the moderation effect inside a fuel block, two fuel block problems with different size were examined. They are a normal size fuel block with 210 fuel pins and a small size fuel block with 12 fuel pins which have the same configuration with the pin problem as shown in Figure 4 and Table 1. Figure 7 shows the configuration of the two problems.

Table 6. k_inf of MHTGR single block.

Packing Fraction	TEMP = 1100 K
	McCARD(M) (σ ≈ 14 pcm)	DeCART(D) with PSM-DH	Diff.(D-M) (pcm)
15%	1.59923	1.59960	37
25%	1.48566	1.48523	−43
35%	1.40028	1.39935	−93

and

Table 7. k_inf of small size block.

Packing Fraction	TEMP = 1100 K
	McCARD(M) (σ ≈ 14 pcm)	DeCART(D) with PSM-DH	Diff.(D-M) (pcm)
15%	1.65946	1.66040	94
25%	1.57386	1.57407	21
35%	1.50224	1.50195	−29

compare the results for the problems. They reveal that the differences of all cases are under 100 pcm. In the small size block, it is noted that there is a rapid change of the moderation effect between the outer fuel pin and the inner fuel pin due to the outmost moderator region. Nevertheless, the code produced the accurate results in the small size block.

Table 8. Burnup calculation results for MHTGR pin problem.

Burnup (Days)	TEMP = 1200 K, PF = 35%
	McCARD(M) (σ ≈ 14 pcm)	DeCART(D) with PSM-DH	Diff.(D-M) (pcm)
0.00	1.25293	1.25215	−78
50.00	1.20219	1.20136	−83
100.00	1.18029	1.17974	−56
150.00	1.15836	1.15828	−8
200.00	1.13718	1.13711	−7
250.00	1.11675	1.11670	−5
300.00	1.09726	1.09733	7
350.00	1.07902	1.07912	10
400.00	1.06180	1.06211	31
450.00	1.04615	1.04626	11
500.00	1.03140	1.03149	8
562.50	1.01411	1.01440	28
625.00	0.99865	0.99871	6
687.50	0.98421	0.98426	5
750.00	0.97105	0.97092	−13
812.50	0.95877	0.95854	−23
875.00	0.94677	0.94700	23
937.50	0.93577	0.93621	44
1000.00	0.92589	0.92607	18
1062.50	0.91629	0.91653	24
1125.00	0.90707	0.90750	43
1187.50	0.89824	0.89894	70
1250.00	0.89035	0.89080	45
1312.50	0.88257	0.88304	47
1375.00	0.87460	0.87563	103
1437.50	0.86740	0.86853	113
1500.00	0.86071	0.86173	102

shows the burnup calculation results for the MHTGR pin problem. It was calculated under the condition of the hot full power for the DH pin with the packing fraction of 35% and the burnup at the 1500 effective full power day is about 98 GWD/MTU. The result shows that the differences between the two codes are within ±120 pcm. It can be seen that the PSM-DH/DeCART also has a good performance in the depletion calculation.

3.2. Large Size Compact and Various Size TRISO Problems

Table 9. k_inf of pin problems with large size compact and pitch.

Half Pitch Size	Compact Radius	Multiplication Factor (PF = 35%)
		TEMP = 300 K			TEMP = 1100 K
		McCARD(M) (σ ≈ 12 pcm)	DeCART(D) with PSM-DH	Diff.(D-M) (pcm)	McCARD(M) (σ ≈ 12 pcm)	DeCART(D) with PSM-DH	Diff.(D-M) (pcm)
2.0	0.8	1.68542	1.68352	−190	1.61091	1.61089	−2
2.0	1.0	1.58182	1.57932	−250	1.49405	1.49323	−82
2.0	1.5	1.30827	1.30644	−183	1.20270	1.20094	−176
2.0	1.8	1.17886	1.17840	−46	1.07542	1.07315	−227

shows the results for the pin problems with very large size compact. The half pitch size and the PF of the pin are fixed by 2.0 cm and 35%, respectively. The material compositions are the same with those of the previous problems. Considering the compact radius of the MHTGR-350 pin, 0.6225 cm, it is noted that they can cover large compact problem. The results reveal that the discrepancy between two codes are within 250 pcm and they are similar to the previous comparisons.

Table 10. k_inf of pin problems with various fuel kernel size.

TRISO Radius	Fuel Kernel Radius	Multiplication Factor (PF = 35%)
		TEMP = 300 K			TEMP = 1100 K
		McCARD(M) (σ ≈ 18 pcm)	DeCART(D) with PSM-DH	Diff.(D-M) (pcm)	McCARD(M) (σ ≈ 18 pcm)	DeCART(D) with PSM-DH	Diff.(D-M) (pcm)
0.0385	0.0175	1.43830	1.43758	−72	1.33052	1.33075	23
0.0410	0.0200	1.39114	1.39032	−82	1.28218	1.28208	−10
0.0460	0.0250	1.31868	1.31744	−124	1.21207	1.21103	−104
0.0485	0.0275	1.29118	1.28986	−132	1.18695	1.18545	−150

shows the results for the pin problems with various fuel kernel and TRISO radius. The compact radius was fixed by 0.6225 cm. In all cases, the results by two codes are similar within 150 pcm. It is clear that they are in a good agreement considering the statistical uncertainty by the random distribution of the particles.

3.3. Computational Efficiency for PSM-DH

Table 11. Calculation time for MHTGR single block problem.

Calculation Module	DeCART with Pre-Generated Library (D) (sec)	DeCART with PSM-DH (P) (sec)	Ratio (P/D)
Resonance Treatment	785.3	477.4	0.61
MOC	1561.3	1196.1	0.77
Total Calculation	2374.7	1699.4	0.72

compares the calculation time in DeCART with the pre-generated library and the PSM-DH for MHTGR single block problem as shown in Figure 5a. Actually, the existing DH treatment method in DeCART is the Sanchez–Pomraning method [23]. It needs much more calculation time than a homogenous case, because it performs the DH treatment for the explicit compact geometry with TRISO and matrix. However, DeCART with PSM-DH treats DH region as a homogeneous region and the calculation time was cut down to 72% compared with that by the existing DH treatment module for the DH problem.

4. Conclusions

In this paper, the extension of the PSM was proposed for performing the resonance treatment of a DH fuel of VHTR and the verification results for various VHTR fuel pins and fuel blocks were presented.

The pointwise homogenized cross-sections for the compact was obtained after solving the slowing down equation for a spherical unit cell composed of an explicit TRISO, a matrix layer, and a moderator layer. The moderator volume was analytically derived using the relation of the Dancoff factor and the mean chord length. Then, the shielded cross-section for the homogenized fuel compact was obtained using the original PSM.

The verification calculations were performed for the fuel pins with various packing fractions, compact sizes, TRISO sizes, and fuel temperatures. Additionally, two fuel block problems with very different sizes were examined and the depletion calculation was carried out for investigating the accuracy of the proposed method. They revealed that the PSM-DH has a good performance.

The PSM-DH has an advantage that problem dependent self-shielded cross-sections can be generated in the lattice calculation step for a VHTR problem. Thus, it is expected that the method could be applied for the development of the various type VHTRs. In the near future, it is planned that an improved model for considering multiple TRISO types in a compact will be examined.