Large Eddy Simulation of Film Cooling with Forward Expansion Hole: Comparative Study with LES and RANS Simulations
Abstract
1. Introduction
2. Geometry and Boundary Conditions
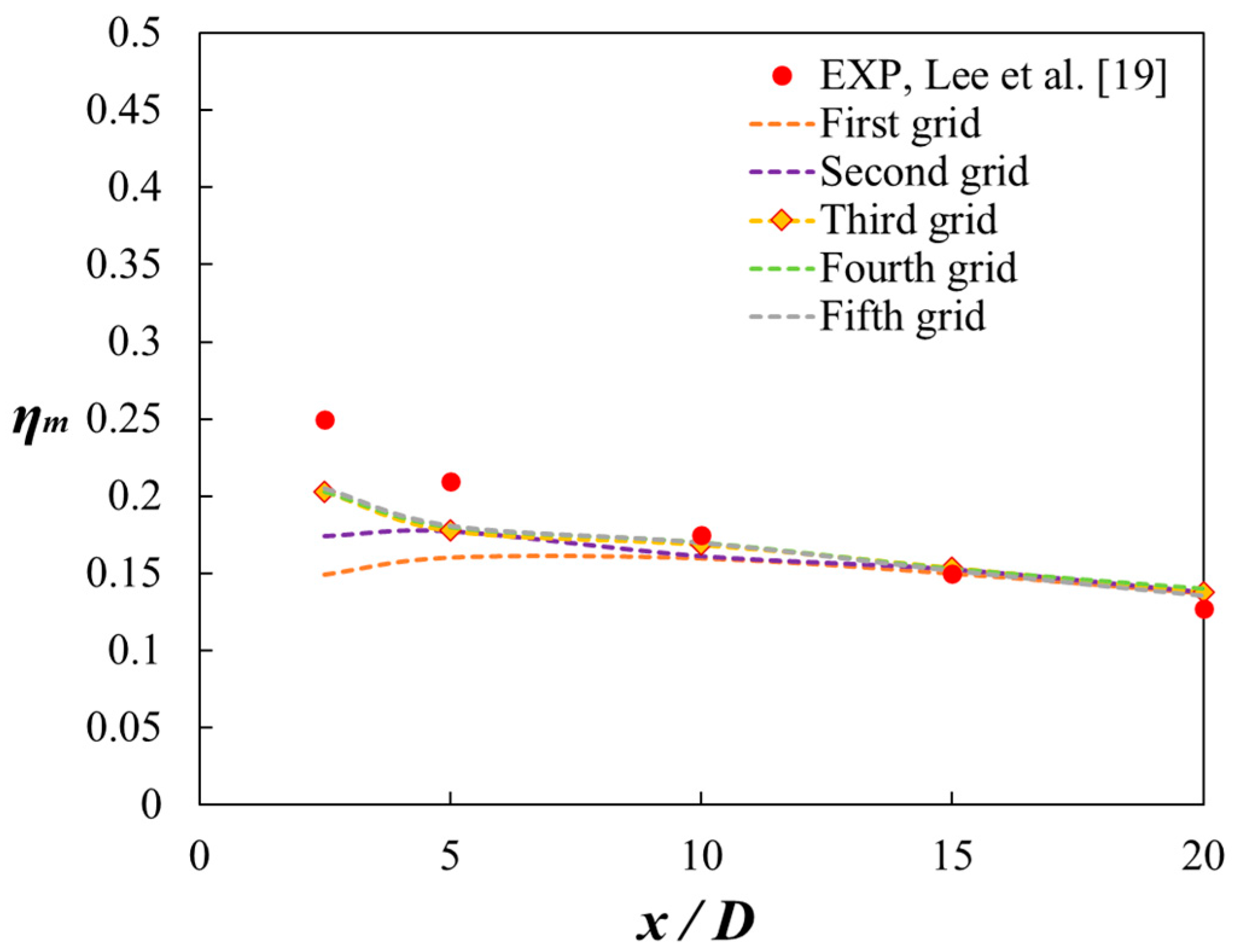
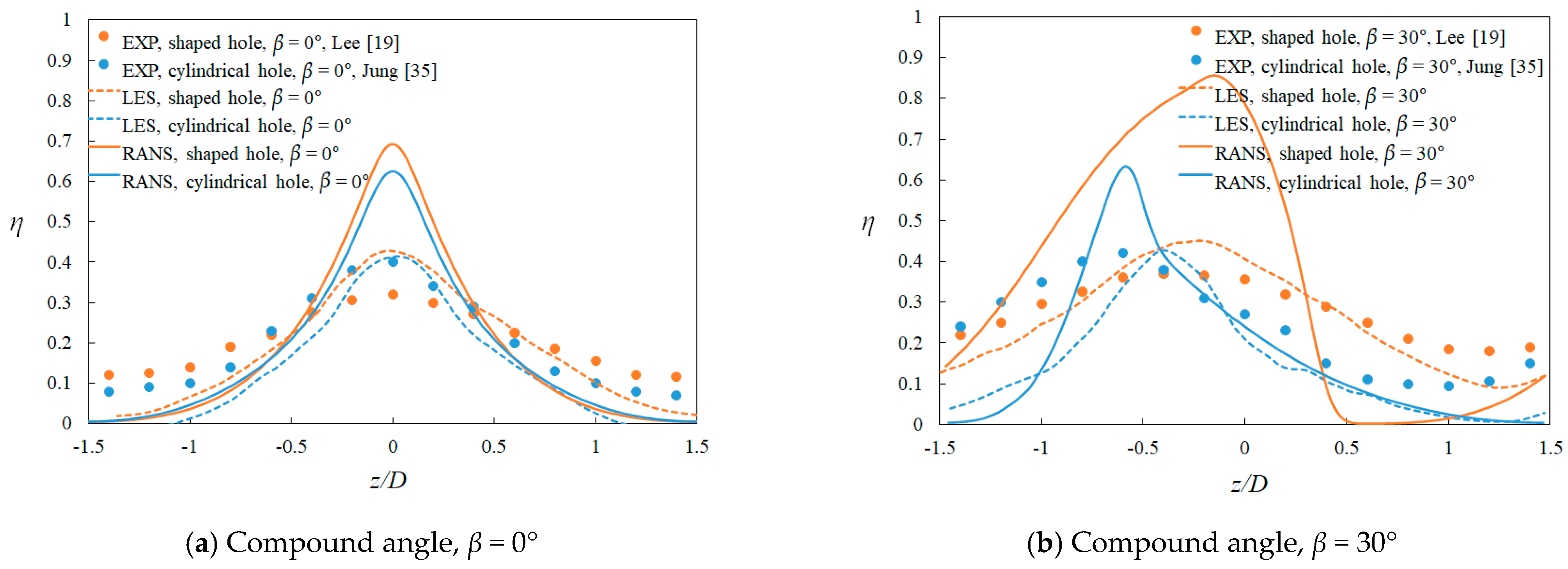
3. Validation of Numerical Methods
4. Results and Discussion
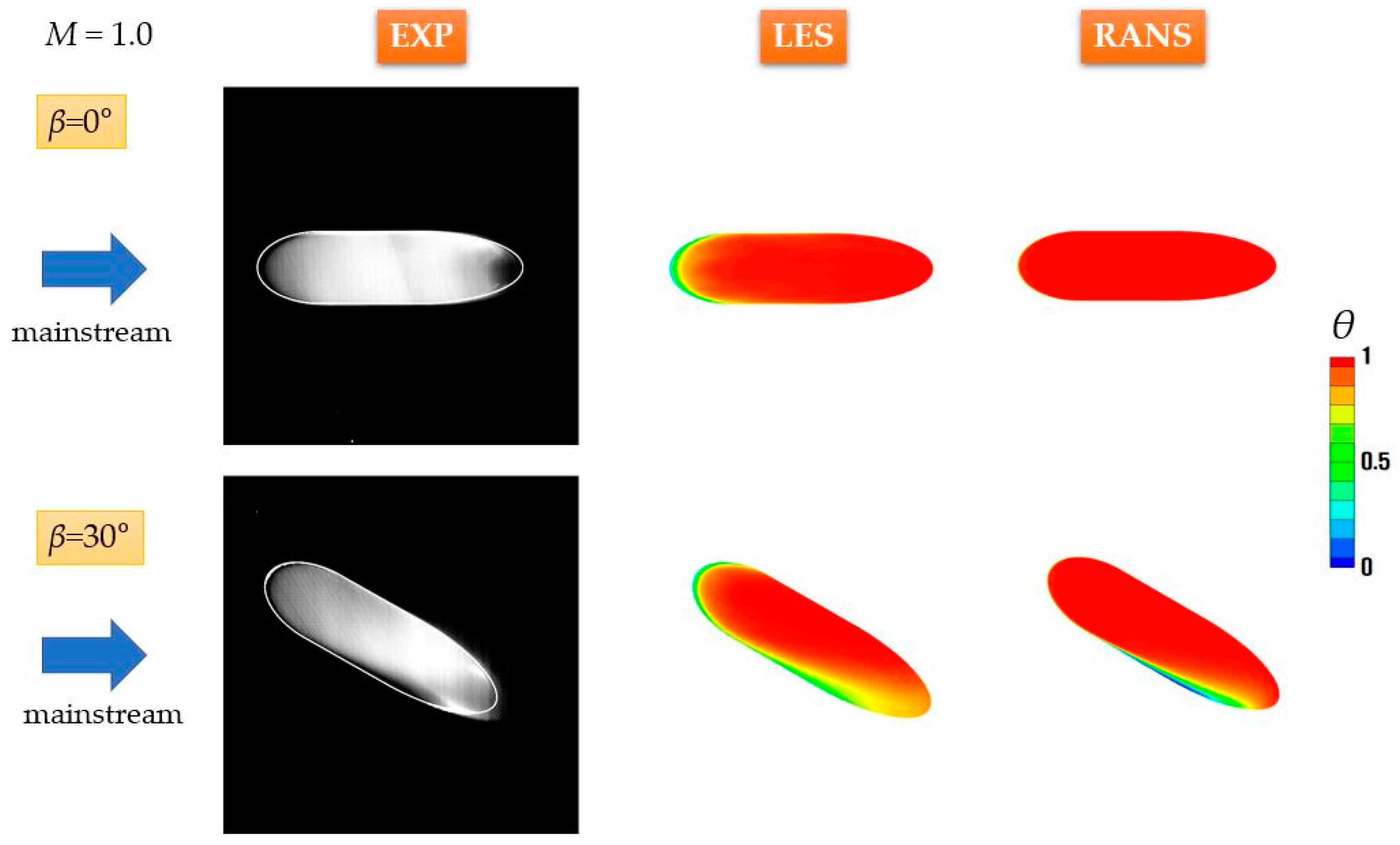
4.1. Contours of Time-Averaged η
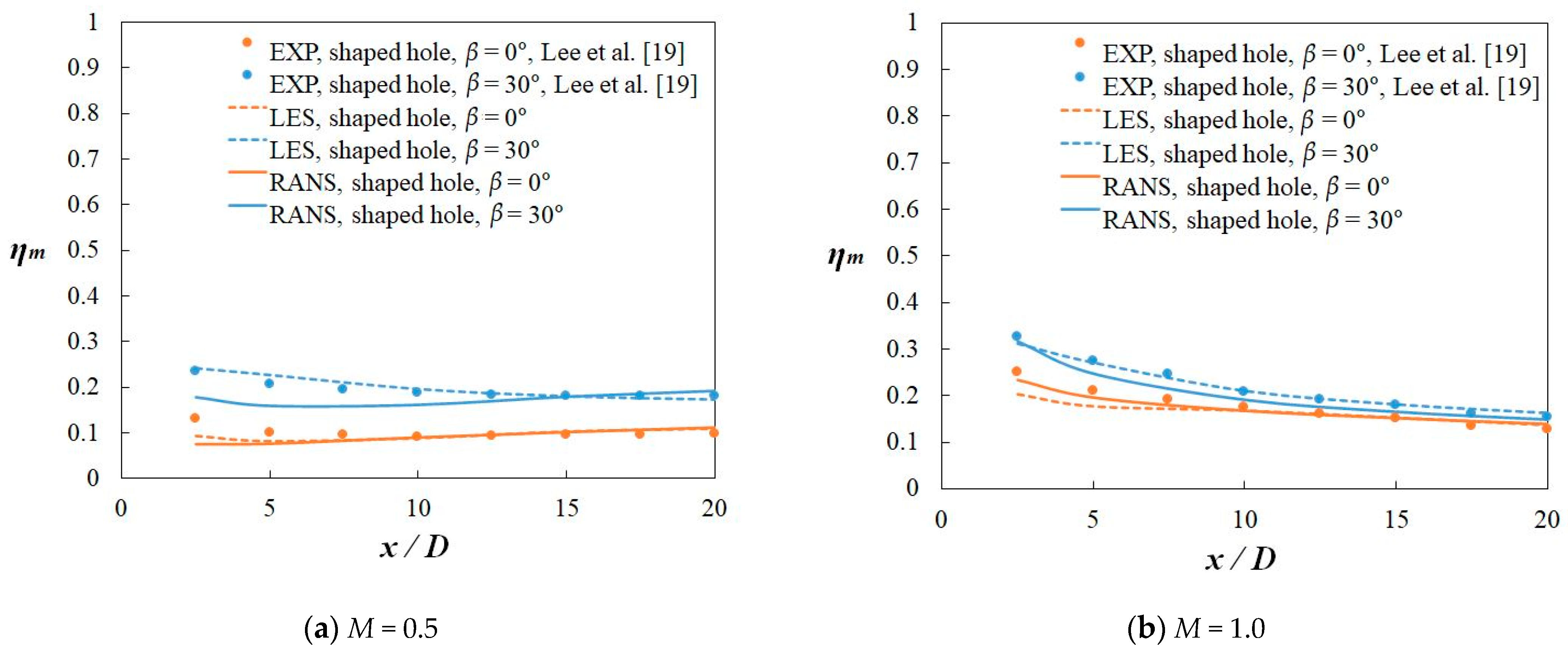
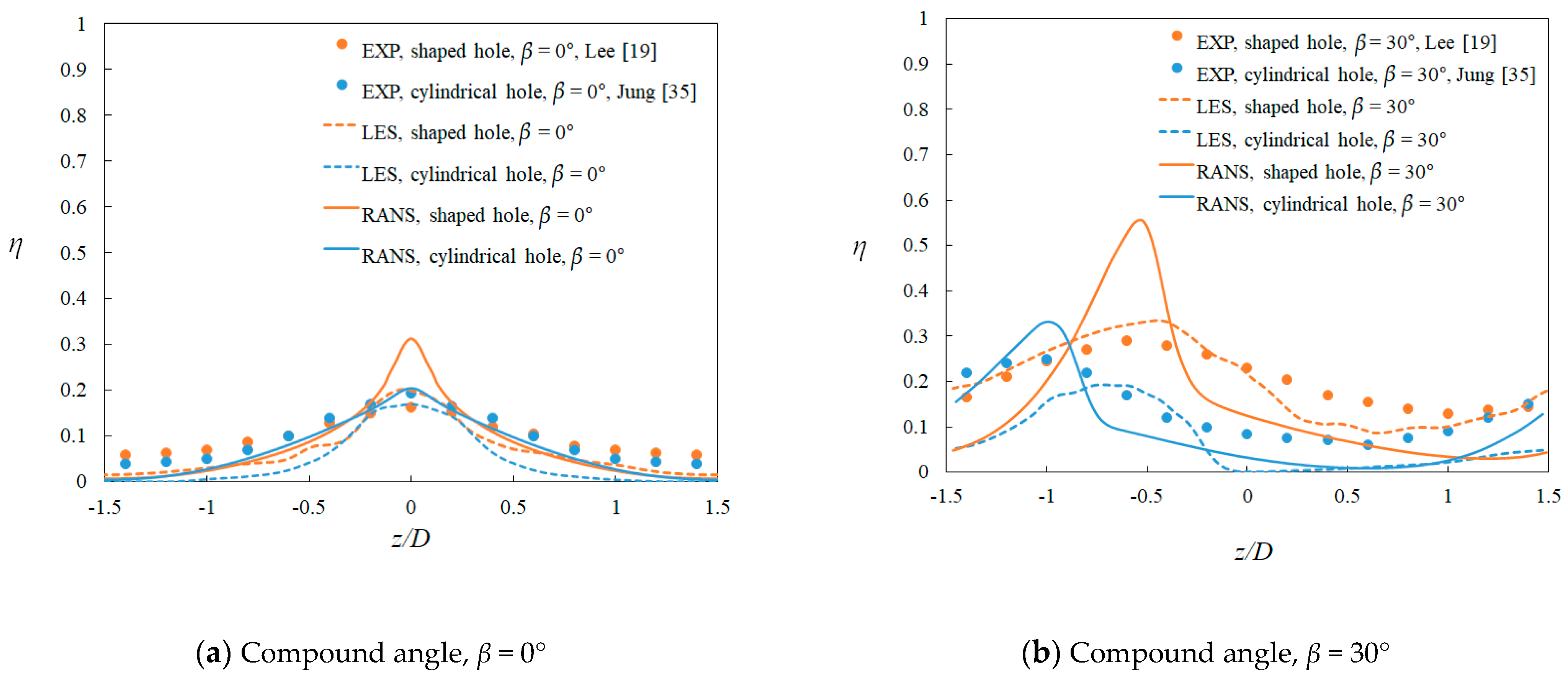
4.2. Time-Averaged Film Cooling Effectiveness
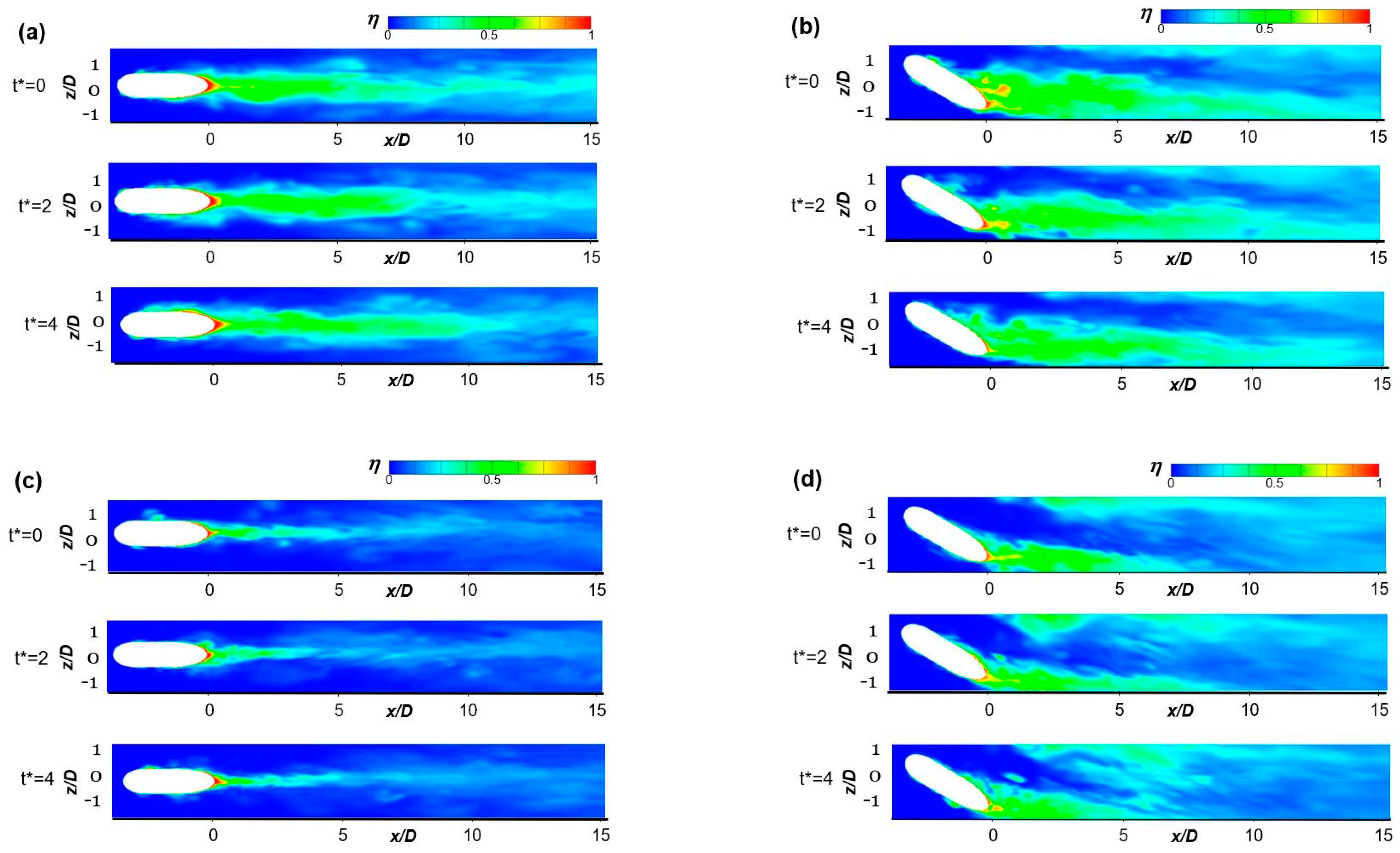
4.3. Contours of Instantaneous Film Cooling Effectiveness on Wall
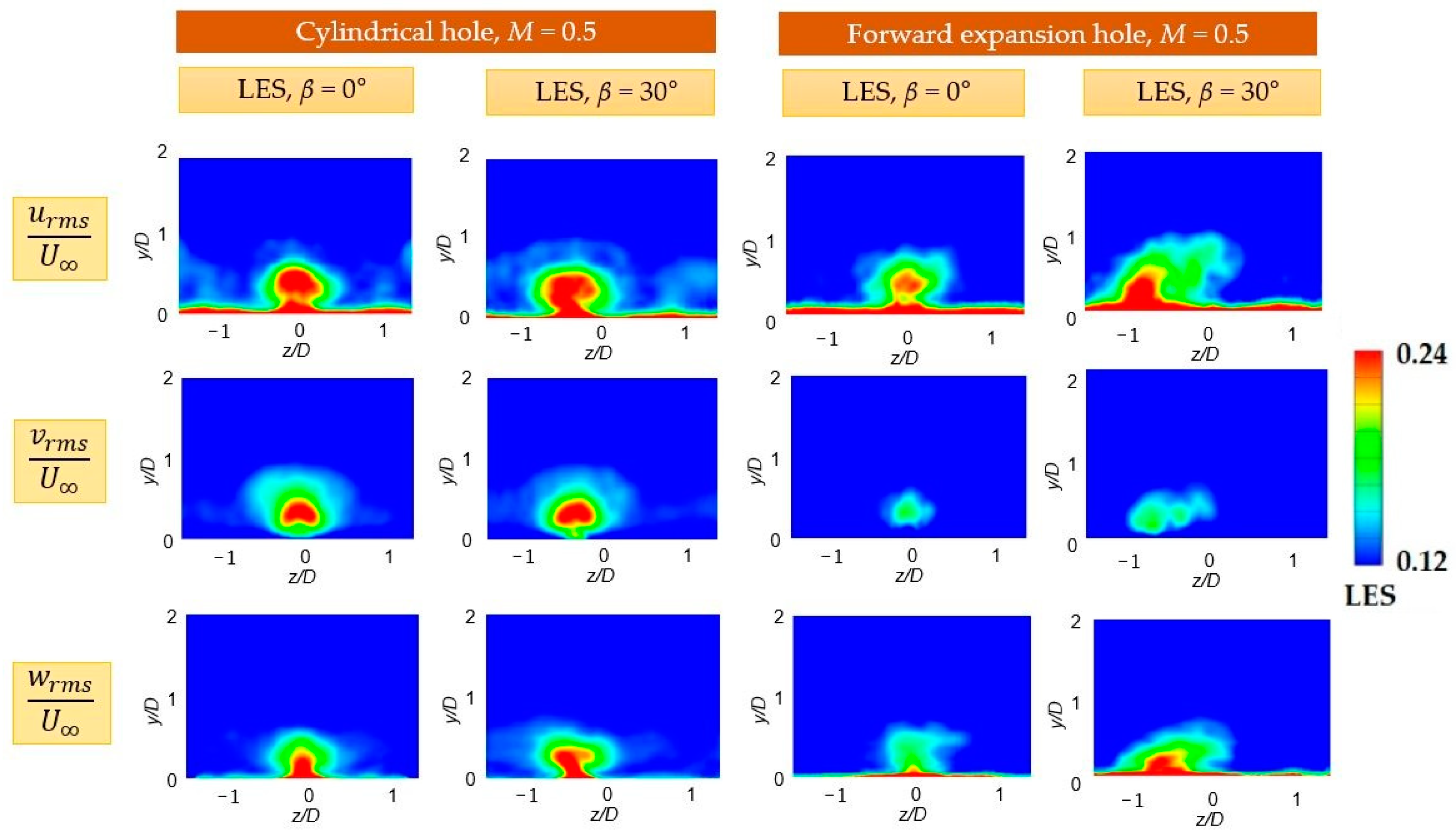
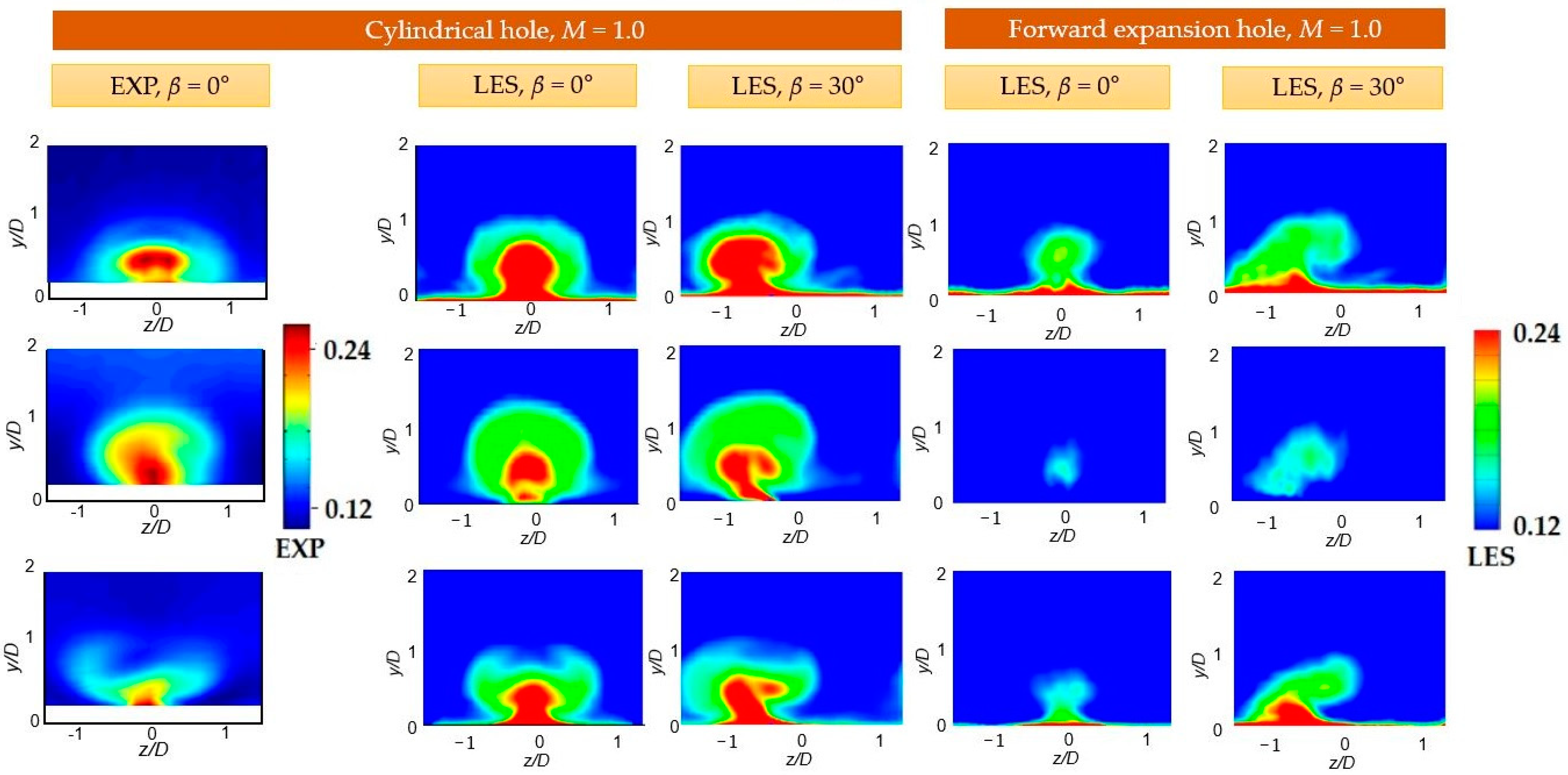
4.4. Contours of Velocity Fluctuation on Streamwise-Normal Plane
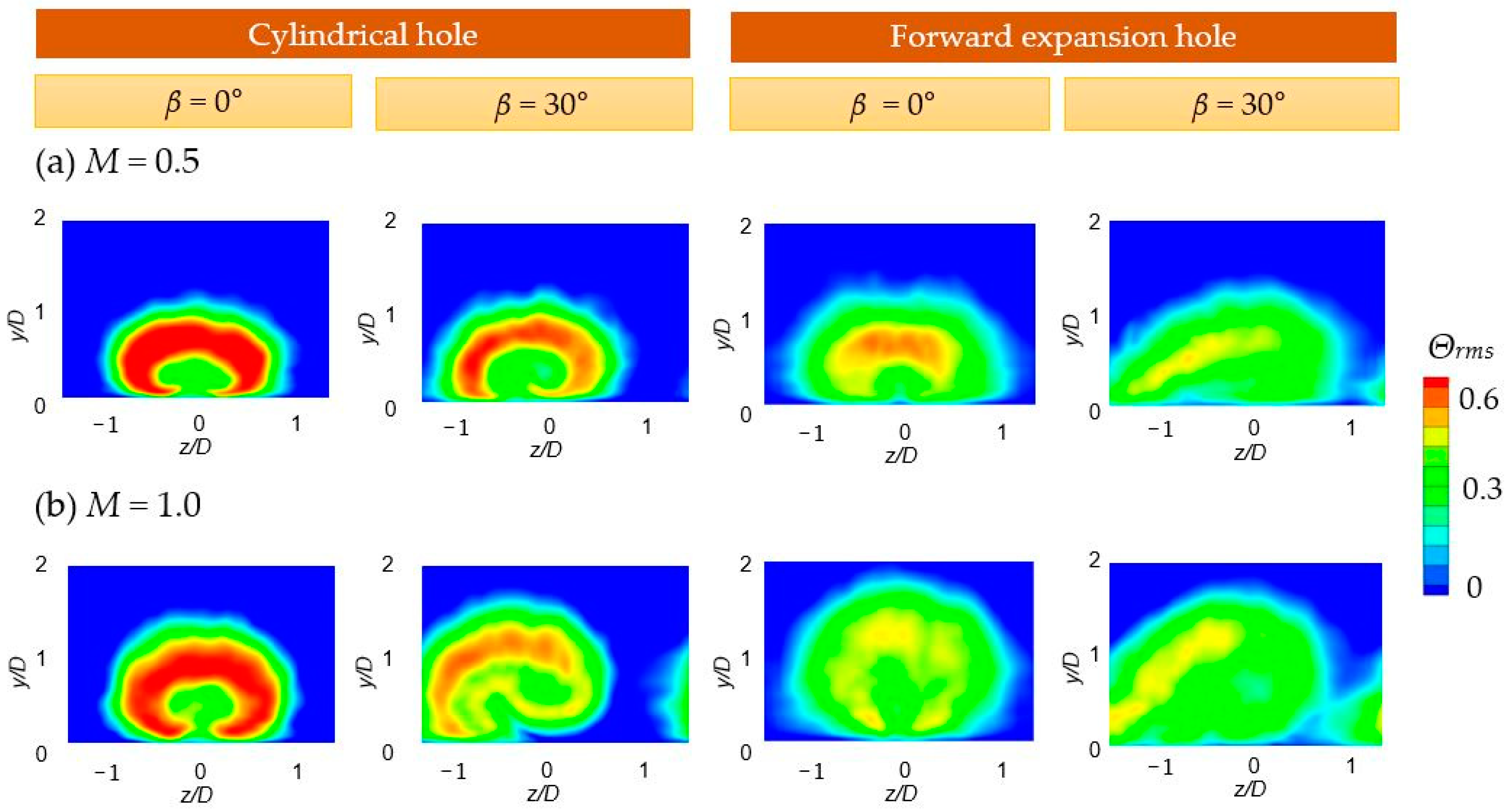
4.5. Contours of Temperature Fluctuations on Streamwise-Normal Plane
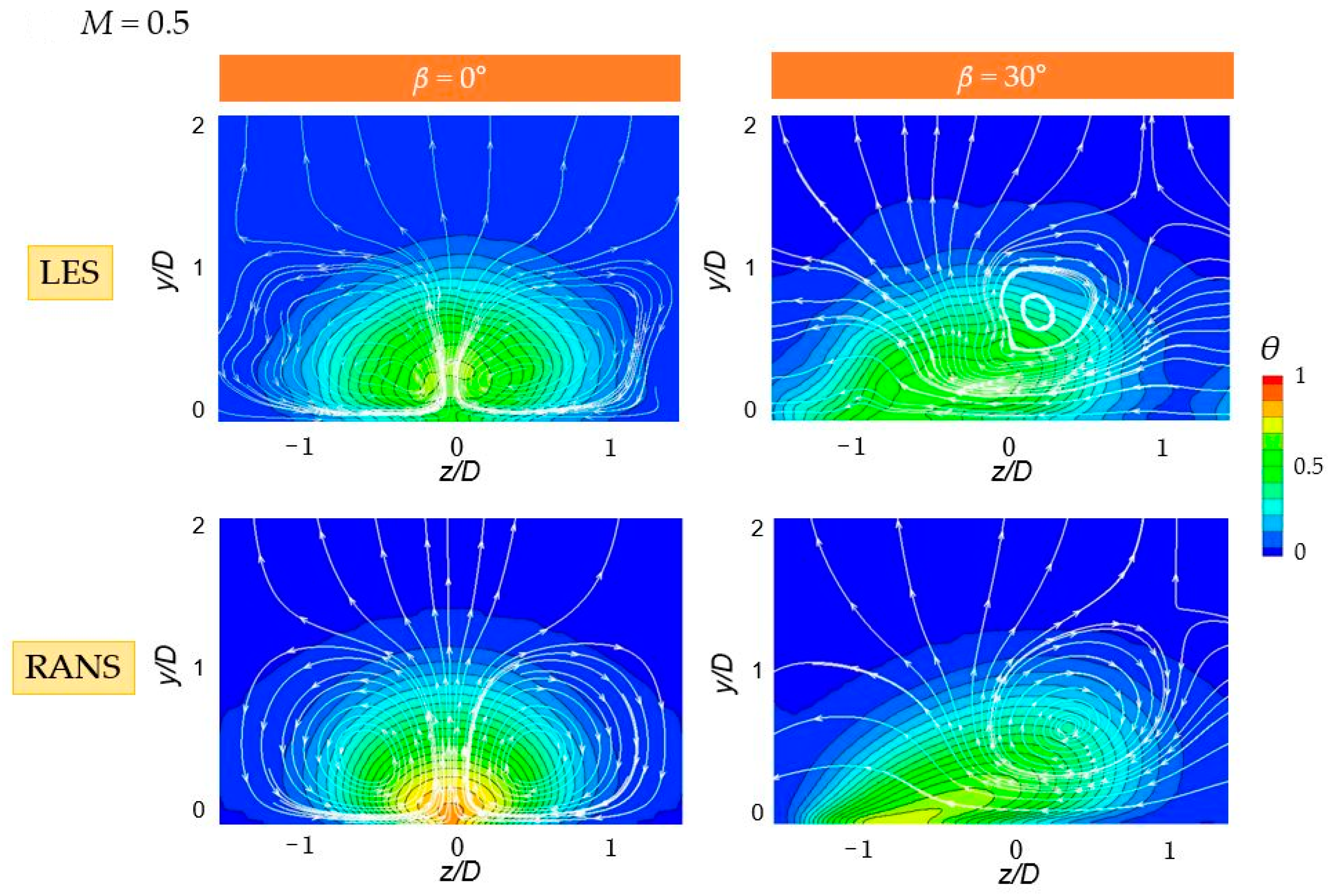
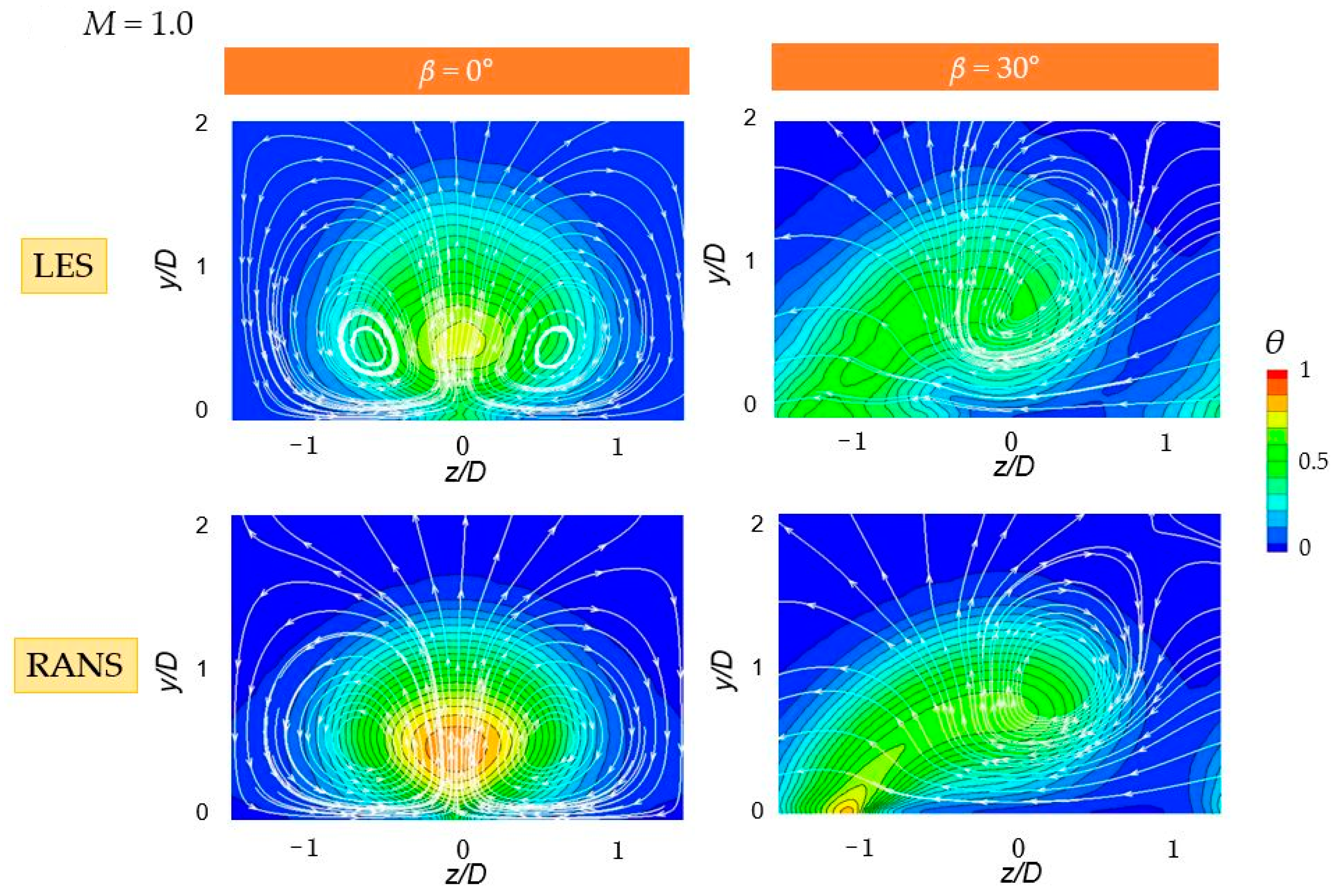
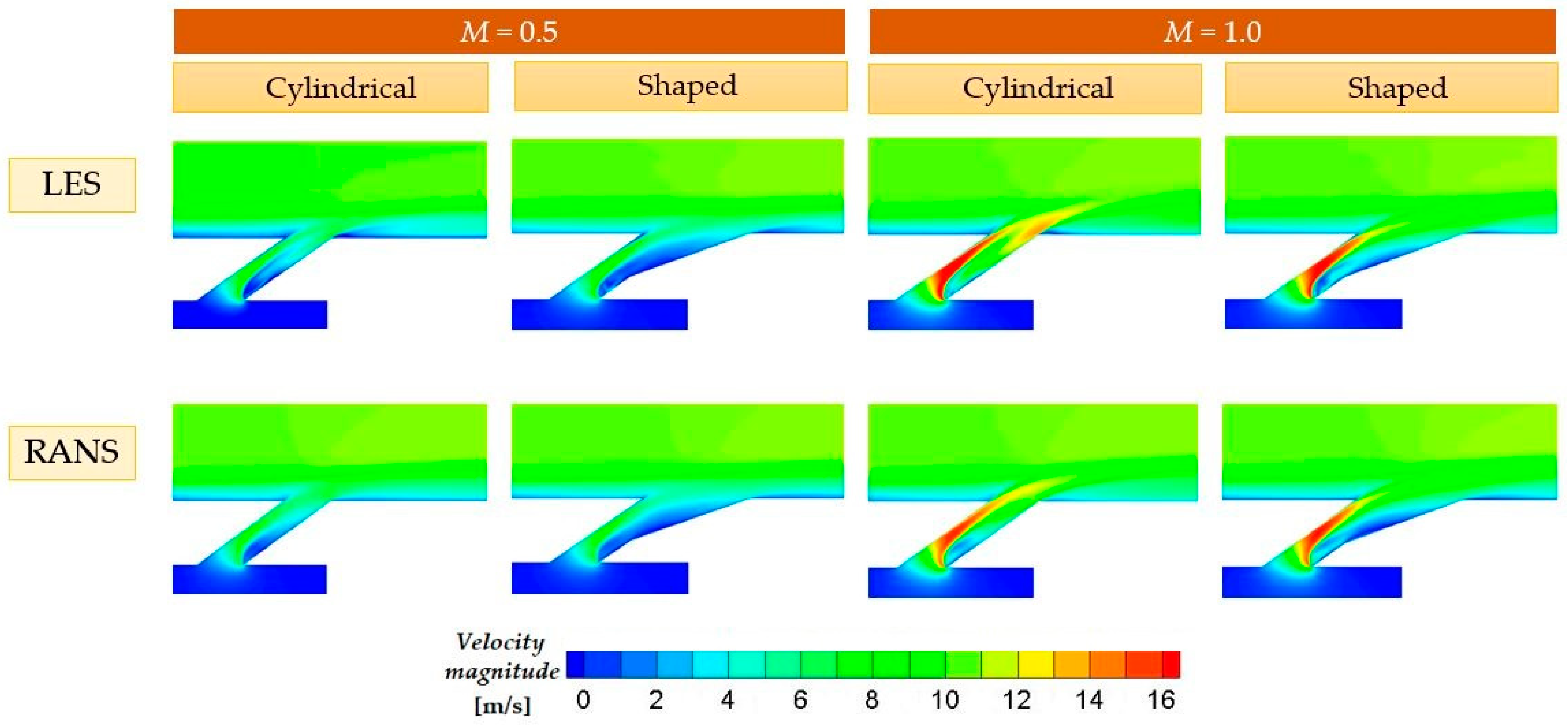
4.6. Time-Averaged Velocity Magnitude Contours in Hole
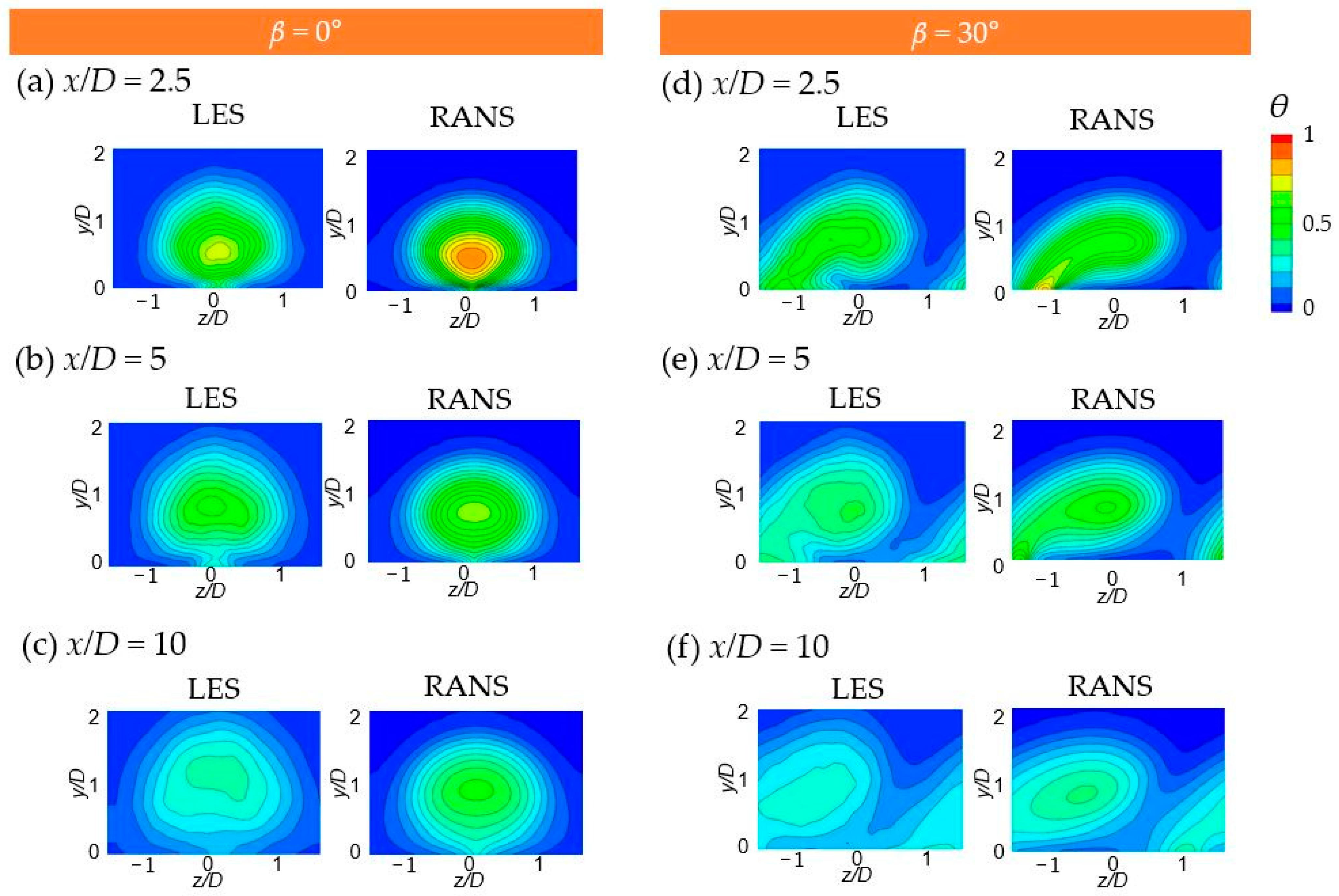
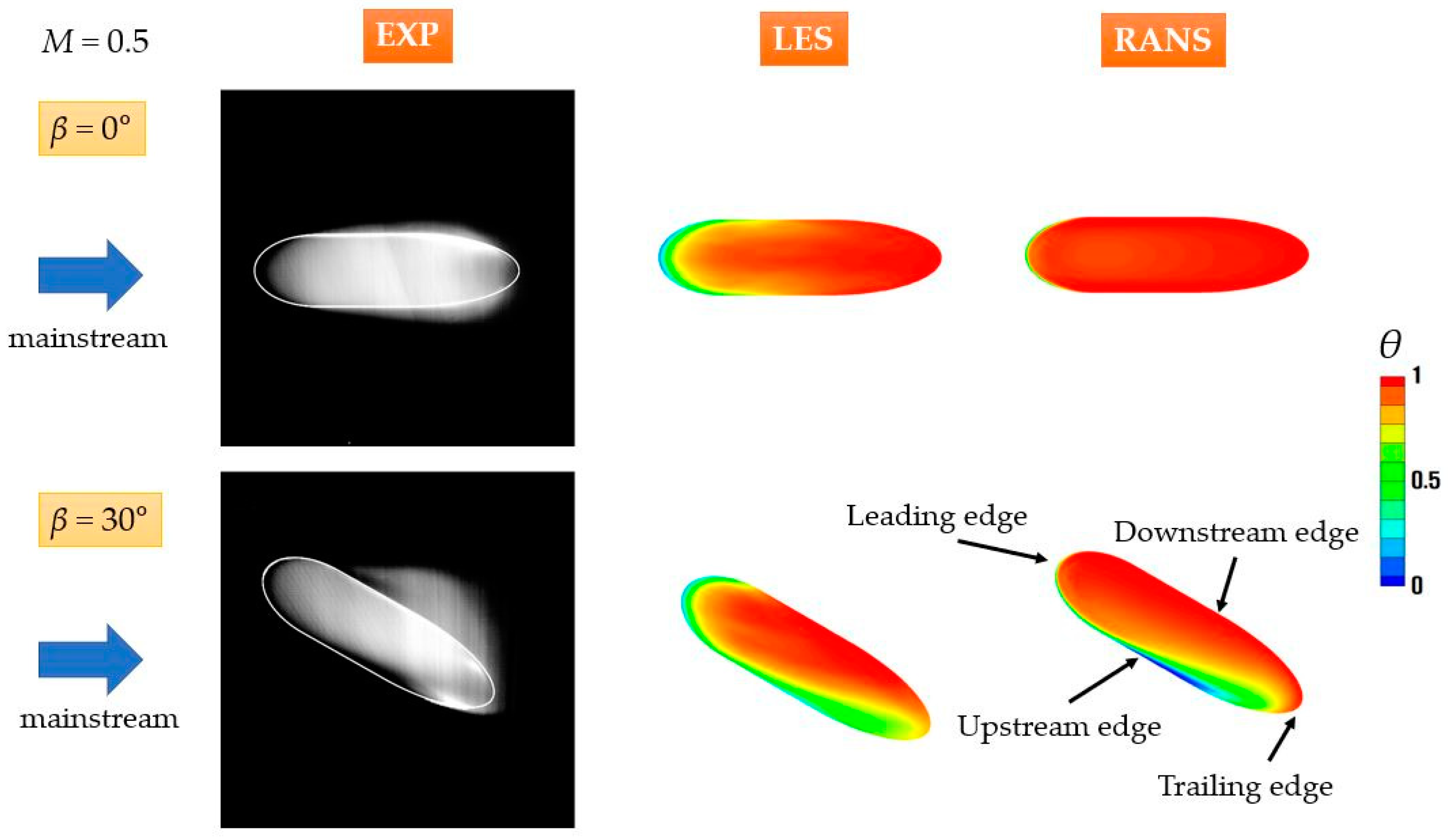
4.7. Mean Dimensionless Temperature Contours at Hole Exit
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| D | diameter of lower hole |
| L | hole length |
| M | Blowing ratio = |
| P | pitch between holes |
| t | time |
| Adiabatic wall temperature | |
| Temperature of mainstream gas | |
| U | Mean velocity |
| injectant velocity | |
| mainstream velocity | |
| Greek Symbols | |
| α | injection angle |
| β = | compound angle (spanwise injection angle) |
| Θ | dimensionless temperature |
| adiabatic film cooling effectiveness | |
| centerline film cooling effectiveness | |
| lateral-averaged film cooling effectiveness | |
| ρ | density |
| injectant density | |
| mainstream density | |
| Subscripts | |
| C | coolant |
| aw | adiabatic wall |
| m | lateral-averaged |
| Abbreviations | |
| LES | Large Eddy Simulation |
| RANS | Reynolds-Averaged Navier–Stokes |
References
- Moran, M.; Shapiro, H.; Boettner, D.; Bailey, M. Fundamentals of Engineering Thermodynamics, 8th ed.; Wiley: Hoboken, NJ, USA, 2014; p. 532. [Google Scholar]
- Mai, T.D.; Ryu, J. Effects of leading-edge modification in damaged rotor blades on aerodynamic characteristics of high-pressure gas turbine. Mathematics 2020, 8, 2191. [Google Scholar] [CrossRef]
- Leedom, D.H.; Acharya, S. Large eddy simulations of film cooling flow fields from cylindrical and shaped holes. In Proceedings of the ASME Turbo Expo 2008, Berlin, Germany, 9–13 June 2008; GT2008-51009. pp. 865–877. [Google Scholar]
- Acharya, S.; Leedom, D.H. Large eddy simulations of discrete hole film cooling with plenum inflow orientation effects. J. Heat Transf. 2013, 135, 011010. [Google Scholar] [CrossRef]
- Baek, S.I.; Ahn, J. Large Eddy Simulation of Film Cooling with Bulk Flow Pulsation: Comparative Study of LES and RANS. Appl. Sci. 2020, 10, 8553. [Google Scholar] [CrossRef]
- Fujimoto, S. Large eddy simulation of film cooling flows using octree hexahedral meshes. In Proceedings of the ASME Turbo Expo 2012, Copenhagen, Denmark, 11–15 June 2012. GT-2012-7009. [Google Scholar]
- Walters, D.K.; Leylek, J.H. Impact of film-cooling jets on turbine aerodynamic losses. ASME J. Turbomach. 2000, 122, 537–545. [Google Scholar] [CrossRef]
- McGovern, K.T.; Leylek, J.H. A detailed analysis of film cooling physics: Part II—Compound-angle injection with cylindrical holes. ASME J. Turbomach. 2000, 122, 113–121. [Google Scholar] [CrossRef]
- Tyagi, M.; Acharya, S. Large eddy simulation of film cooling flow from an inclined cylindrical jet. ASME J. Turbomach. 2003, 125, 734–742. [Google Scholar] [CrossRef]
- Rozati, A.; Tafti, D. Large eddy simulation of leading edge film cooling: Part II—Heat transfer and effect of blowing ratio. In Proceedings of the ASME Turbo Expo 2007, GT2007-27690, Montreal, QC, Canada, 14–17 May 2007. [Google Scholar]
- Johnson, P.; Shyam, V.; Hah, C. Reynolds-Averaged Navier–Stokes Solutions to Flat Plate Film Cooling Scenarios, NASA/TM-2011-217025. Available online: https://ntrs.nasa.gov/api/citations/20110012464/downloads/20110012464.pdf (accessed on 1 February 2021).
- Goldstein, R.J.; Eckert, E.R.G.; Burggraf, F. Effects of hole geometry and density on three-dimensional film cooling. Int. J. Heat Mass Transf. 1974, 17, 595–607. [Google Scholar] [CrossRef]
- Bell, C.M.; Hamakawa, H.; Ligrani, P.M. Film cooling from shaped holes. J. Heat Transf. 2000, 122, 224–232. [Google Scholar] [CrossRef]
- Hyams, D.G.; Leylek, J.H. A detailed analysis of film cooling physics: Part III-Streamwise injection with shaped holes. J. Turbomach. 2000, 122, 122–132. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, J.; Feng, H.; Huang, Y. Large eddy simulation of film cooling flow from a fanshaped hole. Appl. Therm. Eng. 2018, 129, 855–870. [Google Scholar] [CrossRef]
- Oliver, T.A.; Bogard, D.G.; Moser, R.D. Large eddy simulation of compressible, shaped-hole film cooling. Int. J. Heat Mass Transf. 2019, 140, 498–517. [Google Scholar] [CrossRef]
- Wang, Q.; Su, X.; Yuan, X. Large-eddy simulation of shaped hole film cooling with the influence of cross flow. Int. J. Turbo Jet Eng. 2020. ahead-of-print. [Google Scholar]
- Zamiri, A.; You, S.; Chung, J. Large eddy simulation in the optimization of laidback fan-shaped hole geometry to enhance film-cooling performance. Int. J. Heat Mass Transf. 2020, 158, 120014. [Google Scholar] [CrossRef]
- Lee, H.W.; Park, J.J.; Lee, J.S. Flow visualization and film cooling effectiveness measurements around shaped holes with compound angle orientations. Int. J. Heat Mass Transf. 2002, 45, 145–156. [Google Scholar] [CrossRef]
- ANSYS Fluent Theory Guide Version 19. Available online: https://www.ansys.com/products/fluids/ansys-fluent (accessed on 1 February 2021).
- Pointwise Version 18. Available online: http://www.pointwise.com/ (accessed on 1 February 2021).
- Baek, S.I.; Yavuzkurt, S. Effects of flow oscillations in the mainstream on film cooling. Inventions 2018, 3, 73. [Google Scholar] [CrossRef]
- Renze, P.; Schröder, W.; Meinke, M. Large-eddy simulation of film cooling flows with variable density jets. Flow Turbul. Combust. 2008, 80, 119–132. [Google Scholar] [CrossRef]
- Iourokina, I.; Lele, S. Towards large eddy simulation of film cooling flows on a model turbine blade leading edge. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, No. 2005-0670, Reno, NV, USA, 10–13 January 2005. [Google Scholar]
- Ravelli, S.; Abdeh, H.; Barigozzi, G. Numerical Assessment of Density Ratio and Mainstream Turbulence Effects on Leading-Edge Film Cooling: Heat and Mass Transfer Method. J. Turbomach. 2021, 143, 041002. [Google Scholar] [CrossRef]
- White, F. Fluid Mechanics, 8th ed.; McGraw-Hill: New York, NY, USA, 2015. [Google Scholar]
- Ryu, J.; Lele, S.; Viswanathan, K. Study of supersonic wave components in high-speed turbulent jets using an LES database. J. Sound Vib. 2014, 333, 6900–6923. [Google Scholar] [CrossRef]
- Choi, M.G.; Ryu, J. Numerical study of the axial gap and hot streak effects on thermal and flow characteristics in two-stage high pressure gas turbine. Energies 2018, 11, 2654. [Google Scholar] [CrossRef]
- Oh, J.S.; Kang, T.; Ham, S.; Lee, K.S.; Jang, Y.J.; Ryou, H.S.; Ryu, J. Numerical analysis of aerodynamic characteristics of hyperloop system. Energies 2019, 12, 518. [Google Scholar] [CrossRef]
- Le, T.T.G.; Jang, K.S.; Lee, K.S.; Ryu, J. Numerical investigation of aerodynamic drag and pressure waves in hyperloop systems. Mathematics 2020, 8, 1973. [Google Scholar] [CrossRef]
- Lee, H.W. Effects of Bulk Flow Pulsations on Film Cooling with Shaped Holes. Ph.D. Thesis, Seoul National University, Seoul, Korea, 2000. [Google Scholar]
- Lee, S.W.; Kim, Y.B.; Lee, J.S. Flow characteristics and aerodynamic losses of film cooling jets with compound angle orientations. J. Turbomach. 1997, 119, 310–319. [Google Scholar] [CrossRef]
- Baek, S.I.; Ahn, J. Large eddy simulation of film cooling with triple holes: Injectant behavior and adiabatic film cooling effectiveness. Processes 2020, 8, 1443. [Google Scholar] [CrossRef]
- Burd, S.W.; Kaszeta, R.W.; Simon, T.W. Measurements in film cooling flows: Hole L/D and turbulence intensity effects. J. Turbomach. 1998, 120, 791–798. [Google Scholar] [CrossRef]
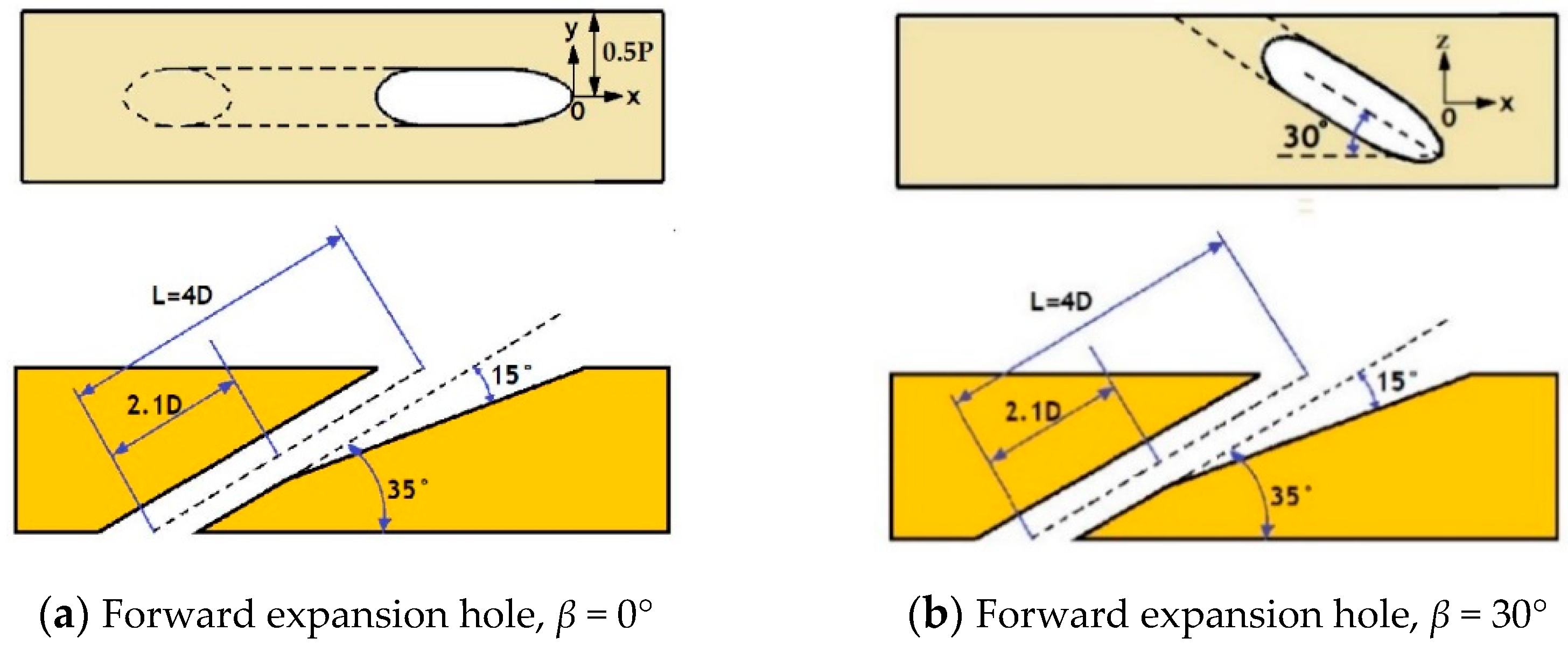
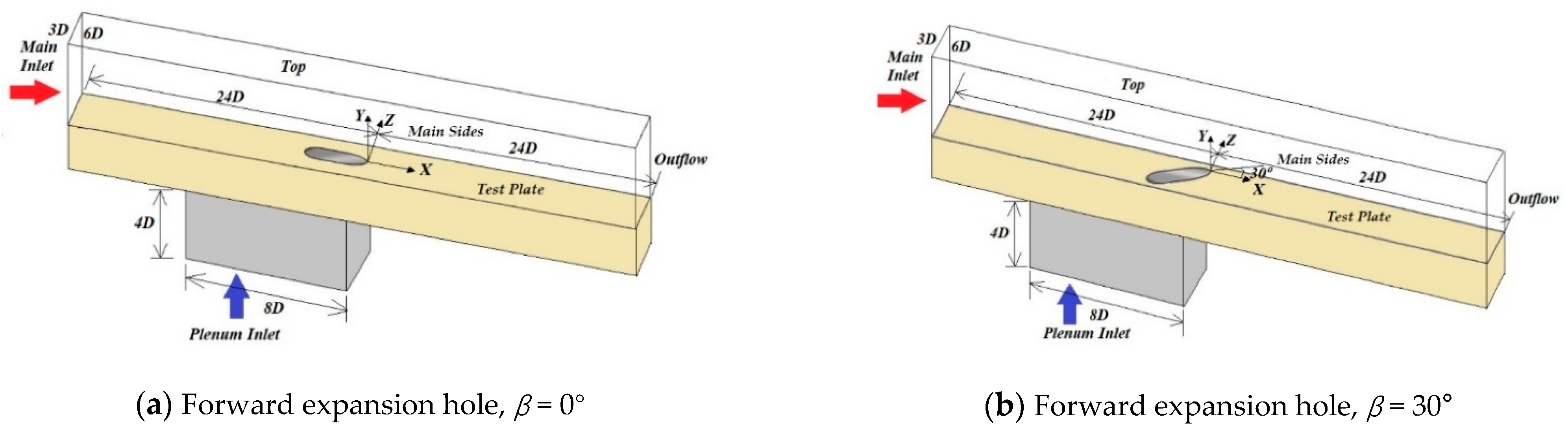
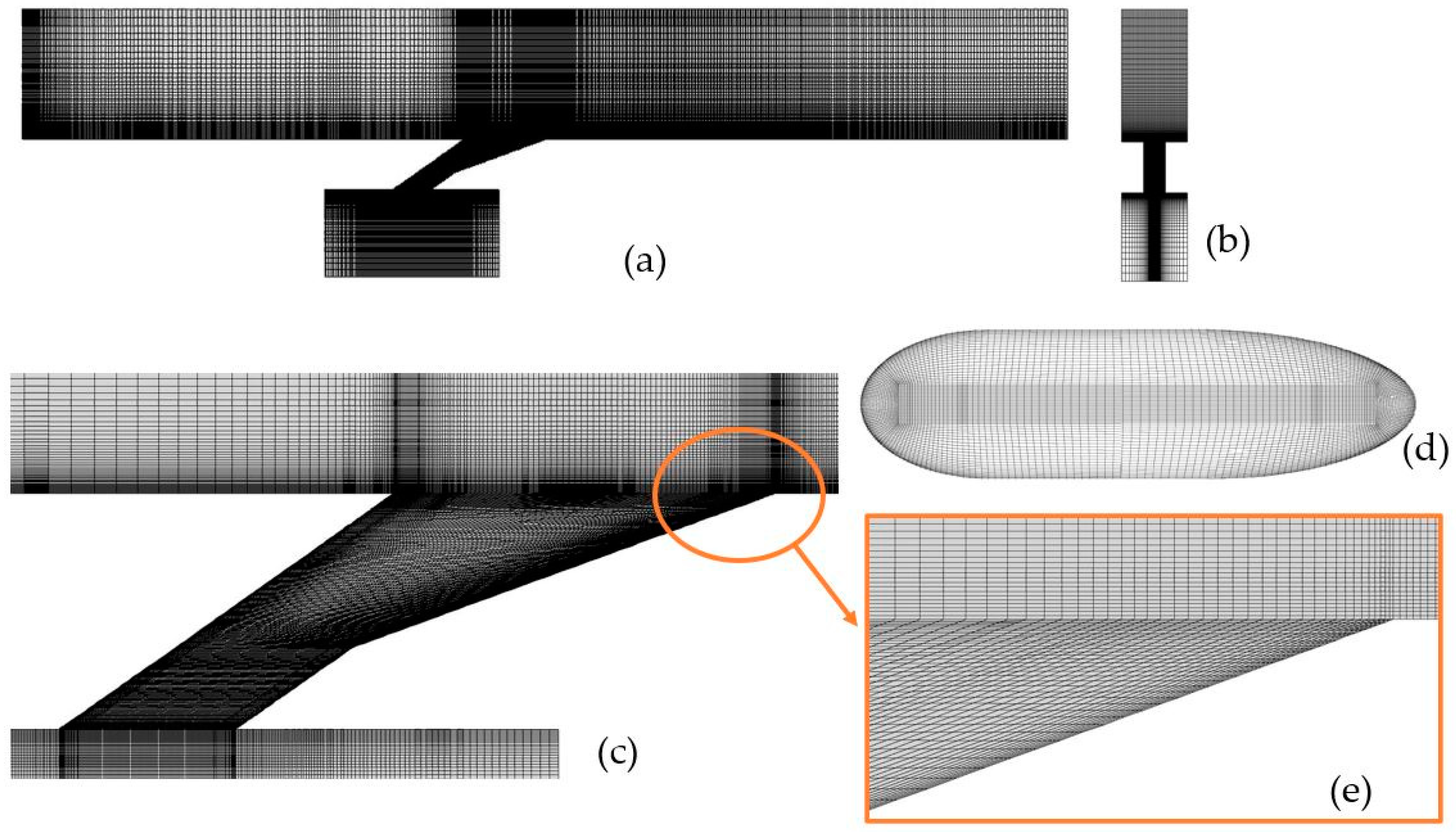
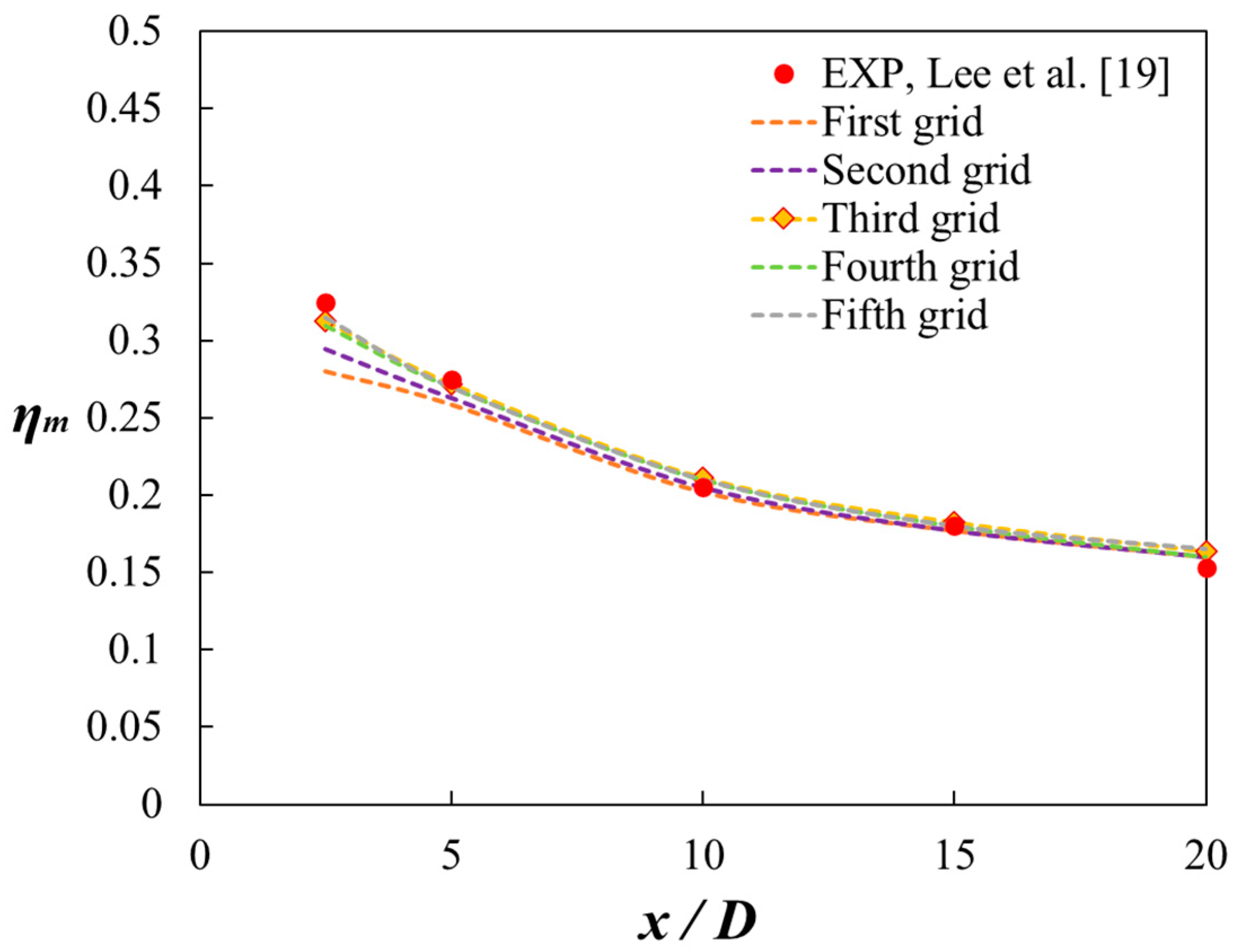
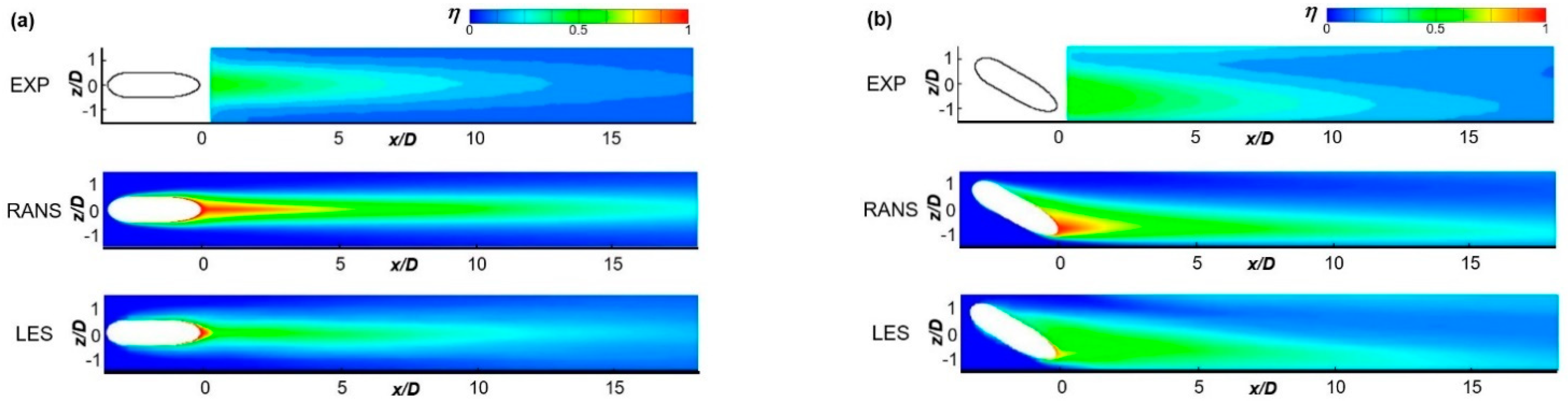
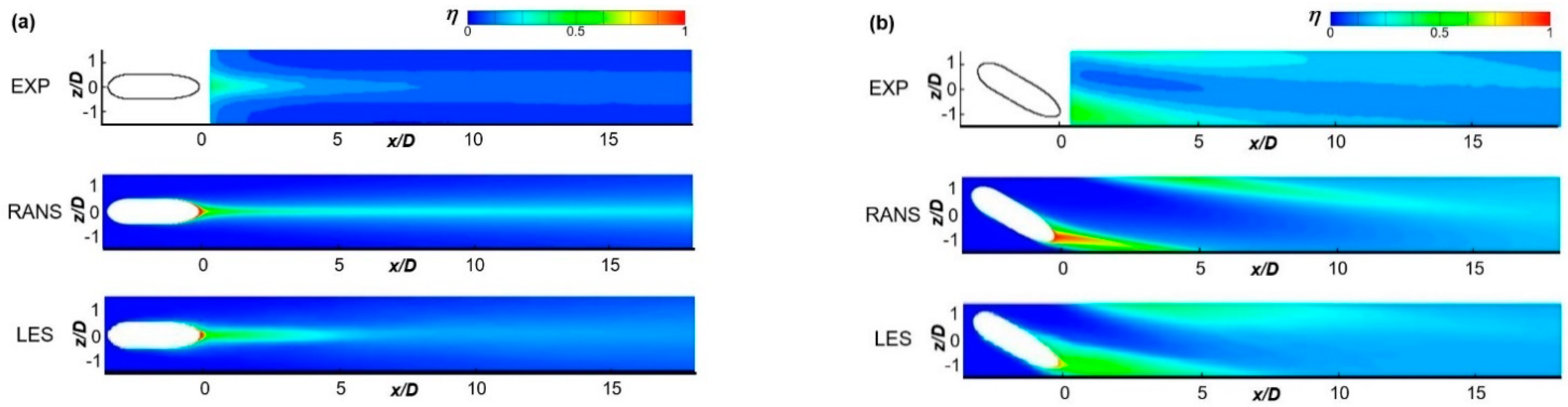
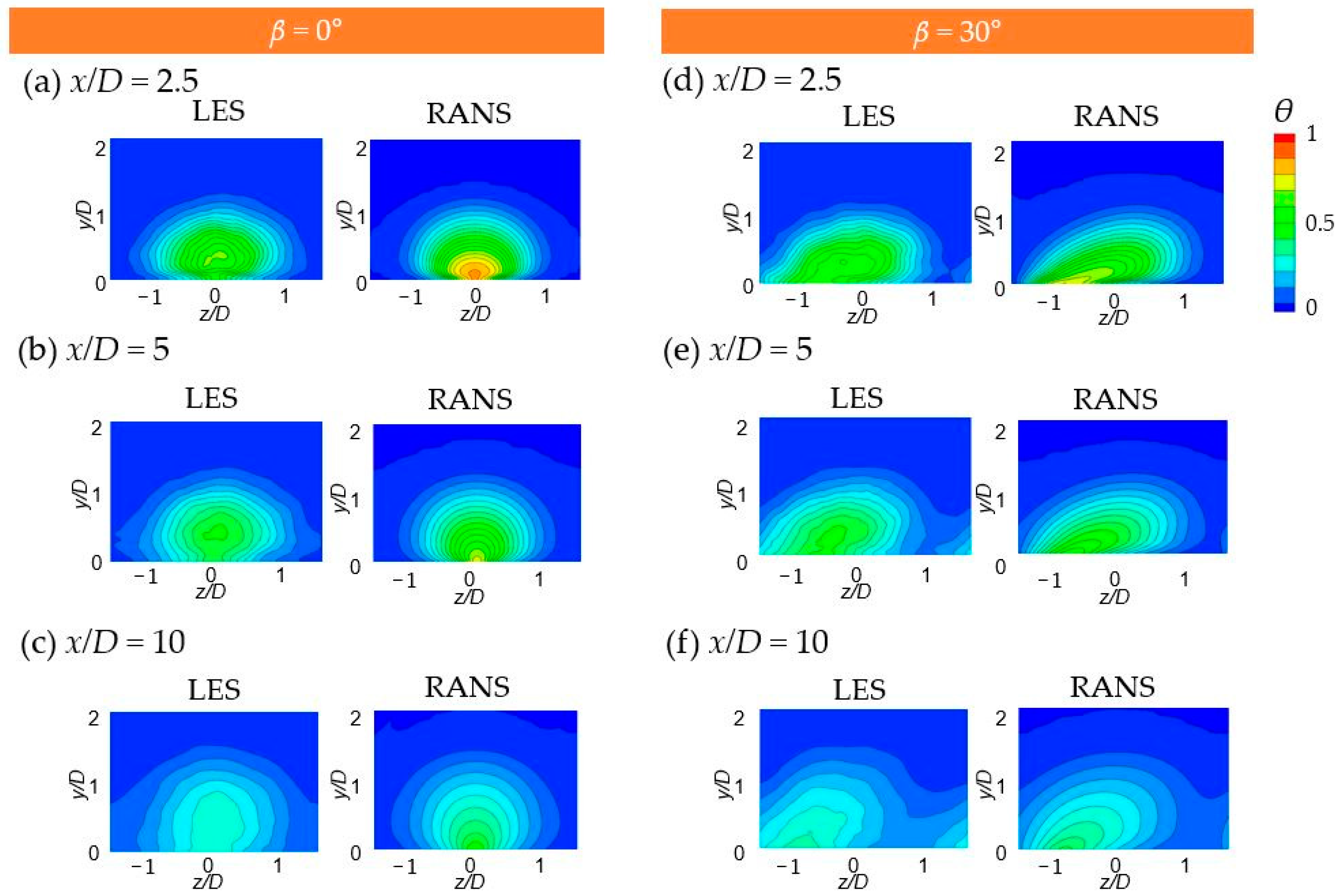
| Surface | Boundary Condition |
|---|---|
| Main inlet | Velocity inlet (u = constant) |
| Plenum inlet | Velocity inlet (u = constant) |
| Top | Symmetry () |
| Test plate | Adiabatic wall (u = v = w = 0) |
| Outflow | Pressure outlet |
| Main sides | Periodic (u(x, y, z, t) = u(x, y, z + P, t), ΔP = 0) |
| Sides of plenum | Wall (u = v = w = 0) |
| Hole wall | Wall (u = v = w = 0) |
| Grid | Number of Cells in x Direction | Number of Cells in y Direction | Number of Cells in z Direction | Number of Cells in Cross Flow Block (Million) | Total Cell Number (Million) |
|---|---|---|---|---|---|
| First | 320 | 70 | 70 | 1.89 | 4.49 |
| Second | 502 | 75 | 76 | 3.18 | 5.78 |
| Third | 552 | 80 | 82 | 3.94 | 6.53 |
| Fourth | 602 | 85 | 86 | 4.72 | 7.31 |
| Fifth | 682 | 90 | 90 | 5.85 | 8.45 |
| Grid | Number of Cells in x Direction | Number of Cells in y Direction | Number of Cells in z Direction | Number of Cells in Cross Flow Block (Million) | Total Cell Number (Million) |
|---|---|---|---|---|---|
| First | 426 | 70 | 92 | 3.06 | 5.65 |
| Second | 480 | 75 | 102 | 3.99 | 6.59 |
| Third | 530 | 80 | 114 | 5.16 | 7.75 |
| Fourth | 560 | 85 | 124 | 6.22 | 8.82 |
| Fifth | 594 | 88 | 134 | 7.32 | 9.91 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baek, S.I.; Ryu, J.; Ahn, J. Large Eddy Simulation of Film Cooling with Forward Expansion Hole: Comparative Study with LES and RANS Simulations. Energies 2021, 14, 2063. https://doi.org/10.3390/en14082063
Baek SI, Ryu J, Ahn J. Large Eddy Simulation of Film Cooling with Forward Expansion Hole: Comparative Study with LES and RANS Simulations. Energies. 2021; 14(8):2063. https://doi.org/10.3390/en14082063
Chicago/Turabian StyleBaek, Seung Il, Jaiyoung Ryu, and Joon Ahn. 2021. "Large Eddy Simulation of Film Cooling with Forward Expansion Hole: Comparative Study with LES and RANS Simulations" Energies 14, no. 8: 2063. https://doi.org/10.3390/en14082063
APA StyleBaek, S. I., Ryu, J., & Ahn, J. (2021). Large Eddy Simulation of Film Cooling with Forward Expansion Hole: Comparative Study with LES and RANS Simulations. Energies, 14(8), 2063. https://doi.org/10.3390/en14082063








