Compact Modelling of Electrical, Optical and Thermal Properties of Multi-Colour Power LEDs Operating on a Common PCB
Abstract
1. Introduction
2. Model Form
- (a)
- Establishing some analytical equations
- (b)
- Analysing whether no redundancy between the elements occurs
- (c)
- Presenting the properties of a typical data set
- (d)
- Explaining how the data processing eliminates the outliers
- (e)
- Presenting the results set
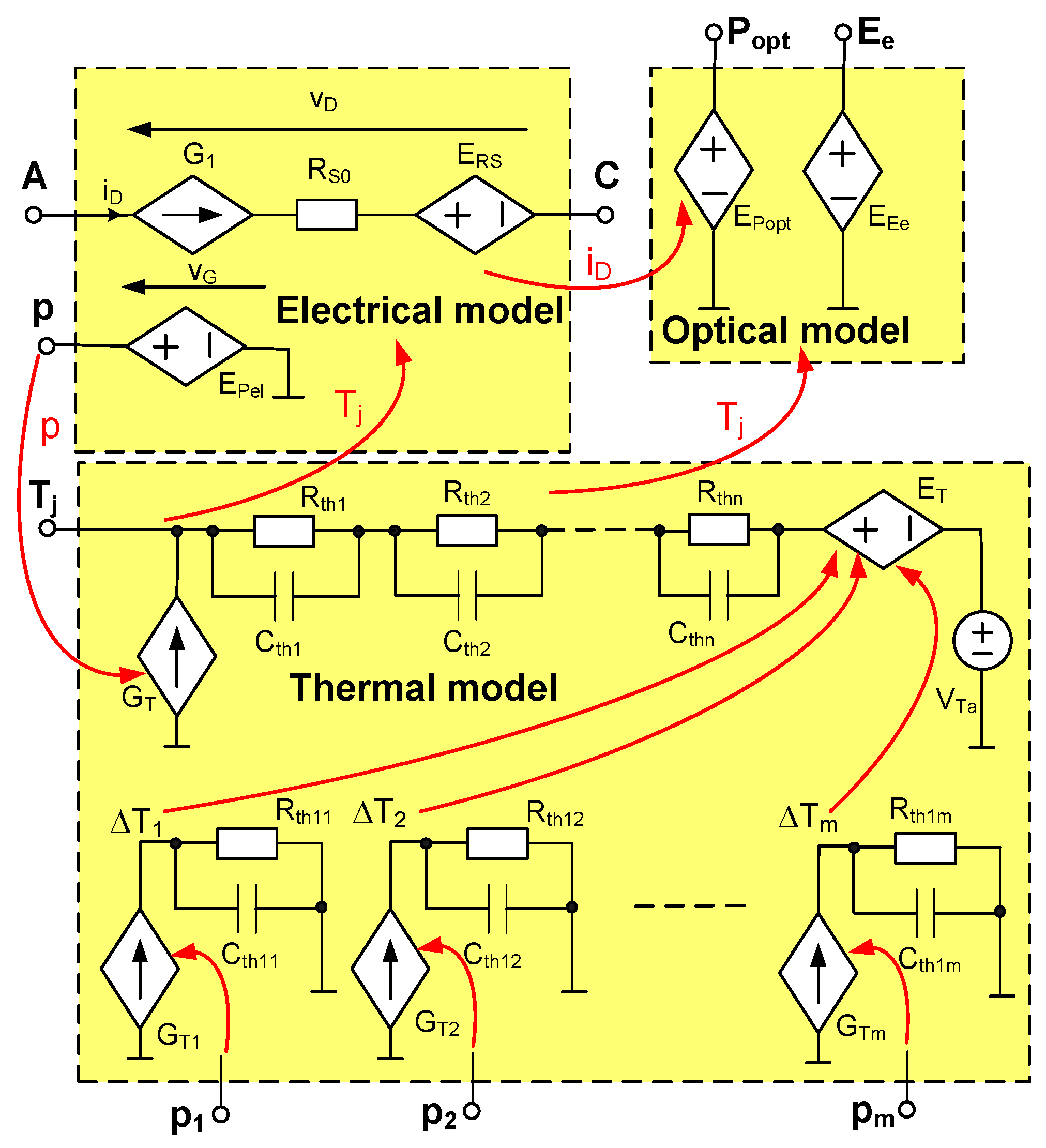
2.1. Electrical Model
2.2. Optical Model
2.3. Thermal Model
3. Model Parameters Estimation
4. Investigated Devices
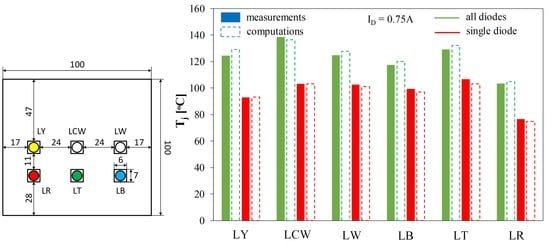
5. Measurement and Computation Results
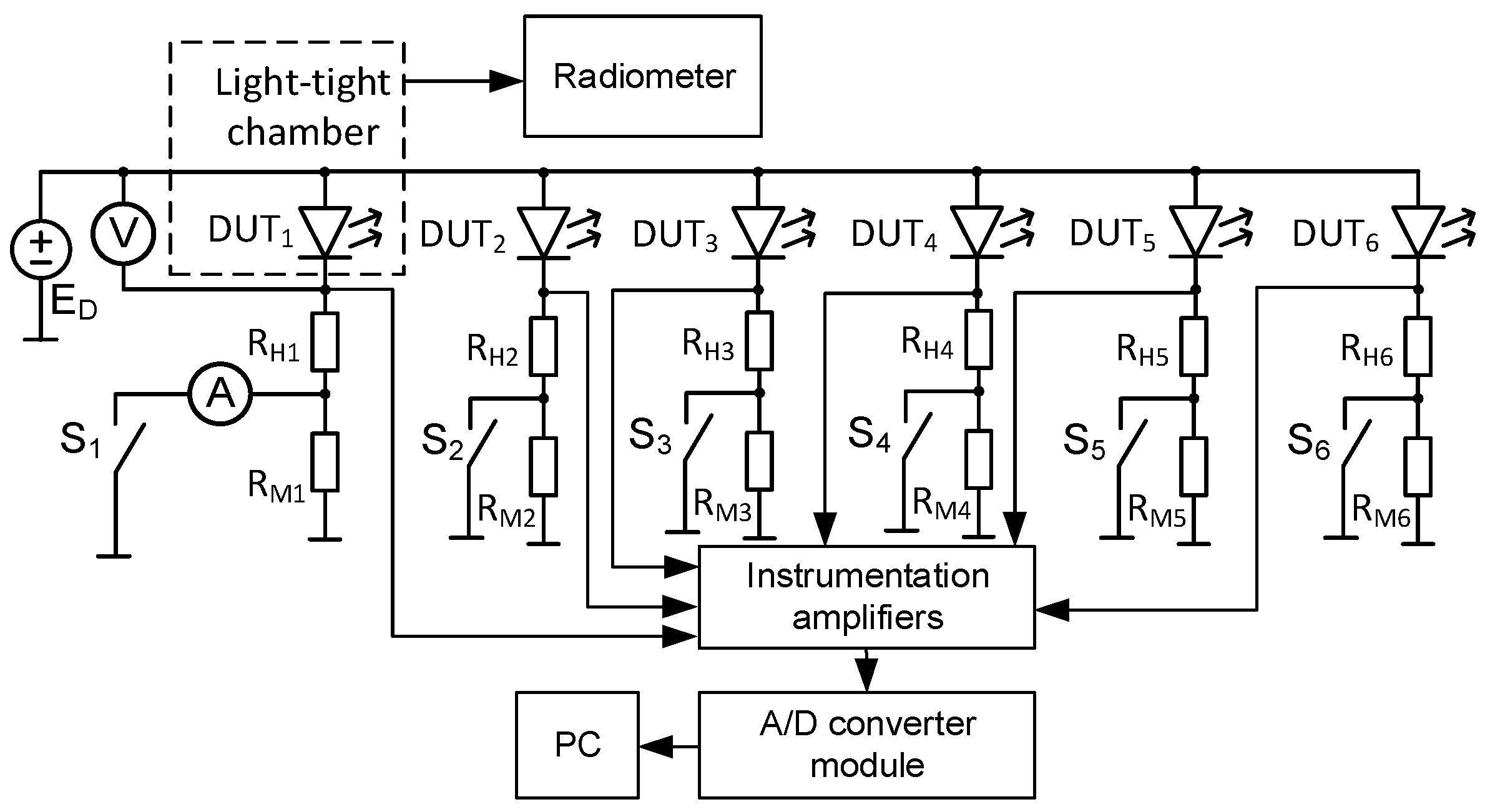
5.1. Measurement Set-Up
5.2. Measurement and Computation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Tj | junction temperature |
| Ta | ambient temperature |
| Popt | optical power |
| Ee | surface power density of the emitted light |
| Zthe(t) | electrical transient thermal impedance |
| vD | forward voltage |
| iD | diode current |
References
- Schubert, E.F. Light Emitting Diodes, 2nd ed.; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- Weir, B. Driving the 21st century’s lights. IEEE Spectr. 2012, 49, 42–47. [Google Scholar] [CrossRef]
- Huang, J.-J.; Kuo, H.-C.; Shen, S.-C. Nitride Semiconductor Light-Emitting Diodes (LEDs). Materials, Technologies and Applications, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Wang, K.; Liu, S.; Luo, X.; Wu, D. Freeform Optics for LED Packages and Applications; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]
- Brugnolotto, E.; Bhogaraju, S.K.; Liu, E.; Conti, F.; Pedron, D.; Signorini, R.; Elger, G. Investigation of Thermomechanical Local Stress Induced in Assembled GaN LEDs. In Proceedings of the 2019 25th International Workshop on Thermal Investigations of ICs and Systems (THERMINIC), Lecco, Italy, 25–27 September 2019; IEEE: New York, NY, USA, 2019; pp. 1–6. [Google Scholar]
- Martin, G.; Yu, J.; Zuidema, P.; Van Der Schans, M. Luminaire Digital Design Flow with Delphi4LED LEDs Multi-Domain Compact Model. In Proceedings of the 2019 25th International Workshop on Thermal Investigations of ICs and Systems (THERMINIC), Lecco, Italy, 25–27 September 2019; IEEE: New York, NY, USA, 2019. [Google Scholar]
- Dziurdzia, B.; Sobolewski, M.; Mikołajek, J.; Wroński, S. Low-voiding solder pastes in LED assembly. Solder. Surf. Mt. Technol. 2020, 32, 201–217. [Google Scholar] [CrossRef]
- Deshayes, Y.; Baillot, R.; Joly, S.; Ousten, Y.; Béchou, L. Overview on Sustainability, Robustness, and Reliability of GaN Single-Chip LED Devices. IEEE Trans. Device Mater. Reliab. 2015, 15, 621–625. [Google Scholar] [CrossRef]
- Pavelka, T.; Ptacek, M. Degradation of LED parameters during operation Brief review of currently used models and measuring methods. In Proceedings of the 2015 16th International Scientific Conference on Electric Power Engineering (EPE), Kouty nad Desnou, Czech Republic, 20–22 May 2015; IEEE: New York, NY, USA, 2015; pp. 523–526. [Google Scholar]
- Hasan, R.; Tomal, A.I. High-performance GaN-based green LEDs. In Proceedings of the 2017 4th International Conference on Advances in Electrical Engineering (ICAEE), Dhaka, Bangladesh, 28–30 September 2017; IEEE: New York, NY, USA, 2017; pp. 54–58. [Google Scholar]
- Lasance, C.J.M.; Poppe, A. Thermal Management for LED Applications; Springer Science Business Media: New York, NY, USA, 2014. [Google Scholar]
- Górecki, K.; Ptak, P. New Method of Measurements Transient Thermal Impedance and Radial Power of Power LEDs. IEEE Trans. Instrum. Meas. 2019, 69, 212–220. [Google Scholar] [CrossRef]
- Janicki, M.; Torzewicz, T.; Samson, A.; Raszkowski, T.; Napieralski, A. Experimental identification of LED compact thermal model element values. Microelectron. Reliab. 2018, 86, 20–26. [Google Scholar] [CrossRef]
- Narendran, N.; Gu, Y. Life of LED-Based White Light Sources. J. Disp. Technol. 2005, 1, 167–171. [Google Scholar] [CrossRef]
- Zhao, M.; Zhong, S.; Fu, X.; Tang, B.; Pecht, M. Deep Residual Shrinkage Networks for Fault Diagnosis. IEEE Trans. Ind. Informatics 2019, 16, 4681–4690. [Google Scholar] [CrossRef]
- Chang, M.-H.; Das, D.; Varde, P.; Pecht, M. Light emitting diodes reliability review. Microelectron. Reliab. 2012, 52, 762–782. [Google Scholar] [CrossRef]
- Blackburn, D.L. Temperature measurements of semiconductor devices—A review. In Proceedings of the Twentieth Annual IEEE Semiconductor Thermal Measurement and Management Symposium (IEEE Cat. No.04CH37545), San Jose, CA, USA, 11 March 2004; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2004; pp. 70–80. [Google Scholar]
- Székely, V. A new evaluation method of thermal transient measurement results. Microelectron. J. 1997, 28, 277–292. [Google Scholar] [CrossRef]
- JEDEC. Standard JESD51-52: Guidelines for Combining CIE 127-2007 Total Flux Measurements with Thermal Measurements of LEDs with Exposed Cooling Surface. 2012. Available online: https://www.jedec.org/document_search?search_api_views_fulltext=Standard+JESD51-52 (accessed on 12 October 2020).
- JEDEC. Standard JESD51-51: Implementation of the Electrical Test Method for the Measurement of Real Thermal Resistance and Impedance of Light-Emitting Diodes with Exposed Cooling. 2012. Available online: https://www.jedec.org/document_search?search_api_views_fulltext=Standard+JESD51-51 (accessed on 12 October 2020).
- CREE. Thermal Management of Cree® XLamp® LEDs. Application Note CLD-AP05REV 3M. Available online: https://www.cree.com/led-components/media/documents/XLampThermalManagement.pdf (accessed on 11 February 2021).
- Efremov, A.A.; Bochkareva, N.I.; Gorbunov, R.I.; Lavrinovich, D.A.; Rebane, Y.T.; Tarkhin, D.V.; Shreter, Y.G. Effect of the joule heating on the quantum efficiency and choice of thermal conditions for high-power blue InGaN/GaN LEDs. Semiconductors 2006, 40, 605–610. [Google Scholar] [CrossRef]
- Treurniet, T.; Lammens, V. Thermal management in color variable multi-chip led modules. In Proceedings of the Twenty-Second Annual IEEE Semiconductor Thermal Measurement And Management Symposium, Dallas, TX, USA, 14–16 March 2006; IEEE: New York, NY, USA, 2006. [Google Scholar]
- Alexeev, A.; Onushkin, G.; Linnartz, J.-P.; Martin, G. Multiple Heat Source Thermal Modeling and Transient Analysis of LEDs. Energies 2019, 12, 1860. [Google Scholar] [CrossRef]
- Wang, C.-P.; Kang, S.-W.; Lin, K.-M.; Chen, T.-T.; Fu, H.-K.; Chou, P.-T. Analysis of Thermal Resistance Characteristics of Power LED Module. IEEE Trans. Electron Devices 2013, 61, 105–109. [Google Scholar] [CrossRef]
- Górecki, K.; Zarębski, J.; Górecki, P.; Ptak, P. Compact Thermal Models of Semiconductor Devices—A Review. Int. J. Electron. Telecommun. 2019, 65, 151–158. [Google Scholar] [CrossRef]
- Poppe, A.; Zhang, Y.; Wilson, J.; Farkas, G.; Szabo, P.; Parry, J.; Rencz, M.; Szekely, V. Thermal Measurement and Modeling of Multi-Die Packages. IEEE Trans. Components Packag. Technol. 2009, 32, 484–492. [Google Scholar] [CrossRef]
- Schweitzer, D.; Ender, F.; Hantos, G.; Szabó, P.G. Thermal transient characterization of semiconductor devices with multiple heat sources—Fundamentals for a new thermal standard. Microelectron. J. 2015, 46, 174–182. [Google Scholar] [CrossRef]
- Rashid, M.H. Spice for Power Electronics and Electric Power; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Górecki, K.; Ptak, P. New dynamic electro-thermo-optical model of power LEDs. Microelectron. Reliab. 2018, 91, 1–7. [Google Scholar] [CrossRef]
- Poppe, A. Multi-domain compact modeling of LEDs: An overview of models and experimental data. Microelectron. J. 2015, 46, 1138–1151. [Google Scholar] [CrossRef]
- Poppe, A. Simulation of LED based luminaries using their multi-domain compact models and CTMs of their thermal environment. Microelectron. Reliab. 2017, 72, 65–74. [Google Scholar] [CrossRef]
- Hui, S.Y.; Qin, Y.X. A General Photo-Electro-Thermal Theory for Light Emitting Diode (LED) Systems. IEEE Trans. Power Electron. 2009, 24, 1967–1976. [Google Scholar] [CrossRef]
- Hui, S.Y.R.; Lee, A.T.L.; Tan, S.-C. New Dynamic Photo-Electro-Thermal Modeling of Light-Emitting Diodes With Phosphor Coating as Light Converter Part I: Theory, Analysis, and Modeling. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 771–779. [Google Scholar] [CrossRef]
- Górecki, K. Modelling mutual thermal interactions between power LEDs in SPICE. Microelectron. Reliab. 2015, 55, 389–395. [Google Scholar] [CrossRef]
- Górecki, K.; Ptak, P. Modelling LED lamps in SPICE with thermal phenomena taken into account. Microelectron. Reliab. 2017, 79, 440–447. [Google Scholar] [CrossRef]
- Poppe, A.; Farkas, G.; Gaál, L.; Hantos, G.; Hegedüs, J.; Rencz, M. Multi-Domain Modelling of LEDs for Supporting Virtual Prototyping of Luminaires. Energies 2019, 12, 1909. [Google Scholar] [CrossRef]
- Liu, S.-M.; Chou, Y.-C. Color Calibration for a Surrounding True-Color LED Display System by PWM Controls. IEEE Trans. Ind. Electron. 2014, 61, 6244–6252. [Google Scholar] [CrossRef]
- Ozluk, B.; Muslu, A.M.; Arik, M. A Comparative Study for the Junction Temperature of Green Light Emitting Diodes (LED)s. IEEE Trans. Compon. Packag. Manuf. Technol. 2019, 9, 2024–2035. [Google Scholar] [CrossRef]
- Onushkin, G.A.; Bosschaart, K.J.; Yu, J.; Van Aalderen, H.J.; Joly, J.; Martin, G.; Poppe, A. Assessment of isothermal electro-optical-thermal measurement procedures for LEDs. In Proceedings of the 2017 23rd International Workshop on Thermal Investigations of ICs and Systems (THERMINIC), Amsterdam, The Netherlands, 27–29 September 2017; IEEE: New York, NY, USA, 2017; pp. 1–6. [Google Scholar]
- Chen, H.T.; Tan, S.-C.; Hui, S.R. Analysis and Modeling of High-Power Phosphor-Coated White Light-Emitting Diodes With a Large Surface Area. IEEE Trans. Power Electron. 2014, 30, 3334–3344. [Google Scholar] [CrossRef]
- Lee, A.T.L.; Chen, H.; Tan, S.-C.; Hui, S.Y. New Dynamic Photo-Electro-Thermal Modeling of Light-Emitting Diodes With Phosphor Coating as Light Converter—Part II: Model Parameter Determination and Practical Verification. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 780–793. [Google Scholar] [CrossRef]
- Tao, X.; Hui, S.Y.R. Dynamic Photoelectrothermal Theory for Light-Emitting Diode Systems. IEEE Trans. Ind. Electron. 2011, 59, 1751–1759. [Google Scholar] [CrossRef]
- Chen, H.-T.; Lin, D.-Y.; Tan, S.-C.; Hui, S.Y.R. Chromatic, Photometric and Thermal Modeling of LED Systems With Nonidentical LED Devices. IEEE Trans. Power Electron. 2014, 29, 6636–6647. [Google Scholar] [CrossRef]
- Baran, K.; Różowicz, A.; Wachta, H.; Różowicz, S.; Mazur, D. Thermal Analysis of the Factors Influencing Junction Temperature of LED Panel Sources. Energies 2019, 12, 3941. [Google Scholar] [CrossRef]
- Baran, K.; Różowicz, A.; Wachta, H.; Różowicz, S. Modeling of Selected Lighting Parameters of LED Panel. Energies 2020, 13, 3583. [Google Scholar] [CrossRef]
- Farkas, G.; Bein, M.C.; Gaal, L. Multi domain modelling of power LEDs based on measured isothermal and transient I-V-L characteristics. In Proceedings of the 2016 22nd International Workshop on Thermal Investigations of ICs and Systems (THERMINIC), Budapest, Hungary, 21–23 September 2016; IEEE: New York, NY, USA, 2016; pp. 181–186. [Google Scholar]
- Górecki, K.; Ptak, P. Thermal, Photometric and Radiometric Properties of Multi-Color LEDs Situated on the Common PCB. Electronics 2020, 9, 1672. [Google Scholar] [CrossRef]
- O’Donnell, K.P.; Chen, X. Temperature dependence of semiconductor band gaps. Appl. Phys. Lett. 1991, 58, 2924–2926. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Avenas, Y.; Dupont, L.; Khatir, Z. Temperature Measurement of Power Semiconductor Devices by Thermo-Sensitive Electrical Parameters—A Review. IEEE Trans. Power Electron. 2012, 27, 3081–3092. [Google Scholar] [CrossRef]
- Székely, V.; Tarnay, K. Accurate algorithm for temperature calculation of devices in nonlinear-circuit-analysis programs. Electron. Lett. 1972, 8, 470. [Google Scholar] [CrossRef]
- Székely, V. Accurate Calculation of Device Heat Dynamics: A Special Feature of the TRANZ-TRAN Circuit-Analysis Program. Electron. Lett. 1973, 9, 132–134. [Google Scholar] [CrossRef]
- Zhu, H.; Lu, Y.; Wu, T.; Guo, Z.; Zhu, L.; Xiao, J.; Tu, Y.; Gao, Y.; Lin, Y.; Chen, Z. A Bipolar-Pulse Voltage Method for Junction Temperature Measurement of Alternating Current Light-Emitting Diodes. IEEE Trans. Electron Devices 2017, 64, 2326–2329. [Google Scholar] [CrossRef]
- Jakopovid, Z.; Bencić, Z.; Koncar, R. Identification Of Thermal Equivalent—Circuit Parameters For Semiconductors. In Proceedings of the 1990 IEEE Workshop on Computers in Power Electronics, Lewisburg, PA, USA, 5–7 August 1990; IEEE: New York, NY, USA, 2005; pp. 251–260. [Google Scholar]
- Datasheet DeltaOhm HD2302. Available online: https://www.deltaohm.com/en/wp-content/uploads/document/Del-taOHM-2302.0-Portabe-Luxmeter-Datasheet-en.pdf (accessed on 12 October 2020).
- Górecki, K.; Górecki, P. The Analysis of Accuracy of Selected Methods of Measuring The Thermal Resistance of IGBTs. Metrol. Meas. Syst. 2015, 22, 455–464. [Google Scholar] [CrossRef][Green Version]
- Lisiecki, J.; Kłysz, S. Estimation of Measurement Uncertainty. Res. Work. Air Force Inst. Technol. 2007, 22, 62. [Google Scholar] [CrossRef]
- OSRAM. LT W5SM, LY W5SM, LW W5SM, LR W5SM, LB W5SM, LCW W5SM Golden Dragon, Datasheet. 2020. Available online: https://www.osram.com/ecat/Golden%20DRAGON%C2%AE%20Plus%20LCW%20W5AM/com/en/class_pim_web_catalog_103489/global/prd_pim_device_2402630/ (accessed on 11 February 2021).
- Oettinger, F.F.; Blackburn, D.L. Semiconductor Measurement Technology: Thermal Resistance Measurements; NIST/SP-400/86; U.S. Department of Commerce: Washington, DC, USA, 1990.
- Auf der Maur, M.; Pecchia, A.; Penazzi, G.; Rodrigues, W.; Di Carlo, A. Efficiency Drop in Green InGaN/GaN Light Emitting Diodes: The Role of Random Alloy Fluctuations. Phys. Rev. Lett. 2016, 116, 27401. [Google Scholar] [CrossRef] [PubMed]
- Liebhard, J.H., IV; Liebhard, J.H., V. A Heat Transfer Textbook, 3rd ed.; Phlogiston Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Górecki, K.; Górecki, P. Nonlinear Compact Thermal Model of the IGBT Dedicated to SPICE. IEEE Trans. Power Electron. 2020, 35, 13420–13428. [Google Scholar] [CrossRef]
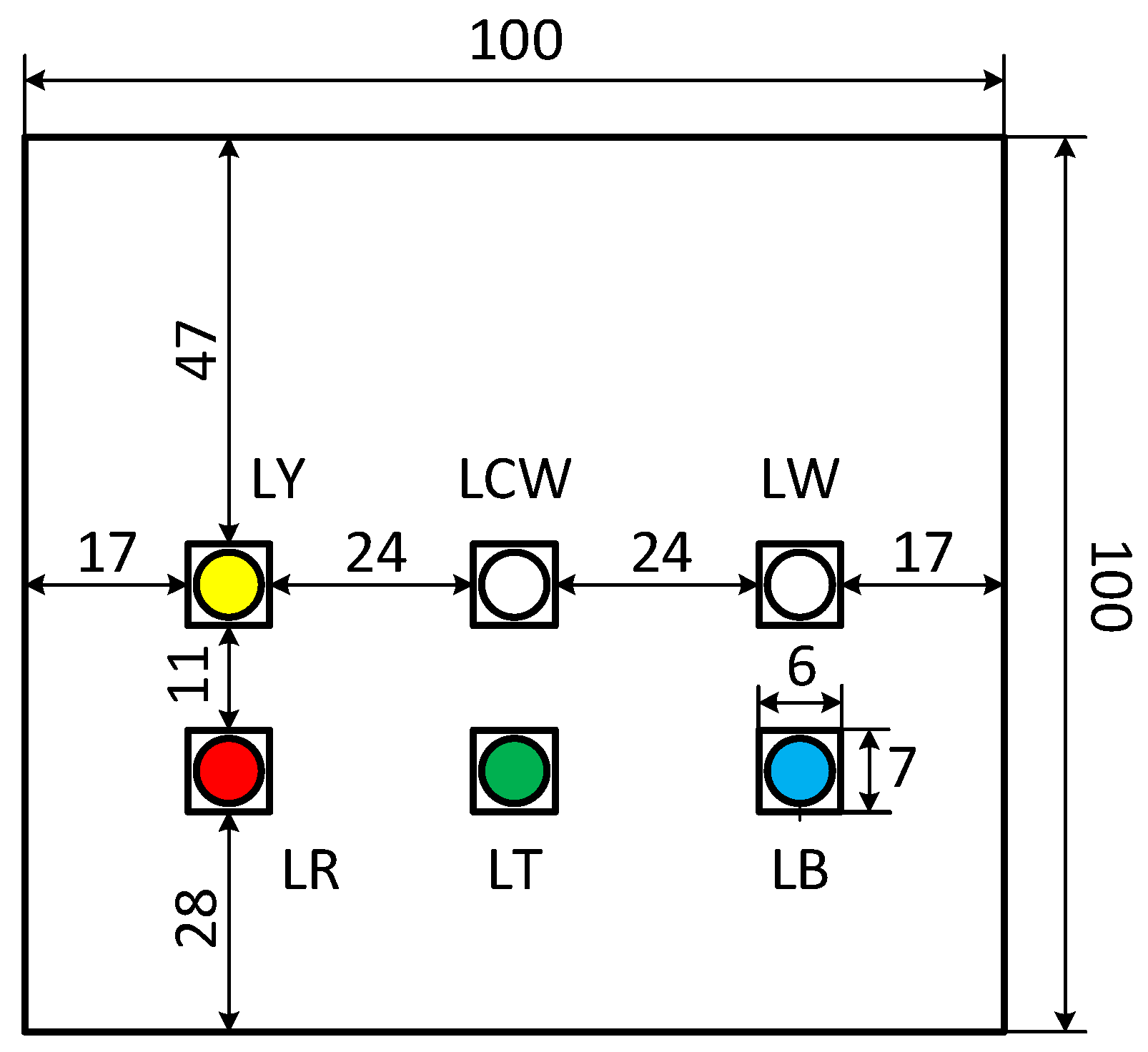
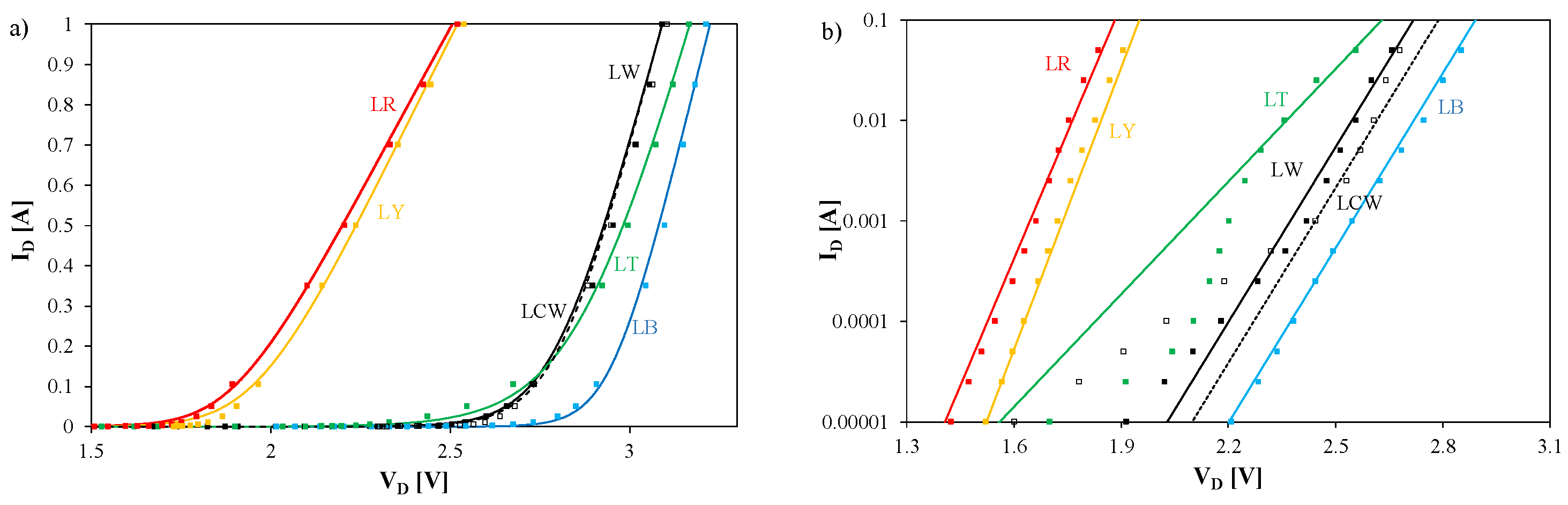
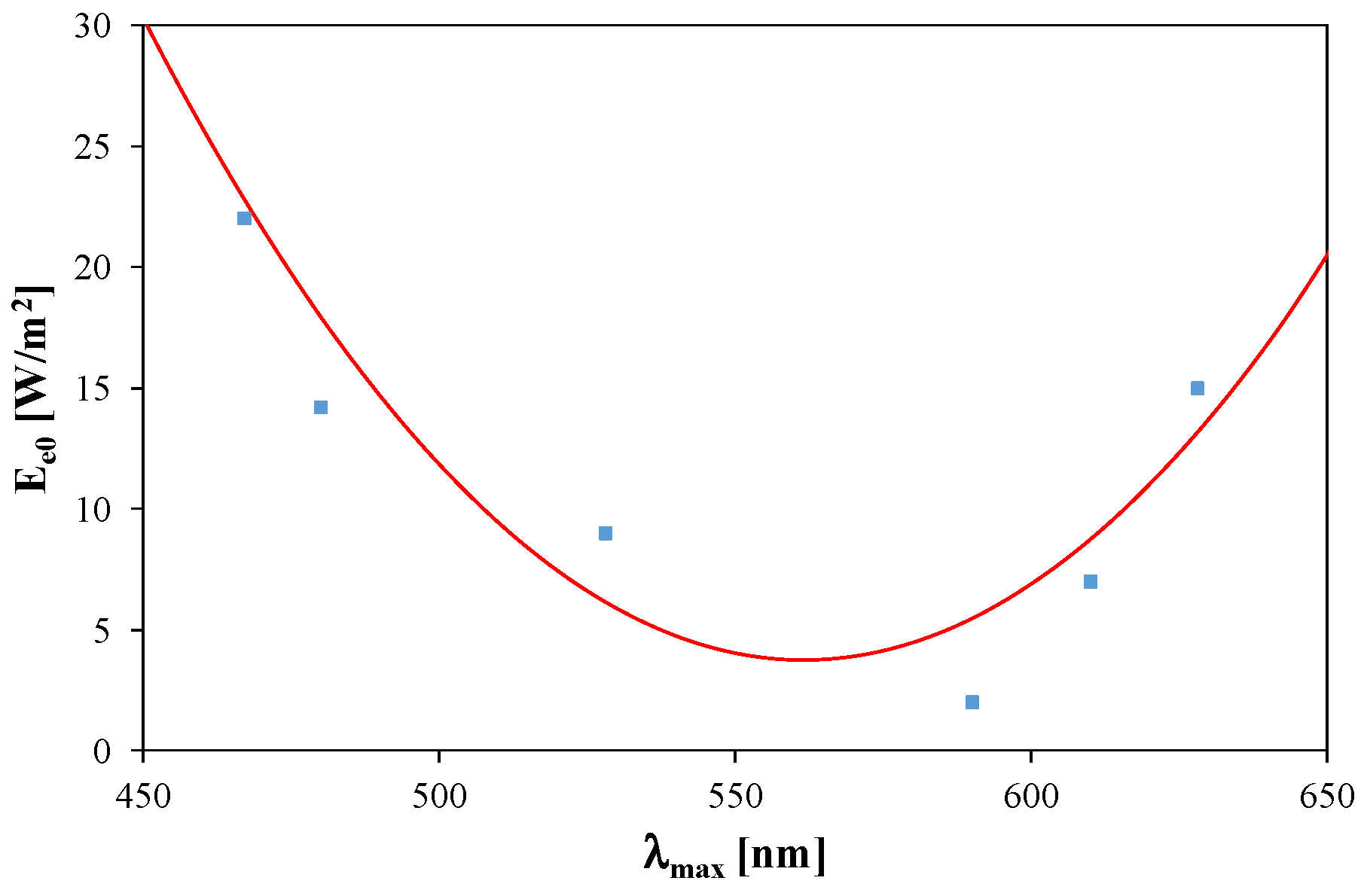
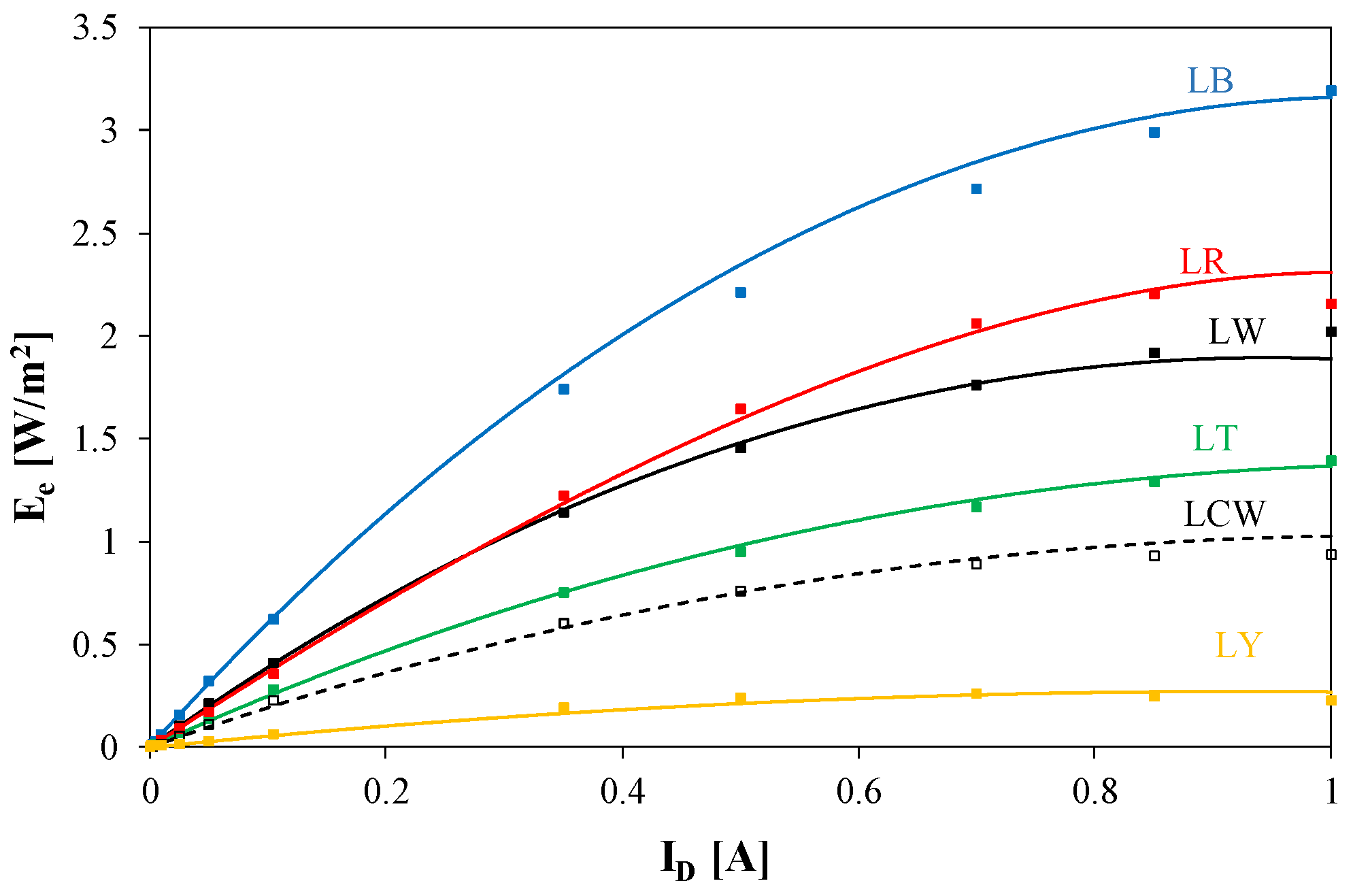
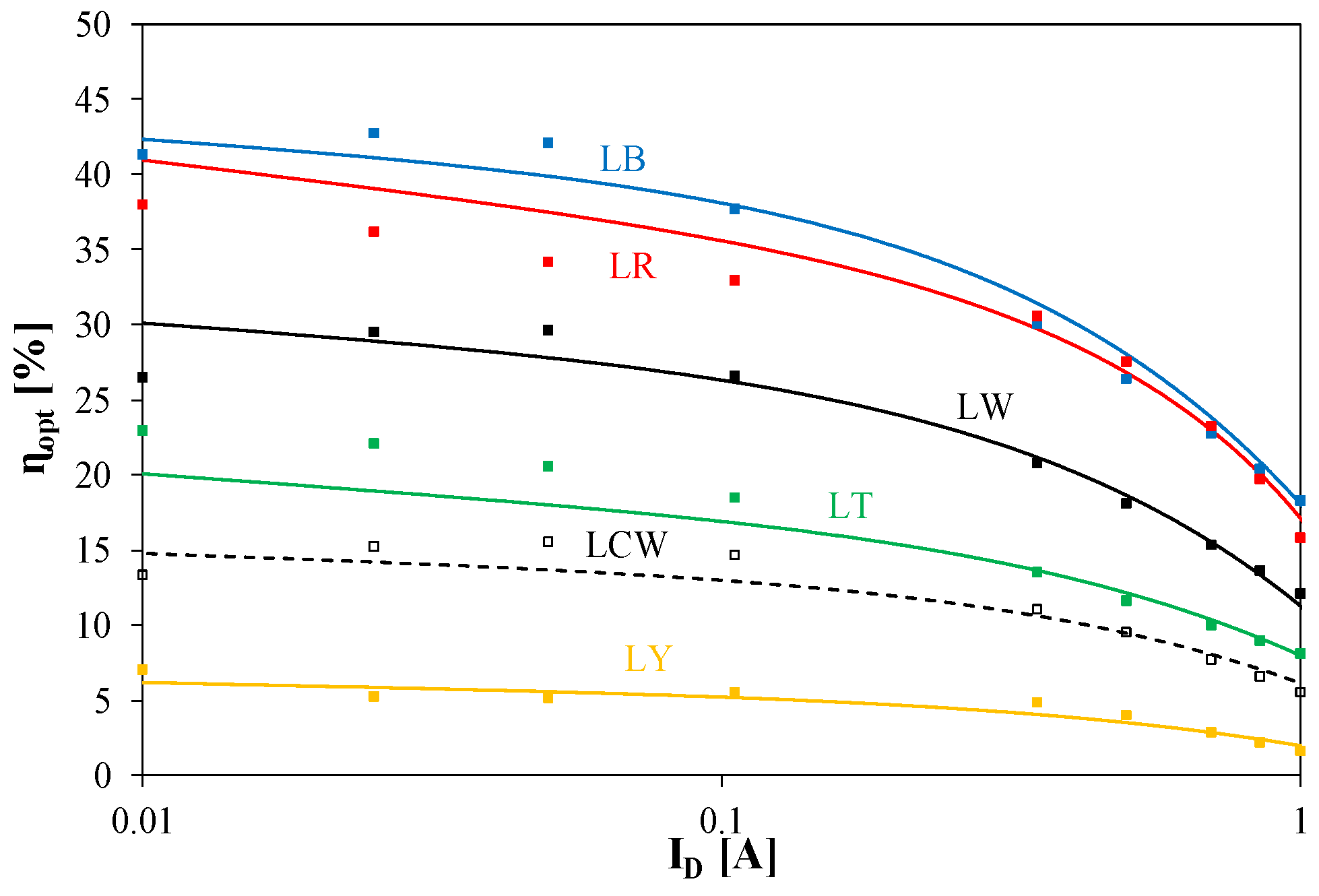
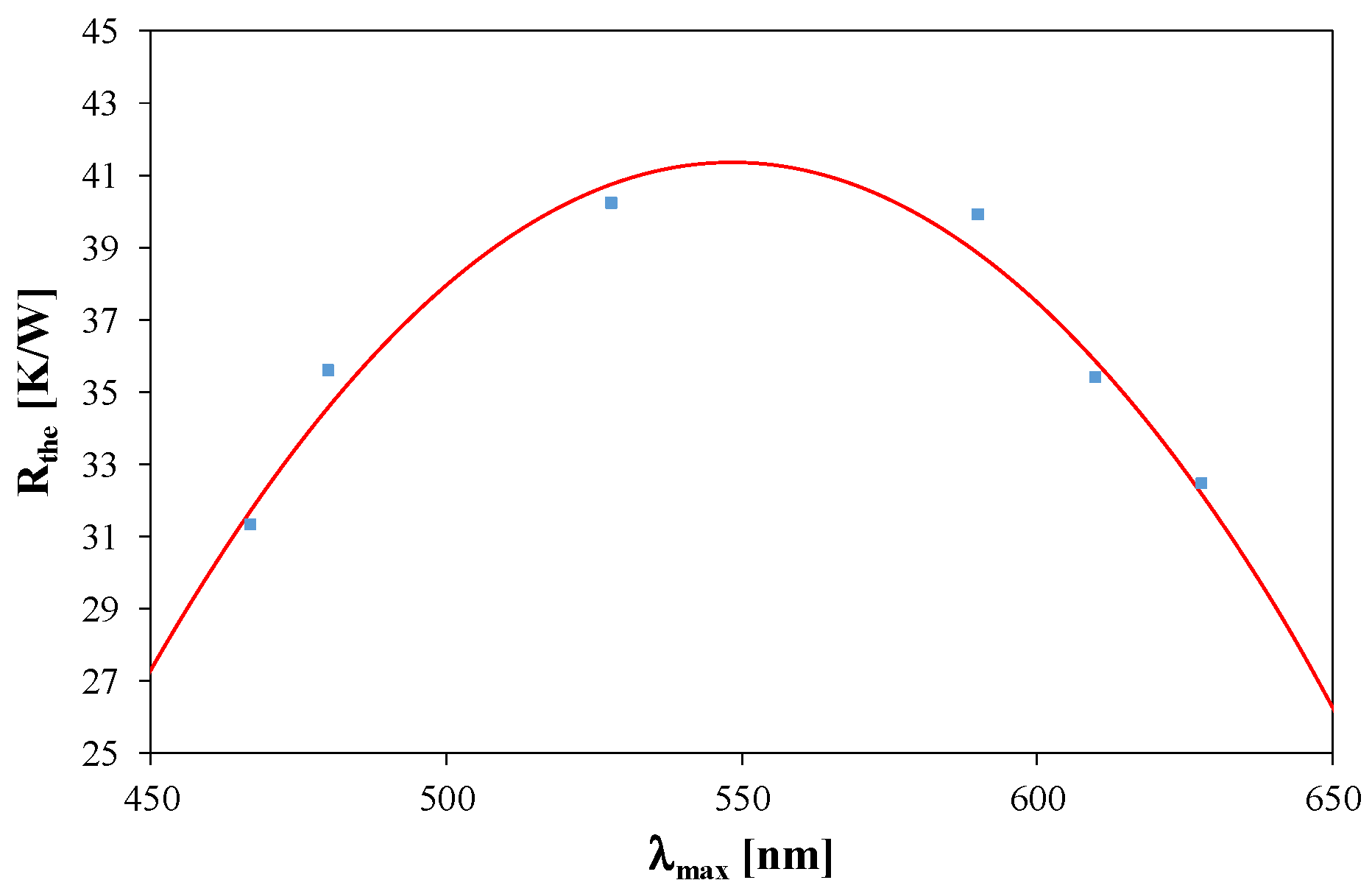
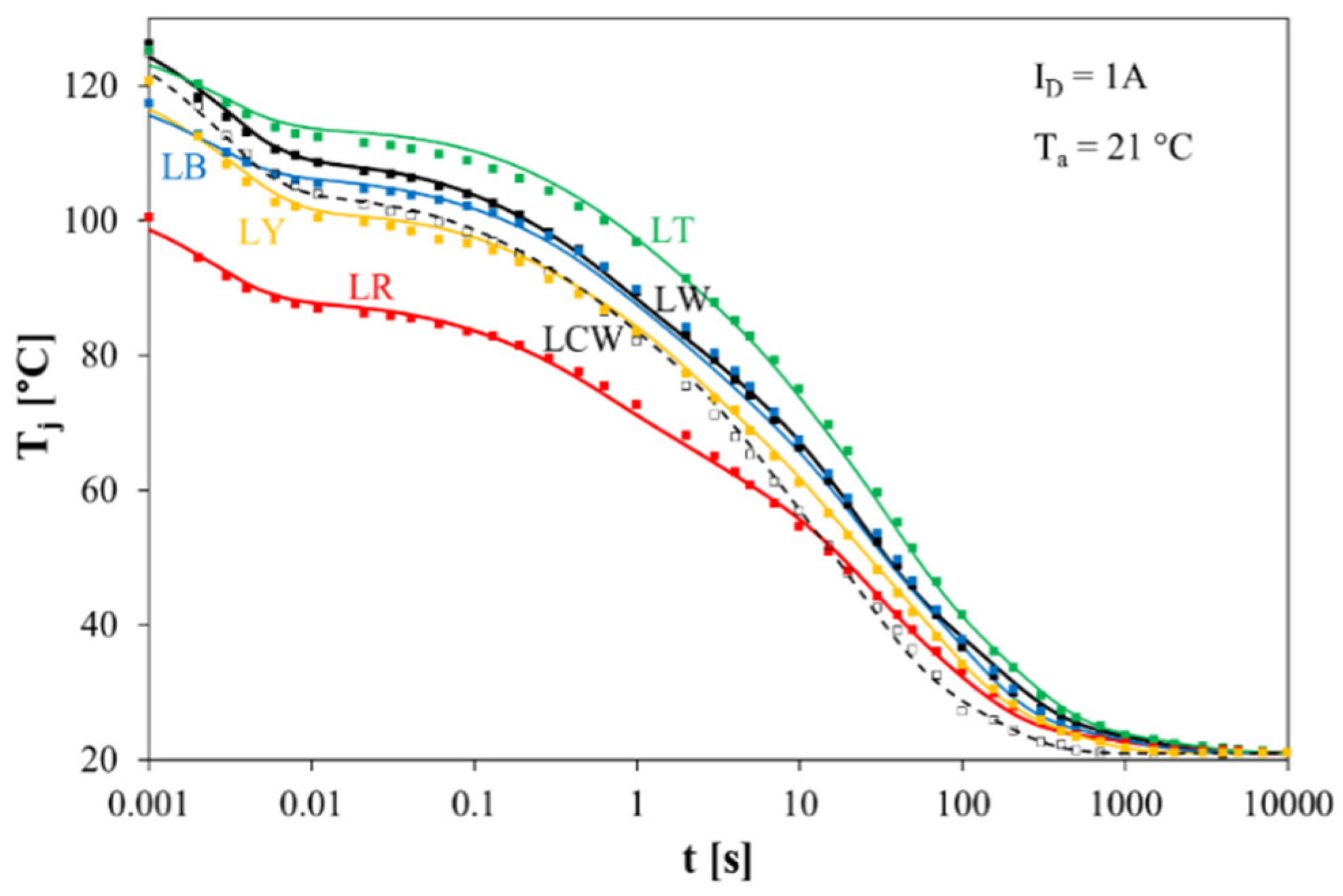
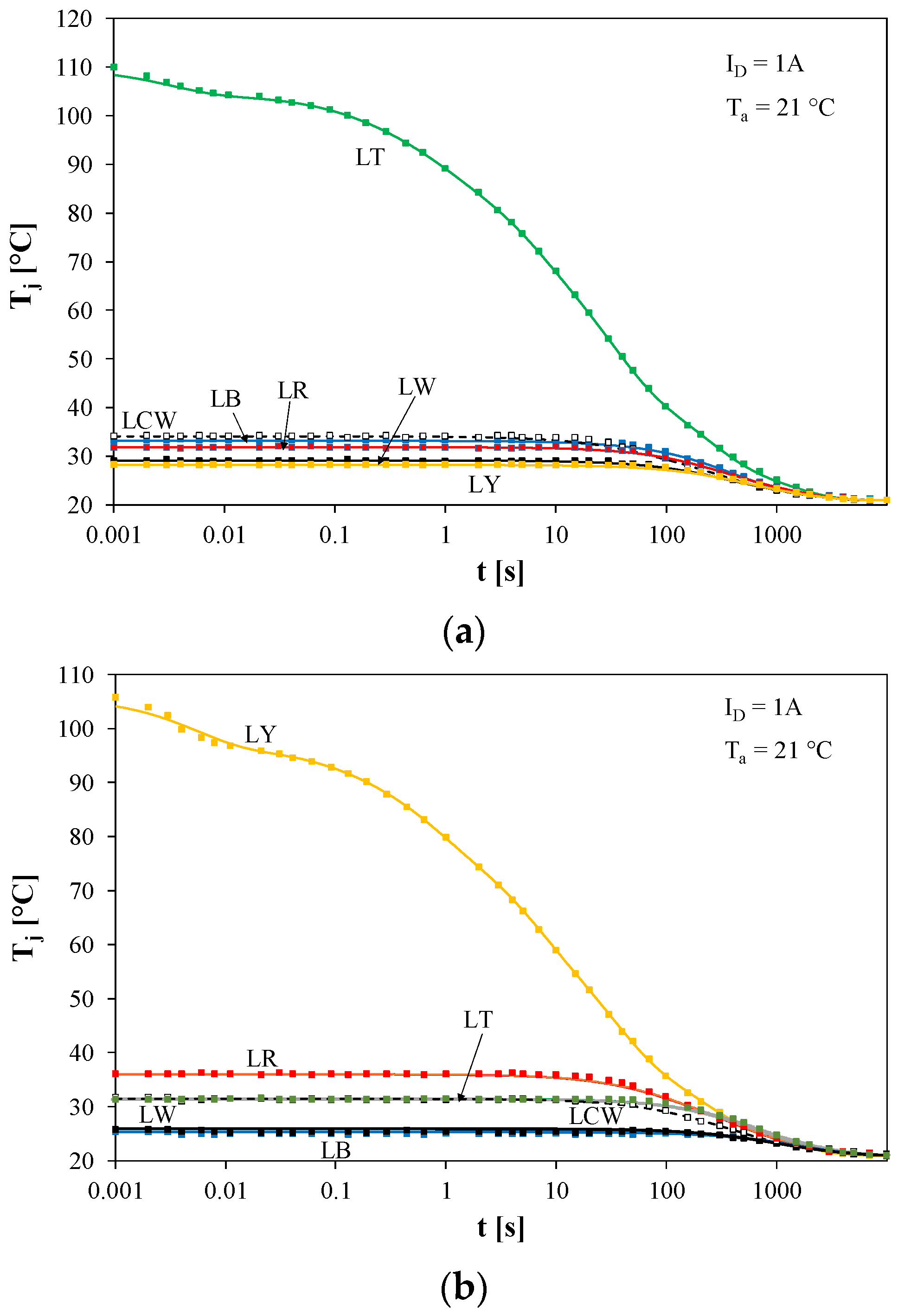
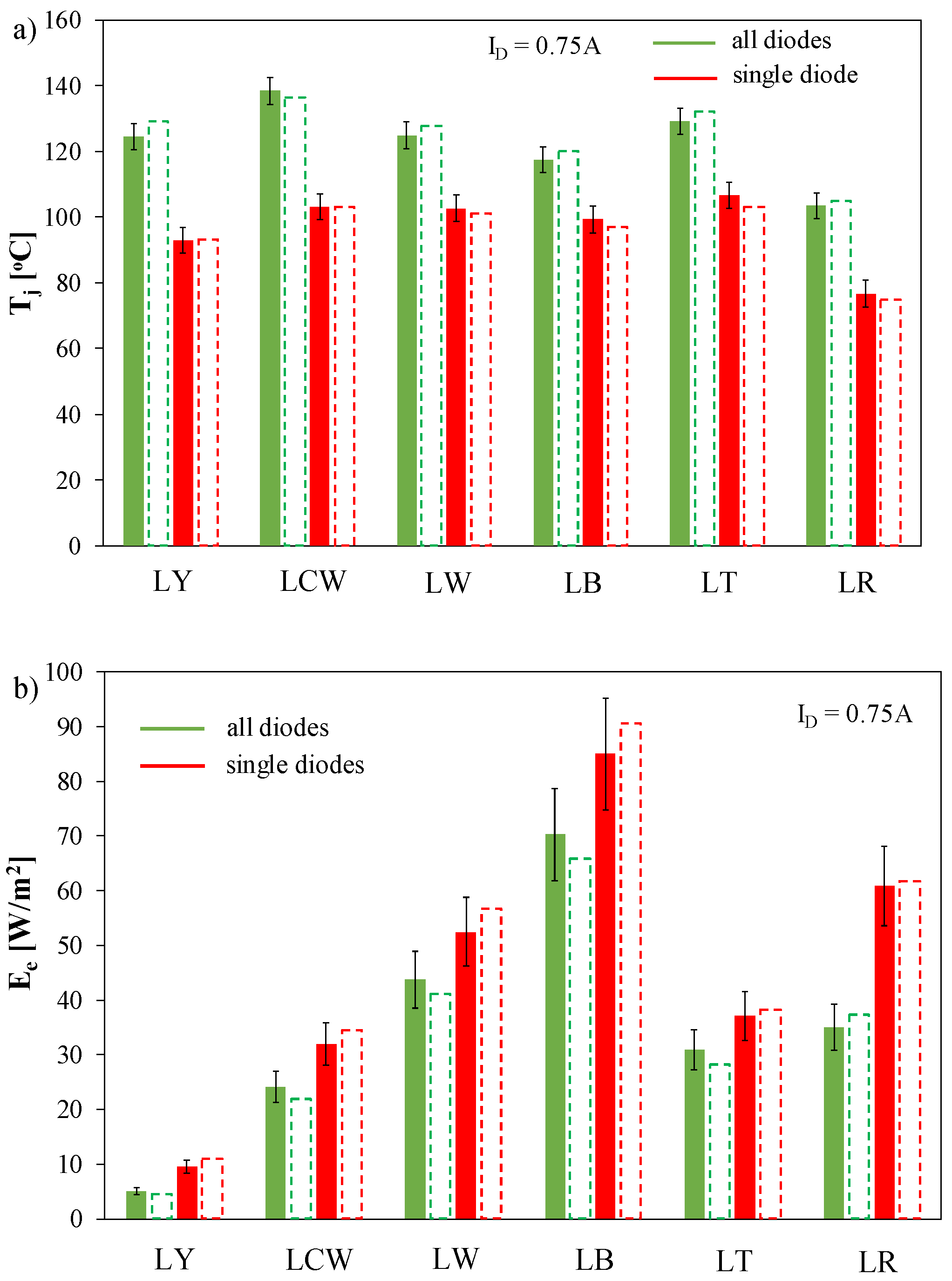
| Diode | LR | LY | LT | LB | LW | LCW |
|---|---|---|---|---|---|---|
| Rthj-s (K/W) | 6.5 | 6.5 | 6.5 | 5 | 5 | 5 |
| ɸv (lm) | 39–71 @400 mA | 39–82 @400 mA | 52–97 @350 mA | 15–33 @350 mA | 71–130 @350 mA | 45–97 @350 mA |
| λmax (nm) | 628 | 590 | 528 | 467 | 480 | 610 |
| Diode | LR | LY | LT | LB | LW | LCW |
|---|---|---|---|---|---|---|
| Vgo (V) | 2.04 | 2.16 | 2.63 | 3.37 | 2.79 | 2.86 |
| I0 (A) | 1.1 | 1.93 | 0.06 | 220 | 0.26 | 0.5 |
| n | 3 | 3.3 | 5.3 | 2.4 | 3.4 | 3.4 |
| RS0 (Ω) | 0.46 | 0.42 | 0.15 | 0.25 | 0.19 | 0.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Górecki, K.; Ptak, P. Compact Modelling of Electrical, Optical and Thermal Properties of Multi-Colour Power LEDs Operating on a Common PCB. Energies 2021, 14, 1286. https://doi.org/10.3390/en14051286
Górecki K, Ptak P. Compact Modelling of Electrical, Optical and Thermal Properties of Multi-Colour Power LEDs Operating on a Common PCB. Energies. 2021; 14(5):1286. https://doi.org/10.3390/en14051286
Chicago/Turabian StyleGórecki, Krzysztof, and Przemysław Ptak. 2021. "Compact Modelling of Electrical, Optical and Thermal Properties of Multi-Colour Power LEDs Operating on a Common PCB" Energies 14, no. 5: 1286. https://doi.org/10.3390/en14051286
APA StyleGórecki, K., & Ptak, P. (2021). Compact Modelling of Electrical, Optical and Thermal Properties of Multi-Colour Power LEDs Operating on a Common PCB. Energies, 14(5), 1286. https://doi.org/10.3390/en14051286