Abstract
Tidal energy is one of the major sources of renewable energy. To accelerate the development of tidal energy, improved designs of Tidal Current Turbine (TCT) are necessary. The effect of tower on performance and wake of TCT is investigated using Computational Fluid Dynamics (CFD) simulations. Transient analysis with transient rotor stator frame change model and shear stress transport turbulence model are utilized in ANSYS CFX. An experimentally validated numerical model with full scale tidal turbine with a blockage ratio of 14.27% and Tip Speed Ratio (TSR) 4.87 is used to simulate the effect of different tower diameters on performance and wake. The effect of different tower diameters is quantified in terms of coefficient of performance (CP). Coefficient of performance for a 3.5 m tower diameter is 0.472 which is followed by 3, 2.5 and 2 m with coefficients of performance of 0.476, 0.478 and 0.476 respectively. Similarly, the coefficient of thrust (CT) on the rotor for 3.5 m tower diameter is 0.902, for 3 m diameter 0.906 and for 2.5 and 2 m diameters are 0.908 and 0.906 respectively.
1. Introduction
Tidal current energy is one of the most predictable forms of renewable energy with significant global potential. Different types of machines can be used to extract this energy from the tidal currents. The widely investigated and reliable one is the Horizontal Axis Tidal Current Turbine (HATCT) [1]. These turbines can be fixed on different types of support structures. Being a part of the whole turbine structure, these supports may affect the turbine performance, blade loads and downstream wake.
Several factors which may affect the performance of tidal current turbines are scrutinized by researchers to further the understanding of turbine design and performance. In this regard, Mujahid et al. quantified the effect of boundary proximity and blockage ratio on the performance of HATCT by using RANS CFD in ANSYS CFX [2]. This study suggested that the performance of the turbine does not change with variation in the blockage ratio for turbines operating in the lower TSR regime. However, a significant increase was observed in the turbine power coefficient with increasing blockage ratios for turbines operating in optimum and higher TSR regimes. Consul, Claudio et al. performed similar investigations for their cross flow marine turbine [3]. Weichao Shi et al. added another important aspect to the field of RANS CFD simulations of TCT and characterized the discernible effects of flow separation on the predicted performance [4]. Jing Liu et al. focused their investigations on the structural design aspects of turbine for its effects on the performance. Their study presented the effect of blade twist and nacelle shape on the performance of TCT through RANS CFD simulations. Results of this study suggested that blades with a twist angle may extract 1.2% more power compared to untwisted blade. Whereas, the nacelle shape has no significant effect on the performance of TCT [5].
The support tower is one of the major cost components of TCT. Therefore, the efficient design of the support tower would be essential to the overall design developments in TCT’s. The design efficiency should not only be limited to the cost and ease of installation but also in terms of its influence on the turbine performance. Although, it is widely believed that the support structure may significantly influence the turbine performance qualitatively as well as quantitatively. However, the research efforts in this direction are limited compared to those focusing the turbine blades for enhancing the performance and reducing the cost of the technology.
The limited number of research studies focusing the turbine support structure has investigated the effect of tower shape, tower cross section and position on the performance of Tidal Current Turbines. In one such study, C. Frost investigated the effect of flow direction and the proximity of tower to rotor on the performance of HATCT by using Reynolds Averaged Navier–Stokes Computational Fluid Dynamics (RANS CFD) to show that both have significant effect on the performance [6]. Similarly, Angus C. W. Creech used CFD with Large Eddy Simulation (LES) for investigating the influence of support structure on the performance and wake characteristics [7]. A. Mason-Jones also utilized RANS CFD numerical model to study the influence of different support tower shapes and velocity shear profile on the performance of HATCT [8]. Although, some of the investigated support shapes were unrealistic, such as diamond aerofoilic and elliptical. However, some more realistic shapes, such as square and circular, were also investigated to characterize their influence on the turbine performance and near wake. Subhash Muchala extended these investigations to tidal turbine arrays and suggested that a support tower may reduce the array power output by about 40% [9]. Recently, Jan Badshah [10] investigated the influence of tower elasticity on the performance of TCT and characterized the fatigue character of a monopile support tower through coupled FSI simulations. The investigations revealed that the variations in power and thrust coefficient of TCT considerably increase due to tower elasticity. The study also presented a very crucial finding that direct thrust force on the tower varies by more than 100% during a turbine rotation cycle. The development of tidal energy technology would require one to lower the cost of technology. The developers are looking into the prospects of large size TCT’s as one of the ways to achieve this objective [11]. However, this would require more detailed information about the influence of support tower on the turbine performance and loads on the blades as well as the support tower itself. Additionally, the influence of the support tower on the downstream wake and its implications for downstream array devices would be critical for further development in the tidal energy technology. This paper attempts to address one of these basic issues and investigates the effect of the tower’s dimeter on the performance and wake of TCT.
This paper is divided into seven sections with Section 2 describing the numerical method utilized for the research. Discussions on dimensionless performance parameters are presented in Section 3. Detail of the mesh setup, sensitivity, boundary conditions and computational domain are provided in Section 4 and Section 5. Important results obtained from this research are presented and discussed in Section 6. The effect of tower diameter on the performance is analyzed in terms of the coefficient of performance, while the effect of tower diameter on the wake is assessed in terms of the downstream velocity deficit. The main conclusions drawn from this research are presented in Section 7.
2. Numerical Method
ANSYS CFX is used to conduct transient CFD simulations by solving the incompressible RANS equations with a second order advection scheme in the finite volume method. The use of RANS CFD simulations for TCT is not novel and the methodology is quite well known and frequently used; for example, in the studies in ref. [12,13,14]. ANSYS CFX employs a node centered finite volume method for solving the governing Navier–Stokes equations. The computational fluid domain is first discretized into a finite set of control volumes and then the continuity, momentum and energy equations are solved for these sets of control volumes.
The methodology is adopted such that the simulations are initially performed in a steady state using Multiple Frame of Reference (MFR) approach. This is accomplished in ANSYS CFX using a frozen rotor frame change model. In this approach, the governing equations are solved in a rotating reference frame and the computational grid is not physically rotated. In a Frozen Rotor model the two frames connect such that their relative position is fixed throughout the calculation. This provides a steady state solution to the Multiple Frame of Reference problem and requires less computational effort [15]. Blades of the turbine are assumed to be neutrally buoyant and the influence of gravity is also neglected. Additionally, the density of water is assumed to be constant and the cavitation is neglected. A Shear Stress Transport (SST) turbulence model is used with an automatic wall function. The SST model belongs to the group of eddy viscosity models, and considers the Reynolds stress term to be proportional to the mean rate of deformation: The SST model combines the Willcox model and standard model to utilize the advantages of both models. This is accomplished using a blending function to apply the model in the viscus sub layer region of the no slip boundary and the model in outer part of the boundary layer. The SST model is known to better predict the onset and amount of flow separation under adverse pressure gradients with better convergence [16]. The limitation of these models is that they are based on the Boussinesq hypothesis with the assumption that turbulence is isotropic. This assumption is inappropriate for large turbulence length scales [17]. Therefore, these models are known to be suboptimal in the near wake due to the presence of large turbulence structures. Contrarily, the Large Eddy Simulation (LES) type models solve the spatially averaged Navier–Stokes equations. In this approach, the large size eddies (i.e., turbulence structures) are directly resolved and eddies smaller than the mesh are modelled. The LES models have been recently used for modeling the spectral distribution of blade bending moments for TCT’s [18,19,20]. However, the requirement of computational resources and efforts are infeasible for most applications. A review of the previous RANS CFD modelling works on tidal turbine over the last decade reveal that the based Shear Stress Transport (SST) model has generally performed better for tidal turbine applications [2,21]. Therefore, the based Shear Stress Transport (SST) model is also used for all the simulations in this study. The results file of the steady state simulation is used as the initial condition for transient simulation. The transient model (time dependent) simulates the rotor in more accurate way as compared to steady state model. This is accomplished using transient rotor stator frame change model and sliding mesh technique in ANSYS CFX. The 2nd order backward Euler time stepping scheme is used to solve the transient term. In a transient rotor stator frame change model, components on both sides of the interface move relative to each other. Although, this approach is more realistic but its computational cost is high and requires higher disk storage compared to a frozen rotor model. The inner cylindrical domain which contains the rotor is physically rotated in a transient rotor stator change model after every time step by utilizing the sliding mesh method. For the rotating domain the mesh motion is enabled with regions of motion specified and the mesh displacement is set relative to the previous mesh.
3. Performance Parameter
In this section two different dimensionless parameters are discussed which are used for the performance of tidal current turbine. First, tip speed ratio is discussed. TSR is the ratio of blade tip to the mean flow velocity
V denotes the velocity of the main stream flow in m/s, and R denotes the radius of the rotor, whereas ω is angular speed of the rotor in rad/s.
The performance of tidal current turbine usually predicts through the use coefficient of power. Coefficient of power is the ratio of the power extracted by the rotor to the power available in the stream. It is denoted mathematically as
P denotes the power extracted by the rotor, denote the density of the water, A denotes the swept area of the rotor and V denotes the velocity of the water mean flow.
The coefficient of thrust is calculated through the following equation
where T denotes the axial force on the rotor.
4. Mesh Set Up
Hybrid mesh is generated with a selective body meshing technique. This meshing technique used is not rare, but is also successfully used by Nitin et al. [22]. The external stationary domain and turbine blades are meshed with hexagonal structured mesh. Only a small portion of 25 m of the external stationary domain in the vicinity of turbine is tetrahedral meshed. The combination of hex and tet mesh is shown in Figure 1a. Figure 1b shows mesh on the turbine structure with tet mesh on hub, nacelle and tower. Conformal mesh is generated on the shared faces between bodies by converting the geometrical model into a single multi body part. The trailing edge and leading edge of the blade is divided into 190 and 180 divisions, whereas the edges of the tip are divided into 90 divisions. The tetrahedral element is 100 mm for the hub and nacelle, and 80 mm for tower is used. The tetrahedral element of 260 mm is set for the internal rotating domain. The external stationary domain is divided into three portions IN, MID and OUT. The MID portion is meshed with the tetrahedral element with an element size of 1000 mm. The length of the OUT and IN portion is divided into 193 and 45 divisions. Width and height of all three portions is same; width is divided into 40 divisions, whereas height is divided into 30 divisions. The bounder layer is applied at the blade surface in order to precisely solve the flow over the blade. The first layer thickness method is utilized by specifying 0.7 mm to the height of first layer thickness and 11 layers of prism are used with a growth rate of 1.2 which is in the prescribed range of 2 ≤ y plus ≤ 300 to take the full advantage of the automatic wall function switch [23]. The total number of elements in the internal rotating domain and external stationary domain is 7 × 106 elements.
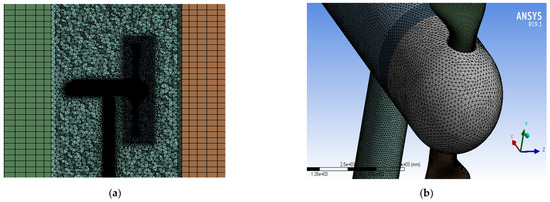
Figure 1.
(a) Mesh detail of external and internal rotating domain (b) mesh of turbine.
5. Computational Domain with Boundary Condition
The computational domain for the problem is set to correspond with the actual channel experiment described in [24]. However, the twin rotor configuration of the original RM1 turbine design is remodeled as a single rotor turbine. This is evident from Figure 2, where a cross sectional view of the computational domain shows that the turbine is located near the side wall of the domain and not at the center. This approach reduces the computational cost of the problem by taking advantage of the design symmetry and does not influence results of the simulation. This approach is not rare and has also been previously used in several other studies for the RANS CFD simulation of the RM1 turbine [25,26,27]. The computational domain is divided into two parts in this study; Internal Rotating Domain (IRD) and External Stationary Domain (ESD). The external stationary domain is divided into three portions, IN, MID and OUT. The dimensions of the ESD are (500 × 55 × 40 m3). The diameter of the cylindrical IRD is 24 m where as its thickness is 5.4 m.
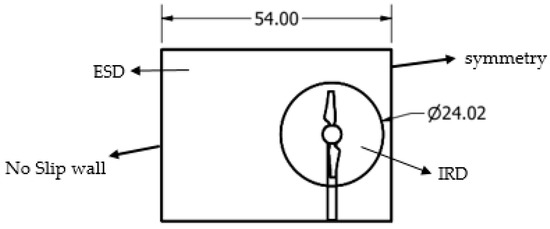
Figure 2.
Front view of computational domain with External Stationary and Internal Rotating Domain.
The blockage ratio of the computational domain, neglecting the blockage due to tower, is 14.3%, which is similar to the experimental channel. However, if we add the contribution of the tower in the total blockage ratio then it would increase to 16.1%, 16.5%, 17% and 17.5% for the 2, 2.25, 3 and 3.5 m tower, respectively. This change in blockage ratio in the range 16.1–17.5% is marginal and is not expected to have any major influence on the turbine performance and downstream wake. This fact is clearly established in the blockage study of this (RM1) turbine in an earlier study by Badshah et al. [2]. Additionally, the argument that this marginal change of 1.4% in the blockage ratio would not much influence the turbine performance and wake is also supported by the experimental study of Chen and Liou [28] and the RANS CFD study of Nitin and Arindam [22] and Koh and Ng [29].
The turbine rotor is enclosed by IRD, in order to model the rotating rotor by using MRF. The back face of the hub is grounded at (x, y, z) = (0, 0, 0), which is used as a domain reference. The rectangular ESD inlet is specified, utilizing a turbulent intensity of 5% and viscosity ratio of 10 thought out all simulations. The outlet BC is specified with 0 pa relative static pressure at ESD for making the boundary conditions robust [30]. On the surfaces of hub, blades, tower and nacelle no slip the wall boundary condition is applied; similarly, no slip wall boundary condition is applied on the one side wall and on the bottom of the plane of the domain. No slip wall boundary condition considers the velocity adjacent to the wall as zero m/s; it is the most commonly used wall boundary condition [30]. At the top of the ESD free slip, a wall boundary condition is applied which assumed that velocity of the water adjacent to the wall is not zero, or in other words the effect of wall friction is neglected; this may result in poor prediction of the performance of TCT. However, if the clearance between blade tip and top surface is greater than or equal to one rotor diameter then the free surface effect on the performance prediction is negligible and is widely used [22,31,32]. Three interfaces are defined at three contacting faces of the IRD and ESD. A transient rotor stator frame change model is used with a general connection interface model, and general grid interface (GGI) method is used to connect the meshes. For the rotating side of all three interfaces boundary condition interface is specified and the mesh motion is also activated. The mesh motion is activated for the no slip wall boundary which is applied to the blade and hub inside the IRD and wall velocity relative to the frame is selected. A complete demonstration of the computational domain is manifest in the Figure 3.
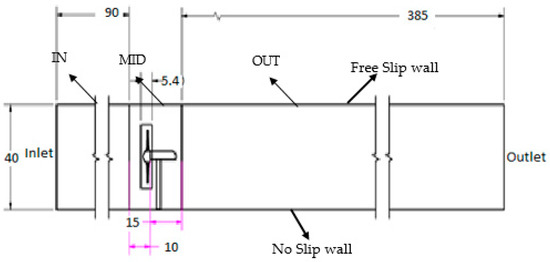
Figure 3.
Demonstration of computational domain.
6. Results and Discussion
The RANS CFD simulation methodology adopted in this paper is already temporally and spatially verified and validated with the circulating water channel experimental measurements by the authors in Badshah [33]. The performance of turbine for 10 complete rotations is modelled in CFD simulations for different tower diameters as shown in Figure 4. The time series show a drift in cycles representing the power coefficient values for the first seven revolutions. The drift in power coefficient values cycle progressively decreases with diminishing marginal drift after the 7th revolution. This is an indication that the values of predicted power coefficient were initially unstable but attained the convergence from 7–10 revolutions. The CFD simulations are generally run for prolonged durations to avoid such instabilities in the convergence of results. Although, an absolute convergence is generally very demanding due to the simulation time and computational resources requirements. However, to limit the uncertainties associated with the results, we have used data from the last (10th) revolution for the discussion on results in this study. Figure 5 shows that the coefficients of performance of turbine during last rotation for different tower diameters. The rotation starts with the position of blades vertically aligned with the tower and ends with the same position after one rotation corresponding to 360°. As rotation proceeds the blades move from a vertically aligned to a horizontal position. The Y-axis represents a corresponding coefficient of performance during blade rotations. Figure 5a shows the variation of CP for tower diameter of 2 and 2.5 m while Figure 5b for 3 and 3.5 m. The coefficient of performance in all diameter cases increases as the blades move from vertical to horizontal positions and decrease as the blades tend towards vertical positions. This phenomenon is called the tower shadow effect, which is also experienced by other researchers in [1,6,7]. The tower diameter has little effect on the overall performance of tidal current turbine. However, the effect exists. With the increase of diameter from 2 to 3.5 m, the increment of 0.5 m the coefficient of performance has been increased. The maximum CP of 0.522 is observed at 2.5 m. This may be due to the combined effect of blockage at this point. The performance of the turbine with the decreasing tower diameter is increasing because the tower shadow effect of the tower is decreasing which affects the performance. Apart from this, the quality of the power extraction is highly affected, as the diameter of the tower increase the fluctuation of the power extraction increase. These fluctuations in the power extraction may have an effect on the fatigue life of the turbine and tower [6,33,34].
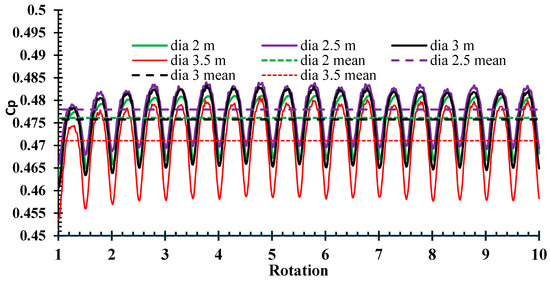
Figure 4.
Coefficient of performance for different tower diameter for 10 rotations.
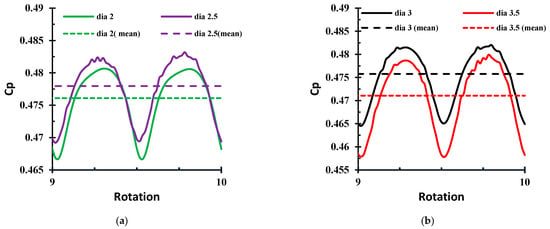
Figure 5.
Coefficient of performance for tower having diameter (a) 2 and 2.5 m (b) 3 and 3.5 m.
Table 1 presents quantitative evaluation of the mean power coefficient ad its fluctuation from the mean value during a rotation cycle for turbines with different tower diameters. The fluctuations from the mean CP are high for the greater diameter. The fluctuation from the mean CP for a tower diameter of 3.5 m is 17.1%, followed by 16.1% for a 3 m diameter tower, and 15.6% and 15.7% for a 2.5 and 2 m diameter, respectively. The difference in CP fluctuation between turbines with towers of 2 and 2.5 m diameter is 0.1%, which is negligible because it is CFD study and CFD results account for small error. Similarly, the difference in fluctuation between 2.5 m diameter tower and 3 m diameter tower is 0.5 and the differences between 3 m diameter and 3.5 m diameter is 1 when the diameter of the tower is increased from 2 to 3.5 m and the fluctuation in the power extraction increases from 15.7% to 17%. This discussion supports the argument that the fluctuation in the power extraction increases by increasing the tower diameter of the turbine.

Table 1.
Fluctuation in the Coefficient of performance for different tower diameter.
Figure 6 shows the coefficient of thrust of the turbine with different diameter towers. Similarly, the coefficient of performance of the last one revolution is discussed here for brevity. The coefficient of thrust on the rotor is maximum when the blades are away from the tower of the turbine and are in a horizontal position. When the blades of the turbine move near the tower or are in a vertically aligned position with the tower the coefficient of thrust on the rotor decreases and reaches its minimum value. As the blades pass the tower the thrust on the rotor gradually increases and reaches its maximum value. The tower diameter has a small effect on the thrust of the rotor of the turbine. Thrust on the rotor for the tower diameter of 3.5 m is a minimum in all cases. The mean thrust on the rotor for the smaller diameter is higher than that of lager diameter towers.
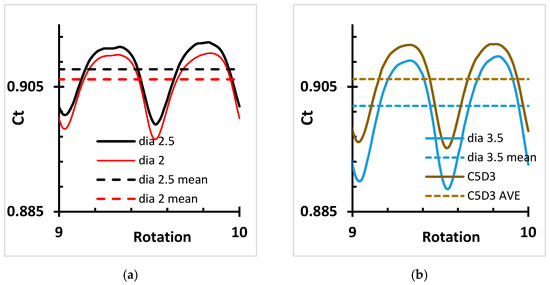
Figure 6.
Coefficient of thrust for tower having diameter (a) 2 and 2.5 m (b) 3 and 3.5 m.
Table 2 illustrates the fluctuation of coefficients of thrust from the mean thrust. The fluctuation in the coefficient of thrust from the mean value is a maximum for the tower diameter of 3.5 m, followed by a 3 m diameter which is 7.8%, whereas the fluctuation in the coefficient of thrust for a 2.5 m diameter and 2 m diameter is 7.8% and 7.62%, respectively. The difference in the coefficient of thrust fluctuation for a 2 m diameter and 2.5 m diameter is 0.4; similarly, this difference between a 2.5 m diameter tower and a 3 m diameter tower is 0.24.

Table 2.
Fluctuation in the coefficients of thrust for different tower diameters.
Figure 7 manifests the velocity contour of the water for different tower diameters. It is clearly observed that velocity deficit beyond the tower in the far wake is a maximum for the tower diameter of 3.5 m, which is represented by a black line; whereas, the velocity deficit for the other tower diameter in the far wake is not significant.
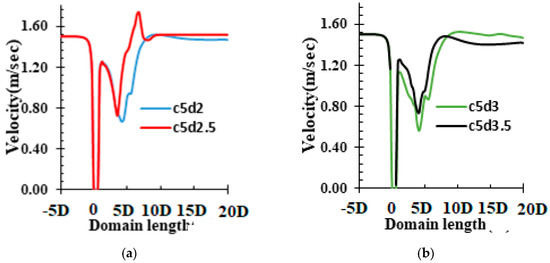
Figure 7.
Velocity contour of the water throughout the domain at the center line of the turbine (a) TCT with tower 2, 2.5 m diameter (b) TCT with tower 3 and 3.5 m diameter.
Figure 8 presents the velocity contour for different tower diameter having same tip to tower clearance. The blue line at the bottom of the domain manifests the wall boundary condition. Velocity next to the wall is considered zero. Similarly, no slip wall boundary condition is applied on the surface of blades, nacelle, tower and hub: that is why velocity at the surface of these parts is zero. Vertical asymmetry in the velocity contours from nacelle above and below throughout the domain is due to the presence of the tower. Beyond the tower velocity of water is small compared to the velocity above the blade tip. The acceleration of the water above the blade tip is due to the blockage of the rotor and tower. The center blue and green portion represents the core wake of the rotor for all turbines as shown in Figure 9a–d. For the tower diameter of 2.5 as shown in Figure 8b the accelerated velocity above the blade tip is mixed with a core wake, while for all other tower diameters the accelerated velocity is not mixed with the core wake of the rotor throughout the domain length. The velocity below the core wake for the tower diameters of 3 m and 3.5 m where the water is accelerated for a certain time which is represented by a brown strip (the arrow is pointing toward the strip) is shown in Figure 8c,d. The fluctuation of velocity of water for towers 3 m in diameter and 3.5 m in diameter is high compared to other two towers.
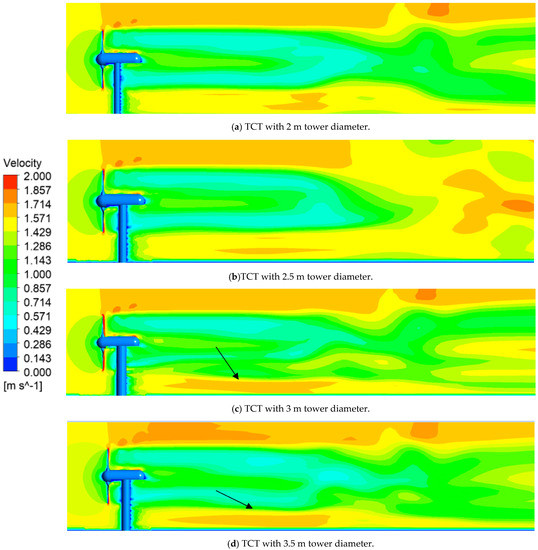
Figure 8.
Velocity contour of the water in X-Y plane throughout the domain.
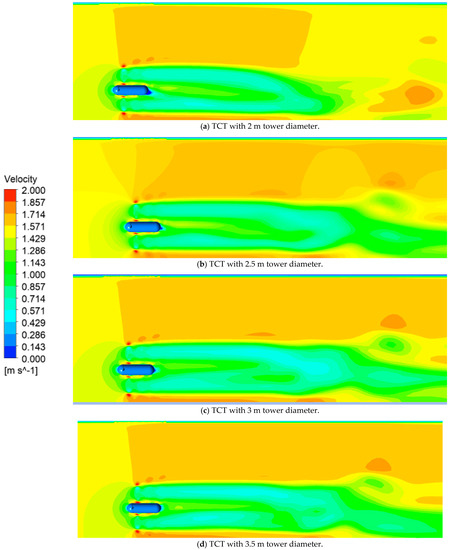
Figure 9.
Velocity contour of the water for different tower diameter in the Z-X plane.
Figure 9 manifests the velocity contour of the Z-X plane. The dark blue in the side of every domain in Figure 9 shows that velocity at this line is zero because no slip wall boundary condition is applied at this side; whereas, the dark blue and green regions beyond the turbine represent the core wake of the turbine. At the other side of every domain in Figure 9, no blue line is experienced because the symmetry boundary condition is applied at this side. In the front of the turbine the light green contour represents the blockage of the rotor. The brown region at the bottom of all parts in Figure 9 shows that velocity accelerates. This acceleration is high in the cases of the 3 and 3.5 m diameters, as shown in Figure 9c,d because the blockage effect of these towers is greater than the blockage effect of the 2 and 2.5 m diameter tower, which is manifest in Figure 9a,b.
7. Conclusions
The effect of different tower diameters on the performance and wake of the tidal current turbine (TCT) is investigated using Computational Fluid Dynamics (CFD). The investigations utilized an already verified and experimentally validated RANS CFD model of the full scale SAFL RM1 turbine [25]. The experimentally validated RANS CFD model with a blockage ratio of 14.3% (neglecting the tower) is used to simulate the effect of different tower diameters on the turbine performance and downstream wake. A tower diameter ranging from 2 to 3.5 m in diameter with the increment of 0.5 m is analyzed. Results showed that coefficient of performance decreases as the blades from vertically aligned positions within the tower go to the horizontal position. It also shows that the CP increases as the blades moves away from the tower for all diameters cases. The largest difference between coefficients of performance is for the 3.5 m diameter and 2.5 m diameter, which is 0.006. This difference is 1.25% of 0.478 (0.478 is the coefficient of performance of 3.5 m diameter tower). Similarly, the fluctuation from the mean value of the coefficient of performance for the 3.5 m diameter is 17.1%, followed by the 3 m, 2.5 m and 2 m diameter towers with respective percent fluctuation from mean value (16.1%, 15.6% and 15.7%). The change between fluctuations for a different tower diameter is nearly one.
The coefficient of thrust on the rotor for the tower diameter of 3.5 m is 0.902; for the 3 m diameter and for the 2.5 m diameter it is 0.906, for the 2 m diameter it is 0.908 and 0.906, the same as the coefficient of performance for the largest difference between the coefficients of thrust, which is for the 3.5 m diameter tower and the 2.5 m diameter tower. This is 0.6% of the 3.5 m diameter of coefficients of thrust. Similarly, the fluctuations from the mean value for the 3.5 m diameter and 3 m diameter are 8.22% and 7.8%, whereas this fluctuation for the 2.5 m diameter and 2 m diameter tower is 7.58% and 7.62%. The rate of change of fluctuation for a different tower diameter is nearly one.
The coefficient of performance and thrust decreases with the increase of tower diameter. Though the decrease in the coefficient of performance and thrust with the increase in diameter is not too high, the fluctuation in power coefficient is considerable and can lead to fatigue failure of the tower and blades. This aspect of fluctuation with change in diameter needs to be considered in future designs of turbine blades and towers.
Author Contributions
Conceptualization, S.B., A.F.R. and M.B.; Formal analysis, Z.U.R.; Funding acquisition, A.F.R.; Investigation, S.B.; Methodology, Z.U.R., A.F.R., M.B., S.J. and M.A.; Project administration, S.B., A.F.R. and M.A.; Resources, S.B.; Software, Z.U.R.; Supervision, S.B. and S.J.; Writing—original draft, Z.U.R. and M.A.; Writing—review and editing, S.B., A.F.R., M.B. and S.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work and APC was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under grant No. D-488-135-1441.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This project was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under grant No. D-488-135-1441. The authors, therefore, gratefully acknowledge DSR technical and financial support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Muchala, S.; Willden, R.H. Influence of support structures on tidal turbine power output. J. Fluids Struct. 2018, 83, 27–39. [Google Scholar] [CrossRef]
- Badshah, M.; Van Zwieten, J.; Badshah, S.; Jan, S. CFD study of blockage ratio and boundary proximity effects on the performance of a tidal turbine. IET Renew. Power Gener. 2019, 13, 744–749. [Google Scholar] [CrossRef]
- Consul, C.A.; Willden, R.H.J.; McIntosh, S.C. Blockage effects on the hydrodynamic performance of a marine cross-flow turbine. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20120299. [Google Scholar] [CrossRef] [PubMed]
- Shi, W.; Wang, D.; Atlar, M.; Seo, K. Flow separation impacts on the hydrodynamic performance analysis of a marine current turbine using CFD. J. Power Energy 2013, 227, 833–846. [Google Scholar] [CrossRef]
- Liu, J.; Lin, H.; Purimitla, S.R.; ET, M.D. The effects of blade twist and nacelle shape on the performance of horizontal axis tidal current turbines. Appl. Ocean Res. 2017, 64, 58–69. [Google Scholar] [CrossRef]
- Frost, C.; Morris, C.E.; Mason-Jones, A.; O’Doherty, D.M.; O’Doherty, T. The effect of tidal flow directionality on tidal turbine performance characteristics. Renew. Energy 2015, 78, 609–620. [Google Scholar] [CrossRef]
- Creech, A.C.; Borthwick, A.G.; Ingram, D. Effects of support structures in an LES actuator line model of a tidal turbine with contra-rotating rotors. Energies 2017, 10, 726. [Google Scholar] [CrossRef]
- Mason-Jones, A.; O’Doherty, D.M.; Morris, C.E.; O’Doherty, T. Influence of a velocity profile & support structure on tidal stream turbine performance. Renew. Energy 2013, 52, 23–30. [Google Scholar]
- Muchala, S.; Willden, R.H. Impact of tidal turbine support structures on realizable turbine farm power. Renew. Energy 2017, 114, 588–599. [Google Scholar] [CrossRef]
- Jan, S.; Badshah, S.; Badshah, M.; Javed, A. Effect of tower elasticity on the performance and fatigue character of monopile support tower for tidal current turbine. Appl. Ocean Res. 2020, 102446. [Google Scholar] [CrossRef]
- Davide, M.; Riccardo, M.; Andreas, U. JRC Ocean Energy Status Report: 2016 Edition; EUR 28407 EN; Publications Office of the European Union: Luxembourg, 2016; p. 4. [Google Scholar]
- Tian, W.; VanZwieten, J.H.; Pyakurel, P.; Li, Y. Influences of yaw angle and turbulence intensity on the performance of a 20 kW in-stream hydrokinetic turbine. Energy 2016, 111, 104–116. [Google Scholar] [CrossRef]
- Shives, M.; Crawford, C. Developing an empirical model for ducted tidal turbine performance using numerical simulation results. Proc. Inst. Mech. Eng. Part A J. Power Energy 2012, 226, 112–125. [Google Scholar] [CrossRef]
- Badshah, M.; Badshah, S.; Kadir, K. Fluid structure interaction modelling of tidal turbine performance and structural loads in a velocity shear environment. Energies 2018, 11, 1837. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS CFX Solver Modelling Guide Release 15; ANSYS Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- ANSYS Inc. ANSYS CFX Solver Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2010. [Google Scholar]
- Tedds, S.; Owen, I.; Poole, R. Near-wake characteristics of a model horizontal axis tidal stream turbine. Renew. Energy 2014, 63, 222–235. [Google Scholar] [CrossRef]
- Ouro, P.; Harrold, M.; Stoesser, T.; Bromley, P. Hydrodynamic loadings on a horizontal axis tidal turbine prototype. J. Fluids Struct. 2017, 71, 78–95. [Google Scholar] [CrossRef]
- Ouro, P.; Stoesser, T. Impact of Environmental Turbulence on the Performance and Loadings of a Tidal Stream Turbine. Flow Turbul. Combust. 2018, 102, 613–639. [Google Scholar] [CrossRef]
- Ahmed, U.; Apsley, D.; Afgan, I.; Stallard, T.J.; Stansby, P.K. Fluctuating loads on a tidal turbine due to velocity shear and turbulence: Comparison of CFD with field data. Renew. Energy 2017, 112, 235–246. [Google Scholar] [CrossRef]
- Abuan, B.E.; Howell, R.J. The performance and hydrodynamics in unsteady flow of a horizontal axis tidal turbine. Renew. Energy 2019, 133, 1338–1351. [Google Scholar] [CrossRef]
- Kolekar, N.; Banerjee, A. Performance characterization and placement of a marine hydrokinetic turbine in a tidal channel under boundary proximity and blockage effects. Appl. Energy 2015, 148, 121–133. [Google Scholar] [CrossRef]
- Ansys, C.J.C.-P.P.M.D. CFX Solver Modeling Guide; ANSYS Inc.: Canonsburg, PA, USA, 2010. [Google Scholar]
- Hill, C.; Neary, V.S.; Gunawan, B.; Guala, M.; Sotiropoulos, F. US Department of Energy Reference Model Program RM1: Experimental Results; Experimental Results (Report No. SAND2014-18783R). Report by University of Minnesota 2014. Available online: https://www.osti.gov/biblio/1172793-department-energy-reference-model-program-rm1-experimental-results (accessed on 1 January 2021).
- Javaherchi, T.; Stelzenmuller, N.; Aliseda, A. Experimental and numerical analysis of the DOE reference model 1 horizontal axis hydrokinetic turbine. In Proceedings of the 1st Marine Energy Technology Symposium, Washington, DC, USA, 27 April 2013. [Google Scholar]
- Javaherchi, T.; Seydel, J.; Stelzenmuller, N.; Aliseda, A. Experimental and numerical analysis of a scale model horizontal axis hydrokinetic turbine. In Proceedings of the 2nd Marine Energy Technology Symposium, Seattle, WA, USA, 15–18 April 2014. [Google Scholar]
- Javaherchi, T.; Stelzenmuller, N.; Aliseda, A. Experimental and numerical analysis of a small array of 45:1 scale horizontal axis hydrokinetic turbines based on the DOE reference model. In Proceedings of the 3rd Marine Energy Technology Symposium, Washington, DC, USA, 27 April 2015. [Google Scholar]
- Chen, T.; Liou, L. Blockage corrections in wind tunnel tests of small horizontal-axis wind turbines. Exp. Therm. Fluid Sci. 2011, 35, 565–569. [Google Scholar] [CrossRef]
- Koh, W.; Ng, E. A CFD study on the performance of a tidal turbine under various flow and blockage conditions. Renew. Energy 2017, 107, 124–137. [Google Scholar] [CrossRef]
- Badshah, M.; Badshah, S.; Jan, S. Comparison of computational fluid dynamics and fluid structure interaction models for the performance prediction of tidal current turbines. J. Ocean Eng. Sci. 2020, 5, 164–172. [Google Scholar] [CrossRef]
- O’Doherty, T.; Mason-Jones, A.; O’doherty, D.; Byrne, C.; Owen, I.; Wang, Y. Experimental and computational analysis of a model horizontal axis tidal turbine. In Proceedings of the 8th European wave and tidal energy conference, Uppsala, Sweden, 7–10 September 2009; pp. 833–841. [Google Scholar]
- Thake, J. Development, Installation and Testing of a Large-Scale Tidal Current Turbine; Technical Report T/06/00210/00/REP; Department of Trade and Industry: London, UK, 2005; pp. 19–26.
- Badshah, M.; Badshah, S.; VanZwieten, J.; Jan, S.; Amir, M.; Malik, S.A. Coupled Fluid-Structure Interaction Modelling of Loads Variation and Fatigue Life of a Full-Scale Tidal Turbine under the Effect of Velocity Profile. Energies 2019, 12, 2217. [Google Scholar] [CrossRef]
- de Souza Custódio Filho, S.; Santana, H.M.; Vaz, J.R.P.; Rodrigues, L.D.; Mesquita, A.L.A. Fatigue life estimation of á hydrokinetic turbine blades. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 281. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).