Equivalent Modeling of Microgrids Based on Optimized Broad Learning System
Abstract
:1. Introduction
- (1)
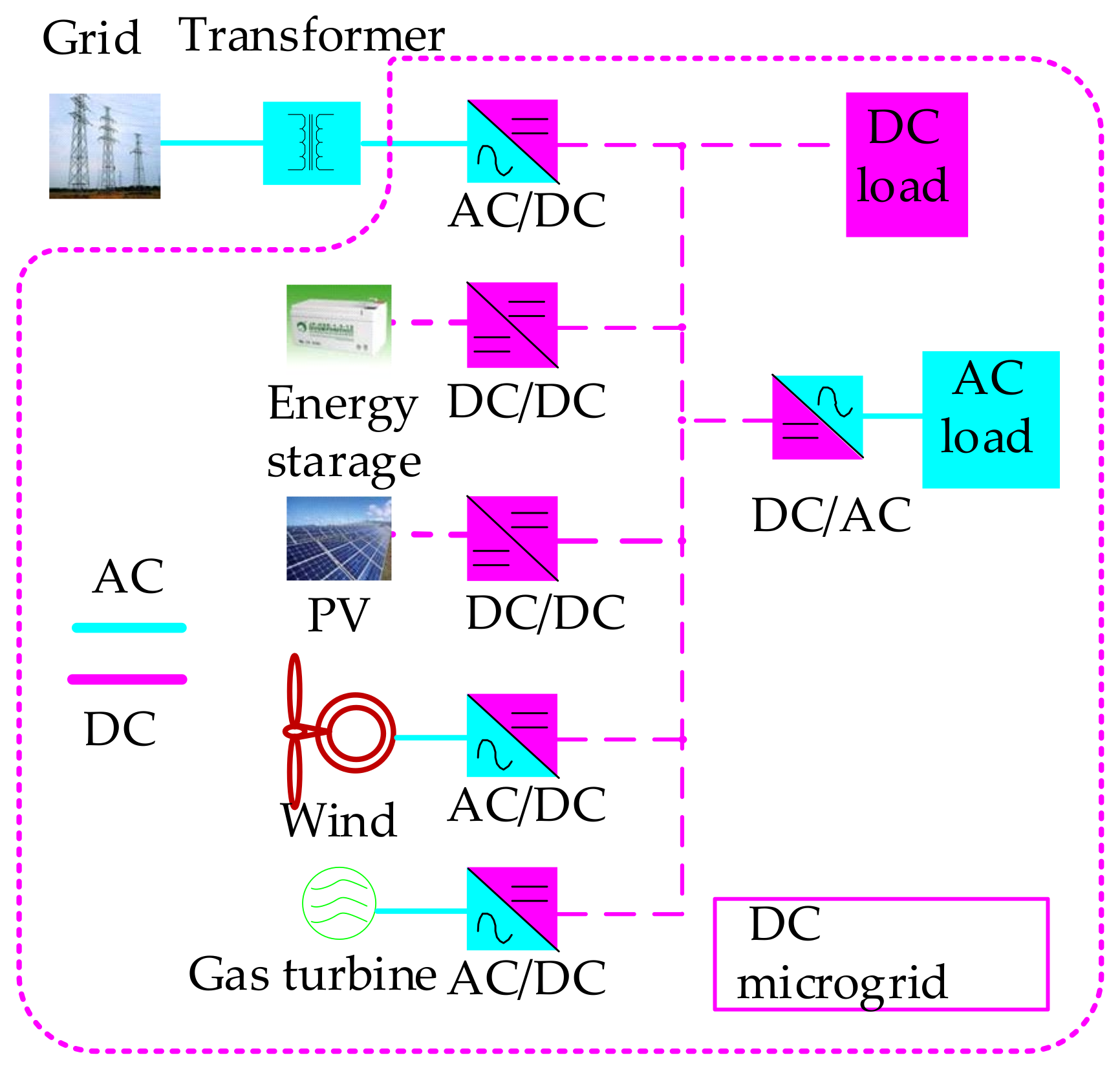
- We treat the DC microgrids as a whole, only collect the voltage and power of the DC microgrids grid-connected access point, and build the model, without considering the specific internal structure of the microgrid.
- (2)
- The BLS structure is used to model the grid-connected DC microgrid, which improves the modeling accuracy and generalization characteristics.
- (3)
- In order to further improve the accuracy of the model, the SSO-BLS algorithm is proposed. The SSO algorithm is used to optimize the and parameters of the BLS network, and thereby improving the performance of the BLS algorithm and improving the accuracy of the grid-connected DC microgrid equivalent model.
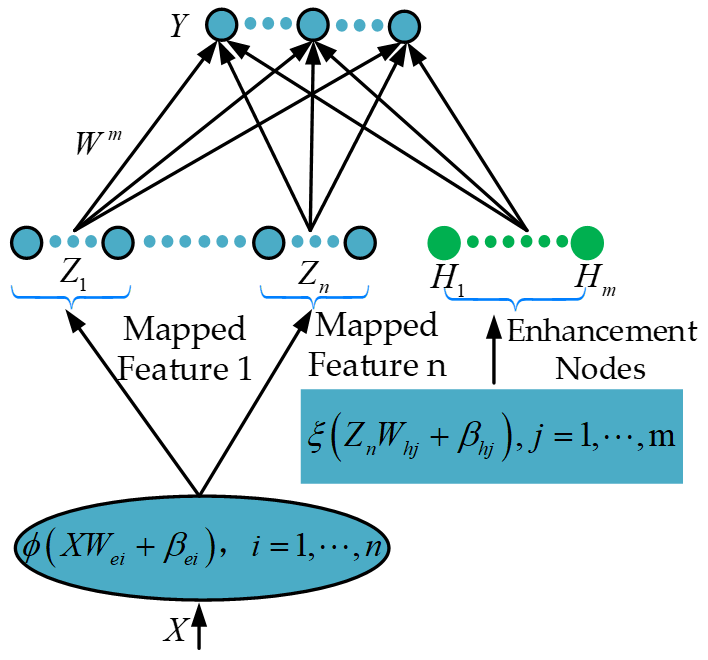
2. BLS
3. Parameter Optimization of BLS Network
4. DC Microgrid Modeling
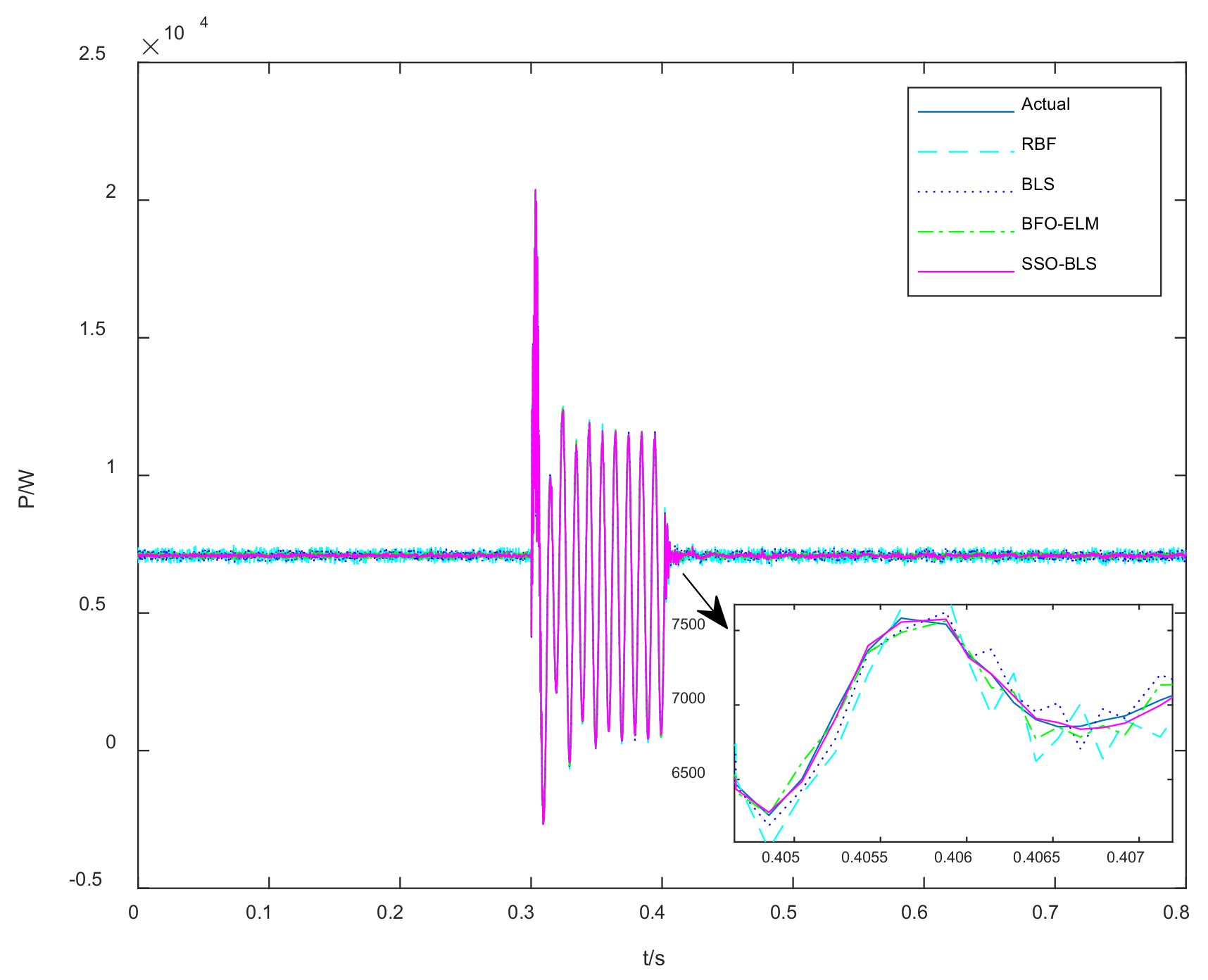
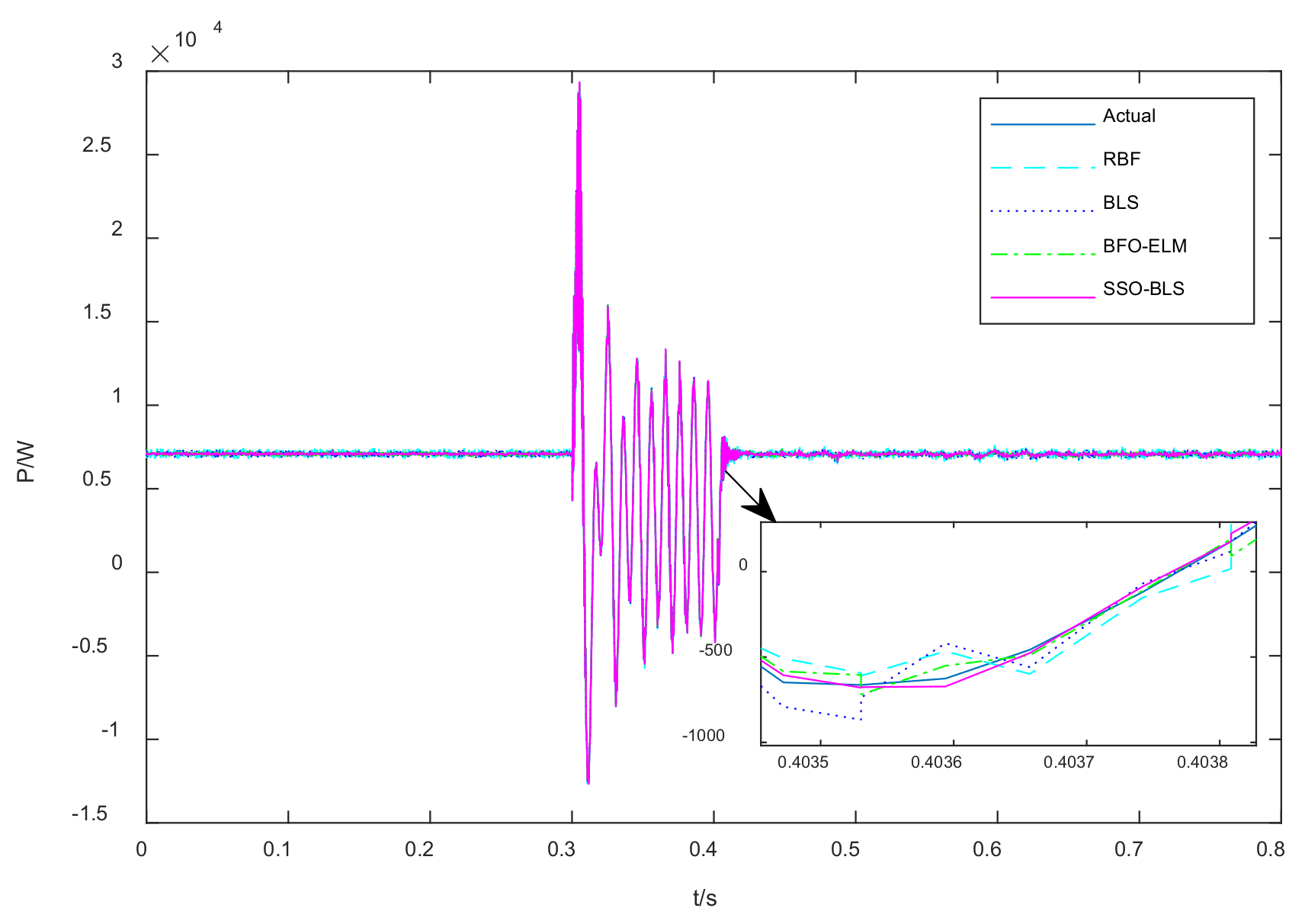
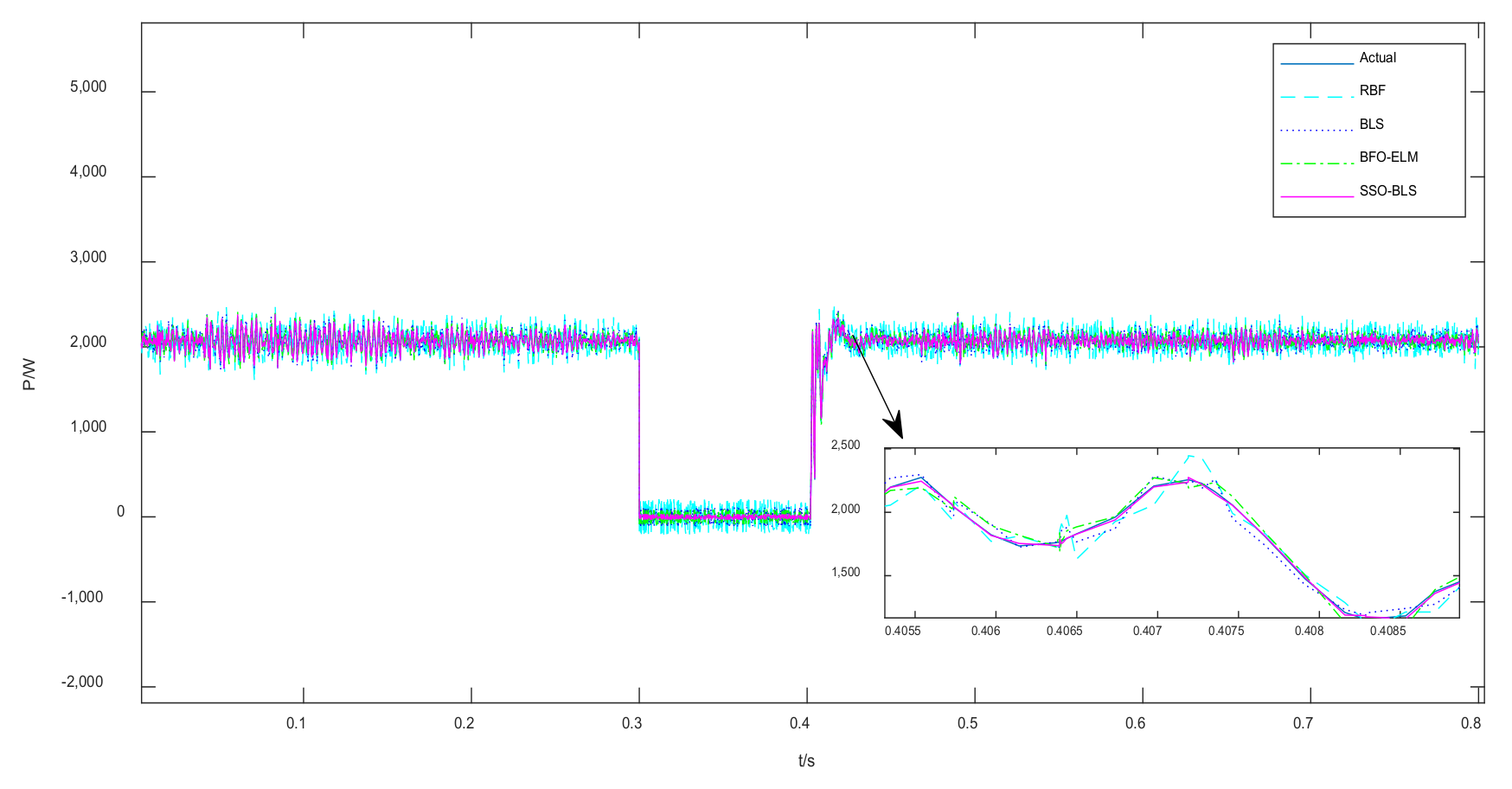
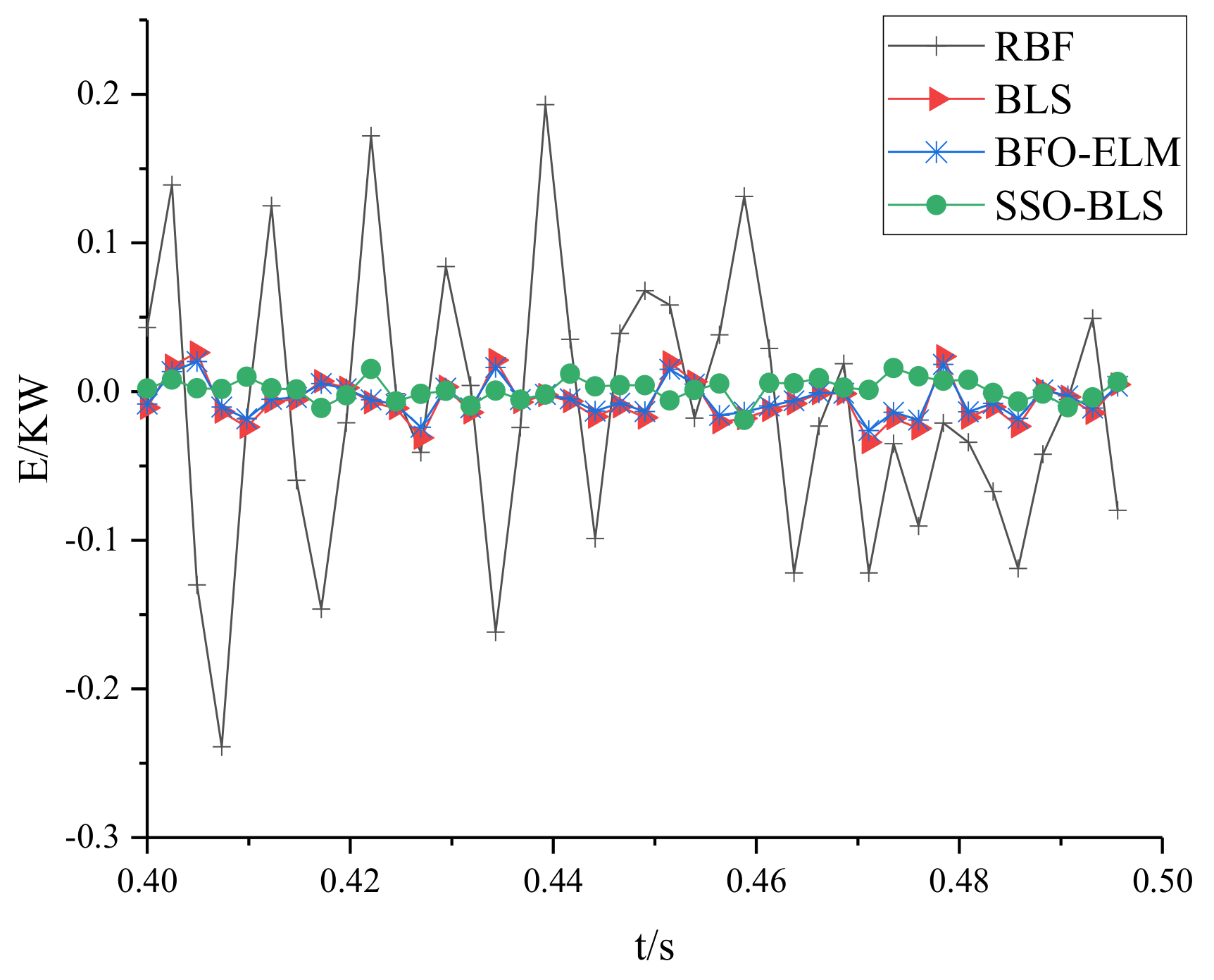
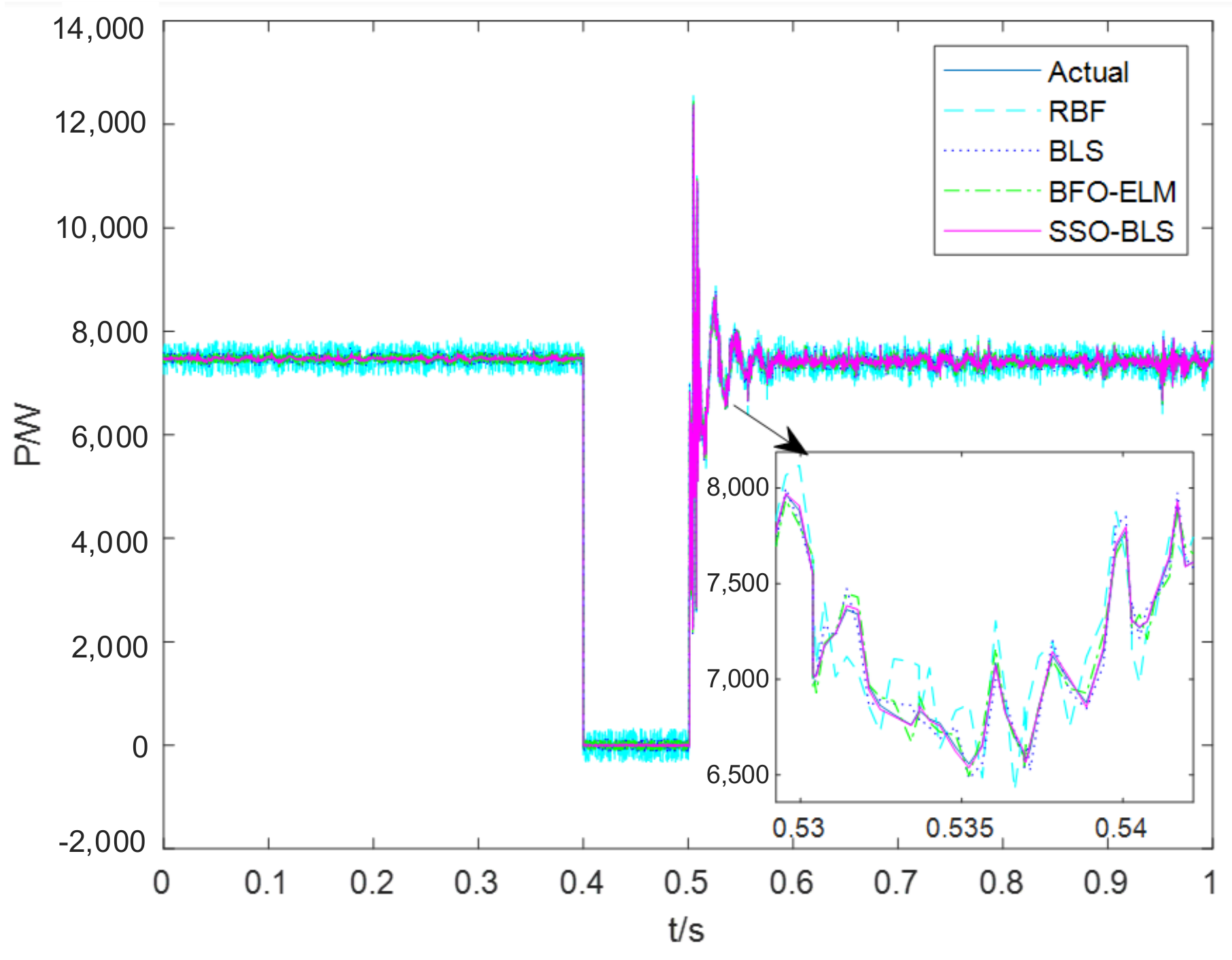
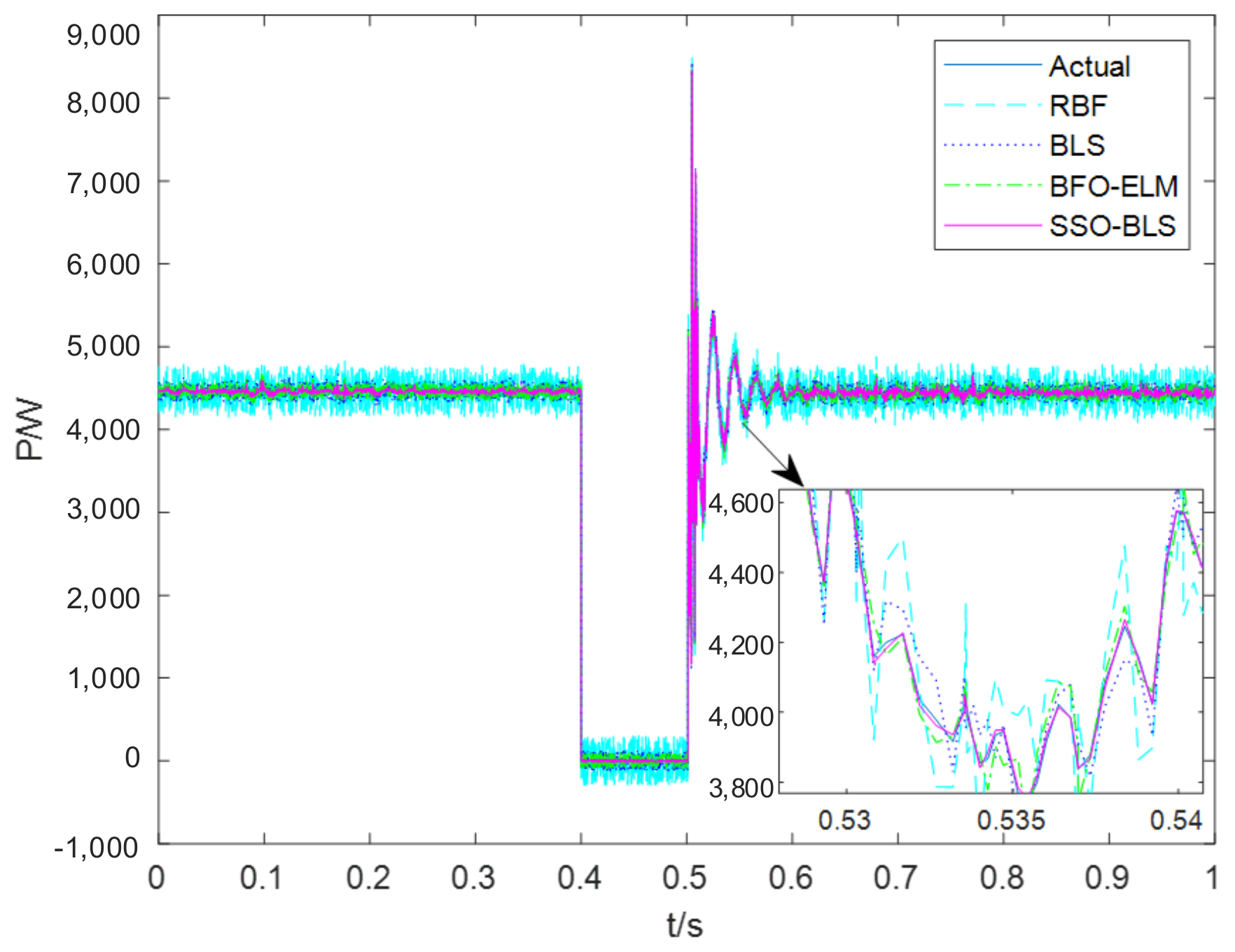
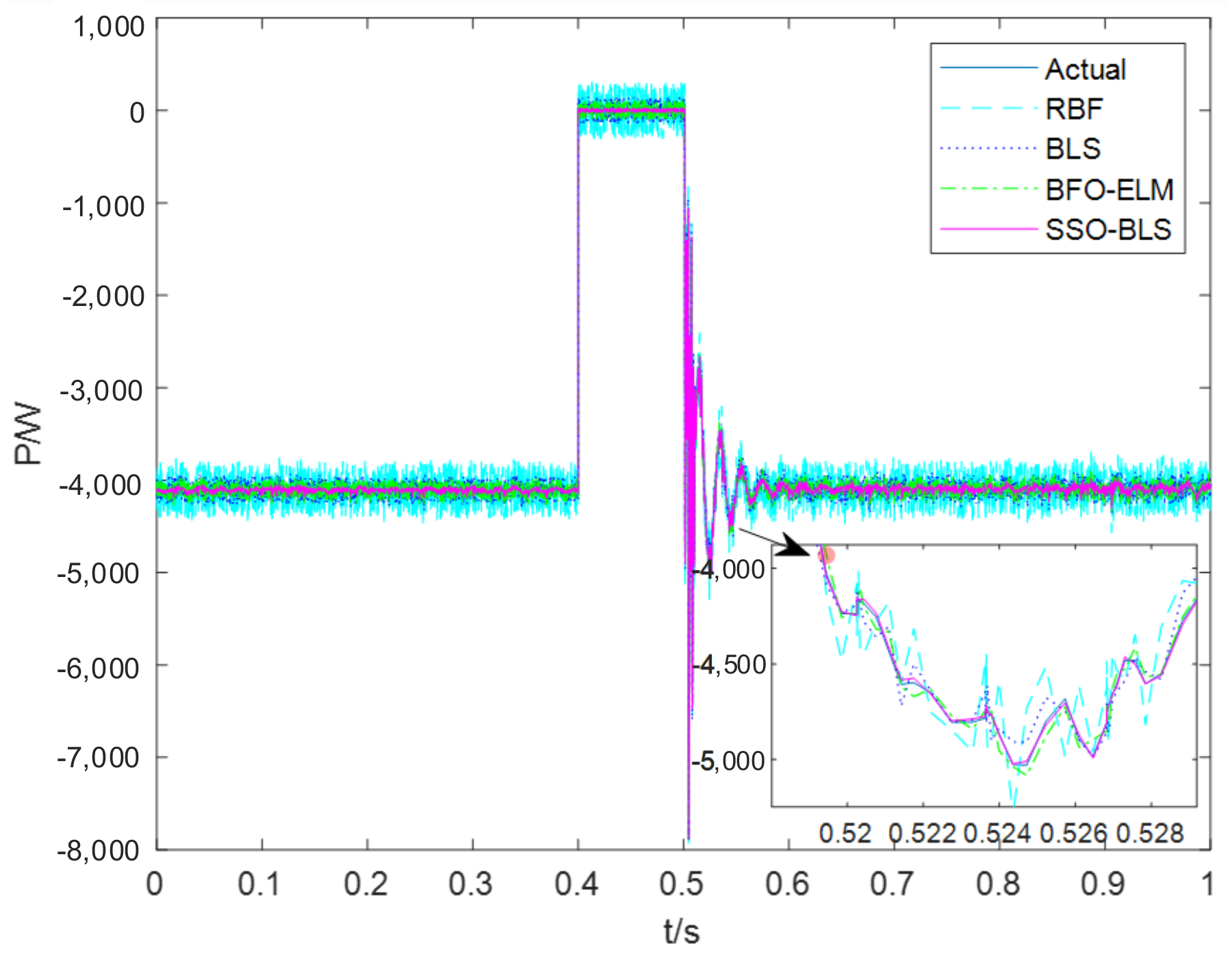
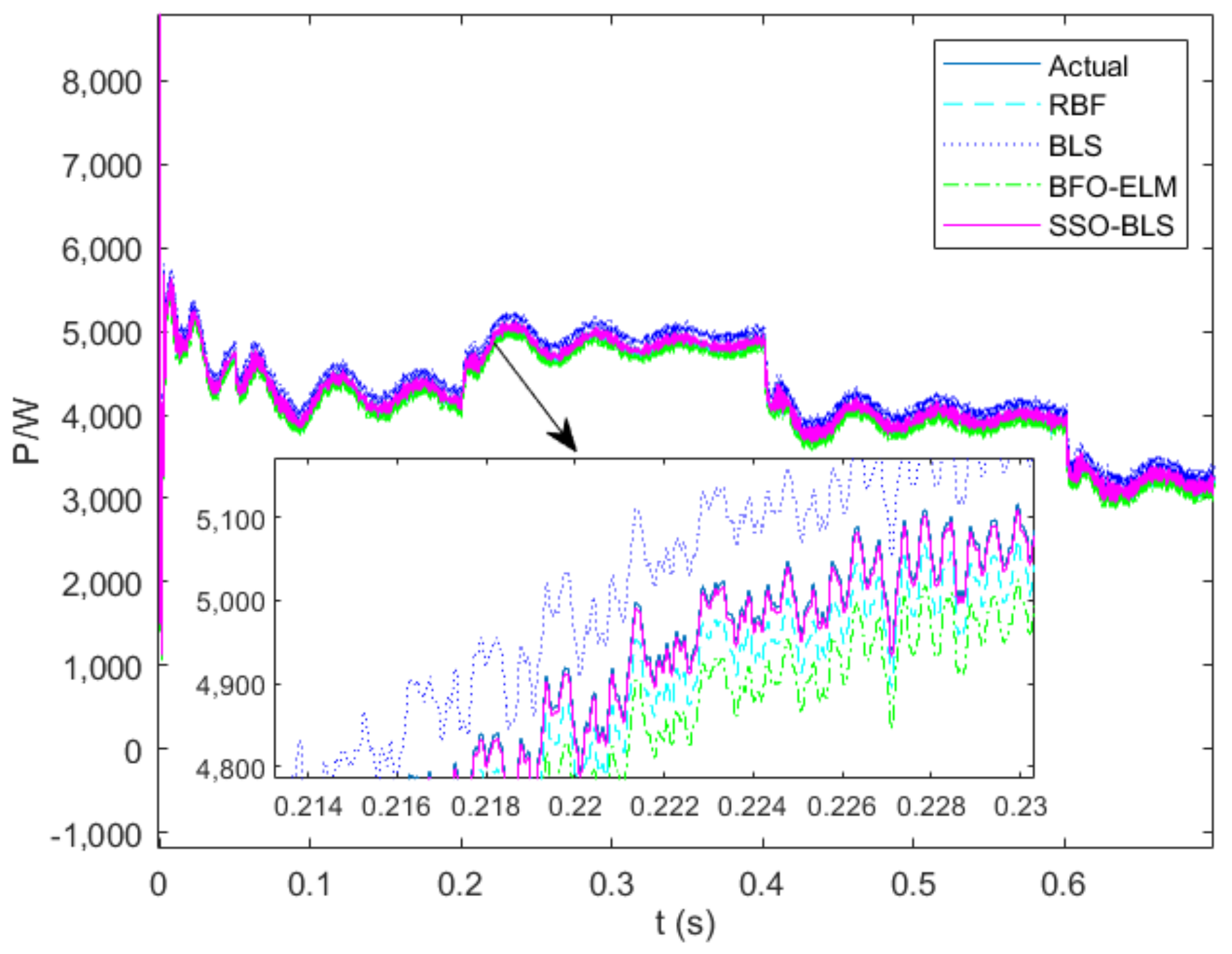
5. Modeling Results and Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, J.; Yao, W.; Zhang, C.K.; Ren, Y.; Jiang, L. Design of robust MPPT controller for grid-connected PMSG-Based wind turbine via per-turbation observation based nonlinear adaptive control. Renew. Energy 2019, 134, 478–495. [Google Scholar] [CrossRef]
- Jately, V.; V., B.V.; Azzopardi, S.; Azzopardi, B. Design and Performance Investigation of a Pilot Micro-Grid in the Mediterranean: MCAST Case Study. Energies 2021, 14, 6846. [Google Scholar] [CrossRef]
- Zhou, W.; Han, L.; Li, G.; Jing, Z. Modeling and simulation of the direct-drive permanent-magnetic wind power system in microgrid based on PSCAD/EMTDC. Electr. Technol. 2016, 17, 52–57. [Google Scholar]
- Wang, L.; Xu, D.; Zhao, H.; Hao, L.; Xu, J.; Qiu, F.; Zhang, B. Research on modeling and simulation method of direct drive permanent magnet wind power generation system. Electron. Meas. Technol. 2019, 328, 50–56. [Google Scholar]
- Brovont, A.D.; Pekarek, S.D. Derivation and Application of Equivalent Circuits to Model Common-Mode Current in Mi-crogrids. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 5, 297–308. [Google Scholar] [CrossRef]
- Giaouris, D.; Papadopoulos, A.; Patsios, C.; Walker, S.; Ziogou, C.; Taylor, P.; Voutetakis, S.; Papadopoulou, S.; Seferlis, P. A systems approach for management of microgrids considering multiple energy carriers, stochastic loads, forecasting and demand side response. Appl. Energy 2018, 226, 546–559. [Google Scholar] [CrossRef] [Green Version]
- Luna, M.; Sferlazza, A.; Accetta, A.; Di Piazza, M.C.; La Tona, G.; Pucci, M. Modeling and Performance Assessment of the Split-Pi Used as a Storage Converter in All the Possible DC Microgrid Scenarios. Theoretical Analysis. Energies 2021, 14, 5616. [Google Scholar] [CrossRef]
- Chen, J.M.; Wang, B.; Lu, Z.X.; Shen, W.P. Photovoltaic power generation prediction based on MEA-BP neural network. In Proceedings of the 2017 32nd Youth Academic Annual Conference of Chinese Association of Automation (YAC), Hefei, China, 19–21 May 2017; pp. 387–392. [Google Scholar]
- Cai, C.; Min, W.; Deng, L.; Zhang, J. Micro-grid dynamic modeling based on RBF Artificial Neural Network. In Proceedings of the International Conference on Power System Technology, Chengdu, China, 20–22 October 2014. [Google Scholar]
- Lopez-Garcia, T.B.; Coronado-Mendoza, A.; Domínguez-Navarro, J.A. Artificial neural networks in microgrids: A review. Eng. Appl. Artif. Intell. 2020, 95, 103894. [Google Scholar] [CrossRef]
- Cai, C.; Deng, L.; Bing, J.; Dai, W.; Jin, Y.; Miao, H. Micro-grid dynamic equivalent modeling based on particle swarm optimization algorithm and rbf artificial neural network. Acta Energ Sol. Sin. 2016, 37, 76–83. [Google Scholar]
- Cai, C.; Cheng, S.; Deng, Z.; Jiang, B.; He, W.G.; Ma, J.X. DC Microgrid Equivalent Modeling Based on Fuzzy-RBF Artificial Neural Network. Power Syst. Technol. 2016, 40, 3446–3452. [Google Scholar]
- Mishra, M.; Panigrahi, R.R.; Rout, P.K. A combined mathematical morphology and extreme learning machine techniques based approach to micro-grid protection. Ain Shams Eng. J. 2019, 10, 307–318. [Google Scholar] [CrossRef]
- Fang, S.; Xu, Y.; Wen, S.; Zhao, T.; Wang, H.; Liu, L. Data-Driven Robust Coordination of Generation and Demand-Side in Photovoltaic Integrated All-Electric Ship Microgrids. IEEE Trans. Power Syst. 2019, 35, 1783–1795. [Google Scholar] [CrossRef]
- Liu, N.; Zhang, Q.; Liu, H. Online short-term load forecasting based on ELM with kernel algorithm in micro-grid environment. Diangong Jishu Xuebao/Trans. China Electrotech. Soc. 2015, 30, 218–224. [Google Scholar]
- Purnomo, D.M.; Purbarani, S.C.; Wibisono, A.; Hendrayanti, D.; Bowolaksono, A.; Mursanto, P.; Ramdhan, D.H.; Jatmiko, W. Genetic algorithm optimization for extreme learning machine based micro-algal growth forecasting of Chlamydomonas sp. In Proceedings of the International Conference on Advanced Computer Science & Information Systems, Depok, Indonesia, 10–11 October 2015. [Google Scholar]
- Shanmugapriya, D.; Padmavathi, G. A wrapper based feature subset selection using ACO-ELM-ANP and GA-ELM-ANP ap-proaches for keystroke dynamics authentication. In Proceedings of the International Conference on Signal Processing Image Processing & Pattern Recognition, Coimbatore, India, 7–8 February 2013. [Google Scholar]
- Hota, P.K.; Barisal, A.K.; Chakrabarti, R. Economic emission load dispatch through fuzzy based bacterial foraging algorithm. Int. J. Electr. Power Energy Syst. 2010, 32, 794–803. [Google Scholar] [CrossRef]
- Dan, Y.; Tao, J. Knowledge worker scheduling optimization model based on bacterial foraging algorithm. Futur. Gener. Comput. Syst. 2021, 124, 330–337. [Google Scholar] [CrossRef]
- Gupta, S.; Katta, A.R.; Baldaniya, Y.; Kumar, R. Hybrid Random Forest and Particle Swarm Optimization Algorithm for Solar Radia-tion Prediction. In Proceedings of the IEEE 5th International Conference on Computing Communication and Automation (ICCCA), Greater Noida, India, 30–31 October 2020. [Google Scholar]
- Huang, Y.; Zhang, X.; Aglzim, E.-H.; Shi, L. Target 5G visible light positioning signal subcarrier extraction method using particle swarm optimization algorithm. In Proceedings of the 2021 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB), Chengdu, China, 4–6 August 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, C.L.P.; Liu, Z. Broad Learning System: An Effective and Efficient Incremental Learning System without the Need for Deep Architecture. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 10–24. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Liu, Z.; Feng, S. Universal Approximation Capability of Broad Learning System and Its Structural Variations. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 1191–1204. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Chen, P.; Dai, L.; Yang, H. A Broad Learning System Based on Pool Computing. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?doi=10.13195/j.kzyjc.2019.1729 (accessed on 20 November 2021).
- Ahmadigorji, M.; Amjady, N. A multiyear DG-incorporated framework for expansion planning of distribution net-works using binary chaotic shark smell optimization algorithm. Energy 2016, 102, 199–215. [Google Scholar] [CrossRef]
- Ya, W.; Russell, J.S. Parameter identification of solid oxide fuel cell by chaotic binary shark smell optimization method. Energy 2019, 188, 73–79. [Google Scholar]
| Power Generator | U | P |
|---|---|---|
| PV | 0.45 kV | 3 kW |
| wind power | 0.45 kV | 5 kW |
| micro gas turbine | 0.45 kV | 5 kW |
| energy storage | 800 Ah | |
| load | 8 kW(DC) | |
| Algorithm | Mean Root Mean Square Error |
|---|---|
| RBF | 0.3216 |
| BLS | 0.1187 |
| BFO-ELM | 0.071 |
| SSO-BLS | 0.038 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Xue, A. Equivalent Modeling of Microgrids Based on Optimized Broad Learning System. Energies 2021, 14, 7911. https://doi.org/10.3390/en14237911
Wang L, Xue A. Equivalent Modeling of Microgrids Based on Optimized Broad Learning System. Energies. 2021; 14(23):7911. https://doi.org/10.3390/en14237911
Chicago/Turabian StyleWang, Lin, and Anke Xue. 2021. "Equivalent Modeling of Microgrids Based on Optimized Broad Learning System" Energies 14, no. 23: 7911. https://doi.org/10.3390/en14237911
APA StyleWang, L., & Xue, A. (2021). Equivalent Modeling of Microgrids Based on Optimized Broad Learning System. Energies, 14(23), 7911. https://doi.org/10.3390/en14237911





