Non-Coaxially Rotating Motion in Casson Martial along with Temperature and Concentration Gradients via First-Order Chemical Reaction

Abstract

The effect of non-coaxial rotation on the transport of mass subjected to first-order chemical reaction is studied analytically. The effects of thermal radiation, buoyancy, constructive and destructive chemical reactions along with Casson fluid in rotating frame are discussed. Time evolution of primary and secondary velocities, energy and solute particles are analyzed. The behavior of flow under the variation of intensity of magnetic field is also investigated. Evolutionary behavior of primary velocity is opposite to the evolutionary behavior of secondary velocity. The impact of buoyant force on primary velocity is opposite to the role of buoyant force on the secondary velocity. The evolutionary behavior of temperature is also examined and a remarkable enhancement in temperature is noticed. Thermal radiation causes the fluid to be cooled down as heat energy is escaped by thermal radiation. Evolutionary behavior of concentration is also analyzed and an increasing of concentration versus time is noted. Destructive chemical reaction results a remarkable reduction in the concentration and vice versa for generative chemical reaction.

1. Introduction

Non-coaxial rotation in fluid regime occurs in many natural and industrial processes. Many industrial processes involve coaxial and non-coaxial rotation of fluid and bodies like disks, cylinder, spheres, etc. Many types of coaxial and non-coaxial rotation of industrial arrangements in fluid flow regime occur in the presence of thermal changes and transport of species. Swirling flows, rotation of pipes during drilling out of oil and transportation of oil through pipes and food processing industrial arrangements are well-known examples of rotational mechanism. Therefore, engineers and scientists have modeled the coaxial and non-coaxial rotation of fluid and computed the solutions by employing several suitable techniques in order to investigate the underlying engineering mechanism. Wide applications related to non-coaxial rotation motion are found in food processing and engineering process, jut engines, pump cleaners, vacuum cleaners, geophysical flows and cooling turbine blades, etc. Therefore, such a developed model is used to study free convection motion in non-coaxial disks while this model is used to study flow behavior at infinite wall of disk. Erdogan [1] modeled Newtonian fluid flow in disk in view of ambient liquid. He derived the exact solution. He also investigated the behavior of wall shear stress under variation of involved parameters. He also studied time evolution of the velocity. Ersoy [2] studied non-coaxial rotational motion in Oldroyd-B liquid. He also studied the impact of porous parameter on the transient and steady flow. Hayat et al. [3] developed a mathematical problem for non-coaxial flow over a permeable disk exposed to transverse magnetic field and derived the exact solution of the developed problem using Laplace transform method. They also analyzed the behavior of boundary layer thickness under the influence of permeability of the disk. Hayat et al. [4] developed mathematical models the flow induced due to non-coaxial rotation of disk and fluid at infinity. They derived modeled IBVP using Laplace Transform. Hayat et al. [5] studied magnetohydrodynamic characteristics for non-coaxial rotating flow induced by non-coaxial oscillations and fluid at infinity. Hayat and Wang [6] modeled flow induced due to the non-coaxial rotation of disk and ambient fluid. Hayat et at. [7] discussed the impact of magnetic field and permeability of disk on the flow induced by non-coaxial rotation of disk and ambient fluid. Hayat et al. [8] modeled flow of second grade fluid over a disk executing non-torsional oscillations while ambient fluid is rotating with uniform angular velocity. Hayat et al. [9] studied the role of magnetic fluid of non-Newtonian fluid. Asghar et at. [10] studied the impact of motion in rotating disk and ambient fluid. Wang [11] modeled the flow of third grade fluid generated by non-coaxial rotations of porous disk and the ambient fluid. Asghar et al. [12] studied the impact of Hall current and velocity on the flow of Newtonian fluid over a disk rotating non-coaxially with respect to rotation of ambient fluid. They found exact solution of the considered problem. Lashkari et al. [13] studied non-coaxially motion. Guria et al. [14] analyzed aspects of energy in rotating disc including Hall current. Chamkha et al. [15] studied hybrid role of nanoparticles in a disk under magnetic field. Dogonchi et al. [16] estimated role of heat generation towards expanding surface. Hayat et al. [17] studied thermal features in cylinder. Saleem et at. [18] estimated energy transfer in Jeffery liquid. Nawaz et at. [19] investigated magneto-nanofluid using finite. Saleem et al. [20] performed Walter’s B liquid in a cone.

Through careful review of existing literature, we came to know that no study on simultaneous transport of heat and mass in the flow of generated by non-coaxial rotation of disk and ambient fluid in the presence of generative/destructive chemical reactions and buoyancy force is conducted so far. The Laplace Transform technique is used to derive exact expressions for velocity, temperature and concentration fields. The derived exact expressions for unknown fields are manipulated to examine the role of key parameters. Finally, the results are briefly described. Developing of model is mentioned in Section 2 whereas Section 2 contains geometry and formulation of dimensionless parameters. Solution approach of developing problem is captured in Section 3. Graphical and physical discussions of various parameters are discussed in Section 4. Consequences of problem are mentioned in Section 5.

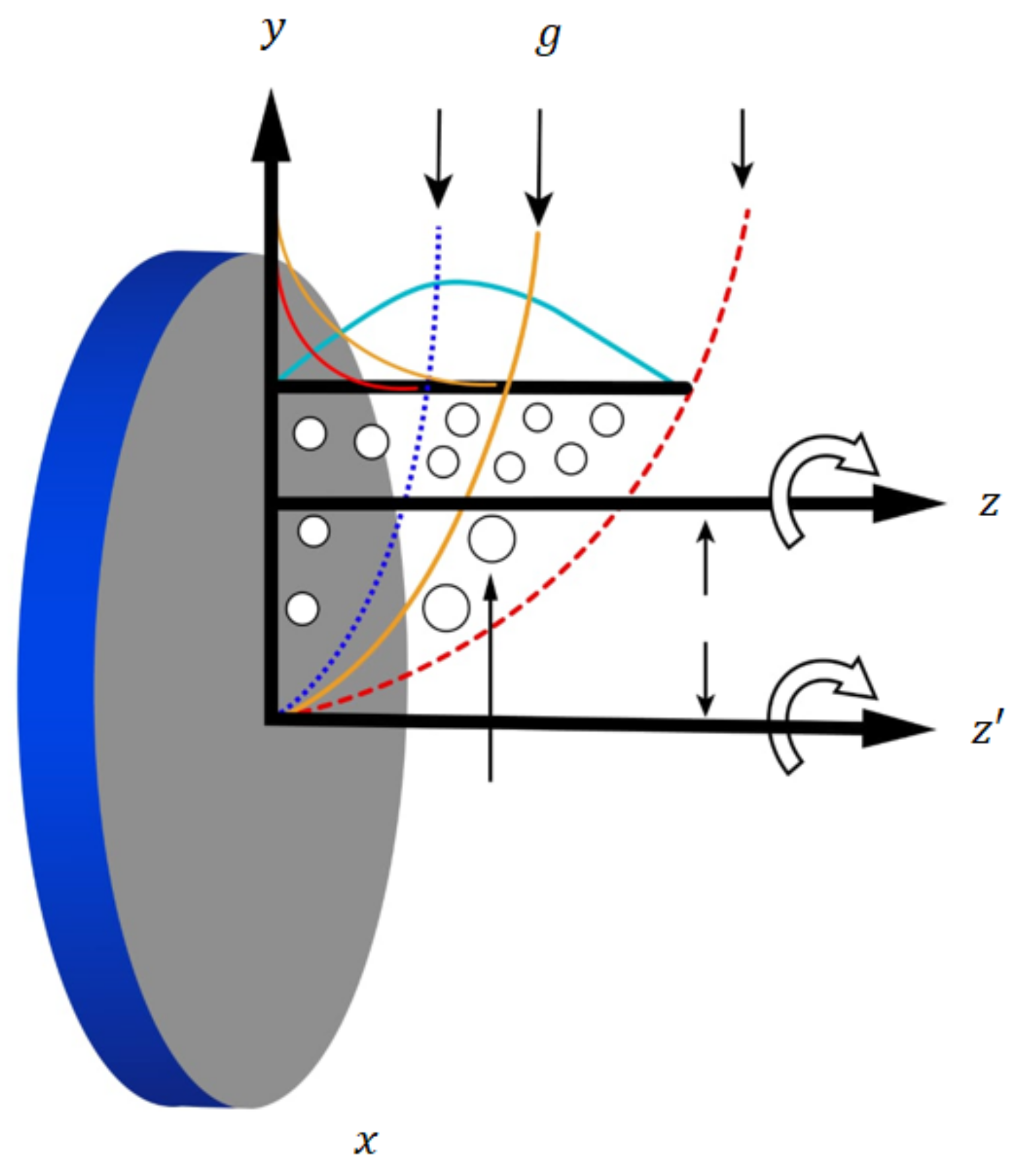
2. Physical Model and Mathematical Modeling

A model of heat energy and solute particles in Casson fluid rotating in a non-coaxial manner over a disk rotating with uniform angular velocity is examined which is shown in Figure 1. Ambient fluid is also rotating about an axis different to the axis of rotation of disk. A disk has temperature greater than heat energy. Initially, temperature of disk is temperature of ambient fluid and concentration at disk is equal to the concentration in ambient fluid. Suddenly, temperature of disk is changed. Similarly, wall concentration becomes different to the concentration in ambient fluid.

It is noticed that motion into particles is developed using wall velocities of disk. The physical meaning of the considered problem is based on wall velocities of disk. Walls become stretched for positive values of $\Omega$ and walls become shrunk for negative value of $\Omega$ whereas walls become stationary for stretch $\Omega =0$. In this considered model, opposite movement of walls is generated for horizontal and vertical velocities. The above-stated circumstances have revealed the following condition [4,5,6].

$$\left.\begin{array}{c}u=-\Omega \left(y-1\right),\hspace{0.17em}T=T_{\infty },\hspace{0.17em}v=x\Omega ,C=C_{\infty } \mathrm{at} 0=t\\ t>0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}u=-y(\Omega ),\hspace{0.17em}\hspace{0.17em}{T}_w=T,\hspace{0.17em}v=x\Omega ,C_w=C\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}, z=0,\hspace{0.17em}\\ z\to \infty ,\hspace{0.17em}\hspace{0.17em}C=C_{\infty },u=\left(-y\Omega +1\right),\hspace{0.17em}v=\Omega x,\hspace{0.17em}{T}_{\infty }=T \end{array}\right\}$$

(1)

In view of these conditions, one can suggest the fields as follows,

$$V=\left[f-\Omega y,\hspace{0.17em}g+\Omega x+,\hspace{0.17em}0\right],\hspace{0.17em}T=T\left(z,\hspace{0.17em}t\right),\hspace{0.17em}C=C\left(z,\hspace{0.17em}t\right),\hspace{0.17em}$$

(2)

Balance laws take the form [4,5,6]

$$\frac{1}{\rho }\frac{\partial p}{\partial x}=2{\Omega }^{2}x+\nu \left(\frac{1}{\beta }+1\right)\hspace{0.17em}\frac{{\partial }^{2}f}{\partial z^2}-\frac{\partial f}{\partial t}+\Omega g-\frac{\sigma B_0^2}{\rho }\left(f-\Omega l\right)-\frac{\mu }{\rho k}f+\frac{\mu \Omega }{\rho k}y,\hspace{0.17em}$$

(3)

$$\frac{1}{\rho }\frac{\partial p}{\partial y}=2{\Omega }^{2}y+\nu \left(1+\frac{1}{\beta }\right)\hspace{0.17em}\frac{{\partial }^{2}g}{\partial z^2}-\frac{\partial g}{\partial t}-\Omega f-\frac{\sigma B_0^2}{\rho }g+{\beta }_T\left(-T_{\infty }+T\right)\overline{g}-\frac{\mu }{\rho k}g-\frac{\mu (\Omega )}{\rho (k)}x,\hspace{0.17em}$$

(4)

$$\frac{\partial T}{\partial t}=\frac{K}{\rho c_p}\frac{{\partial }^{2}T}{\partial z^2}-\frac{1}{\rho c_p}\frac{16{\sigma }_1{T}_{\infty }^3}{3K^{\ast }}\frac{{\partial }^{2}T}{\partial Z^2},\hspace{0.17em}$$

(5)

$$\frac{\partial C}{\partial t}=D\frac{{\partial }^{2}C}{\partial z^2}+\frac{D{K}_T}{T_m}\frac{{\partial }^{2}T}{\partial z^2}-K_1\left(C-C_{\infty }\right),\hspace{0.17em}$$

(6)

Using the ambient condition and eliminating the pressure terms [4,5,6], one obtains

$$\nu \left(1+\frac{1}{\beta }\right)\hspace{0.17em}\frac{{\partial }^{2}f}{\partial z^2}-\frac{\partial f}{\partial t}+\Omega g-\sigma \frac{B_0^2}{\rho }\left(f-\Omega l\right)-\frac{\mu }{\rho k}f\left(\Omega l-f\right)=0,\hspace{0.17em}$$

(7)

$$\nu \left(1+\frac{1}{\beta }\right)\hspace{0.17em}\frac{{\partial }^{2}g}{\partial z^2}-\frac{\partial g}{\partial t}-\Omega f-\sigma \frac{B_0^2}{\rho }g+{\Omega }^{2}l+{\beta }_T\overline{g}\left(T-T_{\infty }\right)-\frac{\mu }{\rho k}g=0,$$

(8)

$$\frac{\partial T}{\partial t}=\frac{K}{\rho c_p}\frac{{\partial }^{2}T}{\partial Z^2}+\frac{1}{\rho C_P}\frac{16{\sigma }_1{T}_{\infty }^3}{3K^{\ast }}\frac{{\partial }^{2}T}{\partial Z^2},$$

(9)

$$\frac{\partial C}{\partial t}=D\frac{{\partial }^{2}C}{\partial z^2}+\frac{D{K}_T}{T_{\infty }}\frac{{\partial }^{2}T}{\partial z^2}-K_1\left(C-C\infty \right),$$

(10)

We obtain

$$\left.\begin{array}{c}\begin{array}{c}T=T,f=\Omega l,\hspace{0.17em}C=C_{\infty },g=0 : t=0,\\ t>0:T=T_{\infty },\hspace{0.17em}g=0,C=C_w,\hspace{0.17em}f=0:z=0\end{array}\\ C=0,\Omega l=f,\hspace{0.17em}0=g,\hspace{0.17em}T=0:z\to \infty \end{array}\right\}\hspace{0.17em}$$

(11)

The desired variables are

$$\tau =\Omega t ,\hspace{0.17em}\hspace{0.33em}\eta =\sqrt{\frac{\Omega }{\nu }}z,\hspace{0.17em}\theta (T_w-T_{\infty })=T-T_{\infty },\hspace{0.17em}\phi (C_w-C_{\infty })=C-C\infty ,\hspace{0.17em}\Gamma =\frac{k\Omega }{\nu },$$

(12)

In Equations (7)–(10), one obtains

$$\left.\begin{array}{c}\left(1+\frac{1}{\beta }\right)\hspace{0.17em}\frac{{\partial }^2\overline{F}}{\partial {\eta }^2}-\left(i\overline{F}+\frac{1}{\Gamma }\overline{F}+p\overline{F}\right)\hspace{0.17em}=-iGr\overline{\theta }\\ \hspace{0.33em}-\frac{1}{p}=\overline{F}\left(0,\hspace{0.17em}p\right),\hspace{0.17em}0=\overline{F}\left(\infty ,\hspace{0.17em}p\right)\end{array}\right\},$$

(13)

$$\left.\begin{array}{c}\frac{{\partial }^2\theta }{\partial {\eta }^2}-\frac{\mathrm{Pr}}{\lambda }\frac{\partial \theta }{\partial \tau }=0,\\ \theta \left(0,\hspace{0.17em}\tau \right)=1,\hspace{0.17em}\theta \left(\infty ,\hspace{0.17em}\tau \right)=0,\hspace{0.17em}\theta \left(\eta ,\hspace{0.17em}0\right)=0,\end{array}\right\},$$

(14)

$$\left.\begin{array}{c}\frac{{\partial }^2\varphi }{\partial {\eta }^2}-Sc\frac{\partial \varphi }{\partial \tau }+ScSr\frac{{\partial }^2\theta }{\partial {\eta }^2}-Scr\varphi =0,\\ \varphi \left(0,\hspace{0.17em}\tau \right)=1,\hspace{0.17em}\varphi \left(\infty ,\hspace{0.17em}\tau \right)=0,\hspace{0.17em}\varphi \left(\eta ,\hspace{0.17em}0\right)=0,\end{array}\right\},$$

(15)

with

$$\begin{array}{c}F\left(\eta ,\hspace{0.17em}\tau \right)=\left(f+ig\right)/\Omega l-1,\hspace{0.17em}\lambda =1+\frac{4}{3N_R},\hspace{0.17em}{N}_R=\frac{K{K}^{\ast }}{4{\sigma }_1{T}_{\infty }^3},\\ Gr=\frac{{\beta }_T\overline{g}\left(T_w-T_{\infty }\right)}{{\Omega }^{2}l},\hspace{0.17em}Pr=\frac{{\nu }_{\rho }{C}_p}{k},\hspace{0.17em}{M}^2=\frac{\sigma B_0^2}{\rho \Omega },\\ Sc=\frac{\nu }{D},\hspace{0.17em}Sr=\frac{D{K}_T\left(T_w-T_{\infty }\right)}{\nu T_m\left(C_w-C_{\infty }\right)},\hspace{0.17em}\gamma =\frac{K_1}{\Omega },\hspace{0.17em}\Gamma =\frac{k\Omega }{\nu },\end{array}$$

3. Exact Solution by Laplace Transform Method

Applying the Laplace Transform on Equations (19)–(21), one obtains problems [21,22,23]. Moreover, system of required ODEs along with boundary conditions is numerical solved by Laplace transformation method. The bulletin code is developed in MATHEMATICA 15.0. Exact solution is obtained via MATHEMATICA 15.0. The required is solution is discussed below.

$$\left.\begin{array}{c}\left(1+\frac{1}{\beta }\right)\hspace{0.17em}\frac{{\partial }^2\overline{F}}{\partial {\eta }^2}-\left(i+\frac{1}{\Gamma }+p\right)\hspace{0.17em}\overline{F}=0\\ \hspace{0.33em}\overline{F}\left(0,\hspace{0.17em}p\right)=-\frac{1}{p} ,\hspace{0.17em}\overline{F}\left(\infty ,\hspace{0.17em}p\right)=0\end{array}\right\},$$

(16)

$$\left.\begin{array}{c}\frac{{\partial }^2\theta }{\partial {\eta }^2}-\frac{Pr}{\lambda }\frac{\partial \theta }{\partial \tau }=0,\\ \theta \left(0,\hspace{0.17em}\tau \right)=1,\hspace{0.17em}\theta \left(\infty ,\hspace{0.17em}\tau \right)=0,\hspace{0.17em}\theta \left(\eta ,\hspace{0.17em}0\right)=0,\end{array}\right\},$$

(17)

$$\left.\begin{array}{c}\frac{{\partial }^2\varphi }{\partial {\eta }^2}-Sc\frac{\partial \varphi }{\partial \tau }+ScSr\frac{{\partial }^2\theta }{\partial {\eta }^2}-Scr\varphi =0,\\ \varphi \left(0,\hspace{0.17em}\tau \right)=1,\hspace{0.17em}\varphi \left(\infty ,\hspace{0.17em}\tau \right)=0,\hspace{0.17em}\varphi \left(\eta ,\hspace{0.17em}0\right)=0,\end{array}\right\},$$

(18)

Equations (18)–(20) are

$$\begin{array}{c}\overline{F}\left(\eta ,\hspace{0.17em}P\right)=-\left[1+\frac{i(Gr)}{\left(i+\frac{1}{\Gamma }+M^2\right)}\right]\hspace{0.17em}\frac{1}{p}{e}^{-\sqrt{\left(p+i+\frac{1}{\Gamma }+M^2\right)}\eta }+\frac{iGr}{\left(i+\frac{1}{\Gamma }+M^2\right)}\frac{e^{-\sqrt{\left(P+i+\frac{1}{\Gamma }+M^2\right)}\eta }}{P-\frac{\lambda \left(i+\frac{1}{\sigma }+M^2\right)}{\left(\left(1+\frac{1}{\beta }\right)\hspace{0.17em}\mathrm{Pr}-\lambda \right)}}+\\ \frac{iGr}{\left(i+\frac{1}{\Gamma }+M^2\right)}\frac{e^{-\sqrt{\frac{\mathrm{Pr}p}{\lambda }}\eta }}{P}-\frac{iGr}{\left(i+\frac{1}{\Gamma }+M^2\right)}\frac{e^{-\sqrt{\frac{\mathrm{Pr}p}{\lambda }}\eta }}{P-\frac{\lambda \left(i+\frac{1}{\Gamma }+M^2\right)}{\left(\left(1+\frac{1}{\beta }\right)\hspace{0.17em}\mathrm{Pr}-\lambda \right)}},\end{array}$$

(19)

$$\left.\overline{\theta }\left(\eta ,\hspace{0.17em}P\right)=\frac{1}{P}{e}^{-\sqrt{\frac{\mathrm{Pr}}{\lambda }p}\eta }\right\},$$

(20)

$$\begin{array}{ll}\phi \left(\eta ,\hspace{0.17em}p\right)& =\frac{1}{p}{e}^{-\sqrt{Sc\left(P+r\right)}\eta }+\frac{ScSrPr}{\mathrm{Pr}-Sc\lambda }\frac{e^{-\sqrt{Sc\left(p+r\right)}\eta }}{\left(p-\frac{Scr\lambda }{\mathrm{Pr}-Sc\lambda }\right)}-\frac{ScSrPr}{Pr-Sc\lambda }\frac{e^{-\sqrt{\frac{Pr}{\lambda }p}\eta }}{\left(p-\frac{Scr\lambda }{Pr-Sc\lambda }\right)}-\\ & \frac{ScSrPr}{Pr-Sc\lambda }\frac{e^{-\sqrt{\frac{\mathrm{Pr}}{\lambda }p}\eta }}{\left(p-\frac{Scr\lambda }{Pr-Sc\lambda }\right)}.\end{array}$$

(21)

Inversion of Laplace transform of above given expression yields

$$\left(f+ig\right)/\Omega l=1-\frac{1}{2}\left(1+\frac{iGr}{\left(i+\frac{1}{\Gamma }+M^2\right)}\right)\hspace{0.17em}\left[\begin{array}{c}{e}^{\sqrt{\left(i+\frac{1}{\Gamma }+M^2\right)}\eta }\mathrm{erf}c\sqrt{\left(\begin{array}{c}\frac{1}{2}\sqrt{\frac{1}{\tau }}+\\ \left(i+\frac{1}{\Gamma }+M^2\right)\end{array}\right)\hspace{0.17em}\tau }\\ +e^{-\sqrt{\left(i+\frac{1}{\sigma }+M^2\right)}\eta }\times \\ \mathrm{erf}c\left(\frac{1}{2}\sqrt{\frac{1}{\tau }}-\sqrt{\left(i+\frac{1}{\Gamma }+M^2\right)\hspace{0.17em}\tau }\right)\end{array}\right]\hspace{0.17em}$$

$$+\frac{iGr}{\left(i+\frac{1}{\Gamma }+M^2\right)}{e}^{\left(\frac{\lambda \left(i+\frac{1}{\Gamma }+M^2\right)}{\left(\left(1+\frac{1}{\beta }\right)Pr-\lambda \right)}\tau \right)}\left[\begin{array}{c}{e}^{-\sqrt{\frac{Pr\left(i+\frac{1}{\Gamma }+M^2\right)}{\left(\left(1+\frac{1}{\beta }\right)\mathrm{Pr}-\lambda \right)}}\eta }\times \\ \mathrm{erf}c\left(\begin{array}{c}\frac{\eta }{2}\sqrt{\frac{1}{\tau }}-\\ \sqrt{\frac{Pr\left(i+\frac{1}{\Gamma }+M^2\right)}{\left(\left(1+\frac{1}{\beta }\right)Pr-\lambda \right)}}\tau \end{array}\right)\\ +e^{\sqrt{\frac{Pr\left(i+\frac{1}{\Gamma }+M^2\right)}{\left(\left(1+\frac{1}{\beta }\right)Pr-\lambda \right)}}\eta }\times \\ \mathrm{erf}c\left(\frac{\eta }{2}\sqrt{\frac{1}{\tau }}+\sqrt{\frac{Pr\left(i+\frac{1}{\Gamma }+M^2\right)}{\left(\left(1+\frac{1}{\beta }\right)\mathrm{Pr}-\lambda \right)}}\tau \right)\end{array}\right]$$

(22)

$$\begin{array}{c}\\ \\ \frac{iGr}{\left(i+\frac{1}{\Gamma }+M^2\right)}\mathrm{erf}c\left(\frac{\eta }{2}\sqrt{\frac{Pr}{\lambda \tau }}\right)-\frac{iGr}{2\left(i+\frac{1}{\Gamma }+M^2\right)}{e}^{\left(\lambda \frac{\left(i+\frac{1}{\Gamma }+M^2\right)}{\left(\left(1+\frac{1}{\beta }\right)\mathrm{Pr}-\lambda \right)}\tau \right)}\times \\ \left[\begin{array}{c}{e}^{\left(-\sqrt{\frac{Pr\left(i+\frac{1}{\Gamma }+M^2\right)}{\left(\left(1+\frac{1}{\beta }\right)Pr-\lambda \right)}}\eta \right)\mathrm{erf}c\left(\frac{\eta }{2}\sqrt{\frac{Pr}{\lambda \tau }}-\sqrt{\lambda \frac{\left(i+\frac{1}{\Gamma }+M^2\right)}{\left(\left(1+\frac{1}{\beta }\right)\mathrm{Pr}-\lambda \right)}\tau }\right)}\\ +\left(e^{\sqrt{\frac{Pr\left(i+\frac{1}{\Gamma }+M^2\right)}{\left(\left(1+\frac{1}{\beta }\right)\mathrm{Pr}-\lambda \right)}}\eta }\right)\mathrm{erf}c\left(\frac{\eta }{2}\sqrt{\frac{Pr}{\lambda \tau }}\right)-\sqrt{\tau \frac{\left(i+\frac{1}{\Gamma }+M^2\right)}{\left(\left(1+\frac{1}{\beta }\right)Pr-\lambda \right)}}\end{array}\right],\end{array}$$

(23)

$$\left.\theta \left(\eta ,\hspace{0.17em}\tau \right)=\mathrm{erf}c\left(\frac{\eta }{2}\sqrt{\frac{Pr}{\lambda \tau }}\right)\right\},$$

$$+\frac{ScSrPr}{2\left(Pr-Sc\lambda \right)}{e}^{\left(\frac{ScSrPr}{Pr-Sc\lambda }\right)}\left[\begin{array}{c}{e}^{-\sqrt{\frac{\lambda \gamma S{c}^2+S{c}^2\gamma \left(Pr-\lambda Sc\right)}{Pr-\lambda Sc}}\eta }\times \\ \mathrm{erf}c\left(\frac{\eta }{2}\sqrt{\frac{Sc}{\tau }}-\sqrt{\frac{\lambda \gamma S{c}^2+S{c}^2\gamma \left(Pr-\lambda Sc\right)}{Pr-\lambda Sc}}\tau \right)\\ +e^{\sqrt{\frac{\lambda \gamma S{c}^2+S{c}^2\gamma \left(Pr-\lambda Sc\right)}{Pr-\lambda Sc}}\eta }\times \\ \mathrm{erf}c\left(\frac{\eta }{2}\sqrt{\frac{Sc}{\tau }}-\sqrt{\frac{\lambda \gamma S{c}^2+S{c}^2\gamma \left(Pr-\lambda Sc\right)}{Pr-\lambda Sc}}\tau \right)\end{array}\right]\hspace{0.17em}$$

$$\phi \left(\eta ,\hspace{0.17em}\tau \right)=\frac{1}{2}\left[e^{\sqrt{Sc\gamma }\eta }\mathrm{erf}c\left(\frac{\eta }{2}\sqrt{\frac{Sc}{\tau }}+\sqrt{\gamma \tau }\right)+e^{-\sqrt{Sc\gamma }\eta }\mathrm{erf}c\left(\frac{\eta }{2}\sqrt{\frac{Sc}{\tau }}-\sqrt{\gamma \tau }\right)\right]\hspace{0.17em}$$

$$\begin{array}{c}\\ \\ -\frac{ScSrPr}{2\left(Pr-Sc\lambda \right)}{e}^{\left(\frac{ScSr\mathrm{Pr}}{\mathrm{Pr}-Sc\lambda }\right)}\left[\begin{array}{c}{e}^{-\sqrt{\frac{\gamma prSc}{\mathrm{Pr}-\lambda Sc}}\eta }\mathrm{erf}c\left(\frac{\eta }{2}\sqrt{\frac{Sc}{\tau }}-\sqrt{\frac{\gamma \lambda Sc}{Pr-\lambda Sc}\tau }\right)\\ +e^{\sqrt{\frac{\gamma PrSc}{Pr-\lambda Sc}}\eta }\mathrm{erf}c\left(\frac{\eta }{2}\sqrt{\frac{Sc}{\tau }}+\sqrt{\frac{\gamma \lambda Sc}{Pr-\lambda Sc}\tau }\right)\end{array}\right]\end{array}$$

(24)

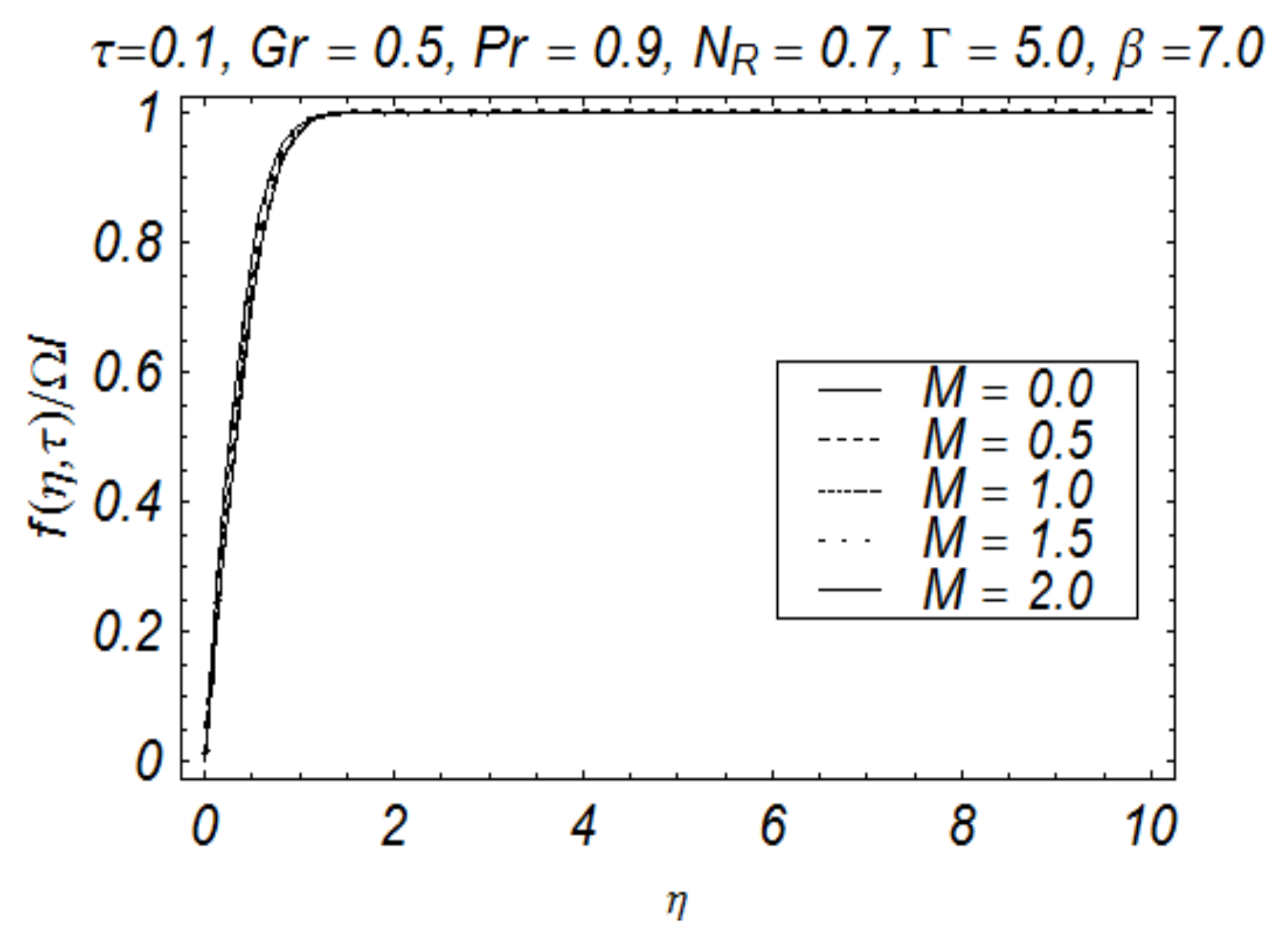
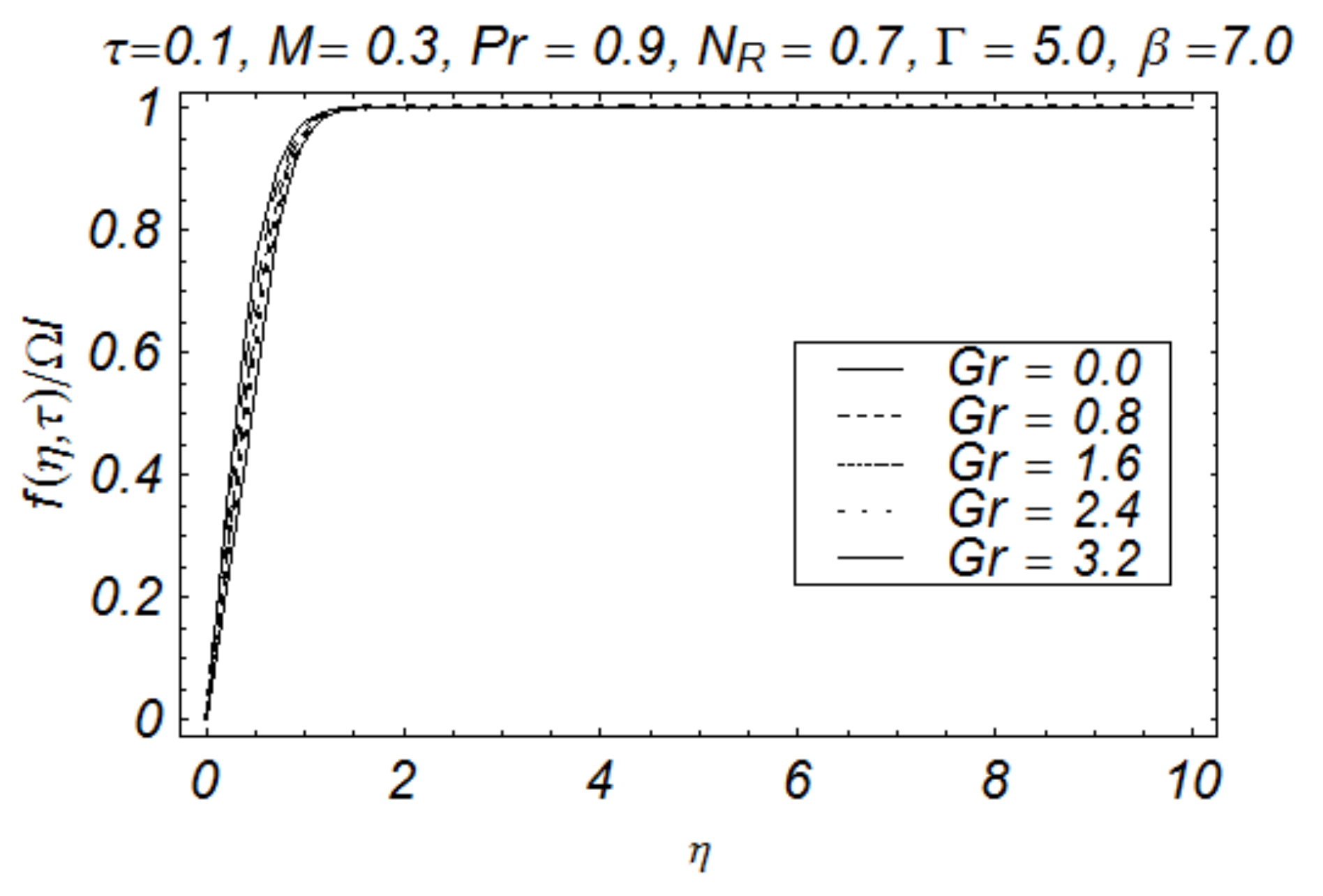
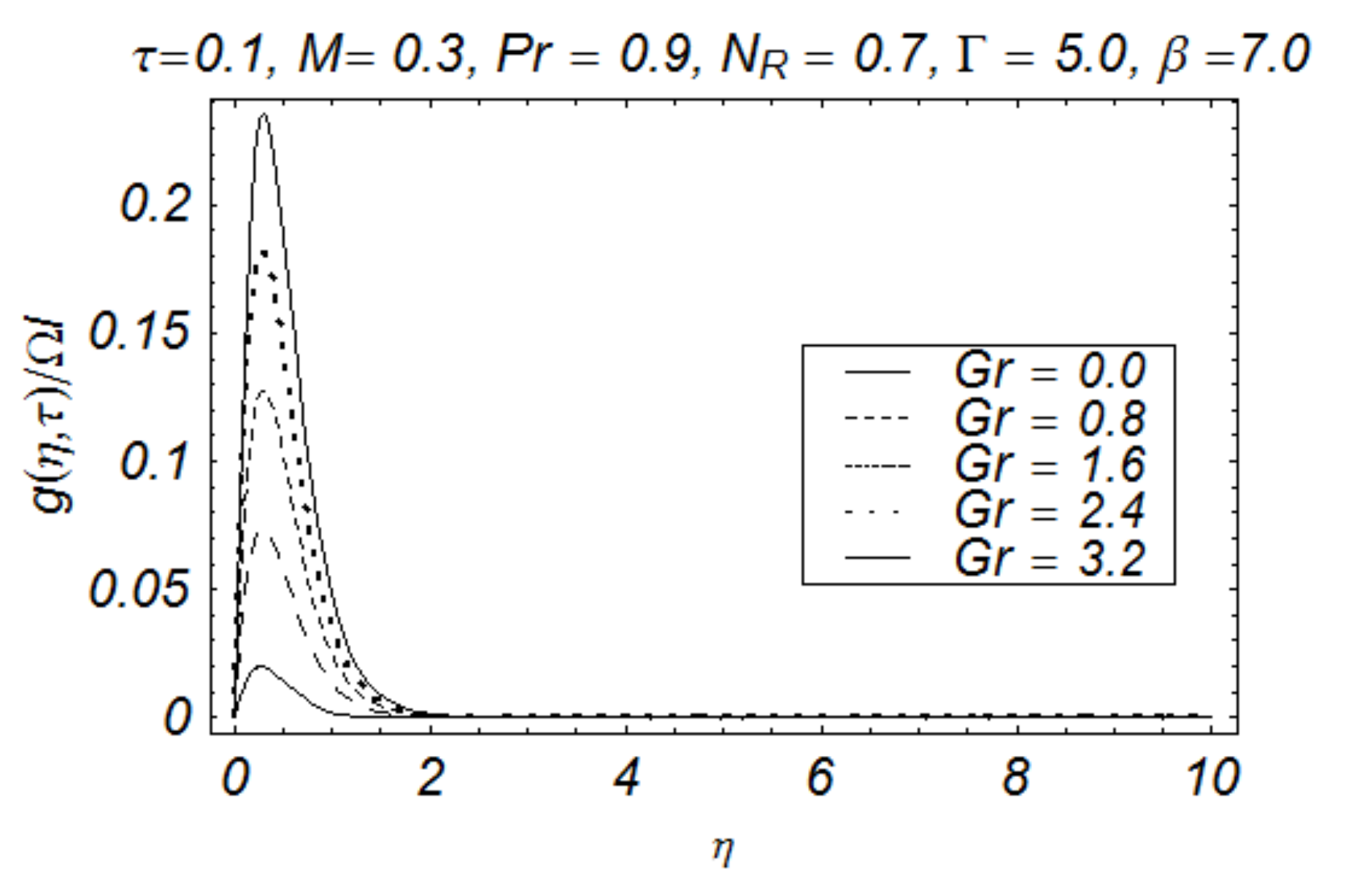
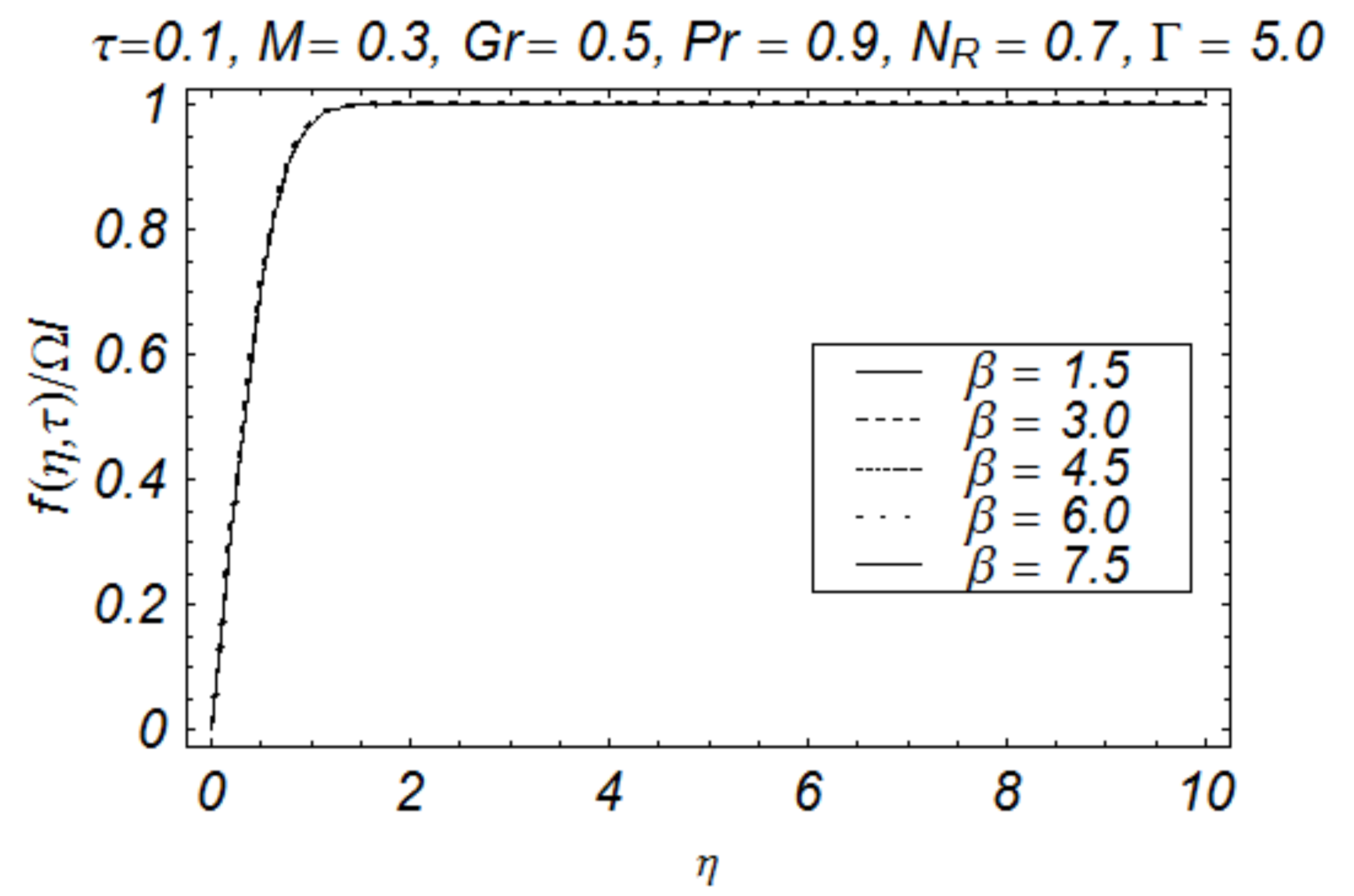
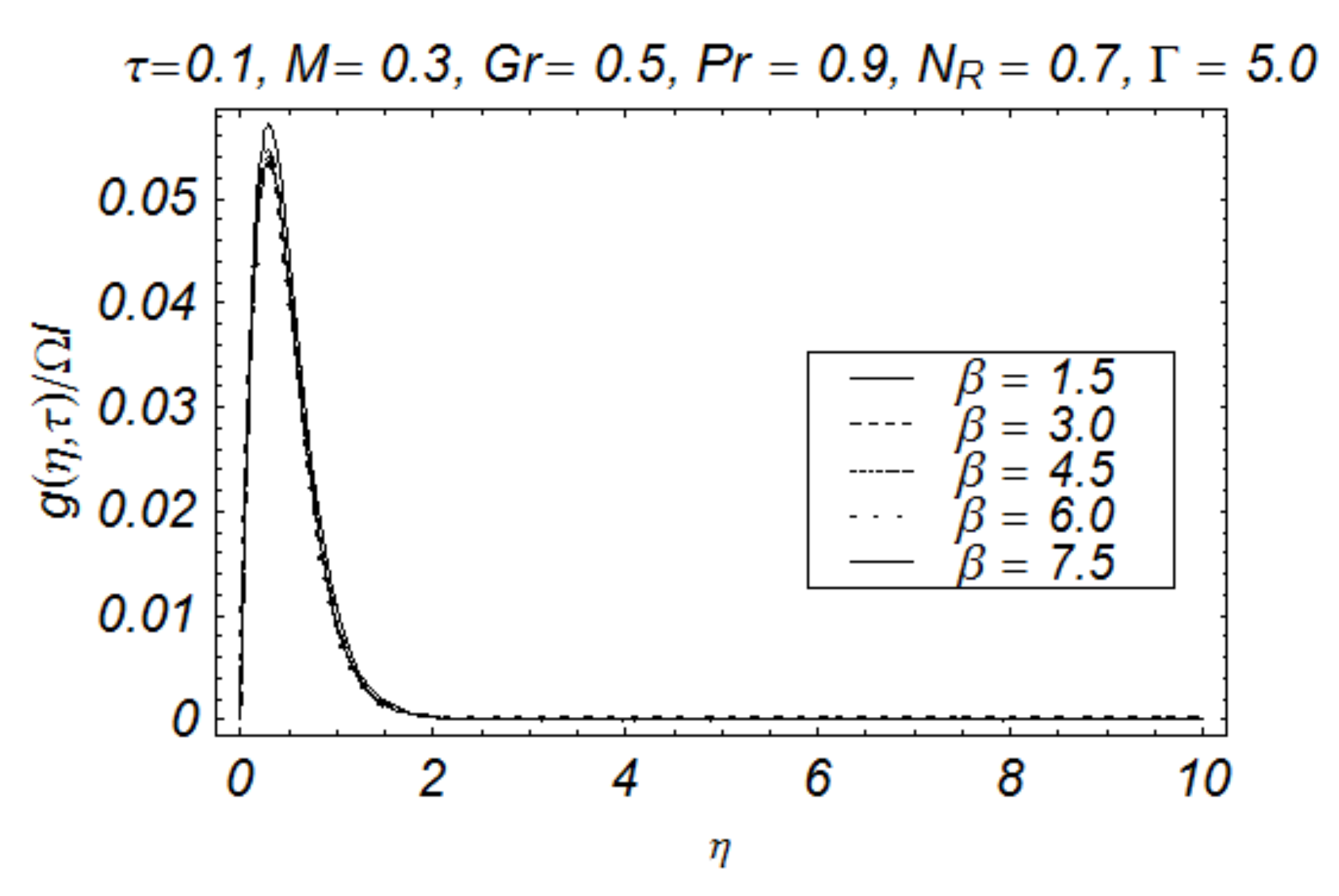
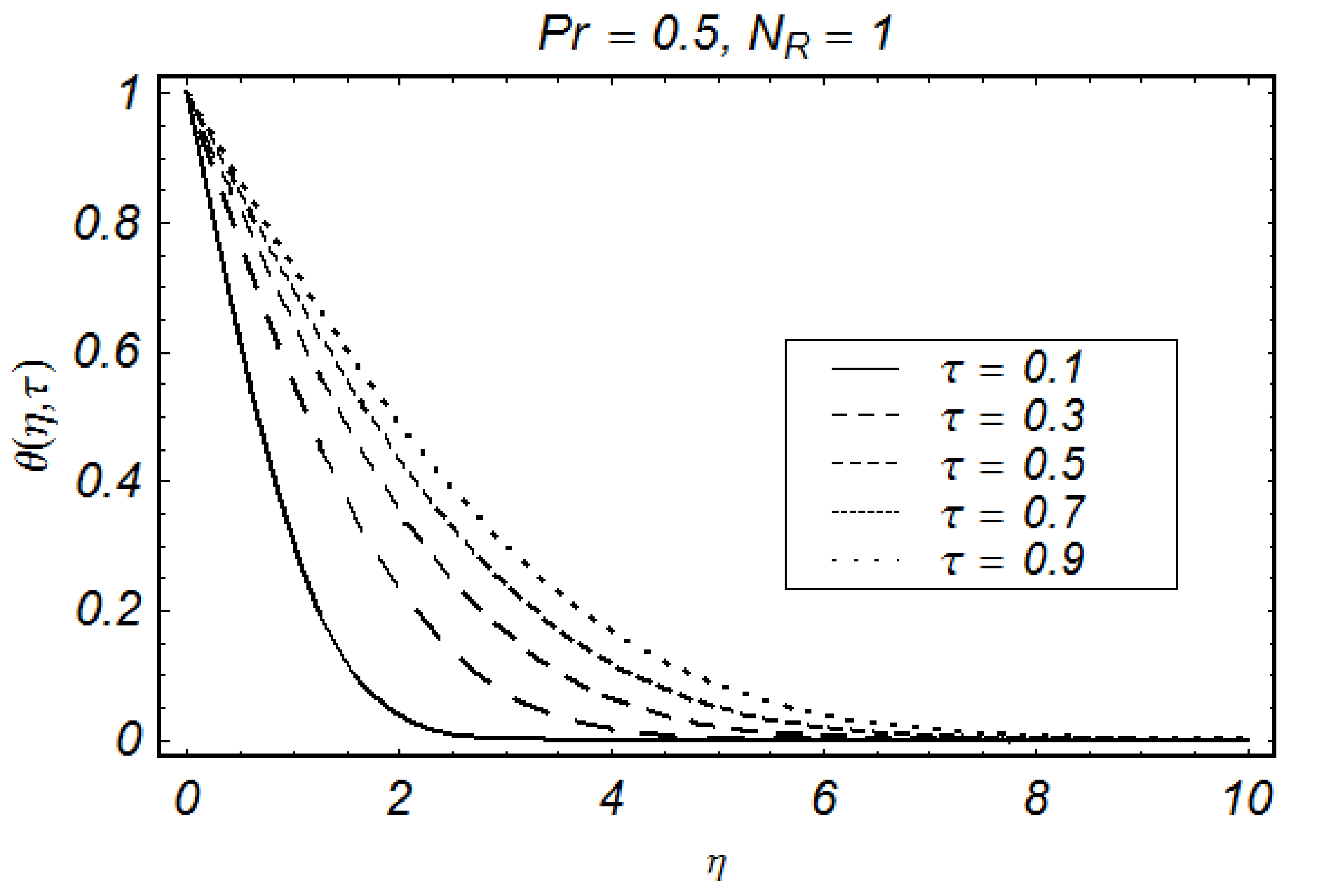
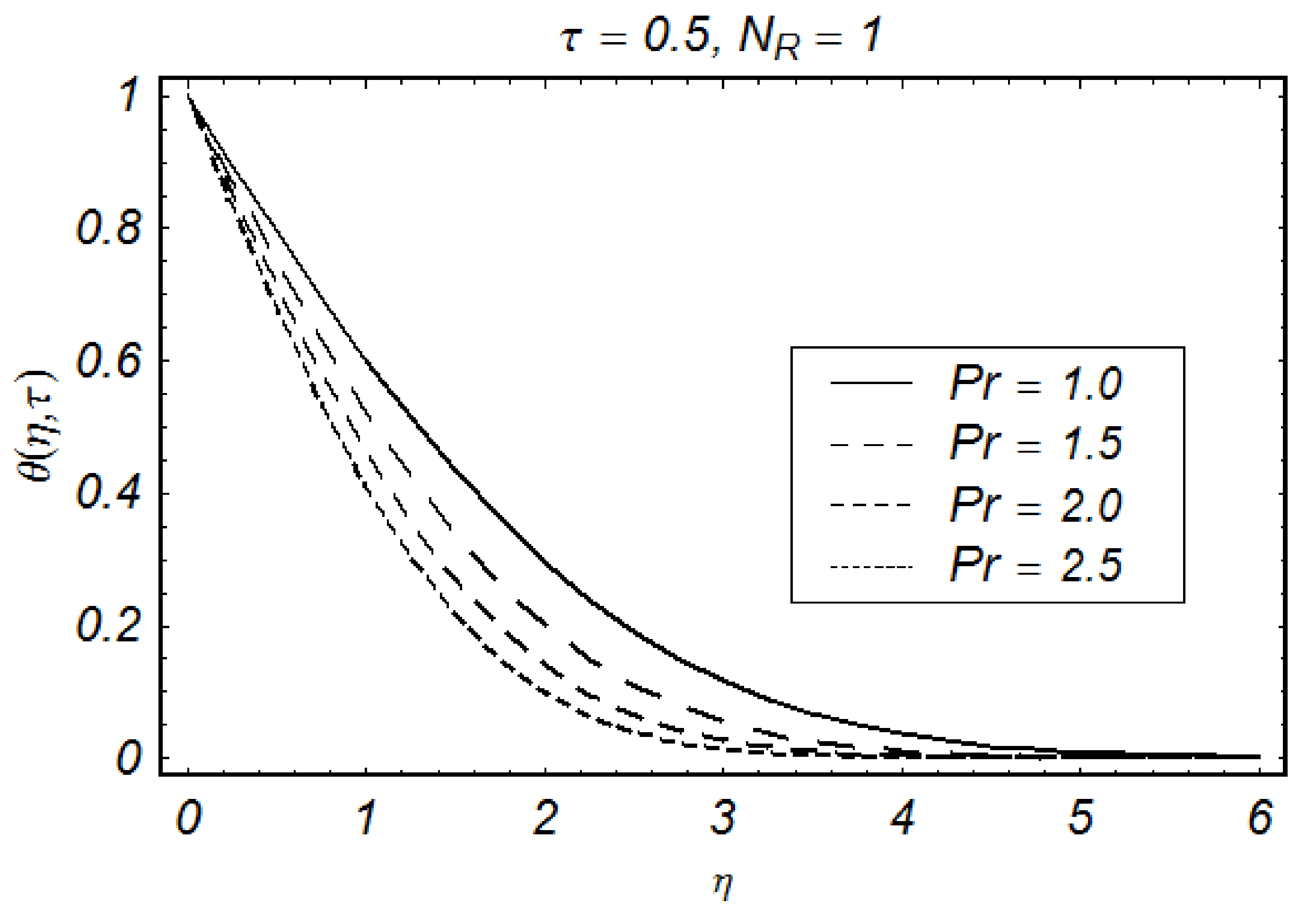
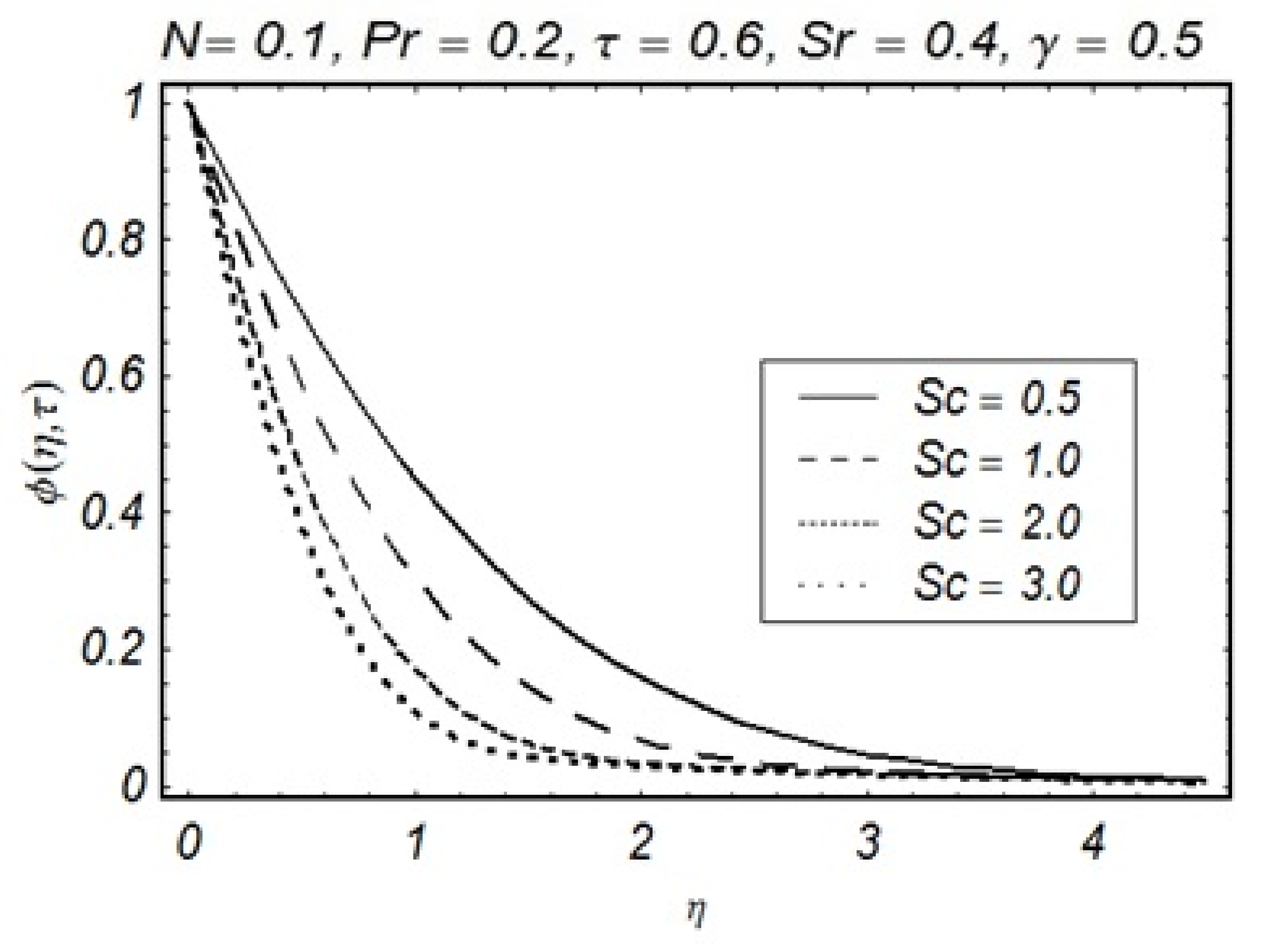
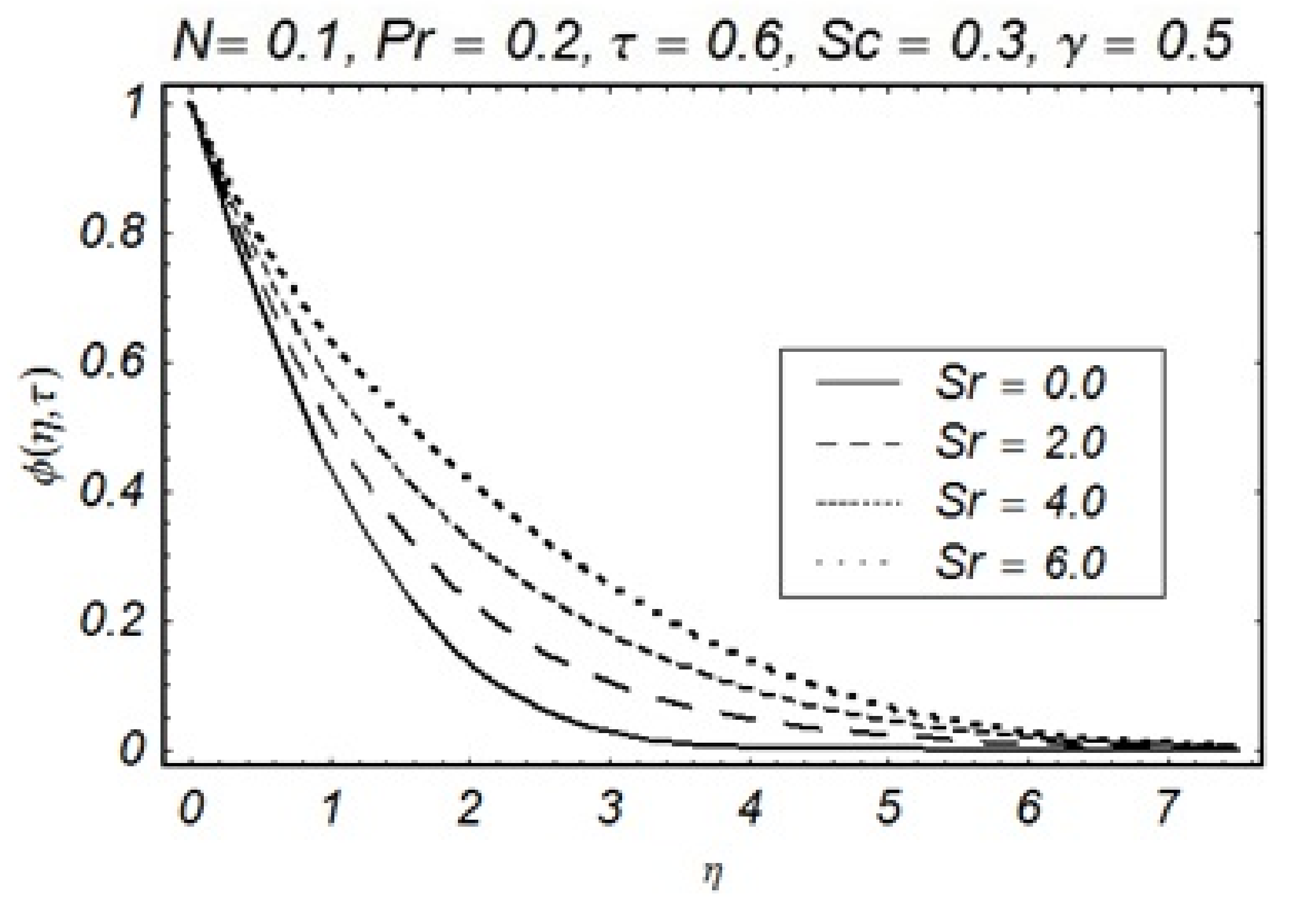
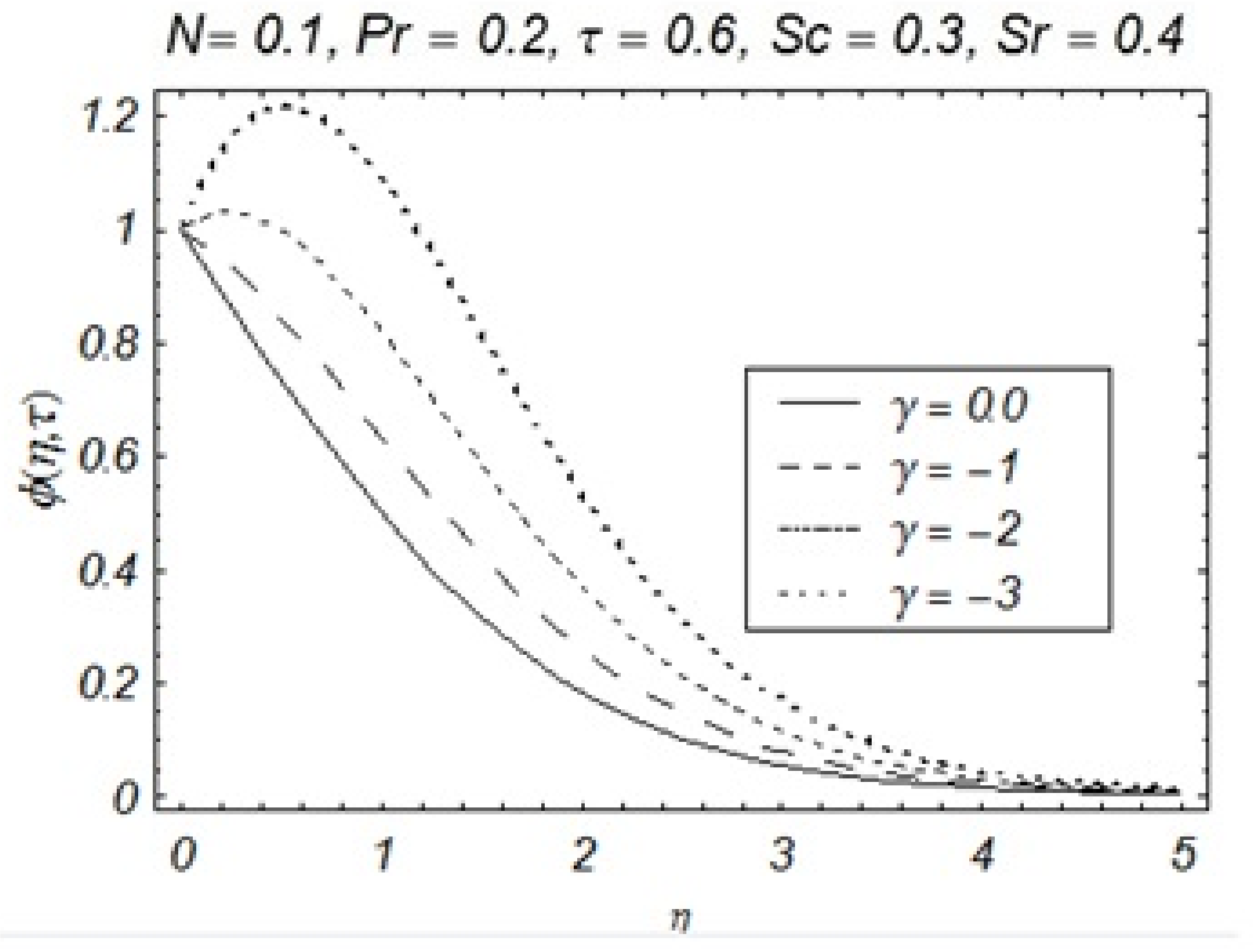
4. Results and Discussion

The exact solution of evolutionary set of partially differential equations is derived and is manipulated versus involved parameters to explore underlying physics. Features of mass diffusion, thermal energy and flow behavior are measured in presence of Casson liquid. An effect of magnetic field is addressed. A rotating disc is considered to measure thermal energy, solute particles and flow behavior considering chemical reaction and thermal radiation. Numerical simulations are obtained by Laplace method using MATHEMATICA 15.0. Graphs of thermal energy, velocities and concentration against various parameters are plotted with help of Laplace method using MATHEMATICA 15.0.A detail discussion is provided below.

Flow analysis: The time evolution of primary and secondary components of velocity is shown by Figure 2 and Figure 3. This graphical representation of velocity components have revealed that $f\left(\eta ,\hspace{0.17em}\tau \right)$ gradually slows down, whereas $g\left(\eta ,\hspace{0.17em}\tau \right)$ increases as time passes when $\tau$ is increased. Moreover, momentum layers of primary velocity are enhanced while momentum layers are declined at secondary velocity. Thus, an opposite trend among primary and secondary velocities are found when $\tau$ is increased. The character of magnetic field on velocities is displayed by Figure 4 and Figure 5. These graphical data represent that flow is accelerated by the Lorentz force. This increasing impact of magnetic field is observed both for $f\left(\eta ,\hspace{0.17em}\tau \right)$ and $g\left(\eta ,\hspace{0.17em}\tau \right)$ (see Figure 4 and Figure 5). Physically, Lorentz forces are developed due to Ohm’s law used in present model. Direction of flow is opposite against applied Lorentz forces. Therefore, resistance force is produced into particles of Casson liquid which resists flow in disk. Another, reason is that negative of Lorentz forces into particles. More viscous fluid is generated against change in magnetic field. Layers of (MBL) have reducing function versus an impact of magnetic field. Guria [24] investigated an impact of magnetic field on secondary and primary velocities. He has included that primary velocity is enhanced but secondary velocity is declined versus an impact of magnetic number. In current model, same behavior of magnetic is investigated on secondary and primary velocities. So, good agreement among current model is verified with already published work by Guria [24]. Computed results have shown that buoyant force has remarkable impact on the flow. The influence of buoyant force on the flow is recorded in Figure 6 and Figure 7. The dual role of Grashof number is observed on velocity for curves for secondary and primary velocities. This effect is produced because of buoyancy. It is noticed that the appearance of buoyancy is used as frictional force into motion of fluid particles. Moreover, it is treated as opposing forces into motion of fluid particles. An impact of Casson number on velocity curves is plotted as shown in Figure 8 and Figure 9. A declination is found into particles motion when Casson number is increased.

Observations related to thermal energy: The time evolution of thermal change in fluid regime is predicted by Figure 10. A remarkable enhancement in TBLT is investigated. A significant reduction in temperature of fluid is observed when $Pr$ is increased (see Figure 11). Further, Prandtl is associated with fraction among thermal and momentum boundary layers. Physically, thermal boundary layers have inverse proportional against an effect of Prandtl number. Thus, an increase in $Pr$ indicates minimum amount of heat energy. Therefore, thermal layers can be adjusted trough variation in Prandtl number. A notable decrease in TBLT is also observed. It noted that the fluid cools down when thermal radiations leaves the fluid regime in the form of electromagnetic wave. This impact of thermal radiations is shown by Figure 12. An effect of thermal radiation is captured into thermal energy. It is revealed that thermal radiation number and temperature profile have inverse proportional relation. Temperature profile is decreased when thermal radiation is boosted. Thermal energy moves away from region of disc trough movement of thermal radiation which carries heat energy along with.

Observations related to concentration profile: Time evolutionary behavior of concentration is shown in Figure 13 which clearly predicts that concentration field increases as time passes. It means that wall concentration diffuses into the fluid with time. The role of Schmidt number on the concentration profile is also studied and outcomes are displayed in Figure 14. This clearly depicts that the solute particles are reducing function of $Sc$. It is a dimensionless number, whereas $Sc$ is the ratio among mass and momentum diffusivities. From a definition point of view, large values of Schmidt number bring declination into diffusion of solute particles. Further, layers associated with concentration have a declination function against Schmidt number. It is also noted that the impact of $\mathrm{Pr}$ on the temperature profile is similar to that of $Sc$ on the concentration profile. The role of $Sr$ on the concentration profile is displayed by Figure 15. Soret number $Sr$ is the coefficient of term in concentration equation which is due to the diffusion species by virtue of temperature differences and an increase in $Sr$ associates an enhancement rate of diffusion of species. The parameter related to $Sr$ is called the Soret number. We note that that fraction among temperature difference and solute particles is referred to as the Soret number. Therefore, an increase in the Soret number brings an enhancement into the temperature difference but reduction is developed into solute particles. Eventually, the concentration profile increases. The impact of chemical reactions on the concentration profile is shown in Figure 16 and Figure 17. Figure 16 captures the impact of destructive chemical reaction on the concentration profile, whereas the impact of generative chemical reaction on concentration profiles is given by Figure 17. Dual behaviors are noticed in solute particles via chemical reaction considered in Figure 16 and Figure 17. A destructive chemical reaction is caused by positive values while generative chemical reaction is developed because of generative chemical reactions.

5. Conclusions

Heat and mass transport in non-coaxial rotational motion of Casson fluid and angular velocity in the presence of reacting medium is modeled and the exact solutions of system of evolutionary set of problems are evaluated by Laplace velocity, temperature and concentration fields’ in view of variation of involved parameters. Numerical simulations are obtained by Laplace method using MATHEMATICA 15.0. Following outcomes are recorded.

• Particle motion becomes slowed down against the intensity of magnetic fields;
• The impact of buoyant force on primary velocity is opposite to the effect of buoyancy on the secondary velocity;
• Applications of non-coaxial rotation motion are found in food processing and engineering processes, jut engines, pump cleaners, vacuum cleaners and geophysical flows;
• TBL (thermal boundary layers) decrease with enhancement in Prandtl number and $\tau$

• Production into thermal energy is declined when thermal radiation is enhanced;
• Growth of layers associated with solute particles is significant against higher values of Soret number but the opposite role in solute particles is observed for values of the Schmidt number;
• The opposite trend in solute particles is noticed for dual behavior of chemical reactions.