A Novel Generator Design Utilised for Conventional Ejector Refrigeration Systems
Abstract
1. Introduction
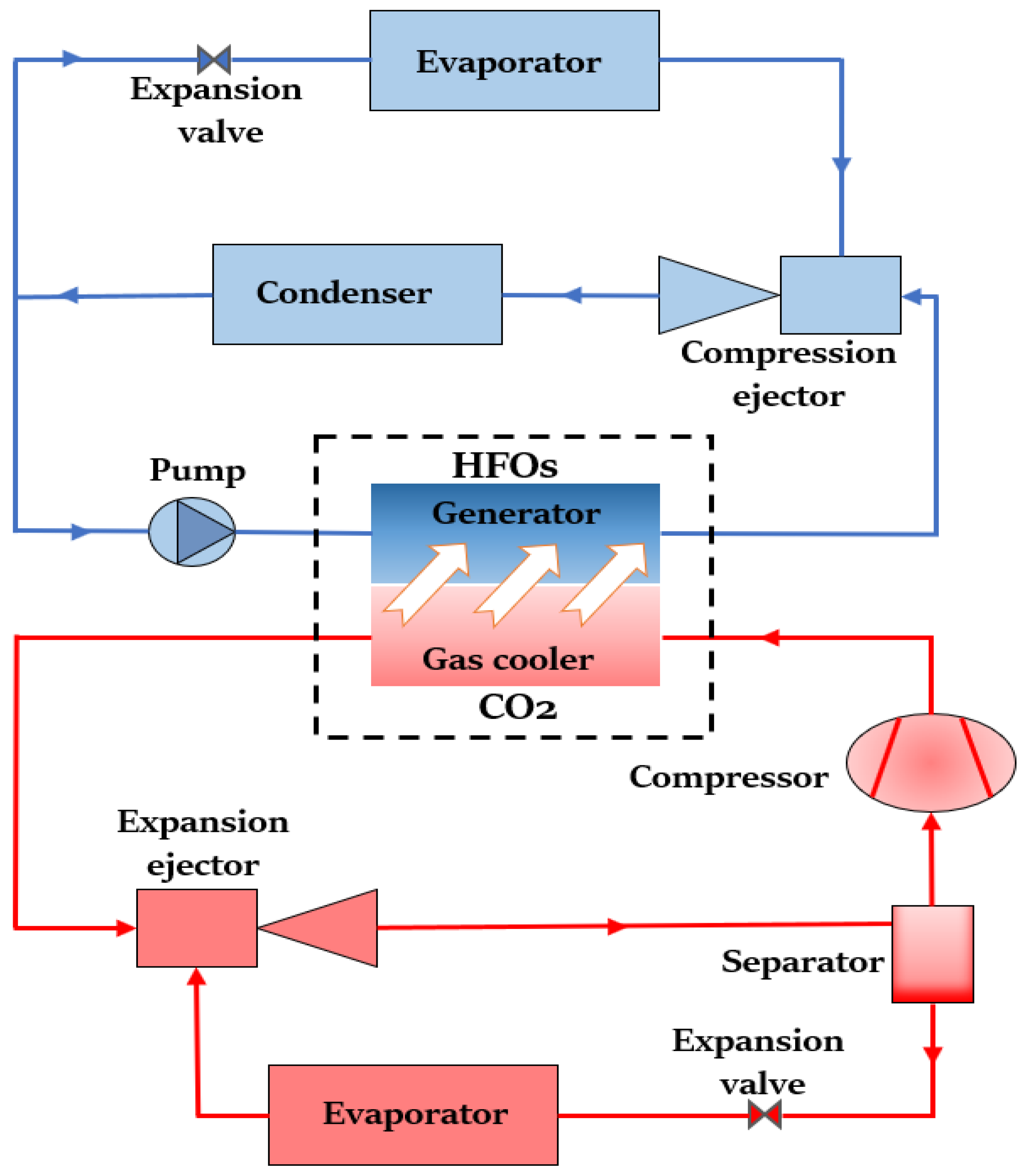
2. System Description
- the heat exchanger operated under steady-state conditions and was considered as one-pass counterflow;
- heat losses to the environment are negligible;
- the maldistribution phenomenon inside the PHE was neglected;
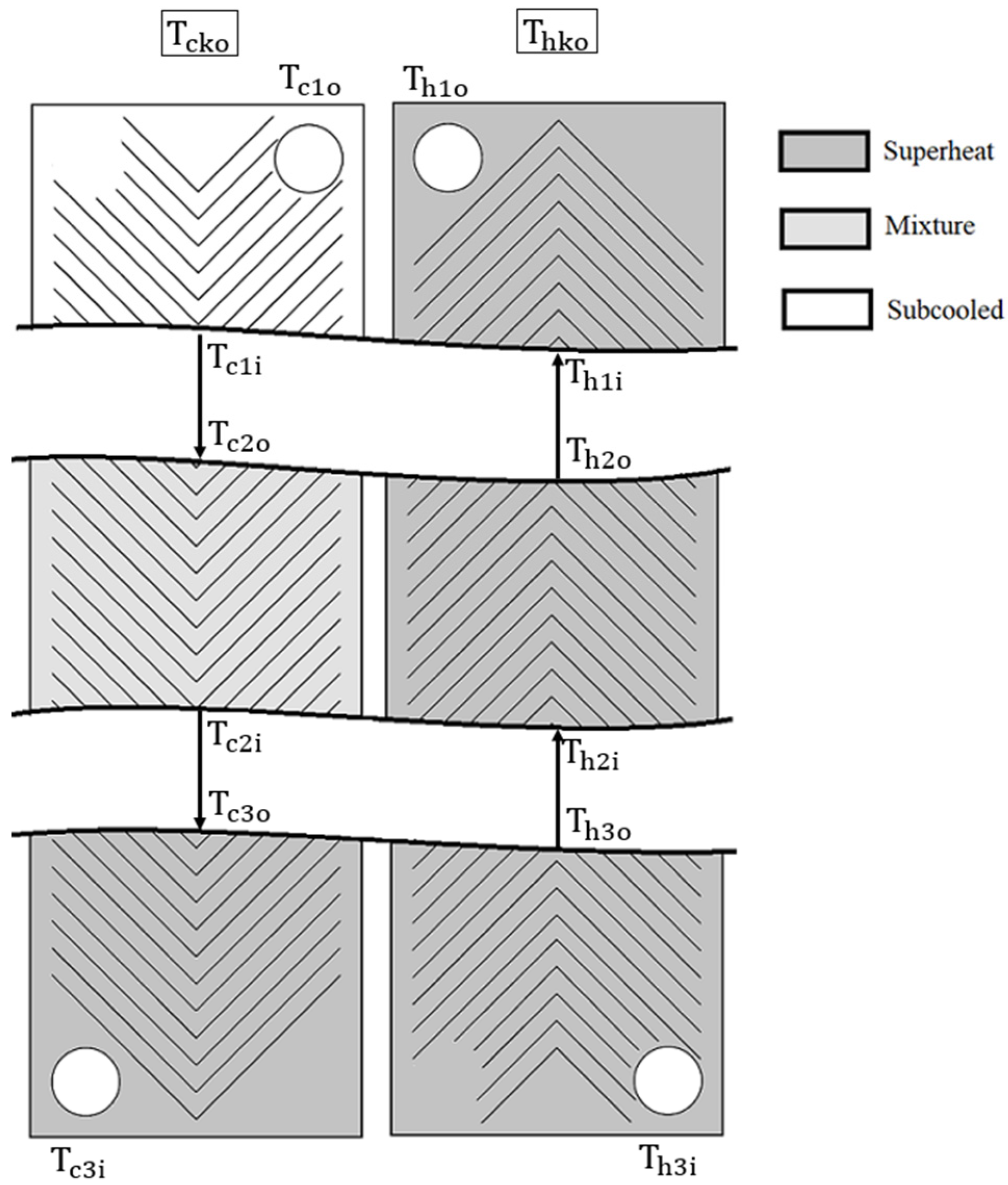
- for the cold stream with a phase change, the plate was divided into three portions;
- a linear temperature difference was considered between the two flow streams;
- the cold stream was modelled at a saturation temperature of 87 °C and an inlet temperature of 25 °C;
- effectiveness was estimated using the ϵ-NTU method; and
- all the thermophysical properties were estimated based on the NIST fluid database (REFPROP v.10).
3. Theoretical Analysis
3.1. Data Reduction
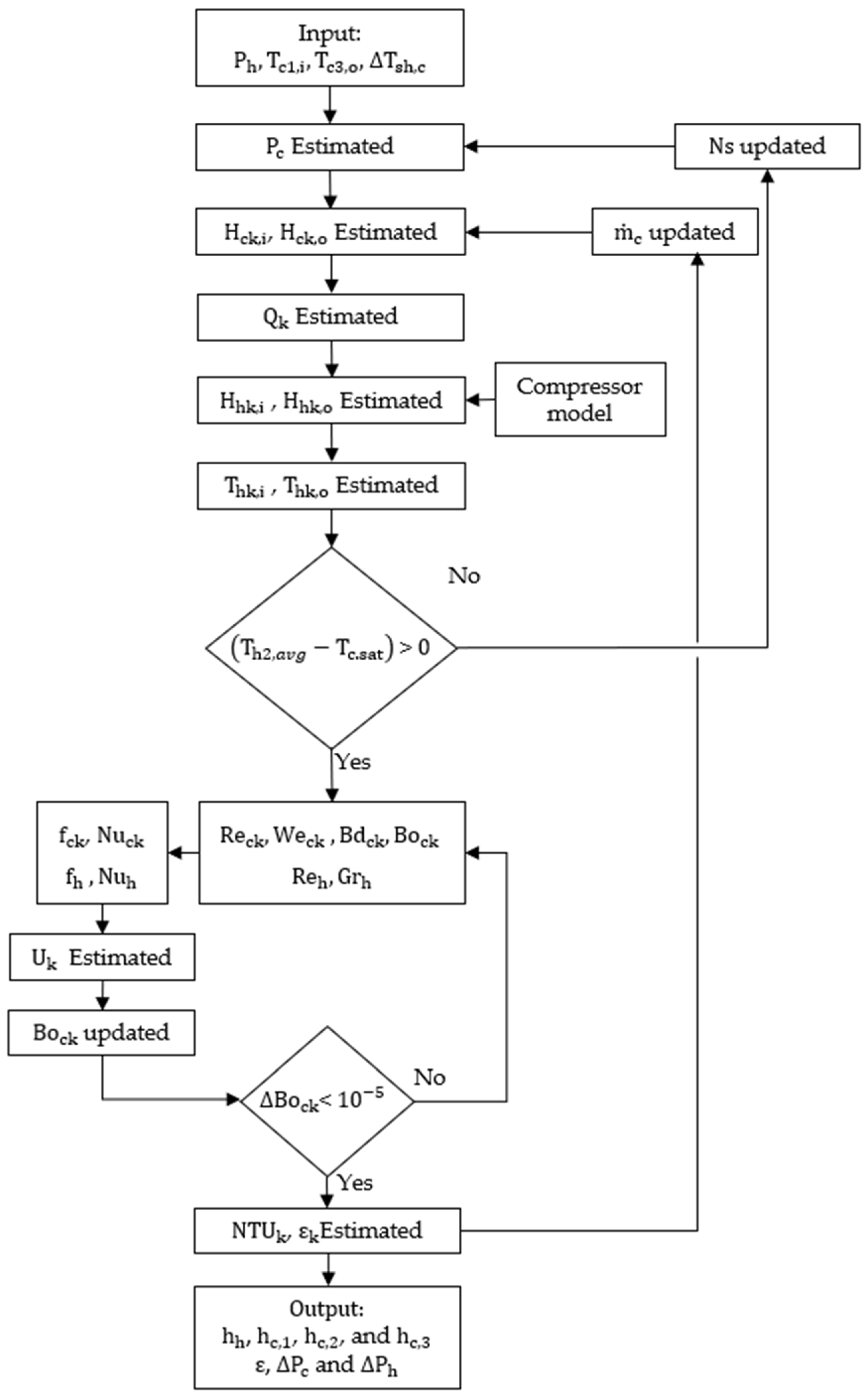
3.2. Calculation Procedures
- The inputs are the hot stream pressure () and the superheat difference (). Afterwards, the saturation pressure () was calculated according to the refrigerant name () at 87 °C.
- The enthalpies were estimated for all artificial inlets and outlets of the cold stream.
- The total heat rate () was evaluated for each artificial section according to the enthalpy difference multiplied by the mass flow rate of the cold stream, Equation (1).
- The inlet enthalpy and the temperature of the hot stream ( and ,respectively) were estimated using the compressor model and the hot stream pressure (). Subsequently, the other enthalpies and temperatures were evaluated using the corresponding heat rate () from each artificial section.
- If the outlet temperature of the hot stream’s second section () is higher than the cold stream saturation temperature (), then the required dimensionless numbers of each stream can be evaluated directly except for the boiling number (Bo), as it requires information on the heat flux between the hot and cold streams (). Based on Amalfi’s review [22], the average between the maximum and the minimum Boiling number was taken as an initial guess with a value of 0.002.
- In the next step, the overall heat transfer coefficient (), the heat flux (), the number of transfer units (NTU), and the effectiveness () will be estimated. When all the data are calculated, the boiling number (Bo) will be updated according to the new heat flux () as well as the overall heat transfer coefficient (), the number of transfer units (NTU), and the effectiveness (). Then, the mass flow rate () will be updated.
- Alternatively, if the outlet temperature of the hot stream’s second section () is lower, then the calculation will be stopped for the current cold stream mass flow rate, and the name (Ns) will be updated to the next step.
- Finally, the output is stored as the effectiveness, the convection coefficients, and the pressure drop matrices at various channel mass fluxes.
4. Discussion
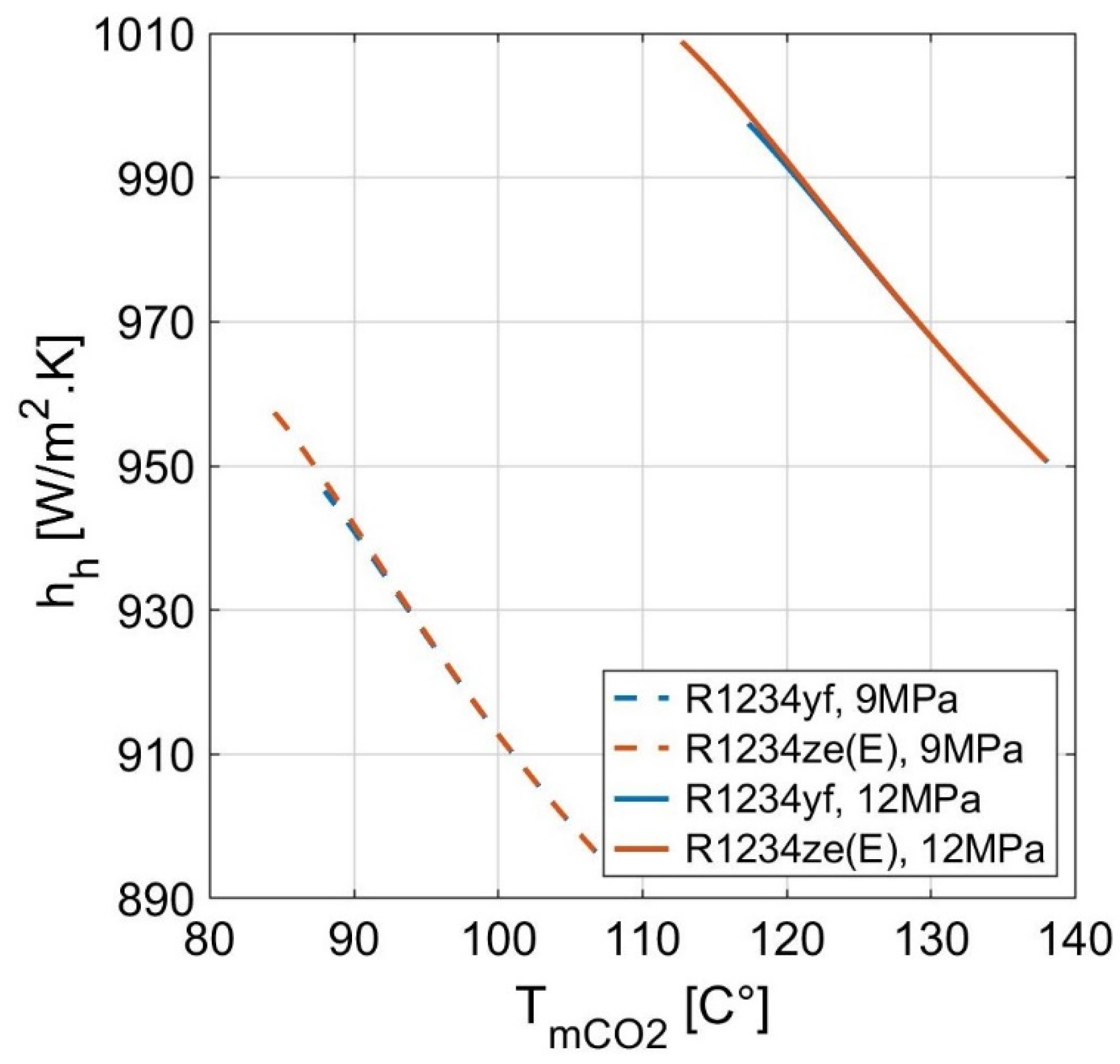
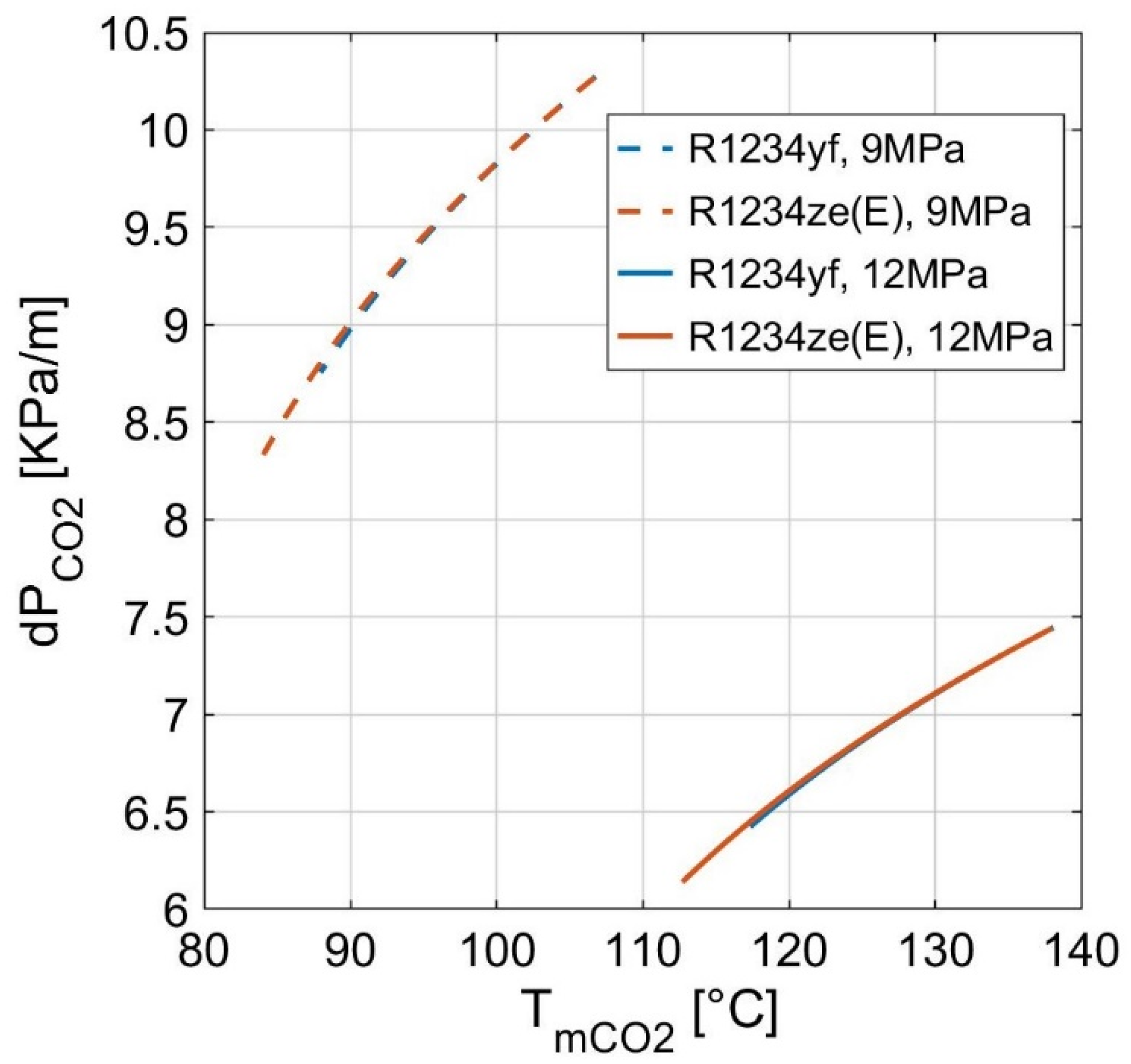
4.1. Effect of Hot Stream Inlet Pressure
4.2. Effect of Superheat
4.3. Effect of Heat Exchanger Size
5. Conclusions
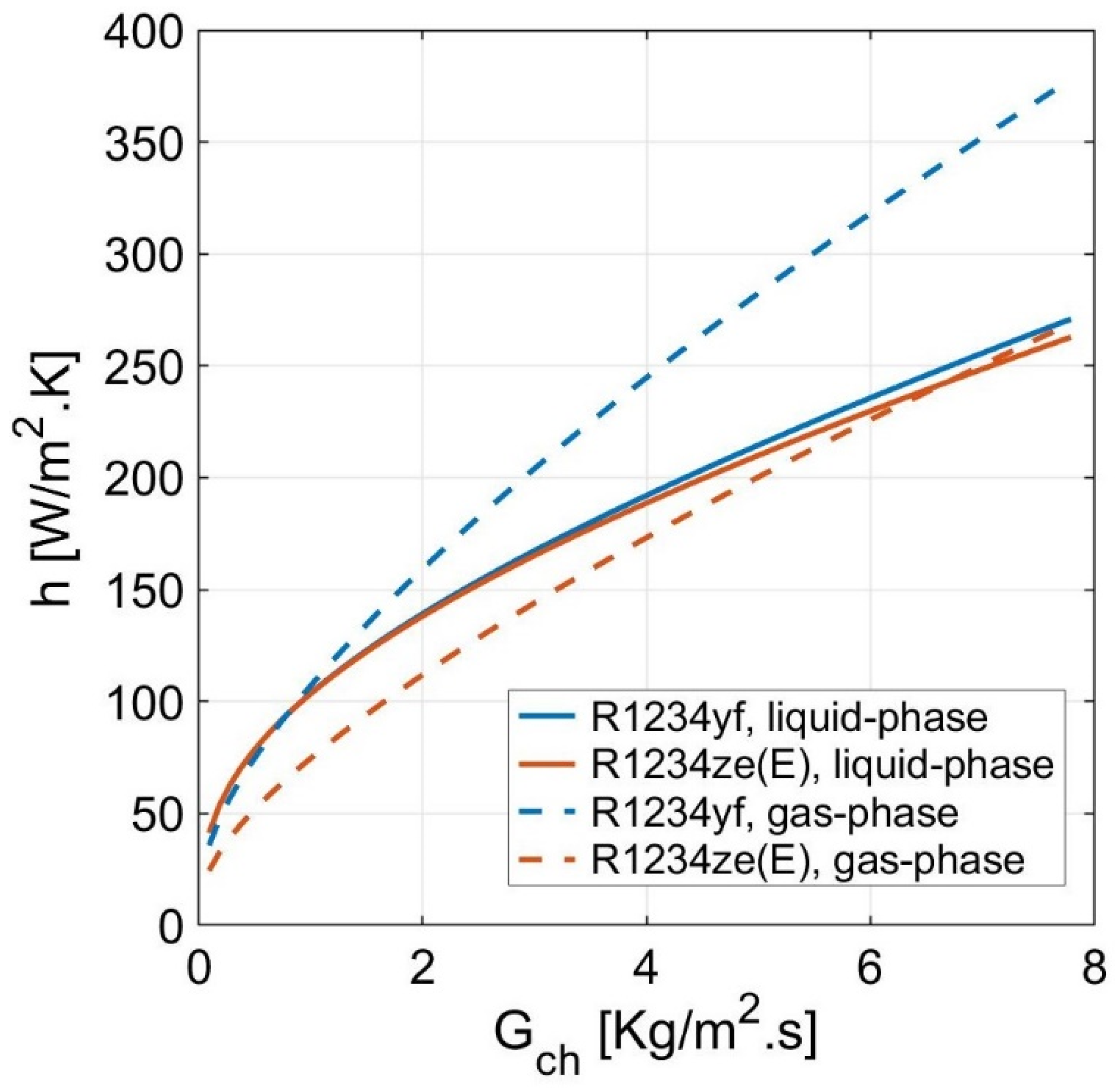
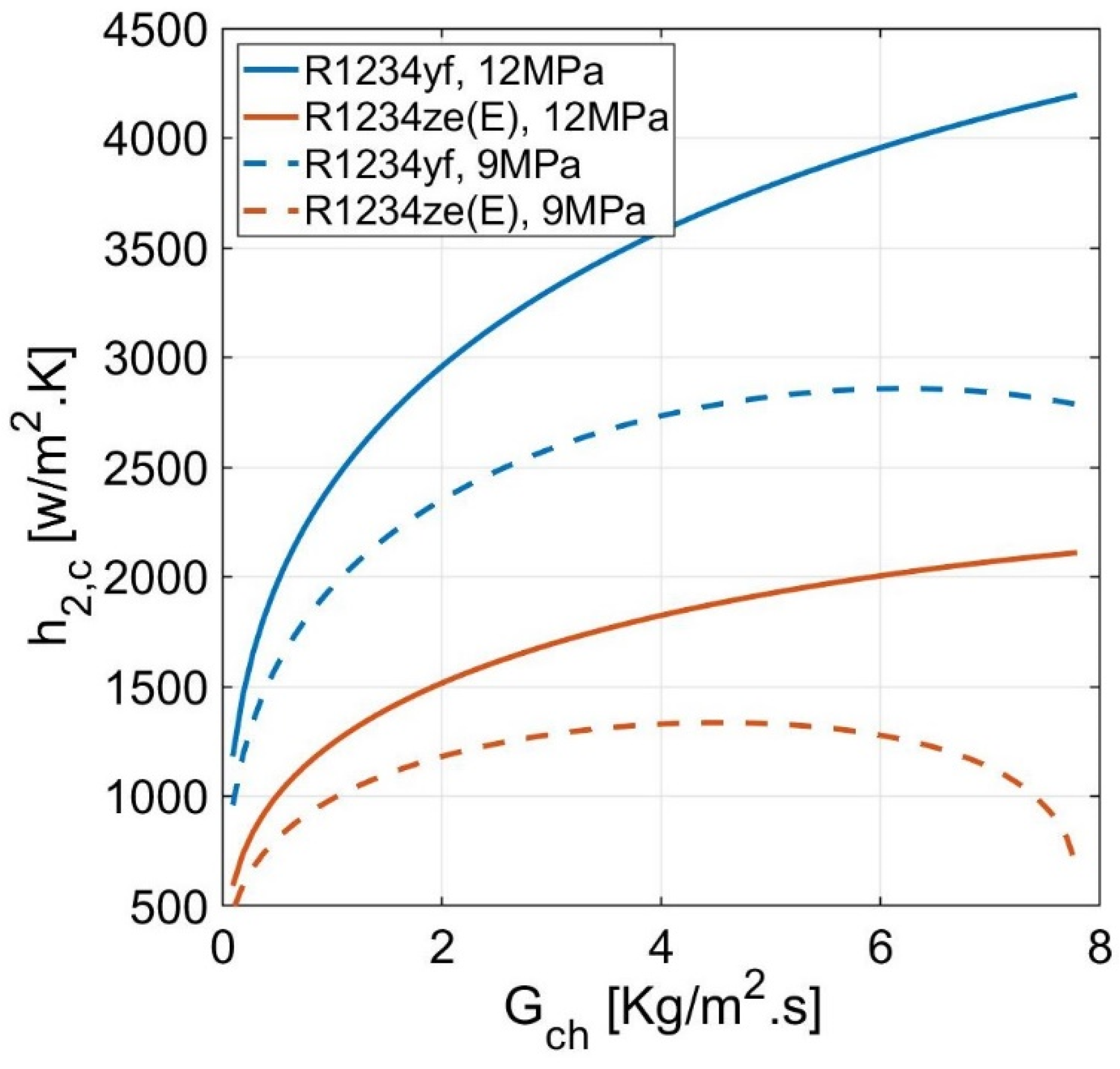
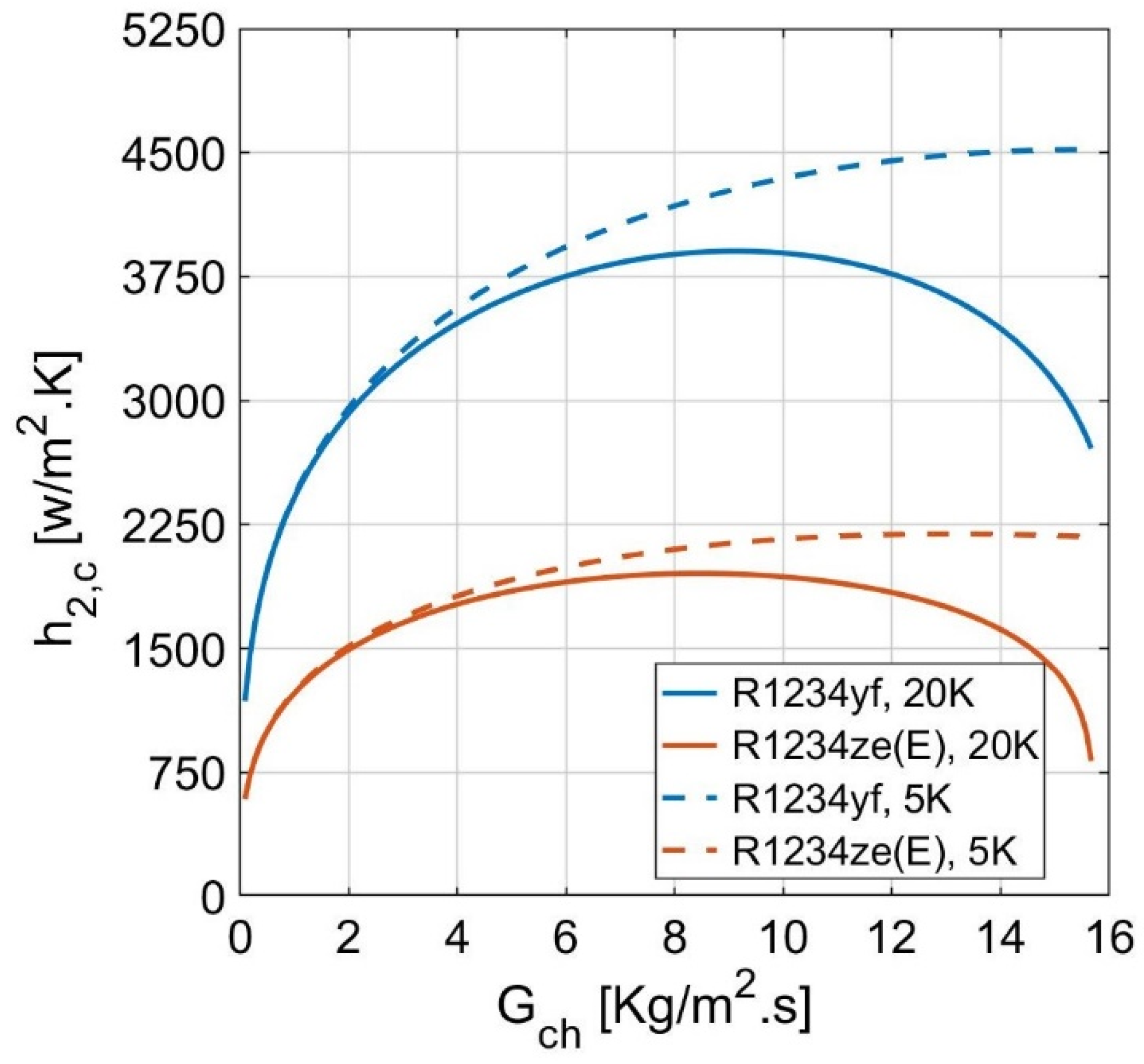
- when increasing the hot stream inlet pressure from 9 to 12 MPa, the two-phase convection coefficients of the HFOs increase significantly with a range of 20–50% and 20–200% for R1234yf and R1234ze(E), respectively;
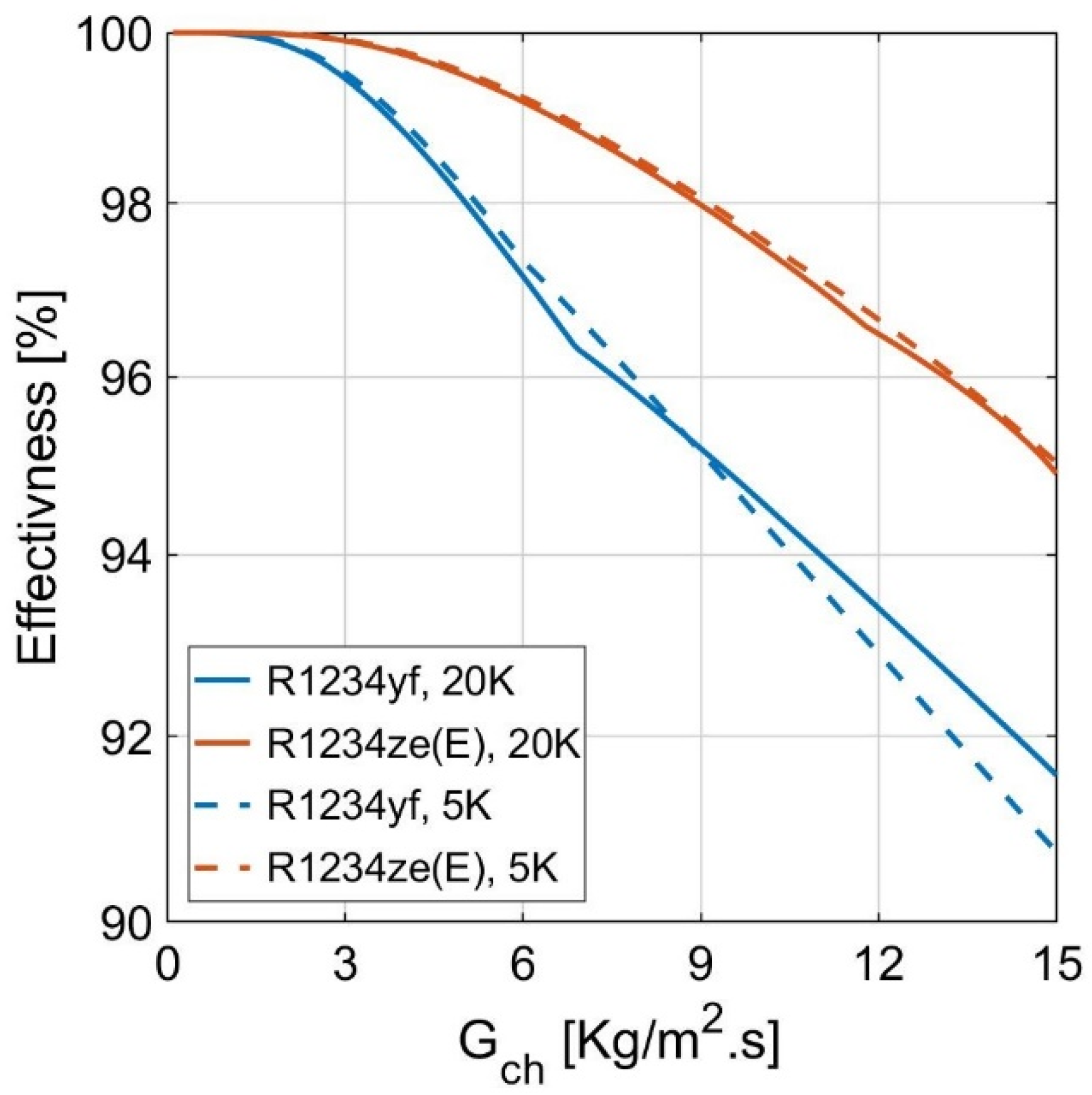
- increasing the cold stream superheat temperature difference from 5 K to 20 K allows the two-phase convection coefficients of the HFOs to increase steeply with a value of 1–20% at low cold channel flow fluxes;
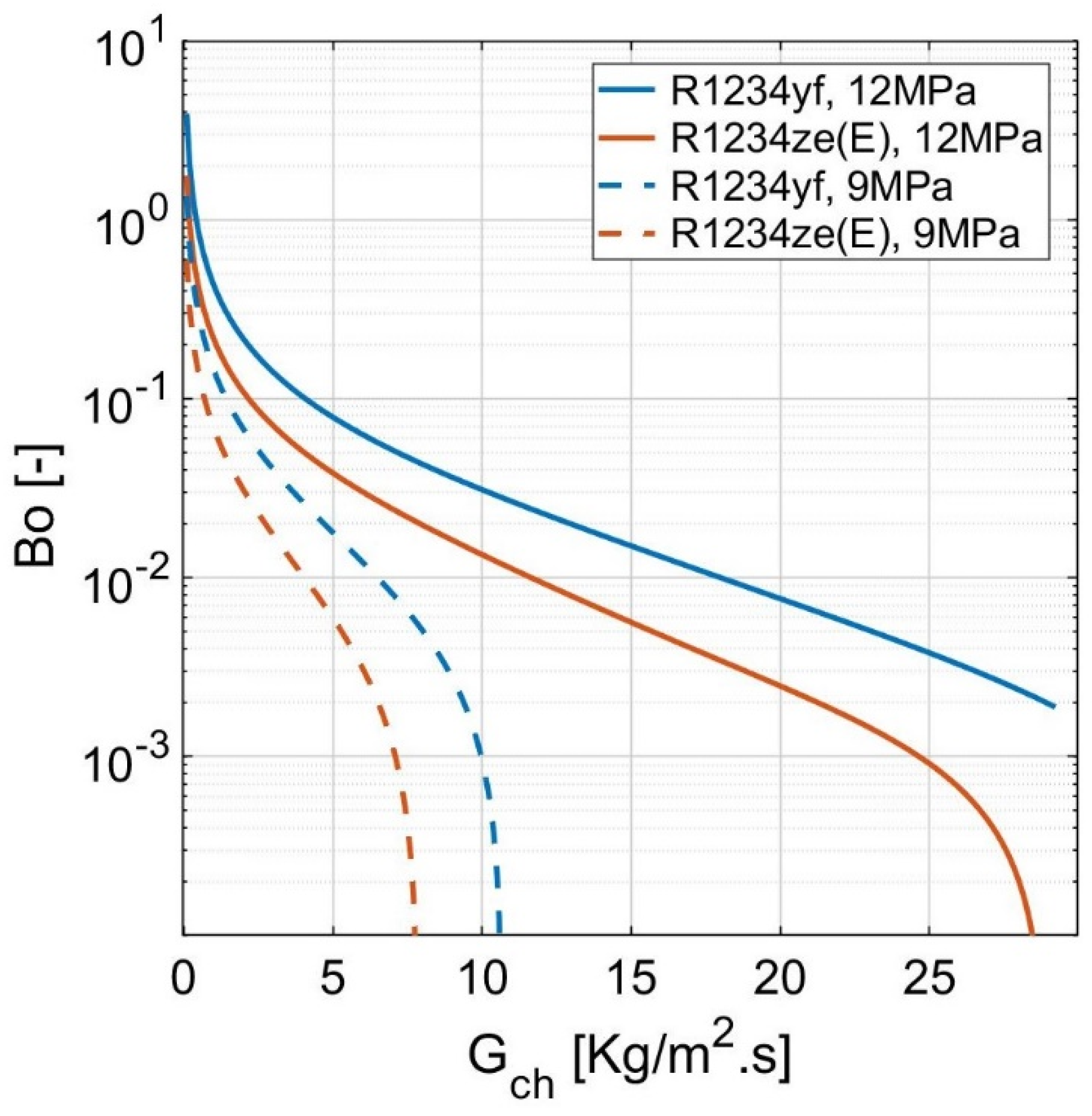
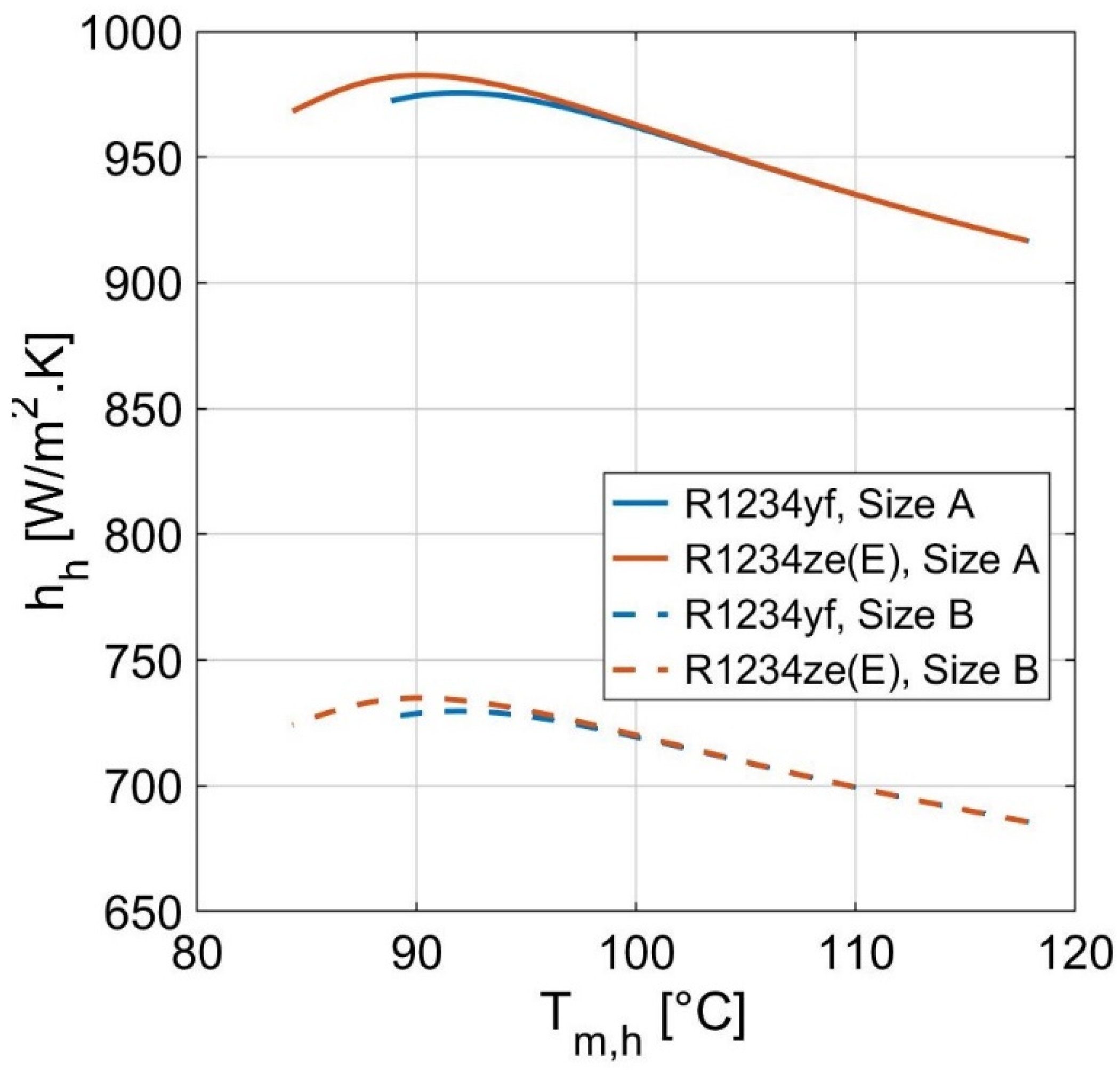
- the two-phase convection coefficient is significantly influenced by the boiling and bond numbers. The working fluid type affects the bond number, while the heat flux dominates the boiling number;
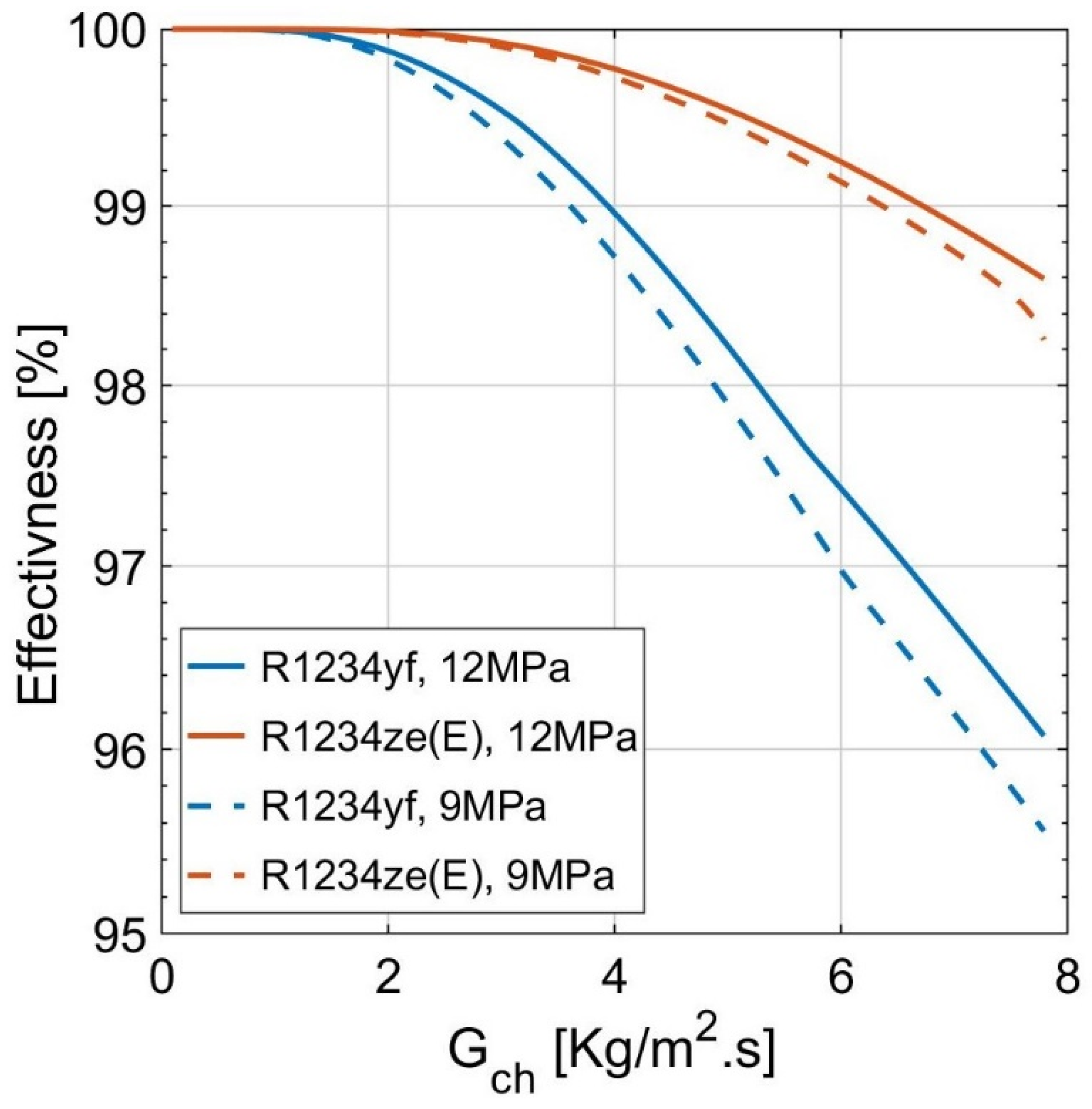
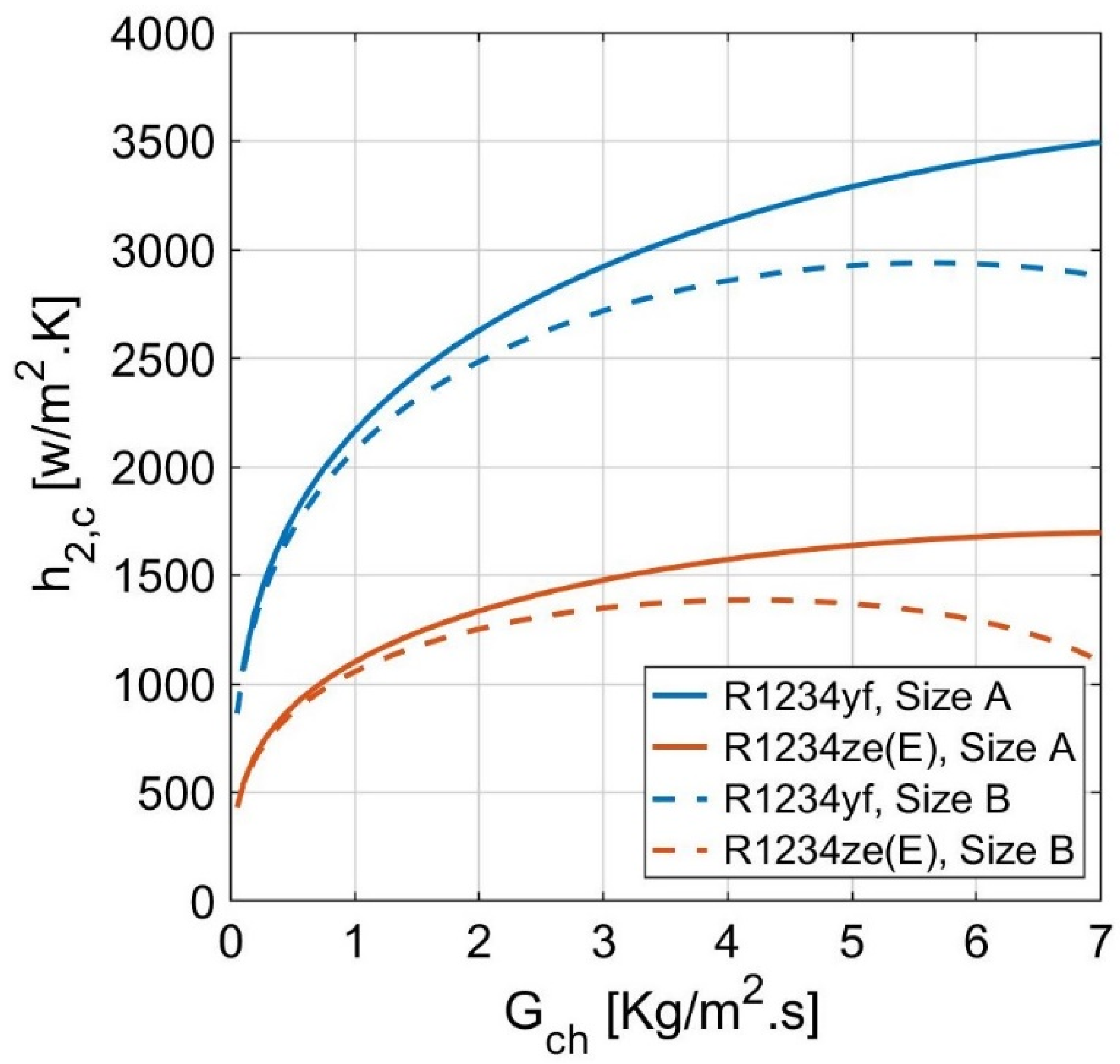
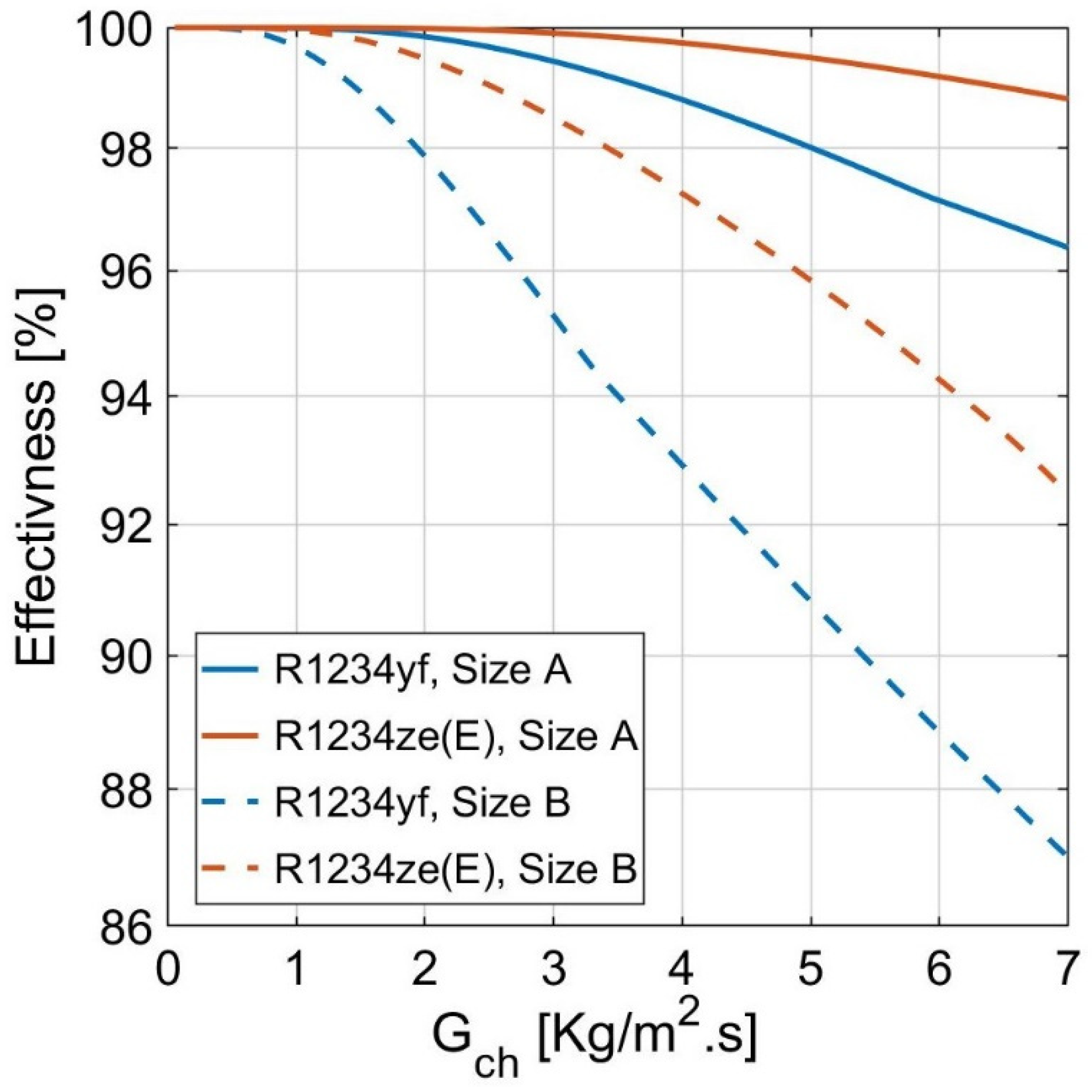
- increasing the plate size influenced both the two-phase convection coefficient and the effectiveness significantly. The two-phase convection coefficients of the HFOs increased with a range of 1–20% and 1–50% for R1234yf and R1234ze(E), respectively. In contrast, the effectiveness increased by 10% for R1234yf and 5% for R1234ze(E);
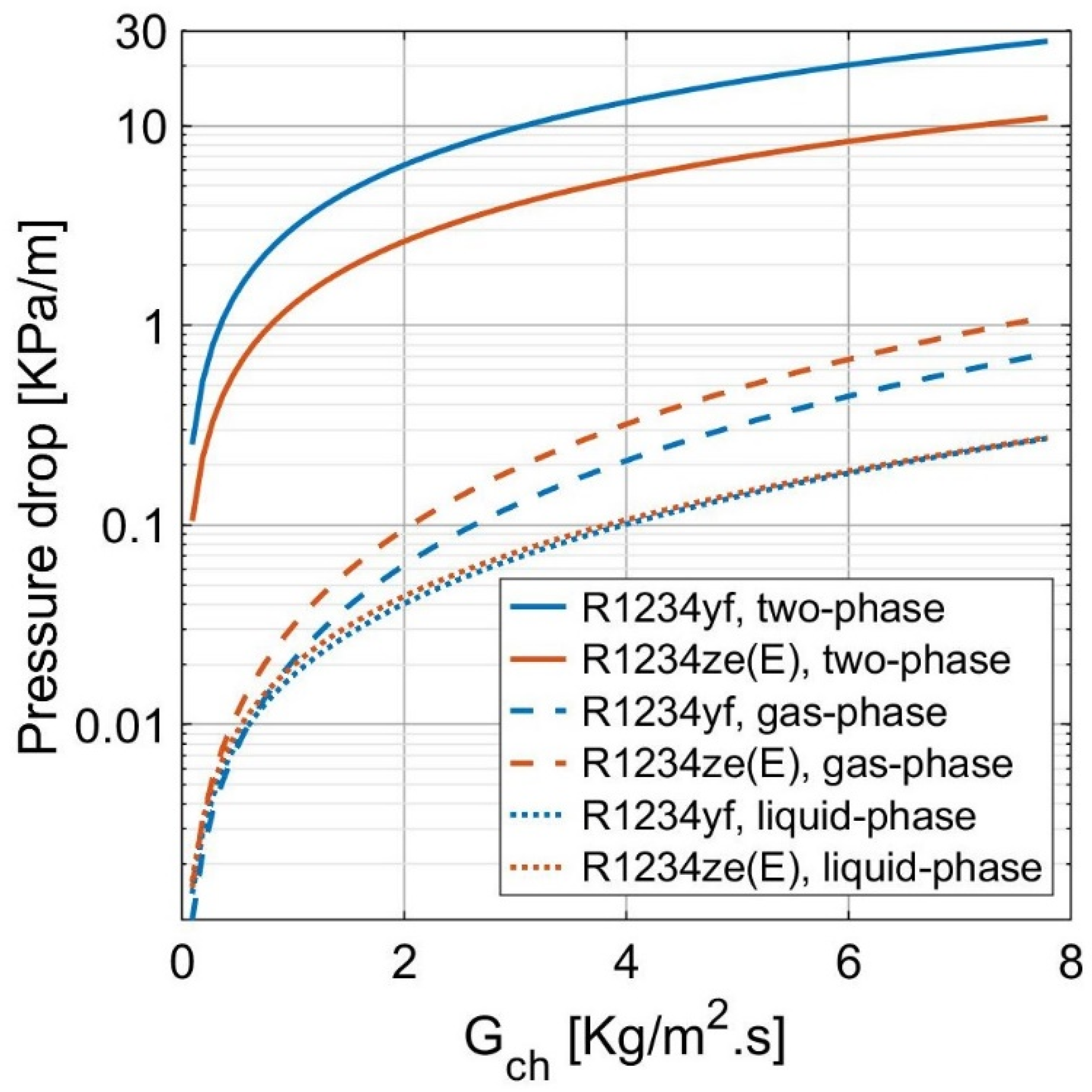
- the two-phase convection coefficient dominates the frictional pressure drop as the flow is turbulent even at a low vapor quality.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Units and Symbols | |
| Mass flow rate (Kg/m2) | |
| A | Area (m2) |
| b | Mean channel gap (m) |
| Bd | Bond number (-) |
| Bo | Boiling number (-) |
| C | Heat capacity (KW/K) |
| Cp | Specific heat (Kj/Kg.K) |
| D | Diameter (m) |
| f | Fanning friction coefficient (-) |
| F | Fouling Factor (m/s2) |
| g | Gravity acceleration (m/s2) |
| G | Mass flux (Kg/m2·s) |
| Gr | Grashof number (-) |
| H | Enthalpy (Kj/Kg) |
| I | Enthalpy of vapourization (Kj/Kg) |
| h | Convection coefficient (-) |
| L | Effective flow length (m) |
| NTU | Number of transfer units (-) |
| Nu | Nusselt number (-) |
| p | Plate pitch (m) |
| P | Pressure (MPa) |
| PHE | Plate heat exchanger (-) |
| Pr | Prandtl number (-) |
| q | Heat flux (KW/ m2) |
| Q | Heat rate (KW) |
| Re | Reynolds number (-) |
| t | Thickness (m) |
| W | Plate width (m) |
| Greek symbols | |
| ∅ | Enlargement factor (-) |
| µ | Dynamic Viscosity (kg/m.s) |
| β | Corrugation Angle (°) |
| Δ | Difference (-) |
| ε | Effectiveness (-) |
| κ | Conductivity (-) |
| λ | Corrugation Pitch (kg/m3) |
| ρ | Density (kg/m3) |
| Surface tension. (N/m) | |
| Subscripts | |
| * | Reduced |
| a | Martin first constant |
| 1 | First partition |
| b | Martin second constant |
| 2 | Second partition |
| 3 | Third partition |
| c | Cold |
| ch | Channel |
| eff | Effective |
| h | Hot |
| hy | Hydraulic |
| i | Inlet |
| k | Artificial partition index |
| l | Liquid |
| lo | Liquid only |
| lv | Liquid vapour difference |
| m | Mean |
| o | Outlet |
| p | Plate |
| s | Refrigerant type index |
| sat | Saturated |
| SH | Superheated |
| sp | Single phase |
| tp | Two phase |
| v | Vapour |
| vo | Vapour only |
| w | Wall |
References
- Tashtoush, B.M.; Al-Nimr, M.A.; Khasawneh, M.A. A comprehensive review of ejector design, performance, and applications. Appl. Energy 2019, 240, 138–172. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F. Computational fluid-dynamics modeling of supersonic ejectors: Screening of turbulence modeling approaches. Appl. Therm. Eng. 2017, 117, 122–144. [Google Scholar] [CrossRef]
- Chen, X.; Omer, S.; Worall, M.; Riffat, S. Recent developments in ejector refrigeration technologies. Renew. Sustain. Energy Rev. 2013, 19, 629–651. [Google Scholar] [CrossRef]
- Charalambous, P.G.; Maidment, G.G.; Kalogirou, S.A.; Yiakoumetti, K. Photovoltaic thermal (PV/T) collectors: A review. Appl. Therm. Eng. 2007, 27, 275–286. [Google Scholar] [CrossRef]
- Nehdi, E.; Kairouani, L.; Elakhdar, M. A solar ejector air-conditioning system using environment-friendly working fluids. Int. J. Energy Res. 2008, 32, 1194–1201. [Google Scholar] [CrossRef]
- Spallina, V.; Romano, M.C.; Chiesa, P.; Lozza, G. Integration of Coal Gasification and Packed Bed CLC process for High Efficiency and Near-zero Emission Power Generation. Energy Procedia 2013, 37, 662–670. [Google Scholar] [CrossRef]
- Li, C.; Wang, R.; Lu, Y. Investigation of a novel combined cycle of solar powered adsorption–ejection refrigeration system. Renew. Energy 2002, 26, 611–622. [Google Scholar] [CrossRef]
- Amalfi, R.L.; Vakili-Farahani, F.; Thome, J.R. Flow boiling and frictional pressure gradients in plate heat exchangers. Part 1: Review and experimental database. Int. J. Refrig. Rev. Int. Du Froid. 2016, 61, 166–184. [Google Scholar] [CrossRef]
- Zohuri, B. Compact Heat Exchangers; Springer International Publishing: Cham, Switzerland, 2017; Volume 58. [Google Scholar]
- Kakaç, S.; Liu, H.; Pramuanjaroenkij, A. Heat Exchangers: Selection, Rating, and Thermal Design, 2nd ed.; Taylor & Francis: Abingdon, UK, 2002. [Google Scholar]
- Zendehboudi, A.; Ye, Z.; Hafner, A.; Andresen, T.; Skaugen, G. Heat transfer and pressure drop of supercritical CO2 in brazed plate heat exchangers of the tri-partite gas cooler. Int. J. Heat Mass Transf. 2021, 178, 121641. [Google Scholar] [CrossRef]
- Amalfi, R.L. Two-Phase Heat Transfer Mechanisms within Plate Heat Exchangers:Experiments, Modeling and Simulations; EPFL: Lausanne, Switzerland, 2016. [Google Scholar]
- Kumar, H. The Plate Heat Exchanger: Construction and Design. In Proceedings of the First U.K. National Conference on Heat Transfer, Leeds, UK, 3–5 July 1984; pp. 1275–1288. [Google Scholar]
- Martin, H. A theoretical approach to predict the performance of chevron-type plate heat exchangers. Chem. Eng. Process. Process. Intensif. 1996, 35, 301–310. [Google Scholar] [CrossRef]
- Focke, W.; Zachariades, J.; Olivier, I. The effect of the corrugation inclination angle on the thermohydraulic performance of plate heat exchangers. Int. J. Heat Mass Transf. 1985, 28, 1469–1479. [Google Scholar] [CrossRef]
- Hayes, N.; Jokar, A.; Ayub, Z.H. Study of carbon dioxide condensation in chevron plate exchangers; heat transfer analysis. Int. J. Heat Mass Transf. 2011, 54, 1121–1131. [Google Scholar] [CrossRef]
- Hayes, N.; Jokar, A.; Ayub, Z.H. Study of carbon dioxide condensation in chevron plate exchangers; pressure drop analysis. Int. J. Heat Mass Transf. 2012, 55, 2916–2925. [Google Scholar] [CrossRef]
- Jokar, A.; Hosni, H.M.; Eckels, S.J. Dimensional analysis on the evaporation and condensation of refrigerant R-134a in minichannel plate heat exchangers. Appl. Thermal Eng. 2006, 26, 2287–2300. [Google Scholar] [CrossRef]
- Lockhart, R.W.; Martinelli, R.C. Proposed Correlation of Data for Isothermal Two-Phase, Two-Component Flow in Pipes. Chem. Eng. Prog. 1949, 45, 9–48. [Google Scholar]
- Chisholm, D. A theoretical basis for the Lockhart-Martinelli correlation for two-phase flow. Int. J. Heat Mass Transf. 1967, 10, 1767–1778. [Google Scholar] [CrossRef]
- Amalfi, R.L.; Vakili-Farahani, F.; Thome, J.R. Flow boiling and frictional pressure gradients in plate heat exchangers. Part 2: Comparison of literature methods to database and new prediction methods. Int. J. Refrig. Rev. Int. Du Froid. 2016, 61, 185–203. [Google Scholar] [CrossRef]
- Finlayson-Pitts, B.J.; Pitts Jr., J.N. Scientific Basis for Control of Halogenated Organics. Chem. Up. Low. Atmos. 2000, 727–761. [Google Scholar] [CrossRef]
- Vallero, D.A. Air pollution calculations: Quantifying pollutant formation, transport, transformation, fate and risks; Elsevier: Amsterdam, The Netherlands, 2019; pp. 377–428. [Google Scholar]
- Wuebbles, D.J. Ozone Depletion and Related Topics: Ozone Depletion Potentials, Encyclopedia of Atmospheric Sciences, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2015; Volume 4, pp. 364–369. [Google Scholar] [CrossRef]
- Longo, G.A.; Mancin, S.; Righetti, G.; Zilio, C. HFC32 vaporisation inside a Brazed Plate Heat Exchanger (BPHE): Experimental measurements and IR thermography analysis. Int. J. Refrig. 2015, 57, 77–86. [Google Scholar] [CrossRef]
- ASHRAE. 2018 ASHRAE Handbook-Refrigeration; ASHRAE: Atlanta, GA, USA, 2018. [Google Scholar]
- Nekså, P.; Walnum, H.T.; Hafner, A. Keynote: CO2—A refrigerant from the past with prospects of being one of the main refrigerants in the futurer. In Proceedings of the 9th IIR-Gustav Lorentzen Conference on Natural Working Fluids, Sydney, Australia, 14–15 April 2010. [Google Scholar]
- United Nations Development Programme. Montreal Protocol on Substances That Deplete the Ozone Layer. 20 Years of Success; United Nations Development Programme: New York, NY, USA, 2007; p. 50. [Google Scholar]
- Karayiannis, T. EHD boiling heat transfer enhancement of R123 and R11 on a tube bundle. Appl. Therm. Eng. 1998, 18, 809–817. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A. An experimental evaluation of the greenhouse effect in the substitution of R134a with CO 2. Energy 2012, 45, 753–761. [Google Scholar] [CrossRef]
- Kruse, H. European research concerning CFC and HCFC substitution. Int. J. Refrig. 1994, 17, 149–155. [Google Scholar] [CrossRef]
- Huang, J.; Sheer, T.J.; Bailey-McEwan, M. Heat transfer and pressure drop in plate heat exchanger refrigerant evaporators. Int. J. Refrig. 2012, 35, 325–335. [Google Scholar] [CrossRef]
- Longo, G. Vaporisation of the low GWP refrigerant HFO1234yf inside a brazed plate heat exchanger. Int. J. Refrig. 2012, 35, 952–961. [Google Scholar] [CrossRef]
- Longo, G.A.; Mancin, S.; Righetti, G.; Zilio, C. HFO1234ze(E) vaporisation inside a Brazed Plate Heat Exchanger (BPHE): Comparison with HFC134a and HFO1234yf. Int. J. Refrig. 2016, 67, 125–133. [Google Scholar] [CrossRef]
- Longo, G.A.; Mancin, S.; Righetti, G.; Zilio, C. Boiling of the new low-GWP refrigerants R1234ze(Z) and R1233zd(E) inside a small commercial brazed plate heat exchanger. Int. J. Refrig. 2019, 104, 376–385. [Google Scholar] [CrossRef]
- Lorentzen, G.; Pettersen, J. A new, efficient and environmentally benign system for car air-conditioning. Int. J. Refrig. 1993, 16, 4–12. [Google Scholar] [CrossRef]
- Ehsan, M.M.; Guan, Z.; Klimenko, A. A comprehensive review on heat transfer and pressure drop characteristics and correlations with supercritical CO 2 under heating and cooling applications. Renew. Sustain. Energy Rev. 2018, 92, 658–675. [Google Scholar] [CrossRef]
- Elbarghthi, A.F.; Hafner, A.; Banasiak, K.; Dvorak, V. An experimental study of an ejector-boosted transcritical R744 refrigeration system including an exergy analysis. Energy Convers. Manag. 2021, 238, 114102. [Google Scholar] [CrossRef]
- Elbarghthi, A.F.; Mohamed, S.; Nguyen, V.V.; Dvorak, V. CFD Based Design for Ejector Cooling System Using HFOS (1234ze(E) and 1234yf). Energies 2020, 13, 1408. [Google Scholar] [CrossRef]
- Elbarghthi, A.F.; Dvorak, V.; Hafner, A.; Banasiak, K. The potential impact of the small-scale ejector on the R744 transcritical refrigeration system. Energy Convers Manag. 2021, 249, 114860. [Google Scholar] [CrossRef]
- Lemmon, E.; Huber, M.; McLinden, M. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 9.1.; Natl Std. Ref. Data Series (NIST NSRDS); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2013. [Google Scholar]
- The European Parliament and the Council of the European Union. REGULATION (EU) No 517/2014. Off. J. Eur. Union 2014, 57, 195–230. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=uriserv:OJ.L_.2014.150.01.0001.01.ENG&toc=OJ:L:2014:150:TOC (accessed on 15 November 2021).
- Minor, B.; Spatz, M. HFO-1234yf Low GWP Refrigerant Update. In Proceedings of the Purdue University International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 15–17 July 2008; Pap. No. 937; pp. 1–8. [Google Scholar]
- Kracik, J.; Dvorak, V.; Van, V.N.; Śmierciew, K. Experimental and Numerical Study on Supersonic Ejectors Working with R-1234ze(E). EPJ Web Conf. 2018, 180, 02047. [Google Scholar] [CrossRef][Green Version]
- Smierciew, K.; Gagan, J.; Butrymowicz, D.; Łukaszuk, M.; Kubiczek, H. Experimental investigation of the first prototype ejector refrigeration system with HFO-1234ze(E). Appl. Therm. Eng. 2017, 110, 115–125. [Google Scholar] [CrossRef]
- Dorin Software Version: 20.12. 2020. Available online: https://www.dorin.com/en/Software/ (accessed on 31 August 2021).
- Incropera, F.P. Fundamentals of Heat and Mass Transfer; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
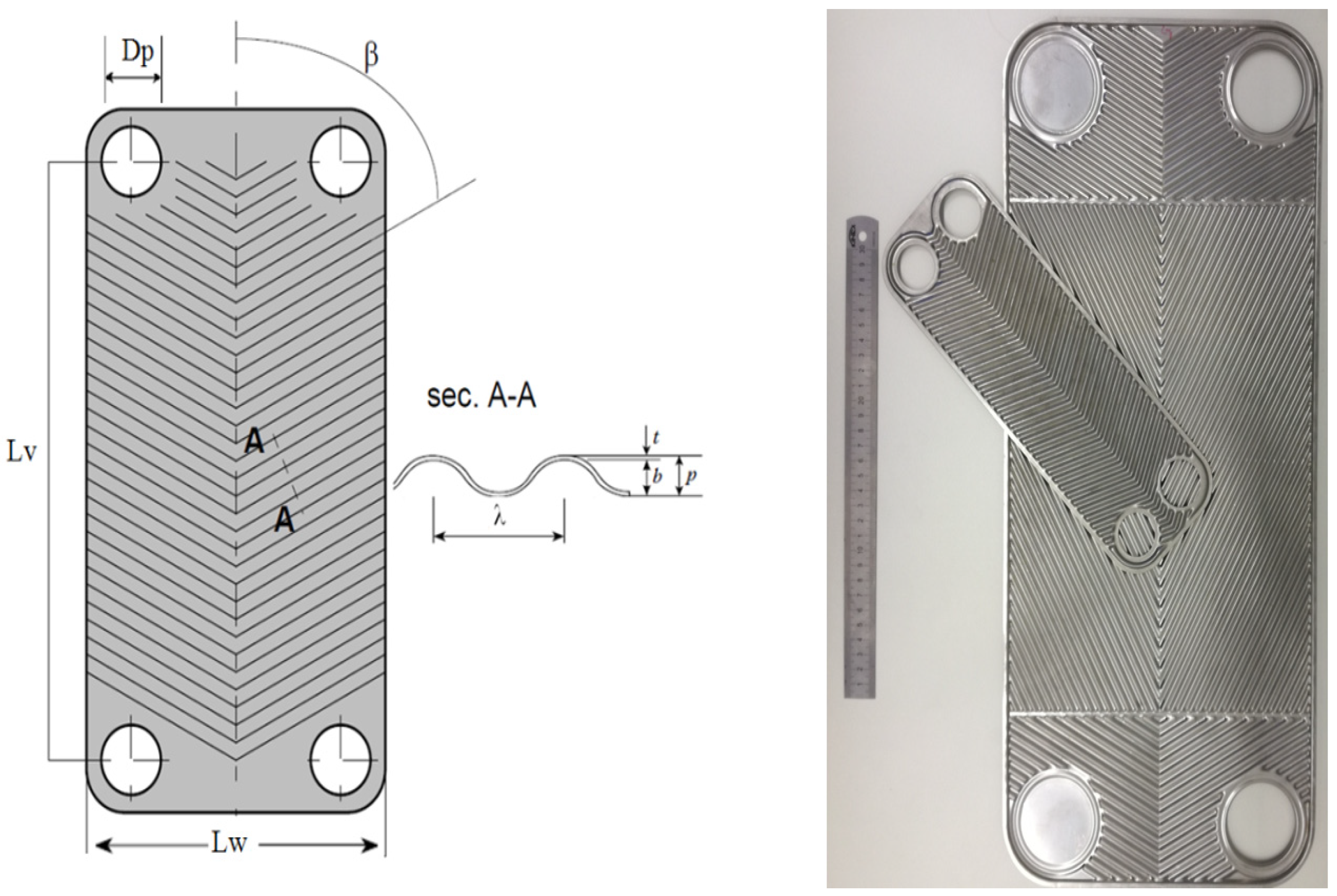
| Geometry Parameters | Plate Size | |
|---|---|---|
| PHE#A | PHE#B | |
| Effective flow length, L (mm) | 485 | 250 |
| Plate thickness t_p (mm) | 0.60 | 0.60 |
| Port diameter D_p (mm) | 55 | 30 |
| Corrugation angle, β (°) | 60 | 60 |
| Plate Pitch, P (mm) | 2.8 | 2.50 |
| Mean Channel Gap, b (mm) | 2.2 | 1.90 |
| Plate width, W (mm) | 245 | 95 |
| Corrugation pitch, λ (mm) | 6.80 | 6.80 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elbarghthi, A.F.A.; Hdaib, M.Y.; Dvořák, V. A Novel Generator Design Utilised for Conventional Ejector Refrigeration Systems. Energies 2021, 14, 7705. https://doi.org/10.3390/en14227705
Elbarghthi AFA, Hdaib MY, Dvořák V. A Novel Generator Design Utilised for Conventional Ejector Refrigeration Systems. Energies. 2021; 14(22):7705. https://doi.org/10.3390/en14227705
Chicago/Turabian StyleElbarghthi, Anas F. A., Mohammad Yousef Hdaib, and Václav Dvořák. 2021. "A Novel Generator Design Utilised for Conventional Ejector Refrigeration Systems" Energies 14, no. 22: 7705. https://doi.org/10.3390/en14227705
APA StyleElbarghthi, A. F. A., Hdaib, M. Y., & Dvořák, V. (2021). A Novel Generator Design Utilised for Conventional Ejector Refrigeration Systems. Energies, 14(22), 7705. https://doi.org/10.3390/en14227705






