Large Eddy Simulation of Film Cooling Involving Compound Angle Hole with Bulk Flow Pulsation
Abstract
:1. Introduction
2. Numerical Method
2.1. Computational Domain and Grid
2.2. Governing Equations and Boundary Conditions
2.2.1. Unsteady RANS Approach
2.2.2. LES Approach
2.2.3. Boundary Conditions
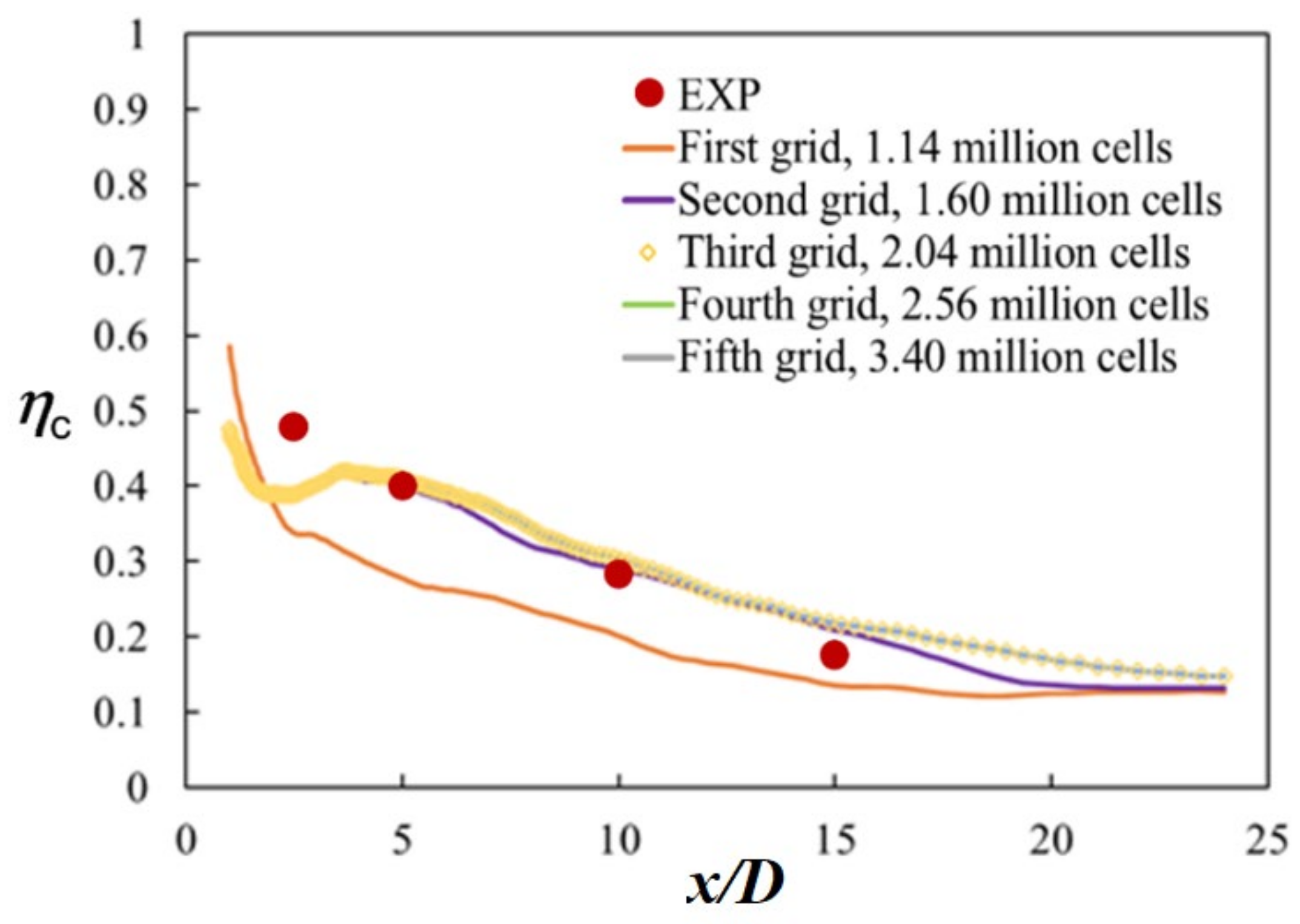
2.3. Validation of Numerical Methods
3. Results and Discussion
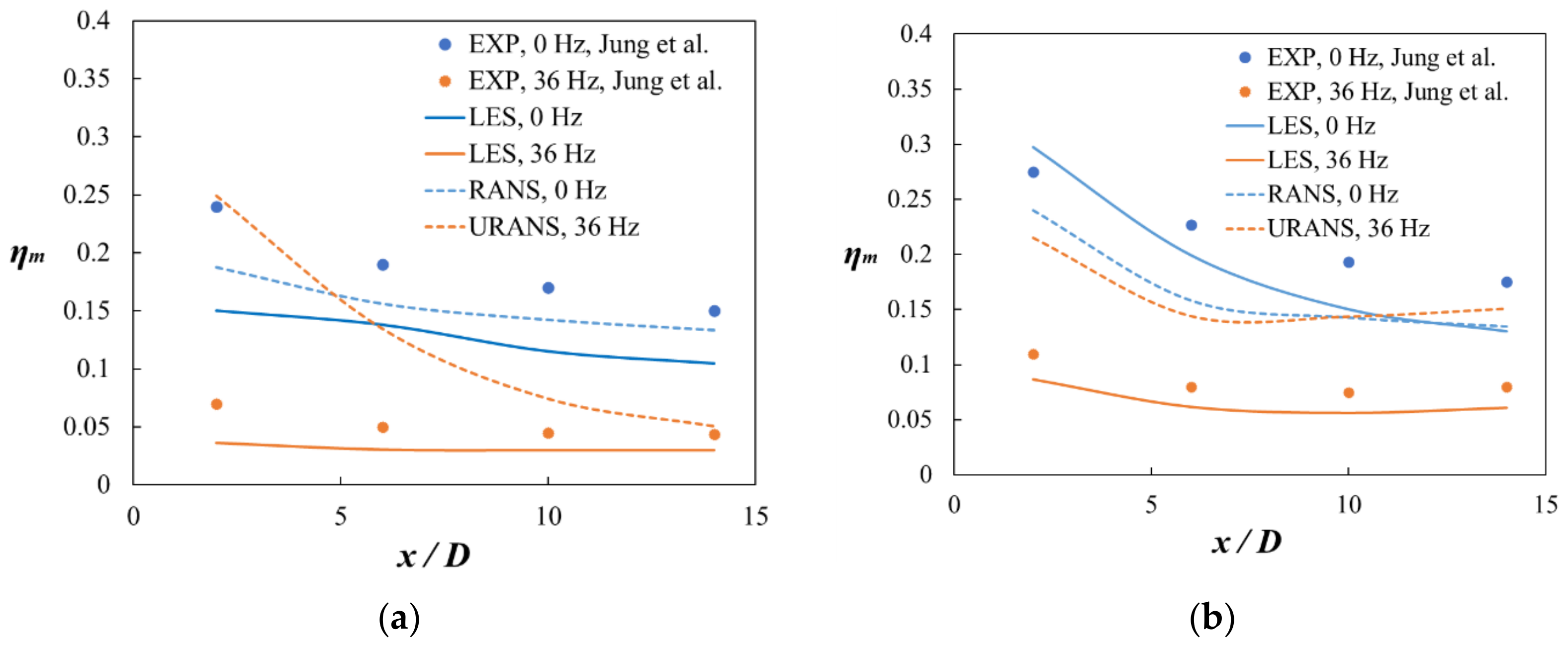
3.1. Spanwise-Averaged Film Cooling Effectiveness
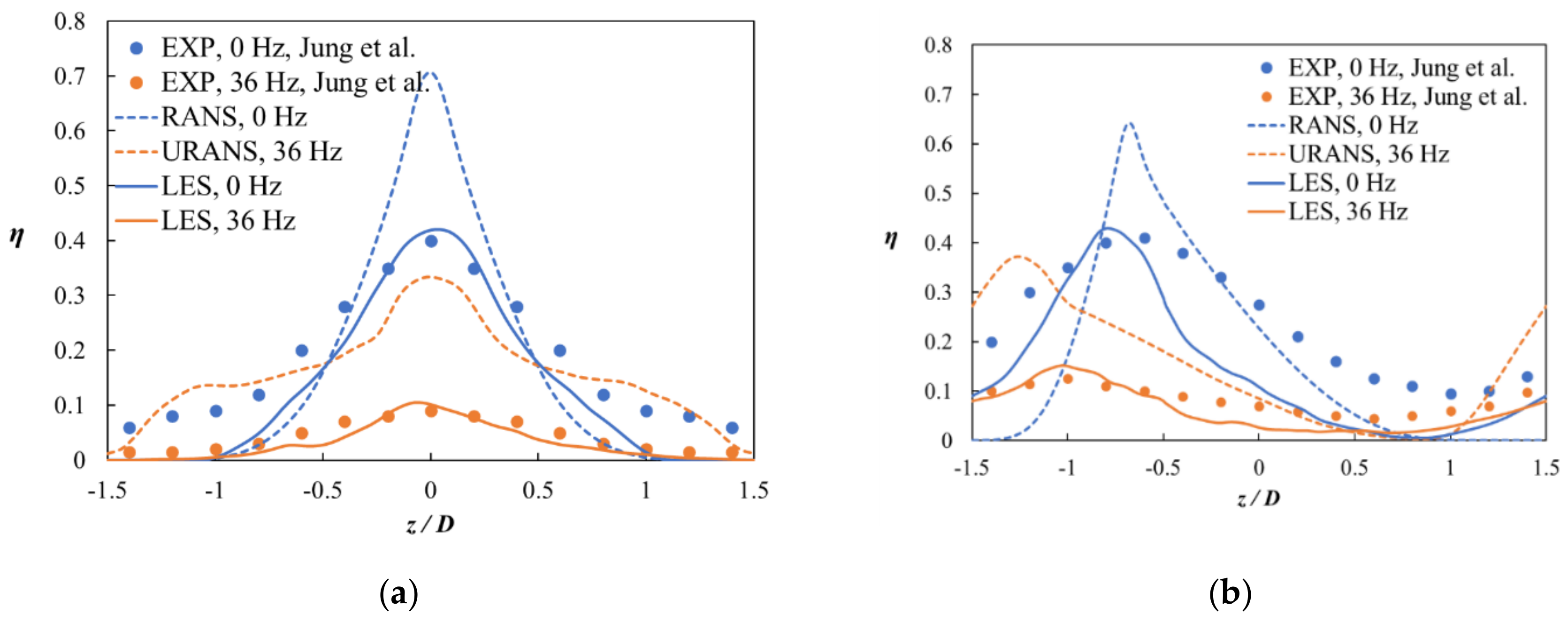
3.2. Distribution of the Time-Averaged Film Cooling Effectiveness at x/D = 5
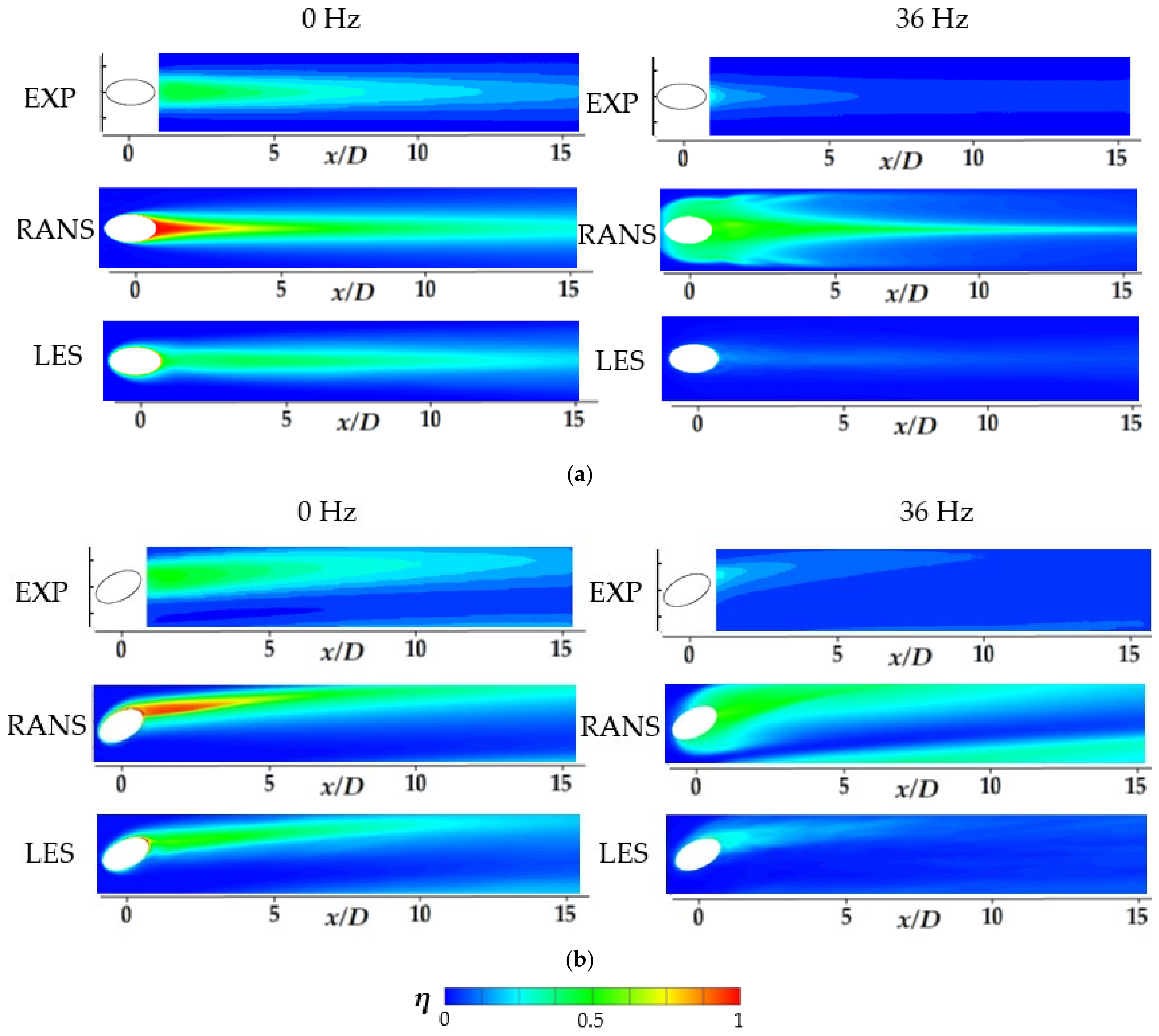
3.3. Time-Averaged Film Cooling Effectiveness Contours
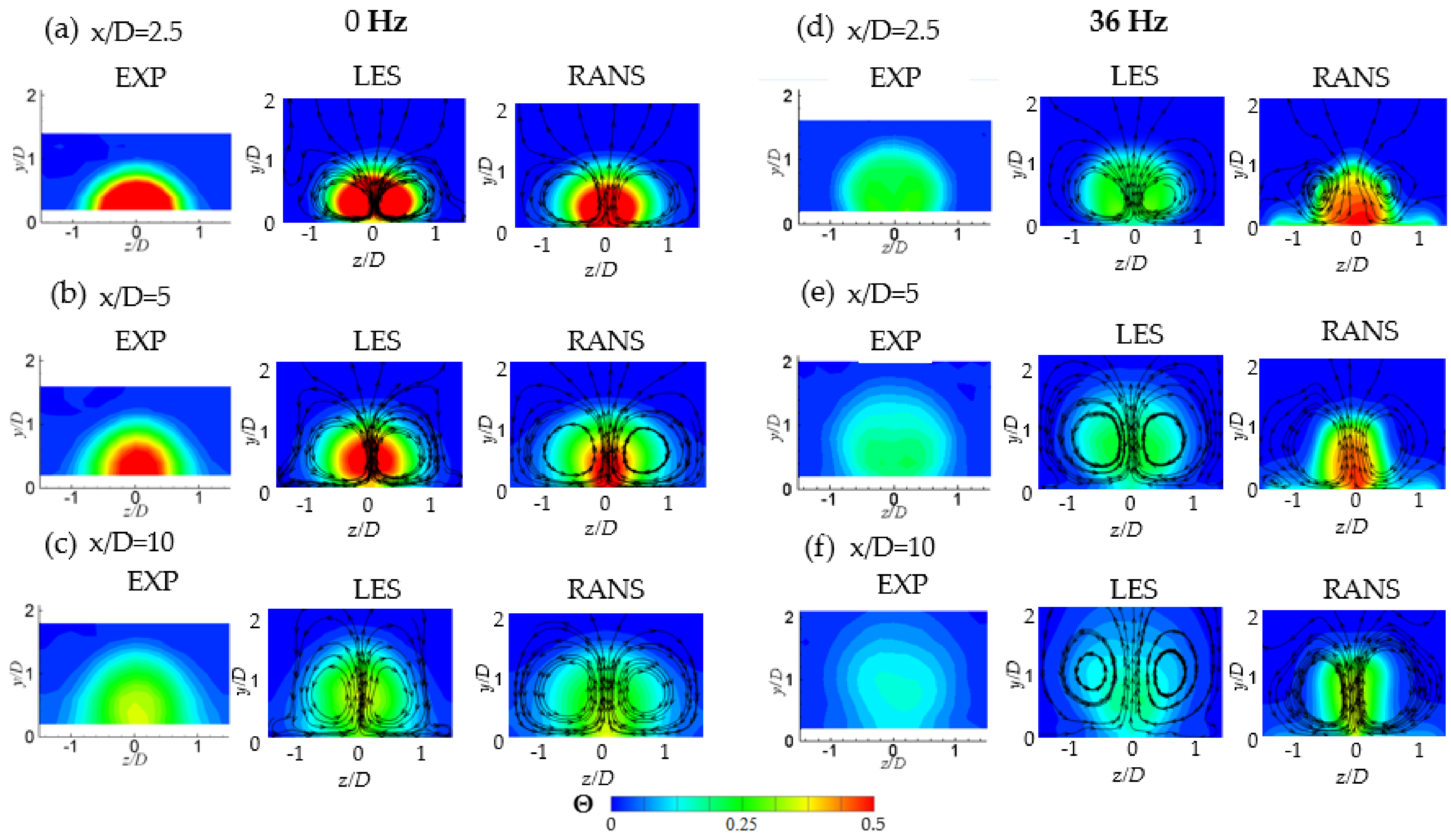
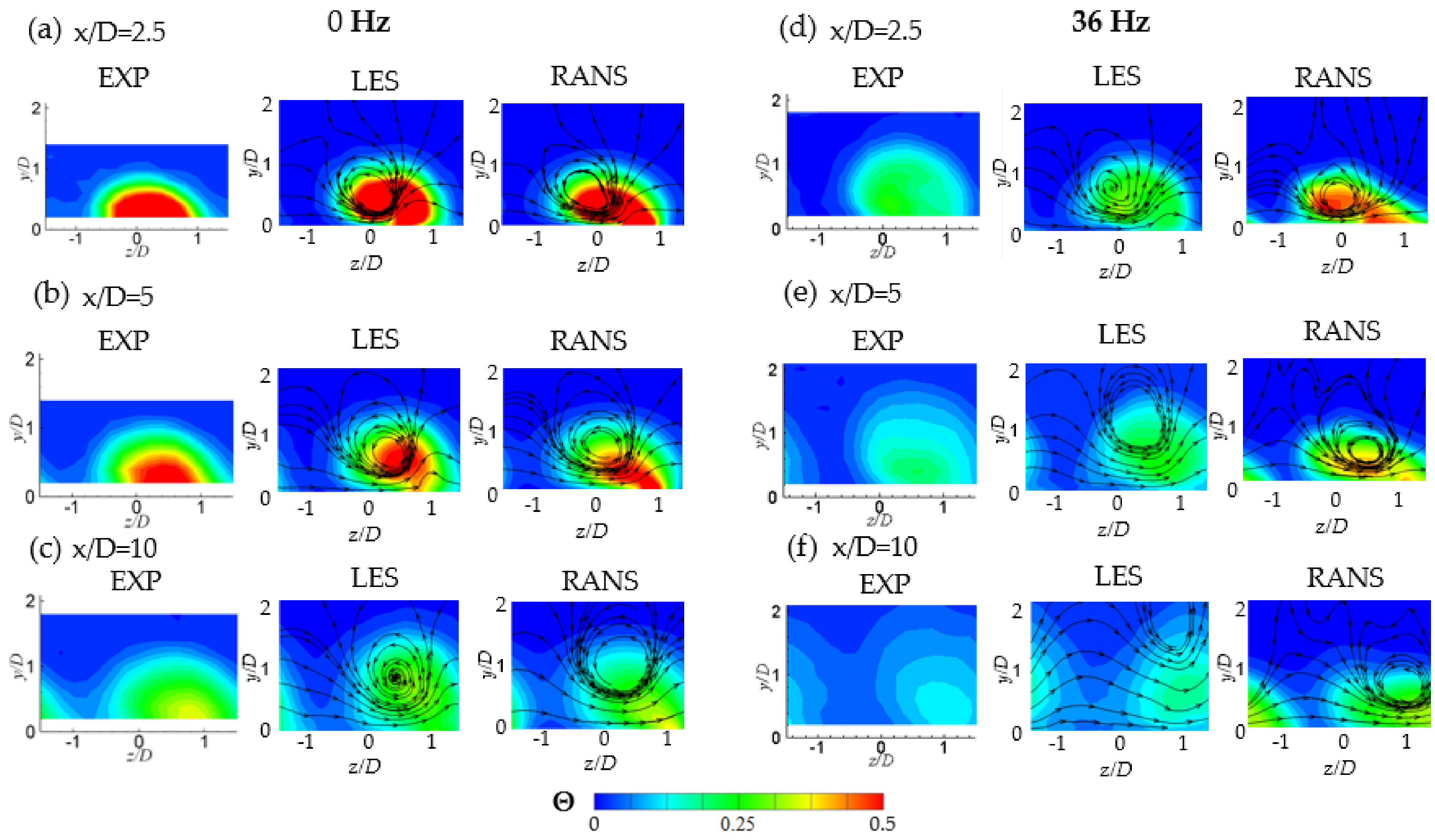
3.4. Time-Averaged Dimensionless Temperature Contours on the Streamwise-Normal Planes
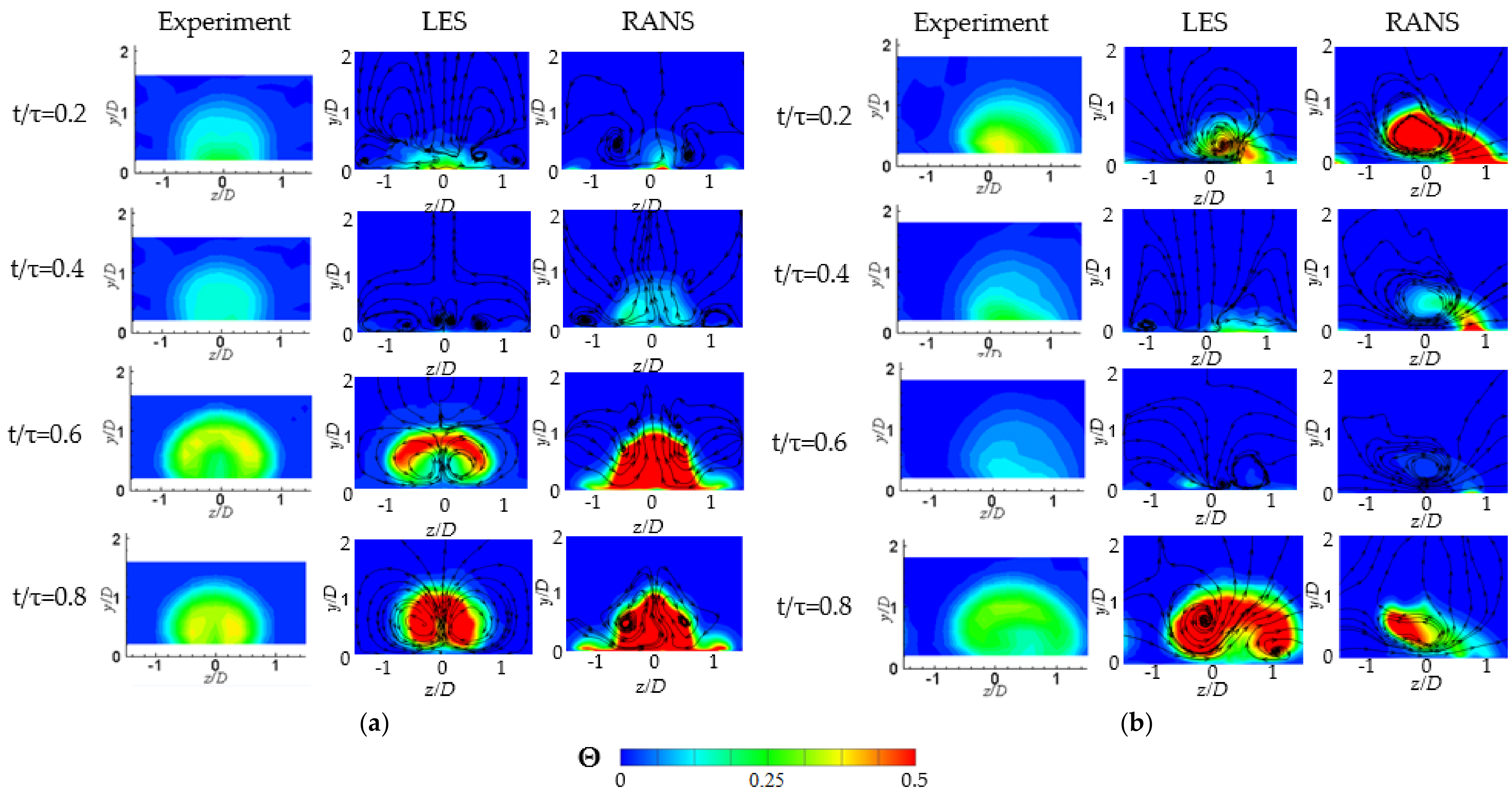
3.5. Contours of Phase-Averaged Dimensionless Temperature at x/D = 5
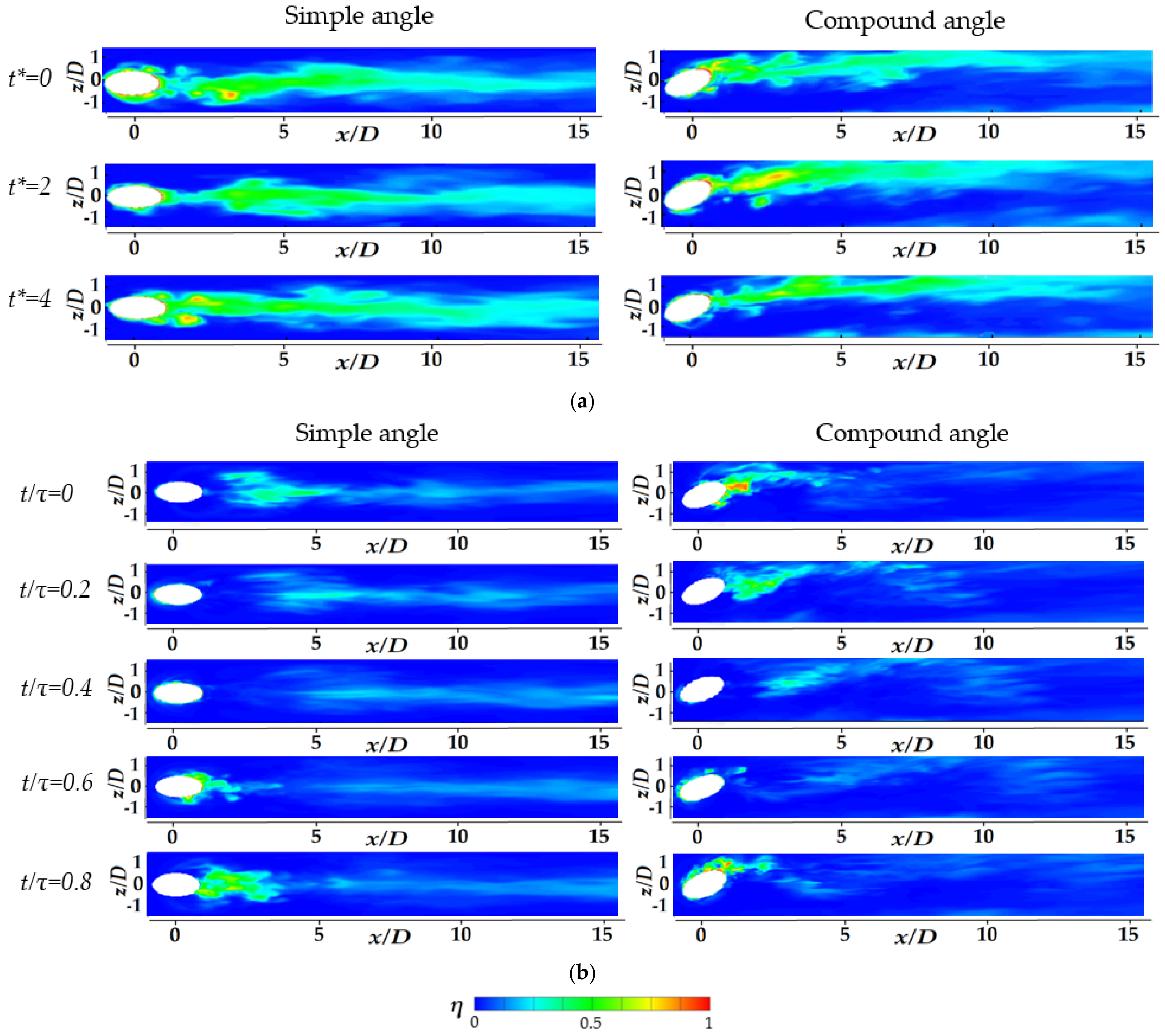
3.6. Instantaneous Dimensionless Temperature Contours for the 30° Orientation Angle on the Spanwise-Normal Plane
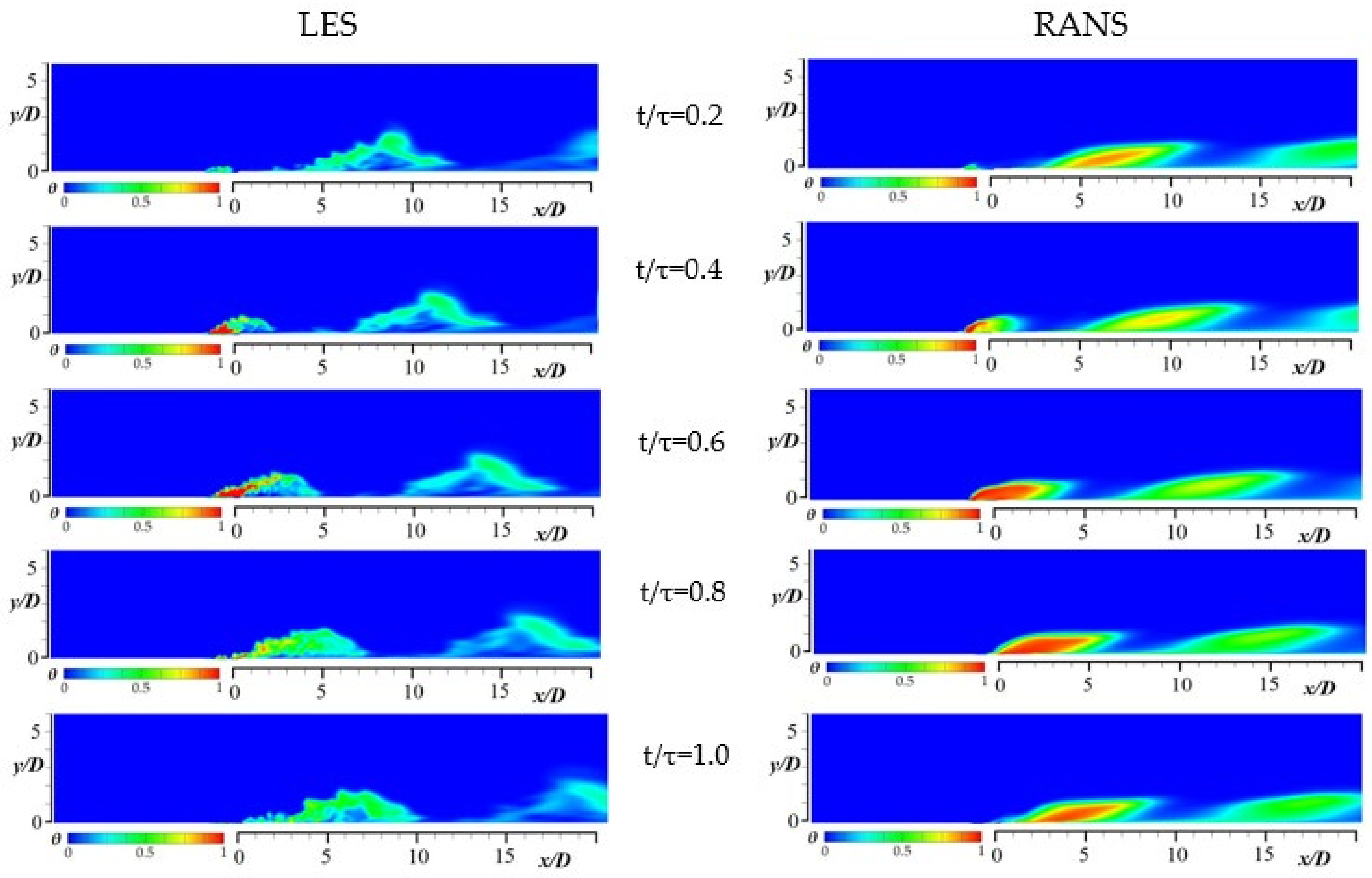
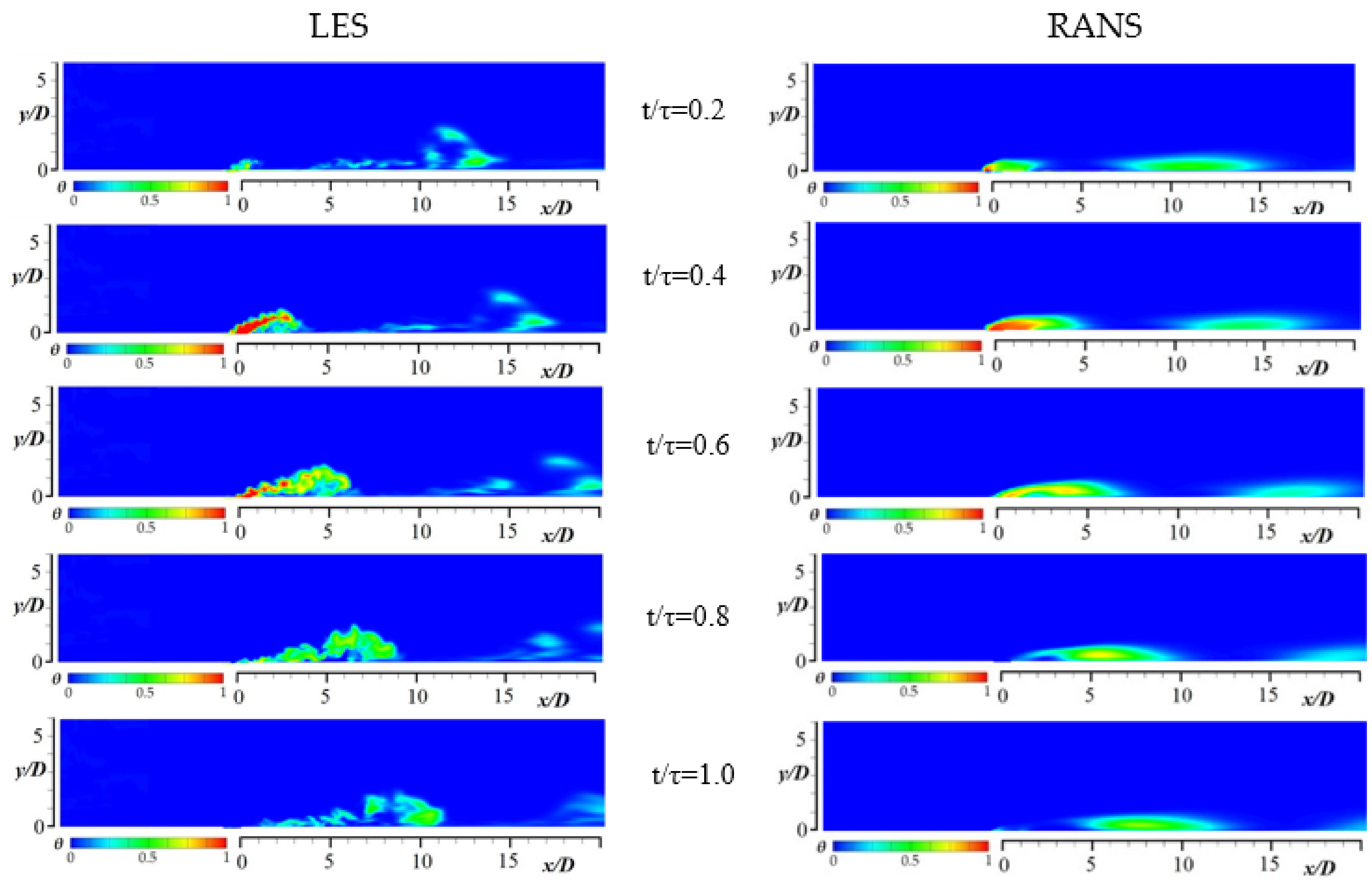
3.7. Instantaneous Film Cooling Effectiveness Contours on the Wall
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Cp = specific heat of fluid (J/kg∙K) |
| Cµ = coefficient of eddy viscosity |
| D = hole diameter |
| g = gravity |
| K = turbulent kinetic energy (W/m2 K) |
| L = hole length |
| M = blowing ratio = |
| p = pressure |
| P = pitch between holes (mm) |
| St = Strouhal number = |
| T = temperature (K) |
| t = time (s) |
| u = turbulent velocity fluctuations (m/s) |
| U = flow velocity (m/s) |
| x = streamwise coordinate |
| y = wall-normal coordinate |
| z = spanwise coordinate |
| Greek symbols |
| β= orientation angle, angle between the streamwise direction and projected injection vector on the x–z plane |
| ε = dissipation rate of turbulent kinetic energy (m2/s3) |
| δ = Kronecker delta |
| κ = thermal conductivity (W/(m∙K)) |
| = adiabatic film cooling effectiveness |
| = spanwise-averaged film cooling effectiveness |
| = density (kg/m3) |
| τij = sub-grid scale turbulent stress (kg/(m·s2)) |
| τ = period (s) |
| μt = sub-grid scale turbulent viscosity (kg/(m·s)) |
| μ = dynamic viscosity (kg/(m·s)) |
| Θ = dimensionless temperature |
| Subscripts |
| aw = adiabatic wall |
| C = coolant |
| G = mainstream gas |
| m = spanwise-averaged |
References
- Moran, M.; Shapiro, H.; Boettner, D.; Bailey, M. Fundamentals of Engineering Thermodynamics, 8th ed.; Wiley: Hoboken, NJ, USA, 2014; p. 532. [Google Scholar]
- Leedom, D.H.; Acharya, S. Large Eddy Simulations of Film Cooling Flow Fields From Cylindrical and Shaped Holes. In Proceedings of the ASME Turbo Expo 2008, Berlin, Germany, 9–13 June 2008; pp. 865–877. [Google Scholar] [CrossRef]
- Baek, S.; Ryu, J.; Ahn, J. Large Eddy Simulation of Film Cooling with Forward Expansion Hole: Comparative Study with LES and RANS Simulations. Energies 2021, 14, 2063. [Google Scholar] [CrossRef]
- Bogard, D.G.; Thole, K. Gas Turbine Film Cooling. J. Propuls. Power 2006, 22, 249–270. [Google Scholar] [CrossRef] [Green Version]
- Walters, D.K.; Leylek, J.H. Impact of Film-Cooling Jets on Turbine Aerodynamic Losses. J. Turbomach. 1999, 122, 537–545. [Google Scholar] [CrossRef]
- Tyagi, M.; Acharya, S. Large Eddy Simulation of Film Cooling Flow From an Inclined Cylindrical Jet. J. Turbomach. 2003, 125, 734–742. [Google Scholar] [CrossRef]
- Rozati, A.; Tafti, D.K. Large Eddy Simulation of Leading Edge Film Cooling—Part II: Heat Transfer and Effect of Blowing Ratio. In ASME Turbo Expo 2007; ASME: Montreal, QC, Canada, 2007. [Google Scholar]
- Na, S.; Shih, T.I.-P. Increasing Adiabatic Film-Cooling Effectiveness by Using an Upstream Ramp. J. Heat Transf. 2006, 129, 464–471. [Google Scholar] [CrossRef]
- Johnson, P.; Shyam, V.; Hah, C. Reynolds-Averaged Navier-Stokes Solutions to Flat Plate Film Cooling Scenarios. NASA/TM-2011-217025. Available online: https://ntrs.nasa.gov/api/citations/20110012464/downloads/20110012464.pdf (accessed on 1 October 2021).
- Schmidt, D.L.; Sen, B.; Bogard, D.G. Film Cooling With Compound Angle Holes: Adiabatic Effectiveness. J. Turbomach. 1996, 118, 807–813. [Google Scholar] [CrossRef]
- Ligrani, P.M.; Lee, J.S. Film Cooling from a Single Row of Compound Angle Holes at High Blowing Ratios. Int. J. Rotating Mach. 1996, 2, 259–267. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.W.; Kim, Y.B.; Lee, J.S. Flow Characteristics and Aerodynamic Losses of Film-Cooling Jets with Compound Angle Orientations. J. Turbomach. 1997, 119, 310–319. [Google Scholar] [CrossRef]
- Jung, I.S.; Lee, J.S. Effects of Orientation Angles on Film Cooling Over a Flat Plate: Boundary Layer Temperature Distributions and Adiabatic Film Cooling Effectiveness. J. Turbomach. 1999, 122, 153–160. [Google Scholar] [CrossRef]
- Seo, H.J.; Lee, J.S.; Ligrani, P.M. The effect of injection hole length on film cooling with bulk flow pulsations. Int. J. Heat Mass Transf. 1998, 41, 3515–3528. [Google Scholar] [CrossRef]
- Coulthard, S.M.; Volino, R.J.; Flack, K.A. Effect of Jet Pulsing on Film Cooling—Part I: Effectiveness and Flow-Field Temperature Results. J. Turbomach. 2006, 129, 232–246. [Google Scholar] [CrossRef]
- Nikitopoulos, D.E.; Acharya, S.; Oertling, J.; Muldoon, F.H. On Active Control of Film-Cooling Flows. In Proceedings of the ASME Turbo Expo, Barcelona, Spain, 8–11 May 2006. [Google Scholar]
- Jung, I.S. Effects of Bulk Flow Pulsations on Film Cooling with Compound Angle Injection Holes. Ph.D. Thesis, Seoul National University, Seoul, Korea, 1998. [Google Scholar]
- Farhadi-Azar, R.; Ramezanizadeh, M.; Taeibi-Rahni, M.; Salimi, M. Compound Triple Jets Film Cooling Improvements via Velocity and Density Ratios: Large Eddy Simulation. J. Fluids Eng. 2011, 133. [Google Scholar] [CrossRef]
- Han, J.-C.; Dutta, S.; Ekkad, S. Gas Turbine Heat Transfer and Cooling Technology, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar] [CrossRef]
- Cengel, Y.; Cimbala, J. Fluid Mechanics, 3rd ed.; McGrawHill: New York, NY, USA, 2014. [Google Scholar]
- White, F. Fluid Mechanics, 8th ed.; McGraw-Hill: New York, NY, USA, 2015. [Google Scholar]
- ANSYS Fluent Theory Guide Version 19. Available online: https://www.ansys.com/products/fluids/ansys-fluent (accessed on 1 October 2021).
- Acharya, S.; Leedom, D.H. Large Eddy Simulations of Discrete Hole Film Cooling with Plenum Inflow Orientation Effects. J. Heat Transf. 2012, 135, 011010. [Google Scholar] [CrossRef]
- Pointwise Version 18. Available online: http://www.pointwise.com/ (accessed on 10 October 2021).
- Baek, S.I.; Yavuzkurt, S. Effects of Flow Oscillations in the Mainstream on Film Cooling. Inventions 2018, 3, 73. [Google Scholar] [CrossRef] [Green Version]
- Renze, P.; Schröder, W.; Meinke, M. Large-eddy Simulation of Film Cooling Flows with Variable Density Jets. Flow Turbul. Combust. 2007, 80, 119–132. [Google Scholar] [CrossRef]
- Iourokina, I.; Lele, S. Towards large eddy simulation of film cooling flows on a model turbine blade leading edge. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar]
- Sakai, E.; Takahashi, T.; Watanabe, H. Large-eddy simulation of an inclined round jet issuing into a crossflow. Int. J. Heat Mass Transf. 2014, 69, 300–311. [Google Scholar] [CrossRef]
- Zamiri, A.; You, S.J.; Chung, J.T. Large Eddy Simulation in the Optimization of Laidback Fan-Shaped Hole Geometry to Enhance Film-Cooling Performance. Int. J. Heat Mass Transf. 2020, 158, 120014. [Google Scholar] [CrossRef]
- Thole, K.; Knost, D.G. Heat transfer and film-cooling for the endwall of a first stage turbine vane. Int. J. Heat Mass Transf. 2005, 48, 5255–5269. [Google Scholar] [CrossRef]
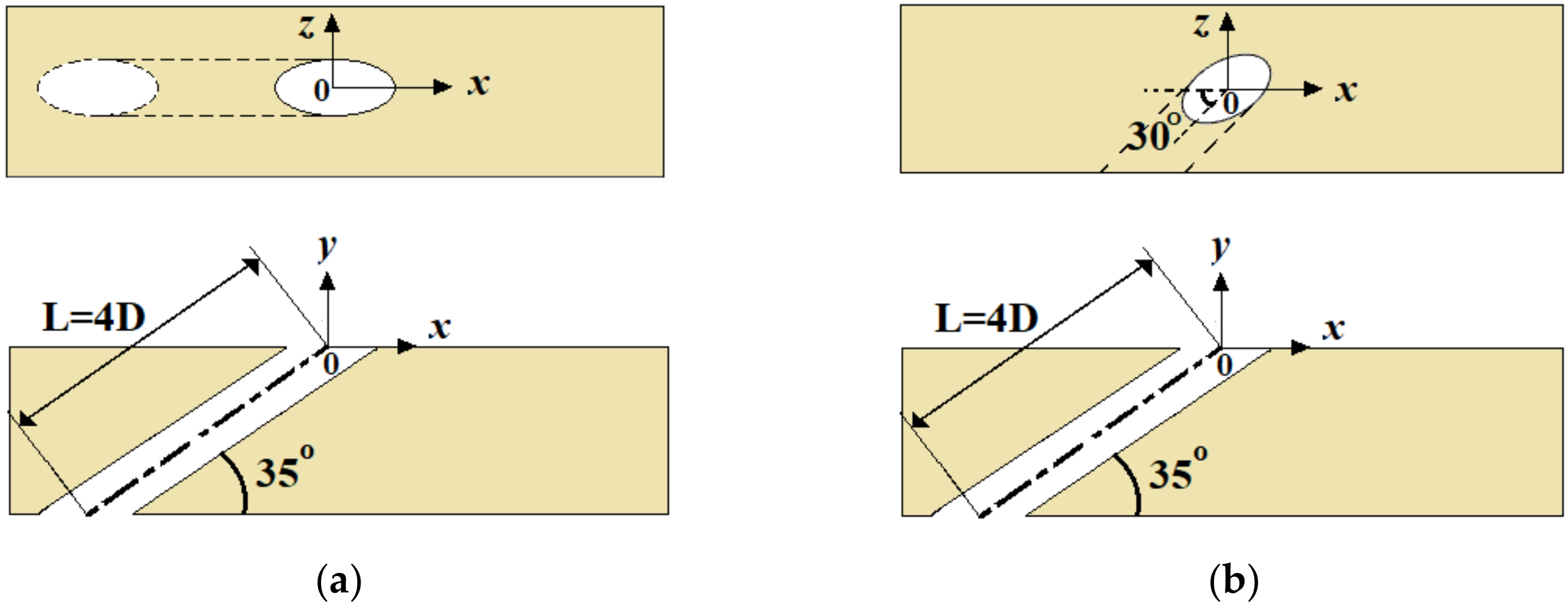
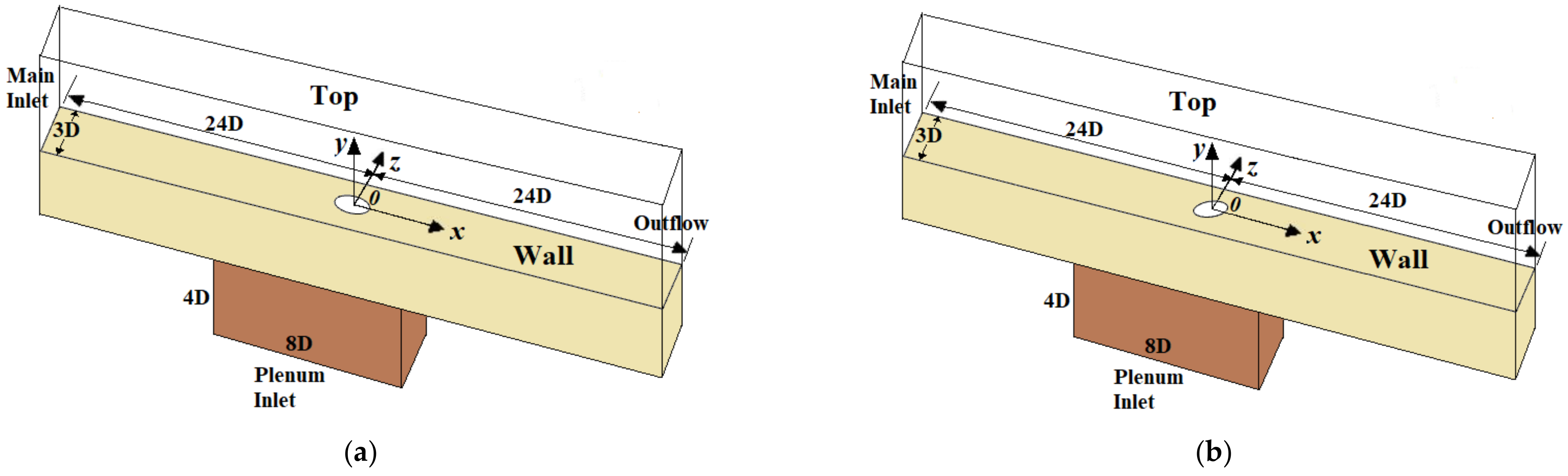
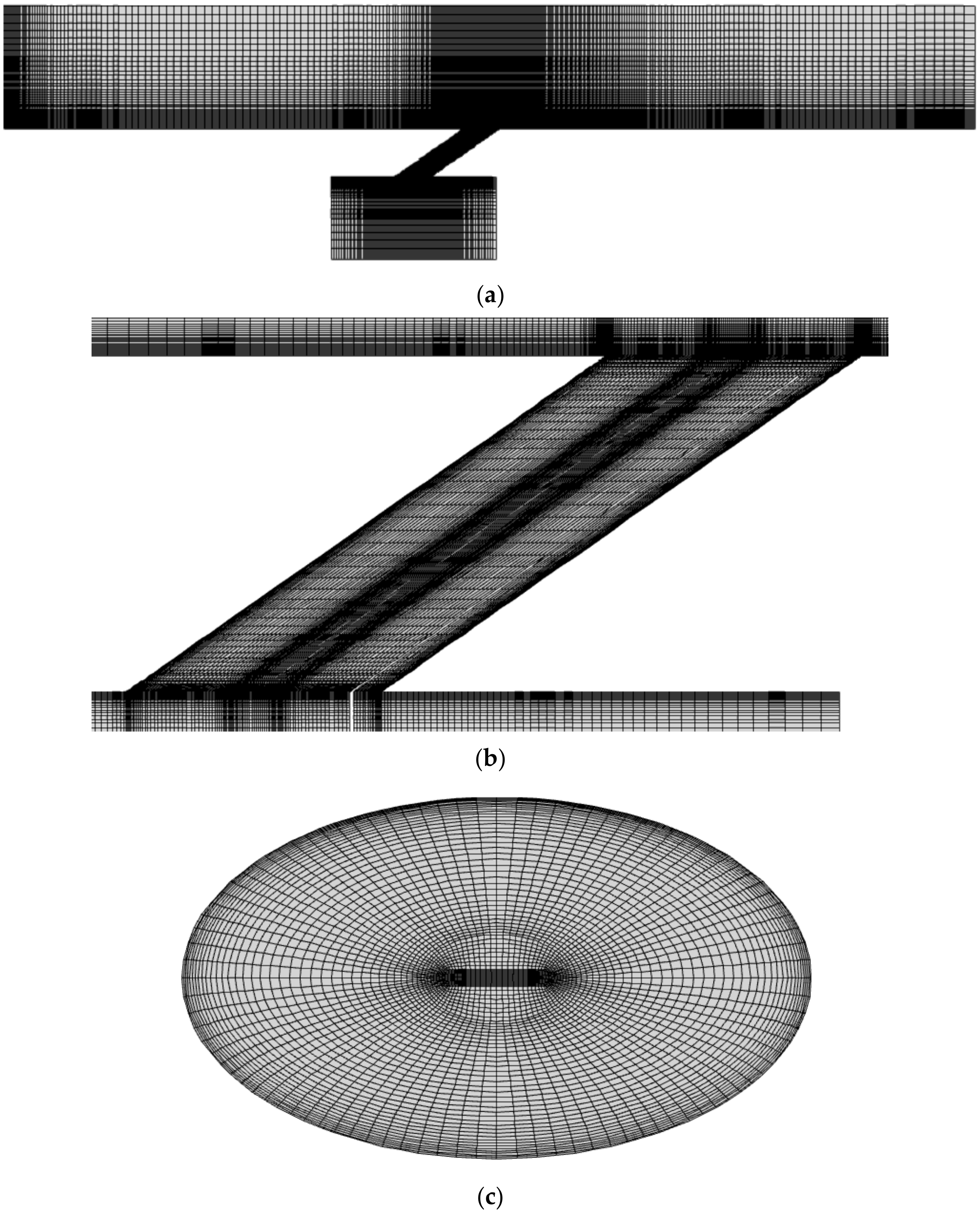
| Surface | Boundary Condition |
|---|---|
| Main inlet | Velocity inlet |
| Plenum inlet | Velocity inlet |
| Top | Symmetry |
| Test plate | Adiabatic wall |
| Outflow | Pressure outlet |
| Main sides | Periodic |
| Sides of plenum | Adiabatic wall |
| Frequency (Hz) | 0 | 36 |
|---|---|---|
| St | 0 | 3.62 |
| β | 0˚ and 30˚ | 0° and 30° |
| A | 0 | 0.54 |
| Frequency (Hz) | 0 | 36 |
|---|---|---|
| St | 0 | 3.62 |
| β | 0° and 30° | 0° and 30° |
| B | 0 | 0.3 |
| Grid | # of Cells in the x Direction | # of Cells in the y Direction | # of Cells in the z Direction | # of Cells in the Main Block (Million) | Total # of Cells (Million) |
|---|---|---|---|---|---|
| First | 242 | 52 | 34 | 0.5 | 1.14 |
| Second | 248 | 62 | 52 | 0.96 | 1.60 |
| Third | 276 | 80 | 56 | 1.41 | 2.04 |
| Fourth | 298 | 94 | 60 | 1.93 | 2.56 |
| Fifth | 312 | 110 | 68 | 2.76 | 3.40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baek, S.-I.; Ahn, J. Large Eddy Simulation of Film Cooling Involving Compound Angle Hole with Bulk Flow Pulsation. Energies 2021, 14, 7659. https://doi.org/10.3390/en14227659
Baek S-I, Ahn J. Large Eddy Simulation of Film Cooling Involving Compound Angle Hole with Bulk Flow Pulsation. Energies. 2021; 14(22):7659. https://doi.org/10.3390/en14227659
Chicago/Turabian StyleBaek, Seung-Il, and Joon Ahn. 2021. "Large Eddy Simulation of Film Cooling Involving Compound Angle Hole with Bulk Flow Pulsation" Energies 14, no. 22: 7659. https://doi.org/10.3390/en14227659
APA StyleBaek, S.-I., & Ahn, J. (2021). Large Eddy Simulation of Film Cooling Involving Compound Angle Hole with Bulk Flow Pulsation. Energies, 14(22), 7659. https://doi.org/10.3390/en14227659







