Modeling Hydraulic Fracturing Using Natural Gas Foam as Fracturing Fluids
Abstract
:1. Introduction
- Collecting the produced gas through pipelines and selling it as liquid natural gas.
- Generating electrical energy with the surplus natural gas.
- Storing the produced gas in suitable reservoirs.
- Injecting the stranded produced gas into the reservoirs for improved oil recovery [1], for example, gas huff-n-puff injection, gas flooding, and foam flooding.
- Using the produced natural gas for hydraulic fracturing [2], for example, NG foam fracturing, natural gas fracturing.

- NG is often free. Operators just need to collect and compress the NG from the field while they need to buy other gases (such as CO2, N2) from other sites and transport them to the asset.
- Stranded natural gas (NG) or flared gas is richer than the gas fed into the pipeline for sale. So, the use of NG or NG foam as a fracturing fluid has advantages over other gases in terms of the phase behavior for some reservoir fluid types. [9] systematically studied the effects of injection fluid composition on the hydrocarbon recovery in a volatile oil reservoir and found that richer gas leads to a higher oil and gas recovery. This indicates that using NG from a gas flare as the fracturing fluid is extremely beneficial to the volatile oil reservoir.
- The use of NG as a fracturing fluid can also contribute to a reduction in carbon emissions and the carbon-neutral/net-zero goal.
2. Model Description
2.1. Main Governing Equations
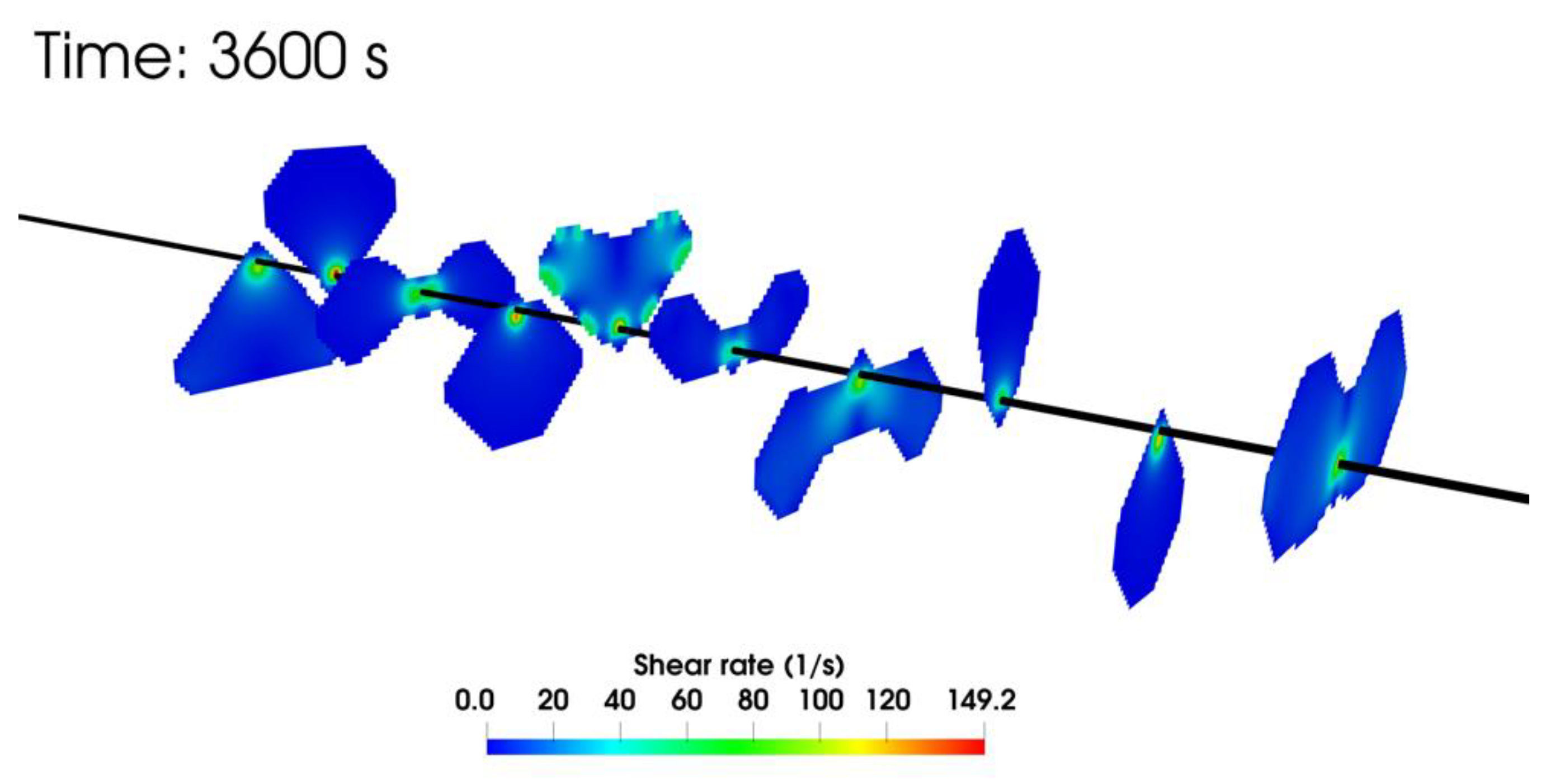
2.2. Modeling of Foam Rheology
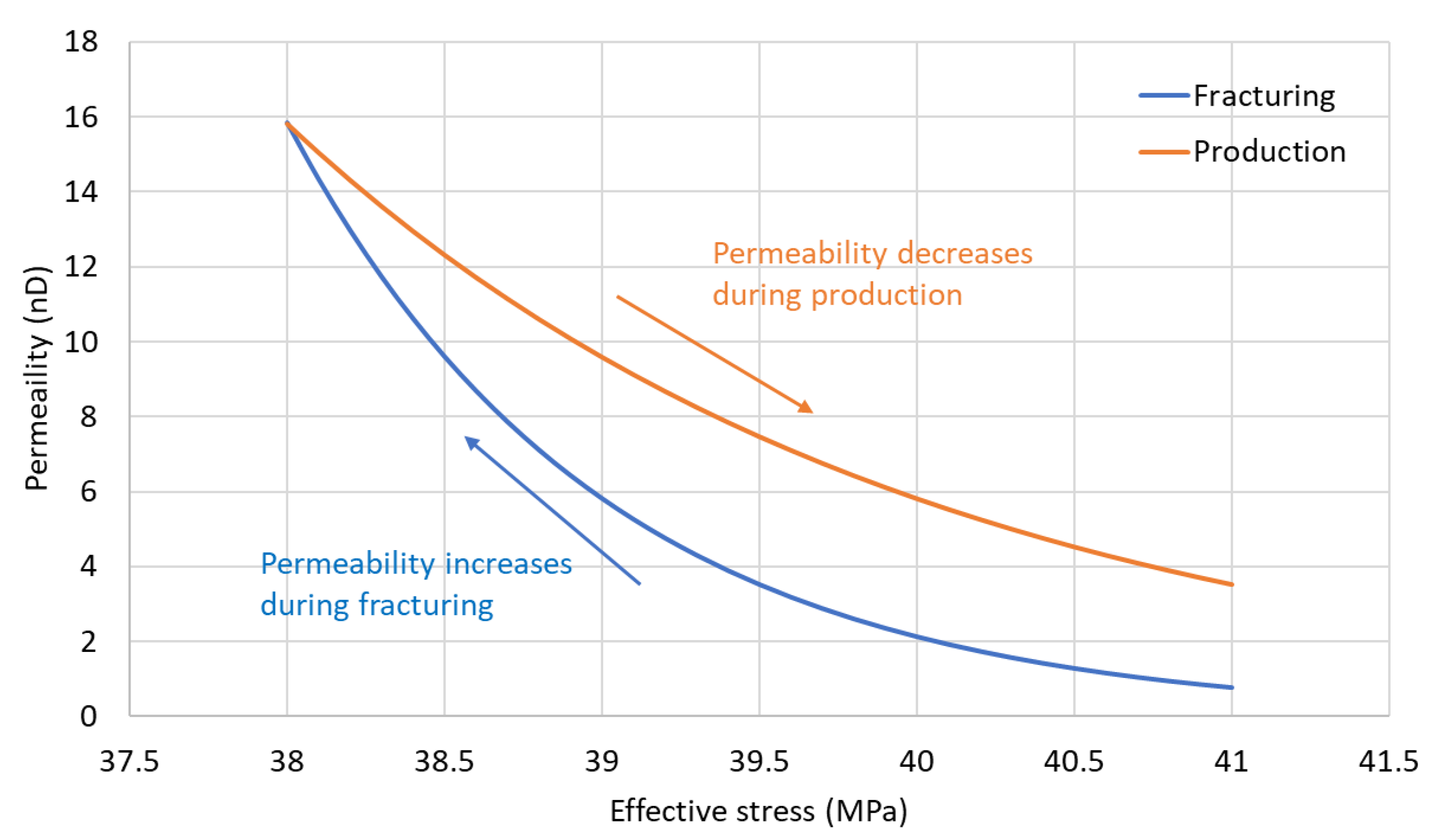
2.3. Stress Dependent Permeability
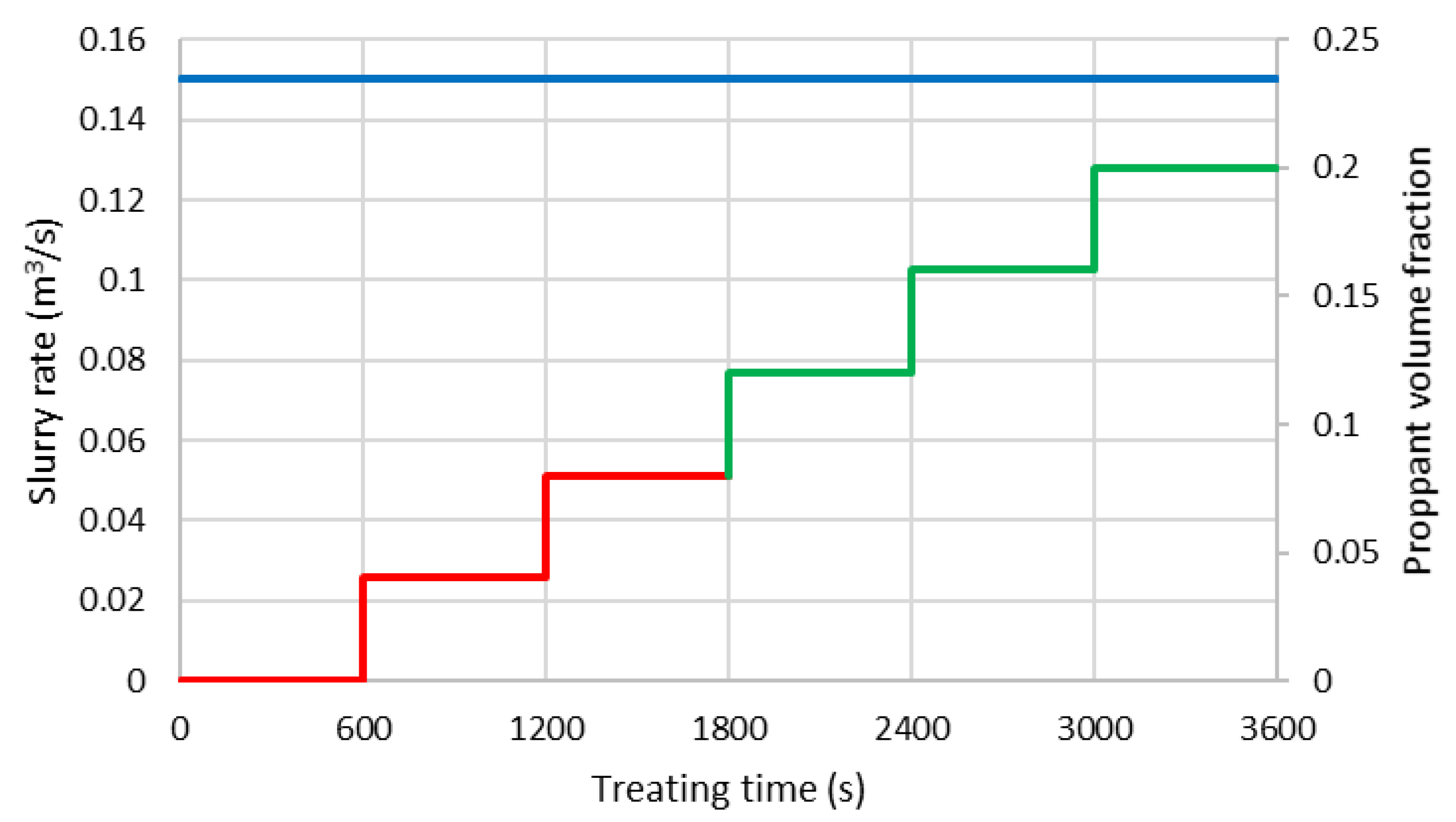
3. Case Setup
4. Results and Discussion
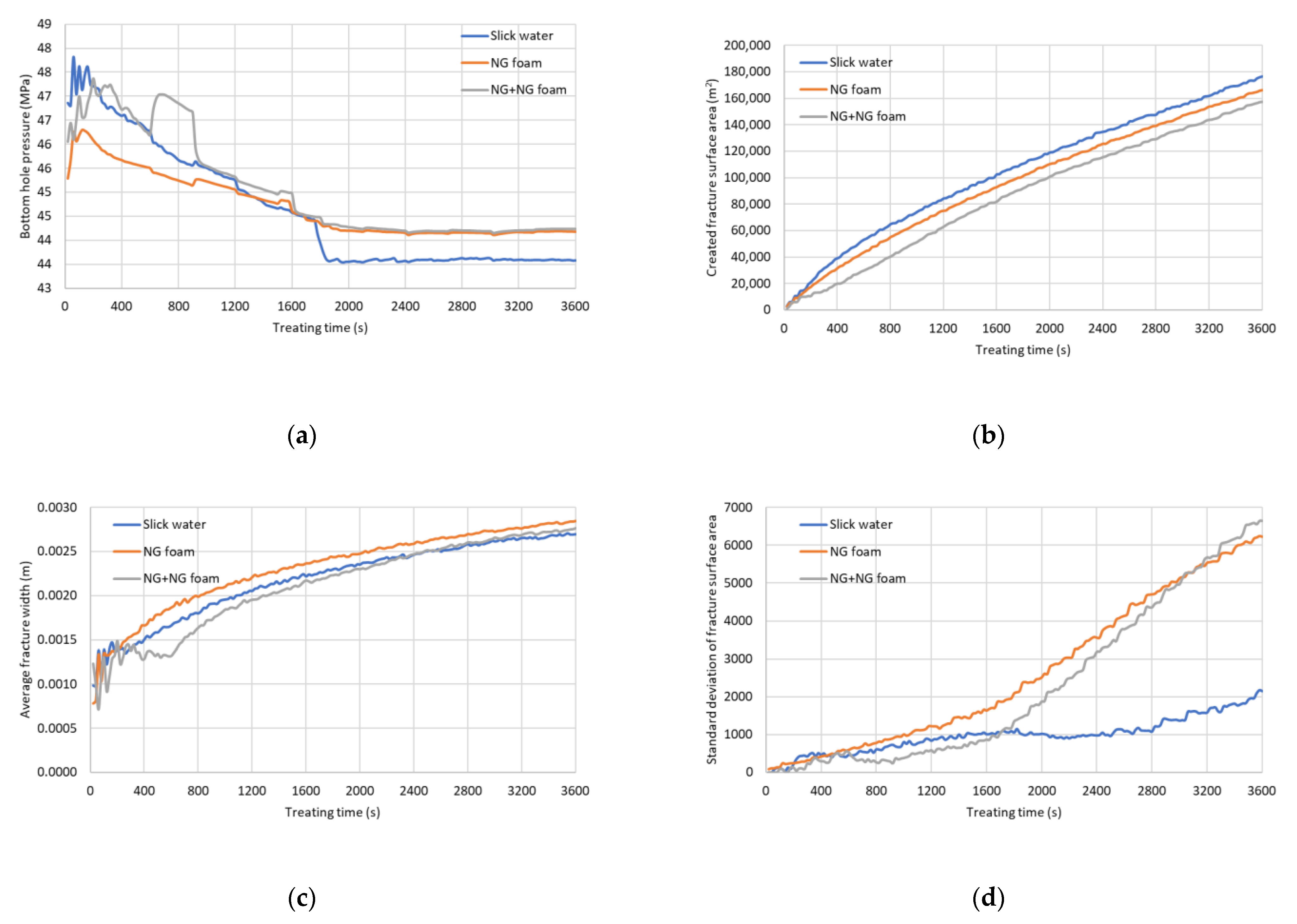
4.1. Results for the Injection Period
| Fracturing Fluid | Ratio of Propped Area to the Created Area | ||
|---|---|---|---|
| Slick water | 176,655 | 68,148 | 0.3858 |
| NG foam | 166,378.5 | 79,320 | 0.4767 |
| NG and NG foam | 159,016 | 77,724 | 0.4888 |
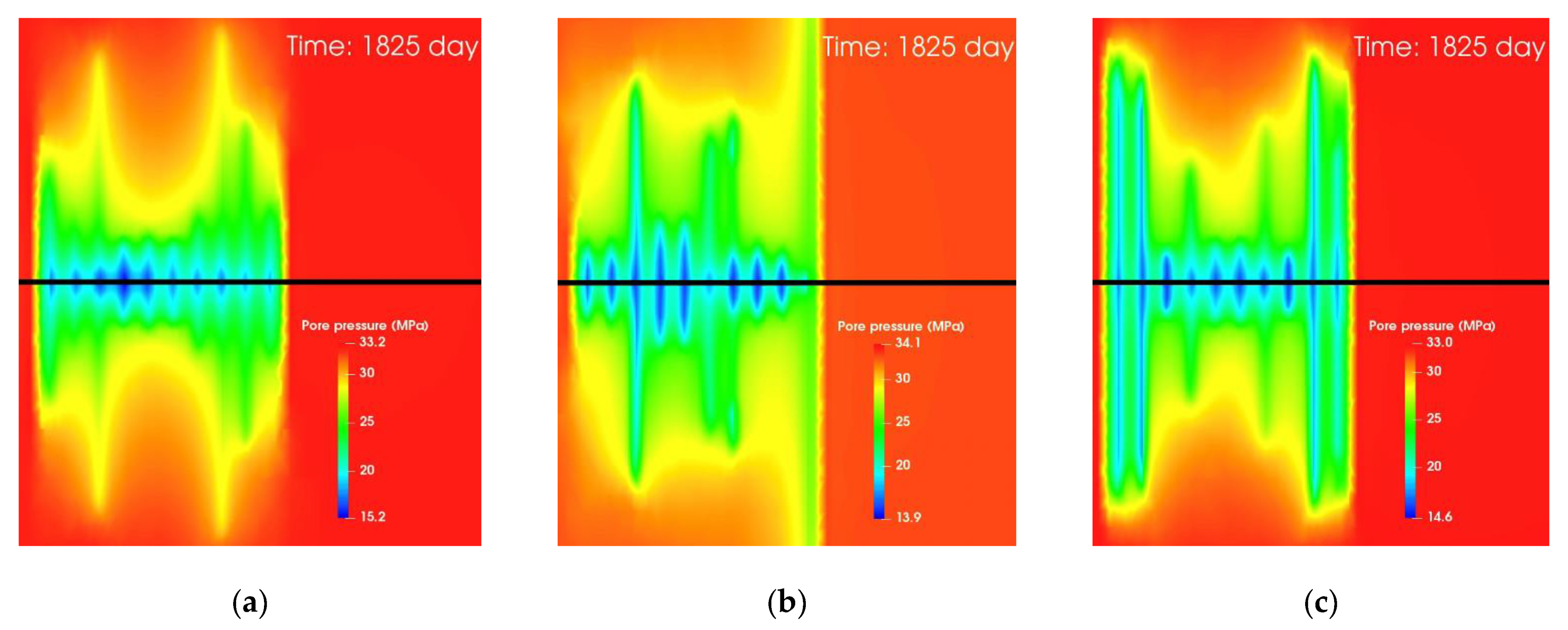
4.2. Results for the Shut-In Period
4.3. Results for the Production Period
5. Conclusions
- The use of NG foam reduces both gas flaring and water usage in well completions potentially saving both capital and reducing the environmental impact. The simulation results presented here can be used to conduct an economic analysis that includes the drilling cost, completion cost, additional cost for gas storage and foam generation, oil/gas/water daily production, oil price to evaluate the cash flow performance of different fracturing fluids and completion designs.
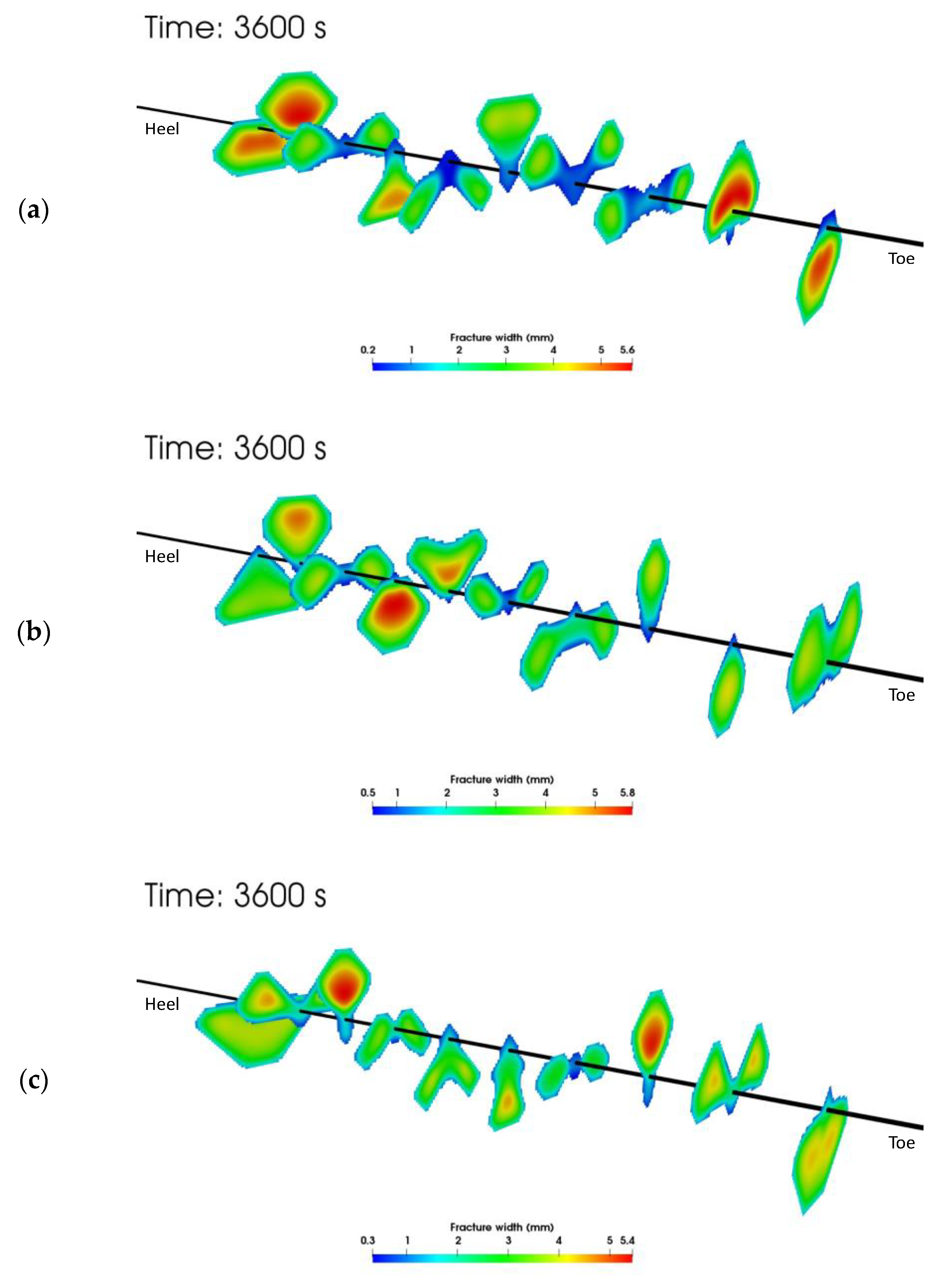
- The use of NG foam gives lower breakdown pressure, smaller created fracture surface area, and larger average fracture width during the hydraulic fracturing than slick water.
- NG foam causes higher effective stress (more compressive) and a larger stress shadow effect than slick water during hydraulic fracturing. More microcracks and higher SRV permeability are expected using NG foam.
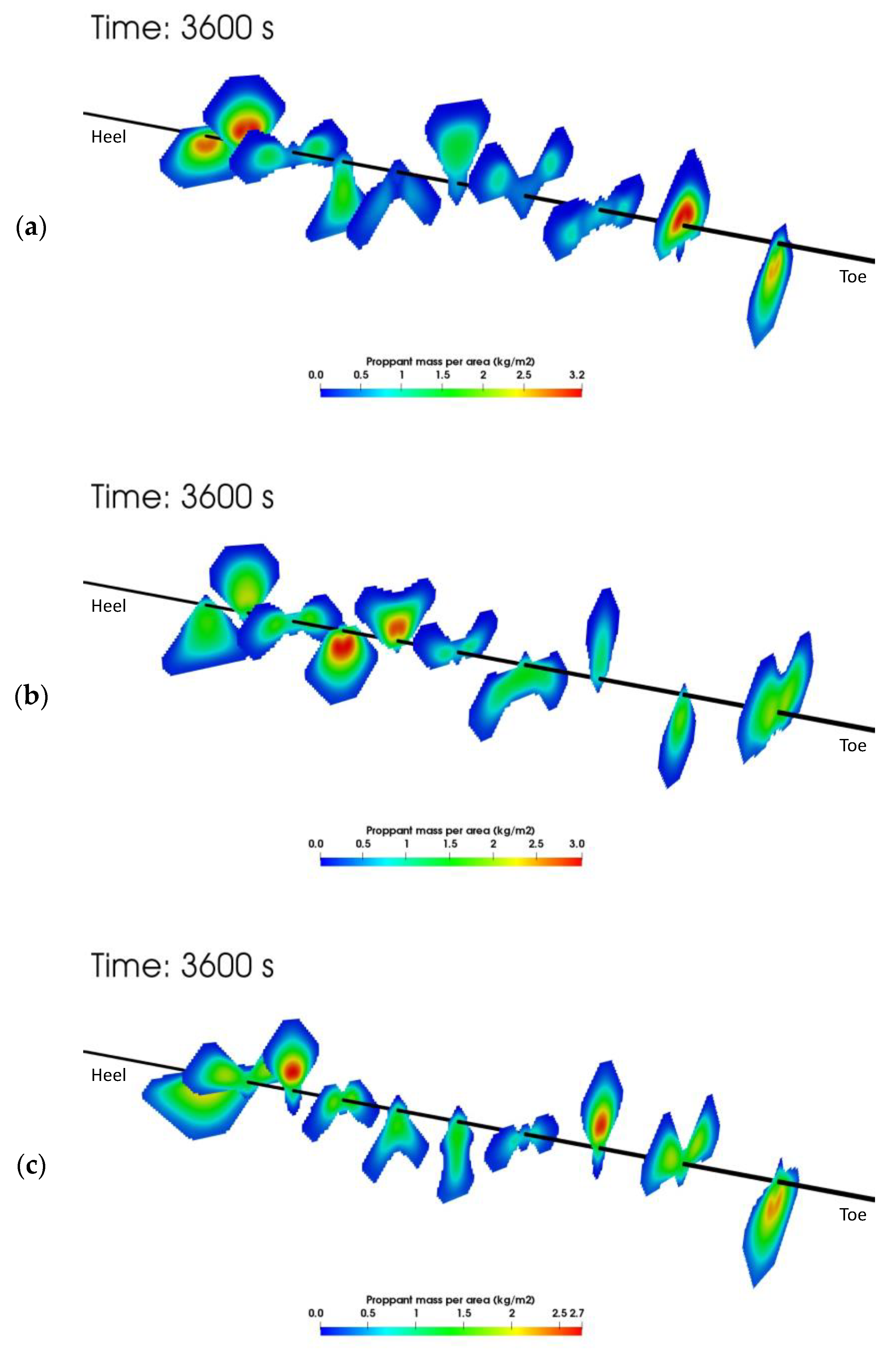
- NG foam has a significantly better sand transport capacity and can thus achieve better proppant placement inside the fractures.
- Higher cluster efficiency and higher oil and gas productivity are observed using NG foam than slick water.
- NG foam leads to more non-uniform fracture growth which may leave unstimulated regions in a newly developed reservoir.
- Precise data input, model calibration, and field pilot tests are essential to obtain more accurately predictable results for NG foam fracturing.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
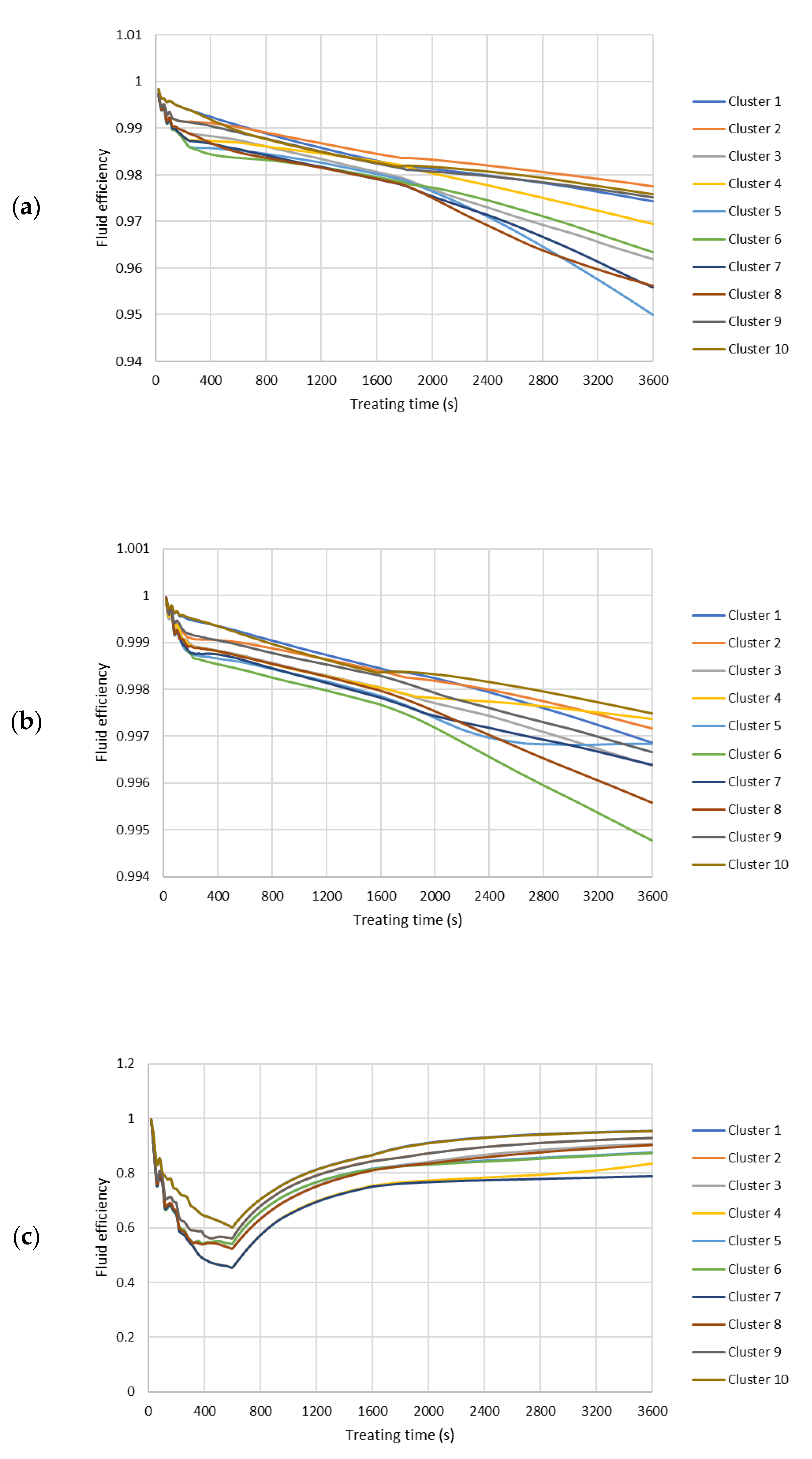

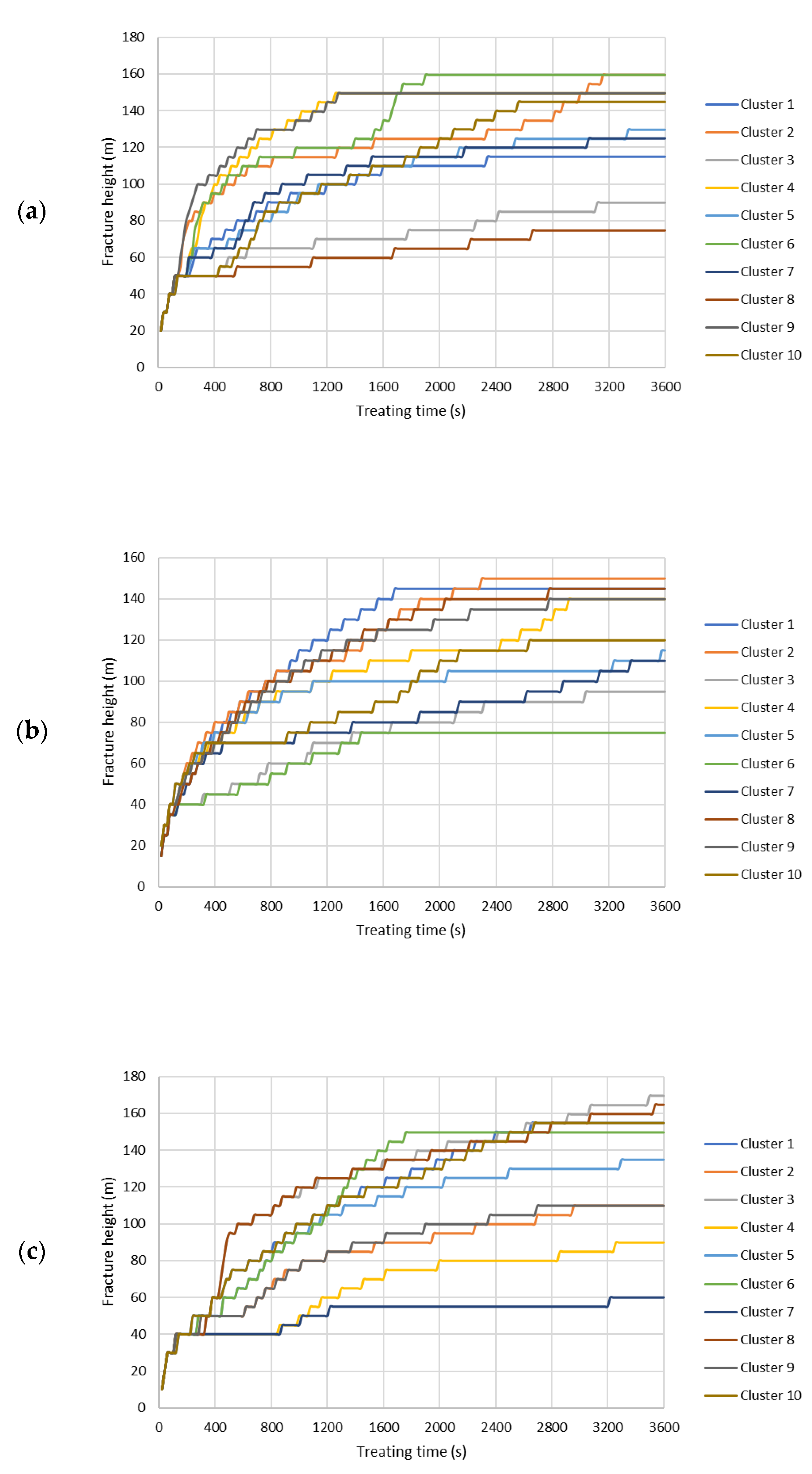
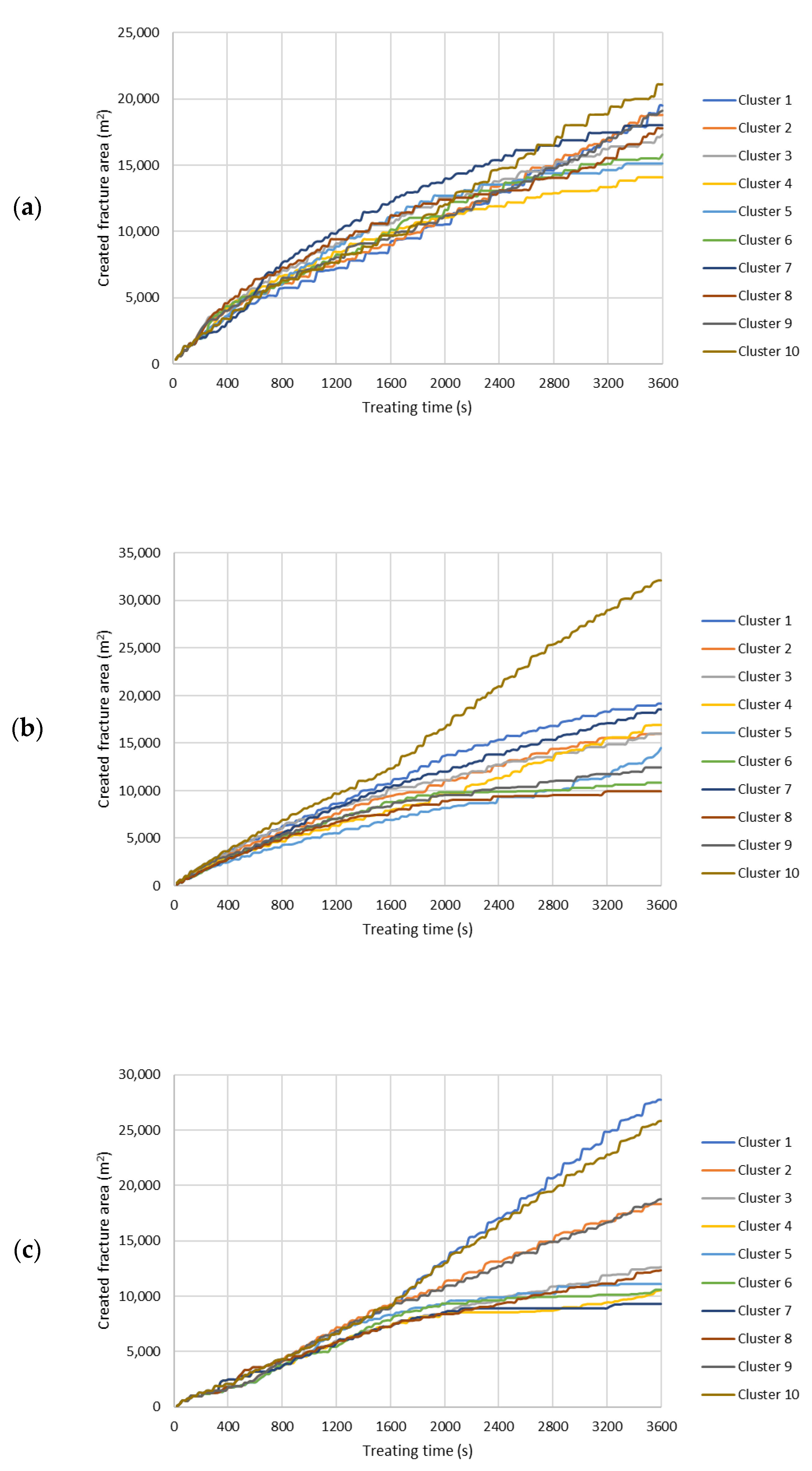
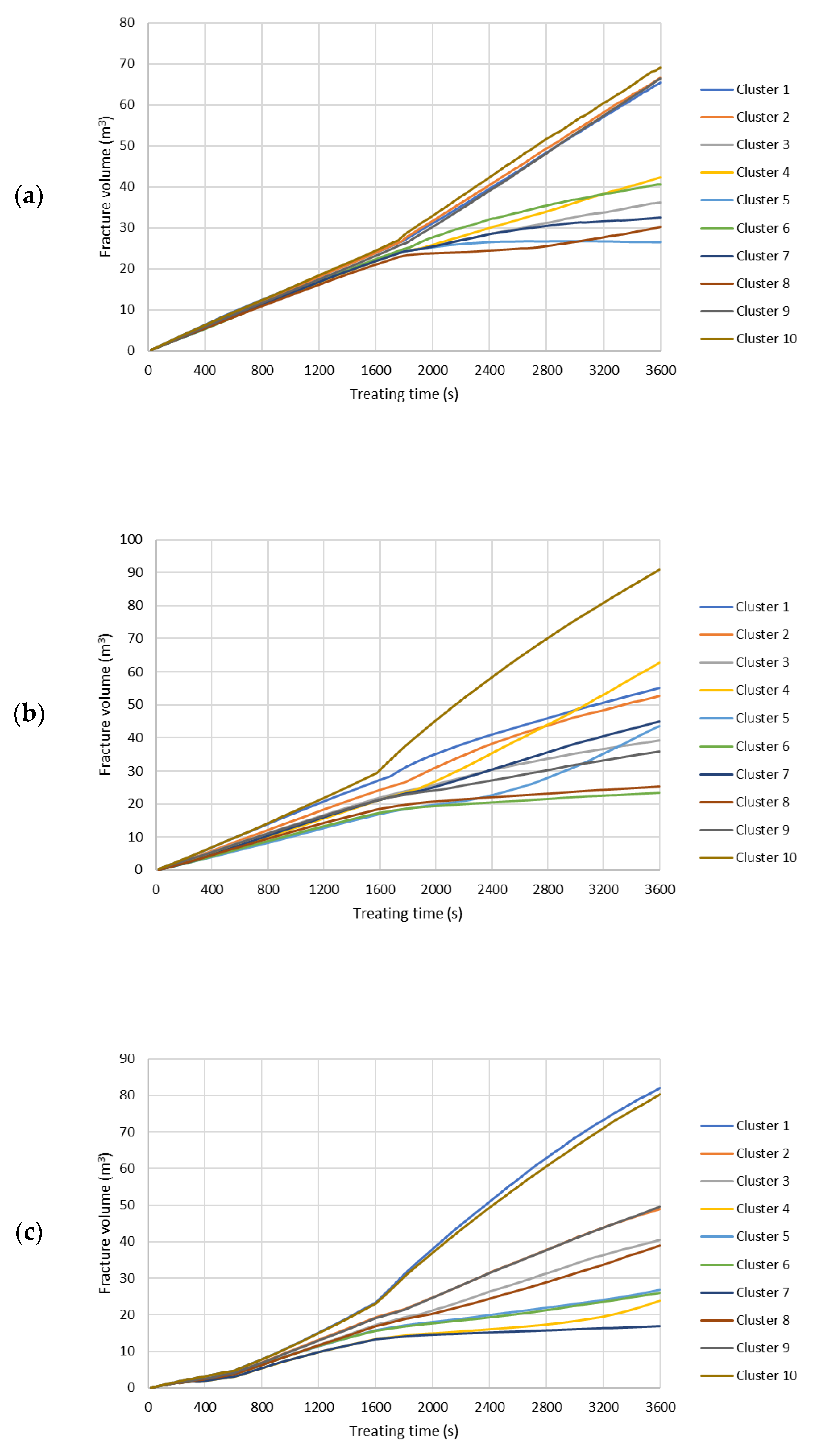


References
- Ozowe, W.O.; Zheng, S.; Sharma, M.M. Selection of Hydrocarbon Gas for Huff-n-Puff IOR in Shale Oil Reservoirs. J. Pet. Sci. Eng. 2020, 195, 107683. [Google Scholar] [CrossRef]
- Pankaj, P.; Phatak, A.; Verma, S. Evaluating Natural Gas-Based Foamed Fracturing Fluid Application in Unconventional Reservoirs. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Brisbane, Australia, 23–25 October 2018. [Google Scholar] [CrossRef]
- U.S. Department of Energy. Natural Gas Gross Withdrawals and Production. 2021. Available online: https://www.eia.gov/dnav/ng/ng_prod_sum_dc_NUS_mmcf_a.htm (accessed on 11 October 2021).
- Ribeiro, L.H.N. Development of a Three-Dimensional Compositional Hydraulic Fracturing Simulator for Energized Fluids. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2013. Available online: http://hdl.handle.net/2152/22805 (accessed on 11 October 2021).
- Khade, S.D.; Shah, S.N. New Rheological Correlations for Guar Foam Fluids. SPE Prod. Facil. 2004, 19, 77–85. [Google Scholar] [CrossRef]
- Ribeiro, L.H.; Sharma, M.M. Multiphase Fluid-loss Properties and Return Permeability of Energized Fracturing Fluids. SPE Prod. Oper. 2012, 27, 265–277. [Google Scholar] [CrossRef]
- Beck, G.; Verma, S. Development and Field Testing Novel Natural Gas (NG) Surface Process Equipment for Replacement of Water as Primary Hydraulic Fracturing Fluid. In Proceedings of the Carbon Storage and Oil and Natural Gas Technologies Review Meeting, Pittsburgh, PA, USA, 13–16 August 2016; pp. 16–18. [Google Scholar]
- Beck, G.; Nolen, C.; Hoopes, K.; Krouse, C.; Poerner, M.; Phatak, A.; Verma, S. Laboratory Evaluation of a Natural Gas-Based Foamed Fracturing Fluid. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017. [Google Scholar] [CrossRef]
- Zheng, S.; Sharma, M.M. The Effects of Geomechanics, Diffusion and Phase Behavior for Huff-n-Puff IOR in Shale Oil Reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 5–7 October 2020. [Google Scholar] [CrossRef]
- Lecampion, B.; Bunger, A.; Zhang, X. Numerical methods for hydraulic fracture propagation: A review of recent trends. J. Nat. Gas Sci. Eng. 2018, 49, 66–83. [Google Scholar] [CrossRef] [Green Version]
- Agrawal, S.; Zheng, S.; Foster, J.T.; Sharma, M.M. Coupling of meshfree peridynamics with the Finite Volume Method for poroelastic problems. J. Pet. Sci. Eng. 2020, 192, 107252. [Google Scholar] [CrossRef]
- Hirose, S.; Sharma, M.M. Numerical Modelling of Fractures in Multilayered Rock Formations Using a Displacement Discontinuity Method. In Proceedings of the 52nd US Rock Mechanics/Geomechanics Symposium, Seattle, WA, USA, 17–20 July 2018. [Google Scholar]
- Li, J.; Li, Y.; Wu, K. An Efficient Higher Order Displacement Discontinuity Method with Joint Element for Hydraulic Fracture Modeling. In Proceedings of the 55th US Rock Mechanics/Geomechanics Symposium, Houston, TX, USA, 18–25 June 2021. [Google Scholar]
- Ouchi, H.; Katiyar, A.; Foster, J.T.; Sharma, M.M. A Peridynamics Model for the Propagation of Hydraulic Fractures in Naturally Fractured Reservoirs. SPE J. 2017, 22, 1082–1102. [Google Scholar] [CrossRef]
- Settgast, R.R.; Fu, P.; Walsh, S.D.; White, J.A.; Annavarapu, C.; Ryerson, F.J. A Fully Coupled Method for Massively Parallel Simulation of Hydraulically Driven Fractures in 3-dimensions. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 627–653. [Google Scholar] [CrossRef]
- Taleghani, A.D.; Gonzalez, M.; Shojaei, A. Overview of numerical models for interactions between hydraulic fractures and natural fractures: Challenges and limitations. Comput. Geotech. 2016, 71, 361–368. [Google Scholar] [CrossRef]
- Weng, X. Modeling of complex hydraulic fractures in naturally fractured formation. J. Unconv. Oil Gas Resour. 2015, 9, 114–135. [Google Scholar] [CrossRef]
- Wu, K.; Olson, J.E. Simultaneous Multifracture Treatments: Fully Coupled Fluid Flow and Fracture Mechanics for Horizontal Wells. SPE J. 2015, 20, 337–346. [Google Scholar] [CrossRef]
- Zhang, F.; Damjanac, B.; Maxwell, S. Investigating hydraulic fracturing complexity in naturally fractured rock masses using fully coupled multiscale numerical modeling. Rock Mech. Rock Eng. 2019, 52, 5137–5160. [Google Scholar] [CrossRef]
- Friehauf, K.E. Simulation and Design of Energized Hydraulic Fractures. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2009. Available online: http://hdl.handle.net/2152/6644 (accessed on 11 October 2021).
- Gu, M. Shale Fracturing Enhancement by Using Polymer-Free Foams and Ultra-Light Weight Proppants. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2013. Available online: http://hdl.handle.net/2152/28733 (accessed on 11 October 2021).
- Manchanda, R.; Zheng, S.; Hirose, S.; Sharma, M.M. Integrating Reservoir Geomechanics with Multiple Fracture Propagation and Proppant Placement. SPE J. 2020, 25, 662–691. [Google Scholar] [CrossRef]
- Zheng, S.; Manchanda, R.; Sharma, M.M. Development of a Fully Implicit 3-D Geomechanical Fracture Simulator. J. Pet. Sci. Eng. 2019, 179, 758–775. [Google Scholar] [CrossRef]
- Zheng, S.; Manchanda, R.; Sharma, M.M. Modeling Fracture Closure with Proppant Settling and Embedment During Shut-in and Production. SPE Drill. Completion 2020, 35, 668–683. [Google Scholar] [CrossRef]
- Zheng, S.; Hwang, J.; Manchanda, R.; Sharma, M.M. An Integrated Model for Multi-Phase Flow, Geomechanics and Fracture Propagation. J. Pet. Sci. Eng. 2020, in press. [Google Scholar]
- Zheng, S.; Manchanda, R.; Gala, D.P.; Sharma, M.M. Pre-loading Depleted Parent Wells to Avoid Frac-Hits: Some Important Design Considerations. SPE Drill. Completion 2020, 36, 170–187. [Google Scholar] [CrossRef]
- Zheng, S.; Sharma, M.M. An Integrated Equation-of-State Compositional Hydraulic Fracturing and Reservoir Simulator. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 5–7 October 2020. [Google Scholar] [CrossRef]
- Lohrenz, J.; Bray, B.G.; Clark, C.R. Calculating Viscosities of Reservoir Fluids from Their Compositions. J. Pet. Technol. 1964, 16, 1–171. [Google Scholar] [CrossRef]
- Yew, C.H.; Weng, X. Mechanics of Hydraulic Fracturing; Gulf Professional Publishing: Houston, TX, USA, 2014. [Google Scholar]
- Shah, S.N. Rheological Characterization of Hydraulic Fracturing Slurries. SPE Prod. Facil. 1993, 8, 123–130. [Google Scholar] [CrossRef]
- Keck, R.G.; Nehmer, W.L.; Strumolo, G.S. A New Method for Predicting Friction Pressures and Rheology of Proppant-laden Fracturing Fluids. SPE Prod. Eng. 1992, 7, 21–28. [Google Scholar] [CrossRef]
- Gao, C.; Gray, K.E. The development of a coupled geomechanics and reservoir simulator using a staggered grid finite difference approach. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017. [Google Scholar] [CrossRef]
- Wang, W.; Fan, D.; Sheng, G.; Chen, Z.; Su, Y. A Review of Analytical and Semi-analytical Fluid Flow Models for Ultra-tight Hydrocarbon Reservoirs. Fuel 2019, 256, 115737. [Google Scholar] [CrossRef]
- Gaswirth, S.B.; Marra, K.R.; Lillis, P.G.; Mercier, T.J.; Leathers-Miller, H.M.; Schenk, C.J.; Klett, T.R.; Le, P.A.; Tennyson, M.E.; Hawkins, S.J.; et al. Assessment of Undiscovered Continuous Oil Resources in the Wolfcamp Shale of the Midland Basin, Permian Basin Province, Texas; No. 2016-3092; US Geological Survey: Reston, VA, USA, 2016. [CrossRef] [Green Version]
- Patterson, R.; Yu, W.; Wu, K. Integration of Microseismic Data, Completion Data, and Production Data to Characterize Fracture Geometry in the Permian Basin. J. Nat. Gas Sci. Eng. 2018, 56, 62–71. [Google Scholar] [CrossRef]
- Sangnimnuan, A.; Li, J.; Wu, K.; Holditch, S.A. Impact of Parent Well Depletion on Stress Changes and Infill Well Completion in Multiple Layers in Permian Basin. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 22–24 July 2019. [Google Scholar] [CrossRef]
- Forrest, J.; Zhu, T.; Xiong, H.; Pradhan, Y. The Effect of Initial Conditions and Fluid PVT Properties on Unconventional Oil and Gas Recoveries in the Wolfcamp Formation in the Midland Basin. In Proceedings of the Unconventional Resources Technology Conference, Houston, TX, USA, 23–25 July 2018. [Google Scholar] [CrossRef]
- Li, L.; Sheng, J.J.; Xu, J. Gas Selection for Huff-n-Puff EOR in Shale Oil Reservoirs based upon Experimental and Numerical Study. In Proceedings of the SPE Unconventional Resources Conference, Calgary, AB, Canada, 15–16 February 2017. [Google Scholar] [CrossRef]
- Cramer, D.; Friehauf, K.; Roberts, G.; Whittaker, J. Integrating DAS, Treatment Pressure Analysis and Video-based Perforation Imaging to Evaluate Limited Entry Treatment Effectiveness. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 23–25 January 2018. [Google Scholar] [CrossRef]
- Romero, J.; Mack, M.G.; Elbel, J.L. Theoretical Model and Numerical Investigation of Near-Wellbore Effects in Hydraulic Fracturing. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 22–25 October 1995. [Google Scholar] [CrossRef]
- Gao, C.; Gray, K.E. A workflow for infill well design: Wellbore stability analysis through a coupled geomechanics and reservoir simulator. J. Pet. Sci. Eng. 2019, 176, 279–290. [Google Scholar] [CrossRef]
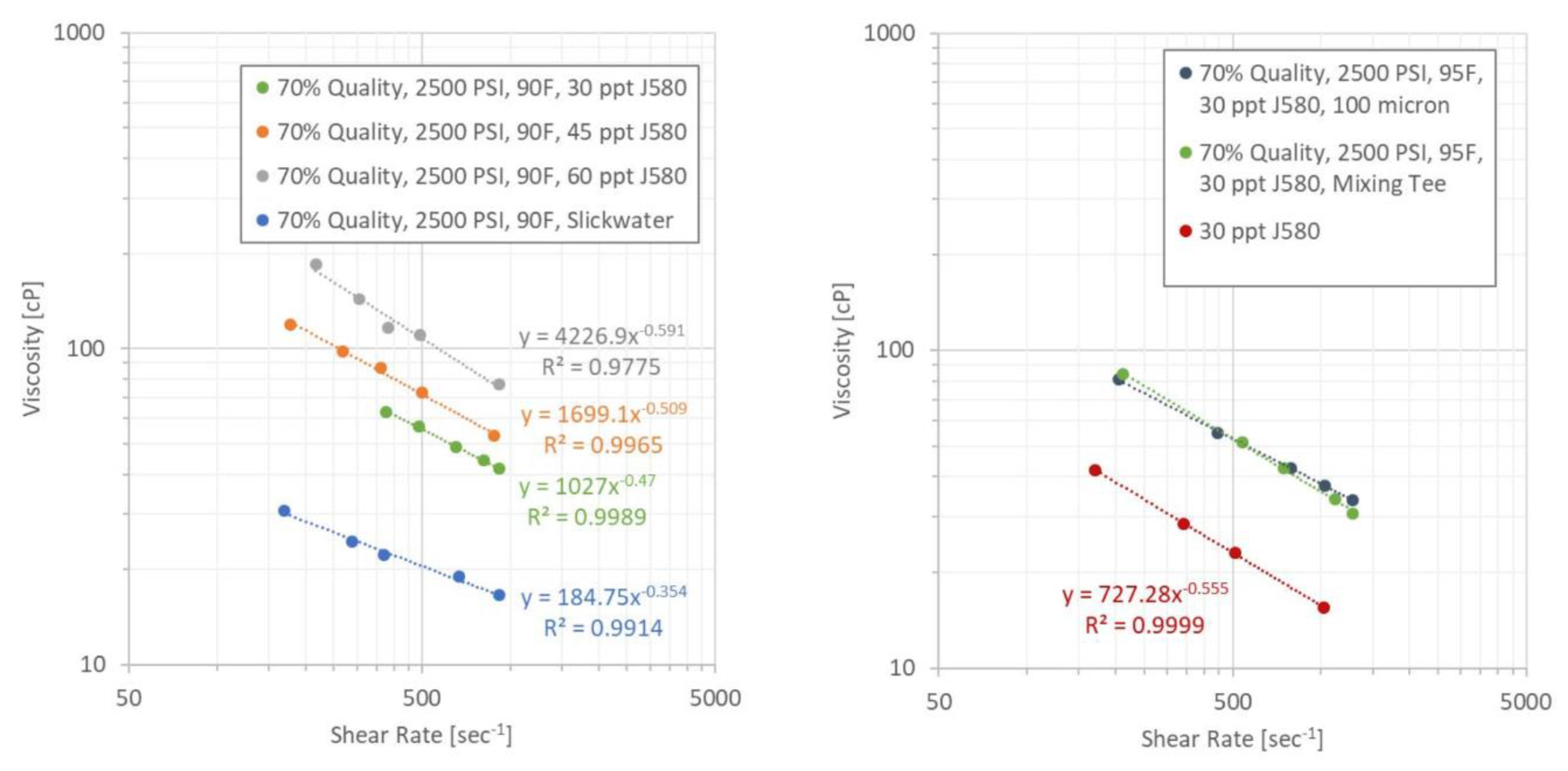






| Fracturing Fluid Name | Consistency Index (k, Pa · sn) | Flow Behavior Index (n, Unitless) |
|---|---|---|
| Slick water | 0.005 | 1 |
| Linear gel | 0.3495 | 0.508 |
| 30 ppt J580 | 0.72726 | 0.445 |
| 0.7 NG foam slick water | 0.18475 | 0.646 |
| 0.7 NG foam 30 ppt J580 | 1.027 | 0.53 |
| 0.7 NG foam 45 ppt J580 | 1.6991 | 0.491 |
| 0.7 NG foam 60 ppt J580 | 4.2269 | 0.409 |
| Rock Layer | Wolfcamp A1 | Wolfcamp A2 | Wolfcamp A3 | Wolfcamp B1 | Wolfcamp B2 | Wolfcamp B3 |
|---|---|---|---|---|---|---|
| Top TVD (m) | 2433.52 | 2449.68 | 2495.70 | 2523.74 | 2539.59 | 2614.88 |
| Thickness (m) | 16.15 | 46.02 | 28.04 | 15.85 | 75.29 | 97.84 |
| Porosity | 0.0646 | 0.0559 | 0.0623 | 0.0909 | 0.093 | 0.0744 |
| Permeability (nD) | 57.3 | 61 | 210 | 449 | 561 | 372 |
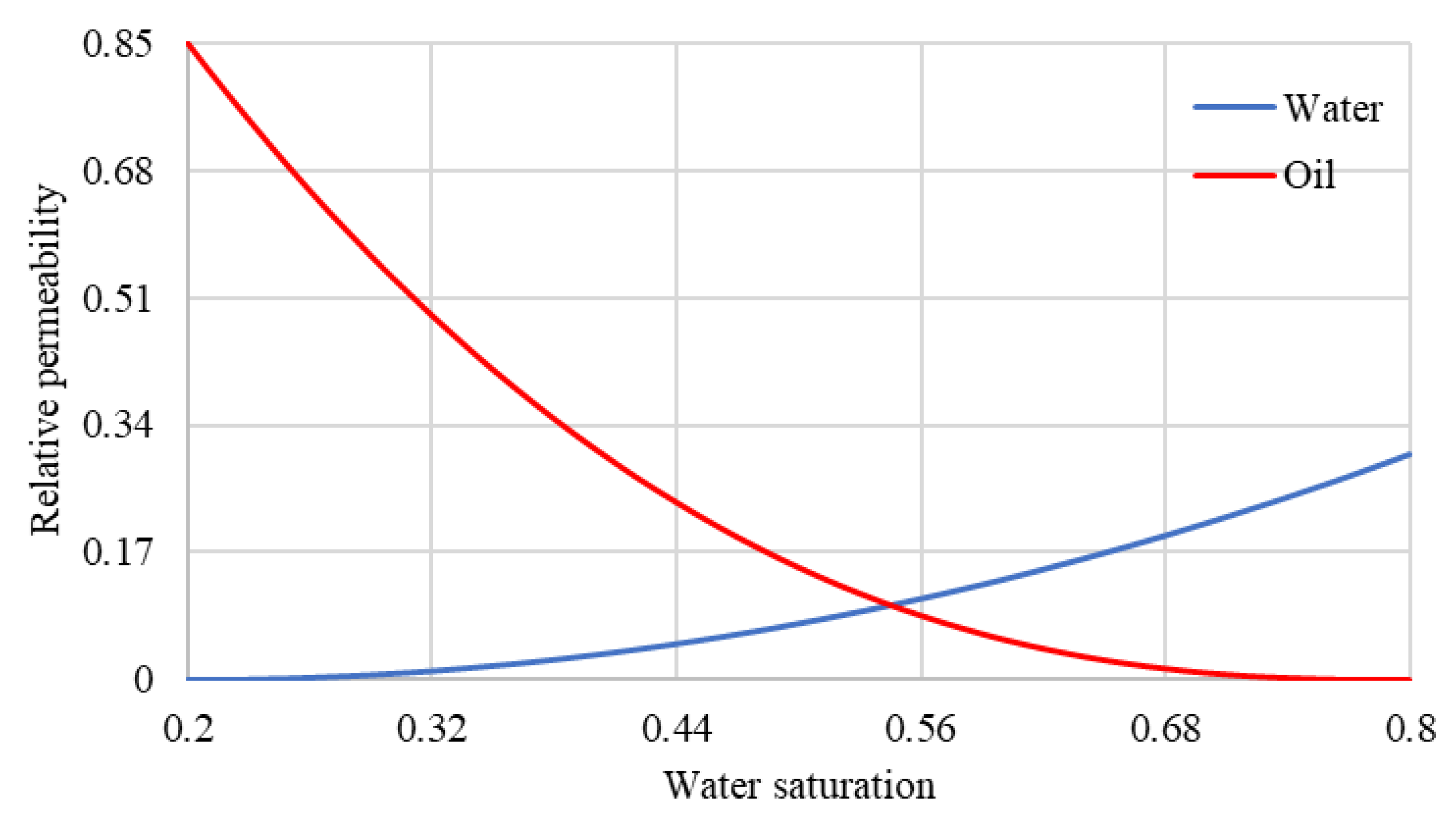
| Water saturation | 0.558 | 0.397 | 0.372 | 0.41 | 0.53 | 0.608 |
| Young’s modulus (GPa) | 22.41 | 17.24–24.48 | 19.99 | 20.68 | 21.37 | 19.31–24.13 |
| Poisson’s Ratio | 0.25–0.27 | 0.25–0.29 | 0.27 | 0.27 | 0.25–0.27 | 0.26–0.29 |
| Temperature (K) | 347.04 | 347.04 | 348.15 | 348.98 | 351.48 | 353.15 |
| Component | z | Pc (Pa) | Tc (K) | Mw (g/mol) | α | Vc (L/mol) |
|---|---|---|---|---|---|---|
| CO2 | 0.0035 | 7376460 | 304.2 | 44.01 | 0.225 | 0.094 |
| N2 | 0.0116 | 3394387.5 | 126.2 | 28.01 | 0.04 | 0.098926184 |
| C1 | 0.3332 | 4600155 | 190.6 | 16.04 | 0.013 | 0.098926184 |
| C2 | 0.0866 | 4883865 | 305.4 | 30.07 | 0.0986 | 0.17281213 |
| C3 | 0.0955 | 4245517.5 | 369.8 | 44.09 | 0.1524 | 0.17281213 |
| IC4 | 0.0106 | 3647700 | 408.1 | 58.12 | 0.1848 | 0.29094571 |
| NC4 | 0.0486 | 3799687.5 | 425.2 | 58.12 | 0.201 | 0.29094571 |
| C5-C6 | 0.0866 | 3181605 | 486.4 | 78.3 | 0.25896667 | 0.499076 |
| C7-C12 | 0.187 | 2502727.5 | 585.1 | 120.6 | 0.3739 | 1.1665888 |
| C12-C21 | 0.075 | 1722525 | 740.1 | 220.7 | 0.61195 | 1.1665888 |
| C22-C80 | 0.0623 | 1307092.5 | 1024 | 443.5 | 1.0456 | 1.1665888 |
| BIP | CO2 | N2 | C1 | C2 | C3 | IC4 | NC4 | C5-C6 |
|---|---|---|---|---|---|---|---|---|
| CO2 | ||||||||
| N2 | 0 | |||||||
| C1 | 0.105 | 0.025 | ||||||
| C2 | 0.13 | 0.01 | 0.0027 | |||||
| C3 | 0.125 | 0.09 | 0.0085 | 0.0017 | ||||
| IC4 | 0.12 | 0.095 | 0.0157 | 0.0055 | 0.0011 | |||
| NC4 | 0.115 | 0.095 | 0.0147 | 0.0049 | 0.0009 | 0 | ||
| C5-C6 | 0.115 | 0.1 | 0.0319 | 0.0165 | 0.0077 | 0.003 | 0.0035 | |
| C7-C12 | 0.115 | 0.11 | 0.047 | 0.0279 | 0.0162 | 0.0089 | 0.0097 | 0.0016 |
| C12-C21 | 0.115 | 0.11 | 0.1003 | 0.0728 | 0.0539 | 0.0402 | 0.0417 | 0.0218 |
| C22-C80 | 0.115 | 0.11 | 0.1266 | 0.0964 | 0.075 | 0.059 | 0.0608 | 0.0365 |
| Parameter | Value | Unit |
|---|---|---|
| Well landing depth | 2577 | |
| Critical stress intensity factor | 5 × 106 | |
| Biot coefficient | 1 | |
| Initial pore pressure | 3.28 × 107 | |
| Initial minimum horizontal stress | 4.13 × 107 | |
| Proppant density | 2650 | |
| Proppant diameter | 175/400 | |
| Asperity height | 1 × 10−4 | |
| Asperity/Proppant initial stiffness | 2 × 1010/2 × 1011 | |
| Proppant maximum packing fraction | 0.62 | |
| Wellbore volume | 55 | |
| Well diameter | 0.1397 | |
| Number of perforation clusters | 10 | |
| Number of perforations per cluster | 3 | |
| Cluster spacing | 15 | |
| Perforation diameter | 0.0127 | |
| Surface pressure | 101325 | |
| Surface temperature | 292.039 | |
| Reservoir simulation box size | ||
| Permeability-stress exponent for hydraulic fracturing | 1 × 10−6 | |
| Permeability-stress exponent for shut-in and production | 5 × 10−7 |
| Fracturing Fluid | Created Fracture Surface Area (m2) | Propped Fracture Surface Area (m2) | Ratio of Propped Area to the Created Area |
|---|---|---|---|
| Slick water | 176,655 | 68,148 | 0.3858 |
| NG foam | 166,378.5 | 79,320 | 0.4767 |
| NG and NG foam | 159,016 | 77,724 | 0.4888 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, S.; Sharma, M.M. Modeling Hydraulic Fracturing Using Natural Gas Foam as Fracturing Fluids. Energies 2021, 14, 7645. https://doi.org/10.3390/en14227645
Zheng S, Sharma MM. Modeling Hydraulic Fracturing Using Natural Gas Foam as Fracturing Fluids. Energies. 2021; 14(22):7645. https://doi.org/10.3390/en14227645
Chicago/Turabian StyleZheng, Shuang, and Mukul M. Sharma. 2021. "Modeling Hydraulic Fracturing Using Natural Gas Foam as Fracturing Fluids" Energies 14, no. 22: 7645. https://doi.org/10.3390/en14227645
APA StyleZheng, S., & Sharma, M. M. (2021). Modeling Hydraulic Fracturing Using Natural Gas Foam as Fracturing Fluids. Energies, 14(22), 7645. https://doi.org/10.3390/en14227645






