A New Modeling Framework for Geothermal Operational Optimization with Machine Learning (GOOML)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Sources
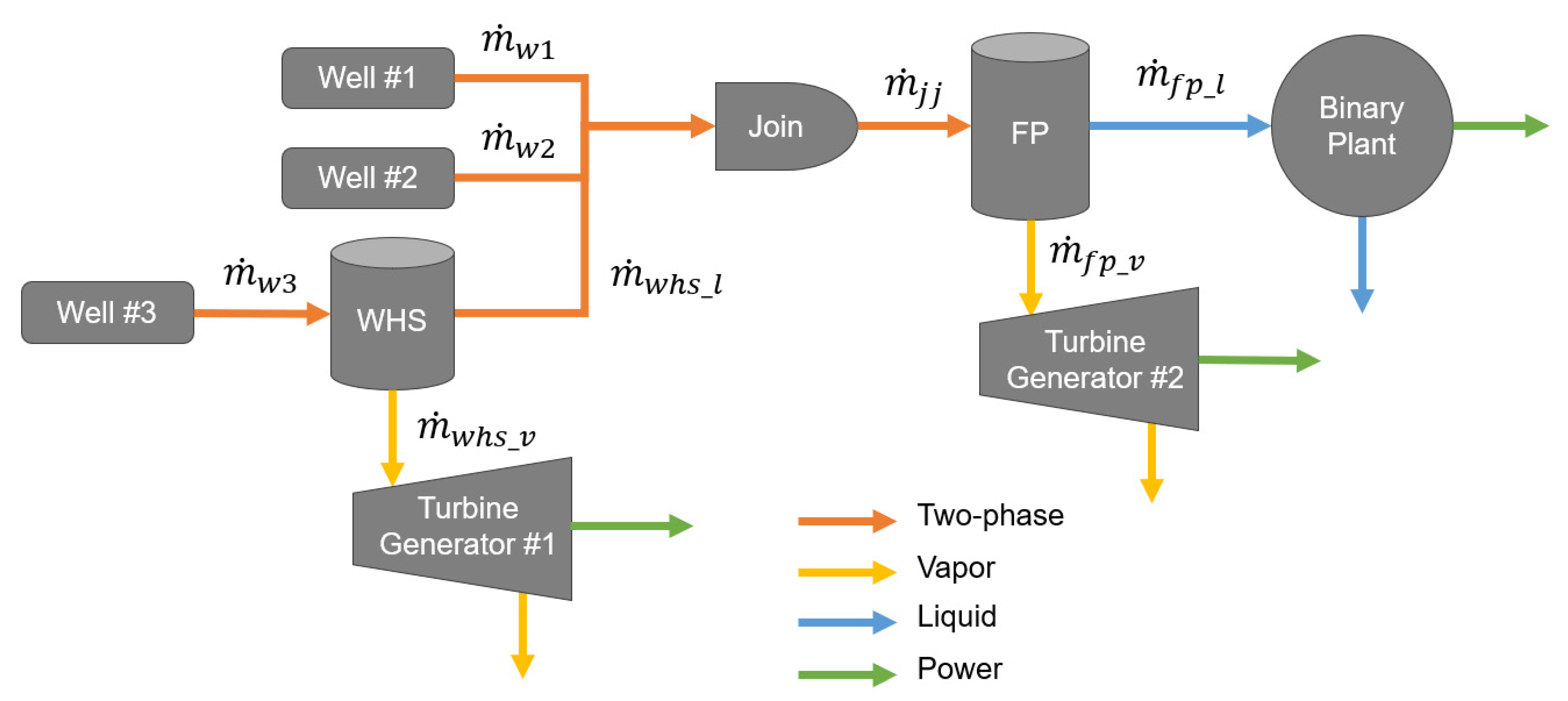
2.2. System Frameworks
2.2.1. Historical System
2.2.2. Forecast System
2.3. Component Models
2.3.1. Well Models
2.3.2. Two-Phase Separator Models (“Flash Plants”)
2.3.3. Power Generating Models
2.3.4. General Utility Component Models
2.4. Modeling Assumptions
3. Results
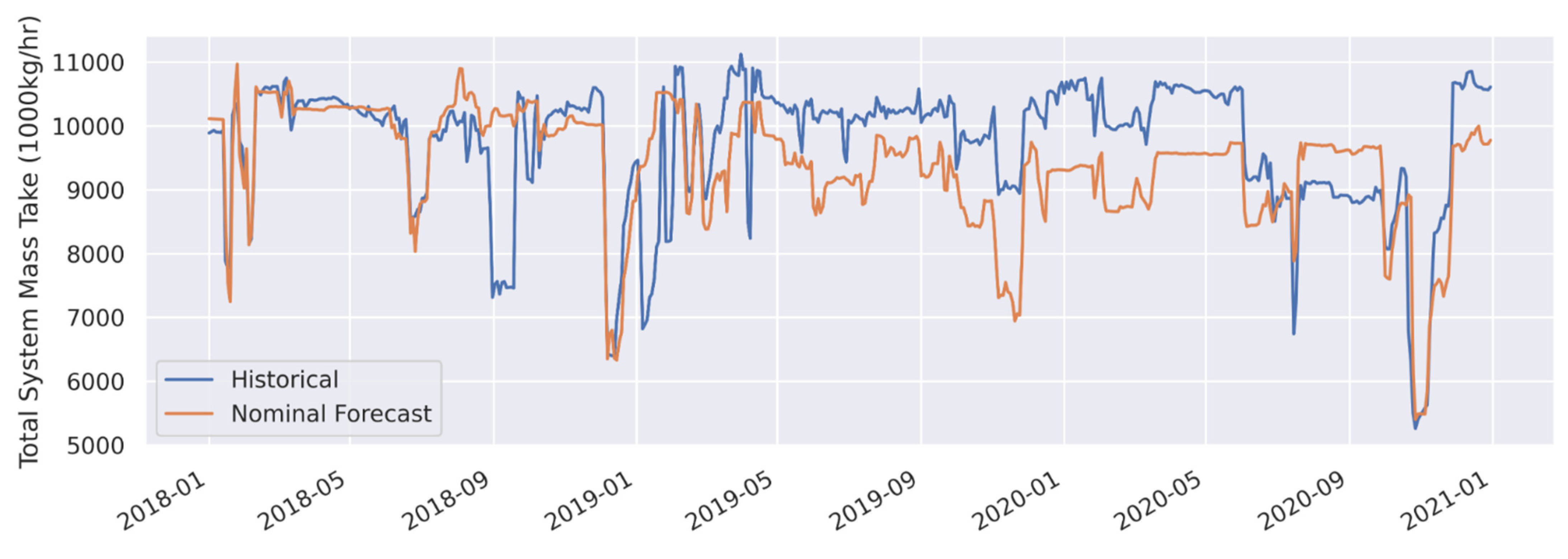
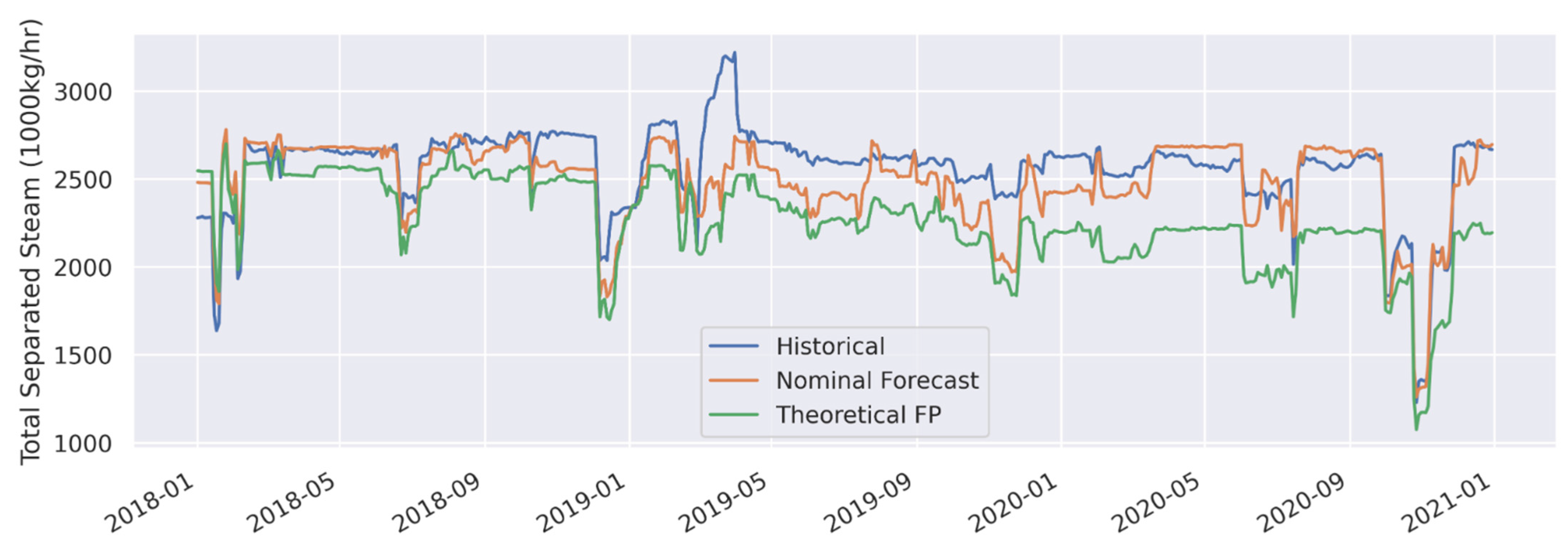
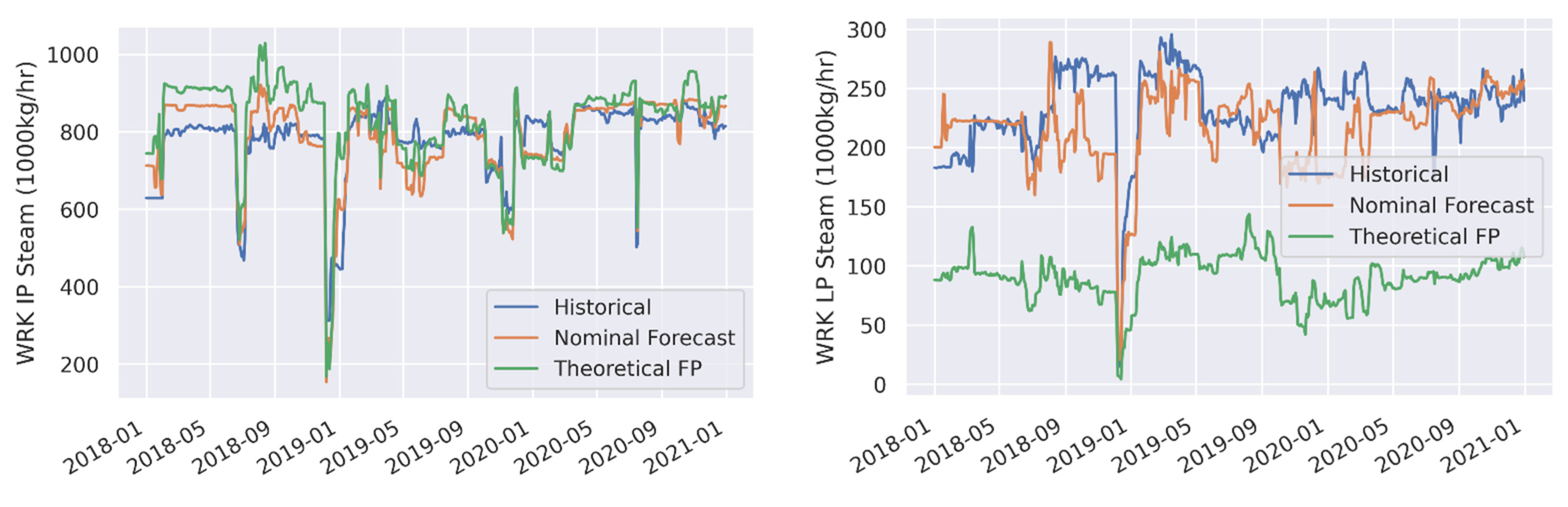
3.1. Forecast Model Validation
3.2. Cross-Validation and Extensibility
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Glossary and Abbreviations
| AI | artificial intelligence |
| as-built | the true physical system including any modifications made during its construction and/or operation as opposed to the nominal system during the design phase |
| binary plant | a power plant that transfers geothermal heat to a secondary fluid with a lower boiling point to drive a turbine generator |
| capacity factor | the ratio of actual power generated to the theoretical maximum output of a power station |
| digital twin | a digital representation of a physical system |
| forecast model | a relational data model that uses trained regressions to predict future operational states |
| GOOML | Geothermal Operational Optimization with Machine Learning |
| hindcast | a forecast model used for validation purposes that is based on some historical data such as known operator actions |
| historical model | a relational data model built using historical data |
| hybrid data-driven thermodynamics model | in the context of this work, GOOML is a hybrid model that relies heavily on traditional thermodynamics (e.g., fluid properties and conservation equations) but uses data-driven machine learning models to determine the behavior of the system within the thermodynamic operational space |
| IP | intermediate pressure |
| join junction | a component where two or more flows are joined to one |
| LP | low pressure |
| mass take | the total mass extracted by a geothermal system |
| MAE | mean absolute error calculated as: where is the GOOML predicted value, is the true historical value, is the number of observations, and is the absolute value operator |
| MBE | mean bias error calculated as: where is the GOOML predicted value, is the true historical value, and is the number of observations |
| ML | machine learning |
| POI | Poihipi power station at the Wairakei Geothermal Field |
| RELU | rectified linear unit |
| separator/flash plant (FP) | a vessel that separates steam and liquid phases from a two-phase flow input, often involving pressure drop and cyclonic separation |
| split junction | a component where input flow is split into two distinct outputs, e.g., steam and liquid in the case of a separator |
| steamfield | a network of wells, pipelines, separators, turbine generators, and binary plants used to harness geothermal energy |
| TG | a turbine generator system that uses steam to generate electricity |
| THI | Te Mihi power station at the Wairakei Geothermal Field |
| TFT | tracer flow test—a method to assess energy and flow rate from a geothermal well |
| two-phase flow | a thermodynamic state of water where both saturated liquid and steam exist simultaneously |
| Willans Line | a highly simplified linear mass-to-power relationship used to represent turbine generator systems |
| WRK | Wairakei power station at the Wairakei Geothermal Field |
| WHS | well head separator—a small two-phase separator dedicated to a single well, typically mounted directly on the well head itself |
References
- IRENA From Baseload to Peak: Renewables Provide A Reliable Solution; International Renewable Energy Agency (IRENA): Masdar City, Abu Dhabi, 2015; p. 16.
- U.S. Energy Information Administration (EIA). Electric Power Monthly with Data for April 2021; U.S. Energy Information Administration (EIA): Washington, DC, USA, 2021; p. 285. [Google Scholar]
- IRENA Renewable Power Generation Costs in 2019; International Renewable Energy Agency (IRENA): Masdar City, Abu Dhabi, 2020; p. 144.
- DiPippo, R. Geothermal Power Plants: Principles, Applications, Case Studies and Environmental Impact; Elsevier Science & Technology: Oxford, UK, 2012; ISBN 9780123947871. [Google Scholar]
- Thain, I.A.; Carey, B. Fifty years of geothermal power generation at Wairakei. Geothermics 2009, 38, 48–63. [Google Scholar] [CrossRef]
- Brosinsky, C.; Westermann, D.; Krebs, R. Recent and prospective developments in power system control centers: Adapting the digital twin technology for application in power system control centers. In Proceedings of the 2018 IEEE International Energy Conference (ENERGYCON), Limassol, Cyprus, 3–7 June 2018; pp. 1–6. [Google Scholar]
- Huang, J.; Zhao, L.; Wei, F.; Cao, B. The Application of Digital Twin on Power Industry. IOP Conf. Ser. Earth Environ. Sci. 2021, 647, 012015. [Google Scholar] [CrossRef]
- GE Digital Twin Analytic Engine for the Digital Power Plant 2016. Available online: https://www.ge.com/digital/sites/default/files/download_assets/Digital-Twin-for-the-digital-power-plant-.pdf (accessed on 13 May 2021).
- COMSOL Multiphysics. 2021. Available online: https://www.comsol.com/ (accessed on 13 May 2021).
- Flownex. 2021. Available online: https://flownex.com/ (accessed on 13 May 2021).
- Aspen HYSYS. Aspentech. Available online: https://www.aspentech.com/en/products/engineering/aspen-hysys (accessed on 13 May 2021).
- Thermolib. Toolbox for Thermodynamic Calculations and Thermodynamic Systems Simulations in MATLAB and Simulink; EUtech Scientific Engineering GmbH. Available online: https://www.mathworks.com/products/connections/product_detail/thermolib.html (accessed on 13 May 2021).
- Wemhoff, A.; Jones, G.; Ortega, A. Villanova Thermodynamic Analysis of Systems (VTAS); Center for Energy-Smart Electronic Systems: Villanova, PA, USA, 2015. [Google Scholar]
- System Advisor Model Version 2020.11.29 (SAM 2020.11.29); National Renewable Energy Laboratory: Golden, CO, USA, 2020.
- Chapman, J.; Lavelle, T.; May, R.; Litt, J.; Guo, T.-H. Toolbox for the Modeling and Analysis of Thermodynamic Systems (T-MATS) User’s Guide; National Aeronautics and Space Administration, Glenn Research Center Cleveland: Cleveland, OH, USA, 2014. [Google Scholar]
- RELAP-7 User’s Guide (Technical Report) | OSTI.GOV. Available online: https://www.osti.gov/biblio/1466669-relap-user-guide (accessed on 13 July 2021).
- NIST/SEMATECH e-Handbook of Statistical Methods; National Institute of Standards and Testing (NIST): Gaithersburg, MD, USA, 2013. [CrossRef]
- Martínez, E.H.; Carlos, M.P.A.; Solís, J.I.C.; Avalos, M.M.D.C.P. Thermodynamic simulation and mathematical model for single and double flash cycles of Cerro Prieto geothermal power plants. Geothermics 2020, 83, 101713. [Google Scholar] [CrossRef]
- Lazalde-Crabtree, H. Design approach of steam-water separators and steam dryers for geothermal applications. Bull. Geotherm. Resour. Counc. 1984, 13, 8. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A system for large-scale machine learning. arXiv 2016, arXiv:1605.08695. [Google Scholar]
- Church, E.F. Steam Turbines, 1st ed.; McGraw-Hill Book Company: New York, NY, USA, 1928. [Google Scholar]
- Linstrom, P.J.; Mallard, W.G. NIST Chemistry WebBook, NIST Standard Reference Database Number 69; National Institute of Standards and Testing (NIST): Gaithersburg, MD, USA, 2013. [Google Scholar] [CrossRef]
- Zarrouk, S.J.; Moon, H. Efficiency of geothermal power plants: A worldwide review. Geothermics 2014, 51, 142–153. [Google Scholar] [CrossRef]
- Mubarok, M.H.; Cater, J.E.; Zarrouk, S.J. Comparative CFD modelling of pressure differential flow meters for measuring two-phase geothermal fluid flow. Geothermics 2020, 86, 101801. [Google Scholar] [CrossRef]
- Xu, K.; Zhang, M.; Li, J.; Du, S.S.; Kawarabayashi, K.; Jegelka, S. How Neural Networks Extrapolate: From Feedforward to Graph Neural Networks. arXiv 2021, arXiv:2009.11848. [Google Scholar]
- Sun, B.; Yang, C.; Wang, Y.; Gui, W.; Craig, I.; Olivier, L. A comprehensive hybrid first principles/machine learning modeling framework for complex industrial processes. J. Process. Control. 2020, 86, 30–43. [Google Scholar] [CrossRef]
- Rätz, M.; Javadi, A.P.; Baranski, M.; Finkbeiner, K.; Müller, D. Automated data-driven modeling of building energy systems via machine learning algorithms. Energy Build. 2019, 202, 109384. [Google Scholar] [CrossRef]
- Liu, Y.; Ling, W.; Young, R.; Cladouhos, T.; Zia, J.; Jafarpour, B. Deep Learning for Prediction and Fault Detection in Geothermal Operations. In Proceedings of the 46th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 15–17 February 2021. [Google Scholar]
- DeepMind AI Reduces Google Data Centre Cooling Bill by 40%. Available online: https://deepmind.com/blog/article/deepmind-ai-reduces-google-data-centre-cooling-bill-40 (accessed on 30 August 2021).
- Li, Y.; Wen, Y.; Tao, D.; Guan, K. Transforming Cooling Optimization for Green Data Center via Deep Reinforcement Learning. IEEE Trans. Cybern. 2020, 50, 2002–2013. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Upflow. GOOML Big Kahuna Forecast Modeling and Genetic Optimization Files [Data Set]; OpenEI, Geothermal Data Repository (GDR); U.S. Department of Energy (DOE) Geothermal Technologies Office: Washington, DC, USA, 2021. [Google Scholar]


| Component | Common Historical Data | Forecast Model | Model Input Features |
|---|---|---|---|
| Single-Phase Well | Pressure, temperature, mass flow | Linear extrapolation with decline | Pressure, temperature, mass flow |
| Two-Phase Well | Pressure, mass flow (TFT estimate), enthalpy (TFT estimate) | TFT deliverability curves with decline | Pressure |
| Separator (Flash Plant) | Output steam pressure, output steam mass flow, output liquid mass flow | Feed-forward neural network, theoretical (thermodynamic-based) | Input mass flow, input enthalpy, input pressure, input steam quality, input velocity, residence time, steam quality at separation pressure, theoretical pressure drop, cyclone design number |
| Turbine Generator | Heat sink temperature, power | Multi-linear regression, Willans Line, theoretical (Carnot-based) | Input mass flow, input enthalpy flow, heat sink temperature, temperature differential |
| Binary Plant | Heat sink temperature, power | Multi-linear regression, theoretical (Carnot-based) | Input enthalpy flow, temperature differential, upstream flow contribution fractions |
| Join Junctions | N/A | N/A | N/A |
| Split Junctions | N/A | N/A | N/A |
| Metric | Model | MAE | MAE (%) | MBE | MBE (%) |
|---|---|---|---|---|---|
| Total System Mass Take (1000 kg/h) | Nominal Forecast | 783 | 8.1 | −328.4 | −3.4 |
| Total Separated Steam (1000 kg/h) | Nominal Forecast | 133 | 5.2 | −76.8 | −3.0 |
| Total Separated Steam (1000 kg/h) | Theoretical FP | 314.2 | 12.3 | −297 | −11.6 |
| WRK IP Steam (1000 kg/h) | Nominal Forecast | 47.5 | 6.1 | 10.9 | 1.4 |
| WRK IP Steam (1000 kg/h) | Theoretical FP | 70.7 | 9.1 | 45.4 | 5.8 |
| WRK LP Steam (1000 kg/h) | Nominal Forecast | 29.3 | 12.6 | −16 | −6.9 |
| WRK LP Steam (1000 kg/h) | Theoretical FP | 142.8 | 61.3 | −142.8 | −61.3 |
| THI IP Steam (1000 kg/h) | Nominal Forecast | 62.5 | 6.8 | −54.2 | −5.9 |
| THI IP Steam (1000 kg/h) | Theoretical FP | 166.6 | 18.2 | −163.8 | −17.9 |
| THI LP Steam (1000 kg/h) | Nominal Forecast | 38.3 | 10.5 | −20.2 | −5.5 |
| THI LP Steam (1000 kg/h) | Theoretical FP | 34.6 | 9.5 | 25.2 | 6.9 |
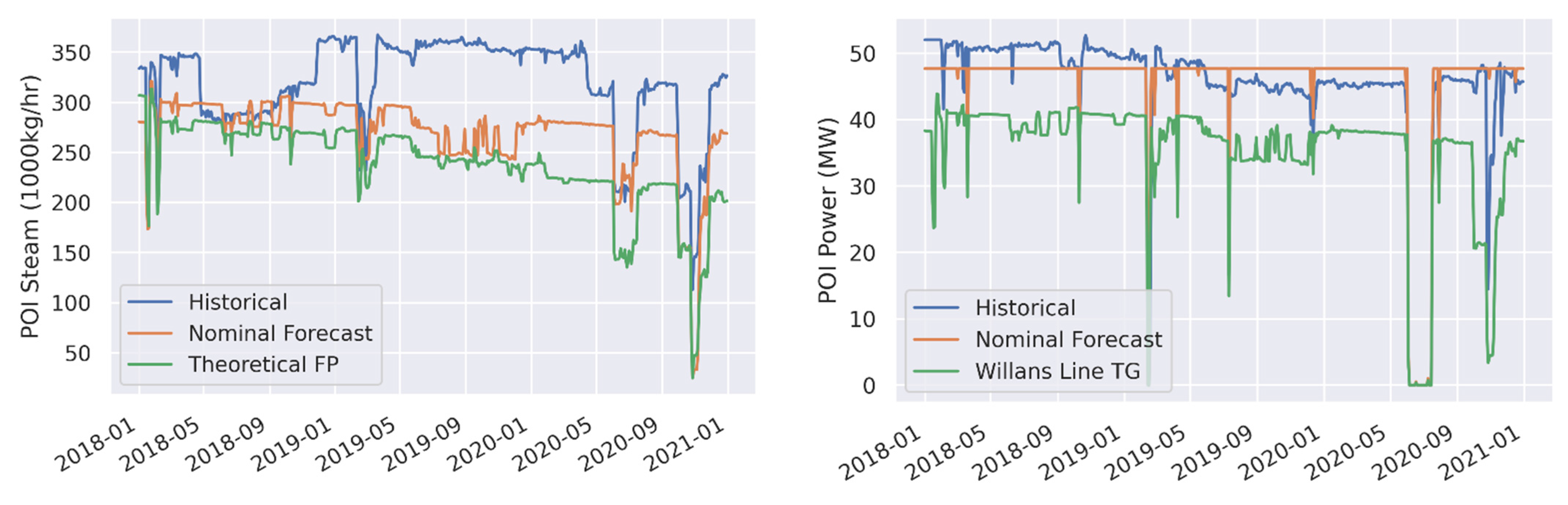
| POI Steam (1000 kg/h) | Nominal Forecast | 52.3 | 16.4 | −49.8 | −15.6 |
| POI Steam (1000 kg/h) | Theoretical FP | 81.1 | 25.4 | −80.7 | −25.3 |
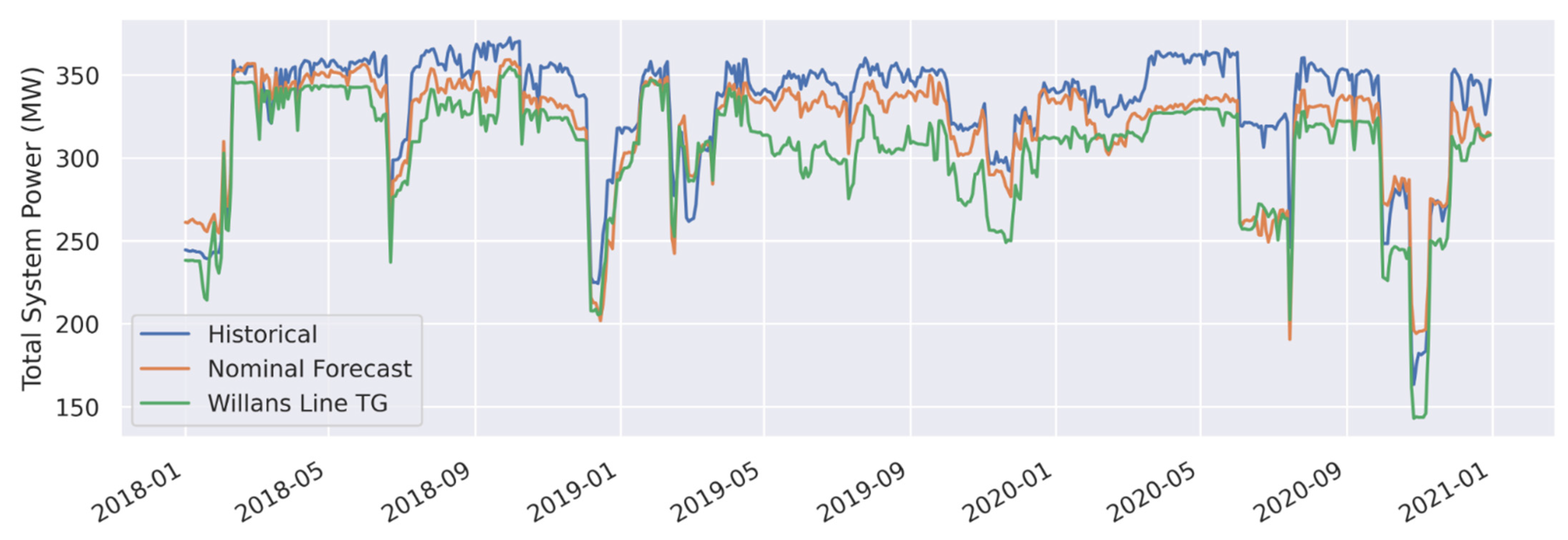
| Total System Power (Gross MWe) | Nominal Forecast | 16.6 | 5.0 | −12.8 | −3.9 |
| Total System Power (Gross MWe) | Willans Line TG | 28.5 | 8.6 | −27.4 | −8.3 |
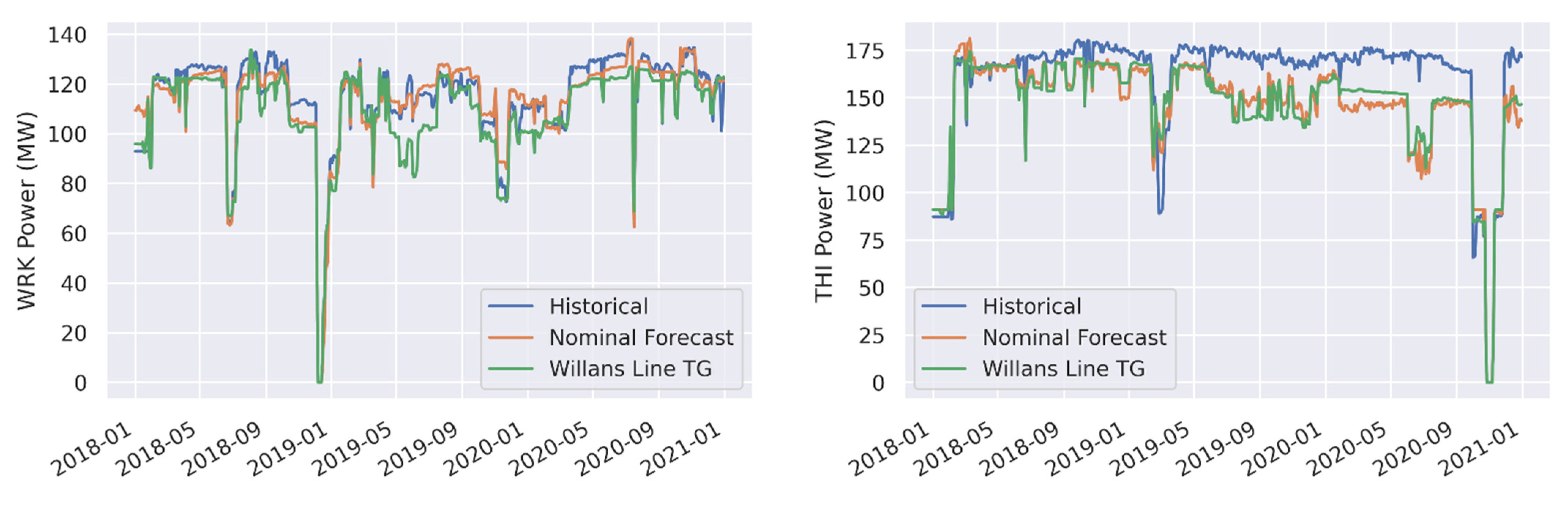
| WRK Power (Gross MWe) | Nominal Forecast | 4.8 | 4.2 | −0.3 | −0.3 |
| WRK Power (Gross MWe) | Willans Line TG | 6.8 | 5.9 | −5.4 | −4.7 |
| THI Power (Gross MWe) | Nominal Forecast | 16.7 | 10.4 | −14 | −8.7 |
| THI Power (Gross MWe) | Willans Line TG | 15.9 | 9.9 | −13.5 | −8.4 |
| POI Power (Gross MWe) | Nominal Forecast | 2.7 | 6.1 | 0.4 | 1.0 |
| POI Power (Gross MWe) | Willans Line TG | 9.8 | 21.9 | −9.6 | −21.5 |
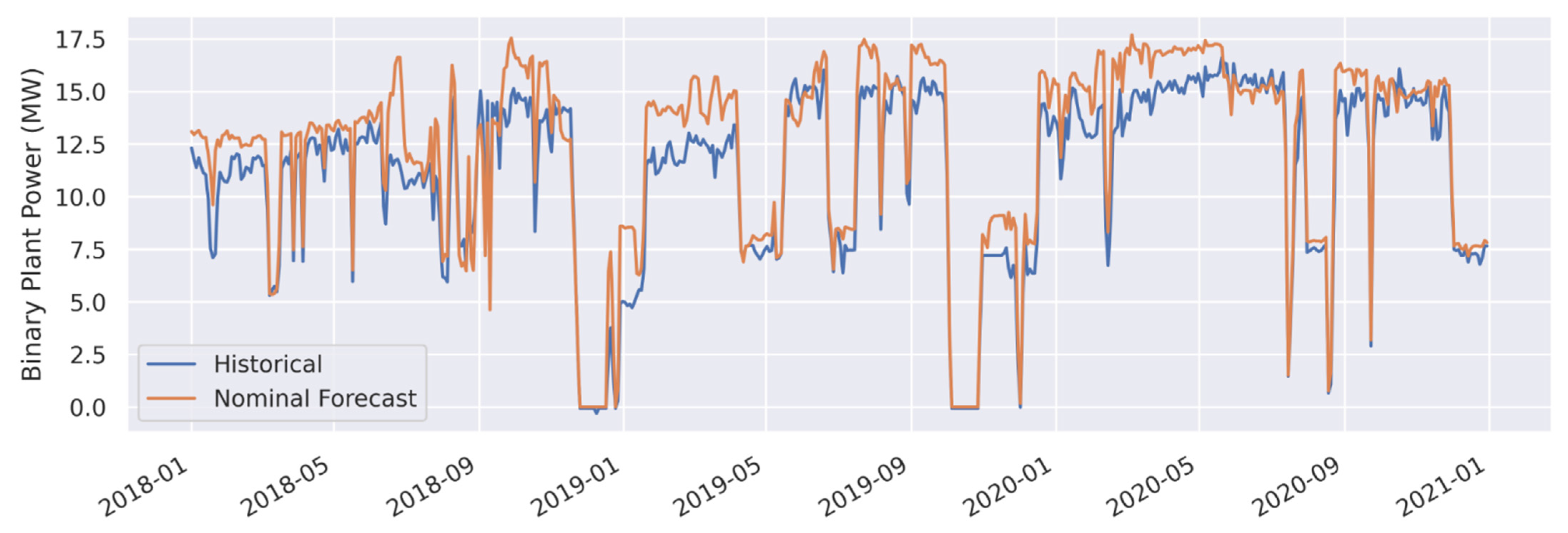
| Binary Plant Power (Gross MWe) | Nominal Forecast | 1.3 | 11.8 | 1.1 | 10.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buster, G.; Siratovich, P.; Taverna, N.; Rossol, M.; Weers, J.; Blair, A.; Huggins, J.; Siega, C.; Mannington, W.; Urgel, A.; et al. A New Modeling Framework for Geothermal Operational Optimization with Machine Learning (GOOML). Energies 2021, 14, 6852. https://doi.org/10.3390/en14206852
Buster G, Siratovich P, Taverna N, Rossol M, Weers J, Blair A, Huggins J, Siega C, Mannington W, Urgel A, et al. A New Modeling Framework for Geothermal Operational Optimization with Machine Learning (GOOML). Energies. 2021; 14(20):6852. https://doi.org/10.3390/en14206852
Chicago/Turabian StyleBuster, Grant, Paul Siratovich, Nicole Taverna, Michael Rossol, Jon Weers, Andrea Blair, Jay Huggins, Christine Siega, Warren Mannington, Alex Urgel, and et al. 2021. "A New Modeling Framework for Geothermal Operational Optimization with Machine Learning (GOOML)" Energies 14, no. 20: 6852. https://doi.org/10.3390/en14206852
APA StyleBuster, G., Siratovich, P., Taverna, N., Rossol, M., Weers, J., Blair, A., Huggins, J., Siega, C., Mannington, W., Urgel, A., Cen, J., Quinao, J., Watt, R., & Akerley, J. (2021). A New Modeling Framework for Geothermal Operational Optimization with Machine Learning (GOOML). Energies, 14(20), 6852. https://doi.org/10.3390/en14206852







