Effect of Light Irradiation on the Diffusion Rate of the Charge Carrier Hopping Mechanism in P3HT–ZnO Nanoparticles Studied by μ+SR
Abstract
1. Introduction
2. Materials and Methods
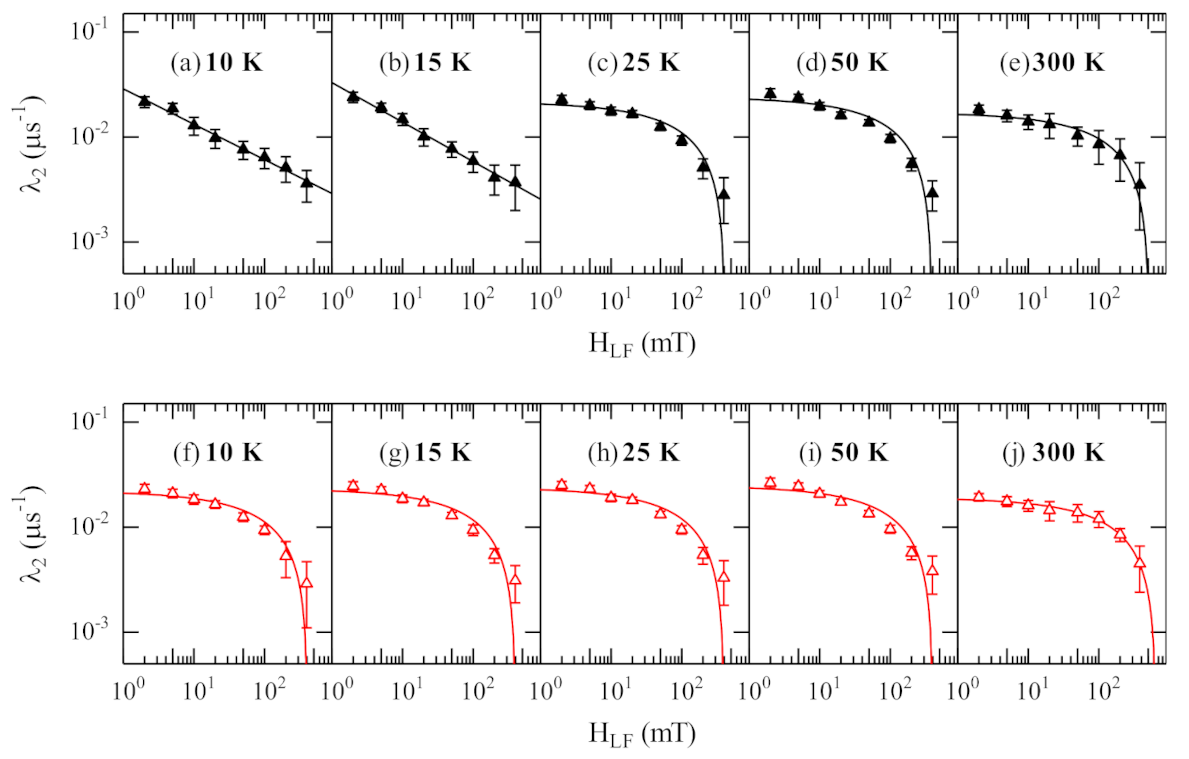
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, S.H.; Saeed, M.A.; Lee, S.Y.; Shim, J.W. Investigating the indoor performance of planar heterojunction based organic photovoltaics. IEEE J. Photov. 2021, 11, 997–1003. [Google Scholar] [CrossRef]
- Liu, R. Hybrid Organic/inorganic nanocomposites for photovoltaic cells. Materials 2014, 7, 2747–2771. [Google Scholar] [CrossRef]
- Yoshikawa, K.; Kawasaki, H.; Yoshida, W.; Irie, T.; Konishi, K.; Nakano, K.; Uto, T.; Adachi, D.; Kanematsu, M.; Uzu, H.; et al. Silicon heterojunction solar cell with interdigitated back contacts for a photoconversion efficiency over 26%. Nat. Energy 2017, 2, 17032. [Google Scholar] [CrossRef]
- Lin, Y.; Firdaus, Y.; Isikgor, F.H.; Nugraha, M.I.; Yengel, E.; Harrison, G.T.; Hallani, R.; El Labban, A.; Faber, H.; Ma, C.; et al. Self-assembled monolayer enables hole transport layer-free organic solar cells with 18% efficiency and improved operational stability. ACS Energy Lett. 2020, 5, 2935–2944. [Google Scholar] [CrossRef]
- Das, N.C.; Sokol, P.E. Hybrid photovoltaic devices from regioregular polythiophene and ZnO nanoparticles composites. Renew. Energy 2010, 35, 2683–2688. [Google Scholar]
- Quist, P.A.C.; Beek, W.J.E.; Wienk, M.M.; Janssen, R.A.J.; Savenije, T.J.; Siebbeles, L.D.A. Photogeneration and decay of charge carriers in hybrid bulk heterojunctions of ZnO nanoparticles and conjugated polymers. J. Phys. Chem. B 2006, 110, 10315–10321. [Google Scholar] [CrossRef]
- Citroni, R.; Di Paolo, F.; Livreri, P. Evaluation of an optical energy harvester for SHM application. Int. J. Electron. Commun. (AEÜ) 2019, 111, 152918. [Google Scholar] [CrossRef]
- Lin, Y.; Magomedov, A.; Firdaus, Y.; Kaltsas, D.; El-Labban, A.; Faber, H.; Naphade, D.R.; Yengel, E.; Zheng, X.; Yarali, E.; et al. 18.4% Organic solar cells using a high ionization energy self-assembled monolayer as hole-extraction interlayer. ChemSusChem 2021, 14, 3569–3578. [Google Scholar] [CrossRef]
- Pattamang, P.; Jiramitmonkon, K.; Piyakulawat, P.; Asawapirom, U.; Tantisantisom, K.; Porntheeraphat, S.; Nukeaw, J.; Pratontep, S. Photoresponse of composites of zinc oxide and poly(3-hexythiophene) under selective uv and white-light illumination. Org. Electron. 2016, 39, 105–112. [Google Scholar] [CrossRef]
- Wright, M.; Uddin, A. Solar energy materials & solar cells organic—Inorganic hybrid solar cells: A comparative review. Sol. Energy Mater. Sol. Cells 2012, 107, 87–111. [Google Scholar]
- Lee, Y.-H.; Yeh, P.-S.; Hsu, Y.-T.; Tong, Z.-H.; Chiang, C.-H. Effective control of solution self-assembly of P3HT/zinc salt complex for in situ template synthesis of P3HT/ZnO nanohybrids. Polymer 2021, 215, 123385. [Google Scholar] [CrossRef]
- Motaung, D.E.; Makgwane, P.R.; Ray, S.S. Metal oxide nanostructures-containing organic polymer hybrid solar cells: Optimization of processing parameters on cell performance. Appl. Surf. Sci. 2015, 355, 484–494. [Google Scholar] [CrossRef]
- Beek, W.J.E.; Wienk, M.M.; Janssen, R.A.J. Hybrid solar cells from regioregular polythiophene and ZnO nanoparticles. Adv. Funct. Mater. 2006, 16, 1112–1116. [Google Scholar] [CrossRef]
- Safriani, L.; Aprilia, A.; Bahtiar, A.; Risdiana; Kartawidjaja, M.; Apriani, T.; Kanazawa, K.; Furukawa, Y. Preparation of ZnO nanoparticles for blend of P3HT:ZnO Nanoparticles:PCBM thin film and its charge carrier dynamics characterization. AIP Conf. Proc. 2013, 1554, 101–104. [Google Scholar]
- Pan, J.; Chen, J.; Huang, Q.; Khan, Q.; Liu, X.; Tao, Z.; Zhang, Z.; Lei, W.; Nathan, A. Size tunable ZnO nanoparticles to enhance electron injection in solution processed QLEDs. ACS Photonics 2016, 3, 215–222. [Google Scholar] [CrossRef]
- Chapel, A.; Dkhil, S.B.; Therias, S.; Gardette, J.-L.; Hannani, D.; Poize, G.; Gaceur, M.; Shah, S.M.; Wong-Wah-Chung, P.; Videlot-Ackermann, C.; et al. Effect of ZnO nanoparticles on the photochemical and electronic stability of P3HT used in polymer solar cells. Sol. Energy Mater. Sol. Cells 2016, 155, 79–87. [Google Scholar] [CrossRef]
- Chin, Y.-M.; Lin, Y.-J.; Liu, D.-S. Enhancement of carrier mobility in poly(3-hexylthiophene) by incorporating ZnO nanoparticles. Thin Solid Films 2013, 548, 453–455. [Google Scholar] [CrossRef]
- Xu, T.; Qiao, Q. Conjugated polymer–inorganic semiconductor hybrid solar cells. Energy Environ. Sci. 2011, 4, 2700–2720. [Google Scholar] [CrossRef]
- Patidar, D.; Kaswan, A.; Saxena, N.S.; Sharma, K. Monodispersed ZnO nanoparticles and their use in heterojunction solar cell. Sci. World J. 2013, 2013, 260521. [Google Scholar] [CrossRef]
- Ebenhoch, B.; Thomson, S.A.J.; Genevicius, K.; Juška, G.; Samuel, I.D.W. Charge carrier mobility of the organic photovoltaic materials PTB7 and PC71BM and its influence on device performance. Org. Electron. 2015, 22, 62–68. [Google Scholar]
- Blundell, S.J. Spin-polarized muons in condensed matter physics. Contemp. Phys. 1999, 40, 175–192. [Google Scholar] [CrossRef]
- Pratt, F.L.; Blundell, S.J.; Jestädt, T.; Lovett, B.W.; Husmann, A.; Marshall, I.M.; Hayes, W.; Monkman, A.; Watanabe, I.; Nagamine, K.; et al. μSR of conducting and non-conducting polymers. Phys. B Condens. Matter. 2000, 289–290, 625–630. [Google Scholar] [CrossRef]
- Ishida, K.; Nagamine, K.; Shirakawa, H. Muon spin rotation and relaxation studies of undoped and iodine-doped polyacetylene. Synth. Met. 1987, 17, 429–432. [Google Scholar] [CrossRef]
- Pratt, F.L.; Valladares, R.M.; Pattenden, P.A.; Blundell, S.J.; Hayes, W.; Monkman, A.P.; Nagamine, K. μSR studies of spin excitations in poylaniline. Synth. Met. 1995, 69, 231–232. [Google Scholar] [CrossRef]
- Pratt, F.L.; Hayes, W.; Mitchell, G.R.; Rossi, B.; Kiani, M.S.; Malhotra, B.D.; Pandey, S.S.; Milton, A.; Monkman, A.P. Muon studies of conducting polymers. Synth. Met. 1993, 55, 677–684. [Google Scholar] [CrossRef]
- Risdiana; Fitrilawati; Siregar, R.E.; Hidayat, R.; Nugroho, A.A.; Tjia, M.O.; Ishii, Y.; Watanabe, I. Field and temperature dependence charge transport characteristic in regio-regular poly(3-octylthiophene-2, 5-diyl) studied by muon spin relaxation. J. Phys. Conf. Ser. 2010, 225, 012003. [Google Scholar]
- Safriani, L.; Risdiana; Fitrilawati; Bahtiar, A.; Aprilia, A.; Siregar, R.E.; Manawan, M.; Sari, D.P.; Angel, J.; Watanabe, I. μSR study with light irradiation of P3HT:ZnO nanoparticles as active material of hybrid solar cells. Mater. Sci. Forum 2019, 966, 404–408. [Google Scholar] [CrossRef]
- Safriani, L.; Risdiana; Fitrilawati; Manawan, M.; Bahtiar, A.; Aprilia, A.; Sari, D.P.; Angel, J.; Watanabe, I. Charge carrier transport in blend of P3HT and ZnO nanoparticles at low temperature studied by µSR. J. Phys. Conf. Ser. 2018, 1080, 012011. [Google Scholar] [CrossRef]
- Safriani, L.; Risdiana; Bahtiar, A.; Aprilia, A.; Siregar, R.E.; Hidayat, R.; Saragi, T.P.I.; Kawasaki, I.; Watanabe, I. Charge carrier dynamics of active material solar cell P3HT:ZnO nanoparticles studied by muon spin relaxation (μSR). Adv. Mater. Res. 2014, 896, 477–480. [Google Scholar] [CrossRef]
- Butler, M.A.; Walker, L.R.; Soos, Z.G. Dimensionality of spin fluctuations in highly anisotropic TCNQ salts. J. Chem. Phys. 1976, 64, 3592–3601. [Google Scholar] [CrossRef]
- Riveli, N.; Adiperdana, B.; Safriani, L.; Suroto, B.J.; Noviyanti, A.R.; Mohammad, I.H.; Rahayu, I.; Manawan, M.; Saragi, T.; Risdiana. Study on the diffusion rate of the charge carrier transport in regio-random P3HT. Mater. Sci. Forum 2019, 966, 471–475. [Google Scholar] [CrossRef]
- Riveli, N.; Risdiana. Study on the diffusion rate of the charge carrier transport in regio-random and regio-regular P3HT. Mater. Sci. Forum 2021, 1028, 204–209. [Google Scholar] [CrossRef]
- Mizoguchi, K. Spin dynamics study in conducting polymers by magnetic resonance. Jpn. J. Appl. Phys. 1995, 34, 1. [Google Scholar] [CrossRef]
- Meulenkamp, E.A. Synthesis and growth of ZnO nanoparticles. J. Phys. Chem. B 1998, 102, 5566–5572. [Google Scholar] [CrossRef]
- Risdiana; Fitrilawati; Hidayat, R.; Siregar, R.E.; Tjia, M.O.; Watanabe, I. µSR study of electron radical dynamics in regio-regular polythiophene. J. Phys. Conf. Ser. 2010, 200, 052024. [Google Scholar]
- Risdiana; Fitrilawati; Hidayat, R.; Siregar, R.E.; Tjia, M.O.; Watanabe, I. Intra- and inter-chain polaron diffusion in regio-random polythiophene studied by muon spin relaxation. Phys. B 2010, 405, S381. [Google Scholar] [CrossRef]
- Risdiana; Adiperdana, B.; Safriani, L.; Bahtiar, A.; Fitrilawati; Siregar, R.E.; Hidayat, R.; Nugroho, A.A.; Tjia, M.O.; Watanabe, I. μSR study of charge carrier diffusion in regioregular poly (3-butylthiophene-2,5-Diyl). Phys. Procedia 2012, 30, 97. [Google Scholar] [CrossRef][Green Version]
- Safriani, L.; Risdiana; Bahtiar, A.; Aprilia, A.; Kawasaki, I.; Watanabe, I. µSR study of charge carrier motion in active layer P3HT:ZnO:PCBM hybrid solar cells. Mater. Sci. Forum 2015, 827, 131. [Google Scholar] [CrossRef]
- Bahtiar, A.; Safriani, L.; Aprilia, A.; Risdiana; Harsojo; Triwikantoro; Darminto; Nugroho, A.A.; Guo, H.; Kawasaki, I.; et al. Study of charge carrier dynamics of P3HT:PCBM blend for active material solar cell using muon spin relaxation. Mater. Sci. Forum 2015, 827, 168–173. [Google Scholar] [CrossRef]
- Pratt, F.L. Repolarization of anisotropic muonium in orientationally disordered solids. Phil. Mag. Lett. 1997, 75, 371–380. [Google Scholar] [CrossRef]
- Pratt, F.L.; Blundell, S.J.; Lovett, B.W.; Nagamine, K.; Ishida, K.; Hayes, W.; Jestadt, T.; Monkman, A.P. Anisotropic polaron motion in conducting polymers studied by muon spin relaxation. Synth. Met. 1999, 101, 323–324. [Google Scholar] [CrossRef]
- Blundell, S.J.; Pratt, F.L.; Marshall, I.M.; Husmann, A.; Hayes, W.; Martin, R.E.; Holmes, A.B. Muon-spin relaxation study of charge carrier dynamics in the conducting polymer PPV. Synth. Met. 2001, 119, 205–206. [Google Scholar] [CrossRef]
- Pratt, F.L.; Ishida, K.; Nagamine, K.; Pattenden, P.A.; Jestadt, T.; Chow, K.H.; Blundel, S.J.; Hayes, W.; Monkman, A.P. Muon studies of spin dynamics in polyaniline. Synth. Met. 1997, 84, 943–944. [Google Scholar] [CrossRef]
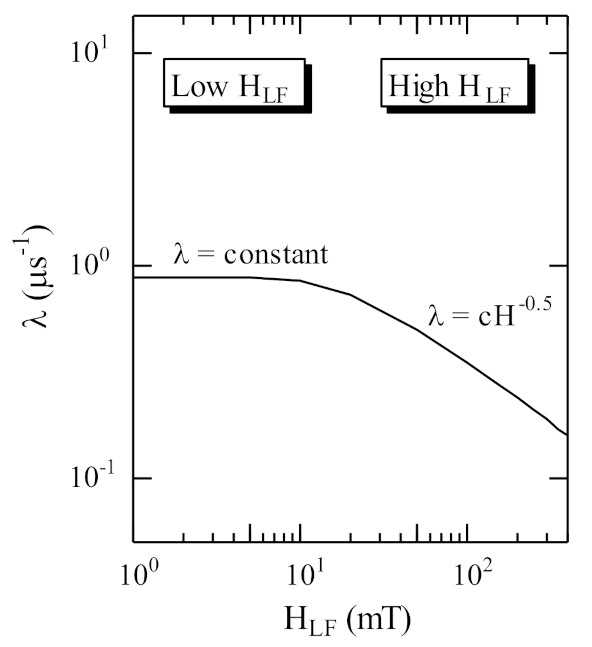
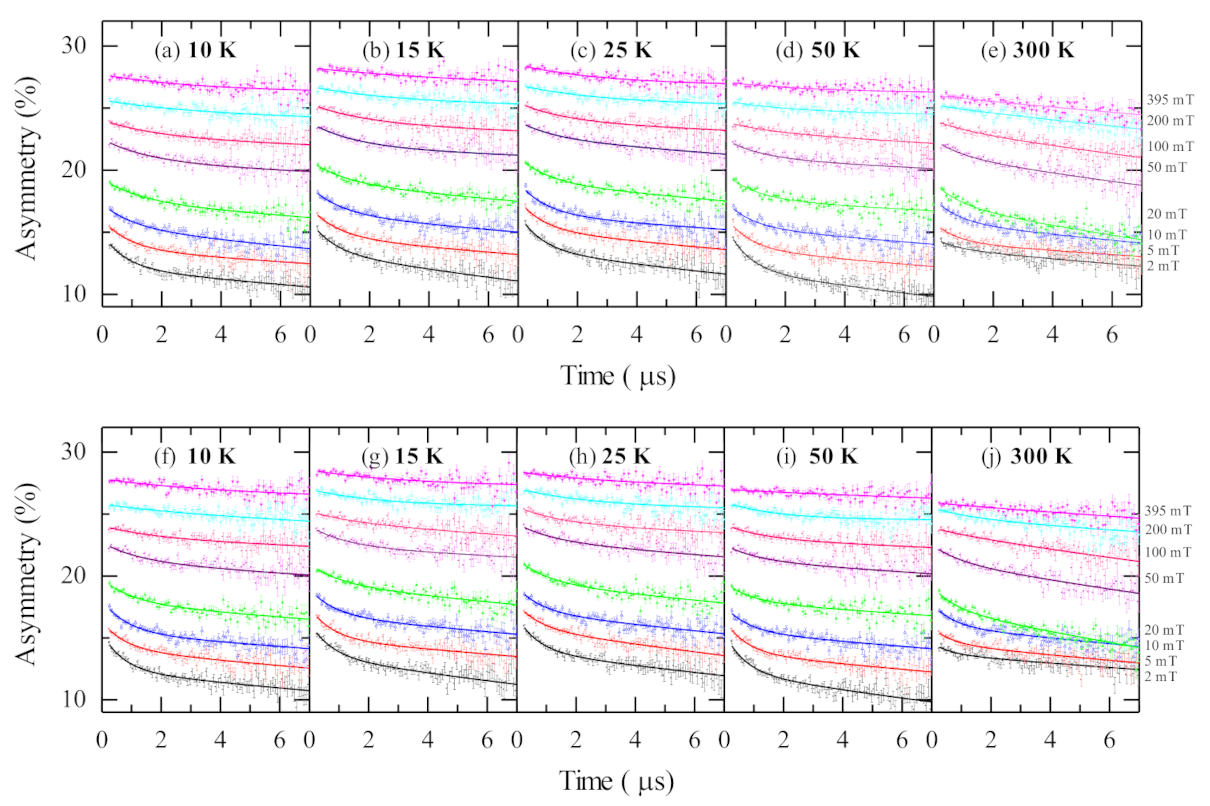
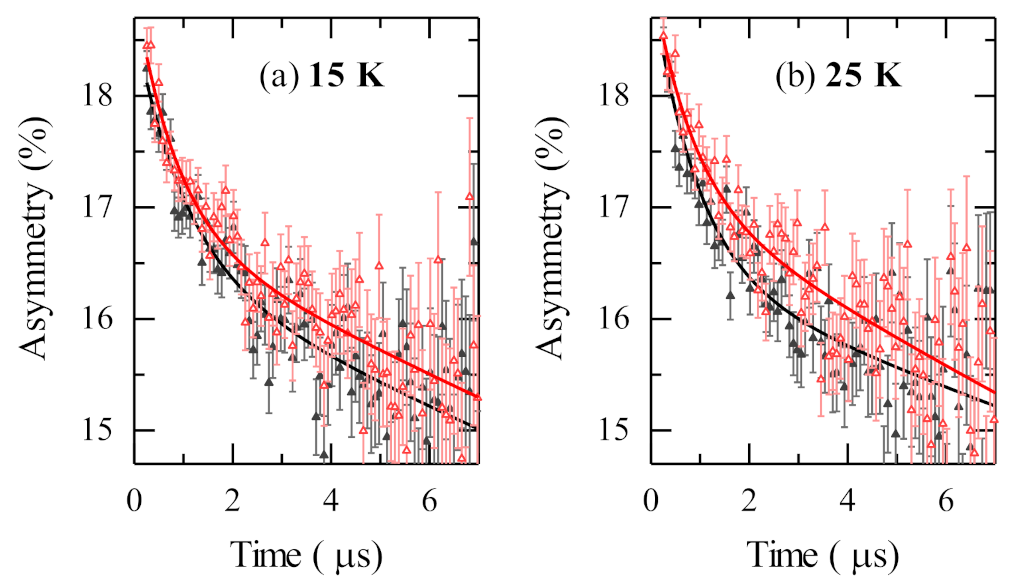
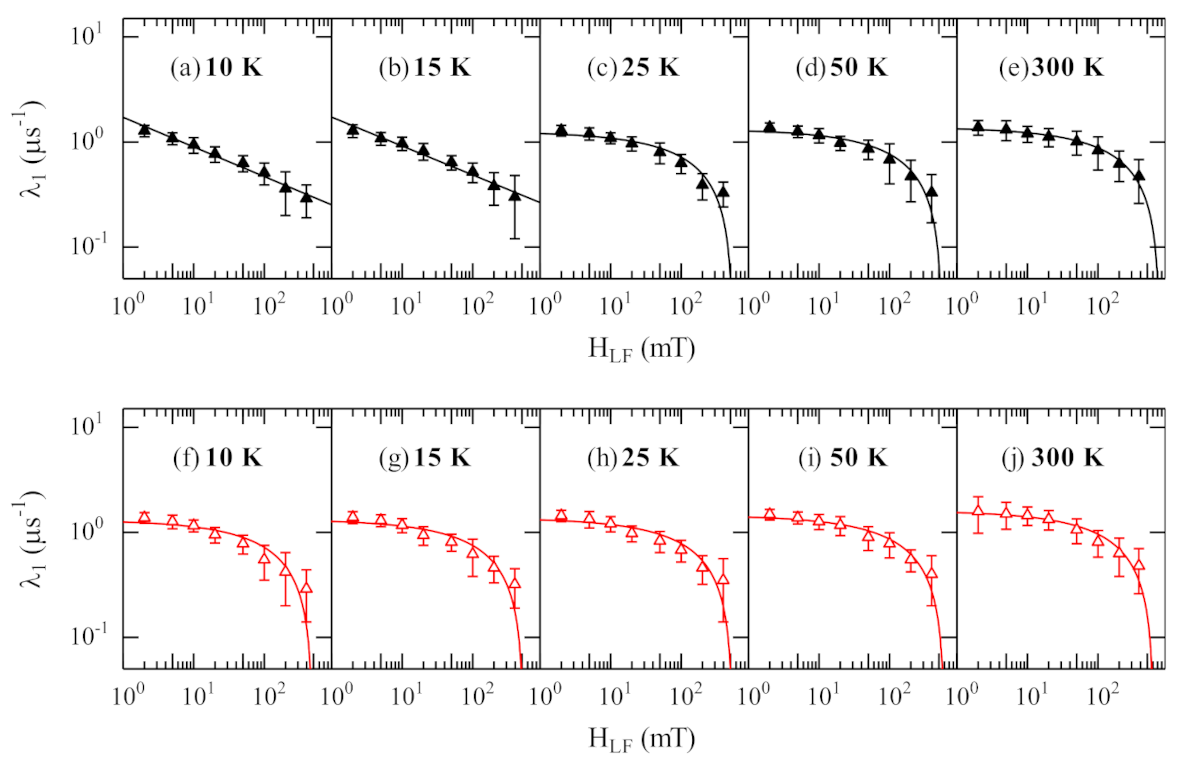
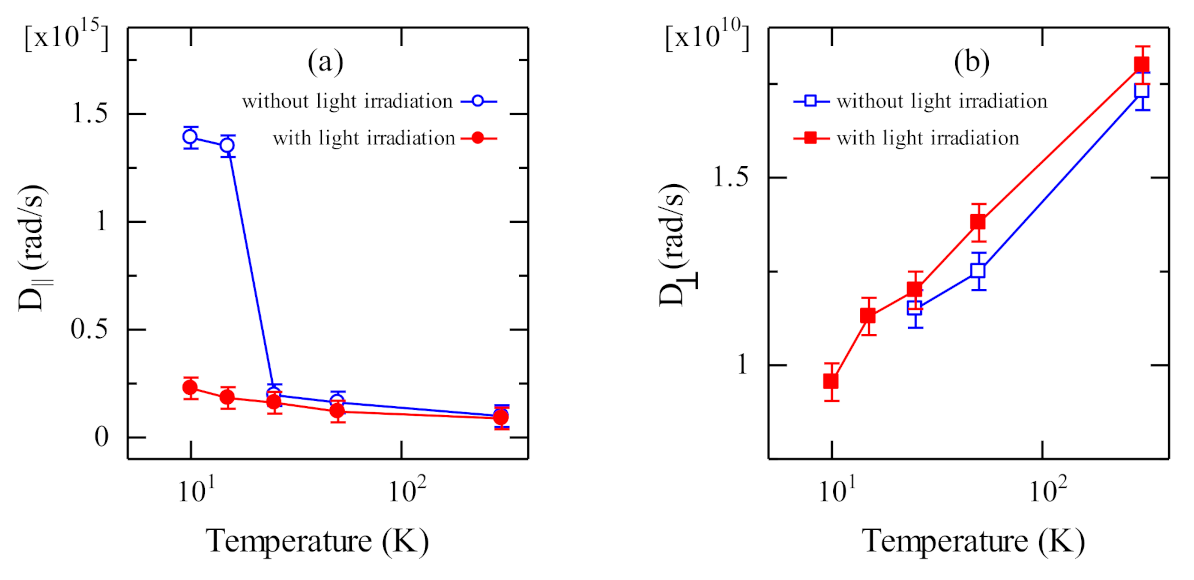
| 10 K | 15 K | 25 K | 50 K | 300 K | |
|---|---|---|---|---|---|
| (×1015 rad/s) | |||||
| (×1010 rad/s) | |||||
| (×104) |
| 10 K | 15 K | 25 K | 50 K | 300 K | |
|---|---|---|---|---|---|
| (×1014 rad/s) | |||||
| (×1010 rad/s) | |||||
| (×104) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pratikna, E.; Safriani, L.; Riveli, N.; Adiperdana, B.; Winarsih, S.; Aprilia, A.; Sari, D.P.; Watanabe, I.; Risdiana, R. Effect of Light Irradiation on the Diffusion Rate of the Charge Carrier Hopping Mechanism in P3HT–ZnO Nanoparticles Studied by μ+SR. Energies 2021, 14, 6730. https://doi.org/10.3390/en14206730
Pratikna E, Safriani L, Riveli N, Adiperdana B, Winarsih S, Aprilia A, Sari DP, Watanabe I, Risdiana R. Effect of Light Irradiation on the Diffusion Rate of the Charge Carrier Hopping Mechanism in P3HT–ZnO Nanoparticles Studied by μ+SR. Energies. 2021; 14(20):6730. https://doi.org/10.3390/en14206730
Chicago/Turabian StylePratikna, Eka, Lusi Safriani, Nowo Riveli, Budi Adiperdana, Suci Winarsih, Annisa Aprilia, Dita Puspita Sari, Isao Watanabe, and Risdiana Risdiana. 2021. "Effect of Light Irradiation on the Diffusion Rate of the Charge Carrier Hopping Mechanism in P3HT–ZnO Nanoparticles Studied by μ+SR" Energies 14, no. 20: 6730. https://doi.org/10.3390/en14206730
APA StylePratikna, E., Safriani, L., Riveli, N., Adiperdana, B., Winarsih, S., Aprilia, A., Sari, D. P., Watanabe, I., & Risdiana, R. (2021). Effect of Light Irradiation on the Diffusion Rate of the Charge Carrier Hopping Mechanism in P3HT–ZnO Nanoparticles Studied by μ+SR. Energies, 14(20), 6730. https://doi.org/10.3390/en14206730






