Prediction of Extreme Conditional Quantiles of Electricity Demand: An Application Using South African Data
Abstract
:1. Introduction
- The study carried out a comparative analysis of EM, AQR and NLQR models in predicting extremely high and low daily peak electricity demand;
- The identification of how electricity demand will change in the distribution networks in five to fifteen years going forward;
- The prediction of extremely high quantiles of DPED could help system operators know the possible largest demand that will enable them to supply adequate electricity to consumers;
- Knowing the possible largest demand of electricity at a given point in time can help system operators shift demand to off-peak periods.
2. Literature Review
3. Methodology
3.1. Semi-Parametric Extremal Mixture Models
Threshold Selection
3.2. Additive Quantile Regression Model
3.3. Nonlinear Quantile Regression
3.4. Combination of Estimated Extreme Quantiles
3.5. Scoring Rules for Quantiles
3.5.1. Continuous Ranked Probability Score
3.5.2. Logarithmic Score
3.5.3. Dawid–Sebastiani Score
3.5.4. Pinball Loss Function
3.5.5. Estimated Intervals’ Widths
4. Empirical Results
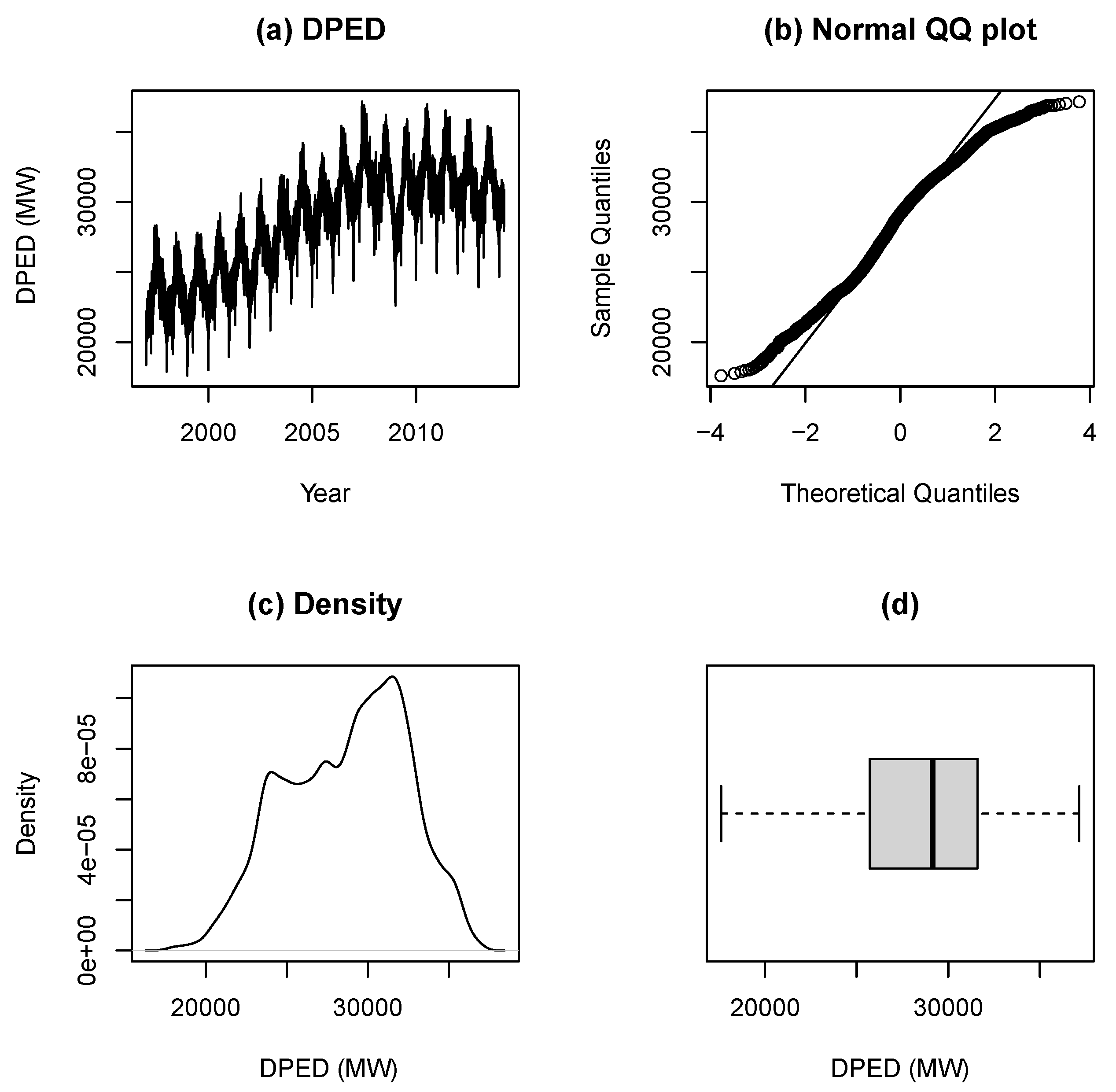
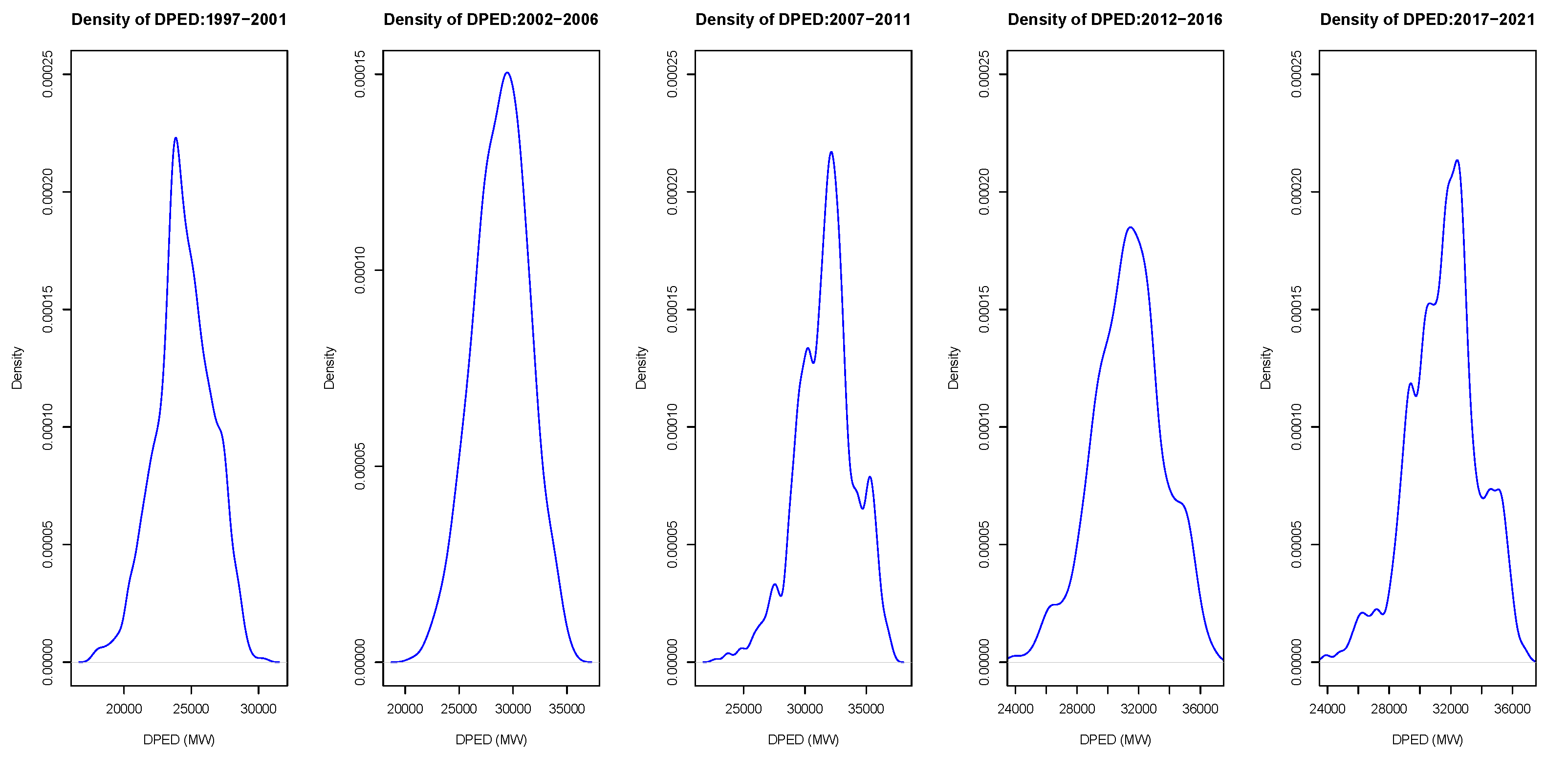
4.1. Data and Software
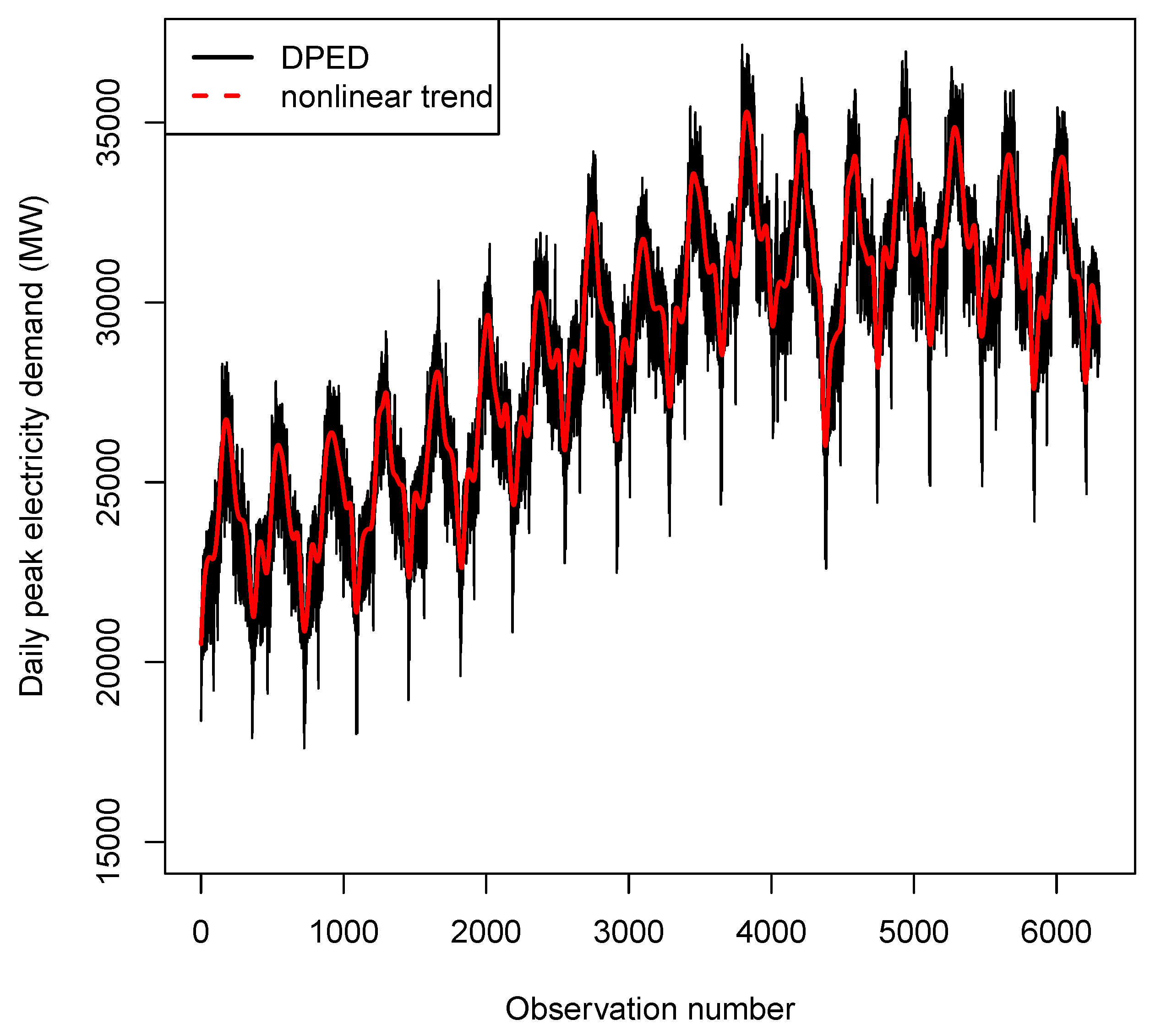
4.2. Exploratory Data Analysis
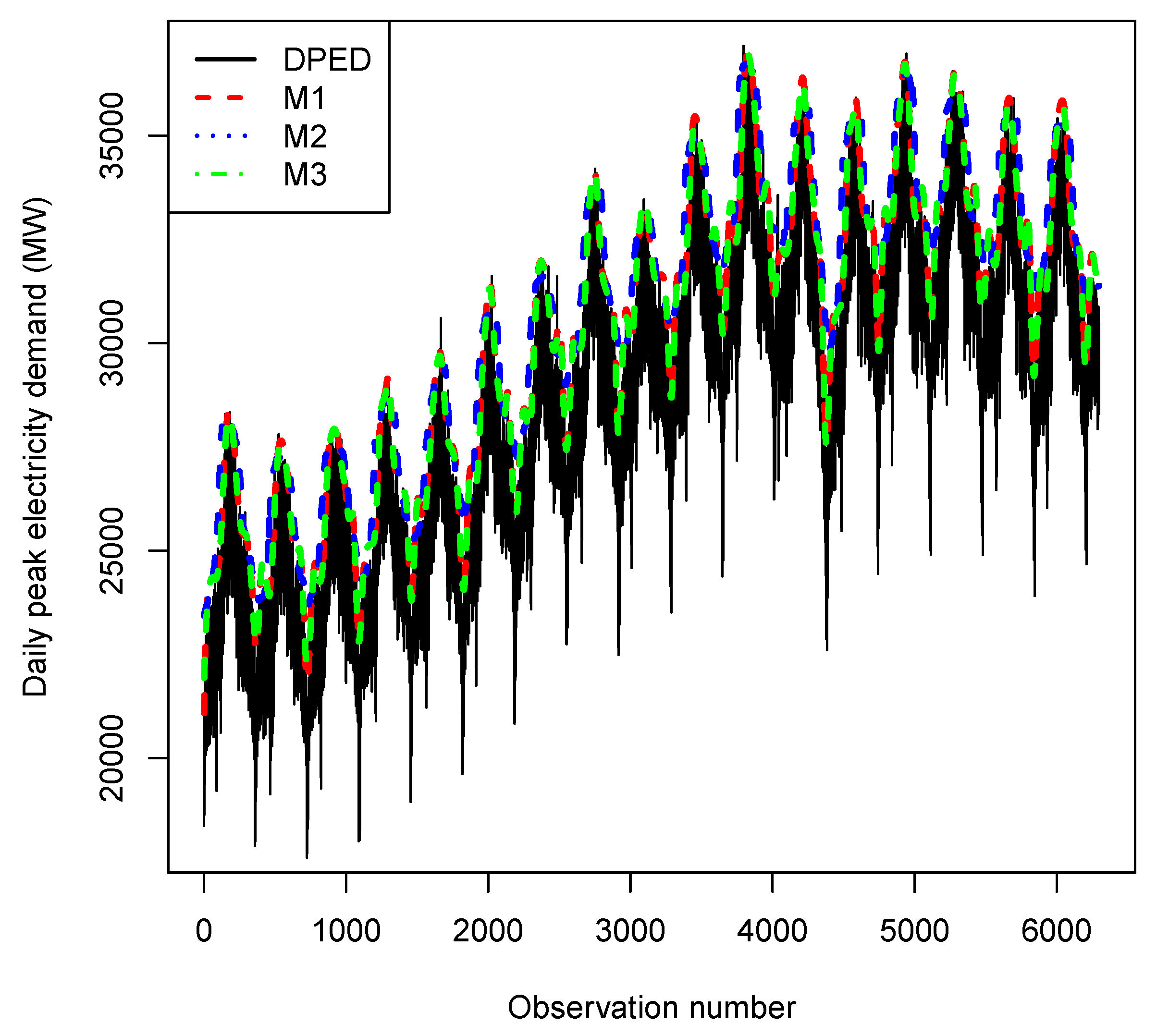
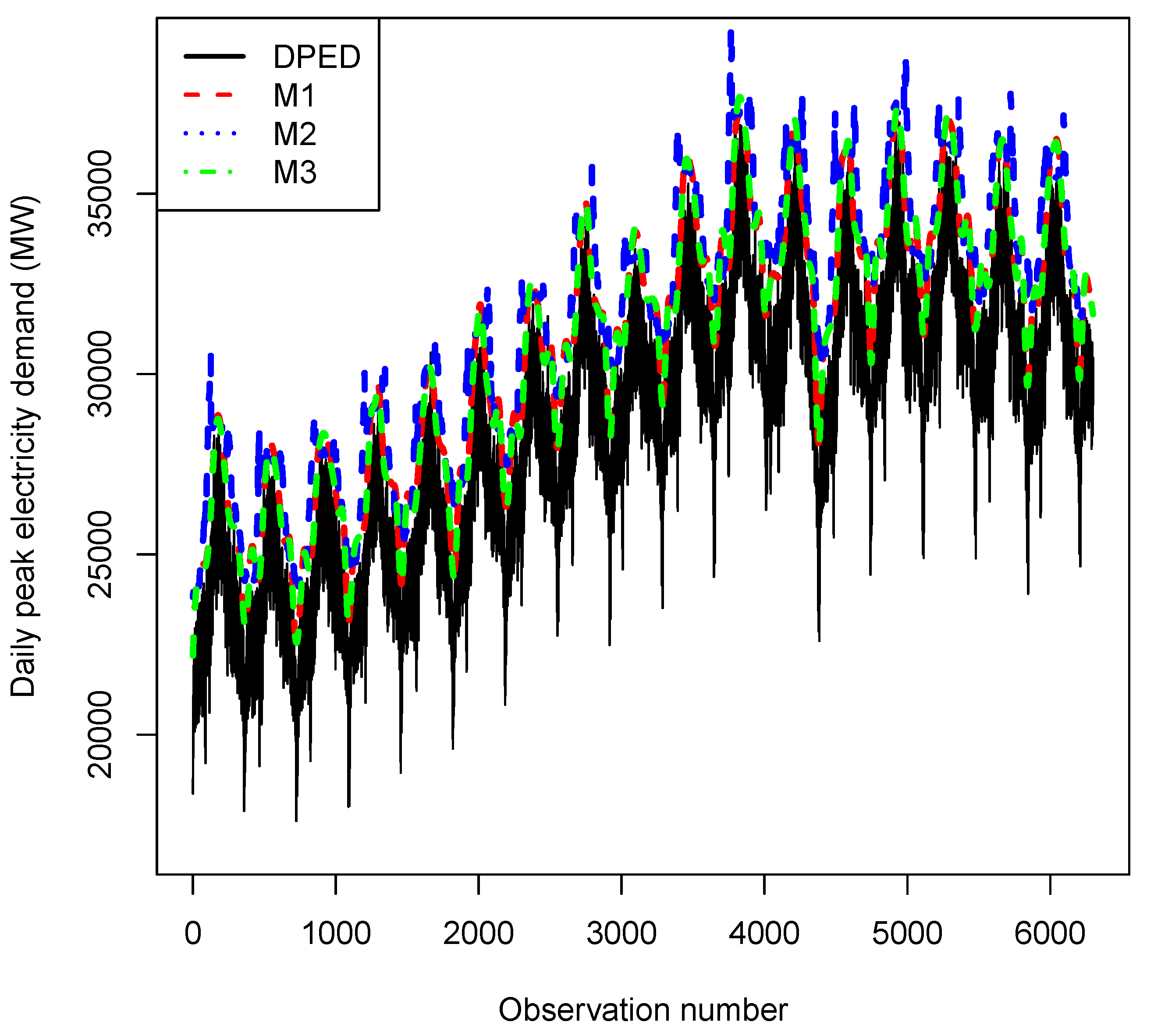
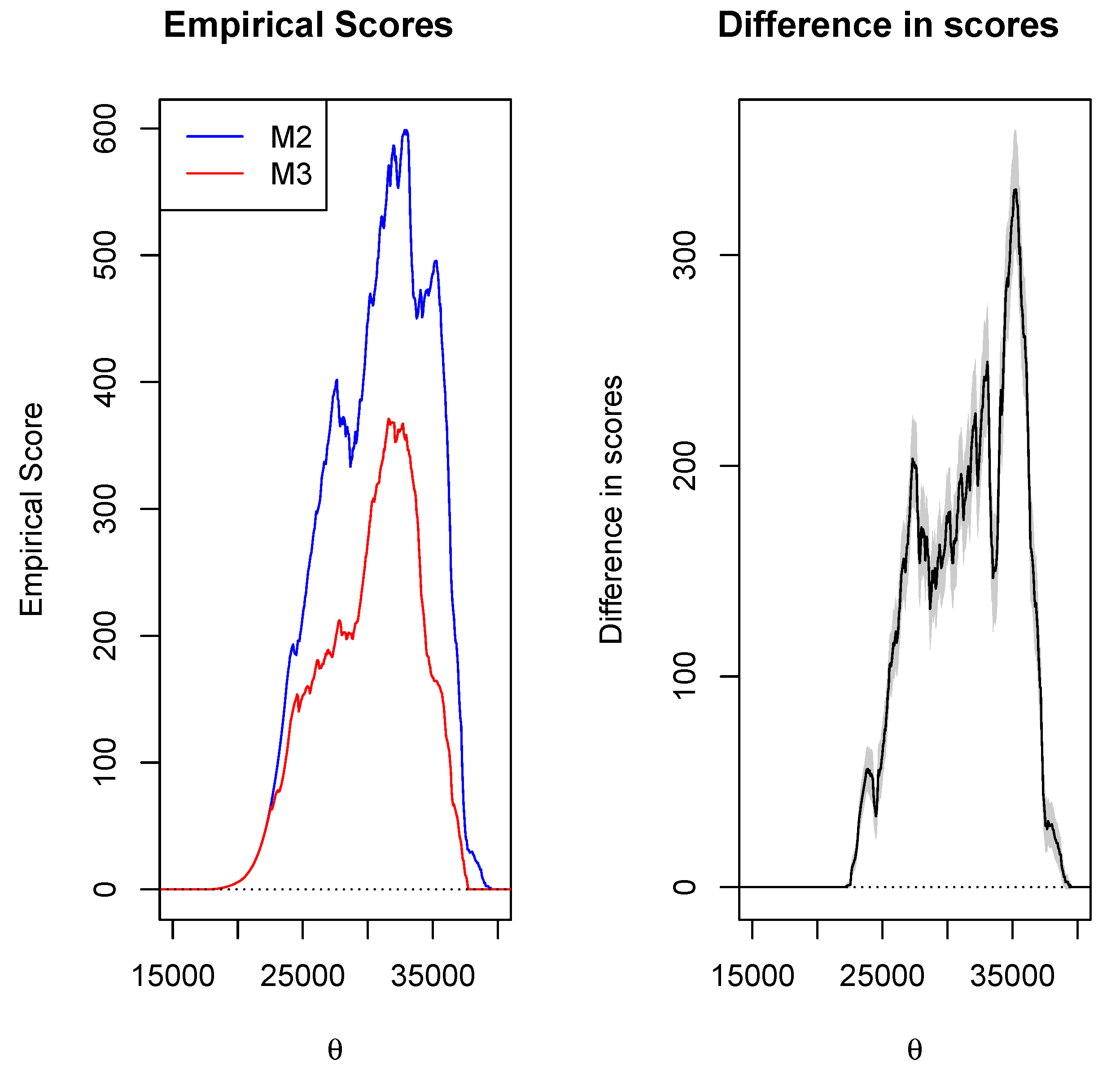
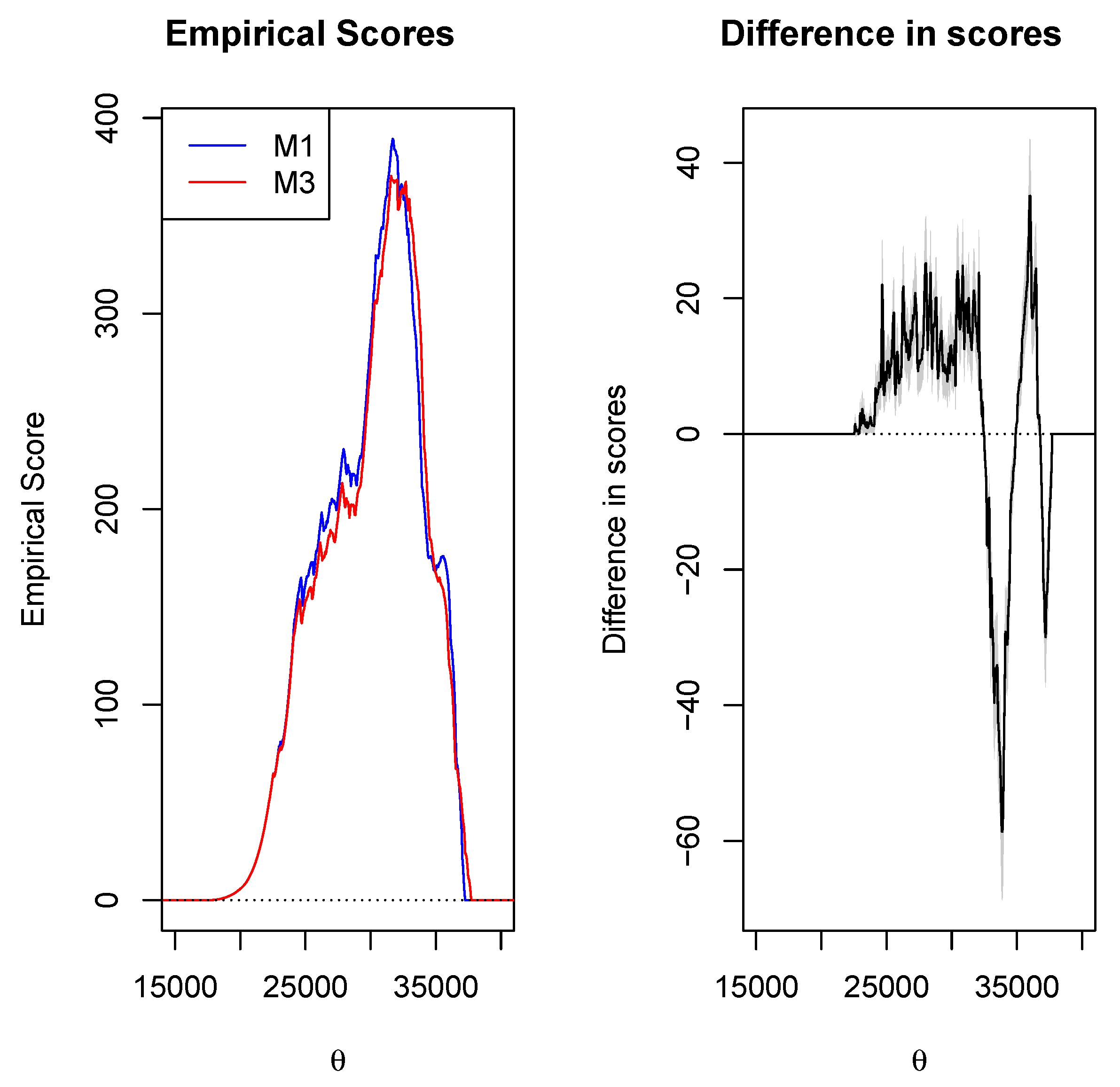
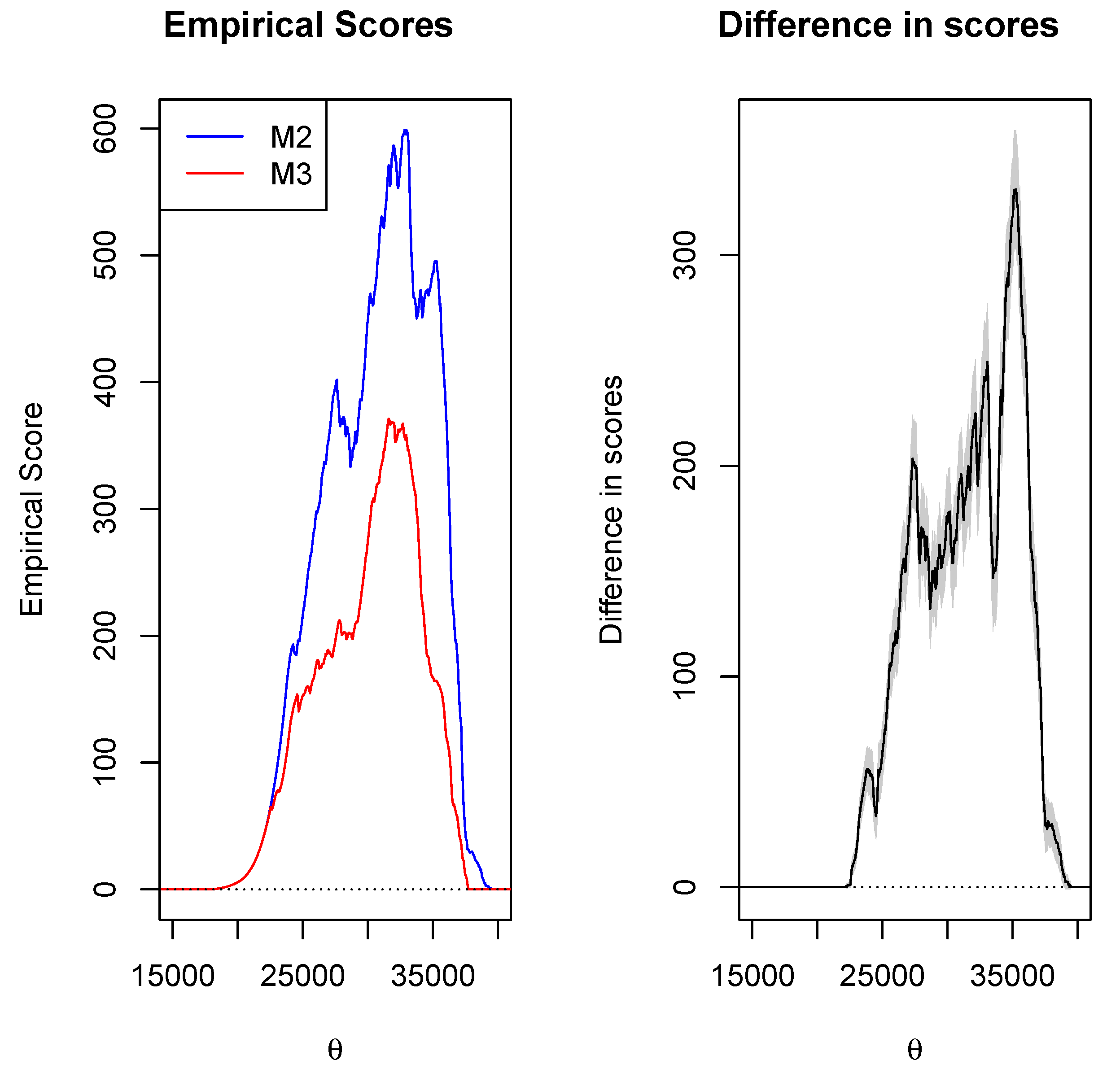
4.3. Results
5. Discussion
- Address the uncertainties that seem to be ignored in practice (for example, the uncertainty in the process that is generating the occurrence of the extreme events);
- Quantify the uncertainties in the estimated parameters of the distribution;
- Predict extremely high quantiles of daily peak electricity demand. This helps system operators know the possible largest demand, which will enable them to supply adequate electricity to consumers and shift load to off-peak periods.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AQR | Additive quantile regression |
| AR | Autoregressive |
| CDF | Cumulative distribution function |
| CP | Coverage probability |
| CRPS | Continuous rank probability score |
| DPD | Daily peak demand |
| DPED | Daily peak electricity demand |
| DSS | Dawid–Sebastiani score |
| EQR | Extreme quantile regression |
| EVT | Extreme value theory |
| GARCH | Generalized autoregressive conditional heteroskedasticity |
| GCV | Generalised cross-validation |
| GDP | Gross domestic product |
| GEVD | Generalised extreme value distribution |
| GJR | Glosten–Jagannathan–Runkle |
| GLD | Generalised logistic distribution |
| GPD | Generalised Pareto distribution |
| GSP | Generalised single Pareto distribution |
| IW | Interval width |
| Lower median | |
| LogS | Logarithmic score |
| Median | |
| MSRE | Mean-squared relative error |
| NDP | National Development Plan |
| NPOT | Nonparametric peaks-over-threshold |
| Probability density function | |
| PL | Pinball loss |
| POT | Peaks-over-threshold |
| QR | Quantile regression |
| quantGAM | Quantile generalised additive model |
| REIPPPP | Renewable Energy Independent Power Producer Program |
| Upper median | |
| USB | United States Bancorp |
References
- Larmuth, J.; Cuellar, A. An updated review of South African CSP projects under the renewable energy independent power producer procurement programme (REIPPPP). In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2019; Volume 2126, p. 040001. [Google Scholar]
- Stands, S.R. Utility-Scale Renewable Energy Job Creation: An Investigation of the South African Renewable Energy Independent Power Producer Procurement Programme (REIPPPP). Bachelor’s Thesis, Stellenbosch University, Stellenbosch, South Africa, 2015. [Google Scholar]
- Do, L.P.C. Using Quantile Regression for Modeling of Electricity Price and Demand. Master’s Thesis, NTNU, Trondheim, Norway, 2015. [Google Scholar]
- Beirlant, J.; Wet, T.D.; Goegebeur, Y. Nonparametric estimation of extreme conditional quantiles. J. Stat. Comput. Simul. 2004, 74, 567–580. [Google Scholar] [CrossRef]
- Gardes, L.; Girard, S.; Lekina, A. Functional nonparametric estimation of conditional extreme quantiles. J. Multivar. Anal. 2010, 101, 419–433. [Google Scholar] [CrossRef] [Green Version]
- Kukush, A.; Beirlant, J.; Goegebeur, Y. Nonparametric estimation of extreme conditional quantiles. In KU Leuven DTEW Research Report; Departement Toegepaste Economische Wetenschappen: Leuven, Belgium, 2005; p. 557. [Google Scholar]
- Wang, H.J.; Li, D. Estimation of extreme conditional quantiles through power transformation. J. Am. Stat. Assoc. 2013, 108, 1062–1074. [Google Scholar] [CrossRef]
- Ndao, P.; Diop, A.; Dupuy, J.F. Nonparametric estimation of the conditional extreme-value index with random covariates and censoring. J. Stat. Plan. Inference 2016, 168, 20–37. [Google Scholar] [CrossRef] [Green Version]
- Sigauke, C.; Verster, A.; Chikobvu, D. Extreme daily increases in peak electricity demand: Tail quantile estimation. Energy Policy 2013, 53, 90–96. [Google Scholar] [CrossRef]
- Diriba, T.A.; Debusho, L.K.; Botai, J. Modeling extreme daily temperature using generalized Pareto distribution at Port Elizabeth, South Africa. Annu. Proc. S. Afr. Stat. Assoc. Conf. 2015, 2015, 41–48. [Google Scholar]
- Sigauke, C.; Nemukula, M.M.; Maposa, D. Probabilistic hourly load forecasting using additive quantile regression models. Energies 2018, 11, 2208. [Google Scholar] [CrossRef] [Green Version]
- Mallor, F.; Omey, E. An introduction to statistical modelling of extreme values. Hub Res. Pap. 2009, 36, 5–31. [Google Scholar]
- Gajowniczek, K.; Zabkowski, T. Two-stage electricity demand modeling using machine learning algorithms. Energies 2017, 10, 1547. [Google Scholar] [CrossRef] [Green Version]
- Chernozhukov, V. Extremal quantile regression. Ann. Stat. 2005, 33, 806–839. [Google Scholar] [CrossRef] [Green Version]
- Lerch, S.; Thorarinsdottir, T.L.; Ravazzolo, F.; Gneiting, T. Forecaster’s dilemma: Extreme events and forecast evaluation. Stat. Sci. 2017, 32, 106–127. [Google Scholar] [CrossRef]
- Jordan, A.; Krüger, F.; Lerch, S. Evaluating probabilistic forecasts with scoringRules. arXiv 2017, arXiv:1709.04743. [Google Scholar] [CrossRef] [Green Version]
- Daouia, A.; Gardes, L.; Girard, S. On kernel smoothing for extremal quantile regression. Bernoulli 2013, 19, 2557–2589. [Google Scholar] [CrossRef]
- Durrieu, G.; Grama, I.; Pham, Q.K.; Tricot, J.M. Nonparametric adaptive estimation of conditional probabilities of rare events and extreme quantiles. Extremes 2018, 18, 437–478. [Google Scholar] [CrossRef]
- D’Haultfœuille, X.; Maurel, A.; Zhang, Y. Extremal quantile regressions for selection models and the black–white wage gap. J. Econom. 2018, 203, 129–142. [Google Scholar] [CrossRef] [Green Version]
- Smith, R.L. Extreme value analysis of environmental time series: An application to trend detection in ground-level ozone. Stat. Sci. 1989, 4, 367–377. [Google Scholar]
- Grama, I.; Spokoiny, V. Statistics of extremes by oracle estimation. Ann. Stat. 2008, 36, 1619–1648. [Google Scholar] [CrossRef]
- Nindhin, K.; Chandran, C. Importance of generalized logistic distribution in extreme value modeling. Appl. Math. 2013, 4, 560–573. [Google Scholar] [CrossRef] [Green Version]
- Sigauke, C. Modelling Electricity Demand in South Africa. Ph.D. Thesis, University of the Free State, Bloemfontein, South Africa, 2014. [Google Scholar]
- Lebotsa, M.E.; Sigauke, C.; Bere, A.; Fildes, R.; Boylan, J.E. Short term electricity demand forecasting using partially linear additive quantile regression with an application to the unit commitment problem. Appl. Energy 2018, 222, 104–118. [Google Scholar] [CrossRef] [Green Version]
- Čepin, M.; Demin, M.; Danilov, M.; Romanenko, I.; Afanasyev, V. Power System Reliability Importance Measures. In Proceedings of the 29th European Safety and Reliability Conference, Hannover, Germany, 22–26 September 2019; pp. 1633–1637. [Google Scholar]
- Sigauke, C.; Nemukula, M.M. Modelling extreme peak electricity demand during a heatwave period: A case study. Energy Systems 2020, 11, 139–161. [Google Scholar] [CrossRef]
- Norouzi, N.; de Rubens, G.Z.; Choubanpishehzafar, S.; Enevoldsen, P. When pandemics impact economies and climate change: Exploring the impacts of COVID-19 on oil and electricity demand in China. Energy Res. Soc. Sci. 2020, 68, 10165. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Ma, X.; Ma, M. A hybrid multi-objective optimizer-based model for daily electricity demand prediction considering COVID-19. Energy 2021, 2019, 119568. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Lin, Z. Impact of COVID-19 pandemic on electricity demand in the UK based on multivariate time series forecasting with bidirectional long short term memory. Energy 2021, 227, 120455. [Google Scholar] [CrossRef]
- Alasali, F.; Nusair, K.; Alhmoud, L.; Zarour, E. Impact of the COVID-19 Pandemic on Electricity Demand and Load Forecasting. Sustainability 2021, 13, 1435. [Google Scholar] [CrossRef]
- Muller, A.; Arnaud, P.; Lang, M.; Lavabre, J. Uncertainties of extreme rainfall quantiles estimated by a stochastic rainfall model and by a generalized Pareto distribution/Incertitudes des quantiles extrêmes de pluie estimés par un modèle stochastique d’averses et par une loi de Pareto généralisée. Hydrol. Sci. J. 2009, 54, 417–429. [Google Scholar] [CrossRef]
- Gardes, L.; Girard, S. Conditional extremes from heavy-tailed distributions: An application to the estimation of extreme rainfall return levels. Extremes 2010, 13, 177–204. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Reeve, D.E. Extreme value prediction via a quantile function model. Coast. Eng. 2013, 77, 91–98. [Google Scholar] [CrossRef] [Green Version]
- Chavez-Demoulin, V.; Embrechts, P.; Sardy, S. Extreme quantile tracking for financial time series. J. Econom. 2014, 181, 44–52. [Google Scholar] [CrossRef]
- Gijbels, I.; Karim, R.; Verhasselt, A. Semiparametric quantile regression using quantile-based asymmetric. Comput. Stat. Data Anal. 2020, 157. [Google Scholar] [CrossRef]
- Taylor, J.W. Evaluating quantile-bounded and expectile-bounded interval forecasts. Int. J. Forecast. 2021, 37, 800–811. [Google Scholar] [CrossRef]
- Durrieu, G.; Grama, I.; Jaunatre, K.; Pham, Q.K.; Tricot, J.M. Extremefit: A Package for Extreme Quantiles. J. Stat. Softw. 2018, 87, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Wu, G.; Qiu, W. Threshold Selection for POT Framework in the Extreme Vehicle Loads Analysis Based on Multiple Criteria. Shock Vib. 2018. [Google Scholar] [CrossRef]
- Verster, A.; De Waal, D.; van der Merwe, S. Selecting an optimum threshold with the Kullback-Leibler deviance measure. JOSA A 2013, 30, 1687–1697. [Google Scholar]
- Gaillard, P.; Goude, Y.; Nedellec, R. Additive models and robust aggregation for GEFCom 2014 probabilistic electric load and electricity price forecasting. Int. J. Forecast. 2016, 32, 1038–1050. [Google Scholar] [CrossRef]
- Fasiolo, M.; Goude, Y.; Nedellec, R.; Wood, S.N. Fast calibrated additive quantile regression. J. Am. Stat. Assoc. 2020, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Koenker, R. Quantile Regression; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- Koenker, R.; Park, B.J. An interior point algorithm for nonlinear quantile regression. J. Econom. 1996, 71, 265–283. [Google Scholar] [CrossRef] [Green Version]
- Manikandan, S. Measures of central tendency: Median and mode. J. Pharmacol. Pharmacother. 2011, 3, 214. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wei, W. Calibration Tests to Evaluate Probabilistic Forecasts and Temporal Modelling to Monitor Infectious Diseases. Ph.D. Thesis, University of Zürich, Zürich, Switzerland, 2016. [Google Scholar]
- Gneiting, T.; Katzfuss, M. Probabilistic forecasting. Annu. Rev. Stat. Appl. 2014, 1, 125–151. [Google Scholar] [CrossRef]
- Hyndman, R.J. Quantile Forecasting with Ensembles and Combinations. 2020. Available online: https://robjhyndman.com/publications/quantile-ensembles/ (accessed on 11 January 2021).
- R Core Team. R: A Language and Environment for Statistical Computing. 2021. Available online: https://www.R-project.org/ (accessed on 22 January 2021).
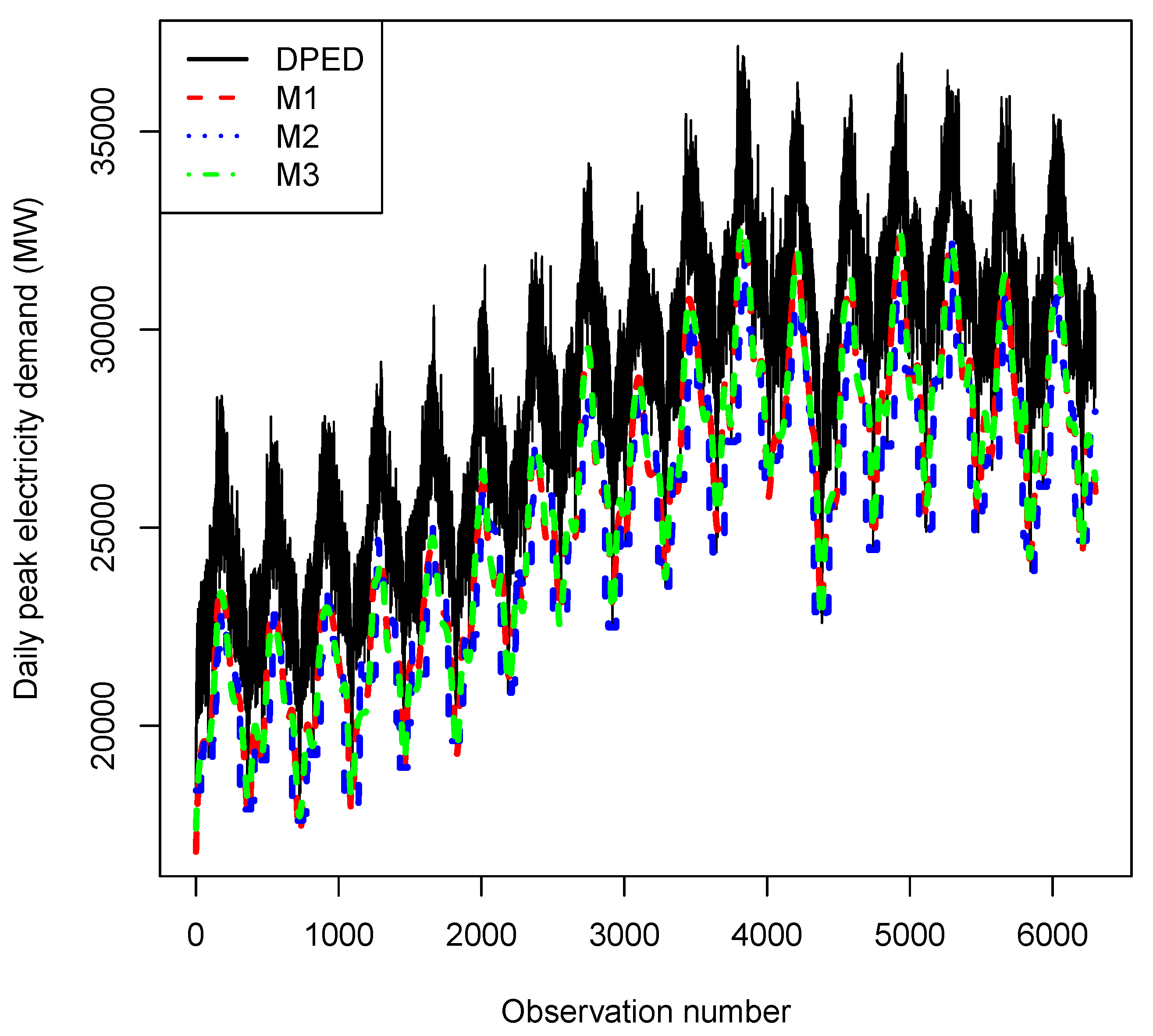
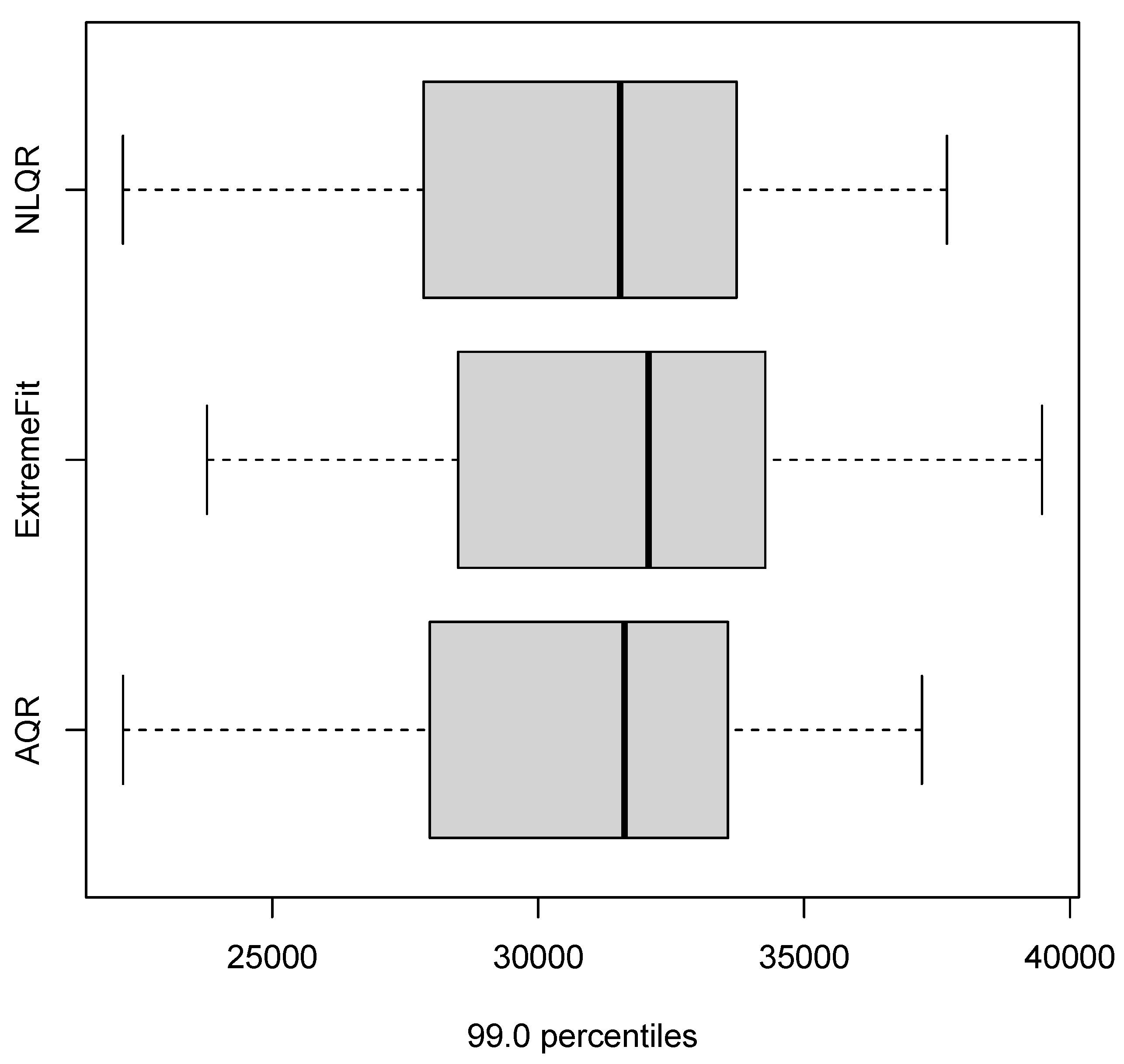
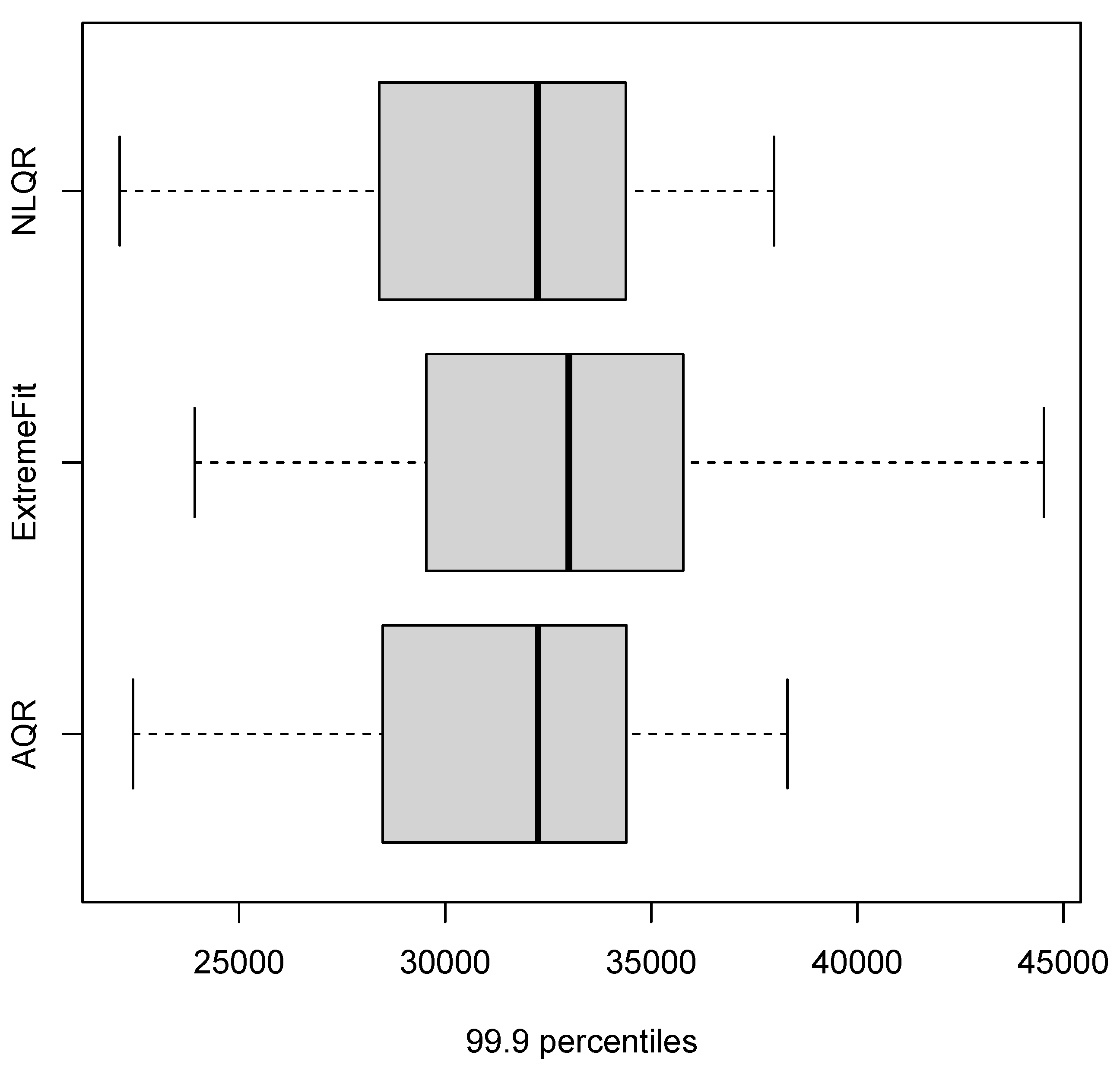
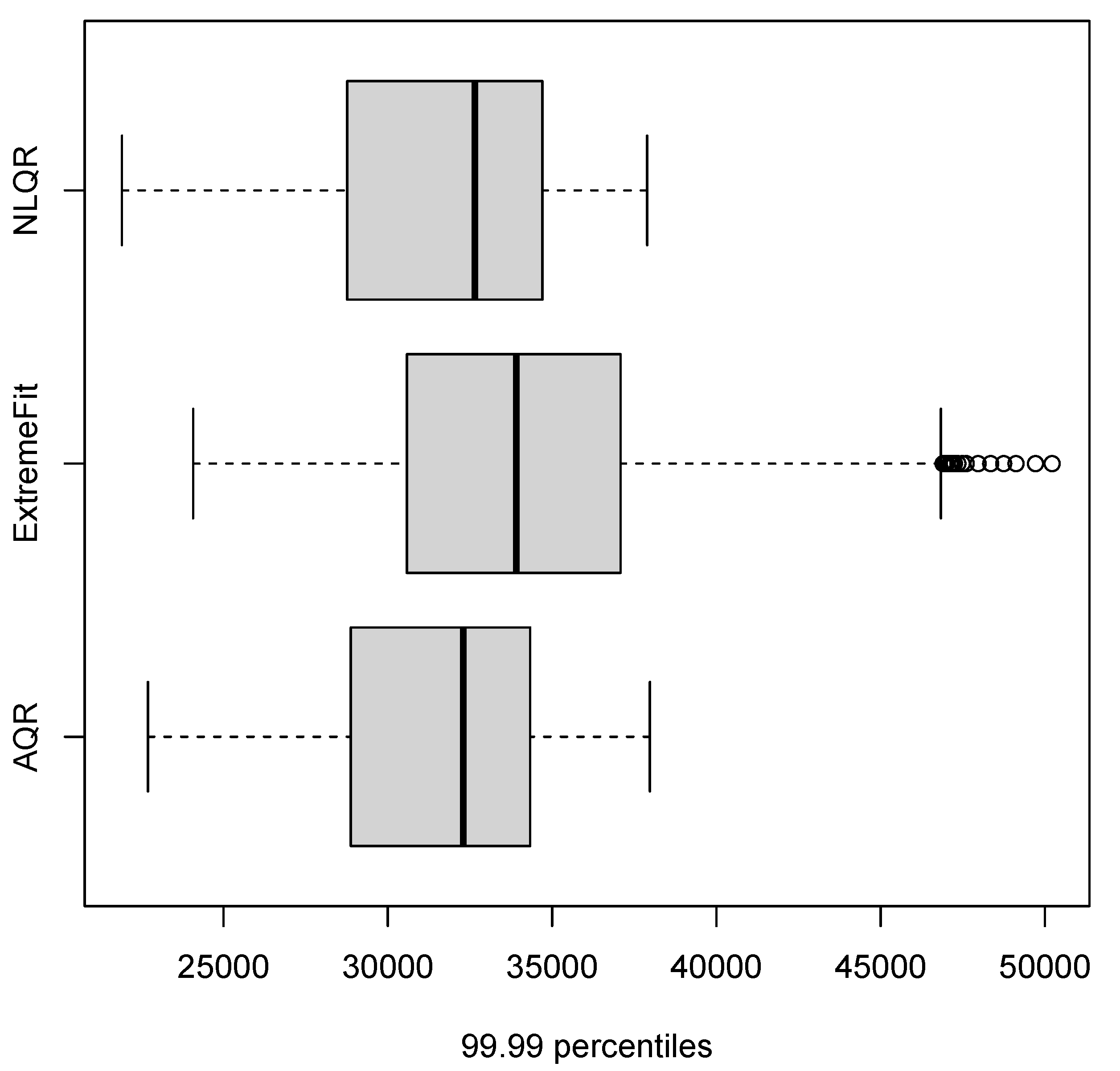
| Authors | Data | Models | Main Findings |
|---|---|---|---|
| Muller et al. [31] | Marseilles hourly rainfall data from 1882–2003 | GPD and SHYPRE hourly rainfall stochastic models. | Results show that both methods give similar results and have similar uncertainties. Moreover, the sensitivity of the GPD to the shape parameter is quite high. |
| Gardes and Girard [32] | French hourly rainfall data from 1993–2000 | Nearest neighbour model. | The results show that the nearest neighbour Hill estimator gives the same weight to all the largest observations. |
| Sigauke et al. [9] | Eskom aggregated DPD data from 2000–2011 | GSP distribution and GPD models. | The Q-Q plot of the GSP distribution incorporates most extreme observations in the tail slightly better than the GPD. |
| Cai and Reeve [33] | Venice sea-level data from 1931–1981 | Semiparametric, QR, and parametric quantile function models. | The performances of the parametric and the semiparametric approaches are very similar at the lower quantile levels. However, the performance of a quantile function modelling approach may vary from dataset to dataset at high quantile levels. |
| Chavez-Demoulin et al. [34] | USB data from 27 June 2002 to 18 May 2010 | NPOT and classical POT models. | The results of NPOT confirmed a rather precise and adapted estimation of high quantile-based risk measures for financial time series. |
| Diriba et al. [10] | Port Elizabeth weather station data from 1949–2013 | GPD model. | The GPD model for the minimum daily winter temperature shows no improvement in the parameter estimates’ precision. |
| Gijbels et al. [35] | Hurricane data from 1971–2017 | Semiparametric and nonparametric models. | The results show that the semiparametric model provides the smallest estimated prediction error compared to the nonparametric model. |
| Taylor [36] | Hourly Nord Pool market prices data from 2013–2018 | AR-GJR-GARCH and AR models. | The results show that the AR-GJR-GARCH model performs better than the AR model for both wider and narrower quantile intervals. |
| Models | Strengths | Weaknesses |
|---|---|---|
| M1 (AQR) | 1. A hybrid model that combines GAMS with QR. 2. Estimation is distribution free. 3. Robust to outliers in the response variable. | 1. Requires a smoothing function of the covariates. 2. Parameters are harder to estimate. 3. Does not give any details about the size of the high level of possible exceedances. |
| M2 (EM) | 1. Semiparametric extremal mixture model. 2. Based on one covariate, which is . | 1. Has limitations on accuracy and stability. 2. Very sensitive to numbers and the location of the measured points. |
| M3 (NLQR) | 1. Inference is performed based on large sample approximation. 2. Robust to outliers in the response variable. | 1. Requires a smoothing parameter. 2. Outliers only have an influence on quantile curves close to them, i.e., they affect extreme quantiles |
| Var | Min | Q1 | Mean | Median | Q3 | Max | Skew | Kurt |
|---|---|---|---|---|---|---|---|---|
| DPED | 17,605 | 25,706 | 28,688 | 29,149 | 31,596 | 37,158 | −0.232 | 2.287 |
| 95.0 percentiles (0.95 quantile) | ||||
| Models | CRPS | LogS | DSS | PL |
| M1 (AQR) | 2144.546 | 9.6088 | 17.4418 | 165.9795 |
| M2 (EM) | 2069.789 | 9.5560 | 17.3701 | 209.2725 |
| M3 (NLQR) | 2155.875 | 9.6116 | 17.4495 | 161.9122 |
| M4 (Median) | 2155.875 | 9.6116 | 17.4495 | 165.5629 |
| 99.0 percentiles (0.99 quantile) | ||||
| Models | CRPS | LogS | DSS | PL |
| M1 (AQR) | 2125.457 | 9.5947 | 17.4256 | 43.2765 |
| M2 (EM) | 2131.232 | inf | 17.4315 | 56.8979 |
| M3 (NLQR) | 2163.629 | inf | 17.4598 | 42.6107 |
| M4 (Median) | 2163.629 | inf | 174598 | 43.2509 |
| 99.9 percentiles (0.999 quantile) | ||||
| Models | CRPS | LogS | DSS | PL |
| M1 (AQR) | 2172.784 | inf | 17.4759 | 5.529 |
| M2 (EM) | 2426.084 | inf | 17.7509 | 7.9267 |
| M3 (NLQR) | 2190.201 | inf | 17.4958 | 5.3599 |
| M4 (Median) | 2190.201 | inf | 17.4958 | 5.4869 |
| 99.99 percentiles (0.9999 quantile) | ||||
| Models | CRPS | LogS | DSS | PL |
| M1 (AQR) | 2168.997 | inf | 17.4747 | 0.6116 |
| M2 (EM) | 2945.86 | inf | 18.3882 | 1.0272 |
| M3 (NLQR) | 2202.221 | inf | 17.5149 | 0.6053 |
| M4 (Median) | 2202.221 | inf | 17.5149 | 0.6274 |
| Interval widths for the 0.01 and 0.99 quantiles (CP = 0.98) | ||||
| Models | Ave IW | Cov Prob | Below 0.01 quantile | Above the 0.99 quantile |
| M1 (AQR) | 5364 | 0.9833 | 59 | 46 |
| M2 (EM) | 6807 | 0.9886 | 52 | 20 |
| M3 (NLQR) | 5312 | 0.9806 | 65 | 57 |
| M4 (Median) | 5385 | 0.9843 | 56 | 43 |
| 5.0 percentiles (0.05 quantile) | ||||
| Models | CRPS | LogS | DSS | PL |
| M1 (AQR) | 3826.125 | 10.3962 | 19.1919 | 226.0744 |
| M2 (EM) | 4225.651 | 10.5635 | 19.6090 | 287.7971 |
| M3 (NLQR) | 3789.174 | 10.3804 | 19.1481 | 220.9624 |
| M4 (Median) | 3789.174 | 10.3804 | 19.1481 | 224.6259 |
| 1.0 percentiles (0.01 quantile) | ||||
| Models | CRPS | LogS | DSS | PL |
| M1 (AQR) | 4529.206 | 10.6899 | 20.0098 | 64.0034 |
| M2 (EM) | 5089.073 | 10.9302 | 20.6903 | 79.2499 |
| M3 (NLQR) | 4523.984 | 10.6905 | 20.0264 | 63.6298 |
| M4 (Median) | 4523.984 | 10.6905 | 20.0264 | 64.45815 |
| 0.1 percentiles (0.001 quantile) | ||||
| Models | CRPS | LogS | DSS | PL |
| M1 (AQR) | 5050.386 | 10.9086 | 20.6212 | 7.793396 |
| M2 (EM) | 5257.614 | 11.0022 | 20.9055 | 8.342102 |
| M3 (NLQR) | 5033.644 | 10.9037 | 20.6112 | 7.756549 |
| M4 (Median) | 5033.644 | 10.9037 | 20.6112 | 7.781235 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maswanganyi, N.; Sigauke, C.; Ranganai, E. Prediction of Extreme Conditional Quantiles of Electricity Demand: An Application Using South African Data. Energies 2021, 14, 6704. https://doi.org/10.3390/en14206704
Maswanganyi N, Sigauke C, Ranganai E. Prediction of Extreme Conditional Quantiles of Electricity Demand: An Application Using South African Data. Energies. 2021; 14(20):6704. https://doi.org/10.3390/en14206704
Chicago/Turabian StyleMaswanganyi, Norman, Caston Sigauke, and Edmore Ranganai. 2021. "Prediction of Extreme Conditional Quantiles of Electricity Demand: An Application Using South African Data" Energies 14, no. 20: 6704. https://doi.org/10.3390/en14206704
APA StyleMaswanganyi, N., Sigauke, C., & Ranganai, E. (2021). Prediction of Extreme Conditional Quantiles of Electricity Demand: An Application Using South African Data. Energies, 14(20), 6704. https://doi.org/10.3390/en14206704







