Fault Diagnosis of DCV and Heating Systems Based on Causal Relation in Fuzzy Bayesian Belief Networks Using Relation Direction Probabilities
Abstract
:1. Introduction
Literature Review
- Integration of data-driven classifier, fuzzy logic, and Bayesian belief network for the combination of data-driven and knowledge-driven diagnosis: The composed diagnostic classifier in this paper includes the knowledge-driven diagnosis theories, that is, fuzzy and Bayesian theories, and data-driven diagnosis strategy based on the intelligent diagnostic classification algorithm. In offline mode, for each fault class, a Relation-Direction Probability (RDP) table is computed and stored in a fault library. In online mode, we determine the similarities between the actual RDP and the offline precomputed RDPs. The combination of BBN and fuzzy logic in our introduced method analyzes the dependencies of the signals using Mutual Information (MI) theory. The method creates a unique RDP table for each class of faults and datasets. This method can also be extended to additional faults by adding RDPs of new fault classes to the offline library. This method provides more understandability, less effort for experts, and higher diagnostic accuracy. Our strategy is less dependent on the expert knowledge and only requires the expert to define fuzzy sets and the whole process can intelligently and automatically classify the faults compared to the other knowledge-based strategies. The evaluation results show that our strategy can accurately map a fault case to the predefined fault in the library.
- Reveal of hidden and intrinsic dependencies of trends or statuses in signals over time in case of faults: In our diagnostic method, a novel strategy is introduced based on the dependency of trends (for sensors) or statuses (for actuators) in different subdomains over time. Therefore, our automatic diagnostic method can find the intrinsic and hidden dependencies of measurement signals and statuses that change concurrently over time in case of a specific fault based on mutual information and fuzzy theory. For example, if a damper stick at open status, the room temperature decreases and makes the heater stick at ON status indirectly because the heater wants to compensate for the heating load due to the damper, which is a hidden dependency between damper and heater status signal.
- Extendibility of the strategy in this paper to complex systems: Finding fault-symptoms dependencies and fault diagnosis in other knowledge-based strategies in the literature are purely based on the expert knowledge, which can be very hard or impossible if the target system is complex with many measurement signals and statuses to the limit that even the experts cannot find the exact and hidden dependencies. However, our approach can automatically find these dependencies and faults in complex systems.
- Mapping and evaluation of the novel diagnostic method for DCV and heating systems: The presented diagnostic fault model covers sensor and actuator faults to map and evaluate the integrated diagnostic method to DCV and heating systems, as an example use case.
- Experimental evaluation of the introduced diagnostic method based on FBBNs compared to deep neural network method using simulation framework: Manufacturers typically are reluctant to provide the full-set fault data. Therefore, the diagnostic method in this paper is implemented in a simulation framework that can inject any desired faults into the system [30]. The evaluation results show a convincing performance of the introduced composed method (knowledge-driven and data-driven) in fault diagnosis in this paper compared to a deep neural network (data-driven method) [31]. A review paper on the state-of-the-art [8] shows the lack of accuracy of the knowledge-driven methods.
- Accurate fault diagnosis independent of prior knowledge and historical data: The other strategies use the BBN theory, but they use historical data, repair logs, or experimental data to calculate the prior conditional probabilities. In the strategy introduced in this paper, the signals only need to be defined as continuous or discrete variables and use the fuzzy theory to categorize the signal values to create the Bayesian network.
2. System Model
- CO2 Sensor Fault: The CO2 sensor fault represents a wrong sensor reading as a constant or noisy value. For example, a constant value of 700 ppm or noisy values within the range of a subdomain from all the subdomains of a domain or attribute. However, this paper assumed the constant fault;
- Temperature Sensor Fault: This type represents a wrong sensor reading with a constant value, for example, 15 °C;
- Damper Actuator Fault: This type of fault represents a stuck-at fault where a damper is stuck at a specific position. For example, if the damper is stuck at its open position, it gets the binary value 1, which means excess low-temperature fresh air comes inside. Therefore, the inside temperature will decrease, and the heater must constantly work to compensate for the heat loss. If the damper is stuck at its closed position, then it gets the value 0, which means that the inside air temperature will increase, and the indoor CO2 concentration will pass the maximum permitted limit;
- Heater Actuator (Thermostat) Fault: This type of fault represents a stuck-at fault where the heater sticks at a specific position. For example, if the heater is stuck at its ON position, it gets the value 1, which means inside air temperature increases. If the heater is stuck at its OFF position, it gets the binary value 0, which means the inside, air temperature tends to decrease.
3. Diagnostic Classifier Based on FBBN
3.1. Data Preparation
3.2. System Attributes and Subdomain Definitions
3.3. Generating Weighted Fuzzy Data Based on Fuzzy Theory
3.4. MI and Probability of Subdomains
3.5. Joint (Intersection) Probability
3.6. Subdomains’ Relation Using MI
3.7. Conditional Probability
- P(A|B) > P(B|A) indicates the direction of dependency between A and B is from B to A. Then, P(B|A) will be eliminated, and P(A|B) will be stored in Table 8.
- P(B|A) > P(A|B) indicates the direction of dependency between A and B is from A to B. Then, P(A|B) will be eliminated, and P(B|A) will be stored in Table 8.
3.8. Relation-Direction Probabilities
3.9. Causal Relation in FBBN Using the Relation Direction Probabilities
3.10. Fault Diagnosis Classification Based on Causal Relations in FBBNs
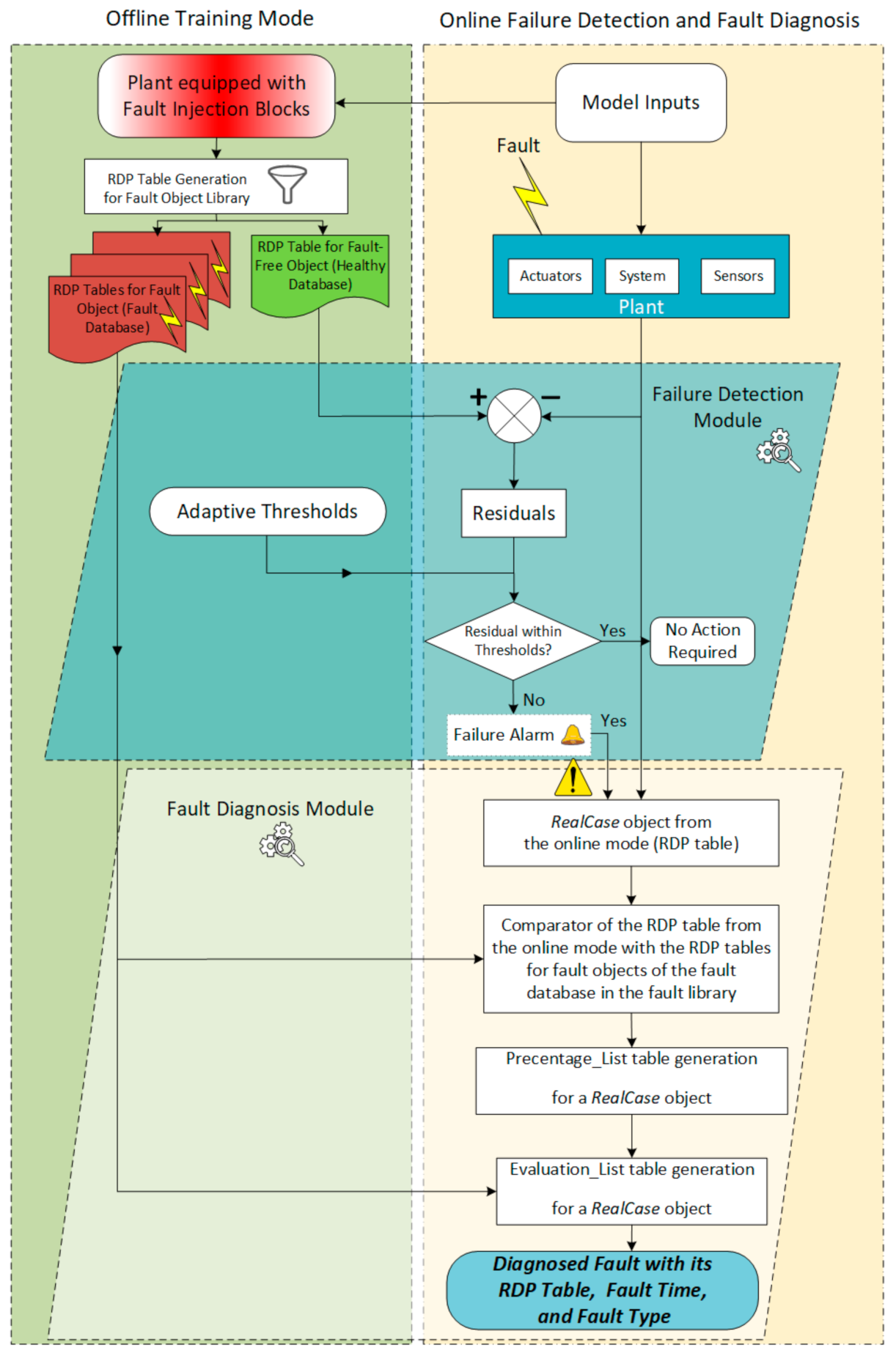
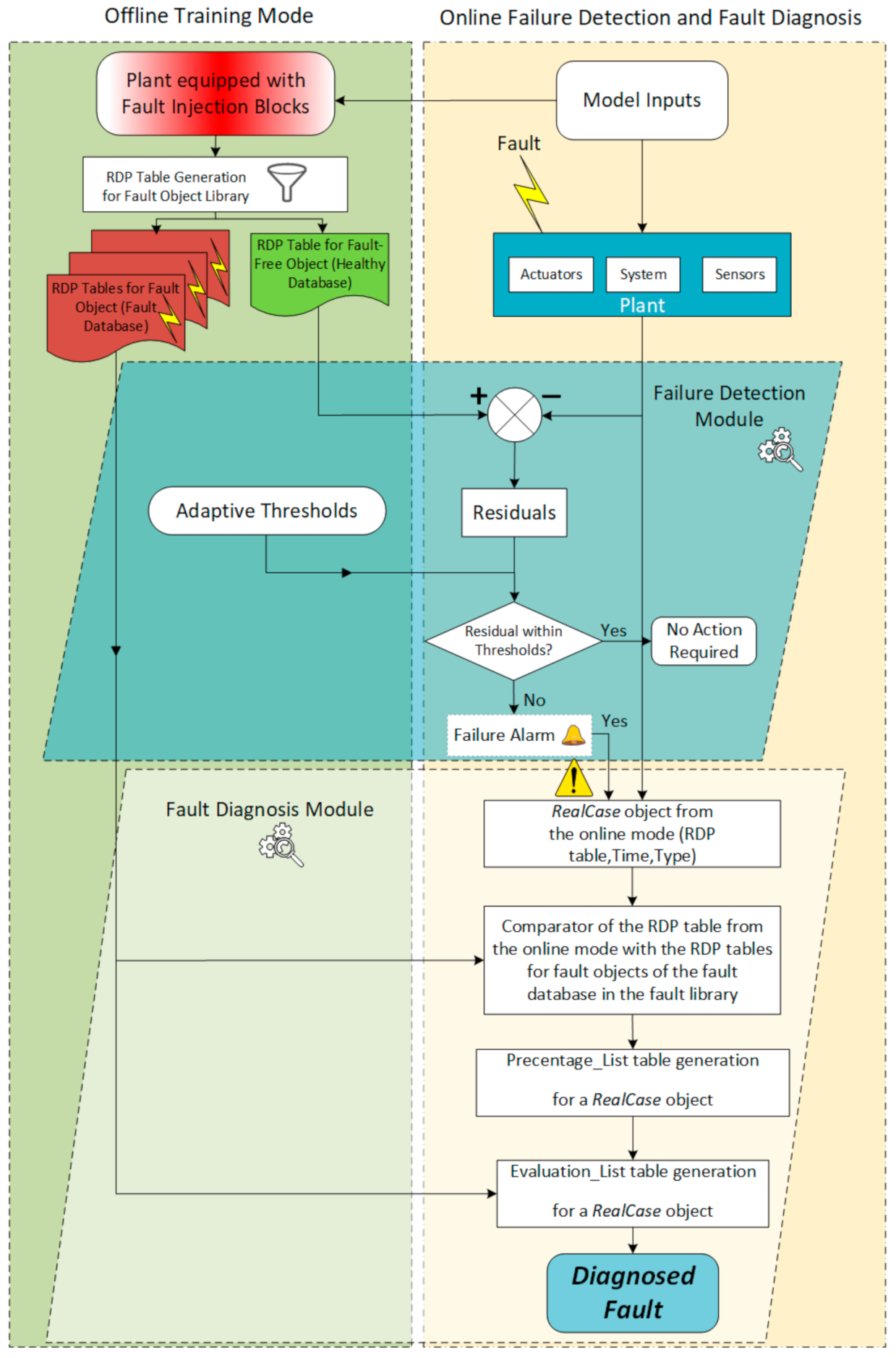
3.10.1. Offline Training Mode
3.10.2. Online Diagnostic Mode
4. Implementation of the Diagnostic Classifier Based on the Example System Model
4.1. Data Preparation in System Model
4.2. Attributes and Subdomains Preparation in System Model
4.2.1. Attributes in System Model
4.2.2. Subdomains in System Model
4.3. Fuzzy Rules in System Model
4.3.1. Fuzzy Membership Functions
4.3.2. Weighted Fuzzy Relational Data Table Based on RDT
4.4. Probability of Subdomains in System Model
4.5. (Intersection) Probability of Subdomain Pairs in System Model
4.6. Subdomains’ Relation Using MI
4.7. Conditional Probabilities
4.8. Relation Direction Probability (RDP) in Example System Model
4.9. FBBN Causal Relation Using the Relation Direction Probabilities
4.10. Fault Diagnosis in System Model
4.10.1. Offline Mode of the Fault Diagnosis in System Model
4.10.2. Online Diagnostic Mode in System Model
5. Evaluation and Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part I: Fault Diagnosis With Model-Based and Signal-Based Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef] [Green Version]
- Wu, S. System-Level Monitoring and Diagnosis of Building HVAC System; University of California: Merced, CA, USA, 2013. [Google Scholar]
- West, S.R.; Guo, Y.; Wang, X.R.; Wall, J. Automated fault detection and diagnosis of HVAC subsystems using statistical machine learning. In Proceedings of the 12th International Conference of the International Building Performance Simulation Association, Sydney, Australia, 14–16 November 2011. [Google Scholar]
- Basarkar, M.; Pang, X.; Wang, L.; Haves, P.; Hong, T. Modeling and Simulation of HVAC Faults in EnergyPlus; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 2011. [Google Scholar]
- Comstock, M.C.; Braun, J.E.; Bernhard, R. Development of Analysis Tools for the Evaluation of Fault Detection and Diagnostics in Chillers; Purdue University: West Lafayette, IN, USA, 1999. [Google Scholar]
- Wen, J.; Li, S. Tools for Evaluating Fault Detection and Diagnostic Methods for Air-Handling Units; ASHRAE RP-1312 Final Report; American Society of Heating, Refrigerating and Air Conditioning Engineers Inc.: Atlanta, GA, USA, 2011. [Google Scholar]
- Steinder, M.Ł.; Sethi, A.S. A survey of fault localization techniques in computer networks. Sci. Comput. Program. 2004, 53, 165–194. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Li, T.; Zhang, X.; Zhang, C. Artificial intelligence-based fault detection and diagnosis methods for building energy systems: Advantages, challenges and the future. Renew. Sustain. Energy Rev. 2019, 109, 85–101. [Google Scholar] [CrossRef]
- Luo, X.J.; Fong, K.F.; Sun, Y.J.; Leung, M.K. Development of clustering-based sensor fault detection and diagnosis strategy for chilled water system. Energy Build. 2019, 186, 17–36. [Google Scholar] [CrossRef]
- Tang, H.; Liu, S. Basic Theory of Fuzzy Bayesian Networks and Its Application in Machinery Fault Diagnosis. In Proceedings of the Fourth International Conference on Fuzzy Systems and Knowledge Discovery (FSKD 2007), Haikou, China, 24–27 August 2007. [Google Scholar]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann: Burlington, MA, USA, 2014. [Google Scholar]
- Qiu, S.; Agogino, A.M.; Song, S.; Wu, J.; Sitarama, S. A fusion of bayesian and fuzzy analysis for print faults diagnosis. In Proceedings of the ISCA 10th International Conference on Intelligent Systems, Arlington, VA, USA, 13–15 June 2001. [Google Scholar]
- Hu, M.; Chen, H.; Shen, L.; Li, G.; Guo, Y.; Li, H.; Li, J.; Hu, W. A machine learning Bayesian network for refrigerant charge faults of variable refrigerant flow air conditioning system. Energy Build. 2018, 158, 668–676. [Google Scholar] [CrossRef]
- Peng, D.; Geng, Z.; Zhu, Q. A multilogic probabilistic signed directed graph fault diagnosis approach based on Bayesian inference. Ind. Eng. Chem. Res. 2014, 53, 9792–9804. [Google Scholar] [CrossRef]
- Chiu, C.-Y.; Lo, C.-C.; Hsu, Y.-X. Integrating bayesian theory and fuzzy logics with case-based reasoning for car-diagnosing problems. In Proceedings of the Fourth International Conference on Fuzzy Systems and Knowledge Discovery (FSKD 2007), Haikou, China, 24–27 August 2007; pp. 344–348. [Google Scholar]
- Kuo, R.J.; Cha, C.L.; Chou, S.H.; Shih, C.W.; Chiu, C.Y. Integration of ant algorithm and case based reasoning for knowledge management. In Proceedings of the International Conference on IJIE, Busan, Korea, 1 December 2003; pp. 10–12. [Google Scholar]
- Zadeh, L.A. Information and control. Fuzzy Sets 1965, 8, 338–353. [Google Scholar]
- Gottwald, S. An early approach toward graded identity and graded membership in set theory. Fuzzy Sets Syst. 2010, 161, 2369–2379. [Google Scholar] [CrossRef]
- Yao, J.Y.; Li, J.; Li, H.; Wang, X. Modeling system based on fuzzy dynamic Bayesian network for fault diagnosis and reliability prediction. In Proceedings of the 2015 Annual Reliability and Maintainability Symposium (RAMS), Palm Harbor, FL, USA, 26–29 January 2015; pp. 1–6. [Google Scholar]
- Intan, R.; Yuliana, O.Y. Fuzzy bayesian belief network for analyzing medical track record. In Advances in Intelligent Information and Database Systems; Springer: Berlin/Heidelberg, Germany, 2010; pp. 279–290. [Google Scholar]
- Cheng, J.; Bell, D.; Liu, W. Learning Bayesian Networks from Data: An Efficient Approach Based on Information Theory. In Handbook of Systemic Autoimmune Diseases; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Mele, F.M. A Model-Based Approach to Hvac Fault Detection and Diagnosis. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, September 2012. [Google Scholar]
- Shiozaki, J.; Miyasaka, F. (Eds.) A Fault Diagnosis Tool for Hvac Systems Using Qualitative Reasoning Algorithms. In Proceedings of the Building Simulation, Kyoto, Japan, 13–15 September 1999; Volume 99. [Google Scholar]
- Shi, Z.; O’Brien, W.; Gunay, H.B. Development of a distributed building fault detection, diagnostic, and evaluation system. ASHRAE Trans. 2018, 124, 23–38. [Google Scholar]
- Zhao, Y.; Xiao, F.; Wang, S. An intelligent chiller fault detection and diagnosis methodology using Bayesian belief network. Energy Build. 2013, 57, 278–288. [Google Scholar] [CrossRef]
- Xiao, F.; Zhao, Y.; Wen, J.; Wang, S. Bayesian network based FDD strategy for variable air volume terminals. Autom. Constr. 2014, 41, 106–118. [Google Scholar] [CrossRef]
- Zhao, Y.; Wen, J.; Xiao, F.; Yang, X.; Wang, S. Diagnostic Bayesian networks for diagnosing air handling units faults—part I: Faults in dampers, fans, filters and sensors. Appl. Therm. Eng. 2017, 111, 1272–1286. [Google Scholar] [CrossRef]
- Cai, B.; Liu, Y.; Fan, Q.; Zhang, Y.; Liu, Z.; Yu, S.; Ji, R. Multi-source information fusion based fault diagnosis of ground-source heat pump using Bayesian network. Appl. Energy 2014, 114, 1–9. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Z.; Gu, X.; He, S.; Yan, Z. Feature selection based on Bayesian network for chiller fault diagnosis from the perspective of field applications. Appl. Therm. Eng. 2018, 129, 674–683. [Google Scholar] [CrossRef]
- Behravan, A.; Obermaisser, R.; Abboush, M. Fault Injection Framework for Demand-Controlled Ventilation and Heating Systems Based on Wireless Sensor and Actuator Networks: BEST PAPER AWARD. In Proceedings of the 2018 IEEE 9th Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON), Vancouver, BC, Canada, 1–3 November 2018; pp. 525–531. [Google Scholar]
- Behravan, A.; Abboush, M.; Obermaisser, R. Deep Learning Application in Mechatronics Systems’ Fault Diagnosis, a Case Study of the Demand-Controlled Ventilation and Heating System. In Proceedings of the 2019 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 26 March 2019–10 April 2019; pp. 1–6. [Google Scholar]
- Avizienis, A.; Laprie, J.-C.; Randell, B.; Landwehr, C. Basic concepts and taxonomy of dependable and secure computing. IEEE Trans. Dependable Secur. Comput. 2004, 1, 11–33. [Google Scholar] [CrossRef] [Green Version]
- Lee, E.A.; Seshia, S.A. Introduction to Embedded Systems: A Cyber-Physical Systems Approach; MIT Press: Cambridge, UK; Cambridge, MA, USA; London, UK, 2017. [Google Scholar]
- Behravan, A.; Mallak, A.; Obermaisser, R.; Basavegowda, D.H.; Weber, C.; Fathi, M. Fault injection framework for fault diagnosis based on machine learning in heating and demand-controlled ventilation systems. In Proceedings of the 2017 IEEE 4th International Conference on Knowledge-Based Engineering and Innovation (KBEI): Iran University of Science and Technology, Tehran, Iran, 22 December 2017; pp. 273–279. [Google Scholar]
- Craig, W.C. Zigbee: Wireless control that simply works. Zigbee Alliance ZigBee Alliance. 2004. Available online: https://www.semanticscholar.org/paper/Zigbee-%3A-%E2%80%9C-Wireless-Control-That-Simply-Works-%E2%80%9D-Craig/4d79defee6653ff9109c13446b87a2b92f4e009d (accessed on 5 August 2021).
- Isermann, R. Fault-Diagnosis Systems: An Introduction from Fault Detection to Fault Tolerance; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Muhammed, T.; Shaikh, R.A. An analysis of fault detection strategies in wireless sensor networks. J. Netw. Comput. Appl. 2017, 78, 267–287. [Google Scholar] [CrossRef]
- Behravan, A.; Obermaisser, R.; Nasari, A. Thermal dynamic modeling and simulation of a heating system for a multi-zone office building equipped with demand controlled ventilation using MATLAB/Simulink. In Proceedings of the 2017 International Conference on Circuits, System and Simulation (ICCSS), London, UK, 14–17 July 2017; pp. 103–108. [Google Scholar]
- Behravan, A.; Obermaisser, R.; Basavegowda, D.H.; Meckel, S. Automatic model-based fault detection and diagnosis using diagnostic directed acyclic graph for a demand-controlled ventilation and heating system in Simulink. In Proceedings of the 2018 Annual IEEE International Systems Conference (SysCon), Vancouver, BC, Canada, 23–26 April 2018; pp. 1–7. [Google Scholar]
- Mutual Information. Available online: https://en.wikipedia.org/wiki/Mutual_information (accessed on 5 August 2021).
- Zeng, G. A unified definition of mutual information with applications in machine learning. Math. Probl. Eng. 2015, 2015, 201874. [Google Scholar] [CrossRef]
- Grandini, M.; Bagli, E.; Visani, G. Metrics for multi-class classification: An overview. arXiv 2020, arXiv:2008.05756. [Google Scholar]
- ThresholdTom. A Confusion Matrix with Predicted Positives in Red and Predicted Negatives in Blue. Available online: https://commons.wikimedia.org/wiki/File:ConfusionMatrixRedBlue.png (accessed on 7 September 2021).
- Makhoul, J.; Kubala, F.; Schwartz, R.; Weischedel, R. Performance measures for information extraction. In Proceedings of DARPA Broadcast News Workshop; Morgan Kaufmann: Burlington, MA, USA, 1999; pp. 249–252. [Google Scholar]
- Frank, S.M.; Lin, G.; Jin, X.; Singla, R.; Farthing, A.; Zhang, L.; Granderson, J. Metrics and Methods to Assess Building Fault Detection and Diagnosis Tools; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2019. [Google Scholar]
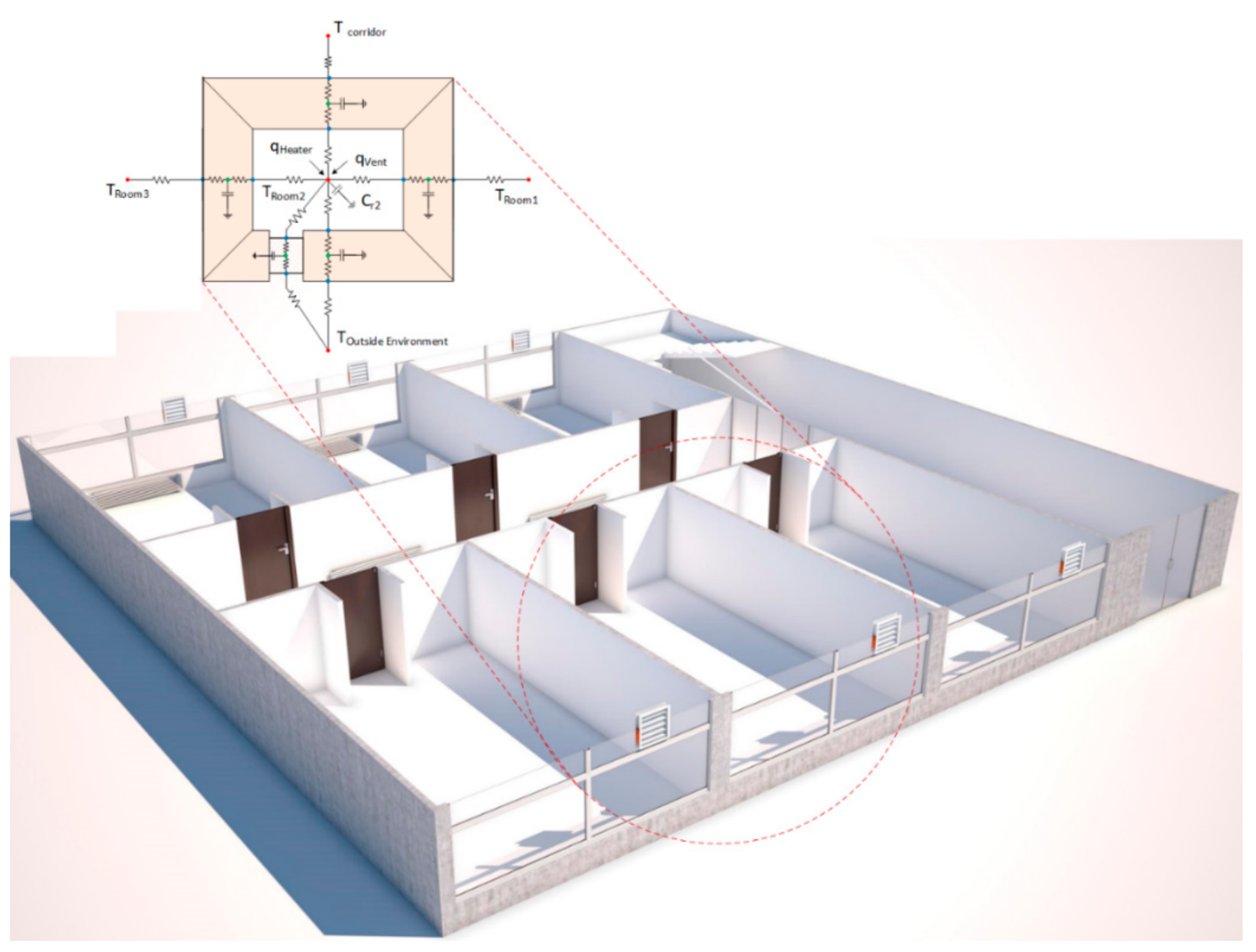



















| Related Works | Application Domain | FDD Method | Approach (e.g., Fuzzy Logic, BBN, Clustering, NN, Classification, …) | Data Collection, e.g., (Simulation/Historical Data) | Diagnostic Method | Assessment (e.g., Accuracy, Understandability, and Effort) | |
|---|---|---|---|---|---|---|---|
| Knowledge-Driven Method (Yes/No) | Data-Driven Method (Yes/No) | ||||||
| Luo et al. [9] | SFDD for chilled water system | Yes | Clustering-based SFDD & Data-Base Gathering Based on Centroid Score (CS) | Real sample information data | No | Yes | Low Expert Effort Low Understandability High Accuracy |
| Qiu et al. [12] | FDD for Printers and print defects | Yes | BBN and fuzzy logic | Expert knowledge, e.g., repair data log | Yes | No | High Expert Effort High Understandability Low Accuracy |
| Tang et al. [10] | FBN in Machinery Fault Diagnosis | Yes | BN and fuzzy logic | Expert Data | Yes | No | High Expert Effort High Understandability Low Accuracy |
| Hu et al. [13] | Refrigerant charge faults of variable refrigerant flow air conditioning system | Yes | Machine learning and Bayesian network | Training data | Yes | Yes | Low Expert Effort High Understandability High Accuracy |
| Peng et al. [14] | 1. A continuous stirred tank heater (CSTH) process 2. A Tennessee Eastman (TE) process | Yes | Multi-logic probabilistic Signed Directed Graph (MSDG) & BN | Historical Data | Yes | No | High Expert Effort High Understandability Low Accuracy |
| Chiu et al. [15] | Car-diagnosing Problems | Yes | Fuzzy logic, Bayesian classifier (with Case-Based Reasoning (CBR)) | Collecting Cases by Experts | Yes | Yes | Low Expert Effort High Understandability High Accuracy |
| Yao et al. [19] | Fault Diagnosis and Reliability Prediction in complex systems (large aircraft equipment) | Yes | Fuzzy logic, Dynamic Bayesian Network (DBN) | Based on observed system, fault statistics and the fuzzy failure probabilities of root nodes | Yes | No | High Expert Effort High Understandability Low Accuracy |
| Zhao et al. [25] | Chiller fault detection | Yes | Bayesian Belief Network (BBN) | Historical Data, Maintenance, Repair log and Expert Knowledge. | Yes | No | High Expert Effort High Understandability Low Accuracy |
| Xiao et al. [26] | Variable Air Volume (VAV) terminals | Yes | Bayesian Network (BN) | Obtained from measurements in building management systems (BMSs) and manual tests | Yes | No | High Expert Effort High Understandability Low Accuracy |
| Cai et al. [28] | Fault diagnosis of ground-source heat pump | Yes | Combination of two Bayesian networks (BN) | Data Based on sensor data and observed information of human being | Yes | No | High Expert Effort High Understandability Low Accuracy |
| Zhao et al. [27] | Air Handling Units (AHUs) in buildings | Yes | Bayesian Belief Network (BBN) | Fault patterns resulted from literature and three AHU fault detection and diagnosis (FDD) projects. | Yes | No | High Expert Effort High Understandability Low Accuracy |
| Intan et al. [20] | Analyzing Medical Track Records | No | Fuzzy logic, BBN based on (MI) | Historical Data | Yes | No | High Expert Effort High Understandability Low Accuracy. |
| Behravan et al. (This Paper) | FDFD in HAVC (DCV and heating) systems | Yes | Fuzzy Logic, BBN Based on Mutual Information (MI), Data-driven Classification | Simulation and Observed Data | Yes | Yes | Low Expert Effort, Low effort for data gathering High Understandability High Accuracy. |
| Samples | Attribute1 | Attribute2 | Attribute3 | Attributem |
|---|---|---|---|---|
| S1 | Value11 | Value12 | Value13 | Value1m |
| S2 | Value 21 | Value 22 | Value23 | Value2m |
| Sn | Valuen1 | Valuen2 | Valuen3 | Valuenm |
| No. | Attributes | Subdomains | Subdomains | Subdomains |
|---|---|---|---|---|
| 1 | Attribute1 | Subdomain11 | Subdomain12 | Subdomain1n |
| 2 | Attribute2 | Subdomain21 | Subdomain22 | Subdomain2e |
| n | Attributen | Subdomainn1 | Subdomainn2 | Subdomainnf |
| Attribute1 | Attribute2 | |||||||
|---|---|---|---|---|---|---|---|---|
| No. of Records | Subdomain11 | Subdomain12 | … | Subdomain1m | Subdomain21 | Subdomain22 | … | Subdomain2e |
| 1 | W11 | W12 | … | W1m | W11 | W12 | … | W1e |
| 2 | W21 | W22 | … | W2m | W21 | W22 | … | W2e |
| … | … | … | … | … | … | … | … | … |
| n | Wn1 | Wn2 | … | Wnm | Wn1 | Wn2 | … | Wne |
| Total Weight | … | … | ||||||
| Attribute1 | Attribute2 | |||||
|---|---|---|---|---|---|---|
| Subdomains | Subdomain11 | Subdomain12 | Subdomain1m | Subdomain21 | Subdomain22 | Subdomain2e |
| Probability of Subdomain | ||||||
| Subdomains | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | … | i-1 | i | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Subdomains | |||||||||||||||||||
| 1 | |||||||||||||||||||
| 2 | P(2,9) | ||||||||||||||||||
| 3 | |||||||||||||||||||
| 4 | |||||||||||||||||||
| 5 | |||||||||||||||||||
| 6 | |||||||||||||||||||
| 7 | P(7,12) | ||||||||||||||||||
| 8 | |||||||||||||||||||
| 9 | |||||||||||||||||||
| 10 | |||||||||||||||||||
| 11 | |||||||||||||||||||
| 12 | |||||||||||||||||||
| 13 | P(13,15) | ||||||||||||||||||
| 14 | |||||||||||||||||||
| 15 | |||||||||||||||||||
| … | |||||||||||||||||||
| i-1 | |||||||||||||||||||
| i | |||||||||||||||||||
| Subdomains | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | … | i | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Subdomains | |||||||||||||||||||
| 1 | |||||||||||||||||||
| 2 | |||||||||||||||||||
| 3 | 1 | 1 | 1 | ||||||||||||||||
| 4 | 1 | ||||||||||||||||||
| 5 | |||||||||||||||||||
| 6 | 1 | ||||||||||||||||||
| 7 | |||||||||||||||||||
| 8 | 1 | ||||||||||||||||||
| 9 | 1 | 1 | |||||||||||||||||
| 10 | |||||||||||||||||||
| 11 | |||||||||||||||||||
| 12 | |||||||||||||||||||
| 13 | 1 | ||||||||||||||||||
| 14 | |||||||||||||||||||
| 15 | |||||||||||||||||||
| 16 | |||||||||||||||||||
| … | |||||||||||||||||||
| i | |||||||||||||||||||
| Subdomains | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Subdomains | |||||||||||||||||||
| 1 | |||||||||||||||||||
| 2 | P(Subdomain2|Subdomain9) | ||||||||||||||||||
| 3 | |||||||||||||||||||
| 4 | |||||||||||||||||||
| 5 | |||||||||||||||||||
| 6 | |||||||||||||||||||
| 7 | |||||||||||||||||||
| 8 | |||||||||||||||||||
| 9 | P(Subdomain9|Subdomain2) | ||||||||||||||||||
| 10 | |||||||||||||||||||
| 11 | |||||||||||||||||||
| 12 | |||||||||||||||||||
| 13 | |||||||||||||||||||
| 14 | |||||||||||||||||||
| 15 | |||||||||||||||||||
| 16 | |||||||||||||||||||
| 17 | |||||||||||||||||||
| 18 | |||||||||||||||||||
| Number of Relations | Parents | Children | Conditional Probabilities |
|---|---|---|---|
| 1 | Subdomaini | Subdomainj | P(Subdomainj | Subdomaini) |
| 2 | Subdomaink | Subdomainw | P(Subdomainw | Subdomaink) |
| n | Subdomainn | Subdomainm | P(Subdomainm | Subdomainn) |
| No. of Faults | 1 | 2 | 3 | n-1 | n |
|---|---|---|---|---|---|
| Objects for Different Fault cases | Fault_Object1 | Fault_Object2 | Fault_Object3 | Fault_Objectn-1 | Fault_Objectn |
| No. of Fault Object in the Offline Library | 1 | 2 | … | i |
|---|---|---|---|---|
| Calculated Percentage of Similarity between the RealCase fault object and each Fault Object in the Offline Fault Library | Percentage of Similarity1 | Percentage of Similarity2 | … | Percentage of Similarityi |
| No. | Type | Time | Percentage |
|---|---|---|---|
| 1 | Offline_FaultType1 | Offline_FaultTime1 | Highest_Percentage1 |
| 2 | Offline_FaultType2 | Offline_FaultTime2 | Highest_Percentage2 |
| 3 | Offline_FaultType3 | Offline_FaultTime3 | Highest_Percentage3 |
| j | Offline_FaultTypej | Offline_FaultTimej | Highest_Percentagej |
| Seconds (Samples) | Daily Temperature | Occupancy Number | Room Temperature | Room CO2 Concentration | Heater Status | Damper Status |
|---|---|---|---|---|---|---|
| 1 | 7.0004 | 0 | 19.9905 | 400 | 0 | 0 |
| 2 | 7.0007 | 0 | 19.9810 | 400 | 0 | 0 |
| 3 | 7.0011 | 0 | 19.9715 | 400 | 0 | 0 |
| 4 | 7.0015 | 0 | 19.9620 | 400 | 0 | 0 |
| 5 | 7.0018 | 0 | 19.9525 | 400 | 0 | 0 |
| … | … | … | … | … | … | … |
| 17,999 | 11.8293 | 6 | 19.5583 | 579.0654 | 1 | 1 |
| 18,000 | 11.8294 | 6 | 19.5570 | 700 | 1 | 1 |
| 18,001 | 11.8295 | 6 | 19.5556 | 700 | 1 | 1 |
| 18,002 | 11.8296 | 6 | 19.5543 | 700 | 1 | 1 |
| 18,003 | 11.8297 | 2 | 19.5530 | 700 | 1 | 1 |
| … | … | … | … | … | … | … |
| 86,399 | 6.9996 | 0 | 16.8578 | 700 | 1 | 1 |
| 86,400 | 7 | 0 | 16.8581 | 700 | 1 | 1 |
| No. | Attributes | Subdomains | Subdomains | Subdomains |
|---|---|---|---|---|
| 1 | Daily Temperature | Low_Daily_Temperature (No. 1) | Middle_Daily_Temperature (No. 2) | High_Daily_Temperature (No. 3) |
| 2 | Occupants Number | Low_Occupancy (No. 4) | Normal_Occupancy (No. 5) | High_Occupancy (No. 6) |
| 3 | Room Temperature | Lower_than_Threshold_ RoomTemperature (No. 7) | Within_Threshold_ RoomTemperature (No. 8) | Upper_than_Threshold_ RoomTemperature (No. 9) |
| 4 | Heater Status | Heater_Status_On (No. 10) | Heater_Status_Off (No. 11) | --------- |
| 5 | Damper Status | Damper_Status_Open (No. 12) | Damper_Status_Close (No. 13) | --------- |
| 6 | Simulation Clock | Healthy_Mode (No. 14) | Faulty_Mode (No. 15) | --------- |
| 7 | Room CO2 Concentration | Lower_than_Threshold_CO2Value (No. 16) | Within_Threshold_CO2Value (No. 17) | Upper_than_Threshold_CO2Value (No. 18) |
| Attributes | Daily Temperature | Occupancy | Room Temperature | Heater Status | Damper Status | Simulation Clock | Room CO2 Concentration | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Subdomains | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
| No. Samples | |||||||||||||||||||
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | |
| 2 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | |
| 3 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | |
| 4 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | |
| 5 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | |
| 17,999 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0.0321 | 0.9679 | 0 | |
| 18,000 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0.5405 | 0.4595 | |
| 18,001 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0.54054 | 0.4595 | |
| 18,002 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0.54054 | 0.4595 | |
| 18,003 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0.54054 | 0.4595 | |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | |
| 86,399 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0.54054 | 0.4595 | |
| 86,400 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0.54054 | 0.4595 | |
| Total Weight | 37,133.7942 | 12,132.4114 | 37,133.7942 | 61,199 | 18,001 | 7200 | 53,381.5449 | 24,902.6097 | 8115.8453 | 85,676 | 724 | 73,790 | 12,610 | 18,000 | 68,400 | 6038.3843 | 48,643.6590 | 31,717.9565 | |
| Attribute | Daily Temperature | Occupancy | Room Temperature | Heater Status | Damper Status | Simulation Clock | Room CO2 Concentration | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Subdomain | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Probability | 0.4298 | 0.1404 | 0.4298 | 0.7083 | 0.2083 | 0.0833 | 0.6178 | 0.2882 | 0.0939 | 0.9916 | 0.0084 | 0.8541 | 0.1459 | 0.2083 | 0.7917 | 0.0699 | 0.5630 | 0.3671 |
| Subdomains | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Subdomains | |||||||||||||||||||
| 1 | 0 | 0.0299 | 0 | 0.4298 | 0 | 0 | 0.4298 | 0 | 0 | 0.4298 | 0 | 0.4298 | 0 | 0 | 0.4298 | 0 | 0.2472 | 0.2123 | |
| 2 | 0 | 0 | 0.0299 | 0.1053 | 0.0351 | 0 | 0.1076 | 0.0204 | 0.0249 | 0.136 | 0.0035 | 0.1053 | 0.0351 | 0.0351 | 0.1053 | 0.0351 | 0.0818 | 0.0707 | |
| 3 | 0 | 0 | 0 | 0.1732 | 0.1732 | 0.0833 | 0.0828 | 0.2803 | 0.0792 | 0.4249 | 0.0049 | 0.3190 | 0.1108 | 0.1732 | 0.2566 | 0.0374 | 0.2812 | 0.1287 | |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5069 | 0.1420 | 0.0594 | 0.7048 | 0.0035 | 0.6250 | 0.0833 | 0.0833 | 0.6250 | 0.0646 | 0.3565 | 0.2872 | |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0917 | 0.0884 | 0.0282 | 0.2035 | 0.0049 | 0.1583 | 0.0501 | 0.0833 | 0.1250 | 0.0030 | 0.1455 | 0.0599 | |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0193 | 0.0578 | 0.0063 | 0.0833 | 0 | 0.0708 | 0.0125 | 0.0417 | 0.0417 | 0.0023 | 0.0610 | 0.0201 | |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0476 | 0 | 0.6153 | 0.0026 | 0.6149 | 0.0029 | 0.0107 | 0.6071 | 0.0050 | 0.3566 | 0.2998 | |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0305 | 0.2835 | 0.0048 | 0.2341 | 0.0541 | 0.1037 | 0.1845 | 0.0267 | 0.2058 | 0.1077 | |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0929 | 0.0010 | 0.0050 | 0.0889 | 0.0939 | 0 | 0.0467 | 0.0526 | 0.0031 | |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.8512 | 0.1404 | 0.2000 | 0.7917 | 0.0664 | 0.5587 | 0.3666 | |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0028 | 0.0056 | 0.0084 | 0 | 0.0035 | 0.0043 | 0.0005 | |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0624 | 0.7917 | 0.0033 | 0.4857 | 0.3650 | |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.1459 | 0 | 0.0666 | 0.0773 | 0.0021 | |
| 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0699 | 0.1351 | 0.0034 | |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.4279 | 0.3637 | |
| 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0166 | 0 | |
| 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.3671 | |
| 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Subdomains | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Subdomains | |||||||||||||||||||
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | |
| 2 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | |
| 3 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | |
| 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Subdomains | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Subdomains | |||||||||||||||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5783 | |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.2653 | 0 | 0.4171 | 0 | 0 | 0 | 0 | 0.5024 | 0 | 0 | |
| 3 | 0 | 0 | 0 | 0 | 0.8315 | 1 | 0 | 0.9724 | 0.8430 | 0 | 0.5829 | 0 | 0.7594 | 0.8315 | 0 | 0.5349 | 0 | 0 | |
| 4 | 1.0 | 0.75 | 0 | 0 | 0 | 0 | 0.8204 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.9247 | 0 | 0.7822 | |
| 5 | 0 | 0.25 | 0 | 0 | 0 | 0 | 0 | 0 | 0.3006 | 0 | 0.5829 | 0 | 0.3431 | 0.4001 | 0 | 0 | 0 | 0 | |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 7 | 1.0 | 0.7659 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.6333 | 0.8165 | |
| 8 | 0 | 0 | 0 | 0 | 0.4244 | 0.6931 | 0 | 0 | 0.3245 | 0 | 0.5687 | 0 | 0.3705 | 0.4978 | 0 | 0.3823 | 0 | 0 | |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.1249 | 0 | 0 | 0 | 0 | 0.6680 | 0 | 0 | |
| 10 | 1.0 | 0 | 0 | 0.9951 | 0 | 1 | 0.9958 | 0 | 0 | 0 | 0 | 0.9967 | 0 | 0 | 1 | 0 | 0.9923 | 0.9985 | |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 12 | 1.0 | 0 | 0 | 0.8824 | 0 | 0 | 0.9952 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0.8627 | 0.9943 | |
| 13 | 0 | 0.25 | 0 | 0 | 0 | 0.1504 | 0 | 0 | 0.9467 | 0 | 0.6644 | 0 | 0 | 0 | 0 | 0.9526 | 0 | 0 | |
| 14 | 0 | 0.25 | 0 | 0 | 0 | 0.4999 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | |
| 15 | 1.0 | 0 | 0 | 0.8824 | 0 | 0 | 0.9827 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.9908 | |
| 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.4171 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 17 | 0.5751 | 0.5822 | 0.6542 | 0 | 0.6982 | 0.7319 | 0 | 0.7140 | 0 | 0 | 0 | 0 | 0 | 0.6484 | 0 | 0 | 0 | 1 | |
| 18 | 0 | 0.5032 | 0 | 0 | 0 | 0 | 0 | 0.3735 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| No. of Relations | Parents | Children | Conditional Probabilities |
|---|---|---|---|
| 1 | Upper_than_Threshold_CO2Value | Low_Daily_Temperature | 0.57827 |
| 2 | Upper_than_Threshold_RoomTemperature | Middle_Daily_Temperature | 0.26533 |
| 3 | Heater_Status_Off | Middle_Daily_Temperature | 0.41713 |
| 4 | Lower_than_Threshold_CO2Value | Middle_Daily_Temperature | 0.50239 |
| 5 | Normal_Occupancy | High_Daily_Temperature | 0.83153 |
| 6 | High_Occupancy | High_Daily_Temperature | 1 |
| 7 | Within_Threshold_RoomTemperature | High_Daily_Temperature | 0.97244 |
| 8 | Upper_than_Threshold_RoomTemperature | High_Daily_Temperature | 0.84297 |
| 9 | Heater_Status_Off | High_Daily_Temperature | 0.58287 |
| 10 | Damper_Status_Close | High_Daily_Temperature | 0.75943 |
| … | … | … | … |
| 65 | Lower_than_Threshold_RoomTemperature | Faulty_Mode | 0.98268 |
| … | … | … | … |
| 70 | Upper_than_Threshold_CO2Value | Within_Threshold_CO2Value | 1 |
| 71 | Middle_Daily_Temperature | Upper_than_Threshold_CO2Value | 0.50319 |
| 72 | Within_Threshold_RoomTemperature | Upper_than_Threshold_CO2Value | 0.37354 |
| No. of Fault Object | Fault_Object1 | Fault_Object2 | Fault_Object3 | … | Fault_Object169 | Fault_Object170 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Details | Type | “CO2SensorLow” | Type | “CO2SensorMiddle” | Type | “CO2SensorHigh” | … | Type | “HeaterActuatorOff” | Type | “HeaterActuatorOn” |
| Time | 5000 | Time | 5000 | Time | 5000 | Time | 85,000 | Time | 85000 | ||
| Data | 86,400 × 10 double | Data | 86,400 × 10 double | Data | 86,400 × 10 double | Data | 86,400 × 10 double | Data | 86,400 × 10 double | ||
| RDP | 144 × 3 string | RDP | 144 × 3 string | RDP | 144 × 3 string | RDP | 144 × 3 string | RDP | 144 × 3 string | ||
| RealCase_Object1 | |
|---|---|
| Type | “Heater_Actuator” |
| Time | 70,393 |
| Value | 0 |
| Percentage_List | 170 × 1 double |
| Evaluation_List | 20 × 3 string |
| No. | Type in Offline Library | Time in Offline Library | Percentage in Percentage_List | |
|---|---|---|---|---|
| 1 | HeaterActuatorOff | 70,000 | 51.3889 | The Diagnosed Case in the First Rank |
| 2 | HeaterActuatorOff | 65,000 | 50 | Second Rank |
| 3 | HeaterActuatorOff | 60,000 | 49.3056 | Third Rank |
| 4 | HeaterActuatorOff | 75,000 | 49.3056 | |
| 5 | HeaterActuatorOff | 55,000 | 47.9167 | Fourth Rank |
| 6 | HeaterActuatorOff | 50,000 | 45.8333 | Fifth Rank |
| 7 | HeaterActuatorOff | 45,000 | 45.1389 | |
| 8 | TemperatureSensorLow | 70,000 | 45.1389 | |
| 9 | HeaterActuatorOff | 80,000 | 45.1389 | |
| 10 | TemperatureSensorLow | 65,000 | 43.75 | |
| 11 | TemperatureSensorHigh | 70,000 | 43.75 | |
| 12 | TemperatureSensorLow | 75,000 | 43.75 | |
| 13 | TemperatureSensorLow | 60,000 | 43.0556 | |
| 14 | TemperatureSensorHigh | 65,000 | 42.3611 | |
| 15 | TemperatureSensorHigh | 75,000 | 42.3611 | |
| 16 | HeaterActuatorOff | 40,000 | 41.6667 | |
| 17 | TemperatureSensorLow | 55,000 | 41.6667 | |
| 18 | TemperatureSensorHigh | 60,000 | 41.6667 | |
| 19 | TemperatureSensorHigh | 55,000 | 40.9722 | |
| 20 | TemperatureSensorLow | 80,000 | 40.9722 |
| Fault Type | Total Number of Injected Fault Cases | Number of Diagnoses (TPs) in Rank1 | Number of Diagnoses (TPs) in Rank 1, 2 | Number of Diagnoses (TPs) in Rank1, 2, 3 | Number of Diagnoses (TPs) in Rank 1, 2, 3, 4 | Number of Diagnoses (TPs) in Rank 1, 2, 3, 4, 5 |
|---|---|---|---|---|---|---|
| CO2 Sensor | 45 | 38 | 41 | 43 | 43 | 43 |
| Damper Actuator | 10 | 10 | 10 | 10 | 10 | 10 |
| Temperature Sensor | 45 | 35 | 40 | 41 | 41 | 42 |
| Heater Actuator | 10 | 10 | 10 | 10 | 10 | 10 |
| Total Number | 110 | 93 | 101 | 104 | 104 | 105 |
| Fault Type | Accuracy for Rank 1 | Accuracy for Rank 1, 2 | Accuracy for Rank 1, 2, 3 | Accuracy for Rank 1, 2, 3, 4 | Accuracy for Rank 1, 2, 3, 4, 5 |
|---|---|---|---|---|---|
| CO2 Sensor | 0.847826087 | 0.913043478 | 0.95652174 | 0.95652174 | 0.956521739 |
| Damper Actuator | 1 | 1 | 1 | 1 | 1 |
| Temperature Sensor | 0.782608696 | 0.891304348 | 0.91304348 | 0.91304348 | 0.934782609 |
| Heater Actuator | 1 | 1 | 1 | 1 | 1 |
| Average Accuracy | 0.907608696 | 0.951086957 | 0.9673913 | 0.9673913 | 0.972826087 |
| Fault Type | Recall for Rank 1 | Recall for Rank 1, 2 | Recall for Rank 1, 2, 3 | Recall for Rank 1, 2, 3, 4 | Recall for Rank 1, 2, 3, 4, 5 |
|---|---|---|---|---|---|
| CO2 Sensor | 0.844444444 | 0.911111111 | 0.95555556 | 0.95555556 | 0.955555556 |
| Damper Actuator | 1 | 1 | 1 | 1 | 1 |
| Temperature Sensor | 0.777777778 | 0.888888889 | 0.91111111 | 0.91111111 | 0.933333333 |
| Heater Actuator | 1 | 1 | 1 | 1 | 1 |
| Average Recall | 0.905555556 | 0.95 | 0.96666667 | 0.96666667 | 0.972222222 |
| Fault Type | F1 for Rank 1 | F1 for Rank 1, 2 | F1 for Rank 1, 2, 3 | F1 for Rank 1, 2, 3, 4 | F1 for Rank 1, 2, 3, 4, 5 |
|---|---|---|---|---|---|
| CO2 Sensor | 0.915662651 | 0.953488372 | 0.97727273 | 0.97727273 | 0.977272727 |
| Damper Actuator | 1 | 1 | 1 | 1 | 1 |
| Temperature Sensor | 0.875 | 0.941176471 | 0.95348837 | 0.95348837 | 0.965517241 |
| Heater Actuator | 1 | 1 | 1 | 1 | 1 |
| Average F1 | 0.947665663 | 0.973666211 | 0.98269027 | 0.98269027 | 0.985697492 |
| Fault Labels | Relevant Elements | TP | FP | TN | FN | TotPop | Precision | Recall | F-Score or F1 | Accuracy |
|---|---|---|---|---|---|---|---|---|---|---|
| CO2 Sensor Rank 1 | 45 | 38 | 0 | 1 | 7 | 46 | 1 | 0.844444444 | 0.915662651 | 0.847826087 |
| CO2 Sensor Rank 1, 2 | 45 | 41 | 0 | 1 | 4 | 46 | 1 | 0.911111111 | 0.953488372 | 0.913043478 |
| CO2 Sensor Rank 1, 2, 3 | 45 | 43 | 0 | 1 | 2 | 46 | 1 | 0.955555556 | 0.977272727 | 0.956521739 |
| CO2 Sensor Rank 1, 2, 3, 4 | 45 | 43 | 0 | 1 | 2 | 46 | 1 | 0.955555556 | 0.977272727 | 0.956521739 |
| CO2 Sensor Rank 1, 2, 3, 4, 5 | 45 | 43 | 0 | 1 | 2 | 46 | 1 | 0.955555556 | 0.977272727 | 0.956521739 |
| Damper Actuator Rank 1 | 10 | 10 | 0 | 1 | 0 | 11 | 1 | 1 | 1 | 1 |
| Damper Actuator Rank 1,2 | 10 | 10 | 0 | 1 | 0 | 11 | 1 | 1 | 1 | 1 |
| Damper Actuator Rank 1, 2, 3 | 10 | 10 | 0 | 1 | 0 | 11 | 1 | 1 | 1 | 1 |
| Damper Actuator Rank 1, 2, 3, 4 | 10 | 10 | 0 | 1 | 0 | 11 | 1 | 1 | 1 | 1 |
| Damper Actuator Rank 1, 2, 3, 4, 5 | 10 | 10 | 0 | 1 | 0 | 11 | 1 | 1 | 1 | 1 |
| Temperature Sensor Rank 1 | 45 | 35 | 0 | 1 | 10 | 46 | 1 | 0.777777778 | 0.875 | 0.782608696 |
| Temperature Sensor Rank 1, 2 | 45 | 40 | 0 | 1 | 5 | 46 | 1 | 0.888888889 | 0.941176471 | 0.891304348 |
| Temperature Sensor Rank 1, 2, 3 | 45 | 41 | 0 | 1 | 4 | 46 | 1 | 0.911111111 | 0.953488372 | 0.913043478 |
| Temperature Sensor Rank 1, 2, 3, 4 | 45 | 41 | 0 | 1 | 4 | 46 | 1 | 0.911111111 | 0.953488372 | 0.913043478 |
| Temperature Sensor Rank 1, 2, 3, 4, 5 | 45 | 42 | 0 | 1 | 3 | 46 | 1 | 0.933333333 | 0.965517241 | 0.934782609 |
| Heater Actuator Rank 1 | 10 | 10 | 0 | 1 | 0 | 11 | 1 | 1 | 1 | 1 |
| Heater Actuator Rank 1, 2 | 10 | 10 | 0 | 1 | 0 | 11 | 1 | 1 | 1 | 1 |
| Heater Actuator Rank 1, 2, 3 | 10 | 10 | 0 | 1 | 0 | 11 | 1 | 1 | 1 | 1 |
| Heater Actuator Rank 1, 2, 3, 4 | 10 | 10 | 0 | 1 | 0 | 11 | 1 | 1 | 1 | 1 |
| Heater Actuator Rank 1, 2, 3, 4, 5 | 10 | 10 | 0 | 1 | 0 | 11 | 1 | 1 | 1 | 1 |
| Type of Classifier | Accuracy | Precision | Recall | F1 or F-Score |
|---|---|---|---|---|
| Combined Classifier (This Study) | 97.28% | 100% | 97.22% | 98.56% |
| Implicit Classifier—Overall | 97.40% | 96.70% | 98.20% | 97.46% |
| Implicit Classifier—For only stuck-at or constant faults | NA | 98.60% | 98.40% | 98.55% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behravan, A.; Kiamanesh, B.; Obermaisser, R. Fault Diagnosis of DCV and Heating Systems Based on Causal Relation in Fuzzy Bayesian Belief Networks Using Relation Direction Probabilities. Energies 2021, 14, 6607. https://doi.org/10.3390/en14206607
Behravan A, Kiamanesh B, Obermaisser R. Fault Diagnosis of DCV and Heating Systems Based on Causal Relation in Fuzzy Bayesian Belief Networks Using Relation Direction Probabilities. Energies. 2021; 14(20):6607. https://doi.org/10.3390/en14206607
Chicago/Turabian StyleBehravan, Ali, Bahareh Kiamanesh, and Roman Obermaisser. 2021. "Fault Diagnosis of DCV and Heating Systems Based on Causal Relation in Fuzzy Bayesian Belief Networks Using Relation Direction Probabilities" Energies 14, no. 20: 6607. https://doi.org/10.3390/en14206607
APA StyleBehravan, A., Kiamanesh, B., & Obermaisser, R. (2021). Fault Diagnosis of DCV and Heating Systems Based on Causal Relation in Fuzzy Bayesian Belief Networks Using Relation Direction Probabilities. Energies, 14(20), 6607. https://doi.org/10.3390/en14206607







