Prediction of Refracturing Timing of Horizontal Wells in Tight Oil Reservoirs Based on an Integrated Learning Algorithm
Abstract
:1. Introduction
2. Characterization of Refracturing Timing Parameters
3. Principle and Method of Refracturing Timing Prediction
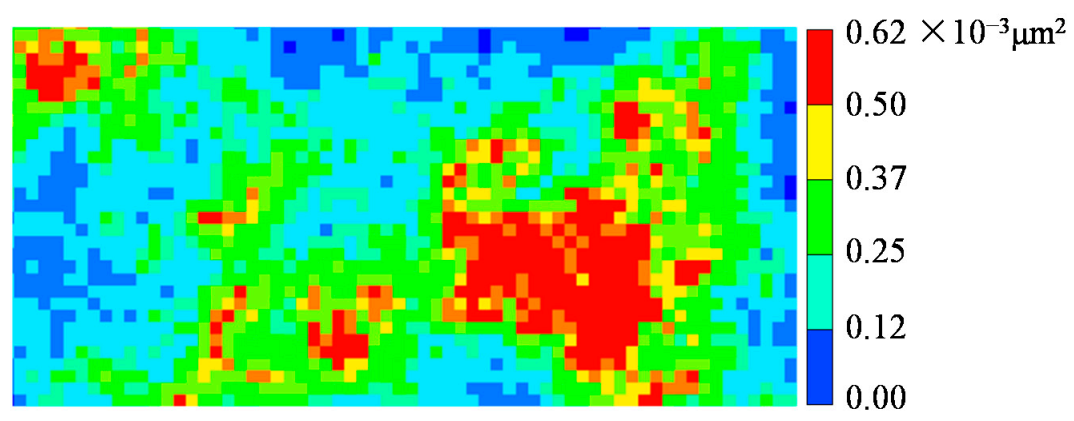
3.1. Sample Set Construction
3.2. Artificial Neural Network Algorithm
3.3. Support Vector Machine Regression Algorithm
3.4. XGBoost Regression Algorithm
- According to conventional experience, a group of initial parameters was selected, and the number of decision trees was set as 50. On this basis, the depth of decision trees (max_depth) and node weights, namely, the regularization coefficient, (min_child_weight) were adjusted. The optimal parameter combination could be found by drawing a heat graph of the loss function with the tree depth and regularization coefficient.
- Adjust the gamma; this parameter determines when the loss function is split, and the smaller the parameter is, the smaller the risk of overfitting is. Therefore, under the premise of ensuring the rationality of the loss function, gamma was taken to be as small as possible.
- Adjust the sampling mode; these parameters mainly involve column sampling (colsample_bytree) and row sampling (subsample). In the same way, the best parameter combination could be found by drawing a heat map of the loss function with two parameters.
- Adjust the learning rate eta; the loss function was compared to complete the eta parameter optimization.
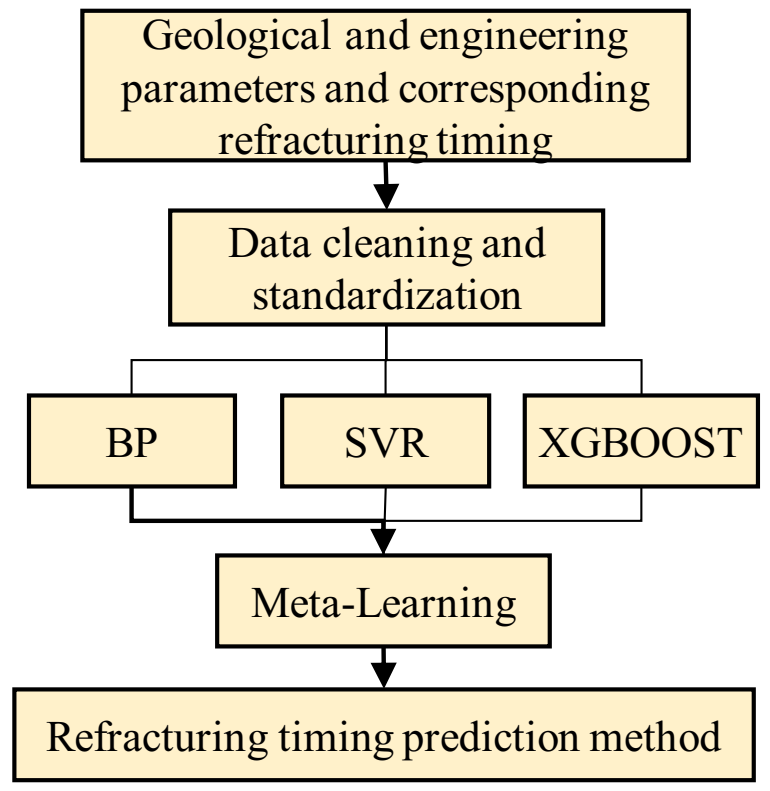
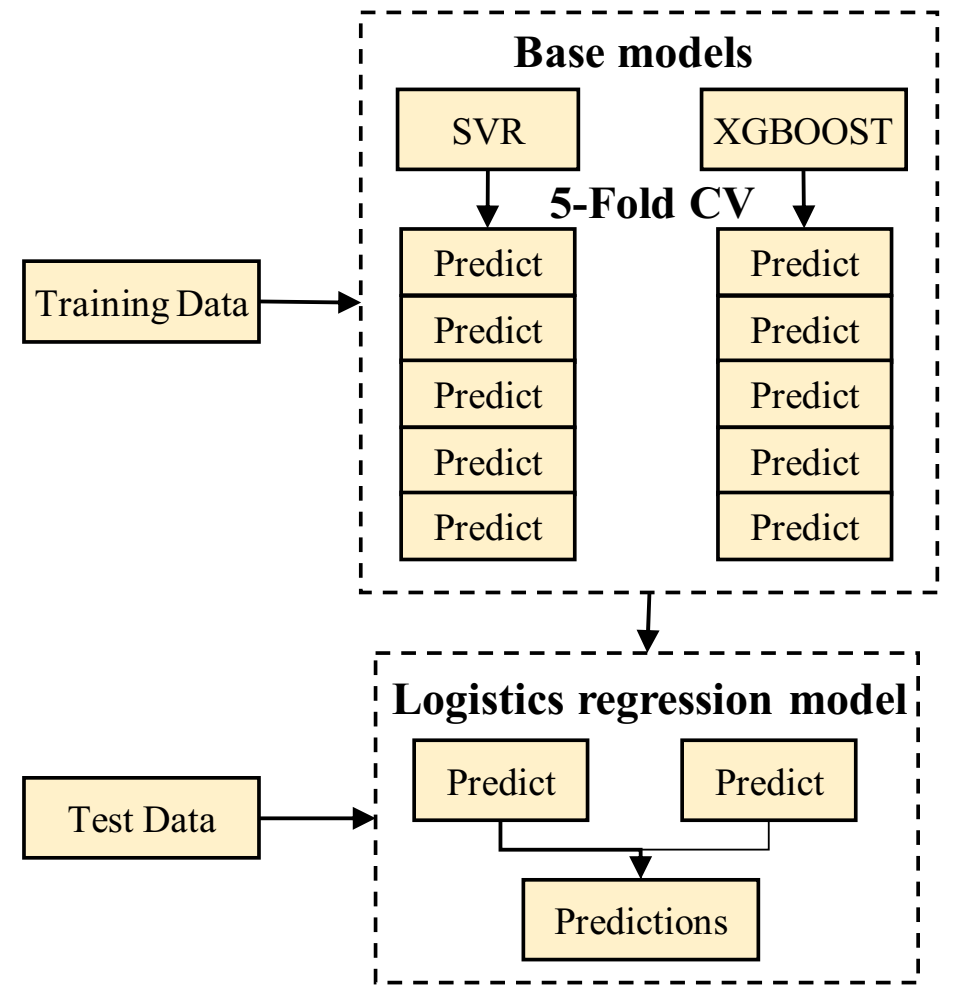
3.5. Integrated Learning Algorithm
4. Algorithm Application and Analysis
4.1. Application Evaluation Analysis of the Algorithm
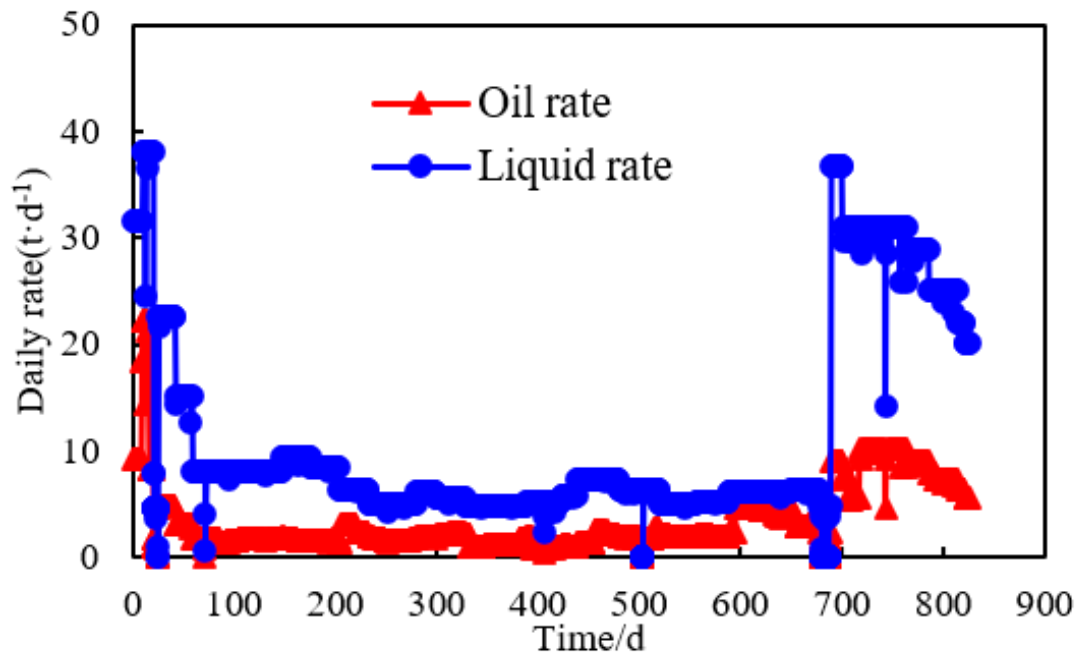
4.2. Field Implementation Effect
5. Conclusions
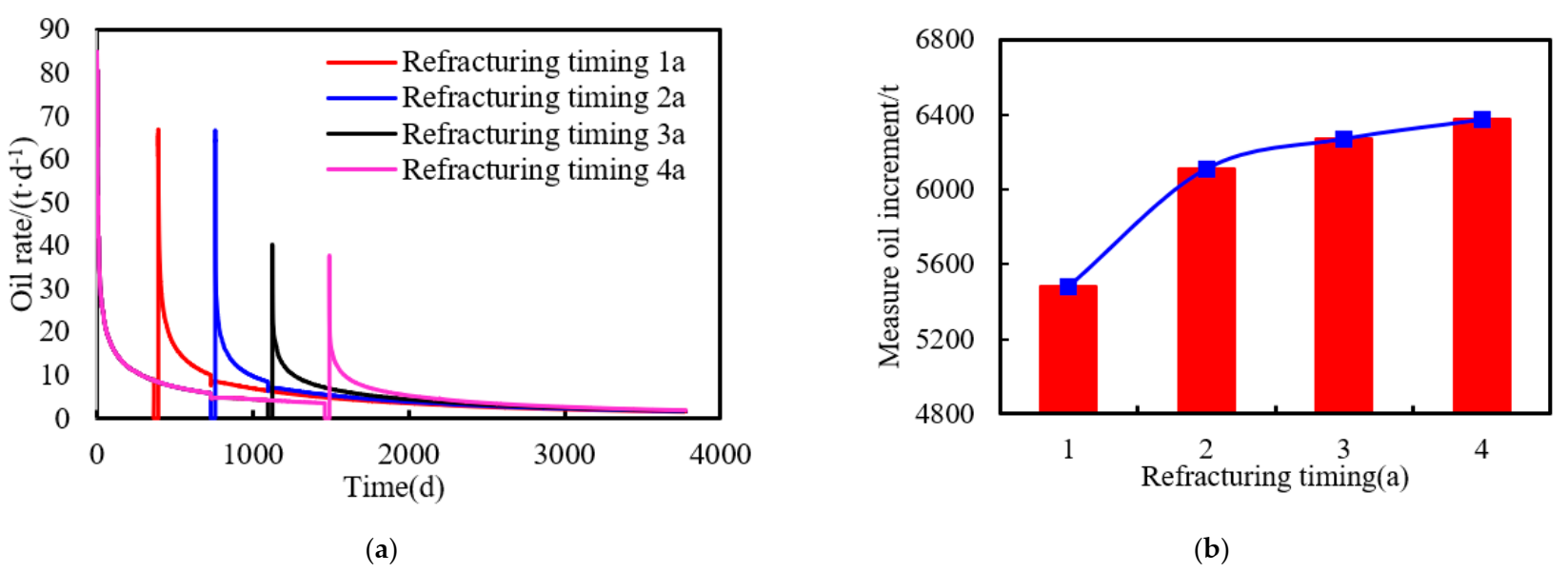
- Based on the increased production of horizontal wells with refracturing measures as the evaluation index, the law of the influence of refracturing timing on the stimulation effect was analyzed. Combined with the economic limit of tight oil horizontal wells, the economic limit daily production of horizontal wells was calculated, and the reasonable refracturing timing was quantitatively characterized.
- Using machine learning techniques to measure the geologic and engineering parameters of horizontal wells, with a total of 11 variables as input, the refracturing time as output, the comprehensive field measurements and a large number of numerical simulation data to construct the learning sample set, and noise reduction processing on the sample set, three kinds of modeling and prediction effect comparisons of machine learning algorithms were chosen; the results showed that the support vector machine and XGBoost regression algorithm of artificial neural network algorithm showed better generalization.
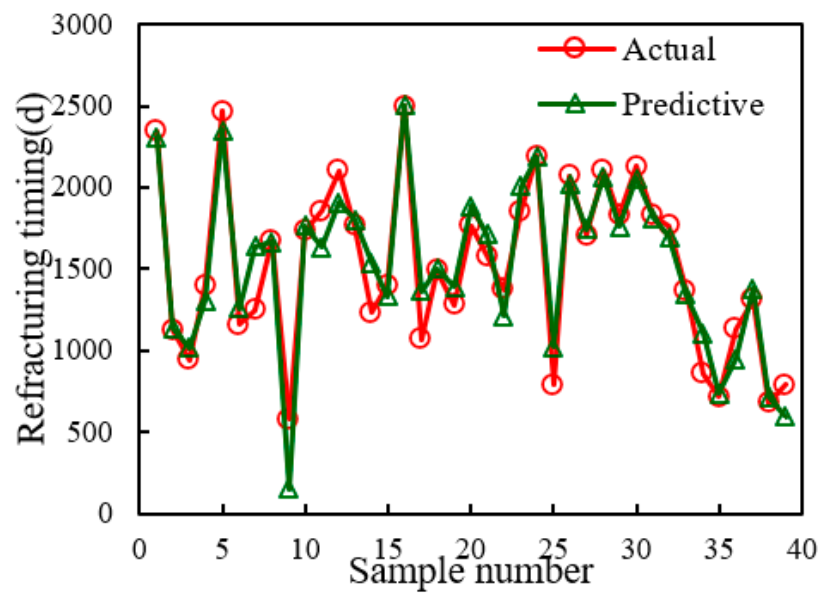
- Through integrated study of the depth of the stacking method, SVR and XGBoost were combined to build the dense oil refracturing horizontal well, based on the integrated study time prediction method. Using 257 groups to build a prediction model in a test set forecast result analysis, it was shown that, compared with a single algorithm model, the prediction accuracy was higher, and the actual and estimated values of the correlation coefficient R2 were 0.945—alternative numerical simulation processes quickly predicted refracturing timing. The prediction model was used to predict the refracturing time of the X34-P6 well in the target reservoir, and the predicted results were in great agreement with the actual value.
- Having a high predictive accuracy, the integrated learning model can serve as a reliable tool for predicting refracturing time. It has high potential for being applied in macro decision making of horizontal well repeated fracturing.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zheng, M.; Li, J.; Wu, X.; Wang, S.; Guo, Q.; Chen, X.; Yu, J. Potential of Oil and Natural Gas Resources of Main Hydrocarbon- Bearing Basins and Key Exploration Fields in China. Earth Sci. 2019, 44, 833–847. [Google Scholar]
- Jia, C.; Zou, C.; Li, J.; Li, D.; Zheng, M. Assessment criteria, main types, basic features and resource prospects of the tight oil in China. Acta Pet. Sin. 2012, 33, 343–350. [Google Scholar]
- Feng, Q.; Xu, S.; Xing, X.; Zhang, W.; Wang, S. Advances and challenges in shale oil development: A critical review. Adv. Geo-Energy Res. 2020, 4, 406–418. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X.; Bao, L.; Feng, Q.; Xu, S. Characterization of hydraulic fracture propagation in tight formations: A fractal perspective. J. Pet. Sci. Eng. 2020, 195, 107871. [Google Scholar] [CrossRef]
- Rui, Z.; Cui, K.; Wang, X.; Lu, J.; Chen, G.; Ling, K.; Shirish, P. A quantitative framework for evaluating unconventional well development. J. Earth Sci. 2018, 166, 900–905. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, Z.; Xu, J. A simulation-based method to determine the coefficient of hyperbolic decline curve for tight oil production. Adv. Geo-Energy Res. 2019, 3, 375–380. [Google Scholar] [CrossRef] [Green Version]
- Wang, F. Refracturing Techique and its Field Test for the Horizontal Well in the Tight Oil. Pet. Geol. Oilfield Dev. Daqing 2018, 37, 171–174. [Google Scholar]
- Su, L.; Bai, X.; Lu, H.; Huang, T.; Wu, H.; Da, Y. Study on repeated stimulation technology and its application to in low-yield horizontal wells in ultra low permeability oil reservoirs, Changqing Oilfield. Oil Drill. Prod. Technol. 2017, 39, 521–527. [Google Scholar]
- Diakhate, M.; Gazawi, A.; Barree, R.D.; Cossio, M.; Barzola, G. Refracturing on horizontal wells in the Eagle Ford Shale in South Texas-one operator’s perspective. Presented at the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 3–5 February 2015. [Google Scholar]
- Lu, M.; Su, Y.; Zhan, S.; Almrabat, A. Modeling for reorientation and potential of enhanced oil recovery in refracturing. Adv. Geo-Energy Res. 2020, 4, 20–28. [Google Scholar] [CrossRef] [Green Version]
- Pang, P.; Liu, Z.; Wang, H.; Zhang, W.; He, J. Numerical Simulation of Refracturing Opportunity. Pet. Geol. Oilfield Dev. Daqing 2015, 34, 83–87. [Google Scholar]
- Guo, J.; Tao, L.; Zeng, F. Optimization of refracturing timing for horizontal wells in tight oil reservoirs: A case study of Cretaceous Qingshankou Formation, Songliao Basin, NE China. Pet. Explor. Dev. 2019, 46, 146–154. [Google Scholar] [CrossRef]
- Zhang, G.; Chen, M.; Yao, F.; Zhao, Z. Study on optimal re-fracturing timing in anisotropic formation and its influencing factors. Acta Pet. Sin. 2008, 29, 885–888, 893. [Google Scholar]
- Da, Y.; Zhao, W.; Bo, X.; Zhang, K.; Li, Z.; Wu, S. Study on fracture pattern law for re-fracturing in low permeability reservoir. Fault-Block Oil Gas Field 2012, 19, 781–784. [Google Scholar]
- Yan, H.; Hou, F.; Zhang, G. Adjusted Refracturing Technology for Horizontal Seam in Daqing Oifield. Pet. Geol. Oilfield Dev. Daqing 2005, 24, 71–73, 108. [Google Scholar]
- Udegbe, E.; Morgan, E.; Srinivasan, S. From Face Detection to Fractured Reservoir Characterization: Big Data Analytics for Restimulation Candidate Selection. Presented at the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017. [Google Scholar]
- Barree, R.D.; Miskimins, J.L.; Svatek, K.J. Reservoir and completion considerations for the refracturing of horizontal wells. Presented at the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 24–26 January 2017. [Google Scholar]
- Oruganti, Y.; Mittal, R.; McBurney, C.J.; Rodriguez, A. Re-Fracturing in Eagle Ford and Bakken to Increase Reserves and Generate Incremental NPV: Field Study. Presented at the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 3–5 February 2015. [Google Scholar]
- Yu, F.; Liu, M.; Hou, J. Discussion about Well and Layer Selection for Refracturing at Late Period of High Water Cut Stage. Pet. Geol. Oilfield Dev. Daqing 2005, 4, 47–48. [Google Scholar]
- Tavassoli, S.; Yu, W.; Javadpour, F.; Sepehrnoori, K. Well screen and optimal time of refracturing: A Barnett shale well. J. Pet. Eng. 2013, 36, 12–22. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.; Wang, S.; Yuan, J.; Li, C.; Zhang, Q. A prediction model of specific productivity index using least square support vector machine method. Adv. Geo-Energy Res. 2020, 4, 460–467. [Google Scholar] [CrossRef]
- Wang, S.; Qin, C.; Feng, Q.; Farzam, J.; Rui, Z. A framework for predicting the production performance of unconventional resources using deep learning. Appl. Energy 2021, 295, 117016. [Google Scholar] [CrossRef]
- Asala, H.I.; Chebeir, J.; Zhu, W.; Taleghani, A.D.; Romagnoli, J. A Machine Learning Approach to Optimize Shale Gas Supply Chain Networks. Presented at the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017. [Google Scholar]
- Morozov, A.; Popkov, D.; Duplyakov, V.; Mutalova, R.; Paderin, G. Data-driven model for hydraulic fracturing design optimization: Focus on building digital database and production forecast. J. Pet. Sci. Eng. 2020, 194, 107504. [Google Scholar] [CrossRef]
- Taherdangkoo, R.; Liu, Q.; Xing, Y.; Butscher, C. Predicting methane solubility in water and seawater by machine learning algorithms: Application to methane transport modeling. J. Contam. Hydrol. 2021, 242, 103844. [Google Scholar] [CrossRef]
- Du, J.; Liu, H.; Ma, D.; Fu, J.; Wang, Y.; Zhou, T. Discussion on effective development techniques for continental tight oil in China. Pet. Explor. Dev. 2014, 41, 217–224. [Google Scholar] [CrossRef]
- Li, Y.; Han, L.; Dong, P.; Han, D. Study on economic limits for horizontal well in low-permeability reservoir. Acta Pet. Sin. 2009, 30, 242–246. [Google Scholar]
- Feng, Q.; Ren, J.; Zhang, X.; Wang, X.; Wang, S.; Li, Y. Study on Well Selection Method for Refracturing Horizontal Wells in Tight Reservoirs. Energies 2020, 13, 4202. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, W.; Liang, J.T.; Wang, S.; Liang, H. Application of statistical machine learning clustering algorithms to improve EUR predictions using decline curve analysis in shale-gas reservoirs. J. Pet. Sci. Eng. 2021, 109216, in press. [Google Scholar] [CrossRef]
- Nguyen, H.; Bui, X.N.; Bui, H.B.; DT, C. Developing an XGBoost model to predict blast-induced peak particle velocity in an open-pit mine: A case study. Acta Geophys. 2019, 67, 477–490. [Google Scholar] [CrossRef]
- Azizi, S.E.; Ahmadloo, M.; Awad, M. Prediction of void fraction for gas–liquid flow in horizontal, upward and downward inclined pipes using artificial neural network. Int. J. Multiph. Flow 2016, 87, 35–44. [Google Scholar] [CrossRef]
- Krawczyk, B.; Minku, L.L.; Gama, J.; Stefanowski, J.; Woniak, M. Ensemble learning for data stream analysis: A survey. Inf. Fusion 2017, 37, 132–156. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Ma, Y.Z.; Gomez, E. Importance of Modeling Heterogeneities and Correlation in Reservoir Properties in Unconventional Formations: Examples of Tight Gas Reservoirs. J. Earth Sci. 2021, 32, 809–817. [Google Scholar] [CrossRef]
- Negash, B.; Yaw, M. Artificial neural network based production forecasting for a hydrocarbon reservoir under water injection. Pet. Explor. Dev. 2020, 47, 357–365. [Google Scholar] [CrossRef]
- Huo, Y.; Jiang, H. A preferred method for gas well re-fracturing well based on BP neural network. Nat. Gas Geosci. 2020, 31, 552–558. [Google Scholar]
- Zheng, J.; Leung, J.Y.; Sawatzky, R.P.; Alvarez, J.M. An AI-based workflow for estimating shale barrier configurations from SAGD production histories. Neural Comput. Appl. 2019, 31, 5273–5297. [Google Scholar] [CrossRef]
- Al-Anazi, A.; Gates, I.D. A support vector machine algorithm to classify lithofacies and model permeability in heterogeneous reservoirs. Eng. Geol. 2010, 114, 267–277. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, G. Principle and Application of Uncertainty Support Vector Machine; Science Press: Beijing, China, 2007; pp. 55–85. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. Presented at the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Sun, Z.; Jiang, B.; Xiao, K.; Li, J. Prediction of fracture aperture in bedrock buried hill oil reservoir based on novel ensemble learning algorithm. Petrpleum Geol. Recovery Effic. 2020, 27, 32–38. [Google Scholar]
- Hope, I.A.; Jorge, A.C.; Vidhyadhar, M.; Ipsita, G.; Jose, A.R. An Integrated Machine-Learning Approach to Shale-Gas Supply-Chain Optimization and Refrac Candidate Identification. Presented at the SPE Reservoir Evaluation & Engineering, San Antonio, TX, USA, 9–11 October 2017. [Google Scholar]
- Bolón-Canedo, V.; Alonso-Betanzos, A. Ensembles for feature selection: A review and future trends. Inf. Fusion 2019, 52, 1–12. [Google Scholar] [CrossRef]
- Ruan, Q.; Wu, Q.; Wang, Y.; Liu, X.; Miao, F. Effective learning model of user classification based on ensemble learning algorithms. Computing 2019, 101, 531–545. [Google Scholar] [CrossRef]


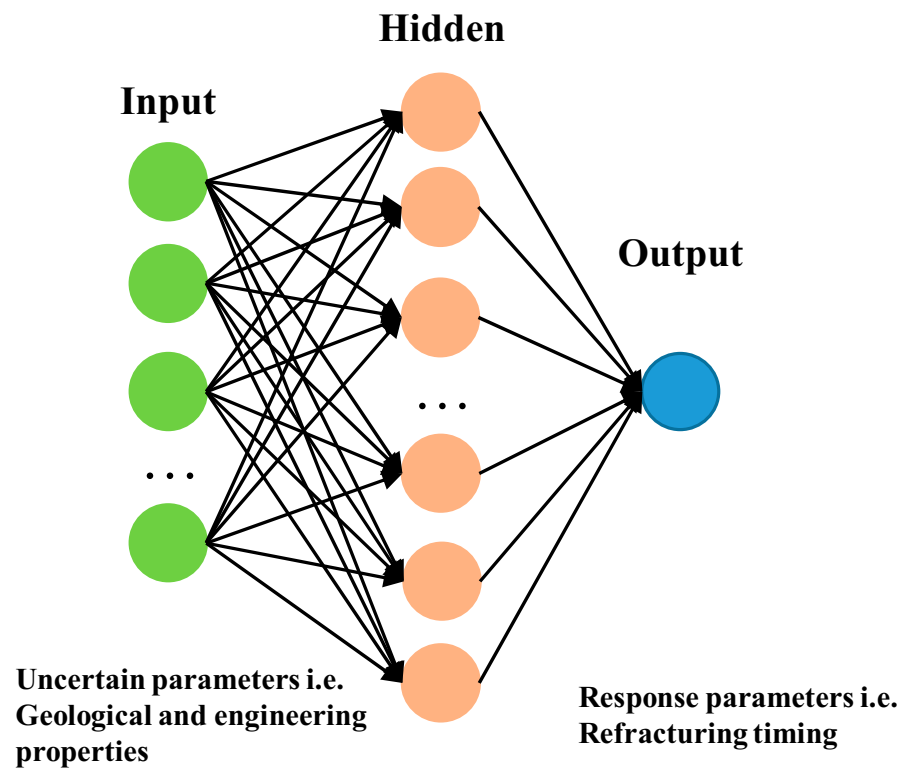



| Input | Output | |
|---|---|---|
| Geological properties | Matrix permeability | Refracturing timing |
| Matrix porosity | ||
| Reservoir pressure | ||
| Effective reservoir thickness | ||
| Oil saturation | ||
| Engineering properties | Fracture half-length | |
| Fracture conductivity | ||
| Fracture spacing | ||
| Fracturing fluid consumption | ||
| Footage of horizontal well | ||
| Bottom hole pressure | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Ren, J.; Feng, Q.; Wang, X.; Wang, W. Prediction of Refracturing Timing of Horizontal Wells in Tight Oil Reservoirs Based on an Integrated Learning Algorithm. Energies 2021, 14, 6524. https://doi.org/10.3390/en14206524
Zhang X, Ren J, Feng Q, Wang X, Wang W. Prediction of Refracturing Timing of Horizontal Wells in Tight Oil Reservoirs Based on an Integrated Learning Algorithm. Energies. 2021; 14(20):6524. https://doi.org/10.3390/en14206524
Chicago/Turabian StyleZhang, Xianmin, Jiawei Ren, Qihong Feng, Xianjun Wang, and Wei Wang. 2021. "Prediction of Refracturing Timing of Horizontal Wells in Tight Oil Reservoirs Based on an Integrated Learning Algorithm" Energies 14, no. 20: 6524. https://doi.org/10.3390/en14206524
APA StyleZhang, X., Ren, J., Feng, Q., Wang, X., & Wang, W. (2021). Prediction of Refracturing Timing of Horizontal Wells in Tight Oil Reservoirs Based on an Integrated Learning Algorithm. Energies, 14(20), 6524. https://doi.org/10.3390/en14206524






