Techno-Economic Efficiency Analysis of Various Operating Strategies for Micro-Hydro Storage Using a Pump as a Turbine
Abstract
1. Introduction
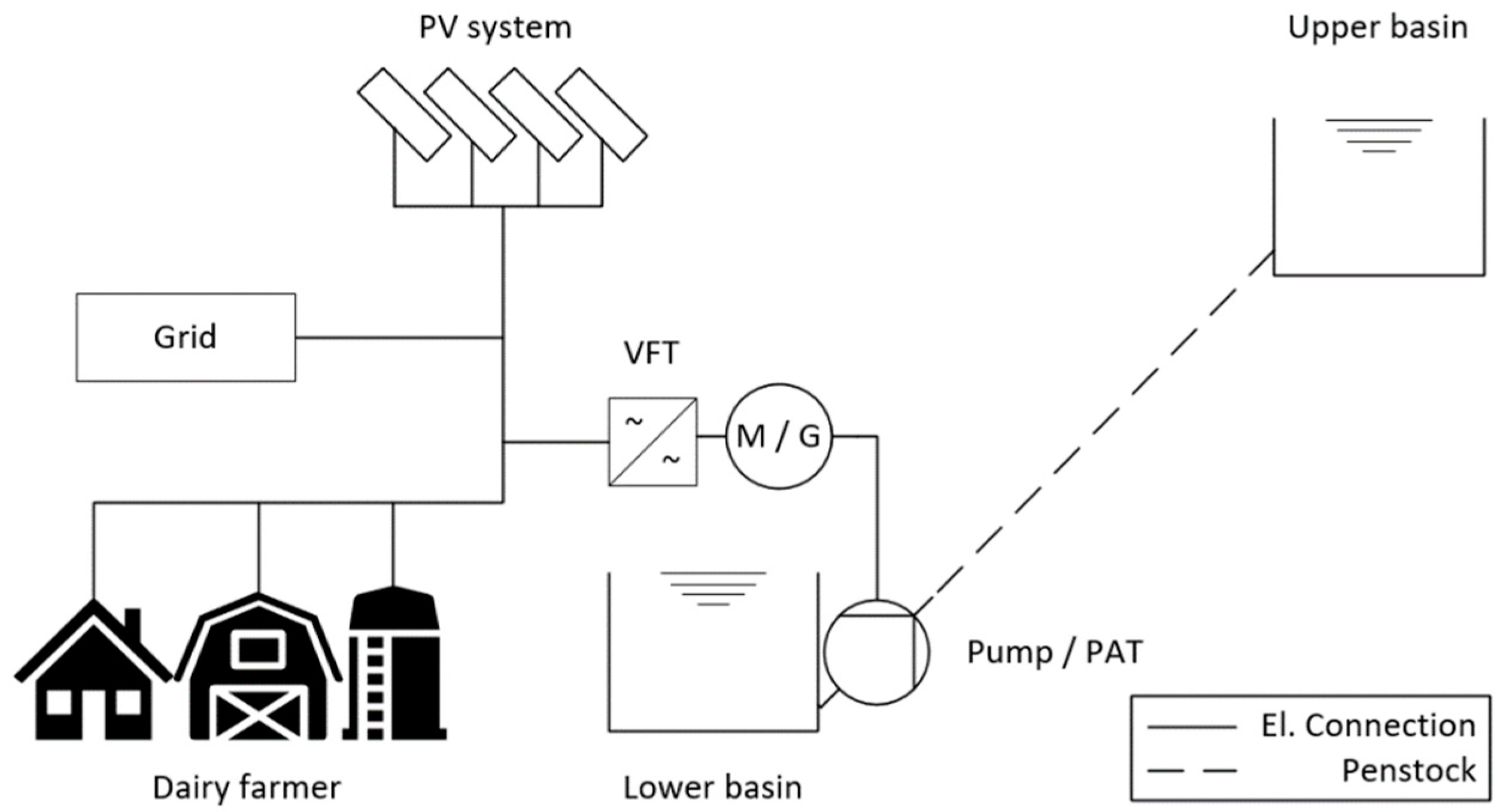
2. Micro-Hydro Storage System and Operating Strategies
2.1. Operating Strategies
2.1.1. Fixed Operating Point
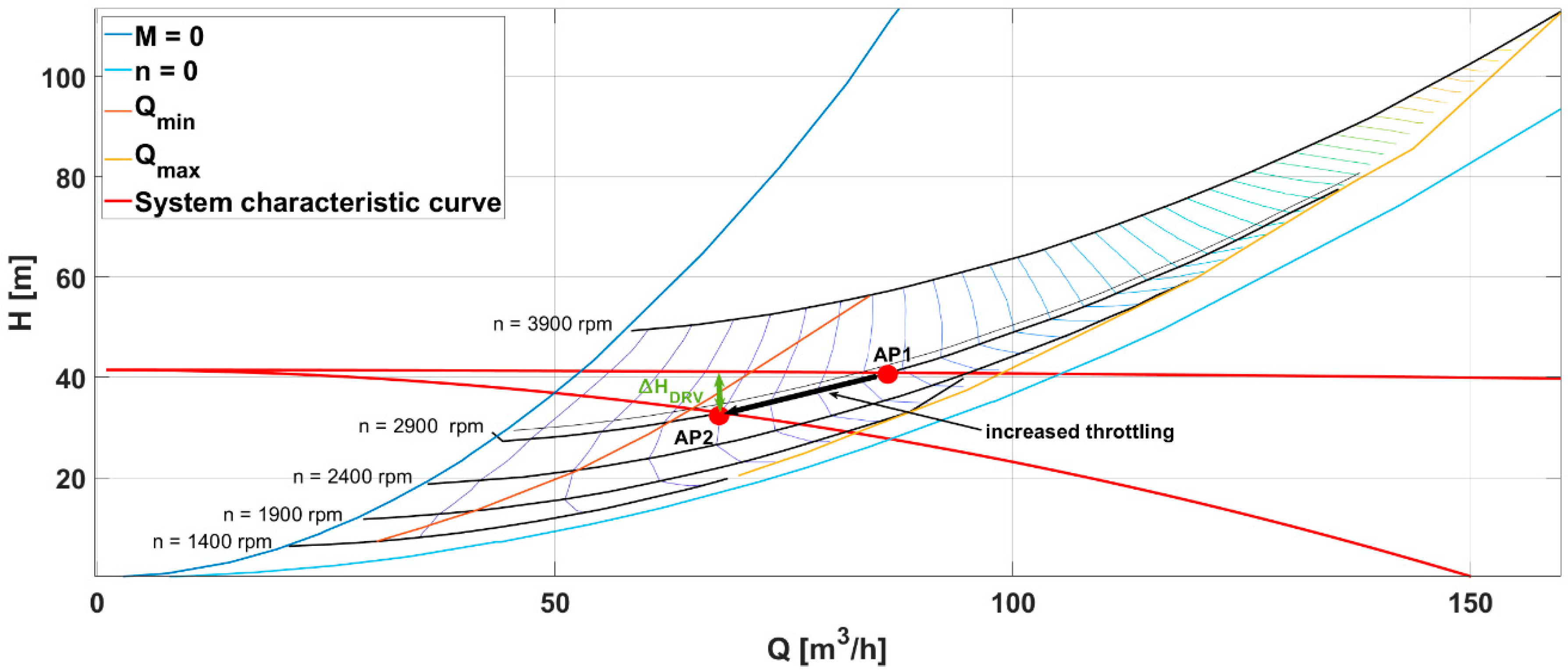
2.1.2. Throttle Control
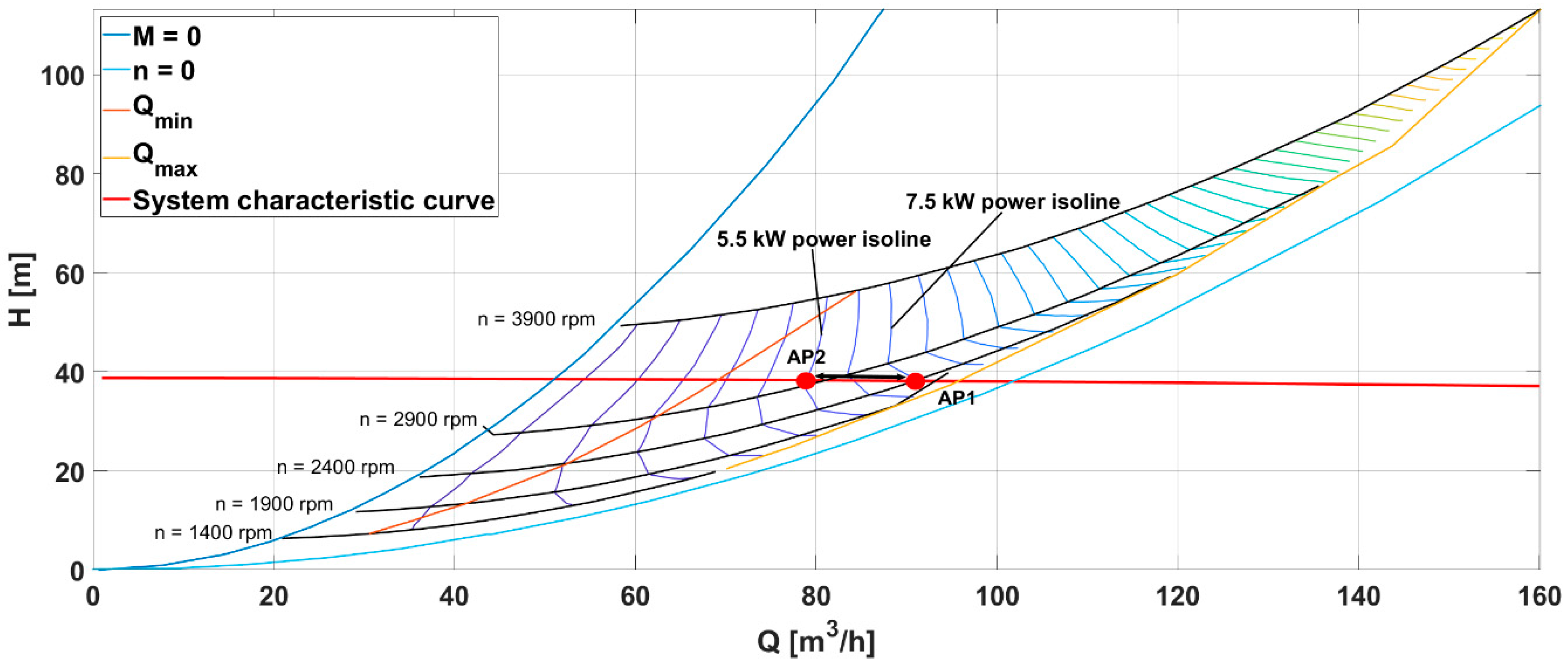
2.1.3. Speed Control with a Frequency Converter
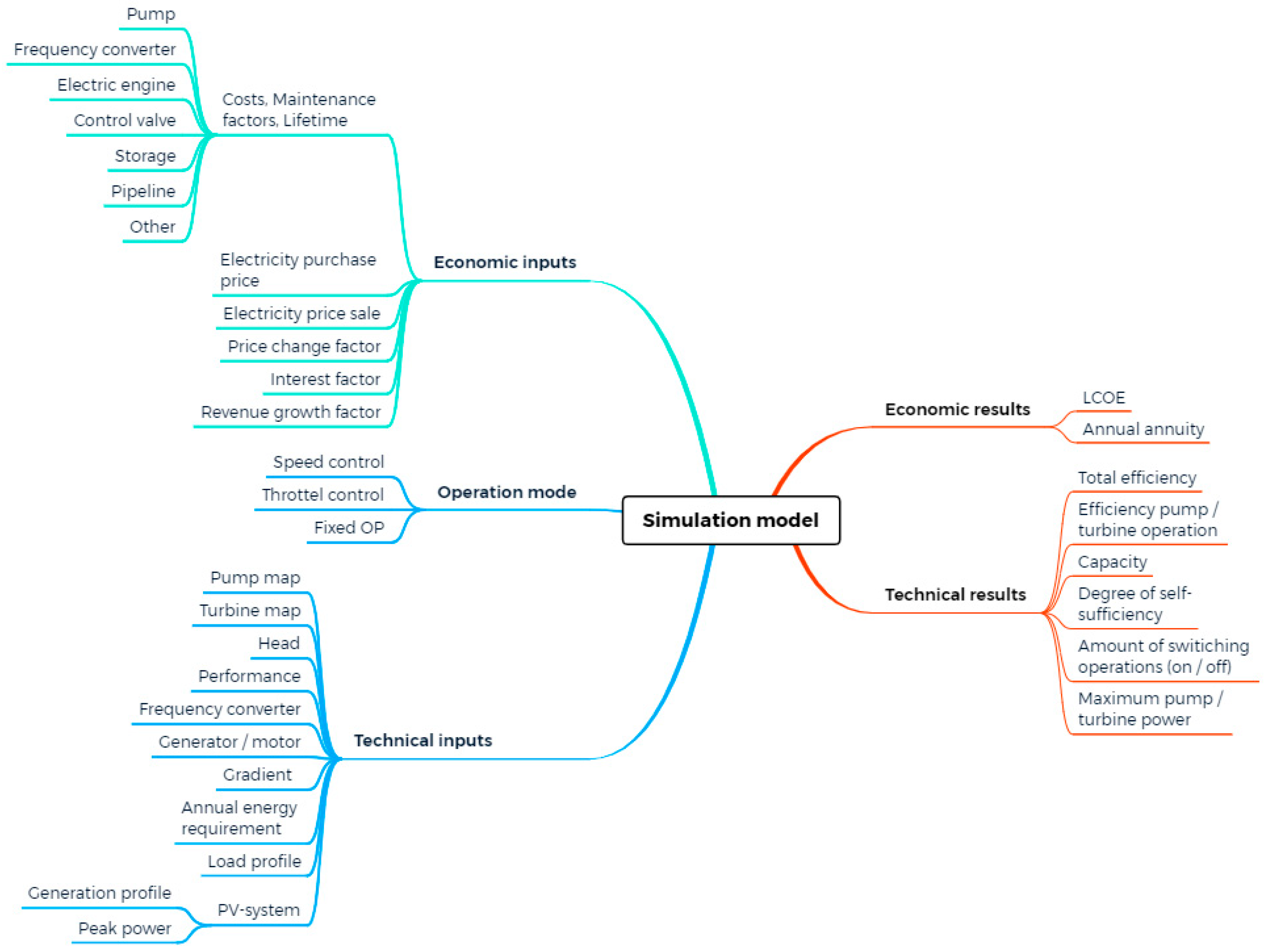
2.2. The Simulation Model
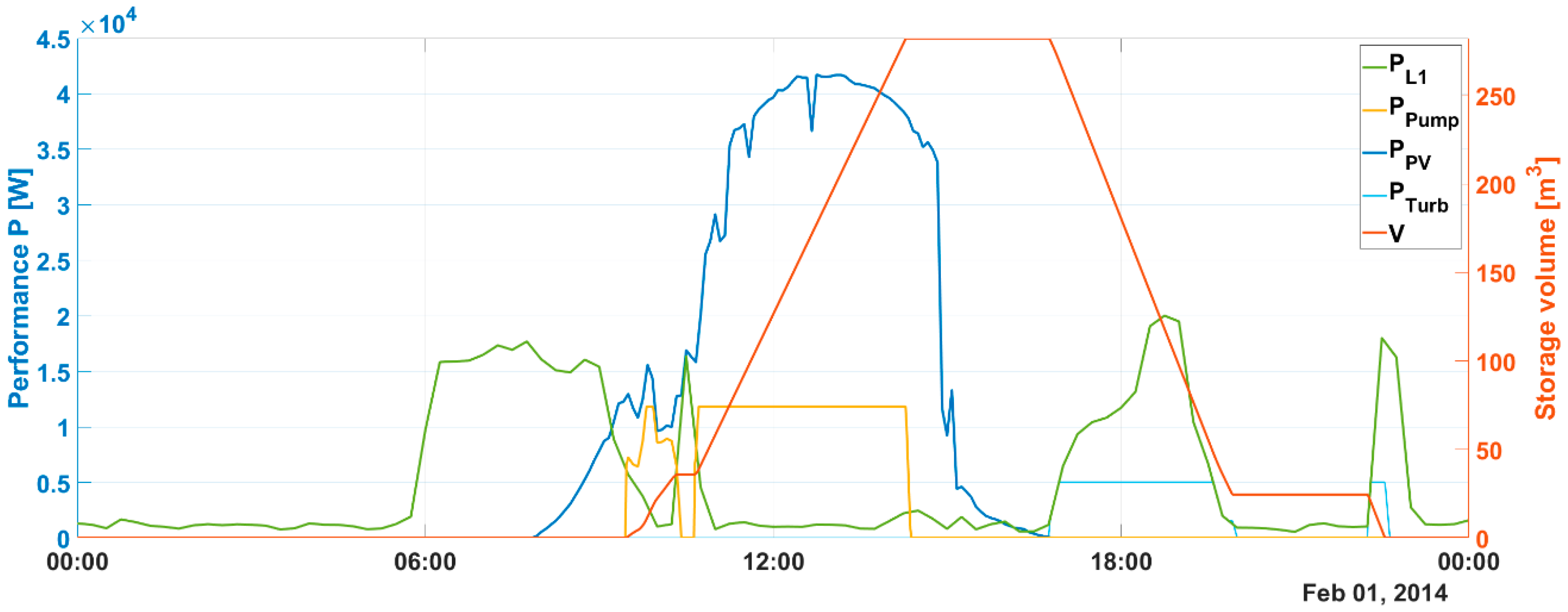
2.2.1. Inputs and Basic Data
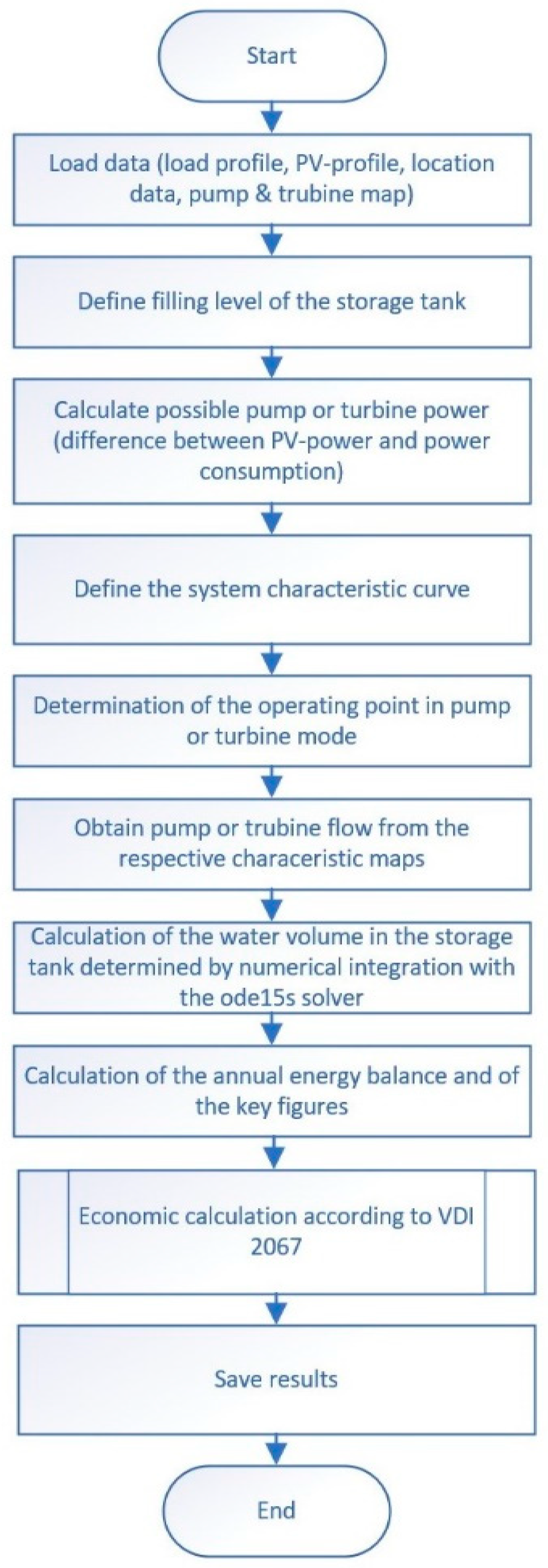
2.2.2. Program Sequence
2.2.3. Finding the Optimal Site
3. Results and Discussion
3.1. Technical Results and Discussion
3.2. Economic Results and Discussion
3.2.1. Annuity Calculation Results for Speed Control
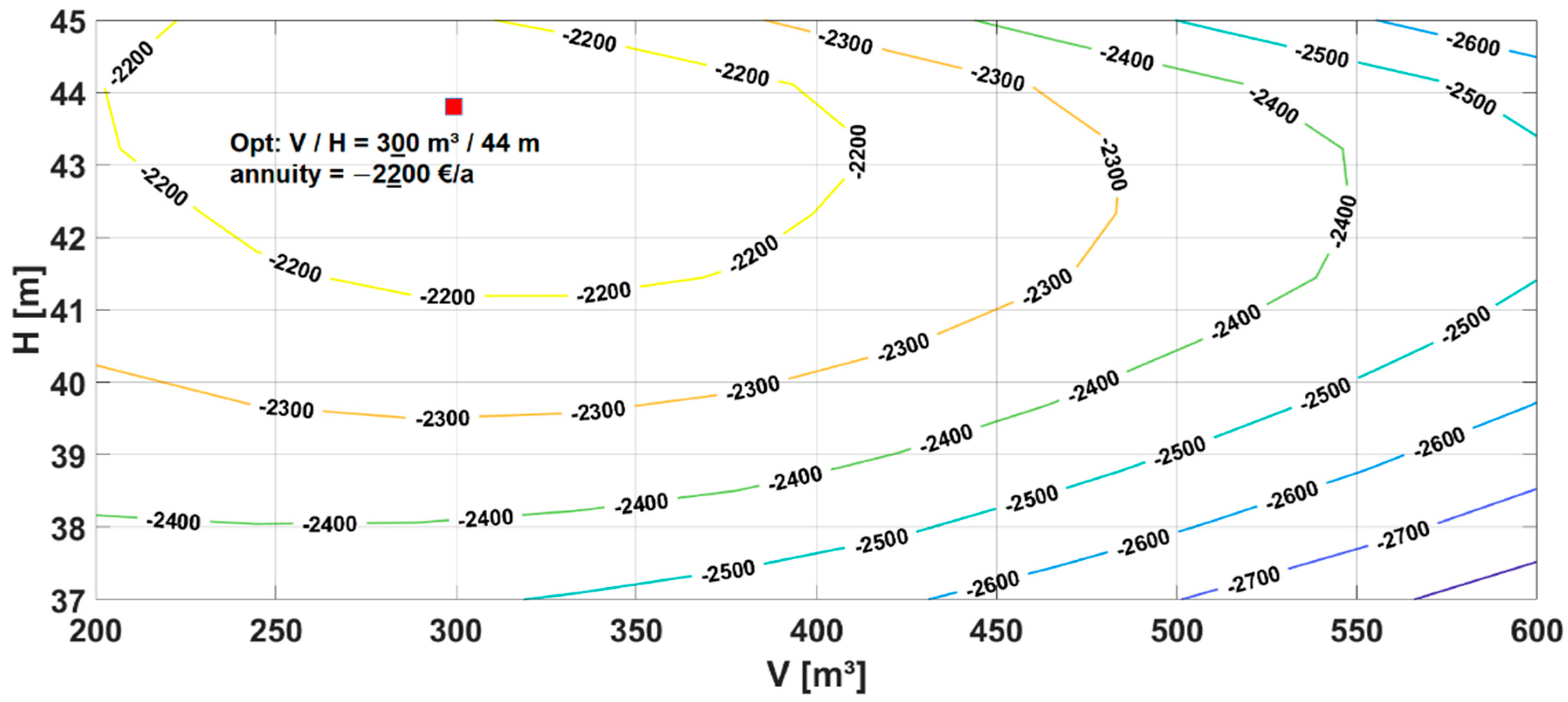
3.2.2. Annuity Calculation Results for the Fixed OP
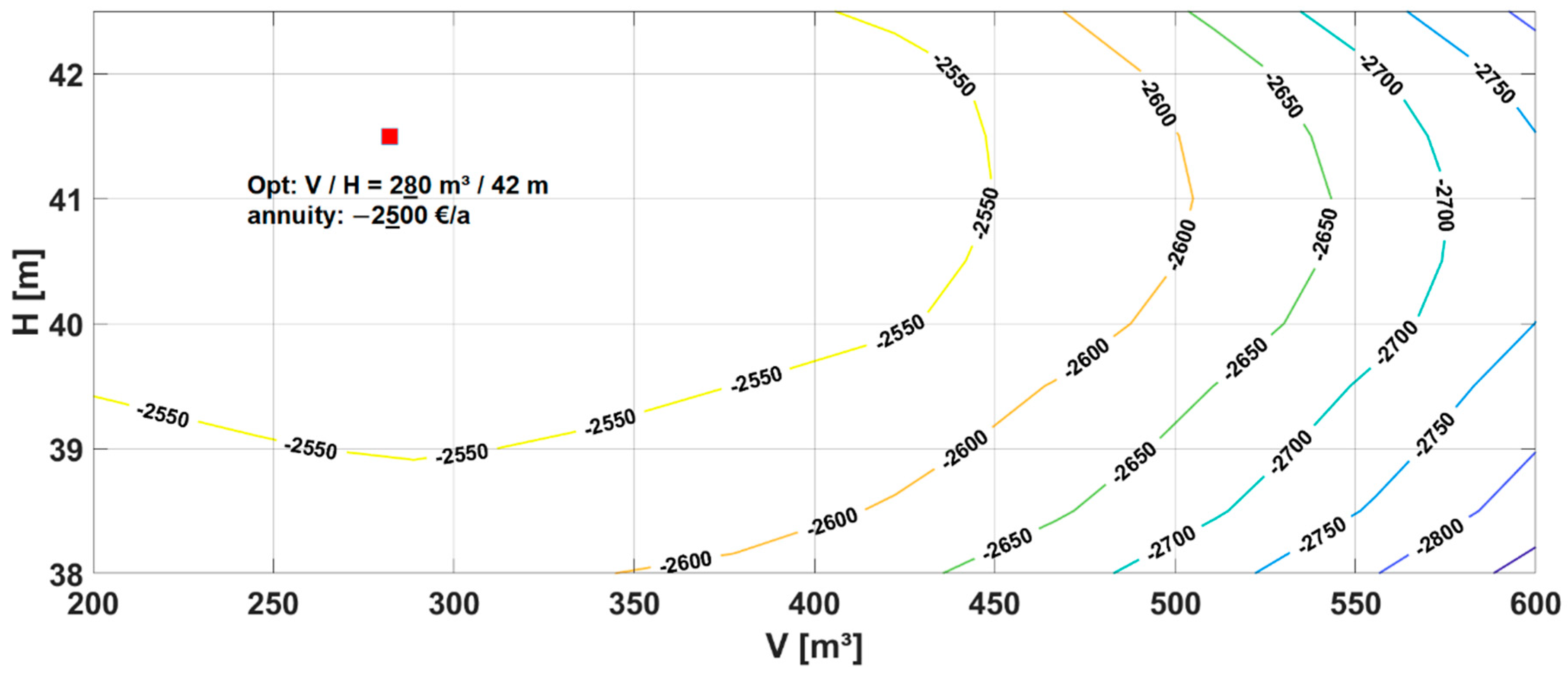
3.2.3. Annuity Calculation Results for Throttle Control
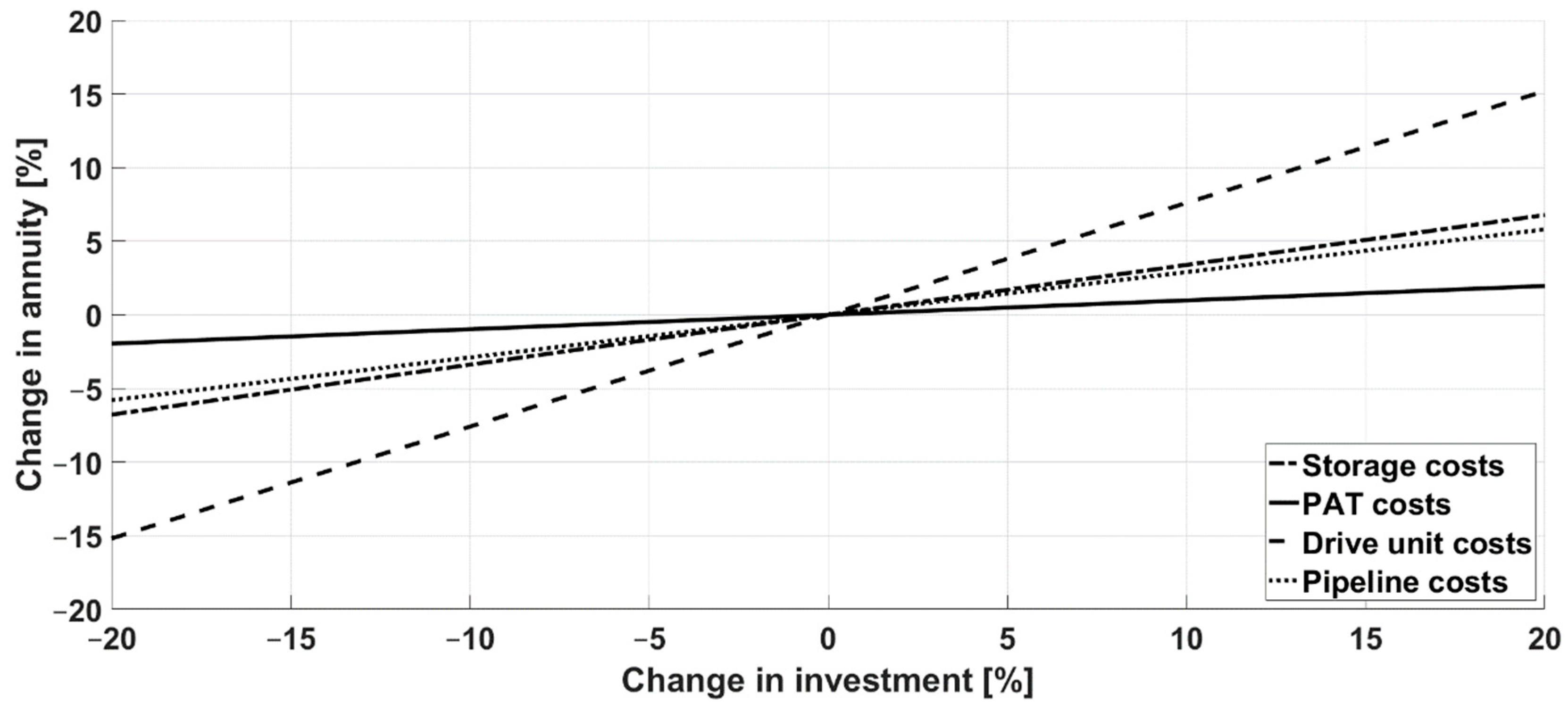
3.2.4. Sensitivity Analysis and Comparison of the Different Operating Modes with Increasing Energy Procurement Costs
3.2.5. LCOE Calculation and Comparison with Other Scientific Research Findings
4. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol/Abbreviation | Interpretation |
| annuity factor | |
| total annual payments or income | |
| annuity of the maintenance costs | |
| annuity of the operation-related costs | |
| annuity of the proceeds | |
| annuity of the capital-related costs | |
| annuity of the other costs | |
| annuity of the demand-related costs | |
| sum of costs | |
| cash value factor | |
| nominal pipeline diameter | |
| possible energy sales proceeds | |
| Darcy friction factor | |
| repair expenditure | |
| service factor | |
| gravitational acceleration | |
| head | |
| head loss | |
| geodetic head | |
| optimized head | |
| discount rate | |
| investment costs storage | |
| investment costs pipeline | |
| investment costs electrical components | |
| investment costs pump | |
| investment costs throttle element | |
| remaining investment costs | |
| levelized cost of energy | |
| pipeline length | |
| torque | |
| rpm | |
| number of replacements | |
| operating and maintenance costs | |
| pressure loss | |
| load profile | |
| maximum power in pump mode | |
| pump power | |
| turbine power | |
| power loss | |
| PV power | |
| number of pump start-ups | |
| interest factor | |
| flow rate | |
| maximum flow rate | |
| minimum flow rate | |
| price change factor | |
| reinvestment costs | |
| residual values | |
| year | |
| observation period | |
| service life | |
| number of turbine start-ups | |
| water velocity | |
| volume flow | |
| storage capacity | |
| optimized storage capacity | |
| energy obtained from the grid | |
| total energy input | |
| total energy requirement | |
| total energy output | |
| energy drawn from the pumped storage | |
| Greek letters | Interpretation |
| individual dynamic loss coefficient of fittings | |
| total dynamic loss coefficient of fittings | |
| efficiency | |
| efficiency of the electrical components in the drive unit | |
| average pump efficiency | |
| electrical pump efficiency | |
| average turbine efficiency | |
| total efficiency | |
| electrical turbine efficiency | |
| coefficient of friction | |
| pi | |
| density |
Appendix A
Appendix A.1. Annuity and Price Change Factor
Appendix A.2. Cost Calculation
Appendix A.2.1. Capital-Related Costs
Appendix A.2.2. Demand-Related Costs
Appendix A.2.3. Operation-Related Costs
Appendix A.2.4. Other Costs
Appendix A.3. Proceeds
Appendix A.4. Annuity of Total Annual Payments
References
- Photovoltaics Report. Available online: https://www.ise.fraunhofer.de/content/dam/ise/de/documents/publications/studies/Photovoltaics-Report.pdf (accessed on 1 June 2020).
- Photovoltaik-Anlagen Dürfen Nach Ende der EEG-Förderung Nicht Einfach Wild Einspeisen. Available online: https://www.pv-magazine.de/2019/08/01/pv-anlagen-duerfen-nach-ende-der-eeg-foerderung-nicht-einfach-wild-einspeisen/ (accessed on 1 June 2020).
- Stock Market Electricity Price at EPEX-Spot Market for Germany/Austria and Germany/Luxemburg. Available online: https://de.statista.com/statistik/daten/studie/289437/umfrage/strompreis-am-epex-spotmarkt/ (accessed on 1 June 2020).
- Bundesnetzsagentur; Bundeskartellamt. Bundesnetzagentur—Monitoringbericht 2019. 2020, p. 298. Available online: https://bundesnetzagentur.de/SharedDocs/Mediathek/Berichte/2019/Monitoringbericht_Energie2019.pdf (accessed on 1 June 2020).
- Strompreise* für Haushalte in den Ländern der EU-28 im Jahr 2018. Available online: https://de.statista.com/statistik/daten/studie/197196/umfrage/elektrizitaetspreise-ausgewaehlter-europaeischer-laender/ (accessed on 1 June 2020).
- Ramos, M.H.; Dadfar, A.; Basharat, M.; Adeyeye, K. Inline pumped storage hydropower towards smart and flexible energy recovery in water networks. Water 2020, 12, 2224. [Google Scholar] [CrossRef]
- De Marchis, M.; Fontanazza, C.M.; Freni, G.; Messineo, A.; Milici, B.; Napoli, E.; Notaro, V.; Puleo, V.; Scopa, A. Energy recovery in water distribution networks. Implementation of pumps as turbine in a dynamic numerical model. Procedia Eng. 2014, 70, 439–448. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, M.H. Pump as Turbine (PAT) design in water distribution network by system effectiveness. Water 2013, 5, 1211–1225. [Google Scholar] [CrossRef]
- Fecarotta, O.; Ramos, H.; Derakhshan, S.; Del Giudice, G.; Carravetta, A. Fine tuning a PAT hydropower plant in a water supply network to improve system effectiveness. J. Water Resour. Plan. Manag. 2018, 144, 04018038. [Google Scholar] [CrossRef]
- Ramos, H.; McNabola, A.; Lopez-Jimenez, P.A.; Perez-Sanchez, M. Smart water management towards future water sustainable networks. Water 2020, 12, 58. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H. Energy production in water distribution networks: A PAT design strategy. Energies 2013, 6, 411–424. [Google Scholar] [CrossRef]
- Madeira, C.F.; Fernandes, F.P.J.; Perez-Sanchez, M.; Lopez-Jimenez, P.A.; Ramos, M.H.; Branco, P.J.C. Electro-hydraulic transient regimes in isolated pumps working as turbines with self-excited induction generators. Energies 2020, 13, 4521. [Google Scholar] [CrossRef]
- Stepanoff, A.J. Centrifugal and Axial Flow Pumps, Design and Applications, 2nd ed.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 1957; Available online: https://wrap.warwick.ac.uk/36099/ (accessed on 1 June 2020).
- Gülich, J.F. Turbinenbetrieb. Allgemeines kennfeld. In Kreiselpumpen; Springer: Berlin/Heidelberg, Germany, 2013; Volume 4, pp. 847–870. [Google Scholar]
- Alatorre-Frenk, C. Cost Minimization in Microhydro Systems Using Pumps-as-Turbines. Ph.D. Thesis, University of Warwick, Coventry, UK, 1994; pp. 55–113. [Google Scholar]
- Derakhshan, S.; Nourbakhsh, A. Experimental study of characteristic curves of centrifugal pumps working as turbine in different specific speeds. Exp. Therm. Fluid Sci. 2008, 32, 800–807. [Google Scholar] [CrossRef]
- Yang, S.; Derakhshan, S.; Kong, F. Theoretical, numerical and experimental prediction of pump as turbine performance. Renew. Energy 2012, 48, 507–513. [Google Scholar] [CrossRef]
- Pugliese, F.; De Paola, F.; Fontana, N.; Giugni, M.; Marini, G. Experimental characterization of two Pumps as Turbines. Renew. Energy 2016, 99, 180–187. [Google Scholar] [CrossRef]
- Stefanizzi, M.; Torresi, M.; Fortunato, B.; Camporeale, S.M. Experimental investigation and performance prediction modeling of a single stage centrifugal pump operation as turbine. Energy Procedia 2017, 126, 589–596. [Google Scholar] [CrossRef]
- Barbarelli, S.; Amelio, M.; Florio, G. Experimental activity at test rig validation correlations to select pumps running as turbines in micro hydro plants. Energy Convers. Manag. 2017, 149, 781–797. [Google Scholar] [CrossRef]
- Anilkumar, T.T.; Simon, S.P.; Padhy, N.P. Residential electricity cost minimization model through open well-pico turbine pumped storage system. Appl. Energy 2017, 195, 23–35. [Google Scholar] [CrossRef]
- Morabito, A.; Steimes, J.; Bontems, O.; Al Zohbi, G.; Hendrick, P. Set-up of a pump as turbine use in micro-pumped hydro energy storage: A case study in Froyennes Belgium. J. Phys. Conf. Ser. 2017, 813, 012033. [Google Scholar] [CrossRef]
- Morabito, A.; Hendrick, P. Pump as turbine applied to micro energy storage and smart water grids: A case study. Appl. Energy 2019, 241, 567–579. [Google Scholar] [CrossRef]
- de Oliveira e Silva, G.; Hendrick, P. Pumped hydro energy storage in buildings. Appl. Energy 2016, 179, 1242–1250. [Google Scholar] [CrossRef]
- Borkowski, D. Analytical model of small hydropower plant working at variable speed. IEEE Trans. Energy Convers. 2018, 33, 1886–1894. [Google Scholar] [CrossRef]
- Barbarelli, S.; Amelio, M.; Florio, G. Predictive model estimating the performances of centrifugal pumps used as turbines. Energy 2016, 107, 103–121. [Google Scholar] [CrossRef]
- Vasudevan, K.R.; Ramachandaramurthy, V.K.; Gomathi, V.; Ekanayake, J.B.; Tiong, S.K. Modelling and simulation of variable speed pico hydel energy storage system for microgrid applications. J. Energy Storage 2019, 24, 100808. [Google Scholar]
- Mohanpurkar, M.; Ouroua, A.; Hovsepian, R.; Luo, Y.; Singh, M.; Muljadi, E.; Gevorgian, V.; Donalek, P. Real-time co-simulation of adjustable-speed pumped storage hydro for transient stability analysis. Electr. Power Syst. Res. 2018, 154, 276–286. [Google Scholar] [CrossRef]
- Schmidt, J.; Kemmetmüller, W.; Kugi, A. Modeling and static optimization of a variable speed pumped storage power plant. Renew. Energy 2017, 111, 38–51. [Google Scholar] [CrossRef]
- Stoppato, A.; Benato, A.; Destro, N.; Mirandola, A. A model for the optimal design and management of a cogenartion system with energy storage. Energy Build. 2016, 124, 241–247. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L.; Peng, J. Pumped storage-based standalone photovoltaic power generation system: Modeling and techno economic optimization. Appl. Energy 2015, 137, 649–659. [Google Scholar] [CrossRef]
- Yang, W.; Yang, J. Advantage of variable-speed pumped storage plants for mitigating wind power variations: Integrated modelling and performance assessment. Appl. Energy 2019, 237, 720–732. [Google Scholar] [CrossRef]
- Simao, M.; Ramos, H. Hybrid pumped hydro storage energy solutions towards wind and PV integration: Improvement on flexibility, reliability and energy costs. Water 2020, 12, 2457. [Google Scholar] [CrossRef]
- Morabito, A.; Furtado, A.; Gilton, C.; Hendrick, P. Variable speed regulation for pump as turbine in micro pumped hydro energy storage. In Proceedings of the 38th IAHR World Congress, Panama City, Panama, 1–6 September 2019. [Google Scholar]
- Recknagel, H.; Sprenger, E.; Schramek, E.-R. Taschenbuch für Heizung + Klimatechnik; Oldenbourg Industrieverlag: München, Germany, 2008. [Google Scholar]
- Beschneiungsanlage Erhält Wasserspeicher. Available online: https://bnn.de/lokales/abb/beschneiungsanlage-erhaelt-waserspeicher (accessed on 30 April 2020).
- Fahrner, H.; (Nationalpark-Hotel Schliffkopf, Schliffkopf, Germany); Lugauer, F.J.; (TUM Campus Straubing for Biotechnology and Sustanability, Weihenstephan-Triesdorf University of Applied Science, Straubing, Germany). Personal communication, 2020.
- Carravetta, A.; Houreh, D.S.; Ramos, H. Rotational speed selection. In Pumps as Turbine; Springer Nature: Cham, Switzerland, 2018; p. 87. [Google Scholar]
- Gülich, J.F. Verhalten der Kreiselpumpen in Anlagen. In Kreiselpumpen; Springer: Berlin/Heidelberg, Germany, 2013; Volume 4, pp. 809–814. [Google Scholar]
- Kainz, J.; (TUM Campus Straubing for Biotechnology and Sustanability, Weihenstephan-Triesdorf University of Applied Science, Straubing, Germany); Lugauer, F.J.; (TUM Campus Straubing for Biotechnology and Sustanability, Weihenstephan-Triesdorf University of Applied Science, Straubing, Germany). Personal communication, 2018.
- Neser, S. Energiebedarf und Einsparmöglichkeiten in der Rinderhaltung; Bayerische Landesanstalt für Landwirtschaft (LfL): Freising, Germany, 2014; Volume 1, pp. 7–22. [Google Scholar]
- Vorpahl, L.; (KSB SE & Co. KGaA, Frankenthal, Germany); Huber, B.; (TUM Campus Straubing for Biotechnology and Sustanability, Straubing, Germany). Personal communication, 2017.
- MAX LAMB GMBH & CO. KG, KAT-ABSRIE-0415. Available online: https://www.lamb.de/fileadmin/KAT-ABSRIE-0415.pdf (accessed on 28 January 2020).
- KSB Aktiengesellscahft. Selecting Centrifugal Pumps; KSB Aktiengesellschaft: Frankenthal, Germany, 2005; Volume 4, pp. 19–31. [Google Scholar]
- Menny, K. Strömungsmaschinen; Teubner: Wiesbaden, Germany, 1985; ISBN 978-3-519-06317-9. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Mathworks. Global Optimization Toolbox: Simulated Annealing (r2019a). Available online: https://de.mathworks.com/help/gads/simulannealbnd.html (accessed on 28 January 2020).
- Quaschning, V. Wasserkraft. Regenerative Energiesysteme; Carl Hanser Verlag: Munich, Germany, 2015; Volume 9, pp. 327–346. [Google Scholar]
- Association of German Engineers. Economic Efficiency of Building Installations—Fundamentals and Economic Calculation; Verein Deutscher Ingenieure e.V.: Düsseldrof, Germany, 2012; pp. 29–36. [Google Scholar]
- Branker, K.; Pathak, M.J.M.; Pearce, J.M. A review of solar photovoltaic levelized cost of electricity. Renew. Sustain. Energy Rev. 2011, 15, 4470–4482. [Google Scholar] [CrossRef]
- Morabito, A.; de Olivia e Silvia, G.; Hendrick, P. Deriaz-pump-turbine for pumped hydro energy storage and micro applications. J. Energy Storage 2019, 24, 100788. [Google Scholar] [CrossRef]


| OP Mode | Storage Capacity | Degree of Self-Sufficiency | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Speed control | 460 m3 | 39 m | 42% | 68% | 62% | 860 | 1000 | 13 kW | 48 kWh | 50% |
| Throttle control | 280 m3 | 42 m | 30% | 63% | 47% | 850 | 990 | 12 kW | 32 kWh | 43% |
| Fixed OP | 300 m3 | 44 m | 35% | 62% | 57% | 920 | 760 | 10 kW | 36 kWh | 44% |
| OP Mode | |||||||
|---|---|---|---|---|---|---|---|
| Speed control | 40 €/m3 | 50 €/m | 16,000 € | 3800 € | 1000 € | 5000 € | 56,000 € |
| Throttle control | 40 €/m3 | 50 €/m | 7200 € | 3800 € | 2500 € | 5000 € | 44,000 € |
| Fixed OP | 40 €/m3 | 50 €/m | 7200 € | 3800 € | 1000 € | 5000 € | 44,000 € |
| Interest Rate | ||||
|---|---|---|---|---|
| Speed control | 0.63 €/kWh | 0.74 €/kWh | 0.86 €/kWh | 0.98 €/kWh |
| Throttle control | 0.85 €/kWh | 0.99 €/kWh | 1.16 €/kWh | 1.33 €/kWh |
| Fixed OP | 0.74 €/kWh | 0.87 €/kWh | 1.01 €/kWh | 1.17 €/kWh |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lugauer, F.J.; Kainz, J.; Gaderer, M. Techno-Economic Efficiency Analysis of Various Operating Strategies for Micro-Hydro Storage Using a Pump as a Turbine. Energies 2021, 14, 425. https://doi.org/10.3390/en14020425
Lugauer FJ, Kainz J, Gaderer M. Techno-Economic Efficiency Analysis of Various Operating Strategies for Micro-Hydro Storage Using a Pump as a Turbine. Energies. 2021; 14(2):425. https://doi.org/10.3390/en14020425
Chicago/Turabian StyleLugauer, Florian Julian, Josef Kainz, and Matthias Gaderer. 2021. "Techno-Economic Efficiency Analysis of Various Operating Strategies for Micro-Hydro Storage Using a Pump as a Turbine" Energies 14, no. 2: 425. https://doi.org/10.3390/en14020425
APA StyleLugauer, F. J., Kainz, J., & Gaderer, M. (2021). Techno-Economic Efficiency Analysis of Various Operating Strategies for Micro-Hydro Storage Using a Pump as a Turbine. Energies, 14(2), 425. https://doi.org/10.3390/en14020425






