Loading Performance of a Novel Shearer Drum Applied to Thin Coal Seams
Abstract
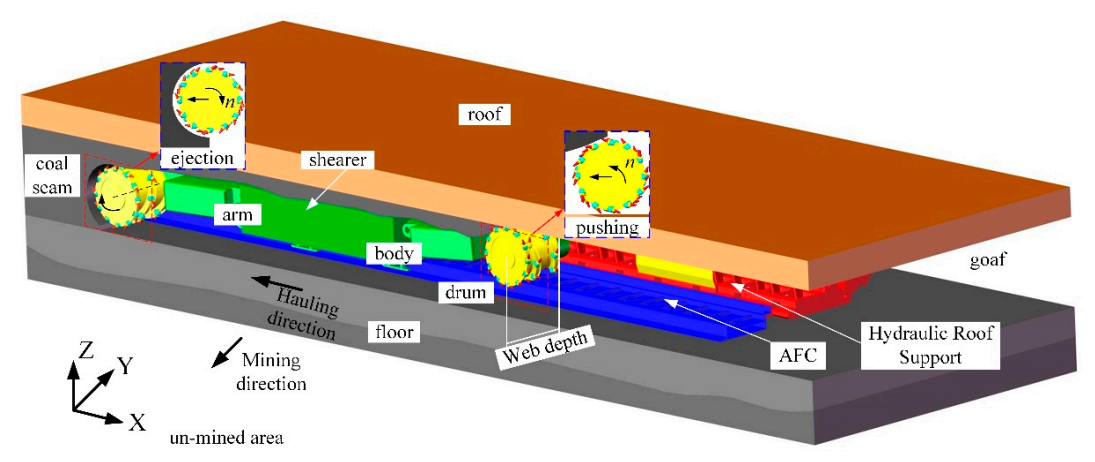
1. Introduction
2. Materials and Methods
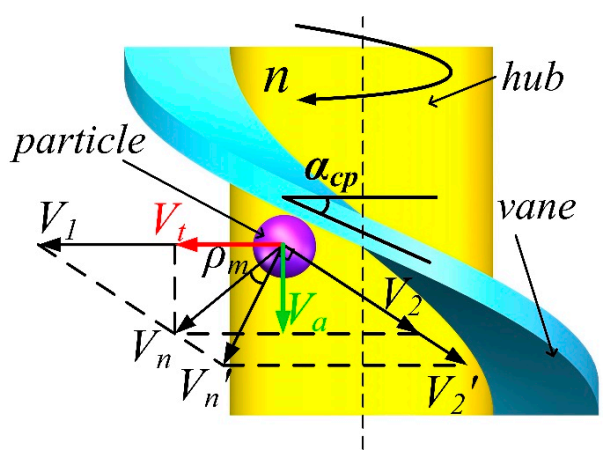
2.1. The Kinematic of the Particle under the Action of Helix Vane
2.2. The Limitation of Coal Flow Speed and Movement Process to Drum Speed
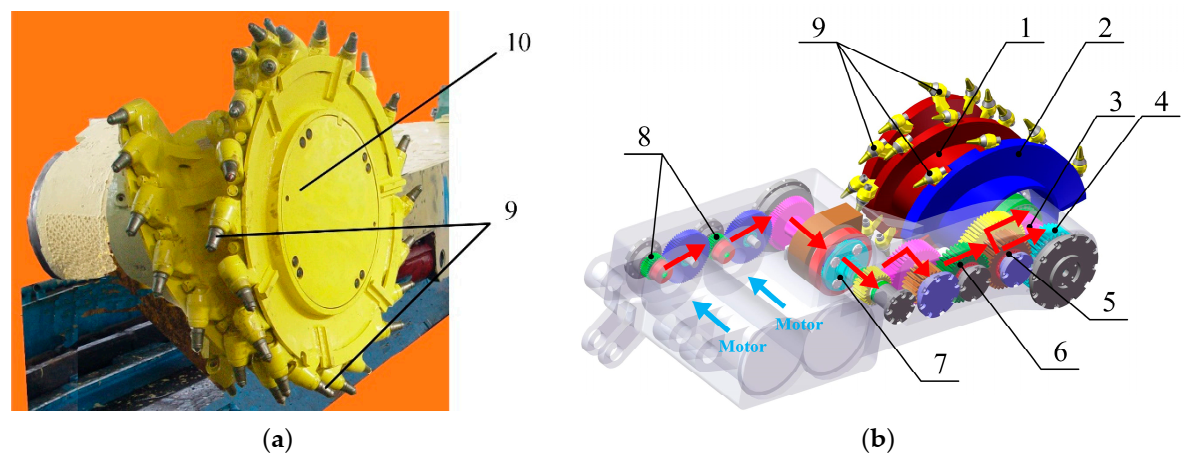
3. The Establishment of Model and Discrete Element Modeling
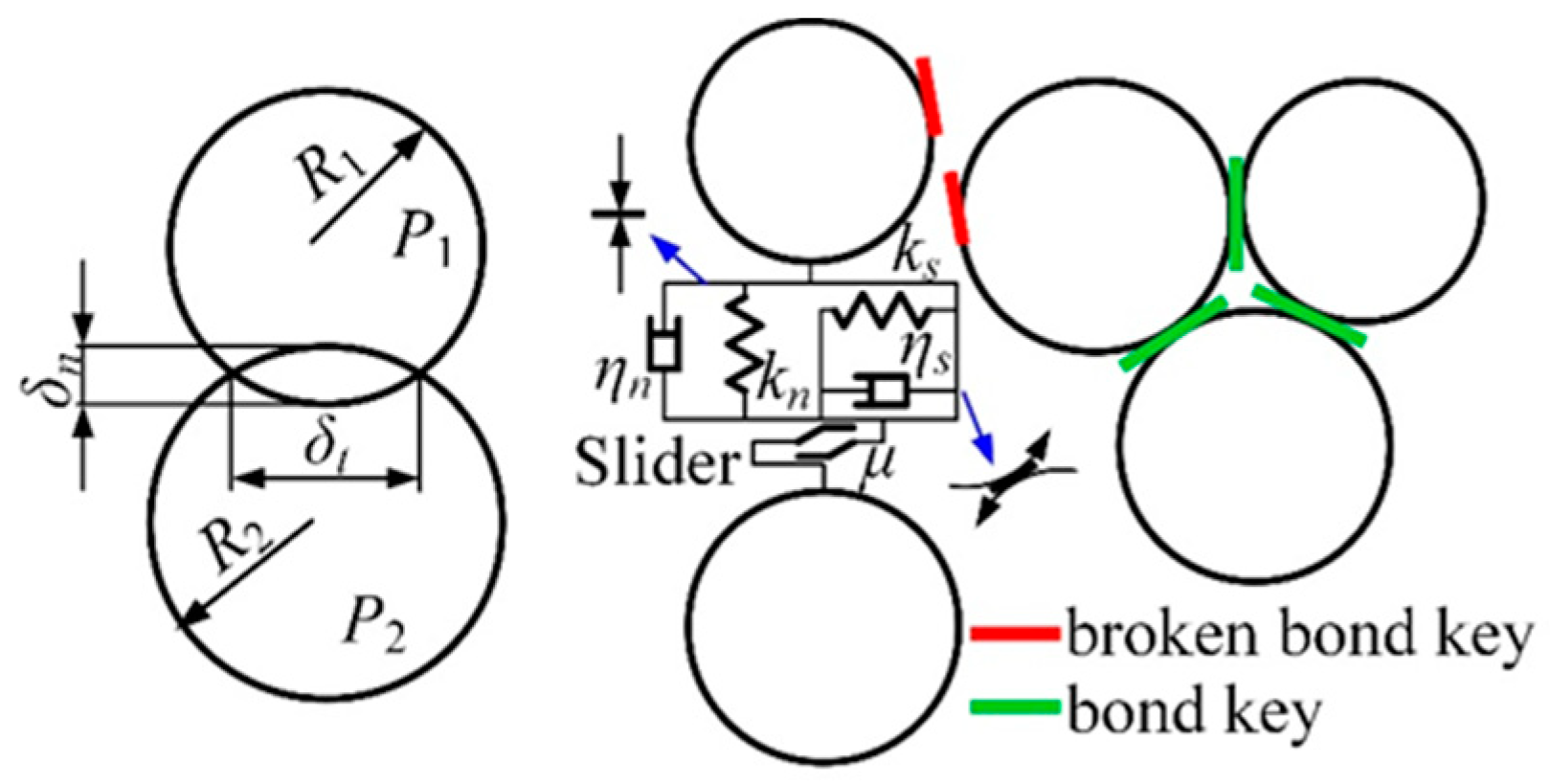
3.1. The Theory of Discrete-Element Method
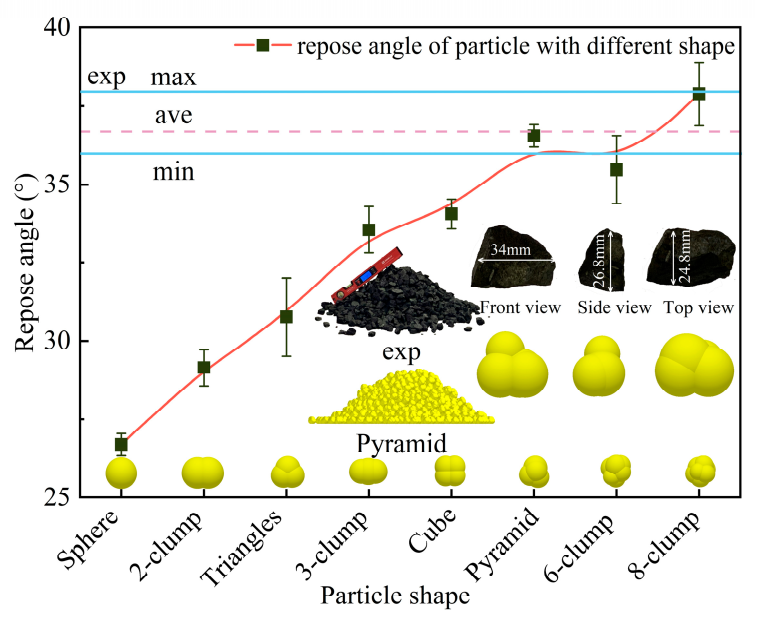
3.2. Model and Calibration of the Particle Shape
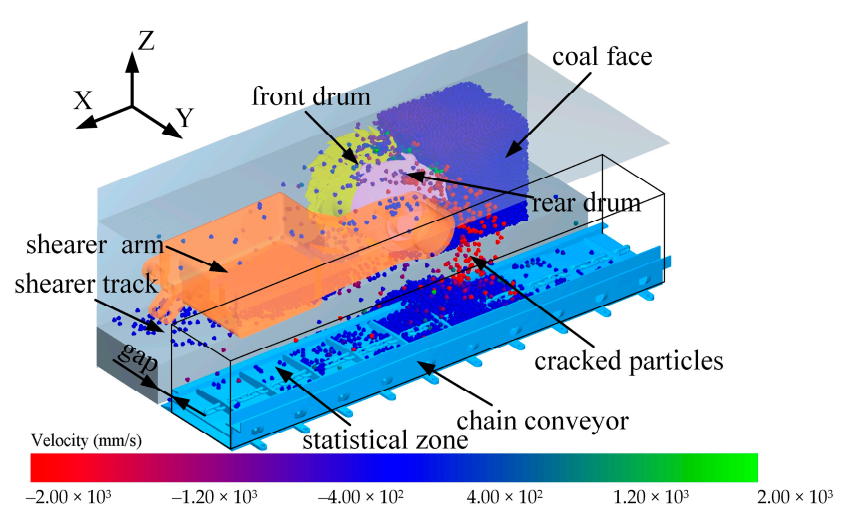
3.3. Establishment of DEM Model
4. Results and Discussion
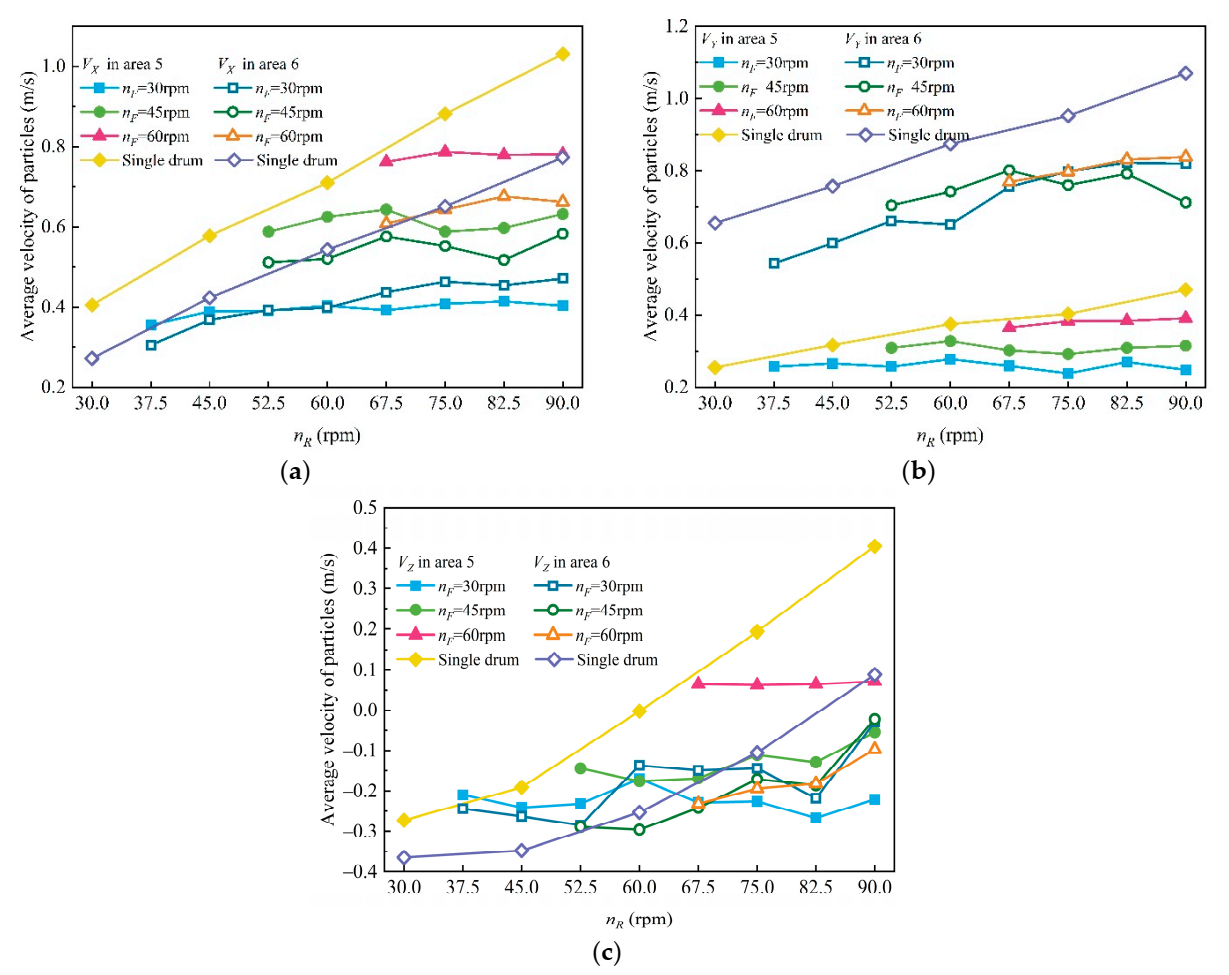
4.1. The Effect of TDRSD on Particle Velocity
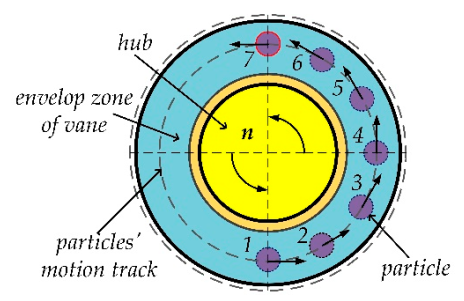
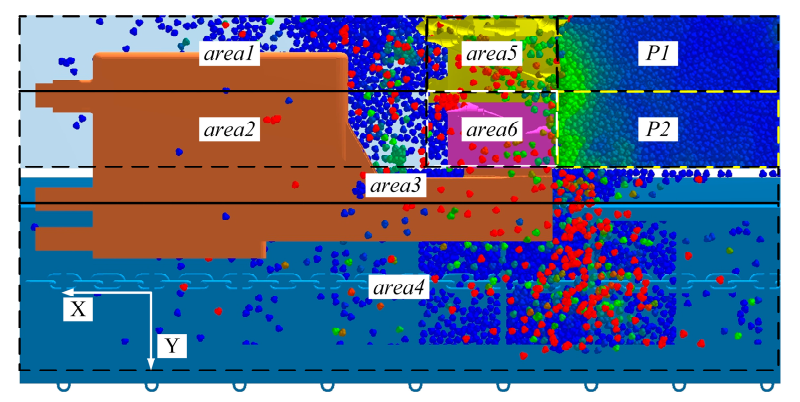
4.2. The Distribution of Particles under the Effect of TDRSD
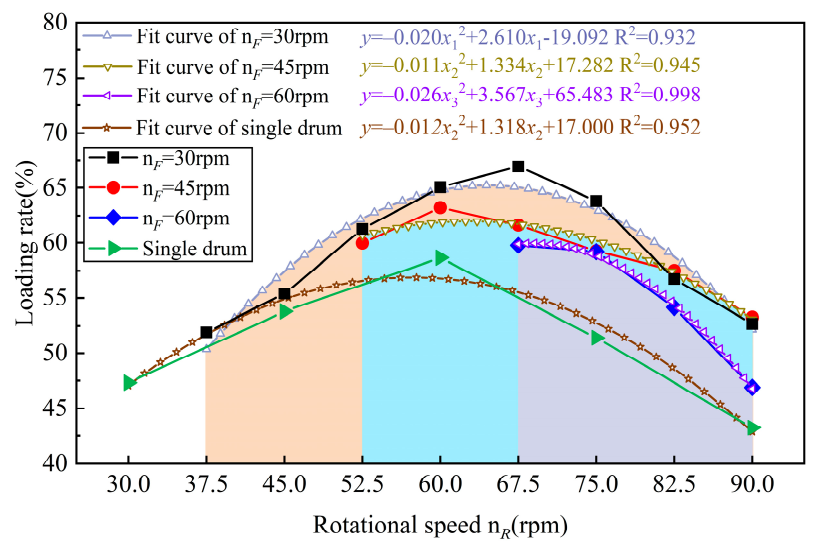
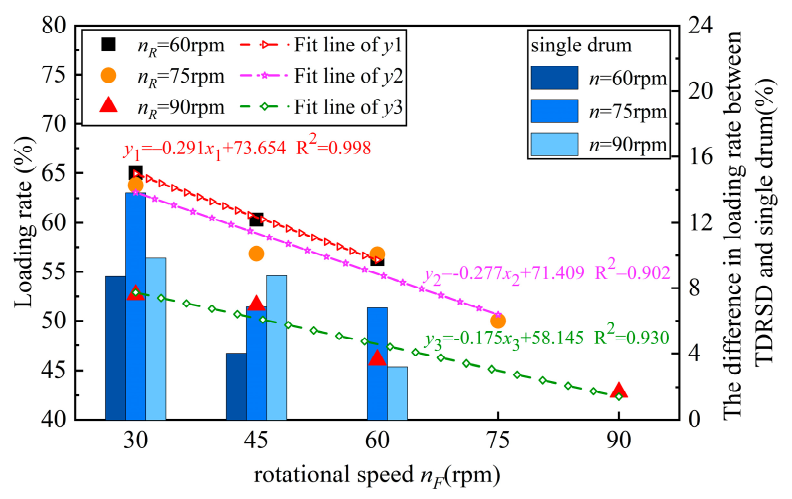
4.3. The Influence of Rotational Speed Matching between the Front and Rear Drums on the Loading Rate
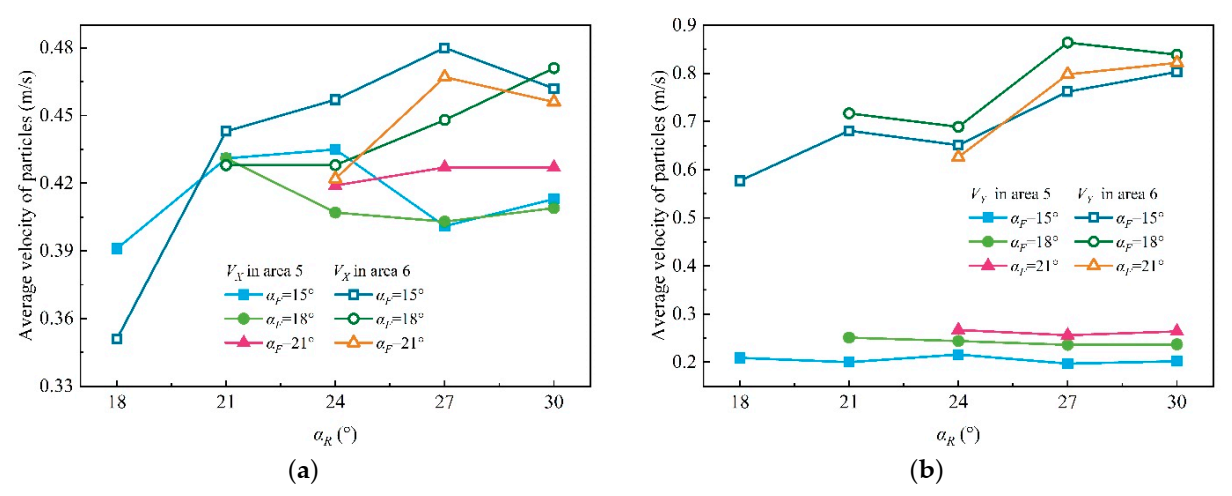
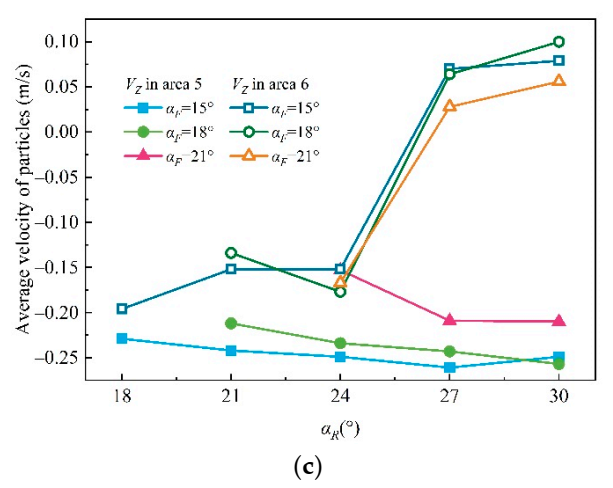
4.4. The Influence of Helix Angle Matching between the Front and Rear Drum on Particle Velocity
4.5. The Distribution of Particles under the Different Helix Angle Matching
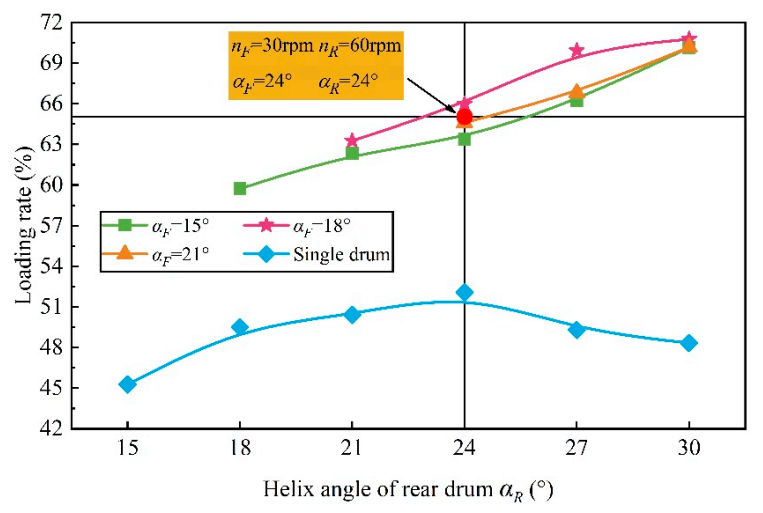
4.6. The Influence of the Helix Angle Matching between the Front and Rear Drum on Loading Performance
5. Conclusions
- (1)
- In the TDRSD, the front drum’s lower rotational speed positively impacted particle conveying. The particles velocity in X-direction had no obvious change with the increase in rotational speed of the rear drum, while the velocity in Y and Z-direction had an obvious increasing trend, which made the particles obtain the ability to cross the gap and played a positive role in particle loading.
- (2)
- The front drum should adopt a lower rotational speed, and the loading performance first increased and then decreased with the increase in the rear drum’s rotational speed. When the front drum’s rotational speed was 30 rpm, and the rear drum’s rotational speed was 60–67.5 rpm, the optimal loading performance was obtained. The optimal loading rate was 66.94%, which is more than 10% higher than that under single drum condition.
- (3)
- The relationship between the helix angle of screw vanes and the maximum web depth was theoretically deduced, and the relationship was optimized based on rotational speed matching. The influence of the front drum’s helix angle on the coal loading performance was not obvious, and the coal loading rate increased continuously with the increase in rear drum’s helix angle. After optimization, the optimal loading performance was obtained in the cases of the front drum’s helix angle was 18° and of the rear drum was 30°, and the coal loading rate was increased by 3.83% compared with TDRSD.
- (4)
- According to the influence of rotational speed matching and helix angle matching on particles loading performance of the drum, the influence degree of the rotational speed matching between the front and rear drum on loading performance was more obvious than that of helix angle matching, which is the decisive factor affecting the coal loading performance of the drum.
Author Contributions
Funding
Conflicts of Interest
References
- Dong, Y.; Di, J.; Wang, X.; Xu, L.; Yang, Z.; Guo, X.; Li, M. Dynamics Experimental Study on Treatment of Acid Mine Drainage by Bacteria Supported in Natural Minerals. Energies 2020, 13, 439. [Google Scholar] [CrossRef]
- Wang, K.; Huang, Y.; Gao, H.; Zhai, W.; Qiao, Y.; Li, J.; Ouyang, S.; Li, W. Recovery Technology of Bottom Coal in the Gob-Side Entry of Thick Coal Seam Based on Floor Heave Induced by Narrow Coal Pilar. Energies 2020, 13, 3368. [Google Scholar] [CrossRef]
- Ma, D.J.; Zhang, X.; Wan, L.R.; Zeng, Q.L.; Ge, H.E. Dynamics Analysis of Shearer Traction Unit Considering the Longitudinal Swing. Energies 2020, 13, 5293. [Google Scholar] [CrossRef]
- Li, X.F.; Wang, S.B.; Ge, S.R.; Malekian, R.; Li, Z.X. Investigation on the influence mechanism of rock brittleness on rock fragmentation and cutting performance by discrete element method. Measurement 2018, 113, 120–130. [Google Scholar]
- Booker, C.M. Theoretical and practical aspects of cutting and loading by shearer drums. Aust. J. Coal Min. Technol. Res. 1983, 3, 1–24. [Google Scholar]
- Ludlow, J.; Jankowski, R.A. Use low shearer drum speeds to achieve deeper coal cutting. Min. Eng. 1984, 36, 251–255. [Google Scholar]
- Hurt, K.G.; Mcstravick, F.G. High performance shearer drum design. Colliery Guardian. 1988, 236, 425–429. [Google Scholar]
- Peng, S.S.; Chang, H.S. Longwall Mining; John Wiley and Sons: New York, NY, USA, 1984. [Google Scholar]
- Ayhan, M.; Eyyuboglu, E.M. Comparison of globoid and cylindrical shearer drums’ loading performance. J. S. Afr. Inst. Min. Metall. 2006, 106, 55–56. [Google Scholar]
- Boloz, L. Unique project of single-cutting head longwall shearer used for thin coal seams exploitation. Arch. Min. Sci. 2013, 58, 1057–1070. [Google Scholar]
- Liu, S.Y.; Du, C.L.; Zhang, J.J.; Jiang, H. Parameters analysis of shearer drum loading performance. Min. Sci. Technol. 2011, 5, 621–624. [Google Scholar] [CrossRef]
- Gao, K.D.; Xu, W.B.; Jiang, S.B.; Du, C.L. Factors affecting thin coal seam shearer drum coal-loading performance by a model test method. J. Cent. South Univ. 2019, 26, 1619–1636. [Google Scholar] [CrossRef]
- Wydro, T. Influence of the plow filling and thread angle onto the plow head efficiency. Arch. Min. Sci. 2015, 60, 143–156. [Google Scholar]
- Cundall, P.A. Computer model for simulating progressive large scale movements in blocky rock systems. In Proceedings of the Symposium of the International Society of Rock Mechanics, Nancy, France, 4–6 October 1971; Volume 1, pp. 2–8. [Google Scholar]
- Cundall, P.A.; Strack, O.A. Discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Shimizu, Y.; Cundall, P.A. Three-Dimensional DEM simulations of bulk handling by screw conveyors. J. Eng. Mech. 2001, 127, 864–872. [Google Scholar] [CrossRef]
- Owen, P.J.; Cleary, P.W. Prediction of screw conveyor performance using the Discrete Element Method (DEM). Powder Tech. 2009, 193, 274–288. [Google Scholar] [CrossRef]
- Orefice, L.; Khinast, J.G. DEM study of granular transport in partially filled horizontal screw conveyors. Powder Tech. 2017, 305, 347–356. [Google Scholar] [CrossRef]
- Pezo, M.; Pezo, L.; Jovanović, A.P.; Terzic, A.; Andric, L.; Loncar, B.; Kojic, P. Discrete element model of particle transport and premixing action in modified screw conveyors. Powder Tech. 2018, 336, 255–264. [Google Scholar] [CrossRef]
- Wang, S.Y.; Li, H.L.; Tian, R.C.; Wang, R.C.; Wang, X.; Sun, Q.J.; Fan, J.W. Numerical simulation of particle flow behavior in a screw conveyor using the discrete element method. Particuology 2018, 43, 137–148. [Google Scholar] [CrossRef]
- He, S.Y.; Guan, J.Q.; Pinson, D.; Yu, A.B.; Zhou, Z.Y. A Discrete Element Method Study of Monodisperse Mixing of Ellipsoidal Particles in a Rotating Drum. Ind. Eng. Chem. Res. 2020, 59, 12458–12470. [Google Scholar] [CrossRef]
- Kuang, S.B.; Li, K.; Yu, A.B. CFD-DEM Simulation of Large-Scale Dilute-Phase Pneumatic Conveying System. Ind. Eng. Chem. Res. 2020, 59, 4150–4160. [Google Scholar] [CrossRef]
- Li, J.P.; Zhou, F.; Yang, D.L.; Yu, B.C.; Li, Y.Z. Effect of swirling flow on large particle pneumatic conveying. Powder Technol. 2020, 362, 745–758. [Google Scholar] [CrossRef]
- Portnikov, D.; Santo, N.; Kalman, H. Simplified model for particle collision related to attrition in pneumatic conveying. Adv. Powder Technol. 2020, 31, 359–369. [Google Scholar] [CrossRef]
- Olaleye, A.K.; Shardt, O.; Walker, G.M.; Van den Akker, H.E. Pneumatic conveying of cohesive dairy powder: Experiments and CFD-DEM simulations. Powder Technol. 2019, 357, 193–213. [Google Scholar] [CrossRef]
- Zhu, X.H.; Luo, Y.X.; Liu, W.J. The rock breaking and ROP increase mechanism for single-tooth impact cutting using DEM. Pet. Sci. 2009, 16, 1134–1147. [Google Scholar] [CrossRef]
- Zhao, L.J.; Jin, X.; Liu, X.H. Numerical research on wear characteristics of drum based on discrete element method (DEM). Eng. Fail. Anal. 2019, 109, 104269. [Google Scholar] [CrossRef]
- Zhang, G.Z.; Dang, W.G.; Herbst, M.; Song, Z.Y. Complex analysis of rock cutting with consideration of rock-tool interaction using distinct element method (DEM). Geomech. Eng. 2020, 20, 421–432. [Google Scholar]
- Zheng, K.H.; Qiu, B.J.; Li, J.P.; Gao, K.D. 3D XCT Mesostructure Characterization and Image-Based Discrete Element (DE) Modelling of Failure Patterns in Coal Gangue Particles (CGPs). Complexity 2019, 2019, 4021368. [Google Scholar] [CrossRef]
- Zhao, L.J.; Liu, H.M.; Zhou, W.C. A study on the dynamic transmission law of spiral drum cutting coal rock based on ANSYS/LS-DYNA simulation. Complexity 2019, 2019, 1482051. [Google Scholar] [CrossRef]
- Liu, S.F.; Lu, S.F.; Wan, Z.J.; Zhang, H.W.; Xing, K.K. Numerical simulation of induced cutting in deep coal. R. Soc. Open Sci. 2019, 6, 190308. [Google Scholar] [CrossRef] [PubMed]
- Li, X.F.; Wang, S.B.; Ge, S.R.; Malekian, R.; Li, Z.X.; Li, Y.F. A study on drum cutting properties with full-scale experiments and numerical simulations. Measurement 2018, 114, 25–36. [Google Scholar] [CrossRef]
- Gao, K.D.; Du, C.L.; Fu, L.; Jiang, H.X. Effect of mining face angle on drum loading performance using discrete element method. Int. J. Earth Sci. Eng. 2014, 7, 41–51. [Google Scholar]
- Gospodarczyk, P. Modeling and simulation of coal loading by cutting drum in flat seams. Arch. Min. Sci. 2016, 61, 365–379. [Google Scholar] [CrossRef]
- Gao, K.D.; Du, C.L.; Dong, J.H.; Zeng, Q.L. Influence of the drum position parameters and the ranging arm thickness on the coal loading performance. Minerals 2015, 5, 723–736. [Google Scholar] [CrossRef]
- Gao, K.D. Feasibility of drum coal loading process simulation using three-dimension discrete element method. Electron. J. Geotech. Eng. 2015, 20, 5999–6007. [Google Scholar]
- Gao, K.D.; Zhang, X.D.; Sun, L.Q.; Zeng, Q.L.; Jiang, K. Complex Effects of Drum Hub Forms and Structural Parameters on Coal Loading Performance. Complexity 2020, 2020, 7036087. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Coetzee, C.J. Calibration of the discrete element method. Powder Technol. 2017, 310, 104–142. [Google Scholar] [CrossRef]
- Markauskas, D.; Kacianauskas, R. Investigation of rice grain flow by multi-sphere particle model with rolling resistance. Granul. Matter 2011, 13, 143–148. [Google Scholar] [CrossRef]
- Coetzee, C.J. Calibration of the discrete element method: Strategies for spherical and non-spherical particles. Powder Tech. 2020, 364, 851–878. [Google Scholar] [CrossRef]
- Fu, L. Study on Cutting and Conveying Performance of Novel Auger Miner Drilling Tool. Ph.D. Thesis, China University of Mining and Technology, Xuzhou, China, 2016. [Google Scholar]






| ρ (kg/m3) | σ | E (GPa) | η | μS | μR | ||
|---|---|---|---|---|---|---|---|
| coal | 1.28 × 103 | 0.28 | 4.25 | coal-coal | 0.50 | 0.80 | 0.10 |
| steel | 7.85 × 103 | 0.30 | 2.06 × 102 | coal-steel | 0.50 | 0.51 | 0.05 |
| n (rpm) | Vq (m/s) | J (m) | Dv (m) | Dc (m) | H (m) | αcp (°) | N | |
|---|---|---|---|---|---|---|---|---|
| Front drum | [30:15:90] | 0.1 | 0.45 | 0.9 | 1.0 | 1.05 | 24 | 2 |
| Rear drum | [37.5:7.5:90] | 0.1 | 0.40 | 0.9 | 1.0 | 1.05 | 24 | 1 |
| n (rpm) | αcp (°) | N | |
|---|---|---|---|
| Front drum | 30 | [15:3:30] | 2 |
| Rear drum | 60 | [15:3:30] | 1 |
| Rotational Speed (rpm) | The Difference in Loading Rate between Single and TDRSD (%) | Loading Rate (%) | |||||
|---|---|---|---|---|---|---|---|
| nF | nR | P1 | ΔP1 | P2 | ΔP2 | ΔP | |
| 60 (single drum) | 20.27 | 36.05 | 56.32 | ||||
| 30 | 60 | 28.01 | +7.74 | 37.03 | +0.98 | +8.72 | 65.04 |
| 45 | 60 | 25.18 | +4.91 | 35.16 | −0.89 | +4.02 | 60.34 |
| 75 (single drum) | 16.47 | 33.52 | 49.99 | ||||
| 30 | 75 | 27.84 | +11.37 | 35.98 | +2.46 | +13.83 | 63.82 |
| 45 | 75 | 22.66 | +6.19 | 34.19 | +0.67 | +6.86 | 56.85 |
| 60 | 75 | 21.69 | +5.22 | 35.10 | +1.58 | +6.80 | 56.79 |
| 90 (single drum) | 15.04 | 27.79 | 42.83 | ||||
| 30 | 90 | 22.96 | +7.92 | 29.71 | +1.92 | +9.84 | 52.67 |
| 45 | 90 | 18.77 | +3.73 | 32.83 | +5.04 | +8.77 | 51.60 |
| 60 | 90 | 16.63 | +1.59 | 29.42 | +1.63 | +3.22 | 46.05 |
| Vq (m/s) | nF (rpm) | nR (rpm) | αF (°) | αR (°) | Loading Rate (%) |
|---|---|---|---|---|---|
| 2.4 | 30 (single drum) | 24 | 46.41 | ||
| 30 | 37.5 | 24 | 24 | 51.92 | |
| 45 | 24 | 24 | 55.40 | ||
| 52.5 | 24 | 24 | 61.26 | ||
| 60 | 24 | 24 | 65.04 | ||
| 67.5 | 24 | 24 | 66.94 | ||
| 75 | 24 | 24 | 63.82 | ||
| 82.5 | 24 | 24 | 56.75 | ||
| 90 | 24 | 24 | 62.67 | ||
| 45 (single drum) | 24 | 52.07 | |||
| 45 | 52.5 | 24 | 24 | 57.47 | |
| 60 | 24 | 24 | 60.34 | ||
| 67.5 | 24 | 24 | 58.93 | ||
| 75 | 24 | 24 | 56.85 | ||
| 82.5 | 24 | 24 | 55.32 | ||
| 90 | 24 | 24 | 51.60 | ||
| 60 (single drum) | 24 | 56.32 | |||
| 60 | 67.5 | 24 | 24 | 57.30 | |
| 75 | 24 | 24 | 56.79 | ||
| 82.5 | 24 | 24 | 52.38 | ||
| 90 | 24 | 24 | 46.05 | ||
| 75 (single drum) | 24 | 49.99 | |||
| 90 (single drum) | 24 | 42.83 | |||
| Vq (m/s) | nF (rpm) | nR (rpm) | αF (°) | αR (°) | Loading Rate (%) |
|---|---|---|---|---|---|
| 2.4 | 60 (single drum) | 15 | 45.27 | ||
| 30 | 60 | 15 | 18 | 59.73 | |
| 15 | 21 | 62.34 | |||
| 15 | 24 | 63.38 | |||
| 15 | 27 | 66.24 | |||
| 15 | 30 | 70.13 | |||
| 60 (single drum) | 18 | 49.51 | |||
| 30 | 60 | 18 | 21 | 63.26 | |
| 18 | 24 | 65.98 | |||
| 18 | 27 | 69.92 | |||
| 18 | 30 | 70.77 | |||
| 60 (single drum) | 21 | 50.40 | |||
| 30 | 60 | 21 | 24 | 63.60 | |
| 21 | 27 | 66.81 | |||
| 21 | 30 | 70.17 | |||
| 60 (single drum) | 24 | 52.07 | |||
| 27 | 49.29 | ||||
| 30 | 48.33 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, K.; Zhang, X.; Sun, L.; Zeng, Q.; Liu, Z. Loading Performance of a Novel Shearer Drum Applied to Thin Coal Seams. Energies 2021, 14, 358. https://doi.org/10.3390/en14020358
Gao K, Zhang X, Sun L, Zeng Q, Liu Z. Loading Performance of a Novel Shearer Drum Applied to Thin Coal Seams. Energies. 2021; 14(2):358. https://doi.org/10.3390/en14020358
Chicago/Turabian StyleGao, Kuidong, Xiaodi Zhang, Liqing Sun, Qingliang Zeng, and Zhihai Liu. 2021. "Loading Performance of a Novel Shearer Drum Applied to Thin Coal Seams" Energies 14, no. 2: 358. https://doi.org/10.3390/en14020358
APA StyleGao, K., Zhang, X., Sun, L., Zeng, Q., & Liu, Z. (2021). Loading Performance of a Novel Shearer Drum Applied to Thin Coal Seams. Energies, 14(2), 358. https://doi.org/10.3390/en14020358





