Abstract
According to the International Electrotechnical Commission (IEC) 61853 standard, the power rating of photovoltaic (PV) modules must be done on a measurement matrix that broadly covers the ranges of operating conditions encountered in the field. These results are becoming more frequent in recent module datasheets. This paper investigates the effectiveness of applying existing empirical PV performance models while using a matrix with 18 operational records, similar to the 22 that were recommended by IEC 61853, as an alternative to the thousands of records that are conventionally used to determine their coefficients. A review of fifteen empirical models is presented and the procedures for determining their coefficients are discussed. In order to validate them, they were applied to data from fourteen PV modules, which remained installed outdoors for about one year, in three locations with distinct climate types. Although the uncertainties that were obtained with the proposed approach, as compared to the conventional one, are about 1% higher for xSi and CdTe modules, and somewhat higher for mSi and CIGS modules, the total uncertainties were only around 5%, a value that is quite adequate for evaluating module performance. Moreover, these uncertainties were from two to five times smaller than those that were obtained by the method that was recommended by IEC 61853 for this purpose.
1. Introduction
The power generation from renewable energy sources, namely, hydropower, wind, solar, and biomass, is increasingly consolidating as a low-cost solution that simultaneously meets short-term economic needs and medium- and long-term decarbonization goals [1]. Among the available technologies, the solar photovoltaic (PV) generation stands out as the current leader in expanding the power generation capacity in the world [2]. Being represented by grid-connected PV systems, it brings together characteristics that make it particularly attractive for utility-scale as well as residential and commercial applications [2,3,4]. Regarding these characteristics, it is pertinent mentioning its: great modularity, operation free of greenhouse gas emissions, and dependence only on the inexhaustible solar irradiation [1,2,3,4]. Nonetheless, PV generation development still depends on appropriate economic and regulatory policies in many countries [1,2,3]. In this context, the accurate modeling of the PV system performance becomes crucial for technical and economic analysis of new and existing PV systems [5,6,7,8,9].
The PV system performance is usually evaluated while using a chain of interchangeable models that allow estimating its electricity production, both in quantity and time [5,6,7]. In this sense, the PV module performance model is the one that plays the most relevant role [7]. The PV module can be considered the basic conversion unit of the system, as the cells that constitute the PV module are typically assumed to be equal and subject to the same environmental and physical integrity conditions [7]. Accordingly, its performance model seeks to estimate how much of the incident solar irradiance will be converted into (direct current) electric power, when mainly considering the influence of its operating temperature on this phenomenon [7,8,10]. Therefore, the results that are provided by this model serve not only as estimates of the expected production of the PV module, but also as reference values that allow for assessing the level of degradation and compliance operating the PV module at hand [11,12,13].
Over the past few decades, several models have been proposed for describing the PV module performance [8,14,15,16]. Traditionally, they are classified into two major categories: “physical models” and “empirical models” [7,8,10].
Much appreciated by the academic community, the physical models describe the operational behavior of the PV module from an equivalent electrical circuit [7,8,10]. Through the analysis of this circuit, it is possible to obtain a parametric equation that allows for representing the full curve of the current-voltage (I–V) relationship expected at PV module terminals under a specific operating condition [7]. Thus, the application of these models to estimate the PV module performance is usually divided into two steps [17]. In the first step, the parameter values must be determined while considering a reference operating condition [17]. Depending on the context, this task can be accomplished through methods that are based on the PV module datasheet or a I–V curve experimentally obtained at PV module terminals in a known operating condition [17,18,19,20,21]. In turn, in the second step, the parameter values must be determined in view of the required operating conditions [17]. This task is commonly done through the so-called “translation equations” [10]. Such equations allow for estimating the values that would be verified for these parameters in a specified operating condition, considering their values determined in the reference operation condition, i.e., in the first step [10,22].
On the other hand, the empirical models are characterized by empirical or semi-empirical expressions that allow for estimating just a single or a few key-points of the I–V curve expected at PV module terminals, but in any operating condition [14,15,16,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. Therefore, their empirical coefficients are usually determined from fitting procedures carried out on numerous operational records of the PV module under study [7]. Not surprisingly, most of these models were developed by laboratories that are involved in systematic PV modules measurements [8].
It is important to note that physical models potentially serve a broader scope of applications, as they can provide the full I–V curve. However, in the cases where the models of both categories can provide the required information on the PV module performance properly, two factors are decisive in choosing one of them: its computational complexity and the input data that are required for its application. In this sense, the empirical models stand out, because they are generally less computationally intensive and more easily adjustable to different PV technologies than physical models [7]. In contrast, the fact that empirical models generally cannot be applied while just considering the PV module datasheet makes physical models predominantly applied to certain types of studies, such as designing new PV systems, where it is not common or even possible to obtain operational records of the PV module at hand.
Regarding this limitation of the empirical models, it is interesting to point out that it is mainly caused by the insufficient amount of operational records that were reported in the PV module datasheet. That is, the minimum requirement for applying an empirical model in a study is that the number of operational records available is at least equal to its number of empirical coefficients; thereby, a system of equations can be deduced for their determination. In turn, the PV module datasheet typically reports information only referring to the short-circuit, open-circuit and maximum power points of the I–V curve verified at “standard test conditions” (STC), i.e., irradiance perpendicularly incident of 1000 W/m², with AM1.5 standard global spectrum, and a PV module operating temperature of 25 °C [37]. Accordingly, as the empirical models usually have two or more empirical coefficients and the PV module datasheet provides a single operational record, it is impossible to apply them without additional information being obtained externally.
Notwithstanding, a path to overcome this situation can be found in the International Electrotechnical Commission (IEC) 61853 standard, entitled “Photovoltaic (PV) module performance testing and energy rating”. Published in 2011, part one of this standard (IEC 61853-1), “Irradiance and temperature performance measurements and power rating”, establishes that a PV module must be tested at twenty-two points of an operating conditions matrix, in which the irradiance incident ranges from 100 to 1100 W/m² and operating temperature, from 15 to 75 °C [38]. Accordingly, part three of this same standard (IEC 61853-3), “Energy rating of PV modules”, recommends an “interpolation method” that is based on bilinear interpolation and linear extrapolation procedures, to estimate the PV modules performance under operating conditions that transcend the points of the IEC 61853-1 matrix [36,39]. However, this recommendation is not restrictive and, therefore, other alternatives, such as empirical models, can be evaluated in order to obtain more accurate results [36].
Although important organizations explicitly recommend adopting IEC 61853-1, such as the Solar American Board for Codes and Standards (Solar ABCs) [40], many PV module manufacturers still decline to test or report such a measurement matrix in the PV module datasheets [41]. Nevertheless, some notable laboratories, such as PV Performance Labs Germany and U.S. Sandia National Laboratories, recently started a movement to popularize IEC 61853-1 in the PV industry [41]. One of their biggest motivations lies precisely in the window of opportunities that the IEC 61853-1 matrix opens to develop new models or alternative approaches to applying existing models [36,42]. Indeed, a novel empirical model that is based on IEC 61853-1 has been freshly proposed by researchers from these laboratories, demonstrating encouraging results [36].
Based on these considerations, this paper aims to investigate the effectiveness of applying existing empirical models while considering a measurement matrix similar to that established by IEC 61853-1 for determining their respective coefficients. In this sense, a comprehensive review of fourteen empirical models, in addition to the newest one aforementioned, was conducted. In order to validate their performance, they were applied to represent fourteen PV modules of different technologies adequately, which remained installed outdoors for about one year, in three locations with distinct climate types. The obtained results confirm that this application approach proposed for the empirical models preserves their intrinsic abilities and, thereby, allows for them to estimate the operational behavior of the PV modules of different technologies in a much more accurate and robust way than the interpolation method that was recommended by IEC 61853-3.
Accordingly, the main contributions of this paper are five-fold:
- to review fifteen outstanding empirical models proposed in the literature over the past forty years;
- to discuss the procedures for determining the coefficients of these empirical models;
- to validate the results obtained by these empirical models considering a measurement matrix similar to that established by IEC 61853-1 for determining their respective coefficients;
- to compare the results obtained by these empirical models with those verified by the interpolation method recommended by IEC 61853-3; and,
- to identify the representation potentials and limitations of these empirical models concerning the different PV module technologies and operating conditions.
In addition to this introductory section, the rest of the paper is organized, as follows. Section 2 presents a review of the fifteen empirical models selected for analysis. Section 3 describes the main data that are related to the PV modules adopted as objects of study, as well as the procedures employed for determining the coefficients of the empirical models and the metrics used to assess their corresponding results. Section 4 reports the results obtained for each empirical model and develops that are discussions based on them. Section 5 draws the main conclusions.
2. A Review of the Empirical Models
Figure 1 depicts the typical I–V curve of a PV module. From its point-to-point multiplication, it is possible to obtain the curve that describes the power-voltage (P–V) relationship of this PV module. Therefore, this curve is additionally shown in Figure 1.
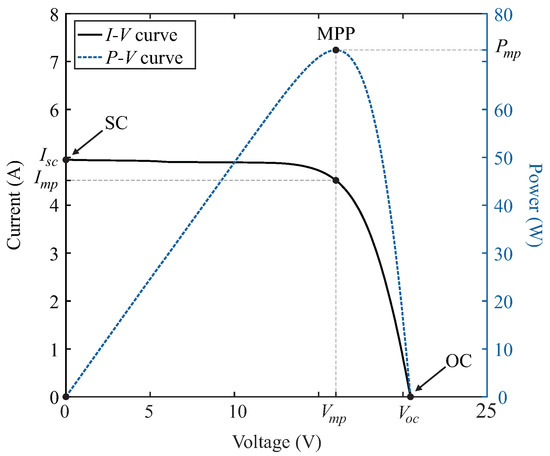
Figure 1.
Characteristic curves of a single-crystalline silicon photovoltaic (PV) module operating under an effective irradiance of 985 W/m² and a temperature of 45 °C [43]. In highlight, the key-points of these curves and their respective coordinates, which is: SC = ; OC = ; MPP = ; or, MPP = .
By analyzing these characteristic curves of the PV module, it is possible to note that they have three key-points: short circuit (SC), open circuit (OC), and maximum power (MPP or, simply, MP). Among these points, one that is of fundamental interest for the PV module performance modeling is the latter. This is because the inverters that make up grid-connected PV systems, especially the most recent ones, are able to guarantee that the PV modules operate at this point with extreme efficiency [8]. Hence, in the case of a system that is composed of an array of PV modules, the input power of the inverter can be properly understood as the product of the maximum power values of current and voltage [8,10].
The way in which empirical models address the PV module maximum power output () can vary significantly. In the practical way, some of the empirical models consider the PV module maximum power output as a straight function of the incident solar irradiance effectively available to be converted () and its operating temperature (), as shown in (1) [23,28].
Following the physical theory behind the concept of electric power, other empirical models consider the PV module maximum power output as the product of its maximum power current () with its maximum power voltage () [24,27,44,45]. The maximum power current and voltage are both given in this case, depending on the operating conditions of the PV module, as shown in (2).
From another perspective, certain empirical models address the PV module maximum power output indirectly, which are linked to evaluation metrics. In this sense, the most commonly used metric is the efficiency that is verified at the maximum power () [25,26,29,30,32,36,46]. In this case, it is determined by the ratio between the PV module maximum power output and its power input, i.e., the product of the effective irradiance with the PV module area (A). Therefore, based on the assumption that such efficiency is given by an empirical function, the PV module maximum power can be calculated, as demonstrated in (3).
Additionally, some empirical models treat the efficiency verified at the maximum power in a normalized manner () to its own value verified in a reference operating condition () [31,33,34]. Thus, the PV module maximum power output can be calculated without the need for knowledge regarding its area, but in view of its own value in the reference operating condition (), as demonstrated in (4).
It is worth mentioning that the empirical models given, as demonstrated in (1), (3) and (4), are also called “single-point efficiency models” or “performance surface models”, as their output can be plotted as a three-dimensional surface () [7,8].
The empirical models that are found in the literature for each of these described formulations are objectively presented below. However, their references are duly cited, allowing for anyone interested in more detailed information to know where to find them. Furthermore, in order to maintain coherence throughout this paper, the functions that correspond to these models have been rewritten following the same pattern. Accordingly, their respective empirical coefficients are represented by “”, where n = , and C is the total number of the empirical model coefficients in question. At the end of this section, an overview of the described empirical models is presented along with some additional comments.
2.1. Power Empirical Models
One of the oldest empirical models found in the literature was presented by Taylor [23] around the mid-1980s. Analyzing the data referring to about four years of operation of fourteen different test systems, this author found that (5) is able to estimate the maximum power output of the PV modules reasonably [23].
Almost 20 years later, Rosell and Ibanez [28] proposed a new and more complex expression for calculating the maximum power output of the PV modules, which is given in (6) [28]. Although the authors do not make it clear how exactly they arrived at this expression, the results that were obtained through it for different PV technologies were very representative [28].
2.2. Voltage-Current Empirical Models
In the second half of the 1990s, King [44] presented a detailed PV module performance model, which is formalized by a set of expressions that allows for explicitly characterizing the key-points of its I–V curve [44]. However, some time later, King et al. [27] improved this set of equations and added two other expressions that allow calculation of the respective current value at the point whose voltage is half the open-circuit voltage and another point whose voltage is half the sum between the open-circuit voltage and the maximum power voltage [27]. Thus, the expressions that were proposed by King et al. [27], which allow to calculate the PV module maximum power output, are given by (7):
where , are, respectively, the maximum power current and voltage that are verified at reference operating condition (,); , are, respectively, the temperature coefficient for maximum power current and voltage (1/°C); is the number of series-connected cells that constitute the PV module under study; and are, respectively, the current and the reference operating temperature of these cells; , is the “thermal voltage” per cell; k is the Boltzmann constant ( J/K), and q is the absolute value of the electron charge ( C).
As can be observed, this set of expressions has been developed when considering the operating temperature () of the cells that constitute the PV module and not the PV module operating temperature () as usual. Accordingly, to estimate such operating temperature, the authors propose that the expression that is given by (7d) be used, where is an empirical coefficient that relates the difference between the cell and the back surface of the PV module (the location where the temperature measurement sensors are properly placed) [27]. Nonetheless, as this coefficient requires measurements that are difficult to carry out in practice, the authors suggest adopting the generic values [27]. For example, = 3 °C is recommended for PV modules that are installed in an open rack and with constructive profile of type “glass/cell/glass”, “glass/cell/polymer sheet”, or “polymer/thin-film/steel” [27].
Furthermore, it is important to note that, although this set of expressions has been developed by King et al. [27] based on data that were collected over the years at U.S. Sandia National Laboratories, they also have elements of physical models, such as the thermal voltage and the coefficient [10]. Interestingly, this latter is associated with a theoretical parameter of physical models, known as “diode ideality factor” and it generally has a value between 1 and 2 for PV cells [20]. Thus, the authors recommend that both this and the other coefficients presented in (7) be determined from specific procedures [27]. In general, these procedures consist of several linear and parabolic regressions and they require a minimum of 600 outdoor measurements of the PV module performance [47]. Moreover, such measurements must meet a series of requirements which are related to the simultaneously observed weather conditions, including the solar irradiance incident on the PV module surface, the air mass (AM) crossed by it, and the wind speed [47]. Appendix B presents a brief description of these requirements.
Despite its complexity, it is essential to mention that the empirical model proposed by King et al. [27] is one of the most popular in the literature [7]. Also known as “Sandia Array Performance Model” (SAPM), it is even used in the software “System Advisor Model” (SAM), which is distributed by U.S. National Renewable Energy Laboratory (NREL) [48]. In this context, the U.S. Sandia National Laboratories provides an up-to-date library of its all coefficients for most of the commercially available PV modules, facilitating its application, even in studies where it is impossible to obtain operating records of the PV module at hand personally [7].
Nevertheless, it is possible to find some variations of this model in the literature, which are easier to apply [24,33,49]. Based on SAPM ancestors [45], Kenny et al. [24] proposed the expressions given by (8) in order to calculate the maximum power current and voltage of the PV module [24]. When developing these expressions, the authors intended to obtain a simple empirical model that would allow for the extrapolating the set of operational records to complete and/or extend its data matrix in the parts where measurements are missing [24].
2.3. Efficiency-Based Empirical Models
In the 2010s, several empirical models were published focusing on the relationship between maximum power efficiency and effective irradiance (–) [25,26,30,32]. In general, the application of these models presumes that the maximum power efficiency is related to the PV module operating temperature by means of a constant rate, as demonstrated in (9), where is the temperature coefficient for maximum power (1/°C) [8]. In this way, such models more effectively explore the impacts of the effective irradiance on the PV module performance, which seems to be more complex and less understood.
In this sense, one of the first empirical models found in the literature was the one proposed by Randall and Jacot [25]. Drawing a parallel between an alternative efficiency formula, which is given by the fill factor metric, as well as the relationships typically verified for short-circuit current and open-circuit voltage in the physical models, these authors obtained the expression given by (10) [25].
At the same period that Randall and Jacot [25] published their model, Williams et al. [26] presented another expression to represent the – relationship, which is given by (11) [26]. Although these authors developed this expression from experimental analysis [26], it is interesting to note that it consists of an extended version of the expression that was proposed by Randall and Jacot [25].
Some time later, Reich et al. [32] proposed a correction to the expression that was proposed by Williams et al. [26]. These authors observed that, at low level of effective irradiance, the expression that is given by (11) resulted in negative maximum power efficiency values [32]. Thus, they included a new coefficient in the expression, “”, which is now given by (12) [32].
From another perspective, Heydenreich et al. [30] proposed a more complex expression to represent the – relationship, which is described in (13) [30]. In general, it was obtained from a common narrative that was adopted by physical models in order to represent the loss mechanisms existing in a PV module [30]. Additionally, it originally applies only to an operating temperature fixed at 25 °C, hence the sub-index shown in (13). Accordingly, when (9) and (13) are applied together, must be equal to 25 °C. Additionally, it is important to mention that this expression proposed by Heydenreich et al. [30] is adopted by the Fraunhofer Institute for Solar Energy Systems (ISE) in studies relating to PV module energy rating [50].
In contrast, some efficiency-based empirical models with a broader scope are also available in the literature [29,36,46]. From experimental tests, Durisch et al. [29] proposed an expression for the strict calculation of the maximum power efficiency that considers, as input variables, the global solar irradiance, air mass, and operating temperature of the cells in the PV module [29]. Nonetheless, rewriting this model in terms of effective irradiance and operating temperature of the PV module, as presented in reference [8], it can be given by (14) [29].
A few years ago, Ransome et al. [35] proposed the so-called “Mechanistic Performance Model” (MPM) [35]. Employed in the Gantner Instruments analysis software, this empirical model is characterized by an expression that considers, as variable input, the effective irradiance, PV module operating temperature, and wind speed [51]. It is worth noting that this latter contributes to decreasing the operating temperature of the PV module; however, its effects are usually only considered when the PV module operating temperature is not directly measured and, therefore, has to be estimated from specific models, such as those that are presented in the references [16,52,53]. Moreover, wind speed measurements are not always taken [43]. Thus, there are two variations of this model that can be applied in the absence of its measurements [36,46]. They are given by (15) and (16), where [36]. According to the authors, the empirical coefficients of these expressions have meanings that are linked to the operational behavior of the PV module and relations that are typical of physical models [51].
More recently, Driesse and Stein [36] proposed a new efficiency-based empirical model already envisioning its application in the context of IEC 61853 [36]. Inspired by the way that Heydenreich et al. [30] developed their empirical model and while considering a series of relations typical of physical models, these authors were able to obtain a set of well-founded expressions that allow for calculating the PV module efficiency [36]. This set of expressions is given in (17).
2.4. Relative Efficiency-Based Empirical Models
One of the first relative efficiency-based empirical models found in the literature was proposed by Montgareuil et al. [31] in the scope of the software “Meteorological, Optical, and Thermal Histories for the Energy Rating of Photovoltaics” (MotherPV) [31]. From a geometric interpretation of the typical I–V curve of a PV module and the logarithmic dependence profile typically observed between its voltage and the effective irradiance, the authors obtained the expressions that were given by (18) [31].
On the other hand, Huld et al. [33] developed a new expression for representing the relative efficiency, which is based on the empirical model proposed by King et al. [27]. By manipulating the product of (7a) with (7b), these authors obtained the expression given in (19) [33]. It is important to highlight that this expression is employed in the software “Photovoltaic Geographical Information System” (PVGIS) [54].
In turn, Silva et al. [34] developed another expression to represent the relative efficiency within the scope of the INNDISOL Project, which is based on the empirical model that was proposed by Durisch et al. [29]. As presented in reference [8], it can be given by (20).
It is interesting to note that the general structure of the empirical models proposed by Silva et al. [34], as well as the one that was proposed by Montgareuil et al. [31], is very similar to that of the efficiency-based empirical models focused on the – relationship, i.e., the empirical models proposed by Randall and Jacot [25], Williams et al. [26], Reich et al. [32], and Heydenreich et al. [30].
2.5. Overview of the Described Models
Once the empirical models have been presented, it is now pertinent to make some discussions about them. In order to assist these discussions, a summary of the main characteristics of the empirical models is presented in Table 1.

Table 1.
Overview of the reviewed empirical models.
Regarding the expressions that characterize these models, some similarities in how they address the effects of effective irradiance and operating temperature on the PV module performance draw attention.
In the case of the effective irradiance, it is observed that a large part of the empirical models describe its effects on the performance of the PV module while using a natural logarithmic term [24,25,26,27,28,30,31,32,33,36]. This interpretation comes from the maximum power voltage behavior, which, in practice, develops a curve with this characteristic in relation to the effective irradiance [31,36]. Nonetheless, it is important to mention that this curve is satisfactorily represented by physical models. That is why all of the empirical models admittedly based on elements and relationships that are typical of physical models, fundamentally have this term [24,25,27,30,33,36]. It is also noteworthy that only the empirical model that was proposed by Taylor [23] does not have any logarithmic term in its expression.
In addition, it is observed that some empirical models approach the effective irradiance in a normalized way [24,27,29,31,33,36]. The main reason for this is that the high values of this variable, when divided by an appropriate reference value, become more reasonable; thereby, the empirical coefficients that are related to such variables also assume more convenient values. In this sense, it is important to highlight that these empirical models typically adopt = 1000 W/m², in allusion to STC. Consequently, this value is also valid for the model that was proposed by Silva et al. [34], which uses it differently from the others.
In the case of the operating temperature, it is frequently observed that the empirical models use the temperature coefficients to simplify or complement the description of its effects on the PV module performance [24,25,26,27,30,31,32,34]. In this regard, it is important to note that is typically shown in the PV module datasheet, while and not always, especially in the case of older PV modules. In situations where these last two temperature coefficients are not reported, auxiliary models can be used for their determination, such as those that are proposed in the references [27,42,55].
Furthermore, it is interesting to note that the use of these temperature coefficients usually involves calculating the deviation of the PV module operating temperature in relation to a reference operating temperature. Additionally, in allusion to the STC, the latter is typically considered to be = 25 °C. It is worth mentioning that this same value is valid for the models that were proposed by: (i) King et al. [27], which differently from the others, adopts the operating temperature of the cells that constitute the PV module in their expressions ( = 25 °C); (ii) Durisch et al. [29], Huld et al. [33], Ransome et al. [35] and Driesse and Stein [36], which use this reference value, even without addressing the temperature coefficients.
Regarding the empirical coefficients, it is verified that some models address the triple of empirical coefficients in relation to others. This is the case of the model that was proposed by Huld et al. [33] when compared to the models proposed by Kenny et al. [24], Randall and Jacot [25] and Silva et al. [34] (see the fifth column of Table 1). Nevertheless, the number of coefficients presented by these models can be considered to be suitable for the context of PV module performance modeling. For clarity purposes, the most popular physical models have up to seven parameters to be determined [20].
Thus, more important than the number of empirical coefficients to be determined is how they relate to themselves intrinsically in the model expression(s). In most of the models, this relationship is linear [23,24,25,26,30,31,33,35], which means that the respective coefficients can be effectively determined through linear regressions. On the other hand, in the models in which this relationship is nonlinear [24,27,28,29,32,34,36], more sophisticated techniques may be needed [31,35]. Even so, it is important to note that the most widely used technique for determining these coefficients is the (linear or nonlinear) least-squares method [29,30,36,54].
Finally, it is relevant to emphasize the involvement of the empirical models with: (i) recent project for the PV module energy rating, such as the model that was proposed by Heydenreich et al. [30,50]; (ii) outstanding PV software, such as the models proposed by King et al. [27,48], Montgareuil et al. [31] and Huld et al. [33,54]; and, (iii) technological application, such as the model that was proposed by Ransome et al. [35,51].
2.6. Additional Comments
From Table 1, it is possible to verify that all of the empirical models described in this section are perfectly capable of being applied considering the IEC 61853-1 matrix. This is because their respective numbers of empirical coefficients are significantly lower than the number of measurements provided by it.
In this sense, it is vital to comment that, during the literature review process, just a single work was found that adequately evaluated the performance of the empirical models when considering the IEC 61853-1 matrix. It is not by chance that this work consists of the study presented by Driesse and Stein [36] to validate the empirical model proposed by them.
In this work, four PV modules of different technologies were considered as study objects [36]. Their respective IEC 61853-1 matrix were obtained in laboratory [36]. Additionally, five extra measurements were made in addition to those that were recommended by the standard to make additional analyzes feasible [36]. In view of these data, the model that was proposed by the authors as well as those proposed by Heydenreich et al. [30], Montgareuil et al. [31], Huld et al. [33], and Ransome et al. [35] (both variations), were applied in the representation of the PV modules. When comparing the results that were obtained from these models and by the interpolation method recommended by IEC 61853-3 [39] (see Appendix A), the authors then carry out comprehensive analyzes.
In general, the obtained results demonstrate that these empirical models, with their coefficients determined from IEC 61853-1 matrix, can satisfactorily estimate the performance of the PV modules in operating conditions that go beyond this matrix [36]. However, this estimation accuracy mainly depends on the model ability to represent the operational behavior of the PV module under different operating conditions and not only the scope of the data that were used for the estimation of their coefficients [36]. Furthermore, the results showed that, in general, the interpolation method that is recommended by IEC 61853-3 [39] has a lower performance than the empirical models, and this method is still much more sensitive to the noise eventually present in the IEC 61853-1 matrix (lack of measurement accuracy) than the empirical models [36].
Nonetheless, it should be noted that these results were obtained when considering only a few PV modules and just some of the empirical models described in this section. Besides that, the performance of these empirical models, when considering the IEC 61853-1 matrix, still needs to be validated in view of the outdoor measurements, such as the operational records of PV modules. Therefore, broader studies still need to be carried out in order to confirm some of the pioneering results that were presented by Driesse and Stein [36] and enrich the discussions regarding applying empirical models in the light of IEC 61853-1 matrix. Hence, the relevance of this paper.
3. Assessment Methodology
The empirical models described in Section 2 have been particularly applied in representing the performance of fourteen PV modules, with eight being of silicon technologies and six of thin-film technologies, in order to make the analysis proposed by this paper feasible. Accordingly, their respective coefficients were determined when considering both a measurement matrix similar to that established by IEC 61853-1 and a set of outdoor operational records made available for these PV modules. At first, the results that were obtained by each empirical models in each of these approaches were evaluated in relation to the outdoor operational records themselves. For this purpose, analytical graphs and assessment metrics were employed, following the best practices of the literature. In the sequence, the performance of the empirical models were compared with each other and with the performance that was observed for the interpolation method recommended by IEC 61853-3 (see Appendix A).
The main data regarding the PV modules adopted as objects of study, as well as the procedures for determining the coefficients of the empirical models and the metrics used to assess their corresponding results, are duly presented below. Moreover, it is worth noting that the methodology that is described in this section has been implemented and computationally implemented in Matlab 2016b and then executed on a PC with an Intel Core i7-4510U @ 2/2.60 GHz, 8 GB RAM, under the Windows 10 64-bit OS.
3.1. PV Modules and Their Operational Records
NREL [43] kindly provided the operational records and datasheets of the fourteen PV modules adopted as objects of study. These PV modules consist of six flat-plate models from five different manufacturers, being one of single-crystalline silicon technology (xSi), two of multi-crystalline silicon technology (mSi), one of cadmium telluride technology (CdTe), and two of copper indium gallium selenide technology (CIGS) [43]. The particular choice of these four PV technologies is because they are the most significant for the global industry in recent years, emphasizing the first two [56], which account for around 95% of the world market.
These PV modules have been divided into two sets, as shown in Table 2. The first was initially installed in Cocoa, Florida state (FL), subtropical climate, and then later moved to the city of Eugene, Oregon state (OR), marine west coast climate; and, the second was installed in Golden, Colorado state (CO), semi-arid climate [43]. In both locations, they were fixed in open-rack outdoors, and systematic measurements of weather, electrical, and thermal variables associated with their performance were recorded for about one year [43].

Table 2.
Characteristics of the PV modules adopted as the object of study [43].
Strictly speaking, in the case of Cocoa-FL and Eugene-OR, the respective I–V curves of the PV modules were measured every 5 min and in the case of Golden-CO, every 15 min [57]. Simultaneously, the solar irradiance incident on the plane of the PV modules’ surfaces was measured at each of these locations while using an appropriate pyranometer (classified as the secondary standard [58]) and its operating temperature by means of a type T thermocouple sensor positioned behind the center of the cell near the center of PV module [57]. The level of cleaning of the PV modules was measured by comparing the daily performance of a PV module to an identical PV module that was cleaned during daily maintenance [57]. Thus, a “soiling factor” () was defined for each operational record of the PV modules. In this sense, = 1 means that the PV module at hand was entirely clean at the time of measurements, and means that some soiling loss has occurred [57].
It is essential to note that the solar irradiance measured on the same plane as the PV modules’ surface () may not represent the solar irradiance that is effectively available to be converted by each of them. The respective soiling that accumulated on their surfaces can cause the solar irradiance obstruction or even its scattering. Therefore, the effective irradiance for a given operational record of these PV modules must be calculated, as given by (21) [27].
Although part two of the IEC 61853 (IEC 61853-2), “Spectral responsivity, incidence angle and module operating temperature measurements”, makes considerations regarding the internal optical losses of the PV module [59], which is, by reflection in its surface and by spectral mismatch, it is important to mention that its impacts on the effective irradiance were not taken into account in the context of this paper. A primary reason for this is that the calculation of these losses usually requires measurements that are explicitly made in the laboratory or equipment not regularly found in monitoring structures of real PV systems [27]. Another reason is that the literature models for calculating these losses still need to be thoroughly investigated regarding their effectiveness, as discussed in references [8,60]. Therefore, the decision to disregard the impacts of such losses was made in order to align this paper with the practical application of the empirical models and avoid introducing other uncertainties in assessing their performances.
When developing the test facilities that are presented above, NREL’s main purpose was to obtain operational records of PV modules of different technologies, which could be used for the reliable validation of PV module performance models [43]. In this way, each operational record of the PV modules was subjected to strict quality control procedures before their availability [57]. Consequently, it can be seen in Table 2 that the number of operation records made available for each of them is less than expected (when considering the aforementioned operation period and measurement intervals). Nevertheless, Figure 2 shows that the operating conditions that were recorded at each installation location of the PV modules cover a wide range of effective irradiance and operating temperature in a very consistent manner.
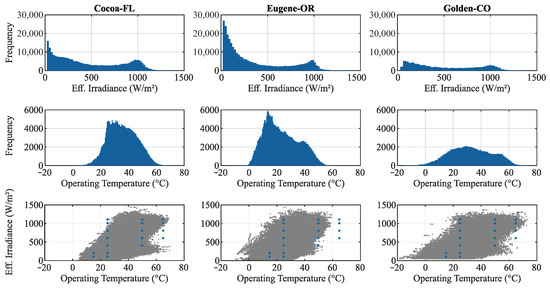
Figure 2.
Overview of the operating conditions recorded for the PV modules under study in Cocoa-Fl (left), Eugene-OR (center) and Golden-CO (right) [43]. In the graphs of effective irradiance versus operating temperature of the PV modules (bottom), the operating conditions in which the characteristics of the PV modules under study were possible to be measured in the laboratory are highlighted [43].
In this sense, it is important to highlight that each PV module was subjected to laboratory tests before its installation (or relocation) in order to update or supplement its respective datasheet information. Accordingly, its temperature coefficients (e.g., , , ) were measured in accordance with IEC 61215 or IEC 61646 [43,61,62]. Likewise, the currents and voltage of maximum power ( and ), short-circuit (), and open-circuit () were measured in the laboratory following the requirements of IEC 61853-1 [43]. However, due to limitations of the available laboratory equipment, it was not possible to fully obtain the measurement matrix that was provided for by this standard [43]. The maximum operating temperature considered for the measurements of the PV modules’ electrical characteristics was 65 °C instead of 75 °C, as shown in Figure 3 [43]. Furthermore, measurements that were related to the operating temperature of 15 °C and effective irradiance of 400, 600, 800, and 1000 W/m² were also not possible to be performed [43].
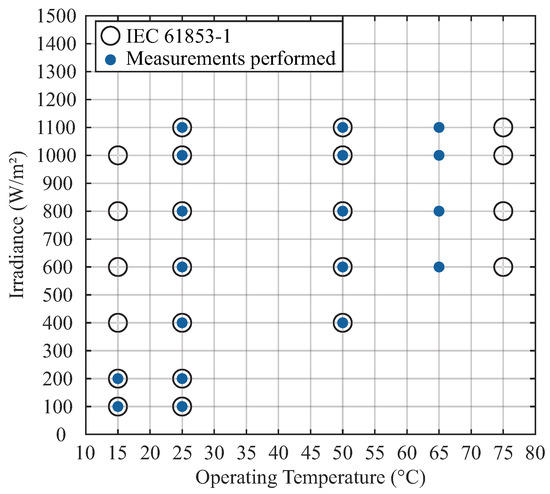
Figure 3.
Comparing the established operating conditions for measuring the electrical characteristics of the PV module by IEC 61853-1 and the operating conditions in which these characteristics were possible to be measured in the laboratory [36,43].
Despite that these measurement matrices respective to IEC 61853-1 are slightly different from the matrix established by such a standard, it is pertinent to note that they meet the objectives of this paper. The measurement points made available correctly comprise the IEC 61853-1 matrix core, as shown in Figure 3. Additionally, the missing points refer to operating conditions verified with a not too high frequency by the PV modules under study, as shown in Figure 2 [43]. Therefore, the conclusions that were obtained by the empirical models in the proposed application approach, i.e., considering these matrices to determine their respective coefficients, can be extended to the case of matrix IEC 61853-1, as long as the due considerations are made.
3.2. Procedures for Determining the Empirical Coefficients
In view of the content that is presented in Section 2, the least-squares method was the technique adopted to determine the coefficients of the empirical models, when considering both the measurement matrix referring to IEC 61853-1 and the operational records that were made available for the PV modules under study.
Modern computing makes use of the nonlinear least-squares method as simple as the linear least-squares method. Thus, the latter must be restricted to particular cases, in which the empirical model is linear, while the former can be used for both nonlinear and linear empirical models. Being aware of this, the nonlinear least-squares method was conveniently chosen as a standard technique in order to determine the coefficients of the empirical models in this work, being performed through the “lsqnonlin” Matlab function.
It is worth mentioning that in the variation of the empirical model proposed by Ransome et al. [35] with five coefficients (C = 5), which is given by (16), a constraint was introduced in the “lsqnonlin” Matlab function in order to ensure that , as recommended by its authors. Similarly, for the empirical model that was proposed by Driesse and Stein [36], constraints have also been introduced to ensure that their coefficients will assume values within the respective ranges that are suggested by its authors [36].
Nonetheless, during the preliminary tests, some complications were observed regarding the determination of the coefficients of the empirical models proposed by King et al. [27], Reich et al. [32] and Driesse and Stein [36].
The empirical model tha was proposed by King et al. [27] has specific procedures for determining each of its coefficients, as explained Section 2. These procedures involve linear and parabolic regressions, which were performed through the “polyfit” Matlab function. Thus, when applying this empirical model with its coefficients being determined considering the measurement matrix referring to IEC 61853-1 made available for the PV modules under study, it was found that such a model returned poor quality solutions. The same was verified, but to a less severe degree, when the measurements that were considered in order to determine the coefficients were the operational records. Some possible reasons that explain such situations are: (i) the reduced number of measurements available in the case of the matrix referring to IEC 61853-1; (ii) the fact that there are no measurements that are related to wind speeds in the operational records of the PV modules, which precludes such measurements from being filtered following all of the weather requirements; and, (iii) the measurement interval of the operational records is greater than that typically considered by the authors.
Aware of that, some alternative procedures were then tested in order to determine the coefficients of the empirical model proposed by King et al. [27]. Coincidentally, the alternative that presented the most satisfactory results both in the case of the measurements used being referring to IEC 61853-1 matrix and in the case of them being the operational records, was the one that involves the total relaxation of the procedures that were specified by its authors. That is, its coefficients were determined while using the nonlinear least-squares method, as performed for the other empirical models, and without any constraint to the values of its coefficients. Notwithstanding, it is worth mentioning that, in the former case, all of the available data referring to IEC 61853-1 matrix were considered without taking their compliance with the weather requirements into account. In turn, in the latter case, 6000 measurements were filtered in the operational records, when only considering the requirements defined for solar irradiance and, of this amount, 4000 were associated with clear sky days and 2000 with cloudy sky days (see Appendix B).
Accordingly, all of the results that will be presented and discussed in Section 4 for the empirical model proposed by King et al. [27] were obtained while using this total relaxed determination procedure. Complementarily, Appendix C presents a sample of the results that were obtained in each alternative procedure tested to determine the coefficients of this empirical model.
Regarding the empirical model that was proposed by Reich et al. [32], it was verified that, for some PV modules, their results to low effective irradiance values had a complex nature. After a thorough investigation, it is concluded that this occurred, because the value that was determined for the coefficient was negative. Under these conditions, the mathematical operation within the term natural logarithm that is expressed in (12) also assumes negative values; thereby, only solutions of a complex nature are feasible. Thus, a constraint was properly added to the process of determining the coefficients of the empirical model that was proposed by Reich et al. [32], in order to ensure that .
Concerning the empirical model proposed by Driesse and Stein [36], an impasse was found when determining its coefficients: “Should the coefficient be calculated or not?”. As claimed by the authors [36], applying their empirical model does not require the knowledge of this coefficient value. Nevertheless, it is possible to notice, in (17c), that the coefficient has an influence on the coefficients and and these three coefficients have a commitment to the estimation of the maximum power voltage of the PV module at hand.
Thus, two procedures were preliminarily tested in order to determine the coefficients that are necessary to apply the empirical model that was proposed by Driesse and Stein [36]. In the first, these coefficients were determined when only considering the PV module maximum power efficiency () fitting and the constraints defined by the authors. In the second, the PV module maximum power voltage () fitting was added, with the value limits of the coefficient being free. Although the coefficients that were determined by both procedures have enabled the model to return results with comparable quality, it was found that those resulting from the second approach were more accurate than those resulting from the first approach.
Therefore, as practiced for the empirical model that was proposed by King et al. [27], all results that will be presented and discussed in Section 4 for the empirical model proposed by Driesse and Stein [36] were obtained using this last determination procedure, which additionally includes the PV module maximum power voltage fitting. Additionally, Appendix C shows a sample of the results that were obtained in each tested procedure to determine its coefficients.
3.3. Assessment Metrics
In accordance with the best practices presented in the literature, three metrics were employed in order to assess the quality of the results that were obtained by the empirical models: “coefficient of determination”, “mean bias error”, and “root mean square error” [36,63,64,65,66].
The coefficient of determination (R²) provides information regarding how well an empirical model can describe the variability verified in practice for the PV module maximum power output [66]. Therefore, this metric can be calculated while using (22), where: is the “i” record of the maximum power measured at the PV module terminals for a given operating condition; is the maximum power estimated by the empirical model at hand for this same operating condition; is the average of the PV module maximum power calculated from the total operational records made available; and, “M” is the number of total operational records made available. It is interesting to note that the closer the coefficient of determination is to 1 (one unity), the greater is the empirical model potential for representing the PV module under study.
In turn, the mean bias error (MBE) is a measure of the empirical model systematic error. This metric can be calculated, as shown in (23) [63]. Additionally, it can take both negative and positive values. Thus, it indicates an empirical model average tendency to underestimate or overestimate the maximum power output of a PV module.
Finally, the root mean square error (RMSE) is a metric that quantifies the effects of systematic (MBE) and non-systematic (standard deviation) errors together [65]. This metric can be calculated by (24) [63]. Unlike the MBE, this metric only assumes positive values. Therefore, the closer its value to zero, the lower the uncertainty that is associated with the empirical model at hand.
4. Experimental Results
The results that were obtained through the methodology described in Section 3 are adequately presented below. Nonetheless, in order to facilitate the discussions about them, it is essential to mention that some simplifications of expressions were adopted. Strictly speaking, applying empirical models while considering a measurement matrix referring to IEC 61853-1 to determine their coefficients will be treated as a “proposed application approach”, or just a “proposed approach”. In turn, applying empirical models considering operational records to determine their coefficients will be treated as a “conventional application approach”, or just a “conventional approach”.
4.1. Overall Results
Figure 4 shows a series of scatter plots, which contrast the maximum power output values that were obtained by the empirical models in the proposed application approach with the respective expected values, i.e., the values that were measured at its terminals. It is worth noting that these values are presented in a normalized way to the corresponding rated powers of the PV modules to facilitate their grouped analysis.
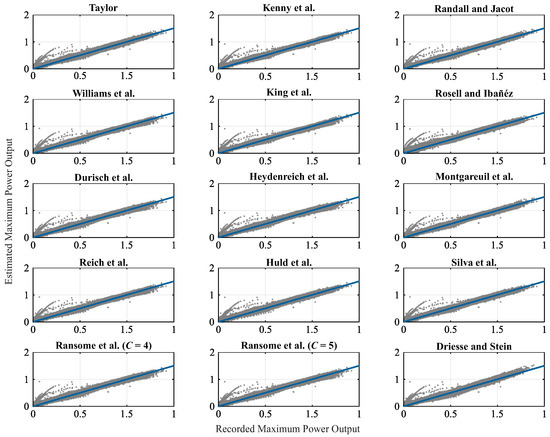
Figure 4.
Maximum power output estimated by the empirical models versus those recorded for the PV modules under study. Both are normalized concerning the respective rated powers of the PV modules.
Thus, it can be seen in Figure 4 that the results that are obtained by the empirical models in the proposed application approach are significantly close to the expected values, with the errors being checked for a narrow and regular range of amplitude. A few discrepant results can be seen, especially for operating conditions in which the maximum power outputs of the PV modules were measured below half of their respective rated powers. However, it is important to mention that they are due to atypical measurements that are verified in the operational records made available for the PV modules and not to represent the empirical models. Consequently, the occurrence of these results is verified simultaneously for all of the empirical models analyzed and even following the same error pattern.
Regarding these atypical measurements, it is worth noting that, as they met the strict quality control procedures performed by NREL, it was decided not to consider them as “outliers” and, thus, keep them in the analysis context of empirical models.
That said, it can be seen in Figure 5 that the results obtained by the interpolation method recommended by IEC 61853-3 are widely dispersed in relation to the expected values, with the errors being checked for a broad and irregular range of amplitude. This situation reveals that the empirical models, when applied in the proposed approach, have greater accuracy and robustness when compared to the interpolation method that was recommended by IEC 61853-3.
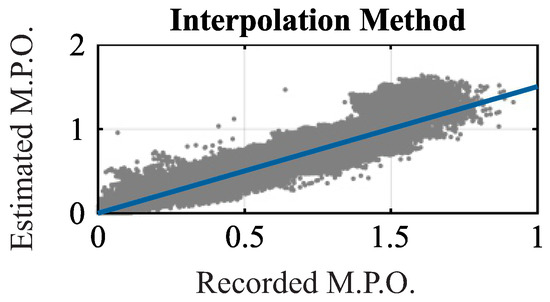
Figure 5.
Maximum power output (M.P.O.) estimated by the interpolation method recommended by IEC 61853-3 versus those recorded for the PV modules under study. Both are normalized concerning the respective rated powers of the PV modules.
4.2. Results on PV Technologies
In spite of the results that are presented above demonstrating that the empirical models present satisfactory performances in the proposed application approach, it is still necessary to quantify how good these performances are and what are their potentials and limitations of representing the behavior of the PV modules. One way of doing this is to compare the quality of the results that were obtained for each empirical model for each type of PV technology under study since the particular characteristics of each PV technology can lead to different conclusions.
Therefore, Table 3 presents an overview of the quality of the results that were obtained by each empirical model for each PV technology in the proposed application approach.

Table 3.
Assessment metrics calculated from the results obtained by each empirical model for each PV technology in the study, when they were applied considering the proposed approach, and by the interpolation method that was recommended by IEC 61853-3.
Right away, the fact that the vast majority of empirical models have presented R² > 0.985 confirms their good potential for representing PV modules in the proposed application approach. It should also be noted that they demonstrated slightly greater sensitivity to behavioral variations of the PV modules of xSi, mSi, and CdTe technologies to the detriment of CIGS technology. Notwithstanding, these sensitivities that were presented by the empirical models were significantly higher than those that were verified by the interpolation method that was recommended by IEC 61853-3, which is observed to have R² < 0.95 for all technologies.
Analyzing the characteristics of the errors verified in the results that were obtained by the empirical models in the proposed application approach, some details draw attention. From the results presented for the MBE in Table 3, it is verified that all of the empirical models demonstrated an average tendency to overestimate the maximum power output of the PV modules of silicon technologies. On the other hand, the vast majority of the empirical models demonstrated an average tendency to underestimate the maximum power output of PV modules of CdTe technology, being the only exception, the empirical model proposed by Kenny et al. [24]. Concerning the PV modules of CIGS technology, a mixed situation is checked. While the empirical models that were proposed by Kenny et al. [24], Randall and Jacot [25], Heydenreich et al. [30], and Silva et al. [34] demonstrated an average tendency to overestimate, the others demonstrated an average tendency to underestimate.
Regarding the amplitude of these systematic errors, it is noted that they are within acceptable limits, which are higher for mSi technology and lower for CIGS technology. Even so, it is pertinent to note that these amplitudes were, in general, smaller than those that were verified by the interpolation method that was recommended by IEC 61853-3 for silicon technologies and slightly higher for thin-film technologies.
In turn, the results that were presented for the RMSE in Table 3 demonstrate that the uncertainties that were associated with the results obtained by the empirical models in the proposed application approach were adequate for the xSi, mSi, and CdTe technologies and are not very good for the CIGS technology. For this latter, these uncertainties were twice as high as that found for other technologies.
Moreover, the fact of the uncertainties that are associated with the results obtained for xSi technology are less than 5% and, for mSi and CdTe technologies, are close to this value, it is something to be commended. This uncertainty level is in agreement with the uncertainties that are typically seen in the measurements and it aligns with that verified for the performance models available in the literature [7,57,65,67,68].
Concerning the results presented for the RMSE in Table 3, it is also possible to verify that the uncertainties associated with the results that were obtained by the empirical models in the proposed application approach for the xSi, mSi, and CdTe technologies are approximately four or five times lower than the respective uncertainties that were verified by the interpolation method recommended by IEC 61853-3. This difference drops to two and a half times for CIGS technology, but it is still quite significant. Accordingly, these results confirm that the empirical models can obtain excellent quality results in the proposed application approach. In fact, their accuracy and robustness are incredibly superior to those from the verified interpolation method recommended by IEC 61853-3.
In this sense, it is pertinent to highlight that: (i) the empirical model that was proposed by King et al. [27] proved to be the most effective in representing PV modules for silicon technologies; (ii) the model proposed by Durisch et al. [29] for CdTe technology; and, (iii) the models proposed by Williams et al. [26] and Reich et al. [32] for CIGS technology. In turn, the model that was proposed by Rosell and Ibanez [28] proved to be the least effective for all PV technologies under study. Additionally, it is important to note that the empirical model that was proposed by Driesse and Stein [36] demonstrated a regular performance, although it was the only one that was developed when considering its application within the scope of the IEC 61853-1 matrix.
In view of these findings, some questions arise: “Do empirical models reach their full potential for representing PV modules in the proposed application approach?”; “Are the performance differences observed between PV technologies typical of the characteristics of the empirical models?”.
The answer to these questions can be found through Table 4, which presents an overview of the quality of the results that were obtained by each empirical model for each PV technology in the conventional application approach.

Table 4.
Assessment metrics calculated from the results obtained by each empirical model for each PV technology in the study, when they were applied when considering the conventional approach.
Hence, when comparing the results that were presented in Table 3 and Table 4 for R², it is possible to notice that the empirical models, when applied in the proposed approach, have their potential to represent the behavior of the PV modules minimally affected compared with what would be found via the conventional application approach. This situation indicates that the respective measurement matrices referring to IEC 61853-1 made available for the PV modules under study were sufficient for properly fitting the coefficients of the empirical models and, consequently, enabling their practical application in the representation of the PV modules. However, using this restricted number of operational records to determine the coefficients affects somewhat the other performance characteristics of the empirical models.
The results that are presented for the MBE in Table 3 and Table 4 demonstrate that originally most empirical models do not present an average tendency as those verified in the proposed application approach. Indeed, the models that were proposed by Taylor [23], Ransome et al. [35] (both variations), and Driesse and Stein [36] stand out for their good balance. The maximum power output values eventually overestimated by them are precisely opposed to the maximum power output values eventually underestimated so that no clear trend, or, in other words, no systematic error is verified in their results for the case of the conventional application approach.
In turn, the results that are presented for the RMSE in Table 3 and Table 4 demonstrate that the uncertainties associated with the results obtained by the empirical models for xSi, mSi, and CdTe technologies are higher than those that were verified for CIGS technology. Meanwhile, the latter’s uncertainties are not observed inadequate in the conventional application approach, as found in the proposed application approach, being close to 5% for the empirical models that were verified as more accurate.
It is also interesting to note that the uncertainty that is associated with the results obtained by the empirical models in the proposed application approach for the CIGS technology is about 5% higher than that verified in the conventional application approach, i.e., twice as large. This difference is less discrepant for the other technologies, reaching almost 3% for the mSi technology and only 1% for the xSi and CdTe technologies. Despite this, all of these differences can be considered to be very satisfactory. This is because, in the proposed application approach, only eighteen operational records were used for determining their coefficients and, in the conventional application approach, tens of thousands are used.
In addition, some curious situations can be observed when comparing the individual performances of the empirical models in the proposed application approach with those respectively verified in the conventional application approach.
The uncertainties that are associated with the results obtained by the empirical model that was proposed by Rosell and Ibanez [28] in the conventional application approach were about 4% to 10% lower than those verified in the proposed application approach. This indicates that this empirical model requires a more comprehensive number of operational records for its effective application.
In contrast, the uncertainties that are associated with the results obtained by the empirical models proposed by Kenny et al. [24], Heydenreich et al. [30] and Driesse and Stein [36] for PV modules of thin-film technologies in the conventional application approach were controversial regarding those that were verified in the proposed application approach, often being larger. This indicates that these empirical models are more sensitive to quality than the quantity of operational records used to efficiently determine their respective coefficients.
Furthermore, it is observed that the empirical model that was proposed by Kenny et al. [24], King et al. [27], and Driesse and Stein [36] presented a greater limitation in the representation of the PV modules of CIGS technology in both application approaches. By analyzing the common features of these models, it is possible that their expressions respectively proposed for estimating the maximum power voltage of the PV modules are not as suitable for this technology as they demonstrate for the others.
From another perspective, the regularity and proximity of the quality verified in the results that were obtained by some empirical models in both application approach, such as those proposed by Taylor [23], Randall and Jacot [25], Williams et al. [26], Durisch et al. [29], Montgareuil et al. [31], Reich et al. [32], Huld et al. [33], Silva et al. [34], and Ransome et al. [35] (both variations), is impressive.
Regarding them, it should be noted that the empirical models that were proposed by Williams et al. [26] and Reich et al. [32] demonstrated a comparable performance for all PV technologies, with the latter even being a reportedly improved version of the former. Nonetheless, their performance is slightly superior to those that were verified for the empirical model proposed by Randall and Jacot [25], which can be considered as a reduced version of them. Similarly, the empirical model that was proposed by Silva et al. [34], which is declared to be a simplified version of the empirical model proposed by Durisch et al. [29], demonstrated a slightly lower performance than the latter. Additionally, in turn, each variation of the empirical model proposed by Ransome et al. [35] demonstrated a performance that was practically equal.
Besides that, it is necessary to point out that the empirical model that was proposed by Taylor [23], even though it has been developed for almost 40 years and is the only one characterized by an expression that does not have any logarithmic term, was able to present a competitive performance in the cases of all PV technologies.
Finally, it is pertinent to highlight that the results that were obtained by the empirical model proposed by Durisch et al. [29] in the conventional application approach were the most effective for all PV technologies, being closely followed by the models that were proposed by Williams et al. [26], Montgareuil et al. [31], Reich et al. [32], and Huld et al. [33].
4.3. Results on Operating Conditions
In order to explore the representation potentials and limitations of the empirical models a little more, Figure 6 shows an overview of the uncertainties that are associated with the results obtained by them in the proposed application approach for the different operating conditions that were recorded for the PV modules under study.
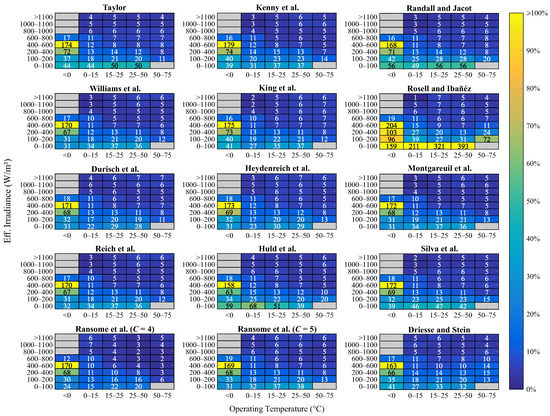
Figure 6.
RMSE values (%) calculated from the results obtained by each empirical model for the different range of operating conditions verified for the PV modules under study, when they were applied when considering the proposed approach.
As can be seen, the performance of empirical models in the proposed application approach has some well-defined behaviors. For effective irradiance levels that are above 800 W/m², the results that were obtained by all empirical models are of excellent quality, regardless of the operating temperature. For operating conditions outside this effective irradiance range, it is observed that, in general, the uncertainty that is associated with the results obtained by the empirical models increases as the level of effective irradiance and operating temperature of the PV modules decreases concomitantly.
The empirical models that are proposed by Rosell and Ibanez [28] and Driesse and Stein [36] deviate somewhat from this rule, because the uncertainty that is associated with their results increases as the level of effective irradiance decreases, even under conditions of elevated temperature operation of the PV modules.
Nevertheless, the worst quality results that were obtained by the empirical models in the proposed application approach were for operating conditions characterized by effective irradiance levels up to 100 W/m² and/or operating temperatures below 0 °C.
In turn, Figure 7 shows an overview of the uncertainties that are associated with the results that were obtained by the interpolation method that was recommended by IEC 61853-3 for the different operating conditions that were recorded for the PV modules under study.
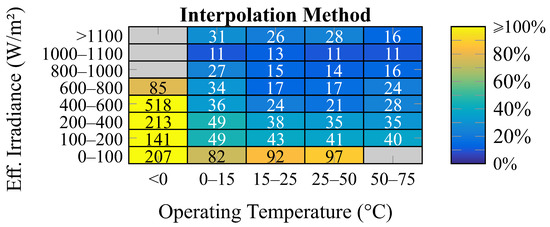
Figure 7.
RMSE values (%) calculated from the results obtained by the interpolation method recommended by IEC 61853-3 for the different range of operating conditions verified for the PV modules under study.
By comparing the results that are presented in Figure 6 and Figure 7, it is possible to notice that the uncertainties that are associated with the results obtained by the interpolation method recommended by IEC 61853-3 are significantly higher than those verified for the empirical models, in practically all of the ranges of operating conditions. The only exception concerning the empirical model proposed by Rosell and Ibanez [28], which has a lower performance than this method, mainly for low levels of effective irradiance.
On the other hand, Figure 8 shows an overview of the uncertainties that are associated with the results obtained by each empirical model in the conventional application approach for the different operating conditions that are verified for the PV modules under study.
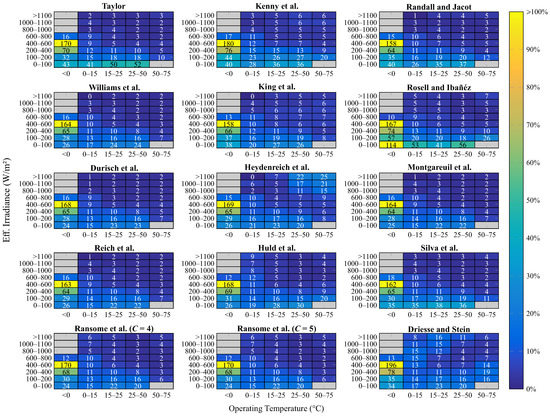
Figure 8.
RMSE values (%) calculated from the results obtained by each empirical model for the different range of operating conditions verified for the PV modules under study, when they were applied considering the conventional approach.
As can be seen, the general performance behavior that was observed for the empirical models in the conventional application approach is similar to that discussed above for the proposed application approach. Hence, it can be concluded that this general performance behavior is due to the representation abilities of the empirical models themselves and not exactly to the amount or dispersion of the operational records used to determine their coefficients.
Some more prominent variations of this performance behavior are observed only for the empirical models by Heydenreich et al. [30] and Driesse and Stein [36]. However, these variations can be attributed to the issues that were previously discussed about determining their coefficients (see Section 4.2).
Regarding the general performance behavior of the interpolation method that was recommended by IEC 61853-3, a different situation is observed. Because it is a strictly mathematical method and of a linear nature, it is due to its lack of ability to represent the nonlinearities of the behavior of the PV modules, when considering the measurement matrices referring to IEC 61853-1 made available to the PV modules under study. Although covering a wide range of operating conditions, the quantity of measurements of these matrices is presumably scarce to allow a more efficient application of this method, especially at low levels of effective irradiance and/or operating temperature. Accordingly, it is interesting to note that a similar situation can be expected for the measurement matrix that was established by IEC 61853-1.
In addition, it can be seen in Figure 6, Figure 7 and Figure 8 that, for operating conditions that are characterized by effective irradiance levels between 200 and 600 W/m² and operating temperature below 0 °C, all of the empirical models obtained results with a strangely accentuated uncertainty. These operating conditions concern a portion of the atypical measurements that were verified in the operational records of the PV modules, which were previously discussed in the view of Figure 4. Thus, the magnitude of these uncertainties must be interpreted with some care, depending on the analysis context.
That said, it is interesting to note that these well-defined behaviors that were observed for the empirical models produce some practical effects on their respective applications. For instance, Table 5 presents an overview of the uncertainties that are associated with the results obtained by each empirical model in the proposed application approach for the PV modules that were installed in each of the three locations considered.

Table 5.
RMSE values (%) calculated from the results obtained by each empirical model for each installation location of the PV modules under study when they were applied considering the proposed approach, and by the interpolation method that was recommended by IEC 61853-3.
As can be verified, the quality of the results that were obtained by the empirical models for the PV modules installed in Cocoa-FL was significantly superior to the results obtained for the PV modules installed in Eugene-OR. Because these are the same PV modules, being monitored by the same test system, and with the information in their datasheets duly updated, the primary explanation for this discrepancy is the different operating conditions verified by them in each location.
The records made in Cocoa-FL were concentrated in operating conditions that were characterized by high levels of effective irradiance and elevated operating temperature, as shown in Figure 2. While, in Eugene-OR, these operational records are more dispersed by low levels of effective irradiance and more recurrent at low operating temperatures. Accordingly, the uncertainties that are associated with the empirical models in the proposed application approach were more significant in the latter location than the former.
This same reasoning can be partially extended to Golden-CO since the manufacturers and models of the PV modules were the same as those that were installed in the other two locations. Because the records that were made in Golden-CO were more dispersed concerning the effective irradiance and the operating temperature of the PV modules, the empirical models demonstrated an intermediate performance as compared to the other two locations.
4.4. Additional Comments
The measurement matrices referring to IEC 61853-1 made available for the PV modules under study have some differences concerning the matrix established by this standard, as shown in Figure 3 and discussed in Section 3. Despite this, most of the conclusions that were obtained from discussions held in this section can be extended for the IEC 61853-1 matrix. This is because the application of the empirical models considering these available measurement matrices (proposed approach) proved to be able to preserve the fundamental performance characteristics of the empirical models, mainly in relation to the operating conditions that were registered for the PV modules.
In other words, if the measurements for high temperatures of the available matrices made available for the PV modules were 75 °C, as established by IEC 61853-1 and not 65 °C, as they were possible to be performed, the impacts on the quality of the results presented would be minimal. Although this second one is more representative than the first one (see Figure 2), the empirical models have intrinsically a very high capacity to represent the behavior of the PV modules in both of the operating conditions (see Figure 6 and Figure 8).
In contrast, if the measurements for the operating temperature of 15 °C and effective irradiance of 400–1000 W/m² had been made available, as established by IEC 61853-1, the most significant effects would be the reduction of the uncertainties that are associated with the results obtained in the operating conditions around these. Consequently, reducing the total uncertainties that are presented for each PV technology and installation location of the PV modules under study also be checked. However, as empirical models generally perform poorly under these operating conditions (see Figure 6 and Figure 8), this reduction is unlikely to be very impactful. Additionally, the occurrence of this reduction would only reinforce the effectiveness of the application of the empirical models considering a matrix of measurements such as that of IEC 61853-1 for the determination of their coefficients, which favors the conclusions obtained from discussions held in this section.
Therefore, it is possible to declare, particularly for those empirical models that have been verified with more regular performance in the results previously presented in this section, i.e., all but the one proposed by Rosell and Ibanez [28], that their respective applications considering a measurement matrix that is similar to that established by IEC 61853-1 for the determination of their coefficients are indeed effective, because:
- it preserves their respective sensitivities and potentials for representing the behavior of PV modules;
- doing this allows for empirical models to obtain good quality results easily, especially for modules of xSi, mSi and CdTe technologies; and
- additionally, incidentally, surprisingly more accurate and robust than those verified by the interpolation method recommended by IEC 61853-3.
Nevertheless, some of the conclusions reached here still need further evaluation. The first is related to the average tendencies that were verified for the empirical models from Table 3. By comparing with the results that are presented in Table 4, it was observed that these average tendencies have a certain dependency on the operational records that are used to determine the coefficients of the empirical models. Thus, as the measurement matrix established by IEC 61853-1 has more measurements than the matrices made available for the PV modules under study and, even for operating conditions to which the performance of the empirical models are notoriously sensitive, different average tendencies can be occasionally observed.
The other is regarding which of the empirical models assessed is the most appropriate for representing each PV technology. As mentioned, the fact that the measurement matrix that was established by IEC 61853-1 has additional measurements for relevant operating conditions can cause a more significant improvement in an empirical model’s performance than in others. Hence, as it was seen that most empirical models presented a comparable performance, one of them may eventually stand out more than that was verified as more effective in the results that are presented here.
Still, the empirical models that were found to be most effective in this paper serve as a first recommendation, such as the empirical model(s) proposed by:
- King et al. [27] for representing xSi and mSi technologies;
- Durisch et al. [29] for representing CdTe technology; and,
- Williams et al. [26] or Reich et al. [32] for representing CIGS technology.
Concerning these empirical models, some issues are worth noting. Regarding the model by King et al. [27], it is essential to emphasize that this has proved to be the most effective for silicon technologies under the relaxed procedures of determining its coefficients, and not under the procedures that were initially proposed by its authors, as explained in Section 3.
With respect to the model that was proposed by Durisch et al. [29], it is relevant to mention that it was the one that proved to be the most effective for all PV technologies in the conventional application approach. Therefore, it is an excellent option for studies, in which such an application approach is proposed.
In relation to the empirical models that were proposed by Williams et al. [26] and Reich et al. [32], it is pertinent to point out that, although the latter was developed based on the former aiming to avoid that results with negative values, this was not verified in practice. In the proposed application approach, both of the empirical models obtained a few negative results for some PV modules operating at extreme conditions, such as very low levels of effective irradiance and operation temperature. Notwithstanding, this deficiency is shared by most of the empirical models and verified in both application approaches. The only empirical models that were observed to be able to obtain only positive results, regardless of the application approach, were those that were proposed by Randall and Jacot [25], Durisch et al. [29], Heydenreich et al. [30], Silva et al. [34], and Driesse and Stein [36]. Thus, special attention should be paid to this issue, depending on the nature of the study at hand.
5. Conclusions
In this paper, an investigation was performed regarding the effectiveness of applying empirical models while using a matrix of measurements very similar to the one that was proposed in IEC 61853-1 in order to determine their coefficients. Accordingly, a comprehensive review of fifteen outstanding empirical models was made, and discussions regarding the procedures for determining their respective coefficients were conducted. In order to validate the performance of the empirical models in this proposed approach, they were applied in the representation of fourteen PV modules of different technologies (xSi, mSi, CdTe, and CIGS), which were installed outdoors for about a year, in three locations with distinct climatic types. The obtained results were compared with those that were verified in the conventional application approach of these empirical models, i.e., when considering the operational records of the PV modules for determining their respective coefficients. Moreover, pertinent comparisons were also made regarding the results that were verified for the interpolation method that was recommended by IEC 61853-3.
Thus, it was concluded that the proposed application approach is, in general, capable of preserving the intrinsic abilities of the empirical models. However, the performance of the empirical models under this application approach is slightly lower than the potential verified via the conventional application approach. More specifically, the uncertainty that was associated with their results was 1% higher than that verified by this latter application approach for the PV modules of xSi and CdTe technologies, reaching almost 3% for those of mSi technology and 5% for those of CIGS technology. Even so, for the xSi, mSi, and CdTe technologies, the total uncertainties that are associated with results obtained by the empirical models in the proposed application approach were around 5%, a value that is quite adequate for the nature of the studies in which these models are commonly applied.
In addition, it was found that the performance of the empirical models in the proposed application approach is much higher in terms of accuracy and robustness than that verified by the interpolation method recommended by IEC 61853-3. In general, the total uncertainties associated with the results obtained by the empirical models were, depending on the PV technology, from 2 to 5 times smaller than those verified for the results obtained by the interpolation method recommended by IEC 61853-3.
Therefore, it is possible to declare that applying the empirical models while considering IEC 61853-1 matrix for determining their respective coefficients is effective and a great option for studies in which only the PV module datasheet, with this matrix duly reported, is available. For instance, empirical models, such as those proposed by King et al. [27], Durisch et al. [29], Williams et al. [26] and Reich et al. [32], may be recommended for studies that are related to designing new PV systems, depending on the PV technology at hand. Aware of this, the representations previously made by other researchers for the manufacturers of PV modules to start testing and reporting the IEC 61853-1 matrix in the datasheets are endorsed here, since this can facilitate the good engineering practice and thereby favor the development of the PV industry. In this context, it is expected that the review, discussions, and results that are presented in this paper will serve as valuable information for PV industry players who work with PV modeling.
Author Contributions
Conceptualization, L.D.; methodology, L.D.; software, L.D.; validation, L.D. and I.S.J.; formal analysis, L.D. and I.S.J.; investigation, L.D.; resources, I.S.J., L.H. and A.M.; data curation, L.D.; writing–original draft preparation, L.D.; writing—review and editing, L.D., I.S.J., L.H. and A.M.; visualization, L.D.; supervision, I.S.J.; project administration, I.S.J., L.H. and A.M.; funding acquisition, L.H. and A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Agência Nacional de Energia Elétrica grant number PD-00673-0052/2018.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Restrictions apply to the availability of these data. Data were obtained through direct contact with Bill Marion/NREL.
Acknowledgments
The authors gratefully acknowledge Bill Marion and the NREL for their kind provision of the dataset, which was used to validate the performance of the empirical models. Also, the authors thank ANEEL, EDP, INERGE, CNPq and FAPEMIG for supporting this research.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A
The interpolation method recommended by IEC 61853-3 stipulates that the PV module maximum power output in a required operating condition (,) must be mathematically estimated straight from the measurement matrix established by IEC 61853-1 [39]. Thus, considering the four nearest neighbor measurements surrounding this operating condition, i.e., = , = , = , and = , being and ; the PV module maximum power output can be estimated through bilinear interpolation, as demonstrate by (A1a)–(A1c) [69]. It is worth noting that , , and are given by the IEC 61853-1 matrix.
However, the required operating condition may be outside the IEC 61853-1 matrix. In this case, the IEC 61853-3 suggests that (one-dimensional) linear extrapolation be applied [39]. So, it can be calculated, as given in (A1d) or (A1e) [66], depending on the situation.
Therefore, following the procedures adopted in the reference [66], the IEC 61853-1 matrix must be initially expanded through linear extrapolation to cover the entire range of operating conditions verified outdoors or even expected for the operation of the PV module under study. Once this is done, the PV module maximum power output can then be systematically estimated through bilinear interpolation for any arbitrated operating condition.
Appendix B
As explained in Section 2, the empirical model proposed by King et al. [27] has specific procedures for determining each of its coefficients. Moreover, these procedures must be performed considering a minimum of 600 measurements of weather, electrical, and thermal variables, which characterize the performance of PV modules [47]. Generally, these measurements are made from an outdoor test facility, where the I–V curves of the PV module at hand are scanned every two minutes, and all other required variables are measured simultaneously [47]. In this test facility, the PV module is kept in operation continuously during daylight hours until a minimum equivalent of 3 clear sky days and 1–2 cloudy sky days are obtained [47]. In practice, this may require a period of one to four weeks [47]. The requirements for classifying the measurements as having made in clear or cloudy sky day are shown in Table A1 and Table A2 [47]. As can be seen, these requirements are fundamentally related to conditions of solar irradiance and wind speed and have a certain degree of flexibility.

Table A1.
Parameters required for qualifying a measurement as referring to a clear sky day [47].
Table A1.
Parameters required for qualifying a measurement as referring to a clear sky day [47].
| Parameter | Required | Preferred |
|---|---|---|
| Global normal irradiance (W/m²) | 800–1050 | 600–1200 |
| DNI/GNI | >0.85 | >0.90 |
| Air mass (absolute value) | 1.5–5.0 | 1.0–7.0 |
| Wind Speed (m/s) | 0–4 | 0–10 |
a Ratio between direct normal (DNI) and global normal irradiance (GNI).

Table A2.
Parameters required for qualifying a measurement as referring to a cloudy sky day [47].
Table A2.
Parameters required for qualifying a measurement as referring to a cloudy sky day [47].
| Parameter | Required | Preferred |
|---|---|---|
| Global normal irradiance (W/m²) | 200–400 | 100–500 |
| DNI/GNI | 0–0.85 (<0.05) | |
a Ratio between direct normal (DNI) and global normal irradiance (GNI). b The bulk of the measurements should occur at DNI/GNI < 0.05.
More information about them, as well as the specific procedures defined by the authors to determine each coefficient, can be precisely found in the references [27,47].
Appendix C
Some procedures for determining the coefficients of the empirical models proposed by King et al. [27] and Driesse and Stein [36], had to be preliminarily tested, as discussed in Section 3. Thus, the RMSE associated with the results obtained by each of these models in each of the tested procedures is presented in Table A3. It is worth mentioning that these results include the fourteen PV modules adopted as objects of study.

Table A3.
RMSE values (%) calculated from the global results obtained by the empirical models proposed by King et al. [27] and Driesse and Stein [36], in each tested procedure to determine their respective coefficients.
Table A3.
RMSE values (%) calculated from the global results obtained by the empirical models proposed by King et al. [27] and Driesse and Stein [36], in each tested procedure to determine their respective coefficients.
| Empirical Model | Procedure for Determining | Proposed | Conventional |
|---|---|---|---|
| the Coefficients | Approach | Approach | |
| King et al. [27] | Original procedure | 50.46 | 10.72 |
| King et al. [27] | Total relaxed procedure | 9.20 | 8.34 |
| Driesse and Stein [36] | Procedure based on | 11.87 | 12.31 |
| Driesse and Stein [36] | Procedure based on and | 9.54 | 8.13 |
References
- International Renewable Energy Agency. Renewable Power Generation Costs in 2019; Report; International Renewable Energy Agency: Abu Dhabi, UAE, 2020. [Google Scholar]
- REN21. Renewables 2020 Global Status Report; Report; REN21 Secretariat: Paris, France, 2020. [Google Scholar]
- Masson, G.; Kaizuka, I. Trends 2019 in Photovoltaic Applications; International Energy Agency: Onehemisphere, Sweden, 2019. [Google Scholar]
- Malinowski, M.; Leon, J.I.; Abu-Rub, H. Solar photovoltaic and thermal energy systems: Current technology and future trends. Proc. IEEE 2017, 105, 2132–2146. [Google Scholar] [CrossRef]
- Stein, J. PV Performance Modeling Methods and Practices; Technical Report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2017.
- Stein, J.S. Energy Prediction and System Modeling. In Photovoltaic Solar Energy; Wiley Online Library: Chichester, UK, 2017; pp. 564–578. [Google Scholar]
- Goss, B.; Cole, I.; Koubli, E.; Palmer, D.; Betts, T.; Gottschalg, R. Modelling and prediction of PV module energy yield. In The Performance of Photovoltaic (PV) Systems; Woodhead Publishing: Cambridge, UK, 2017; pp. 103–132. [Google Scholar]
- De la Parra, I.; Muñoz, M.; Lorenzo, E.; García, M.; Marcos, J.; Martínez-Moreno, F. PV performance modelling: A review in the light of quality assurance for large PV plants. Renew. Sustain. Energy Rev. 2017, 78, 780–797. [Google Scholar] [CrossRef]
- Richter, M.; Tjengdrawira, C.; Vedde, J.; Green, M.; Frearson, L.; Herteleer, B.; Jahn, U.; Herz, M.; Kontges, M.; Stridh, B.; et al. Technical Assumptions Used in PV Financial Models Review of Current Practices and Recommendations; International Energy Agency: Paris, France, 2017. [Google Scholar]
- Petrone, G.; Ramos-Paja, C.A.; Spagnuolo, G.; Xiao, W. Photovoltaic Sources Modeling; Wiley: Chichester, UK, 2017. [Google Scholar]
- Woyte, A.; Richter, M.; Moser, D.; Mau, S.; Reich, N.; Jahn, U. Monitoring of photovoltaic systems: Good practices and systematic analysis. In Proceedings of the 28th European Photovoltaic Solar Energy Conference, Paris, France, 30 September–4 October 2013; pp. 3686–3694. [Google Scholar]
- Köntges, M.; Kurtz, S.; Packard, C.; Jahn, U.; Berger, K.; Kato, K.; Friesen, T.; Liu, H.; Van Iseghem, M. Review of Failures of Photovoltaic Modules Final; International Energy Agency: Paris, France, 2015. [Google Scholar]
- Pearsall, N. Prediction and measurement of photovoltaic system energy yield. In The Performance of Photovoltaic (PV) Systems; Woodhead Publishing: Cambridge, UK, 2017; pp. 183–208. [Google Scholar]
- Skoplaki, E.; Palyvos, J.A. On the temperature dependence of photovoltaic module electrical performance: A review of efficiency/power correlations. Sol. Energy 2009, 83, 614–624. [Google Scholar] [CrossRef]
- Rus-Casas, C.; Aguilar, J.; Rodrigo, P.; Almonacid, F.; Pérez-Higueras, P. Classification of methods for annual energy harvesting calculations of photovoltaic generators. Energy Convers. Manag. 2014, 78, 527–536. [Google Scholar] [CrossRef]
- Rawat, R.; Kaushik, S.; Lamba, R. A review on modeling, design methodology and size optimization of photovoltaic based water pumping, standalone and grid connected system. Renew. Sustain. Energy Rev. 2016, 57, 1506–1519. [Google Scholar] [CrossRef]
- Laudani, A.; Fulginei, F.R.; Salvini, A. Identification of the one-diode model for photovoltaic modules from datasheet values. Sol. Energy 2014, 108, 432–446. [Google Scholar] [CrossRef]
- Chin, V.J.; Salam, Z.; Ishaque, K. Cell modelling and model parameters estimation techniques for photovoltaic simulator application: A review. Appl. Energy 2015, 154, 500–519. [Google Scholar] [CrossRef]
- Abbassi, R.; Abbassi, A.; Jemli, M.; Chebbi, S. Identification of unknown parameters of solar cell models: A comprehensive overview of available approaches. Renew. Sustain. Energy Rev. 2018, 90, 453–474. [Google Scholar] [CrossRef]
- Deotti, L.M.P.; Pereira, J.L.R.; da Silva Júnior, I.C. Parameter extraction of photovoltaic models using an enhanced Lévy flight bat algorithm. Energy Convers. Manag. 2020, 221, 113114. [Google Scholar] [CrossRef]
- De Soto, W.; Klein, S.A.; Beckman, W.A. Improvement and validation of a model for photovoltaic array performance. Sol. Energy 2006, 80, 78–88. [Google Scholar] [CrossRef]
- Ibrahim, H.; Anani, N. Variations of PV module parameters with irradiance and temperature. Energy Procedia 2017, 134, 276–285. [Google Scholar] [CrossRef]
- Taylor, R.W. System and module rating: Advertised versus actual capability. Sol. Cells 1986, 18, 335–344. [Google Scholar] [CrossRef]
- Kenny, R.P.; Friesen, G.; Chianese, D.; Bernasconi, A.; Dunlop, E.D. Energy rating of PV modules: Comparison of methods and approach. In Proceedings of the 3rd World Conference on Photovoltaic Energy Conversion, Osaka, Japan, 11–18 May 2003; Volume 2, pp. 2015–2018. [Google Scholar]
- Randall, J.; Jacot, J. Is AM1. 5 applicable in practice? Modelling eight photovoltaic materials with respect to light intensity and two spectra. Renew. Energy 2003, 28, 1851–1864. [Google Scholar] [CrossRef]
- Williams, S.R.; Betts, T.R.; Helf, T.; Gottschalg, R.; Beyer, H.; Infield, D. Modelling long-term module performance based on realistic reporting conditions with consideration to spectral effects. In Proceedings of the 3rd World Conference on Photovoltaic Energy Conversion, Osaka, Japan, 11–18 May 2003; Volume 2, pp. 1908–1911. [Google Scholar]
- King, D.L.; Kratochvil, J.A.; Boyson, W.E. Photovoltaic Array Performance Model; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2004.
- Rosell, J.; Ibanez, M. Modelling power output in photovoltaic modules for outdoor operating conditions. Energy Convers. Manag. 2006, 47, 2424–2430. [Google Scholar] [CrossRef]
- Durisch, W.; Bitnar, B.; Mayor, J.C.; Kiess, H.; Lam, K.H.; Close, J. Efficiency model for photovoltaic modules and demonstration of its application to energy yield estimation. Sol. Energy Mater. Sol. Cells 2007, 91, 79–84. [Google Scholar] [CrossRef]
- Heydenreich, W.; Müller, B.; Reise, C. Describing the world with three parameters: A new approach to PV module power modelling. In Proceedings of the 23rd European PV Solar Energy Conference and Exhibition (EU PVSEC), Valencia, Spain, 1–4 September 2008; pp. 2786–2789. [Google Scholar]
- Montgareuil, A.; Sicot, L.; Martin, J.; Mezzasalma, F.; Merten, J. A new tool for the MotherPV method: Modelling of the irradiance coefficient of photovoltaic modules. In Proceedings of the 24th European Photovoltaic Solar Energy Conference, Hamburg, Germany, 21–25 September 2009; pp. 21–25. [Google Scholar]
- Reich, N.V.; Van Sark, W.; Alsema, E.; Lof, R.; Schropp, R.; Sinke, W.; Turkenburg, W. Crystalline silicon cell performance at low light intensities. Sol. Energy Mater. Sol. Cells 2009, 93, 1471–1481. [Google Scholar] [CrossRef]
- Huld, T.; Gottschalg, R.; Beyer, H.G.; Topič, M. Mapping the performance of PV modules, effects of module type and data averaging. Sol. Energy 2010, 84, 324–338. [Google Scholar] [CrossRef]
- Silva, J.; Asenjo, B.; Vela, N.; Chenlo, F. Caracterización de módulos fotovoltaicos de diversas tecnologías en el marco del proyecto INNDISOL. In Proceedings of the XV Congreso Ibérico y X Congreso Iberoamericano de Energía Solar, Vigo, Spain, 19–22 June 2012. [Google Scholar]
- Ransome, S.; Sutterlueti, J.; Instruments, G.; Solutions, E. A Systematic comparison of 12 empirical models used for energy yield prediction VS PV technology. In Proceedings of the 33rd European Photovoltaic Solar Energy Conference (EU PVSEC), Amsterdam, The Netherlands, 25–29 September 2017. [Google Scholar]
- Driesse, A.; Stein, J. From IEC 61853 Power Measurements to PV System Simulations; Technical Report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2020.
- Photovoltaic, C.S.T. Modules—Design Qualification and Type Approval; International Electrotechnical Commission: Geneva, Switzerland, 2005; Volume 1215, p. 2005-05. [Google Scholar]
- IEC. Photovoltaic (PV) Module Performance Testing and Energy Rating—Part 1: Irradiance and Temperature Performance Measurements and Power Rating; International Electrotechnical Commission: Geneva, Switzerland, 2011. [Google Scholar]
- IEC. Photovoltaic (PV) Module Performance Testing and Energy Rating—Part 3: Energy Rating of PV Modules; International Electrotechnical Commission: Geneva, Switzerland, 2018. [Google Scholar]
- TamizhMani, G.; Kuitche, J.; Mikonowicz, A. Nameplate, Datasheet and Sampling Requirements of Photovoltaic Modules; Solar ABCs Report; Arizona State University: Tempe, AZ, USA, 2012. [Google Scholar]
- Driesse, A.; Stein, J. Making the Most of Module Matrix Measurements: IEC 61853-1; Technical Report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2019.
- Dobos, A.P.; Freeman, J.M. Significant Improvement in PV Module Performance Prediction Accuracy Using a New Model Based on IEC-61853 Data; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2019. [Google Scholar]
- Marion, B.; Anderberg, A.; Deline, C.; del Cueto, J.; Muller, M.; Perrin, G.; Rodriguez, J.; Rummel, S.; Silverman, T.J.; Vignola, F.; et al. New data set for validating PV module performance models. In Proceedings of the 2014 IEEE 40th Photovoltaic Specialist Conference (PVSC), Denver, CO, USA, 8–13 June 2014; pp. 1362–1366. [Google Scholar]
- King, D.L. Photovoltaic module and array performance characterization methods for all system operating conditions. In AIP Conference Proceedings; American Institute of Physics: Melville, NY, USA, 1997; Volume 394, pp. 347–368. [Google Scholar]
- King, D.L.; Kratochvil, J.A.; Boyson, W.E. Field Experience with a New Performance Characterization Procedure for Photovoltaic Arrays; Technical Report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 1998.
- Ransome, S. Validating Energy Yield Modelling with the NREL Outdoor Dataset. In Proceedings of the 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC & 34th EU PVSEC), Waikoloa, HI, USA, 10–15 June 2018; pp. 2713–2718. [Google Scholar]
- King, B.H.; Hansen, C.W.; Riley, D.; Robinson, C.D.; Pratt, L. Procedure to Determine Coefficients for the Sandia Array Performance Model (SAPM); Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2016.
- Gilman, P.; Dobos, A.P.; DiOrio, N.; Freeman, J.; Janzou, S.; Ryberg, D. SAM Photovoltaic Model: Technical Reference Update; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2018.
- Williams, S.; Betts, T.; Gottschalg, R.; Infield, D.; van der Borg, N.; Burgers, A.; De Moor, H.; Warta, W.; Friesen, G.; Chianese, D.; et al. Evaluating the state of the art of photovoltaic performance modelling in Europe. In Proceedings of the 20th European Photovoltaic Solar Energy Conference, Barcelona, Spain, 6–10 June 2005; pp. 1937–1941. [Google Scholar]
- Dirnberger, D.; Müller, B.; Reise, C. PV module energy rating: Opportunities and limitations. Prog. Photovolt. Res. Appl. 2015, 23, 1754–1770. [Google Scholar] [CrossRef]
- Ransome, S.; Sutterlueti, J. How to Choose the Best Empirical Model for Optimum Energy Yield Predictions. In Proceedings of the 2017 IEEE 44th Photovoltaic Specialist Conference (PVSC), Washington, DC, USA, 25–30 June 2017; pp. 652–657. [Google Scholar]
- Akhsassi, M.; El Fathi, A.; Erraissi, N.; Aarich, N.; Bennouna, A.; Raoufi, M.; Outzourhit, A. Experimental investigation and modeling of the thermal behavior of a solar PV module. Sol. Energy Mater. Sol. Cells 2018, 180, 271–279. [Google Scholar] [CrossRef]
- Charles Lawrence Kamuyu, W.; Lim, J.R.; Won, C.S.; Ahn, H.K. Prediction model of photovoltaic module temperature for power performance of floating PVs. Energies 2018, 11, 447. [Google Scholar] [CrossRef]
- Huld, T.; Friesen, G.; Skoczek, A.; Kenny, R.P.; Sample, T.; Field, M.; Dunlop, E.D. A power-rating model for crystalline silicon PV modules. Sol. Energy Mater. Sol. Cells 2011, 95, 3359–3369. [Google Scholar] [CrossRef]
- Batzelis, E.I. Simple PV performance equations theoretically well founded on the single-diode model. IEEE J. Photovolt. 2017, 7, 1400–1409. [Google Scholar] [CrossRef]
- ISE. Photovoltaics Report; Fraunhofer Institute for Solar Energy Systems: Freiburg, Germany, 2020. [Google Scholar]
- Marion, W.; Anderberg, A.; Deline, C.; Glick, S.; Muller, M.; Perrin, G.; Rodriguez, J.; Rummel, S.; Terwilliger, K.; Silverman, T. User’s Manual for Data for Validating Models for PV Module Performance; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2014.
- KP. CMP 22 Pyranometer. In Instruction Manual; Kipp and Zonen: Delft, The Netherlands, 2016. [Google Scholar]
- IEC. Photovoltaic (PV) Module Performance Testing and Energy Rating—Part 2: Spectral Responsivity, Incidence Angle and Module Operating Temperature Measurements; International Electrotechnical Commission: Geneva, Switzerland, 2016. [Google Scholar]
- Freeman, J.; Freestate, D.; Hobbs, W.; Riley, C. Using measured plane-of-array data directly in photovoltaic modeling: Methodology and validation. In Proceedings of the 2016 IEEE 43rd Photovoltaic Specialists Conference (PVSC), Portland, OR, USA, 5–10 June 2016; pp. 2653–2656. [Google Scholar]
- IEC. Terrestrial Photovoltaic (PV) Modules—Design Qualification and Type Approval; International Electrotechnical Commission: Geneva, Switzerland, 2016. [Google Scholar]
- IEC. Thin-Film Terrestrial Photovoltaic (PV) Modules—Design Qualification and Type Approval; International Electrotechnical Commission: Geneva, Switzerland, 2008. [Google Scholar]
- Marion, B. Comparison of predictive models for photovoltaic module performance. In Proceedings of the 2008 33rd IEEE Photovoltaic Specialists Conference, San Diego, CA, USA, 11–16 May 2008; pp. 1–6. [Google Scholar]
- Stein, J.S.; Cameron, C.P.; Bourne, B.; Kimber, A.; Posbic, J.; Jester, T. A standardized approach to PV system performance model validation. In Proceedings of the 2010 35th IEEE Photovoltaic Specialists Conference, Honolulu, HI, USA, 20–25 June 2010; pp. 001079–001084. [Google Scholar]
- Richter, M.; De Brabandere, K.; Kalisch, J.; Schmidt, T.; Lorenz, E. Best practice guide on uncertainty in PV modelling. In Public Report Performance Plus WP2 Deliverable D; 3E: Brussels, Belgium, 2015; Volume 2. [Google Scholar]
- Illiich, P. Evaluation of Photovoltaic Modeling Algorithms for Various Weather Conditions Based on Granular Intra-Array Module and Weather Measurements Taken at NIST—Validation of IEC 61853-3 Committee Draft Sub-Models and Spatial PV Array Analysis. Master’s Thesis, University of Applied Sciences Technikum Vienna, Vienna, Austria, 2017. [Google Scholar]
- Friesen, G.; Gottschalg, R.; Beyer, H.; Williams, S.; van Sark, W.; Guérin de Montgareuil, A.; Van Der Borg, N.; Huld, T.; Müller, B.; De Keizer, A.; et al. Intercomparison of different energy prediction methods within the european project “performance”—Results of the 1st round robin. In Proceedings of the 22nd European Photovoltaic Solar Energy Conference, WIP-Renewable Energies, Milan, Italy, 3–7 September 2007; pp. 2659–2663. [Google Scholar]
- Cameron, C.P.; Boyson, W.E.; Riley, D.M. Comparison of PV system performance-model predictions with measured PV system performance. In Proceedings of the 2008 33rd IEEE Photovoltaic Specialists Conference, San Diego, CA, USA, 11–16 May 2008; pp. 1–6. [Google Scholar]
- Whitaker, C.; Newmiller, J. Photovoltaic Module Energy Rating Procedure. Final Subcontract Report; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 1998.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).