Multi-Objective Teaching–Learning-Based Optimization with Pareto Front for Optimal Design of Passive Power Filters
Abstract
:1. Introduction
1.1. Background
1.2. Aim and Contributions
1.3. Paper Organization
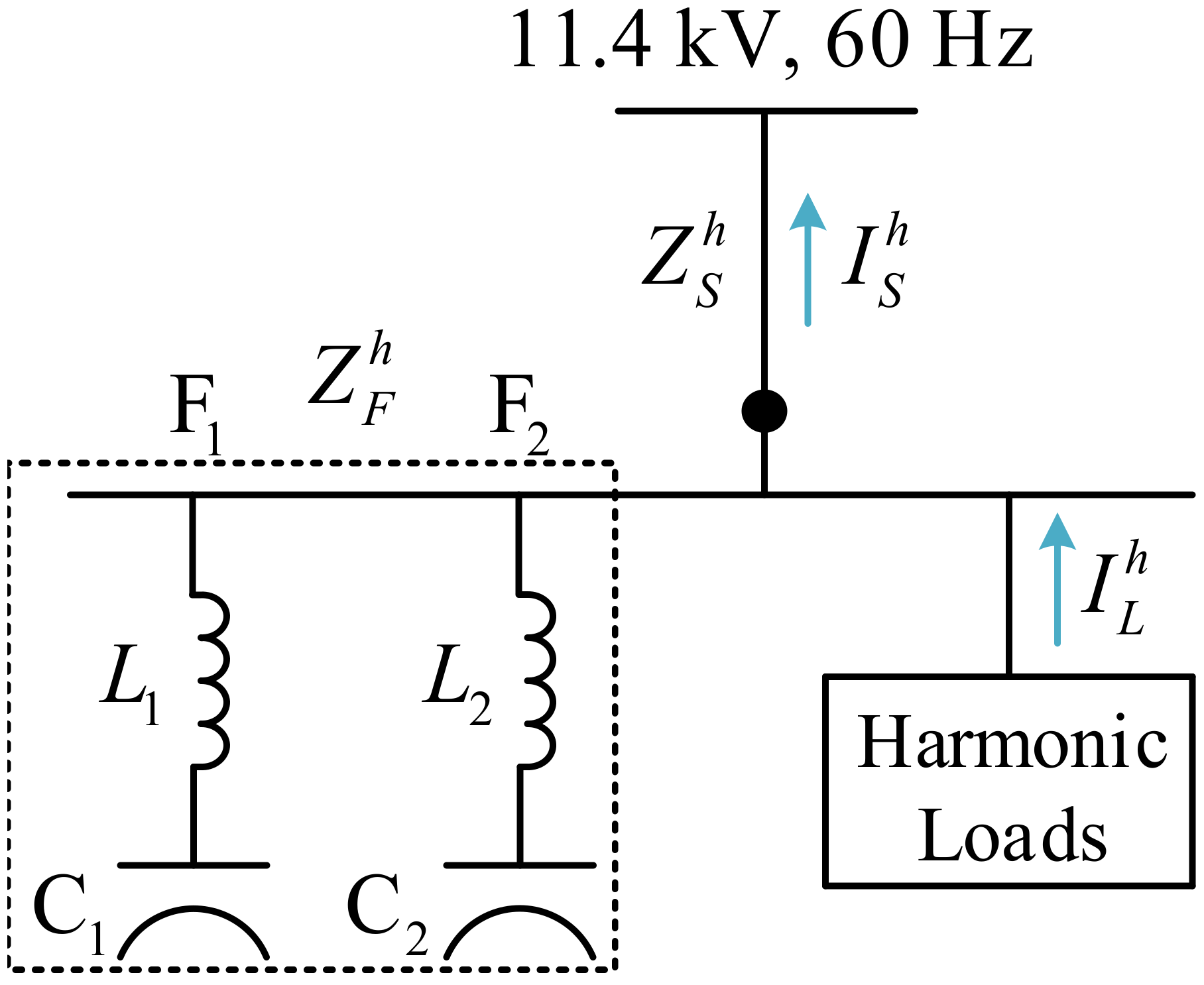
2. Passive Power Filter Model
3. Problem Formulation
3.1. Objective Functions
3.1.1. Minimizing Total Harmonic Distortion of Current
- harmonic order;
- highest harmonic order considered;
- rms of fundamental current;
- rms of harmonic current with integer order.
3.1.2. Minimizing Total Harmonic Distortion of Voltage
- harmonic order;
- highest harmonic order considered;
- rms of fundamental voltage;
- rms of harmonic voltage with integer order.
3.1.3. Minimizing Initial Investment Cost
- i type of filters;
- number of filters of type i;
- resistance of j-th filter of type i;
- the inductance of j-th filter of type i;
- the capacitance of j-th filter of type i;
- reactive power capacity of j-th filter of type i;
- the power loss of j-th filter of type i;
3.1.4. Maximizing Total Fundamental Reactive Power Compensation
- fundamental reactive power produced by j-th filter of i-th type.
3.2. Constraints
3.2.1. Total Harmonic Distortion
- maximum tolerance for total harmonic distortions of currents;
- maximum tolerance for total harmonic distortions of voltages.
3.2.2. Individual Harmonic Distortion
- maximum tolerance for harmonic current at h-th order;
- maximum tolerance for harmonic voltage at h-th order.
3.2.3. Total Fundamental Reactive Power Compensation
- maximum reactive power compensation;
- minimum reactive power compensation.
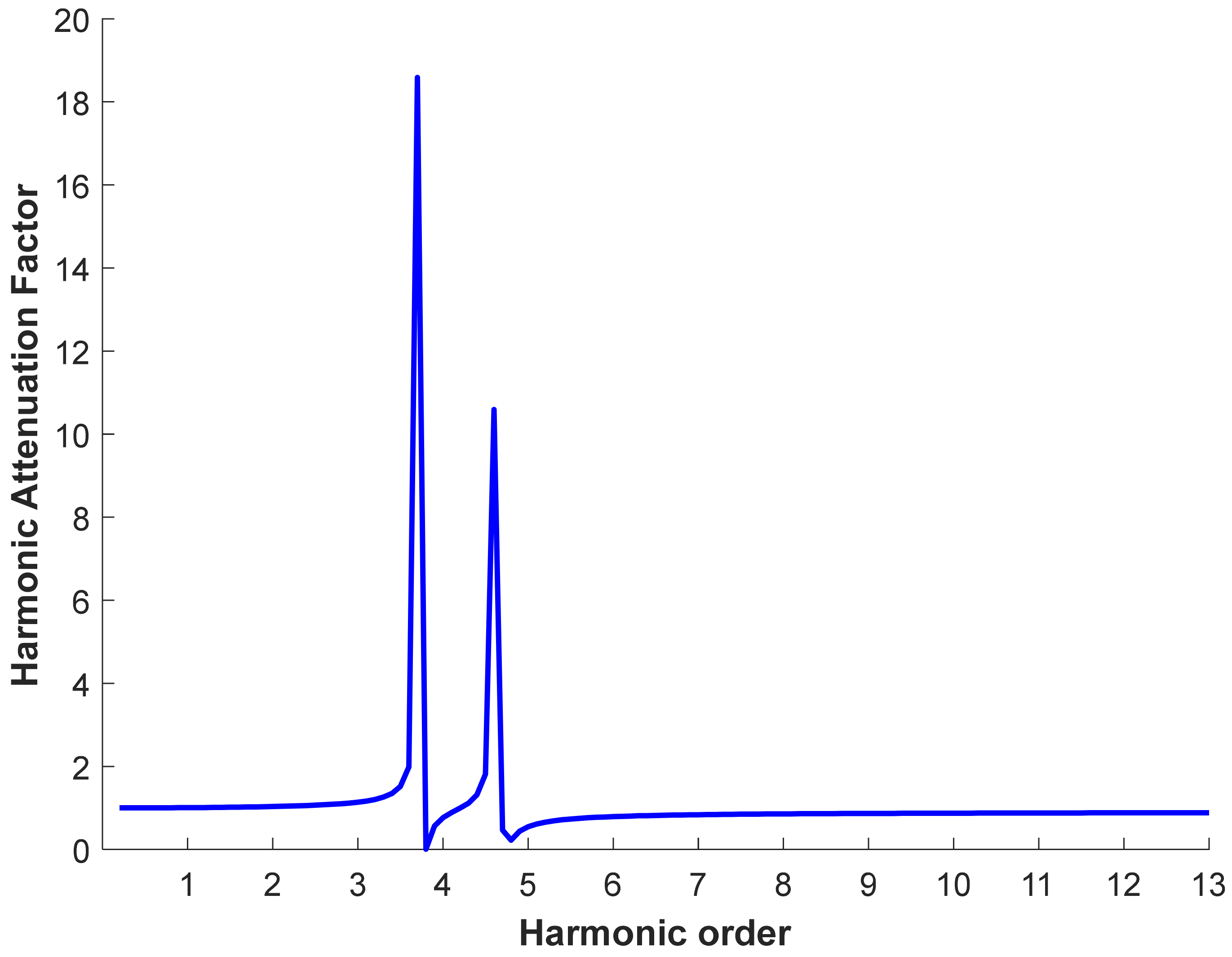
3.2.4. Harmonic Resonance
- order of harmonic to be mitigated;
- order of critical harmonic;
- the impedance of j-th filter of i-th type;
- the impedance of multiple passive power filters.
3.2.5. Perturbations
- Percentage variation of frequency for a power system:
- Percentage variation of resistance for a PPF:
- Percentage variation of inductance for a PPF:
- Percentage variation of capacitance for a PPF:where
- , the upper limit and lower limit of the percentage variation of frequency for a power system in [−1%, 1%];
- , the upper limit and lower limit of the percentage variation of resistance for a PPF in [−3%, 3%];
- , the upper limit and lower limit of the percentage variation of inductance for a PPF in [−3%, 3%];
- , the upper and lower limits of the percentage variation of capacitance for a PPF in [−3%, 3%].
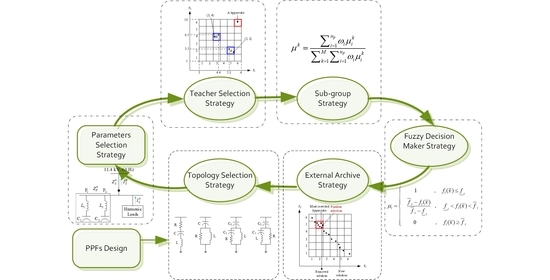
4. Proposed Multi-Objective TLBO
4.1. Teacher Phase
- ii-th iteration;
- mean grade of the learners in subject j at the i-th iteration;
- grade of learner k in subject j at the i-th iteration;
- grade of the teacher in the subject j at the i-th iteration;
- random number in the range [0,1].
4.2. Learner Phase
4.3. Pareto Optimality
- vector of decision variables;
- vector of an objective function;
- inequality constraint;
- equality constraint;number of objective functions;
- number of inequality constraints;
- number of equality constraints.
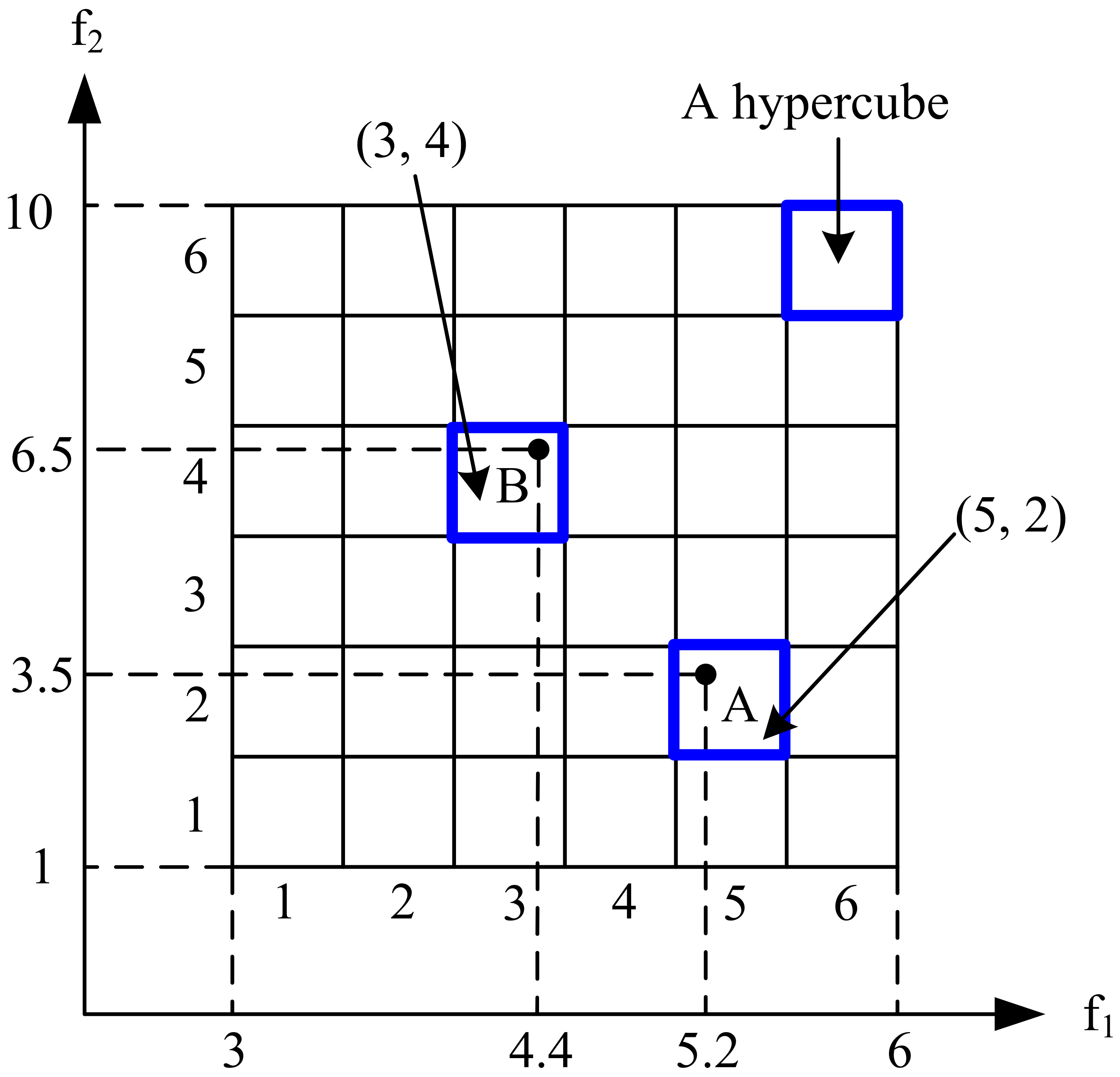
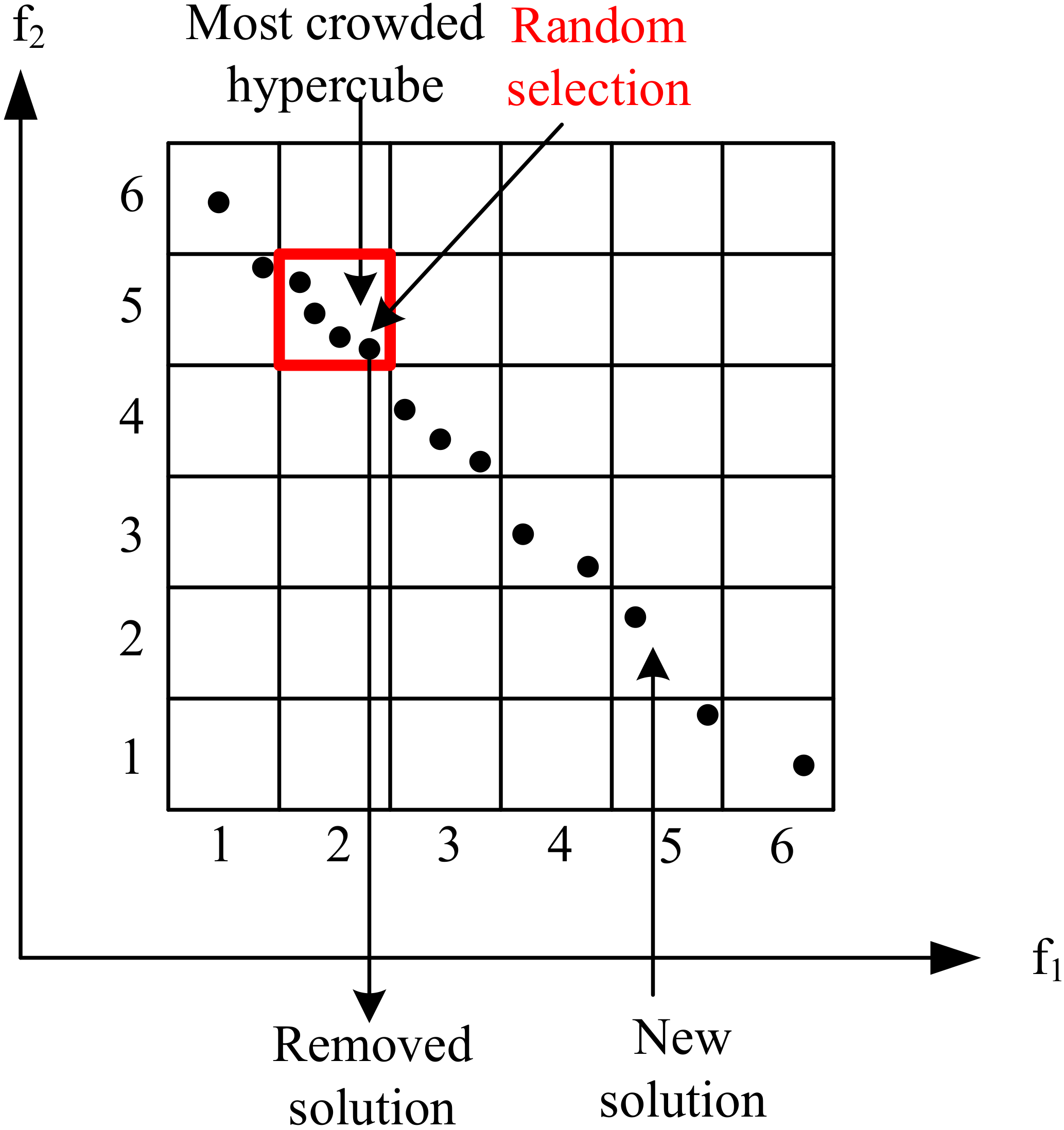
4.4. External Archive Strategy
4.5. Fuzzy Decision-Making Strategy
- membership value of the i-th objective function ;
- , the upper and lower bounds of the i-th objective function.
- nominal membership value of the non-dominated solution k;
- number of non-dominated solutions in the external archive;
- weighting factor of objective function i, and .
4.6. Sub-Group Search Strategy
- Step 1: The number of groups is determined by the number or attributes of the objective functions. The score criteria for each sub-group are defined by (27) and (28) with the corresponding weighting factors.
- Step 2: The NDSs in the external archive are evaluated according to the score criteria of each sub-group. The roulette wheel selection method was used to choose the teacher for each sub-group.
- Step 3: Learners are uniformly and randomly distributed into each sub-group.
- Step 4: According to the score criteria of each sub-group, the solutions of the previous and current generations are evaluated to determine the replacement of the previous generation.
- Step 5: Steps 2 to 4 are repeated until the termination criterion is satisfied.
4.7. Teacher Selection Strategy
- Step 1: Initialize population;
- Step 2: Determine the type of group and score criteria for each sub-group;
- Step 3: Evaluate the multi-objective functions with multi-constraints;
- Step 4: Store the first NDS in the external archive.
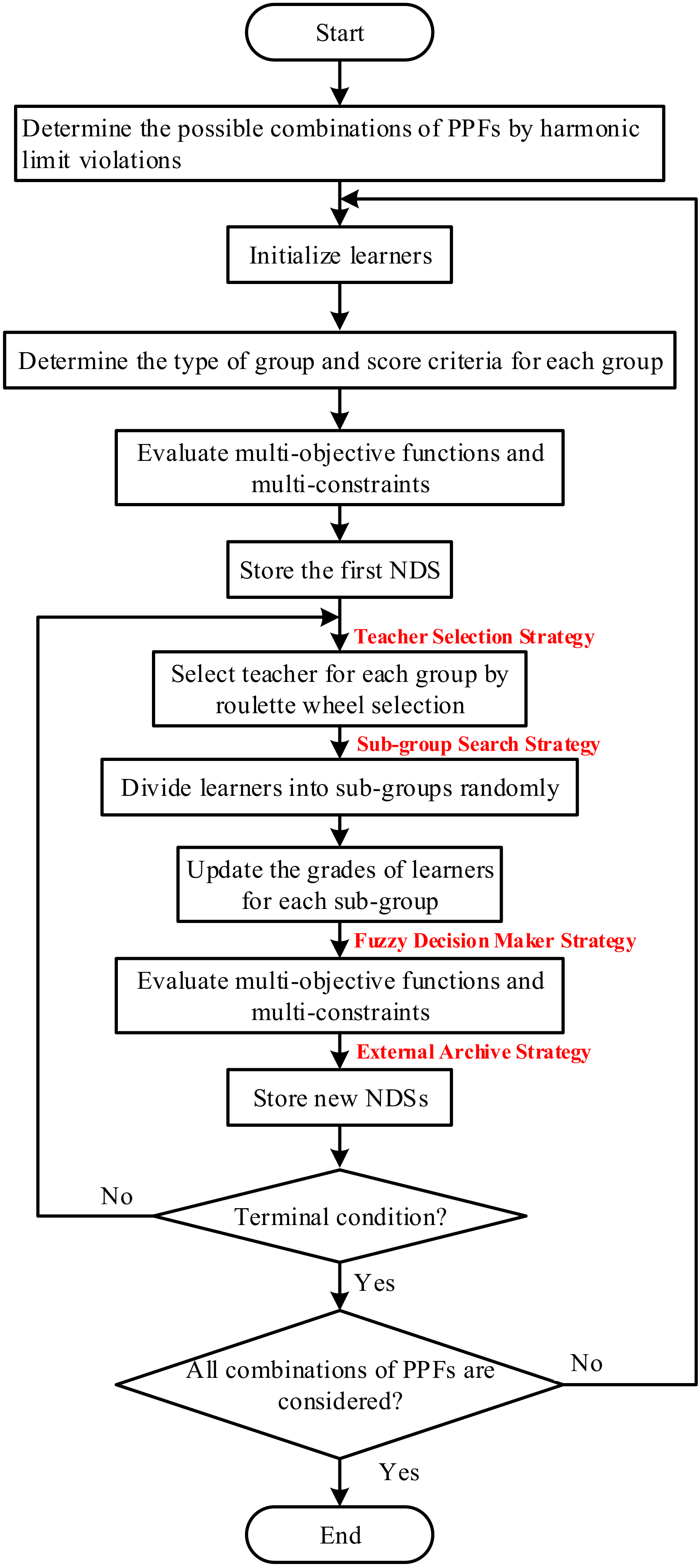
- Step 5: Select the teacher for each sub-group using roulette wheel selection;
- Step 6: Divide learners into sub-groups randomly;
- Step 7: Update the grades of learners if the evaluation criteria for each sub-group are satisfied;
- Step 8: Evaluate the multi-objective functions with multi-constraints;
- Step 9: Store new NDSs in the external archive.
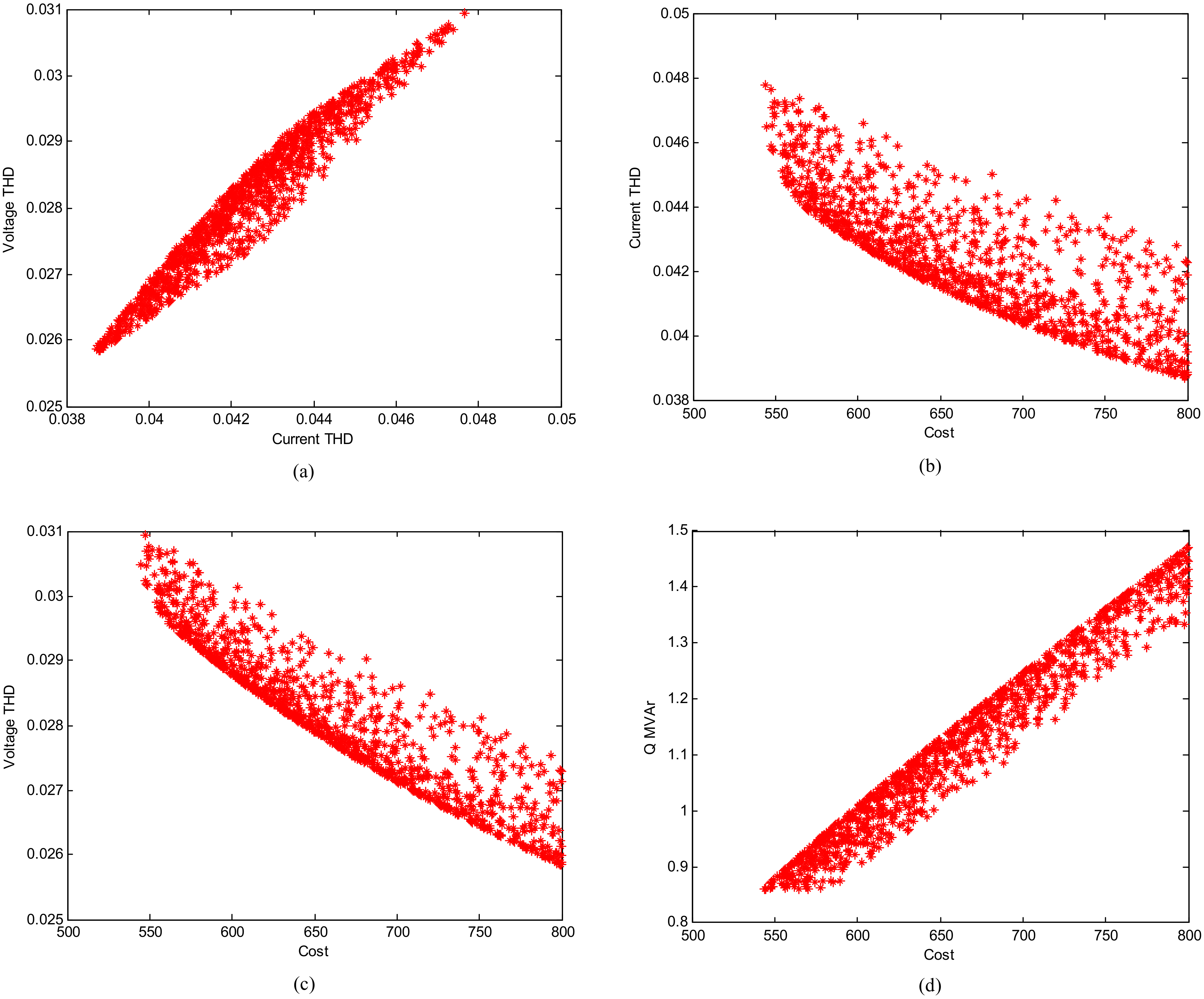
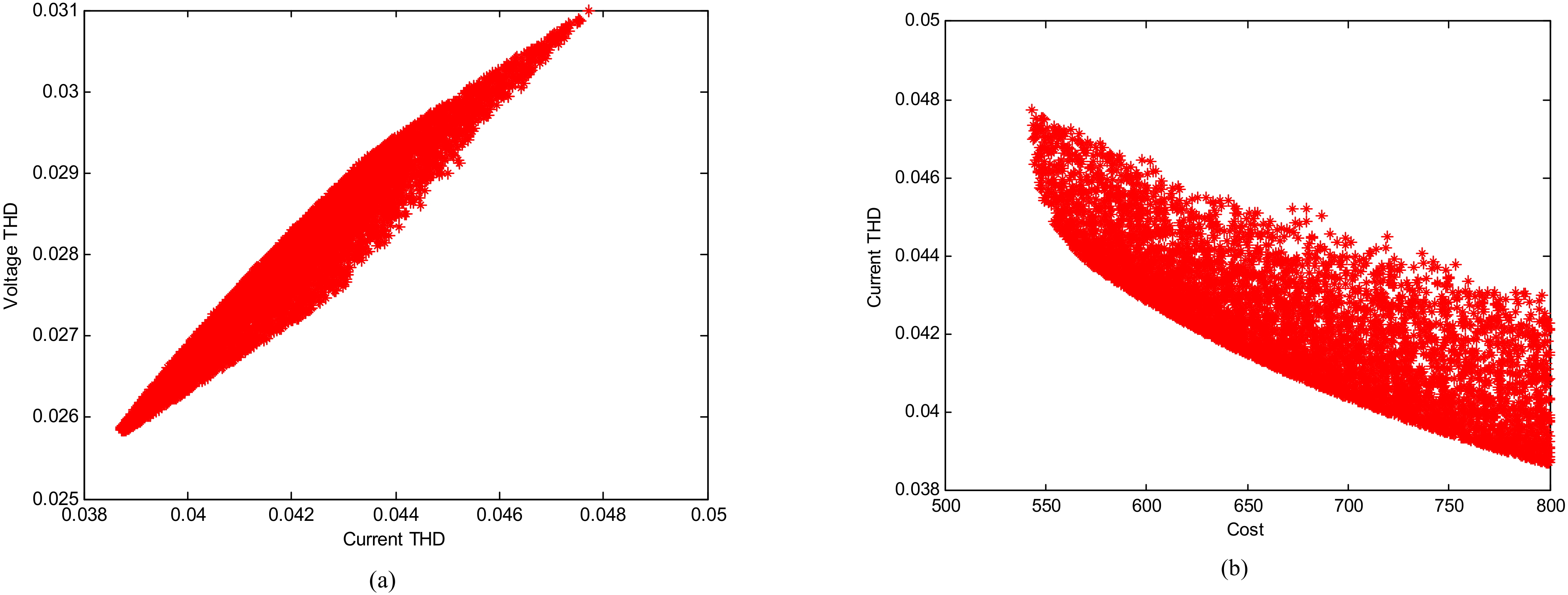
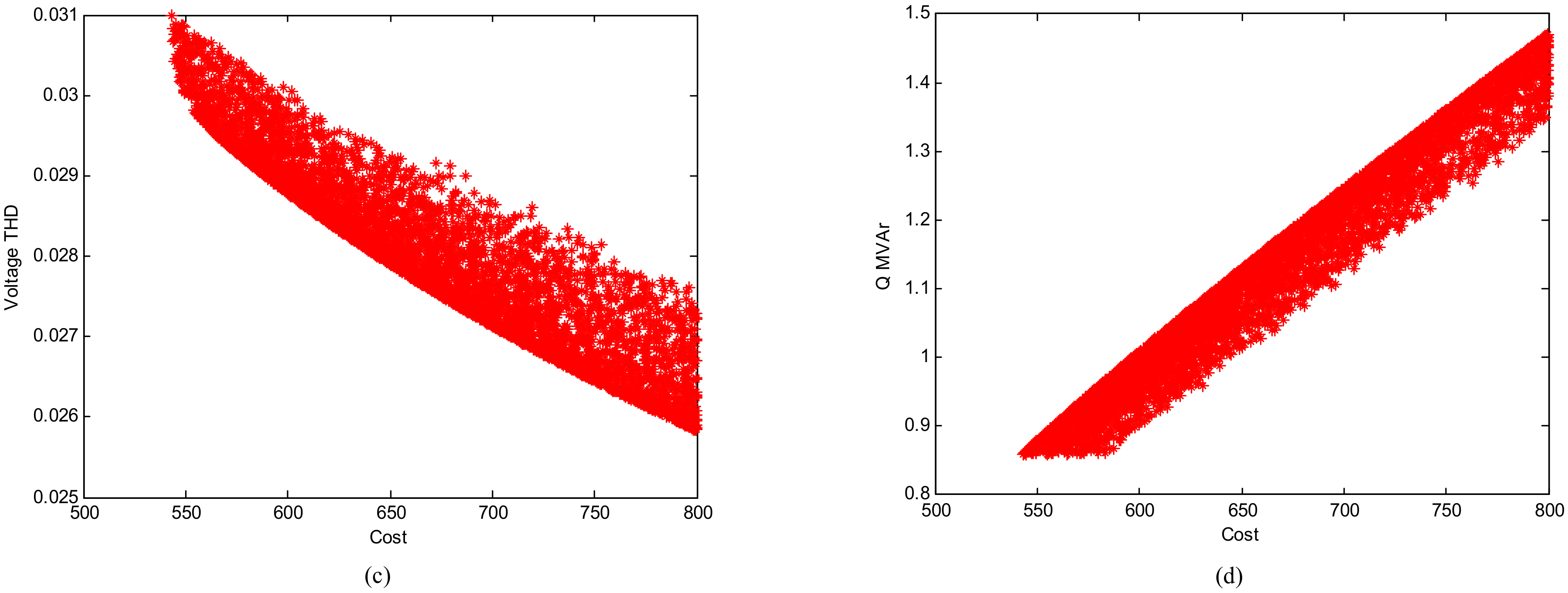
5. Simulation Results
5.1. Basic Comparison Study
- harmonic currents through power supply terminal;
- harmonic currents;
- system impedance;
- filter impedance.
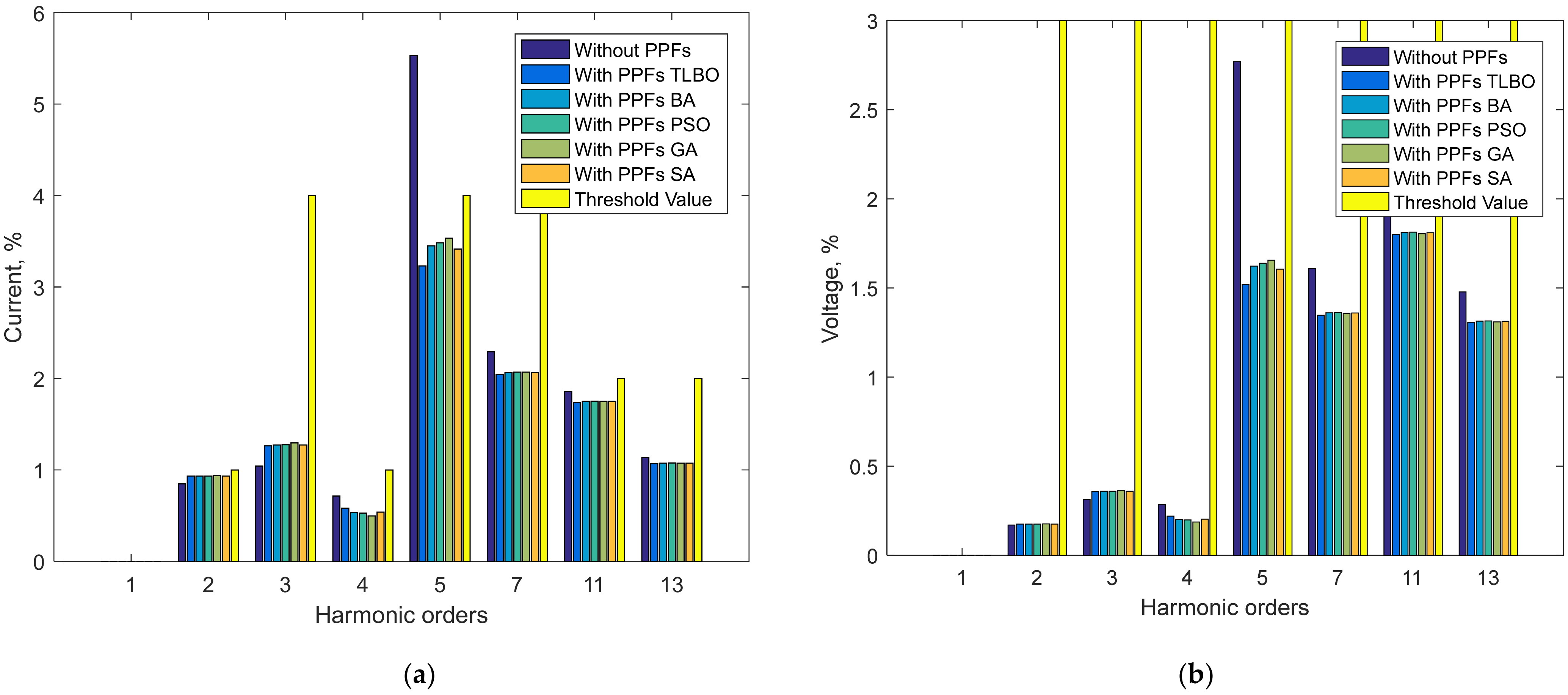
| Method | TLBO | BA | PSO | GA | SA |
|---|---|---|---|---|---|
| Single-tuned () | |||||
| Single-tuned () | |||||
| (%) | 4.65 | 4.82 | 4.84 | 4.87 | 4.80 |
| (%) | 3.05 | 3.11 | 3.12 | 3.12 | 3.11 |
| Cost | 545.46 | 546.55 | 547.23 | 572.47 | 545.99 |
| Harmonic Orders | Current, A | Voltage, V | Current, % | Voltage, % | IEEE Standard 519 | |
|---|---|---|---|---|---|---|
| Current, % | Voltage, % | |||||
| 2 | 7.26 | 11.55 | 0.93 | 0.18 | 1 | 3 |
| 3 | 9.85 | 23.51 | 1.27 | 0.36 | 4 | 3 |
| 4 | 4.54 | 14.45 | 0.58 | 0.22 | 1 | 3 |
| 5 | 25.13 | 100.03 | 3.23 | 1.52 | 4 | 3 |
| 7 | 15.91 | 88.64 | 2.04 | 1.35 | 4 | 3 |
| 11 | 13.53 | 118.51 | 1.74 | 1.80 | 2 | 3 |
| 13 | 8.31 | 86.03 | 1.07 | 1.31 | 2 | 3 |
| THD (%) | 4.65 | 3.05 | - | - | 5 | 5 |
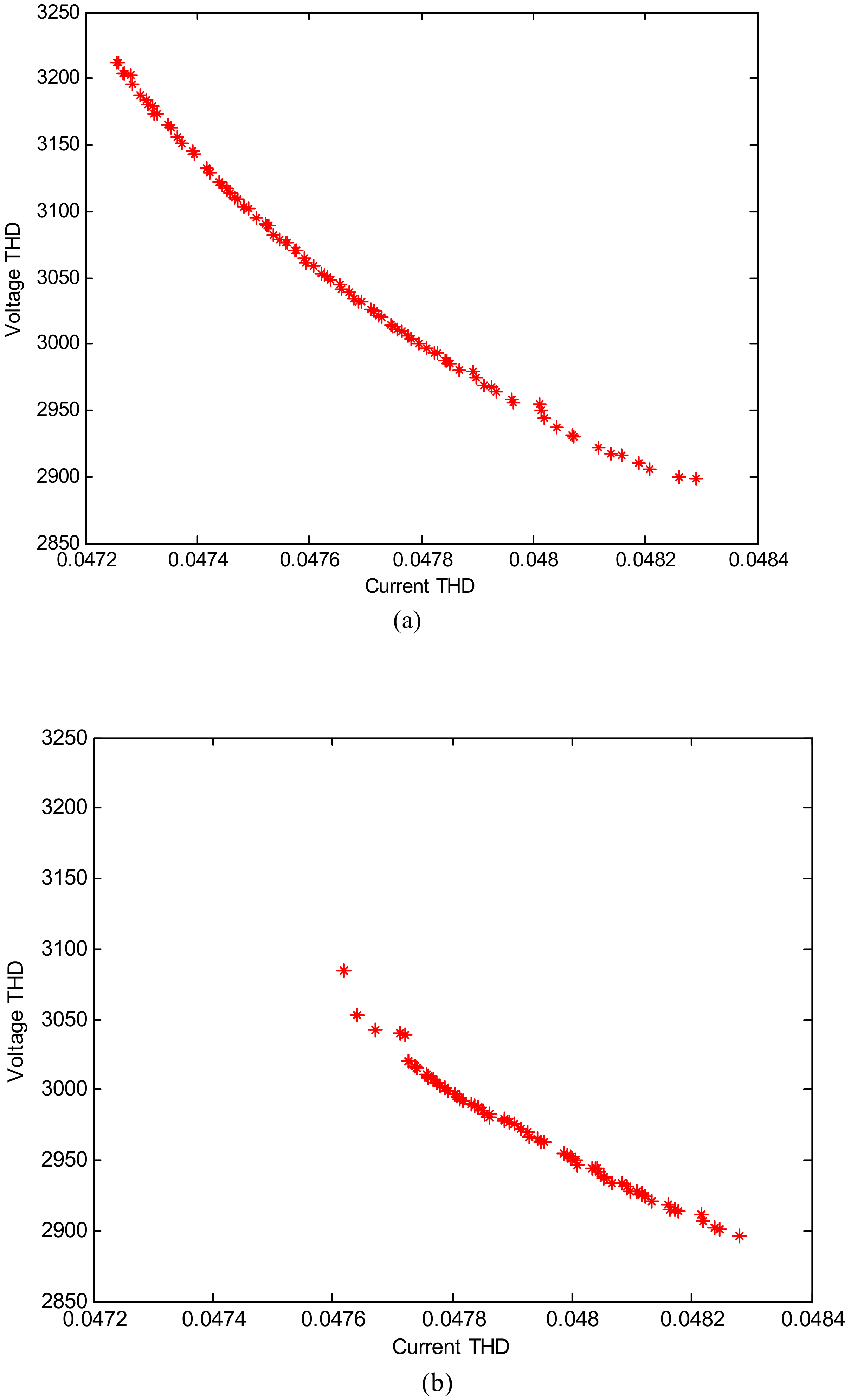
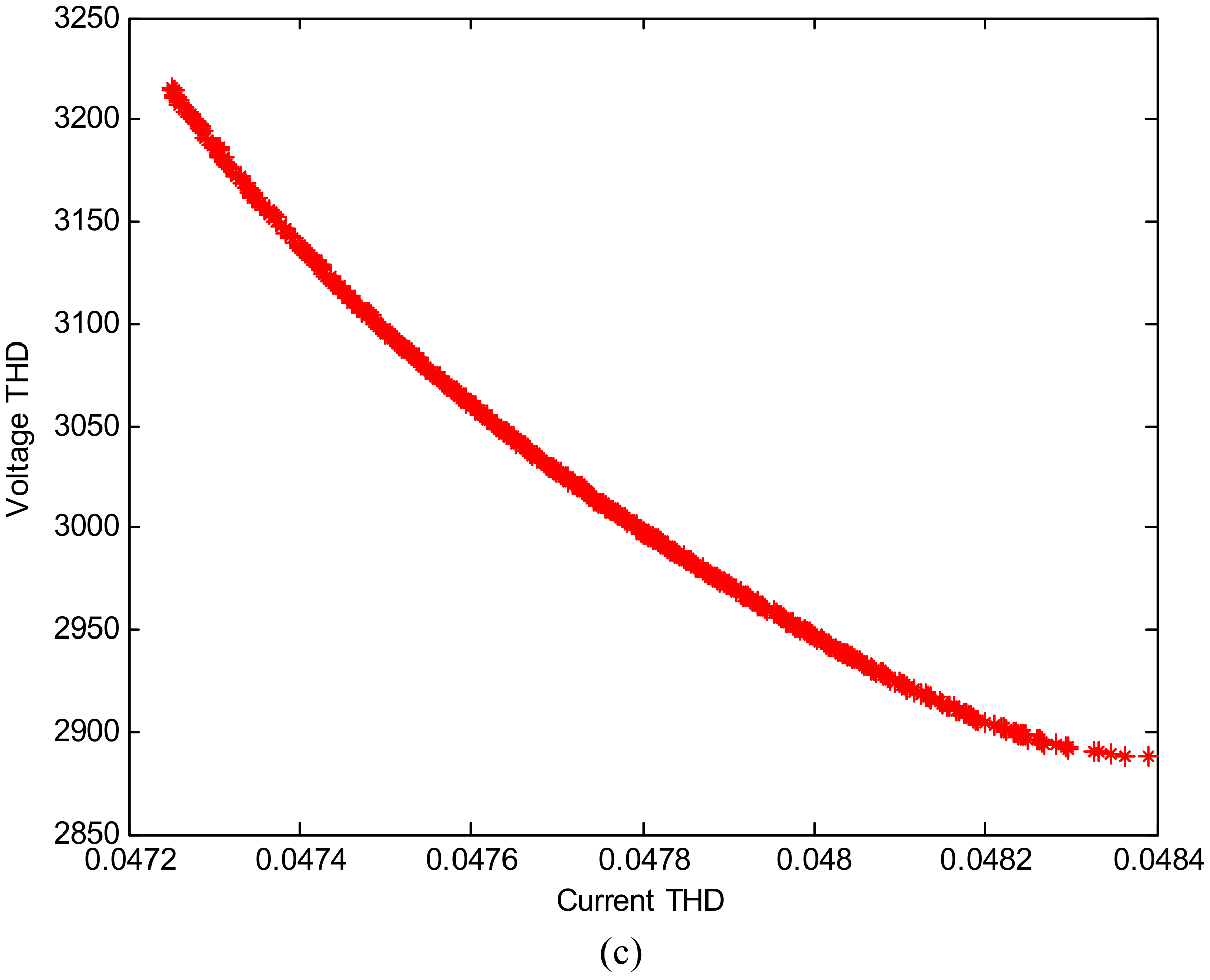
5.2. Accuracy Study
5.3. Performance Test
- Step 1: Check individual harmonic distortion; the individual harmonic distortion is evaluated for the node candidates.
- Step 2: Select the maximum number of PPF combinations; the harmonic limit violations set the maximum number of PPFs.
- Step 3: Select the pivot point; to develop a harmonic suppression strategy, a pivot point needs to be selected for the harmonic components. The pivot point is determined by the distribution of the major harmonic components. In most cases, the fifth-order harmonic is regarded as the pivot point.
- Step 4: Determine the possible combinations of PPFs; once the pivot point is determined, the corresponding topology combination of PPFs can be selected to eliminate the major harmonic components. The following rules can determine the topology combination of PPFs: (1) If the major harmonic component occurs at the pivot point, all types of PPFs can be regarded as candidates for evaluation; (2) if the major harmonic components occur below the pivot point (i.e., second-, third-, and fourth-order harmonics), the ST and CD PPFs are regarded as candidates for evaluation; (3) conversely, if the major harmonic components occur above the pivot point (i.e., seventh-, ninth-, eleventh-, and high-order harmonics), the SD and TD PPFs are regarded as candidates for evaluation.
- Step 5: Verify the feasible combinations of PPFs; the initial number and possible combination of PPFs are selected in accordance with the above rules. Not all combinations of PPFs can be used to search for the NDSs for PPF design. If the first NDS for PPF design can be found in a limited number of the initial population, this topology combination of PPFs can be regarded as a feasible combination of PPFs. Otherwise, proceed to Step 6.
- Step6: Recheck individual harmonic distortions; the individual harmonic distortion with the existing PPFs is reevaluated to determine the additional combinations of PPFs.
- Step 7: Determine the additional combinations of PPFs; according to the remaining major harmonic components, the additional combinations of PPFs are generated by the above rules. The feasible combinations of PPFs are verified until the number of PPFs exceeds the predefined threshold.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| the capacitance of j-th filter of type i; | |
| , | upper and lower limits of percentage variation of capacitance for a PPF; |
| Euclidean distance; | |
| rms of fundamental current; | |
| rms of harmonic current with integer order; | |
| harmonic currents; | |
| harmonic currents through power supply terminal; | |
| vector of an objective function; | |
| , | upper and lower limits of percentage variation of frequency for a power system; |
| , | upper and lower bounds of the i-th objective function; |
| inequality constraint; | |
| GD | generational distance; |
| highest harmonic order considered; | |
| upper tolerance for harmonic current at h-th order; | |
| upper tolerance for harmonic voltage at h-th order; | |
| harmonic order; | |
| order of critical harmonic; | |
| order of harmonic to be mitigated; | |
| equality constraint; | |
| to | cost weighting coefficients; |
| , | upper and lower limits of the percentage variation of inductance for a PPF; |
| the inductance of j-th filter of type i; | |
| number of non-dominated solutions in the external archive; | |
| mean grade of the learners in subject j at the i-th iteration; | |
| number of filters of type i; | |
| number of objective functions; | |
| number of inequality constraints; | |
| number of equality constraints; | |
| power loss of j-th filter of type i; | |
| reactive power capacity of j-th filter of type i; | |
| total fundamental reactive power; | |
| fundamental reactive power produced by j-th filter of i-th type; | |
| , | upper and lower limits of reactive power compensation; |
| , | upper and lower limit of percentage variation of resistance for a PPF; |
| resistance of j-th filter of type i; | |
| random number in the range [0,1]; | |
| teaching factor; | |
| upper tolerance for total harmonic distortions of currents; | |
| upper tolerance for total harmonic distortions of voltages; | |
| rms of fundamental voltage; | |
| rms of harmonic voltage with integer order; | |
| grade of the teacher in the subject j at the i-th iteration; | |
| grade of learner k in subject j at the i-th iteration; | |
| vector of decision variables; | |
| the impedance of j-th filter of i-th type; | |
| the impedance of multiple passive power filters; | |
| filter impedance; | |
| system impedance; | |
| set coefficient for i-type filter; | |
| harmonic attenuation factor; | |
| the weighting factor of objective function I; | |
| membership value of the i-th objective function ; | |
| nominal membership value for the non-dominated solution k. |
References
- Eroğlu, H.; Cuce, E.; Cuce, P.M.; Gul, F.; Iskenderoğlu, A. Harmonic problems in renewable and sustainable energy systems: A comprehensive review. Sustain. Energy Technol. Assess. 2021, 48, 101566. [Google Scholar] [CrossRef]
- Baliyan, A.; Jamil, M.; Rizwan, M. Power Quality Improvement Using Harmonic Passive Filter in Distribution System. In Advances in Energy Technology; Springer: Berlin/Heidelberg, Germany, 2021; pp. 435–445. [Google Scholar] [CrossRef]
- Gheisarnejad, M.; Mohammadi-Moghadam, H.; Boudjadar, J.; Khooban, M.H. Active Power Sharing and Frequency Recovery Control in an Islanded Microgrid with Nonlinear Load and Nondispatchable DG. IEEE Syst. J. 2019, 14, 1058–1068. [Google Scholar] [CrossRef]
- Ismael, S.M.; Aleem, S.H.A.; Abdelaziz, A.Y.; Zobaa, A.F. State-of-the-art of hosting capacity in modern power systems with distributed generation. Renew. Energy 2018, 130, 1002–1020. [Google Scholar] [CrossRef]
- Li, D.; Yang, K.; Zhu, Z.Q.; Qin, Y. A Novel Series Power Quality Controller with Reduced Passive Power Filter. IEEE Trans. Ind. Electron. 2016, 64, 773–784. [Google Scholar] [CrossRef]
- Mboving, A.; Stéphane, C. Investigation on the Work Efficiency of the LC Passive Harmonic Filter Chosen Topologies. Electronics 2021, 10, 896. [Google Scholar] [CrossRef]
- Bollen, M.H.J.; Das, R.; Djokic, S.; Ciufo, P.; Meyer, J.; Rönnberg, S.; Zavodam, F. Power Quality Concerns in Implementing Smart Distribution-Grid Applications. IEEE Trans. Smart Grid 2016, 8, 391–399. [Google Scholar] [CrossRef] [Green Version]
- Kalair, A.; Abas, N.; Kalair, A.; Saleem, Z.; Khan, N. Review of harmonic analysis, modeling and mitigation techniques. Renew. Sustain. Energy Rev. 2017, 78, 1152–1187. [Google Scholar] [CrossRef]
- Gandoman, F.H.; Ahmadi, A.; Sharaf, A.M.; Siano, P.; Pou, J.; Hredzak, B.; Agelidis, V.G. Review of FACTS technologies and applications for power quality in smart grids with renewable energy systems. Renew. Sustain. Energy Rev. 2018, 82, 502–514. [Google Scholar] [CrossRef]
- Yang, N.; Le, M. Three-phase harmonic power flow by direct Z BUS method for unbalanced radial distribution systems with passive power filters. IET Gener. Transm. Distrib. 2016, 10, 3211–3219. [Google Scholar] [CrossRef]
- Yang, N.-C.; Le, M.-D. Loop frame of reference based harmonic power flow for unbalanced radial distribution systems. Int. J. Electr. Power Energy Syst. 2016, 77, 128–135. [Google Scholar] [CrossRef]
- Yang, N. Three-phase power flow calculations using direct Z BUS method for large-scale unbalanced distribution networks. IET Gener. Transm. Distrib. 2016, 10, 1048–1055. [Google Scholar] [CrossRef]
- Yang, N.-C.; Tseng, W.-C. Adaptive three-phase power-flow solutions for smart grids with plug-in hybrid electric vehicles. Int. J. Electr. Power Energy Syst. 2015, 64, 1166–1175. [Google Scholar] [CrossRef]
- Yang, N. Three-phase power flow calculations by direct Z LOOP method for microgrids with electric vehicle charging demands. IET Gener. Transm. Distrib. 2013, 7, 1002–1010. [Google Scholar] [CrossRef]
- Chen, T.-H.; Yang, N.-C. Simplified annual energy loss evaluation method for branch circuits of a home or building. Energy Build. 2010, 42, 2281–2288. [Google Scholar] [CrossRef]
- Yang, N.-C.; Chen, T.-H. Assessment of loss factor approach to energy loss evaluation for branch circuits or feeders of a dwelling unit or building. Energy Build. 2012, 48, 91–96. [Google Scholar] [CrossRef]
- Yang, N.-C.; Tseng, W.-C. Impact assessment of a hybrid energy-generation system on a residential distribution system in Taiwan. Energy Build. 2015, 91, 170–179. [Google Scholar] [CrossRef]
- Yang, N.-C.; Chen, H.-C. Decomposed Newton algorithm-based three-phase power-flow for unbalanced radial distribution networks with distributed energy resources and electric vehicle demands. Int. J. Electr. Power Energy Syst. 2018, 96, 473–483. [Google Scholar] [CrossRef]
- Yang, N.; Chen, H. Three-phase power-flow solutions using decomposed quasi-Newton method for unbalanced radial distribution networks. IET Gener. Transm. Distrib. 2017, 11, 3594–3600. [Google Scholar] [CrossRef]
- Chou, C.-J.; Liu, C.-W.; Lee, J.-Y.; Lee, K.-D. Optimal planning of large passive-harmonic-filters set at high voltage level. IEEE Trans. Power Syst. 2000, 15, 433–441. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.-M. Passive filter design using genetic algorithms. IEEE Trans. Ind. Electron. 2003, 50, 202–207. [Google Scholar] [CrossRef]
- Makram, E.; Subramaniam, E.; Girgis, A.; Catoe, R. Harmonic filter design using actual recorded data. IEEE Trans. Ind. Appl. 1993, 29, 1176–1183. [Google Scholar] [CrossRef]
- Das, J. Passive Filters—Potentialities and Limitations. IEEE Trans. Ind. Appl. 2004, 40, 232–241. [Google Scholar] [CrossRef]
- Chang, G.W.; Wang, H.-L.; Chuang, G.-S.; Chu, S.-Y. Passive Harmonic Filter Planning in a Power System with Considering Probabilistic Constraints. IEEE Trans. Power Deliv. 2008, 24, 208–218. [Google Scholar] [CrossRef]
- He, N.; Xu, D.; Huang, L. The Application of Particle Swarm Optimization to Passive and Hybrid Active Power Filter Design. IEEE Trans. Ind. Electron. 2009, 56, 2841–2851. [Google Scholar] [CrossRef]
- Chang, Y.-P.; Tseng, W.-K.; Tsao, T.-F. Application of combined feasible-direction method and genetic algorithm to optimal planning of harmonic filters considering uncertainty conditions. IEE Proc.-Gener. Transm. Distrib. 2005, 152, 729–736. [Google Scholar] [CrossRef]
- Ko, C.-N.; Chang, Y.-P.; Wu, C.-J. A PSO Method with Nonlinear Time-Varying Evolution for Optimal Design of Harmonic Filters. IEEE Trans. Power Syst. 2008, 24, 437–444. [Google Scholar] [CrossRef]
- Chu, R.; Wang, J.-C.; Chiang, H.-D. Strategic planning of LC compensators in nonsinusoidal distribution systems. IEEE Trans. Power Deliv. 1994, 9, 1558–1563. [Google Scholar] [CrossRef]
- Ortmeyer, T.; Hiyama, T. Distribution system harmonic filter planning. IEEE Trans. Power Deliv. 1996, 11, 2005–2012. [Google Scholar] [CrossRef]
- Chang, G.W.; Wang, H.-L.; Chu, S.-Y. Strategic placement and sizing of passive filters in a power system for controlling voltage distortion. IEEE Trans. Power Deliv. 2004, 19, 1204–1211. [Google Scholar] [CrossRef]
- Nassif, A.B.; Xu, W.; Freitas, W. An Investigation on the Selection of Filter Topologies for Passive Filter Applications. IEEE Trans. Power Deliv. 2009, 24, 1710–1718. [Google Scholar] [CrossRef]
- Kawann, C.; Emanuel, A. Passive shunt harmonic filters for low and medium voltage: A cost comparison study. IEEE Trans. Power Syst. 1996, 11, 1825–1831. [Google Scholar] [CrossRef]
- Lin, K.-P.; Lin, M.-H.; Lin, T.-P. An advanced computer code for single-tuned harmonic filter design. IEEE Trans. Ind. Appl. 1998, 34, 640–648. [Google Scholar] [CrossRef]
- Bajaj, M.; Sharma, N.K.; Pushkarna, M.; Malik, H.; Alotaibi, M.A.; Almutairi, A. Optimal Design of Passive Power Filter Using Multi-Objective Pareto-Based Firefly Algorithm and Analysis Under Background and Load-Side’s Nonlinearity. IEEE Access 2021, 9, 22724–22744. [Google Scholar] [CrossRef]
- Badugu, R.; Acharya, D.; Das, D.K.; Prakash, M. Class Topper Optimization Algorithm based Optimum Passive Power Filter Design for Power System. In Proceedings of the 2021 5th International Conference on Computing Methodologies and Communication (ICCMC), Erode, India, 8–10 April 2021; pp. 648–652. [Google Scholar]
- Wang, Y.; Liu, H.; Yin, K.; Yuan, Y. A Full-Tuned Filtering Method for Dynamic Tuning Passive Filter Power Electronics. J. Control. Autom. Electr. Syst. 2021, 1–11. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, K.; Liu, H.; Yuan, Y. A Method for Designing and Optimizing the Electrical Parameters of Dynamic Tuning Passive Filter. Symmetry 2021, 13, 1115. [Google Scholar] [CrossRef]
- Azab, M. Multi-objective design approach of passive filters for single-phase distributed energy grid integration systems using particle swarm optimization. Energy Rep. 2019, 6, 157–172. [Google Scholar] [CrossRef]
- Wang, S.; Ding, X.; Wang, J. Multi-objective optimization design of passive filter based on particle swarm optimization. In Proceedings of the Journal of Physics: Conference Series. J. Physics Conf. Ser. 2020, 1549, 032017. [Google Scholar] [CrossRef]
- Yang, N.; Le, M. Multi-objective bat algorithm with time-varying inertia weights for optimal design of passive power filters set. IET Gener. Transm. Distrib. 2015, 9, 644–654. [Google Scholar] [CrossRef]
- Yang, N.-C.; Le, M.-D. Optimal design of passive power filters based on multi-objective bat algorithm and pareto front. Appl. Soft Comput. 2015, 35, 257–266. [Google Scholar] [CrossRef]
- Rao, R.; Savsani, V.; Vakharia, D. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Rao, R.V.; Kalyankar, V. Parameter optimization of modern machining processes using teaching–learning-based optimization algorithm. Eng. Appl. Artif. Intell. 2013, 26, 524–531. [Google Scholar] [CrossRef]
- Nayak, M.; Nayak, C.; Rout, P. Application of Multi-Objective Teaching Learning based Optimization Algorithm to Optimal Power Flow Problem. Procedia Technol. 2012, 6, 255–264. [Google Scholar] [CrossRef] [Green Version]
- Niknam, T.; Azizipanah-Abarghooee, R.; Narimani, M.R. A new multi objective optimization approach based on TLBO for location of automatic voltage regulators in distribution systems. Eng. Appl. Artif. Intell. 2012, 25, 1577–1588. [Google Scholar] [CrossRef]
- Lata, P.; Vadhera, S. Reliability Improvement of Radial Distribution System by Optimal Placement and Sizing of Energy Storage System using TLBO. J. Energy Storage 2020, 30, 101492. [Google Scholar] [CrossRef]
- Lata, P.; Vadhera, S. TLBO-based approach to optimally place and sizing of energy storage system for reliability enhancement of radial distribution system. Int. Trans. Electr. Energy Syst. 2020, 30, e12334. [Google Scholar] [CrossRef]
- Coello, C.C.; Toscano-Pulido, G.; Lechuga, M. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Shabanpour-Haghighi, A.; Seifi, A.R.; Niknam, T. A modified teaching–learning based optimization for multi-objective optimal power flow problem. Energy Convers. Manag. 2014, 77, 597–607. [Google Scholar] [CrossRef]
- IEEE Std 519-1992. Recommended Practices and Requirements for Harmonic Control in Electrical Power System; IEEE Industry Applications Society: New York, NY, USA, 1993. [Google Scholar]
- Van Veldhuizen, D.A.; Lamont, G.B. Multiobjective Evolutionary Algorithm Research: A History and Analysis, 1998. Citeseer. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.35.8924 (accessed on 18 August 2021).

| Type | ||
|---|---|---|
| ST | ||
| SD | ||
| TD | ||
| CD |
| Set No. | ST | SD | TD | CD |
|---|---|---|---|---|
| 1 | 1 | 1 | 1.2 | 1.2 |
| 2 | 1.2 | 1.4 | 1.6 | 1.6 |
| 3 | 1.6 | 1.8 | 2.0 | 2.0 |
| 4 | 2.0 | 2.2 | 2.4 | 2.4 |
| 5 | 2.4 | 2.5 | 2.8 | 2.8 |
| Item | Feasible Ranges of Parameters |
|---|---|
| Short-circuit current | 8268–19,695 A |
| System short circuit capacity | 163–388 MVA |
| Equivalent system impedance | 0.3342–0.7961 Ω |
| System voltage level | 11.4 kV |
| System frequency | 60 Hz |
| Harmonic Orders | Current, A | Voltage, V | IEEE Standard 519 | |||
|---|---|---|---|---|---|---|
| Current, A | Current, % | Voltage, V | Voltage, % | |||
| 1 | 828.37 | 6581.79 | - | - | - | - |
| 2 | 7.02 | 11.18 | 8.28 | 1 | 197.5 | 3 |
| 3 | 8.64 | 20.63 | 33.1 | 4 | 197.5 | 3 |
| 4 | 5.92 | 18.85 | 8.28 | 1 | 197.5 | 3 |
| 5 | 45.8 | 182.3 | 33.1 | 4 | 197.5 | 3 |
| 7 | 19.0 | 105.9 | 33.1 | 4 | 197.5 | 3 |
| 11 | 15.4 | 134.9 | 16.6 | 2 | 197.5 | 3 |
| 13 | 9.4 | 97.28 | 16.6 | 2 | 197.5 | 3 |
| THD (%) | 6.55 | 4.11 | - | 5 | - | 5 |
| Item | Feasible Ranges of Parameters |
|---|---|
| Number of iterations | 200 |
| Population size | 20 |
| Number of objectives | 4 |
| Number of constraints | 22 |
| Number of groups | 4 |
| Size of external archive | 100 |
| Number of divisions | 30 |
| Maximum number of PPFs set | 2 |
| Maximum initial IC | 1000 pu |
| R for PPFs | 0.01–100 Ω |
| L for PPFs | 0.01–50 mH |
| C for PPFs | 0.01–100 μF |
| Parameter | TLBO | BA | PSO | GA |
|---|---|---|---|---|
| Number of iterations | 200 | 200 | 200 | 200 |
| Population size | 20 | 20 | 20 | 20 |
| Other related parameters | - | Maximum frequency, Minimum frequency, Constants, | Cognitive parameter, Social parameter, | EliteCount = 2; CrossoverFraction = 0.8; MutationRate = 0.1; MaximumSurvivalRate = 2; |
| Algorithm | Generational Distance | ||||
|---|---|---|---|---|---|
| Best | Worst | Average | Median | Std. Dev. | |
| MOTLBO | 0.00000053 | 0.0013 | 0.0000689 | 0.0000571 | 0.000068 |
| MOBA | 0.00000094 | 0.0106 | 0.0000921 | 0.0000708 | 0.000220 |
| MOPSO | 0.00000193 | 0.0177 | 0.0001251 | 0.0000874 | 0.000566 |
| Type of Filters | Parameter | THDI | THDV | PF | QF | Cost | |||||
| * | |||||||||||
| ST | 4.60 | 86.35 | 4.99 | 2.98 | 0.98 | 4484 | 635 | ||||
| ST | 4.07 | 96.35 | 4.83 | 2.88 | 0.99 | 4999 | 705 | ||||
| ST | 11.05 | 26.58 | 3.77 | 2.74 | 0.95 | 2596 | 538 | ||||
| ST | 18.31 | 23.69 | |||||||||
| ST | 10.31 | 28.47 | 3.73 | 2.68 | 0.96 | 3024 | 592 | ||||
| ST | 14.22 | 30.07 | |||||||||
| ST | 10.16 | 28.89 | 4.01 | 2.80 | 0.96 | 3064 | 589 | ||||
| SD | 20.96 | 8.68 | 31.18 | ||||||||
| ST | 9.81 | 29.95 | 3.87 | 2.53 | 0.99 | 5609 | 929 | ||||
| SD | 20.54 | 5.67 | 78.06 | ||||||||
| ST | 10.16 | 29.19 | 4.10 | 2.92 | 0.95 | 2606 | 788 | ||||
| TD | 38.41 | 23.45 | 21.01 | 21.01 | |||||||
| ST | 9.07 | 33.04 | 4.20 | 2.85 | 0.98 | 4652 | 1254 | ||||
| TD | 47.81 | 31.83 | 46.27 | 46.27 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, N.-C.; Liu, S.-W. Multi-Objective Teaching–Learning-Based Optimization with Pareto Front for Optimal Design of Passive Power Filters. Energies 2021, 14, 6408. https://doi.org/10.3390/en14196408
Yang N-C, Liu S-W. Multi-Objective Teaching–Learning-Based Optimization with Pareto Front for Optimal Design of Passive Power Filters. Energies. 2021; 14(19):6408. https://doi.org/10.3390/en14196408
Chicago/Turabian StyleYang, Nien-Che, and Sun-Wei Liu. 2021. "Multi-Objective Teaching–Learning-Based Optimization with Pareto Front for Optimal Design of Passive Power Filters" Energies 14, no. 19: 6408. https://doi.org/10.3390/en14196408
APA StyleYang, N.-C., & Liu, S.-W. (2021). Multi-Objective Teaching–Learning-Based Optimization with Pareto Front for Optimal Design of Passive Power Filters. Energies, 14(19), 6408. https://doi.org/10.3390/en14196408