A Robust Optimization Approach for Optimal Power Flow Solutions Using Rao Algorithms

Abstract

This paper offers three easy-to-use metaphor-less optimization algorithms proposed by Rao to solve the optimal power flow (OPF) problem. Rao algorithms are parameter-less optimization algorithms. As a result, algorithm-specific parameter tuning is not required at all. This quality makes these algorithms simple to use and able to solve various kinds of complex constrained optimization and engineering problems. In this paper, the main aim to solve the OPF problem is to find the optimal values of the control variables in a given electrical network for fuel cost minimization, real power losses minimization, emission cost minimization, voltage profile improvement, and voltage stability enhancement, while all the operating constraints are satisfied. To demonstrate the efficacy of Rao algorithms, these algorithms have been employed in three standard IEEE test systems (30-bus, 57-bus, and 118-bus) to solve the OPF problem. The OPF results of Rao algorithms and the results provided by other swarm intelligence (SI)/evolutionary computing (EC)-based algorithms published in recent literature have been compared. Based on the outcomes, Rao algorithms are found to be robust and superior to their competitors.

1. Introduction

With the inclusion of different kinds of power electronic appliances and renewable energy sources in modern inter-connected restructured power systems, the importance of solving the OPF problem is increasing day by day. Optimal power flow results are needed for economic operation, planning, and control of the existing electrical grid and future expansion planning. In a given electrical network, the OPF solution must regulate the control or decision variables set in a feasible region that optimizes pre-defined objective functions. In the formulation of the OPF problem, fuel cost minimization (FCM) is frequently used as a primary objective function in addition to other objectives like voltage stability enhancement (VSE), voltage profile improvement (VPI), real power losses minimization (RPLM), and emission cost minimization (ECM) via readjustment of control variables, taking into account both operational and physical constraints [1]. The mathematical formulation of the OPF problem is complex. It is a highly non-linear, high-dimensional, non-differential, multi-modal, and non-convex problem with discrete and continuous control variables. Carpentier introduced a first-time OPF problem based on the economic load dispatch in the early 1960s [2,3].

Many classical optimization techniques (COTs) [4,5] such as linear programming, non-linear programming, mixed integer programming, interior point method, etc., were employed during the early decades to handle OPF problems. While some COTs have outstanding convergence properties, many of them are often used in the industry. Their disadvantages include the following: most of the conventional algorithms are deterministic, except hill-climbing, thus they are unable to find the global optimal solution, and they cannot efficiently manage binary or integer variables. In addition, conventional optimization methods require initial points (except for linear programming and convex optimization), thus the COTs are not appropriate for solving the OPF problem.

Various evolutionary computing-based algorithms were proposed in recent literature to overcome the demerits of classical optimization techniques and solve the complex constrained optimization problem. In a couple of years, the EC techniques are attracting power engineers and researchers to solve OPF problems because of their efficacy in handling various types of engineering and complex optimization problems [6,7]. Some of these techniques are the: bat search algorithm (BSA) [8]; improved colliding bodies optimization (ICBO) [9]; back-hole-based optimization (BHBO) [10]; multi-agent-based differential evolution approach (MADE) [11]; adaptive group search optimization (AGSO) [12]; biogeography-based optimization (BBO) [13]; moth swarm algorithm (MSA) [14]; water evaporation algorithm (WEA) [15]; symbiotic organisms search algorithm (SOS) [16]; tree-seed algorithm (TS) [17]; differential search algorithm (DSA) [18]; salp swarm optimizer algorithm (SSO) [19], etc.

Rao algorithms and many modified versions of Rao algorithms have been used to solve a wide range of optimization problems including the optimal reactive power dispatch with renewable energy [20], multi-objective optimization of selected thermodynamic cycles [21], constrained design optimization of selected mechanical system components [22], engineering design optimization [23], estimation of photovoltaic cell parameters [24], classification of Parkinson’s disease [25], OPF problem with renewable energy sources [26], multi-objective design optimization of selected heat sinks [27], and many more.

The authors found that all EC/SI-based algorithms have some advantages and disadvantages through the literature survey. Two main parts of any EC/SI-based algorithm are exploration and exploitation, or intensification and diversification. Some algorithms have good exploration capability but poor exploitation, and vice versa. Some algorithms are more suitable to solve certain types of problems than others. It is logically proved that any single EC/SI-based optimization algorithm does not have the potential to solve various types of engineering and complex optimization problems, thus, the “No Free Lunch” theorem encourages the development of new algorithms [28].

Meta-heuristic algorithms, notwithstanding their benefits, have several drawbacks. They need parameter tuning to find the near-global best solution. It has been observed that parameter tuning of meta-heuristic optimization algorithms plays a very important role and is a very crucial and time-costly task for solving a given optimization problem. Therefore in this paper, the authors proposed a robust optimization technique called Rao algorithms to resolve the OPF problem. The proposed algorithms are comparatively new meta-heuristic optimization algorithms developed by Rao [29,30].

Rao algorithms are parameter-less optimization algorithms. As a result, algorithm-specific parameter tuning is not required at all. This quality makes these algorithms simple to apply for solving different kinds of optimization problems. The working principle of Rao algorithms is based on the worst and best solutions achieved throughout the optimization and random interaction between the candidate solutions.

The main contributions of this paper are:

• To develop Rao algorithms to solve OPF problems with six objective functions, namely FCM, VSE under normal and contingency conditions, VPI, RPLM, and ECM.
• To apply Rao algorithms to solve various multi-objective OPF problems by transforming the multi-objective OPF problem into a single objective OPF problem using weighing factors.
• To check the efficiency and supremacy of Rao algorithms by applying these algorithms to solve the OPF problem in three standard IEEE (30-bus, 57-bus, and 118-bus) test systems.
• To compare the simulation outcomes acquired by Rao algorithms for the above-mentioned objective functions with the results of other methods mentioned in recent literature.
• The OPF results demonstrate that the suggested Rao algorithms are efficient and robust in most of the cases over other popular methods, which are reported in recent literature.

In this paper, the authors propose Rao algorithms, which are recently devolved powerful optimization algorithms, to solve OPF problems considering technical and economical objective functions in three standard IEEE (30-bus, 57-bus, and 118-bus) systems. The rest of the paper is organized as follows: Section 2 covers the representation of OPF problems; Section 3 provides details of Rao algorithms to solve OPF problems; Section 4 provides the OPF results attained by Rao algorithms; and in Section 6, the conclusion is provided.

2. Problem Formulation

The OPF problem formulation aims to find the optimal setting of the control variables for a given electrical network that optimizes the pre-defined objective functions while all operating constraints and power flows are within the operating limit [10,11]. Mathematically, the objective function, together with the operating constraints of the OPF problem selected in this work, is given by Equations (1)–(3):

$$\mathrm{Minimize}{Z}_{min}\left(m, n\right)$$

(1)

Subject to the constraints;

$$g\left(m, n\right)=0$$

(2)

and

$$h \left(m, n\right) \le 0\left(3\right)$$

(3)

$Z_{min}\left(m, n\right)$ is an objective function that needs to be optimized; g is the equality constraints representing the non-linear load flow equations; and h is the inequality constraints representing the system operating limits.

The dependent variables (m) and control variables (n) are described in Equations (4) and (5):

$$m=\left[P_{g_1},V_1\dots V_{NLB},Q_{g1},\dots Q_{gNGN},S_1,\dots S_{Ntl}\right]$$

(4)

$$n=\left[P_{g_2}\dots P_{g_{ NGN}}, V_{g_1}\dots V_{g_{NGN}}, Q_{C_1}\dots Q_{C_{NC}}, T_1\dots T_{NTR}\right]$$

(5)

where, $P_g$ and $Q_g$ denote the active and reactive power outputs of generator units. $V_L$ and $V_g$ represent the load and generator bus voltages, respectively. $Q_C$ and $T_{TR}$ represent the shunt VAR compensation and transformer tap-setting, respectively. $P_{g_1}$ is the slack bus active power output. NGN, NC, NTR, NLB, and Ntl correspond to the number of generators, number of VAR compensation units, numbers of regulating transformers, number of load buses, and number of transmission lines, respectively.

Constraints

Two types of constraints are involved in the OPF problem, namely equality and inequality [31].

(a) 

Equality Constraints

The equality constraints g (m, n) represent the load flow equation and can be described by Equations (6) and (7):

$$P_{Loss}={{\displaystyle \sum }}_{i=1}^{NB}{P}_{gi}-{{\displaystyle \sum }}_{i=1}^{NB}{P}_{di}$$

(6)

$$Q_{Loss}={{\displaystyle \sum }}_{i=1}^{NB}{Q}_{gi}-{{\displaystyle \sum }}_{i=1}^{NB}{Q}_{di}$$

(7)

where $P_{Loss}$ and $Q_{Loss}$ denote the total active and reactive power loss for a given electrical system, respectively. NB represents the number of buses. $P_{di}$ and $Q_{di}$ are the active and reactive power demands at the ith bus.

(b) 

Inequality Constraints

The operational limits of various power system equipment are expressed by the inequality constraints h (m, n), which are described by Equations (8)–(14):

• Generator Constraints:

For each generator unit, the active powers ($P_{gk}$), reactive powers ($Q_{gk}$), and bus voltage ($V_{gk}$) should lie in between their minimum and maximum limits.

$$P_{g_k}^{min}\le P_{g_k}\le P_{g_k}^{max}k=1\dots \dots NGN$$

(8)

$$V_{g_k}^{min}\le V_{g_k}\le V_{g_k}^{max}k=1\dots \dots NGN$$

(9)

$$Q_{g_k}^{min}\le Q_{g_k}\le Q_{g_k}^{max}k=1\dots \dots NGN$$

(10)

• Shunt VAR compensator constraints:

The controllable VAR sources ($Q_{C_k}$) are regulated to their lowest and maximum limits:

$$Q_{C_k}^{min}\le Q_{C_k}\le Q_{C_k}^{max}k=1\dots NC$$

(11)

• Transformer Constraints:

Transformer tap settings ($T_k$) are retained within the maximum and minimum limits.

$$T_k^{min}\le T_k\le T_k^{max}k=1\dots \dots NTR$$

(12)

• Security Constraints:

The voltage at load buses ($V_{L_k}$) and the power flow in transmission lines ($S_{l_k}$) should be retained within their respective minimum and maximum limits.

$$V_{L_k}^{min}\le V_{L_k}\le V_{L_k}^{max}k=1\dots \dots NLB$$

(13)

$$S_{l_k}\le S_{l_k}^{max}k=1\dots \dots Ntl$$

(14)

(c) 

Incorporation of Constraints

The penalty factor approach is used in the OPF problem to efficiently include the working limits of operating constraints, such as bus voltage constraints, line flows, and generator constraints. The penalty factor approach penalizes each violation by multiplying it by a large number so that infeasible solutions are rejected and only feasible solutions are considered. To find feasible solutions [30], the above-mentioned inequality constraints are included and the augmented objective function is obtained by Equation (15).

$$Z_{aug}=Z_{min}(.)+C_1.H\left(P_{g_1}\right)+C_2{{\displaystyle \sum }}_{i=1}^{NGN}H\left(Q_{g_i}\right)+C_3{{\displaystyle \sum }}_{i=1}^{NLB}H\left(V_{L_i}\right)+C_4{{\displaystyle \sum }}_{i=1}^{Ntl}H\left(S_{l_i}\right)$$

(15)

$$H\left(x_i\right)=\{\begin{array}{c}{\left(x_i-x_{i,max}\right)}^2 if x_i>x_{i,max}\\ {\left(x_{i,min}-x_i\right)}^2 if x_i<x_{i,min}\\ 0 if x_{i,min}\le x_i\le x_{i,max}\end{array}$$

(16)

where H($x_i$) is the penalty function of variable $x_i$. Here, $x_i$ shows a dependent variable. In addition, $x_{i,max}$, and $x_{i,min}$ are the upper and lower limits of the variable $x_i$, respectively.

The three variants of the proposed Rao algorithms are applied to solve the OPF problems considering inherent complexities such as non-linear, multi-extremism, high dimensionality, and non-convexity property. In this paper, all the control variables are considered to be continuous.

3. Rao Algorithms

The proposed Rao algorithms employ the worst and best solutions, which can be obtained during the phases of optimization and random interaction among candidate solutions. The key benefit of the proposed algorithms is their algorithm-specific parameter-less property and hence these algorithms can be easily implemented for solving different types of optimization problems [21,22,23,29].

Assume that there is an ‘m’ population size (i.e., candidate solutions, k = 1, 2, …, m) and ‘n’ design variables (i.e., j = 1, 2, 3, …, n) for any iteration i. The best candidate will provide the best value of an objective function in all the candidate solutions, while the worst candidate will give the worst value of the objective function. During the ith iteration, $\mathrm{if} R_{i,j,k}$ is the jth variable value for the kth candidate, its value is updated according to Equations (17)–(19).

$$R_{j,k,i}{}^{\prime }=R_{j,k,i}+{\alpha }_{1,j,i}\left(R_{j,best,i}-R_{j,worst,i}\right)$$

(17)

$$R_{j,k,i}{}^{\prime }=R_{j,k,i}+{\alpha }_{1,j,i} \left(R_{j,best,i}-R_{j,worst,i}\right) +{\alpha }_{2,j,i} \left(\left|R_{j,k,i}\mathrm{or} R_{j,l,i}\right|- \left| R_{j,l,i}\mathrm{or} R_{j,k,i}\right|\right)$$

(18)

$$R_{j,k,i}{}^{\prime }=R_{j,k,i}+{\alpha }_{1,j,i} (R_{j,best,i}-|R_{j,worst,i}|) +{\alpha }_{2,j,i} \left(\left|R_{j,k,i}\mathrm{or} R_{j,l,i}\right|- \left(R_{j,l,i}\mathrm{or} R_{j,k,i}\right)\right)$$

(19)

In Equations (17)–(19), the value of the jth variable for the best candidate is $R_{j,best,i}$ and the value of the jth variable for the worst candidate is $R_{j,worst,i}$. The modified value of $R_{j,k,i}$ is $R_{j,k,i}{}^{\prime }$. For the jth variable, ${\alpha }_{1,j,i}$ and ${\alpha }_{2,j,i}$ are the two random numbers in the range (0, 1) during the ith iteration [29].

The term “$R_{j,k,i}$ or $R_{j,l,i}$” in Equations (17)–(19) shows that the solution for candidate k is compared with any randomly picked candidate solution l and the information is shared based on objective function values. If the kth solution’s objective function value is better than the lth solution’s objective function value, the term “$R_{j,k,i}$ or $R_{j,l,i}$” becomes $R_{j,k,i}$ and in that case, “$R_{j,l,i} \mathrm{or} R_{j,k,i}$” becomes $R_{j,l,i}$. Similarly, the term “$R_{j,k,i}$ or $R_{j,l,i}$” becomes $R_{j,l,i}$ when the objective function value of the lth solution is better than the fitness value of kth solution and in such condition, the expression “$R_{j,l,i} \mathrm{or} R_{j,k,i}$” becomes $R_{j,k,i}$.

The flowchart of the Rao algorithm is shown in Figure 1. The flowcharts for the Rao-2 and Rao-3 algorithms will be the same, except that Equation (17) will be replaced by Equations (18) and (19) in either chart, respectively.

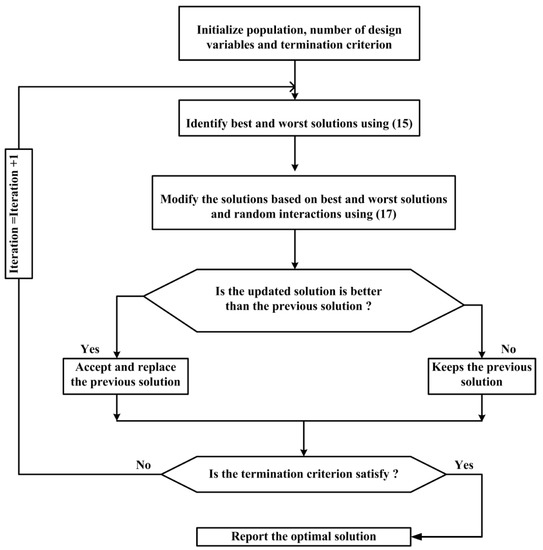
Figure 1. Flowchart of Rao-1 algorithm. Adapted from ref. [29].

Computational Steps of Rao Algorithms for the OPF Problem

The following are the computational steps for applying Rao algorithms:

• Randomly generate the initial population with control variables and set the stopping criteria, i.e., It_max.
• Set iterations count to It = 0.
• Identify the worst and best solutions in the population by observing the value of the augmented objective function (15).
• Update the solutions based on the worst and best solutions (17).
• Proceed to step 6 if the updated solution is better than the previous solution; otherwise, proceed to step 7.
• Replace the old solution with the new one. Go to step 8.
• Keep the old solution.
• If It < It_max, increase the count of iteration (i.e., It = It + 1) by 1 and go to step 3. Otherwise go to step 9.
• Stop and display objective function value of best results.

4. OPF Results and Discussion

Three standard test systems, IEEE (30-, 57-, and 118-bus), are used to check the efficacy of the Rao algorithms considering various objective functions. Several trials have been carried out but the best results obtained and presented in this paper are with the population size (pop.) = 40 and the maximum number of iterations (It_max) = 100 for the IEEE 30-bus system, while pop. = 50 and It_max = 150 for the IEEE 57-bus and IEEE 118-bus systems. All the computations were carried out on a 1.7 GHz Intel Processor, 4GB RAM, Core i3, and 64-bit operating system using the MATLAB-13a computing environment on a personal computer (PC).

In various cases of these systems, the converged solution strictly followed all the lower and upper operating limits, which included reactive and active power generation output, line loading, and load bus voltage magnitudes. Under this condition, the value of the penalty was observed to be zero, which guarantees a feasible solution. It has been seen that Rao algorithms’ numerical results are better in most of the cases than the reported results as mentioned in recent literature.

Performance of Rao-1, Rao-2, and Rao-3 is found to be competitive with one another as mentioned in [30]. In this paper, different topologies have been considered because the different topologies have different problem dimensions and complexities. The proposed Rao algorithms have been applied on three standard IEEE test systems, i.e., 30-bus, 57-bus, and 118-bus, which have 24 control variables, 33 control variables, and 130 control variables, respectively, to test the efficacy of the proposed algorithm for different problems dimensions.

4.1. IEEE 30-Bus Test System

The system data along with control variables’ operating limits are taken from Reference [32] and given in Table 1. The emission and fuel cost coefficients of the IEEE 30-bus system are taken from [33]. For this system, 30 runs were performed using Rao algorithms to solve the different objective functions of the OPF problem and the best results out of 30 independent trials are given in this paper.

Table 1. Details of the IEEE 30-bus test system.

Control Variables	Nbus	Ntl	NGN	NLB	NC	NTR	Voltage Limit (PQ Bus)	Voltage Limit (PV Bus)
24 (05+06+09+04)	30	41	6 (@ G1, G2, G5, G8, G11, G13)	24	9 (@ Sh 10, Sh 12, Sh 15, Sh 17, Sh 20, Sh 21, Sh 23, Sh 24, Sh29)	4 (@ Nt 11, Nt 12, Nt 15 & Nt 36)	(0.94:1.06)	(0.95:1.1)

4.1.1. Case 1: Fuel Cost Minimization (FCM)

Here, the first objective of the OPF problem is to reduce the total cost of generation or the fuel cost [8]. This function can be described as Equation (20):

$$F_{cost}\left(a,b\right)={\displaystyle \sum }_{i=1}^{NGN }{f}_i\left(P_{g_i}\right) \left(\$/h\right)$$

(20)

All the generating units’ cost characteristics are quadratic and can be stated as Equation (21).

$$f_i\left(P_{g_i}\right)=A_i+B_i{P}_{g_i}+C_i{P}_{g_i}^2 \left(\$/h\right)$$

(21)

The minimum cost attained by the Rao-3 algorithm is 799.9683 $/h, while Rao-2 and Rao-1 algorithms provided the minimum fuel cost of 799.9918 $/h and 800.4391 $/h, respectively. Table 2 compares the simulation results of Case 1 obtained by the proposed algorithms and other reported algorithms listed in recent literature. The OPF results of the proposed Rao-3 algorithm and optimal control variable settings are presented in Table 3. Based on the outcomes, it is clear that the Rao-3 algorithm provided the least value of the fuel cost as compared to the other methods. This demonstrates the effectiveness of the proposed Rao-3 algorithm as compared to Rao-2 and Rao-1 algorithms, as well as other competitors for this case. The fuel cost convergence characteristics of Case 1 are presented in Figure 2.

Table 2. Case 1: FCM in the IEEE 30-bus system.

Algorithm	Fuel Cost ($/h)	Time (s)
Rao-3	799.9683	89.56
Rao-2	799.9918	89.74
Rao-1	800.4391	91.62
MSA [14]	800.5099	-
MPSO [14]	800.5164	-
MDE [14]	800.8399	-
MFO [14]	800.6863	-
FPA [14]	802.7983	-
DSA [18]	800.3887	-
EEA [34]	800.0831
Jaya [35]	800.479	-
QOJA [36]	800.352	-
MSO [37]	801.571	-
IMFO [38]	800.3848	-
MFO [38]	800.6206	-
GA [38]	800.4346	-
PSO [38]	800.4075	-
TLBO [38]	800.4104	-
ARCBBO [39]	800.5159	-
RCBBO [39]	800.8703	-
GWO [40]	801.41	-
DE [40]	801.23	-
MGBICA [41]	801.1409	-
GBICA [41]	801.1513	-
ABC [42]	800.66	-
SKH [43]	800.5141	-
ECHT-DE [44]	800.4148	-
SF-DE [44]	800.4131	133.1
SP-DE [44]	800.4293	-
MGOA [45]	800.4744	-
Tabu Search [46]	800.29	-

Table 3. Optimum values of control variables for Case 1, Case 2, and Case 3 of the IEEE 30-bus system.

S. Number	Control Variable	Case 1 (FCM)			Case 2 (VPI)			Case 3 (VSE)
		Rao-1	Rao-2	Rao-3	Rao-1	Rao-2	Rao-3	Rao-1	Rao-2	Rao-3
Generator active power output
1	PG2	0.4869	0.4923	0.4879	0.4957	0.4855	0.4827	0.4884	0.4906	0.4873
2	PG5	0.2131	0.2134	0.2144	0.2137	0.2166	0.2176	0.2127	0.2158	0.2119
3	PG8	0.2078	0.2059	0.2093	0.2228	0.2188	0.2253	0.2044	0.2087	0.2149
4	PG11	0.1186	0.1195	0.1192	0.1253	0.1243	0.1227	0.1221	0.1143	0.1159
5	PG13	0.12	0.12	0.12	0.12	0.12	0.12	0.12	0.1201	0.1201
Generator voltage
6	VG1	1.1	1.0933	1.0944	1.0444	1.0504	1.0492	1.0909	1.0941	1.0948
7	VG2	1.0707	1.0751	1.0752	1.0253	1.032	1.0319	1.0748	1.0745	1.0758
8	VG5	1.0299	1.0441	1.0444	1.0078	1.0122	1.0118	1.0475	1.0435	1.043
9	VG8	1.0405	1.0491	1.0486	1.0044	1.0059	1.0072	1.052	1.0489	1.0493
10	VG11	1.1	1.1	1.0994	1.0751	1.073	1.0724	1.0999	1.0981	1.1
11	VG13	1.0592	1.0498	1.0574	0.9904	0.9696	0.9771	1.0551	1.0558	1.048
Tap settings
12	T6–9	1.1	1.0992	1.0659	1.1	1.1	1.1	1.0806	1.0382	1.1
13	T6–10	0.9	0.9	0.9267	0.9	0.9	0.9002	0.9004	0.9451	0.9014
14	T4–12	0.9763	0.9711	0.969	0.9451	0.9218	0.9229	0.9708	0.9745	0.9635
15	T28–27	0.9813	0.9735	0.9759	0.9708	0.9699	0.9713	0.9815	0.9738	0.9821
Shunt VAR source
16	QSh10	0.0369	0.05	0.0442	0.05	0.0499	0.0496	0.0457	0.0214	0.0484
17	QSh12	0.0003	0.05	0.0026	0	0.05	0.003	0.0053	0.05	0.05
18	QSh15	0.0453	0.05	0.05	0.0495	0.05	0.05	0.0481	0.0335	0.0479
19	QSh17	0.05	0.0492	0.0495	0	0.0001	0.0003	0.0499	0.0493	0.0368
20	QSh20	0.0419	0.05	0.0414	0.0496	0.05	0.05	0.0264	0.046	0.049
21	QSh21	0.05	0.0499	0.05	0.0499	0.05	0.0498	0.0499	0.0466	0.0498
22	QSh23	0.0332	0.037	0.0352	0.0496	0.05	0.0497	0.0432	0.0404	0.0418
23	QSh24	0.05	0.0493	0.0497	0.05	0.05	0.0491	0.05	0.0489	0.0476
24	QSh29	0.0278	0.0178	0.029	0.033	0.0265	0.0285	0.0333	0.0309	0.05
Fuel cost ($\h)		800.4391	799.9918	799.9683	803.4877	803.5375	803.5304	800.0492	800.001	800.025
TVD (pu)		0.9714	1.1168	1.1356	0.1031	0.0993	0.1001	1.1481	1.1409	1.1449
Emission (ton/h)		0.3362	0.3351	0.3351	0.3315	0.3338	0.3331	0.3357	0.3355	0.3354
PLoss(MW)		9.0613	8.91	8.8872	9.7465	9.8209	9.7724	8.941	8.9086	8.9098
L-index (LI)		0.1307	0.1285	0.1281	0.1404	0.1404	0.1408	0.128	0.1278	0.1264

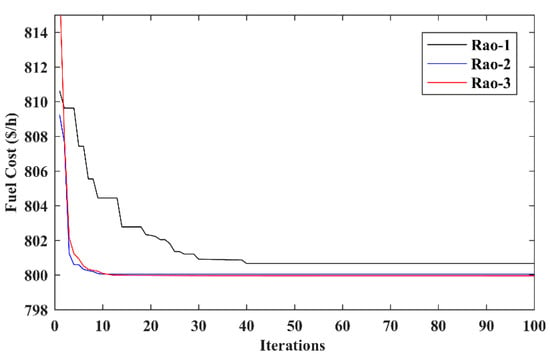
Figure 2. Convergence characteristics for the IEEE 30-bus system, Case 1.

4.1.2. Case 2: Voltage Profile Improvement (VPI)

The main motive of the second case is to minimize the voltage variation in all the load buses from 1.0 pu [31] along with the fuel cost. The multi-objective function is transformed into a single objective function by using the weighted sum method using Equation (22):

$$F_{TVD}\left(a,b\right)={\displaystyle \sum }_{i=1}^{NGN }{f}_i(.)\$/h+{\phi }_{VD}{\displaystyle \sum }_{iϵNLB}\left|V_i-1\right|$$

(22)

In the combined objective function, the value of the weighting factor (${\phi }_{VD}$) assigned to voltage deviation was taken as 160.

The OPF results attained using Rao algorithms are compared with other reported results in Table 4. As can be observed from Table 4, the Rao-2 algorithm provided the minimum total voltage deviation as 0.0993 pu, which is the least among the Rao algorithm variants. In this case, the minimum total voltage deviation obtained by the proposed Rao algorithms are slightly higher than some reported results. Such types of situations will be there only because the different papers might have selected different weighting factors.

Table 4. Case 2: VPI in the IEEE 30-bus system.

Algorithm	Fuel Cost ($/h)	TVD (pu)	Time (s)
Rao-3	803.5304	0.1001	88.14
Rao-2	803.5375	0.0993	87.36
Rao-1	803.4877	0.1031	89.91
MSA [14]	803.3125	0.1084	-
MPSO [14]	803.9787	0.1202	-
MDE [14]	803.2122	0.1265	-
MFO [14]	803.7911	0.1056	-
FPA [14]	803.6638	0.1366	-
IMFO [38]	803.5715	0.0954	-
MFO [38]	803.5173	0.1007	-
GA [38]	803.2347	0.1018	-
PSO [38]	803.4736	0.0978	-
TLBO [38]	803.5675	0.0939	-
ECHT-DE [44]	803.7198	0.09454	123.3
SF-DE [44]	803.4241	0.09772	-
SP-DE [44]	803.4196	0.09776	-
MGOA [45]	803.4176	0.1107	-
GOA [45]	803.4488	0.1709	-

TVD = total voltage deviation.

The optimal control variable settings are presented in Table 3, while the load (PQ) bus voltage profile obtained by the Rao-2 algorithm in Case 2 is shown in Figure 3. Based on the OPF results, it is clear that the Rao-2 algorithm provided the least value of the total voltage deviation as compared to the other variants of the Rao method. This demonstrates the effectiveness of the Rao-2 algorithm in comparison to the Rao-1 and Rao-3 algorithms for this case.

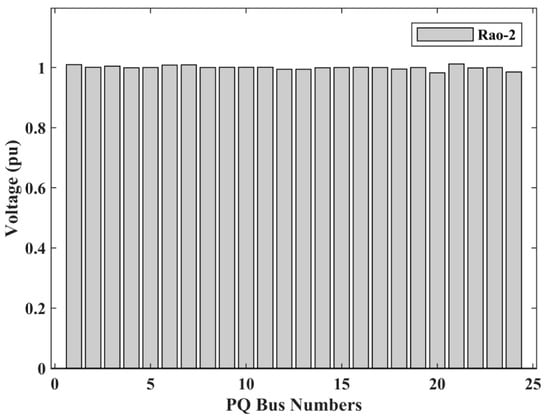
Figure 3. Load bus voltage profile for the IEEE 30-bus system, Case 2.

4.1.3. Case 3: Voltage Stability Enhancement (VSE)

The system voltage stability can be increased by reducing the L-index [8]. In this paper, fuel cost minimization and voltage stability enhancement were considered using the two-fold objective function as in Equation (23):

$$F_{Lmax}\left(a,b\right)={{\displaystyle \sum }}_{i=1}^{NGN}{f}_i(.)\$/h+{\phi }_{L}L$$

(23)

where ${\phi }_L$ is the weight factor.

The control variables’ settings of this case obtained using the three variants of Rao algorithms are given in Table 5. The OPF results of Rao algorithms and the results provided by other reported results published in recent literature have been compared in Table 5. The OPF results in Table 5 prove that the Rao-3 algorithm is best among three variants of Rao algorithms for Case 3. As can be observed from Table 5, the Rao-3 algorithm provided a minimum L-index value of 0.1264, which is the least among the Rao variants. In this case, the minimum L-index values obtained by the proposed Rao algorithms are slightly higher than some reported results but the fuel cost is less. Such types of situations will be there only because the different papers might have selected different weighting factors.

Table 5. Case 3: VSE in the IEEE 30-bus system.

Algorithm	Fuel Cost ($/h)	L-Index	Time (s)
Rao-3	800.0250	0.1264	87.94
Rao-2	800.0010	0.1278	88.50
Rao-1	800.0492	0.1280	88.11
MSA [14]	801.2248	0.1371	-
MPSO [14]	801.6966	0.1375	-
MDE [14]	802.0991	0.1374	-
MFO [14]	801.668	0.1376	-
FPA [14]	801.1487	0.1376	-
IMFO [38]	800.4762	0.1255	-
MFO [38]	800.9415	0.1266	-
GA [38]	800.4385	0.1254	-
PSO [38]	800.5815	0.128	-
TLBO [38]	800.4738	0.1247	-
ECHT-DE [44]	800.4321	0.13739	130.4
SF-DE [44]	800.4203	0.13745	-
SP-DE [44]	800.4365	0.13748	-
Bisection method [47]	958.8330	0.1050	-

L-index = voltage collapse proximity indicator.

4.1.4. Case 4: Voltage Stability Enhancement (VSE) during Contingency

In Case 4, voltage stability has been improved considering single line outage (n − 1) contingency [8]. The prime objective in this case is to improve voltage stability and reduce the fuel cost under a single line (connected between bus number 2 to bus number 6) outage condition. Table 6 compares the OPF results of Case 4 obtained by the proposed Rao algorithms with other efficient optimization algorithms reported in the recent literature. The results shown in Table 6 demonstrate the Rao-3 algorithm’s dominance over other recently developed optimization methods. The control variables’ settings obtained in this case using the three Rao algorithms are given in Table 7.

Table 6. Case 4: VSE during contingency results in the IEEE 30-bus system.

Algorithm	Fuel Cost ($/h)	L-Index	Time (s)
Rao-3	818.5353	0.1363	90.65
Rao-2	810.3012	0.1439	92.32
Rao-1	827.3375	0.1485	91.87
MSA [14]	804.4838	0.1392	-
MPSO [14]	807.6519	0.1405	-
MDE [14]	806.6668	0.1398	-
MFO [14]	804.556	0.1394	-
FPA [14]	805.5446	0.1415	-

Table 7. Optimum values of control variables of Case 4, Case 5, and Case 6 of the IEEE 30-bus system.

S. Number	Control Variable(p.u)	Case 4 (VSE) during Contingency			Case 5 (RPLM)			Case 6 (ECM)
		Rao-1	Rao-2	Rao-3	Rao-1	Rao-2	Rao-3	Rao-1	Rao-2	Rao-3
Generator active power output
1	PG2	0.4034	0.4515	0.4811	0.8	0.8	0.8	0.6633	0.6631	0.7421
2	PG5	0.2951	0.2132	0.214	0.5	0.5	0.5	0.5	0.5	0.4638
3	PG8	0.2935	0.2808	0.2416	0.35	0.35	0.35	0.35	0.35	0.3154
4	PG11	0.168	0.12	0.1279	0.3	0.3	0.3	0.3	0.3	0.2867
5	PG13	0.2854	0.12	0.12	0.4	0.4	0.4	0.4	0.4	0.3127
Generator voltage
6	VG1	1.0414	1.1	1.02	1.066	1.0616	1.0718	1.0737	0.9963	1.0473
7	VG2	1.0035	1.469	1.02	1.0509	1.0577	1.0679	1.0677	0.95	1.0441
8	VG5	1.0416	1.095	1.092	1.025	1.0381	1.0484	1.0477	0.956	1.0317
9	VG8	1.0799	1.095	1.08	1.0409	1.0495	1.0552	1.0539	1.0932	1.0488
10	VG11	1.0602	1.06	1.1	1.02	1.1	1.1	1.1	0.9539	1.0924
11	VG13	1.0237	1.0714	1.1	1.0452	1.07	1.063	1.0613	1.1	1.0719
Tap settings
12	T6–9	0.9602	1.0496	0.914	1.1	1.0858	1.0822	1.0445	0.9063	1.0493
13	T6–10	1.0208	1.0657	0.9747	0.9108	0.9001	0.9	0.9518	0.9054	1.0764
14	T4–12	1.0379	1.0012	0.9549	1.0307	0.9977	0.9966	0.9928	0.9762	1.0378
15	T28–27	0.9724	0.9327	0.9256	1.0072	0.9772	0.9774	0.9761	0.9156	1.0724
Shunt VAR source
16	QSh10	0.021	0.05	0.05	0.05	0	0	0.0293	0.0317	0.0217
17	QSh12	0.0324	0.05	0.05	0.045	0.0479	0.0478	0.05	0.0414	0.0429
18	QSh15	0.032	0.05	0.05	0.0495	0.039	0.0471	0.0448	0	0.0342
19	QSh17	0.0151	0.05	0.05	0.05	0.0499	0.0498	0.05	0.0349	0.0343
20	QSh20	0.0283	0.05	0.05	0.05	0.0413	0.0412	0.0413	0.0018	0.0122
21	QSh21	0.0344	0.05	0.05	0.05	0.05	0.05	0.05	0.05	0.0433
22	QSh23	0.0147	0.05	0.05	0.0427	0.0371	0.0341	0.0332	0.05	0.0358
23	QSh24	0.0282	0.05	0.05	0.05	0.05	0.05	0.05	0.05	0.0458
24	QSh29	0.0232	0.05	0.05	0.0205	0.0257	0.0252	0.0236	0.05	0.0383
Fuel cost ($\h)		827.3375	810.3012	818.5353	968.1496	967.6830	967.5828	942.3443	944.1722	915.2185
TVD (pu)		0.5925	0.5754	0.7439	0.4125	1.0361	1.1277	1.1261	0.821	0.5493
Emission (ton/h)		0.2792	0.3324	0.3375	0.2066	0.2066	0.2066	0.2037	0.204	0.2126
PLoss (MW)		9.2645	11.3868	14.145	3.3041	3.1086	3.0675	3.2162	3.9623	4.2325
L-index		0.1485	0.1439	0.1363	0.1391	0.1302	0.1289	0.1286	0.1328	0.1467

4.1.5. Case 5: Real Power Loss Minimization (RPLM)

In Case 5, RPLM was selected as a prime objective function [29]. Mathematically, $F_{Loss}$ can be represented by Equation (24).

$$F_{Loss}\left(a,b\right)={{\displaystyle \sum }}_{i=1}^{NB}{P}_{gi}-{{\displaystyle \sum }}_{i=1}^{NB}{P}_{di}$$

(24)

The function $F_{Loss}$ is selected for the power loss as described in Equation (24). The minimum power loss attained by the Rao-3 algorithm is 3.0675 MW, while Rao-2 and Rao-1 algorithms provided minimum power losses of 3.1086 MW and 3.3041 MW, respectively. The results of Rao algorithms and optimal control variable settings are presented in Table 7. Table 8 compares the simulation results of Case 5 obtained by the proposed algorithms and other published methods proposed in recent literature. Based on the OPF outcomes, it can be concluded that the Rao-3 algorithm provided the least value of power loss as compared to the other methods. The power loss convergence characteristics of Case 5 are presented in Figure 4.

Table 8. Case 5: RPLM in the IEEE 30-bus system.

Algorithm	Power Loss (MW)	Time (s)
Rao-3	3.0675	85.72
Rao-2	3.1086	90.89
Rao-1	3.3041	89.07
MSA [14]	3.1005	-
MPSO [14]	3.1031	-
MDE [14]	3.1619	-
MFO [14]	3.1111	-
FPA [14]	3.5661	-
MSO [37]	3.4052	-
IMFO [38]	3.0905	-
MFO [38]	3.139	-
GA [38]	3.118	-
PSO [38]	3.103	-
TLBO [38]	3.088	-
SKH [43]	3.0987	-
ECHT-DE [44]	3.0850	-
SF-DE [44]	3.0845	-
SP-DE [44]	3.0844	136.4

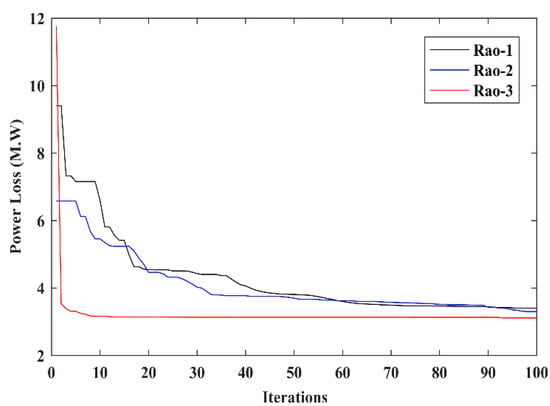
Figure 4. Convergence characteristics for the IEEE 30-bus system, Case 5.

4.1.6. Case 6: Emission Cost Minimization

For a given electrical network, the total emission cost [29] can be calculated using Equation (25):

$$F_{ECOST}\left(x,u\right)={\displaystyle \sum }_{i=1}^{NGN }{\delta }_i+{\mu }_i{P}_{G_i}+{\gamma }_i{P}_{G_i}^2+{\xi }_i\mathit{exp}\left({\lambda }_i{P}_{G_i}\right) \left(\raisebox{1ex}{$ton$}\!\left/ \!\raisebox{-1ex}{$h$}\right.\right)$$

(25)

The objective function $F_{ECOST}$ is selected for total emission cost minimization as described in Equation (25). Table 9 compares the results obtained by the proposed Rao algorithms for Case 6 with other efficient optimization algorithms reported in the recent literature. The results shown in Table 9 demonstrate the dominance of the Rao-1 algorithm over other variants of Rao techniques. The convergence characteristics offered by the three Rao algorithms are shown in Figure 5. The control variables’ settings for Case 6 obtained using the three Rao algorithms are given in Table 7. As can be noted from Table 9, the MGOA [45] algorithm offered the least emission value in comparison to the Rao-1 algorithm in this case, but Rao algorithm variants offered better results in most of the cases.

Table 9. Case 6: ECM in the IEEE 30-bus system.

Algorithm	Emission (ton/h)	Time (s)
Rao-3	0.2126	87.87
Rao-2	0.2040	85.45
Rao-1	0.2037	89.82
MSA [14]	0.2048	-
MPSO [14]	0.2325	-
MDE [14]	0.2093	-
MFO [14]	0.2049	-
FPA [14]	0.2052	-
DSA [18]	0.2058	-
MSO [37]	0.2175	-
IMFO [38]	0.2048	-
MFO [38]	0.2048	-
GA [38]	0.2048	-
PSO [38]	0.2048	-
TLBO [38]	0.2048	-
MGBICA [41]	0.2048	-
GBICA [41]	0.2049	-
ABC [42]	0.2048	-
SKH [43]	0.2048	-
ECHT-DE [44]	0.2048	138.2
SF-DE [44]	0.2048	-
SP-DE [44]	0.2048	-
MGOA [45]	0.2025	-
GOA [45]	0.2050	-

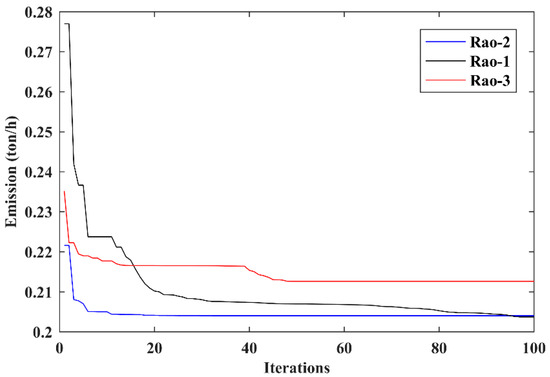
Figure 5. Convergence characteristic for the IEEE 30-bus system, Case 6.

4.2. IEEE 57-Bus System

To evaluate the effectiveness of the Rao algorithms, they are applied to the IEEE 57-bus system to solve OPF problems. The system data, shunt capacitor data, transformer data, and control variables’ limits are taken from [48] and are shown in Table 10. The active and reactive power demands of this system on the 100 MVA base are 12.508 and 3.364 pu, respectively. Thirty independent runs were taken using Rao algorithms to solve the OPF problem for this system and the best results obtained are given in this paper.

Table 10. Details of the IEEE 57-bus system.

Control Variable	Nbus	Ntl	NGN	NLB	NC	NTR	Voltage Limit (PQ Bus)	Voltage Limit (PV Bus)
33 (06+07+03+17)	57	80	7 (@ G1, G2, G3 G6, G8 G9, G12)	50	3(@ Sh18, Sh25, Sh23)	17 (@ Nt19, Nt20, Nt31 Nt 35, Nt 36, Nt 37, Nt 41, Nt46, Nt54, Nt58, Nt59, Nt65, Nt66, Nt71, Nt73, Nt76 & Nt80)	(0.94:1.06)	(0.9:1.1)

4.2.1. Case 7: Fuel Cost Minimization (FCM)

FCM is selected as the primary objective as in Case 1 and defined in Equation (20). Table 11 compares the simulation results of Case 7 as obtained by the proposed Rao algorithms and by other methods reported in recent literature. The minimum cost attained by the Rao-3 algorithm is 41,659.2621 $/h, while Rao-2 and Rao-1 algorithms offered the minimum fuel cost of 41,872.0668 $/h and 41,771.1088 $/h, respectively. Based on the OPF outcomes, it is clear that the Rao-3 algorithm provided the least fuel cost as compared to other methods. This demonstrates the effectiveness of the proposed Rao-3 algorithm as compared to Rao-2 and Rao-1 algorithms, as well as other reported algorithms. The OPF results of the proposed Rao-3 algorithm and optimal control variable settings are presented in Table 12. The fuel cost characteristic of Case 7 is presented in Figure 6.

Table 11. Case 7 (FCM) results in the IEEE 57-bus system.

Algorithm	Fuel Cost ($/h)	Time (s)
Rao-3	41,659.2621	131.23
Rao-2	41,872.0668	132.94
Rao-1	41,771.1088	131.87
MSA [14]	41,673.7231	-
MPSO [14]	41,678.6762	-
MDE [14]	41,695.8123	-
MFO [14]	41,686.4119	-
FPA [14]	41,701.9592	-
TSA [17]	41,685.07	75.61
DSA [18]	41,686.82	-
SSA [19]	41,672.30	80.61
MSO [37]	41,747.20	-
IMFO [38]	41,692.7178	-
MFO [38]	41,719.8471	-
GA [38]	41,700.4162	-
PSO [38]	41,684.4009	-
TLBO [38]	41,694.7778	-
SKH [43]	41,676.9152	-
ECHT-DE [44]	41,670.562	-
SF-DE [44]	41,667.85	-
SP-DE [44]	41,667.82	219.9
MGOA [45]	41,671.0980	-
GOA [45]	41,679.6792	-

Table 12. Optimum values of control variables of Case 7 and Case 8 for the IEEE 57-bus system.

S. Number	Control Variable (p.u)	CASE 7 (FCM)			CASE 8 (VPI)
		Rao-1	Rao-2	Rao-3	Rao-1	Rao-2	Rao-3
Generator active power output
1	PG2	0.8722	0.9999	0.8857	0.8822	0.8866	0.4027
2	PG3	0.42	0.5217	0.4494	0.4506	0.4497	0.42
3	PG6	0.7856	0.3264	0.7324	0.7298	0.7183	0.3135
4	PG8	4.6615	4.5567	4.6028	4.6168	4.5992	4.814
5	PG9	0.8309	0.94	0.9588	0.963	0.9726	0.962
6	PG12	3.639	3.9341	3.5953	3.5936	3.607	4.087
Generator voltage
7	VG1	1.0791	1.0629	1.0603	1.0484	1.0322	0.9965
8	VG2	1.0822	1.0694	1.0637	1.0526	1.0362	1.014
9	VG3	1.0602	1.0556	1.0529	1.043	1.0255	1.0097
10	VG6	1.0611	1.0493	1.0615	1.057	1.04	1.0032
11	VG8	1.0656	1.0626	1.0741	1.0757	1.0592	1.0135
12	VG9	1.0508	1.0484	1.0541	1.0502	1.0329	1.0148
13	VG12	1.0518	1.046	1.0462	1.0342	1.0175	1.044
Tap settings
14	T4–18	1.0824	1.001	1.1	0.982	1.0872	0.9031
15	T4–18	1.0075	1.0173	0.9416	1.0113	0.9243	1.0393
16	T21–20	1.0187	1.0649	1.0154	0.9892	0.991	0.9757
17	T24–25	1.0879	1.0289	0.9447	1.017	0.9452	1.1
18	T24–25	1.0887	0.9164	1.0887	1.0503	1.0952	1.0996
19	T24–26	1.0277	0.9031	1.0327	1.1	1.0224	1.0152
20	T7–29	1.0149	1.0082	0.9954	1.034	1.014	1.0054
21	T34–32	1.0011	0.9549	0.9565	0.938	0.9356	0.9334
22	T11–41	1.0006	0.9111	0.9083	0.9	0.9008	0.9002
23	T15–45	1.01	1.1	0.9781	0.989	0.9691	0.9524
24	T14–46	0.9841	0.9489	0.9612	0.9866	0.9651	0.9798
25	T10–51	1.0997	0.9788	0.9748	1.0039	0.9848	1.0138
26	T13–49	0.9037	0.9328	0.936	0.9553	0.9357	0.9001
27	T11–43	1.0938	1.0018	0.9771	1.0047	0.9745	0.9781
28	T40–56	0.9067	0.9	0.9975	1.0041	0.9975	0.9849
29	T39–57	0.9182	0.9	0.9675	0.9415	0.9384	0.9
30	T9–55	1.0134	1.1	1.0026	1.0285	1.0115	1.0146
Shunt VAR source
31	Qsh18	0.1858	0.0559	0.1724	0.0127	0.0628	0.0003
32	Qsh25	0.2803	0.1939	0.1439	0.163	0.1747	0.3
33	Qsh53	0.2381	0.1577	0.1267	0.1705	0.1481	0.3
Fuel cost ($\h)		41,771.1088	41,872.0668	41,659.2621	41,688.4417	41,691.1102	42,043.2728
TVD (pu)		1.5465	1.6713	1.6953	0.9882	0.7645	0.5725
L-index		0.231	0.2411	0.2349	0.2438	0.2415	0.2297
PLoss (MW)		17.364	16.4837	14.7262	15.4719	15.4214	18.0100

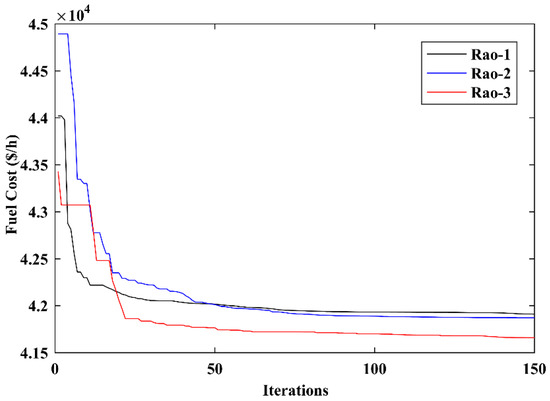
Figure 6. Convergence characteristics for the IEEE 57-bus system, Case 7.

4.2.2. Case 8: Voltage Profile Improvement (VPI)

In Case 8, improvement of the voltage profile is considered as an objective function in addition to the fuel cost, as defined in Equation (22). The optimal control variables’ settings are presented in Table 12. The minimum total voltage deviation attained by the Rao-3 algorithm is 0.5725 pu, while Rao-1 and Rao-2 algorithms provided the minimum total voltage deviations of 0.9882 and 0.9882 pu, respectively. Table 13 compares the simulation results of Case 8 obtained by the proposed Rao algorithms and other proposed methods reported in recent literature. Based on the OPF outcomes shown in Table 13, it can be concluded that the Rao-3 algorithm provided the least total voltage deviation compared to the other methods. This demonstrates the effectiveness of the proposed Rao-3 algorithm over Rao-1 and Rao-2 algorithms, as well as other algorithms. PQ bus voltage profiles obtained in Case 8 are shown in Figure 7.

Table 13. Case 8: VPI results in the IEEE 57-bus system.

Algorithm	Fuel Cost ($/h)	TVD (pu)	Time (s)
Rao-3	42,043.2728	0.5725	134.25
Rao-2	41,691.1102	0.7645	136.34
Rao-1	41,688.4417	0.9882	131.87
MSA [14]	41,714.9851	0.67818	-
MPSO [14]	41,721.6098	0.67813	-
MDE [14]	41,717.3874	0.6781	-
MFO [14]	41,718.8659	0.67796	-
FPA [14]	41,726.3758	0.69723	-
TSA [17]	54,045.17	0.72	75.41
DSA [18]	41,699.4	0.762	-
IMFO [38]	41,692.7178	0.7182	-
MFO [38]	41,719.8471	0.7551	-
GA [38]	41,700.4162	0.8051	-
PSO [38]	41,684.4009	0.7624	-
TLBO [38]	41,694.7778	0.712	-
ECHT-DE [44]	41,694.82	0.81659	-
SF-DE [44]	41,697.52	0.77572	-
SP-DE [44]	41,697.50	0.77253	203.6
MGOA [45]	41,697.9735	0.7381	-
GOA [45]	41,715.1396	0.8260	-

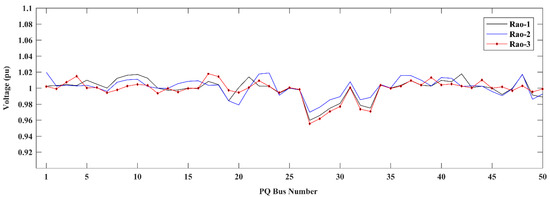
Figure 7. Voltage profile for the IEEE 57-bus system.

4.2.3. Case 9: Voltage Stability Enhancement (VSE)

In Case 9, the VSE is considered in addition to the fuel cost, as defined in Equation (23). The control variables’ values obtained using the three Rao algorithms are provided in Table 14. The results of Case 9 attained by the proposed Rao methods and the optimization algorithms mentioned in the recent literature are compared in Table 15. The OPF results shown in Table 15 also prove the dominance of the Rao-3 algorithm over other optimization algorithms for this case.

Table 14. Optimum values of control variables of Case 9 and Case 10 for the IEEE 57-bus test system.

S. Number	Control Variable (p.u)	Case 9 (VSE)			Case 10 (RPLM)
		Rao-1	Rao-2	Rao-3	Rao-1	Rao-2	Rao-3
Generator active power output
1	PG2	0.8747	0.9749	0.9637	0.3048	0.3	0.3
2	PG3	0.4513	0.4486	0.4518	1.3241	1.322	1.3549
3	PG6	0.7085	0.7029	0.7067	0.9937	0.9999	0.9996
4	PG8	4.6141	4.5994	4.5916	3.1132	3.0842	3.0604
5	PG9	0.9998	0.9324	0.934	0.9978	0.9999	0.99998
6	PG12	3.5892	3.572	3.5912	4.1	4.1	4.0999
Generator voltage
7	VG1	1.047	1.0873	1.0873	1.0542	1.0723	1.0712
8	VG2	1.0502	1.1	1.1	1.0559	1.0722	1.0721
9	VG3	1.0425	1.0672	1.0676	1.0563	1.067	1.0666
10	VG6	1.0569	1.0621	1.062	1.0623	1.0633	1.0631
11	VG8	1.0717	1.0689	1.0697	1.0654	1.0697	1.0695
12	VG9	1.0465	1.0507	1.0509	1.0492	1.0576	1.0572
13	VG12	1.0328	1.0384	1.0382	1.0441	1.0572	1.0567
Tap settings
14	T4–18	1.0999	0.9016	0.9	1.1	0.9117	1.1
15	T4–18	0.9081	1.1	1.0428	1.0023	1.082	0.9014
16	T21–20	1.0138	1.0321	1.0025	0.998	1.042	1.0128
17	T24–25	1.083	1.1	1.0999	0.9036	1.0356	1.0902
18	T24–25	1.1	1.0998	1.1	1.0698	0.9704	0.9354
19	T24–26	1.0252	1.0268	1.0262	1.0086	1.0109	1.0098
20	T7–29	0.9991	0.9993	0.9986	0.9953	0.9963	0.9961
21	T34–32	0.9423	0.9522	0.9476	0.9318	0.9528	0.9526
22	T11–41	0.9112	0.9129	0.9002	0.9111	0.9174	0.9025
23	T15–45	0.9707	0.9909	0.9916	0.9733	0.9892	0.9889
24	T14–46	0.9539	0.9695	0.9686	0.9671	0.9751	0.9722
25	T10–51	0.9676	0.9709	0.9699	0.9797	0.9821	0.9819
26	T13–49	0.9076	0.9389	0.9365	0.9411	0.9449	0.9451
27	T11–43	0.9643	0.9782	0.9811	0.9776	0.9817	0.9939
28	T40–56	0.9945	0.9924	1.0152	0.9826	0.9938	0.993
29	T39–57	0.9753	0.9655	0.9639	0.96	0.9624	0.9638
30	T9–55	0.9912	0.9934	0.9978	0.9986	0.9961	0.9947
Shunt VAR source
31	Qsh18	0.1139	0.0375	0.0002	0.2771	0.0002	0.0239
32	Qsh25	0.2412	0.2613	0.2576	0.1081	0.1448	0.1554
33	Qsh53	0.1405	0.1428	0.1293	0.1445	0.1339	0.129
Fuel cost ($\h)		41,670.4726	41,692.9720	41,692.6149	44,418.4740	44,438.1623	44,600.2741
TVD (pu)		1.7637	1.7835	1.8735	1.5278	1.7464	1.793
PLoss (MW)		15.0175	15.561	15.4768	10.005	9.766	9.759
L-index		0.22	0.2191	0.2186	0.2434	0.2353	0.2330

Table 15. Case 9: VSE results in the IEEE 57-bus system.

Algorithm	Fuel Cost ($/h)	L-Index	Time (s)
Rao-3	41,692.6149	0.2186	131.78
Rao-2	41,692.9720	0.2191	132.54
Rao-1	41,670.4726	0.2200	132.76
MSA [14]	41,675.9948	0.27481	-
MPSO [14]	41,694.1407	0.27918	-
MDE [14]	41,689.5878	0.27677	-
MFO [14]	41,680.1937	0.27467	-
FPA [14]	41,684.1859	0.27429	-
DSA [18]	41,761.22	0.2383	-
IMFO [38]	41,673.6204	0.23525	-
MFO [38]	41,688.6522	0.2395	-
GA [38]	41,670.0872	0.2413	-
PSO [38]	41,670.1755	0.242	-
TLBO [38]	41,685.353	0.24787	-
SKH [43]	43,937.1058	0.2721	-
ECHT-DE [44]	41,671.09	0.28152	-
SF-DE [44]	41,667.53	0.28022	214.4
SP-DE [44]	41,668.45	0.28092	-
MGOA [45]	41,682.4031	0.2297	-
GOA [45]	41,698.1175	0.2395	-

4.2.4. Case 10: Real Power Loss Minimization (RPLM)

The function $F_{Loss}$ is selected for the RPLM as described in Equation (24). The minimum power loss attained by the Rao-2 algorithm is 9.759 MW, while Rao-1 and Rao-3 algorithms provided the power losses of 10.005 MW and 9.770 MW, respectively. Results of the proposed Rao algorithms and optimal control variable settings are presented in Table 14. Table 16 compares the simulation results of this case as obtained by the proposed Rao algorithms and other methods reported in recent literature. The OPF results shown in Table 16 demonstrate the superiority of the Rao-2 algorithm over Rao-1 and Rao-3, as well as the other competitors. The power loss convergence characteristic of Case 10 is presented in Figure 8.

Table 16. Case 10: RPLM results in the IEEE 57-bus system.

Algorithm	Power Loss (MW)	Time (s)
Rao-3	9.7590	131.26
Rao-2	9.7660	132.18
Rao-1	10.005	135.77
TSA [17]	12.473	76.17
SSA [19]	11.321	81.17
SKH [34]	10.6877	-
MSO [37]	12.7435	-
CKHA [49]	11.1224	-

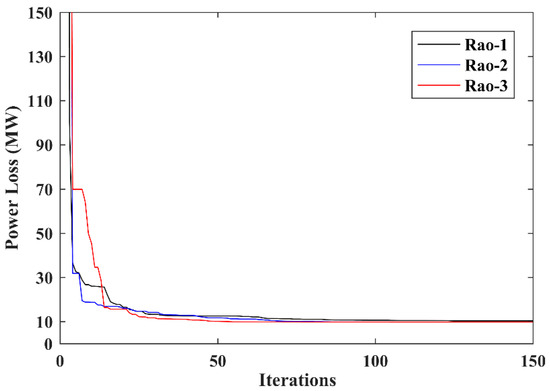
Figure 8. Convergence characteristic for the IEEE 57-bus system, Case 10.

4.3. IEEE 118-Bus System

To demonstrate the scalability of Rao algorithms and prove their efficacy to solve large-scale problems, all three versions of Rao algorithms were applied to solve the OPF problem in the IEEE 118-bus test system. The IEEE 118-bus test system has 54 generation units, two reactors, and 12 capacitors, 186 branches, and nine tap-changing transformers. The system data along with the control variable operating limits are given in Reference [48]. Thirty independent runs were taken using Rao algorithms to solve the OPF problem for the proposed test system and the best results obtained out of 30 trials are shown in this section.

Case 11: Fuel Cost Minimization (FCM)

In Case 11, fuel cost is selected as the primary objective as in Case 1. The minimum cost attained by the Rao-3 algorithm is 129,220.6794 $/h, while Rao-2 and Rao-1 algorithms offered the minimum fuel costs of 129,256.5242 $/h and 129,241.1787 $/h, respectively. The OPF result of the proposed Rao-3 algorithm and the optimal control variable settings are presented in Table 17. Table 18 compares the OPF results of Case 11 obtained by the proposed Rao algorithms and other methods reported in recent articles. Based on the OPF outcomes, it is clear that the Rao-3 algorithm provided the least fuel cost as compared to the other methods. This demonstrates the effectiveness of the proposed Rao-3 algorithm over Rao-1 and Rao-2 algorithms, as well as other algorithms. The fuel cost characteristics of Case 11 is presented in Figure 9.

Table 17. Optimum values of control variables of Case 11 for the IEEE 118-bus test system.

S. Number	Control Variables	Initial	Rao-3	S. Number	Control Variables	Initial	Rao-3	S. Number	Control Variables	Initial	Rao-3
1	PG1	0	0.07872	45	PG103	0.4	0.33181	89	VG77	1.006	1.00706
2	PG4	0	0.07685	46	PG104	0	0.24175	90	VG80	1.04	1.02122
3	PG6	0	0.0662	47	PG105	0	0.06467	91	VG85	0.985	1.03344
4	PG8	0	0.1337	48	PG107	0	0.0083	92	VG87	1.015	1.01663
5	PG10	4.5	4.27188	49	PG110	0	0.03809	93	VG89	1.005	1.02186
6	PG12	0.85	0.58259	50	PG111	0.36	0.33608	94	VG90	0.985	0.9779
7	PG15	0	0.02101	51	PG112	0	0.18375	95	VG91	0.98	0.96364
8	PG18	0	0.00159	52	PG113	0	0.00423	96	VG92	0.99	1.0142
9	PG19	0	0.00782	53	PG116	0	0.0008	97	VG99	1.01	0.98147
10	PG24	0	0.0178	54	VG1	0.995	1.02416	98	VG100	1.017	1.03575
11	PG25	2.2	2.1492	55	VG4	0.998	1.03241	99	VG103	1.01	1.05908
12	PG26	3.14	2.84427	56	VG6	0.99	1.03808	100	VG104	0.971	1.05774
13	PG27	0	0.31058	57	VG8	1.015	0.97062	101	VG105	0.965	1.05895
14	PG31	0.07	0.09645	58	VG10	1.05	0.9431	102	VG107	0.952	1.05859
15	PG32	0	0.00434	59	VG12	0.99	1.05326	103	VG110	0.973	0.96628
16	PG34	0	0.17751	60	VG15	0.97	1.01875	104	VG111	0.98	0.95313
17	PG36	0	0.32141	61	VG18	0.973	1.0552	105	VG112	0.975	0.94652
18	PG40	0	0.46268	62	VG19	0.962	1.02694	106	VG113	0.993	1.03236
19	PG42	0	0.68702	63	VG24	0.992	1.04181	107	VG116	1.005	0.97069
20	PG46	0.19	0.25232	64	VG25	1.05	1.04186	108	T5–8	0.985	0.9002
21	PG49	2.04	1.87987	65	VG26	1.015	0.95537	109	T26–25	0.96	1.03159
22	PG54	0.48	0.30277	66	VG27	0.968	1.03944	110	T30–17	0.96	0.9885
23	PG55	0	0.74996	67	VG31	0.967	1.03063	111	T38–37	0.935	0.95581
24	PG56	0	0.35764	68	VG32	0.963	1.02981	112	T63–59	0.96	1.09927
25	PG59	1.55	1.53703	69	VG34	0.984	1.02045	113	T64–61	0.985	0.91596
26	PG61	1.6	1.65333	70	VG36	0.98	1.03052	114	T65–66	0.935	1.08267
27	PG62	0	0.09242	71	VG40	0.97	0.98601	115	T68–69	0.935	0.90129
28	PG65	3.91	3.98068	72	VG42	0.985	0.97303	116	T81–80	0.935	1.0949
29	PG66	3.92	3.33319	73	VG46	1.005	1.03671	117	QSh5	0	0.0397
30	PG70	0	0.12369	74	VG49	1.025	1.00562	118	Qsh34	0	0.13264
31	PG72	0	0.04355	75	VG54	0.955	0.96514	119	Qsh37	0	0.29284
32	PG73	0	0.01357	76	VG55	0.952	0.98114	120	Qsh44	0	0.22743
33	PG74	0	0.05	77	VG56	0.954	0.96645	121	Qsh45	0	0.16846
34	PG76	0	0.05541	78	VG59	0.985	1.04398	122	Qsh46	0	0.01255
35	PG77	0	0.05941	79	VG61	0.995	1.05939	123	Qsh48	0	0.00779
36	PG80	4.77	3.5775	80	VG62	0.998	1.05898	124	Qsh74	0	0.27942
37	PG85	0	0.12274	81	VG65	1.005	0.96444	125	Qsh79	0	0.01159
38	PG87	0.04	0.01293	82	VG66	1.05	1.05809	126	Qsh82	0	0.3
39	PG89	6.07	4.56372	83	VG69	1.035	1.04551	127	Qsh83	0	0.15625
40	PG90	0	0.06063	84	VG70	0.984	0.94113	128	Qsh105	0	0.13484
41	PG91	0	0.01788	85	VG72	0.98	0.94008	129	Qsh107	0	0.26686
42	PG92	0	0.05746	86	VG73	0.991	0.94036	130	Qsh110	0	0.01831
43	PG99	0	0.00446	87	VG74	0.958	1.00781
44	PG100	2.52	2.33746	88	VG76	0.943	0.96203
								Fuel Cost ($/h)		131,220.0208	129,220.6794
								TVD (p.u)		1.4389	1.5416
								PLoss (MW)		132.8101	109.1203
								QLoss (MW)		782.6073	745.9912
								PG69 (slack bus)		513.8101	471.2005

Table 18. Case 11 (FCM) results in the IEEE 118-bus system.

Algorithm	Fuel Cost ($/h)	Time (s)
Rao-3	129,220.6794	164.19
Rao-2	129,256.5242	169.24
Rao-1	129,241.1787	167.33
GPU-PSO [1]	129,627.03	-
IMFO [38]	131.8200	-
PSOGSA [50]	129,733.58	-

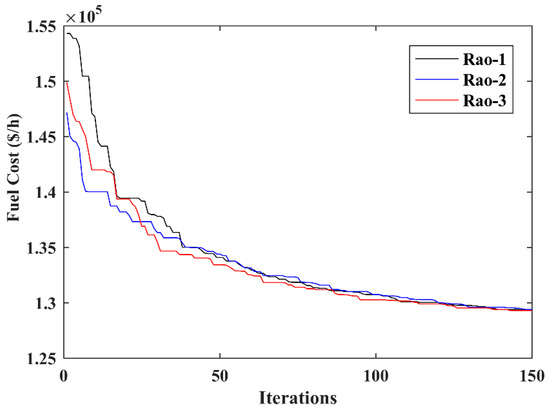
Figure 9. Fuel cost convergence characteristic of Rao algorithms for Case 11.

5. Statistical Comparison of Rao-1, Rao-2, and Rao-3

Table 19 presents a statistical summary of 30 independent runs performed using three variants of Rao algorithms.

Table 19. Statistical analysis of the various cases using the Rao algorithms.

Algorithm	Best	Worst	Mean	Standard Deviation	Best	Worst	Mean	Standard Deviation
Case 1					Case 7
Rao-3	799.9683	801.8023	800.8813	0.0186	41,659.2621	41,674.4259	41,669.0213	1.7866
Rao-2	799.9918	801.9718	800.9032	0.0203	41,872.0668	41,894.0668	41,887.0668	2.2906
Rao-1	800.4391	802.1403	801.2391	0.0223	41,771.1088	41,782.4437	41,776.6512	2.1860
Case 5					Case 10
Rao-3	3.0675	3.1182	3.0714	0.0288	9.7590	9.8460	9.7971	0.0318
Rao-2	3.1086	3.1761	3.1271	0.0360	9.7660	9.8541	9.8065	0.0339
Rao-1	3.3041	3.4065	3.3389	0.0408	10.0050	10.9451	10.4515	0.0351
Case 6					Case 11
Rao-3	0.2126	0.2246	0.2206	0.0166	129,220.6794	129,440.3458	129,331.6023	4.0910
Rao-2	0.2040	0.2065	0.2048	0.0131	129,256.5242	129,541.2740	129,402.0961	4.7350
Rao-1	0.2037	0.2049	0.2043	0.0110	129,241.1787	129,511.7206	129,381.4028	4.5210

6. Conclusions

In this paper, newly developed algorithm-specific parameter-less optimization techniques, through Rao algorithms, are proposed to solve the OPF problem. The suggested Rao algorithms were found to be superior to other EC/SI-based methods, as these algorithms do not involve tuning the algorithm-specific parameters. Various objectives considered for solving the OPF problem in this paper included the minimization of fuel cost, minimization of total voltage deviation, enhancement of voltage stability under normal and contingency conditions, minimization of real power loss, and minimization of emission cost.

To demonstrate the efficacy of the Rao algorithms and their capacity to solve OPF problems in different scale power systems with complex constraints and large dimensions, the algorithms are applied on the standard IEEE 30-bus system with 24 control variables, the IEEE 57-bus system with 33 control variables, and the IEEE 118-bus system with 130 control variables. The simulation results achieved by the proposed Rao algorithms were compared with recently developed optimization algorithms, which proved superiority in most cases of the proposed Rao algorithms, particularly Rao-2 and Rao-3 algorithms in terms of robustness and quality of solutions. The results confirm their capability to solve complex optimization problems as well as large dimensional OPF problems. As the proposed Rao algorithms are parameter tuning-free and are capable of solving complex and large dimensional OPF problems, they can be employed to solve OPF problems in practical power systems.