Abstract
Distribution networks are currently subject to a huge revolution in terms of assets being installed. In particular, the massive spread of renewable energy sources has drastically changed the way of approaching the grid. For example, renewables affected (i) the production of the legacy power plants, (ii) the quality of the supplied energy, decreasing it, (iii) the fault detection and location, etc. To mitigate the significant drawbacks of the renewables’ presence, several intelligent electronic devices have been (and are being) developed and installed among the grid. The aim is to increase grid monitoring and knowledge of its status. However, considering the significant number of nodes of the distribution network, compared to the transmission one, the process of installing new equipment is not effortless and is also quite expensive. This work aims at emphasizing a new concept of distributed monitoring systems, based on the phasor measurement unit’s current measurements, and a controlling algorithm to exploit it. The idea underneath the work is to avoid the out-of-service time needed and the costs associated with the installation of voltage sensors. Therefore, this paper describes an algorithm that exploits measurements from existing equipment and current measurements from PMUs to obtain information on the load and the node voltages. The algorithm is then tested on simulated power networks of increasing complexity and verified with an uncertainty evaluation. The results obtained from the simulation confirm the applicability and effectiveness of the algorithm and the benefits of a current-based monitoring system.
1. Introduction
It is well known that distribution and transmission networks (DN and TN, respectively) have different characteristics and they must be treated accordingly. For example, TNs typically consist of long transmission lines and a few-nodes structure. On the contrary, DNs have thousands of nodes and a meshed structure that contains short branches and a multitude of loads [1]. Such differences among the two types of networks are even more emphasized when their monitoring and control is considered. As a matter of fact, the spread of renewable energy sources (RES) in the low and medium voltage (LV and MV, respectively) portions of the network has some drawbacks that must be considered. For example, (i) RES are changing the typical DN power flow, which is monodirectional, to a bidirectional one [2]; (ii) the unprogrammed availability of produced energy results in dispatchment problems with the traditional power plants [3]; (iii) the electronic devices typically used associated with RES to adjust voltage and power levels are the most famous source of disturbances that affect power quality (PQ) [4,5].
To address these problems the DN is being instrumentalized with energy meters, phasor measurement units (PMUs), and all kinds of intelligent electronic devices (IEDs). This way, system operators (SOs) may have a higher awareness of the status of the network, resulting in countermeasures to face and solve PQ issues and other undesired conditions [6].
The problem associated with the massive deployment of IEDs among the DN is the availability of accurate and cheap sensors to be used as the source of information to be sent to the IEDs. The accuracy is needed to collect reliable voltage and current measurements, which are the inputs of typical algorithms that monitor and control the network [7,8,9,10]. However, this is an aspect that is addressed by the standards associated with the new generation of sensors, the low-power instrument transformers (LPITs). In particular, the standard containing the general aspects in terms of accuracy (but not limited to it) is the IEC 61869-6 [11].
As for the cheapness of the sensors and the IEDs, it is a key aspect that must be considered because of the above-mentioned peculiar topology of the DN. In other words, considering the number of nodes involved, if the distributed measurement system (DMS) is expensive, SOs will not deploy it, or they will just install it in a few key nodes. In addition to the costs of the instrumentation to be installed, a DMS developer should also consider the costs for the SOs of installation and the associated outages of service for the affected customers. This part of the cost, most of the time, is several orders of magnitude greater than the one needed for the instrumentation.
To this purpose, this paper starts from this idea of costs reduction for the SOs, to develop a DMS concept based only on current measurements. The DMS is based on measurements collected from PMUs and asynchronous equipment already available in the field. Afterward, the collected measures are used to run an ad hoc developed algorithm that estimates the phase of the voltage in each node of the network. Of course, the idea of using current measurements for running algorithms for network monitoring is not new. As described in [12,13,14,15,16,17], several methods have already been presented. However, they typically rely on (i) pseudo measurements, (ii) information on the network impedances, (iii) voltage phasors among the network, and (iv) other a priori information. The added value of this work is that none of the previously listed information is needed, even if it can be a posteriori added to increase the level of knowledge of the network. In other words, this article aims at emphasizing the idea of using only current measurements to perform the management and control of the network (which is difficult to find in the literature).
In light of the above, the algorithm is tested on two different simulated networks. First of all, a simple 4-nodes network was used to understand the idea underneath the algorithm. Second, the well-known IEEE 13-bus test feeder [18] was used as a benchmark grid to confirm the algorithm’s applicability to whatever kind of network. Afterward, an uncertainty evaluation, based on the Monte Carlo method (MCM) was performed considering the typical accuracy classes of the instrument transformers (ITs). Note that assessing the uncertainty propagated by an algorithm due to the contributions of uncertainty that affect its input quantities is crucial for the algorithm validation.
Finally, from the results it is possible to confirm all the benefits resulting from the current-based DMS (hence, from the output of the work): (i) reduction of the installation costs and penalties attributed to the DSOs for the energy not supplied; (ii) availability of reliable and accurate load profiles 24/7 to enhance the forecasting activities, (iii) estimates of the voltage profiles thanks to typical already-installed equipment, (iv) increasing monitoring for faster fault detection and location, which is fundamental for the prestige of a DSO, (v) PQ improvement thanks to the current behavior awareness.
The remainder of the work is structured as follows. Section 2 presents the motivation and the algorithm considered in this study. The DMS and the benchmark power networks are detailed in Section 3. In Section 4, instead, the algorithm is tested and validated through the uncertainty evaluation. Finally, the main achievements and future applications are collected in Section 5.
2. Motivation and Algorithm
2.1. Motivation
One of the main goals of a SO is to manage the grid in the most efficient way. This includes cost reduction for all those unnecessary activities. Therefore, considering the number of costs that a SO has to face [19], one of the potential ways of expenditure limitation is reducing the installation costs. This expenditure item could be significant and most of the time predominant compared to the devices to be installed. The reason is that for all critical or voltage-related activities, the considered portion of the network must be powered off during the entire duration of the installations. Furthermore, this operation results in penalty fees for the DSO and a disservice for the affected customers.
Consequently, this paper focuses on a current-based DMS which relies only on current measurements in order to avoid all the aforementioned limitations and costs. In addition, another goal is to emphasize the idea that a lot of information related to the network can be extracted starting from current measurements.
For example, most of the faults are current-based or detectable by monitoring the current. Therefore, a completely observable grid from the current perspective becomes a more reliable grid in which predictive maintenance and seasonal fault detection can be performed [20,21,22,23,24]. Another example concerns the PQ. In fact, depending on the load, the current might be subjected to distortions in addition to the main component (50 or 60 Hz). Therefore, acquiring the current measurements from the network helps SOs’ analysis of the anomalies source [25,26,27,28].
2.2. The Algorithm
This section is dedicated to the description of the algorithm developed for the DMS. The goals of the algorithm are mainly two:
- Current monitoring and load profile generation.
- Phase estimation of the voltage at the load nodes.
The first goal is achieved considering that the measuring device is a PMU and, according to its standard IEC 60255 [29], the reporting rate varies from one to hundreds of frames per second. Such reporting rates are perfectly suitable for generating load current profiles. In fact, as typically found in the literature [30,31], the information on the load is commonly known or forecasted every 15 min up to every hour. Therefore, the current measures collected from the PMU will directly populate the desired outcome.
As for the second goal, the estimate of the voltage phase is obtained by merging the information coming from the PMU with the one coming from already installed and asynchronous devices like the smart termination and the rilevatore di guasto direzionale e misure (RGDM) [32,33]. The first device is a combined voltage and current sensor installed in the cable termination arriving at the secondary substation. The latter device, instead, is an IED that collects voltage and current measurements and gives information to the protection devices. However, the RGDM is not synchronized with the GPS and hence, it does not provide information on the absolute phase of voltages and currents. This is mainly due to the GPS unavailability in most of the substations, which can be either underground or in places where there is limited connection.
Consequently, the PMU provides the information on the current phasor every 1 s (for the sake of clarity), giving the absolute phase. Instead, the RGDM sends to the SO the information on the phase displacement between the current and the voltage () every 15 min. Such a value, like all the others coming from the RGDM, is an average value of measurements performed every second. The RGDM also provides the timestamp associated with the 15 min results, even if not synchronized with the GPS. Therefore, the estimate of the voltage phase is obtained averaging the phase values measured by the PMU and summing it to given by the RGDM:
With this estimation process the distribution of the load is intrinsically obtained, treated as a random variable, and hence the distribution of the voltage phase.
3. Distributed Monitoring System
This section describes the two considered networks for the algorithm application and testing. In detail, Section 3.1 describes a simple 4-nodes portion of the network while Section 3.2 contains the algorithm implementation in the well-known IEEE 13-bus test feeder.
3.1. Four-Nodes Network
3.1.1. Description
One of the two networks considered in this work is quite simple, and it is shown in Figure 1. The choice of a simple network has been taken to emphasize more the concept behind the article, than the achievable complexity which is theoretical and as demonstrated with the example in Section 3.2, has no limits.
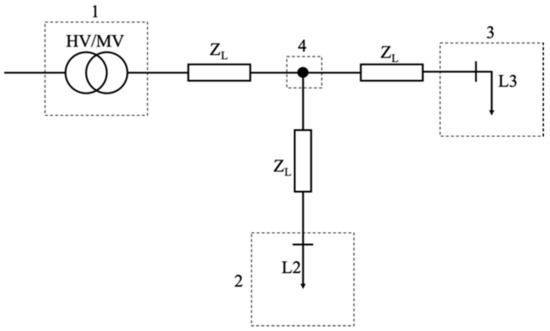
Figure 1.
Equivalent single-phase schematic of the considered 4-nodes network.
Figure 1 shows a 4-nodes structure in which Node 1 is the high to medium voltage transformer (HV/MV); Node 2 and Node 3 are passive nodes with variable loads (L2 and L3, respectively) which can be considered as simple customers or secondary substations; and Node 4 is a conjunction node in which all the currents of the circuit pass through. Finally, ZL is the line impedance modeled with the series of a resistor and an inductor (R-L impedance). Such a choice is the common one for DNs.
More details on the amplitude of the considered quantities are given in Section 4, in which the algorithm validation is described.
3.1.2. DMS Positioning and Comments
The idea behind the work is the implementation of DMSs which only perform current measurements. This is to avoid the need for interrupting the voltage supply every time a new installation is performed. Furthermore, the information coming from the current measurements is more significant, for different purposes, than the voltage ones because they reflect the load variations and conditions. This is even more emphasized if the current measurements are coming from a synchronized instrument like a PMU. In fact, the synchrophasors would provide measurements that could be used in combination with all the others coming from the PMU installed among the grid.
To this purpose, in the considered network of Figure 1, we adopted PMUs as measurement devices for the DMS. Furthermore, the best placement of the PMU, just one for the network of Figure 1, is Node 4. This way, the three currents of the network are fully monitored.
The presence of only current measuring devices may be considered not enough for the implementation of a DMS. However, in light of the actual situation of the network, some comments are necessary. First, primary substations (Node 1 in Figure 1) are typically equipped with accurate instrumentation to collect voltage and current measurements. This is necessary to fully monitor a key network location like the primary substation. Second, all of them and sometimes even the secondary substations are interconnected through the SCADA system; hence, an existing communication system or database is commonly present and used by SOs. Third, and in particular for the Italian case, most of the secondary substations (Node 2 and 3 in Figure 1) are already equipped with smart terminations and RGDM (as abovementioned).
As a final remark, note that whatever algorithm developed for the DN must match and consider the actual conditions of the grid to avoid inapplicable solutions and to maximize the exploitable information.
3.2. IEEE 13-Bus Test Feeder
3.2.1. Description
Figure 2 depicts the IEEE 13-bus test feeder, which is a common benchmark network used by researchers and SOs to simulate the DN. Overall, the network operates at 4.16 kV (the voltage level is not significant in the context of this work) and has quite short branches. On the contrary, it is relatively highly loaded, and it contains a single voltage regulator at the substation, overhead and underground lines, shunt capacitors, an in-line transformer, and unbalanced loading. Between nodes 671 and 692 there is also a breaker, which is not used for the tests described in Section 4. In detail, nine loads can be found inside the network, of which one is distributed between Node 632 and Node 671 while the others are loads localized at specific nodes.
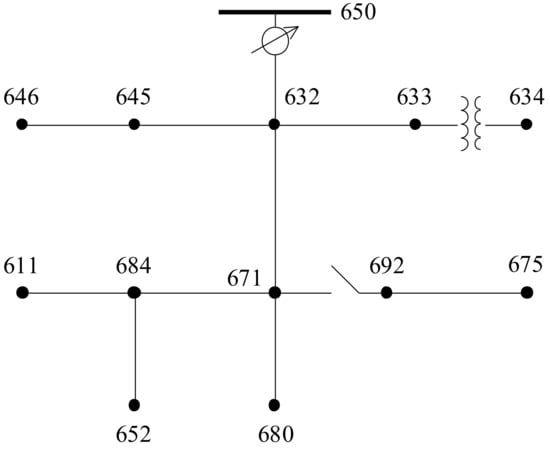
Figure 2.
Equivalent single-phase schematic of the IEEE 13-bus test feeder.
As for the two transformers, the main 115 kV/4.16 kV, 2500 kVA one is located at the top of the network at Node 650. The second transformer instead decreases the MV to LV levels with a ratio of 4.16 kV/0.48 kV. It features 500 kVA of rated power, and it is located after Node 633.
Considering that all the information on the grid can be found in [18], only the significant information is briefly recalled.
Table 1 contains distances between the nodes, while Table 2 collects the load at the specific nodes, presented in terms of active and reactive power per phase (Ph-1, Ph-2, and Ph-3).

Table 1.
Distances between each node of the network. (See [18]).

Table 2.
Load, in terms of active and reactive powers, at each node. (See [18]).
With the same logic, Table 3 lists the distributed loads between each couple of nodes of the network.

Table 3.
Load, in terms of active and reactive powers, between each couple of nodes. (See [18]).
3.2.2. DMS and Comments
The IEEE 13-bus test feeder has been chosen for the algorithm implementation due to its topology and completeness. In fact, it contains common and diverse elements which can be found in every DN. It is also a suitable benchmark network to prove that what is presented for the 4-node case can be extended to almost all kinds of networks.
Another comment to be made on the network in Figure 2 concerns observability. As a matter of fact, the minimum number of PMUs that provide sufficient information to the SO is 2. Such two PMUs are optimally placed in Node 632 and 684 if one considers the breaker open time higher than the close time. On the contrary, if the aim is the full observability of the network, a potential PMU placement would be at the nodes 645, 633, 671, 611, and 675. This results in five PMUs observing a 13 nodes network (38% of nodes observed). Note that these results are obtained on an electrotechnical and experience base and do not involve any ad hoc placement algorithm.
4. Validation
The first part of this Section 4.1, is dedicated to the tests on the 4-node network. The aim is to verify, in a multitude of conditions, the applicability of the algorithms and the robustness of the results. Afterward, Section 4.2 contains a simple extension of what is presented in Section 4.1 but on the most complex network. Finally, Section 4.3 presents an uncertainty propagation study aimed at assessing the contribution of the uncertainty sources on the measured quantities.
4.1. Four-Nodes Network
4.1.1. Simulation Details
What is described in the previous section has been validated by means of the Simulink environment of MatLab®. The schematic of Figure 1 has been recreated with the characteristics listed in Table 4. Two notes on the values inside the table: (i) the voltage supply refers to Node 1 which is the injection node. The initial phase for this node is set to zero. Of course, any initial phase angle can be attributed to the reference node, without affecting the results; therefore, the choice is just for the sake of simplicity (of simulation and reading). The simulation step, instead, is set to 10 μs to simulate common data acquisition systems, acquiring at 100 kSa/s, capable of measuring voltages and currents in the PQ frequency range. The distribution line distances among the nodes (1-4, 4-2, and 4-3) are all set to 5 km considering an average value of the distribution lines. Furthermore, the length of the lines is a variable that does not affect the effectiveness of the algorithm; in fact, such lengths are quite different from those used for the IEEE 13-bus feeder.

Table 4.
Simulation details for the 4-node network.
Turning to the loads of the network, the selected power factors (PFs) are 0.9 and 0.8 for L2 and L3, respectively. This choice has been made considering the fines applied by the SOs to the customers if the PF is lower than those values. Additionally, note that the PF is a quantity that may vary in shorter time intervals compared to the 15 min variations. Furthermore, it is a quantity coming from the RGDM, hence it is not a variable that has to be estimated, and it is the average of a 15 min measurement window.
As for the load profiles, the core choice of the simulation has been selected according to the literature. In [34,35,36] it has been demonstrated how in DNs the load has variations up to 100 % during the day and smooth variations of 30 min time intervals are considered. A final note, as anticipated, in literature it is possible to find several works dealing with the load profile monitoring. It is quite common that the time between acquisition lies between 30 min and 1 h. However, despite such a time, PMUs are an order of magnitude faster. Therefore, they will always be the PMUs acquisitions to be down-sampled to those of the other devices if comparisons or computations must be performed.
4.1.2. Simulation Tests
The aim of the tests was to assess whether the algorithm was effectively following the load profile variation in different configurations.
Considering the 15 min interval between the outputs of the RGDM, the load profiles have been set with one limited variation every 15 min for 50 times. The load variations involve both the active and reactive parts so that the PF is kept constant for the entire simulation, as explained above. L2 and L3 have different load profiles to increase the coherence of the simulation with reality. To run the tests, three pairs of load profiles, referred to as A, B, and C have been used. They are depicted in Figure 3. As can be seen, the p.u. notation is adopted to focus on the load variations, which are diverse, and include several potential cases.
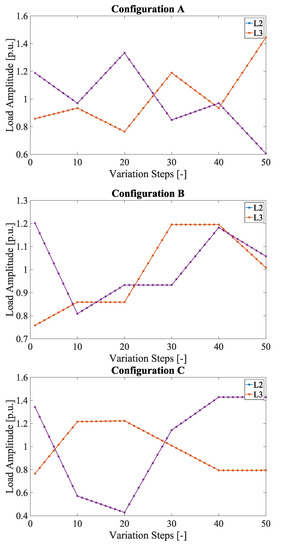
Figure 3.
Load profiles for L2 and L3 for the three configurations (A–C).
Inside each step variation of the load, the simulated PMU extracts 100 synchrophasor of the currents of the circuit, namely , , and for the current between nodes 1-4, 4-2, and 4-3, respectively. Instead, the simulated RGDM saves only one value of in each of the 50 steps.
A final note on the simulation duration, as detailed in Table 4, the 15 min per 50 times duration has been compressed and scaled to a 10 s simulation.
4.1.3. Simulation Results
The first result is simply aimed at emphasizing the usefulness of a PMU in the load profile assessment and recording. For this purpose, Figure 4 shows the comparison between the power variation of the load and the current being measured by the PMU (in one of the treated cases). Consequently, the current-based DMS would introduce benefits for all the load forecasting and load profile generation algorithms that typically use data with time intervals around 15–45 min. On the contrary, the increasing amount of data—resulting from the higher reporting rate of a PMU—will emphasize a new problem that is being currently faced by DSOs and utilities: data storage. However, this problem is easily addressed with specific techniques that pre-process data and keep only the significant information.
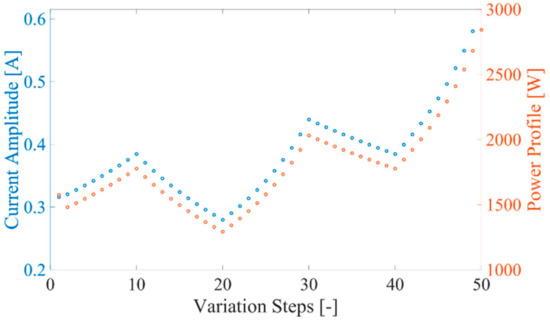
Figure 4.
Comparison between the power load profile and the current measured by the PMU.
The main results are presented in Figure 5, Figure 6, Figure 7 and Figure 8, in which the estimated voltage phase in nodes 2 and 3 is compared with the reference voltage phase obtained from the simulation model. Considering the coherence among the results, for case A both results are shown in Figure 5 and Figure 6, while one case for each configuration has been included for configurations B and C (Figure 7 and Figure 8). In detail, the voltage phase of L3 is presented for configurations A, B, and C, in Figure 6, Figure 7 and Figure 8, respectively.
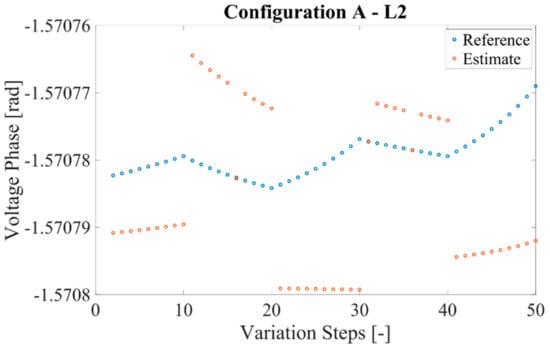
Figure 5.
Reference and estimate of the voltage phase for configuration A and L2.
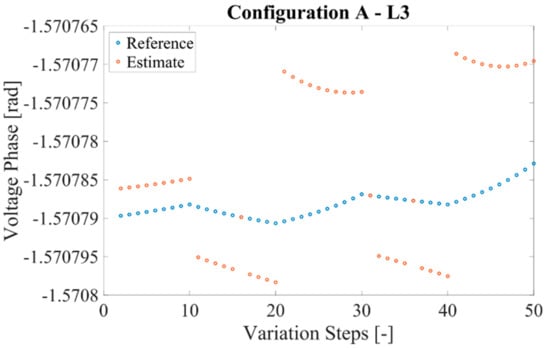
Figure 6.
Reference and estimate of the voltage phase for configuration A and L3.
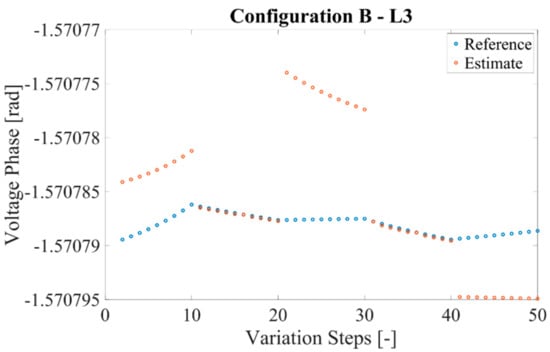
Figure 7.
Reference and estimate of the voltage phase for configuration B and L3.
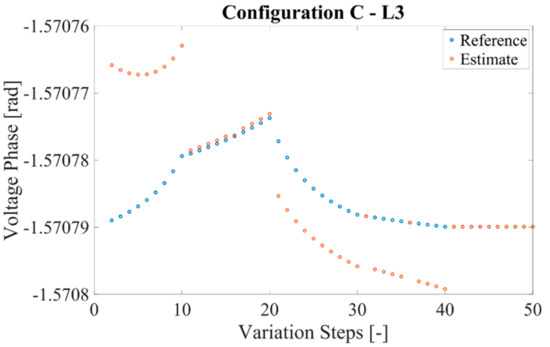
Figure 8.
Reference and estimate of the voltage phase for configuration C and L3.
Note from the graphs how the estimates match with the reference values, for all the considered configurations. This means that the estimated phase may be used by the SOs to assess the voltage on that specific node and potentially intervene with countermeasures.
A comment is required on the behavior of the estimates. From the graph, it can be noted slight discrepancies while the load is varying. This can be attributed to the constant variation of the load, obtained modifying the simulation’s parameters, which highlights the computational limits of the simulator. However, all the obtained discrepancies with respect to the reference value are in the order of tens of microradian. Such a value is certainly negligible compared to the typical accuracies of the sensors deployed in the field and a good result considering the source of the information, which is for half, asynchronous.
From the results of the tests performed on the 4-node network, it can be concluded that current-based DMSs allow the gathering of crucial information from the grid. In particular, considering that almost all MV or LV customers have energy meters connected to their loads, the information of the current can be combined with the available powers coming from them. Furthermore, the current monitoring allows the creation of ad-hoc load profiles for each customer, resulting in better planning and managing of the generation sources for the SOs.
Finally, DSOs should find a trade-off between the level of detail and the reporting rate of the monitored quantities, and the data amount, costs, and accuracy associated with them. At present, and confirmed by literature and experience, DSOs adopt reporting rates (from power and energy meters) ranging from 15 min to 1 h. Such information can be interpreted as obstacles to the deployment and use of new instrumentation and IEDs.
4.2. IEEE 13-Bus Test Feeder
In this second part of the validation tests, the algorithm is implemented on the IEEE 13-bus test feeder.
4.2.1. Simulation Details
An overview of the Simulink schematic representing the IEEE 13-bus test feeder is depicted in Figure 9.
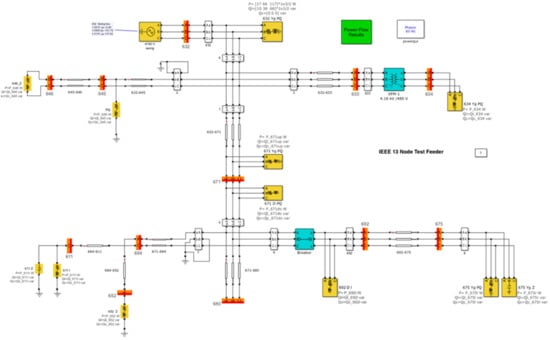
Figure 9.
Overview of the Simulink schematic representing the IEEE 13-bus test feeder.
In addition to the network details described in Section 3.2.1, the simulation is run for 1 s and at 60 Hz. The idea is to test as many different values as possible (considering both the benchmark networks) to confirm the wide applicability of the presented concept. Furthermore, considering the good results obtained for the 4-node network, in this set of tests the burdens are kept constant to the values listed in Table 2 and Table 3.
4.2.2. Simulation Tests
By referring to the schematic of the IEEE 13-bus network in Figure 2, and considering its topology and involved assets, the outputs of the simulation tests are the phases at nodes 634, 645, 684, and 692. The reasons for that are easily explained:
- Node 680 is just a terminal; no load is connected.
- Nodes 652 and 611 are loads connected with a very short wire to Node 684. Therefore, combining the two burdens the information on Node 684 can be found.
- Between Node 633 and 634 there is a transformer; therefore, considering negligible the phase distortion that it introduces, the phase of the voltage at node 633 can be obtained.
- There are no loads between Node 692 and Node 675. Therefore, the voltage phase of the two nodes differs by the amount introduced by the line impedance. Such contribution can be easily removed for the sake of algorithm validation (or corrected if a SO knows its line impedances).
To obtain what is above described, a realistic network configuration would involve 2 PMUs, one in Node 632 and one in Node 671.
4.2.3. Simulation Results
The results of the simulation described in Section 4.2.2 are presented in Table 5. It contains, for each node and each phase the estimated phase of the voltage and the reference one obtained from the simulation . The last column of the table shows the error between two such values (), calculated as the difference between the estimated and reference value.

Table 5.
Estimated and reference value of the node voltage phases.
As can be seen from the results, the estimates are fully coherent with the reference values. This confirms the applicability of the method. Furthermore, in absolute terms, the discrepancies between the values are negligible compared to the typical accuracy characteristics of the assets involved in the measurement chain (PMU, sensors, energy meters, etc.). This aspect is explored in the next section.
Other comments from the results, also in light of those obtained in the 4-nodes configurations, are that the algorithm is independent of (i) the number of phases of the network, (ii) the voltage level, (iii) the types and PF of the loads, (iv) the operating frequencies, (v) the number of nodes, and (vi) the length of the branches.
The results also support the adoption of current DMSs to perform monitoring and predictive maintenance. In fact, up to now, the state estimation algorithm is mainly focused on voltages. However, the information of the current phasor is crucial to obtain full awareness of the load profiles and the current levels of each cable. Furthermore, with a simple algorithm like the one above illustrated and tested; it is possible to extend the knowledge of the network, obtaining an accurate estimate of the voltage phase in each node.
4.3. Uncertainty Propagation
4.3.1. Introduction
This section concludes the paper with a focus on a critical aspect as far as measurements are concerned. In fact, the uncertainty propagation, through the measurement chain used for an application, is fundamental (even if based on preliminary assumptions) to assess the quality of the results. For example, the uncertainty associated with the results, due to the measurement chain, may become greater than the sensitivity required to an algorithm of method. Therefore, when a new method, algorithm, or approach is developed it is fundamental to perform an uncertainty evaluation that avoids presenting meaningless results.
So, in this section the results obtained in Section 4.1 are analyzed considering the contribution to the uncertainty in a real measurement chain. In particular, for the considered network the sources of uncertainty are:
- The sensors used to measure the currents used by the PMUs;
- The PMUs;
- The sensors used to measure the voltages and currents needed for the power computation (inside the RGDM or whatever energy meter).
- The energy/power meters.
Starting from the sensors for the PMUs, the final quantity of interest is the phase of the voltage at the nodes. Therefore, it is necessary to attribute uncertainty to the phase of the measured currents. This is straightforward considering that IEC 61869-10 [37] specifies limits for the ratio error and phase displacement for the low-power current transformers (LPCTs) for each specified accuracy class. Analogously, for the low-power voltage transformers, the limits are given in IEC 61869-11 [38]. Another comment on the contribution to the uncertainty is that, in accordance with common PMUs, their uncertainty is negligible compared to those of the sensors described in [37]. Hence, in the measurement chain sensor + PMU, the overall contribution to the uncertainty is considered, for the MCM purpose, one of the sensors (and in particular of the accuracy class 0.5).
As for the power/energy meters, slightly different considerations are valid. In particular, the idea is based on the evaluation of the load phase starting from the active and reactive power measurements. Therefore, the uncertainty contributions associated with those two parameters must be used. To this purpose, the limits given in IEC 50470-2 apply [39] and are used in what follows. In particular, it must be considered that the typical values provided in [39] are in order of 2–3%, hence significantly higher than those of a 0.5 accuracy class sensor. For this reason, for the measurement chain sensor + energy meter, the overall contribution to the uncertainty is considered as coming from the energy meter.
4.3.2. Monte Carlo Method
The uncertainty propagation, aimed at assessing the uncertainty associated with the phase information acquired with the PMUs and the IEDs, is performed utilizing the Monte Carlo Method.
For the sake of the simulation, LPCT with a 0.5 accuracy class has been used for the current measurements performed sent to the PMUs, and 2.5% accuracy on active and reactive power has been used for the measurements collected with the power meter.
Afterward, 100 thousand simulations were performed, in which the current phase and the active and reactive powers were corrupted with the uncertainty contributions taken from uniform distributions. Finally, the estimated voltage phase was computed along with its associated standard deviation.
The application of the MCM to the A, B, and C configurations, described in Section 4.1.2, provided interesting results. The mean standard deviation associated with the phase obtained from the PMUs was in the order of 5·10−3 rad and the one computed starting from the powers is in the order of 10−2 rad. In Figure 10 their behavior is presented, for the sake of clarity, for the configuration C and load L2.
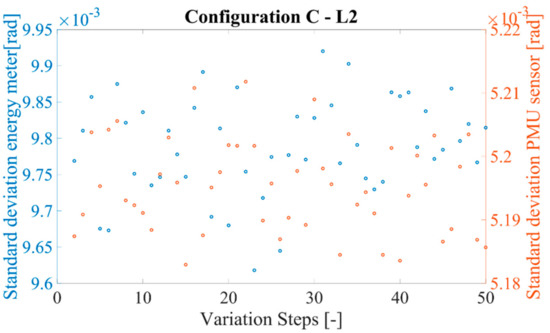
Figure 10.
Behavior of the standard deviations associated to the PMUs and power meters measurements.
From Figure 10 it can be observed that a simple device like an energy meter provides results with an uncertainty comparable with those obtained from the PMU. This is easily explained considering that the bottleneck was the sensor that made negligible PMUs contributions to the uncertainty.
Figure 11 instead presents the comparison between the estimated phase and the reference one, already shown in Figure 8, with the added information on the uncertainty.
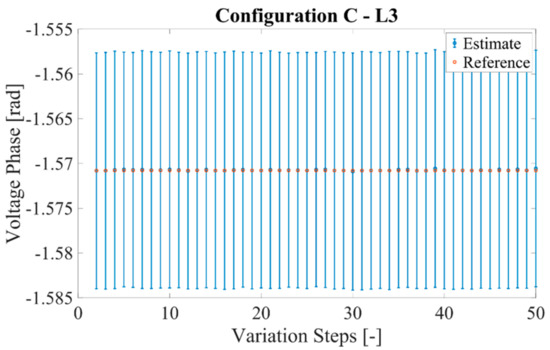
Figure 11.
Estimated and reference voltage phases of Figure 8 with the error bars obtained with the MCM.
It is clear from the picture that (i) the simulation discrepancies found in Section 4, are completely negligible compared to the overall uncertainty associated with the phase measurements, which is now in the order of tens of milliradian; (ii) the uncertainty evaluation is always crucial and very significant when a new algorithm, method, or approach must be assessed; (iii) the in-field conditions, hence the sensor contributions, are key factors that drastically change the laboratory conditions.
The aspect of the actual in-field conditions must be also emphasized. As a matter of fact, the installed devices significantly affected whatever kind of algorithm could be developed. In particular, algorithms (like the presented one) typically reach accuracies up to part per millions or higher during the simulation testing. However, as soon as the uncertainty contribution from the field is added, their efficiency is lowered by several orders of magnitude. This should change the perspective of the algorithm developers, who should better focus and immediately include the huge contribution of the measurement devices to test their solutions.
Final comments on the presented solution are as follows. On the one hand, the use of current-based DMSs allows us to obtain a double benefit for the SO: (i) cost reduction for the in-field installation, hence the possibility to install more devices, increasing the percentage of the monitored grid; (ii) monitoring of all the currents of the network, which are the key quantities to detect and locate faults, plus they allow to quantify the load profile and variations.
On the other hand, the presented algorithm has been adapted to a peculiar Italian situation. However, this, or in general, whichever algorithm can be improved if other sources of information coming from the grid are available. For example, (i) adding the knowledge of the grid impedances to the current-based DMS would allow for the estimation of the voltage drop in each branch and hence the voltage at each node; (ii) few synchronized voltage measurements would guarantee an accurate estimate of the voltage profiles; etc.
Finally, the motivation of this work is based on the author’s perspective that low-cost PMUs are starting their penetration of the market. Combining this aspect with the use of open ring current sensors (like Rogowski coils or hall effect sensors), the result can be quantified as significant savings on the device and installation costs.
5. Conclusions
The need for monitoring distribution networks is crucial for system operators. However, this need must match with the actual and in-field requirements. This typically results in excellent but not applicable solutions due to physical or economic requirements. Therefore, in this paper, we presented and supported the idea of distributed measurement systems based only on current measurements obtained without powering off the network. The study focuses on the case of current measurements obtained from synchronized instruments, such as phasor measurement units. In the paper, such a measurement system has been applied on a simple 4-nodes network and the IEEE 13-bus test feeder. Afterward, the algorithm for estimating the phase of the voltages of the network was described and tested in various load profile configurations of the two networks. From the results, it emerged that the proposed solution and algorithm effectively estimate the voltage phase in several conditions of the network. The performance of the algorithm was then evaluated by running an uncertainty evaluation process with the Monte Carlo method. This included the significant contribution to the uncertainty from the measurement devices. The uncertainty evaluation showed how the bottleneck of the algorithm is typically due to the accuracy limitation of the in-field deployed devices, and not to the algorithm itself.
Author Contributions
Conceptualization, A.M. and R.T.; methodology, R.T.; validation, L.P.; formal analysis, R.T.; investigation, A.M.; resources, L.P.; data curation, A.M.; writing—original draft preparation, A.M.; writing—review and editing, R.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by EdgeFLEX, grant number 883710. This project received funding from European Union’s Horizon 2020 research and innovation program.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Hammer, B.; Fuhr, C.; Hanson, J.; Konigorski, U. Differences of power flows in transmission and distribution networks and implications on inverter droop control. In Proceedings of the ICCEP 2019—7th International Conference on Clean Electrical Power: Renewable Energy Resources Impact, Otranto, Italy, 2–4 July 2019; pp. 46–54. [Google Scholar]
- Erick, A.O.; Folly, K.A. Reinforcement Learning Approaches to Power Management in Grid-tied Microgrids: A Review. In Proceedings of the 2020 Clemson University Power Systems Conference (PSC), Clemson, SC, USA, 10–13 March 2020; pp. 1–6. [Google Scholar]
- Antonelli, M.; Desideri, U.; Franco, A. Effects of large scale penetration of renewables: The Italian case in the years 2008–2015. Renew. Sustain. Energy Rev. 2018, 81, 3090–3100. [Google Scholar] [CrossRef]
- Dias, T.C.; Roque, L.A.A.M.; Ribeiro, P.F. Power electronics in the context of renewables, power quality and smart grids. In Proceedings of the International Conference on Harmonics and Quality of Power, ICHQP, Belo Horizonte, Brazil, 16–19 October 2016; pp. 170–175. [Google Scholar]
- Fu, Q.; Montoya, L.F.; Solanki, A.; Nasiri, A.; Bhavaraju, V.; Abdallah, T.; Yu, D.C. Microgrid Generation Capacity Design with Renewables and Energy Storage Addressing Power Quality and Surety. IEEE Trans. Smart Grid 2012, 3, 2019–2027. [Google Scholar] [CrossRef]
- Al-Badi, A.H.; Ahshan, R.; Hosseinzadeh, N.; Ghorbani, R.; Hossain, E. Survey of Smart Grid Concepts and Technological Demonstrations Worldwide Emphasizing on the Oman Perspective. Appl. Syst. Innov. 2020, 3, 5. [Google Scholar] [CrossRef] [Green Version]
- Mingotti, A.; Peretto, L.; Tinarelli, R. A novel equivalent power network impedance approach for assessing the time reference in asynchronous measurements. In Proceedings of the I2MTC 2017—2017 IEEE International Instrumentation and Measurement Technology Conference, Turin, Italy, 22–25 May 2017. [Google Scholar]
- Mingotti, A.; Peretto, L.; Tinarelli, R. An equivalent synchronization for phasor measurements in power networks. In Proceedings of the AMPS 2017—IEEE International Workshop on Applied Measurements for Power Systems, Liverpool, UK, 20–22 September 2017. [Google Scholar]
- Gao, W.; Tang, N.; Mu, X. A distribution network reconfiguration algorithm based on hopfield neural network. In Proceedings of the 4th International Conference on Natural Computation, ICNC, Jinan, China, 18–20 October 2008. [Google Scholar]
- Muhamedagic, A.; Mujezinovic, A. State estimation algorithm for radial distribution networks. In Proceedings of the ICAT 2017—26th International Conference on Information, Communication and Automation Technologies, Sarajevo, Bosna i Hercegovina, 26–28 October 2017. [Google Scholar]
- IEC 61869-6:2016. Instrument Transformers—Part 6: Additional General Requirements for Low-Power Instrument Transformers; International Standardization Organization: Geneva, Switzerland, 2016. [Google Scholar]
- Almutairi, S.; Miao, Z.; Fan, L. Performance of Branch-Current Based Distribution System State Estimation. In Proceedings of the 2018 North American Power Symposium (NAPS), Fargo, ND, USA, 9–11 September 2018; pp. 1–6. [Google Scholar]
- Baran, M. Branch current based state estimation for distribution system monitoring. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–4. [Google Scholar]
- Noopura, S.P.; Kumar, R.J.R.; Jain, A.; Jayan, M.V. Fast decoupled state estimation based on current equations. In Proceedings of the 2015 IEEE Innovative Smart Grid Technologies—Asia, ISGT ASIA, Bangkok, Thailand, 3–6 November 2015. [Google Scholar]
- Pau, M.; Pegoraro, P.A.; Sulis, S. Efficient Branch-Current-Based Distribution System State Estimation Including Synchronized Measurements. IEEE Trans. Instrum. Meas. 2013, 62, 2419–2429. [Google Scholar] [CrossRef]
- Xu, G.W.; Zheng, R.J.; Chang, K.-C. Design of Leakage Current Monitoring System for Low Voltage Power Grid Based on NB-IoT; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Yu, M.; Han, Y. Auto-monitoring System for Residual Current Circuit Breakers. IEEJ Trans. Electr. Electron. Eng. 2021, 16, 842–851. [Google Scholar] [CrossRef]
- IEEE PES AMPS DSAS Test Feeder Working Group. Available online: https://site.ieee.org/pes-testfeeders/resources/ (accessed on 25 July 2021).
- Prettico, G.; Flammini, M.G.; Andreadou, N.; Vitiello, S.; Fulli, G.; Masera, M. Distribution System Operators Observatory 2018, Overview of the Electricity Distribution System in Europe; JRC Science for Policy Report; European Commission: Ispra, Italy, 2019. [Google Scholar]
- Peretto, L.; Tinarelli, R.; Ghaderi, A.; Mingotti, A.; Mazzanti, G.; Valtorta, G.; Amoroso, G.; Danesi, S. Monitoring Cable current and Laying Environment Parameters for Assessing the Aging Rate of MV Cable Joint Insulation. In Proceedings of the 2018 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Cancun, Mexico, 21–24 October 2018; pp. 390–393. [Google Scholar]
- Alsheryani, R.M.; Alkaabi, S.S.; Alkaabi, S.S.; Aldhaheri, A.M.; Khouri, F.I.; Alharmoodi, S.I.; Alhajeri, A.S. Applying artificial intelligence (AI) for predictive maintenance of power distribution networks: A case study of al ain distribution company. In Proceedings of the 2019 International Conference on Electrical and Computing Technologies and Applications ICECTA 2019, Ras Al Khaimah, United Arab Emirates, 19–21 November 2019. [Google Scholar]
- Biasse, J.-M.; Ferraro, V.; Brun, P.; Yang, Y.; Wang, G. New features for MV switchgear are now available to move to condition based maintenance. In Proceedings of the CMD 2016—International Conference on Condition Monitoring and Diagnosis 2016, Xi’an, China, 25–28 September 2016; pp. 198–201. [Google Scholar]
- Osladil, M.; Kozubik, L. Smart asset management in view of recent analytical technologies. In Proceedings of the 2015 16th International Scientific Conference on Electric Power Engineering, EPE, Kouty nad Desnou, Czech Republic, 20–22 May 2015; pp. 60–62. [Google Scholar]
- Zavoda, F.; Lemire, R.; Abbey, C. Implementing predictive distribution maintenance using a universal controller. In Proceedings of the IEEE Power Engineering Society Transmission and Distribution Conference, Chicago, IL, USA, 14–17 April 2014. [Google Scholar]
- Bingham, R.P. Measurement instruments for power quality monitoring. In Proceedings of the 2008 IEEE/PES Transmission and Distribution Conference and Exposition, Chicago, IL, USA, 21–24 April 2008. [Google Scholar]
- Issouribehere, P.E.; Barbero, J.C.; Issouribehere, F.; Barbera, G.A. Power quality measurements in a steel industry with electric arc furnaces. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008. [Google Scholar]
- Stanciu, N.; Stanescu, D.; Szabo, W. Evaluating measurement uncertainty in electric current measurement in PQ determination. Eurocon 2013, 815–822. [Google Scholar] [CrossRef]
- Mingotti, A.; Peretto, L.; Tinarelli, R.; Zhang, J. Use of COMTRADE fault current data to test inductive current transformers. In Proceedings of the 2019 IEEE International Workshop on Metrology for Industry 4.0 and IoT, MetroInd 4.0 and IoT, Naples, Italy, 4–6 June 2019; pp. 103–107. [Google Scholar]
- IEC 60255-1:2009. Measuring Relays and Protection Equipment—Part 1: Common Requirements; International Standardization Organization: Geneva, Switzerland, 2009. [Google Scholar]
- Li, R.; Gu, C.; Zhang, Y.; Li, F. Implementation of load profile test for electricity distribution networks. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Ramos, S.; Duarte, J.M.M.; Soares, J.; Vale, Z.; Duarte, F.J. Typical load profiles in the smart grid context a clustering methods comparison. In Proceedings of the IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Gentilini, I.; Weichold, J.; Calone, R.; Bolcato, G.; Giammanco, F.; Stalder, M. The smart termination: An innovative component to enable smart grids development. In Proceedings of the 22nd International Conference and Exhibition on Electricity Distribution, Stockholm, Sweden, 10–13 June 2013. [Google Scholar]
- Mingotti, A.; Peretto, L.; Tinarelli, R.; Angioni, A.; Monti, A.; Ponci, F. A Simple Calibration Procedure for an LPIT plus PMU System Under Off-Nominal Conditions. Energies 2019, 12, 4645. [Google Scholar] [CrossRef] [Green Version]
- Besagni, G.; Vilà, L.P.; Borgarello, M. Italian Household Load Profiles: A Monitoring Campaign. Buildings 2020, 10, 217. [Google Scholar] [CrossRef]
- Pilo, F.; Pisano, G.; Troncia, M. Updated Typical Daily Load Profiles for LV Distribution Networks Customers. In Proceedings of the 2019 1st International Conference on Energy Transition in the Mediterranean Area (SyNERGY MED), Cagliari, Italy, 28–30 May 2019; pp. 1–6. [Google Scholar]
- Tang, X.; Hasan, K.N.; Milanovic, J.V.; Bailey, K.; Stott, S.J.; Sgtott, S.J. Estimation and Validation of Characteristic Load Profile through Smart Grid Trials in a Medium Voltage Distribution Network. IEEE Trans. Power Syst. 2017, 33, 1848–1859. [Google Scholar] [CrossRef]
- IEC 61869-10:2018. Instrument Transformers—Part 10: Additional Requirements for Low-Power PASSIVE Current Transformers; International Standardization Organization: Geneva, Switzerland, 2018. [Google Scholar]
- IEC 61869-11:2018. Instrument Transformers—Part 11: Additional Requirements for Low-POWER Passive Voltage Transformers; International Standardization Organization: Geneva, Switzerland, 2018. [Google Scholar]
- IEC 50470-2:2006+A1:2018. Electricity Metering Equipment (a.c.)—Part 2: Particular Requirements—Electromechanical Meters for Active Energy (Class Indexes A and B); International Standardization Organization: Geneva, Switzerland, 2018. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).