Numerical and Experimental Investigation of Internal Flow Characteristics and Pressure Fluctuation in Inlet Passage of Axial Flow Pump under Deflection Flow Conditions
Abstract
:1. Introduction
2. Experimental Setup and Uncertainty Analysis
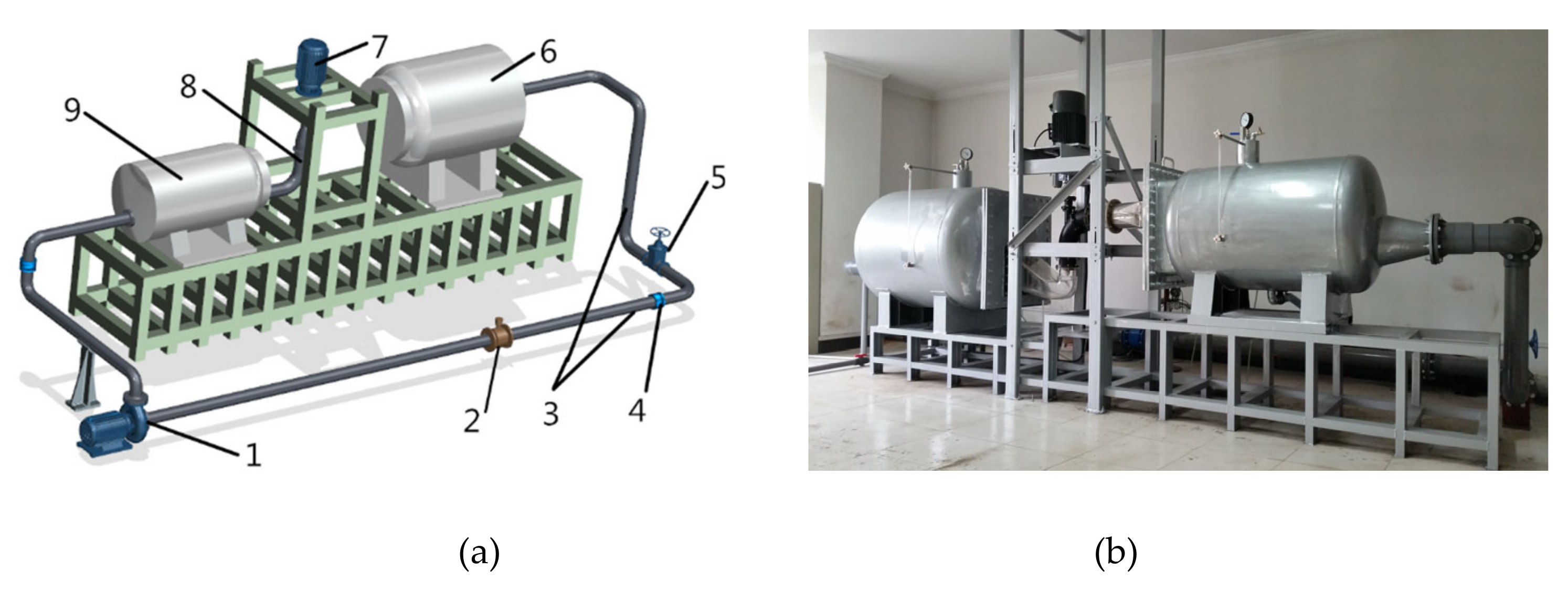
2.1. Pump Device
2.2. Uncertainty Analysis of Experiment
2.2.1. Uncertainty Analysis of Pumping System
2.2.2. Uncertainty Analysis of Pressure Fluctuation Test
3. Numerical Simulation Model and Method
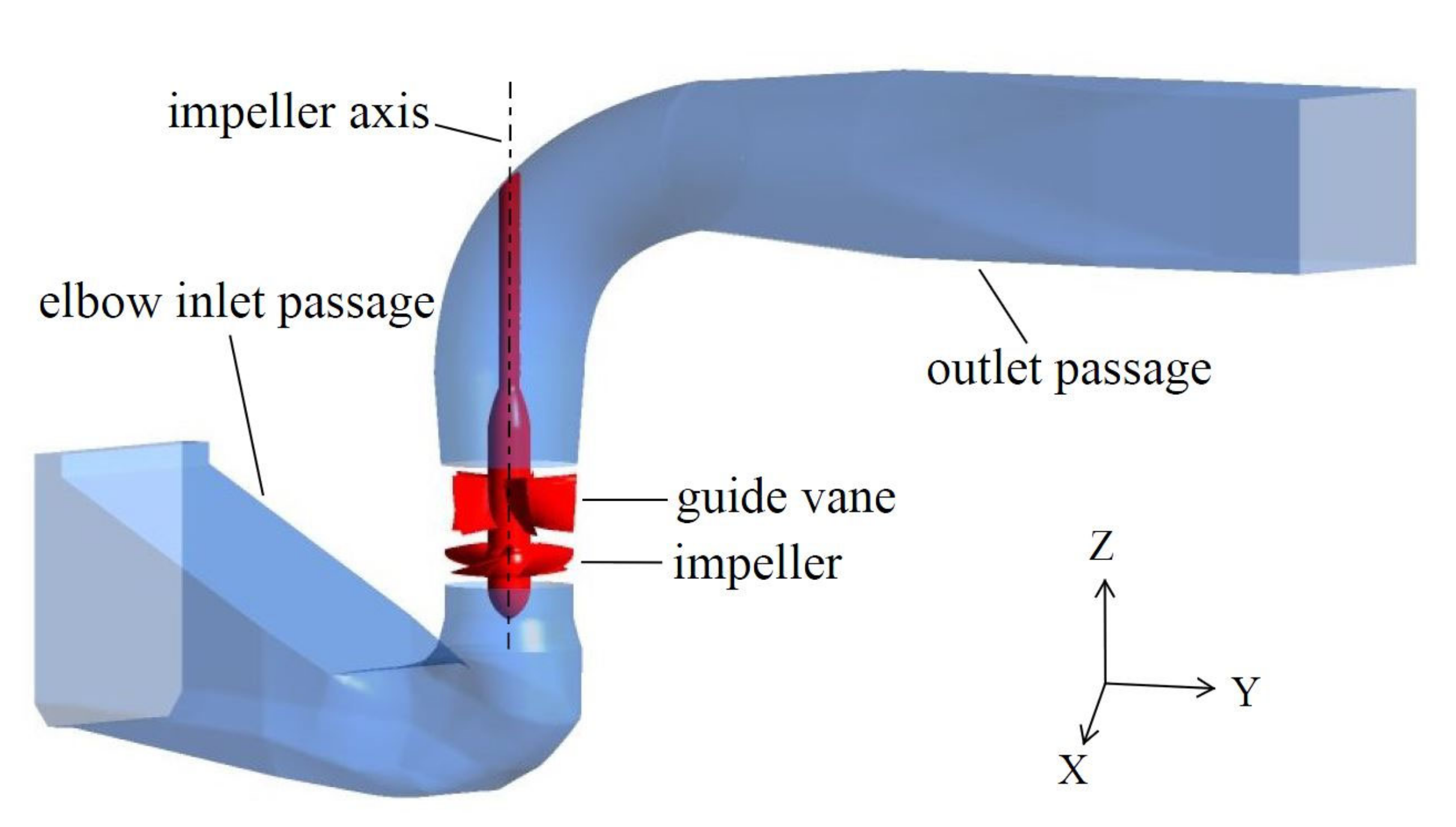
3.1. Numerical Calculation Model
3.2. Governing Equation and Turbulence Model
3.3. Boundary Condition Setting
3.4. Analysis of Grid Irrelevance of Computational Model
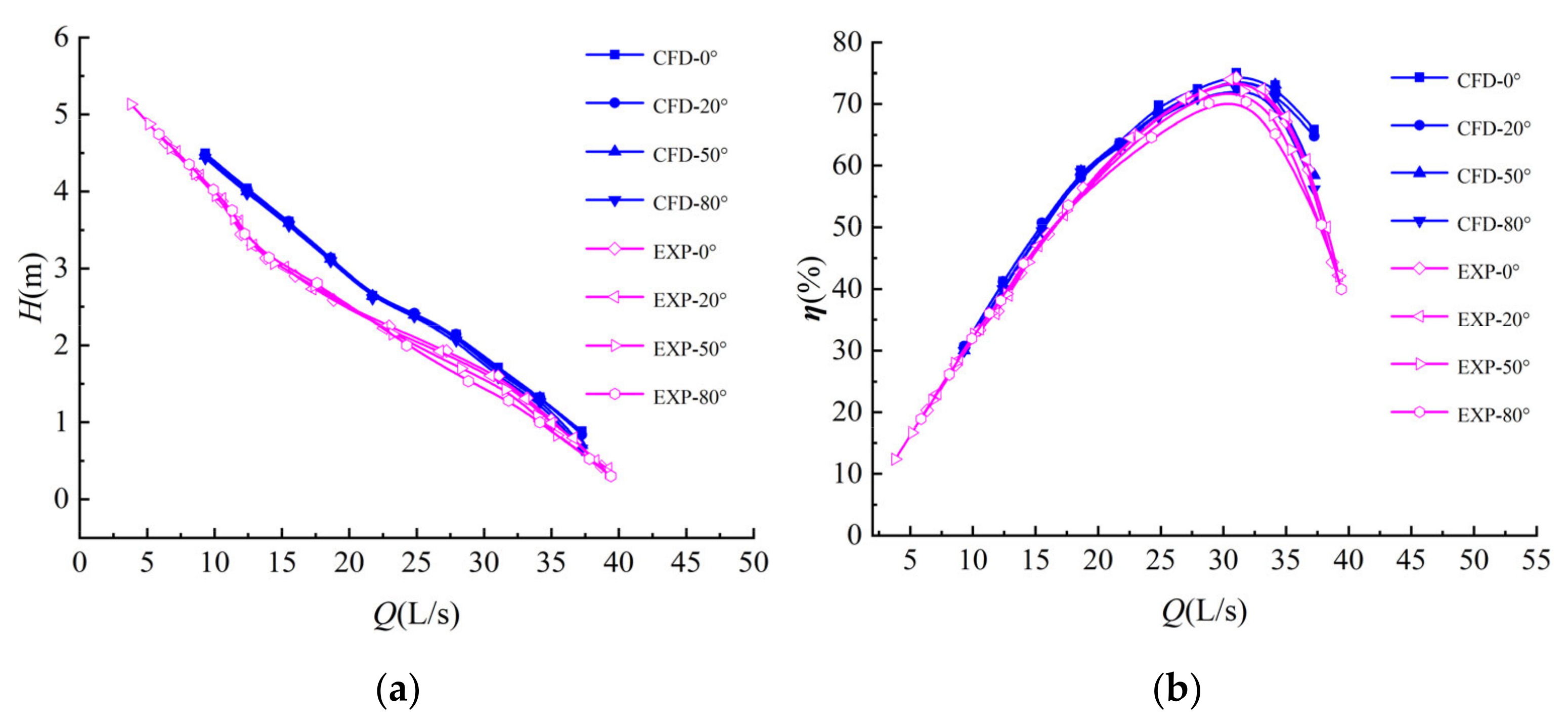
3.5. Validation of the Numerical Simulation
4. Results and Analysis
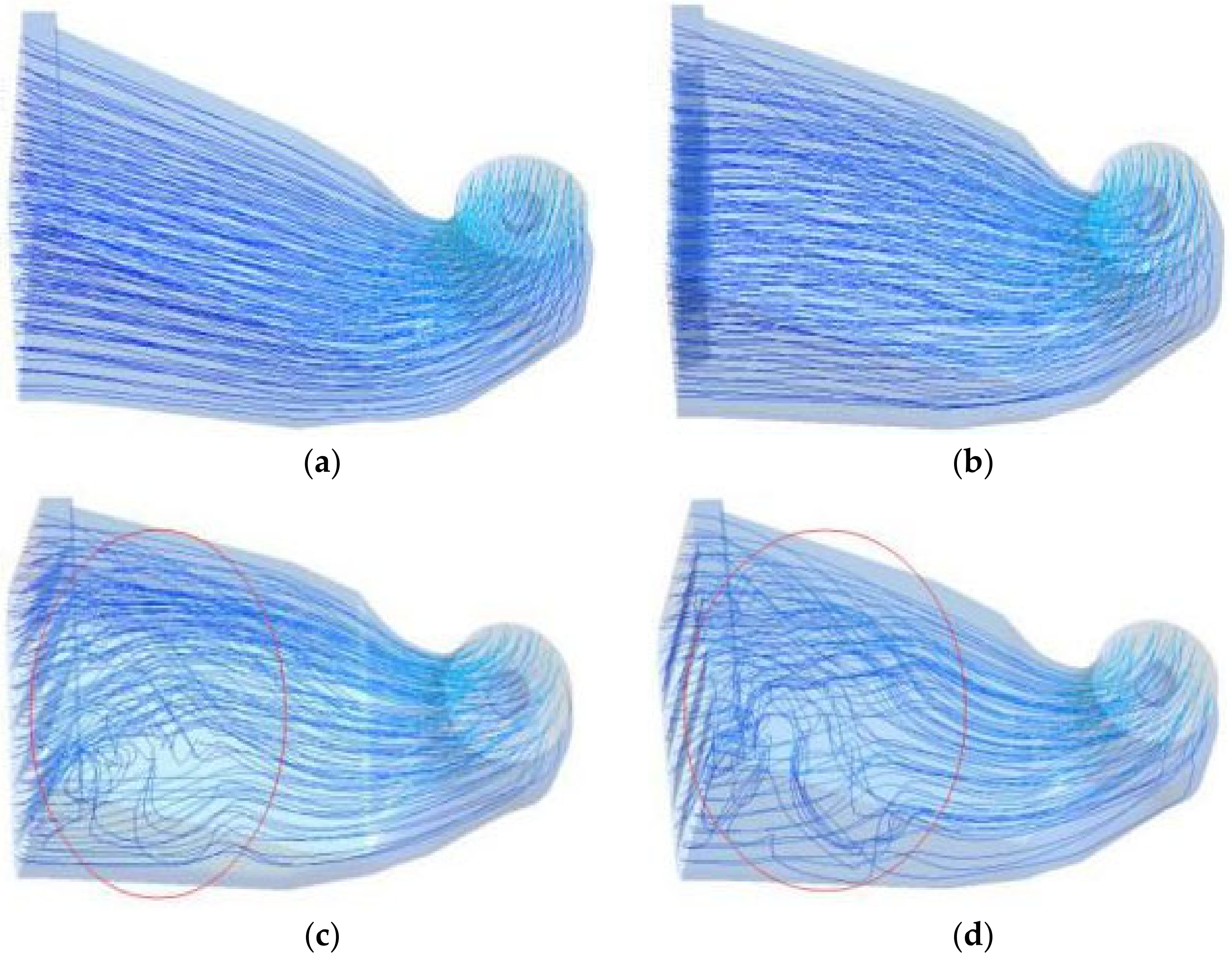
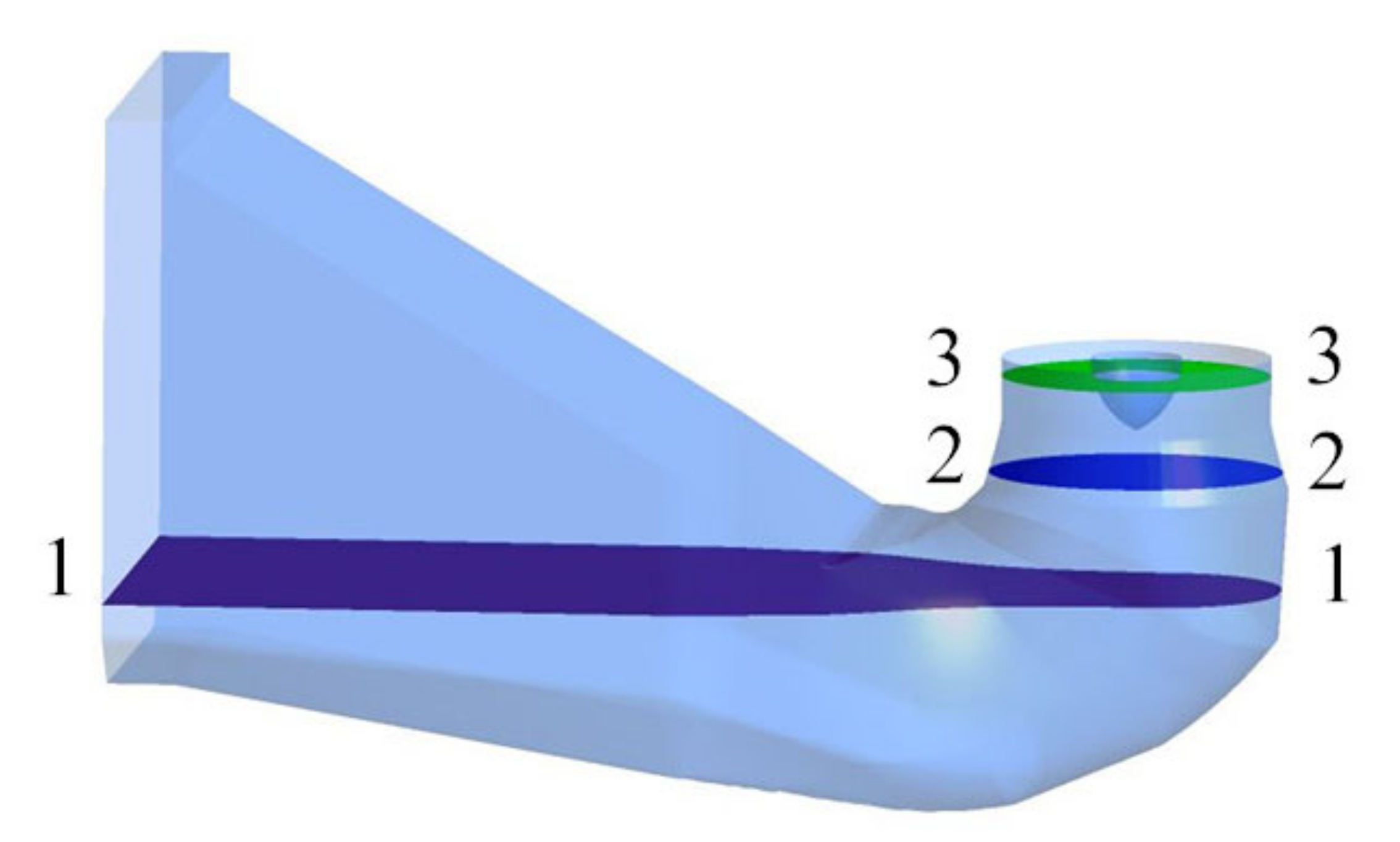
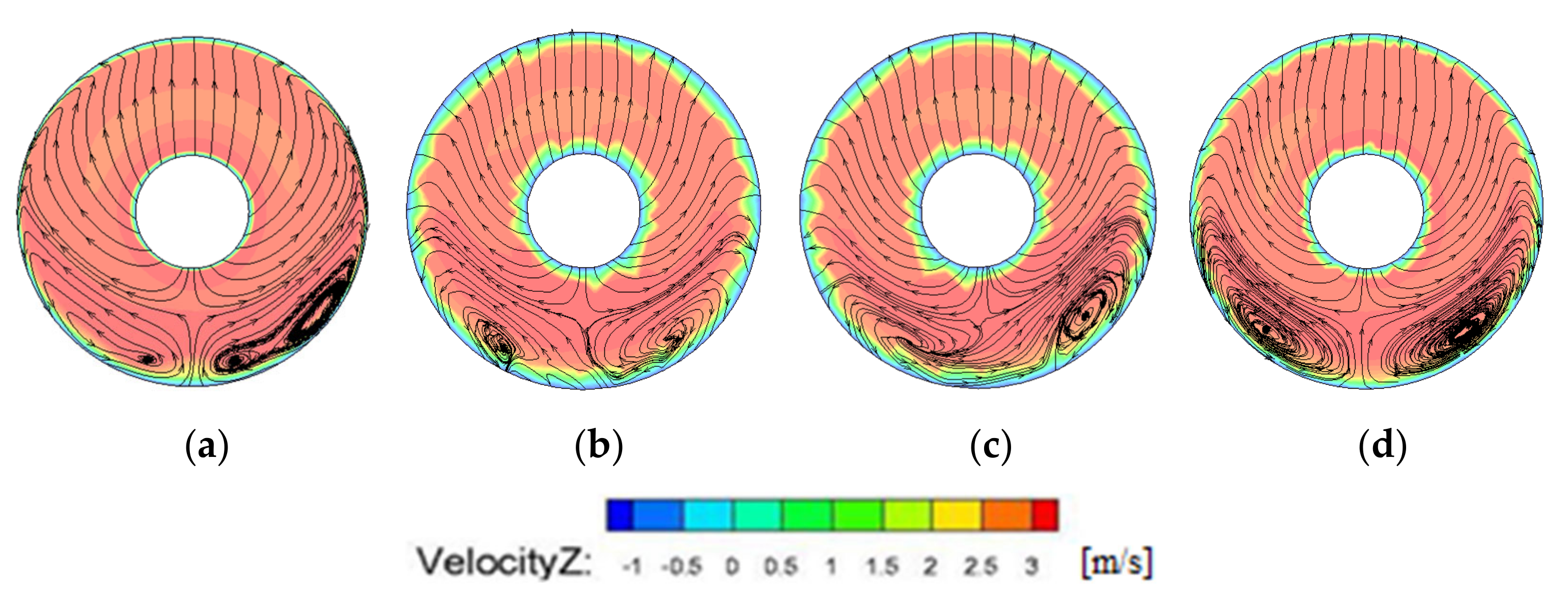
4.1. Analysis of Flow Characteristics in Inlet Passage
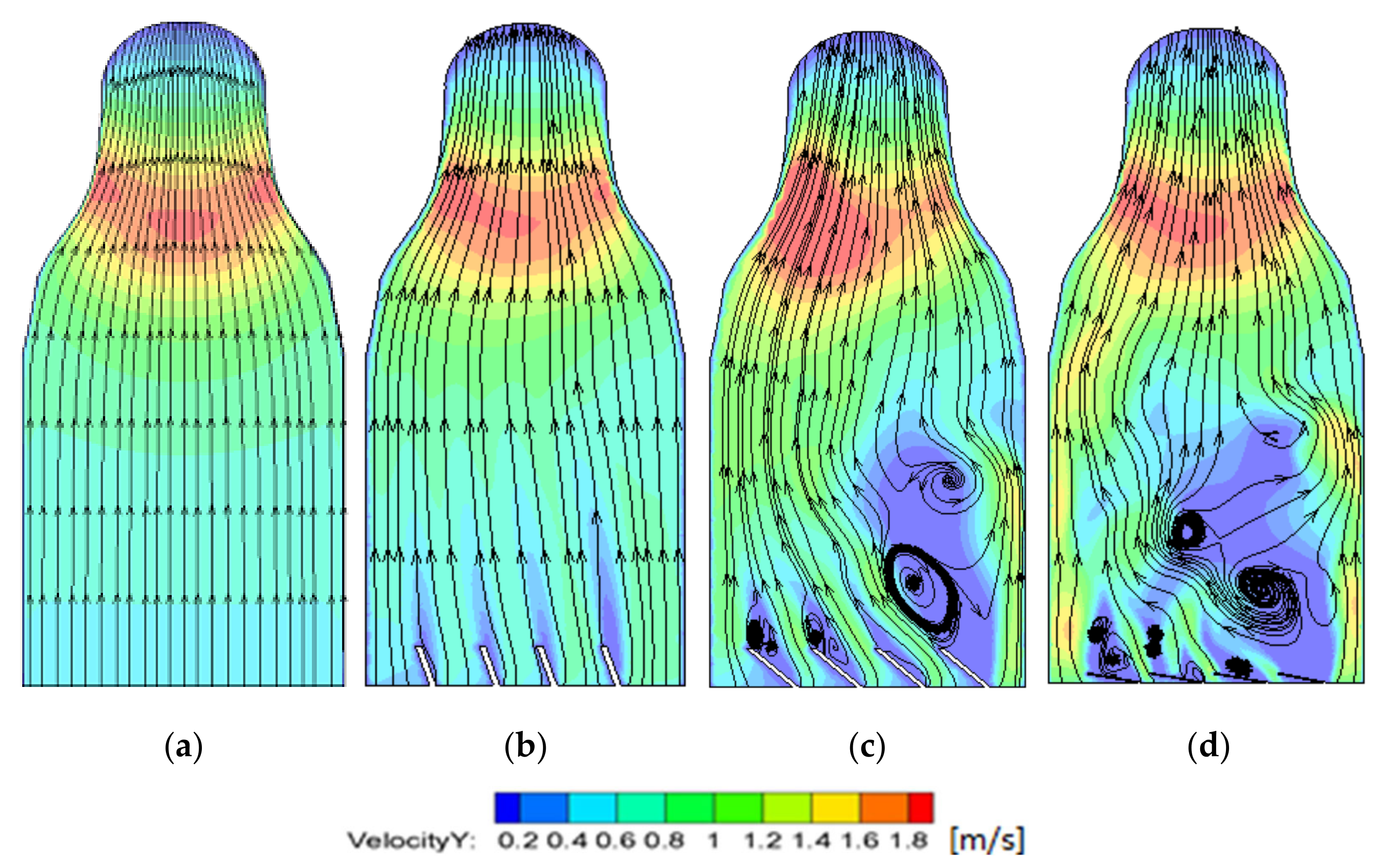
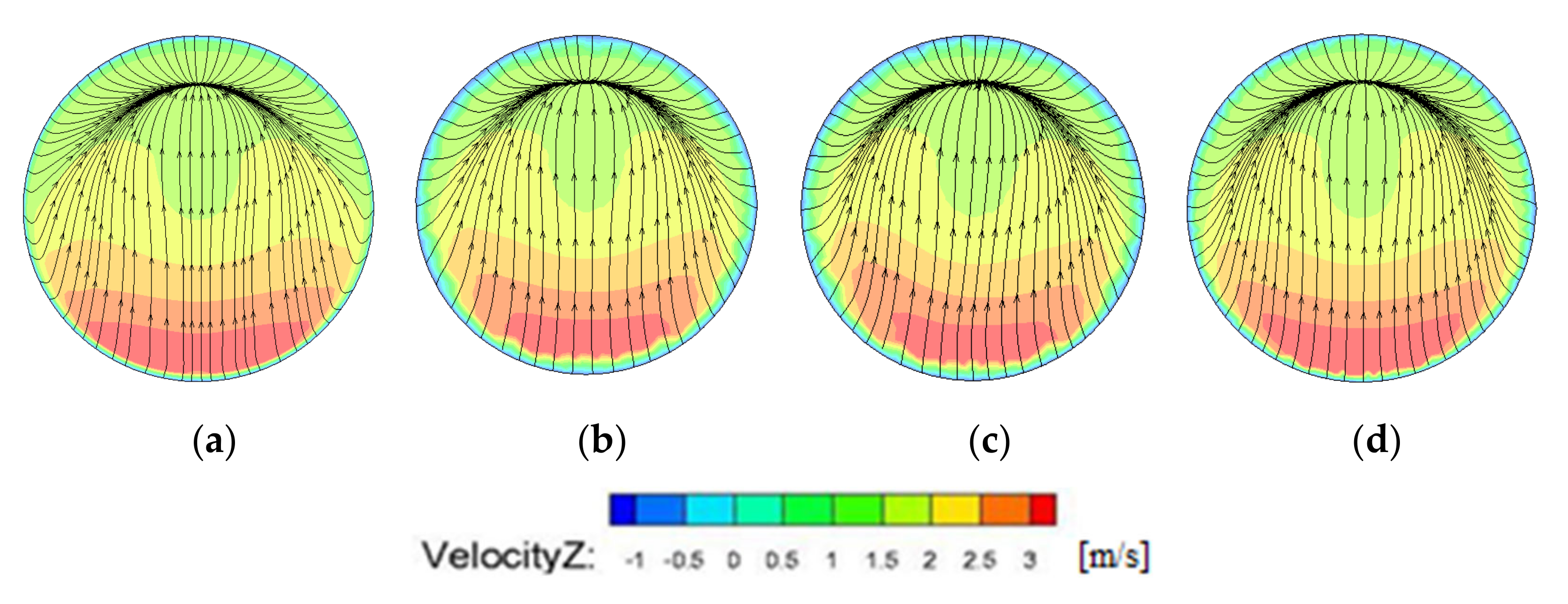
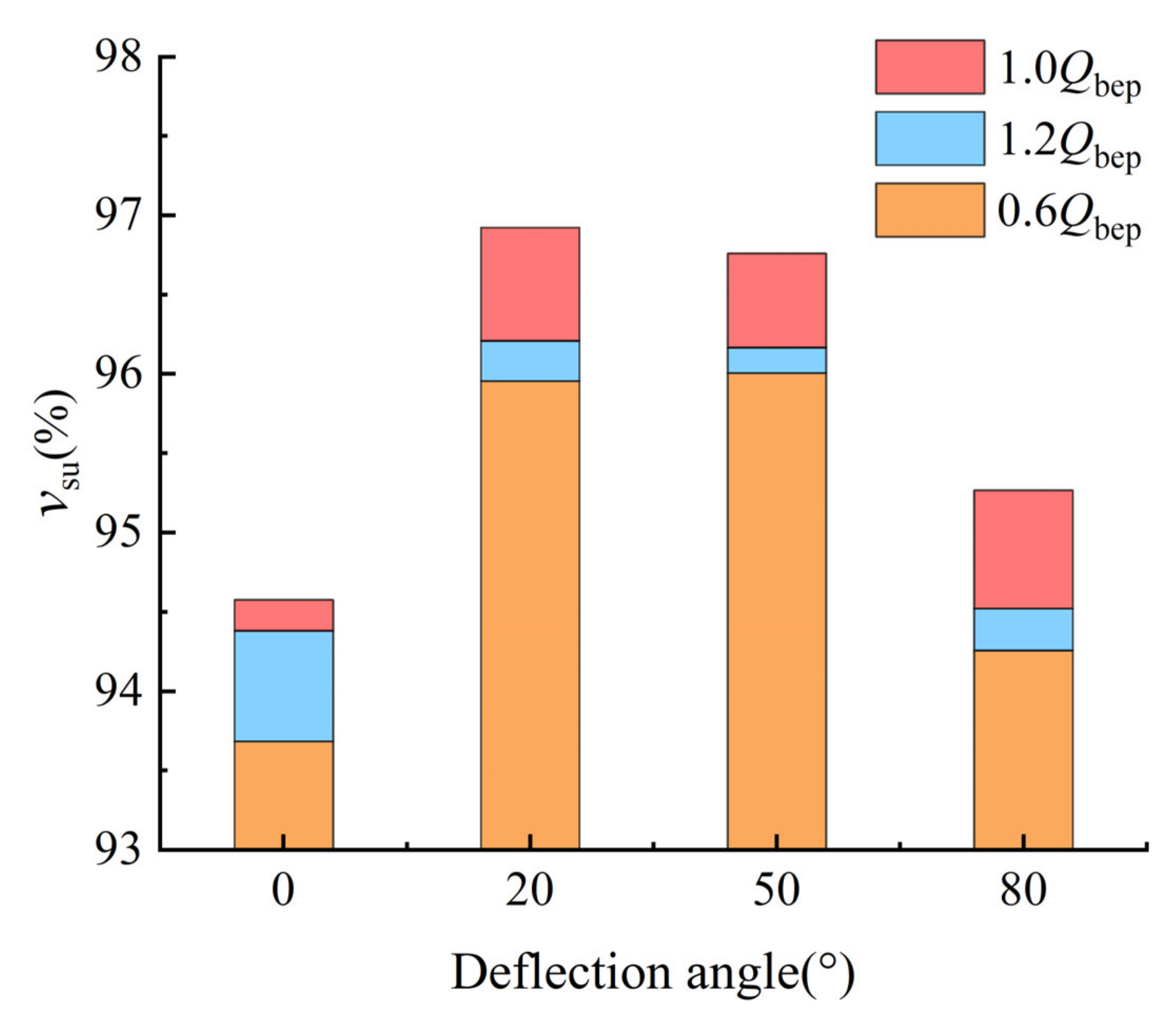
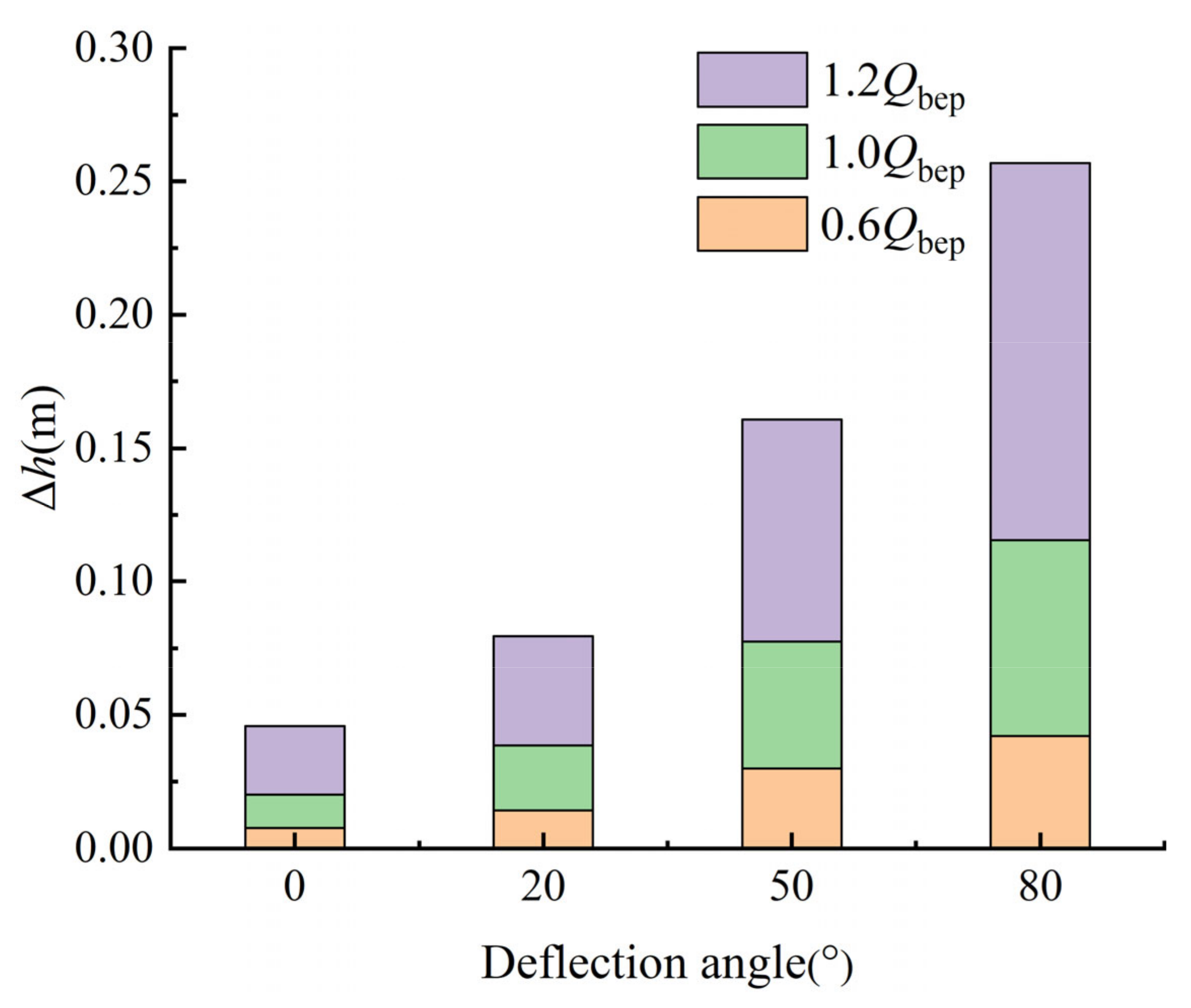
4.2. Analysis of Axial Velocity Uniformity at Outlet of Inlet Passage and the Hydraulic Loss of Inlet Passage
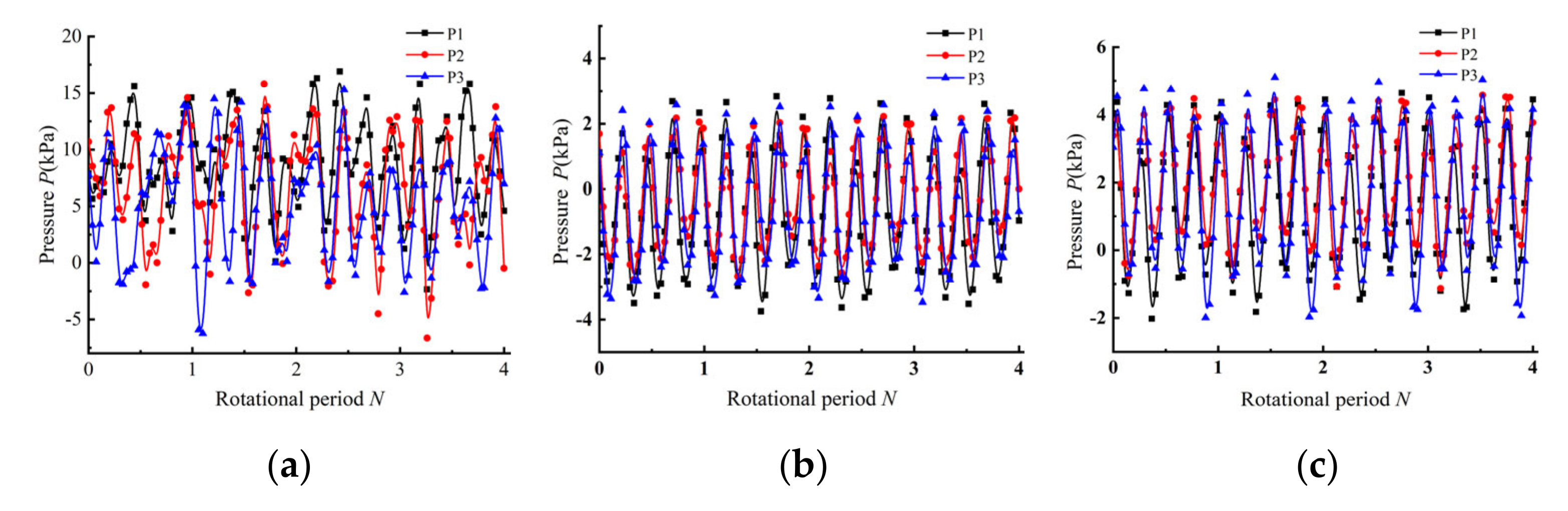
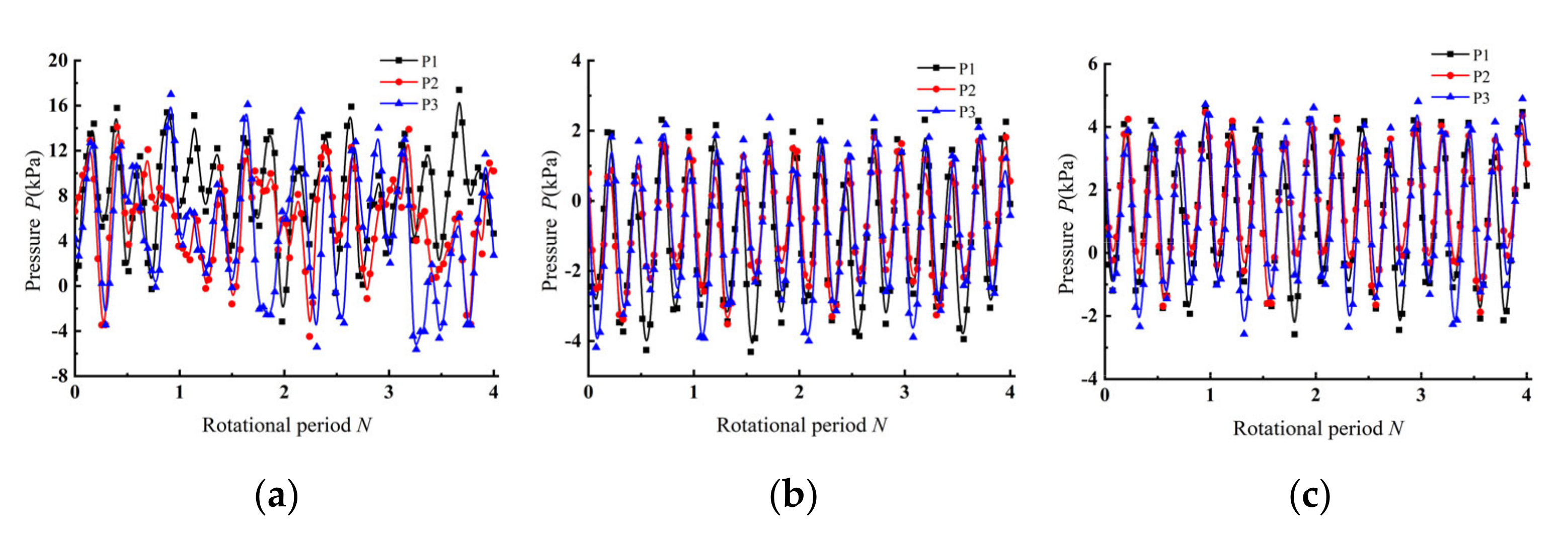
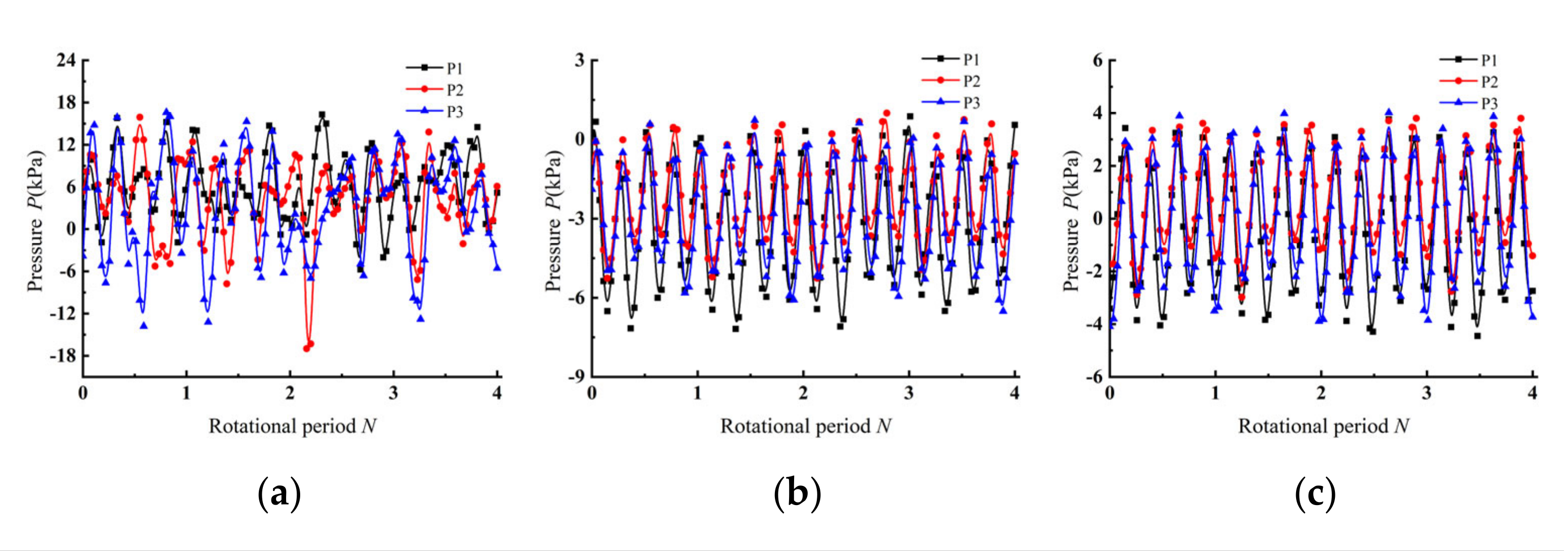
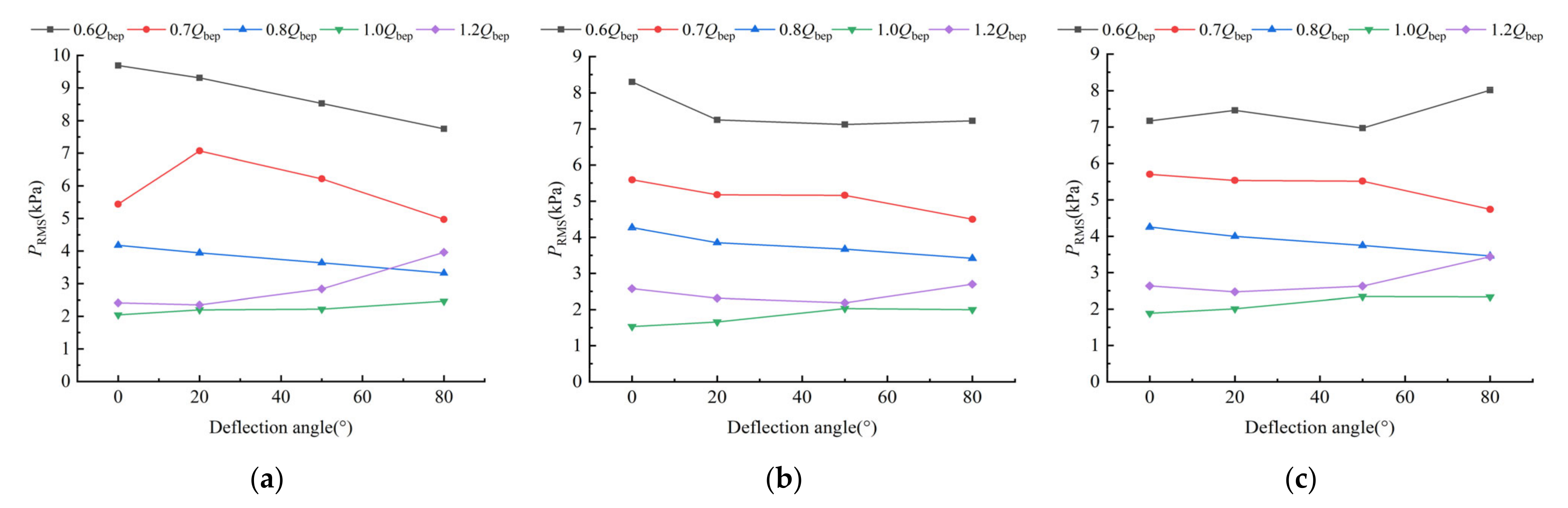
4.3. Time Domain Analysis of Pressure Pulsation at the Outlet Monitoring Point of the Inlet Passage
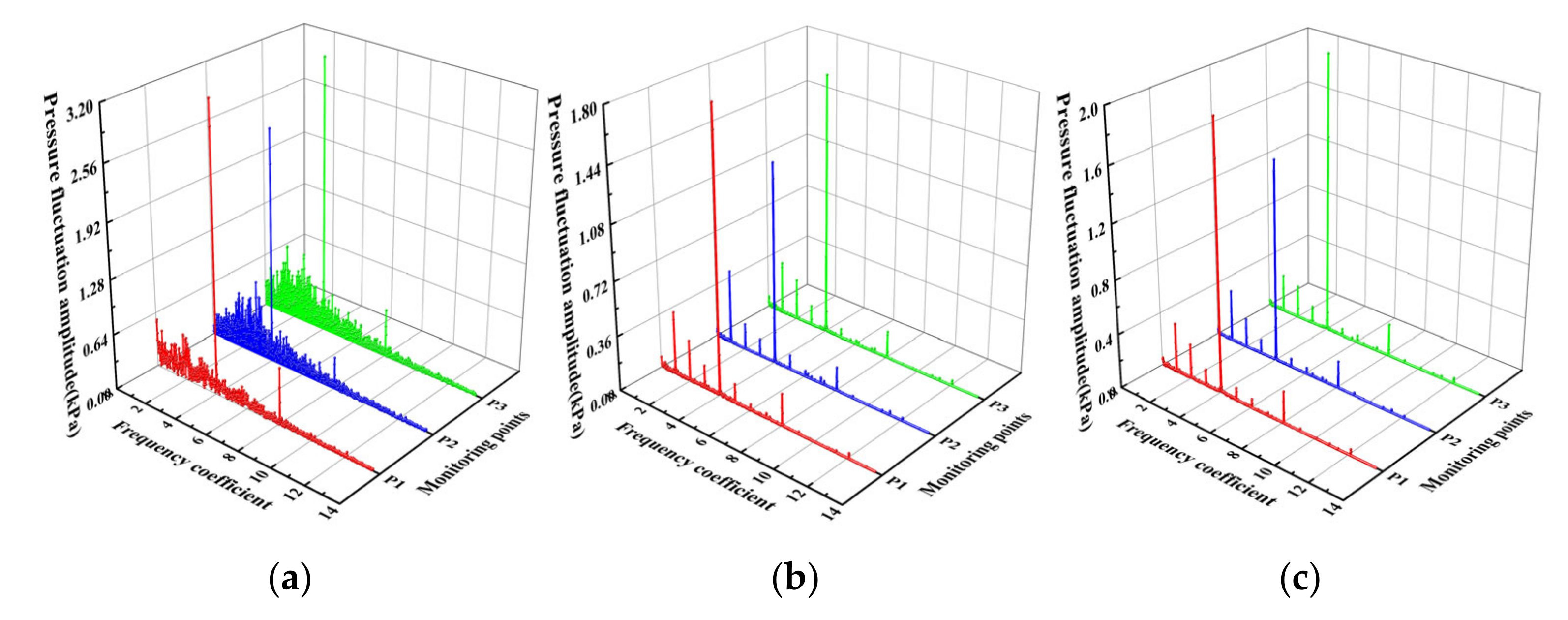
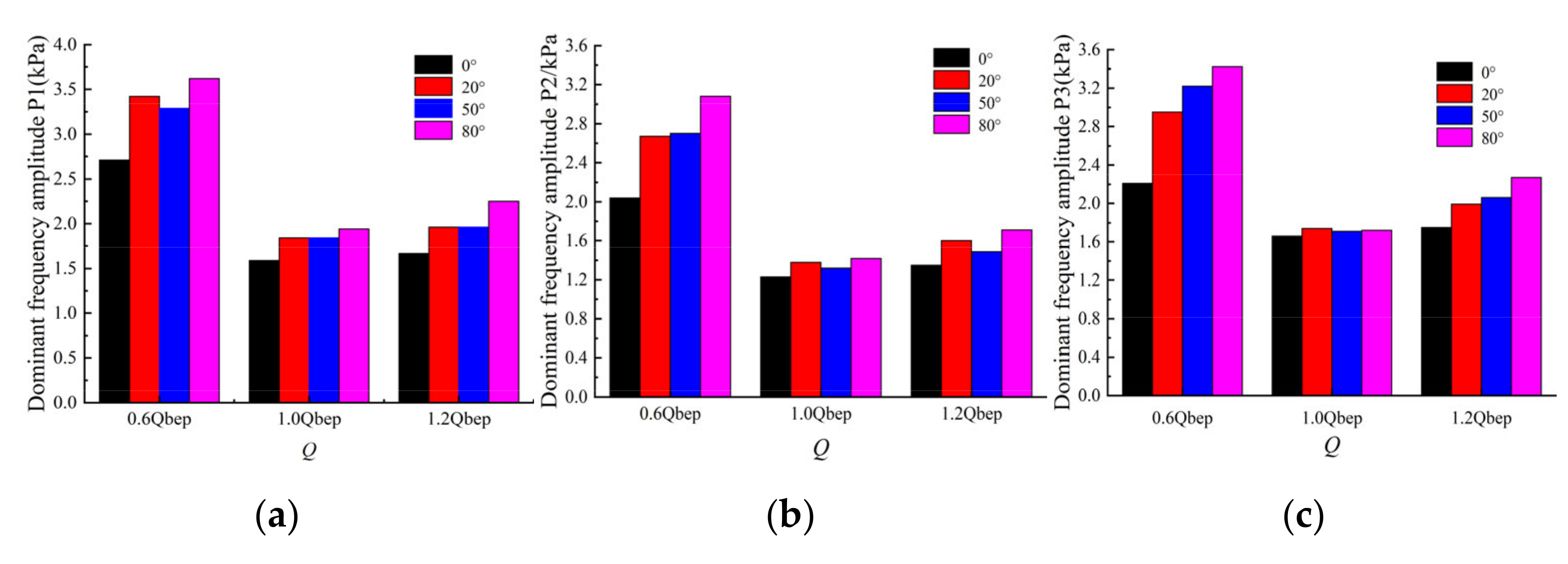
4.4. Frequency Domain Analysis of Pressure Pulsation at the Outlet Monitoring Point of the Inlet Passage
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| D | Diameter of the impeller (m) |
| Eη | Total uncertainty (%) |
| Eη,S | Systematic uncertainty (%) |
| Eη,R | Random uncertainty (%) |
| Q | Flow rate (m2/s) |
| Qbep | Optimal flow rate (m2/s) |
| H | Total head (m) |
| η | Efficiency of the pump device (%) |
| ρ | Density of water (kg/m3) |
| Δh | Hydraulic loss (m) |
| Pin | pressure at the inlet section of the inlet passage (Pa) |
| Pout | pressure at the outlet section of the inlet passage (Pa) |
| g | Local gravity acceleration (m/s2) |
| vsu | Uniformity of the axial velocity (%) |
| μ | Fluid dynamic viscosity (m2/s) |
| NF | Multiple frequency |
References
- Liu, C. The developments of axial flow pump system researches in China. In Proceedings of the Fluids Engineering Division Summer Meeting, Washington, DC, USA, 10–14 July 2016. [Google Scholar]
- Yang, F.; Liu, C.; Tang, F.; Zhou, J.; Luo, C. Analysis of hydraulic performance for vertical axial-flow pumping system with cube-type inlet passage. Trans. Chin. Soc. Agric. Eng. 2014, 30, 62–69. [Google Scholar]
- Jiao, W.; Cheng, L.; Zhang, D.; Zhang, B.; Su, Y.; Wang, C. Optimal design of inlet passage for waterjet propulsion system based on flow and geometric parameters. Adv. Mater. Sci. Eng. 2019, 2019, 2320981. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.S.; Shi, W.D.; Bin, C.; Guan, X.F. Unsteady flow analysis and experimental investigation of axial-flow pump. J. Hydrodyn. 2010, 22, 35–43. [Google Scholar] [CrossRef]
- Zhang, W.P.; Shi, L.J.; Tang, F.P.; Duan, X.H.; Liu, H.Y.; Sun, Z.Z. Analysis of inlet flow passage conditions and their influence on the performance of an axial-flow pump. Proc. Inst. Mech. Eng. Part A-J. Power Energy 2020, 235, 733–746. [Google Scholar] [CrossRef]
- Liu, C.; Jin, Y. Numerical Simulation on three dimensional flow in two-way reversible pumping system. Trans. Chin. Soc. Agric. Eng. 2011, 42, 74–78. [Google Scholar]
- Tokyay, T.E.; Constantinescu, S.G. Validation of a large-eddy simulation model to simulate flow in pump intakes of realistic geometry. J. Hydraul. Eng.-ASCE. 2006, 132, 1303–1315. [Google Scholar] [CrossRef]
- Yang, F.; Xie, C.L.; Liu, C.; Yuan, Y.; Shi, L.J. Influence of axial-flow pumping system operating conditions on hydraulic performance of elbow inlet conduit. Trans. Chin. Soc. Agric. Eng. 2016, 47, 15–21. [Google Scholar]
- Zhang, D.S.; Shi, W.D.; Pan, D.Z.; Dubuisson, M. Numerical and experimental investigation of tip leakage vortex cavitation patterns and mechanisms in an axial flow pump. J. Fluids Eng.-Trans. ASME 2015, 137, 121103. [Google Scholar] [CrossRef]
- Xie, C.L.; Tang, F.P.; Zhang, R.T.; Zhou, W.; Zhang, W.P.; Yang, F. Numerical calculation of axial-flow pump’s pressure fluctuation and model test analysis. Adv. Mech. Eng. 2018, 10, 1687814018769775. [Google Scholar] [CrossRef]
- Choi, Y.D.; Kurokawa, J.; Matsui, J. Performance and internal flow characteristics of a very low specific speed centrifugal pump. J. Fluids Eng.-Trans. ASME 2006, 128, 341–349. [Google Scholar] [CrossRef]
- Kan, K.; Zheng, Y.; Chen, Y.J.; Xie, Z.S.; Yang, G.; Yang, C.X. Numerical study on the internal flow characteristics of an axial-flow pump under stall conditions. J. Mech. Sci. Technol. 2018, 32, 4683–4695. [Google Scholar] [CrossRef]
- Mu, T.; Zhang, R.; Xu, H.; Zheng, Y.; Fei, Z.D.; Li, J.H. Study on improvement of hydraulic performance and internal flow pattern of the axial flow pump by groove flow control technology. Renew. Energy 2020, 160, 756–769. [Google Scholar] [CrossRef]
- Wang, L.; Liu, H.L.; Wang, K.; Zhou, L.; Jiang, X.P.; Li, Y. Numerical Simulation of the Sound Field of a Five-Stage Centrifugal Pump with Different Turbulence Models. Water 2019, 11, 1777. [Google Scholar] [CrossRef] [Green Version]
- Chen, E.Y.; Ma, Z.L.; Zhao, G.P.; Li, G.P.; Yang, A.L.; Nan, G.F. Numerical investigation on vibration and noise induced by unsteady flow in an axial-flow pump. J. Mech. Sci. Technol. 2016, 30, 5397–5404. [Google Scholar] [CrossRef]
- Furukawa, A.; Shigemitsu, T.; Watanabe, S. Performance test and flow measurement of contra-rotating axial flow pump. J. Therm. Sci. 2007, 16, 7–13. [Google Scholar] [CrossRef]
- Feng, J.J.; Luo, X.Q.; Guo, P.C.; Wu, G.K. Influence of tip clearance on pressure fluctuations in an axial flow pump. J. Mech. Sci. Technol. 2016, 30, 1603–1610. [Google Scholar] [CrossRef]
- Zhang, W.P.; Tang, F.P.; Shi, L.J.; Hu, Q.J.; Zhou, Y. Effects of an inlet vortex on the performance of an axial-flow pump. Energies 2020, 13, 2854. [Google Scholar] [CrossRef]
- Momosaki, S.; Usami, S.; Watanabe, S.; Furukawa, A. Numerical simulation of internal flow in a contra-rotating axial flow pump. In IOP Conference Series: Earth and Environmental Science, Volume 12, 25th IAHR Symposium on Hydraulic Machinery and Systems 20–24 September 2010 ‘Politehnica’ University of Timişoara, Timişoara, Romania; IOP Publishing Ltd.: Bristol, UK, 2010; Volume 12, p. 012046. [Google Scholar]
- Shervani-Tabar, M.T.; Ettefagh, M.M.; Lotfan, S.; Safarzadeh, H. Cavitation intensity monitoring in an axial flow pump based on vibration signals using multi-class support vector machine. Proc. Inst. Mech. Eng. Part C-J. Eng. Mech. Eng. Sci. 2018, 232, 3013–3026. [Google Scholar] [CrossRef]
- The People’s Republic of China Water Industry Standard. Code for Model Pump and Its Installation Acceptance Tests (SL140-2006); Publishing House of Electronics Industry: Beijing, China, 2006. [Google Scholar]
- Cheng, Y.; Lien, F.S.; Yee, E.; Sinclair, R. A comparison of large eddy simulations with a standard k–ε Reynolds-averaged Navier–Stokes model for the prediction of a fully developed turbulent flow over a matrix of cubes. J. Wind Eng. Ind. Aerodyn. 2003, 91, 1301–1328. [Google Scholar] [CrossRef]
- Li, X.H.; Zhang, S.J.; Zhu, B.L.; Hu, Q.B. The study of the k-ε turbulence model for numerical simulation of centrifugal pump. In Proceedings of the 2006 7th International Conference on Computer-Aided Industrial Design and Conceptual Design, Hangzhou, China, 17–19 November 2006; pp. 1–5. [Google Scholar]
- Hou, Q.F.; Zou, Z.S. Comparison between standard and renormalization group k-ε models in numerical simulation of swirling flow tundish. ISIJ Int. 2005, 45, 325–330. [Google Scholar] [CrossRef] [Green Version]
- Shaheed, R.; Mohammadian, A.; Gildeh, H.K. A comparison of standard k–ε and realizable k–ε turbulence models in curved and confluent channels. Environ. Fluid Mech. 2019, 19, 543–568. [Google Scholar] [CrossRef]
- Balabel, A.; El-Askary, W.A. On the performance of linear and nonlinear k–ε turbulence models in various jet flow applications. Eur. J. Mech. B-Fluids 2011, 30, 325–340. [Google Scholar] [CrossRef]
- Shi, L.J.; Tang, F.P.; Xie, R.S.; Zhang, W.P. Numerical and experimental investigation of tank-type axial-flow pump device. Adv. Mech. Eng. 2017, 9, 1687814017695681. [Google Scholar] [CrossRef] [Green Version]
- Suh, J.W.; Kim, J.W.; Choi, Y.S.; Kim, J.H.; Joo, W.G.; Lee, K.Y. Multi-objective optimization of the hydrodynamic performance of the second stage of a multi-phase pump. Energies 2017, 10, 1334. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.J. Analysis Method of Water Pump and Pumping Station; China Water Conservancy and Hydropower Press: Beijing, China, 2020. [Google Scholar]
- Ariff, M.; Salim, S.M.; Cheah, S.C. Wall y+ approach for dealing with turbulent flow over a surface mounted cube: Part 1—low Reynolds number. In Proceedings of the Seventh International Conference on CFD in the Minerals and Process Industries, Melbourne, Australia, 9–11 December 2009; pp. 1–6. [Google Scholar]










| Terms | Equipment | Type | Systematic Error |
|---|---|---|---|
| Flow | Electromagnetic flowmeter | EJA110A | ±0.1% |
| Head | Differential pressure | LDG-125S | ±0.01% |
| Torque and speed | Transmitter | JW-3 | ±0.1% |
| Torque speed sensor |
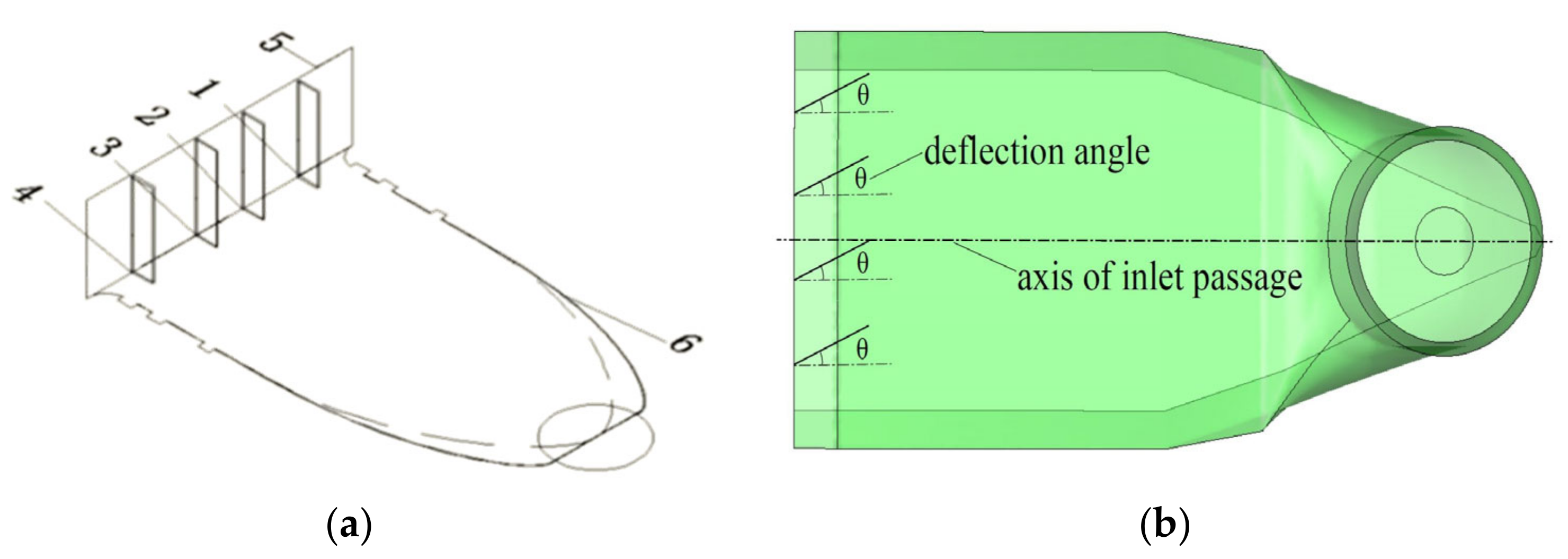
| Deflection Angle(°) | Inlet Area Blockage Ratio (%) | Deflection Angle(°) | Inlet Area Blockage Ratio (%) |
|---|---|---|---|
| 0 | 6.07 | 50 | 57.31 |
| 20 | 25.21 | 80 | 68.54 |
| Locations | Type |
|---|---|
| Inlet of model pump | Total pressure, 1 standard atmosphere |
| Outlet of model pump | Mass flow rate |
| Solid wall surface | No-slip wall |
| Convergence criterion | 10−5 |
| Interface on both sides of impeller | Stage |
| Static and static interface | None |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Li, Z.; Yuan, Y.; Liu, C.; Zhang, Y.; Jin, Y. Numerical and Experimental Investigation of Internal Flow Characteristics and Pressure Fluctuation in Inlet Passage of Axial Flow Pump under Deflection Flow Conditions. Energies 2021, 14, 5245. https://doi.org/10.3390/en14175245
Yang F, Li Z, Yuan Y, Liu C, Zhang Y, Jin Y. Numerical and Experimental Investigation of Internal Flow Characteristics and Pressure Fluctuation in Inlet Passage of Axial Flow Pump under Deflection Flow Conditions. Energies. 2021; 14(17):5245. https://doi.org/10.3390/en14175245
Chicago/Turabian StyleYang, Fan, Zhongbin Li, Yao Yuan, Chao Liu, Yiqi Zhang, and Yan Jin. 2021. "Numerical and Experimental Investigation of Internal Flow Characteristics and Pressure Fluctuation in Inlet Passage of Axial Flow Pump under Deflection Flow Conditions" Energies 14, no. 17: 5245. https://doi.org/10.3390/en14175245
APA StyleYang, F., Li, Z., Yuan, Y., Liu, C., Zhang, Y., & Jin, Y. (2021). Numerical and Experimental Investigation of Internal Flow Characteristics and Pressure Fluctuation in Inlet Passage of Axial Flow Pump under Deflection Flow Conditions. Energies, 14(17), 5245. https://doi.org/10.3390/en14175245







