Abstract
Currently, built LED luminaires are usually multi-source. This causes a large number of photometric and simulation problems connected with computer lighting visualization. This paper highlights three key issues with these luminaires: a change in the traditional understanding of the coordinate system for these luminaires, the photometric test distance of these luminaires and the need for the photometric separation of a single LED in the computer lighting simulation process. An optical model of a linear LED luminaire used in floodlighting was formulated on this basis. The presented conclusions refer to practical applications. Thus, it is necessary to address the crucial points that specify the coordinate system for the multi-source LED luminaire by its designer and present the information in a datasheet. The other important points concern determining the appropriate photometric test distance for the multi-source LED luminaires of a given type and creating photometric files for the different distances in the operation of the luminaire. Taking the above ideas into account will lead to an improvement in the quality and accuracy of lighting measurements and simulations.
1. Introduction
Each new type of light source has been developed in a way so as to increase its average life, luminous efficacy, color rendition or ease of dimming [1,2,3,4,5,6,7]. At the same time, the new light sources have constrained a certain specification of a luminaire design as the result of their geometry (Figure 1) [8,9,10]. Therefore, rotationally symmetrical luminaires (shades, chandeliers, reflectors, etc.) of relatively small dimensions were the most suitable ones for incandescent lamps or, nowadays, for electroluminescent retrofits with an E27 base on such lamps (Figure 1a) [11,12,13]. Fluorescent lamps, especially linear ones, were dedicated to the elongated luminaire design (Figure 1b) [14,15]. Discharge lamps basically preserved the elongated shape of the arc tube, but this feature became less pronounced compared to fluorescent lamps. Therefore, luminaires for discharge lamps (Figure 1c) were less dominant in terms of length, although this feature was still easily noticeable [16,17,18]. In luminaires for discharge lamps, the existence of the main light radiation plane perpendicular to the luminaire length was the reason for the popularization of the C-ɤ coordinate system [19,20]. It was also a consequence of the existence of the dominant dimension of the luminaire length. The era of light-emitting diodes (LEDs) has brought out a rarely seen feature of luminaires, i.e., a multi-source nature (Figure 1d) [21,22,23,24]. This nature arises from the fact that a single LED chip is characterized by low power and a low luminous flux [3,25,26]. This is why LED luminaires need to have many (sometimes even several dozen) single LED chips to meet certain parameters of the luminous environment. Consequently, the miniaturization of the light source and its multi-source nature have caused many problems in lighting technology practice that so far have been marginal [27].
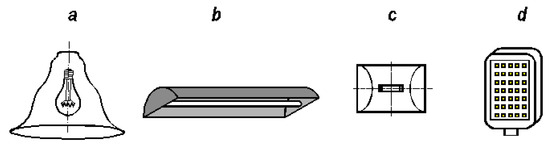
Figure 1.
Typical designs of the luminaires for various types of light sources: (a) incandescent, (b) fluorescent, (c) discharge, (d) LED.
One of them is, for example, the issue of determining the photometric center of luminaires consisting of multiple light sources. For conventional types, which usually have a single light source, the photometric center is referred to as the geometrical center of the light source [28]. However, in multi-source LED luminaires, this is not possible because there are many LED chips. In addition, the different geometries of this type of luminaire are another impediment. This fact may harm the accuracy of the measurements of the luminous intensity distribution and the determination of the photometric test distance. As a result, it may cause the computer simulation of the lighting to be incorrect [29].
Another problem is defining an appropriate photometric system for a multi-source luminaire. There are different coordinate systems of photometry [28]. Currently, the most popular is the C-gamma system (Figure 2A). It is based on a bundle of half-planes whose common straight line is the optical axis of the luminaire, and any direction in space is defined by the two angles (C and gamma). It is the most intuitive coordinate system of spatial orientation around a luminaire, and is widely used in regulations and technical reports in European countries. In contrast, a slightly different coordinate system is used in North America, mainly due to the development of the IESNA (Illuminating Engineering Society of North America). The main differences between these two coordinate systems are shown in Figure 2B. The IESNA version is also based on a bundle of half-planes with a common straight line being the optical axis of the luminaire and two angles, V and H. The critical difference is in determining the position of the first plane (respectively C = 0 or H = 0). The first plane in the C-gamma system is consistent with the transverse dimension of the luminaire, while in the system proposed by IESNA, it is compatible with the longer dimension of the luminaire. Additionally, considering the multi-source nature of LED luminaires, it can introduce many problems and lead to both misunderstandings and incorrect calculations of lighting parameters. A detailed examination of this subject is presented in Section 2, which is the basis for further research outlined in this article.
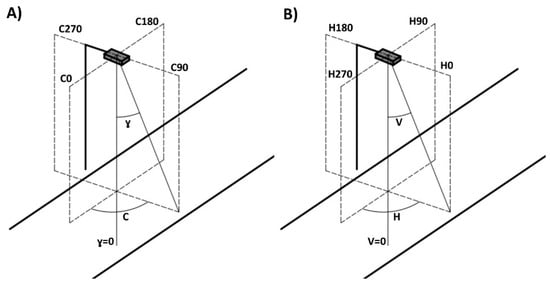
Figure 2.
Typical photometric coordinate systems: (A) C-gamma and (B) “VH” by IESNA.
Therefore, this article aims to identify and investigate the problems associated with the photometry of multi-source LED luminaires using a C-gamma coordinate system. The study will be carried out based on a laboratory experiment consisting of two multi-source LED luminaires with different geometry. Moreover, the appropriate computer simulations of lighting effects obtained for a given typical use case will be presented. Both the measurements and simulations will enable recommendations to be made regarding the photometry of multi-source LED luminaires to improve the accuracy of computer visualization of lighting effects.
2. The Need to Change the Traditional Understanding of the Coordinate System for a Luminaire
Traditionally, understanding the coordinate system of a luminaire was connected with its dimensions and consisted of distinguishing the optical, longitudinal and transverse axes [30]. This was a consequence of using discharge lamps in the luminaires that were characterized by the existence of a dominant length dimension (Figure 3). The photometric plane C0 was usually perpendicular to the direction of the length of the light source. Therefore, this plane was perpendicular to the length of the luminaire and it was related to the main light radiation direction. On the basis of the external appearance of the optical system, the identification of this plane and its photometric features was often impossible due to the grooving or matting of the shade. That is why the procedure for determining the luminaire coordinate system moved to the outer dimensions of the luminaire [20].
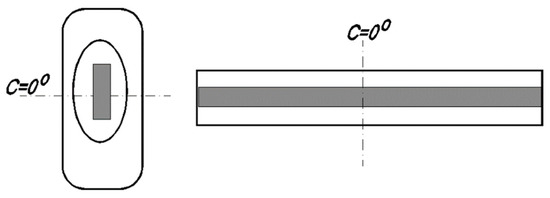
Figure 3.
According to the traditional understanding, the position of the C0 plane depends on the shape of the luminaire dimension and should be perpendicular to the longitudinal axis of the luminaire.
The multi-source nature of LED luminaires has changed the current understanding and definition of the coordinate system related to the luminaires. This is a consequence of the fact that single chips forming the whole light source can be mounted on the mounting board in any way, consequently giving it any size. Moreover, this complex multi-point light source does not have to be composed of identical elementary lenses. If the LED luminaire consists of, for example, 10 identical single chips, they can be mounted inside the circle area, be placed one after the other or take a rectangular shape (Figure 3). Each time, the luminous intensity distribution of each of these three matrix shape variations will be the same as long as the individual chips are moved parallelly, without any rotation. According to the traditional understanding of the coordinate system related to the dimensions of the luminaire, each of these luminaires would have a C0 plane located in relation to the separation of the longitudinal and transverse dimensions of the luminaire axes (Figure 4).
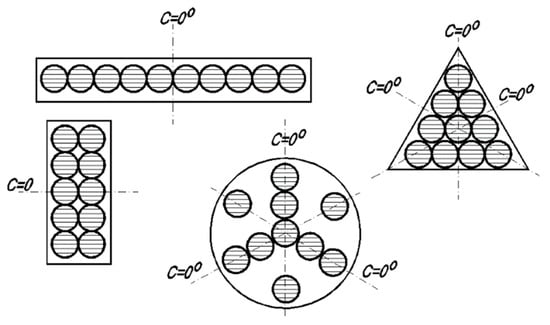
Figure 4.
In many cases, an error is made when the coordinate system is set only on the basis of the outer dimensions of the luminaire. Therefore, the C0 plane defined based on the longitudinal and transverse directions and the optical axis is not the main plane for shaping the luminous intensity distribution.
One important observation emerges from the analysis presented above. Determining the coordinate system of the luminaire in the multi-source LED luminaires should be changed from the dimensions of the luminaire to the dimensions of the elementary diode. Therefore, this basically entails the analysis of the main plane to shape the luminous intensity distribution of the elementary LED chip (Figure 5). In Figure 4 and Figure 5, the optical system of each LED is defined by horizontal lenticular strips.
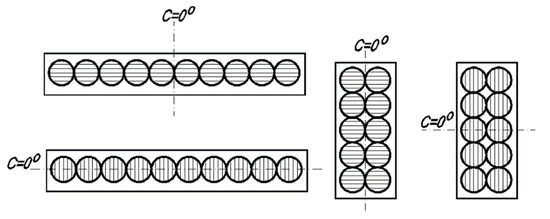
Figure 5.
In the multi-source LED luminaires, it is not the luminaire dimension that determines the coordinate system for the luminaire, but the optical system of a single LED chip. The luminaires with the same dimensions may have this coordinate system placed in a different way.
The aforementioned problem becomes crucial if the multi-row LED matrix is equipped with lenses of different shapes and LED chips of different power. This leads to the conclusion that it is the luminaire designer who should make a decision about the location of the coordinate system for the multi-source LED luminaire. This designer’s decision should be clearly shown on both the luminaire housing (shade) and the drawing in the datasheet. Otherwise, it may cause misunderstandings and entirely different interpretations of the technical documentation regarding the lighting design. Therefore, in turn, it can also be the reason for a deterioration in the quantitative and qualitative characteristics of a given type of lighting.
3. The Dependence of the Photometric Test Distance on the Geometrical Configuration of the LED Matrix
3.1. The Photometric Test Distance
The photometric test distance is a basic term in lighting technology [19,20,31]. For conventional luminaires with one light source and a reflector, it can be determined theoretically as the distance from which each point located on the optical axis of the luminaire is illuminated by all elementary reflections performed on the reflector surface (Figure 6a) [32]. Therefore, in this case, the photometric test distance depends on the dimensions of the reflector and the light source [33]. Consequently, photometric distance law can be applied during laboratory measurements for a given luminaire (1) [19]. When it comes to the diffuse reflection optics, it is relatively easy to calculate the photometric test distance as it is, approximately, the five times largest dimension of the luminaire [20]. However, it is different for luminaires with systems based on specular reflection. In this case, it is recommended that this photometric distance be determined during a laboratory experiment on a photometric bench. For conventional luminaires with a mirror reflector, there have been some attempts to describe the photometric test distance by the means of the formulas relating it to the dimensions and parameters of the reflector, such as its focal length or the luminous surface [34]. Nevertheless, these formulas have not been adopted in the photometry due to the specific problematic nature of their application.
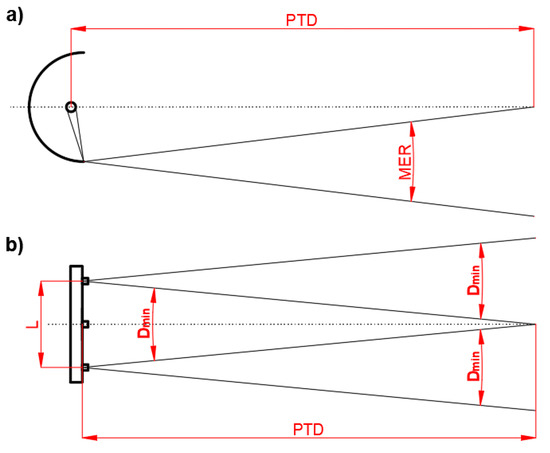
Figure 6.
Graphical definition of the photometric test distance (PTD) for: (a) the conventional luminaires and (b) the multi-source LED luminaires; MER—the minimal elementary reflection, Dmin—the minimal divergence, L—the maximum distance between diodes.
For multi-source LED luminaires, the photometric test distance not only depends on the overall dimensions of the light source, it is also influenced by the geometry of the LED chip positioning and the individual minimal divergence of the luminous intensity distribution beam of a given LED chip (Figure 6b). Therefore, if these two parameters are known, the photometric test distance can be calculated using the dependence (2). It is worth emphasizing here that this dependence (2) was proposed for the calculations of the photometric test distance for a projector-type luminaire [33]. However, to what extent is this dependence suitable for the multi-source LED luminaires in the laboratory tests? This issue will be discussed based on the experimental research that was conducted:
where:
E is the illuminance [lx];
I is the luminous intensity [cd];
R is the distance between the light source and the sensor [m];
T is the angle between the surface and the direction of illumination [°];
L is the maximum distance between diodes [m];
Dmin is the minimum divergence [°].
It should also be added that the problem of adopting the appropriate photometric test distance for multi-source LED luminaires to obtain far-field results was described in the standard CIE S 025:2015 “Test method for led lamps, led luminaires and led modules” [35]. This standard shows the relationship between the half-peak divergence of the chip, the size of the luminaire, the spacing between the chips and the photometric test distance. The approach presented in this standard can be useful for determining the photometric test distance, but only for luminaires with a lambertian or semi-lambertian nature of radiation. However, for mirror, shiny or light-transmitting luminaires, determining the photometric test distance using this method does not work because it introduces significant errors. This is evidenced by the fact that, for automotive headlights with a diameter of nearly 20 cm, the photometric test distance was set at 25 m. However, it should be remembered that, in order to be sure that the appropriate photometric test distance is obtained, measurements should be made from an infinite distance from the source of radiation. It is impossible to do this in real circumstances, therefore it is recommended that the determination of the photometric test distance is calculated in a laboratory experiment. In this case, a sufficiently large photometric test distance should be obtained so that the light source (luminaire) can be analyzed as a point. It also means that the photometer’s head covers all the reflected rays coming from a given source so that photometric distance law can be applied with the smallest relative error. Our experience shows that the adoption of the normative recommendations may lead to an overestimation of the value of the photometric test distance. In turn, this fact can lead to a situation in which the conditions of near-field photometry will be inappropriate and, as this article will show, it has a great impact on the issue of the visualization of lighting effects. Therefore, it is worth considering the possibility of introducing an optical model of the mid-field region [36]. This model can be used to improve the effects of lighting visualization in the software using the classic simulation approach based on .ies and .ldt photometric files.
The research outlined in this article is relatively complex. It consists of both photometric measurements and computer simulations of lighting effects performed for many cases. The diagram showing the individual steps of the research and the sections in which they were described is presented in Figure 7.
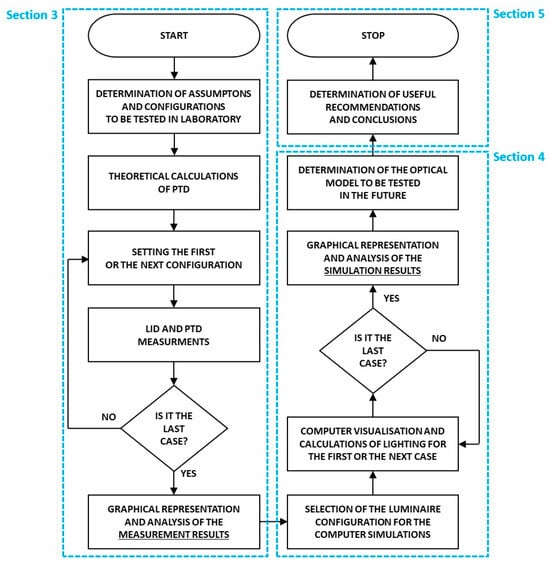
Figure 7.
The step diagram of the conducted research.
3.2. The Laboratory Experiment
For the purposes of the experiment, two luminaires were built—a linear LED luminaire and a surface LED luminaire. The views of these luminaires are presented in Figure 8. These LED luminaires are commonly used in various applications, such as in architectural lighting [29]. Each of the luminaires was equipped with five LED chips, for which it was possible to change the lenses forming a beam spread, and six different optical systems were used. This is why the creation of the rotationally symmetrical luminous intensity distributions with the half-peak divergence ranging from 8.5° to 120° could be achieved (Figure 9). There was also the possibility of changing the distance between the individual chips. For the linear luminaire, measurements were taken for the following chip distances: 35 mm, 105 mm and 210 mm. Similarly, for the surface luminaire, measurements were taken for the following chip distances: 50 mm, 105 mm and 210 mm. The luminous intensity distributions for the applied lenses were measured via the traditional method using a goniophotometer [30,37,38]. Later, the values of divergences were determined for the individual cases: the half-peak divergence for 50% of the maximum luminous intensity and the minimum divergence for 90% of the maximum luminous intensity [39]. The comparison of these values is presented in Table 1. Obtaining the minimum divergence value made it possible to calculate the photometric test distance (PTDc) using the dependence (2).
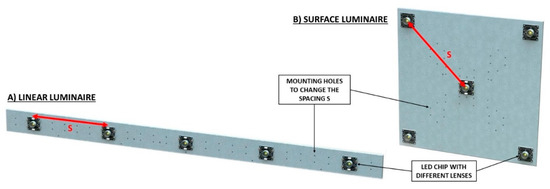
Figure 8.
The views of the test luminaires: S—spacing between diodes.
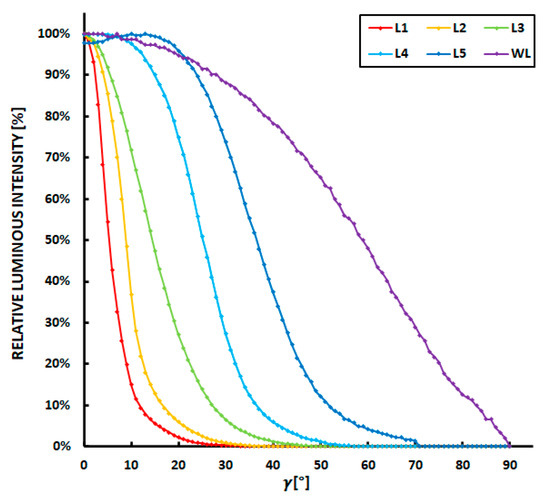
Figure 9.
The luminous intensity distribution curves for the selected lenses: L1 (8.5°), L2 (14°), L3 (30°), L4 (45°), L5 (70°), WL (120°).
Next, each of the luminaires was placed on a photometric bench that was 5 m in length (Figure 10). At the other end of the bench, there was a precisely calibrated illuminance meter (class A). The illuminance measurements were taken for the distance between 0.2 m and 5 m, in steps of 0.1 m each from the luminaire. Afterwards, based on the dependence (1), the luminous intensity value was determined. Thanks to this, it was possible to obtain the luminous intensity characteristic as a function of the distance I = f(R) for every analyzed case. The example characteristic for one case is presented in Figure 11. With the increase in distance, the luminous intensity grew, and at some point, its value began to stabilize, which was in line with the theoretical predictions. However, in reality, it is impossible to obtain the same luminous intensity value after obtaining the photometric test distance. It is connected, among other things, with fluctuations in the voltage of the power supply and the stability of the radiation source itself (in this case, the multi-source LED luminaire). That is why the decision was made that the photometric test distance obtained on the basis of the measurements (PTDM) would be used for the situation where the obtained luminous intensity values for the successive distances did not differ by more than 1%, rounded to hundredths (cm). This procedure is presented in Figure 11. In order to compare the photometric test distance values that were obtained based on the PTDM measurements with the PTDC calculations, the dependence (3) was used to determine their relative difference. Its positive value meant that the result obtained from the measurements was higher than the one obtained by means of the calculations. A negative value indicated that it was the opposite.
where:
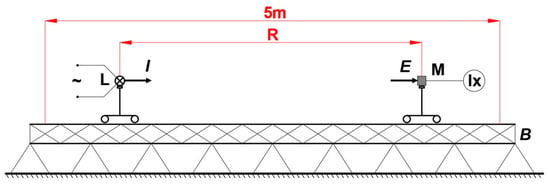
Figure 10.
The scheme of the laboratory setup: B—the photometric bench, L—the test luminaire, M—the illuminance meter, R—the distance between illuminance meter and test luminaire, I—the luminous intensity, E—the illuminance.
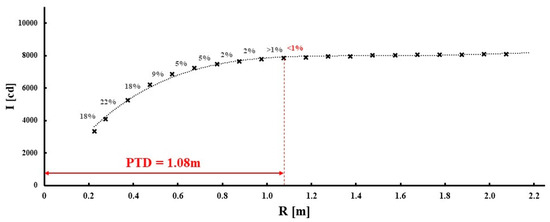
Figure 11.
The method of the photometric test distance (PTD) determination based on the measurement results.
- δPTD—is the relative difference of photometric test distance [%];
- PTDM—is the measured photometric test distance [m];
- PTDC—is the calculated photometric test distance [m].
3.3. The Results of the Experiment and Discussion
Table 1 shows the results of the calculations of the photometric test distance based on the dependence (2) and obtained as a result of laboratory measurements. For a few cases, it was impossible to determine the photometric test distance by means of the measurements due to the limited dimensions of the available photometric bench. At first, it is worth noting that the highest photometric test distances were obtained for the lenses of 8.5° and 14° with the lowest half-peak divergence lenses. This was also the case regardless of the geometric arrangement of the LED chips (regardless of whether it was the linear or the surface luminaire). It was also observed that the longer the distance between individual chips in the multi-source luminaire, the higher the obtained photometric distance. It happened regardless of the type of optics applied or the theoretical or experimental approach. When comparing the results for the linear and surface luminaires, it was also clear that the surface luminaire could be treated as geometrically focused as opposed to the linear luminaire. All these observations are in line with the theoretical predictions and they also confirm that the experimental measurements were conducted correctly.

Table 1.
The results of the calculations and measurements of the photometric test distance (PTD) for the test luminaires.
Table 1.
The results of the calculations and measurements of the photometric test distance (PTD) for the test luminaires.
| LENS TYPE | HPD Datasheet * [°] | Dmin Measured [°] | LINEAR LED LUMINAIRE | SURFACE LED LUMINAIRE | ||
|---|---|---|---|---|---|---|
| PTD Calculated [m] | PTD Measured [m] | PTD Calculated [m] | PTD Measured [m] | |||
| S = 35 mm/L = 140 mm | S = 50 mm/L = 100 mm | |||||
| L1 | 8.5° | 4.6° | 1.74 | 1.77 | 1.24 | 1.30 |
| L2 | 14° | 8.3° | 0.97 | 1.10 | 0.69 | 0.80 |
| L3 | 30° | 11.1° | 0.72 | 0.77 | 0.51 | 0.70 |
| L4 | 45° | 30.1° | 0.26 | 0.50 | 0.19 | 0.40 |
| L5 | 70° | 47.8° | 0.16 | 0.50 | 0.11 | 0.40 |
| WL | 120° | 54.0° | 0.14 | 0.32 | 0.10 | 0.40 |
| S = 105 mm/L = 420 mm | S = 105 mm/L = 210 mm | |||||
| L1 | 8.5° | 4.6° | 5.21 | >5 ** | 2.60 | 2.52 |
| L2 | 14° | 8.3° | 2.91 | 3.10 | 1.45 | 1.52 |
| L3 | 30° | 11.1° | 2.16 | 2.40 | 1.08 | 1.12 |
| L4 | 45° | 30.1° | 0.78 | 0.90 | 0.39 | 0.50 |
| L5 | 70° | 47.8° | 0.47 | 0.67 | 0.24 | 0.40 |
| WL | 120° | 54.0° | 0.41 | 0.67 | 0.21 | 0.51 |
| S = 210 mm/L = 840 mm | S = 210 mm/L = 420 mm | |||||
| L1 | 8.5° | 4.6° | 10.41 | >5 ** | 5.21 | >5 ** |
| L2 | 14° | 8.3° | 5.82 | >5 ** | 2.91 | 3.80 |
| L3 | 30° | 11.1° | 4.31 | 4.57 | 2.16 | 3.10 |
| L4 | 45° | 30.1° | 1.56 | 1.70 | 0.78 | 1.00 |
| L5 | 70° | 47.8° | 0.95 | 1.60 | 0.47 | 1.00 |
| WL | 120° | 54.0° | 0.82 | 1.20 | 0.41 | 0.90 |
* The half-peak divergence (HPD) from the manufacturer’s datasheet; ** The maximum length of the photometric bench was 5 m.
Based on the dependence (3), the relative differences between the values of the photometric test distance obtained as the result of the measurements and the calculations were determined. These results are presented in Figure 12. As far as both multi-source LED luminaires are concerned, a clear trend can be observed. The higher the beam divergence, the bigger the relative error between the values obtained because of the measurements and the calculations. This relative error can be more than 50%. Nevertheless, taking into account the absolute values, it is worth highlighting that when it comes to the optics with a large beam divergence (more than 45°), the photometric test distance decreases below 1 m. In the photometric laboratories, however, the luminaires are usually examined from a distance of several meters. Therefore, in the case of the luminaires with the wide distribution of individual diodes, the problem of not reaching the appropriate distance for the far-field photometry will probably not occur. However, this problem will definitely be much bigger when it comes to the narrow optics located at large distances apart from each other. For the half-peak divergences not exceeding 30°, the obtained relative errors are not higher than 12% for the linear luminaire and 30% for the surface luminaire. This means that the values obtained during the measurements were much higher compared to the theoretical formula (2), which had to be corrected according to the obtained relative error. Nevertheless, the validation of the photometric test distance for the luminaire tested with a given spatial location of chips and their individual luminous intensity distributions should be performed. It is worth emphasizing here that the described tests were only performed for rotationally symmetrical luminous intensity distributions, which is considered to be the simplest optical system. As for the luminous intensity distribution of planar symmetry (e.g., axially symmetrical, asymmetrical), the problem of difference in photometric test distance will be more complex. The consequence of the described problem is linked to an incorrect computer simulation and especially to an unrealistic visualization of the lighting effects. This issue is discussed in Section 4.
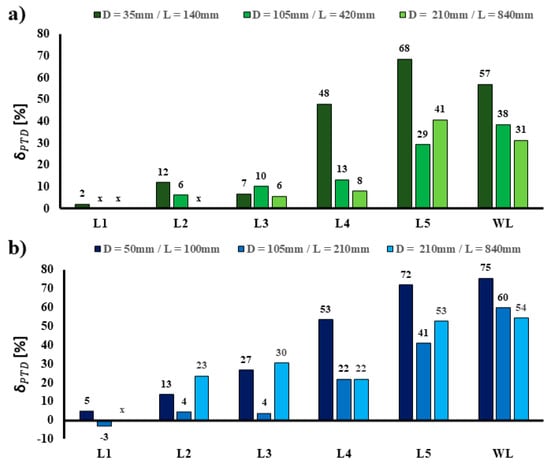
Figure 12.
The relative differences between the photometric test distances obtained as a result of the calculations and the measurements: (a)—for the linear LED luminaire, (b)—for the surface LED luminaire.
4. The Need for the Photometric Separation of Each Single Diode
Multi-source LED lamps, especially linear ones, consist of many elementary light points. Such luminaires are usually measured in a traditional way (in the sense of preparing the .ies or the .ldt photometric files) from a distance resulting from luminous intensity characteristics of the entire lamp. That is why, if the luminaire is 1 m long and consists of 20 elementary chips, the photometric data refers to the entire luminaire. This fact indicates that this luminaire is intended to illuminate the objects or planes located at a considerable big distance (far-field photometry). Meanwhile, the linear LED luminaires used in floodlighting are mainly used for local lighting solutions. Therefore, such luminaires are used for architectural details with linear dimensions (i.e., baluster railings, tympanums, etc.) and are located at a close distance to the luminaire [29]. In such a situation, the individual parts of the object are not illuminated by the entire luminaire but only by a few elementary lenses that are closest to it. Thus, depending only on the manufacturers’ photometric data for the entire lamp will lead to significant errors in the computer simulation of lighting. The reasons for this undesirable situation are as follows:
- The model of the luminous intensity distribution of the entire lamp usually assumes that the light is emitted from the geometric center point of the luminaire;
- The values of the calculated lighting parameters in the areas of the illuminated object close to the luminaire are different when compared with the reality confirmed by measurements;
- The simulation image of a spotlight is different from its real observed appearance.
Therefore, it is necessary to find a solution which will link reality with the computer-simulated effects that can now result in almost photorealistic accuracy [40,41,42,43,44]. In order to solve this problem, the luminous intensity distribution of the entire luminaire is most often rescaled for one LED chip. This is achieved by dividing the luminous intensity distribution determined for the entire luminaire by the number of its LED lenses. Such a miniaturized luminous intensity distribution is assigned to each elementary lens placed in the luminaire, taking into account its real location. The aforementioned problem is exemplified in the illumination of a typical architectural detail which is usually illuminated with the use of a linear multi-source LED luminaire. This is why a triangular tympanum with a base of 10 m and a height of 3 m was used for the computer simulation of lighting effects. The model of this tympanum was made with 3dS Max software. This software is often used for computer simulations of architectural lighting and it uses a renderer with a radiosity algorithm [45,46]. The reflectance of the material applied to the surfaces of tympanum was 50%. The tympanum was floodlit with a line of luminaires located at its base at a distance of 20 cm from its surface. These luminaries consisted of five LED chips and the luminaire dimensions as seen from the top were 50 cm × 5 cm. A single diode had a diameter of 1 cm. The tympanum lighting simulations (both visualization and luminance distribution) were carried out in various variants. The simulation of the lighting was performed using the luminous intensity distribution for the entire luminaire for near-field and far-field photometry [47,48,49]. Separating the luminous intensity distribution of the individual chips was also performed. This separation was achieved by five photometric files of a single diode set in the same way as in the real luminaire. In each of the variants, the total luminous flux of the luminaire was the same and equaled 195 lm. The following possible variants were distinguished:
- A—a photometric file of the luminaire obtained for far-field photometry with the light emitting from a point;
- B—a photometric file of the luminaire obtained for far-field photometry with the light emitting from a rectangular strip with a length and width corresponding to the dimensions of the luminaire;
- C—a photometric file of the luminaire obtained for near-field photometry with the light emitting from a point;
- D—a photometric file of the luminaire obtained for near-field photometry with the light emitting from a rectangular strip with a length and the width corresponding to the dimensions of the luminaire;
- E—five photometric files of a single diode with the light emitting from a point;
- F—five photometric files of a single diode with the light emitting from a circle with the area corresponding to the output area of the lens of one diode.
The dimensions of the surface from which the light was emitted in variants B, D and E equaled the real dimensions of the luminaire and the chips selected for testing. The obtained qualitative effects are presented in Figure 13. The results of the calculations of the luminance distribution (average luminance Lavg, maximum luminance Lmax and their Lmax/Lavg ratio) are shown in Table 2.
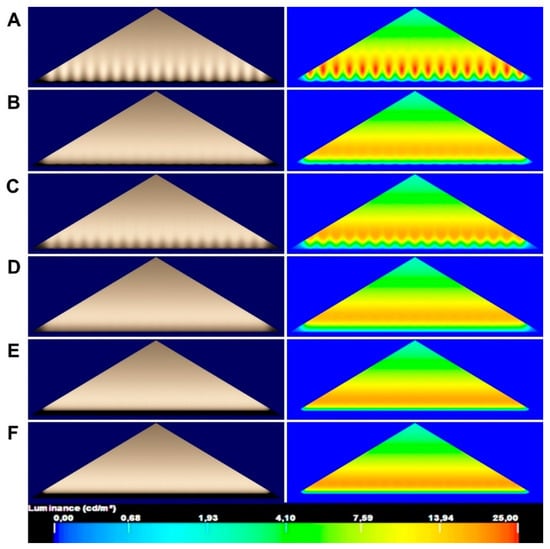
Figure 13.
The visualizations and luminance distributions of the lighting for the tympanum (10 m/3 m) with the linear LED luminaires for different simulation variants. Both the photometric separation effect of the individual LED lenses of the luminaire and the photometric file carried out from a close distance improve the accuracy and created a more natural image of the visualization and the luminance distribution.

Table 2.
The results of the calculations of luminance for the illuminated tympanum in different lighting simulation cases.
The visualization differences shown in Figure 13 are the result of using a different approach to the luminous intensity distributions of the same multi-source luminaire following the description of the presented cases above (A–F). At first, attention should be paid to some quantitative aspects (Table 2). It can be concluded that the method for simulating the lighting of the tympanum has only a slight impact on the level of average luminance obtained. In the extreme case, the difference in the obtained average luminance value is only 0.37 cd/m2. In the context of the achieved level (approx. 12 cd/m2), it should be stated that it is impossible for an observer to be able to see this difference. Therefore, it can be concluded that the calculations of the other parameters, e.g., relating to the light pollution, will be correct regardless of the simulation approach applied [50]. The obtained maximum luminance levels are also similar for cases B–F. In this respect, it is possible to distinguish case A where the highest values of the maximum luminance of approx. 1.5 times higher than in the remaining cases were obtained. This is because, in this case, the photometric file created for the far-fiaeld photometry was used and the light was emitting from the center point of each luminaire.
However, the situation is very different when it comes to the obtained aesthetic effect and the luminance distribution. The method for simulating the lighting effect has a strong impact on the obtained unaesthetic effect. In the visualization in cases A, B and C as well as in the luminance distribution, the unaesthetic oversized luminance spots (burnouts) become visible. These burnouts are in fact the distortion of the lighting reality resulting from the incorrectly defined assumptions of the computer simulation of the lighting. The images shown in Figure 13A,C are obtained by treating the linear luminaire as the light source focused at one point. Figure 13B,D exclude this assumption and show the results of calculations in which the light distribution in the luminaire model occurs uniformly from a given surface area. The luminance distribution obtained for these cases is characterized by the significantly lower luminance gradient compared to the simulation from the point, and the unaesthetic burnouts do not occur. In the real luminaire, the light distribution is not uniform across the entire output surface of the luminaire. Therefore, cases E and F shown in Figure 13 represent the variant of the individual LED lenses photometrically separated at the same number as in the real luminaire. In these cases, it can be seen that the difference between the light distributions from the point and the surface is blurred. Thus, it can be concluded that both the obtained visualization and the luminance distribution for these cases are the most accurate ones and reflect the reality.
The aforementioned problem of differences in both visualization and luminance distribution also arises from the existence of the multi-source nature of LED luminaires. The linear LED luminaires for illumination at a short distance from the object cannot be represented in the simulations. This is because the luminous intensity distribution is emitted from its optical center or the luminous intensity distribution is measured for far-field photometry. Then both the quantitative effect and the visualization image are distorted. The differences in the calculated luminance distribution shown in Figure 13 mainly result from the inconsistency of the method for determining the luminous intensity distribution of the luminaire and its later application. The photometric data obtained at the standard photometric distance should not be used in the applications where this luminaire illuminates objects that are located close by. This inconsistency can be seen clearly in Figure 14. This figure shows the luminous intensity distribution curves of the same linear LED luminaire that was used to illuminate the tympanum, measured at a distance of 0.8 m (the near-field) and 9.5 m (the far-field). The differences in the shape (the different beam divergences from the C0 and C90 planes) and the measured luminous intensity values (up to several hundred candelas) explain the visualization inaccuracies. Regardless, the authors consider it necessary to change the approach to determining the luminous intensity distribution of the linear LED luminaires, especially those that are used to illuminate the object from a short distance. During the simulation process, the elementary luminous intensity distribution of a single LED lens should be used instead of the luminous intensity distribution relating to the entire luminaire. Although this procedure may extend the computation time (the rendering as a result of the larger number of light sources) in the larger designs, the obtained aesthetic effect is the closest effect to reality.
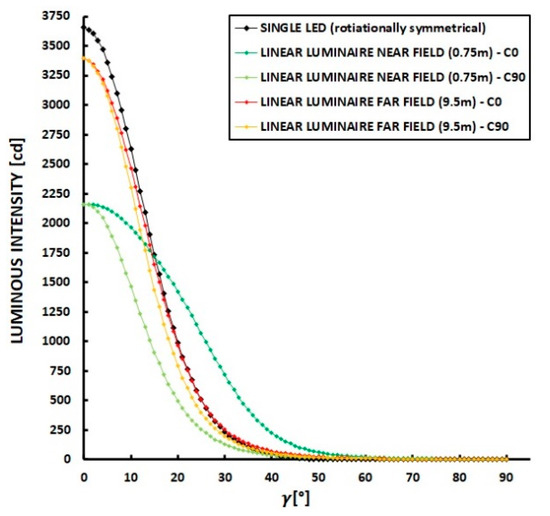
Figure 14.
The luminous intensity distribution curves of the same linear LED luminaire used in the previous simulations (Figure 8 and Figure 9), measured at different distances from the luminaire and for a single LED applied in this luminaire. The curves are scaled for the light source with a luminous flux of 1000 lm.
The need to present a new optical model of LED line illumination which especially allows to improve the visual effect of lighting simulation arises on the basis on the conducted research. This model takes into account the photometry of mid-field region based on the approximation of the luminous intensity distribution of the far-field and the near-field. The corresponding mathematical form of this model is shown by the formula (4). Depending on this formula, the approximation function fa appears. This function depends on the nature of the variability of the luminous intensity distribution of the linear LED luminaire in the section between the near-field and the far-field. If a linear nature of this variability was assumed, then the value of this function would be 2:
where:
- EP—illuminance at point P of the object;
- EP,i—illuminance from the following LED chip;
- n—number of LED chips;
- IP,i,nf—luminous intensity of the i-th diode in the direction of point P according to the near-field model;
- IP,i,ff—luminous intensity of the i-th diode in the direction of point P according to the far-field model;
- rP,i—distance of the i-th diode from point P;
- fa—approximation function of the mid-field region model.
However, it should be noted that the precise determination of the value of this approximation function requires separate precise study. Therefore, further research is planned to verify the proposed approach empirically. It will be an extension of the issues discussed in this article. This research will also be based on laboratory measurements of parameters such as illuminance and luminance for given cases. There will also be the performance of appropriate simulation models using advanced software, e.g., 3dS MAX. A comparison of the simulation results with those obtained based on the simulation tests will be made. All works will be aimed at determining the applicability of the proposed optical model in terms of its advantages and limitations for use on an industrial scale.
5. Conclusions
The development of light-emitting diodes has led to many improvements in contemporary lighting technology and illuminating engineering. However, it has also created many measurement (photometric) and simulation problems. As this technology has been developing at such a fast pace, some technical issues have been unresolved or omitted. In fact, these issues can lead to unnecessary confusion, and therefore there is a clear need to solve them or change the existing traditional approach. This paper discusses three main open issues related to the classical photometry of multi-source luminaires and the simulation of the lighting effects for this type of equipment. Based on the conducted considerations, measurements and simulations, the authors determined the following three main areas connected with the measurements and simulations for the multi-source LED luminaires:
- The coordinate system for multi-source luminaires should be definitively determined by their manufacturer. It needs to be marked in the technical documentation and related to the coordinate system for the plane shaping the luminous intensity distribution of a single LED chip.
- The photometric test distance of multi-source LED luminaires should be verified in an experimental way by a photometric laboratory. This helps to define the near-field or far-field photometry and prepare the proper, high-quality input data such as photometric files for different distances.
- The simulations of the effects of a lighting solution with multi-source LED luminaires should be performed with the greatest of care for the realism of the obtained effect. Therefore, the appropriate photometric data for the proper distance need to be used. The manufacturers of lighting equipment should specify the distance for which the measurements of the luminous intensity distributions were taken. They should also provide various photometric files for the designer’s use. Therefore, the lighting designer responsible for a given project should use the appropriate photometric files of the luminaires according to the real distance they will work in.
In addition, the issues considered in this paper have allowed the authors to determine the optical model of a linear LED luminaire used in floodlighting based on mid-field region photometry. This model can and should be used to improve the accuracy of computer calculations of lighting effects and the quality of the visualization. The model will be tested in the near future based on the comparison between the measurements and the computer simulations.
Author Contributions
Conceptualization, K.S. and W.Ż.; methodology, K.S. and W.Ż.; validation, K.S. and W.Ż.; formal analysis, K.S.; investigation, K.S. and K.K.; resources, K.S. and K.K.; data curation, K.S. and K.K.; writing—original draft preparation, K.S. and W.Ż.; writing—review and editing, K.S. and W.Ż.; visualization, K.S. and W.Ż.; supervision, K.S.; project administration, K.S.; funding acquisition, K.S. All authors have read and agreed to the published version of the manuscript.
Funding
The authors received no external financial support for the research and authorship. Article Processing Charges (APC) were covered by the IDUB Open Science program at the Warsaw University of Technology.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Acknowledgments
Authors would like to thank the Authorities of the Electrical Power Engineering Institute (Warsaw University of Technology) for the financial support of English proofreading.
Conflicts of Interest
The authors declare no conflict of interest.
Correction Statement
This article has been republished with a minor correction to resolve a typographical error in formula (2). This change does not affect the scientific content of the article.
References
- Tabaka, P.; Rozga, P. Assessment of methods of marking LED sources with the power of equivalent light bulb. Bull. Pol. Acad. Sci. Tech. Sci. 2017, 65, 883–890. [Google Scholar] [CrossRef]
- Malik, R.; Ray, K.; Mazumdar, S. A Low-Cost, Wide-Range, CCT-Tunable, Variable-Illuminance LED Lighting System. LEUKOS J. Illum. Eng. Soc. 2020, 16, 157–176. [Google Scholar] [CrossRef]
- Wiśniewski, A. Źródła Światła (eng. Light Sources); SEP COSIW: Warsaw, Poland, 2013; ISBN 978-83-61163-34-3. (In Polish) [Google Scholar]
- Shailesh, K.R.; Kurian, C.P.; Kini, S.G. Understanding the reliability of LED luminaires. Light. Res. Technol. 2018, 50, 1179–1197. [Google Scholar] [CrossRef]
- Casamayor, J.L.; Su, D.; Ren, Z. Comparative life cycle assessment of LED lighting products. Light. Res. Technol. 2018, 50, 801–826. [Google Scholar] [CrossRef]
- Protzman, J.B.; Houser, K.W. LEDs for general illumination: The state of the science. LEUKOS J. Illum. Eng. Soc. 2006, 3, 121–142. [Google Scholar] [CrossRef]
- Pracki, P.; Wiśniewski, A.; Czyżewski, D.; Krupiński, R.; Skarżyński, K.; Wesołowski, M.; Czaplicki, A. Strategies influencing energy efficiency of lighting solutions. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 711–719. [Google Scholar] [CrossRef]
- Lee, X.H.; Yang, J.T.; Chang, J.H.; Chien, W.T.; Lo, Y.C.; Lin, C.C.; Sun, C.C. An LED-based luminaire for badminton court illumination. Light. Res. Technol. 2017, 49, 396–406. [Google Scholar] [CrossRef]
- Żagan, W.; Zalewski, S.; Słomiński, S.; Kubiak, K. Methods for designing and simulating optical systems for luminaires. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 739–750. [Google Scholar] [CrossRef]
- Royer, M. Lumen maintenance and Light loss factors: Consequences of current design practices for LEDs. LEUKOS J. Illum. Eng. Soc. 2014, 10, 77–86. [Google Scholar] [CrossRef]
- Ojanen, M.; Kärhä, P.; Nevas, S.; Sperling, A.; Mäntynen, H.; Ikonen, E. Double-coiled tungsten filament lamps as absolute spectral irradiance reference sources. Metrologia 2012, 49. [Google Scholar] [CrossRef]
- Bertenshaw, D.R. The standardisation of light and photometry—A historical review. Light. Res. Technol. 2020, 52, 816–848. [Google Scholar] [CrossRef]
- Penny, A.G. Changes in the Dimensions of Incandescent Filament Lamps. Light. Res. Technol. 1962, 27, 37–40. [Google Scholar] [CrossRef]
- Tabaka, P.; Rózga, P. Analysis of selected parameters of compact fluorescent lamps during their long-term operation. Metrol. Meas. Syst. 2020, 27, 541–557. [Google Scholar] [CrossRef]
- Tähkämö, L.; Bazzana, M.; Zissis, G.; Puolakka, M.; Halonen, L. Life cycle assessment of a fluorescent lamp luminaire used in industry—A case study. Light. Res. Technol. 2014, 46, 453–464. [Google Scholar] [CrossRef]
- Chammam, A.; Nsibi, W.; Nejib Nehdi, M.; Mrabet, B.; Sellami, A. Behaviour of a high-intensity discharge lamp fed by a high-frequency dimmable electronic ballast. Light. Res. Technol. 2017, 49, 277–284. [Google Scholar] [CrossRef]
- Jack, A.G. Studies concerned with improvement of the low pressure sodium discharge lamp. Light. Res. Technol. 1978, 10, 150–155. [Google Scholar] [CrossRef]
- Cifuentes, L. High-pressure discharge lamps: Approaches to modelling. Light. Res. Technol. 1991, 23, 161–165. [Google Scholar] [CrossRef]
- Rea, M. Lighting Handbook: Reference & Application; IESNA: New York, NY, USA, 2000; ISBN 0879951508. [Google Scholar]
- Oleszyński, T. Miernictwo Techniki Świetlnej (Eng. Metrology of Lighting Technology); PWN: Warsaw, Poland, 1957. (In Polish) [Google Scholar]
- Li, M.; Chen, K.; Rupp, A.; Chu, D.; Vangari, D. Luminous flux and current uniformity analysis in linear LED modules. LEUKOS J. Illum. Eng. Soc. 2015, 11, 19–29. [Google Scholar] [CrossRef]
- Słomiński, S. Advanced modelling and luminance analysis of LED optical systems. Bull. Pol. Acad. Sci. Tech. Sci. 2019, 67, 1107–1116. [Google Scholar] [CrossRef]
- Barbosa, J.L.F.; Simon, D.; Calixto, W.P. Design optimization of a high power LED matrix luminaire. Energies 2017, 10, 639. [Google Scholar] [CrossRef]
- Martin, G.; Marty, C.; Bornoff, R.; Poppe, A.; Onushkin, G.; Rencz, M.; Yu, J. Luminaire digital design flow with multi-domain digital twins of LEDs. Energies 2019, 12, 2389. [Google Scholar] [CrossRef]
- Raypah, M.E.; Sodipo, B.K.; Devarajan, M.; Sulaiman, F. Estimation of Luminous Flux and Luminous Efficacy of Low-Power SMD LED as a Function of Injection Current and Ambient Temperature. IEEE Trans. Electron. Devices 2016, 63, 2790–2795. [Google Scholar] [CrossRef]
- Czyżewski, D. Research on luminance distributions of chip-on-board light-emitting diodes. Crystals 2019, 9, 645. [Google Scholar] [CrossRef]
- Zalewski, S. Digital recording of photometric data for multisource luminaires. Prz. Elektrotech. 2012, 88, 220–222. [Google Scholar]
- International Commission on Illumination. Technical Report No. 121: The Photometry and Goniophotometry of Luminaires; CIE: Vienna, Austria, 1996. [Google Scholar]
- Żagan, W.; Skarżyński, K. The “layered method”—A third method of floodlighting. Light. Res. Technol. 2020, 52, 641–653. [Google Scholar] [CrossRef]
- International Commission on Illumination. Technical Report No. 70: The Measurement of Absolute Luminous Intensity Distribution; CIE: Vienna, Austria, 1987. [Google Scholar]
- Dybczyński, W. The influence of distance on the photometry of luminous intensity. Prz. Elektrotech. 2003, 79, 274–277. (In Polish) [Google Scholar]
- Żagan, W. Oprawy Oświetleniowe—Kształtowanie Rozsyłu Strumienia Świetlnego i Rozkładu Luminancji (Eng. Luminaires—The Modelling of Luminous Flux and Luminance Distribution); OWPW: Warsaw, Poland, 2012; ISBN 978-83-7814-054-2. (In Polish) [Google Scholar]
- Holmes, J.G. A reference distance for the photometry of projectors. Light. Res. Technol. 1981, 13, 96–98. [Google Scholar] [CrossRef]
- Jacobs, V.; Blattner, P.; Ohno, Y.; Bergen, T.; Krueger, U.; Hanselaer, P.; Rombauts, P.; Schmidt, F. Analyses of errors associated with photometric distance in goniophotometry. In Proceedings of the 28 Session of CIE, Manchester, UK, 28 June–4 July 2015; pp. 458–468. [Google Scholar]
- International Commission on Illumination. CIE S 025/E:2015 Test Method for Led Lamps, Led Luminaires and Led Modules; CIE: Vienna, Austria, 2015. [Google Scholar]
- Sun, C.-C.; Lee, T.-X.; Ma, S.-H.; Lee, Y.-L.; Huang, S.-M. Precise optical modeling for LED lighting verified by cross correlation in the midfield region. Opt. Lett. 2006, 31, 2193. [Google Scholar] [CrossRef] [PubMed]
- Sametoglu, F. Construction of two-axis goniophotometer for measurement of spatial distribution of a light source and calculation of luminous flux. Acta Phys. Pol. A 2011, 119, 783–791. [Google Scholar] [CrossRef]
- Jacobs, V.; Forment, S.; Rombauts, P.; Hanselaer, P. Near-field and far-field goniophotometry of narrow-beam LED arrays. Light. Res. Technol. 2015, 47, 470–482. [Google Scholar] [CrossRef]
- Website of International Commission on Illumination CIE. Available online: http://cie.co.at/e-ilv (accessed on 11 June 2021).
- Wachta, H.; Baran, K.; Leśko, M. The meaning of qualitative reflective features of the facade in the design of illumination of architectural objects. AIP Conf. Proc. 2019, 2078, 020102. [Google Scholar] [CrossRef]
- Reinhart, C.; Pierre-Felix, B. Experimental validation of autodesk® 3ds max® design 2009 and daysim 3.0. LEUKOS J. Illum. Eng. Soc. 2009, 6, 7–35. [Google Scholar] [CrossRef]
- Joon, J.S. Principles of Photorealism to develop photorealistic visualisation for Interface Design: A review. In Proceedings of the 2010 Seventh International Conference on Computer Graphics, Imaging and Visualization, Sydney, Australia, 7–10 August 2010; pp. 17–25. [Google Scholar] [CrossRef]
- Stojanov, I.; Ristevski, B.; Kotevski, Z.; Savoska, S. Application of 3ds Max for 3D Modelling and Rendering. In Proceedings of the International Conference on Applied Internet and Information Technologies, Bitola, North Macedonia, 3–4 June 2016; pp. 133–144. [Google Scholar] [CrossRef]
- Krupinski, R. Simulation and analysis of floodlighting based on 3D computer graphics. Energies 2021, 14, 1042. [Google Scholar] [CrossRef]
- Geebelen, B.; Van Der Voorden, M.; Neuckermans, H. Fast and accurate simulation of long-term daylight availability using the radiosity method. Light. Res. Technol. 2005, 37, 295–310. [Google Scholar] [CrossRef]
- Website of Autodesk 3ds Max Help. Available online: https://help.autodesk.com/view/3DSMAX/2021/ENU/?query=radiosity (accessed on 11 June 2021).
- Stannard, S.; Brass, J. Application distance photometry. J. Illum. Eng. Soc. 1990, 19, 39–46. [Google Scholar] [CrossRef]
- Ngai, P.Y.; Zhang, J.X.; Quan, Y. On computation using far-field and near-field photometry. J. Illum. Eng. Soc. 1993, 22, 118–149. [Google Scholar] [CrossRef]
- Audenaert, J.; Acuña, R.P.C.; Hanselaer, P.; Leloup, F.B. Practical limitations of near-field goniophotometer measurements imposed by a dynamic range mismatch. Opt. Express 2015, 23, 2240. [Google Scholar] [CrossRef] [PubMed]
- Skarżyński, K. Methods of Calculation of Floodlighting Utilisation Factor at the Design Stage. Light Eng. 2018, 26, 144–152. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).