Enhancing Global Maximum Power Point of Solar Photovoltaic Strings under Partial Shading Conditions Using Chimp Optimization Algorithm

Abstract

This paper proposes the application of a metaheuristic algorithm inspired by the social behavior of chimps in nature, called Chimp Optimization Algorithm (ChOA), for the maximum power point tracking of solar photovoltaic (PV) strings. In this algorithm, the chimps hunting process is mathematically articulated, and new mechanisms are designed to perform the exploration and exploitation. To evaluate the ChOA, it is applied to some fixed dimension benchmark functions and engineering problem application of tracking maximum power from solar PV systems under partial shading conditions. Partial shading condition is a common problem that appears in the solar PV modules installed in domestic areas. This shading alters the power developed by the solar PV panel, and exhibits multiple peaks on the power variation with voltage (P-V) characteristic curve. The dynamics of the solar PV system have been considered, and the mathematical model of a single objective function has been framed for tuning the optimal control parameter with the suggested algorithm. Implementing various practical shading patterns of solar PV systems with the ChOA algorithm has shown improved solar power point tracking performance compared to other algorithms in the literature.

1. Introduction

Day by day, due to the exponential advancement in the demand of electrical energy, the dependency on fossil-fuels-based power plants has increased gradually, thereby, the cost of unit power generation is increasing [1]. Solar photovoltaic (PV) systems are treated as the main alternative to the traditional methods, which can sustainably develop energy [2]. Kumar et al. [3] presented that the Indian government has planned to develop 200 GW of renewable energy by the year 2022. The solar power generation is trending globally, where the statistics of major share are shown in Figure 1, International Renewable Energy Agency (IRENA), March 2021 [4].

To harvest the maximum energy from solar PV panels regardless of environmental issues and load changes, the panel must be operated at a point, namely maximum power point (MPP), and the tracking of that point is termed as Maximum Power Point Tracking (MPPT). Yang et al. [5] examined solar power point tracking performance under ideal situations. Subudhi et al. [6] discussed the pitfalls of traditional MPPT methods like perturb and observe/hill-climbing methods, which can be confused during those time intervals characterized by swiftly changing environmental conditions. Mohammed et al. [7] have studied the perturb and observe (P&O) technique to extract more energy from the solar PV module. Li et al. [8] designed a novel global MPP (GMPP) technique that depends on increment in the power, and analyzed the algorithm behavior and convergence rate under various shading patterns. Mohammed et al. [9] executed the incremental conductance method for tracing MPP of the PV system. Seyedmahmoudin et al. [10] focused on the idea of a novel Differential Evolution and Particle Swarm Optimization (DEPSO) algorithm for MPPT under various shading conditions. Yuxiang shi et al. [11] designed a low-frequency ripple-free algorithm for tracking MPP of grid integrated PV system, and tested it on a 5 KW solar plant experimental setup. Eltamay et al. [12] applied the Gray Wolf Algorithm (GWO) along with Fuzzy Controllers (FC) to show the most optimized way of damping the oscillations near and around GMPP. Bader et al. [13] established fuzzy- based controller for harnessing maximum energy from solar PV strings. Martin et al. [14] explored a novel MPPT approach that stands on faked vision. This technique used a camera to identify the shade on the portion of the solar PV module and provides the voltage signal which converges the MPP. The authors reported that this novel MPPT approach provides tracking efficiency in the range of around 99%. Satishkumar and Maheshkumar [15] designed a variable step-size adaptive P&O algorithm under rapid changes in climatic conditions. The authors showed the proposed algorithm coordinate action lead for a quick response with minimum oscillations around MPP. Narenderreddy et al. [16] studied a novel predictive model control algorithm built on a tree-structured multilevel inverter to mitigate the issues related to load disturbances and harmonics. Shubhajit et al. [17] examined the variant PSO, and it is found to be low cost and higher efficiency. Rehman et al. [18] advised the application of optimization approach to catch proper configuration to reduce cost and effective solutions.

Javad et al. [19] employed a novel modified firefly optimization algorithm under partially shaded conditions and compared with PSO approach. Nagadurga et al. [20] focused on the PSO algorithm for MPP tracking at various irradiation levels, and they found that the PSO technique provides more output under changing environmental conditions than the P&O method from their simulation results. Mingxuan et al. [21] addressed a two-stage PSO algorithm merged with a shuffeled frog leaping algorithm under partial shading climatic conditions to extract extreme global power. Ramli et al. [22] discussed several MPPT tracking techniques for the PV system under regular and partial shading conditions. The same work was presented by Bhavneshkumar et al. [23] taking the water-pump system as a load to the PV system. Sundareswaran et al. [24] proposed a novel artificial bee colony for extracting GMPP under shaded climate situations. Nagadurga et al. [25] compared the teaching-learning-based optimization (TLBO) algorithm with the PSO technique, and the authors showed that implementation of TLBO is easy due to its simple tuning parameters. Helwa et al. [26] investigated different ways to track the sun and extract maximum energy for improving the input given to the power converter. Jeba et al. [27] examined the fractional-order Proportional, Integral, and Derivative (PID) controller-based solar PV systems. Gangwar et al. [28] investigated the method of harnessing maximum energy from the solar system by arranging the panels in a particular pattern called Phyllotaxy. The authors carried out their research work on different phyllotaxy patterns like 1/3, 2/5, 3/8, etc., and compared the results with conventional arrangements for harnessing the energy from the sun. Gil-Velasco and Aguilar-Castillo [29] studied the harvesting of energy from PV systems using the P&O method and reported that the experimental results were in line with the simulation results. Angadi et al. [30] investigated the performance optimization of solar PV systems by applying a perturbation-based MPPT algorithm.

An extensive literature study shows the application of different metaheuristic techniques for the considered research problem of MPP tracking. Further, the standalone PSO and GWO techniques are quite successful in achieving efficient MPP tracking performance. It has been noted from various literature studies that PSO, GWO and some of its variants facing the problem of stuck in local peak remains to persist under shading conditions by the works of [22,23,24,25]. The satisfactory presentation of optimization techniques mainly depends on tuning their algorithm parameters and exploration capabilities. Hence, with complexity increment, the available optimization techniques from literature were not enough for the research objective fulfillment. To explore the capabilities of exploration and exploitation, the No Free Lunch (NFL) theorem prompts Chimp Optimization Algorithm (ChOA) for MPP extraction under partially shaded conditions. Khishe et al. [31] developed ChOA for training an artificial neural network to apply underwater acoustic datasets. The superior performance characteristics resulted from ChOA algorithm recommends its application in extracting optimal parameters for various research problems. Therefore, the present research work explores the optimization method ChOA, which determines the suitable duty cycle supplied for boost converter to achieve maximum energy from the solar PV system. ChOA has various benefits like fewer control parameters, flexibility of implementation, optimum balance between exploration and exploitation stages, and the capability to escape premature convergence. Furthermore, the simulation work of ChOA is compared with the other algorithms from the existing literature, and it is critically analyzed to identify the better optimization technique for solar PV systems under dynamic weather conditions.

The rest of the paper is presented as follows. Section 2 describes the MOAs for tracking MPP. Section 3 presents the realization of the proposed technique on some fixed dimension benchmark functions. The extraction of maximum power point from solar PV system with the proposed ChOA is detailed in Section 4. The application of the ChOA algorithm is shown in Section 5. Finally, Section 6 summarizes the main conclusions.

2. Metaheuristic Optimization Algorithms (MOAs) for Tracking MPP

For solving engineering optimization problems, MOA have increasingly been employed in the past few years. The present research work explores the key hunting characteristics of chimps, namely ChOA for real-world engineering problem of global power point extraction of PV strings.

2.1. Chimp Optimization Algorithm (ChOA): Background and Social Hierarchy

Chimp’s (agents) community is fission-fusion in nature, where the sequence of society is time-invariant. Furthermore, every community representative has an individual skill and a unique function that they might modify over time. Seeing this information, the approach of the self-reliant group is planned in this technique. Therefore, individual assembly of chimps tries to detect the hunt space with their peculiar talent for the specific task. Chimps are categorized as: (i) Driver; (ii) Barrier; (iii) Chaser, and (iv) Attackers. Chimps have a distinct duty in the hunt operation in favor of winning hunts. Drivers chase the prey with no attempt to catch them. Barriers establish themselves in leaves to form a barrier transversely the getaway route of the prey. Chasers can travel quickly behind the prey to catch them. Attackers wish to have higher intellectuality to forecast the subsequent movement of the prey. Hence, an attacker is compensated by a better portion of meat once the successful hunt is completed. Attackers’ essential job correlates absolutely with becoming old and their physical capability. Moreover, chimps can switch duty through the precise hunt, or remain their duty throughout the whole practice. It has been observed that chimps chase to achieve the prey for societal trade-in favors like support, sex, or grooming. “Social incentives” also-ran merely worn by chimps in addition to humans. Hence, it gives chimps specific assets more than former social predators. Further, sexual impulse motivates chimps to proceed towards the closing stage of the chase. The hunt procedure of chimps can be separated into two major stages: first, the “Exploration” stage subsists of (i) Driving, (ii) Blocking, and (iii) Chasing the prey; second, the exploitation stage consists of striking the prey.

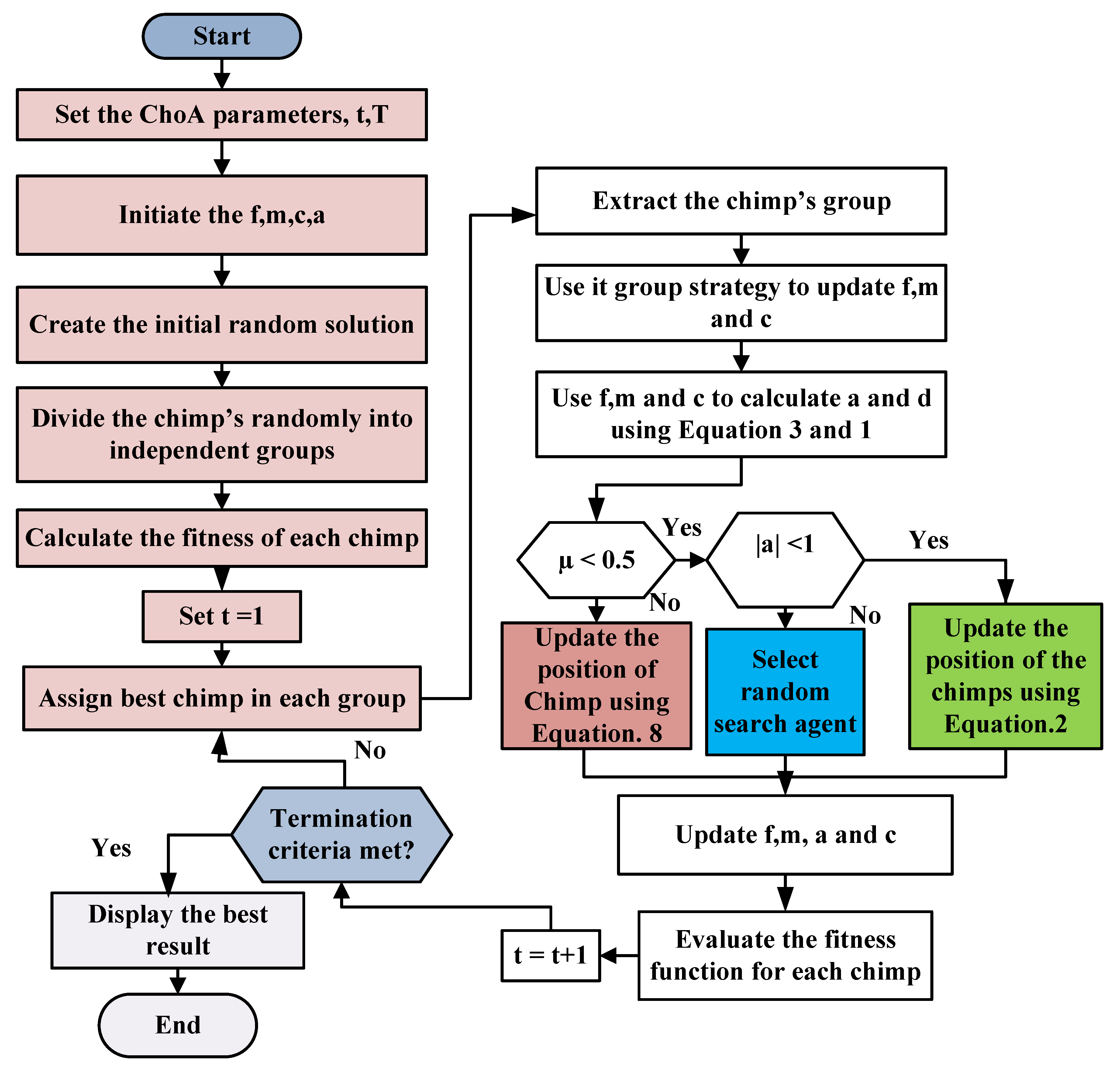
2.2. Mathematical Model of Chimp Optimization Algorithm

The hunting process is done in two phases, exploration and exploitation. For the modeling of driving the prey and chasing the prey, Equations (1) and (2) are used:

$$\mathrm{D}=\left|{\mathrm{C}\ast \mathrm{X}}_{\mathrm{prey}}\left(\mathrm{t}\right)-{\mathrm{m}\ast \mathrm{X}}_{\mathrm{Chimp}}\left(\mathrm{t}\right)\right|$$

(1)

$${\mathrm{X}}_{\mathrm{chimp}}\left(\mathrm{t}+1\right)={\mathrm{X}}_{\mathrm{Prey}}\left(\mathrm{t}\right)-\mathrm{a}\ast \mathrm{D}$$

(2)

where

• t: Current iteration
• a, m and c: Coefficient vectors
• ${\mathrm{X}}_{\mathrm{prey}}$: Prey position vector
• ${\mathrm{X}}_{\mathrm{Chimp}}$: Chimp position vector

The values of a, m and C are designed using Equations (3)–(5):

$$\mathrm{a}=2\ast f\ast {\mathrm{r}}_1-f$$

(3)

$$\mathrm{C}=2{\ast \mathrm{r}}_2$$

(4)

$$\mathrm{m}=\mathrm{Chaotic}\mathrm{Vector}$$

(5)

where $f$ decreases from the value 2.5 to 0 non-linearly in the exploration and exploitation stages through the iteration process. ${\mathrm{r}}_1$ and ${\mathrm{r}}_2$ are random vectors in the range of [0, 1], a and C are regulation vectors, D gives the distance between the X_Chimp and X_prey. Chaotic vector $\mathrm{m}$ is computed on several chaotic maps such that the result of the sexual motivation of chimps in the searching process. The report of this chaotic vector $\mathrm{m}$ will be explained in Section 2.4. In traditional swarm intelligent optimization techniques, all agents (particle) have identical behavior throughout the search space so that the particles are able to be treated as a group with the same hunt strategy. In the following, different strategies of chimp independent groups to revise $f$ will be modeled mathematically. The chimps’ independent groups updating process can be realized by taking any continuous function from [31].

The independent group’s updating process can be executed by constant parameters. These parameters are identified in a specific manner throughout each iteration f to be reduced. Each self-determining group applies their model to seek the exploration space locally as well as globally. The perfect version of the chimp optimization algorithm with distinct autonomous groups is chosen, shown in

Table 1. Dynamic coefficient of f vector.

Group	Barrier	Attacker	Driver	Chaser
f	$1.95-2{\mathrm{t}}^{1/3}/{\mathrm{T}}^{1/4}$	$1.95-2{\mathrm{t}}^{1/4}/{\mathrm{T}}^{1/3}$	$\left(-3\raisebox{1ex}{${\mathrm{t}}^3$}\!\left/ \!\raisebox{-1ex}{${\mathrm{T}}^3$}\right.\right)+1.5$	$\left(-2\raisebox{1ex}{${\mathrm{t}}^3$}\!\left/ \!\raisebox{-1ex}{${\mathrm{T}}^3$}\right.\right)+1.5$

, and the dynamic coefficient of f that has been proposed is shown in Figure 2. T denotes in Table 1 the maximum number of iterations, and t specifies the present iteration. These dynamic coefficients of vector f have been selected with different curves and slopes to facilitate a precise searching nature for chimps’ independent groups for refining the behavior of ChOA.

2.3. Exploration Phase

While attacking, the chimps might examine the prey’s locality with the help of different stages like driving, chasing, and blocking to enclose the prey. Certainly, the chase is generally managed by attackers. Drivers, barriers, and chasers are periodically engaged in the hunting process. During the first iteration, there is no knowledge regarding the optimum position of the prey. Therefore, the location of the attacker must be the position of the prey, i.e., the corresponding barrier, driver, and chaser location are reorganized according to the attacker’s position. Obtained best solution is to store, and the other chimps are required to revise their position for prominent chimp’s location.

The other ChOA parameter that changes the exploration process is C given in Equation (4). C is a random vector in the range of [0, 2]. This parameter offers random weights for prey to check whether (C > 1) or (C < 1). It also helps ChOA to get its stochastic nature along with the optimization procedure and minimizes the chance of trapping in local optima value. C is desirable to develop continuous random values and complete the exploration phase from starting to ending period iterations. The exercise of encircling the prey by the chimps is mathematically modeled as in Equations (6) and (7):

$$\begin{gathered} {\mathrm{D}}_{\mathrm{Attacker}}=\left|{\mathrm{C}}_1{\ast \mathrm{X}}_{\mathrm{Attacker}}-{\mathrm{m}}_1\ast \mathrm{X}\right|;{\mathrm{D}}_{\mathrm{Barrier}}=\left|{\mathrm{C}}_2{\ast \mathrm{X}}_{\mathrm{barrier}}-{\mathrm{m}}_2\ast \mathrm{X}\right| \\ {\mathrm{D}}_{\mathrm{Chaser}}=\left|{\mathrm{C}}_3{\ast \mathrm{X}}_{\mathrm{chaser}}-{\mathrm{m}}_3\ast \mathrm{X}\right|;{\mathrm{D}}_{\mathrm{Driver}}=\left|{\mathrm{C}}_4{\ast \mathrm{X}}_{\mathrm{driver}}-{\mathrm{m}}_4\ast \mathrm{X}\right| \end{gathered}$$

$$\begin{gathered} {\mathrm{X}}_1={\mathrm{X}}_{\mathrm{Attacker}}-{\mathrm{a}}_1\ast \left({\mathrm{D}}_{\mathrm{Attacker}}\right);{\mathrm{X}}_2={\mathrm{X}}_{\mathrm{Barrier}}-{\mathrm{a}}_2\ast \left({\mathrm{D}}_{\mathrm{Barrier}}\right) \\ {\mathrm{X}}_3={\mathrm{X}}_{\mathrm{Chaser}}-{\mathrm{a}}_3\ast \left({\mathrm{D}}_{\mathrm{Chaser}}\right);{\mathrm{X}}_4={\mathrm{X}}_{\mathrm{Driver}}-{\mathrm{a}}_4\ast \left({\mathrm{D}}_{\mathrm{Driver}}\right) \end{gathered}$$

(6)

$$\mathrm{X}\left(\mathrm{t}+1\right)=\frac{{\mathrm{X}}_1+{\mathrm{X}}_2+{\mathrm{X}}_3+{\mathrm{X}}_4}{4}$$

(7)

2.4. Attacking Mode (Exploitation Stage)

The attacking process is modeled mathematically as the value of f decreases 2.5 to 0 linearly, to reinforce the procedure of attacking and exploiting the prey’s location. It is found that the scope of the vector decrement is very similar to the f. The most explicit terminology is a random vector with a range of [−2f and 2f]. Every time, the casual value of a stretch out within the value of [−1 and 1], and the subsequent placement of a chimp may be at any location over the available position and the condition of the prey. Even though the projected blocking, driving, and chasing mechanisms in some way highlight the investigation limit, ChOA may, in any case, be in danger of trap into nearby minima. Consequently, an additional operator is essential to highlight the searching ability in the exploitation period. In this optimization algorithm, the chimps are departing to hunt the prey. As described in Figure 3, the vector $\mathrm{a}$ is modeled numerically to fit this behavior. Therefore, the disparity $\left|a\right|$ > 1 enforce the chimps to wander commencing the prey and $\left|a\right|$ < 1 power chimps to converge at the location of the prey.

Chaotic Maps (Sexual Motivation)

The chaotic behavior of chimps helps in final stage to further alleviate the problems of stuck in local optima, and slow convergence rate while solving the high dimensional engineering application problems. The mathematical model is expressed by Equation (8):

$${\mathrm{X}}_{\mathrm{Chimp}}\left(\mathrm{t}+1\right)=\{\begin{array}{c}{\mathrm{X}}_{\mathrm{Prey}}\left(\mathrm{t}\right)-a\ast \mathrm{D} \mathrm{if} \mathsf{\mu }<0.5\\ \mathrm{Chaotic}\_\mathrm{value} \mathrm{if} \mathsf{\mu }>0.5\end{array}$$

(8)

where $\mathsf{\mu }$ is a random number in [0, 1].

To improve the performance of the ChOA various chaotic maps to provide random behavior have been used in this work as shown in Figure 4. The corresponding function definitions are explained as follows.

No	Name	Chaotic Map	Range
1	Quadratic	${\mathrm{x}}_{\mathrm{i}+1}={\mathrm{x}}_{\mathrm{i}}^2-\mathrm{c},\mathrm{c}=1$	(0, 1)
2	Logistic	${\mathrm{x}}_{\mathrm{i}+1}={\mathsf{\alpha }\mathrm{x}}_{\mathrm{i}}\left(1-{\mathrm{x}}_{\mathrm{i}}\right),\mathsf{\alpha }=4$	(0, 1)
3	Bernoulli	${\mathrm{x}}_{\mathrm{i}+1}=2{\mathrm{x}}_{\mathrm{i}}$	(0, 1)

The schematic flowchart of the chimp optimization algorithm is shown in Figure 5. The process starts by randomly taking the initial population of chimps with the individual chimp groups. The objective function evaluates the chimps’ positions. Then, the corresponding steps are repeated until the stopping criteria is satisfied.

3. Testing of the ChOA on Some Fixed Dimension Benchmark Functions

For the given issue, every optimization technique is characteristically stochastic for getting the ideal solution, which implies that the execution changes over various iterations. The recommended ChOA algorithm has been realized by considering two fixed dimensional multimodal test systems, given in

Table 2. Fixed dimension benchmark functions.

Function	Range	Dim
${\mathrm{F}}_1\left(\mathrm{X}\right)=4{\mathrm{X}}_1^2-2.1{\mathrm{X}}_1^4+\frac{1}{3}{\mathrm{X}}_1^6+{\mathrm{X}}_1{\mathrm{X}}_2-4{\mathrm{X}}_1^2+4{\mathrm{X}}_2^4$	[−5, 5]	2
${\mathrm{F}}_2\left(\mathrm{X}\right)=3.5{\mathrm{X}}_1^2-2.1{\mathrm{X}}_1^4+\frac{1}{6}{\mathrm{X}}_1^6+{\mathrm{X}}_1{\mathrm{X}}_2-6.5{\mathrm{X}}_1^2+4{\mathrm{X}}_2^4$	[−5, 5]	2

. The considered test functions have one global optimum along with numerous local optima, thus, they decide the searchability of the optimization strategy.

The statistical investigation with the ChOA strategy has been applied on the considered fixed measurement multimodal benchmark works and introduced in

Table 3. Analysis of statistical results on the fixed benchmark functions.

Function		ChOA	GWO	PSO
${\mathrm{F}}_1\left(\mathrm{X}\right)=4{\mathrm{X}}_1^2-2.1{\mathrm{X}}_1^4+\frac{1}{3}{\mathrm{X}}_1^6+{\mathrm{X}}_1{\mathrm{X}}_2-4{\mathrm{X}}_1^2+4{\mathrm{X}}_2^4$	Mean	−1.03163	−1.03163	−1.03158
	SD	6.25 × 10−16	2.63 × 10−8	2.95 × 10−5
	Best	−1.03163	−1.03163	−1.03163
	Worst	−1.03163	−1.03163	−1.03152
${\mathrm{F}}_2\left(\mathrm{X}\right)=3.5{\mathrm{X}}_1^2-2.1{\mathrm{X}}_1^4+\frac{1}{6}{\mathrm{X}}_1^6+{\mathrm{X}}_1{\mathrm{X}}_2-6.5{\mathrm{X}}_1^2+4{\mathrm{X}}_2^4$	Mean	−26.8026	−26.8026	−26.7927
	SD	1.00 × 10−14	5.26 × 10−6	0.010597
	Best	−26.8026	−26.8026	−26.8026
	Worst	−26.8026	−26.8026	−26.7547

. The investigated strategy is analyzed with other most recent strategies with similar algorithm parameters of group size 30. The mean value, Equation (9), standard deviation, Equation (10), worst, and best optimum values found over 25 specific runs are delineated in Table 3 for ChOA, GWO, and PSO.

$${\mathrm{F}}_{\mathrm{Mean}}=\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{f}}_{\mathrm{i}}}{\mathrm{N}}$$

(9)

$${\mathrm{F}}_{\mathrm{SD}}=\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}({\left({\mathrm{f}}_{\mathrm{i}}-{\mathrm{F}}_{\mathrm{mean}}\right)}^2)}{\mathrm{N}}$$

(10)

From the results in Table 3, it can be seen that the variations of ChOA strategy let ideal qualities be contrasted with the fundamental algorithm for the most extreme numeral cases. The utilization of ChOA improved the performance in various kinds of functions. The presentation of proposed strategies relating to the fixed benchmark functions are shown in Figure 6, which shows the evaluation between the convergence curves of different heuristic methods. It shows the 2D portrayal of the three-dimensional boundary space, the search history of every emphasis projected on X₁ and X₂ axes only and indicates the fitness values of the various techniques being used in contrast. The search history plots are joining towards different optimal points showing diverse optima figures nearby one global value. The movement of ideal characteristics got over various iterations can be seen and escape being hit in nearby local optima with the suggested optimization technique can be observed. The proposed algorithm has the mixed characteristics of integrated algorithms, which brought about effective and enhanced the system’s performance.

4. Extraction of Maximum Power Point from Solar PV System with the Proposed ChOA

The application of ChOA technique is implemented in the field of the MPPT of the solar photovoltaic system under partial shading conditions. The experiments are performed on the numerically displayed PV system that resembles the actual powered PV system. The overall solar power network implies different equipment used for the harness of power from the source end to the load utility end. Subsequently, the solar PV system characteristics under various shading conditions are studied. The mathematic model of the solar PV cell is formulated as below.

4.1. Modelling of PV Cell

This section describes the analysis of a solar PV cell, a primary block of solar module/panel. It is needed to achieve exact I-V & P-V characteristics of PV cells to get an excellent use of the available insolation generated from the solar system. However, it is always challenging to reproduce the same I-V and P-V characteristics on the datasheet of the panel under all climatic conditions. For PV panel modeling, the data required are (i) Open-circuit voltage of the panel (V_oc); (ii) Current under short-circuit (I_sc); (iii) Maximum voltage near MPP (V_MPP); and (iv) Current near MPP (I_MPP). In contempt about this data, PV panel further required photocurrent developed at standard test condition (I_N), diode reverse saturation current (I_o), the resistance of the terminal of the panel (R_S), shunt resistance (R_Sh), and fill factor. The solar cell equivalent circuit is presented in Figure 7.

The photo current equation of the solar cell is expressed using Equation (11), given by Winston et al.

$$\mathrm{I}={\mathrm{N}}_{\mathrm{P}}\left\{{\mathrm{I}}_{\mathrm{PV}}-{\mathrm{I}}_0\left[\exp (\frac{\mathrm{V}+{\mathrm{IR}}_{\mathrm{S}}}{{\mathrm{V}}_{\mathrm{t}}{\mathrm{N}}_{\mathrm{s}}})\right]-1\right\}-\left(\frac{\mathrm{V}+{\mathrm{IR}}_{\mathrm{s}}}{{\mathrm{R}}_{\mathrm{P}}}\right)$$

(11)

where

Ns	Total number of cells connected in series.
NP	Total number of cells connected in parallel.
I0	Saturation current of the diode in A.
I PV	Photo current generated by the cell under standard test conditions in A.
RS	Series resistance in Ω.
RP	Shunt resistance in Ω.
a	Fill factor.

4.2. Maximum Power Extracting Controllers in PV Module during Partial Shading Condition

In large generating power stations, several numbers of PV panels are arranged in series to improve the voltage and parallel connection to enhance the current rating. Passing clouds and the shadow of large buildings, trees, and other moving objects may lead to improper irradiation on the panels. During shading conditions, the power output of some modules decreases drastically. Hence, it exhibits several peaks on the P-V curve, which is shown in Figure 8. To effort the priority of MPPT techniques, the simulation results of P-V characteristics of the KC200GT panel are presented in the same Figure 8. For climatic conditions such as irradiation and temperature, an exclusive operating point is observed on the I-V and P-V characteristic curve, noted as MPP. This unique operating point keeps changing its point according to the changes in weather conditions. Since the generated unit cost and furnishing cost are very high for solar PV generation, it is a force to operate the panel at MPP to harness maximum energy from the panel under swiftly changing weather conditions. Hence, the MPPT control circuit became an integrated part of the PV system.

The placement of power electronic converters between the PV panel and load will adequately regulate the interior resistance presented by the PV module and, thereby, operate the module to engage near the maximum operating conditions. Various researchers [32] employed numerous MPPT techniques based on the swarm intelligence to amend the driving point of the load associated with adjustment of the duty ratio of the DC-DC type boost converter.

By varying the duty cycle pattern of the converter, the yield voltage can fluctuate from the least to the most extreme worth of the design value of the converter. When d=0, then the output voltage obtained is low, and when the duty cycle tending to unity (maximum value), then the output voltage obtained by the power converter is large means maximum value. Therefore, 0 and 1 are the operating range of the duty cycle for the boost converter.

4.3. Formulation Objective Function

The functional behavior of the power curve in Figure 8 is non-convex, and the behavior of the power curve can be expressed by Equation (12):

$${\mathrm{P}}_{\mathrm{PV}}\left(\mathrm{t}\right)=\mathrm{F}\left({\mathrm{V}}_{\mathrm{PV}}\left(\mathrm{t}\right),{\mathrm{I}}_{\mathrm{PV}}\left(\mathrm{t}\right),\mathsf{\gamma }\left(\mathrm{t}\right)\right)$$

(12)

$\mathrm{where}$

${\mathrm{P}}_{\mathrm{PV}}$	PV power in watts.
${\mathrm{V}}_{\mathrm{PV}}$	PV voltage in volts.
${\mathrm{I}}_{\mathrm{PV}}$	PV current in Amps.

where $\mathsf{\gamma }$ represents all the decision variable other than the voltage and current, and defines the power curve at the time t.

In this work, ChOA for the non-convex optimization problem is presented for maximum power point tracking, and the procedure is outlined in algorithm. The objective of the MPPT technique is to maximize the amount of power drawn from the solar photovoltaic system by adjusting the duty cycles (decision variable) of the DC-DC boost converter. The duty cycle in each iteration is optimally selected [33] by ChOA algorithm for the objective of maximum power drawn from the PV string. This condition can be tested by using Equations (12) and (13):

$${\mathrm{P}}_{\mathrm{PV}}\left({\mathrm{d}}_{\mathrm{i}}^{\mathrm{K}}\right)>{\mathrm{P}}_{\mathrm{PV}}\left({\mathrm{d}}_{\mathrm{i}}^{\mathrm{k}-1}\right)$$

(13)

where ${\mathrm{P}}_{\mathrm{PV}}\left({\mathrm{d}}_{\mathrm{i}}^{\mathrm{K}}\right)$ present power of kth particle at kth iteration.

${\mathrm{P}}_{\mathrm{PV}}\left({\mathrm{d}}_{\mathrm{i}}^{\mathrm{k}-1}\right)$ is the previous power of kth particle at (k − 1)th iteration. Duty cycle (d) of the boost converter is the decision variable subjected to constraints given by Equation (14):

$${\mathrm{d}}_{\min }^{0.05}<{\mathrm{d}}_{\mathrm{i}}^{\mathrm{K}+1}<{\mathrm{d}}_{\max }^{0.95}$$

(14)

4.4. ChOA Algorithm Implementation for MPPT fo Solar PV Systems

The relevance of the proposed algorithm for planning the MPPT controller includes some key advances. The PV system model is created with the assistance of conditions as shown in Section 4.1. The objective function ought to be drawn on the perceptions of investigated system, and an appropriate technique is utilized to acquire the optimum power from the PV system.

ChOA is initiated by setting up random residents of chimps (agents), which is the duty ratio of boost converter used in the experiment. In the next step, all the chimps (particles) randomly spread into four groups (attackers, chaser, barrier, and driver), and the global peak power (P_m) in every cluster is solved by calculating their particular objective function (fitness function) values. f coefficient of each chimp is updated by its group strategy. The vibrant coefficients of f have been shown in Table 1 and Figure 2. The next stage is the driver, attacker, barrier, and chaser assessment of the available prey location. Later, every solution of the candidate revises its closeness from the prey. Likewise, the flexible regulation of the coefficients motivates the local optima prevention and quick movement towards the prey. Finally, chaotic maps comfort to speedy convergence with no getting trapped into local optima position. The pseudo-code of ChOA is given below.

Pseudo-code of ChOA Algorithm for MPPT tracking under the shading condition.

Algoritm 1 Pseudocode of ChOA

Load the chimp population (duty cycle of the DC-DC converter) Initialize the algorithm-specific parameters like f, m, a and c Compute the position of individual chimp Separate chimps aimlessly into different groups Until the stopping criterion is satisfied Determine the fitness function of each chimp Fitness function for Maximum power extraction from solar PV strings is $\mathrm{P}\left({\mathrm{d}}_{\mathrm{i}}^{\mathrm{K}}\right)>\mathrm{P}\left({\mathrm{d}}_{\mathrm{i}}^{\mathrm{k}-1}\right)$ dAttacker = Best search agent in the chimp population dChaser = Second best search agent dbarrier = Third best serach agent ddriver = Fourth best search agent    While (t < maximum number of iteration)       for each chimp;         Extract the chimps group         Update the parameters f, m and c using group strategy         Use parameters f, m and c to determine a and then d       end for       for each search chimp         if (α < 0.5)            if (|a| < 1) update location of each chimp agent         else if (|a| > 1) Select random search agent         end if else if (α > 0.5) update the position of the chimp end if end for Update f, m, a and c Update dAttacker, dChaser, dbarrier and ddriver t = t + 1 end while return dAttacker

5. Results and Discussions

A DC-DC boost converter integrated PV system is implemented to verify the suggested method, and the Simulink experimental setup is shown in Figure 9. For doing extensive research work under different shading conditions of solar PV strings, the KC200GT solar panel is used to simulate PV modules. Four such solar PV modules are joined in series that furnished with a boost type converter. The boost type switching circuit specification used in this simulation work in the input inductance is 10 mH, frequency = 25 kHz, capacitance (C_out) = 330 µF. Figure 9 shows the simulation circuit of the KC200 GT PV module under different shading patterns using MATLAB 2016a software.

Table 4. Specifications of the solar PV module (KYOCERA solar KC200GT).

Parameter	Value
Number of cells	54
Voc—open-circuit voltage in (V)	32.9 V
Isc—short Circuit Current in (A)	8.21 A
VMpp—Maximum voltage at MPP (V)	26.3 V
IMpp—Maximum current at MPP (A)	7.61 A
PMpp (W)	200.143 W
Number of series-connected strings	1
Number of parallel-connected strings	1

shows the parameters of the solar PV system.

A broad comparison along with the other swarm intelligent PSO technique toward the above solar PV system is carried out in MATLAB/Simulink 2016a platform to validate the examined algorithm. The power output of the PV system is calculated and compared with local and global maximum power values based on the type of algorithm applied to the PV system. The sampling time interval is taken as 1 s such that the system will grasp the steady-state condition ahead of GMPP is reached.

In optimization-based maximum power tracking methods, tuning parameters will alter the algorithm performance during the searching process, some tuning parameters are fixed, and some are varying. The specification used for the PSO optimization algorithm are C₁ = C₂ = 2, population size = 50, number of design variable equal to one, iterations = 10, weighting factor = 0.8 [10]. A small population size will lead to fast convergence and the feasibility of getting trapped to local optimal will be increased. Hence, while choosing population size in swarm intelligent techniques, e.g., PSO, adjustment between tracking accuracy, and convergence speed must be made. PSO, GWO, and ChOA algorithms are applied for observing steady and dynamic behavior of solar PV strings under shading conditions by giving random control signal (duty ratios) to the boost converter according to the algorithm mechanism. The tuning parameters of the benchmark algorithm are shown in

Table 5. Tuning parameters of benchmark algorithm.

Algorithm	Specification	Value
PSO	Inertia coefficient(W)	0.8–1.2
	Design variables	1
	Number of runs	10
	Cognitive and social learning coefficient (C1&C2)	2
	Probability of search ratio	0.02
GWO	No. of agents (wolf)	10
	Positive Limit	5
	Negative limit	−5
	Number of iterations	10
ChOA	f	Details given in Table 1
	r1, r2	Random values
	m	chaotic
	No of search agents	10
	iterations	10

.

To analyze the proposed algorithm, two shading patterns are considered for this PV system module: Shading Pattern 1: G₁ = 800 W/m², G₂ = 600 W/m², G₃ = 400 W/m² and G₄ = 200 W/m²; Shading Pattern 2: G₁ = 1000 W/m², G₂ = 1000 W/m², G₃ = 500 W/m² and G₄ = 500 W/m². Figure 10 shows the variation of power curves for these shading conditions, and global maximum powers (P_MPP) for particular pattern, including: Pattern 1, P_MPP = 267.41 W, Pattern 2: P_MPP = 443.056 W, and Pattern 3, P_MPP = 800.23 W.

5.1. Shading Pattern1

The irradiation of solar PV module for the first pattern of shading is studied as 800 W/m², 600 W/m², 400 W/m², and 200 W/m². The power curve of PV strings under the first shading pattern is shown in Figure 11. There are four peaks present in the Power curve during the first shading pattern. Under this shading condition, the global MPP is 257.41 W. From these simulation results, it was analyzed that the GMPP obtained under the first pattern using ChOA is 257.41 W. The tracking of the GMPP process started for ChOA and PSO algorithms by initializing the random values for the duty cycle, and then by running the algorithm duty ratio (d) is revised.

Figure 12 illustrates the simulation results for this case with a performance comparison between the proposed technique with another swarm intelligent technique of PSO. From Figure 9, the elaborate simulation outcomes (PV output power, voltage, and duty ratio) of a PV system with distinct MPPT techniques under the shading patterns of 800 W/m², 600 W/m², 400 W/m², and 200 W/m² are derived. As shown in Figure 12, the maximum power point trackers start the initialization to establish the search space to cover the entire P-V curve shown in Figure 8 under the first shading pattern to extract GMPP of 257.41 W. The simulation results obtained from chimp optimization have less oscillation during the searching process of MPP under shading conditions. In specific, the power output of the solar PV module converges to the MPP with fewer oscillations. Further, the suggested chimp algorithm converges enough rapidly, reaching to the optimal values only in few seconds, but PSO average convergence time is high from the simulation results shown in Figure 12. It is analyzed that ChOA and PSO methods have the capability of chasing global maximum power during different shading conditions. The qualitative analysis for maximum power extraction with various shading conditions is presented in

Table 6. Summarization of statistical simulation results like power, voltage, and current of PV module under partial shading conditions.

Different Shading Patterns	Parameter	MPPT Methods
		ChOA	PSO	GWO (Mohanthy et al. [34])	Bat (Roacha et al. [35])
M1 = [1000, 900, 800, 700]	Maximum power	625.5319 W	625.4645 W	622.4625 W	624.321 W
	Duty @MPP	0.3196	0.4026	0.302	0.321
	Voltage	115.23 V	112.8706 V	110.023 V	111.212 V
	Current	5.5656 A	5.5687 A	3.975 A	3.865 A
M2 = [800, 650, 100, 500]	Maximum power	335.6 W	331.2 W	329.7 W	329.75 W
	Duty @GMPP	0.3296	0.3021	0.297	0.257
	Voltage	84.57 V	83.4 V	80.7 V	81.2 V
	Current	3.9489 A	3.85 A	2.95 A	3.12 A
M3 = [650, 850, 400, 900]	Maximum power	350.0825 W	349.5 W	325.5 W	329.56 W
	Duty @GMPP	0.6127	0.6027	0.507	0.527
	Voltage	53.6725 V	53.21 V	51.5 V	52.5 V
	Current	6.5915 A	6.312 A	6.123 A	6.223 A
M4 = [500, 600, 1000, 400]	Maximum power	260.2923 W	258.2 W	256.2 W	257.2 W
	Duty @GMPP	0.5163	0.5026	0.4062	0.496
	Voltage	56.4194 V	55.41 V	53.55 V	54.12 V
	Current	4.3234 A	4.123 A	4.091 A	4.112 A
M5 = [400, 100, 850, 250]	Maximum power	171.8035 W	170.5W	165.5 W	168.5 W
	Duty @GMPP	0.4630	0.4630	0.4203	0.445
	Voltage	86.3148 V	85.31 V	84.4 V	84.6 V
	Current	2.8733 A	2.853 A	2.583 A	2.612 A
M6 = [350, 400, 700, 150]	Maximum power	232.75 W	230.133 W	214.5 W	216.5 W
	Duty @GMPP	0.2704	0.2541	0.2543	0.252
	Voltage	87.543 V	86.4692 V	85.54 V	86.12 V
	Current	2.9210 A	2.8177 A	2.718 A	2.725 A

.

5.2. Shading Pattern 2

In this scenario, PV modules receive the irradiation as 1000 W/m², 1000 W/m², 500 W/m², and 500 W/m². This creates three peaks in the characteristic curve of PV module and forms a complex situation for tracking GMPP. The location of GMPP is shown in Figure 13.

For shading patterns 1000 W/m², 1000 W/m², 500 W/m², and 1000 W/m² from Figure 13, the GMPP is 441.314 W. The exhaustive simulation results from the PV systems with proposed algorithms under a second shading pattern of 1000 W/m², 1000 W/m², 500 W/m², 500 W/m² are shown in Figure 14, illustrated that the convergence time for ChOA was less comparative with the other intelligent techniques. As can be seen in Figure 12 and Figure 14, the GWO and PSO MPPT algorithms presented high disturbance in the occurrence of transients in the output voltage and power curve of boost converter, the key reasons for the existence of these oscillations are variations in the solar PV system operating conditions and load changes. Since the proposed ChOA has resulted as a devised method with a better damping of oscillations over an extensive range of operating conditions with faster speed of convergence and optimally tuning the decision variable d (duty cycle) of the power converter to get the MPP with sustained oscillations. Meanwhile, the GWO and PSO algorithm requires the complete rescan along the curve to fetch the new GMPP, according to the changes in operating conditions thereby reducing the overall system efficiency.

Certainly, from Figure 15, the results show that the ChOA has good exploration potential. ChOA is the most efficient technique. By cause of four distinct exploration mechanisms in chasing the prey, which leads to global optima in the prime iteration phases, the chaotic mechanism ensures the best results. From Figure 15, the results of iteration versus best fit show the convergence criteria of ChOA are practically superior to the other heuristic techniques like GWO and PSO for the shading patterns of 800 W/m², 600 W/m², 400 W/m², and 200 W/m². The updating procedure of ChOA coefficients permit chimps to catch Global MPP in the search space within a short span. It may be constructed that ChOA and PSO techniques are fit for identifying the GMPP, and the execution of ChOA is desirable over the PSO and GWO technique due to its faster convergence rate.

To verify the expected output from the proposed technique, both PSO and ChOA approaches are simulated in the MATLAB/SIMULINK environment under different partial shading patterns (M1 to M6), and related to GWO and bat optimization algorithms in the earlier studies reported by Mohanthy et al. [34] and Rocha et al. [35]. The statistical simulation results are summarized in Table 6. It shows the information such as a comparison of ChOA and PSO optimization techniques under different shading patterns from M₁ to M₆ for the KC200GT solar PV module within the simulation period of 1 sec. It was identified from the simulation results that the shading pattern M₁ will develop maximum power to the solar photovoltaic system. It was observed from the simulation results of different shading conditions that ChOA will work executively for partial shading conditions and gave better performance superior to PSO because of speed and certainty. The statistical simulation results show that the ChOA technique tracks more voltage and power output from the solar PV system compared to the PSO, GWO, and bat optimization techniques. A summary of the statistical simulation results is presented in Table 6. The statistical analysis shows that the switching signal (duty ratio) for boost converter to yield more power from solar PV module is in the range of 0.2 to 0.6 for different shading patterns (M₁ to M₆).

With the ChOA approach, PSO and GWO algorithms from the well-organized prose are still carried out for maximum power tracking, a comparative study is realized among this soft computing maximum power tracking techniques with previous work, as shown in

Table 7. Summary of the comparison of soft computing implemented in this work with the recent literature.

Authors	Optimization Technique for MPPT Tracking	Variable Specification	Charge Controller	Dynamic Response	Tracking Speed	Contribution of the Work
Eltamaly et al. [12]	Hybrid GWO-FLC	Duty cycle	Boost Converter	High	Fast	Developed the flow chart for hybrid GWA along with fuzzy logic controller
Nagadurga et al. [20]	PSO	Duty Cycle	Boost Converter	Good	Slow	Proposed increment in PV power using PSO technique
Nagadurga et al. [25]	TLBO technique	Duty Cycle	Boost Converter	Medium	Moderate	Examined the TLBO algorithm for different weather conditions
Javad et al. [19]	FA	Voltage	Boost Converter	Medium	Fast	Proposed FA for extracting global peak power during shading conditions
Present study	Chimp Optimization technique	Duty Cycle	Boost Converter	Fast	Moderate	Proposed chimp optimization technique for MPPT under partial shading conditions

.

Three various shading patterns are initiated in the Simulink environment and the mentioned algorithms are tested for these insolation patterns.

Table 8. Comparison of statistical results of ChOA and PSO simulation analysis.

Optimization Technique	Parameter	Shading Pattern M1	Shading Pattern M2	Shading Pattern M3
ChOA	Minimum iterations	2	3	2
	Maximum iteration	4	5	6
	Convergence time to trace GMPP(s)	0.10	0.12	0.10
	Efficiency	100	99.99	99.85
PSO	Minimum iterations	2	4	3
	Maximum iteration	6	8	9
	Convergence time to trace GMPP(s)	0.14	0.16	0.23
	Efficiency	98.56	98.99	98.66

summarizes the statistical data of ChOA and PSO approaches. It is shown from the statistical results that implementing ChOA increases the efficiency of tracking for a maximum power of the solar PV system compared to the PSO approach. The numerical simulation results showed that ChOA is more accurate and has a faster convergence rate than the PSO algorithm.

6. Conclusions

In this work, a heuristic optimization technique, namely, ChOA, is realized for the optimization of shading solar PV modules that have GMPP and LMPP on the P-V characteristic curve. ChOA is an efficient approach for harnessing maximum power from the solar PV system. This algorithm provides rapid convergence due to the better balance among the exploration and exploitation processes. However, the ChOA method has a tremendous chance of tracing global optimal and helps enhance the power obtained from the solar system. Various shading patterns are created in the MATLAB/Simulink platform, and two algorithms such as ChOA and PSO are implemented for these shading patterns. ChOA is easy to implement and has a quick convergence value compared to the PSO technique. The ChOA was contrasted with notable optimization techniques from the existing research work. From the simulation test results, the ChOA method has a high ability to search GMPP, eliminating oscillation in power output near and around MPP, and a more accurate and fast convergence rate than the PSO technique. The concluding remarks from this study are listed as follows:

❖

For the problem of MPPT tracking under partial shading conditions dividing the chimps into four individual groups ensures exploration and exploitation of the search space.

❖

The utilization of chaotic maps guides the ChOA strategy to clear up nearby optima stagnation.

❖

ChOA algorithm exploits four types of population-based search agents; prevention of local optima is very high.

❖

Chimps stores explore space info above the sequence of iteration. Chimps relatively use memory to preserve the conquer resolution captured until now.

Many research guidelines can be suggested for upcoming research studies with the help of the proposed ChOA to solve a variety of engineering and industrial optimization problems. Further, changing ChOA to solve multi-objective optimization problems can be explored as the best improvement. However, the capability of chOA can be analyzed with other hunting-based optimization techniques for resolving distinct optimization issues, e.g., engineering design, data acquisition, neural networks, and computer analysis.