Machine Learning—A Review of Applications in Mineral Resource Estimation
Abstract
:1. Introduction
2. Methodology
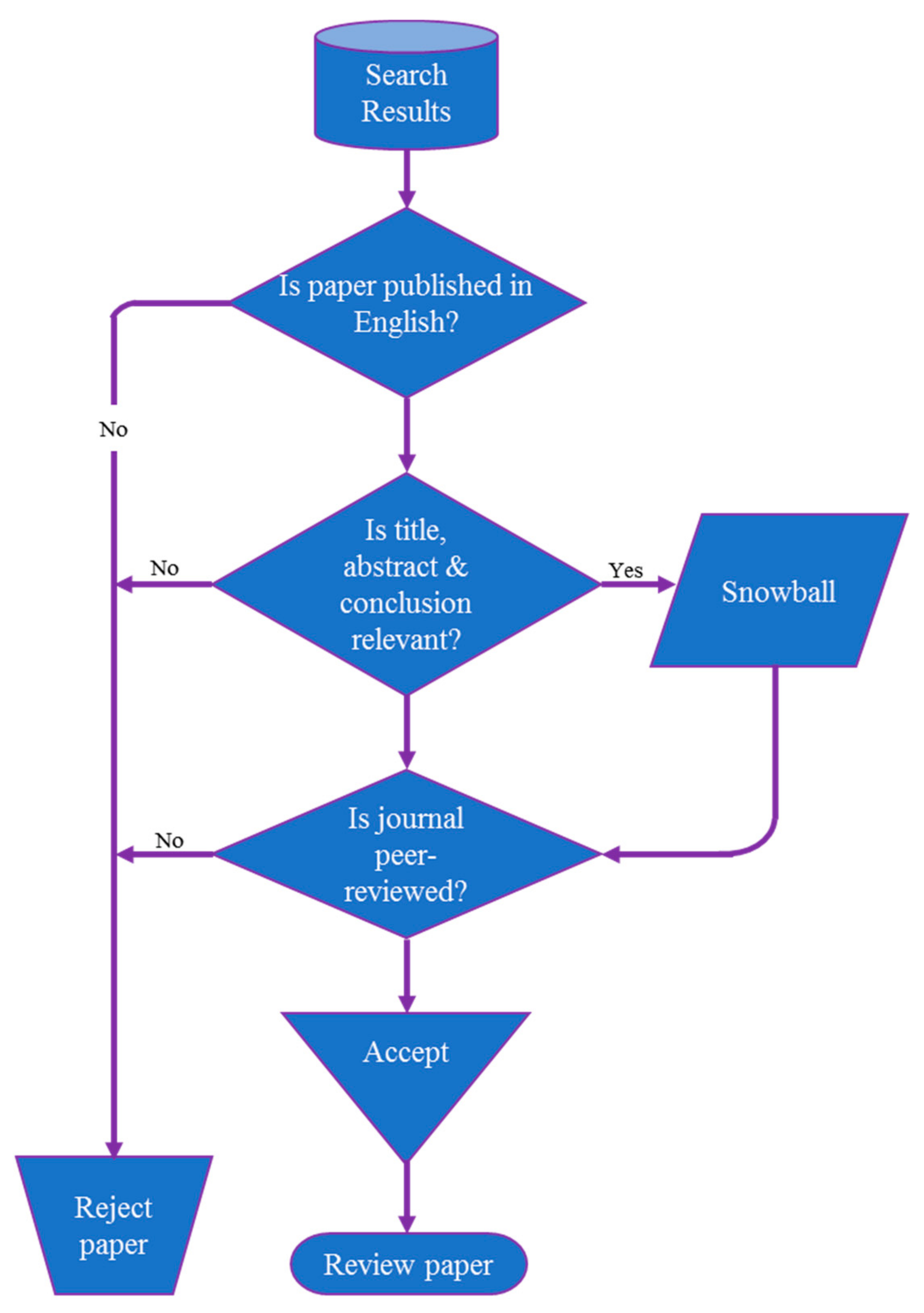
2.1. Review Scope
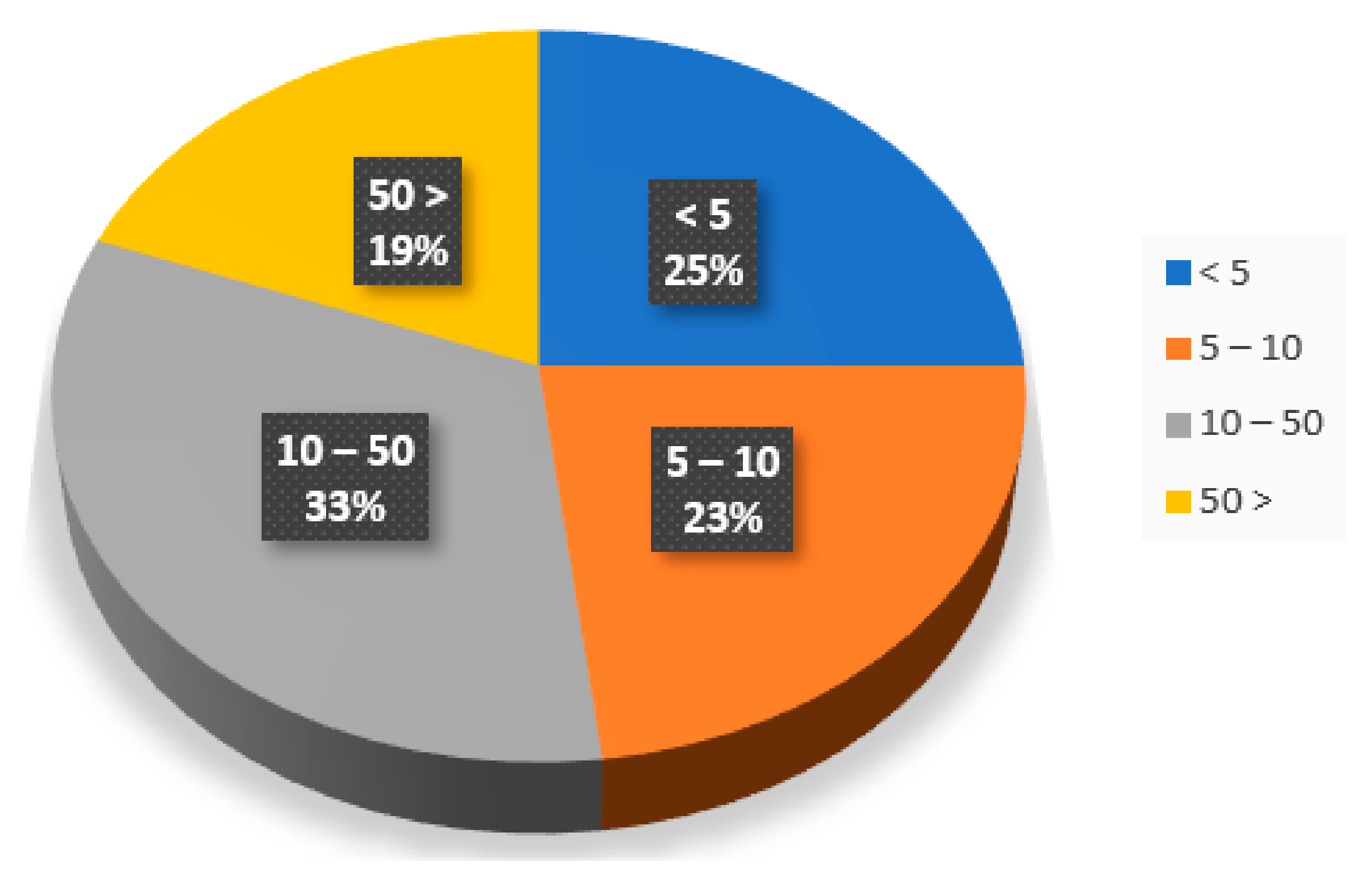
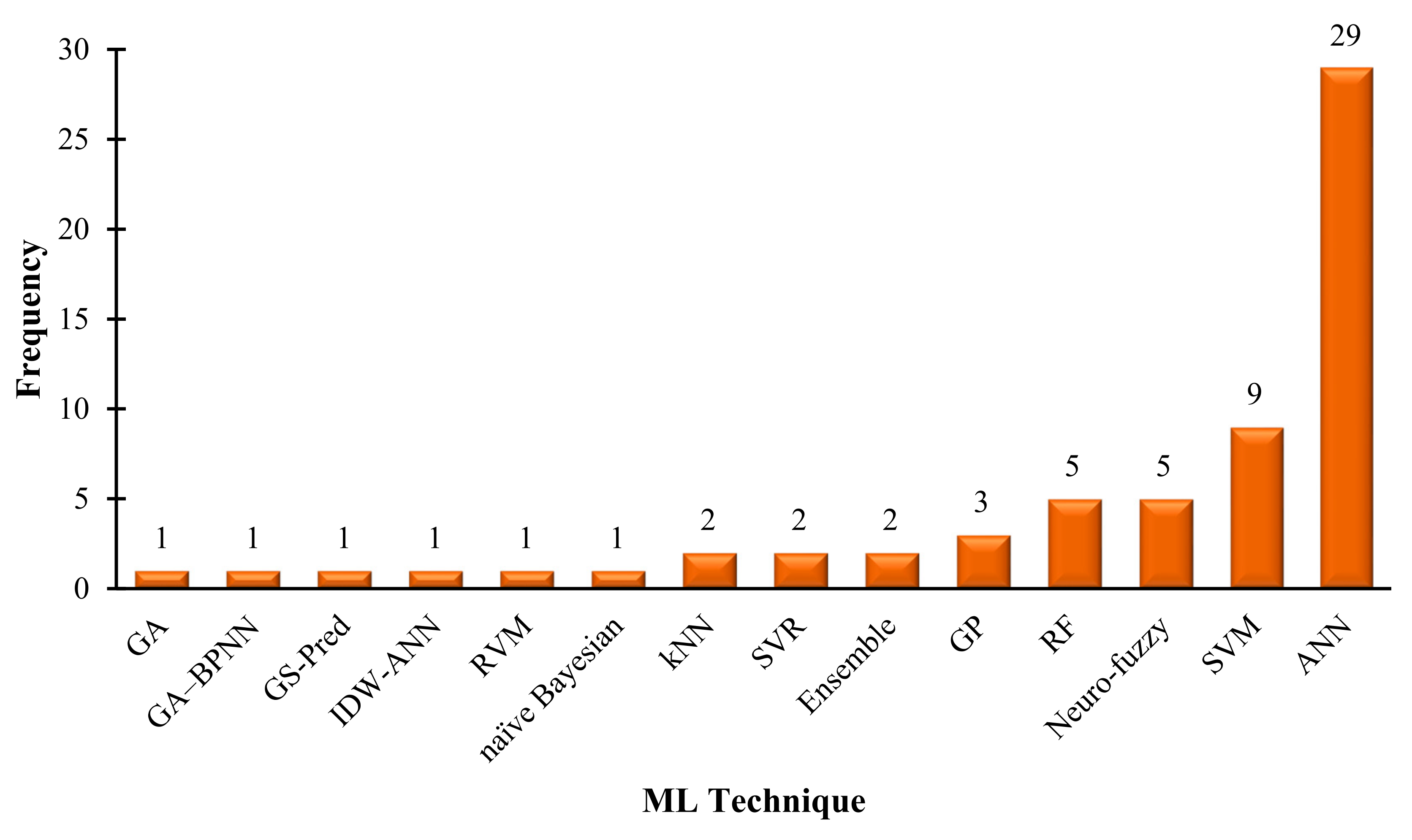
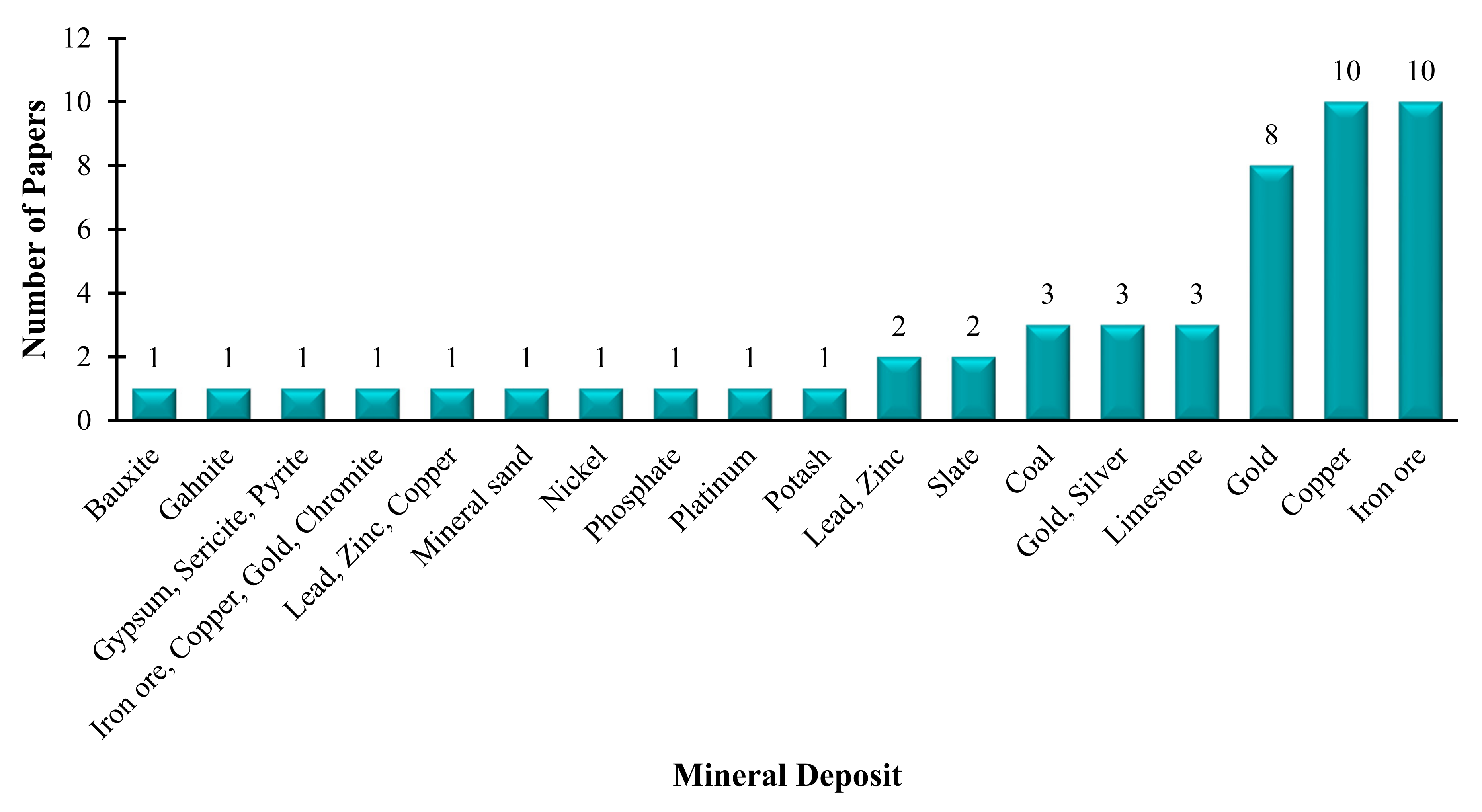
2.2. Review Summary
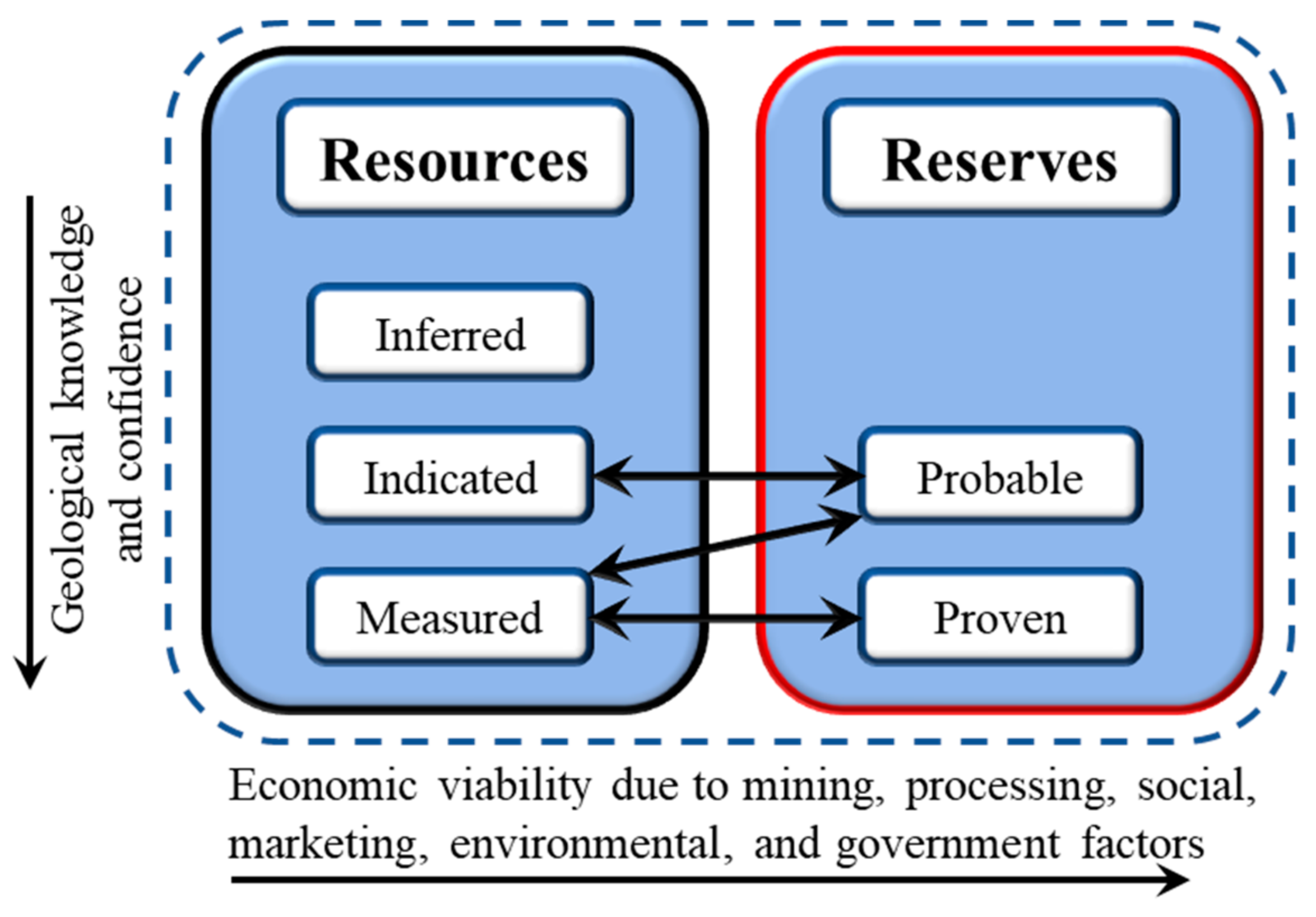
3. Conventional Resource Estimation Techniques
3.1. Inverse Distance Weighting (IDW)
3.2. Kriging
4. Machine Learning Techniques
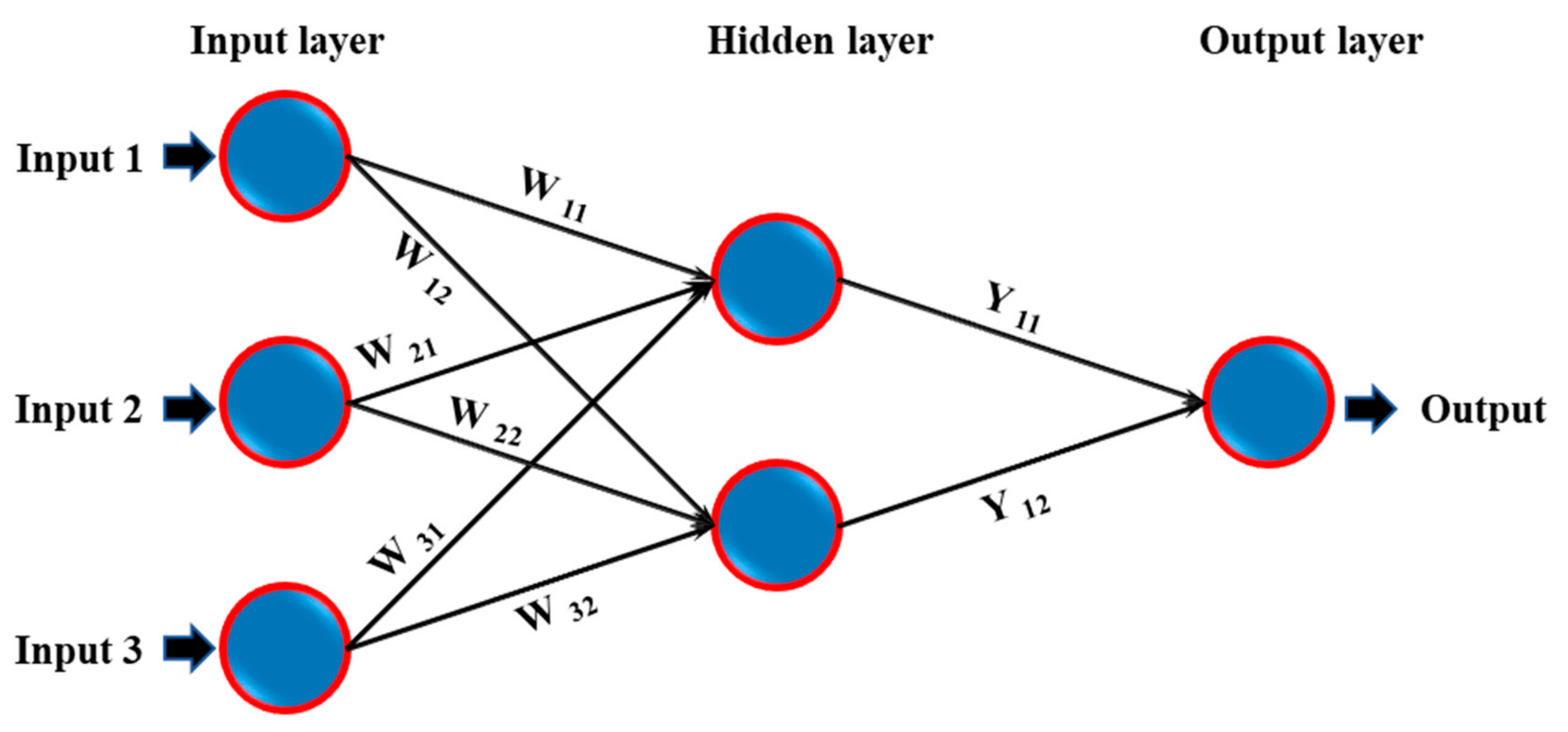
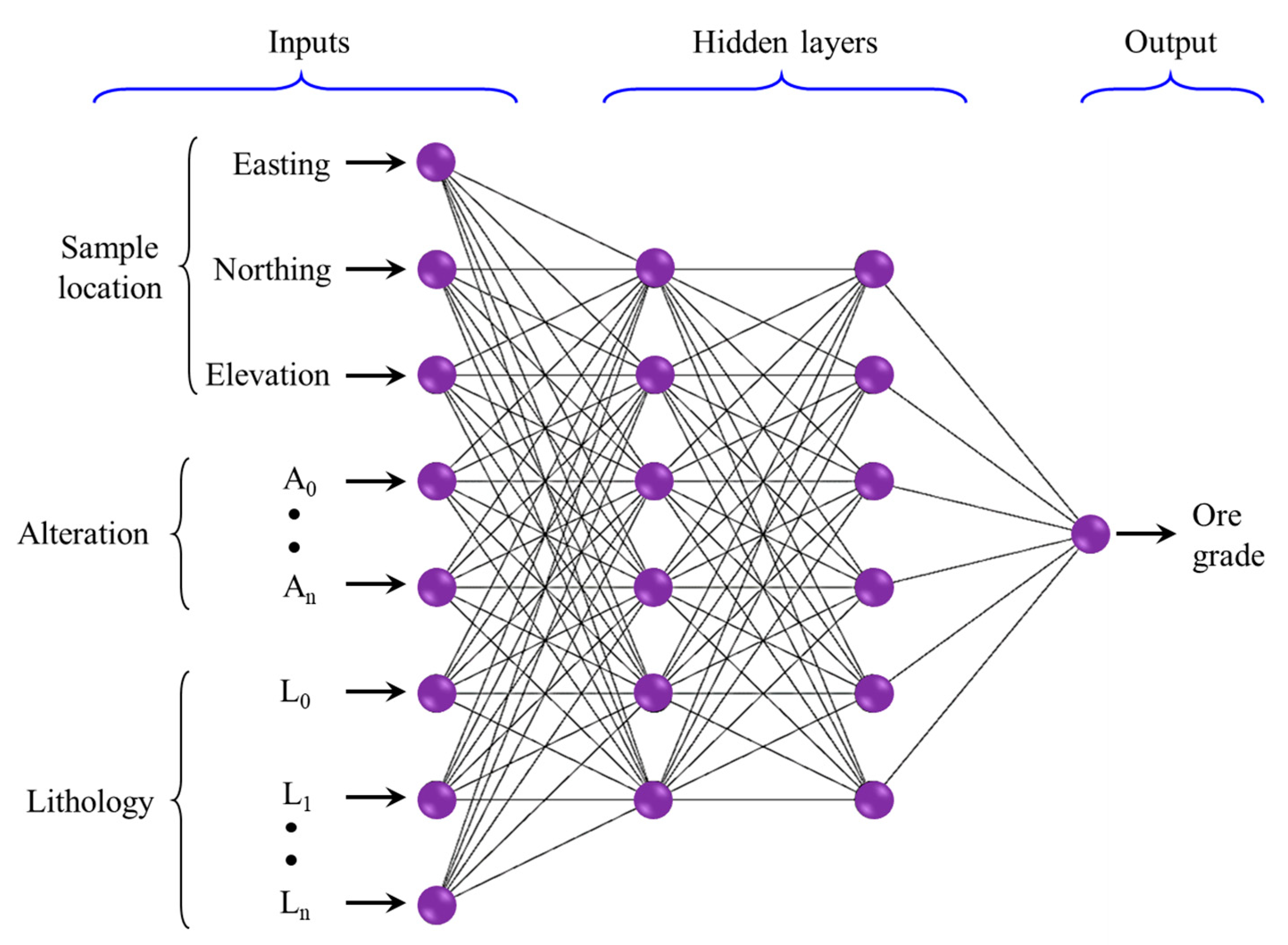
4.1. Artificial Neural Network (ANN)
4.2. Support Vector Machines (SVM)
4.3. Random Forest (RF)
4.4. Emerging and Hybrid Algorithms
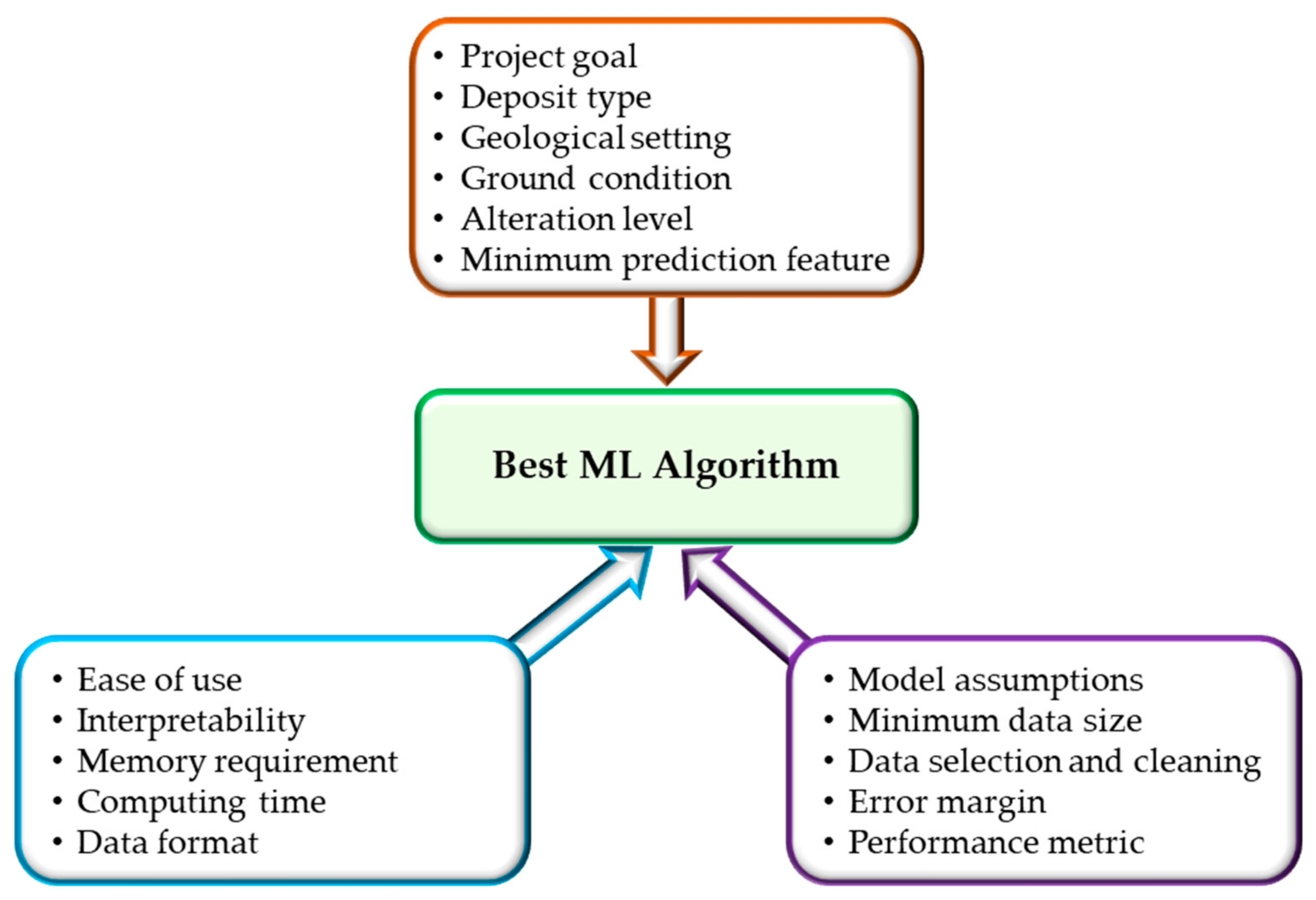
5. Discussion and Future Directions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Coates, D.R. Mineral resources. In Geology and Society; Coates, D.R., Ed.; Springer: Boston, MA, USA, 1985; pp. 19–46. [Google Scholar]
- Dubiński, J. Sustainable Development of Mining Mineral Resources. J. Sustain. Min. 2013, 12, 1–6. [Google Scholar] [CrossRef] [Green Version]
- McMahon, G.; Moreira, S. The Contribution of the Mining Sector to Socioeconomic and Human Development. 2014. Available online: http://hdl.handle.net/10986/18660 (accessed on 20 May 2020).
- Löf, O.; Ericsson, M. Mining’s contribution to national economies. Eng. Min. J. 2018, 219, 48–56. [Google Scholar]
- Van Gosen, B.S.; Verplanck, P.L.; Long, K.R.; Gambogi, J.; Seal, R.R., II. The Rare-Earth Elements: Vital to Modern Technologies and Lifestyles; US Geological Survey: Reston, VA, USA, 2014. [Google Scholar]
- Henckens, M.L.C.M.; Biermann, F.H.B.; Driessen, P.P.J. Mineral resources governance: A call for the establishment of an International Competence Center on Mineral Resources Management. Resour. Conserv. Recycl. 2019, 141, 255–263. [Google Scholar] [CrossRef]
- Crowson, P.C.F. Mineral reserves and future minerals availability. Miner. Econ. 2011, 24, 1–6. [Google Scholar] [CrossRef]
- Zerzour, O.; Gadri, L.; Hadji, R.; Mebrouk, F.; Hamed, Y. Geostatistics-Based Method for Irregular Mineral Resource Estimation, in Ouenza Iron Mine, Northeastern Algeria. Geotech. Geol. Eng. 2021, 39, 3337–3346. [Google Scholar] [CrossRef]
- Tokoglu, M. Comparative Analysis of 3D Domain Modelling Alternatives: Implications for Mineral Resource Estimates; Colorado School of Mines: Golden, CO, USA, 2018. [Google Scholar]
- Abzalov, M.Z.; Bower, J. Geology of bauxite deposits and their resource estimation practices. Appl. Earth Sci. 2014, 123, 118–134. [Google Scholar] [CrossRef]
- Rossi, M.E.; Deutsch, C.V. Mineral Resource Estimation; Springer Science & Business Media: Berlin, Germany, 2014. [Google Scholar]
- Hartman, H.L.; Mutmansky, J.M. Introductory Mining Engineering, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Yunsel, T.Y. A practical application of geostatistical methods to quality and mineral reserve modelling of cement raw materials. J. S. Afr. Inst. Min. Metall. 2012, 112, 239–249. [Google Scholar]
- Shurygin, D.N.; Vlasenko, S.V.; Shutkova, V.V. Estimation of the Error in the Calculation of Mineral Reserves Taking into Account the Heterogeneity of the Geological Space; IOP Publishing: Bristol, UK, 2019; Volume 272, p. 22139. [Google Scholar]
- Wellmer, F.-W.; Dalheimer, M.; Wagner, M. Economic Evaluations in Exploration; Springer Science & Business Media: Berlin, Germany, 2007; ISBN 3540735593. [Google Scholar]
- Jones, O.; Lilford, E.; Chan, F. The Business of Mining: Mineral Project Valuation; CRC Press: Boca Raton, FL, USA, 2018; ISBN 0429622686. [Google Scholar]
- JORC. Australasian Code for Reporting of Exploration Results, Mineral Resources and Ore Reserves (The JORC Code). 2012. Available online: http://www.jorc.org/docs/JORC_code_2012.pdf (accessed on 20 May 2020).
- Dominy, S.C.; Noppé, M.A.; Annels, A.E. Errors and uncertainty in mineral resource and ore reserve estimation: The importance of getting it right. Explor. Min. Geol. 2002, 11, 77–98. [Google Scholar] [CrossRef]
- Abuntori, C.A.; Al-Hassan, S.; Mireku-Gyimah, D.; Ziggah, Y.Y. Evaluating the performance of Extreme Learning Machine technique for ore grade estimation. J. Sustain. Min. 2021, 20, 56–71. [Google Scholar] [CrossRef]
- Shirmard, H.; Farahbakhsh, E.; Muller, D.; Chandra, R. A review of machine learning in processing remote sensing data for mineral exploration. arXiv 2021, arXiv:2103.07678. [Google Scholar]
- Samson, M. Mineral Resource Estimates with Machine Learning and Geostatistics. Master’s Thesis, University of Alberta, Edmonton, AB, Canada, 2020. [Google Scholar]
- Cevik, S.I.; Ortiz, J.M. Machine Learning in the Mineral Resource Sector: An Overview. 2020. Available online: http://hdl.handle.net/1974/28545 (accessed on 20 January 2020).
- Jalloh, A.B.; Kyuro, S.; Jalloh, Y.; Barrie, A.K. Integrating artificial neural networks and geostatistics for optimum 3D geological block modeling in mineral reserve estimation: A case study. Int. J. Min. Sci. Technol. 2016, 26, 581–585. [Google Scholar] [CrossRef]
- Yasrebi, A.B.; Hezarkhani, A.; Afzal, P.; Karami, R.; Tehrani, M.E.; Borumandnia, A. Application of an ordinary kriging–artificial neural network for elemental distribution in Kahang porphyry deposit, Central Iran. Arab. J. Geosci. 2020, 13, 1–14. [Google Scholar] [CrossRef]
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine learning in agriculture: A review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef] [Green Version]
- Ali, D.; Frimpong, S. Artificial intelligence, machine learning and process automation: Existing knowledge frontier and way forward for mining sector. Artif. Intell. Rev. 2020, 53, 6025–6042. [Google Scholar] [CrossRef]
- Hyder, Z.; Siau, K.; Nah, F. Artificial intelligence, machine learning, and autonomous technologies in mining industry. J. Database Manag. 2019, 30, 67–79. [Google Scholar] [CrossRef]
- Zhang, S.E.; Nwaila, G.T.; Tolmay, L.; Frimmel, H.E.; Bourdeau, J.E. Integration of machine learning algorithms with Gompertz Curves and Kriging to estimate resources in gold deposits. Nat. Resour. Res. 2021, 30, 39–56. [Google Scholar] [CrossRef]
- Jung, D.; Choi, Y. Systematic Review of machine learning applications in mining: Exploration, exploitation, and reclamation. Minerals 2021, 11, 148. [Google Scholar] [CrossRef]
- McCoy, J.T.; Auret, L. Machine learning applications in minerals processing: A review. Miner. Eng. 2019, 132, 95–109. [Google Scholar] [CrossRef]
- Dumakor-Dupey, N.K.; Arya, S.; Jha, A. Advances in blast-induced impact prediction—A review of machine learning applications. Minerals 2021, 11, 601. [Google Scholar] [CrossRef]
- Wee, B.V.; Banister, D. How to Write a Literature Review Paper? Transp. Rev. 2016, 36, 278–288. [Google Scholar] [CrossRef] [Green Version]
- Jalali, S.; Wohlin, C. Systematic literature studies: Database searches vs. backward snowballing. In Proceedings of the 2012 ACM-IEEE International Symposium on Empirical Software Engineering and Measurement, Lund, Sweden, 19–20 September 2012. [Google Scholar]
- Haldar, S.K. Mineral resource and ore reserve estimation. In Mineral Exploration; Elsevier: Amsterdam, The Netherlands, 2018; pp. 145–165. [Google Scholar]
- Afeni, T.B.; Akeju, V.O.; Aladejare, A.E. A comparative study of geometric and geostatistical methods for qualitative reserve estimation of limestone deposit. Geosci. Front. 2020, 12, 243–253. [Google Scholar] [CrossRef]
- Glacken, I.M.; Snowden, D.V. Mineral resource estimation. In Mineral Resource and Ore Reserve Estimation—The AusIMM Guide to Good Practice; Edwards, A.C., Ed.; The Australasian Institute of Mining and Metallurgy: Melbourne, Australia, 2001; pp. 189–198. [Google Scholar]
- Wu, X.; Zhou, Y. Reserve estimation using neural network techniques. Comput. Geosci. 1993, 19, 567–575. [Google Scholar] [CrossRef]
- Varouchakis, E.A. Geostatistics. In Spatiotemporal Analysis of Extreme Hydrological Events; Elsevier: Amsterdam, The Netherlands, 2018; ISBN 9780128116890. [Google Scholar]
- Gandhi, S.M.; Sarkar, B.C. Geostatistical resource/reserve estimation. In Essentials of Mineral Exploration and Evaluation; Elsevier: Amsterdam, The Netherlands, 2016; pp. 289–308. [Google Scholar]
- Shahbeik, S.; Afzal, P.; Moarefvand, P.; Qumarsy, M. Comparison between ordinary kriging (OK) and inverse distance weighted (IDW) based on estimation error case study: Dardevey iron ore deposit, NE Iran. Arab. J. Geosci. 2014, 7, 3693–3704. [Google Scholar] [CrossRef]
- Zarco-Perello, S.; Simões, N. Ordinary kriging vs inverse distance weighting: Spatial interpolation of the sessile community of Madagascar reef, Gulf of Mexico. PeerJ 2017, 5, e4078. [Google Scholar] [CrossRef] [Green Version]
- Osterholt, V.; Dimitrakopoulos, R. Simulation of orebody geology with multiple-point geostatistics-application at Yandi channel Iron ore deposit, WA, and implications for resource uncertainty. In Advances in Applied Strategic Mine Planning; Springer Science & Business Media: Berlin, Germany, 2018; pp. 335–352. [Google Scholar]
- Chen, Y.; Jiang, X.; Wang, Y.; Zhuang, D. Spatial characteristics of heavy metal pollution and the potential ecological risk of a typical mining area: A case study in China. Process Saf. Environ. Prot. 2018, 113, 204–219. [Google Scholar] [CrossRef]
- Dominy, S.C.; Hunt, S.P. Evaluation of gold deposits-Part 2: Results of a survey of estimation methodologies applied in the Eastern Goldfields of Western Australia. Trans. Inst. Min. Metall. Sect. B Appl. Earth Sci. 2001, 10, 167–175. [Google Scholar] [CrossRef]
- Yasrebi, A.B.; Afzal, P.; Wetherelt, A.; Foster, P.; Madani, N.; Javadi, A. Application of an inverse distance weighted anisotropic method (IDWAM) to estimate elemental distribution in Eastern Kahang Cu-Mo porphyry deposit, Central Iran. Int. J. Min. Miner. Eng. 2016, 7, 340. [Google Scholar] [CrossRef]
- Al-hassan, S.; David, A. Competitiveness of Inverse Distance Weighting Method for the Evaluation of Gold Resources in Fluvial Sedimentary Deposits: A Case Study. J. Geosci. Geomat. 2015, 3, 122–127. [Google Scholar] [CrossRef]
- Trong, V.D.; Bao, T.D.; Fomin, S.I. Ordinary kriging comparison and inverse distance weighting for quality assessment of Vietnam cement limestone deposits. In Proceedings of the International Multidisciplinary Scientific GeoConference Surveying Geology and Mining Ecology Management, Albena, Bulgaria, 29 June–5 July 2017. [Google Scholar] [CrossRef]
- Mallick, M.K.; Choudhary, B.S.; Budi, G. Geological reserve estimation of limestone deposit: A comparative study between ISDW and OK. Model. Meas. Control C 2020, 81, 72–77. [Google Scholar] [CrossRef]
- Ali Akbar, D. Reserve estimation of central part of Choghart north anomaly iron ore deposit through ordinary kriging method. Int. J. Min. Sci. Technol. 2012, 22, 573–577. [Google Scholar] [CrossRef]
- Daya, A.A.; Bejari, H. A comparative study between simple kriging and ordinary kriging for estimating and modeling the Cu concentration in Chehlkureh deposit, SE Iran. Arab. J. Geosci. 2015, 8, 6003–6020. [Google Scholar] [CrossRef]
- Yasrebi, J.; Saffari, M.; Fathi, H.; Karimian, N.; Moazallahi, M.; Gazni, R. Evaluation and comparison of ordinary kriging and inverse distance weighting methods for prediction of spatial variability of some chemical parameters. Res. J. Biol. Sci. 2009, 4, 93–102. [Google Scholar]
- Daya, A. Ordinary kriging for the estimation of vein type copper deposit: A case study of the Chelkureh, Iran. J. Min. Metall. A Min. 2015, 51, 1–14. [Google Scholar] [CrossRef]
- Hekmatnejad, A.; Emery, X.; Alipour-Shahsavari, M. Comparing linear and non-linear kriging for grade prediction and ore/waste classification in mineral deposits. Int. J. Min. Reclam. Environ. 2019, 33, 247–264. [Google Scholar] [CrossRef]
- Taboada, J.; Saavedra, Á.; Iglesias, C.; Giráldez, E. Estimating quartz reserves using compositional kriging. Abstr. Appl. Anal. 2013, 2013, 1–6. [Google Scholar] [CrossRef]
- Zuo, R. Machine Learning of mineralization-related geochemical anomalies: A Review of potential methods. Nat. Resour. Res. 2017, 26, 457–464. [Google Scholar] [CrossRef]
- Shanmuganathan, S. Artificial neural network modelling: An introduction. In Studies in Computational Intelligence; Springer Science & Business Media: Berlin, Germany, 2016; pp. 1–14. [Google Scholar]
- Prieto, A.; Prieto, B.; Ortigosa, E.M.; Ros, E.; Pelayo, F.; Ortega, J.; Rojas, I. Neural networks: An overview of early research, current frameworks and new challenges. Neurocomputing 2016, 214, 242–268. [Google Scholar] [CrossRef]
- Fung, C.C.; Iyer, V.; Brown, W.; Wong, K.W. Comparing the performance of different neural networks architectures for the prediction of mineral prospectivity. In Proceedings of the 2005 International Conference on Machine Learning and Cybernetics, Guangzhou, China, 18–21 August 2005; Volume 1, pp. 394–398. [Google Scholar]
- Leite, E.P.; de Souza Filho, C.R. Artificial neural networks applied to mineral potential mapping for copper-gold mineralizations in the Carajás Mineral Province, Brazil. Geophys. Prospect. 2009, 57, 1049–1065. [Google Scholar] [CrossRef]
- Rigol-Sanchez, J.P.; Chica-Olmo, M.; Abarca-Hernandez, F. Artificial neural networks as a tool for mineral potential mapping with GIS. Int. J. Remote Sens. 2003, 24, 1151–1156. [Google Scholar] [CrossRef]
- Lee, S.; Oh, H.-J. Application of artificial neural network for mineral potential mapping. In Artificial Neural Networks-Application; BoD–Books on Demand: Norderstedt, Germany, 2011. [Google Scholar]
- Oh, H.J.; Lee, S. Application of artificial neural network for gold-silver deposits potential mapping: A case study of Korea. Nat. Resour. Res. 2010, 19, 103–124. [Google Scholar] [CrossRef]
- Singer, D.A.; Kouda, R. Application of a feedforward neural network in the search for kuroko deposits in the hokuroku district, Japan. Math. Geol. 1996, 28, 1017–1023. [Google Scholar] [CrossRef]
- Harris, D.V.; Pan, G. Mineral favorability mapping: A comparison of artificial neural networks, logistic regression, and discriminant analysis. Nat. Resour. Res. 1999, 8, 93–109. [Google Scholar] [CrossRef]
- Nie, W.; Fang, J.; Wen, S.; Feng, Q.; He, Y.; Yang, X. Estimation and improvement of recovery of low grade copper oxide using sulfide activation flotation method based on GA–BPNN. Processes 2021, 9, 583. [Google Scholar] [CrossRef]
- Al-Alawi, S.M.; Tawo, E.E. Application of Artificial Neural Networks in Mineral Resource Evaluation. J. King Saud Univ. Eng. Sci. 1998, 10, 127–138. [Google Scholar] [CrossRef]
- Yama, B.R.; Lineberry, G.T. Artificial neural network application for a predictive task in mining. Min. Eng. 1999, 51, 59–64. [Google Scholar]
- Koike, K.; Matsuda, S.; Suzuki, T.; Ohmi, M. Neural network-based estimation of principal metal contents in the Hokuroku District, Northern Japan, for exploring Kuroko-type deposits. Nat. Resour. Res. 2002, 11, 135–156. [Google Scholar] [CrossRef]
- Tahmasebi, P.; Hezarkhani, A. Application of adaptive neuro-fuzzy inference system for grade estimation; case study, sarcheshmeh porphyry copper deposit, Kerman, Iran. Aust. J. Basic Appl. Sci. 2010, 4, 408–420. [Google Scholar]
- Tahmasebi, P.; Hezarkhani, A. Application of a Modular Feedforward Neural Network for Grade Estimation. Nat. Resour. Res. 2011, 20, 25–32. [Google Scholar] [CrossRef]
- Matías, J.M.; Vaamonde, A.; Taboada, J.; González-Manteiga, W. Comparison of kriging and neural networks with application to the exploitation of a slate mine. Math. Geol. 2004, 36, 463–486. [Google Scholar] [CrossRef]
- Chatterjee, S.; Bhattacherjee, A.; Samanta, B.; Pal, S.K. Ore grade estimation of a limestone deposit in India using an artificial neural network. Appl. GIS 2006, 2, 3.1–3.20. [Google Scholar] [CrossRef]
- Kaplan, U.E.; Topal, E. A new ore grade estimation using combine machine learning algorithms. Minerals 2020, 10, 847. [Google Scholar] [CrossRef]
- Tutmez, B. An uncertainty oriented fuzzy methodology for grade estimation. Comput. Geosci. 2007, 33, 280–288. [Google Scholar] [CrossRef]
- Tutmez, B.; Tercan, A.E.; Kaymak, U. Fuzzy modeling for reserve estimation based on spatial variability. Math. Geol. 2007, 39, 87–111. [Google Scholar] [CrossRef]
- Tutmez, B. Use of hybrid intelligent computing in mineral resources evaluation. Appl. Soft Comput. J. 2009, 9, 1023–1028. [Google Scholar] [CrossRef]
- Tahmasebi, P.; Hezarkhani, A.; Mortazavi, M. Application of discriminant analysis for alteration separation; Sungun copper deposit, East Azerbaijan, Iran. Aust. J. Basic Appl. Sci. 2010, 6, 565. [Google Scholar]
- Tahmasebi, P.; Hezarkhani, A. A hybrid neural networks-fuzzy logic-genetic algorithm for grade estimation. Comput. Geosci. 2012, 42, 18–27. [Google Scholar] [CrossRef] [Green Version]
- Li, X.-L.; Xie, Y.-L.; Guo, Q.-J.; Li, L.-H. Adaptive ore grade estimation method for the mineral deposit evaluation. Math. Comput. Model. 2010, 52, 1947–1956. [Google Scholar] [CrossRef]
- Singh, R.K.; Ray, D.; Sarkar, B.C. Recurrent neural network approach to mineral deposit modelling. In Proceedings of the Proceedings of the 4th IEEE International Conference on Recent Advances in Information Technology, Dhanbad, India, 15–17 March 2018. [Google Scholar]
- Huang, Y.; Wänstedt, S. Application of Kalman learning algorithm multilayer neural network to estimates of ore grades. Int. J. Surf. Min. Reclam. Environ. 1998, 12, 19–27. [Google Scholar] [CrossRef]
- Jafrasteh, B.; Fathianpour, N. A hybrid simultaneous perturbation artificial bee colony and back-propagation algorithm for training a local linear radial basis neural network on ore grade estimation. Neurocomputing 2017, 235, 217–227. [Google Scholar] [CrossRef]
- Samanta, B. Radial basis function network for ore grade estimation. Nat. Resour. Res. 2010, 19, 91–102. [Google Scholar] [CrossRef]
- Samanta, B.; Bandopadhyay, S. Construction of a radial basis function network using an evolutionary algorithm for grade estimation in a placer gold deposit. Comput. Geosci. 2009, 35, 1592–1602. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Chatterjee, S.; Bandopadhyay, S. Goodnews Bay Platinum resource estimation using least squares support vector regression with selection of input space dimension and hyperparameters. Nat. Resour. Res. 2011, 20, 117–129. [Google Scholar] [CrossRef]
- Li, X.; Li, L.; Zhang, B.; Guo, Q. Hybrid self-adaptive learning based particle swarm optimization and support vector regression model for grade estimation. Neurocomputing 2013, 118, 179–190. [Google Scholar] [CrossRef]
- Zuo, R.; Carranza, E.J.M. Support vector machine: A tool for mapping mineral prospectivity. Comput. Geosci. 2011, 37, 1967–1975. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Sanchez-Castillo, M.; Chica-Olmo, M.; Chica-Rivas, M. Machine learning predictive models for mineral prospectivity: An evaluation of neural networks, random forest, regression trees and support vector machines. Ore Geol. Rev. 2015, 71, 804–818. [Google Scholar] [CrossRef]
- Geranian, H.; Tabatabaei, S.H.; Asadi, H.H.; Carranza, E.J.M. Application of discriminant analysis and support vector machine in mapping gold potential areas for further drilling in the Sari-Gunay gold deposit, NW Iran. Nat. Resour. Res. 2016, 25, 145–159. [Google Scholar] [CrossRef]
- Mahvash Mohammadi, N.; Hezarkhani, A. Application of support vector machine for the separation of mineralised zones in the Takht-e-Gonbad porphyry deposit, SE Iran. J. Afr. Earth Sci. 2018, 143, 301–308. [Google Scholar] [CrossRef]
- Ghezelbash, R.; Maghsoudi, A.; Carranza, E.J.M. Performance evaluation of RBF- and SVM-based machine learning algorithms for predictive mineral prospectivity modeling: Integration of S-A multifractal model and mineralization controls. Earth Sci. Inform. 2019, 12, 277–293. [Google Scholar] [CrossRef]
- Abbaszadeh, M.; Hezarkhani, A.; Soltani-Mohammadi, S. Proposing drilling locations based on the 3D modeling results of fluid inclusion data using the support vector regression method. J. Geochem. Explor. 2016, 165, 23–34. [Google Scholar] [CrossRef]
- Abbaszadeh, M.; Hezarkhani, A.; Soltani-Mohammadi, S. Classification of alteration zones based on whole-rock geochemical data using support vector machine. J. Geol. Soc. India 2015, 85, 500–508. [Google Scholar] [CrossRef]
- Abbaszadeh, M.; Hezarkhani, A.; Soltani-Mohammadi, S. An SVM-based machine learning method for the separation of alteration zones in Sungun porphyry copper deposit. Geochemistry 2013, 73, 545–554. [Google Scholar] [CrossRef]
- Taboada, J.; Matías, J.M.; Ordóñez, C.; García, P.J. Creating a quality map of a slate deposit using support vector machines. J. Comput. Appl. Math. 2007, 204, 84–94. [Google Scholar] [CrossRef] [Green Version]
- Das Goswami, A.; Mishra, M.K.; Patra, D. Adapting pattern recognition approach for uncertainty assessment in the geologic resource estimation for Indian iron ore mines. In Proceedings of the International Conference on Signal Processing, Communication, Power and Embedded System, Sankt Goar, Germany, 23–25 May 2016. [Google Scholar]
- Zhang, X.; Song, S.; Li, J.; Cheng, W. Robust LS-SVM regression for ore grade estimation in a seafloor hydrothermal sulphide deposit. Acta Oceanol. Sin. 2013, 32, 16–25. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, S.; You, K.; Zhang, X.; Wu, C. Relevance vector machines using weighted expected squared distance for ore grade estimation with incomplete data. Int. J. Mach. Learn. Cybern. 2017, 8, 1655–1666. [Google Scholar] [CrossRef]
- Tipping, M.E. The relevance vector machine. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Suganthan, P.N. Random Forests with ensemble of feature spaces. Pattern Recognit. 2014, 47, 3429–3437. [Google Scholar] [CrossRef]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Ao, Y.; Li, H.; Zhu, L.; Ali, S.; Yang, Z. The linear random forest algorithm and its advantages in machine learning assisted logging regression modeling. J. Pet. Sci. Eng. 2019, 174, 776–789. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăgu, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R.; Dixon, B. GIS-based groundwater potential mapping using boosted regression tree, classification and regression tree, and random forest machine learning models in Iran. Environ. Monit. Assess. 2016, 188, 1–27. [Google Scholar] [CrossRef]
- Baudron, P.; Alonso-Sarría, F.; García-Aróstegui, J.L.; Cánovas-García, F.; Martínez-Vicente, D.; Moreno-Brotóns, J. Identifying the origin of groundwater samples in a multi-layer aquifer system with Random Forest classification. J. Hydrol. 2013, 499, 303–315. [Google Scholar] [CrossRef]
- McKay, G.; Harris, J.R. Comparison of the data-driven random forests model and a knowledge-driven method for mineral prospectivity mapping: A case study for gold deposits around the Huritz Group and Nueltin Suite, Nunavut, Canada. Nat. Resour. Res. 2016, 25, 125–143. [Google Scholar] [CrossRef]
- Jafrasteh, B.; Fathianpour, N.; Suárez, A. Comparison of machine learning methods for copper ore grade estimation. Comput. Geosci. 2018, 22, 1371–1388. [Google Scholar] [CrossRef]
- Sheng, L.; Zhang, T.; Niu, G.; Wang, K.; Tang, H.; Duan, Y.; Li, H. Classification of iron ores by laser-induced breakdown spectroscopy (LIBS) combined with random forest (RF). J. Anal. At. Spectrom. 2015, 30, 453–458. [Google Scholar] [CrossRef]
- O’Brien, J.J.; Spry, P.G.; Nettleton, D.; Xu, R.; Teale, G.S. Using random forests to distinguish gahnite compositions as an exploration guide to broken hill-type Pb-Zn-Ag deposits in the broken hill domain, Australia. J. Geochem. Explor. 2014, 149, 74–86. [Google Scholar] [CrossRef]
- Schnitzler, N.; Ross, P.S.; Gloaguen, E. Using machine learning to estimate a key missing geochemical variable in mining exploration: Application of the Random Forest algorithm to multi-sensor core logging data. J. Geochem. Explor. 2019, 205, 106344. [Google Scholar] [CrossRef]
- Matin, S.S.; Chelgani, S.C. Estimation of coal gross calorific value based on various analyses by random forest method. Fuel 2016, 177, 274–278. [Google Scholar] [CrossRef]
- Seeger, M. Gaussian processes for machine learning. Int. J. Neural Syst. 2004, 14, 69–106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning. 2006. Available online: http://www.gaussianprocess.org/gpml/chapters/RW.pdf (accessed on 20 May 2020).
- Chen, F.; Chen, S.; Peng, G. Using Sequential Gaussian Simulation to Assess Geochemical Anomaly Areas of Lead Element; Springer: Berlin, Germany, 2013. [Google Scholar]
- Wang, J.; Zuo, R. Identification of geochemical anomalies through combined sequential Gaussian simulation and grid-based local singularity analysis. Comput. Geosci. 2018, 118, 52–64. [Google Scholar] [CrossRef]
- Soltani, F.; Afzal, P.; Asghari, O. Delineation of alteration zones based on Sequential Gaussian Simulation and concentration-volume fractal modeling in the hypogene zone of Sungun copper deposit, NW Iran. J. Geochem. Explor. 2014, 140, 64–76. [Google Scholar] [CrossRef]
- Afzal, P.; Madani, N.; Shahbeik, S.; Yasrebi, A.B. Multi-Gaussian kriging: A practice to enhance delineation of mineralized zones by Concentration-Volume fractal model in Dardevey iron ore deposit, SE Iran. J. Geochem. Explor. 2015, 158, 10–21. [Google Scholar] [CrossRef]
- Bazdar, H.; Fattahi, H.; Ghadimi, F. Hybrid ANN with invasive weed optimization algorithm, a new technique for prediction of gold and silver in Zarshuran gold deposit, Iran. Q. J. Tethys 2015, 3, 273–285. [Google Scholar]
- Mahmoudabadi, H.; Izadi, M.; Menhaj, M.B. A hybrid method for grade estimation using genetic algorithm and neural networks. Comput. Geosci. 2009, 13, 91–101. [Google Scholar] [CrossRef]
- Yu, S.; Zhu, K.; He, Y. A hybrid intelligent optimization method for multiple metal grades optimization. Neural Comput. Appl. 2012, 21, 1391–1402. [Google Scholar] [CrossRef]
- Chatterjee, S.; Bhattacherjee, A. Genetic algorithms for feature selection of image analysis-based quality monitoring model: An application to an iron mine. Eng. Appl. Artif. Intell. 2011, 24, 786–795. [Google Scholar] [CrossRef]
- Patel, A.K.; Chatterjee, S.; Gorai, A.K. Development of a machine vision system using the support vector machine regression (SVR) algorithm for the online prediction of iron ore grades. Earth Sci. Inform. 2019, 12, 197–210. [Google Scholar] [CrossRef]
- Patel, A.K.; Chatterjee, S. Computer vision-based limestone rock-type classification using probabilistic neural network. Geosci. Front. 2016, 7, 53–60. [Google Scholar] [CrossRef] [Green Version]
- Perez, C.A.; Estévez, P.A.; Vera, P.A.; Castillo, L.E.; Aravena, C.M.; Schulz, D.A.; Medina, L.E. Ore grade estimation by feature selection and voting using boundary detection in digital image analysis. Int. J. Miner. Process. 2011, 101, 28–36. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, J.; Wang, Y.; Dou, D.; Xia, W. Ash content prediction of coarse coal by image analysis and GA-SVM. Powder Technol. 2014, 268, 429–435. [Google Scholar] [CrossRef]
- Kanevski, M. Machine Learning for Spatial Environmental Data: Theory, Applications, and Software; EPFL Press: Lausanne, Switzerland, 2009. [Google Scholar]
- Li, J.; Heap, A.D.; Potter, A.; Daniell, J.J. Application of machine learning methods to spatial interpolation of environmental variables. Environ. Model. Softw. 2011, 26, 1647–1659. [Google Scholar] [CrossRef]
- Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine learning in geosciences and remote sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef] [Green Version]
- Karami, R.; Afzal, P. Estimation of elemental distributions by combining artificial neural network and Inverse Distance Weighted (IDW) based on lithogeochemical data in Kahang porphry deposit, Central Iran. Univers. J. Geosci. 2015, 3, 59–65. [Google Scholar] [CrossRef]
- Dutta, S.; Bandopadhyay, S.; Ganguli, R.; Misra, D. Machine learning algorithms and their application to ore reserve estimation of sparse and imprecise data. J. Intell. Learn. Syst. Appl. 2010, 2, 86. [Google Scholar] [CrossRef] [Green Version]
- Das Goswami, A.; Mishra, M.K.; Patra, D. Investigation of general regression neural network architecture for grade estimation of an Indian iron ore deposit. Arab. J. Geosci. 2017, 10. [Google Scholar] [CrossRef]
- Lishchuk, V.; Lund, C.; Ghorbani, Y. Evaluation and comparison of different machine-learning methods to integrate sparse process data into a spatial model in geometallurgy. Miner. Eng. 2019, 134, 156–165. [Google Scholar] [CrossRef]
- Ishikawa, S.T.; Gulick, V.C. An automated mineral classifier using Raman spectra. Comput. Geosci. 2013, 54, 259–268. [Google Scholar] [CrossRef]
- Fouedjio, F.; Klump, J. Exploring prediction uncertainty of spatial data in geostatistical and machine learning approaches. Environ. Earth Sci. 2019, 78, 38. [Google Scholar] [CrossRef]
- Nwaila, G.T.; Zhang, S.E.; Frimmel, H.E.; Manzi, M.S.D.; Dohm, C.; Durrheim, R.J.; Burnett, M.; Tolmay, L. Local and target exploration of conglomerate-hosted gold deposits using machine learning algorithms: A case study of the Witwatersrand gold ores, South Africa. Nat. Resour. Res. 2020, 29, 135–159. [Google Scholar] [CrossRef]
- Caté, A.; Perozzi, L.; Gloaguen, E.; Blouin, M. Machine learning as a tool for geologists. Lead. Edge 2017, 36, 215–219. [Google Scholar] [CrossRef]
- Chen, L.; Ren, C.; Li, L.; Wang, Y.; Zhang, B.; Wang, Z.; Li, L. A comparative assessment of geostatistical, machine learning, and hybrid approaches for mapping topsoil organic carbon content. ISPRS Int. J. Geo-Inf. 2019, 8, 174. [Google Scholar] [CrossRef] [Green Version]
- Jafrasteh, B.; Fathianpour, N.; Suárez, A. Advanced Machine Learning Methods for Copper Ore Grade Estimation; European Association of Geoscientists & Engineers: Houten, The Netherlands, 2016. [Google Scholar]
- Afeni, T.B.; Lawal, A.I.; Adeyemi, R.A. Re-examination of Itakpe iron ore deposit for reserve estimation using geostatistics and artificial neural network techniques. Arab. J. Geosci. 2020, 13, 657. [Google Scholar] [CrossRef]
- Kapageridis, I.K. Input space configuration effects in neural network-based grade estimation. Comput. Geosci. 2005, 31, 704–717. [Google Scholar] [CrossRef]
- Erdogan Erten, G.; Yavuz, M.; Deutsch, C.V. Grade estimation by a machine learning model using coordinate rotations. Appl. Earth Sci. 2021, 130, 57–66. [Google Scholar] [CrossRef]
- Chatterjee, S.; Bandopadhyay, S.; Machuca, D. Ore grade prediction using a genetic algorithm and clustering Based ensemble neural network model. Math. Geosci. 2010, 42, 309–326. [Google Scholar] [CrossRef]
- Zhou, Z.H. Ensemble Methods: Foundations and Algorithms; CRC Press: Boca Raton, FL, USA, 2012; ISBN 9781439830055. [Google Scholar]
- Li, Y.; Gao, J.; Li, Q.; Fan, W. Ensemble learning. In Data Classification: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2014; ISBN 9781466586758. [Google Scholar]
- Chatterjee, S.; Bandopadhyay, S.; Rai, P. Genetic algorithm-based neural network learning parameter selection for ore grade evaluation of limestone deposit. Min. Technol. 2008, 117, 178–190. [Google Scholar] [CrossRef]
- Tahmasebi, P.; Hezarkhani, A. Application of Optimized Neural Network by Genetic Algorithm, IAMG09; Stanford University: Stanford, CA, USA, 2009. [Google Scholar]
- Samanta, B.; Bandopadhyay, S.; Ganguli, R. Data segmentation and genetic algorithms for sparse data division in Nome placer gold grade estimation using neural network and geostatistics. Explor. Min. Geol. 2002, 11, 69–76. [Google Scholar] [CrossRef]
- Tang, Y.; Salakhutdinov, R. Learning stochastic feedforward neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–8 December 2013. [Google Scholar]
- Ling, H.; Samarasinghe, S.; Kulasiri, D. Stochastic neural networks for modelling random processes from observed data. In Artificial Neural Network Modelling; Springer: Berlin, Germany, 2016. [Google Scholar]
- Kapageridis, I.K.; Denby, B.; Hunter, G. Integration of a neural ore grade estimation tool in a 3D resource modeling package. In Proceedings of the International Joint Conference on Neural Networks, Washington, DC, USA, 10–16 July 1999. [Google Scholar]
- Kapageridis, I.K. Application of Artificial Neural Network Systems to Grade Estimation from Exploration Data. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 1999. [Google Scholar]
- Žliobaitė, I.; Pechenizkiy, M.; Gama, J. An overview of concept drift applications. Big Data Anal. New Algorithms New Soc. 2016, 16, 91–114. [Google Scholar]
- Žliobaitė, I. Learning under concept drift: An overview. arXiv 2010, arXiv:1010.4784. [Google Scholar]
- Zhukov, A.V.; Sidorov, D.N.; Foley, A.M. Random Forest Based Approach for Concept Drift Handling; Springer: Berlin, Germany, 2016; pp. 69–77. [Google Scholar]
- Zenisek, J.; Holzinger, F.; Affenzeller, M. Machine learning based concept drift detection for predictive maintenance. Comput. Ind. Eng. 2019, 137, 106031. [Google Scholar] [CrossRef]
- Namitha, K. Concept drift detection in data stream clustering and its application on weather data. Int. J. Agric. Environ. Inf. Syst. 2020, 11, 67–85. [Google Scholar] [CrossRef]
- Fdez-Riverola, F.; Iglesias, E.L.; Díaz, F.; Méndez, J.R.; Corchado, J.M. Applying lazy learning algorithms to tackle concept drift in spam filtering. Expert Syst. Appl. 2007, 33, 36–48. [Google Scholar] [CrossRef] [Green Version]
- Sayadi, A.R.; Tavassoli, S.M.M.; Monjezi, M.; Rezaei, M. Application of neural networks to predict net present value in mining projects. Arab. J. Geosci. 2014, 7, 1067–1072. [Google Scholar] [CrossRef]
- Zhang, H.; Nguyen, H.; Bui, X.N.; Nguyen-Thoi, T.; Bui, T.T.; Nguyen, N.; Vu, D.A.; Mahesh, V.; Moayedi, H. Developing a novel artificial intelligence model to estimate the capital cost of mining projects using deep neural network-based ant colony optimization algorithm. Resour. Policy 2020, 66, 101604. [Google Scholar] [CrossRef]
- Ganguli, R.; Dagdelen, K.; Grygiel, E. System engineering. In SME Mining Engineering Handbook; Darling, P., Ed.; SME: Englewood, CO, USA, 2011; pp. 839–853. [Google Scholar]




| Implementation | Count |
|---|---|
| Historical and field data | 1 |
| Laboratory-scale data | 1 |
| Experimental and laboratory-scale data | 2 |
| Historical data | 3 |
| Simulated and field data | 3 |
| Field data | 42 |
| Technique | Deposit | Year |
|---|---|---|
| Ensemble | Gold | 2021 |
| IDW-ANN | Copper | 2015 |
| GA | Iron | 2012 |
| GA-BPNN | Copper | 2021 |
| GS-Pred | Gold | 2020 |
| RVM | Copper, Silver | 2015 |
| kNN | Gold | 2017, 2020 |
| SVR | Copper, Iron | 2013, 2019 |
| RF | Iron, Gahnite, Copper | 2014, 2015, 2016 |
| GP | Copper, Gold | 2016, 2017, 2018 |
| Neuro-fuzzy | Copper, Coal | 2007, 2009, 2010, 2012 |
| SVM | Platinum, Copper, Nickel, Slate, Silver, Gold | 2007, 2011, 2013, 2016, 2018 |
| ANN | Bauxite, Gold, Silver, Limestone, Zinc, Lead, Iron, Phosphate, Copper, Chromite, Potash, Slate, Gypsum, Sericite, Pyrite, Copper, Mineral sand | 1993, 1996, 1998, 1999, 2002, 2004, 2005, 2006, 2008, 2009, 2010, 2011, 2012, 2015, 2016, 2017, 2018, 2020 |
| Algorithm | Variables | Deposit | Dataset | Result | Reference |
|---|---|---|---|---|---|
| ANN | Drillhole location and composite grade values | Copper | 25 drill holes | A maximum absolute error of 80% was obtained for the training set. The estimate reflected actual grade distribution as high grades, but few cases were underestimated because they were few. | [37] |
| ANN | Input variables are X and Y coordinates, while target variables are the thickness of mineralized lengths of the deposit and the corresponding content of alumina and silica | Bauxite | 163 drill holes | The results showed that the input variables could explain 79% of the variability in the target variables. | [66] |
| ANN | Drillhole spatial location (X, Y, and Z) and sample length | Mineral sand | 2880 composite samples from 302 drillholes | The model showed accurate predictions of ore grade with R2 of 0.889; however, underpredicted for high-grade values that had relatively few training cases. | [23] |
| ANN and kNN | Geological information (lithology and alteration) and sample location (X, Y, and Z) | Gold | 123 drill holes | The model predicted the grades on a test dataset with a mean absolute error (MAE) of 0.507 and R2 is 0.528. | [73] |
| Algorithm | Variables | Deposit | Dataset | Result | Reference |
|---|---|---|---|---|---|
| SVM | The model incorporated information (drillhole coordinates) from 4 (Case 1) and 16 (Case 2) neighborhood samples as input parameters to estimate grades for unsampled locations | Platinum | 470 drill holes | The models recorded higher R values than kriging, but the grades were underestimated. | [86] |
| SVM | Slate quality evaluation based on sandy intercalations, quartz-filled microfractures, flat-lying schistosity planes, pyrite or other sulfurs affected by oxidation, surface alterations, crenulation schistosity, and kink bands | Slate | 10 boreholes | The SVM result compared well with kriging with the advantage of easy interpretation, better control over outliers, and greater sparsity. | [96] |
| Algorithm | Variables | Deposit | Dataset | Result | Reference |
|---|---|---|---|---|---|
| RF | Emission spectral lines of Si and Ti as the input data and ore class as output data | Iron ore | 300 analytical spectra were acquired from 10 classes of iron ores | The model exhibits better predictive power with an accuracy of 97.5% for all spectral data as the input and prediction accuracy of 100% for iron ore samples. | [111] |
| RF | Compositions of gahnite in sulfide-bearing rocks | Polymetallic | 533 | The model classified gahnite into various schemes with misclassification rates of 1.6, 3.3, and 4.7%. | [112] |
| Algorithm | Variables | Deposit | Dataset | Result | Reference |
|---|---|---|---|---|---|
| SLPSO–SVR | Contour map of copper distribution was used as input data and copper grade was the target variable | Copper | 200 groups of sample data | The model has advantages of rapid training, generality, and accuracy grade estimation approach. | [87] |
| GP | Hole location was used as predictor variable and grade as target variable | Copper | 603 drill holes | GP performed better than other models. | [110] |
| ELM | Input data is X, Y, and Z coordinate, and the output is ore grade. | Gold | 3759 drill holes | ELM with sigmoid activation function better than other models with R2 of 0.9193. | [19] |
| Machine Vision and Image classification | A total of 280 image features were extracted from ore sample images captured on a belt conveyor. | Iron ore | 280 image features | The model showed a satisfactory prediction of iron ore grade with R2 of 0.9402. | [125] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dumakor-Dupey, N.K.; Arya, S. Machine Learning—A Review of Applications in Mineral Resource Estimation. Energies 2021, 14, 4079. https://doi.org/10.3390/en14144079
Dumakor-Dupey NK, Arya S. Machine Learning—A Review of Applications in Mineral Resource Estimation. Energies. 2021; 14(14):4079. https://doi.org/10.3390/en14144079
Chicago/Turabian StyleDumakor-Dupey, Nelson K., and Sampurna Arya. 2021. "Machine Learning—A Review of Applications in Mineral Resource Estimation" Energies 14, no. 14: 4079. https://doi.org/10.3390/en14144079
APA StyleDumakor-Dupey, N. K., & Arya, S. (2021). Machine Learning—A Review of Applications in Mineral Resource Estimation. Energies, 14(14), 4079. https://doi.org/10.3390/en14144079






