Efficient Ranking-Based Whale Optimizer for Parameter Extraction of Three-Diode Photovoltaic Model: Analysis and Validations
Abstract
:1. Introduction
- Slow convergence toward the best solution because of the distance control factor that reduces gradually with the iterations;
- Using the current positions in the next generation, even if it is worse, may reduce the probability of getting to better solutions;
- After half the maximum iterations, the exploration operator will be terminated and hence stagnation inside local minima is inevitable if the best-so-far solution is so.
- Proposing a new updating scheme to replace the unbeneficial solutions under the ranking method for reducing the probability of stagnation into local optimal and then integrating the WOA with this strategy in a variant named RWOA to utilize each solution within the optimization process as possible;
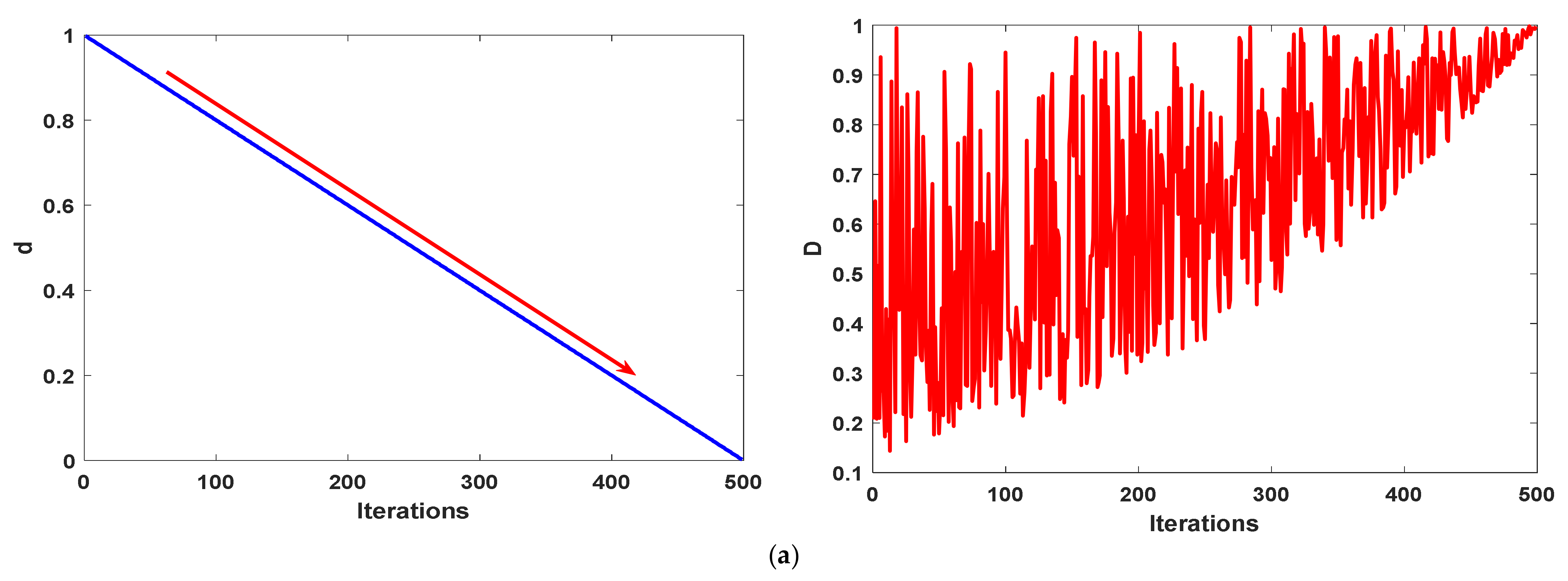
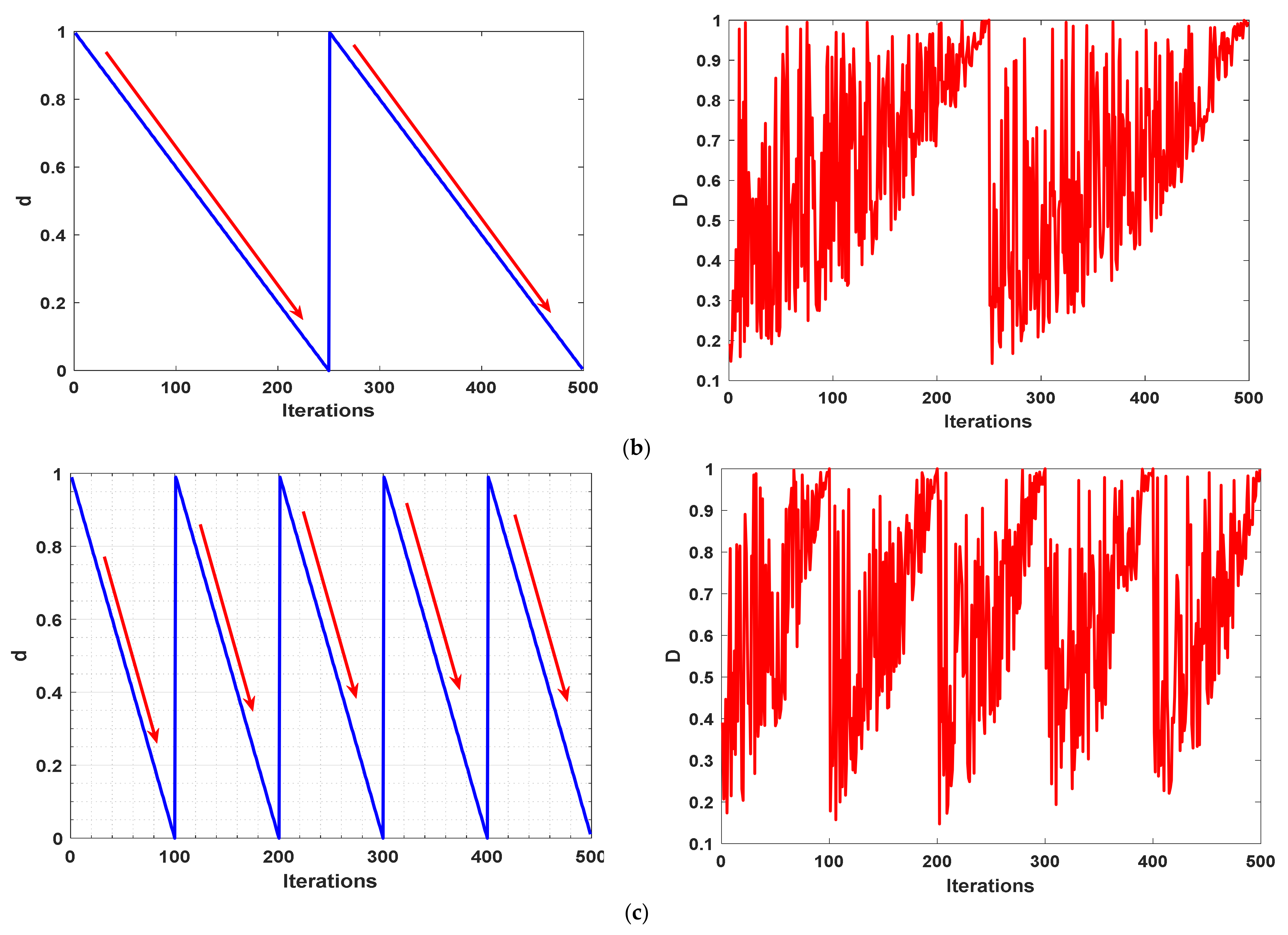
- Developing a novel strategy called a cyclic exploration and exploitation strategy to promote both local and global search of the RWOA for reaching further better outcomes in a new variant of RWOA called HWOA;
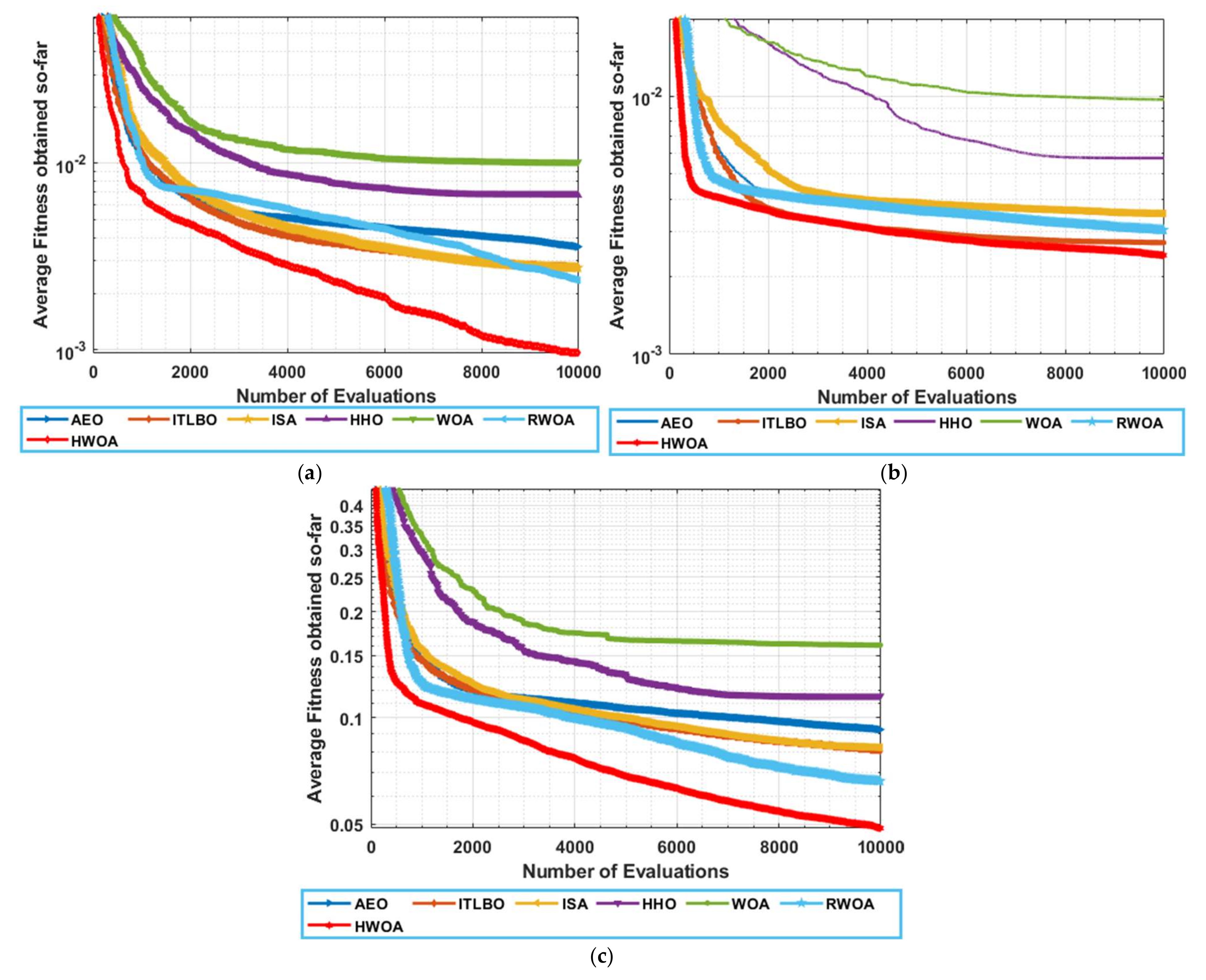
- Our findings show that RWOA is competitive in some cases and superior in the others in terms of final accuracy and convergence speed compared to five well-established algorithms for estimating the unknown parameters of RTC France and two PV modules (Photowatt-PWP201 and Kyocera KC200GT); however, the HWOA can be superior in all cases.
2. Mathematical Formulation of the Three-Diode Model
3. Proposed Approaches: RWOA and HWOA
WOA, Overview
- The first strategy is based on using a spiral shape to spin around their prey;
- The second uses a shrinking circle—called an encircling mechanism—to attack the prey.
- Low premature convergence toward the best solution;
- Local minima problem.
- Each whale in the population is used as much as possible based on the ranking method suggested in [20];
- The whales selected using the previous method are replaced by a novel formula to accelerate convergence;
- Memory saving is used to avoid reducing the diversity between the individuals of the population and subsequently reducing the probability of becoming trapped into local minima;
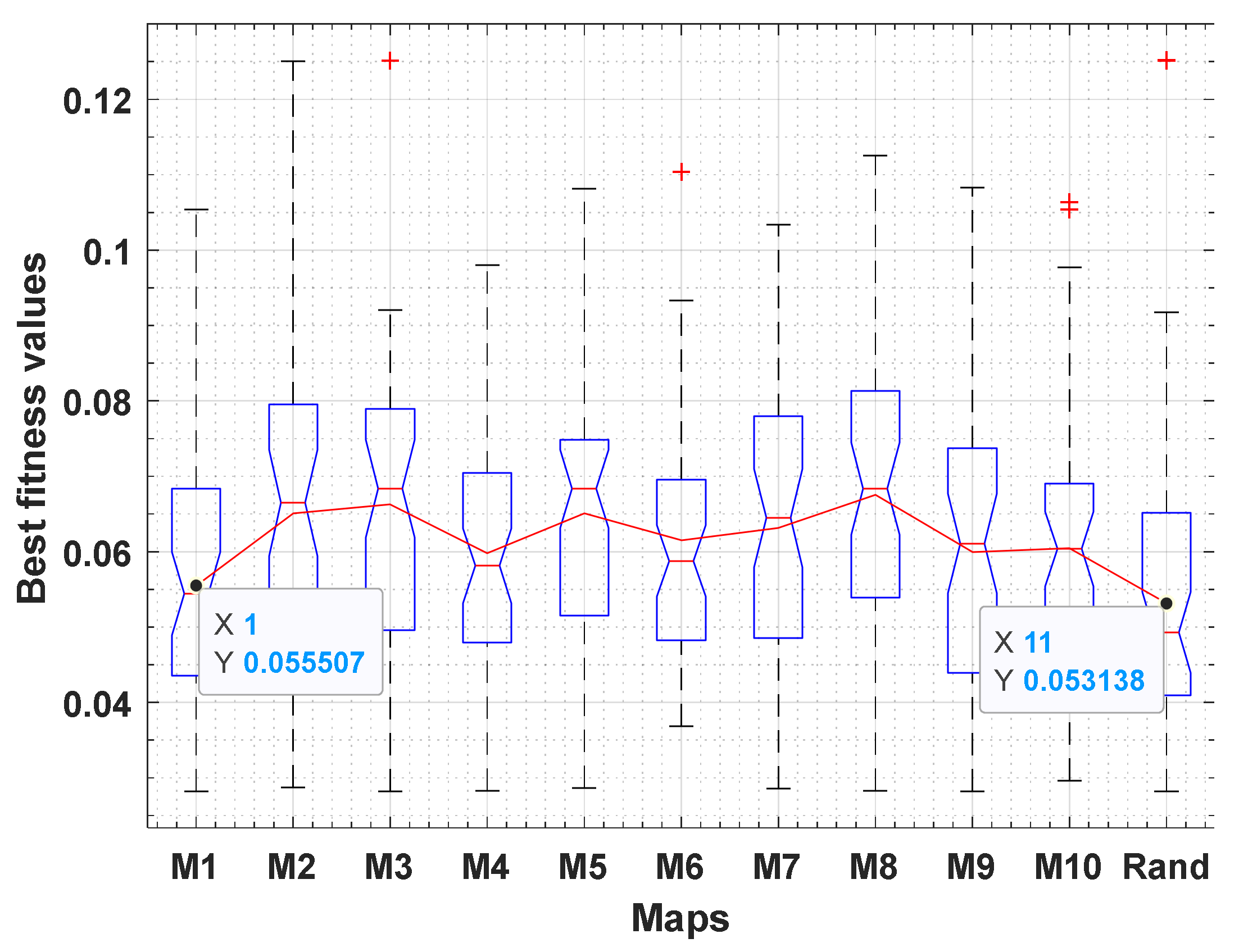
- Finally, to distribute the whales efficiently within the boundary of the optimization problem, ten chaotic maps are investigated for their suitability to be incorporated in the proposed approach.
| Algorithm 1 Initialization (N, d, LB, UB) |
| 1. create an array W of size 2. //initialization 3. for i = 1: N 4. for j = 1: d 5. create a random number r between 0 and 1; 6. W (i + 1, j) = LB(j) + r × (UB(j) − LB(j)); 7. end for 8. end for 9. Return W. |
| Algorithm 2 The Steps of RWOA |
| 1. Calling initialization (N, d, LB, UB) 2. . 3. Evaluate the fitness of using Equation (17). 4. , set the current fitness values in a vector called old fitness, . 5. : is a ranking vector of N cells with an initial value 0 6. Find the best whale 7. 8. while ( < ) 9. for each whale 10. Update a, A, p, C, and l 11. if () 12. if () 13. Update using Equation (4) 14. else 15. Update using Equation (11) 16. end if 17. else 18. Update using Equation (9) 19. end if 20. If 21. Calculate using Equation (14) 22. Update using Equation (16) 23. End 24. If < 25. 26. 27. 28. Else 29. 30. 31. End 32. Calculating the fitness of the using Equation (17) 33. end for 34. Update the best whale with if better 35. ++ 36. end while. |
| Algorithm 3 The Steps of HWOA |
| 1. Calling initialization (N, d, LB, UB) 2. . 3. Evaluate the fitness of using Equation (17) 4. , set the current fitness values in a vector called old fitness, 5. : is a ranking vector of N cells with an initial value 0 6. Find the best whale 7. 8. while ( < ) 9. for each whale 10. Update a, A, p, C, and l 11. if () 12. if () 13. Update using Equation (4) 14. else 15. Update using Equation (11) 16. end if 17. else 18. Update using Equation (9) 19. end if 20. If 21. Calculate using Equation (14) 22. Update using Equation (16) 23. End 24. Calculating the fitness of the using Equation (17) 25. end for 26. for each whale 27. Generate two random numbers between 0 and 1. 28. if 29. Update using Equation (19) 30. else 31. Update using Equation (20) 32. end if 33. if < 34. 35. 36. 37. else 38. 39. 40. end 41. end for 42. Update the best whale with if better. 43. ++ end while. |
4. Experimental Settings
5. Results and Discussion
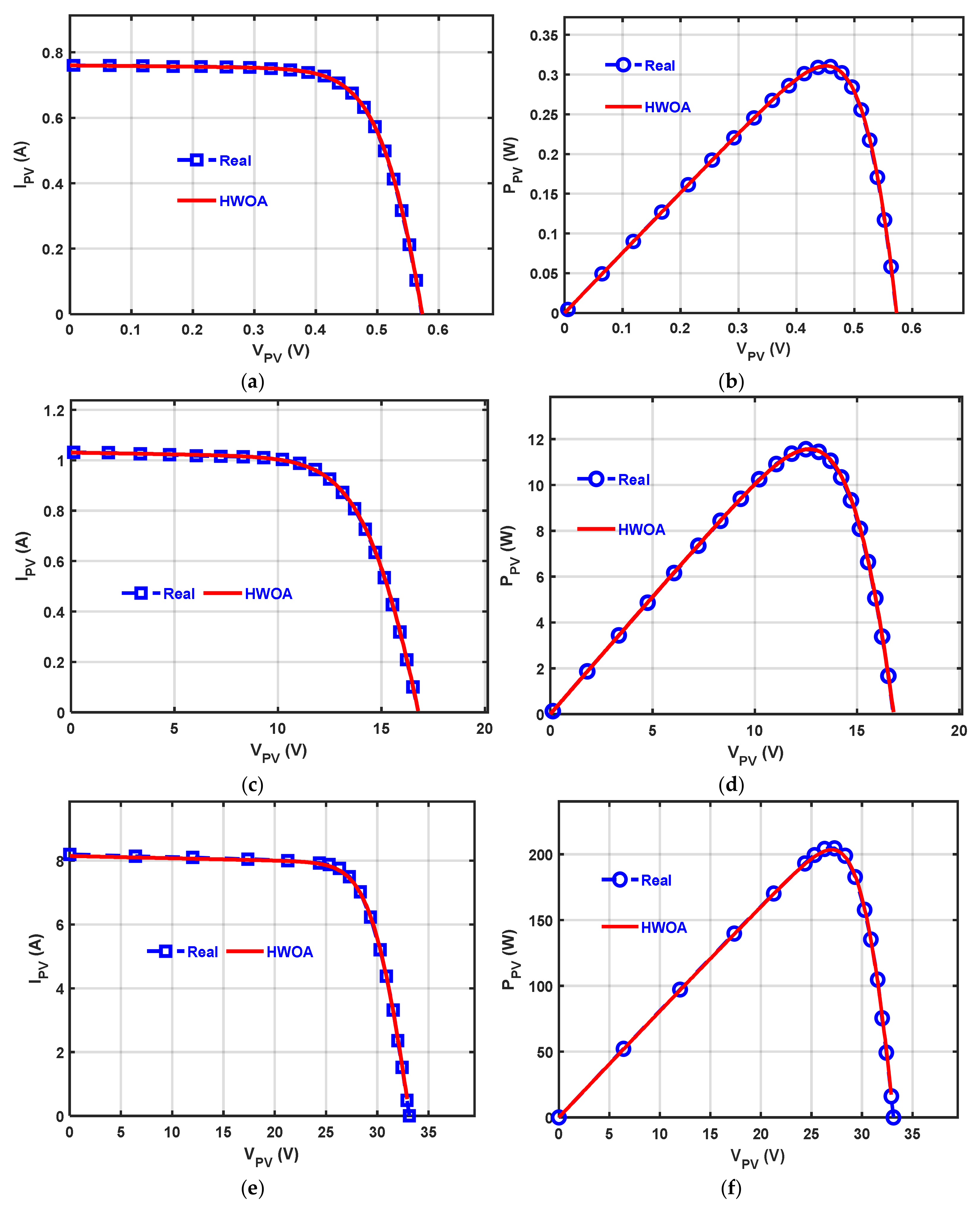
5.1. RTC France Cell
5.2. Photowatt-PWP201 Module
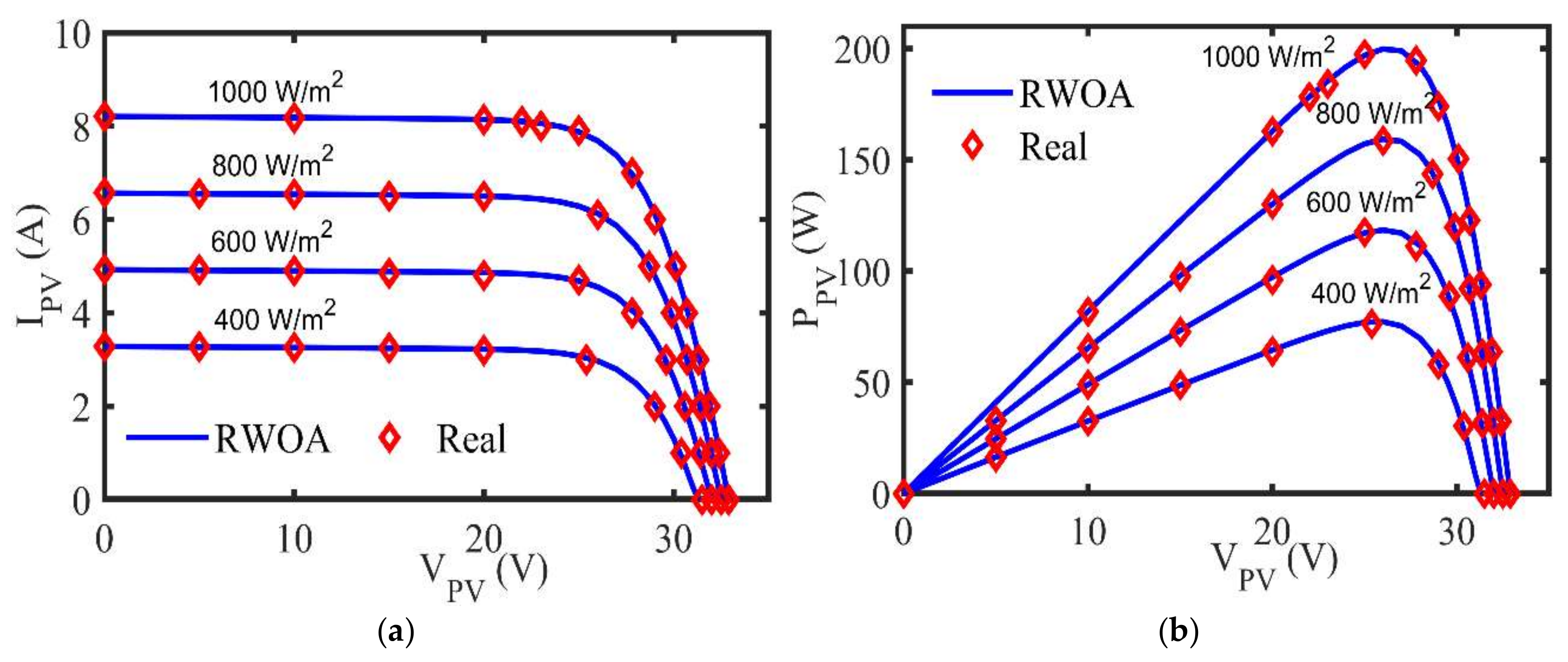
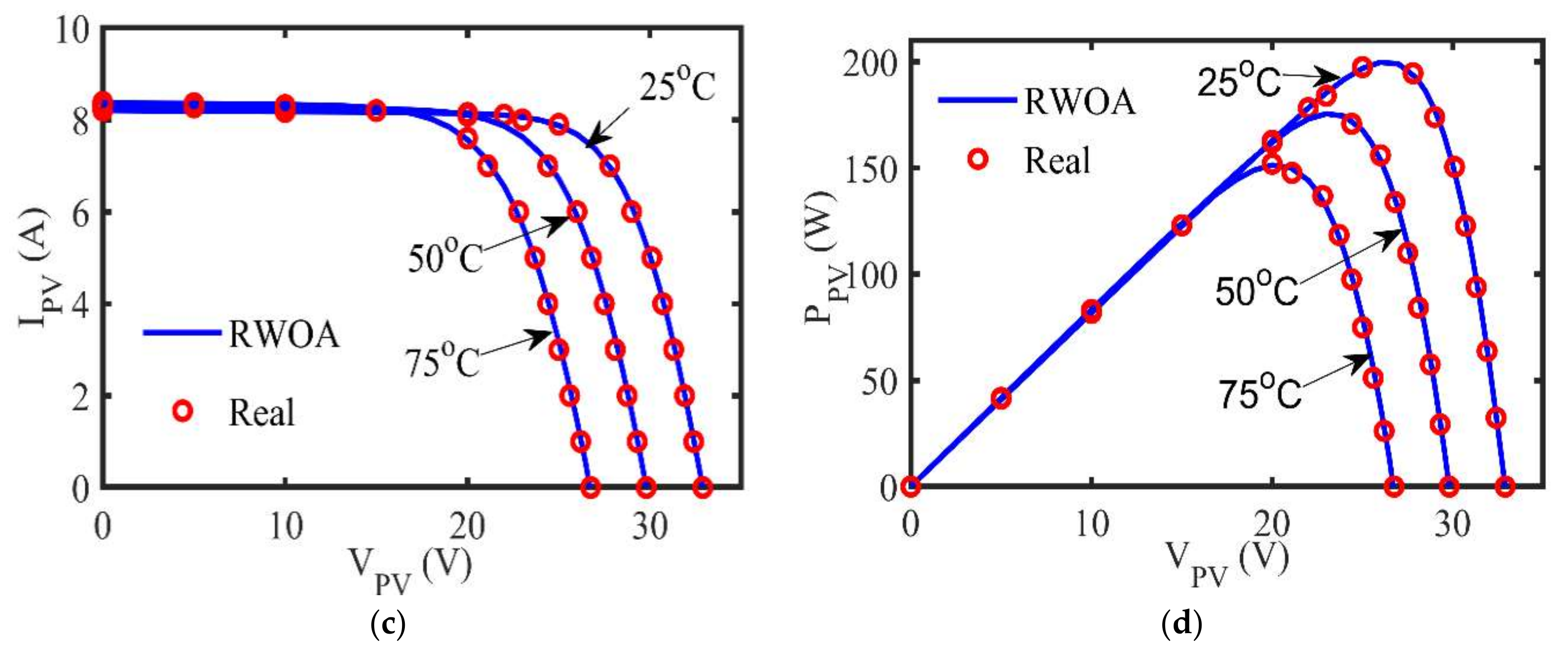
5.3. Kyocera KC200GT-204.6W
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; Rousis, A.O.; Strbac, G. On microgrids and resilience: A comprehensive review on modeling and operational strategies. Renew. Sustain. Energy Rev. 2020, 134, 110313. [Google Scholar] [CrossRef]
- Ibrahim, I.A.; Hossain, M.; Duck, B.C.; Nadarajah, M. An improved wind driven optimization algorithm for parameters identification of a triple-diode photovoltaic cell model. Energy Convers. Manag. 2020, 213, 112872. [Google Scholar] [CrossRef]
- Bharadwaj, P.; Lehman, B. Modelling Flexible a-Si PV for Increased Energy Capture and Improved Reliability. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2020; pp. 2794–2799. [Google Scholar]
- Ahmad, T.; Sobhan, S.; Nayan, M.F. Comparative Analysis between Single Diode and Double Diode Model of PV Cell: Concentrate Different Parameters Effect on Its Efficiency. J. Power Energy Eng. 2016, 4, 31–46. [Google Scholar] [CrossRef] [Green Version]
- Askarzadeh, A.; Rezazadeh, A. Parameter identification for solar cell models using harmony search-based algorithms. Sol. Energy 2012, 86, 3241–3249. [Google Scholar] [CrossRef]
- Khanna, V.; Das, B.K.; Bisht, D.; Vandana; Singh, P.K. A three diode model for industrial solar cells and estimation of solar cell parameters using PSO algorithm. Renew. Energy 2015, 78, 105–113. [Google Scholar] [CrossRef]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Shongwe, S.; Hanif, M. Comparative Analysis of Different Single-Diode PV Modeling Methods. IEEE J. Photovolt. 2015, 5, 938–946. [Google Scholar] [CrossRef]
- Bai, J.; Liu, S.; Hao, Y.; Zhang, Z.; Jiang, M.; Zhang, Y. Development of a new compound method to extract the five parameters of PV modules. Energy Convers. Manag. 2014, 79, 294–303. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Parameters extraction of three-diode photovoltaic model using computation and Harris Hawks optimization. Energy 2020, 195, 117040. [Google Scholar] [CrossRef]
- ElAzab, O.S.; Hasanien, H.M.; Elgendy, M.A.; Abdeen, A.M. Parameters estimation of single- and multiple-diode photovoltaic model using whale optimisation algorithm. IET Renew. Power Gener. 2018, 12, 1755–1761. [Google Scholar] [CrossRef]
- Wei, T.; Yu, F.; Huang, G.; Xu, C. A Particle-Swarm-Optimization-Based Parameter Extraction Routine for Three-Diode Lumped Parameter Model of Organic Solar Cells. IEEE Electron Device Lett. 2019, 40, 1511–1514. [Google Scholar] [CrossRef]
- El-Hameed, M.A.; Elkholy, M.M.; El-Fergany, A.A. Three-diode model for characterization of industrial solar generating units using Manta-rays foraging optimizer: Analysis and validations. Energy Convers. Manag. 2020, 219, 113048. [Google Scholar] [CrossRef]
- Allam, D.; Yousri, D.; Eteiba, M. Parameters extraction of the three diode model for the multi-crystalline solar cell/module using Moth-Flame Optimization Algorithm. Energy Convers. Manag. 2016, 123, 535–548. [Google Scholar] [CrossRef]
- ElAzab, O.S.; Hasanien, H.M.; Alsaidan, I.; Abdelaziz, A.Y.; Muyeen, S.M. Parameter Estimation of Three Diode Photovoltaic Model Using Grasshopper Optimization Algorithm. Energies 2020, 13, 497. [Google Scholar] [CrossRef] [Green Version]
- Diab, A.A.Z.; Sultan, H.M.; Do, T.D.; Kamel, O.M.; Mossa, M.A. Coyote Optimization Algorithm for Parameters Estimation of Various Models of Solar Cells and PV Modules. IEEE Access 2020, 8, 111102–111140. [Google Scholar] [CrossRef]
- Yousri, D.; Thanikanti, S.B.; Allam, D.; Ramachandaramurthy, V.K.; Eteiba, M. Fractional chaotic ensemble particle swarm optimizer for identifying the single, double, and three diode photovoltaic models’ parameters. Energy 2020, 195, 116979. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Elazab, O.S.; Hasanien, H.M.; Elgendy, M.A.; Abdeen, A.M. Whale optimisation algorithm for photovoltaic model identification. J. Eng. 2017, 2017, 1906–1911. [Google Scholar] [CrossRef]
- Li, S.; Gong, W.; Yan, X.; Hu, C.; Bai, D.; Wang, L.; Gao, L. Parameter extraction of photovoltaic models using an improved teaching-learning-based optimization. Energy Convers. Manag. 2019, 186, 293–305. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Elhoseny, M.; Chakrabortty, R.K.; Ryan, M. A Hybrid COVID-19 Detection Model Using an Improved Marine Predators Algorithm and a Ranking-Based Diversity Reduction Strategy. IEEE Access 2020, 8, 79521–79540. [Google Scholar] [CrossRef]
- Nunes, H.G.G.; Pombo, J.; Mariano, S.; Calado, M.; de Souza, J.F. A new high performance method for determining the parameters of PV cells and modules based on guaranteed convergence particle swarm optimization. Appl. Energy 2018, 211, 774–791. [Google Scholar] [CrossRef]
- Yousri, D.; Rezk, H.; Fathy, A. Identifying the parameters of different configurations of photovoltaic models based on recent artificial ecosystem-based optimization approach. Int. J. Energy Res. 2020, 44, 11302–11322. [Google Scholar] [CrossRef]
- Selem, S.I.; El-Fergany, A.A.; Hasanien, H.M. Artificial electric field algorithm to extract nine parameters of triple-diode photovoltaic model. Int. J. Energy Res. 2021, 45, 590–604. [Google Scholar] [CrossRef]
- Fathy, A.; Rezk, H. Robust electrical parameter extraction methodology based on Interior Search Optimization Algorithm applied to supercapacitor. ISA Trans. 2020, 105. [Google Scholar] [CrossRef]
- Chou, J.-S.; Truong, D.-N. A novel metaheuristic optimizer inspired by behavior of jellyfish in ocean. Appl. Math. Comput. 2021, 389, 125535. [Google Scholar] [CrossRef]
- Ma, X.; Li, M.; Du, L.; Qin, B.; Wang, Y.; Luo, X.; Li, G. Online extraction of physical parameters of photovoltaic modules in a building-integrated photovoltaic system. Energy Convers. Manag. 2019, 199, 112028. [Google Scholar] [CrossRef]
- Yadir, S.; Bendaoud, R.; El-Abidi, A.; Amiry, H.; Benhmida, M.; Bounouar, S.; Zohal, B.; Bousseta, H.; Zrhaiba, A.; Elhassnaoui, A. Evolution of the physical parameters of photovoltaic generators as a function of temperature and irradiance: New method of prediction based on the manufacturer’s datasheet. Energy Convers. Manag. 2020, 203, 112141. [Google Scholar] [CrossRef]
- Aly, S.P.; Ahzi, S.; Barth, N. An adaptive modelling technique for parameters extraction of photovoltaic devices under varying sunlight and temperature conditions. Appl. Energy 2019, 236, 728–742. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; El-Fergany, A.; Abouhawwash, M.; Askar, S.S. Parameters identification of pv triple-diode model using improved generalized normal distribution algorithm. Mathematics 2021, 9, 995. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Chakrabortty, R.K.; Ryan, M.J.; El-Fergany, A. An improved artificial jellyfish search optimizer for parameter identification of photovoltaic models. Energies 2021, 14, 1867. [Google Scholar] [CrossRef]




| Parameter | LB | UB |
|---|---|---|
| Algorithms | RMSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| AEO [23] | 0.75922 | 1.238 × 10−7 | 6.438 × 10−7 | 4.294 × 10−9 | 0.03505 | 85.16681 | 1.43068 | 1.68675 | 1.41757 | 0.00129701 |
| ITLBO [20] | 0.76049 | 1.401 × 10−7 | 3.675 × 10−7 | 1.071 × 10−9 | 0.03676 | 57.43669 | 1.42406 | 1.66862 | 1.65840 | 0.00077984 |
| ISA [25] | 0.76050 | 1.141 × 10−8 | 1.350 × 10−6 | 4.648 × 10−7 | 0.03899 | 70.30744 | 1.24034 | 1.78686 | 1.90577 | 0.00081148 |
| HHO [10] | 0.75969 | 2.036 × 10−8 | 1.531 × 10−8 | 1.264 × 10−6 | 0.03720 | 108.84172 | 1.29243 | 1.51025 | 1.74264 | 0.00122689 |
| WOA [18] | 0.76050 | 1.170 × 10−6 | 3.306 × 10−7 | 7.065 × 10−7 | 0.02743 | 429.58132 | 1.70700 | 1.70299 | 1.69958 | 0.00352126 |
| RWOA | 0.76050 | 2.639 × 10−6 | 5.205 × 10−8 | 1.049 × 10−8 | 0.03841 | 64.45417 | 2.00000 | 1.34115 | 1.40000 | 0.00075626 |
| HWOA | 0.76050 | 7.668 × 10−7 | 8.966 × 10−8 | 1.193 × 10−6 | 0.03795 | 60.85709 | 1.95480 | 1.37604 | 1.99836 | 0.00075148 |
| Algorithms | AEO [23] | ITLBO [20] | ISA [25] | HHO [10] | WOA [18] | RWOA | HWOA |
|---|---|---|---|---|---|---|---|
| Best | 0.0012970061 | 0.0007798428 | 0.0008114755 | 0.0012268860 | 0.0035212594 | 0.0007562561 | 0.0007514822 |
| Worst | 0.0058557573 | 0.0075862070 | 0.0049871863 | 0.0180751229 | 0.0182047656 | 0.0085551216 | 0.0058540672 |
| Avg | 0.0038307293 | 0.0029920966 | 0.0027888508 | 0.0073241072 | 0.0098232146 | 0.0024644842 | 0.0010557685 |
| SD | 0.0012625166 | 0.0014567314 | 0.0009987475 | 0.0037530593 | 0.0025490806 | 0.0016299982 | 0.0007712976 |
| Time (s) | 1.8484064800 | 2.4445874020 | 1.1383867480 | 4.2349410020 | 2.2107720220 | 2.5196325380 | 1.3130094500 |
| Rank | 5 | 4 | 3 | 6 | 7 | 2 | 1 |
| Points | ITLBO [20] | HWOA | Points | ITLBO [20] | HWOA |
|---|---|---|---|---|---|
| 1 | 0.00042140 | 0.00059436 | 14 | 0.00063736 | 0.00094555 |
| 2 | 0.00024578 | 0.00014751 | 15 | 0.00043540 | 0.00023563 |
| 3 | 0.00052240 | 0.00049222 | 16 | 0.00018622 | 0.00019598 |
| 4 | 0.00060074 | 0.00056986 | 17 | 0.00105762 | 0.00087708 |
| 5 | 0.00112908 | 0.00104595 | 18 | 0.00084037 | 0.00055163 |
| 6 | 0.00107938 | 0.00095619 | 19 | 0.00055482 | 0.00082578 |
| 7 | 0.00002304 | 0.00016786 | 20 | 0.00050983 | 0.00065411 |
| 8 | 0.00088337 | 0.00074426 | 21 | 0.00067192 | 0.00064497 |
| 9 | 0.00040942 | 0.00031250 | 22 | 0.00000501 | 0.00017199 |
| 10 | 0.00032050 | 0.00030689 | 23 | 0.00092424 | 0.00113327 |
| 11 | 0.00089763 | 0.00079535 | 24 | 0.00060347 | 0.00048777 |
| 12 | 0.00084004 | 0.00061514 | 25 | 0.00148841 | 0.00135363 |
| 13 | 0.00156924 | 0.00125975 | 26 | 0.00075850 | 0.00117864 |
| RTC | PWP201 | KC200GT | ||||
|---|---|---|---|---|---|---|
| Algorithms | h | p-Value | h | p-Value | h | p-Value |
| HWOA vs. AEO | 1 | 3.1949811 × 10−16 | 1 | 5.1397061 × 10−10 | 1 | 5.6387345 × 10−17 |
| HWOA vs. ITLBO | 1 | 2.7981570 × 10−14 | 1 | 9.6808330 × 10−5 | 1 | 3.5812605 × 10−16 |
| HWOA vs. ISA | 1 | 3.1940068 × 10−15 | 1 | 7.2511469 × 10−14 | 1 | 5.0379086 × 10−16 |
| HWOA vs. HHO | 1 | 3.7391900 × 10−17 | 1 | 2.1975265 × 10−17 | 1 | 5.0154613 × 10−17 |
| HWOA vs. WOA | 1 | 7.9688116 × 10−18 | 1 | 9.5403423 × 10−18 | 1 | 8.4619555 × 10−18 |
| HWOA vs. RWOA | 1 | 2.1162998 × 10−10 | 1 | 1.2795224 × 10−6 | 1 | 3.9885266 × 10−6 |
| Algorithms | RMSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| AEO [23] | 1.03167 | 2.299 × 10−6 | 4.908 × 10−6 | 2.116 × 10−7 | 0.03423 | 23.20661 | 1.31099 | 1.98340 | 1.87961 | 0.00212391 |
| ITLBO [20] | 1.03094 | 3.314 × 10−6 | 8.137 × 10−8 | 2.028 × 10−9 | 0.03361 | 26.15666 | 1.34608 | 1.80984 | 1.70548 | 0.00215662 |
| ISA [25] | 1.03033 | 2.399 × 10−6 | 3.636 × 10−7 | 1.082 × 10−9 | 0.03436 | 26.49586 | 1.32168 | 1.37055 | 1.95677 | 0.00216172 |
| HHO [10] | 1.02678 | 2.052 × 10−6 | 2.572 × 10−6 | 2.259 × 10−6 | 0.03163 | 78.98323 | 1.36586 | 1.44777 | 1.51062 | 0.00313249 |
| WOA [18] | 1.02626 | 5.197 × 10−6 | 2.776 × 10−6 | 5.301 × 10−6 | 0.03173 | 474.24080 | 1.97039 | 1.94977 | 1.40202 | 0.00340767 |
| RWOA | 1.03170 | 3.101 × 10−6 | 1.000 × 10−9 | 1.000 × 10−9 | 0.03376 | 23.59534 | 1.33896 | 2.00000 | 2.00000 | 0.00209360 |
| HWOA | 1.03170 | 2.594 × 10−6 | 1.005 × 10−9 | 1.000 × 10−9 | 0.03436 | 22.16526 | 1.32049 | 2.00000 | 1.99996 | 0.00205067 |
| Algorithms | AEO [23] | ITLBO [20] | ISA [25] | HHO [10] | WOA [18] | RWOA | HWOA |
|---|---|---|---|---|---|---|---|
| Best | 0.0021239070 | 0.0021566228 | 0.0021617217 | 0.0031324927 | 0.0034076744 | 0.0020936002 | 0.0020506744 |
| Worst | 0.0045855675 | 0.0039748826 | 0.0049328947 | 0.0133624679 | 0.0339653392 | 0.0048751104 | 0.0037856010 |
| Avg | 0.0031909775 | 0.0028101343 | 0.0034395527 | 0.0049863792 | 0.0092443412 | 0.0029661832 | 0.0024630570 |
| SD | 0.0005529085 | 0.0004478418 | 0.0005988061 | 0.0021315308 | 0.0066477865 | 0.0005826925 | 0.0003765776 |
| Time (s) | 2.0259489840 | 2.5425894060 | 1.0690436680 | 4.1146105580 | 2.1864761820 | 2.5288949540 | 1.1371688640 |
| Rank | 4 | 2 | 5 | 6 | 7 | 3 | 1 |
| Points | AEO [23] | HWOA | Points | AEO [23] | HWOA |
|---|---|---|---|---|---|
| 1 | 0.00202612 | 0.00196520 | 14 | 0.00070850 | 0.00107830 |
| 2 | 0.00150929 | 0.00155811 | 15 | 0.00051425 | 0.00072990 |
| 3 | 0.00205488 | 0.00218585 | 16 | 0.00206436 | 0.00208065 |
| 4 | 0.00001616 | 0.00017725 | 17 | 0.00234223 | 0.00215810 |
| 5 | 0.00211195 | 0.00188234 | 18 | 0.00129039 | 0.00094117 |
| 6 | 0.00405118 | 0.00381960 | 19 | 0.00115746 | 0.00069973 |
| 7 | 0.00398503 | 0.00379324 | 20 | 0.00015724 | 0.00066030 |
| 8 | 0.00178349 | 0.00167704 | 21 | 0.00102009 | 0.00150851 |
| 9 | 0.00011291 | 0.00009277 | 22 | 0.00295107 | 0.00337354 |
| 10 | 0.00333524 | 0.00316378 | 23 | 0.00028751 | 0.00060339 |
| 11 | 0.00363641 | 0.00331901 | 24 | 0.00020045 | 0.00002180 |
| 12 | 0.00327006 | 0.00285082 | 25 | 0.00041889 | 0.00039876 |
| 13 | 0.00208071 | 0.00163878 | 26 | 0.00194215 | 0.00209381 |
| Algorithms | RMSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| AEO [23] | 8.13273 | 1.457 × 10−7 | 6.419 × 10−7 | 5.324 × 10−8 | 0.00317 | 142.95143 | 1.33878 | 1.99886 | 1.67833 | 0.06162560 |
| ITLBO [20] | 8.09277 | 8.870 × 10−8 | 2.782 × 10−9 | 5.431 × 10−7 | 0.00328 | 347.12120 | 1.30285 | 1.75460 | 1.88985 | 0.06196293 |
| ISA [25] | 8.13193 | 1.794 × 10−8 | 1.432 × 10−6 | 4.577 × 10−9 | 0.00394 | 12.38224 | 1.20240 | 1.86530 | 1.53053 | 0.05929216 |
| HHO [10] | 8.13923 | 1.000 × 10−9 | 1.956 × 10−8 | 2.460 × 10−8 | 0.00418 | 138.06531 | 1.06811 | 1.26960 | 1.46177 | 0.05470326 |
| WOA [18] | 8.15932 | 3.135 × 10−9 | 1.579 × 10−9 | 4.621 × 10−7 | 0.00277 | 500.00000 | 2.00000 | 2.00000 | 1.42904 | 0.07293691 |
| RWOA | 8.20030 | 1.000 × 10−9 | 1.310 × 10−9 | 1.053 × 10−9 | 0.00460 | 2.65765 | 1.04687 | 2.00000 | 1.94552 | 0.02821562 |
| HWOA | 8.20186 | 1.000 × 10−9 | 1.000 × 10−9 | 1.000 × 10−9 | 0.00459 | 2.63009 | 1.04687 | 2.00000 | 1.69348 | 0.02822241 |
| Algorithms | AEO [23] | ITLBO [20] | ISA [25] | HHO [10] | WOA [18] | RWOA | HWOA |
|---|---|---|---|---|---|---|---|
| Best | 6.16256 × 10−2 | 6.19629 × 10−2 | 5.92922 × 10−2 | 5.47033 × 10−2 | 7.29369 × 10−2 | 2.82156 × 10−2 | 2.82224 × 10−2 |
| Worst | 1.20377 × 10−1 | 1.18683 × 10−1 | 1.11085 × 10−1 | 2.09556 × 10−1 | 2.53518 × 10−1 | 1.25166 × 10−1 | 8.74320 × 10−2 |
| Avg | 9.26133 × 10−2 | 8.08383 × 10−2 | 8.24407 × 10−2 | 1.15432 × 10−1 | 1.60725 × 10−1 | 6.62490 × 10−2 | 4.86870 × 10−2 |
| SD | 1.45518 × 10−2 | 1.12456 × 10−2 | 1.15311 × 10−2 | 3.13564 × 10−2 | 4.59415 × 10−2 | 1.98688 × 10−2 | 1.29875 × 10−2 |
| Time (s) | 2.13778639 | 2.59146917 | 0.92115676 | 3.92217410 | 2.16986671 | 2.48034050 | 1.06056147 |
| Rank | 5 | 3 | 4 | 6 | 7 | 2 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdel-Basset, M.; Mohamed, R.; El-Fergany, A.; Askar, S.S.; Abouhawwash, M. Efficient Ranking-Based Whale Optimizer for Parameter Extraction of Three-Diode Photovoltaic Model: Analysis and Validations. Energies 2021, 14, 3729. https://doi.org/10.3390/en14133729
Abdel-Basset M, Mohamed R, El-Fergany A, Askar SS, Abouhawwash M. Efficient Ranking-Based Whale Optimizer for Parameter Extraction of Three-Diode Photovoltaic Model: Analysis and Validations. Energies. 2021; 14(13):3729. https://doi.org/10.3390/en14133729
Chicago/Turabian StyleAbdel-Basset, Mohamed, Reda Mohamed, Attia El-Fergany, Sameh S. Askar, and Mohamed Abouhawwash. 2021. "Efficient Ranking-Based Whale Optimizer for Parameter Extraction of Three-Diode Photovoltaic Model: Analysis and Validations" Energies 14, no. 13: 3729. https://doi.org/10.3390/en14133729
APA StyleAbdel-Basset, M., Mohamed, R., El-Fergany, A., Askar, S. S., & Abouhawwash, M. (2021). Efficient Ranking-Based Whale Optimizer for Parameter Extraction of Three-Diode Photovoltaic Model: Analysis and Validations. Energies, 14(13), 3729. https://doi.org/10.3390/en14133729









