Distributed Learning Applications in Power Systems: A Review of Methods, Gaps, and Challenges
Abstract
1. Introduction
2. Review Methodology
- Are there any publications that have implemented various forms of distributed learning in power systems?
- What applications can distributed learning frameworks have in power systems?
- What are the main benefits of distributed learning for power systems?
- What kind of data is exchanged in distributed learning methods in power systems?
- What are some possible research areas for implementing distributed learning in power systems?
- 1.
- The article should have a learning-based structure. This could include any type of learning algorithm where the aim is to construct a mathematical representation for an unknown model.
- 2.
- The article should focus on solving a power system-related problem.
- 3.
- It should use a distributed structure where there is data exchange between multiple agents or between agents and a central server.
- 4.
- Only research articles that have tested their algorithms on a case study and have presented the results should be included.
- Multidisciplinary databases:
- – MDPI;
- – Elsevier;
- – Springer;
- – Arxiv; and
- – Wiley Online Library.
- Specific databases:
- – ACM Digital Library; and
- – IEEE Xplore Library.
- Machine learning keywords: [learning, distributed learning, federated learning, assisted learning, ADMM, dual decomposition, primal decomposition, consensus gradient, and privacy.]
- Power system keywords: [power system, voltage control, resiliency, renewable energy, energy, energy management, electric vehicle, and agent.]
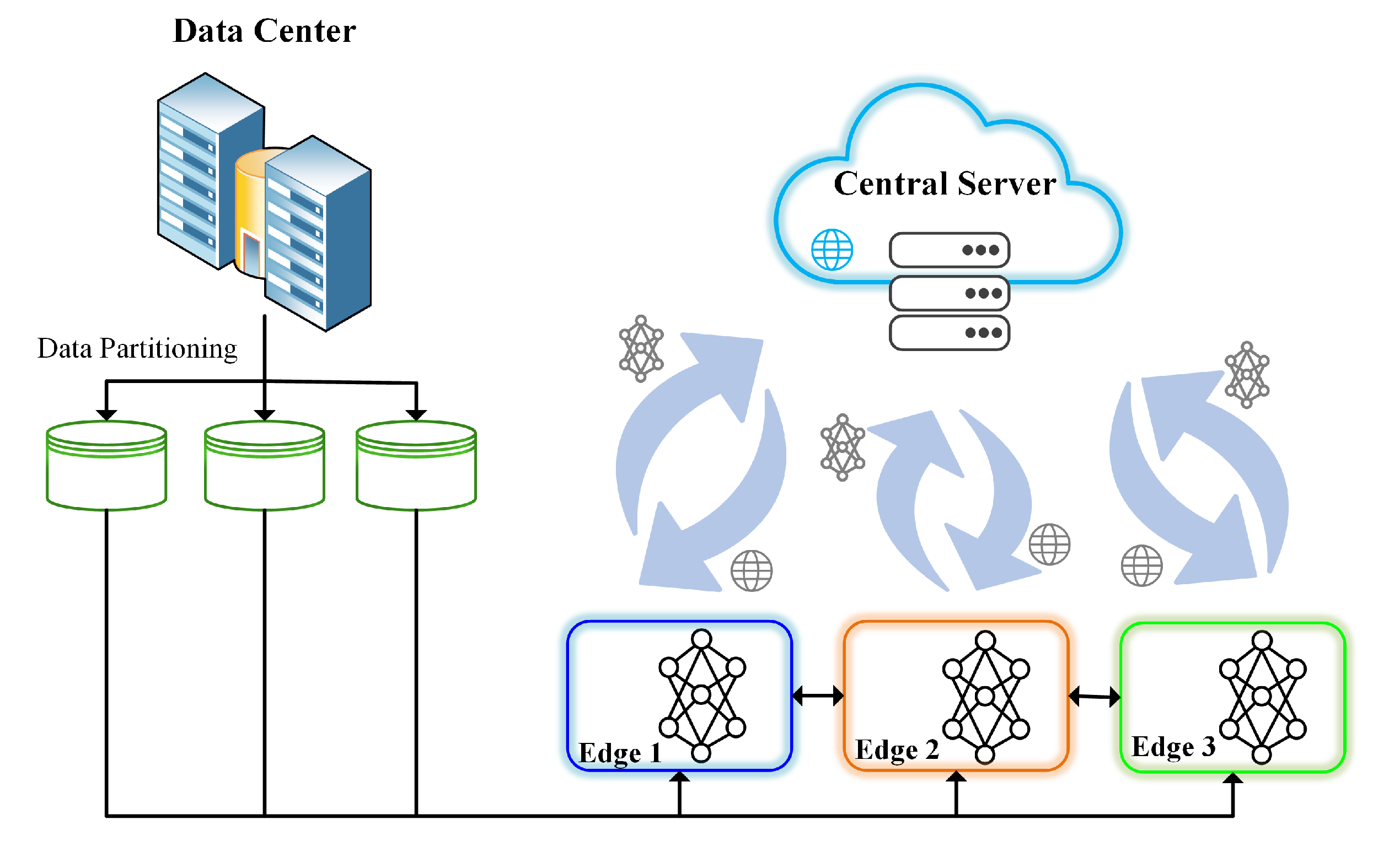
3. Distributed Learning Overview
4. Applications of Distributed Learning
4.1. Voltage Control
4.2. Renewable Energy Forecast
4.3. Demand Prediction
4.4. Energy Management
4.5. Transient Stability Enhancement
4.6. Resilience Enhancement
4.7. Economic Dispatch
4.8. Energy Storage Systems Control
4.9. Other Applications
5. Research Gaps and Challenges
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Siebert, L.C.; Aoki, A.R.; Lambert-Torres, G.; Lambert-de Andrade, N.; Paterakis, N.G. An Agent-Based Approach for the Planning of Distribution Grids as a Socio-Technical System. Energies 2020, 13, 4837. [Google Scholar] [CrossRef]
- Marinakis, V. Big Data for Energy Management and Energy-Efficient Buildings. Energies 2020, 13, 1555. [Google Scholar] [CrossRef]
- Alimi, O.A.; Ouahada, K.; Abu-Mahfouz, A.M. A Review of Machine Learning Approaches to Power System Security and Stability. IEEE Access 2020, 8, 113512–113531. [Google Scholar] [CrossRef]
- Hossain, E.; Khan, I.; Un-Noor, F.; Sikander, S.S.; Sunny, M.S.H. Application of Big Data and Machine Learning in Smart Grid, and Associated Security Concerns: A Review. IEEE Access 2019, 7, 13960–13988. [Google Scholar] [CrossRef]
- Wu, N.; Peng, C.; Niu, K. A Privacy-Preserving Game Model for Local Differential Privacy by Using Information-Theoretic Approach. IEEE Access 2020, 8, 216741–216751. [Google Scholar] [CrossRef]
- Keshk, M.; Turnbull, B.; Moustafa, N.; Vatsalan, D.; Choo, K.R. A Privacy-Preserving-Framework-Based Blockchain and Deep Learning for Protecting Smart Power Networks. IEEE Trans. Ind. Inform. 2020, 16, 5110–5118. [Google Scholar] [CrossRef]
- Liu, E.; Cheng, P. Mitigating Cyber Privacy Leakage for Distributed DC Optimal Power Flow in Smart Grid With Radial Topology. IEEE Access 2018, 6, 7911–7920. [Google Scholar] [CrossRef]
- Yang, L.; Chen, X.; Zhang, J.; Poor, H.V. Cost-Effective and Privacy-Preserving Energy Management for Smart Meters. IEEE Trans. Smart Grid 2015, 6, 486–495. [Google Scholar] [CrossRef]
- Alsharif, A.; Nabil, M.; Sherif, A.; Mahmoud, M.; Song, M. MDMS: Efficient and Privacy-Preserving Multidimension and Multisubset Data Collection for AMI Networks. IEEE Internet Things J. 2019, 6, 10363–10374. [Google Scholar] [CrossRef]
- Knirsch, F.; Eibl, G.; Engel, D. Error-Resilient Masking Approaches for Privacy Preserving Data Aggregation. IEEE Trans. Smart Grid 2018, 9, 3351–3361. [Google Scholar] [CrossRef]
- Li, Y.; Hu, B. A Consortium Blockchain-Enabled Secure and Privacy-Preserving Optimized Charging and Discharging Trading Scheme for Electric Vehicles. IEEE Trans. Ind. Inform. 2021, 17, 1968–1977. [Google Scholar] [CrossRef]
- Zhang, Q.; Fan, W.; Qiu, Z.; Liu, Z.; Zhang, J. A New Identification Approach of Power System Vulnerable Lines Based on Weighed H-Index. IEEE Access 2019, 7, 121421–121431. [Google Scholar] [CrossRef]
- Mak, T.W.K.; Fioretto, F.; Shi, L.; Van Hentenryck, P. Privacy-Preserving Power System Obfuscation: A Bilevel Optimization Approach. IEEE Trans. Power Syst. 2020, 35, 1627–1637. [Google Scholar] [CrossRef]
- Feng, X.; Lan, J.; Peng, Z.; Huang, Z.; Guo, Q. A Novel Privacy Protection Framework for Power Generation Data based on Generative Adversarial Networks. In Proceedings of the 2019 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Macao, China, 1–4 December 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Ge, Y.; Ye, H.; Loparo, K.A. Agent-Based Privacy Preserving Transactive Control for Managing Peak Power Consumption. IEEE Trans. Smart Grid 2020, 11, 4883–4890. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Wen, F.; Shahidehpour, M. Privacy-Preserving Optimal Dispatch for an Integrated Power Distribution and Natural Gas System in Networked Energy Hubs. IEEE Trans. Sustain. Energy 2019, 10, 2028–2038. [Google Scholar] [CrossRef]
- Ye, Y.; Li, S.; Liu, F.; Tang, Y.; Hu, W. EdgeFed: Optimized Federated Learning Based on Edge Computing. IEEE Access 2020, 8, 209191–209198. [Google Scholar] [CrossRef]
- Shen, P.; Li, C.; Zhang, Z. Distributed Active Learning. IEEE Access 2016, 4, 2572–2579. [Google Scholar] [CrossRef]
- Mowla, N.I.; Tran, N.H.; Doh, I.; Chae, K. AFRL: Adaptive federated reinforcement learning for intelligent jamming defense in FANET. J. Commun. Netw. 2020, 22, 244–258. [Google Scholar] [CrossRef]
- Ahmed, L.; Ahmad, K.; Said, N.; Qolomany, B.; Qadir, J.; Al-Fuqaha, A. Active Learning Based Federated Learning for Waste and Natural Disaster Image Classification. IEEE Access 2020, 8, 208518–208531. [Google Scholar] [CrossRef]
- Hua, G.; Zhu, L.; Wu, J.; Shen, C.; Zhou, L.; Lin, Q. Blockchain-Based Federated Learning for Intelligent Control in Heavy Haul Railway. IEEE Access 2020, 8, 176830–176839. [Google Scholar] [CrossRef]
- Wang, N.; Li, J.; Ho, S.S.; Qiu, C. Distributed machine learning for energy trading in electric distribution system of the future. Electr. J. 2021, 34, 106883. [Google Scholar] [CrossRef]
- Farhoumandi, M.; Zhou, Q.; Shahidehpour, M. A review of machine learning applications in IoT-integrated modern power systems. Electr. J. 2021, 34, 106879. [Google Scholar] [CrossRef]
- Zhang, D.; Han, X.; Deng, C. Review on the research and practice of deep learning and reinforcement learning in smart grids. CSEE J. Power Energy Syst. 2018, 4, 362–370. [Google Scholar] [CrossRef]
- Khodayar, M.; Liu, G.; Wang, J.; Khodayar, M.E. Deep learning in power systems research: A review. CSEE J. Power Energy Syst. 2020, 1–13. [Google Scholar] [CrossRef]
- Chen, J.; Ran, X. Deep Learning With Edge Computing: A Review. Proc. IEEE 2019, 107, 1655–1674. [Google Scholar] [CrossRef]
- Chiu, T.C.; Shih, Y.Y.; Pang, A.C.; Wang, C.S.; Weng, W.; Chou, C.T. Semisupervised Distributed Learning With Non-IID Data for AIoT Service Platform. IEEE Internet Things J. 2020, 7, 9266–9277. [Google Scholar] [CrossRef]
- Yang, Z.; Bajwa, W.U. ByRDiE: Byzantine-Resilient Distributed Coordinate Descent for Decentralized Learning. IEEE Trans. Signal Inf. Process. Netw. 2019, 5, 611–627. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, J.; Wang, F. Stability-Based Generalization Analysis of Distributed Learning Algorithms for Big Data. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 801–812. [Google Scholar] [CrossRef]
- Li, H.; Zhang, H.; Wang, Z.; Zhu, Y.; Han, Q. Distributed consensus-based multi-agent convex optimization via gradient tracking technique. J. Frankl. Inst. 2019, 356, 3733–3761. [Google Scholar] [CrossRef]
- Shalev-Shwartz, S.; Shamir, O.; Srebro, N.; Sridharan, K. Stochastic Convex Optimization; COLT: Berlin, Germany, 2009. [Google Scholar]
- Magnússon, S.; Shokri-Ghadikolaei, H.; Li, N. On Maintaining Linear Convergence of Distributed Learning and Optimization Under Limited Communication. IEEE Trans. Signal Process. 2020, 68, 6101–6116. [Google Scholar] [CrossRef]
- Huang, Z.; Hu, R.; Guo, Y.; Chan-Tin, E.; Gong, Y. DP-ADMM: ADMM-Based Distributed Learning With Differential Privacy. IEEE Trans. Inf. Forensics Secur. 2020, 15, 1002–1012. [Google Scholar] [CrossRef]
- Zhang, T.; Zhu, Q. Dynamic Differential Privacy for ADMM-Based Distributed Classification Learning. IEEE Trans. Inf. Forensics Secur. 2017, 12, 172–187. [Google Scholar] [CrossRef]
- Gu, C.; Li, J.; Wu, Z. An adaptive online learning algorithm for distributed convex optimization with coupled constraints over unbalanced directed graphs. J. Frankl. Inst. 2019, 356, 7548–7570. [Google Scholar] [CrossRef]
- Falsone, A.; Margellos, K.; Garatti, S.; Prandini, M. Dual decomposition for multi-agent distributed optimization with coupling constraints. Automatica 2017, 84, 149–158. [Google Scholar] [CrossRef]
- Niu, Y.; Wang, H.; Wang, Z.; Xia, D.; Li, H. Primal-dual stochastic distributed algorithm for constrained convex optimization. J. Frankl. Inst. 2019, 356, 9763–9787. [Google Scholar] [CrossRef]
- Yang, Q.; Chen, G. Primal-Dual Subgradient Algorithm for Distributed Constraint Optimization Over Unbalanced Digraphs. IEEE Access 2019, 7, 85190–85202. [Google Scholar] [CrossRef]
- McMahan, H.B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-Efficient Learning of Deep Networks from Decentralized Data, 2017. arXiv 2017, arXiv:cs.LG/1602.05629. [Google Scholar]
- Bonawitz, K.; Eichner, H.; Grieskamp, W.; Huba, D.; Ingerman, A.; Ivanov, V.; Kiddon, C.; Konečný, J.; Mazzocchi, S.; McMahan, H.B.; et al. Towards Federated Learning at Scale: System Design. arXiv 2019, arXiv:cs.LG/1902.01046. [Google Scholar]
- Savazzi, S.; Nicoli, M.; Rampa, V. Federated Learning With Cooperating Devices: A Consensus Approach for Massive IoT Networks. IEEE Internet Things J. 2020, 7, 4641–4654. [Google Scholar] [CrossRef]
- Shen, S.; Zhu, T.; Wu, D.; Wang, W.; Zhou, W. From distributed machine learning to federated learning: In the view of data privacy and security. In Concurrency and Computation: Practice and Experience; Wiley Online Library: Hoboken, NJ, USA, 2020. [Google Scholar]
- Yang, Q.; Liu, Y.; Chen, T.; Tong, Y. Federated Machine Learning: Concept and Applications. ACM Trans. Intell. Syst. Technol. 2019, 10. [Google Scholar] [CrossRef]
- Li, L.; Fan, Y.; Tse, M.; Lin, K.Y. A review of applications in federated learning. Comput. Ind. Eng. 2020, 149, 106854. [Google Scholar] [CrossRef]
- Zhang, C.; Xie, Y.; Bai, H.; Yu, B.; Li, W.; Gao, Y. A survey on federated learning. Knowl. Based Syst. 2021, 216, 106775. [Google Scholar] [CrossRef]
- Xian, X.; Wang, X.; Ding, J.; Ghanadan, R. Assisted Learning: A Framework for Multi-Organization Learning. In Advances in Neural Information Processing Systems; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.F., Lin, H., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 14580–14591. [Google Scholar]
- Mor, G.; Vilaplana, J.; Danov, S.; Cipriano, J.; Solsona, F.; Chemisana, D. EMPOWERING, a Smart Big Data Framework for Sustainable Electricity Suppliers. IEEE Access 2018, 6, 71132–71142. [Google Scholar] [CrossRef]
- Tousi, M.; Hosseinian, S.H.; Menhaj, M.B. A Multi-agent-based voltage control in power systems using distributed reinforcement learning. Simulation 2011, 87, 581–599. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, H.; Wang, Y.; He, H. A Distributed Iterative Learning Framework for DC Microgrids: Current Sharing and Voltage Regulation. IEEE Trans. Emerg. Top. Comput. Intell. 2020, 4, 119–129. [Google Scholar] [CrossRef]
- Karim, M.A.; Currie, J.; Lie, T. A distributed machine learning approach for the secondary voltage control of an Islanded micro-grid. In Proceedings of the 2016 IEEE Innovative Smart Grid Technologies—Asia (ISGT-Asia), Melbourne, VIC, Australia, 28 November–1 December 2016; pp. 611–616. [Google Scholar] [CrossRef]
- Tousi, M.R.; Hosseinian, S.H.; Menhaj, M.B. Voltage Coordination of FACTS Devices in Power Systems Using RL-Based Multi-Agent Systems. AUT J. Electr. Eng. 2009, 41, 39–49. [Google Scholar] [CrossRef]
- da Silva, R.G.; Ribeiro, M.H.D.M.; Moreno, S.R.; Mariani, V.C.; dos Santos Coelho, L. A novel decomposition-ensemble learning framework for multi-step ahead wind energy forecasting. Energy 2021, 216, 119174. [Google Scholar] [CrossRef]
- Sommer, B.; Pinson, P.; Messner, J.W.; Obst, D. Online distributed learning in wind power forecasting. Int. J. Forecast. 2021, 37, 205–223. [Google Scholar] [CrossRef]
- Pinson, P. Introducing distributed learning approaches in wind power forecasting. In Proceedings of the 2016 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Beijing, China, 16–20 October 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Goncalves, C.; Bessa, R.J.; Pinson, P. Privacy-preserving Distributed Learning for Renewable Energy Forecasting. IEEE Trans. Sustain. Energy 2021, 1. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J. A Distributed Approach for Wind Power Probabilistic Forecasting Considering Spatio-Temporal Correlation Without Direct Access to Off-Site Information. IEEE Trans. Power Syst. 2018, 33, 5714–5726. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J. A Distributed Approach for Wind Power Probabilistic Forecasting Considering Spatiotemporal Correlation without Direct Access to Off-site Information. In Proceedings of the 2020 IEEE Power Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; p. 1. [Google Scholar] [CrossRef]
- Howlader, A.M.; Senjyu, T.; Saber, A.Y. An Integrated Power Smoothing Control for a Grid-Interactive Wind Farm Considering Wake Effects. IEEE Syst. J. 2015, 9, 954–965. [Google Scholar] [CrossRef]
- Bui, V.H.; Nguyen, T.T.; Kim, H.M. Distributed Operation of Wind Farm for Maximizing Output Power: A Multi-Agent Deep Reinforcement Learning Approach. IEEE Access 2020, 8, 173136–173146. [Google Scholar] [CrossRef]
- Saputra, Y.M.; Hoang, D.T.; Nguyen, D.N.; Dutkiewicz, E.; Mueck, M.D.; Srikanteswara, S. Energy Demand Prediction with Federated Learning for Electric Vehicle Networks. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, Z.; Ogbodo, M.; Huang, H.; Qiu, C.; Hisada, M.; Abdallah, A.B. AEBIS: AI-Enabled Blockchain-Based Electric Vehicle Integration System for Power Management in Smart Grid Platform. IEEE Access 2020, 8, 226409–226421. [Google Scholar] [CrossRef]
- Ebell, N.; Gütlein, M.; Pruckner, M. Sharing of Energy Among Cooperative Households Using Distributed Multi-Agent Reinforcement Learning. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe), Bucharest, Romania, 29 September–2 October 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Albataineh, H.; Nijim, M.; Bollampall, D. The Design of a Novel Smart Home Control System using Smart Grid Based on Edge and Cloud Computing. In Proceedings of the 2020 IEEE 8th International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 12–14 August 2020; pp. 88–91. [Google Scholar] [CrossRef]
- Kohn, W.; Zabinsky, Z.B.; Nerode, A. A Micro-Grid Distributed Intelligent Control and Management System. IEEE Trans. Smart Grid 2015, 6, 2964–2974. [Google Scholar] [CrossRef]
- Hu, R.; Kwasinski, A. Energy Management for Microgrids Using a Hierarchical Game-Machine Learning Algorithm. In Proceedings of the 2019 1st International Conference on Control Systems, Mathematical Modelling, Automation and Energy Efficiency (SUMMA), Lipetsk, Russia, 20–22 November 2019; pp. 546–551. [Google Scholar] [CrossRef]
- Gao, L.m.; Zeng, J.; Wu, J.; Li, M. Cooperative reinforcement learning algorithm to distributed power system based on Multi-Agent. In Proceedings of the 2009 3rd International Conference on Power Electronics Systems and Applications (PESA), Hong Kong, China, 20–22 May 2009; pp. 1–4. [Google Scholar]
- Ernst, D.; Glavic, M.; Wehenkel, L. Power systems stability control: Reinforcement learning framework. IEEE Trans. Power Syst. 2004, 19, 427–435. [Google Scholar] [CrossRef]
- Rogers, G. Power System Oscillations; Springer US: Boston, MA, USA, 2000; pp. 1–6. [Google Scholar] [CrossRef]
- Hadidi, R.; Jeyasurya, B. A real-time multiagent wide-area stabilizing control framework for power system transient stability enhancement. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–8. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Chen, T.; Su, W.; Jin, T. Proactive Resilience of Power Systems Against Natural Disasters: A Literature Review. IEEE Access 2019, 7, 163778–163795. [Google Scholar] [CrossRef]
- Mahzarnia, M.; Moghaddam, M.P.; Baboli, P.T.; Siano, P. A Review of the Measures to Enhance Power Systems Resilience. IEEE Syst. J. 2020, 14, 4059–4070. [Google Scholar] [CrossRef]
- Karim, M.A.; Currie, J.; Lie, T.T. Distributed Machine Learning on Dynamic Power System Data Features to Improve Resiliency for the Purpose of Self-Healing. Energies 2020, 13, 3494. [Google Scholar] [CrossRef]
- Ghorbani, M.J.; Choudhry, M.A.; Feliachi, A. A Multiagent Design for Power Distribution Systems Automation. IEEE Trans. Smart Grid 2016, 7, 329–339. [Google Scholar] [CrossRef]
- Ghorbani, M.J. A Multi-Agent Design for Power Distribution Systems Automation. Ph.D. Thesis, West Virginia University, Morgantown, WV, USA, 2014. [Google Scholar] [CrossRef]
- Ghorbani, J.; Choudhry, M.A.; Feliachi, A. A MAS learning framework for power distribution system restoration. In Proceedings of the 2014 IEEE PES T D Conference and Exposition, Chicago, IL, USA, 14–17 April 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Hong, J. A Multiagent Q-Learning-Based Restoration Algorithm for Resilient Distribution System Operation. Master’s Thesis, University of Central Florida, Orlando, FL, USA, 2017. [Google Scholar]
- Kim, K.K.K. Distributed Learning Algorithms and Lossless Convex Relaxation for Economic Dispatch with Transmission Losses and Capacity Limits. Math. Probl. Eng. 2019, 2019. [Google Scholar] [CrossRef]
- Zhu, F.; Yang, Z.; Lin, F.; Xin, Y. Decentralized Cooperative Control of Multiple Energy Storage Systems in Urban Railway Based on Multiagent Deep Reinforcement Learning. IEEE Trans. Power Electron. 2020, 35, 9368–9379. [Google Scholar] [CrossRef]
- Al-Saffar, M.; Musilek, P. Reinforcement Learning-Based Distributed BESS Management for Mitigating Overvoltage Issues in Systems With High PV Penetration. IEEE Trans. Smart Grid 2020, 11, 2980–2994. [Google Scholar] [CrossRef]
- Li, K.; Guo, Y.; Laverty, D.; He, H.; Fei, M. Distributed Adaptive Learning Framework for Wide Area Monitoring of Power Systems Integrated with Distributed Generations. Energy Power Eng. 2013, 5, 962–969. [Google Scholar] [CrossRef]
- Jouini, T.; Sun, Z. Distributed learning for optimal allocation of synchronous and converter-based generation. arXiv 2021, arXiv:math.OC/2009.13857. [Google Scholar]
- Bollinger, L.; Evins, R. Multi-Agent Reinforcement Learning for Optimizing Technology Deployment in Distributed Multi-Energy Systems; European Group for Intelligent Computing in Engineering: Plymouth, UK, 2016. [Google Scholar]
- Gusrialdi, A.; Chakrabortty, A.; Qu, Z. Distributed Learning of Mode Shapes in Power System Models. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami, FL, USA, 17–19 December 2018; pp. 4002–4007. [Google Scholar] [CrossRef]
- Al-Saffar, M.; Musilek, P. Distributed Optimization for Distribution Grids With Stochastic DER Using Multi-Agent Deep Reinforcement Learning. IEEE Access 2021, 9, 63059–63072. [Google Scholar] [CrossRef]
- Al-Saffar, M.; Musilek, P. Distributed Optimal Power Flow for Electric Power Systems with High Penetration of Distributed Energy Resources. In Proceedings of the 2019 IEEE Canadian Conference of Electrical and Computer Engineering (CCECE), Edmonton, AB, Canada, 5–8 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- You, S. A Cyber-secure Framework for Power Grids Based on Federated Learning. engrXiv 2020. [Google Scholar] [CrossRef]
- Cao, H.; Liu, S.; Zhao, R.; Xiong, X. IFed: A novel federated learning framework for local differential privacy in Power Internet of Things. Int. J. Distrib. Sens. Netw. 2020, 16, 1550147720919698. [Google Scholar] [CrossRef]
- Afzalan, M.; Jazizadeh, F. A Machine Learning Framework to Infer Time-of-Use of Flexible Loads: Resident Behavior Learning for Demand Response. IEEE Access 2020, 8, 111718–111730. [Google Scholar] [CrossRef]
- Gholizadeh, N.; Abedi, M.; Nafisi, H.; Marzband, M.; Loni, A. Fair-optimal bi-level transactive energy management for community of microgrids. IEEE Syst. J. 2021, 15, 1–11. [Google Scholar] [CrossRef]
- Mamuya, Y.D.; Lee, Y.D.; Shen, J.W.; Shafiullah, M.; Kuo, C.C. Application of Machine Learning for Fault Classification and Location in a Radial Distribution Grid. Appl. Sci. 2020, 10, 4965. [Google Scholar] [CrossRef]
- Gush, T.; Bukhari, S.B.A.; Mehmood, K.K.; Admasie, S.; Kim, J.S.; Kim, C.H. Intelligent Fault Classification and Location Identification Method for Microgrids Using Discrete Orthonormal Stockwell Transform-Based Optimized Multi-Kernel Extreme Learning Machine. Energies 2019, 12, 4504. [Google Scholar] [CrossRef]
- Karim, M.A.; Currie, J.; Lie, T.T. Dynamic Event Detection Using a Distributed Feature Selection Based Machine Learning Approach in a Self-Healing Microgrid. IEEE Trans. Power Syst. 2018, 33, 4706–4718. [Google Scholar] [CrossRef]
- Cui, M.; Wang, J.; Chen, B. Flexible Machine Learning-Based Cyberattack Detection Using Spatiotemporal Patterns for Distribution Systems. IEEE Trans. Smart Grid 2020, 11, 1805–1808. [Google Scholar] [CrossRef]
- Rafiei, M.; Niknam, T.; Khooban, M.H. Probabilistic Forecasting of Hourly Electricity Price by Generalization of ELM for Usage in Improved Wavelet Neural Network. IEEE Trans. Ind. Inform. 2017, 13, 71–79. [Google Scholar] [CrossRef]
- Li, W.; Yang, X.; Li, H.; Su, L. Hybrid Forecasting Approach Based on GRNN Neural Network and SVR Machine for Electricity Demand Forecasting. Energies 2017, 10, 44. [Google Scholar] [CrossRef]
- Zhu, H.; Lian, W.; Lu, L.; Dai, S.; Hu, Y. An Improved Forecasting Method for Photovoltaic Power Based on Adaptive BP Neural Network with a Scrolling Time Window. Energies 2017, 10, 1542. [Google Scholar] [CrossRef]
- Khodayar, M.; Kaynak, O.; Khodayar, M.E. Rough Deep Neural Architecture for Short-Term Wind Speed Forecasting. IEEE Trans. Ind. Inform. 2017, 13, 2770–2779. [Google Scholar] [CrossRef]
- Shi, Z.; Yao, W.; Zeng, L.; Wen, J.; Fang, J.; Ai, X.; Wen, J. Convolutional neural network-based power system transient stability assessment and instability mode prediction. Appl. Energy 2020, 263, 114586. [Google Scholar] [CrossRef]
- Duan, J.; Shi, D.; Diao, R.; Li, H.; Wang, Z.; Zhang, B.; Bian, D.; Yi, Z. Deep-Reinforcement-Learning-Based Autonomous Voltage Control for Power Grid Operations. IEEE Trans. Power Syst. 2020, 35, 814–817. [Google Scholar] [CrossRef]
- Araya, D.B.; Grolinger, K.; ElYamany, H.F.; Capretz, M.A.; Bitsuamlak, G. An ensemble learning framework for anomaly detection in building energy consumption. Energy Build. 2017, 144, 191–206. [Google Scholar] [CrossRef]
- Jindal, A.; Dua, A.; Kaur, K.; Singh, M.; Kumar, N.; Mishra, S. Decision Tree and SVM-Based Data Analytics for Theft Detection in Smart Grid. IEEE Trans. Ind. Inform. 2016, 12, 1005–1016. [Google Scholar] [CrossRef]
- Zhao, J.; Li, L.; Xu, Z.; Wang, X.; Wang, H.; Shao, X. Full-Scale Distribution System Topology Identification Using Markov Random Field. IEEE Trans. Smart Grid 2020, 11, 4714–4726. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, J.; Poor, H.V. A Learning-to-Infer Method for Real-Time Power Grid Multi-Line Outage Identification. IEEE Trans. Smart Grid 2020, 11, 555–564. [Google Scholar] [CrossRef]
- Venayagamoorthy, G.K.; Sharma, R.K.; Gautam, P.K.; Ahmadi, A. Dynamic Energy Management System for a Smart Microgrid. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1643–1656. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.Z.; Zhou, J.; Huang, Z.L.; Bi, X.L.; Ge, Z.Q.; Li, L. A multilevel deep learning method for big data analysis and emergency management of power system. In Proceedings of the 2016 IEEE International Conference on Big Data Analysis (ICBDA), Hangzhou, China, 12–14 March 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Donnot, B.; Guyon, I.; Schoenauer, M.; Panciatici, P.; Marot, A. Introducing machine learning for power system operation support. arXiv 2017, arXiv:stat.ML/1709.09527. [Google Scholar]
- Fioretto, F.; Mak, T.W.K.; Hentenryck, P.V. Predicting AC Optimal Power Flows: Combining Deep Learning and Lagrangian Dual Methods. arXiv 2019, arXiv:eess.SP/1909.10461. [Google Scholar]
- Dalal, G.; Mannor, S. Reinforcement learning for the unit commitment problem. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, G.; Giannakis, G.B. Real-Time Power System State Estimation and Forecasting via Deep Unrolled Neural Networks. IEEE Trans. Signal Process. 2019, 67, 4069–4077. [Google Scholar] [CrossRef]
- Duchesne, L.; Karangelos, E.; Wehenkel, L. Machine learning of real-time power systems reliability management response. In Proceedings of the 2017 IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Kim, D.I.; Wang, L.; Shin, Y.J. Data Driven Method for Event Classification via Regional Segmentation of Power Systems. IEEE Access 2020, 8, 48195–48204. [Google Scholar] [CrossRef]
- Wen, S.; Wang, Y.; Tang, Y.; Xu, Y.; Li, P.; Zhao, T. Real-Time Identification of Power Fluctuations Based on LSTM Recurrent Neural Network: A Case Study on Singapore Power System. IEEE Trans. Ind. Inform. 2019, 15, 5266–5275. [Google Scholar] [CrossRef]
- Khodayar, M.; Wang, J.; Wang, Z. Energy Disaggregation via Deep Temporal Dictionary Learning. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 1696–1709. [Google Scholar] [CrossRef]
- Khokhar, S.; Mohd Zin, A.A.; Memon, A.P.; Mokhtar, A.S. A new optimal feature selection algorithm for classification of power quality disturbances using discrete wavelet transform and probabilistic neural network. Measurement 2017, 95, 246–259. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, J.; Jiang, L.; Tan, R.; Niyato, D.; Li, Z.; Lyu, L.; Liu, Y. Privacy-Preserving Blockchain-Based Federated Learning for IoT Devices. IEEE Internet Things J. 2021, 8, 1817–1829. [Google Scholar] [CrossRef]
- Zhang, W.; Lu, Q.; Yu, Q.; Li, Z.; Liu, Y.; Lo, S.K.; Chen, S.; Xu, X.; Zhu, L. Blockchain-Based Federated Learning for Device Failure Detection in Industrial IoT. IEEE Internet Things J. 2021, 8, 5926–5937. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Marchal, S.; Miettinen, M.; Fereidooni, H.; Asokan, N.; Sadeghi, A.R. DÏoT: A Federated Self-learning Anomaly Detection System for IoT. In Proceedings of the 2019 IEEE 39th International Conference on Distributed Computing Systems (ICDCS), Dallas, TX, USA, 7–10 July 2019; pp. 756–767. [Google Scholar] [CrossRef]
- Jiang, J.C.; Kantarci, B.; Oktug, S.; Soyata, T. Federated Learning in Smart City Sensing: Challenges and Opportunities. Sensors 2020, 20, 6230. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.; Xiong, Z.; Niyato, D.; Zou, Y.; Zhang, Y.; Guizani, M. Reliable Federated Learning for Mobile Networks. IEEE Wirel. Commun. 2020, 27, 72–80. [Google Scholar] [CrossRef]
- Melis, L.; Song, C.; De Cristofaro, E.; Shmatikov, V. Exploiting Unintended Feature Leakage in Collaborative Learning. In Proceedings of the 2019 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 19–23 May 2019; pp. 691–706. [Google Scholar] [CrossRef]
- McMahan, H.B.; Ramage, D.; Talwar, K.; Zhang, L. Learning Differentially Private Recurrent Language Models. arXiv 2018, arXiv:cs.LG/1710.06963. [Google Scholar]
- Li, T.; Sahu, A.K.; Talwalkar, A.; Smith, V. Federated Learning: Challenges, Methods, and Future Directions. IEEE Signal Process. Mag. 2020, 37, 50–60. [Google Scholar] [CrossRef]
- Prakash, S.; Dhakal, S.; Akdeniz, M.; Avestimehr, A.S.; Himayat, N. Coded Computing for Federated Learning at the Edge. arXiv 2020, arXiv:cs.DC/2007.03273. [Google Scholar]
- Wu, Q.; He, K.; Chen, X. Personalized Federated Learning for Intelligent IoT Applications: A Cloud-Edge Based Framework. IEEE Open J. Comput. Soc. 2020, 1, 35–44. [Google Scholar] [CrossRef]
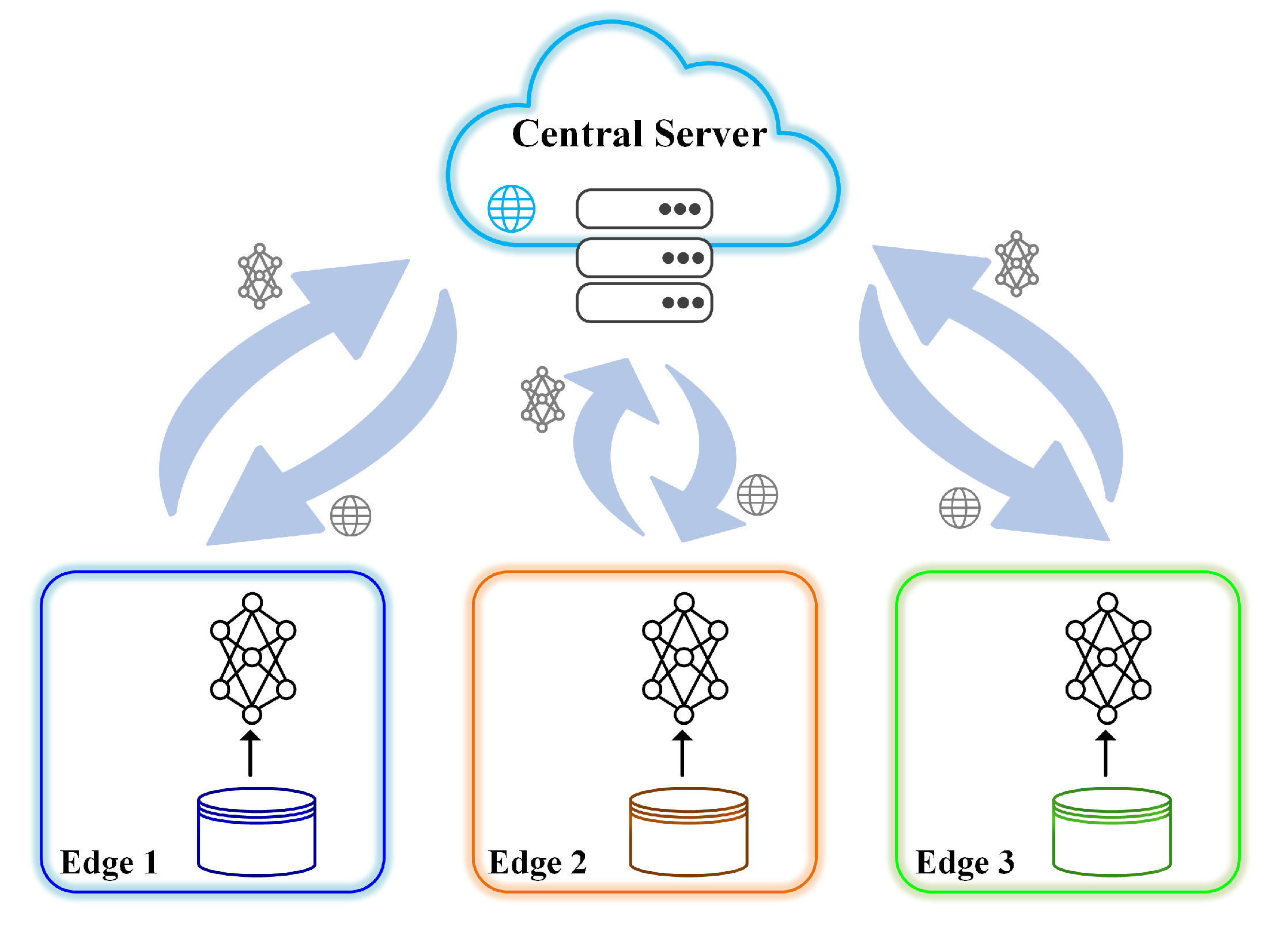
| Method | Data Source | Communication with Central Server | Communication between Agents |
|---|---|---|---|
| Distributed Learning | Central server | ✓ | ✓ |
| Federated Learning | Agents | ✓ | × |
| Assisted Learning | Agents | × | ✓ |
| Ref. | Application | Agents | Central Server | Machine Learning Algorithm | Exchanged Data |
|---|---|---|---|---|---|
| [48] | Voltage control | STATCOMs | - | Q-learning | Rewards, value functions |
| [49] | Voltage control | Voltage control units | - | Actor–critic framework | Powerflow information |
| [50] | Voltage control | Synchronous generators | Virtual server | Multilayer perceptron | Control actions |
| [51] | Voltage control | FACTs | - | SARSA Q-learning | Rewards, value functions |
| [53] | Wind power forecast | Neighbor wind turbine operators | Wind turbine operator | ADMM, mirror-descent | Partial power predictions, model coefficients of sites encryption matrix |
| [54] | Wind power forecast | Neighbor wind turbine operators | Wind turbine operator | ADMM | Partial power predictions |
| [56,57] | Wind power forecast | Wind farm operators | Power system operator | ADMM | Partial power predictions |
| [59] | Wind power maximization | Wind turbine operators | Transmission system operator | Deep Q-learning | Rewards |
| [60,61] | EV demand prediction | Charging stations | Charging station provider | Federated learning | Gradient information |
| [62] | Energy sharing among households | Households | Utility | Q-learning | Rewards |
| [64] | Microgrid energy management | Element controllers | Microgrid management server | Hamiltonians | Control variables |
| [65] | Microgrid energy management | Element controllers | Virtual server | Reinforcement learning | Load ratio |
| [66] | Wind–PV management | Wind turbines PV systems | - | Reinforcement learning | Action history |
| [69] | Increasing power system stability margins | Generator excitation systems, power system stabilizers | - | Reinforcement learning | States, rewards |
| [72] | Resiliency enhancement | Network regions | - | Ensemble learning | Rotor angle |
| [73,74,75,76] | Resiliency enhancement | Feeder agents | Substation agent | Q-learning | Measurements |
| [77] | Economic dispatch | Generators | Transmission system operator | Primal-dual decomposition | Lagrange multipliers |
| [78,79] | Energy Storage Control | Energy storage systems | Virtual server | Q-learning | Rewards |
| [80] | Wide-area monitoring | Synchrophasors | Virtual server | Incremental learning | Measured data |
| [81] | Optimal allocation | Generation units | - | Log-linear learning | Generation types |
| [82] | Technology deployment | Technology types | Market agent | Q-learning, Actor–critic framework | Energy prices, production prices |
| [83] | Mode shapes estimation | Local estimators | - | Linear regression | Electro-mechanical states |
| [84,85] | OPF | Microgrids | Central critic server | Deep reinforcement learning | Loss gradients |
| [87] | NILM | Households | Utility | Federated learning | Gradient information |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gholizadeh, N.; Musilek, P. Distributed Learning Applications in Power Systems: A Review of Methods, Gaps, and Challenges. Energies 2021, 14, 3654. https://doi.org/10.3390/en14123654
Gholizadeh N, Musilek P. Distributed Learning Applications in Power Systems: A Review of Methods, Gaps, and Challenges. Energies. 2021; 14(12):3654. https://doi.org/10.3390/en14123654
Chicago/Turabian StyleGholizadeh, Nastaran, and Petr Musilek. 2021. "Distributed Learning Applications in Power Systems: A Review of Methods, Gaps, and Challenges" Energies 14, no. 12: 3654. https://doi.org/10.3390/en14123654
APA StyleGholizadeh, N., & Musilek, P. (2021). Distributed Learning Applications in Power Systems: A Review of Methods, Gaps, and Challenges. Energies, 14(12), 3654. https://doi.org/10.3390/en14123654







