Quantifying the Effects of Wave—Current Interactions on Tidal Energy Resource at Sites in the English Channel Using Coupled Numerical Simulations
Abstract
1. Introduction
- Instrument measurement uncertainties are reasonably small and well understood if best practices are followed during instrument deployment and data analysis.
- Extrapolation procedures for tidal energy data are established, but the correct evaluation in site conditions with asymmetric tidal flows is challenging. Incorporating and quantifying wave–current interactions when measuring and predicting the tidal resource is a key uncertainty factor for wave exposed sites.
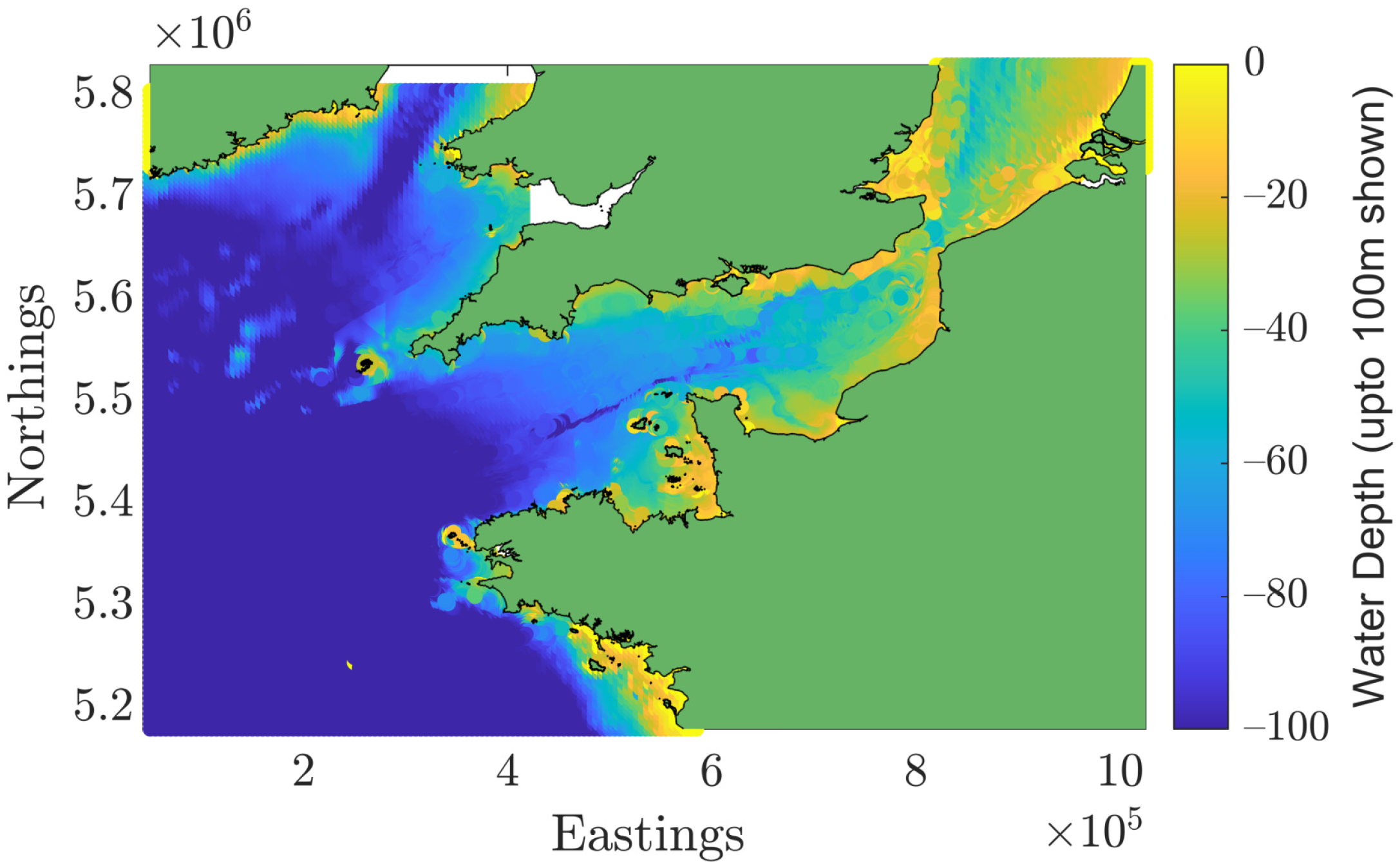
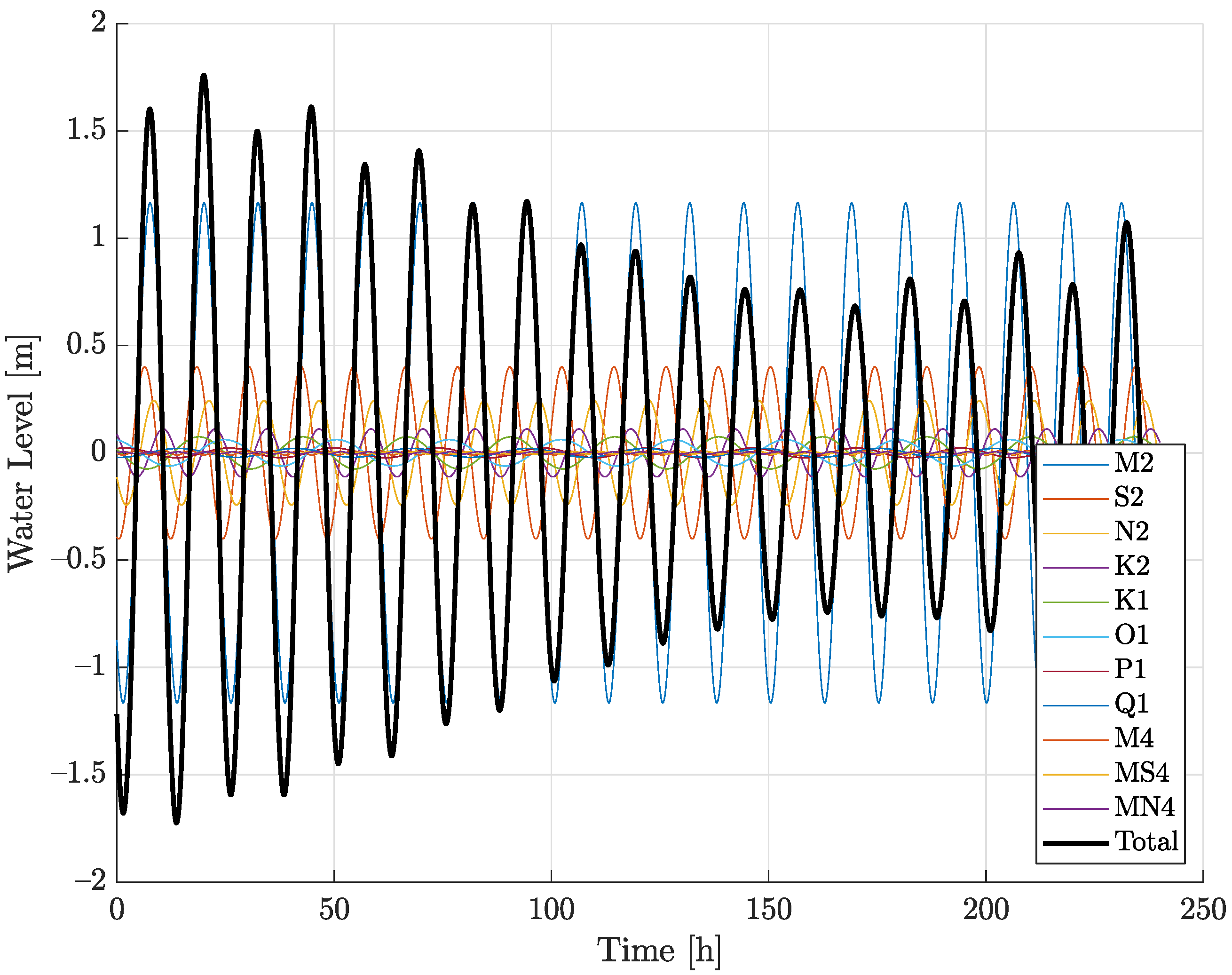
2. Modeling
| Site | Description |
|---|---|
| PTEC, Isle of Wight | Located 2.5 km off the southern tip of the Isle of Wight the site runs east–west for approximately 5 km and is approximately 1 km across. Spring peak flows are up to 4 ms. As of 2021, a 30 MW tidal array demonstration project is currently in the planning stages. The site has a potential capacity of 300 MW [26,27]. The mean water depth at the model output point used in this study is 65 m. |
| Alderney | Le Raz Blanchard is the highly energetic race between the island of Alderney and the Normandy coast. With spring peak flows of over 5 ms [28]. It is one of the most powerful tidal stream sites in Europe. An initial 7–20 MW array is planned to begin in 2021-2022 with up to 2–3 GW of tidal turbines are planned in the future [29]. It is estimated in [5] that the potential resource is as high as 5.10 GW. The mean water depth at the model output point used in this study is 38 m. |
| Guernsey | There are several areas around Guernsey with fast flows that could be suitable for tidal energy extraction. This study looks at Big Roussel, the race between the two small islands of Sark and Herm. It has peak flows of up to 3 ms [30]. Coles et al. [5] estimated that there is a maximum capacity of 0.12–0.24 GW. The mean water depth at the model output point used in this study is 40 m. |
2.1. Effects of Waves on Currents
2.1.1. Stokes Drift and Mass Flux
2.1.2. Streaming
2.1.3. Wave Induced Turbulence
2.1.4. Forcing by Radiation Stress Gradients
2.1.5. Enhancement of the Bed Shear Stresses
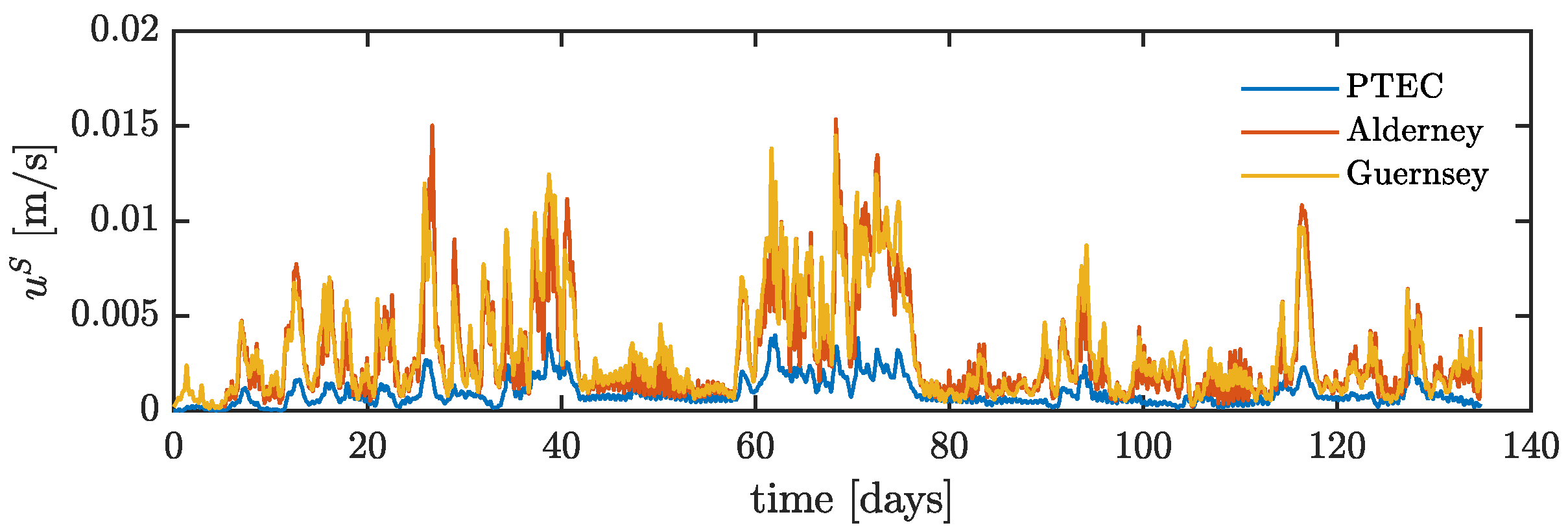
3. Results and Analysis
3.1. General Characterization
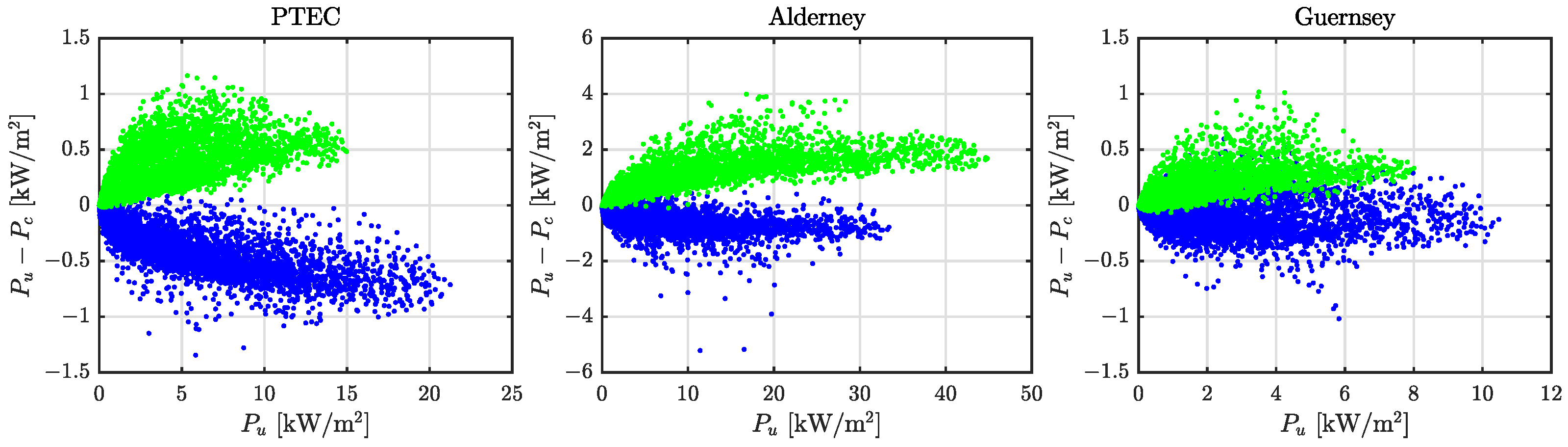
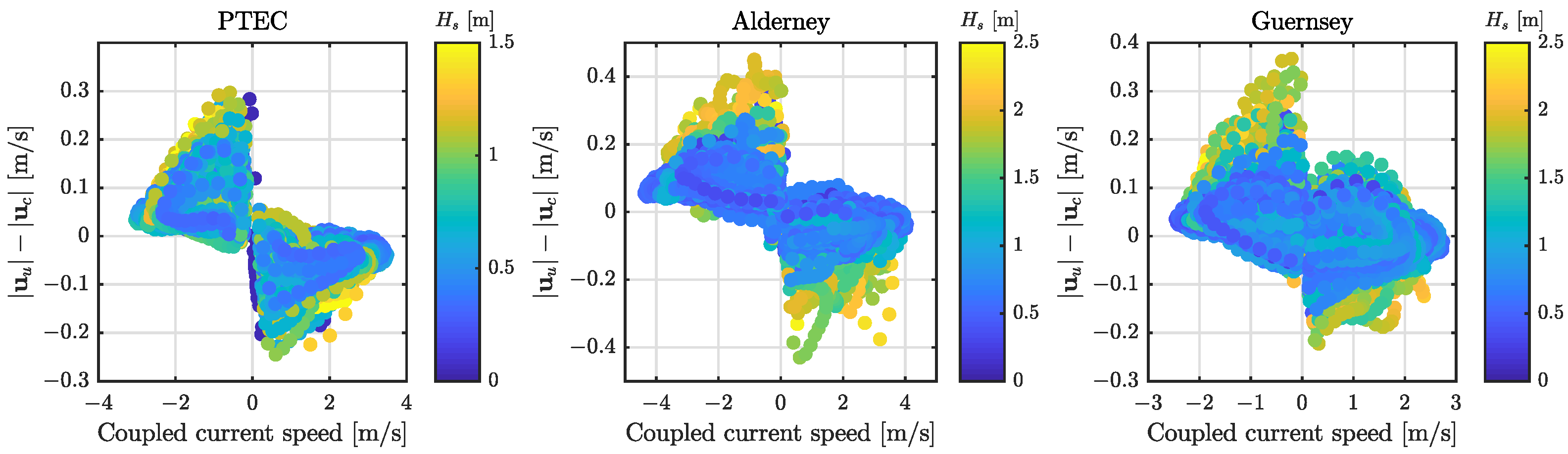
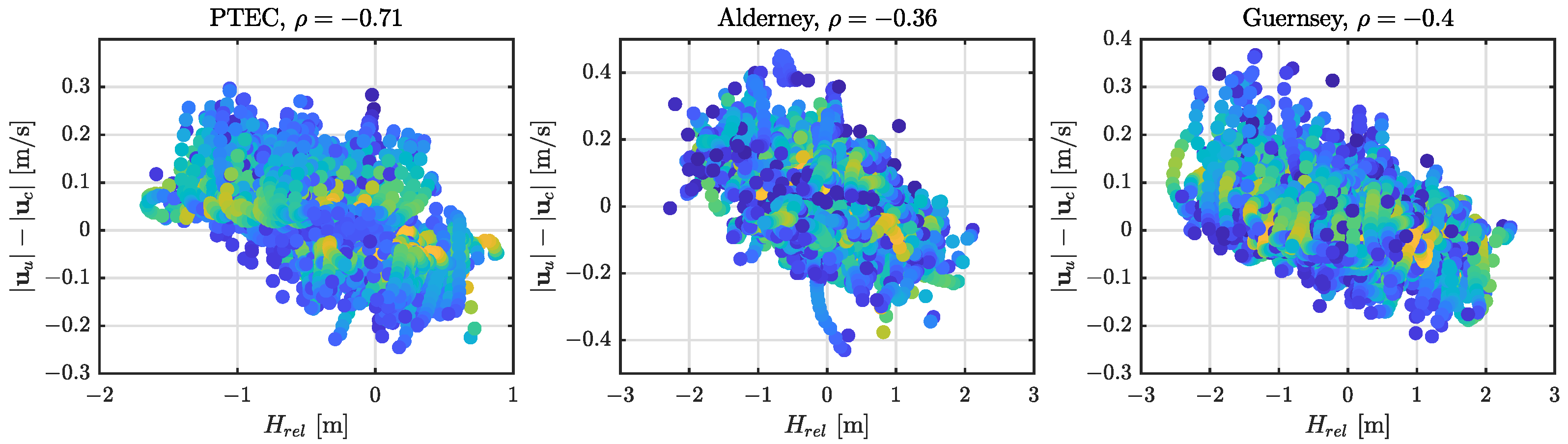
3.2. Difference in Flow between Coupled and Uncoupled Runs
4. Analysis
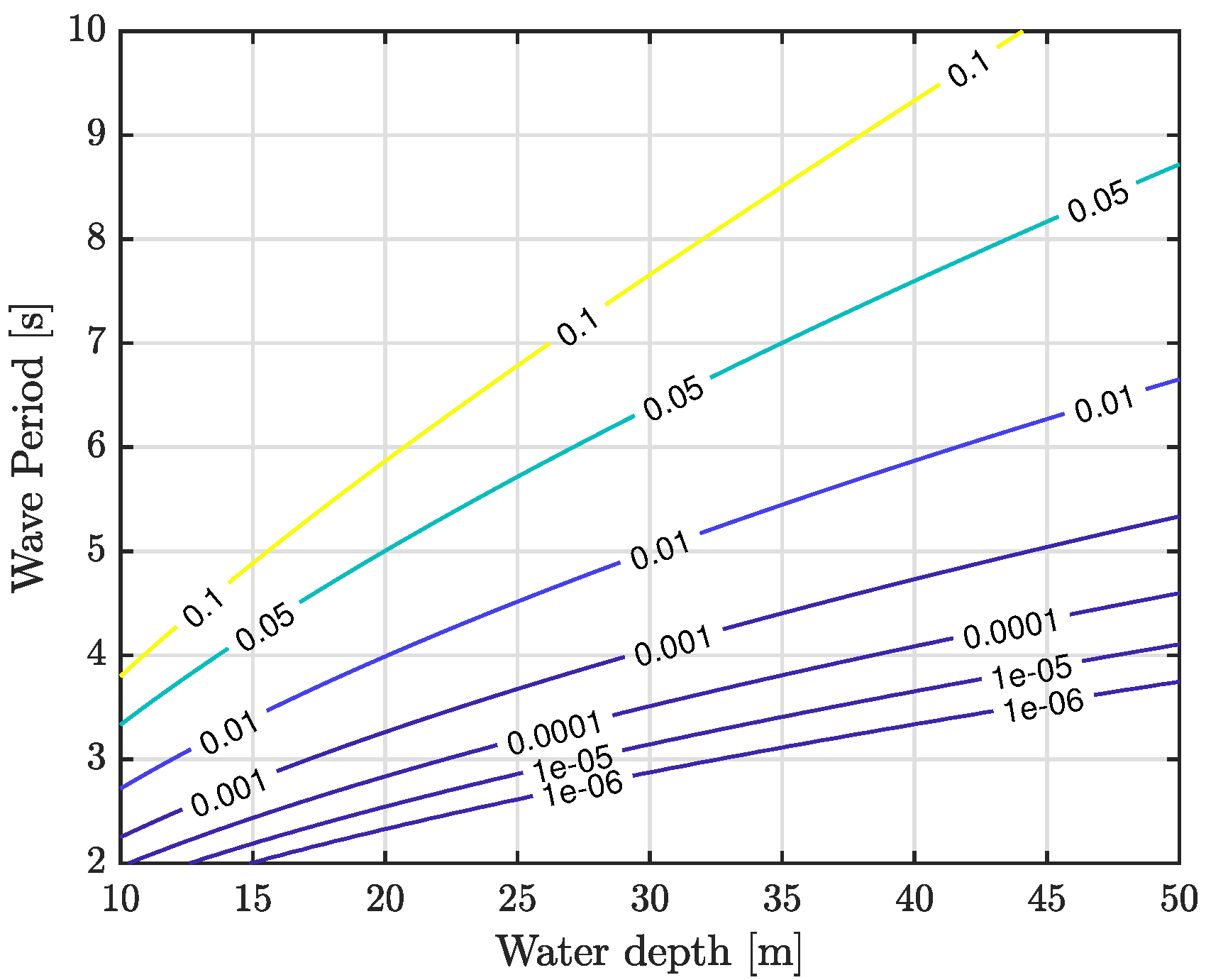
4.1. Stokes Drift
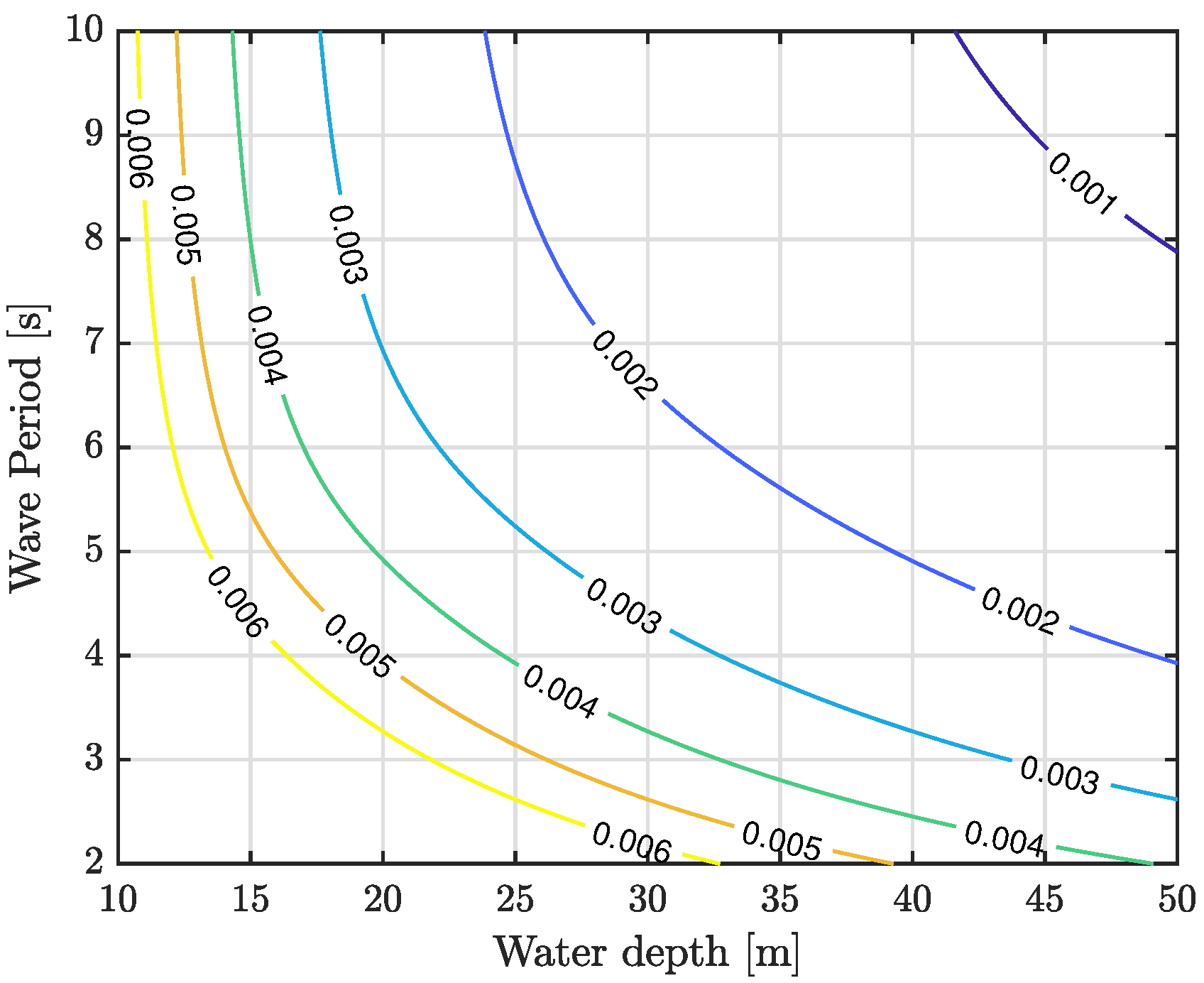
4.2. Enhancement of the Bed Shear Stresses
4.3. Forcing by Radiation Stress Gradients
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Crown Estate. UK Wave and Tidal Key Resource Areas Project—Technical Methodology Report; Technical Report; The Crown Estate: London, UK, 2013. [Google Scholar]
- Ocean Energy Europe. Ocean Energy: Key Trends and Statistics 2020; Technical Report; OEE: Brussles, Belgium, 2021. [Google Scholar]
- Draper, S.; Adcock, T.A.; Borthwick, A.G.; Houlsby, G.T. Estimate of the tidal stream power resource of the Pentland Firth. Renew. Energy 2014, 63, 650–657. [Google Scholar] [CrossRef]
- Hashemi, R.; Neill, S.; Davies, G. A numerical study of wave and current fields around Ramsey Island-tidal energy resource assessment. In Proceedings of the XIXth TELEMAC-MASCARET User Conference 2012, Oxford, UK, 18–19 October 2012; pp. 135–141. [Google Scholar]
- Coles, D.S.; Blunden, L.S.; Bahaj, A.S. Assessment of the energy extraction potential at tidal sites around the Channel Islands. Energy 2017, 124, 171–186. [Google Scholar] [CrossRef]
- Sutherland, G.; Foreman, M.; Garrett, C. Tidal current energy assessment for Johnstone Strait, Vancouver Island. Proc. Inst. Mech. Eng. Part A J. Power Energy 2007, 221, 147–157. [Google Scholar] [CrossRef]
- Blanchfield, J.; Garrett, C.; Rowe, A.; Wild, P. Tidal stream power resource assessment for Masset Sound, Haida Gwaii. Proc. Inst. Mech. Eng. Part A J. Power Energy 2008, 222, 485–492. [Google Scholar] [CrossRef]
- Karsten, R.H.; McMillan, J.M.; Lickley, M.J.; Haynes, R.D. Assessment of tidal current energy in the Minas Passage, Bay of Fundy. Proc. Inst. Mech. Eng. Part A J. Power Energy 2008, 222, 493–507. [Google Scholar] [CrossRef]
- Fairley, I.; Evans, P.; Wooldridge, C.; Willis, M.; Masters, I. Evaluation of tidal stream resource in a potential array area via direct measurements. Renew. Energy 2013, 57, 70–78. [Google Scholar] [CrossRef]
- Thiébaut, M.; Sentchev, A. Tidal stream resource assessment in the Dover Strait (eastern English Channel). Int. J. Mar. Energy 2016, 16, 262–278. [Google Scholar] [CrossRef]
- Lewis, M.; Neill, S.; Robins, P.; Hashemi, M. Resource assessment for future generations of tidal-stream energy arrays. Energy 2015, 83, 403–415. [Google Scholar] [CrossRef]
- Campbell, R.; Martinez, A.; Letetrel, C.; Rio, A. Methodology for estimating the French tidal current energy resource. Int. J. Mar. Energy 2017, 19, 256–271. [Google Scholar] [CrossRef]
- Lewis, M.J.; Neill, S.P.; Hashemi, M.R.; Reza, M. Realistic wave conditions and their influence on quantifying the tidal stream energy resource. Appl. Energy 2014, 136, 495–508. [Google Scholar] [CrossRef]
- Hashemi, M.R.; Neill, S.P.; Robins, P.E.; Davies, A.G.; Lewis, M.J. Effect of waves on the tidal energy resource at a planned tidal stream array. Renew. Energy 2015, 75, 626–639. [Google Scholar] [CrossRef]
- Wiberg, P.L.; Sherwood, C.R. Calculating wave-generated bottom orbital velocities from surface-wave parameters. Comput. Geosci. 2008, 34, 1243–1262. [Google Scholar] [CrossRef]
- González-Santamaría, R.; Zou, Q.; Pan, S.; Padilla-Hernandez, R. Modelling wave-tide interactions at a wave farm in the southwest of England. In Proceedings of the Coastal Engineering Conference. American Society of Civil Engineers (ASCE), Shanghai, China, 30 June–5 July 2010; p. 34. [Google Scholar] [CrossRef]
- Lewis, M.J.; Palmer, T.; Hashemi, M.R.; Robins, P.; Saulter, A.; Brown, J.; Lewis, H.; Neill, S. Wave-tide interaction modulates nearshore wave height. Ocean. Dyn. 2019, 69, 367–384. [Google Scholar] [CrossRef]
- ORE Catapult. Wave and Tidal Energy Yield Uncertainty: Literature Review and Reference Document; Technical Report; ORE Catapult: Glasgow, UK, 2015. [Google Scholar]
- O’Cathain, M.; Stock-Williams, C.; Carnus, T. Wave & Tidal Energy Production Estimates: Converting Resource Uncertainties into Energy Uncertainties. In Proceedings of the European Wave and Tidal Energy Conference, Aalborg, Denmark, 2–5 September 2013; 2013. [Google Scholar]
- Shah, S.; Buckland, H.; Thies, P.R.; Bruce, T. Combining Tidal Energy Yield Estimates. In Proceedings of the Asian Wave and Tidal Energy Conference, Singapore, 25–27 October 2016. [Google Scholar]
- Deltares. Delft3D-FLOW: User Manual; Technical Report; Deltares: Delft, The Netherlands, 2021. [Google Scholar]
- TUDelft. SWAN: Scientific and Technical Documentation; Technical Report; TU Delft: Delft, The Netherlands, 2010. [Google Scholar]
- Deltares. Delft3D—Flexible Mesh Technical Reference Manual; Technical Report; Deltares: Delft, The Netherlands, 2018. [Google Scholar]
- Kernkamp, H.W.; Van Dam, A.; Stelling, G.S.; De Goede, E.D. Efficient scheme for the shallow water equations on unstructured grids with application to the Continental Shelf. Ocean. Dyn. 2011, 61, 1175–1188. [Google Scholar] [CrossRef]
- Martyr-Koller, R.C.; Kernkamp, H.W.; van Dam, A.; van der Wegen, M.; Lucas, L.V.; Knowles, N.; Jaffe, B.; Fregoso, T.A. Application of an unstructured 3D finite volume numerical model to flows and salinity dynamics in the San Francisco Bay-Delta. Estuarine Coast. Shelf Sci. 2017, 192, 86–107. [Google Scholar] [CrossRef]
- Power Technology. EMEC, PTEC to Develop Large-Scale Tidal Energy Site in UK; Verdict Media Limited. Available online: https://powerlinks.news/emec/news/and-ptec-to-develop-large-scale-tidal-energy-site-in-uk (accessed on 17 June 2021).
- Perpetuus; Royal HaskoningDHV. Environmental Impact Statement; Technical Report; Royal HaskoningDHV: Amersfoort, The Netherlands, 2016. [Google Scholar]
- Bahaj, A.S.; Myers, L. Analytical estimates of the energy yield potential from the Alderney Race (Channel Islands) using marine current energy converters. Renew. Energy 2004, 29, 1931–1945. [Google Scholar] [CrossRef]
- Atlantis, S. Raz Blanchard|Tidal Projects|SIMEC Atlantis Energy. Available online: https://simecatlantis.com/projects/raz-blanchard-alderney/ (accessed on 17 June 2021).
- Blunden, L.S.; Bahaj, A.S. Initial evaluation of tidal stream energy resources at Portland Bill, UK. Renew. Energy. Pergamon 2006, 31, 121–132. [Google Scholar] [CrossRef]
- EDINA Marine Digimap Service. Arcsecond Gridded Bathymetry [ASC Geospatial Data]; EDINA: Edinburgh, UK, 2013. [Google Scholar]
- SHOM. Service Hydrographique et Océanographique de la Marine; SHOM: Brest, France, 2016. [Google Scholar]
- GEBCO Bathymetric Compilation Group 2020. The GEBCO_2020 Grid—A Continuous Terrain Model of the Global Oceans and Land; British Oceanographic Data Centre, National Oceanography Centre, NERC: Southampton, UK, 2020. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient Inverse Modeling of Barotropic Ocean Tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions 1. Model description and validation. J. Geophys. Res. Ocean. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- ECMWF. Copernicus Climate Change Service (C3S); Climate Data Store (CDS), European Centre for Medium Range Weather Forecasts: Reading, UK, 2021; Available online: https://cds.climate.copernicus.eu/ (accessed on 17 June 2021).
- Van Nieuwkoop, J.C.C.; Smith, H.C.M.; Smith, G.H.; Johanning, L. Wave resource assessment along the Cornish coast (UK) from a 23-year hindcast dataset validated against buoy measurements. Renew. Energy 2013, 58, 1–14. [Google Scholar] [CrossRef]
- Kutupoğlu, V.; Çakmak, R.E.; Akpınar, A.; van Vledder, G.P. Setup and evaluation of a SWAN wind wave model for the Sea of Marmara. Ocean. Eng. 2018, 165, 450–464. [Google Scholar] [CrossRef]
- Silva, D.; Soares, C.G. Assessment of the wave power resource at Madeira archipelago with the SWAN model. In Developments in Renewable Energies Offshore: Proceedings of the 4th International Conference on Renewable Energies Offshore (RENEW 2020, Lisbon, Portugal, 12–15 October 2020; CRC Press: Boca Raton, FL, USA, 2020; p. 45. [Google Scholar]
- ECMWF. 2D Wave Specta (ERA5); Climate Data Store (CDS), European Centre for Medium Range Weather Forecasts: Reading, UK, 2021; Available online: https://www.ecmwf.int/en/forecasts/documentation-and-support/2d-wave-spectra (accessed on 17 June 2021).
- Soulsby, R.L.; Hamm, L.; Klopman, G.; Myrhaug, D.; Simons, R.R.; Thomas, G.P. Wave-current interaction within and outside the bottom boundary layer. Coast. Eng. 1993, 21, 41–69. [Google Scholar] [CrossRef]
- Groeneweg, J. Wave-Current Interactions in a Generalized Lagrangian mean Formulation. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1999. [Google Scholar]
- Fredsøe, J.; Deigaard, R. Mechanics of Coastal Sediment Transport; Advanced Series on Ocean Engineering; World Scientific: Singapore, 1992; Volume 3. [Google Scholar] [CrossRef]
- Dingemans, M.W.; Radder, A.C.; De Vriend, H.J. Computation of the driving forces of wave-induced currents. Coast. Eng. 1987, 11, 539–563. [Google Scholar] [CrossRef]
- Komen, G.J.; Hasselmann, S.; Hasselmann, K. On the Existence of a Fully Developed Wind-Sea Spectrum. J. Phys. Oceanogr. 1984, 14, 1271–1285. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.; Bouws, E.; Carlson, H.; Cartwright, D.; Enke, K.; Ewing, J.; Gienapp, H.; Hasselmann, D.; Kruseman, P.; et al. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Ergaenzungsheft Zur Dtsch. Hydrogr. Z. Reihe A 1973, 12, 1–95. [Google Scholar]
- Fredsøe, J. Turbulent Boundary Layer in Wave-current Motion. J. Hydraul. Eng. 1984, 110, 1103–1120. [Google Scholar] [CrossRef]
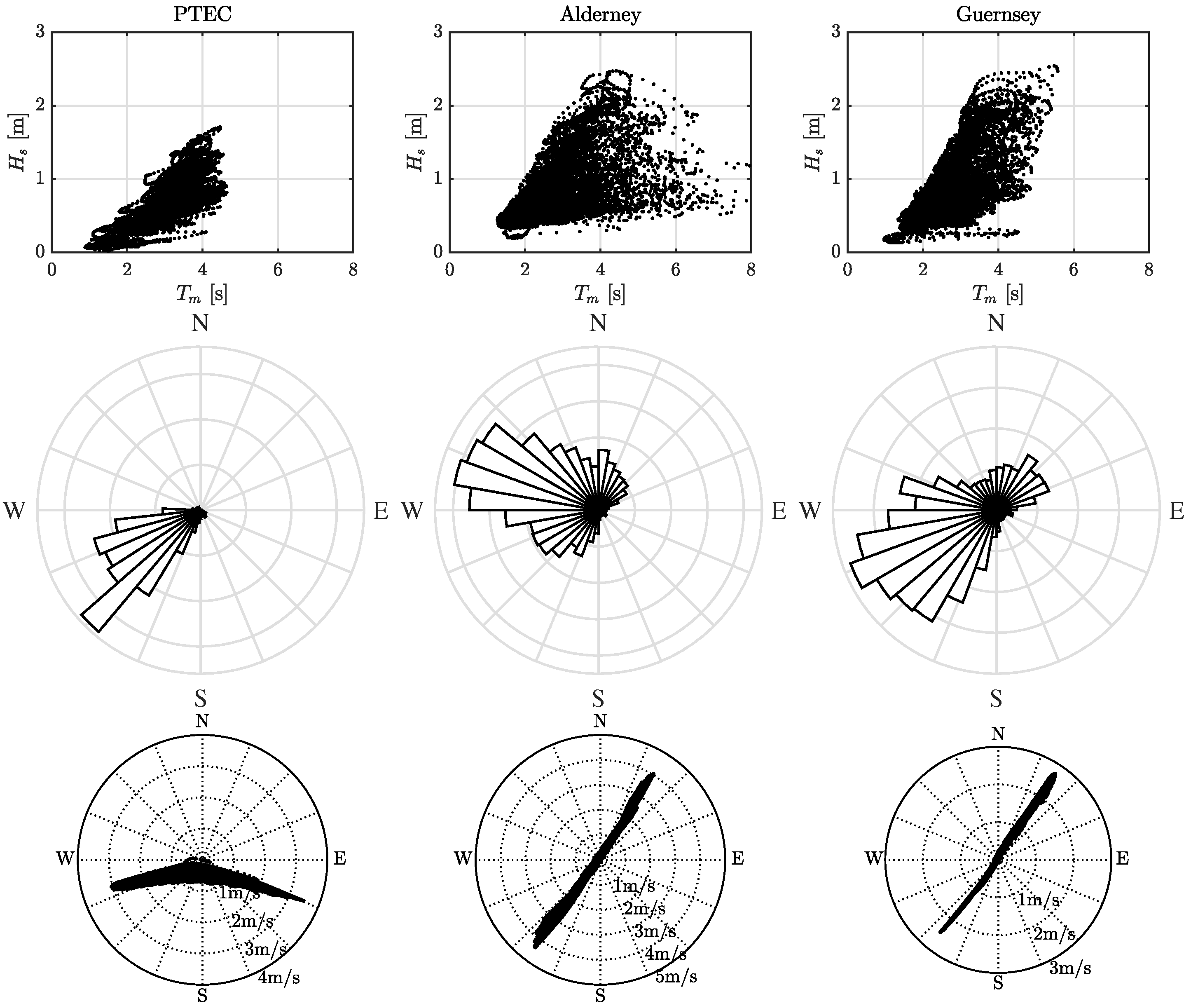

| Easterly | Westerly | Overall | ||||
|---|---|---|---|---|---|---|
| [kW/m] | [kW/m] | [kW/m] | ||||
| PTEC | 4.7 | +7.0% | 3.5 | −8.4% | 4.1 | +0.7% |
| Alderney | 5.9 | +7.0% | 8.4 | −9.6% | 7.1 | −2.5% |
| Guernsey | 2.0 | +2.6% | 1.5 | −9.0% | 1.8 | −1.5% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hardwick, J.; Mackay, E.B.L.; Ashton, I.G.C.; Smith, H.C.M.; Thies, P.R. Quantifying the Effects of Wave—Current Interactions on Tidal Energy Resource at Sites in the English Channel Using Coupled Numerical Simulations. Energies 2021, 14, 3625. https://doi.org/10.3390/en14123625
Hardwick J, Mackay EBL, Ashton IGC, Smith HCM, Thies PR. Quantifying the Effects of Wave—Current Interactions on Tidal Energy Resource at Sites in the English Channel Using Coupled Numerical Simulations. Energies. 2021; 14(12):3625. https://doi.org/10.3390/en14123625
Chicago/Turabian StyleHardwick, Jon, Ed B. L. Mackay, Ian G. C. Ashton, Helen C. M. Smith, and Philipp R. Thies. 2021. "Quantifying the Effects of Wave—Current Interactions on Tidal Energy Resource at Sites in the English Channel Using Coupled Numerical Simulations" Energies 14, no. 12: 3625. https://doi.org/10.3390/en14123625
APA StyleHardwick, J., Mackay, E. B. L., Ashton, I. G. C., Smith, H. C. M., & Thies, P. R. (2021). Quantifying the Effects of Wave—Current Interactions on Tidal Energy Resource at Sites in the English Channel Using Coupled Numerical Simulations. Energies, 14(12), 3625. https://doi.org/10.3390/en14123625







