Heat Release Kinetics upon Water Vapor Sorption Using Cation-Exchanged Zeolites and Prussian Blue Analogues as Adsorbents: Application to Short-Term Low-Temperature Thermochemical Storage of Energy

Abstract

In view of potential uses in short-term thermochemical heat storage by sorption of water vapor, the capacity to release a sufficient heat amount at the appropriate rate of a Prussian blue analogue (PBA) containing hexacyanocobaltate vacancies has been compared with those of 13X type zeolites possessing Na⁺, Ce³⁺, Ce⁴⁺, or Tb³⁺ extra-framework compensating cations. The extended structural and surface characterization demonstrated good reproducibility of the preparation procedures performed on a 10-g scale. The adsorbents were tested under dynamic conditions of gas flow with the aid of either a gas flow calorimeter (120 mL h⁻¹ helium flow) to measure the amount and rate of the integral heat release or a laboratory-scale test rig (15,000 to 22,800 mL h⁻¹ nitrogen flow) to monitor the outlet temperature of nitrogen heated by adsorption. For a regeneration temperature of 353 K and a partial H₂O pressure of 2.8 kPa in helium, the PBA sample yielded an integral heat ranging between 900 and 1020 kJ kg⁻¹ with a very slow heat release lasting for even 12–14 h. The zeolite-based materials generated between 350 and 950 kJ kg⁻¹ more rapidly (up to 6–7 h), depending on the nature and the content of compensating cations, as well as on the dehydration state achieved during regeneration. With the laboratory-scale test rig, the efficiency of heat extraction by convection was about 65% for Na-13X and only 38% for PBA, and it diminished with decreasing flow rate.

1. Introduction

Low-temperature thermochemical storage based on solid-vapor adsorption offers a promising alternative to numerous concepts tested in the scientific and technical literature. In this frame, the envisaged objective is to harvest solar energy during a sunny period and store this energy until the next period of “darkness” [1,2,3,4,5]. In the case of daily or short-term storage, it is potentially possible to benefit from the thermal energy released during the discharging step as the auxiliary heat source, which may be activated on demand when the targeted indoor temperature cannot be attained by the main heating system. Compared to other types of thermal energy storage technologies in a mature state (e.g., sensible or latent heat storage), the main advantages of the storage by sorption are the reliability and the easiness of the operating principle. Indeed, it is based on the quite well-controlled and usually reversible changes in the chemical potential of a solid adsorbent, as well as a relatively weak dependence of the restored energy on the charging and discharging temperatures. This allows avoiding heavy investments in thermal insulation so as to prevent energy loss in the intermediate interval. The quantity of heat released upon discharging and its constancy in time with repeated charging–discharging cycles, as well as the thermal stability of the working materials under specific conditions of the charging step, are key criteria evaluated in the selection of appropriate adsorbents [5,6]. Fundamental laboratory studies or experimental tests performed with different prototypes of heat storage unit have revealed that such classical adsorbents as silica gels, amorphous mesoporous silicas, and zeolites of different types are capable of producing a sufficiently high heat effect while keeping their structural and textural integrity simultaneously (e.g., [5,6,7,8,9,10] and references therein). It appears clear that various materials attain their optimal performance under particular operating conditions, but none of them really stands out significantly above the others. In consequence, the current trend is either to still search for completely new adsorbents (e.g., [11,12,13,14,15]) or to find optimal operating conditions for the existing materials.

Natural and modified zeolites have been intensively tested as adsorbents in view of their use in thermochemical heat storage by adsorption of water vapor [9,10,16,17,18,19]. In general, zeolites are known to adsorb much water vapor already at quite moderate relative pressures of water. However, high regeneration temperatures are required. In the context of future implementation of storage systems, the crystalline structure of the aluminosilicate framework was demonstrated to be subjected to a significant aging process during repeated hydration–dehydration cycles even at low temperatures, thus resulting in the appearance of an X-ray amorphous phase [20]. This observation was confirmed for three pelletized 13X samples from different industrial manufacturers submitted up to 3500 cycles.

One of the options followed in tuning the thermal performance of zeolite materials was to impregnate their surface with hygroscopic salt hydrates (e.g., MgSO₄, MgCl₂, CaCl₂) [16,17,19,21]. A significant improvement in the heat and mass transfer, as well as an increase in the overall surface area available for water adsorption, were observed in relation to the nature of the porous host framework. For example, the highest heat yield of 1090 kJ per kg of composite sample was measured for commercial Na-Y beads impregnated with 15 wt% MgSO₄, compared to zeolites H-Y, Na-X, and Mordenite impregnated with the same quantity of salt [16]. These results were obtained after a thermal pre-treatment performed at 423 K for 3 h under helium flow conditions. The subsequent adsorption of water vapor was performed at 296 K by applying a vapor pressure of 2.6 kPa [16]. An alternative option examined was to propose zeolite frameworks containing different extra-framework compensating cations [9,18,22]. On the basis of experimental adsorption isotherms measured at 298, 318, 338, and 358 K, Aprea et al. calculated the integral heat of adsorption of water vapor onto synthetic (13X-type) and natural (HEU-type clinoptilolite-rich tuff) zeolites containing various compensating cations [9]. They demonstrated a positive effect of cation exchange on the thermal performance of zeolites. Indeed, the specific heat storage density increased in the following order: Na⁺ < Cd²⁺ < Sr²⁺ < Zn²⁺. It is worth noting that zeolite samples were degassed, prior to adsorption measurements, by a vacuum treatment at 423 K for 3 h. The enhanced heat of water adsorption at a relative vapor pressure of 2.8 kPa, as measured by flow calorimetry, was also reported for a commercial 13X zeolite modified by cation exchange with Mg²⁺ and Ca²⁺ ions when the vacuum pretreatment was performed at 473 K [18]. Higher heat values attaining even 1140 kJ kg⁻¹ were obtained under the same dehydration and hydration conditions for cerium-exchanged 13X samples [22]. In these two cases, a significant decrease in the heat quantity was monitored in two subsequent cycles preceded by a vacuum treatment overnight either at room temperature [18] or at 353 K [22]. Simultaneously, a kind of thermal instability of 13X zeolites could be related to the mobility of extra-framework compensating cations, strongly depending on the difference in the hydration state of the material between the charging and discharging steps. In order to remedy this shortcoming, it was suggested that substituting the pristine compensating Na⁺ cations with some multivalent ones possessing higher hydration energies could improve the structural stability due to stronger cation–framework interactions while enhancing the heat release upon adsorption. A decrease in the regeneration temperature to 353 K could also be envisaged even though the complete sample dehydration was not achieved.

On the other hand, the range of potential adsorbents to be applied in gas separation has been broadened for the last decade owing to the development of Metal–Organic Frameworks (MOFs) and porous cyano-bridged coordination polymers such as Prussian blue analogues (PBA). Indeed, the latter possess high porosity and desired chemical selectivity towards certain gaseous components [23,24,25,26,27]. Versatile solid structures belonging to both families may be derived on the basis of the molecular chemistry concepts while taking advantage of their chemical and structural flexibility combined with the possibility of post-synthesis modifications. In particular, they can contain coordinatively unsaturated metal sites (CUS) when vacant Lewis acid sites on the metal ions or cluster nodes are created [28]. These CUS may play an important role in modulating the hydrophilic–hydrophobic surface balance, especially in the case of PBA materials, which exhibit very high stability under hydrothermal conditions [29]. Prussian blue analogues are represented by a general formula A_aM[M’(CN)₆]_b⎕_c·xH₂O (A is an alkaline ion, M and M’ designate transition metal ions, and ⎕ represents a cyanometallate vacancy) and they crystallize in a face-centered cubic structure [30]. The [M’(CN)₆]_b⎕ complexes are linked to octahedral Mⁿ⁺ ions through cyano-bridges to generate a 3D porous framework. The presence of cyanometallate vacancies implies that the Mⁿ⁺ ions complete their six-coordinated geometry with water molecules. The latter may be subsequently removed to generate CUS, which in turn may interact specifically with a variety of molecular species. Despite their remarkable properties and hydrothermal stability, these materials were never investigated in view of their use as adsorbents in thermochemical energy storage.

In light of the above discussion, the intention of the present study was to test the capacity of a selected PBA material to produce sufficient heat amounts upon adsorption of water vapor and compare its thermal performances with those of cation-exchanged zeolites. In a broader context, the opportunity was taken to address some technical aspects affecting the performance of porous adsorbents in the case of short-term heat storage in open storage systems operating in the “moist-air flow” mode. Therefore, both the overall amount of heat released during the discharging step and the kinetics of heat release over a given period appeared as the main parameters to be studied thoroughly.

In line with our previous studies [15,22], special attention was paid to avoid potentially detrimental conditions of high partial pressures of water vapor during the discharging step, combined with elevated temperatures applied to regenerate the adsorbent during the charging step. This research strategy was followed despite the fact that the “mild” regeneration conditions would possibly result in a decreased energy release upon adsorption of water vapor. Moreover, the restriction imposed on the regeneration temperature may also be justified by its dependence on the maximum air temperatures to be attained at the outlet from solar air collectors functioning in different climatic zones during summer and winter periods [31,32]. An adequate experimental study was programmed to seek to answer whether the PBA sample could compete on certain aspects with benchmark zeolite adsorbents, either commercial faujasite-type zeolite or modified zeolite structures obtained by substituting the pristine extra-framework compensating cations by trivalent ones. Two types of experimental equipment used to date differed in the way the thermal energy was extracted during the discharging step (i.e., adsorption of water vapor onto dehydrated adsorbent). Namely, the models of heat transfer by conduction within the adsorbent bed or by convection in the carrier gas were tested. For this purpose, it was necessary to reproduce on a 10-g scale the preparation procedures previously developed to obtain PBA and 13X zeolites containing cerium and terbium compensating cations.

2. Materials and Methods

2.1. Materials

The raw zeolite material further subjected to cation exchange procedures was a 13X commercial sample purchased from Sigma–Aldrich. The chemical formula for this sample was Na₈₇.₈(SiO₂)₁₀₈.₉(AlO₂)₈₃.₁·xH₂O with an atomic Si:Al ratio of 1.27 [22]. For the purpose of this study, it will be further referred to as Na-13X. High purity (ACS reagent grade, assay ≥ 99.0%) terbium(III) nitrate hexahydrate, Tb(NO₃)₃.6H₂O, cerium(III) nitrate hexahydrate, Ce(NO₃)₃.6H₂O, ammonium sulfate, (NH₄)₂SO₄, tripotassium hexacyanocobaltate(III), K₃[Co(CN)₆], and cobalt(II) nitrate hexahydrate, Co(NO₃)₂·6H₂O were also Sigma–Aldrich products. The ALPHAGAZ 2 grade helium and nitrogen (Air Liquide, France) as well as the 18.2 MΩ cm ultrapure water (PURELAB^® Chorus 1, ELGA Veolia, France) were used in the gas adsorption and calorimetry experiments.

2.2. Adsorbent Samples and Their Characterization

Two zeolite samples were obtained by exchanging sodium compensating ions in the commercial 13X zeolite with either terbium(III) or cerium(III) cations according to the preparation and purification protocols reported previously [22,33]. For each type of material, the procedures were repeated twice, and the two batches were subsequently mixed together to obtain around 10 g of a unique sample.

The chemical formulas of the two zeolite samples were determined based on the results of Wavelength Dispersive X-ray Fluorescence (WDXRF) obtained with a PANalytical’s Axios Max spectrometer and Energy Dispersive X-ray Spectroscopy (EDX) on the scanning electron microscope (SEM; FEI Quanta 200 FEG).

The sodium exchange rate for the cerium-containing zeolite was found to be about 97%, and its chemical formula was thus Na₂.₆Ce₂₇.₄(SiO₂)₁₀₉(AlO₂)₈₃·xH₂O. This sample was subsequently heated at 723 K in the air for 12 h so as to oxidize extra-framework Ce³⁺ cations to Ce⁴⁺ ones [22]. The ultimate material was named Ce-13X. Two terbium-containing zeolite samples, differing in cation exchange ratio, were prepared: Tb65-13X (65 wt% of Na⁺ exchanged) and Tb95-13X (95 wt%). The chemical formula of the latter was Na₄.₆Tb₂₄.₄(SiO₂)₁₀₈.₆(AlO₂)₈₃.₄·xH₂O. The invariability of the zeolite structure after cation exchange or water adsorption experiments was verified by X-ray diffraction (XRD) at room temperature (see Sections 3 and 6 in the Supplementary Material).

A lacunary Prussian blue analogue was synthesized on a 10-g scale by following the procedure described previously [27,29]. Its chemical composition was confirmed by determining the overall atomic K:Co ratio by means of Energy Dispersive X-ray Spectroscopy (EDX), as well as by identifying the presence of the main structural features characteristic of the PBA cyano-bridged network with the use of Fourier-transform infrared spectroscopy (FT-IR) and Powder X-Ray Diffraction (PXRD). Additionally, changes in the surface hydration state or thermal stability of this sample were tested through thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC). The experimental details of all those techniques are described in the Supplementary Materials (Sections 4 and 6).

The chemical formula of this material was K₀.₀₃Co²⁺[Co³⁺(CN)₆]₀.₆₈⎕₀.₃₂·4.7H₂O, where the ⎕ symbol was used to represent the hexacyanocobaltate vacancies. This sample will be further referred to as PBA.

For both zeolite and PBA samples, the adsorption and desorption isotherms for gaseous N₂ were measured at 77 K by means of micromeritics 3Flex (Version 5.01) sorption equipment. Each sample was previously degassed overnight at 423 K under a secondary vacuum. The equivalent specific surface area (S_ap) was calculated on the basis of the Brunauer–Emmett–Teller (BET) model adapted to describe micropore-containing solids as a rational approximation and by taking 0.162 nm² as a cross-sectional area for one adsorbed N₂ molecule [34]; the BET transform was analyzed in the range of low relative pressures p/p₀, where p₀ was the saturated vapor pressure. The volume of micropores and the external surface area were determined by applying the α_S-plot procedure to the adsorption isotherm.

Other characterization techniques applied within the framework of the present study and the results obtained are described in the Supplementary Material.

2.3. Measurements of Water Vapor Uptake by Materials under Static and Flow Conditions

The retention affinity and capacity of Ce-13X and PBA towards water vapor were quantified by measuring the adsorption isotherms under static conditions at 298 K using a homemade sorption apparatus described previously [35]. Prior to the sorption measurements, around 100 mg of each sample were subjected to a thermal treatment either at 353 K or at 423 K under a secondary vacuum, better than 0.01 Pa (10⁻⁵ Torr). The amount adsorbed corresponding to a given equilibrium pressure was calculated by following the manometric/volumetric measurement principles. The sorption measurements were performed in a Setaram C80 differential and isothermal microcalorimeter, thus allowing to simultaneously determining the adsorbed amount and the corresponding differential heat of adsorption [36]. The processing of calorimetry data is detailed in the Supplementary Material (Section 1, Figure S1).

The heat release kinetics and capacity of all samples were tested under dynamic conditions of a gas flow passing through an adsorbent bed placed in the calorimetric cell of a 4 V ms microscale flow microcalorimeter [15,18,22]. A weighted sample (about 100 mg) was placed in the calorimetric cell and first degassed at 353 K for 48 h with the aid of an RV3 rotary vane pump (Midisciences, France). In the successive desorption (dehydration) stages, the degassing was carried out still at 353 K but under a continuous helium flow of 120 mL h⁻¹. Each saturation (adsorption) stage was achieved by flowing a mixture of water vapor in helium at a partial pressure of 2.8 kPa through the adsorbent bed for about 24 h. An in-line mounted saturation glass vessel filled with ultrapure water and thermostated by a water bath at 296 K was used to saturate the 120 mL h⁻¹ flow of pure helium continuously before directing it into the calorimetric cell [15,22]. The end of the heat release upon adsorption was set by waiting until the complete return of the thermal signal to baseline. This time interval was strongly dependent on the type of sample studied. The experimental set-up is described in the Supplementary Material (Section 1, Figure S2). The total heat evolved during a saturation run corresponding to the integral heat of adsorption. Ten successive dehydration–saturation cycles were carried out for each sample. It was also possible to simultaneously monitor the variations in the heat of adsorption as a function of time to obtain the heat release kinetics. For this purpose, the recorded thermal profile was partially integrated across the 40 s time intervals by means of the built-in software, and the sliced-time heat values were plotted against the corresponding time-sliced intervals.

A homemade laboratory-scale test rig was developed to continuously monitor the temperature of the gas flowing out after the adsorption of water vapor onto ca. 6.5 g sample placed inside a rigid PVC cylindrical reactor with a volume of ca. 37 cm³. Each new sample was first pre-treated in a vacuum at 423 K in an external degassing rig and then placed inside the reactor. The dry gaseous nitrogen used to dehydrate the solid sample was heated to 353 K when passing at a flow rate of 880 mL min⁻¹ through a heating coil. To perform an adsorption step, an in-line mounted saturation stainless steel vessel thermostated at 296 K was employed to control the humidity content in gaseous nitrogen flowing through the reactor at a flow rate of either 250 or 380 mL min⁻¹ (i.e., 15,000 or 22,800 mL h⁻¹). The dehydration and saturation periods lasted for about 18 h and were separated by a 4 h cooling interval. The experimental set-up is described in more detail in the Supplementary Material (Section 2, Figure S3).

3. Results and Discussion

With the aim of comparing the performances of various systems, the materials prepared on a scale of 10 g for the purpose of the present study were tested accordingly so as to demonstrate that their main properties are similar to those reported previously [22,29,33].

The results of the XRD study reported in the Supplementary Material (Section 3, Figure S4) for the pristine Na-13X and three zeolites (i.e., Ce-13X, Tb65-13X, and Tb95-13X) indicate that cation-exchanged samples have a cubic crystal structure of the 13X framework with the space group of Fd3m. The unit cell parameter, a, and cell volume, v, are as follows: a = 24.9859 Å and v = 15,598.0143 ų, Na-13X; a = 25.028 Å and v = 15,677.55 ų, Ce-13X; a = 24.9132 Å and v = 15,463.37 ų, Tb65-13X and Tb95-13X. Furthermore, the XPS study made on Ce-13X (the XPS spectra are reported in Figure S5 in the Supplementary Material) has revealed that the Ce³⁺ content in the sample is ca. 84 at % and that of Ce⁴⁺ is ca. 16 at %.

In the case of PBA, LeBail refinement applied to the XRD pattern (Supplementary Material: Section 4, Figure S6) provides a solid argument that the space group is identified as $Fm\overline{3}m$ type having a unit cell parameter a = 10.2091(3) Å in good accordance with the results reported for similar samples [37,38,39].

3.1. Surface Properties of Zeolite and PBA Materials

The description of adsorbents should obviously include their textural properties, which are essential in modulating their sorption capacity towards many different gases and vapors. The N₂ adsorption–desorption isotherms obtained for four zeolites and PBA after a vacuum degassing pre-treatment at 423 K are presented in Figure S8 in the Supplementary Material. The equivalent specific surface areas and porous parameters inferred from the analysis of these adsorption curves are given in

Table 1. Equivalent specific surface area (S_ap), micropore volume (V_µ), and external surface area (S_ext) for the samples studied in the present work, as obtained on the basis of the N₂ adsorption at 77 K after an overnight vacuum pre-treatment at 423 K.

Sample	Sap (m2 g−1)	Vµ (cm3 g−1)	Sext (m2 g−1)
Na-13X	861	0.29	2
Ce-13X	521	0.18	9
Tb65-13X	622	0.2	4
Tb95-13X	608	0.2	10
PBA	896	0.23	158

.

Both Na-13X and PBA are highly microporous, as shown by the shape of the sorption isotherms (Figure S8), strongly reminiscent of type I according to the IUPAC classification [40]. This is confirmed by the great extent of their surface areas and micropore volumes. In the case of Na-13X, its textural parameters agree well (within experimental uncertainty) with those obtained for a 13X sample taken from another commercial batch [18]. Surprisingly, its equivalent specific surface area is much greater than that of a similar sample measured by means of another sorption apparatus after a vacuum degassing at 473 K [22]. These results illustrate well the difficulty in determining the intrinsic values of textural parameters when the dry state of a hydrophilic and microporous adsorbent cannot be attained clearly and unambiguously. Therefore, the measurements are dependent on the experimental uncertainty due to the variability of the initial state of the sample (e.g., sample aging, surface hydration state) and the pre-treatment procedures applied. By analogy, the difference between the equivalent specific surface area of the present Ce-13X sample and that of similar adsorbent studied previously (i.e., 578 m² g⁻¹ for Ce3-13X [22]) can be ascribed to different degassing temperatures (i.e., 423 K against 473 K) thereby leading to different hydration states of the zeolite framework and extra-framework compensating cations. Poorer repeatability of cation exchange and/or sample oxidation processes on a larger scale may be an additional reason. Another argument may be made on the basis of various crystallographic sites occupied by extra-framework cations in 13X zeolites. According to the results of Monte Carlo simulations [18,22], Na⁺, Ce³⁺, and Ce⁴⁺ ions occupy the type I’ sites (in the sodalite cage toward the hexagonal prism) and the type II sites (close to the 6-ring window of the supercage) preferentially; some of them may also be located in the type III′ sites (close to the 12-ring window of the supercage). On the contrary, the type III’ site appears to be the preferential location in the dry zeolite saturated with Tb³⁺ ions [33]. It should be noted that the 12-ring windows constitute the pore inlet openings in the 13X framework. Furthermore, various cations differ in size depending on their hydration state; e.g., for three cations, the radii of the bare ions, r, and those of the cations with their first hydration shells, r + Δr, are as follows [41]: r = 102 pm and Δr = 116 pm, Na⁺; r = 92 pm and Δr = 223 pm, Tb³⁺; r = 101 pm and Δr = 207 pm, Ce³⁺; r = 80 pm and Δr = 283 pm, Ce⁴⁺. Therefore, these findings might, to a certain extent, account for the subtle differences in the micropore volume (and thus in the equivalent specific surface area) among the samples, especially if the compensating cations remain to a great extent hydrated after vacuum pre-treatment.

The thermal performance of adsorbents in thermochemical energy storage is strictly related to their capacity of adsorbing water vapor under given operating conditions. The temperature and the duration of the sample dehydration process corresponding to the charging stage in the storage cycle are presumed to have an impact on this performance.

The situation is quite complex for some Prussian blue analogues (PBA), for example, Co²⁺[Co³⁺(CN)₆]₀.₆₆, for which the original hydrophobic character may be reversibly switched to hydrophilic one through water coordination to CUS [29]. For the PBA sample achieved within the framework of the present study, thermogravimetric analysis in oxidizing (air) atmosphere (see Figure S7 in the Supplementary Material) has revealed its thermal and oxidative stability up to about 535 K. The removal of the coordinated and physically adsorbed water molecules occurred up to 480–500 K, with the steepest decrease in the mass loss being observed between 353 and 423 K. To better explore the relationship between the surface character and the conditions applied during the degassing procedure, the adsorption of water vapor onto PBA was carried out after vacuum pre-treatment at 353 and 423 K. 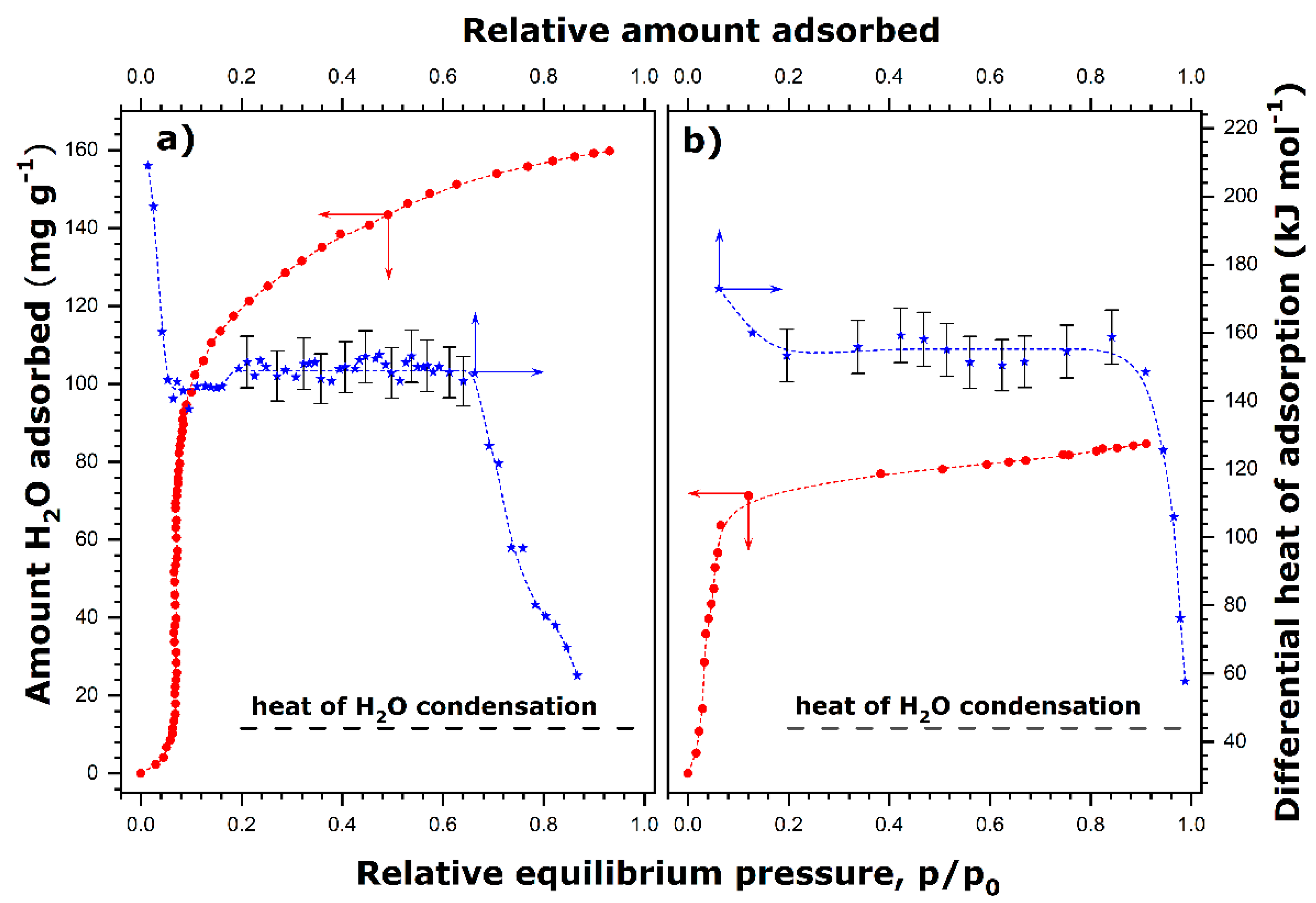Figure 1 shows the adsorption equilibrium isotherms and the related heat of adsorption curves.

When the degassing temperature is equal to 423 K, a sigmoidal-shaped adsorption curve is obtained (Figure 1a) in line with the results reported for similar materials by Boudjema et al. [29]. In the initial adsorption range where the sorption isotherm is a convex function, the differential heat of adsorption firstly takes high values, at least 200 kJ mol⁻¹, and then decreases rapidly to values lying between 143 and 155 kJ mol⁻¹, which remain fairly constant in a large interval of surface coverage ratio, Θ (Figure 1a). Following the same line of reasoning, this initial portion of the adsorption isotherm can be attributed to the strong interaction of water molecules with the CUS. Then, the heat curve has an extended plateau in a range up to Θ ≈ 0.7. This adsorption range corresponds well to the quasi-vertical portion of the adsorption isotherm, where the adsorption of water vapor is highly cooperative and thus resembles the two-dimensional condensation of adsorbed water [42]. Multiply hydrogen bonding of oncoming water molecules with those that were adsorbed in the first stage and between themselves clearly makes an important contribution to the total energy of water adsorption on a previously homogenized surface. Beyond Θ = 0.7, the differential heat decreases with the steadily increasing quantity of adsorption down to a value close to the heat of water condensation (i.e., about 44 kJ mol⁻¹ at 298 K [43]). The amount of adsorbed water seems to level off at high relative pressures, thus reaching an adsorption plateau value of about 160 mg per gram of adsorbent (i.e., 8.9 mmol g⁻¹).

The adsorption and heat curves obtained under milder degassing conditions (353 K) possess similar key characteristics, even though some quantitative differences may be revealed (Figure 1b). Chiefly, the two-dimensional condensation of adsorbed water accompanied by a fairly constant value of the differential molar heat of adsorption (150–160 kJ mol⁻¹) dominates the adsorption process since it occurs practically from Θ ≈ 0.1 to Θ ≈.9. Moreover, the maximum quantity of water adsorption attains a smaller value of 105 mg g⁻¹ (i.e., 5.8 mmol g⁻¹). The initial convex portion of the isotherm is greatly reduced compared to that obtained under conditions of a higher degassing temperature. This indicates a more hydrophilic character of the PBA surface at the beginning of adsorption due to a greater number of water molecules on the CUS after the degassing treatment at 353 K.

In comparison, Figure 2 shows analogous adsorption and heat curves determined on a selected zeolite sample after the degassing treatment at 353 K. An adsorption curve similar to the Type I isotherm with a steep initial portion is obtained even though the sample could not be completely dehydrated at this temperature [18]. The maximum quantity of adsorption of about 54 mg g⁻¹ is much smaller than the one obtained for PBA. The differential heat of adsorption attains high values (about 230 kJ mol⁻¹) at low relative quantities of adsorption. This may correspond to the interaction of water molecules with extra-framework cerium cations. Then, it decreases monotonously down to about 100 kJ mol⁻¹. This final value seems to indicate a rather moderate interaction of water vapor on the zeolite surface, likely due to confinement effects [44]. Altogether, Ce-13X keeps its very hydrophilic character after a “mild” degassing treatment. Therefore, it is reasonable to suppose that zeolite samples can still be useful in thermochemical heat storage when the regeneration temperature is not very high and the adsorption of water vapor is carried out at low humidity levels.

3.2. Impact of the Variability of Regeneration Conditions on the Heat Release Performance of Zeolite and PBA Materials in Repeated Cycles

In order to elucidate the effects of changing operating conditions on the capacity of storing energy, the solid samples were subjected to ten regular dehydration–saturation cycles. The dehydration of the adsorbent surface before each of the ten saturation cycles was performed according to the conclusions drawn from adsorption and batch calorimetry studies in Section 3.1 (Figure 1 and Figure 2). The sample was heated at 353 K inside the calorimeter for a given period of time either under vacuum (prior to the first cycle) or under a continuous helium flow of 120 mL h⁻¹ (the subsequent cycles). It was further slowly cooled down to room temperature for 24 h under the same helium flow. In the standard procedure, the duration of each heating step was changed alternatively on a 24- and 48-h shift basis so as to perform two dehydration–saturation cycles per week.

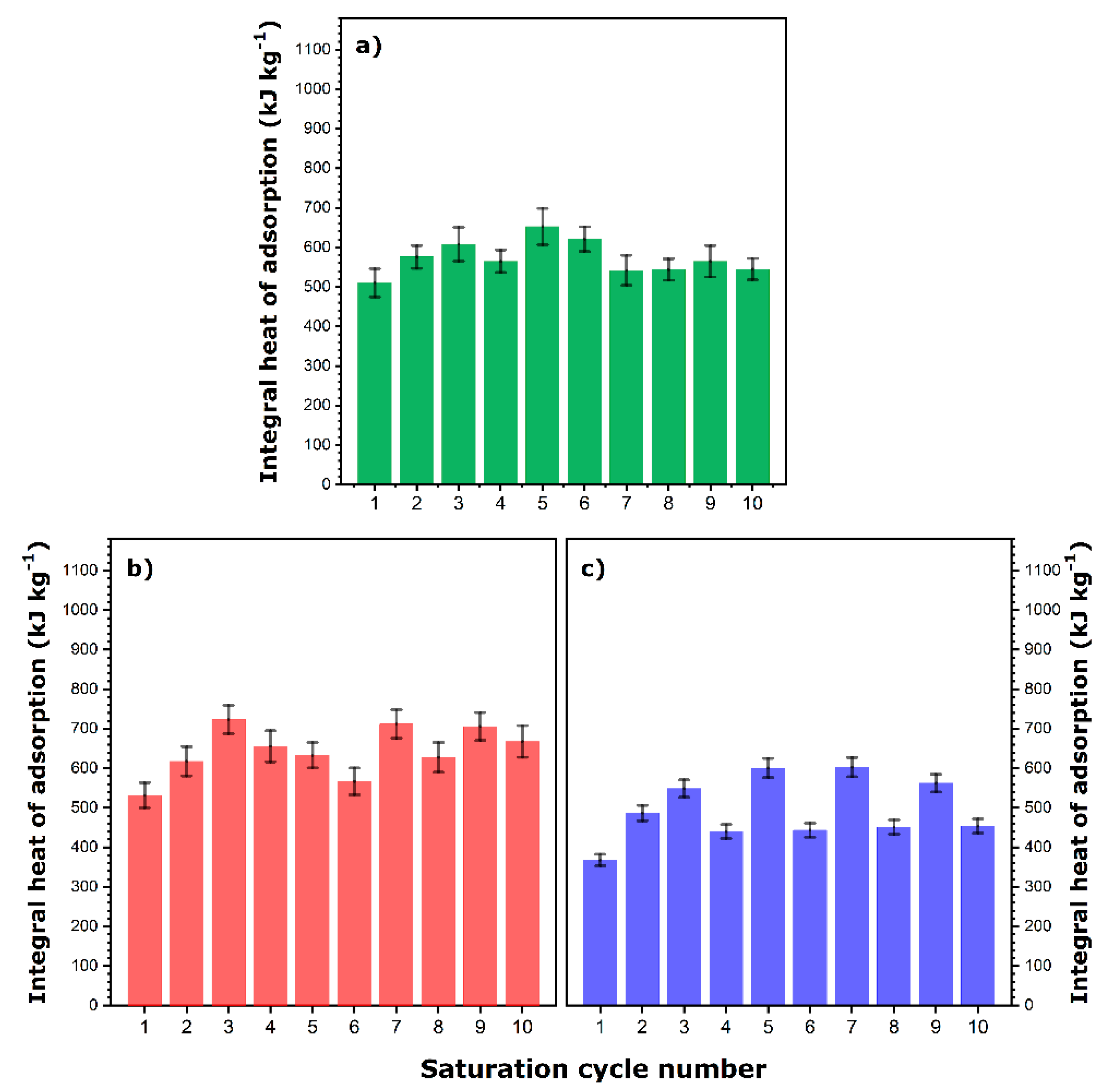
The integral values of the heat released in ten saturation cycles are presented in Figure 3 and Figure 4. Additionally, the hydrothermal stability of the samples upon continuous cycling under changing temperature and humidity conditions was checked accordingly. Figure S9 in the Supplementary Material shows the XRD patterns of the unprocessed sample, and that recovered after the last saturation cycle. Since the number and the position of the peaks do not change in the XRD patterns (despite variations in the peak intensity), it is evident that all materials keep their structural integrity at least during the repeated dehydration–saturation procedure lasting continuously up to 5 weeks.

Figure 3a presents the results of calorimetry measurements obtained with Na-13X. It is worth noting that the integral heat of adsorption depends on the degassing conditions applied before a given saturation stage and particularly on the duration of the heating step. Indeed, the averaged heat value obtained after a heating step of 24 h is equal to 659 ± 26 kJ kg⁻¹, whereas the corresponding value for the time period of 48 h attains 776 ± 27 kJ kg⁻¹. In addition, the integral heat of adsorption for the first saturation cycle is 952 ± 38 kJ kg⁻¹, which indicates that the 48-h vacuum pre-treatment at 353 K applied dehydrates Na-13X zeolite to a greater extent than that achieved subsequently by flushing the sample with gaseous helium at the same temperature. It should be pointed out here that this first-cycle heat of adsorption is clearly greater than that obtained previously under different, less controlled and less repeatable, pre-activation conditions (i.e., 784 ± 45 kJ kg⁻¹ after 24-h vacuum treatment at 423 K outside the calorimeter and degassing inside the calorimetric cell during a few hours by the continuous helium flow of 120 mL h⁻¹ [22]). The previously advanced arguments based on the variability of surface properties due to insufficient dehydration treatment can be repeated again. Finally, this heat value is comparable, within the experimental error, to the one measured with Na-Y zeolite (i.e., 978 kJ kg⁻¹) for a similar H₂O pressure of 2.6 kPa when the pre-activation treatment was carried out at 423 K during 3 h by the 3000 mL h⁻¹ flow of helium [16].

In the case of PBA, the impact of the variability of the dehydration conditions on the thermal performance during the subsequent saturation stage was monitored by changing the duration of the heating step in a less regular manner while always maintaining the same temperature of 353 K. The duration of this heating step prior to each saturation run is detailed in Figure 3b. The integral heat recorded during the first saturation cycle is 920 ± 42 kJ kg⁻¹, whereas the averaged heat values measured after short- and long-time heating steps are, respectively, 893 ± 29 and 1012 ± 58 kJ kg⁻¹. Besides the first cycle, the adsorption of water vapor onto PBA releases more heat per unit mass of adsorbent compared to that onto Na-13X, thus confirming the potential of these molecule-based materials. Again, fairly irregular changes in the integral heat of saturation as a function of the duration of the heating step are observed. This means that whatever the heating time, the complete and reversible surface dehydration cannot be achieved under the operating conditions applied in the present study.

In the next step, the thermal performance of the cation-exchanged zeolite samples was compared to that of the pristine Na-13X. The results are shown in Figure 4.

In the case of Ce-13X (Figure 4a), the heat released during the first saturation cycle, as well as the averaged heat values recorded after 24-h and 48-h heating steps, are equal to 511 ± 36, 570 ± 28, and 592 ± 42 kJ kg⁻¹, respectively. In addition, the first value is almost half that measured on a similar adsorbent (i.e., Ce3-13X sample in [22]) after an off-site degassing at 423 K. This likely indicates that the zeolite sample was not sufficiently dehydrated at 353 K despite the relatively long duration of the vacuum degassing. Clearly, some additional sample activation is observed during the subsequent dehydration–saturation cycles.

Similar trends in the integral heat of adsorption corresponding to short and long dehydration cycles can be observed for Tb65-13X (Figure 4b) and especially for Tb95-13X (Figure 4c). To facilitate the comparison among the samples, the three characteristic enthalpy values were gathered in

Table 2. Averaged values of the integral heat released upon the adsorption of water vapor in three representative saturation cycles.

Sample	Integral Heat of Water Adsorption (kJ kg−1)
	1st Cycle	After Short-Time Heating	After Long-Time Heating
Na-13X	952 ± 38	659 ± 26	776 ± 27
Ce-13X	511 ± 36	570 ± 28	592 ± 42
Tb65-13X	532 ± 32	627 ± 35	694 ± 36
Tb95-13X	368 ± 15	455 ± 17	579 ± 24
PBA	920 ± 42	893 ± 29	1012 ± 58

. It can be observed that the regeneration of a zeolite sample containing a much greater amount of multivalent Tb³⁺ cations instead of monovalent Na⁺ ones is incomplete. In turn, this results in the decreased performance of this sample in the adsorption of water vapor.

An additional test was performed to illustrate also the importance of the cooling step on the thermal performance of adsorbents. For a selected sample (Ce-13X), the experimental protocol was changed in that the cooling step was removed prior to the first saturation cycle. As a result, this first hydration was carried out at 353 K. The comparison of the heat values measured in four cycles by following two types of protocol is given in Figure S10 in the Supplementary Material. In line with the exothermic character of the adsorption phenomenon, the integral heat of adsorption decreases from 511 ± 36 kJ kg⁻¹ at 296 K to 328 ± 23 kJ kg⁻¹ at 358 K. When the standard operating conditions are restored in the subsequent cycles, the heat values become comparable within experimental error.

From the discussion above, it can be concluded that 13X zeolites containing various extra-framework compensating cations do not exhibit the expected improved thermal performance in adsorption of small amounts of water vapor if the dehydration of adsorbents is carried out either under vacuum or under a helium flow at 353 K. This is particularly true in the case of multivalent compensating cations characterized by strong interactions with the zeolite framework and high hydration energies. In this context, it may be noted that the Gibbs free energies of hydration for the four types of cation studied here are as follows [41]: −365 kJ mol⁻¹, Na⁺; −3200 kJ mol⁻¹, Ce³⁺; −3400 kJ mol⁻¹, Tb³⁺; −6120 kJ mol⁻¹, Ce⁴⁺. It is thus understandable that such multivalent compensating cations still preserve most of their hydration shells at the end of the sample regeneration stage. Higher degassing temperatures are needed to fully benefit from the improved thermal performance of 13X zeolites due to the increased hydration energies of their compensating cations.

3.3. Heat Release Kinetics of Zeolite and PBA Materials in Repeated Cycles

Besides the integral heat of adsorption released during each discharging stage, the kinetics of heat release is also of great interest for further use of adsorbents in heat storage by adsorption of water vapor. The complete kinetic curves acquired with the five adsorbents in ten dehydration–saturation cycles are presented in the Supplementary Material (Figures S11–S15). The most general conclusion to be drawn from the comparison of these results is that the rate at which the cumulative heat of adsorption changes clearly depends on the dehydration treatment applied prior to a given saturation step. To highlight some general trends in this regard, Figure 5 presents the kinetic curves of gradual heat release monitored in the following cycles: the first saturation cycle, as well as two other cycles chosen, as being representative for long-time and short-time heating steps (i.e., saturation cycles n° 7 and 8). Note that the heat recovery rate represents sliced-time values of the heat of adsorption across a 40-sec time interval.

For all adsorbents, the kinetic profiles have right-skewed bell-like shapes. The kinetic behavior of PBA is characterized by a broad time window inside which noticeable heat effects are observed (brown lines in Figure 5a–c). Irrespective of the saturation cycle, the maximum heat extraction rate is generally reached 7–8 h after the beginning. This value is about 35 W kg⁻¹ for the first saturation cycle (Figure 5a) and the one after a short-time heating (Figure 5c); it increases to about 45 W kg⁻¹ when the heating step is prolonged (Figure 5b). The time windows are shorter for zeolite samples, and the maximum heat extraction rates are reached 2–4 h after the beginning (depending strongly on the cycle). For Na-13X (black lines in Figure 5a–c), the time window becomes narrower in the order: 1st cycle > cycle after long-time heating > cycle after short-time heating. On the contrary, the maximum heat recovery rate is quite similar for the three cycles (56.0 ± 0.8 kJ kg⁻¹). In the case of three cation-exchanged zeolites, the broadest time window is obtained after a long-time heating step. The maximum extraction rate changes from one saturation cycle to another: the average of the three values is 30 ± 3, 38.5 ± 1.8, and 30 ± 5 kJ kg⁻¹ for Ce-13X (green lines), Tb65-13X (red lines), and Tb95-13X (blue lines), respectively.

One trend in the kinetic behavior of the three cation-exchanged zeolites deserves to be emphasized here. With the only exception of the first saturation cycle, the heat release accompanying the adsorption of water vapor onto Ce-13X, Tb65-13X, and Tb95-13X are characterized by slower kinetics compared to that observed for Na-13X. This feature is one of the requirements that should be addressed when implementing storage technology.

3.4. Thermal Performance of Materials Measured by Laboratory-Scale Test Rig

According to the calorimetric measurement principle [45,46], heat generated inside the calorimetric cell is transferred to its outer surface by means of conduction when the gas flow rate is sufficiently low. Therefore, the helium flow rate of 120 mL h⁻¹ applied in the calorimetry system does not allow the effluent gas to be heated efficiently. The amount of the convective heat transfer from the solid–gas interface by means of a gas flowing through the adsorbent bed may be increased by greatly increasing the flow rate. In the homemade laboratory-scale test rig employed in the present study, helium was replaced by pure nitrogen, and the flow rate during adsorption was increased by almost 200 times, namely up to 22,800 mL h⁻¹. The sensible heat, Q_s, in a heating process of nitrogen can be calculated as follows:

Q_s = C_p ∙ ρ_g ∙ R_V ∙ ∆T,

(1)

where C_p is the specific heat capacity of the gas (1.04 kJ kg⁻¹ deg⁻¹ for N₂ at 300 K [43]), ρ_g is the mass density of the gas (1.126 kg m⁻³ for N₂ at 300 K [43]), R_V is the volume flow rate of the gas, and ∆T denotes the temperature difference. This equation may be thus applied to evaluate the maximum temperature of the effluent gas that may be obtained in the test rig if the heat produced upon adsorption is totally transformed to the sensible heat Q_s without any heat loss. The maximum temperature obviously cannot be too high to avoid the thermal degradation of the material used for the reactor (i.e., for PVC, the glass transition temperature is in the range 343–373 K, whereas the melting point lies between 433 and 573 K [47]). The maximum heat extraction rates taken for the estimation were 35 W kg⁻¹ for PBA and 56 W kg⁻¹ for Na-13X. With an adsorbent mass of 6.5 g inside the reactor and a volume flow rate of 22,800 mL h⁻¹, the temperature of N₂ flowing out of the reactor should increase from 296 K to 327 K in the case of PBA or 345 K in the case of Na-13X.

Figure 6 presents the results of a single cycle test (black lines) carried out by making use of 6.5 g of Na-13X or PBA.

In the case of Na-13X (Figure 6a), the maximum temperature obtained experimentally (i.e., 344 K) is close to the theoretical value. It is attained after about 22 min, much earlier than the maximum heat recovery rate for this adsorbent in Figure 5. For PBA (Figure 6b), the maximum experimental temperature (i.e., 315 K) is far from the theoretical value, and it is reached after 56 min. Altogether, the convective extraction of the heat released upon adsorption of water vapor yields temperature profiles that are different from those corresponding to the heat recovery rate as a function of time in Figure 5. The first reason is due to the accelerated supply of water vapor to the adsorbent surface. Calculating the area under each curve by integration allows the total extracted heat to be calculated on the basis of Equation (1). The resulting values are 431 and 343 kJ kg⁻¹ for Na-13X and PBA, respectively. When compared to the averaged heat values obtained after a heating step of 24 h in the calorimetry experiment (see Table 2), they stand for around 65 and 38% of the integral heat of adsorption. Beyond the differences in the operating conditions between the two types of experiment and lower heat extraction efficiency of dry nitrogen compared to that of helium, it is clear that the volume flow rate of nitrogen applied (i.e., 22,800 mL h⁻¹) is still too small for the heat loss by conduction through the insulation to be avoided in the test rig.

To verify the last hypothesis, an additional two-cycle test was performed with the use of the same sample and by decreasing the flow rate of nitrogen to 15,000 mL h⁻¹. The option of increasing the flow rate was discarded so as to avoid a too great consumption of carrier gas during the experiment. The adsorbent placed inside the reactor was dehydrated between the first and the second cycles by a flow of nitrogen heated to about 353 K. The resulting temperature profiles were added to Figure 6 (red and blue lines).

For both adsorbents, the maximum temperature decreases to a great extent in comparison with the first experiment. Additionally, the temperature profile becomes more and more flattened, especially during the second hydration cycle (blue lines in Figure 6a,b). The areas under the curves lead to the following values of heat extracted by convection, respectively, in the first and the second cycles: 343 and 358 kJ kg⁻¹ for Na-13X; 215 and 249 kJ kg⁻¹ for PBA. On average, the percentage of the integral heat of adsorption thus decreases from 65% to ~53% for Na-13X and from 38% to ~26% for PBA when the flow rate passes from 22,800 to 15,000 mL h⁻¹. These results indicate that the conduction heat loss in the test rig is significant, and much greater flow rates would be necessary to recover the heat of adsorption only by convection. This is particularly true when using PBA as an adsorbent, probably because the intrinsic kinetics of heat release upon adsorption of water vapor on its surface is much slower, as shown in Figure 5 (brown lines).

4. Conclusions

Thermal performances of powdered 13X type zeolites and a Prussian blue analogue (PBA) were compared in view of potential applications in short-term low-temperature thermochemical storage of thermal energy by sorption of water vapor. The experimental conditions chosen were (i) low partial pressures of sorbate (i.e., 2.8 kPa) during the discharging step and (ii) moderate regeneration temperatures (i.e., 353 K) during the charging step.

As measured by gas flow calorimetry with the use of a 120 mL h⁻¹ flow of helium as a carrier gas, the zeolite-based materials could generate an integral heat of adsorption lying in the range between 350 and 950 kJ kg⁻¹. These results were found to depend on the nature and content of extra-framework compensating cations, as well as on the dehydration state achieved during regeneration. In contrast with the results of previous studies, cation exchange in Na-13X zeolite did not lead to an increase in the thermal performance of adsorbents towards water vapor under milder dehydration conditions (in the absence of a vacuum pre-treatment at 423 K). However, on a more positive note, the kinetics of heat release were found to be slowed down in comparison with the pristine Na-13X. Remarkably, the PBA sample yielded an enhanced integral heat of adsorption ranging between 900 and 1020 kJ kg⁻¹ with a very slow heat release lasting for even 12–14 h. These properties will prove particularly relevant for uses in short-term heat storage where the heat release should last during the day or night. On the basis of these results, it can be confirmed that these porous molecule-based materials can equal or sometimes even exceed the thermal performances of benchmark adsorbents such as zeolites.

The temperature of the gaseous nitrogen measured in the laboratory-scale test rig at the outlet of a 37 cm³ adsorber containing about 6.5 g of the solid sample was found to depend chiefly on the gas flow rate applied. Decreasing this flow rate from 22,800 to 15,000 mL h⁻¹ caused a significant decrease in the maximum outlet temperature with the concomitant flattening of the overall temperature profile over time. In general, the efficiency of heat extraction by convection was about 65% for Na-13X and only 38% for PBA, and it diminished with decreasing flow rate. In order to boost the gas flow, it would be necessary to produce adsorbents in the appropriate, granulated form. This, in turn, may pose issues related to gas moving along certain preferential pathways while bypassing a fraction of the porous matrix. In the light of the results achieved in the present study, it may be concluded that placing the temperature sensors in contact with the adsorbent bed within the reactor could be an adequate way of recovering most of the heat amount released during the adsorption of water vapor onto zeolites and PBA.