Abstract
Implementation of alternative energy supply solutions requires the broad involvement of local communities. Hence, smart energy solutions are primarily investigated on a local scale, resulting in integrated community energy systems (ICESs). Within this framework, the distributed generation can be optimally utilised, matching it with the local load via storage and demand response techniques. In this study, the boat demand flexibility in the Ballen marina on Samsø—a medium-sized Danish island—is analysed for improving the local grid operation. For this purpose, suitable electricity tariffs for the marina and sailors are developed based on the conducted demand analysis. The optimal scheduling of boats and battery energy storage system (BESS) is proposed, utilising mixed-integer linear programming. The marina’s grid-flexible operation is studied for three representative weeks—peak tourist season, late summer, and late autumn period—with the combinations of high/low load and photovoltaic (PV) generation. Several benefits of boat demand response have been identified, including cost savings for both the marina and sailors, along with a substantial increase in load factor. Furthermore, the proposed algorithm increases battery utilisation during summer, improving the marina’s cost efficiency. The cooperation of boat flexibility and BESS leads to improved grid operation of the marina, with profits for both involved parties. In the future, the marina’s demand flexibility could become an essential element of the local energy system, considering the possible increase in renewable generation capacity—in the form of PV units, wind turbines or wave energy.
1. Introduction
The concept of smart grids, implemented in local-scale systems, has attracted the far-reaching attention of governments, grid companies, and stakeholders [1,2]. By complementing local grids with adequate information and communication technologies, policies, and technical advancements, it is possible to significantly increase energy efficiency and enable greater utilisation of renewable energy [3,4]. Nevertheless, the implementation of intelligent grids is not possible without including consumers to a great extent. For this purpose, demand-side management (DSM) techniques are devised to influence the energy usage patterns, efficiently matching local supply and demand [5]. Within this framework, demand response (DR) is a part of DSM measures. DR initiatives allow the controllable loads—such as thermal loads or electric vehicles (EVs)—to be deferred to off-peak periods, providing financial incentives for participating consumers [6,7]. This action brings several advantages, including environmental benefits, congestion management, and reduced energy prices [8,9]. This way, the well-established approach of the generation-following load is inverted, controlling the demand via price signals or load control measures, with economic motivation for participating consumers [10]. In this context, DR initiatives can be broadly classified into incentive-based and price-based programs [5].
In incentive-based programmes, participating customers receive payments for load reduction, typically in the form of electricity bill discounts. In this regard, the prominent initiatives include direct load control (DLC), interruptible/curtailable load, demand bidding and buyback, and emergency demand response (EDR) programmes [2,5,11]. In contrast, price-based programmes provide consumers with time-varying energy prices. The price signals are devised to shift the electricity demand—higher rates naturally discourage extensive energy consumption at peak hours. In this category, time-of-use (TOU) tariffs, critical peak pricing (CPP) inclining block rate, and real-time pricing (RTP) are the most relevant programmes [12,13,14]. Within this framework, TOU and RTP programmes are widely recognized as the most efficient initiatives, suitable for future DR implementations [5].
Aiming at green goals, sustainable transport is an essential challenge, which needs to be addressed with innovative approaches. Understanding its importance, the Danish government targets 500,000 electric cars on the roads by 2030 [15]. Nevertheless, the additional load on power systems—created by the rising number of EVs—brings several challenges to the existing electrical grid. Notably, grid congestions, power balancing, and voltage issues are anticipated as possible detriments [8]. Therefore, grid integration possibilities of EVs are investigated in several publications [16,17,18]. With adequate coordination and management strategies, EVs provide a significant level of flexibility, utilising their synergies with RES and mitigating induced problems [7,19].
Besides electric cars, the other modes of electric transport are also in focus for increasing their integration with the grid. Reference [20] investigates the rail transport flexibility to minimise the energy cost and optimise the traction system loading. On the other hand, Reference [21] analyses the synergies between metro trains and electric cars, utilising metro regenerative braking energy for car charging. Furthermore, maritime transport can be used for improving the efficiency of marina distribution systems. In [22], the optimal scheduling algorithm for hybrid ferries is proposed. Nevertheless, the majority of vessel-flexibility studies focus on optimal scheduling of generation and voyage, not considering the interactions between vessels and onshore electrical grid [23,24,25,26]. The boat demand flexibility can become an essential element of smart marina energy systems, complementing the integrated operation of renewable generation and BESSs [3,27,28].
In the coastal locations, the renewable generation potential is substantial, taking advantage of the natural surroundings. The prevalent wind turbines and PV units can be complemented by harnessing wave energy, as indicated in various studies [29,30,31]. Furthermore, the implementation of energy storage techniques is vital for the efficient operation of renewables-based grids, benefiting from the adequate modelling of BESSs [32]. This way, the community energy systems—comprising local generation, storage systems, and DR techniques—are considered a suitable approach for increasing grid efficiency, utilising appropriate control strategies [33].
This paper proposes the optimal scheduling of the boat electricity demand in the ICES of Ballen marina on Samsø. The objective of the boat scheduling strategy is to increase the cost efficiency of energy usage for both marina and sailors, as well as to increase the marina’s load factor. Furthermore, the cooperation of boat flexibility and the marina’s distribution system—comprising PV units and BESS—is investigated under the developed hourly-varying tariff for the marina and TOU tariff for sailors. The boat flexibility is modelled and analysed, expanding the scope of previous research on marina energy systems.
The remainder of this paper is organised as follows. Section 2 presents the marina’s energy system outline, along with its challenges and opportunities. The marina’s boat demand is analysed in Section 3. Subsequently, Section 4 sets out the devised electricity pricing schemes for the marina and sailors. The modelling of boat flexibility is performed in Section 5. Thereafter, Section 6 provides the methods used for this study. The simulation results of the prepared study cases are provided and discussed in Section 7. Finally, the conclusions and future works are presented in Section 8.
2. Ballen Marina on Samsø
Local energy initiatives are an emerging issue throughout Europe due to the numerous encouragements from policymakers, as well as the unquestionable need for smarter and more efficient energy solutions [34]. The rising involvement of local communities enables the implementation of ICESs in diverse locations, with proven benefits on many levels. Moreover, this concept is especially appealing for islands, where the positive effects of local multi-energy solutions are remarkable [35].
The ongoing demonstration programme—via the European Union’s Horizon 2020 SMILE project—investigates the ICES of Ballen marina, located on the medium-sized Danish island of Samsø, aiming to increase the harbour’s self-sufficiency and reduce energy cost. Despite the cable connection between Samsø and the mainland, the discrepancies between buying and selling electricity prices encourage improving the self-consumption of locally generated energy. It is especially important in terms of inconsistent marina’s load, highly dependent on tourism. For this reason, the integration of PV generation, BESS, and flexible loads is currently under examination. The essential parameters of the Ballen marina are presented in Table 1 [3,36,37].

Table 1.
Overview of Ballen marina parameters.
The smart energy systems, consisting of energy storage systems (ESSs) and local renewable generation, can be effectively complemented by the DR techniques, demonstrating considerable improvements in the operation of ICESs. The potential benefits of load flexibility are considerable, including technical, economic, and ecological advantages [8]. Therefore, the flexible operation of the Ballen marina’s demand is investigated here, with the aim to increase cost-efficiency of the energy consumption, as well as load factor, by peak-shaving and valley-filling strategies.
In Ballen marina, docking boats constitute the most significant electrical load, accounting for approximately 75% of the total demand, which is supported by the local PV generation in around 45%. For this reason, in terms of flexibility potential, boats are primarily considered. The number of arriving boats is closely associated with the tourism season. From the DR point of view, the most interesting period is summer, due to the highest number of electricity consumers visiting the marina. Moreover, since the load is higher than PV generation during the peak tourist season, the BESS is mostly empty, as outlined in [28]. This is undesired and leaves room for further improvements. Hence, the better utilisation of BESS during summer, as well as time-variable energy prices and DR techniques, is investigated in this paper.
3. Marina’s Demand Analysis
The analysis was performed based on a data set from 2019, containing the recorded marina’s boat demand. For the analysis, the week with the highest demand was chosen, which was 15–21 July 2019 (from Monday to Sunday). The weekly boat demand profile is presented in Figure 1.
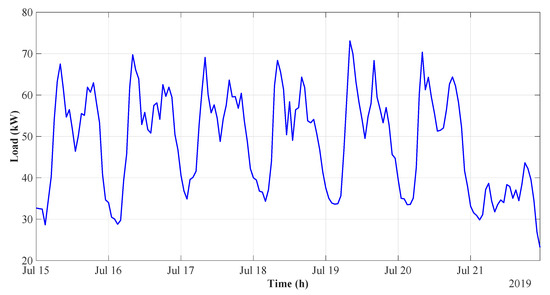
Figure 1.
Weekly boat demand.
For the chosen period, a similar daily boat demand pattern is clearly observable from Monday to Saturday (15–20 July), while Sunday (21 July) presents a considerably lower number of docking boats. For this reason, Sunday is excluded from further load variance analysis—nevertheless, it is still taken into account in the flexibility simulations. It is noted that this trend is only valid for the chosen summer period—the load distribution between the days of a week may be different for other seasons of the year. Thereafter, the weekly mean boat demand for each hour—along with the standard deviation—is calculated, as presented in Figure 2.
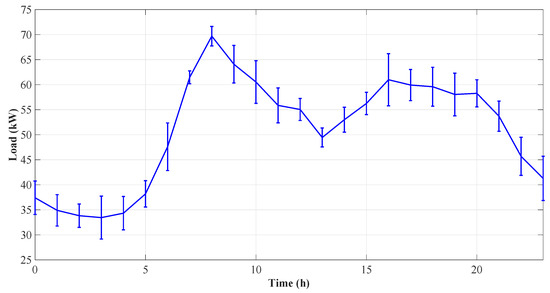
Figure 2.
Weekly mean boat demand with standard deviation.
Principally, four particular boat demand periods—for a typical summer day—can be distinguished:
- Night valley: 21.00–6.00.
- Morning peak: 6.00–10.00.
- Noon valley: 10.00–15.00.
- Afternoon peak: 15.00–21.00.
Within this framework, the highest load value can be observed at 8.00 (during the morning peak), while the lowest boat demand is seen at 3.00 (during the night valley). Furthermore, the afternoon peak reaches the crest value at 16.00, whilst the noon valley is the lowest at 13.00.
From observing the standard deviation, it is noted that the morning peak has a significantly lower variance compared to the afternoon peak. For this reason, it is substantially easier to accurately predict and manage the morning demand. This can be done with a combination of forecasting techniques and intelligence of the harbour’s master.
Ultimately, the economic benefits of boat flexibility are dependent on the price signals. Thus, the Elspot prices for the DK1 area are taken into consideration [38] in this work. In this context, the mean boat demand is compared with the mean Elspot prices for the analysed week, as presented in Figure 3.
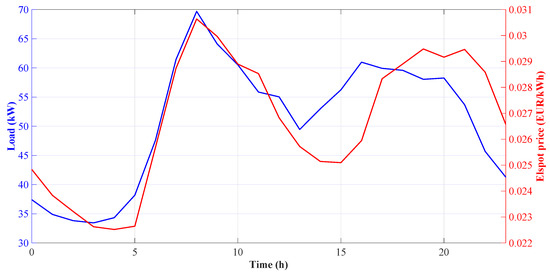
Figure 3.
Weekly mean boat demand and Elspot prices.
The visual inspection of the plot indicates the possible correlation between boat demand and Elspot prices. Therefore, the correlation analysis is performed, assessing the correlation based on the two following parameters [39]:
- Pearson correlation coefficient r: statistical measure of the linear correlation between two data sets, in the range of . A value of indicates perfect negative correlation, whereas signifies perfect positive correlation.
- p-value: probability of obtaining test results equal to or more extreme than the observed results. Very small p-values indicate that null hypothesis can be rejected. Typically, the null hypothesis is tested under the significance level of , leading to 95% confidence interval.
The correlation test is carried out under the null hypothesis of no correlation between mean boat demand and Elspot prices:
The results prove a very strong positive correlation between these variables, with the Pearson correlation coefficient of . The correlation is significant, with the p-value of , which is lower than the significance level of 5%. Therefore, the null hypothesis can be rejected, accepting the alternative one , which states that the correlation (not causation) between these data sets exists:
Moreover, it should be stressed that the hour with the highest demand corresponds to the time of the highest energy price. This fact implies that load shifting can be profitable for both marina and sailors, decreasing the energy cost for both involved parties. Since shifting peak demand to the valley period is equivalent to buying energy at a cheaper price, there is a considerable opportunity to improve the marina’s load factor and cost efficiency. In this manner, the peak load could be shifted to off-peak hours, utilising the price signals. Furthermore, the lower standard deviation of the morning peak indicates its higher predictability, which is advantageous for developing an adequate price-based DR programme.
Finally, the practical constraints of boat flexibility also signify the importance of the morning peak rather than the afternoon one. In a 24 h time frame, the charging action of boats—which arrive in the morning—could be ideally postponed to the later hours. Nevertheless, some purposes of sailors’ electricity usage are unlikely to be shifted, such as meal preparation and social activities.
4. Electricity Pricing
The local grid flexibility requires a suitable pricing mechanism, encouraging changes in electricity usage patterns. At the end of 2020, all Danish electricity consumers gained access to flex settlements, allowing them to use the tariff option with hourly changing energy prices. This required installation of electricity meters equipped with hourly consumption remote reading capability. The flex settlements are intended to influence energy consumption, accordingly to the variable renewable generation. This way, consumers can economically benefit from their flexibility, enabling greater integration of renewable energy at the same time [40]. A similar idea of energy pricing is intended for the Ballen marina, where switching to the hourly-varying tariff is currently under consideration.
4.1. Hourly-Varying Tariff for Marina
The marina currently trades energy with the utility grid at hourly-varying pricing rates. Furthermore, the smart metering system is already installed on the marina site, enabling remote switching and measurements for each of the 340 sockets. Thus, the hourly pricing scheme in the Ballen marina is modelled based on the illustrative Danish tariff [41].
The aforementioned tariff comprises Elspot prices , released one day ahead on the Nord Pool wholesale market. The inherent component of the energy buying price is the transport charge , consisting of the electricity transmission and distribution fees. Furthermore, this price also consists of other fees and taxes , including—among other things—the Public Service Obligations (PSO) charge. In this manner, the energy buying cost for each hour is calculated as:
where i denotes index of time slot.
Considering the illustrative tariff, the energy transport charge is assumed to be equal to EUR/kWh. Moreover, the other fees and taxes are modelled as EUR/kWh. It is noted that the Elspot energy prices are the only time-varying component in the buying price—the idea of dynamic electricity taxation is still under development in Denmark [42].
Subsequently, the energy selling price at each hour is assumed to be equal to the Elspot price at the corresponding time:
Taking into account the mean Elspot price of EUR/kWh, it is calculated that fees and taxes account for 85.7% of the total energy-buying price, on average. Within this framework, the battery’s energy arbitrage—understood as pre-charging and selling energy back to the grid—can be considered as an infeasible option since the additional components in the buying price are significantly higher than variations in Elspot prices.
Furthermore, due to significant taxes in energy buying price, the potential benefits from time-varying Elspot prices are substantially diminished. From the developed pricing model, the maximum buying price (0.20 EUR/kWh)—including fees and taxes—is only 10% higher than the minimum price (0.18 EUR/kWh) for the analysed week. Nevertheless, BESS pre-charging from the grid during the low price period and storing the energy for later use—when the prices are higher—should be investigated as a possible battery control option.
Besides, the hourly-changing prices open up new opportunities for improving the marina’s grid operation. Notably, the dynamic tariff enables greater involvement of the marina’s electricity consumers. In this context, sailors could economically benefit from their flexibility, shifting their consumption to off-peak periods and therefore helping with peak load shaving. For this reason, the TOU tariff for sailors in the Ballen marina is developed, encouraging their participation in the DR programme.
4.2. Time of Use Tariff for Sailors
The hourly-varying energy pricing scheme—envisaged for the Ballen marina—needs to be transformed into a viable tariff, which would be offered to arriving sailors. Currently, sailors are being charged with a flat energy price of 0.34 EUR/kWh [43]. Given the marina’s energy buying price of 0.21 EUR/kWh [38], a 38% margin is imposed on it. To influence changes in electricity consumption and understand price-induced flexibility, the flat tariff is replaced with one of the DR programmes in this work. The simplest and most widely implemented price-based initiative is the TOU tariff, with different prices at fixed day periods. This tariff is also the most comprehensible one, with clear financial benefits for participating consumers. Therefore, a suitable TOU tariff for the Ballen marina is developed, taking into account the harbour’s load characteristics.
Based on the boat demand analysis in Section 3, four distinctive demand periods have been determined, which can be simplified to three time zones for the TOU tariff. The time zones are devised to have divergent prices, encouraging sailors to consume electricity during off-peak hours. To improve the intelligibility of the tariff, a colour indicator has been assigned to each time zone.
The green zone is set for the off-peak day period, covering the entire night demand valley. The energy price in this zone should be the lowest one; however, the price normally must be not lower than the actual marina’s buying cost. Subsequently, the yellow zone is applied during the noon valley, with the price equal to the currently used flat tariff price. Ultimately, the red zone is established for both morning and afternoon peak demand periods. The price for this time zone should be the highest one, discouraging electricity usage in these periods. Taking this information into account, the following prices and hours have been proposed for each time zone:
- Green zone: 0.22 EUR/kWh, 21.00–6.00.
- Yellow zone: 0.34 EUR/kWh, 10.00–15.00.
- Red zone: 0.40 EUR/kWh, 6.00–10.00 and 15.00–21.00.
It is noted that—under this pricing scheme—the marina’s hourly savings from boat flexibility and BESS action are not directly conveyed to sailors. Nonetheless, these activities allow the marina to offer a cheaper off-peak price for them. Further, the time zones of the developed TOU tariff—along with the mean boat demand for the analysed week—are graphically presented in Figure 4.
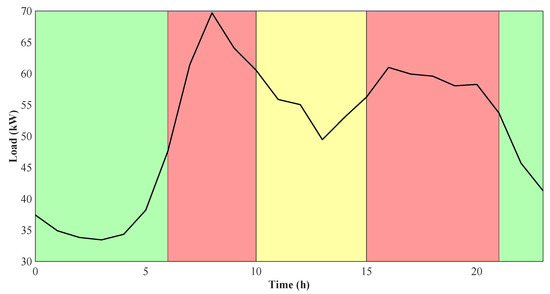
Figure 4.
TOU tariff time zones.
The tariff is developed based on the weekly data; however, the trend of peak and off-peak hours is preserved for the entire year. Therefore, the tariff can be in effect all year round, assuming that sailors react to the price signals. Consequently, the DR optimisation model is developed to determine the optimal boat flexibility patterns, making use of time-varying energy prices.
5. Modelling of Demand Response
The implementation of hourly-varying prices for the marina, along with the TOU tariff for sailors, enables the possibilities for cost-efficient usage of electricity. Essentially, the DR scheme consists of two main operations—peak shaving and valley filling. In this manner, the DR model is developed, with the aim to determine the optimal load shifting action. Subsequently, the formulated model is utilised in mixed-integer linear programming optimisation.
The simulations are carried out over a time horizon of to determine the optimal action over a 24-h time frame. This way, the optimisation is performed separately for each day in the analysed week. The length of each time slot is assumed as . Firstly, the DR power at each time slot is modelled as:
where / denotes increase and decrease in power, respectively, with regard to the predicted load .
The increase in power is equivalent to the valley-filling action. Considering one of the DR objectives—which concerns increasing load factor (defined as in Equation (31)) —the resulting load should not be greater than the daily mean load . Nevertheless, in practical terms, the off-peak demand is unlikely to be ever increased that high to reach the mean load. For this reason, the maximum valley-filling action is constrained by the flexibility factor , signifying the highest difference between the mean and predicted load:
where denotes DR power increase binary decision variable.
For the base scenario, the flexibility factor is assumed as . It is noted that if the predicted load is greater than the mean demand, the values of are negative. Thus, the decision variable needs to be equal to 0 to satisfy the constraint. Thereby, the load increasing action is permitted only if the predicted load is below the mean—in the demand valley.
Similarly, the decrease in power —equivalent to the peak shaving action—is constrained by the same flexibility factor , which here indicates the maximum difference between the predicted and mean demand:
where denotes DR power decrease binary decision variable.
In this case, the decision variable permits the load increasing action only if the predicted load is above the mean, signifying the demand peak. Subsequently, the decision variables are restricted to be binary integers:
Furthermore, only one decision variable is allowed to be active at each time slot:
The DR action is anticipated to change the shape of the demand curve without affecting the total consumed energy. In other words, no strategic energy conservation or load growth (reducing or increasing energy consumption) [10] is allowed. Thus, the sum of the DR load needs to be equal to the sum of the predicted load :
This constraint also indicates that the total increase in power has to be equal to the total peak shaving action over a daily time horizon. It is noted that—in real-life situations—the more flattened demand curve would lead to lower power losses, and therefore lower consumed energy. Nevertheless, the power losses associated with boat demand are disregarded in this work. Subsequently, the power exchange with the public utility is modelled as in [28]:
where denotes power import/export from/to the grid, is power import/export binary decision variable, signifies maximum power import/ export, and is power exchange with the grid.
To complete the model, the power balance constraint—including DR load , power exchange , and PV generation —is formulated as:
Finally, the optimisation problem is formulated, utilising the developed boat-flexibility model. The initial model does not take into account the BESS, which will be added at a later stage. The success of DR programmes depends primarily on the reaction of participating energy consumers to the price signals. Therefore, the consumers become the essential party to the implementation of smart grid solutions. In this work, sailors are assumed to schedule their electricity consumption in the most cost-efficient way, reacting to the TOU tariff’s price signals. For this reason, the optimisation objective is defined as the minimisation of sailors’ energy cost. The time-varying energy price for sailors—under the TOU tariff—is denoted as . Thus, the optimisation problem is formulated as:
Constraints (6)–(10) are devised to limit the DR action. Further, constraints (11)–(14) are set to establish marina’s energy exchange with the public grid. Finally, constraint (16) is used to preserve power balance for each time slot.
In addition, the flowchart of the optimal load shifting action is presented in Figure 5.
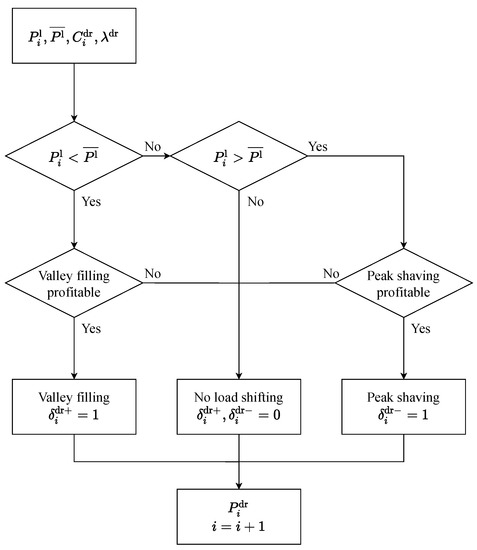
Figure 5.
Demand response flowchart.
Subsequently, the optimisation model is used to determine the optimal flexible load operation in the Ballen marina.
6. Proposed Optimal Operation of Marina’s Energy System
The weekly simulations, with time slots, are conducted in the MathWorks MATLAB R2021a environment, employing mixed-integer linear programming optimisation. The following study cases are considered:
- Base Scenario,
- Cost-Efficient Operation of BESS,
- Boat Flexibility and BESS,
- Late Summer and Late Autumns Seasons.
Firstly, the base scenario is outlined, with the assumption of all boats participating in the DR programme. The initial simulations consider the boat flexibility during the peak tourist season, assuming the flexibility factor of . Within this framework, the cost savings and grid operation improvements are evaluated. Moreover, the flexibility factor sensitivity is analysed for the impact of this parameter on the load-shifting performance.
The final three study cases take into consideration the BESS—installed in the Ballen marina—to determine the optimal marina’s energy system operation. For this reason, the battery model needs to be included in the optimisation problem. Hence, the BESS optimisation model presented in [28] is adopted:
where denotes battery charging/discharging efficiency, is battery round-trip efficiency, is battery state of charge, is battery charging/discharging power, is battery capacity, is battery maximum charging/discharging rate, is battery maximum/minimum state of charge, is battery charging/discharging binary decision variable, is battery maximum power, and signifies battery power.
The maximum state of charge (SOC) is assumed as , with regard to the battery capacity. Similarly, the minimum SOC assumed as . These two constraints are established to prevent the accelerated battery ageing [44].
The presented model is augmented, introducing the time horizon of . Applying this adjustment, the additional constraint needs to be included, preventing simultaneous battery discharging and power export actions. In this manner, only one of the battery discharging and power export binary decision variables is allowed to be active at each time slot:
This constraint prevents energy arbitrage from the BESS. In other words, the energy stored in the battery is not being sold to the public utility. The proposed marina’s energy management system (EMS) outline—including boat flexibility and BESS—is shown in Figure 6.
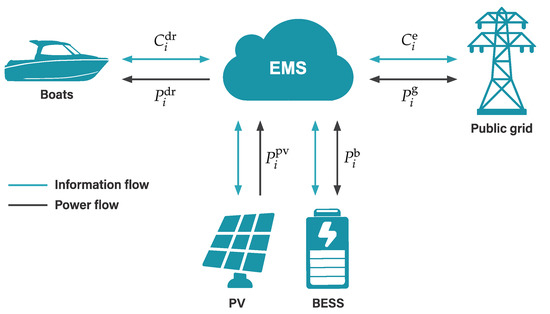
Figure 6.
Marina’s energy management system.
Within this framework, the optimal scheduling of BESS is analysed, with the aim to increase battery utilisation—defined as the proportion of hours during which BESS is active—and the marina’s cost efficiency during summer. Subsequently, the BESS and boat flexibility models are combined, investigating the optimal operation of the entire marina’s energy system. Finally, the marina’s grid operation in the late summer and late autumn seasons is studied, employing the developed control algorithm.
The DR programme performance is assessed based on the marina’s and sailors’ energy cost, as well as the load factor. In this respect, the marina’s energy cost C is calculated as:
Similarly, the energy cost for sailors is given by:
Finally, the load factor is calculated as:
where denotes the average load and is the maximum load during the simulation week.
7. Results and Discussion
In this section, the results of the four introduced simulation scenarios are presented and evaluated. Furthermore, the optimisation problems for the final three study cases—which include the BESS installed on the marina site—are formulated and utilised in the simulations.
7.1. Base Scenario
The simulation of the base scenario was carried out for the analysed summer week (15–21 July 2019). The scenario assumes that all boats, docking in the Ballen marina, participate in the DR programme. Within this framework, sailors schedule their electricity usage in the most cost-efficient way, shifting their demand to low-price periods. Moreover, the flexibility factor is fixed as .
The simulation results of the Ballen marina’s DR—for all boats participating—are presented in Figure 7.
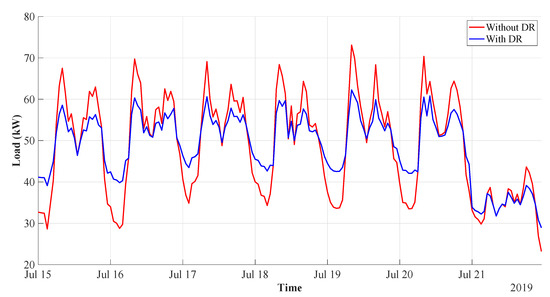
Figure 7.
DR for all boats participating.
The visual inspection of the plot indicates that the load factor has improved. Furthermore, the demand was properly shifted from peak to off-peak hours, leaving the total weekly demand unchanged. For the sake of clarity, the load shifting action is graphically presented in Figure 8.
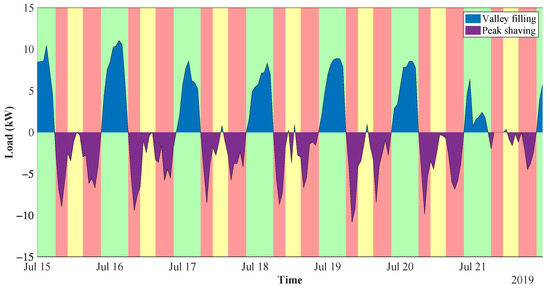
Figure 8.
Load shifting in DR programme.
The results confirm that time zones of the TOU tariff have been correctly designed, making the peak shaving and valley filling action beneficial for sailors. During the noon valley, the load has been either decreased or slightly increased, depending on the profitability of each action for the particular day. The maximum price difference—between green and red zones—is equal to 0.18 EUR/kWh. Thus, the participating sailors would save this amount for every unit of shifted energy.
The total load during the analysed week is equal to 8167 kWh, whereas PV supplies 1510 kWh, accounting for 18.5% of the weekly demand. Hence, the remaining energy of 6657 kWh (81.5% of the weekly load) is imported from the public grid. Since the load is much higher than the PV generation during the simulation week, no energy export occurs.
The possible cost savings for the marina are due to importing the energy during periods of lower prices, thanks to load shifting. The energy supplied by the local PV generation is assumed to be free for the marina, whereas it does not affect the price offered to sailors. In this respect, the Elspot price, the energy import from the public utility—for the scenarios with and without DR—and the PV generation for the analysed week are presented in Figure 9.
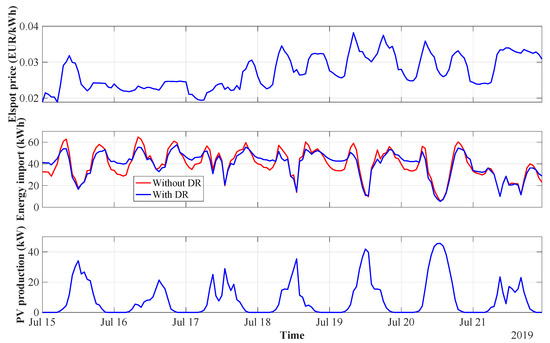
Figure 9.
Elspot prices, energy import, and PV production.
The opportunities for decreasing the marina’s energy cost—which depends on the hourly-varying Elspot prices—are visible during high-price periods when the energy import is minimised by the peak shaving action. Nevertheless, the maximum price difference for the investigated week is equal to only 0.02 EUR/kWh. For this reason, the direct cost savings for the marina are anticipated to be lower than for sailors, taking into consideration the different types of tariffs developed for both parties. Further, the key simulation results for all boats taking part in the load shifting—for the entire summer week—have been quantified and presented in Table 2.

Table 2.
Simulation results for all boats participating in DR programme for a week.
The relevant measure of flexibility is the shifted energy, calculated as a sum of all clipped peaks. Equivalently, this parameter is equal to the sum of all valley-filling actions since no energy conservation is taken into account. In this scenario, the shifted energy accounts for 4.2% of the total load. With the increase of this parameter, greater cost savings and demand curve flattening can be achieved.
The most significant DR implementation result is observable in the load factor, improving this parameter by 17.4%. This outcome is advantageous for the marina’s energy system on many levels. First of all, the future grid enhancements could be postponed, considering the possible peak demand increase during the next summer seasons. Secondly, the load shifting could mitigate possible voltage regulation problems caused by uneven load distribution between the piers. Moreover, the decrease in energy losses would be another positive effect of the improved load factor. Finally, in the future, more boats could be docked and charged in the marina without hindering the grid operation.
Despite the hourly-varying energy tariff for the marina, the marina’s electricity buying cost has been only slightly reduced, leading to 0.2% savings. In this regard, the direct cost reduction is insignificant compared to the potential additional cost of the DR implementation. However, the indirect benefits for the marina could be still relevant, such as the advantages of load factor increase.
Furthermore, the cost savings for sailors—under the TOU tariff—are equal to 2.1%, which is a relatively low result. Thus, the cost-efficiency of load shifting may be insufficient to convince sailors to participate in the DR programme. The price incentives would need to be accompanied by educational programmes, enhancing the knowledge about the ecological benefits of appropriate energy usage. Otherwise, further financial inducements should be offered to sailors, such as additional incentives or a further decrease in off-peak energy price; however, this may be not a valid business case for the marina.
The essential parameter of the developed DR model—having an impact on the outcomes—is the flexibility factor, constraining the maximum load-shifting action. The assumption of has resulted in a reasonable load profile, which is likely to be achieved in the real-life price-based DR implementation. Nevertheless, it is important to study how changing this parameter affects the DR simulation results. For this purpose, the sensitivity analysis is carried out for five different values of : 0%, 25%, 50%, 75%, and 100%. The flexibility factor of indicates that no load shifting can be applied. Conversely, signifies that a flat load curve is aimed towards, with the load factor approaching . The results of the flexibility factor sensitivity analysis are presented in Figure 10.
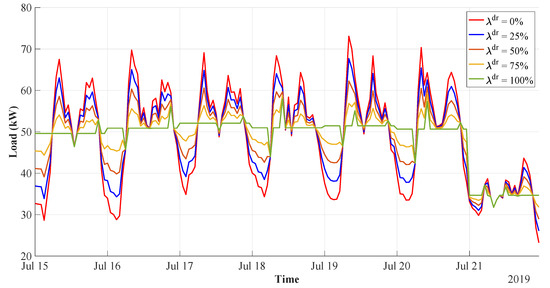
Figure 10.
DR for different flexibility factors.
It is observed that the variations in the flexibility factor significantly affect the load profile shape. When this parameter is increased, the demand curve is flattened, obtaining almost a flat profile at average daily demand in the case of . Nevertheless, it is anticipated to be practically infeasible to level out the profile to that extent. Thereafter, the simulation results are outlined in Table 3.

Table 3.
Simulation results for different flexibility factors.
With different flexibility factors, the shifted energy varies from 2.1% () to 8.5% () of the total load. Moreover, this parameter has a substantial impact on the load factor, improving it by 26.2% in the best scenario. Notwithstanding this, the effect of the flexibility factor on the marina’s and sailors’ energy cost is much lower, leading to at most 0.3% and 4.3% savings, respectively. The initially adopted factor of proves considerable improvement of the marina’s grid operation while maintaining realistic assumptions. Hence, this value is used for all subsequent simulations.
Afterwards, the implementation of BESS for increasing cost efficiency is examined.
7.2. Cost-Efficient Operation of BESS
As indicated in previous research [28], the battery is underutilised in the summer period, being idle from 15 to 24 July. With the objective of minimising energy exchange with the public utility, the BESS needs not act during the peak tourist season since the load is significantly higher than the PV generation. Thus, no energy export is required to be prevented by its action. In the future, this issue could be mitigated by increasing the renewable generation capacity—in the form of PV units, wind turbines, or wave energy—which in turn would improve the operation of the marina’s ICES from both technical and economic perspectives. Nevertheless, the existing PV plant size and hourly-changing pricing scheme suggest the need for investigating the possibilities of different BESS scheduling—with the aim of minimising the energy cost.
The cost-efficient BESS operation—under the developed hourly-varying marina’s tariff—is determined, utilising the battery optimisation model presented in Section 6. For this purpose, the battery’s objective function is reshaped: instead of minimising the energy exchange, the objective is defined as minimising energy cost for the marina. Moreover, the power balance constraint—with marina’s load, PV generation, BESS action, and power exchange—is included:
Thereby, the optimisation problem is formulated as:
In this context, the flowchart of the optimal cost-efficient battery operation—which comprises charging from the PV plant, pre-charging from the public grid, and supplying local demand—is presented in Figure 11.
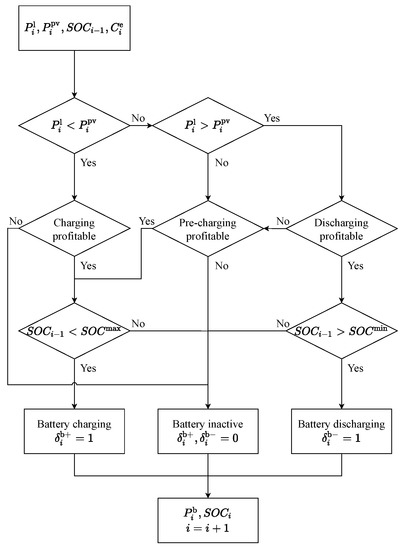
Figure 11.
Cost-efficient battery operation flowchart.
To avoid emptying the battery before midnight—when it cannot charge from the PV units—the beginning of the 24-h optimisation windows is shifted from 24.00 to 12.00. This way, new optimisation windows begin at the time of typically highest PV generation. With this approach, the optimisation needs to start 12 h before and stop 12 h after the analysed period—which is applied for all scenarios that include BESS. Since the battery is mostly empty during the summer period, the initial SOC for all forthcoming simulations is assumed as , equal to 2.5%. The BESS operation is investigated, assuming a typical round-trip efficiency value of . The simulation results of the cost-efficient BESS operation, along with the load and Elspot prices, are presented in Figure 12.
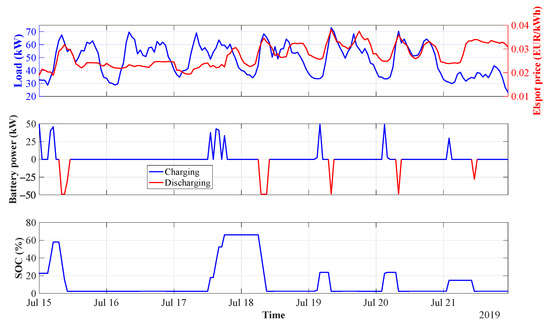
Figure 12.
Cost-efficient operation of BESS.
Taking advantage of the hourly-varying energy prices, the battery utilisation increases from 0% to 12.5% during the summer week. Since the local PV generation is fully self-consumed by the load, the battery charges only from the public grid. The overall grid import increased by 0.3% from the base scenario as a consequence of the battery losses. It is clearly seen that the BESS pre-charges during periods of low load and low prices, whereas the discharging action is performed when load and prices are highest. The battery does not reach , as the periods of low prices—during which pre-charging from the public grid is profitable—do not last longer than 4 h. In this manner, the optimisation objective constrains the BESS to be fully pre-charged. During the day of low variations in the price (16 July 2019), the battery has remained inactive. This event indicates that the pre-charging action during that day would lead to battery losses, which would be more costly than the possible benefits from varying electricity prices. Nonetheless, the BESS was successfully activated on the other days of the week, proving minimisation of energy cost for the marina.
Subsequently, the boat flexibility and battery models are combined, with the aim to determine the optimal operation of the entire marina’s smart energy system.
7.3. Boat Flexibility and BESS
In the pivotal scenario of the Ballen marina’s grid operation, the boat flexibility should cooperate with the battery system, ensuring benefits for both marina and sailors. For this purpose, the models of DR and BESS are integrated, forming a single optimisation problem. First, the power balance constraint is modified, incorporating DR power, battery action, power exchange, and PV generation:
The objective function is designed to minimise the overall energy cost, defined as a sum of sailors’ and marina’s costs. This way, the benefits will be provided for both involved parties. Within this framework, the optimisation problem—combining DR and BESS operation—is formulated as:
The load-shifting profitability is dependent on the TOU tariff for sailors, whereas the cost savings for the marina are subject to the price variations of the Elspot-based tariff. In this manner, PV generation and battery action do not affect the energy prices for sailors. Nonetheless, the BESS is scheduled with respect to the shifted demand, coordinating its action with the DR programme. Hence, the boats and BESS are scheduled simultaneously to provide the lowest overall energy cost, combining the algorithms presented in Figure 5 and Figure 11.
The simulations of the integrated DR and BESS operation are carried out with the assumption of all boats participating () and the flexibility factor of . The results for the summer week are presented in Figure 13.
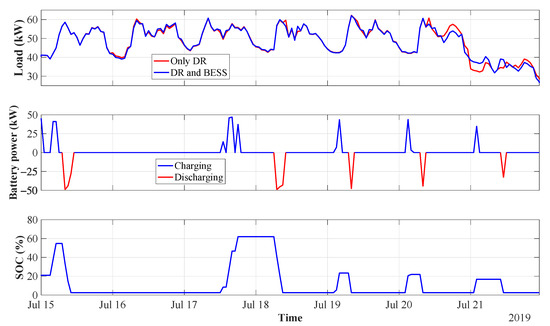
Figure 13.
DR and BESS in summer.
The obtained results are similar to the outcomes of the separate optimisation of the DR and BESS action. Nevertheless, minor changes in the battery operation can be observed as the marina’s demand profile is reshaped by the load shifting. Moreover, the optimal DR action is also only marginally different—since the optimisation windows’ beginning is shifted from 24.00 to 12.00. Further, the simulation results of four performed study cases are outlined in Table 4.

Table 4.
Simulation results for DR and BESS in summer.
It is observed that the boat flexibility has a greater impact on the marina’s energy cost compared to the BESS operation in the considered week. Moreover, the battery alone cannot improve the load factor—as well as the energy cost for sailors—since its action does not affect the shape of the demand curve. Nonetheless, the battery utilisation of 12.5% was achieved for the scenarios, which include BESS. Within this framework, the combination of DR and BESS deployment is the most beneficial scenario for both marina and sailors.
Finally, the integrated DR and BESS operation is analysed for two different seasons when grid operation characteristics are considerably divergent.
7.4. Late Summer and Late Autumn Seasons
The preceding analysis concerns the peak tourist season, with high load and consequently PV generation shortage. This study is extended with two seasons, during which the marina’s grid is facing different challenges. Essentially, the periods with low load and either high or low PV generation are the most interesting. In the first case, the energy export—due to PV production excess—is substantial, and the cooperation of DR and BESS could partly mitigate it. In the latter one, the PV production is low and should be reasonably distributed, with the aim to increase self-consumption and minimise energy cost.
In this manner, two representative weeks during different seasons are chosen for further analysis:
- Late summer: 9–15 September 2019, low load (341 kWh) and high PV generation (1759 kWh).
- Late autumn: 21–27 October 2019, low load (324 kWh) and low PV generation (355 kWh).
First, the simulations are carried out for the late summer week, utilising the developed optimisation algorithm (35). The simulation results of the DR and BESS cooperation are presented in Figure 14.
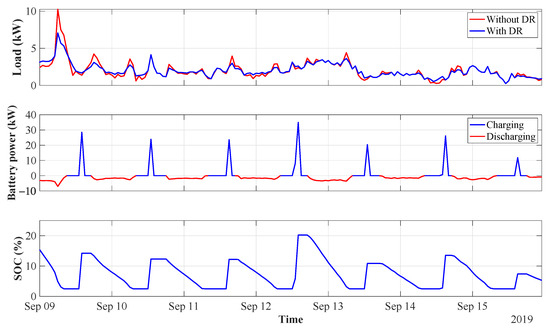
Figure 14.
DR and BESS in late summer.
The late summer load profile demonstrates a considerably different shape compared to the previously examined peak tourist season week. The characteristic boat demand periods are not easily distinguishable, and the peak demand does not exceed 11 kW. Nevertheless, the DR action has successfully levelled out the main peak on 9 September, also shifting the load on the other days.
In this period, the battery acts as a buffer for excess PV generation. This way, the BESS charges only the amount of power that is necessary to supply the load until the end of the 24 h time horizon. The remaining surplus PV production is sold to the public grid, with profit for the marina. The self-sufficiency of 100% is obtained, with the battery utilisation of 63.1%.
Thereafter, the optimisation results of the DR and BESS action for the late autumn week—with low load and low PV generation—are shown in Figure 15.
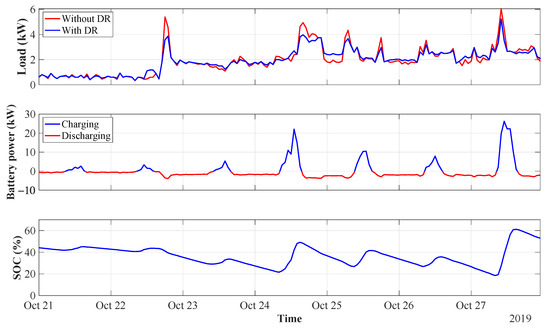
Figure 15.
DR and BESS in late autumn.
Similarly, the demand curve does not clearly indicate the peak and valley periods. However, the load factor is visually increased by the performed load shifting. The battery acts in a similar way as in the previous scenario. The self-sufficiency of 100% is achieved while locally consuming the entire PV generation. Furthermore, the BESS is utilised at 100%, being active for the entire simulation period. Within this framework, the developed optimisation strategy is concluded to be adequate also for periods with low load and high/low PV production.
Ultimately, the simulation results of the integrated DR and BESS optimisation for the analysed weeks are presented in Table 5.

Table 5.
Simulation results for late summer and late autumn weeks.
During the late summer week, the shifted energy accounts for 5.3% of the total demand. The initial load factor is relatively low, and as a consequence, the load shifting results in a 44.9% increase of this parameter. Moreover, the combined DR and BESS operation results in a 100% reduction in energy import and an 11.2% decrease in energy export. The high PV production leads to a negative weekly energy price for the marina, which is interpreted as a profit from selling the excess energy. The optimisation of boat flexibility and battery action results in a 412.5% increase in the marina’s profit for the considered week, corresponding to 33 EUR of additional earnings. Nevertheless, the cost savings for sailors amount to 2.7%—under the TOU tariff—since the shifted energy is relatively low.
On the other hand, the baseline load factor is improved by 16.0% for the late autumn week. The energy import and export are completely eliminated, ensuring free marina’s operation. Nevertheless, the sailors’ energy cost is decreased by only 1.9%, as a result of 4.6% shift in the weekly demand.
The observed enhancements of the marina’s cost efficiency—for both considered weeks—are mostly due to the minimisation of the energy exchange. Nonetheless, the benefits of boat flexibility are less unambiguous compared to the peak tourist season. Therefore, the DR programme implementation is concluded to be more vital for periods of higher boat demand.
8. Conclusions
The docking boats are the primary load of the Ballen marina, with the highest number of visiting sailors during the summer season. The demand analysis has shown the possibilities for harnessing their flexibility, utilising the envisaged hourly-varying pricing scheme for marina and the TOU tariff for sailors. Considering the simulation results, a significant improvement in the load factor has been observed, positively impacting the marina’s grid operation. Furthermore, the cost-efficient operation of integrated DR and BESS results in cost savings for both sailors and marina, as well as the greater utilisation of the battery in summer. The developed optimisation strategy proves its suitability also for periods of lower boat demand, minimising the energy cost for sailors and the energy exchange with the public grid. The DR implementation demonstrates the greatest potential during the periods of the highest load. Notwithstanding this, the economic benefits for sailors—under the TOU tariff—are relatively low, which could necessitate further investigations into controlling land-based marina’s loads, such as heat pumps, water pumps, washing machines, EV charging, and the sauna. In addition, the marina’s demand flexibility may become a vital element of its energy system, considering the desirable increase in the local renewable generation capacity. It could also include the possibilities of exploring sustainable coastal and marine technologies, such as wave energy. Future works will focus on evaluating the flexibility potential of marina’s EVs and assessing the benefits from vehicle-to-grid (V2G) technology implementation.
Author Contributions
Conceptualization, methodology, software, formal analysis, investigation, writing—original draft preparation and visualization, D.J.; data curation, D.J. and J.J.; validation, supervision and writing—review and editing, J.R.P., P.P., B.B.-J., and J.J.; project administration and funding acquisition, B.B.-J. and J.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 731249 (SMILE project).
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy restrictions.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BESS | Battery energy storage system |
| CPP | Critical peak pricing |
| DLC | Direct load control |
| DR | Demand response |
| DSM | Demand-side management |
| EDR | Emergency demand response |
| EMS | Energy management system |
| ESS | Energy storage system |
| EV | Electric vehicle |
| ICES | Integrated community energy system |
| PSO | Public Service Obligations |
| PV | Photovoltaic |
| RTP | Real-time pricing |
| SOC | State of charge |
| TOU | Time-of-use |
| V2G | Vehicle-to-grid |
References
- Smart Grid Strategy: The Intelligent Energy System of the Future; Technical Report; Danish Ministry of Climate, Energy and Building: Copenhagen, Denmark, 2013.
- Albadi, M.H.; El-Saadany, E.F. Demand Response in Electricity Markets: An Overview. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–5. [Google Scholar]
- Carli, R.; Dotoli, M.; Jantzen, J.; Kristensen, M.; Ben Othman, S. Energy scheduling of a smart microgrid with shared photovoltaic panels and storage: The case of the Ballen marina in Samsø. Energy 2020, 198, 1–16. [Google Scholar] [CrossRef]
- Ma, R.; Chen, H.; Huang, Y.; Meng, W. Smart Grid Communication: Its Challenges and Opportunities. IEEE Trans. Smart Grid 2013, 4, 36–46. [Google Scholar] [CrossRef]
- Deng, R.; Yang, Z.; Chow, M.; Chen, J. A Survey on Demand Response in Smart Grids: Mathematical Models and Approaches. IEEE Trans. Ind. Inform. 2015, 11, 570–582. [Google Scholar] [CrossRef]
- Dall’Anese, E.; Mancarella, P.; Monti, A. Unlocking Flexibility: Integrated Optimization and Control of Multienergy Systems. IEEE Power Energy Mag. 2017, 15, 43–52. [Google Scholar] [CrossRef]
- Ipakchi, A.; Albuyeh, F. Grid of the future. IEEE Power Energy Mag. 2009, 7, 52–62. [Google Scholar] [CrossRef]
- Strbac, G. Demand side management: Benefits and challenges. Energy Policy 2008, 36, 4419–4426. [Google Scholar] [CrossRef]
- Chiu, W.; Sun, H.; Poor, H.V. Demand-side energy storage system management in smart grid. In Proceedings of the 2012 IEEE Third International Conference on Smart Grid Communications (SmartGridComm), Tainan, Taiwan, 5–8 November 2012; pp. 73–78. [Google Scholar]
- Arteconi, A.; Hewitt, N.J.; Polonara, F. State of the art of thermal storage for demand-side management. Appl. Energy 2012, 93, 371–389. [Google Scholar] [CrossRef]
- Palensky, P.; Dietrich, D. Demand Side Management: Demand Response, Intelligent Energy Systems, and Smart Loads. IEEE Trans. Ind. Inform. 2011, 7, 381–388. [Google Scholar] [CrossRef]
- Jordehi, A.R. Optimisation of demand response in electric power systems, a review. Renew. Sustain. Energy Rev. 2019, 103, 308–319. [Google Scholar] [CrossRef]
- Vardakas, J.S.; Zorba, N.; Verikoukis, C.V. A Survey on Demand Response Programs in Smart Grids: Pricing Methods and Optimization Algorithms. IEEE Commun. Surv. Tutorials 2015, 17, 152–178. [Google Scholar] [CrossRef]
- Datchanamoorthy, S.; Kumar, S.; Ozturk, Y.; Lee, G. Optimal time-of-use pricing for residential load control. In Proceedings of the 2011 IEEE International Conference on Smart Grid Communications, Brussels, Belgium, 17–20 October 2011; pp. 375–380. [Google Scholar] [CrossRef]
- DR. Regeringen Klar Med Udspil til Transportaftale: Målet er 500.000 Elbiler i 2030. Available online: https://www.dr.dk/nyheder/politik/regeringen-klar-med-udspil-til-transportaftale-maalet-er-500000-elbiler-i-2030 (accessed on 29 September 2020).
- Shao, S.; Pipattanasomporn, M.; Rahman, S. Grid Integration of Electric Vehicles and Demand Response With Customer Choice. IEEE Trans. Smart Grid 2012, 3, 543–550. [Google Scholar] [CrossRef]
- Rizvi, S.A.A.; Xin, A.; Masood, A.; Iqbal, S.; Jan, M.U.; Rehman, H. Electric Vehicles and their Impacts on Integration into Power Grid: A Review. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Saele, H.; Petersen, I. Electric vehicles in Norway and the potential for demand response. In Proceedings of the 2018 53rd International Universities Power Engineering Conference (UPEC), Glasgow, UK, 4–7 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Mohammad, A.; Zamora, R.; Lie, T.T. Integration of Electric Vehicles in the Distribution Network: A Review of PV Based Electric Vehicle Modelling. Energies 2020, 13, 4541. [Google Scholar] [CrossRef]
- Yang, H.; Shen, W.; Yu, Q.; Liu, J.; Jiang, Y.; Ackom, E.; Dong, Z.Y. Coordinated demand response of rail transit load and energy storage system considering driving comfort. Csee J. Power Energy Syst. 2020, 6, 749–759. [Google Scholar] [CrossRef]
- Calvillo, C.F.; Sánchez-Miralles, A.; Villar, J. Synergies of Electric Urban Transport Systems and Distributed Energy Resources in Smart Cities. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2445–2453. [Google Scholar] [CrossRef]
- Hein, K.; Yan, X.; Wilson, G. Multi-Objective Optimal Scheduling of a Hybrid Ferry with Shore-to-Ship Power Supply Considering Energy Storage Degradation. Electronics 2020, 9, 849. [Google Scholar] [CrossRef]
- Kanellos, F.D.; Tsekouras, G.J.; Hatziargyriou, N.D. Optimal Demand-Side Management and Power Generation Scheduling in an All-Electric Ship. IEEE Trans. Sustain. Energy 2014, 5, 1166–1175. [Google Scholar] [CrossRef]
- Shang, C.; Srinivasan, D.; Reindl, T. Economic and Environmental Generation and Voyage Scheduling of All-Electric Ships. IEEE Trans. Power Syst. 2016, 31, 4087–4096. [Google Scholar] [CrossRef]
- Shang, C.; Srinivasan, D.; Reindl, T. NSGA-II for joint generation and voyage scheduling of an all-electric ship. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 5113–5119. [Google Scholar] [CrossRef]
- Huang, Y.; Lan, H.; Hong, Y.Y.; Wen, S.; Fang, S. Joint voyage scheduling and economic dispatch for all-electric ships with virtual energy storage systems. Energy 2020, 190, 116268. [Google Scholar] [CrossRef]
- Ponnaganti, P.; Bak-Jensen, B.; Pillai, J. Maximizing the self-consumption of Solar-PV using Battery Energy Storage System in Samsø-Marina. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Europe, ISGT-Europe 2019. IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Bucharest, Romania, 29 September–2 October 2019. [Google Scholar] [CrossRef]
- Jozwiak, D.; Pillai, J.R.; Ponnaganti, P.; Bak-Jensen, B.; Jantzen, J. Integrated Community Energy Systems: Case Study of Ballen Marina on Samsø. In Proceedings of the 2021 International Conference on Smart Energy Systems and Technologies (SEST), Vaasa, Finland, 6–8 September 2021. [Google Scholar]
- Rusu, E.; Onea, F. Estimation of the wave energy conversion efficiency in the Atlantic Ocean close to the European islands. Renew. Energy 2016, 85, 687–703. [Google Scholar] [CrossRef]
- Rusu, E. Wave energy assessments in the Black Sea. J. Mar. Sci. Technol. 2009, 14, 359–372. [Google Scholar] [CrossRef]
- Bonanno, A.; Franzitta, V.; Muzio, F.P.; Trapanese, M. A multiphysics approach to the design of a seawave energy conversion system. In Proceedings of the 2008 IEEE International Conference on Sustainable Energy Technologies, Singapore, 24–27 November 2008; pp. 665–668. [Google Scholar] [CrossRef]
- Franzitta, V.; Viola, A.; Trapanese, M. Description of Hysteresis in Lithium Battery by Classical Preisach Model. Adv. Mater. Res. 2012, 622–623, 1099–1103. [Google Scholar] [CrossRef]
- Tran, Q.T.T.; Riva Sanseverino, E.; Zizzo, G.; Di Silvestre, M.L.; Nguyen, T.L.; Tran, Q.-T. Driven Primary Regulation for Minimum Power Losses Operation in Islanded Microgrids. Energies 2018, 11, 2890. [Google Scholar] [CrossRef]
- Gangale, F.; Vasiljevska, J.; Covrig, C.F.; Mengolini, A.; Fulli, G. Smart Grid Projects Outlook 2017: Facts, Figures and Trends in Europe; Technical Report; Joint Research Centre: Luxembourg, Luxembourg, 2017. [Google Scholar]
- Marczinkowski, H.M.; Østergaard, P.A. Evaluation of electricity storage versus thermal storage as part of two different energy planning approaches for the islands Samsø and Orkney. Energy 2019, 175, 505–514. [Google Scholar] [CrossRef]
- Jantzen, J.; Bak-Jensen, B. Deliverable D3.1: Specifications and Data Report for the Samsø Demonstrator; Technical Report; Smart Island Energy Systems: Brussels, Belgium, 2017. [Google Scholar]
- Marczinkowski, H.M. Deliverable D8.2: Short and Medium-Term Scenarios for the Three Pilot Islands; Technical Report; Smart Island Energy Systems: Brussels, Belgium, 2018. [Google Scholar]
- Jantzen, J.; Kristensen, M. The Ballen2016 Data Set. Available online: http://arkiv.energiinstituttet.dk/643/ (accessed on 29 October 2020).
- Agresti, A. Statistical Methods for the Social Sciences, 5th ed.; Pearson: New York, NY, USA, 2018. [Google Scholar]
- Energinet.dk. Flexafregning af Kunders Elforbrug. Available online: https://energinet.dk/El/Private-elkunder/Flexafregning (accessed on 3 February 2021).
- Elpris. SPOT PLUS Prisen. Available online: https://elpris.dk/ (accessed on 25 February 2021).
- Albertsen, L.H.; Andersen, M.; Boscán, L.R.; Santos, A.Q. Implementing dynamic electricity taxation in Denmark. Energy Policy 2020, 143, 111543. [Google Scholar] [CrossRef]
- Samsø Kommune. Takster 2021. Available online: https://www.samsoe.dk/kommunen/oekonomi/takster-2021 (accessed on 16 April 2021).
- Wikner, E.; Thiringer, T. Extending Battery Lifetime by Avoiding High SOC. Appl. Sci. 2018, 8, 1825. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).