The Impact of Active and Passive Thermal Management on the Energy Storage Efficiency of Metal Hydride Pairs Based Heat Storage
Abstract
1. Introduction
2. Mathematical Model
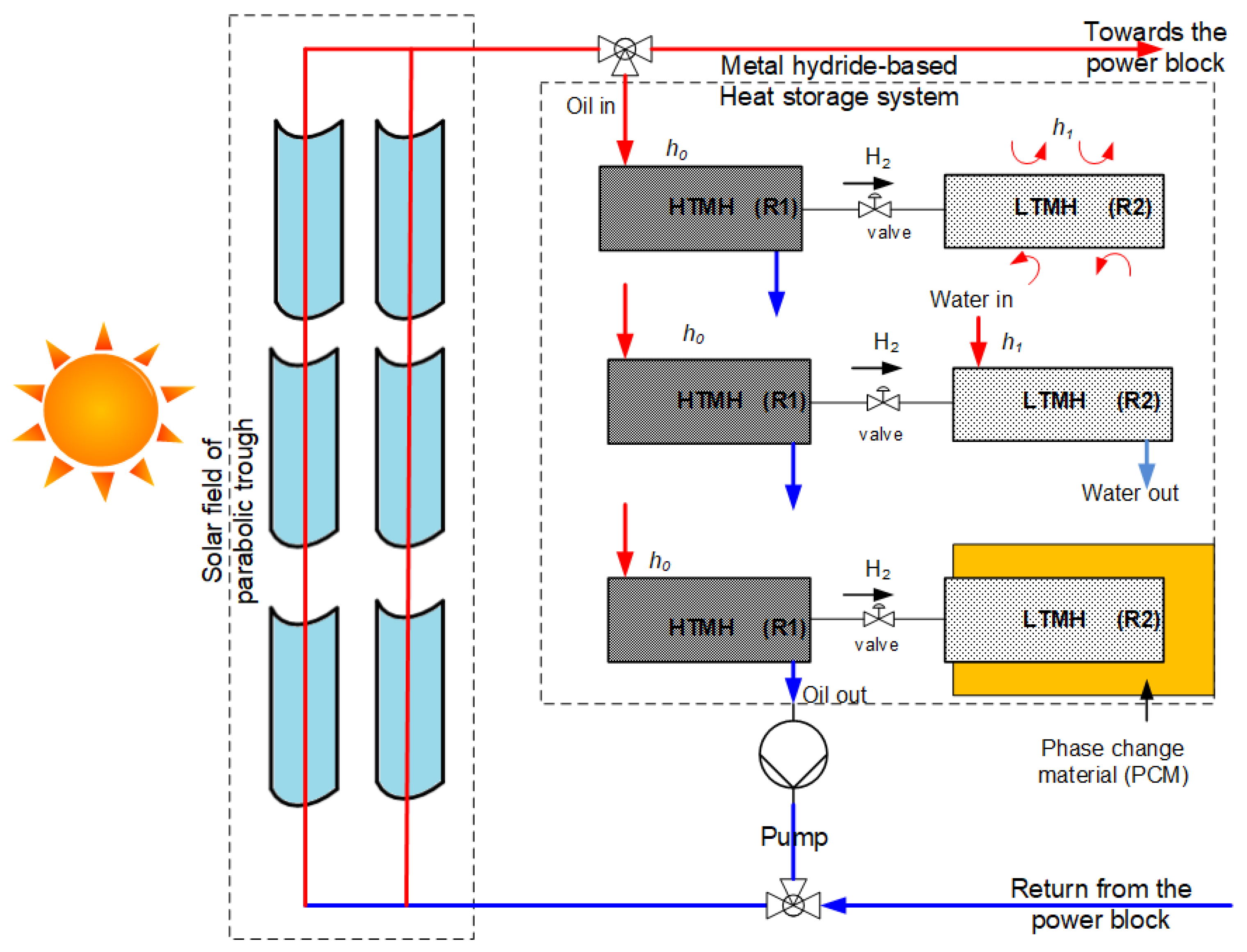
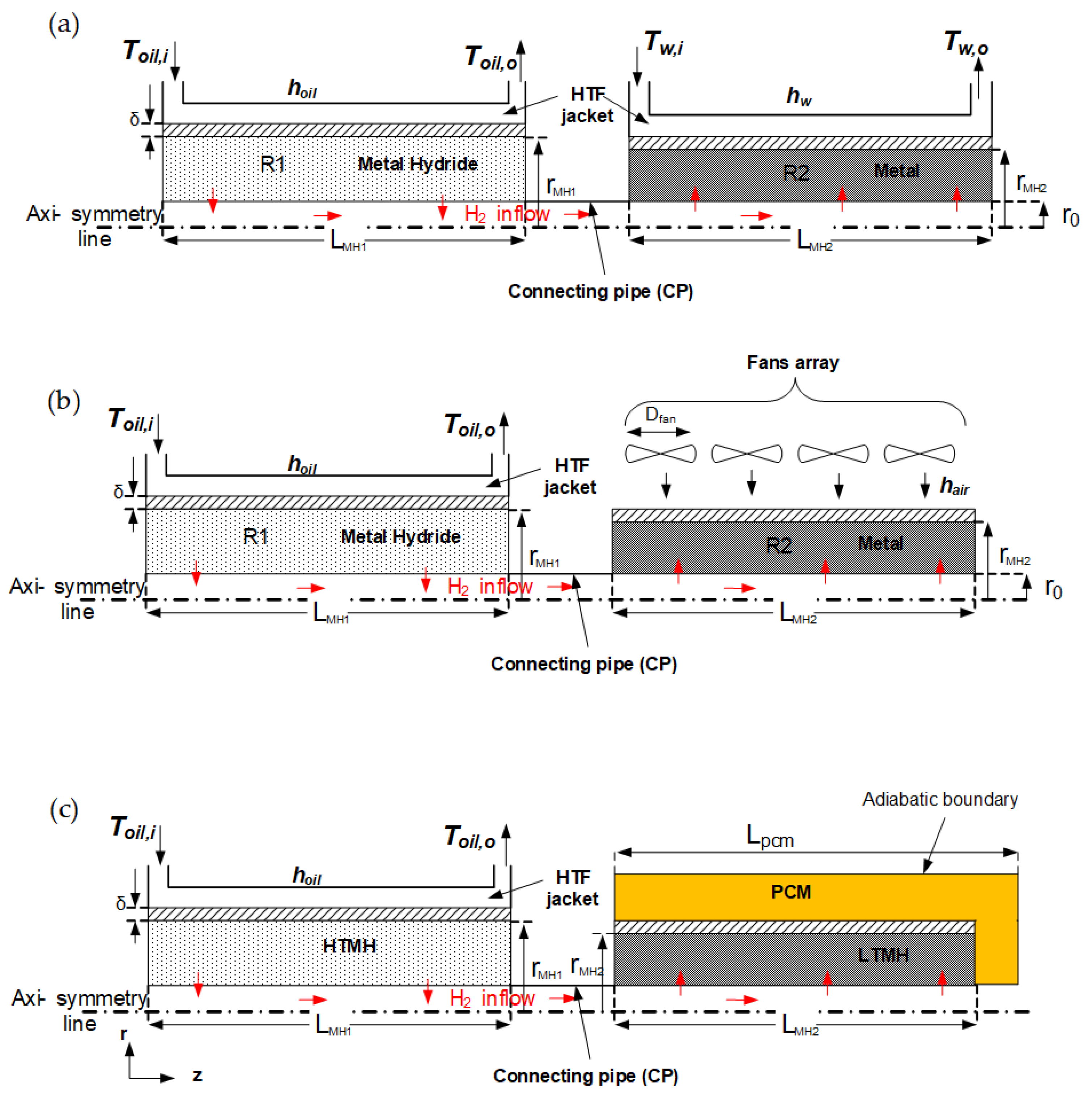
2.1. Problem Description
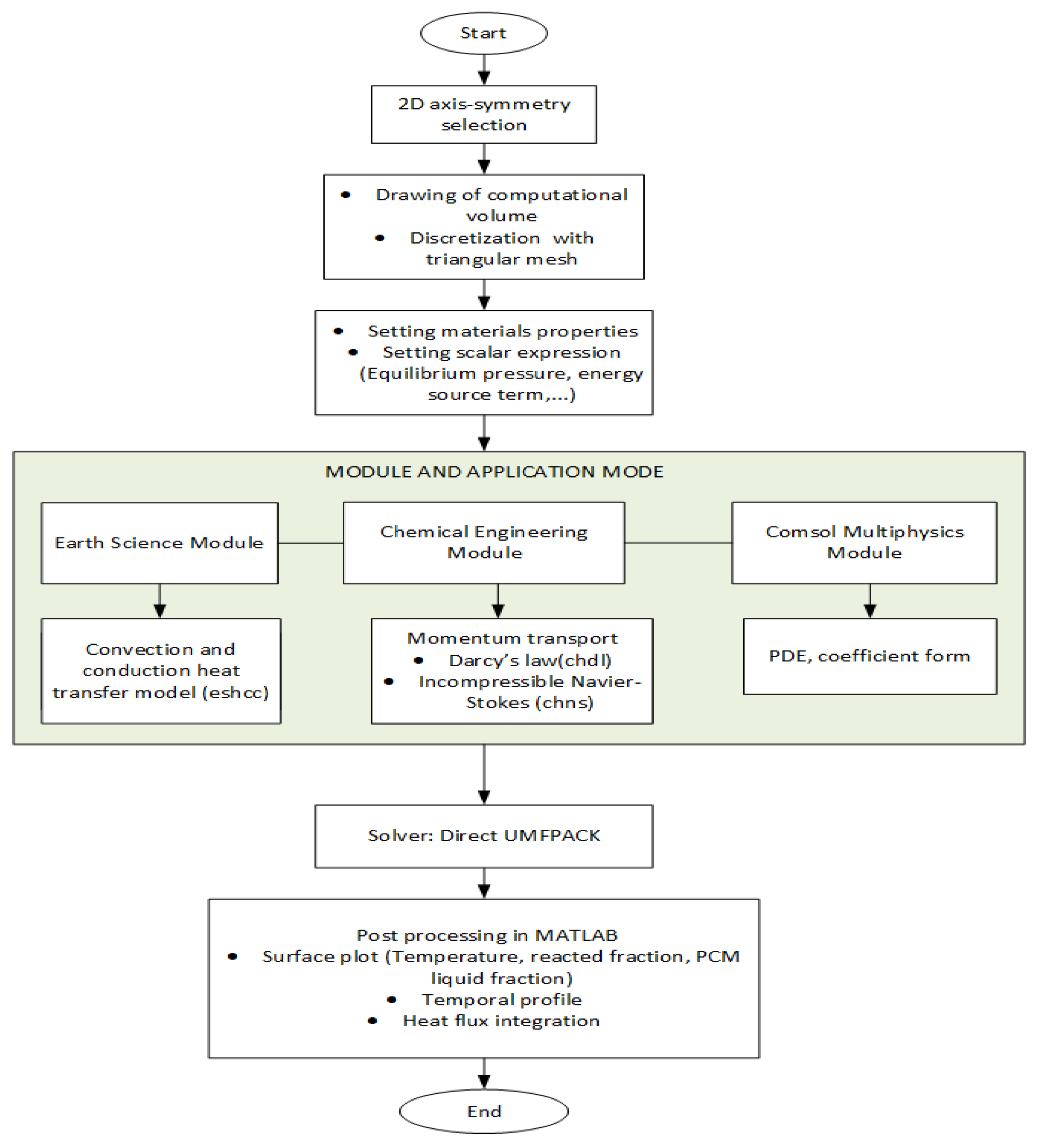
2.2. Computational Model
2.3. Governing Equations
- The thermal equilibrium between the H2 and the metal hydride is assumed;
- The intrinsic physical properties of the hydrides are constant during each step of the thermal energy storage;
- The jacket is perfectly insulated (adiabatic wall);
- The radiative heat transfer is neglected;
- Hydrogen is considered to be an ideal gas;
- The hysteresis phenomenon is not considered in the equilibrium pressure of metal hydrides.
- The thermo-physical properties of the PCMs are assumed to be constant;
- The PCM’s latent heat is independent of the temperature;
- The effect of natural convection is negligible;
2.4. Heat Transfer Calculation
2.4.1. Forced Convection
2.4.2. Free Convection
2.5. Fan and Pumping Powers
2.6. Performance Evaluation
- The volumetric heat storage density is as follows:
- The heat discharging specific power is as follows:
- The energy storage efficiency is as follows:
3. Results and Discussion
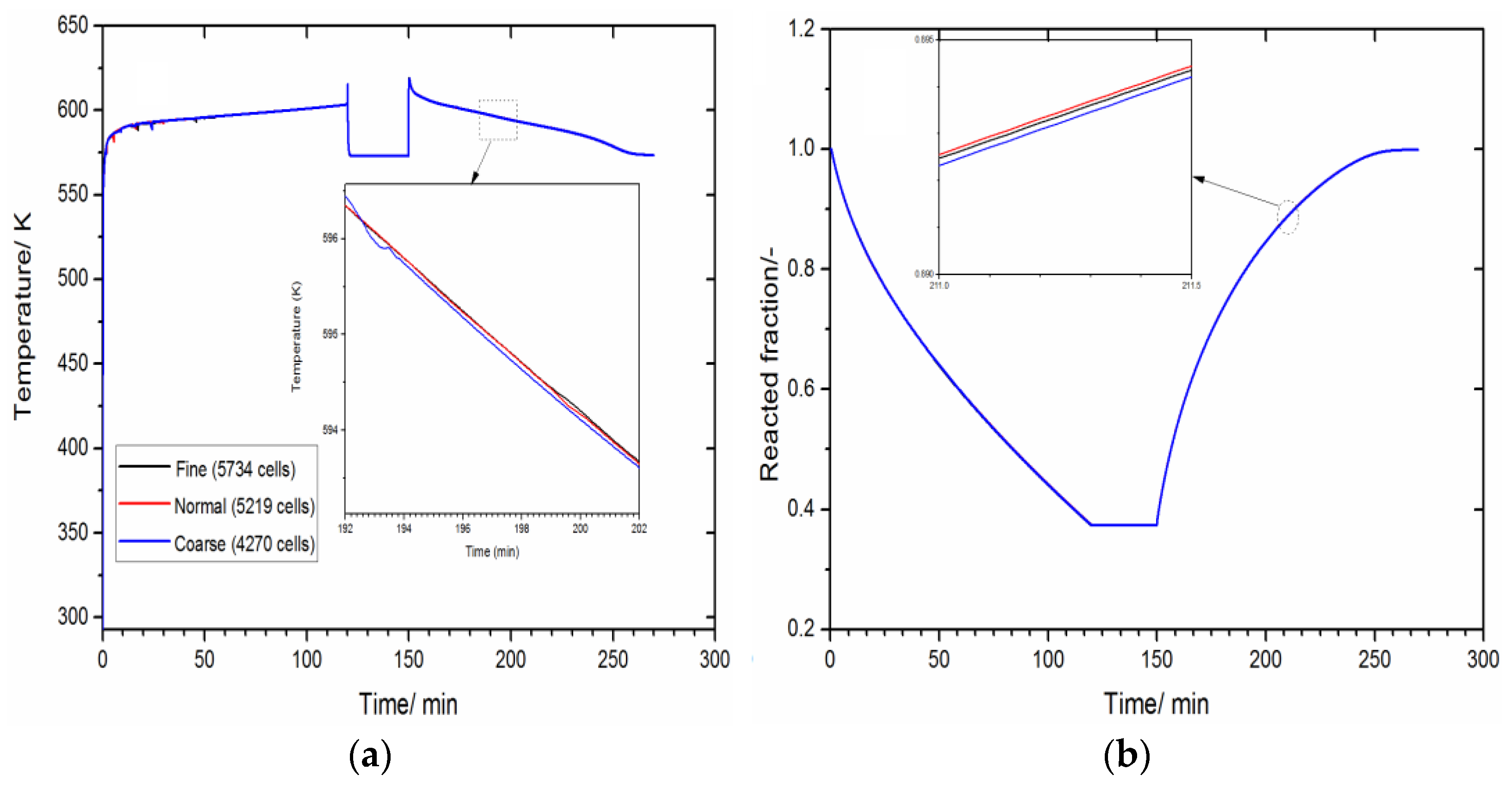
3.1. Numerical Setting and Model Validation
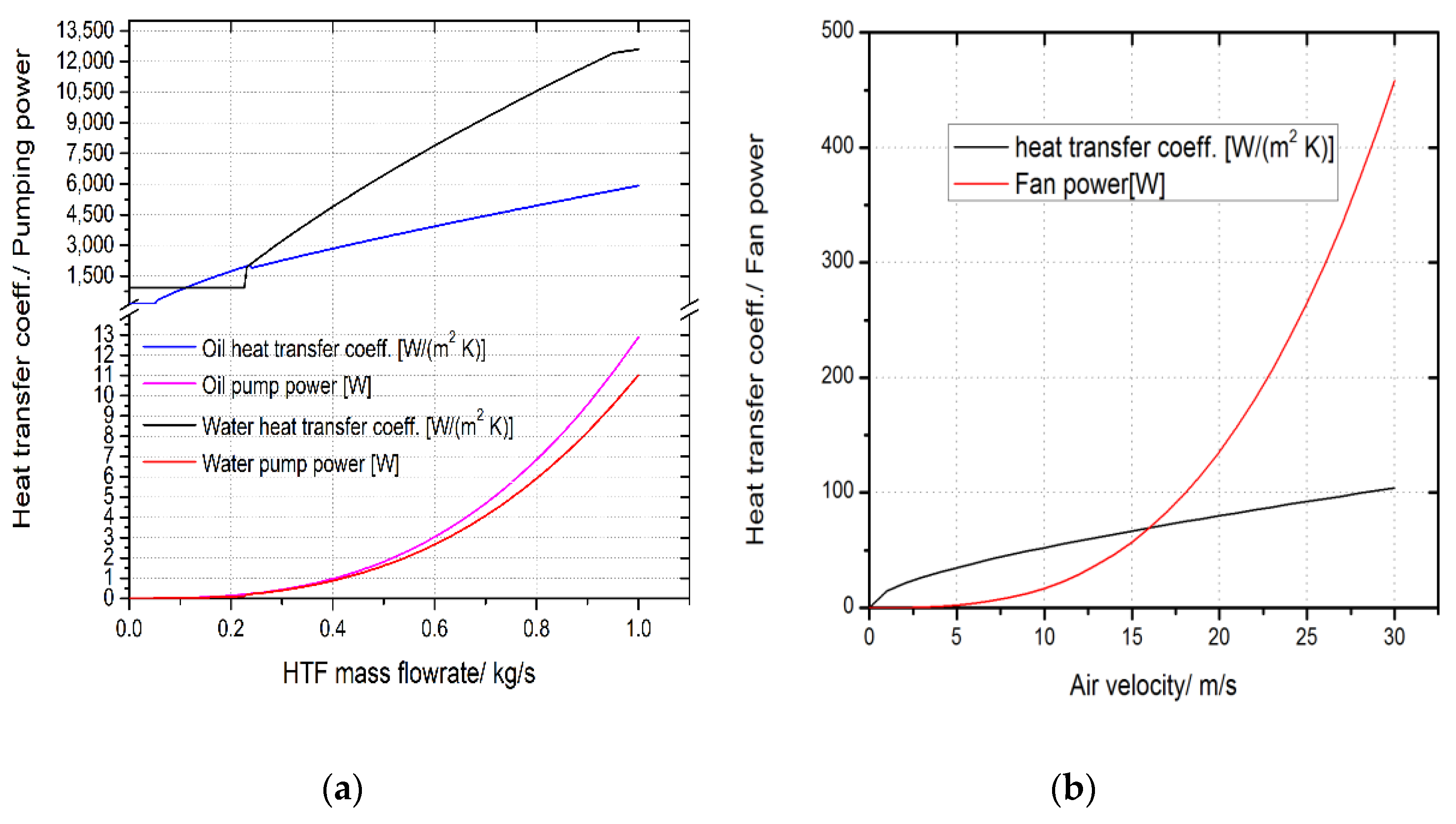
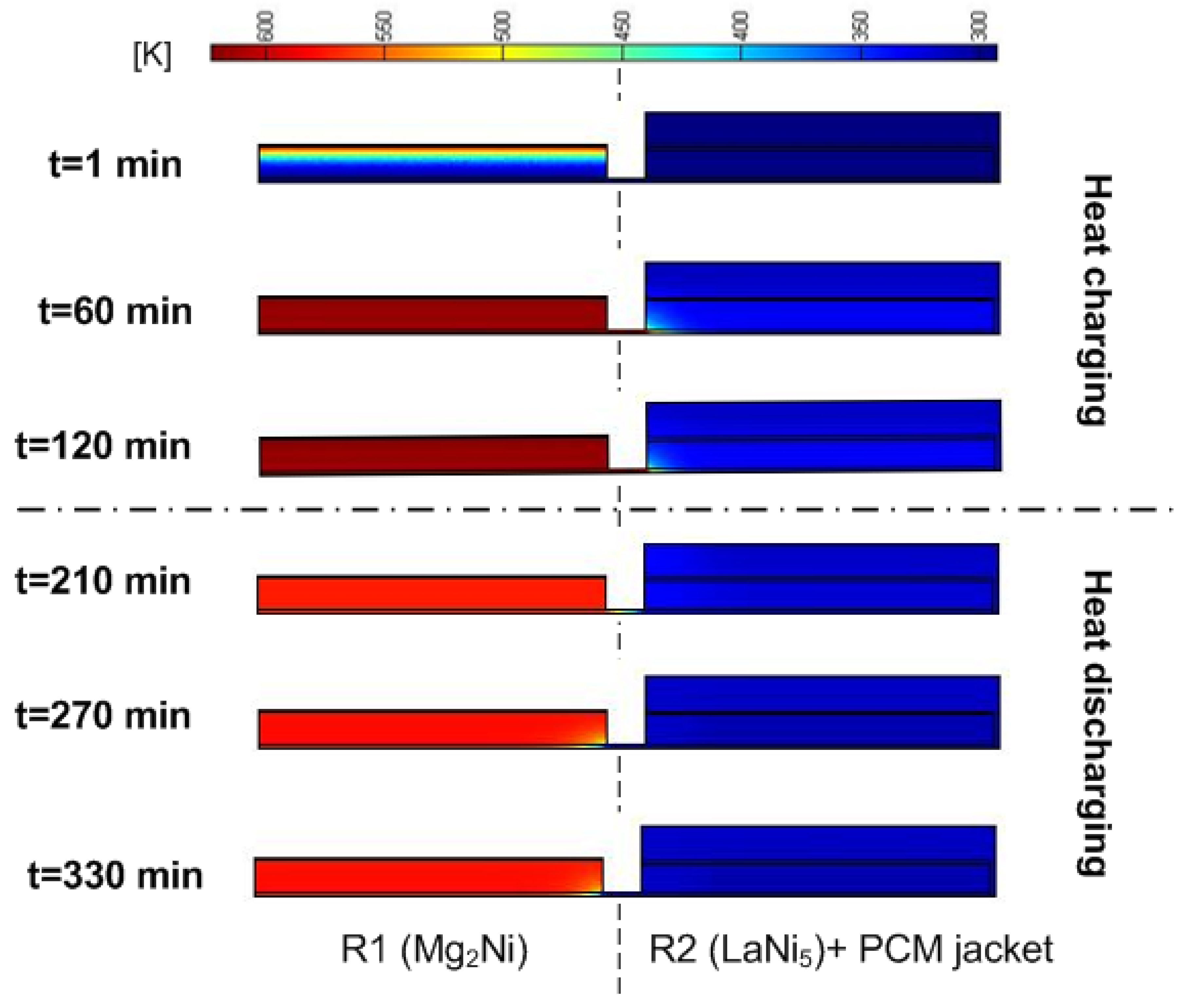
3.2. Heat Transfer Versus Pumping HTF
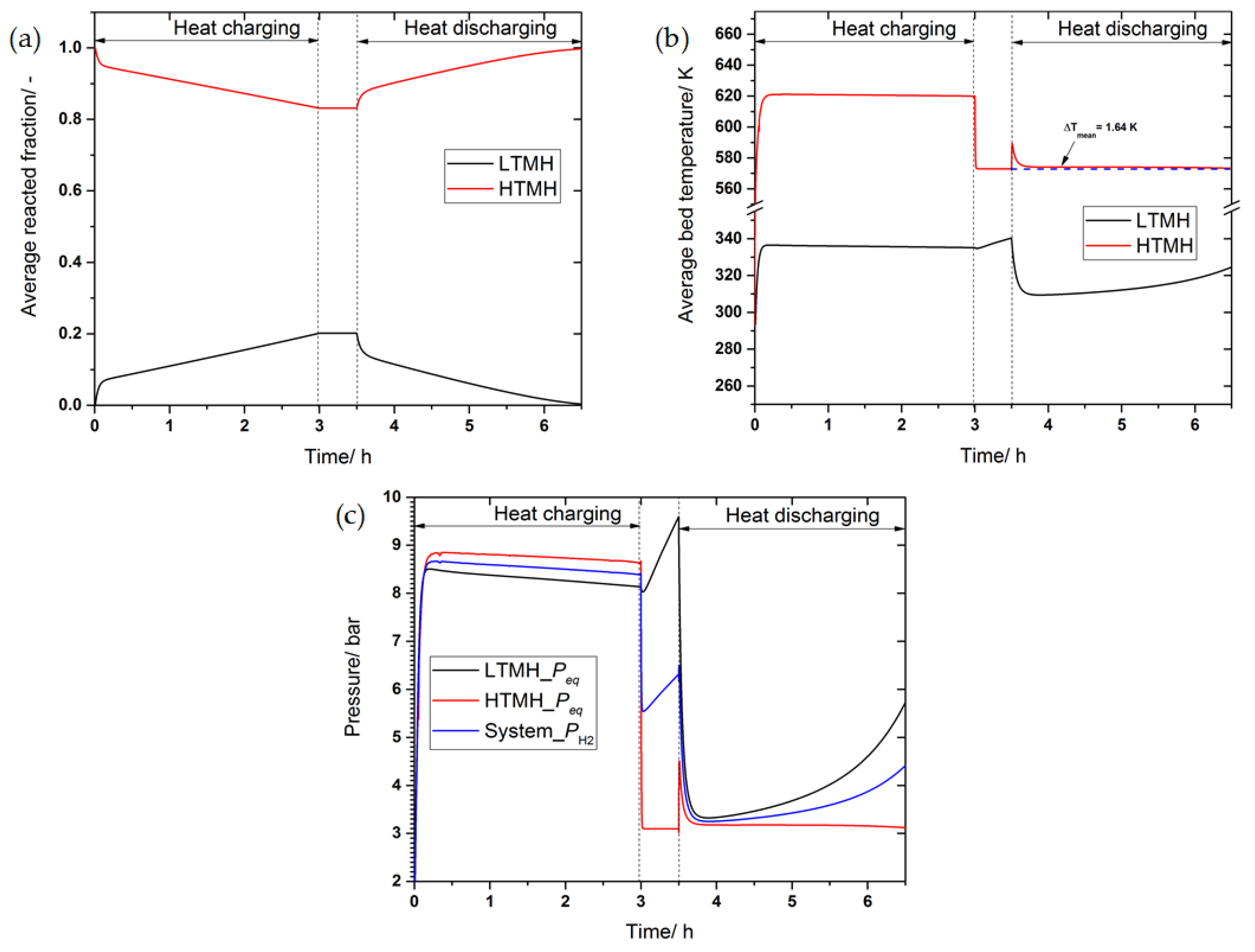
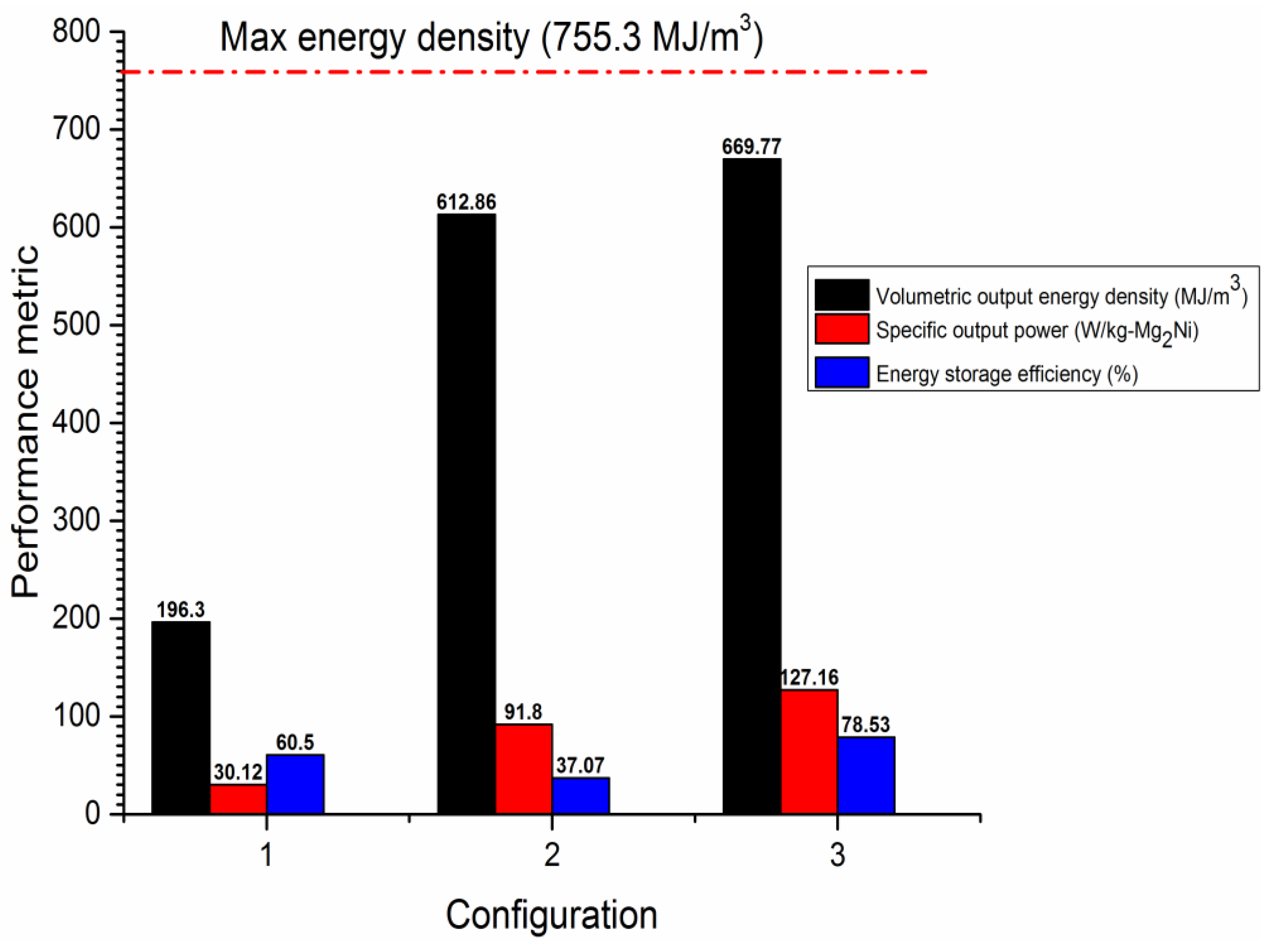
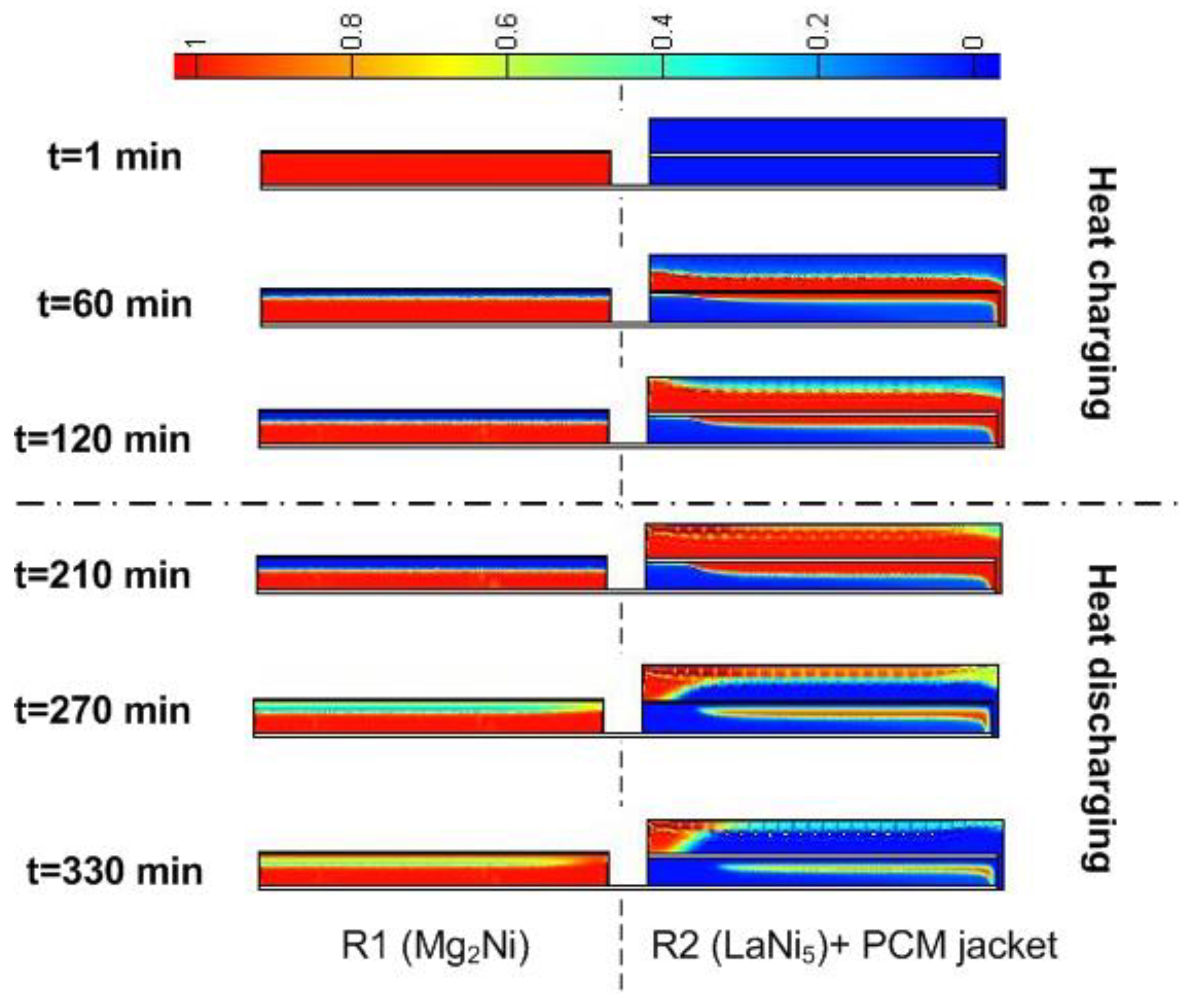
3.3. The Effect of Convective Heat Transfer on the Performance of the Heat Storage System
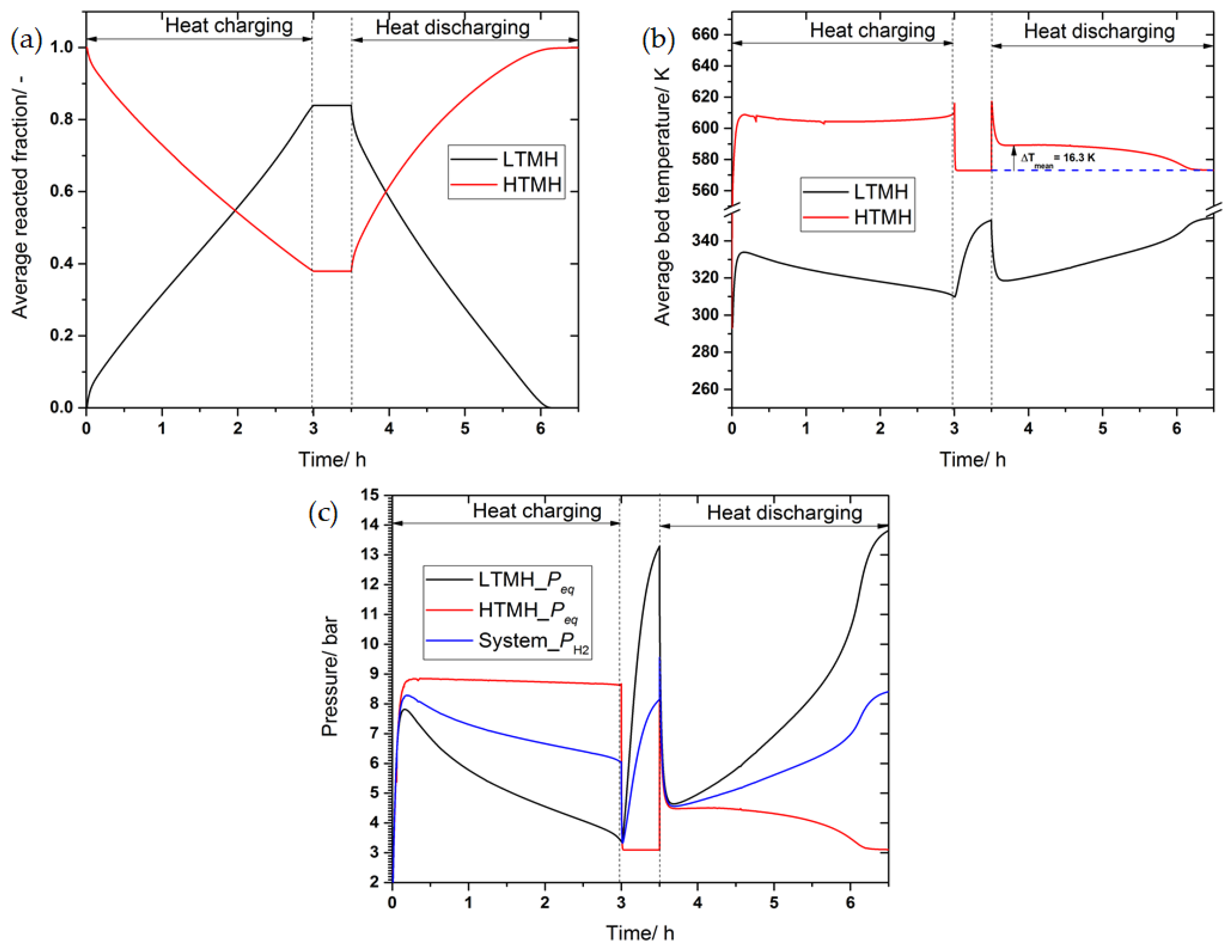
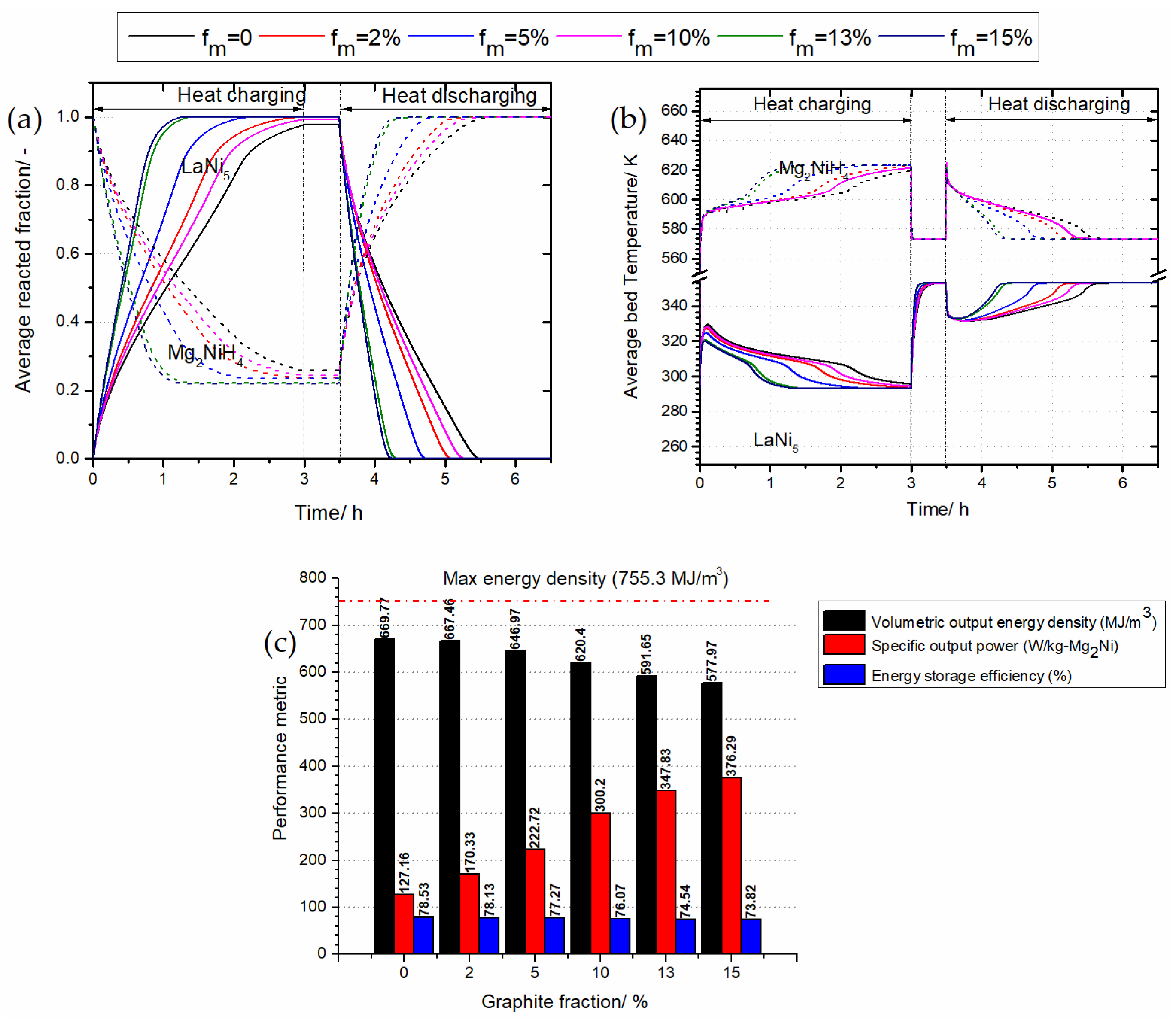
3.4. The Effect of Thermal Conductivity Improvement on the System’s Performance
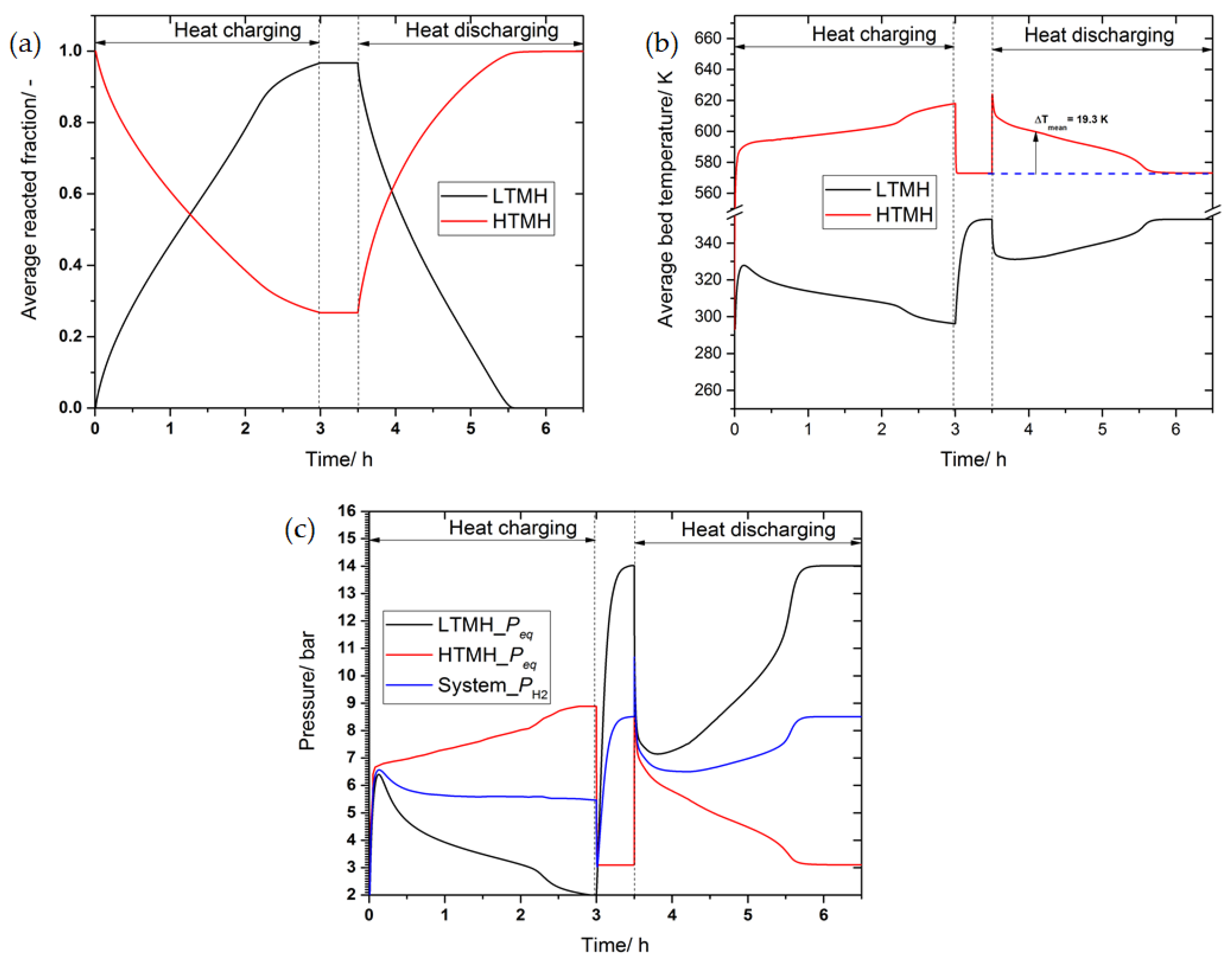
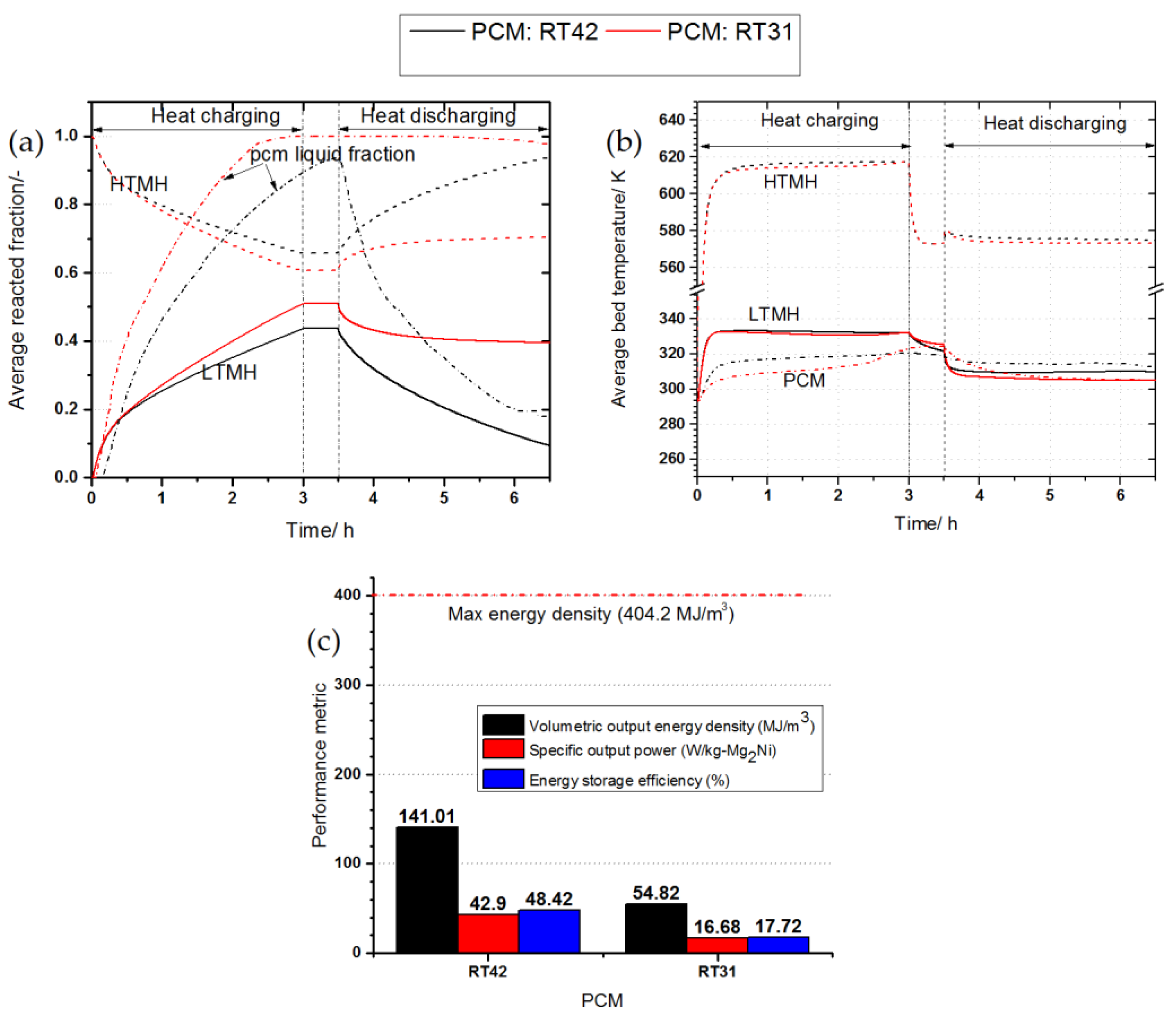
3.5. The Effect of Phase Change Material on the System’s Performance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Cp | Heat capacity (J·kg−1·K−1) | Velocity (m·s−1) | |
| Cf | hydraulic friction factor | V | Volume (m3) |
| CP | Connecting pipe | wt | H2 weight capacity (%) |
| D | Diameter (m) | Greek letters | |
| dh | Hydraulic diameter (m) | α | Conversion fraction, thermal diffusivity in Equation (23) (m2·s−1) |
| Ea,d | Activation energy (J·mol−1) | β | Thermal expansion in Equation (23) (K−1) |
| fm | Graphite volume fraction | ε | Bed porosity |
| h0,1 | Convective heat transfer coefficient (W·m−2·K−1) | η | Power efficiency of pump and motor, energy storage efficiency |
| HTF | Heat transfer fluid | λ | Thermal conductivity (W·m−1·K−1) |
| HTMH | High-temperature metal hydride | µ | Dynamic viscosity (Pa·s) Equation |
| ΔH | Reaction heat (J·mol−1 H2) Latent heat (kJ/kg) | ν | Kinematic viscosity (m2·s−1) |
| ka,d | Reaction rate constant (s−1) | ρ | Density (kg·m−3) |
| Keff | Permeability (m2) | Superscript | |
| L | Reactor length (m) | ¯¯ | Spatial average |
| LTMH | Low-temperature metal hydride | Subscript | |
| Mg | H2 molecular weight (kg·mol−1) | a | Activation, absorption |
| Mass flow rate (kg·s−1) | c | Cooling, charging | |
| Outward normal unit vector to the heat transfer interfaces | d | Desorption, discharging | |
| NuD | Nusselt number | eff | effective |
| p | Pressure (Pa) | eq | equilibrium |
| PCM | Phase change material | f | fluid |
| Pr | Prandtl number | g | gas |
| ΔP | Hydraulic pressure drop (Pa) | h | heating |
| Q | Heat exchanged (J) | i | inlet |
| r | Radius (m) | l | liquid |
| RaD | Rayleigh number | m | melting |
| Rg | Universal gas constant J·mol−1·K−1 | MH | Metal hydride |
| ReD | Reynolds number | o | outlet |
| ΔS | Entropy change of the reaction (J·mol−1·K−1) | s | storage system, solid |
| T | Temperature (K) | tr | transition |
| t | Time (s) | w | water |
| ΔT | HTF temperature difference (K) | ||
References
- Feng, P.; Liu, Y.; Ayuba, I.; Wu, Z.; Yang, F.; Zhang, Z. Optimal design methodology of metal hydride reactors for thermochemical heat storage. Energy Convers. Manag. 2018, 174, 239–247. [Google Scholar] [CrossRef]
- Nyallang, S.N.; Lototskyy, M.; Tolj, I. Selection of metal hydrides-based thermal energy storage: Energy storage efficiency and density targets. Int. J. Hydrogen Energy 2018, 43, 22568–22583. [Google Scholar]
- Reiser, A.; Bogdanovic, B.; Schlichte, K. The application of Mg-based metal hydrides as heat energy storage systems. Int. J. Hydrogen Energy 2000, 25, 425–430. [Google Scholar] [CrossRef]
- Bogdanovic, B.; Ritter, A.; Spliethoff, B. A process steam generator based on the high-temperature magnesium hydride/magnesium heat storage system. Int. J. Hydrogen Energy 1995, 20, 811–822. [Google Scholar] [CrossRef]
- Zhao, B.; Cheng, M.; Liu, C.; Dai, Z. Cyclic thermal characterization of a molten-salt packed-bed thermal energy storage for concentrating solar power. Appl. Energy 2017, 195, 761–773. [Google Scholar] [CrossRef]
- Li, X.; Xu, E.; Song, S.; Wang, X.; Yuan, G. Dynamic simulation of two-tank indirect thermal energy storage system with molten salt. Renew. Energy 2017, 113, 1311–1319. [Google Scholar] [CrossRef]
- Abdulla, A.; Reddy, K.S. Effect of operating parameters on thermal performance of molten salt packed-bed thermocline thermal energy storage system for concentrating solar power plants. Int. J. Therm. Sci. 2017, 121, 30–44. [Google Scholar] [CrossRef]
- Yin, H.; Ding, J.; Jiang, R.; Yang, X. Thermocline characteristics of molten-salt thermal energy storage in porous packed-bed tank. Appl. Therm. Eng. 2017, 110, 855–863. [Google Scholar] [CrossRef]
- Mahfuz, M.H.; Kamyar, A.; Afshar, O.; Sarraf, M.; Anisur, M.R.; Kibria, M.A.; Saidur, R.; Metselaar, I.H.S.C. Exergetic analysis of a solar thermal power system with PCM storage. Energy Convers. Manag. 2014, 78, 486–492. [Google Scholar] [CrossRef]
- Ma, F.; Zhang, P. Investigation on the performance of a high-temperature packed bed latent heat thermal energy storage system using Al-Si alloy. Energy Convers. Manag. 2017, 150, 500–514. [Google Scholar] [CrossRef]
- Thaker, S.; Oni, A.O.; Kumar, A. Techno-economic evaluation of solar-based thermal energy storage systems. Energy Convers. Manag. 2017, 153, 423–434. [Google Scholar] [CrossRef]
- Corgnale, C.; Hardy, B.; Motyka, T.; Zidan, R.; Teprovich, J.; Peters, B. Screening analysis of metal hydride based thermal energy storage systems for concentrating solar power plants. Renew. Sustain. Energy Rev. 2014, 38, 821–833. [Google Scholar] [CrossRef]
- Sekhar, B.S.; Muthukumar, P.; Saikia, R. Tests on a metal hydride based thermal energy storage system. Int. J. Hydrogen Energy 2012, 37, 3818–3824. [Google Scholar] [CrossRef]
- Sheppard, D.A.; Paskevicius, M.; Buckley, C.E. Thermodynamics of hydrogen desorption from NaMgH3 and its application as a solar heat storage medium. Chem. Mater. 2011, 23, 4298–4300. [Google Scholar] [CrossRef]
- Fang, Z.Z.; Zhou, C.; Fan, P.; Udell, K.S.; Bowman, R.C.; Vajo, J.J.; Kekelia, B. Metal hydrides based high energy density thermal battery. J. Alloys Compds. 2015, 645, 184–189. [Google Scholar] [CrossRef]
- Paskevicius, M.; Sheppard, D.A.; Williamson, K.; Buckley, C.E. Metal hydride thermal heat storage prototype for concentrating solar thermal power. Energy 2015, 88, 469–477. [Google Scholar] [CrossRef]
- Poupin, L.; Humphries, T.D.; Mark Paskevicius, M.; Buckley, C.E. An experimental high temperature thermal battery coupled to a low temperature metal hydride for solar thermal energy storage. Sustain. Energy Fuels. 2020, 4, 285–292. [Google Scholar] [CrossRef]
- Bogdanovic, B.; Ritter, A.; Spliethoff, B. Active MgH2-Mg Systems for Reversible Chemical Storage. Angew. Chem. Int. Ed. Engl. 1990, 29, 223–234. [Google Scholar] [CrossRef]
- Ward, P.A.; Corgnale, C.; Teprovich, J.A.; Motyka, T.; Hardy, B.; Peters, B.; Zidan, R. High performance metal hydride based thermal energy storage systems for concentrating solar power applications. J. Alloys Compds. 2015, 645, S374–S378. [Google Scholar] [CrossRef]
- Bao, Z.; Yuan, S. Performance investigation of thermal energy storage systems using metal hydrides adopting multi-step operation concept. Int. J. Hydrogen Energy 2016, 41, 5361–5370. [Google Scholar] [CrossRef]
- Bao, Z. Performance investigation and optimization of metal hydride reactors for high temperature thermochemical heat storage. Int. J. Hydrogen Energy 2015, 40, 5664–5676. [Google Scholar] [CrossRef]
- d’Entremont, A.; Corgnale, C.; Hardy, B.; Zidan, R. Simulation of high temperature thermal energy storage system based on coupled metal hydrides for solar driven steam power plants. Int. J. Hydrogen Energy 2018, 43, 817–830. [Google Scholar] [CrossRef]
- Malleswararao, K.; Aswin, N.; Srinivasa, S.; Murthy, S.S.; Dutta, P. Performance prediction of a coupled metal hydride based thermal energy storage system. Int. J. Hydrogen Energy 2020, 45, 16239–16253. [Google Scholar] [CrossRef]
- Mellouli, S.; Askri, F.; Edacherian, A.; Alqahtani, T.; Algarnia, S.; Abdelmajid, J.; Phelan, P. Performance analysis of a thermal energy storage system based on paired metal hydrides for concentrating solar power plants. Appl. Therm. Eng. 2018, 144, 1017–1029. [Google Scholar] [CrossRef]
- Bao, Z.; Yang, F.; Wu, Z.; Nyallang, N.S.; Zhang, Z. Optimal design of metal hydride reactors based on CFD—Taguchi combined method. Energy Convers. Manag. 2013, 65, 322–330. [Google Scholar] [CrossRef]
- Afzal, M.; Mane, R.; Sharma, P. Heat transfer techniques in metal hydride hydrogen storage: A review. Int. J. Hydrogen Energy 2017, 42, 30661–30682. [Google Scholar] [CrossRef]
- Yang, F.S.; Wang, G.X.; Zhang, Z.X.; Rudolph, V. Investigation on the influences of heat transfer enhancement measures in a thermally driven metal hydride heat pump. Int. J. Hydrogen Energy 2010, 35, 9725–9735. [Google Scholar] [CrossRef]
- Ron, M.; Gruen, D.; Mendelsohn, M.; Sheft, I. Preparation and properties of porous metal hydride compacts. J. Less Common Metals 1980, 74, 445–448. [Google Scholar] [CrossRef]
- Isselhorst, A.; Groll, M. Two-stage metal hydride heat transformer laboratory model. J. Alloys Compds 1995, 231, 888–894. [Google Scholar] [CrossRef]
- Werner, R.; Groll, M. Two-stage metal hydride heat transformer laboratory model: Results of reaction bed tests. J. Less Common Metals 1991, 172–174, 1122–1129. [Google Scholar] [CrossRef]
- Klein, H.P.; Groll, M. Development of a two-stage metal hydride system as topping cycle in cascading sorption systems for cold generation. Appl. Therm. Eng. 2002, 22, 631–639. [Google Scholar] [CrossRef]
- Chaise, A.; de Rango, P.; Marty, P.; Fruchart, D.; Miraglia, S.; Olives, R.; Garrier, S. Enhancement of hydrogen sorption in magnesium hydride using expanded natural graphite. Int. J. Hydrogen Energy 2009, 34, 8589–8596. [Google Scholar] [CrossRef]
- Pohlmann, C.; Röntzsch, L.; Kalinichenka, S.; Hutsch, T.; Kieback, B. Magnesium alloy-graphite composites with tailored heat conduction properties for hydrogen storage applications. Int. J. Hydrogen Energy 2010, 35, 12829–12836. [Google Scholar] [CrossRef]
- Muthukumar, P.; Groll, M. Metal hydride based heating and cooling systems: A review. Int. J. Hydrogen Energy 2010, 35, 3817–3831. [Google Scholar] [CrossRef]
- Mellouli, S.; Abhilash, E.; Askri, F.; Nasrallah, S.B. Integration of thermal energy storage unit in a metal hydride hydrogen storage tank. Appl. Therm. Eng. 2016, 102, 1185–1196. [Google Scholar] [CrossRef]
- Mâad, H.B.; Miled, A.; Askri, F.; Nasrallah, S.B. Numerical simulation of absorption-desorption cyclic processes for metal-hydrogen reactor with heat recovery using phase-change material. Appl. Therm. Eng. 2016, 96, 267–276. [Google Scholar] [CrossRef]
- Darzi, A.A.R.; Afrouzi, H.H.; Moshfegh, A.; Farhadi, M. Absorption and desorption of hydrogen in long metal hydride tank equipped with phase change material jacket. Int. J. Hydrogen Energy 2016, 41, 9595–9610. [Google Scholar] [CrossRef]
- Nyamsi, S.N.; Yang, F.; Zhang, Z. An optimization study on the finned tube heat exchanger used in hydride hydrogen storage system- analytical method and numerical simulation. Int. J. Hydrogen Energy 2012, 37, 16078–16092. [Google Scholar] [CrossRef]
- Nyallang, N.S.; Tolj, I.; Lototskyy, M. Metal hydride beds-phase change materials: Dual-mode thermal energy storage for medium-high temperature industrial waste heat recovery. Energies 2019, 12, 3949. [Google Scholar] [CrossRef]
- Nyallang, N.S.; Lototskyy, M.; Tolj, I. Optimal design of combined two-tank latent and metal hydrides-based thermochemical heat storage systems for high-temperature waste heat recovery. Energies 2020, 13, 4216. [Google Scholar]
- Abdin, Z.; Webb, C.J.; Gray, E.M. One-dimensional metal-hydride tank model and simulation in Matlab -Simulink. Int. J. Hydrogen Energy 2018, 43, 5048–5067. [Google Scholar] [CrossRef]
- Laurencelle, F.; Goyette, J. Simulation of heat transfer in metal hydride reactor with aluminum foam. Int. J. Hydrogen Energy 2007, 32, 2957–2964. [Google Scholar] [CrossRef]
- Chung, C.A.; Lin, C.S. Prediction of hydrogen desorption performance of Mg2Ni hydride reactors. Int. J. Hydrogen Energy 2009, 34, 9409–9423. [Google Scholar] [CrossRef]
- Incropera, F.; DeWitt, D.; Bergman, T.; Lavine, A. Fundamentals of Heat and Mass Transfer, 6th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007; p. 580. [Google Scholar]
- Perry, R.; Green, D.W.; Maloney, J.O. Perry’s Chemical Engineers’ Handbook, 7th ed.; McGraw Hill: New York, NY, USA, 1997; Chapter 6: Tables 4–6. [Google Scholar]
- Siyabi, I.A.; Khanna, S.; Mallick, T.; Sundaram, S. An experimental and numerical study on the effect of inclination angle of phase change materials thermal energy storage system. J. Energy Storage 2019, 23, 57–68. [Google Scholar] [CrossRef]
- Lizana, J.; Chacartegui, R.; Barrios-Padura, A.; Valverde, J.M. Advances in thermal energy storage materials and their applications towards zero energy buildings: A critical review. Appl. Energy 2017, 203, 219–239. [Google Scholar] [CrossRef]
| Mg2Ni [43] | LaNi5 [2] | |
|---|---|---|
| Enthalpy of formation/kJ·mol−1 | 64.5 | 30.5 |
| Entropy of formation/J·mol−1 K−1 | 122.2 | 108 |
| Activation energy, abs-des/kJ·mol−1 | 52.20/63.46 | 21.17/16.47 |
| Rate constant abs-des/s−1 | 175/5452.2 | 59.18/9.57 |
| Density/kg·m−3 | 3200 | 8400 |
| Specific heat, M-MH/J·kg−1·K−1 | 697 | 419 |
| Max hydrogen capacity/wt% | 3.6 | 1.39 |
| Porosity | 0.5 | 0.5 |
| Permeability/m2 | 1.3 × 10−12 | 1.3 × 10−12 |
| Effective thermal conductivity/W·m−1·K−1 | 1 | 1 |
| Hydride thickness/m | 0.027 | 0.025 |
| H2 filter radius, r0/m | 0.003 | 0.003 |
| Hydraulic diameter dh/m | 0.003 | 0.003 |
| Reactor length LMH/m | 0.45 | 0.45 |
| Parameter | Value/Range | ||||
|---|---|---|---|---|---|
| SS316L | Graphite | Water (298 K) | Therminol VP-1 [6] (623 K) | Dry Air (293 K) | |
| Density ρ/kg·m−3 | 7990 | 2200 | 1000 | 761 | 1.2 |
| Specific heat, Cp/J·kg−1·K−1 | 500 | 710 | 4180 | 2454 | 1000 |
| Thermal conductivity/W·m−1·K−1 | 16.2 | 17.9 | 0.59 | 0.086 | 0.025 |
| Dynamic viscosity/mPa.s | - | - | 0.89 | 0.177 | 18.1 × 10−3 |
| Cooling fluid temperature Tc/K | - | - | 293 | 573 | 293 |
| Heating fluid temperature Th/K | - | - | 353 | 623 | 353 |
| PCM | Melting Temperature/°C | Density, Solid/Liquid/kg∙m−3 | Thermal Conductivity/W∙m−1∙K−1 | Specific Heat, Cp/J·kg−1·K−1 | Latent Heat of Fusion/kJ∙kg−1 | Volumetric Heat Capacity/MJ∙m−3 |
|---|---|---|---|---|---|---|
| RT31 | 31 | 880/760 | 0.2 | 2000 | 165 | 145 |
| RT42 | 42 | 880/760 | 0.2 | 2000 | 165 | 145 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nyamsi, S.N.; Tolj, I. The Impact of Active and Passive Thermal Management on the Energy Storage Efficiency of Metal Hydride Pairs Based Heat Storage. Energies 2021, 14, 3006. https://doi.org/10.3390/en14113006
Nyamsi SN, Tolj I. The Impact of Active and Passive Thermal Management on the Energy Storage Efficiency of Metal Hydride Pairs Based Heat Storage. Energies. 2021; 14(11):3006. https://doi.org/10.3390/en14113006
Chicago/Turabian StyleNyamsi, Serge Nyallang, and Ivan Tolj. 2021. "The Impact of Active and Passive Thermal Management on the Energy Storage Efficiency of Metal Hydride Pairs Based Heat Storage" Energies 14, no. 11: 3006. https://doi.org/10.3390/en14113006
APA StyleNyamsi, S. N., & Tolj, I. (2021). The Impact of Active and Passive Thermal Management on the Energy Storage Efficiency of Metal Hydride Pairs Based Heat Storage. Energies, 14(11), 3006. https://doi.org/10.3390/en14113006








