Investigation of Heat Diffusion at Nanoscale Based on Thermal Analysis of Real Test Structure
Abstract
1. Introduction
1.1. State of the Art
1.2. MEMS Test Structure Description
2. Mathematical Description of Proposed Methodology
2.1. General Description
2.2. Structure Cross-Sectional Area Discretization
2.3. Dual-Phase-Lag Approximation Scheme for Test Structure
2.4. Heat Transfer Enhancement
3. Thermal Simulation and Results Analysis
3.1. Material Characterization and Initial Simulation Results
- τT = 60 ps, τq = 3 ps (all layers)
- τT = 2.6 ps, τq = 0.0916 ps (platinum resistors) and τT = 60 ps, τq = 3 ps (all remaining layers).
3.2. Final Simulation Results and Comparison to Real Measurements of the Test Structure
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Description | SI Unit |
| Latin symbols | ||
| T | Temperature rise distribution in analyzed area in relations to ambient temperature | K |
| a | Constant describing an interaction between gas molecules and solid walls | - |
| b | Inter-atomic distance | m |
| cp | Specific heat of a material for a constant pressure (cp) | |
| cv | Volumetric heat capacity being a product of a specific heat of a material for a constant pressure (cp) and its density (ρ) | |
| Quotient of Planck constant and the value of 2∙π | J∙s | |
| k | Material thermal conductivity | |
| kB | Boltzmann constant | |
| q | Heat flux density | |
| qV | Volume density of internally generated heat | |
| Δs | Mesh nodes distance | m |
| t | Time variable | s |
| x | Space variable | mn |
| Greek symbols | ||
| αx | Order of a fractional Grünwald–Letnikov space derivative | - |
| Λ | Molecule’s mean free path length | m |
| ρ | Material density | |
| τT | Temperature time lag | s |
| τq | Heat flux time lag | s |
| Matrix and vectors | ||
| Vector including only 1 values | - | |
| a × b | Matrix dimensions; a reflect number of rows, b is the number of columns | - |
| Derivatives | ||
| ∂ | Derivative symbol | - |
| First derivative of function f | - | |
| Second derivative of function f | - | |
| Fractional Grünwald–Letnikov derivative of order α around point 0 for s variable | - | |
| Mathematical operators | ||
| Difference operator corresponding to changes for Dt →0 | - | |
| Multiplication operator | - | |
| ∇ | Nabla operator | - |
| Δ | Laplace operator | - |
| GLΔαx | Fractional order of Laplace operator | - |
| ∇ ◦ | Divergence operator in orthogonal Euclidean space | - |
| Sets’ union operator | - | |
| T | Transposition operator | - |
| Sets and spaces | ||
| Finite set of elements | - | |
| Open interval between a and b | - | |
| span{a,b} | Linear subspace generated by vectors a and b | - |
| Functions | ||
| Ensemble average | - | |
| Rounding of α value to the smallest integer number higher or equal to α | - | |
| diag(∙) | Matrix function creating a diagonal matrix from a vector | - |
| repmat(∙) | Matrix function replicating a given vector and composing a matrix of required dimensions | - |
| round(α,k) | Rounding of α value to kth digit after decimal point | - |
| Maximum of the set including f function values | - | |
| Special Gamma function | - |
References
- Fourier, J.-B.J. Théorie Analytique de la Chaleur; Firmin Didot: Paris, France, 1822. [Google Scholar]
- Fourier, J.-B.J. The Analytical Theory of Heat; Cambridge University Press: London, UK, 1878. [Google Scholar]
- Raszkowski, T.; Samson, A. The Numerical Approaches to Heat Transfer Problem in Modern Electronic Structures. Comput. Sci. 2017, 18, 71–93. [Google Scholar] [CrossRef]
- Raszkowski, T.; Zubert, M.; Janicki, M.; Napieralski, A. Numerical solution of 1-D DPL heat transfer equation. In Proceedings of the 22nd International Conference Mixed Design of Integrated Circuits and Systems (MIXDES), Torun, Poland, 25–27 June 2015; pp. 436–439. [Google Scholar]
- Zubert, M.; Janicki, M.; Raszkowski, T.; Samson, A.; Nowak, P.S.; Pomorski, K. The Heat Transport in Nanoelectronic Devices and PDEs Translation into Hardware Description Languages. Bulletin de la Société des Sciences et des Lettres de Łódź Série Recherches sur les Déformations 2014, LXIV, 69–80. [Google Scholar]
- Nabovati, A.; Sellan, D.P.; Amon, C.H. On the lattice Boltzmann method for phonon transport. J. Comput. Phys. 2011, 230, 5864–5876. [Google Scholar] [CrossRef]
- Zubert, M.; Raszkowski, T.; Samson, A.; Janicki, M.; Napieralski, A. The distributed thermal model of fin field effect transistor. Microelectron. Reliab. 2016, 67, 9–14. [Google Scholar] [CrossRef]
- Zubert, M.; Raszkowski, T.; Samson, A.; Zając, P. Methodology of determining the applicability range of the DPL model to heat transfer in modern integrated circuits comprised of FinFETs. Microelectron. Reliab. 2018, 91, 139–153. [Google Scholar] [CrossRef]
- Tzou, D.Y. Macro-to Microscale Heat Transfer: The Lagging Behavior, 2nd ed.; Willey: Hoboken, NJ, USA, 2015. [Google Scholar]
- Jou, D.; Casas-Vázquez, J.; Lebon, G. Extended Irreversible Thermodynamics. Rep. Prog. Phys. 1988, 51, 1105–1179. [Google Scholar] [CrossRef]
- Jou, D.; Casas-Vázquez, J.; Lebon, G. Extended Irreversible Thermodynamics, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Tzou, D.Y. An Engineering Assessment to the Relaxation Time in Thermal Waves. Int. J. Heat Mass Transf. 1993, 36, 1845–1851. [Google Scholar] [CrossRef]
- Tzou, D.Y. A Unified Field Approach for Heat Conduction from Macro- to Micro-Scales. J. Heat Transf. 1995, 117, 8–16. [Google Scholar] [CrossRef]
- Grmela, M.; Öttinger, H.C. Dynamics and thermodynamics of complex fluids. I. Development of a general formalism. Phys. Rev. E 1997, 56, 6620–6632. [Google Scholar] [CrossRef]
- Öttinger, H.C.; Grmela, M. Dynamics and thermodynamics of complex fluids. II. Illustrations of a general formalism. Phys. Rev. E 1997, 56, 6633–6655. [Google Scholar] [CrossRef]
- Pavelka, M.; Klika, V.; Grmela, M. Multiscale Thermo-Dynamics Introduction to GENERIC; de Gruyter: Berlin, Germany, 2018. [Google Scholar] [CrossRef]
- Anufriev, R.; Gluchko, S.; Volz, S.; Nomura, M. Quasi-Ballistic Heat Conduction due to Lévy Phonon Flights in Silicon Nanowires. ACS Nano 2018. [Google Scholar] [CrossRef] [PubMed]
- Kröger, M.; Hütter, M. Automated symbolic calculations in nonequilibrium thermodynamics. Comput. Phys. Commun. 2010, 181, 2149–2157. [Google Scholar] [CrossRef]
- Zhukovsky, K. Exact Negative Solutions for Guyer–Krumhansl Type Equation and the Maximum Principle Violation. Entropy 2017, 19, 440. [Google Scholar] [CrossRef]
- Van, P.; Berezovski, A.; Fülöp, T.; Gróf, G.; Kovács, R.; Lovas, Á.; Verhás, J. Guyer-Krumhansl-type heat conduction at room temperature. EPL (Europhys. Lett.) 2017, 118. [Google Scholar] [CrossRef]
- Pop, E.; Sinha, S.; Goodson, K.E. Heat Generation and Transport in Nanometer-Scale Transistors. Proc. IEEE 2006, 94, 1587–1601. [Google Scholar] [CrossRef]
- Podlubny, I. Geometric and Physical Interpretation of Fractional Integration and Fractional Differentiation. arXiv 2001. arXiv:math/0110241v1. [Google Scholar]
- Li, C.P.; Deng, W. Remarks on fractional derivatives. Appl. Math. Comput. 2007, 187. [Google Scholar] [CrossRef]
- Li, C.P.; Qian, D.L.; Chen, Y.Q. On Riemann-Liouville and Caputo Derivatives. Discret. Dyn. Nat. Soc. 2011, 2011, 562494. [Google Scholar] [CrossRef]
- Li, C.P.; Zhao, Z.G. Introduction to fractional integrability and differentiability. Eur. Phys. J. Spec. Top. 2011, 193, 5–26. [Google Scholar] [CrossRef]
- Cattaneo, M.C. A form of heat conduction equation which eliminates the paradox of instantaneous propagation. C.R. Acad. Sci. I Math. 1958, 247, 431–433. [Google Scholar]
- Cattaneo, C. Sur une forme de l’equation de la chaleur eliminant le paradoxe d’une propagation instantanee (in French). Comptes Rendus de l’Académie des Sciences 1958, 247, 431–433. [Google Scholar]
- Vernotte, P. Les paradoxes de la theorie continue de l’equation de la chaleur (in French). C. R. Acad. Sci. 1958, 246, 3154–3155. [Google Scholar]
- Vermeersch, B.; De Mey, G. Non-Fourier thermal conduction in nano-scaled electronic structures. Analog Integr. Circ. Signal Process. 2008, 55, 197–204. [Google Scholar] [CrossRef]
- Kovács, R.; Ván, P. Generalized heat conduction in heat pulse experiments. Int. J. Heat Mass Transf. 2015, 83, 613–620. [Google Scholar] [CrossRef]
- Raszkowski, T.; Samson, A.; Zubert, M. Temperature Distribution Changes Analysis Based on Grünwald-Letnikov Space Derivative. Bull. Soc. Sci. Lettres Łódź 2018, LXVIII, 141–152. [Google Scholar]
- Sobczak, A.; Topilko, J.; Zajac, P.; Pietrzak, P.; Janicki, M. Compact Thermal Modelling of Nanostructures Containing Thin Film Platinum Resistors. In Proceedings of the 21st International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), 6–27 July 2020. in press. [Google Scholar]
- Janicki, M.; Topilko, J.; Sobczak, A.; Zajac, P.; Pietrzak, P.; Napieralski, A. Measurement and Simulation of Test Structures Dedicated to the Investigation of Heat Diffusion at Nanoscale. In Proceedings of the 20th International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Hannover, Germany, 24–27 March 2019. [Google Scholar] [CrossRef]
- Raszkowski, T.; Samson, A.; Zubert, M. Investigation of Heat Distribution using Non-integer Order Time Derivative. Bull. Soc. Sci. Lettres Łódź Série Rech. Déformations 2018, LXVIII, 79–92. [Google Scholar]
- Curtiss, C.F.; Hirschfelder, J.O. Integration of stiff equations. Proc. Natl. Acad. Sci. USA 1952, 38, 235–243. [Google Scholar] [CrossRef]
- Ascher, U.M.; Petzold, L.R. Computer Methods for Ordinary Differential-Algebraic Equations; SIAM: Philadelphia, PA, USA, 1998. [Google Scholar]
- Süli, E.; Mayers, D. An Introduction to Numerical Analysis; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Auzinger, W.; Herfort, W.N. A uniform quantitative stiff stability estimate for BDF schemes. Opusc. Math. 2006, 26, 203–227. [Google Scholar]
- Raszkowski, T.; Samson, A.; Zubert, M. Dual-Phase-Lag Model Order Reduction Using Krylov Subspace Method for 2-Dimensional Structures. Bull. Soc. Sci. Lettres Łódź Série Rech. Déformations 2018, LXVIII, 55–68. [Google Scholar]
- Raszkowski, T.; Samson, A.; Zubert, M.; Janicki, M.; Napieralski, A. The numerical analysis of heat transfer at nanoscale using full and reduced DPL models. In Proceedings of the International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Dresden, Germany, 3–5 April 2017. [Google Scholar]
- Bahrami, M.; Yanavovich, M.M.; Culham, J.R.; Thermophys, J. Thermal joint resistance of conforming rough surfaces with gas-filled gaps. AIAA J. Thermophys. Heat Transf. 2004, 18, 318–325. [Google Scholar] [CrossRef]
- Bahrami, M.; Culham, J.R.; Yanavovich, M.M.; Schneider, G.E. Review of thermal joint resistance models for non-conforming rough surfaces. AMSE J. Appl. Mech. Rev. 2006, 59, 1–12. [Google Scholar] [CrossRef]
- Volokitin, A.I.; Persson, B.N.J. Radiative heat transfer between nanostructures. Phys. Rev. B 2001, 63, 205404. [Google Scholar] [CrossRef]
- Volokitin, A.I.; Persson, B.N.J. Resonant photon tunneling enhancement of the radiative heat transfer. Phys. Rev. B 2004, 69, 045417. [Google Scholar] [CrossRef]
- Raszkowski, T. Numerical Modelling of Thermal Phenomena in Nanometric Semiconductor Structures. Ph.D. Dissertation, Lodz University of Technology, Lodz, Poland, 2019. (In Polish). [Google Scholar]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Górecki, K.; Górecki, P. Compact electrothermal model of laboratory made GaN Schottky diodes. Microelectron. Int. 2020, Paper version in press 3/2020. [Google Scholar] [CrossRef]
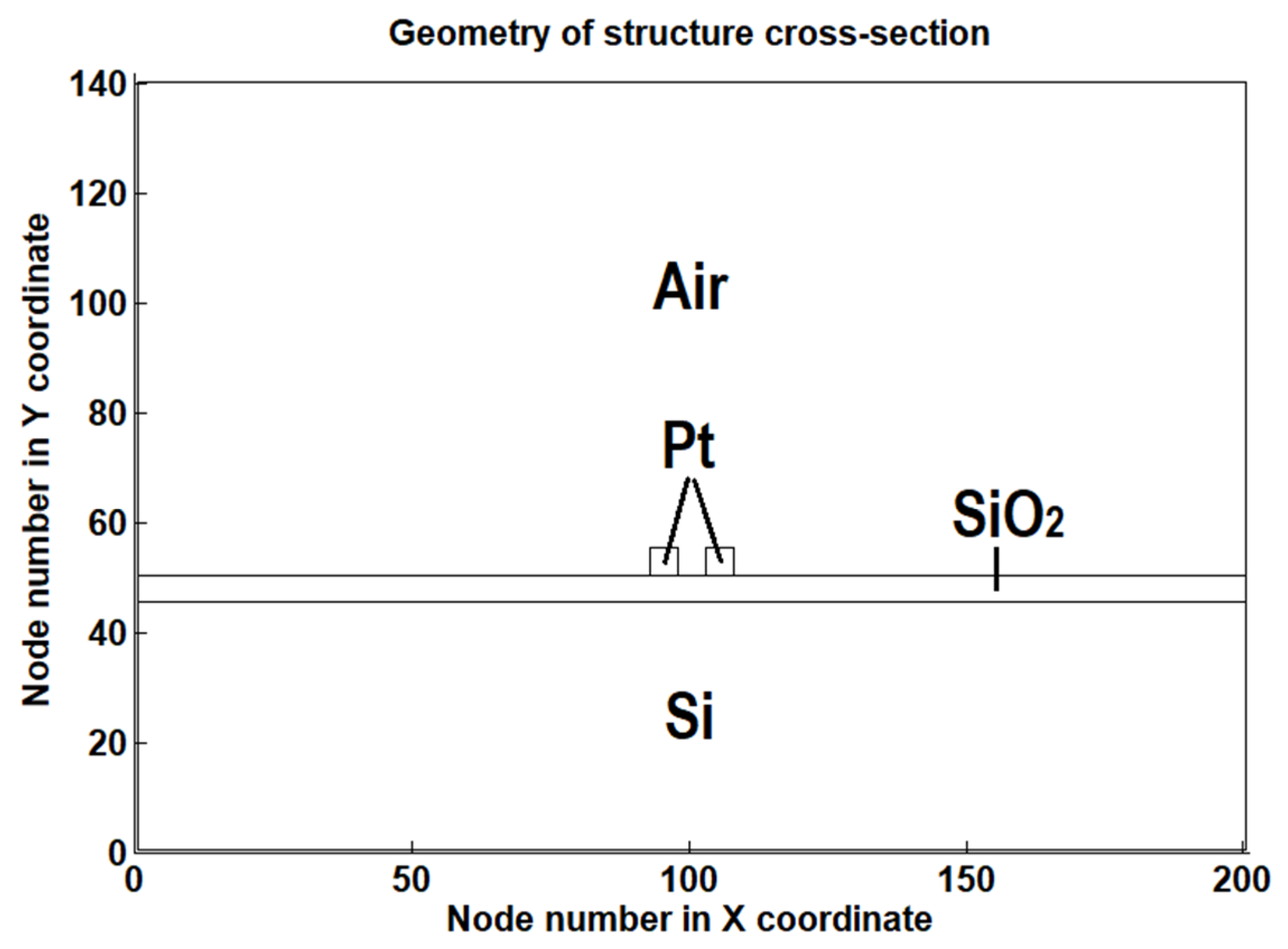
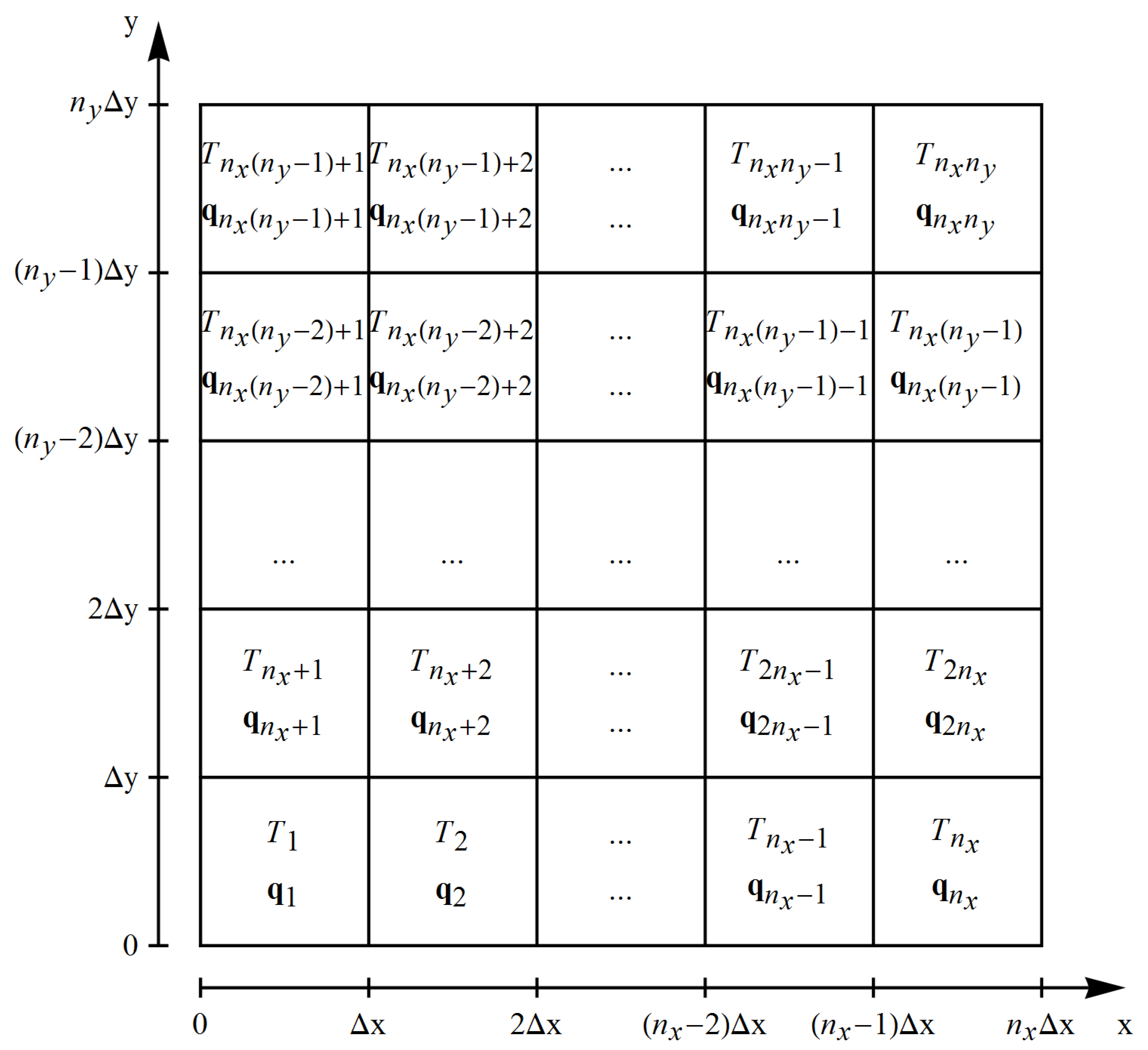

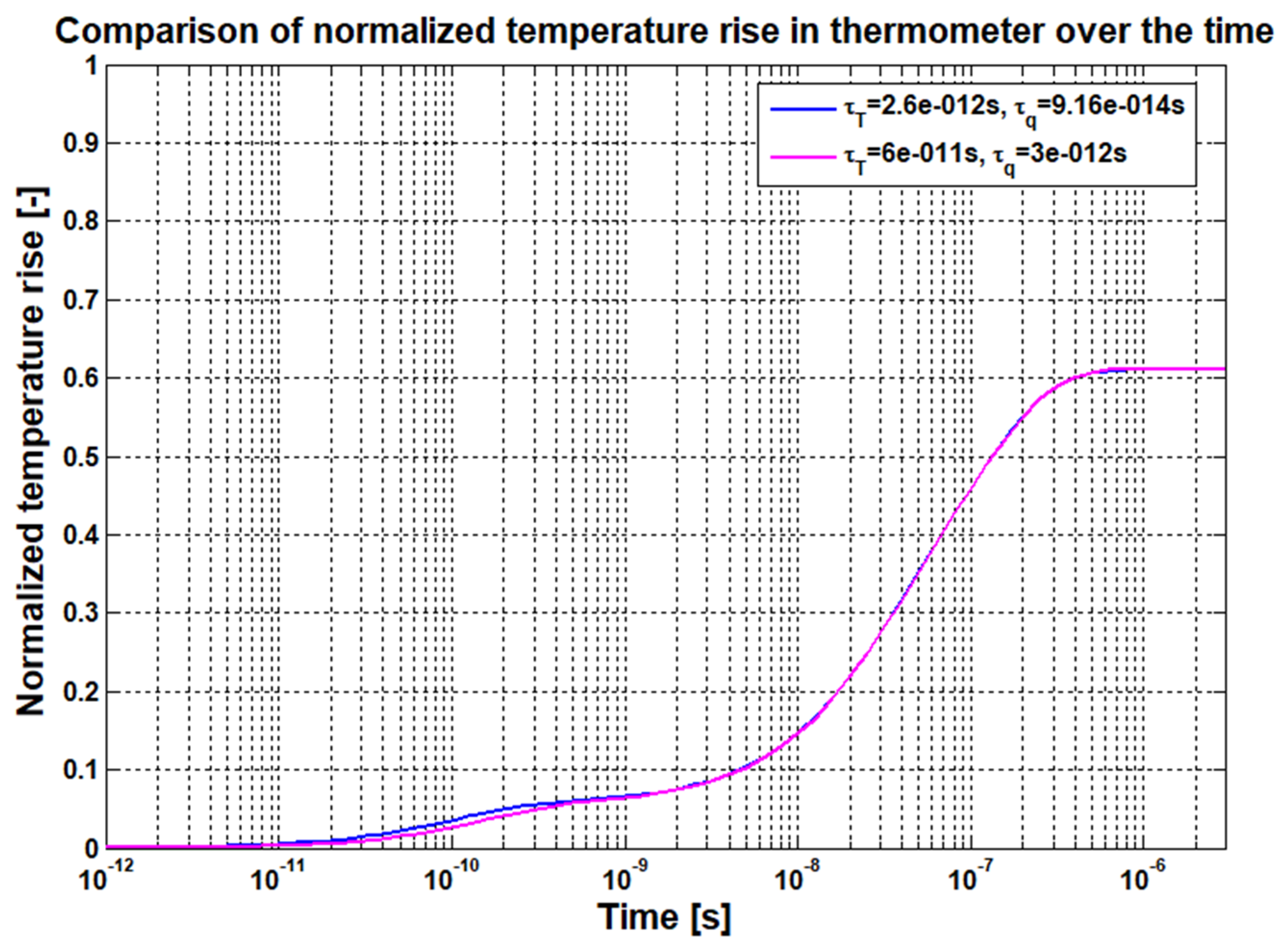
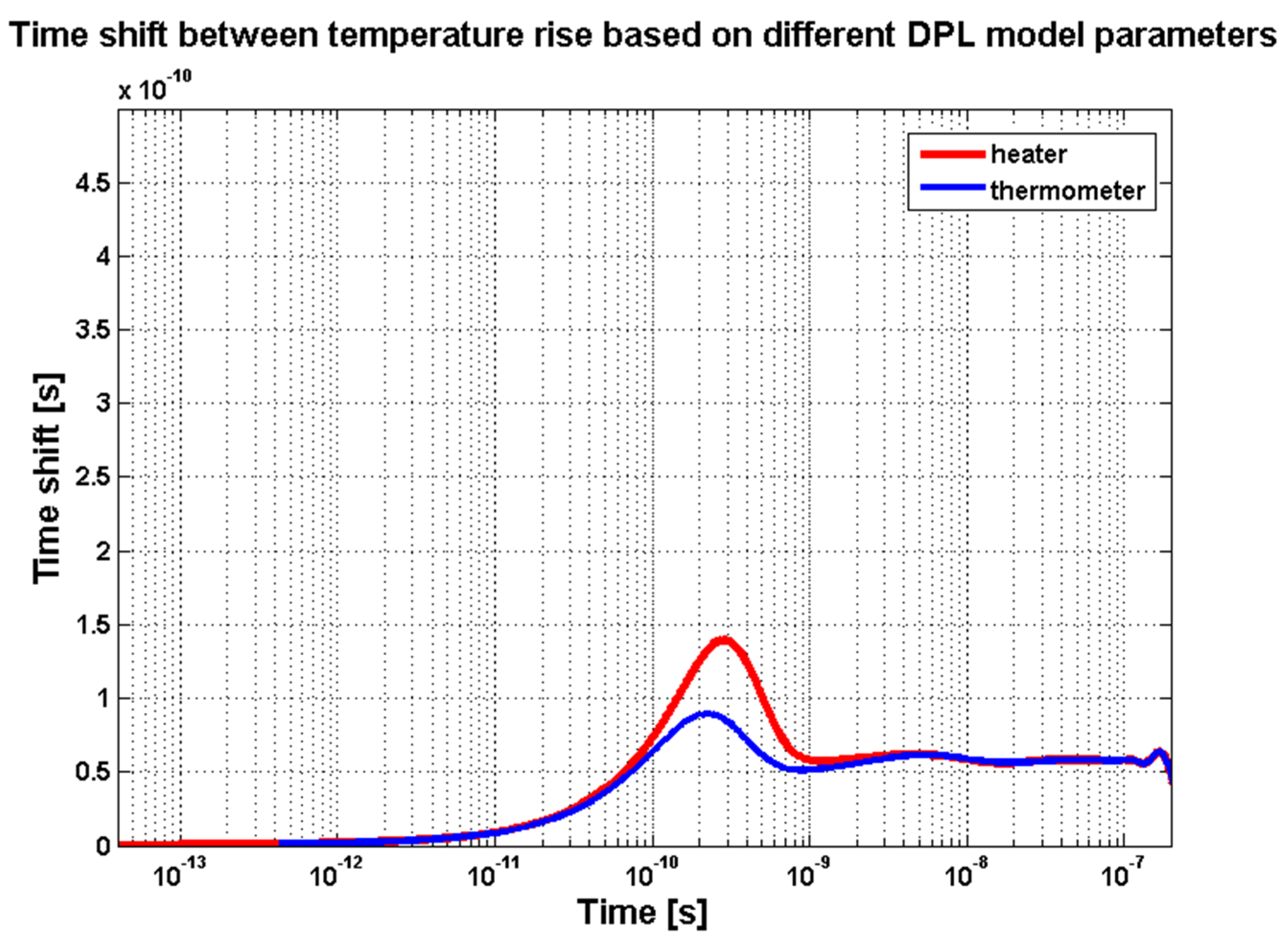
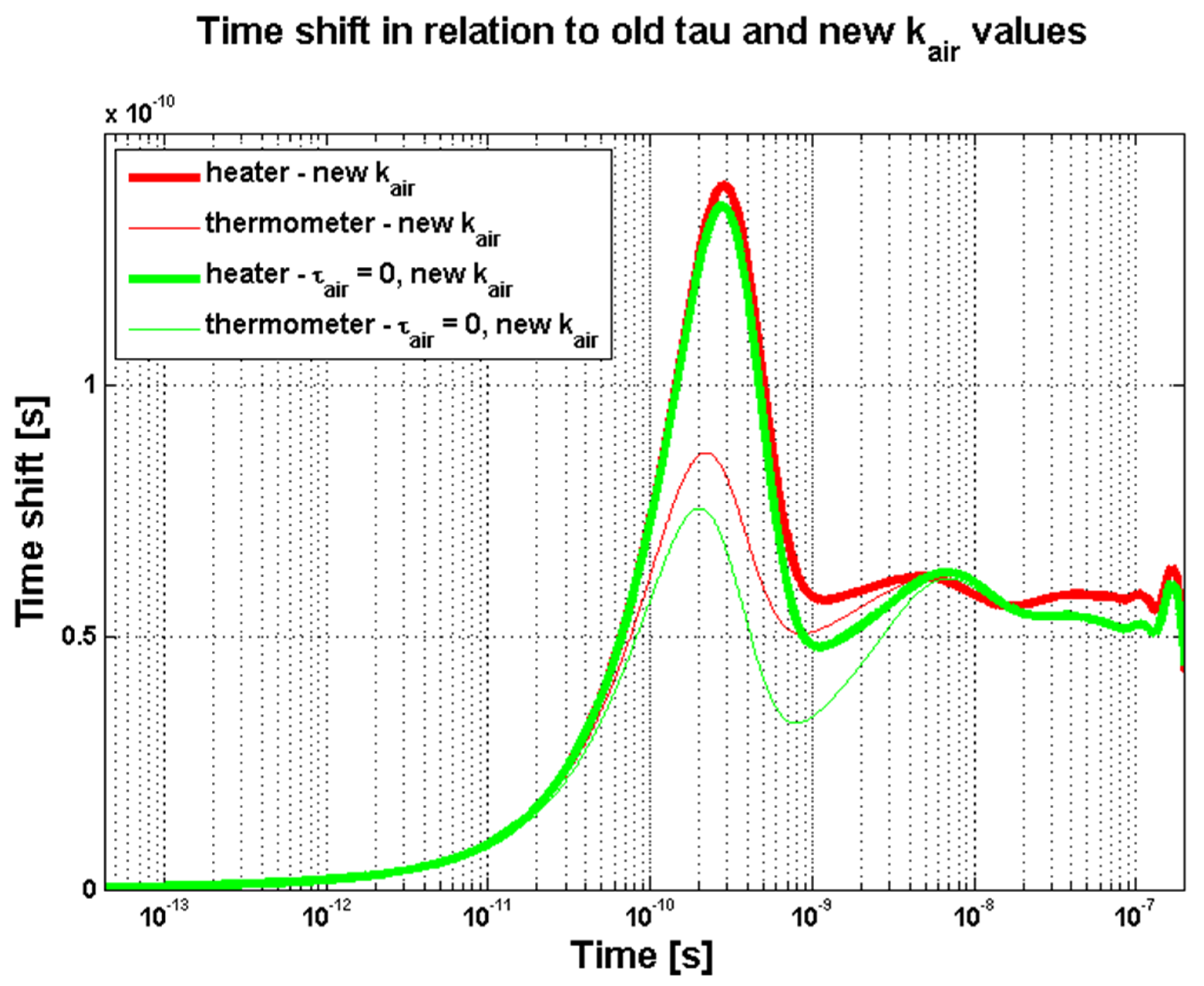
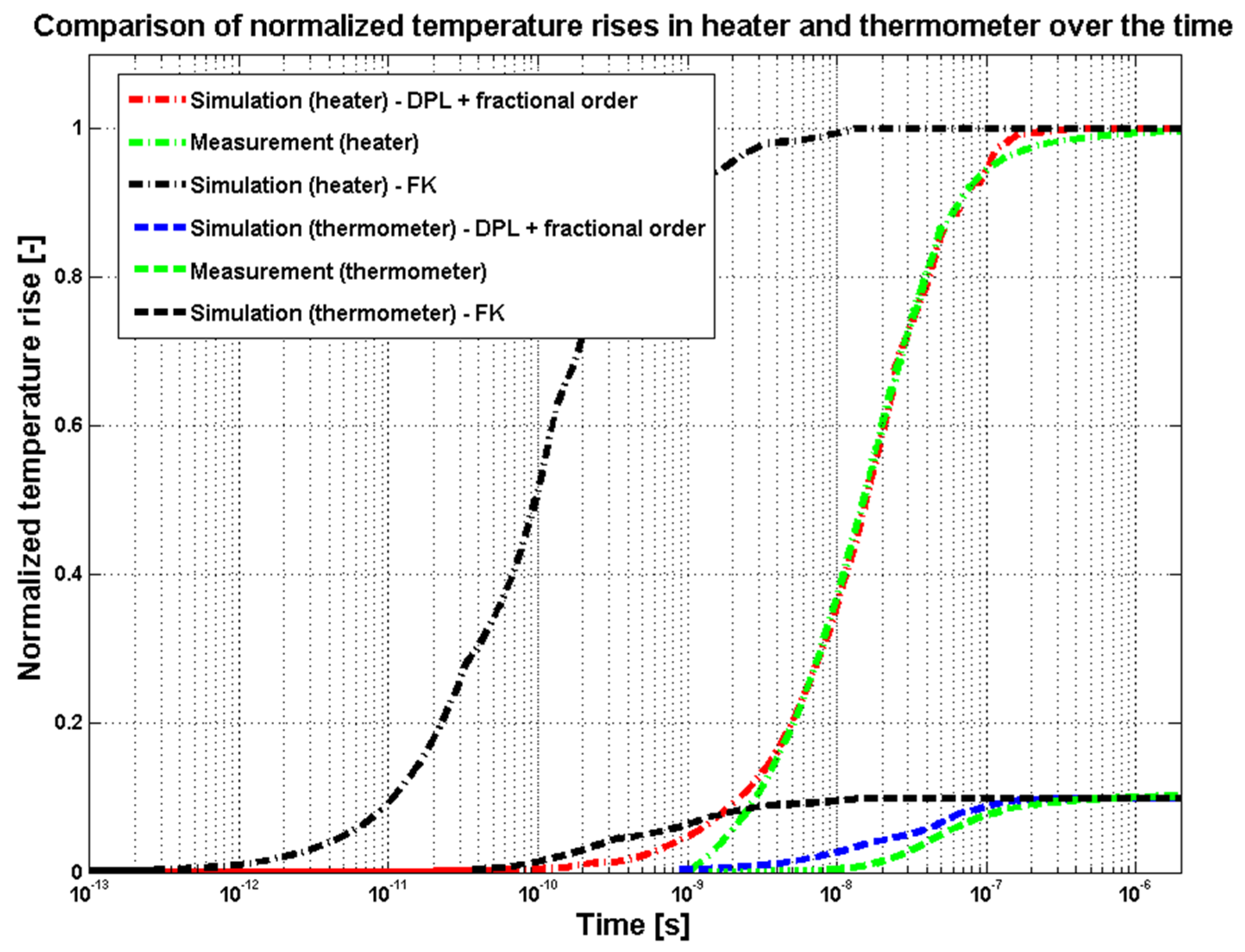
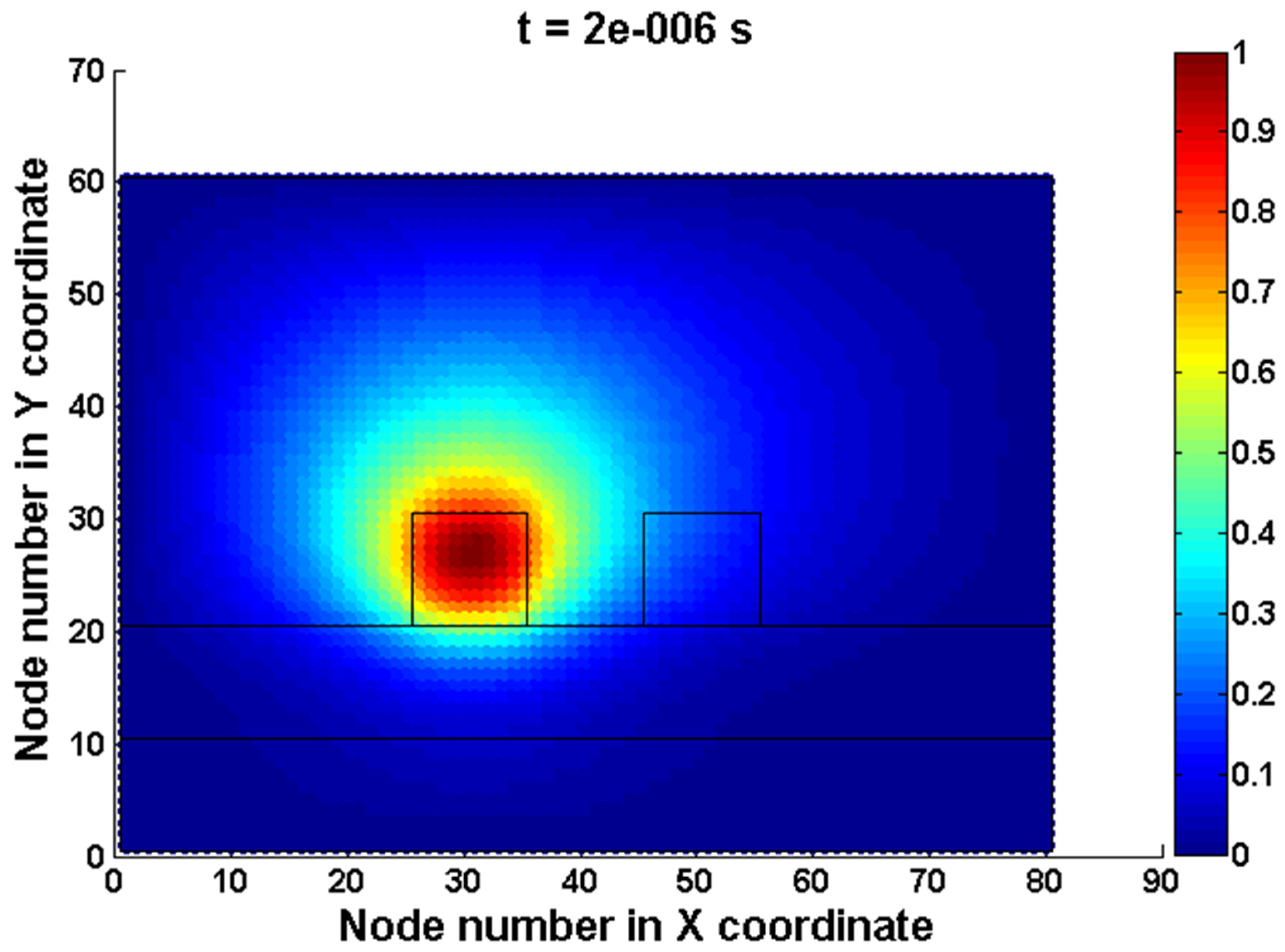
| Heat Transfer Model | Derived Time Delayed PDE |
|---|---|
| (a) | |
| DPL equation [12,13] for τT > τq > 0, Maxwell–Cattaneo–Vernotte equation [26,27,28] for τq > 0, τT = 0 (more details in Vermeersch and De Mey as well as Kovács and Ván papers [29,30]), and F–K Equations (1)–(2) for τq = τT = 0: | ⇓ |
| (b) | |
| Ballistic-conductive heat transfer model for τq > 0, τQ > 0, k12∙k12 ≤ 0 (more details [30]) | |
| (c) | |
| Proposed DPL model [12,13], with fractional order of the temperature function space derivative based on Grünwald–Letnikov theory for τq > 0, τT > 0, 2 < αx < 2.5 (more details in [31]): | ⇓ |
| Layer | Material | |||
|---|---|---|---|---|
| 1 (wafer) | Silicon (Si) | 148 | 2330 | 712 |
| 2 (oxide) | Silicon dioxide (SiO2) | 1.38 | 2220 | 745 |
| 3 (heater) | Platinum (Pt) | 71.6 | 21,450 | 133 |
| 4 (thermometer) | Platinum (Pt) | 71.6 | 21,450 | 133 |
| 5 (ambient) | Air | 0.0263 * | 1.1614 | 1.007 |
| Temperature Distribution Simulation | MSE | RMSE | SSE | R2 | Corr |
|---|---|---|---|---|---|
| Heater | 8.5837∙10−4 | 0.0293 | 0.6034 | 0.9572 | 0.9973 |
| Thermometer | 9.5540∙10−5 | 0.0098 | 0.0472 | 0.9554 | 0.9748 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raszkowski, T.; Zubert, M. Investigation of Heat Diffusion at Nanoscale Based on Thermal Analysis of Real Test Structure. Energies 2020, 13, 2379. https://doi.org/10.3390/en13092379
Raszkowski T, Zubert M. Investigation of Heat Diffusion at Nanoscale Based on Thermal Analysis of Real Test Structure. Energies. 2020; 13(9):2379. https://doi.org/10.3390/en13092379
Chicago/Turabian StyleRaszkowski, Tomasz, and Mariusz Zubert. 2020. "Investigation of Heat Diffusion at Nanoscale Based on Thermal Analysis of Real Test Structure" Energies 13, no. 9: 2379. https://doi.org/10.3390/en13092379
APA StyleRaszkowski, T., & Zubert, M. (2020). Investigation of Heat Diffusion at Nanoscale Based on Thermal Analysis of Real Test Structure. Energies, 13(9), 2379. https://doi.org/10.3390/en13092379





