Power Prediction of Airborne Wind Energy Systems Using Multivariate Machine Learning
Abstract
1. Introduction
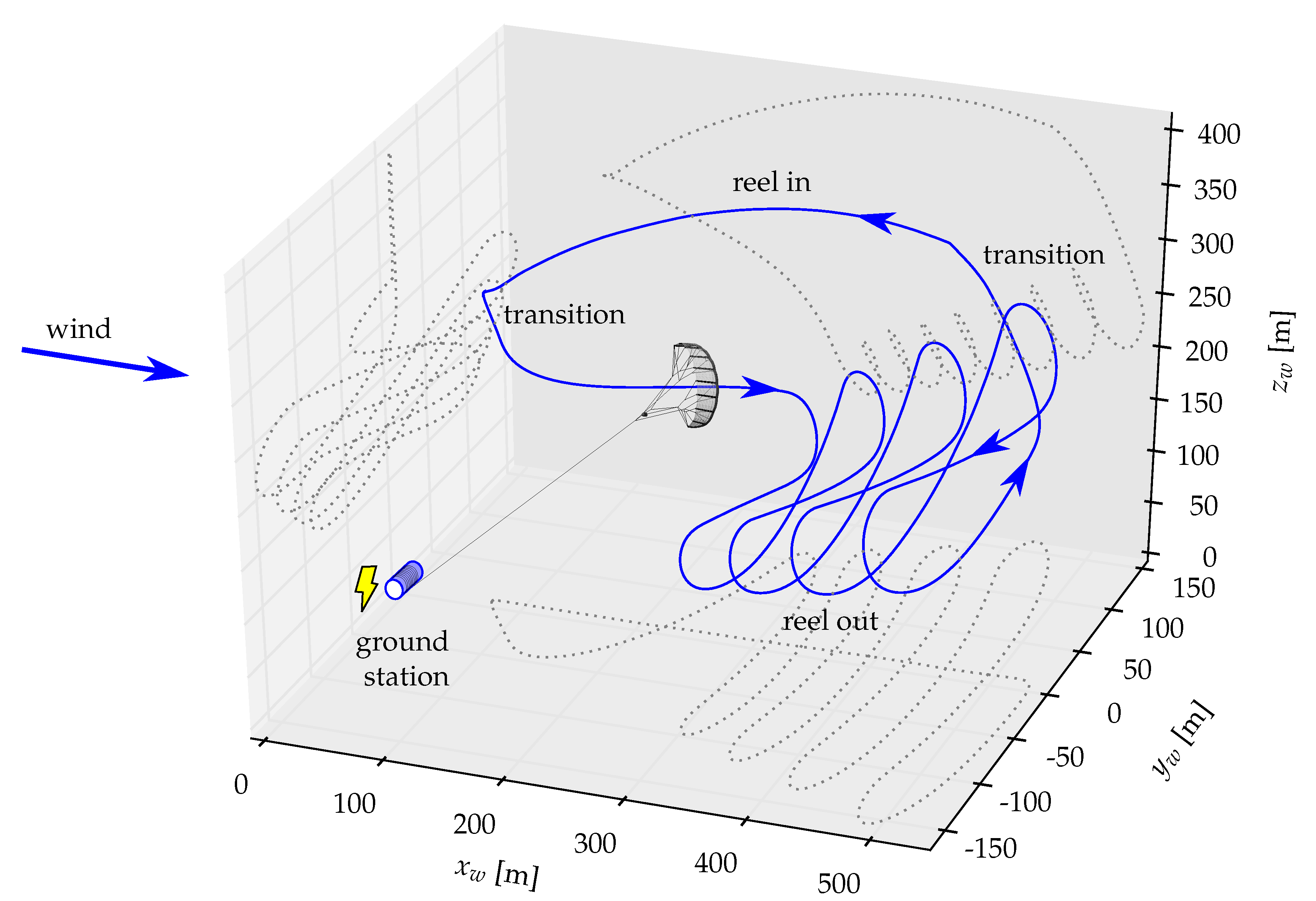
1.1. Airborne Wind Energy
1.2. Machine Learning Methods in AWE
1.3. Contribution and Organization
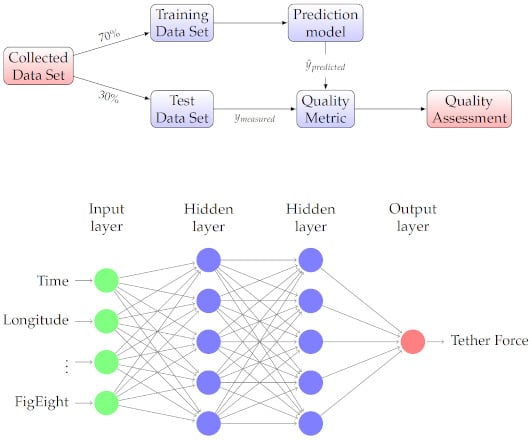
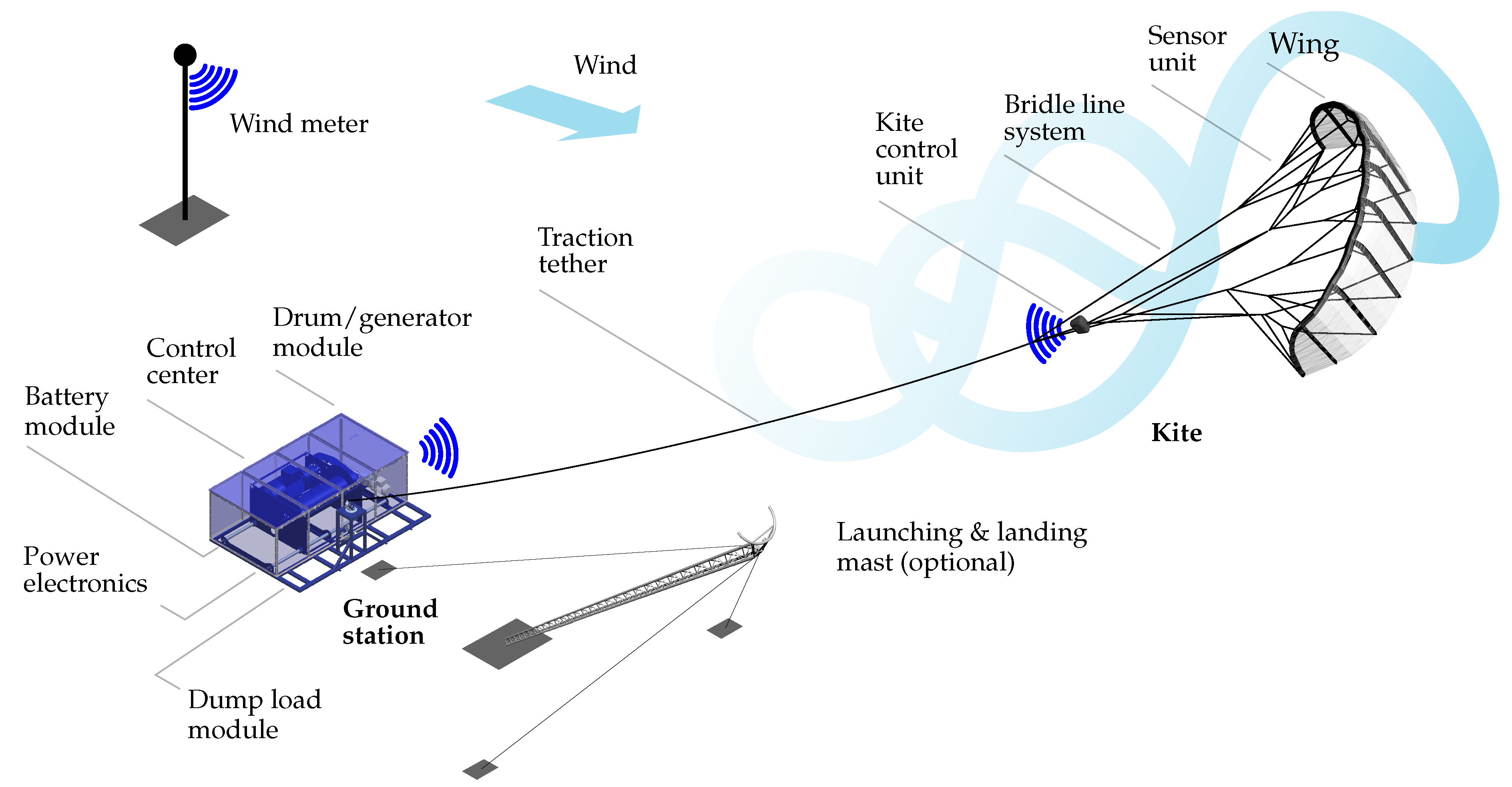
2. System Setup and Data Collection
2.1. System Components
2.2. Data Collection
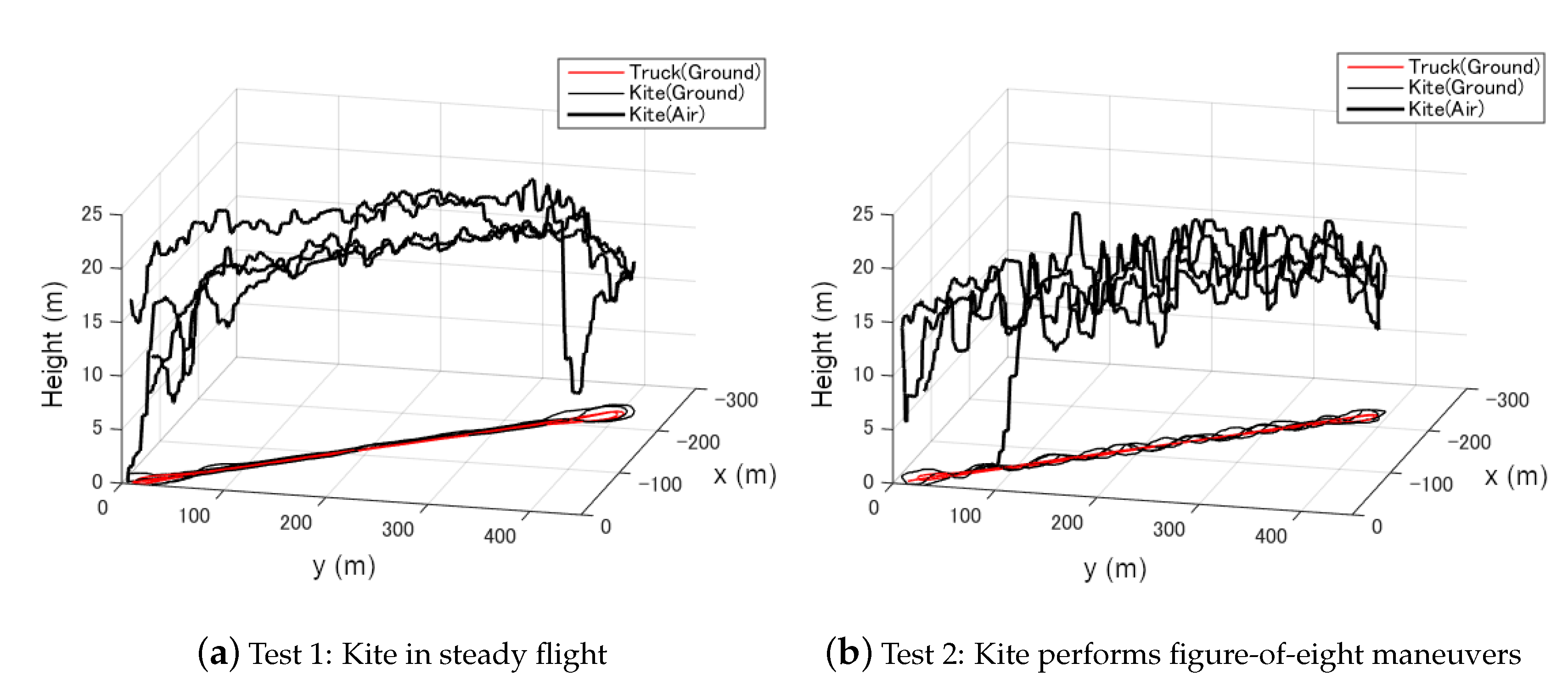
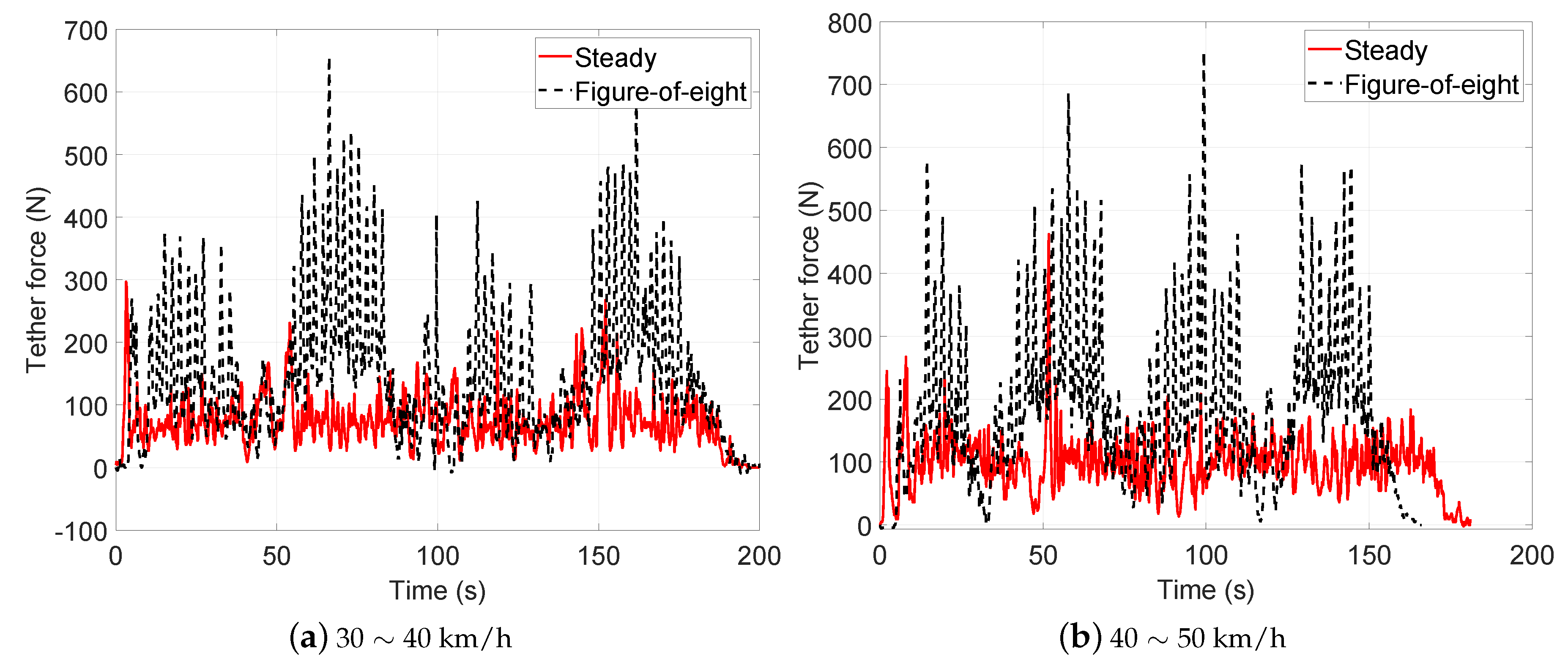
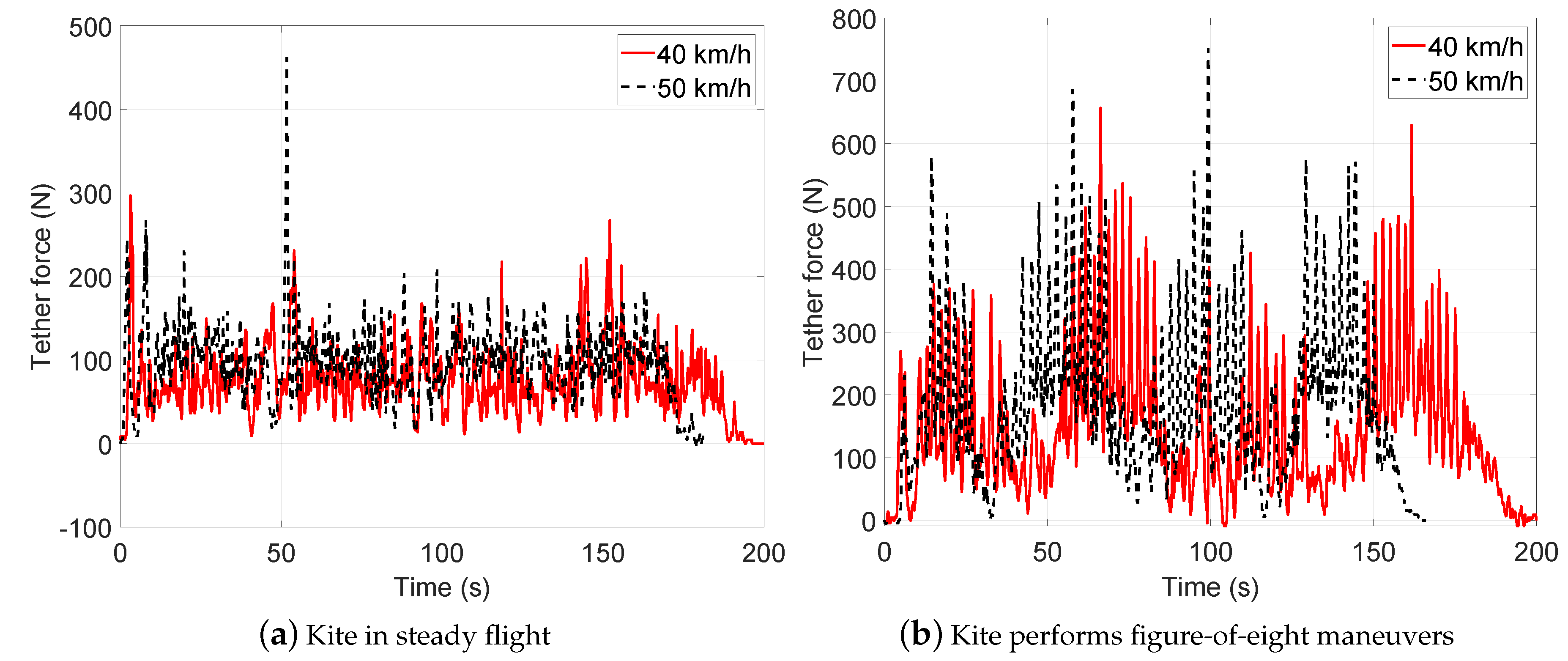
3. Design of Experiment (DOE)
- Test 1: Steady flight with towing speed 30∼40 km/h and CLL = 13.8 m
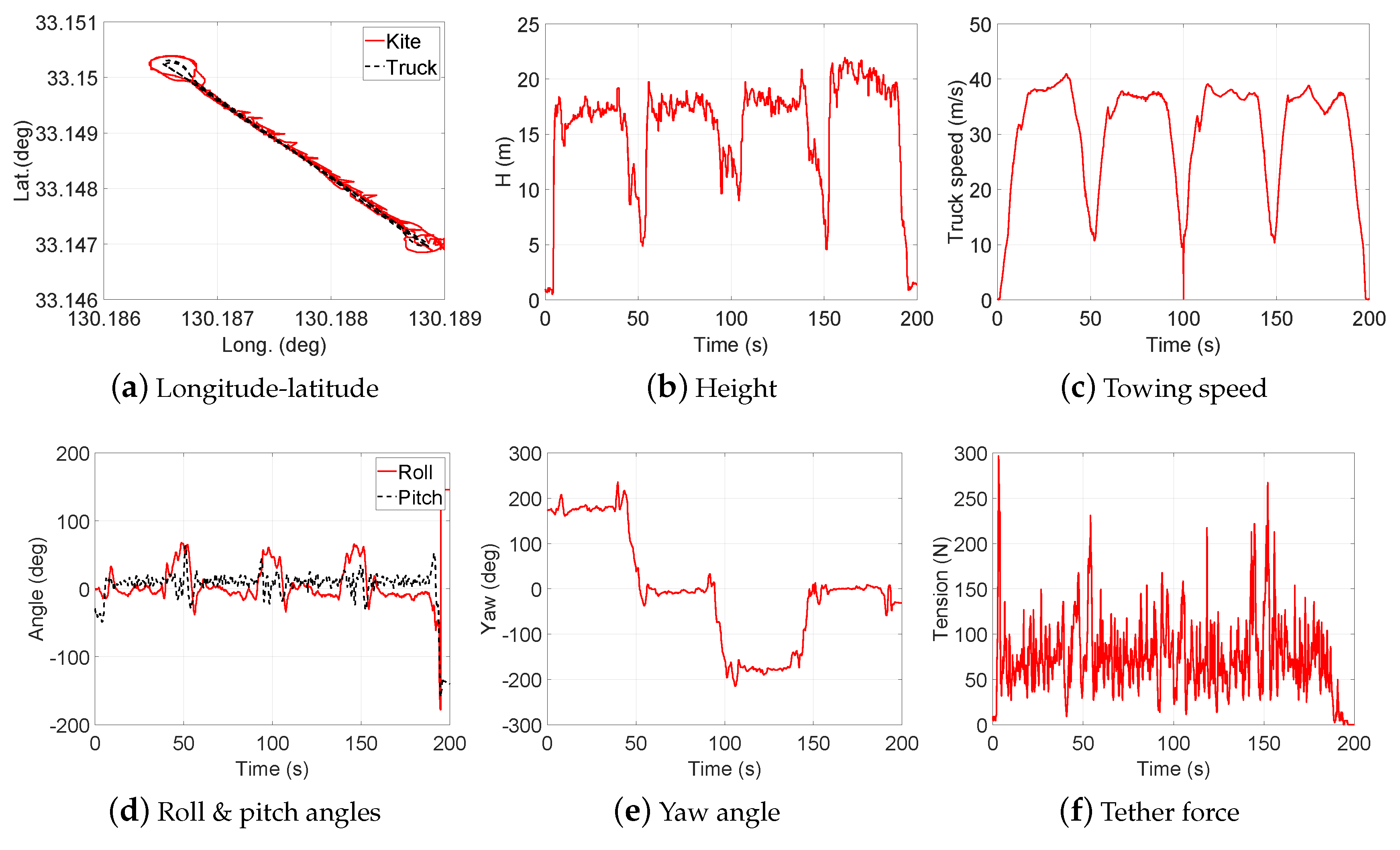
- Test 2: Figure-of-eight maneuvers with towing speed 30∼40 km/h and CLL = 13.8 m
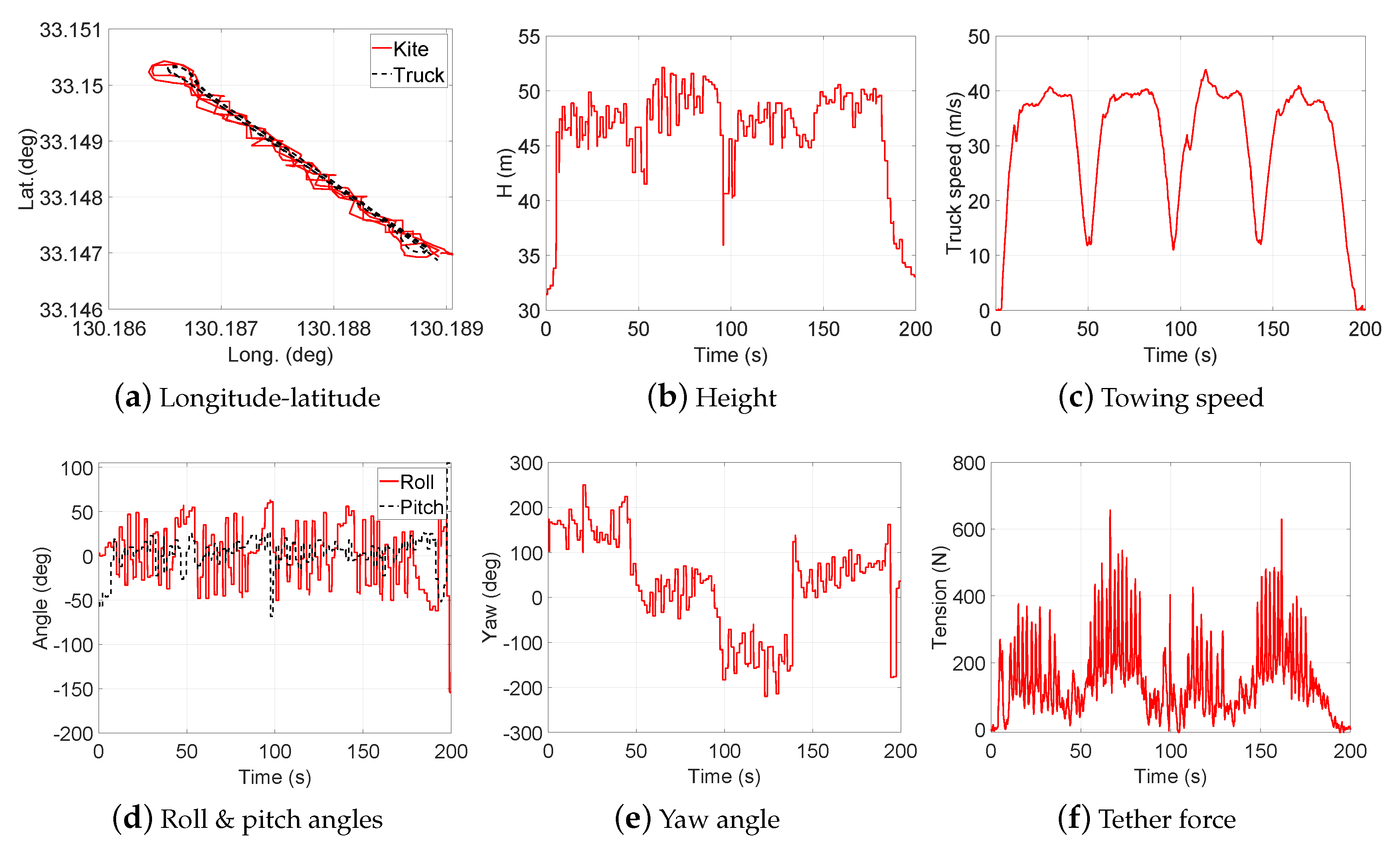
- Test 3: Steady flight with towing speed 40∼50 km/h and CLL = 13.8 m

- Test 4: Figure-of-eight maneuvers with towing speed 40∼50 km/h and CLL = 13.8 m
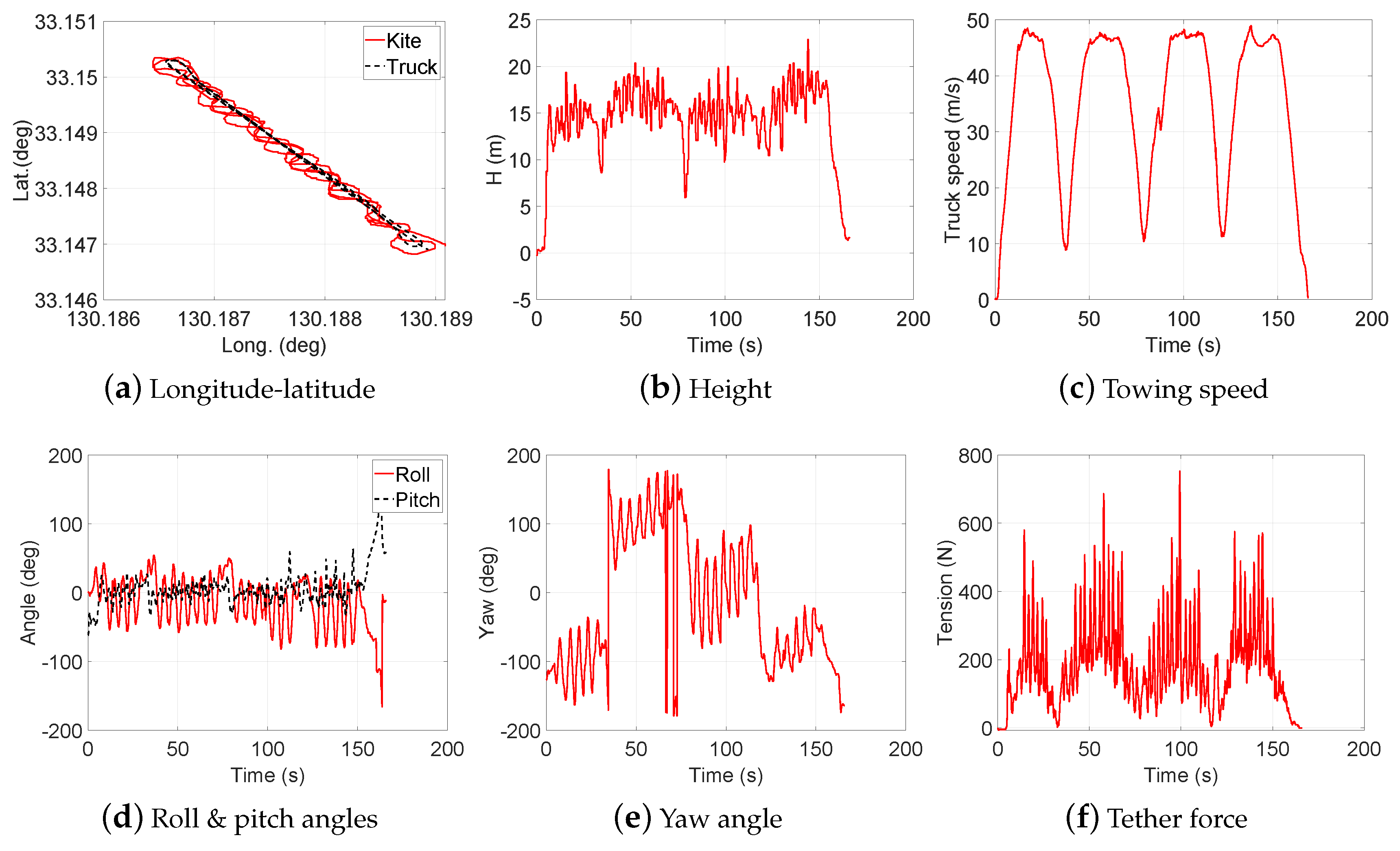
- Test 5: Steady flight with towing speed 30∼40 km/h and CLL = 13.6 m
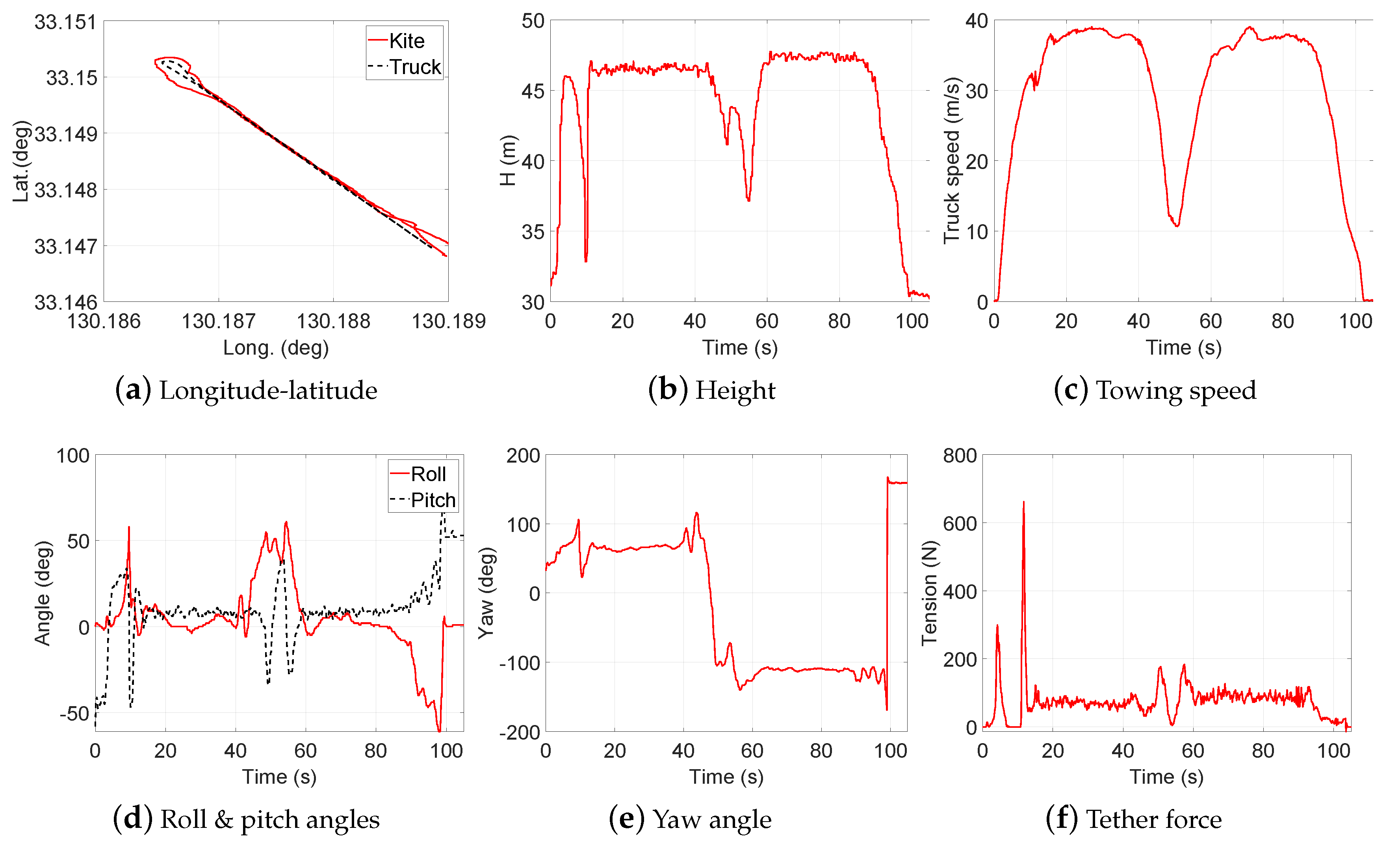
- Test 6: Steady flight with towing speed 30∼40 km/h and CLL = 13.4 m
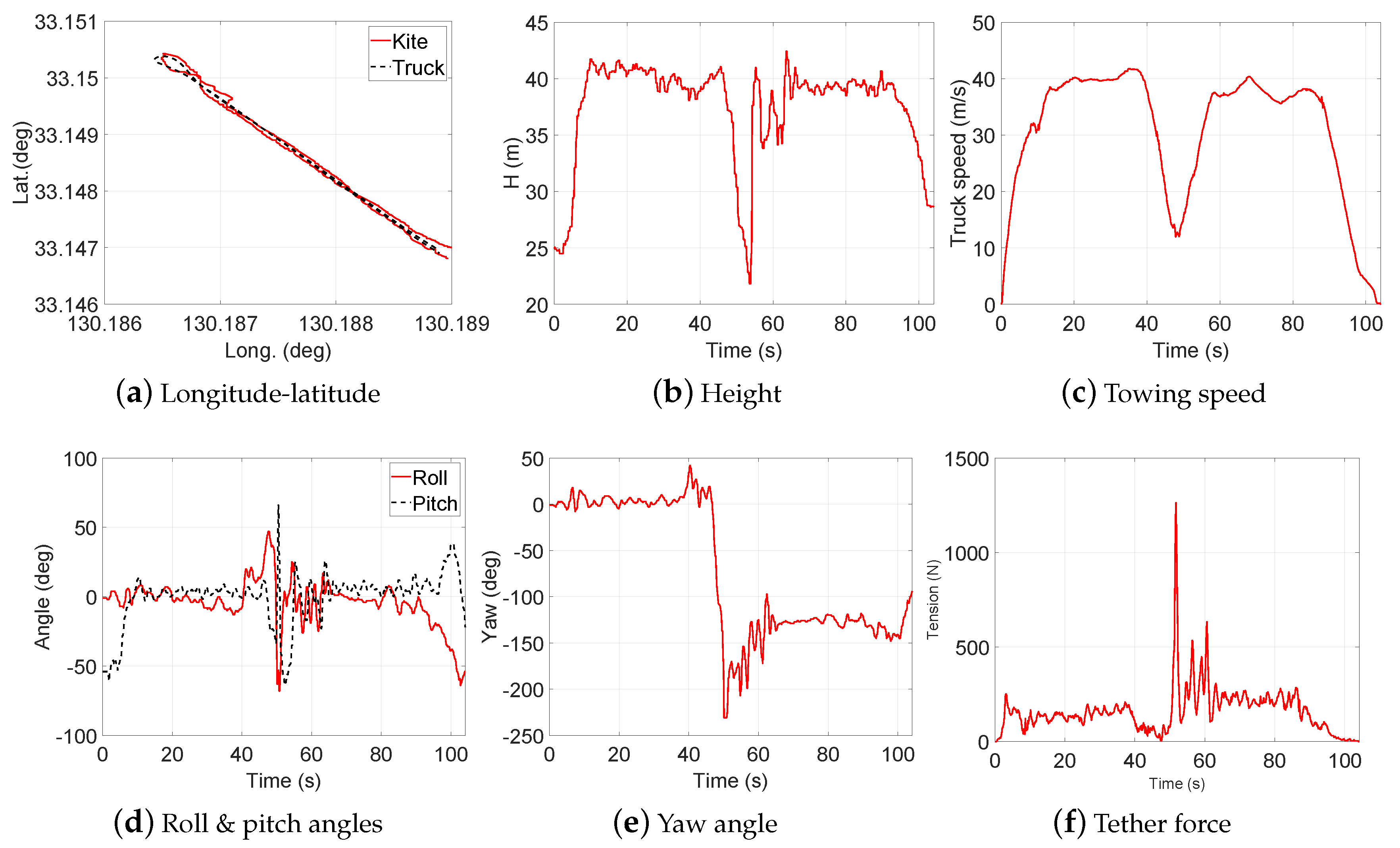
- Test 7: Steady flight with towing speed 40∼50 km/h and CLL = 13.6 m
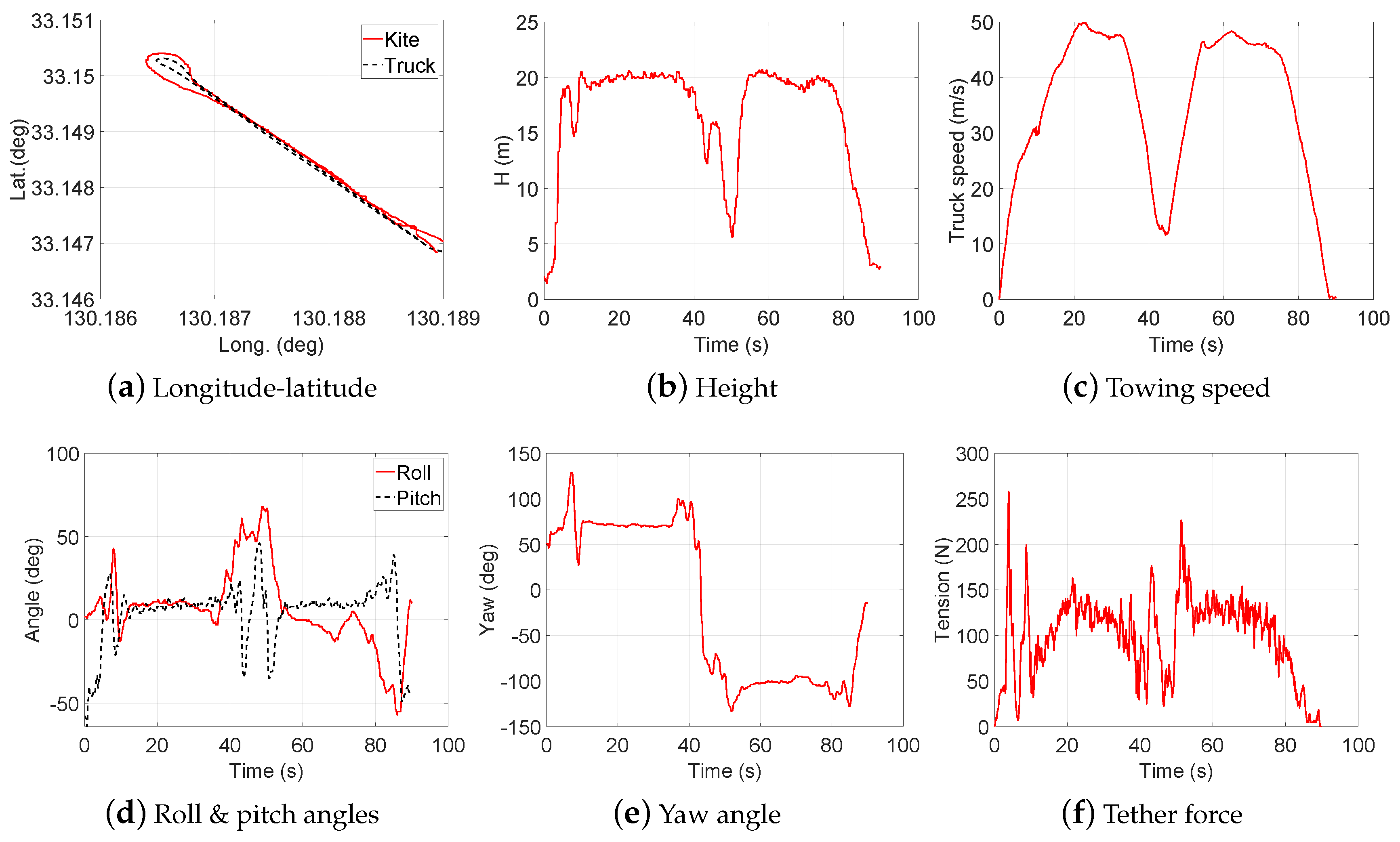
4. Data Analysis and Preprocessing
4.1. Handling Categorical Variables
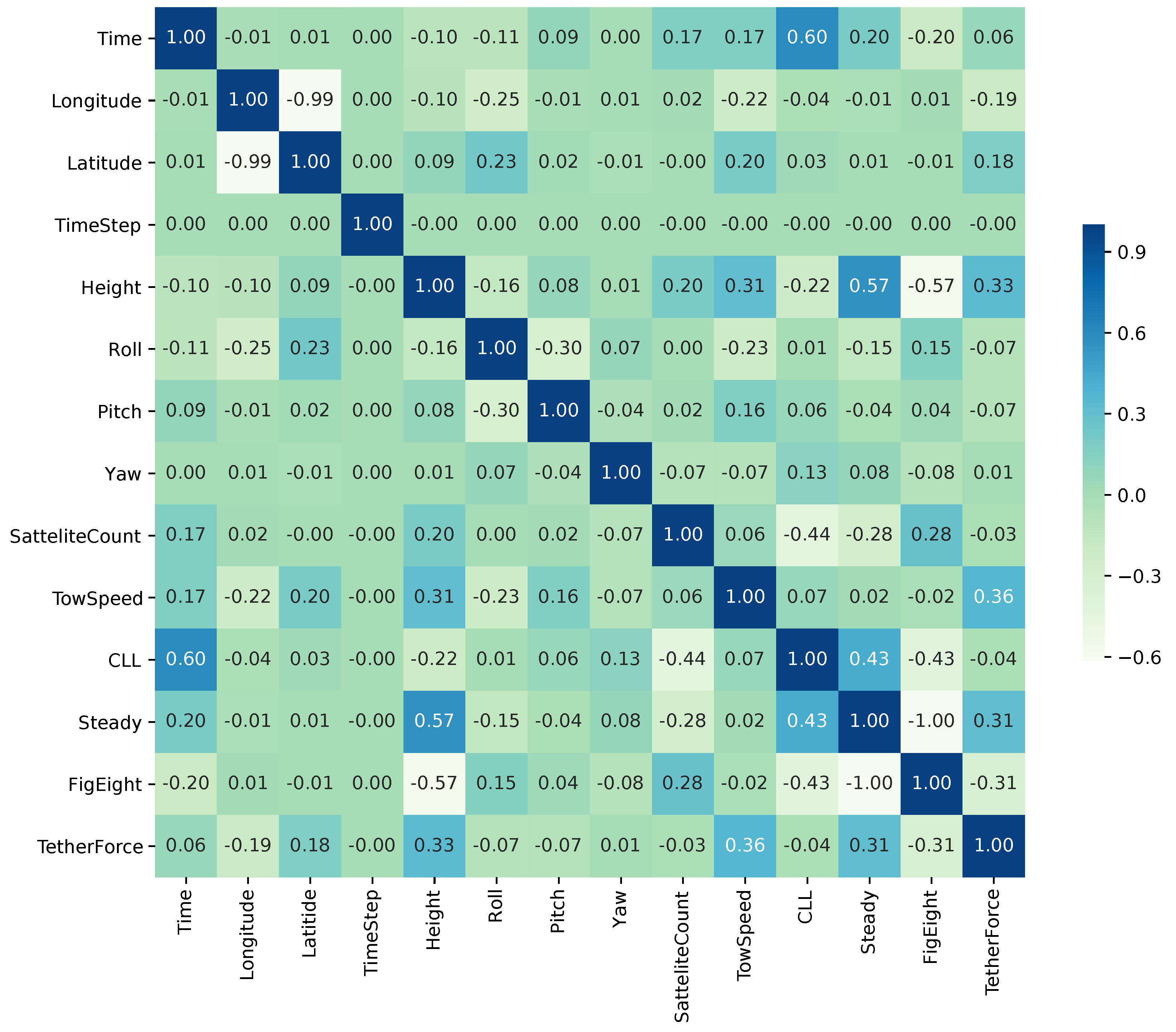
4.2. Global Sensitivity Analysis
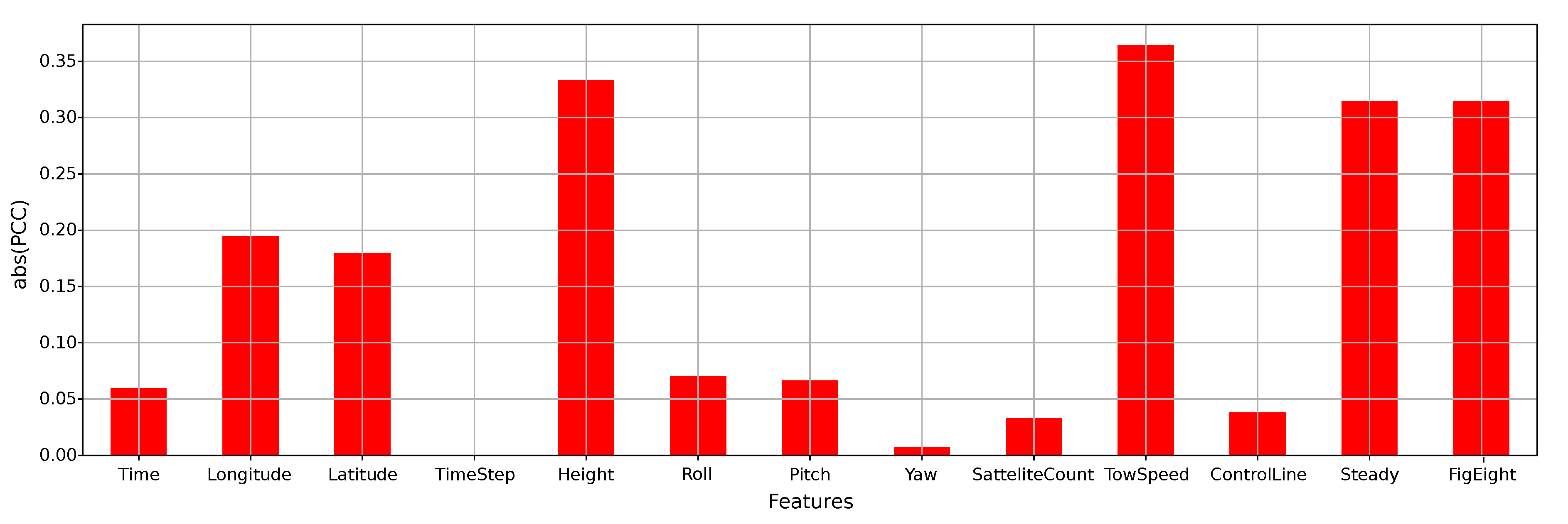
4.3. Feature Ranking and Selection
4.4. Model-Based Sensitivity Analysis
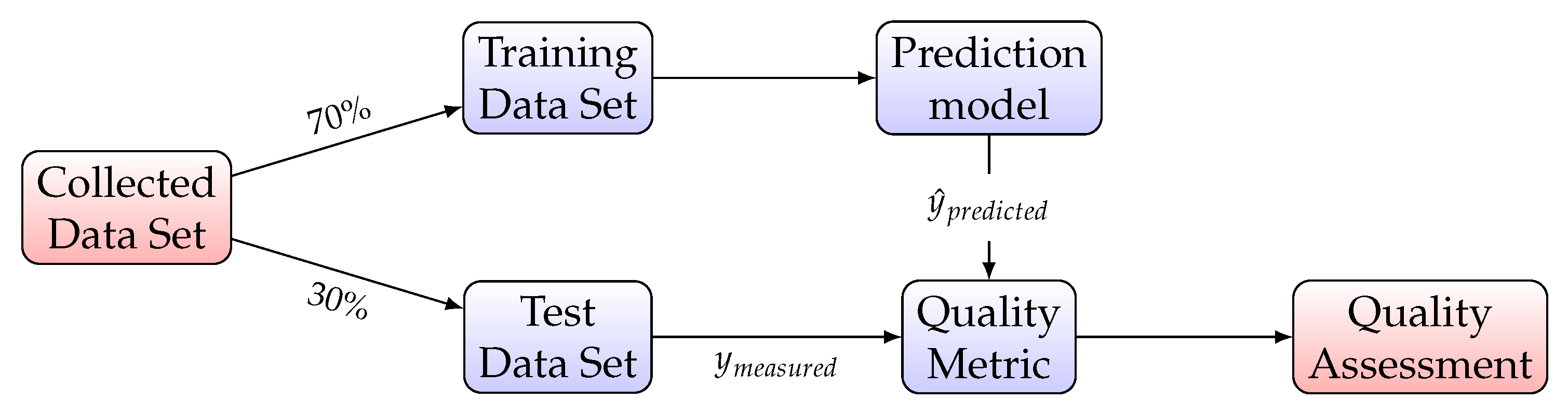
5. Regression Model Construction
5.1. Multivariate Regression
5.2. Quality Metrics
- Mean Square Error: expected value of the squared (quadratic) error
- Coefficient of Determination (): represents the proportion of variance (of y) that has been explained by the independent variables in the model, providing an indication of goodness of fit and therefore a measure of how well unseen samples are likely to be predicted by the model, through the proportion of explained variancewhere and . Best possible score is 1 and it can be negative, because the model can be arbitrarily worse. A constant model that always predicts the expected value of y, disregarding the input features, would get a score of 0.
- Maximum Residual Error: captures the worst case error between the predicted value and the true value. In a perfectly fitted single output regression model, it would be 0 on the training set. This metric shows the extent of error that the model had when it was fitted
- Explained Variance: best possible score is 1, lower values are worse.
- Mean Absolute Error: expected value of the absolute error loss or -norm loss
6. ML Experimental Results
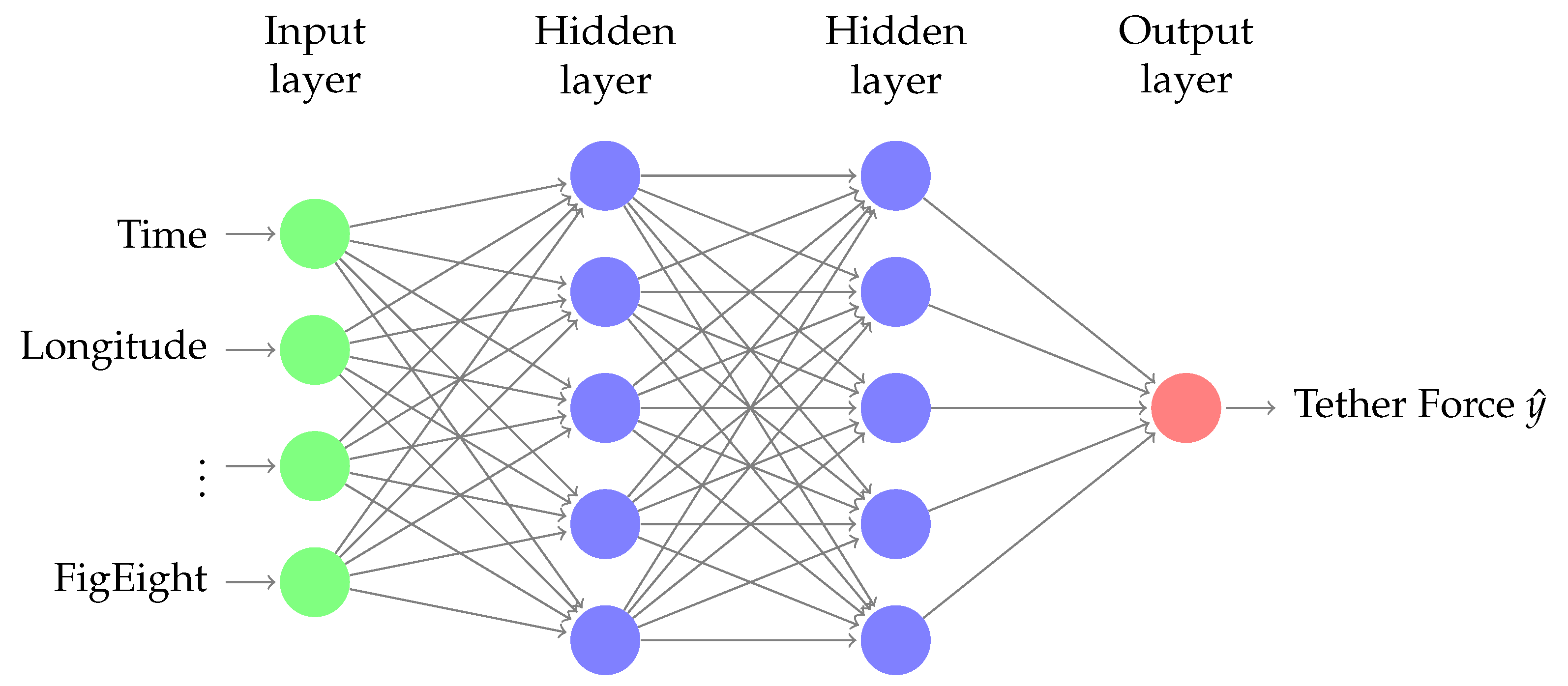
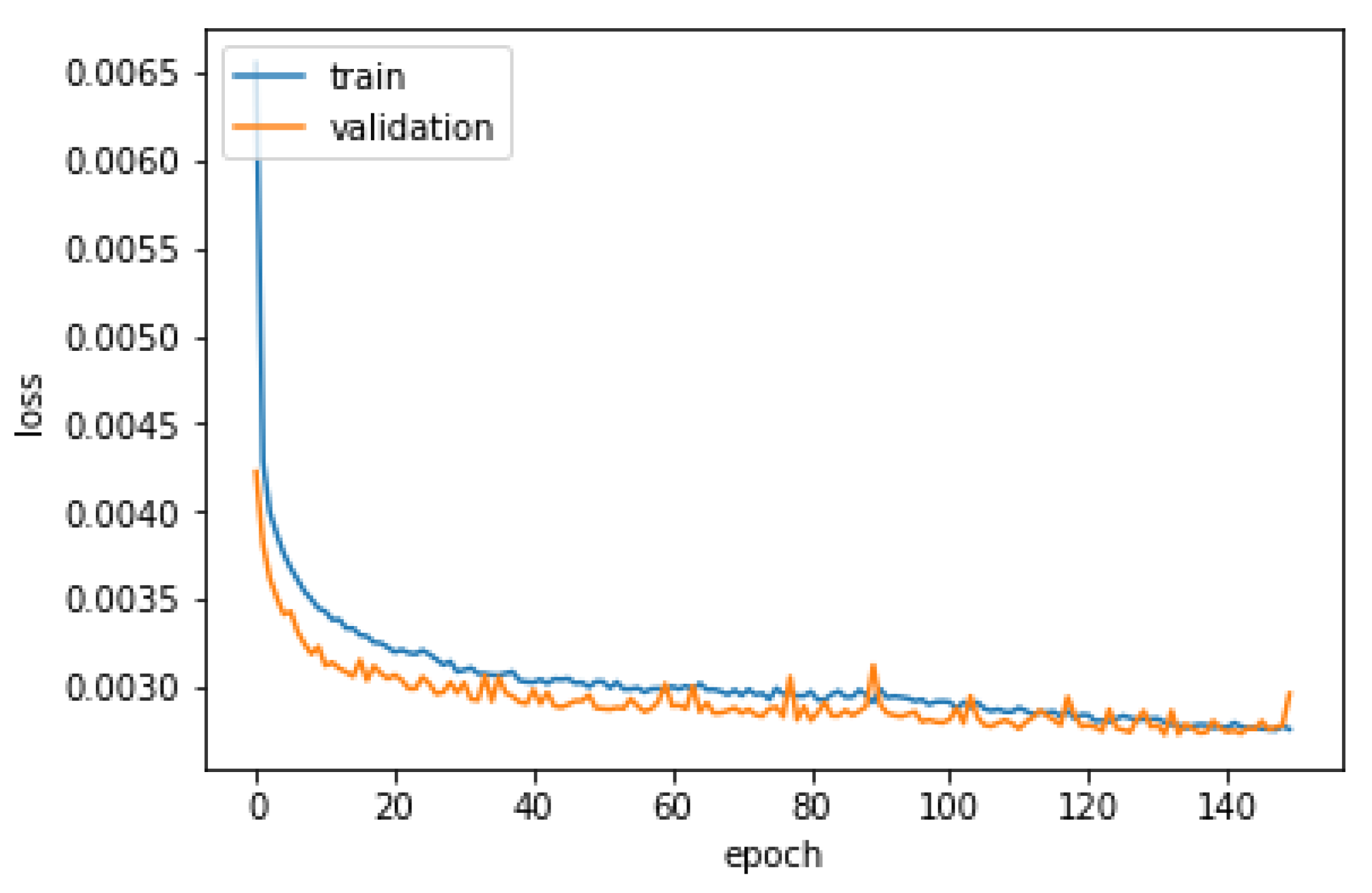
6.1. Neural Network Regression
6.2. Comparing Regression Models
7. Conclusions and Future Work
- Our sensitivity analysis results have validated our intuitive understanding of measurement ranking in impacting the predicted tether force, and hence the generated power.
- The performance of different ML algorithms was assessed, including neural networks, linear regression and ensemble methods, in terms of training time and different accuracy metrics. Different regression algorithms resulted in different performance scores, emphasizing the need for further studies around the training data set and hyperparameter tuning.
- Our preliminary investigations highlighted the potential of ML modeling methods in predicting tether force and traction power in AWE applications.
- the steering actuation of the KCU, either directly measured as a linear motion of the control lines, or derived from the rotation of the motor,
- the apparent wind speed at the kite,
- the angle of attack of the apparent wind velocity vector with the wing, and
- the side slip angle of the apparent wind velocity vector with the wing.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Availability
References
- Schmehl, R. (Ed.) Airborne Wind Energy: Advances in Technology Development and Research; Green Energy and Technology; Springer: Singapore, 2018. [Google Scholar]
- Ahrens, U.; Diehl, M.; Schmehl, R. (Eds.) Airborne Wind Energy; Green Energy and Technology; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Cherubini, A.; Papini, A.; Vertechy, R.; Fontana, M. Airborne Wind Energy Systems: A review of the technologies. Renew. Sustain. Energy Rev. 2015, 51, 1461–1476. [Google Scholar] [CrossRef]
- Mendonça, A.K.D.S.; Vaz, C.R.; Lezana, Á.G.R.; Anacleto, C.A.; Paladini, E.P. Comparing patent and scientific literature in airborne wind energy. Sustainability 2017, 9, 915. [Google Scholar] [CrossRef]
- Samson, J.; Katebi, R.; Vermillion, C. A critical assessment of airborne wind energy systems. In Proceedings of the 2nd IET Renewable Power Generation Conference, Beijing, China, 9–11 September 2013; pp. 4–7. [Google Scholar]
- Loyd, M.L. Crosswind kite power (for large-scale wind power production). J. Energy 1980, 4, 106–111. [Google Scholar] [CrossRef]
- Ockels, W.J. Laddermill, a novel concept to exploit the energy in the airspace. Aircr. Des. 2001, 4, 81–97. [Google Scholar] [CrossRef]
- Williams, P.; Lansdorp, B.; Ockesl, W. Optimal crosswind towing and power generation with tethered kites. J. Guid. Control Dyn. 2008, 31, 81–93. [Google Scholar] [CrossRef]
- Cherubini, A.; Vertechy, R.; Fontana, M. Simplified model of offshore airborne wind energy converters. Renew. Energy 2016, 88, 465–473. [Google Scholar] [CrossRef]
- AWESCO Network. Airborne Wind Energy—An Introduction to an Emerging Technology. Available online: http://www.awesco.eu/awe-explained (accessed on 14 February 2020).
- Fagiano, L.; Zgraggen, A.U.; Morari, M.; Khammash, M. Automatic crosswind flight of tethered wings for airborne wind energy: Modeling, control design, and experimental results. IEEE Trans. Control Syst. Technol. 2013, 22, 1433–1447. [Google Scholar]
- Van der Vlugt, R.; Peschel, J.; Schmehl, R. Design and Experimental Characterization of a Pumping Kite Power System. In Airborne Wind Energy; Ahrens, U., Diehl, M., Schmehl, R., Eds.; Green Energy and Technology; Springer: Berlin/Heidelberg, Germany, 2013; Chapter 23; pp. 403–425. [Google Scholar]
- Fechner, U. A Methodology for the Design of Kite-Power Control Systems. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2016. [Google Scholar]
- Bechtle, P.; Schelbergen, M.; Schmehl, R.; Zillmann, U.; Watson, S. Airborne Wind Energy Resource Analysis. Renew. Energy 2019, 141, 1103–1116. [Google Scholar] [CrossRef]
- Kitenergy S.r.l. Available online: http://www.kitenergy.net/ (accessed on 14 February 2020).
- KiteGen S.r.l. Available online: http://www.kitegen.com/en/ (accessed on 14 February 2020).
- Skysails Power GmbH. Available online: https://skysails-power.com/ (accessed on 14 February 2020).
- Kitepower B.V. Available online: https://kitepower.nl/ (accessed on 14 February 2020).
- Salma, V.; Friedl, F.; Schmehl, R. Reliability and Safety of Airborne Wind Energy Systems. Wind Energy 2019, 23, 340–356. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Baldi, P.; Brunak, S. Bioinformatics: The Machine Learning Approach, 2nd ed.; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Kourou, K.; Exarchos, T.P.; Exarchos, K.P.; Karamouzis, M.V.; Fotiadis, D.I. Machine learning applications in cancer prognosis and prediction. Comput. Struct. Biotechnol. J. 2015, 13, 8–17. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in PyTorch. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th {USENIX} Symposium on Operating Systems Design and Implementation ({OSDI} 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Rushdi, M.; Yoshida, S.; Dief, T.N. Simulation of a Tether of a Kite Power System Using a Lumped Mass Model. In Proceedings of the International Exchange and Innovation Conference on Engineering & Science (IECES), Fukuoka, Japan, 18–19 October 2018; pp. 42–47. [Google Scholar]
- Van der Vlugt, R.; Bley, A.; Schmehl, R.; Noom, M. Quasi-Steady Model of a Pumping Kite Power System. Renew. Energy 2019, 131, 83–99. [Google Scholar] [CrossRef]
- Dief, T.N.; Fechner, U.; Schmehl, R.; Yoshida, S.; Rushdi, M.A. Adaptive Flight Path Control of Airborne Wind Energy Systems. Energies 2020, 13, 667. [Google Scholar] [CrossRef]
- Rapp, S.; Schmehl, R.; Oland, E.; Haas, T. Cascaded Pumping Cycle Control for Rigid Wing Airborne Wind Energy Systems. J. Guid. Control Dyn. 2019, 42, 2456–2473. [Google Scholar] [CrossRef]
- Rushdi, M.; Hussein, A.; Dief, T.N.; Yoshida, S.; Schmehl, R. Simulation of the Transition Phase for an Optimally-Controlled Tethered VTOL Rigid Aircraft for Airborne Wind Energy Generation. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Licitra, G. Identification and Optimization of an Airborne Wind Energy System. Ph.D. Thesis, University of Freiburg, Breisgau, Germany, 2018. [Google Scholar]
- Diwale, S.S.; Lymperopoulos, I.; Jones, C.N. Optimization of an airborne wind energy system using constrained gaussian processes. In Proceedings of the 2014 IEEE Conference on Control Applications (CCA), Nice, France, 8–10 October 2014; pp. 1394–1399. [Google Scholar]
- Oehler, J.; Schmehl, R. Aerodynamic characterization of a soft kite by in situ flow measurement. Wind Energy Sci. 2019, 4, 1. [Google Scholar] [CrossRef]
- Baheri, A.; Vermillion, C. Altitude optimization of airborne wind energy systems: A Bayesian optimization approach. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 1365–1370. [Google Scholar]
- Wood, T.A.; Hesse, H.; Smith, R.S. Predictive control of autonomous kites in tow test experiments. IEEE Control Syst. Lett. 2017, 1, 110–115. [Google Scholar] [CrossRef]
- Licitra, G.; Bürger, A.; Williams, P.; Ruiterkamp, R.; Diehl, M. System Identification of a Rigid Wing Airborne Wind Energy System. arXiv 2017, arXiv:1711.10010. [Google Scholar]
- Licitra, G.; Koenemann, J.; Bürger, A.; Williams, P.; Ruiterkamp, R.; Diehl, M. Performance assessment of a rigid wing Airborne Wind Energy pumping system. Energy 2019, 173, 569–585. [Google Scholar] [CrossRef]
- Dief, T.N.; Fechner, U.; Schmehl, R.; Yoshida, S.; Ismaiel, A.M.; Halawa, A.M. System identification, fuzzy control and simulation of a kite power system with fixed tether length. Wind Energy Sci. 2018, 3, 275–291. [Google Scholar] [CrossRef]
- Dief, T.N.; Rushdi, M.; Halawa, A.; Yoshida, S. Hardware-in-the-Loop (HIL) and Experimental Findings for the 7 kW Pumping Kite Power System. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Clifton, A.; Kilcher, L.; Lundquist, J.; Fleming, P. Using machine learning to predict wind turbine power output. Environ. Res. Lett. 2013, 8, 024009. [Google Scholar] [CrossRef]
- Heinermann, J.; Kramer, O. Machine learning ensembles for wind power prediction. Renew. Energy 2016, 89, 671–679. [Google Scholar] [CrossRef]
- Treiber, N.A.; Heinermann, J.; Kramer, O. Wind power prediction with machine learning. In Computational Sustainability; Lässig, J., Kersting, K., Morik, K., Eds.; Springer: Cham, Switzerland, 2016; Volume 645, pp. 13–29. [Google Scholar]
- Ti, Z.; Deng, X.W.; Yang, H. Wake modeling of wind turbines using machine learning. Appl. Energy 2020, 257, 114025. [Google Scholar] [CrossRef]
- Breukels, J. An Engineering Methodology for Kite Design. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2011. [Google Scholar]
- Bosch, A.; Schmehl, R.; Tiso, P.; Rixen, D. Dynamic nonlinear aeroelastic model of a kite for power generation. J. Guid. Control Dyn. 2014, 37, 1426–1436. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Schmehl, R.; Noom, M.; van der Vlugt, R. Traction Power Generation with Tethered Wings. In Airborne Wind Energy; Green Energy and Technology; Ahrens, U., Diehl, M., Schmehl, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Chapter 2; pp. 23–45. [Google Scholar]
- Chollet, F. Keras: The Python Deep Learning Library. Available online: https://keras.io (accessed on 23 March 2020).
- Géron, A. Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems, 2nd ed.; O’Reilly Media: Sebastopol, CA, USA, 2019. [Google Scholar]





| Kite Position | Kite Orientation | Towing Speed (km/h) | Tether Force (N) (Output) | |||||
|---|---|---|---|---|---|---|---|---|
| Longitude () | Latitude () | Height (m) | Roll () | Pitch () | Yaw () | |||
| min | 130.186294 | 33.146762 | 38.500000 | −178.000000 | −159.000000 | −196.000000 | 0.000000 | 0.000000 |
| max | 130.189163 | 33.150520 | 90.880000 | 176.000000 | 129.000000 | 179.000000 | 50.661459 | 1263.870000 |
| mean | 130.187766 | 33.148546 | 73.816240 | 0.936829 | 5.592179 | −16.135081 | 32.737716 | 118.015877 |
| std | 0.000823 | 0.001138 | 12.354317 | 30.846308 | 22.635880 | 101.824154 | 12.295361 | 94.366362 |
| 25% | 130.186996 | 33.147449 | 66.250000 | −12.000000 | 1.000000 | −112.000000 | 26.057640 | 63.420000 |
| median | 130.187774 | 33.148536 | 77.750000 | 0.000000 | 8.000000 | −2.000000 | 36.877950 | 97.395000 |
| 75% | 130.188507 | 33.149593 | 84.440000 | 13.000000 | 14.000000 | 67.000000 | 40.105059 | 147.225000 |
| Test No. | Towing Speed (km/h) | Flight Mode | CLL (m) |
|---|---|---|---|
| 1 | 30∼40 | Steady flight | 13.8 |
| 2 | 30∼40 | Figure-of-eight maneuvers | 13.8 |
| 3 | 40∼50 | Steady flight | 13.8 |
| 4 | 40∼50 | Figure-of-eight maneuvers | 13.8 |
| 5 | 30∼40 | Steady flight | 13.6 |
| 6 | 30∼40 | Steady flight | 13.4 |
| 7 | 40∼50 | Steady flight | 13.6 |
| TetherForce | TowSpeed | Height | Steady | FigEight | |
|---|---|---|---|---|---|
| TetherForce | 1.000000 | 0.364342 | 0.333041 | 0.314789 | −0.314789 |
| TowSpeed | 0.364342 | 1.000000 | 0.308207 | 0.017213 | −0.017213 |
| Height | 0.333041 | 0.308207 | 1.000000 | 0.568476 | −0.568476 |
| Steady | 0.314789 | 0.017213 | 0.568476 | 1.000000 | −1.000000 |
| FigEight | −0.314789 | −0.017213 | −0.568476 | −1.000000 | 1.000000 |
| Layer (Type) | Output Shape | Param # |
|---|---|---|
| Dense_9 (Dense) | (None, 12) | 168 |
| Dense_10 (Dense) | (None, 8) | 104 |
| Dense_11 (Dense) | (None, 1) | 9 |
| Model | MSE | Coef. of Det. | Max_Error | Exp_Var | MAE | Train_Time |
|---|---|---|---|---|---|---|
| Voting Regressor | 2733.279160 | 0.678340 | 573.467337 | 0.678418 | 32.411861 | 0.43750 |
| Neural Network | 3623.617703 | 0.573562 | 553.713162 | 0.591568 | 39.140221 | 22.03125 |
| Gradient Boosting | 3890.056241 | 0.542207 | 791.537785 | 0.542208 | 37.028307 | 0.46875 |
| Decision Tree Regressor | 4206.607833 | 0.504954 | 1005.660000 | 0.504978 | 30.291717 | 0.06250 |
| Nonlinear Regression | 4709.975147 | 0.445717 | 671.062801 | 0.445805 | 43.167692 | 0.03125 |
| linear Regression | 5487.650725 | 0.354197 | 702.994674 | 0.354205 | 49.385283 | 0.00000 |
| Ridge Regression | 5552.731547 | 0.346539 | 729.976413 | 0.346563 | 49.595747 | 0.00000 |
| Lasso Regression | 5557.930973 | 0.345927 | 731.646629 | 0.345952 | 49.619318 | 0.00000 |
| Elastic Net Regression | 6154.191023 | 0.275757 | 784.324714 | 0.275797 | 52.908989 | 0.00000 |
| Adaptive Boosting | 7211.143207 | 0.151372 | 496.412500 | 0.260536 | 62.991571 | 0.15625 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rushdi, M.A.; Rushdi, A.A.; Dief, T.N.; Halawa, A.M.; Yoshida, S.; Schmehl, R. Power Prediction of Airborne Wind Energy Systems Using Multivariate Machine Learning. Energies 2020, 13, 2367. https://doi.org/10.3390/en13092367
Rushdi MA, Rushdi AA, Dief TN, Halawa AM, Yoshida S, Schmehl R. Power Prediction of Airborne Wind Energy Systems Using Multivariate Machine Learning. Energies. 2020; 13(9):2367. https://doi.org/10.3390/en13092367
Chicago/Turabian StyleRushdi, Mostafa A., Ahmad A. Rushdi, Tarek N. Dief, Amr M. Halawa, Shigeo Yoshida, and Roland Schmehl. 2020. "Power Prediction of Airborne Wind Energy Systems Using Multivariate Machine Learning" Energies 13, no. 9: 2367. https://doi.org/10.3390/en13092367
APA StyleRushdi, M. A., Rushdi, A. A., Dief, T. N., Halawa, A. M., Yoshida, S., & Schmehl, R. (2020). Power Prediction of Airborne Wind Energy Systems Using Multivariate Machine Learning. Energies, 13(9), 2367. https://doi.org/10.3390/en13092367