Finite-Element Simulation for Thermal Modeling of a Cell in an Adiabatic Calorimeter
Abstract
1. Introduction
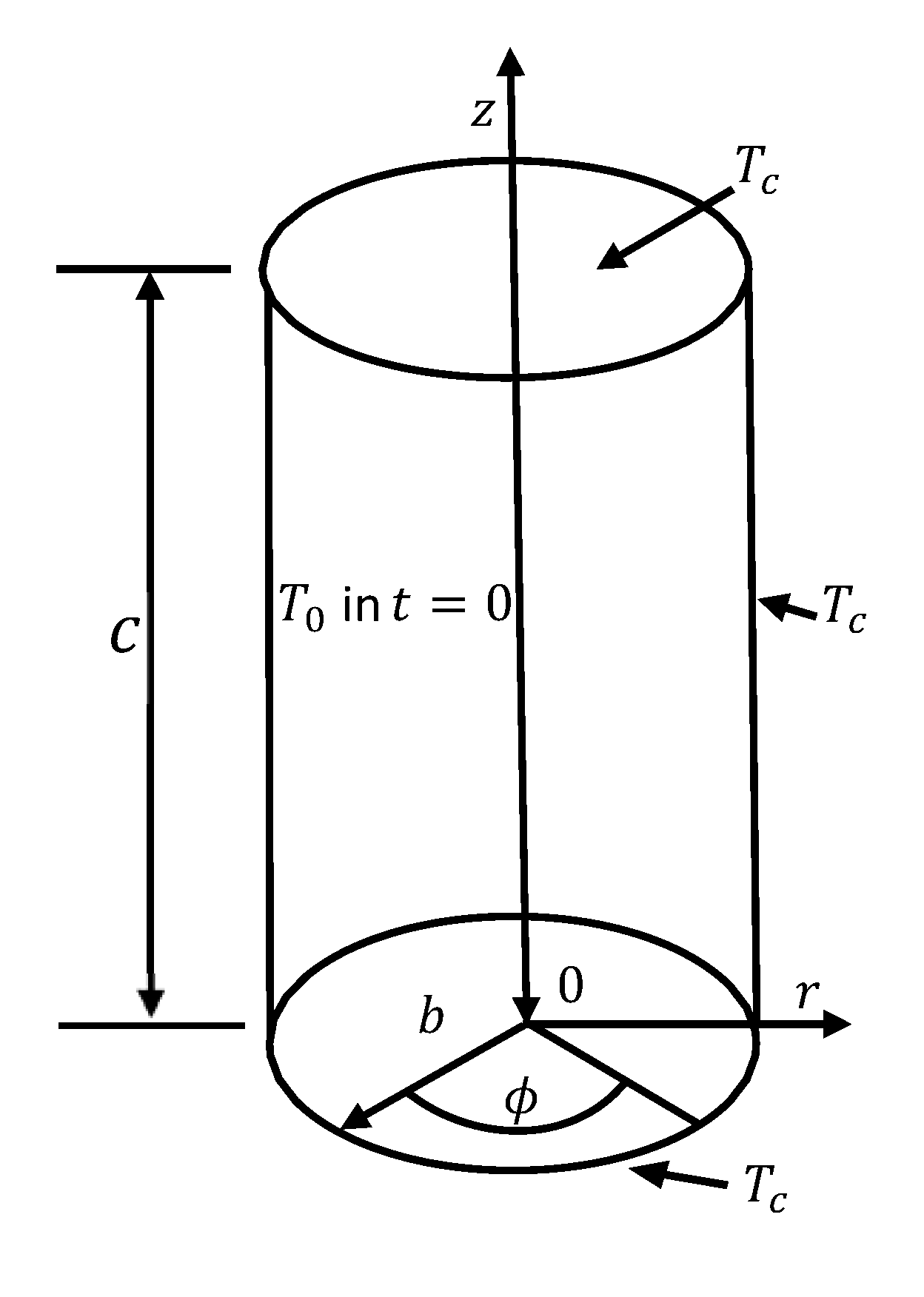
2. Theoretical Analysis
Mathematical Formulation
3. Numerical Solution
Model to Compare the Analytical Solution
4. Analysis Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Q | Amount of heat |
| m | Mass |
| Temperature variation | |
| I | Current |
| V | Voltage |
| t | Time |
| °C | Celsius grade |
| Thermal diffusivity | |
| k | Thermal conductivity |
| Density | |
| Heat capacity | |
| b | Constant in radial coordinates |
| c | Constant in z coordinates |
| Temperature constant | |
| Represent a change of variable for T | |
| Initially temperature | |
| Bessel functions of order | |
| Eigenfunction | |
| Bessel functions of order | |
| Solution for Bessel functions of order | |
| Eigenvalue evaluated in radius b | |
| Summation of eigenvalue evaluated in radius b | |
| Eigenfunction for z coordinate | |
| Summation of eigenvalue evaluated in height | |
| C | Normal function |
| Bessel functions evaluated in 0 | |
| CENAM | Centro Nacional de Metrologia |
References
- Hoseinzadeh, S.; Heyns, P.S.; Kariman, H. Numerical investigation of heat transfer of laminar and turbulent pulsating Al2O3/water nanofluid flow. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 1149–1166. [Google Scholar] [CrossRef]
- Sarafraz, M.; Safaei, M.R. Diurnal thermal evaluation of an evacuated tube solar collector (ETSC) charged with graphene nanoplatelets-methanol nano-suspension. Renew. Energy 2019, 142, 364–372. [Google Scholar] [CrossRef]
- Tan, Z.C.; Shi, Q.; Liu, B.P.; Zhang, H.T. A fully automated adiabatic calorimeter for heat capacity measurement between 80 and 400 K. J. Therm. Anal. Calorim. 2008, 92, 367–374. [Google Scholar] [CrossRef]
- Lang, B.E.; Boerio-Goates, J.; Woodfield, B.F. Design and construction of an adiabatic calorimeter for samples of less than 1 cm3 in the temperature range T = 15 K to T = 350 K. J. Chem. Thermodyn. 2006, 38, 1655–1663. [Google Scholar] [CrossRef]
- Kobashi, K.; Kyômen, T.; Oguni, M. Construction of an adiabatic calorimeter in the temperature range between 13 and 505 K, and thermodynamic study of 1-chloroadamantane. J. Phys. Chem. Solids 1998, 59, 667–677. [Google Scholar] [CrossRef]
- Sorai, M.; Kaji, K.; Kaneko, Y. An automated adiabatic calorimeter for the temperature range 13 K to 530 K The heat capacities of benzoic acid from 15 K to 305 K and of synthetic sapphire from 60 K to 505 K. J. Chem. Thermodyn. 1992, 24, 167–180. [Google Scholar] [CrossRef]
- Tan, Z.C.; Shi, Q.; Liu, X. Construction of High-Precision Adiabatic Calorimeter and Thermodynamic Study on Functional Materials. In Calorimetry: Design, Theory and Applications in Porous Solids; IntechOpen: Rijeka, Croatia, 2018; p. 1. [Google Scholar] [CrossRef]
- Matsuo, T.; Suga, H. Adiabatic microcalorimeters for heat capacity measurement at low temperature. Thermochim. Acta 1985, 88, 149–158. [Google Scholar] [CrossRef]
- Magee, J.W.; Deal, R.J.; Blanco, J.C. High-temperature adiabatic calorimeter for constant-volume heat capacity measurements of compressed gases and liquids. J. Res. Natl. Inst. Stand. Technol. 1998, 103, 63. [Google Scholar] [CrossRef]
- Sun, M.T.; Chang, C.H. The error analysis of a steady-state thermal conductivity measurement method with single constant temperature region. J. Heat Transf. 2007. [Google Scholar] [CrossRef]
- Yari, A.; Hosseinzadeh, S.; Galogahi, M. Two-dimensional numerical simulation of the combined heat transfer in channel flow. Int. J. Recent Adv. Mech. Eng. 2014, 3, 55–67. [Google Scholar] [CrossRef]
- Kaur, G.; Singh, M.; Kumar, J.; De Beer, T.; Nopens, I. Mathematical Modelling and Simulation of a Spray Fluidized Bed Granulator. Processes 2018, 6, 195. [Google Scholar] [CrossRef]
- Al-Najem, N.; Özişik, M. On the solution of three-dimensional inverse heat conduction in finite media. Int. J. Heat Mass Transf. 1985, 28, 2121–2128. [Google Scholar] [CrossRef]
- Renaud, J.; Rossomme, S.; Sarfehnia, A.; Vynckier, S.; Palmans, H.; Kacperek, A.; Seuntjens, J. Development and application of a water calorimeter for the absolute dosimetry of short-range particle beams. Phys. Med. Biol. 2016, 61, 6602–6619. [Google Scholar] [CrossRef] [PubMed]
- Amoabeng, K.O.; Lee, K.H.; Choi, J.M. Modeling and Simulation Performance Evaluation of a Proposed Calorimeter for Testing a Heat Pump System. Energies 2019, 12, 4589. [Google Scholar] [CrossRef]
- Karvinen, H.; Hasani Aleni, A.; Salminen, P.; Minav, T.; Vilaça, P. Thermal Efficiency and Material Properties of Friction Stir Channelling Applied to Aluminium Alloy AA5083. Energies 2019, 12, 1549. [Google Scholar] [CrossRef]
- Mohammed, H.A.; Narrein, K. Thermal and hydraulic characteristics of nanofluid flow in a helically coiled tube heat exchanger. Int. Commun. Heat Mass Transf. 2012. [Google Scholar] [CrossRef]
- Pitarch, J.L.; Sala, A.; de Prada, C. A Systematic Grey-Box Modeling Methodology via Data Reconciliation and SOS Constrained Regression. Processes 2019, 7, 170. [Google Scholar] [CrossRef]
- Moreno-Piraján, J.C.; Giraldo, L. Isoperibolic Titration Calorimetry as a Tool for the Prediction of Thermodynamic Properties of Cyclodextrins. Energies 2008, 1, 93–104. [Google Scholar] [CrossRef]
- Özisik, N.; Bayazitoglu, Y.A. Elements of Heat Transfer; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Zhi-Cheng, T.; Jinchun, Y.; Yi, S.; Shuxia, C.; Lixing, Z. An adiabatic calorimeter for heat capacity measurements in the temperature range 300–600 K and pressure range 0.1–15 MPa. Thermochim. Acta 1991, 183, 29–38. [Google Scholar] [CrossRef]
- Zhong, Q.; Dong, X.; Zhao, Y.; Wang, J.; Zhang, H.; Li, H.; Guo, H.; Shen, J.; Gong, M. Adiabatic calorimeter for isochoric specific heat capacity measurements and experimental data of compressed liquid R1234yf. J. Chem. Thermodyn. 2018, 125, 86–92. [Google Scholar] [CrossRef]
- Gadalla, M.; Ghommem, M.; Bourantas, G.; Miller, K. Modeling and Thermal Analysis of a Moving Spacecraft Subject to Solar Radiation Effect. Processes 2019, 7, 807. [Google Scholar] [CrossRef]
- Zhu, H.; Sun, B.; Jiang, J.; Xu, W. Measurement of hazardous reactions under extreme conditions with a house-built high-performance adiabatic calorimeter. J. Therm. Anal. Calorim. 2020. [Google Scholar] [CrossRef]
- Kossoy, A. An in-depth analysis of some methodical aspects of applying pseudo-adiabatic calorimetry. Thermochim. Acta 2020, 683. [Google Scholar] [CrossRef]
- Choi, Y.; Jeon, K.; Park, Y.; Hyun, S. Numerical simulation of heat-loss compensated calorimeter. Int. J. Comput. Methods Exp. Meas. 2019, 7, 285–296. [Google Scholar] [CrossRef]
- Ding, J.; Yu, L.; Wang, J.; Xu, Q.; Yang, S.; Ye, S. A symmetric dual-channel accelerating rate calorimeter with the varying thermal inertia consideration. Thermochim. Acta 2019, 678. [Google Scholar] [CrossRef]
- Ivsic, B.; Dadic, M.; Malaric, R.; Martinovic, Z. Thermal considerations on adiabatic coaxial line for microcalorimeter measurements. In Proceedings of the 2019 2nd International Colloquium on Smart Grid Metrology (SMAGRIMET), Split, Croatia, 9–12 April 2019. [Google Scholar] [CrossRef]
- Sarafraz, M.; Arya, A.; Nikkhah, V.; Hormozi, F. Thermal performance and viscosity of biologically produced silver/coconut oil nanofluids. Chem. Biochem. Eng. Q. 2016, 30, 489–500. [Google Scholar] [CrossRef]
- Sarafraz, M.M.; Tlili, I.; Tian, Z.; Bakouri, M.; Safaei, M.R.; Goodarzi, M. Thermal Evaluation of Graphene Nanoplatelets Nanofluid in a Fast-Responding HP with the Potential Use in Solar Systems in Smart Cities. Appl. Sci. 2019, 9, 2101. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Durán, J.E.E.; Rodríguez-Reséndiz, J.; Ramirez, J.M.O.; Zamora-Antuñano, M.A.; Lira-Cortes, L. Finite-Element Simulation for Thermal Modeling of a Cell in an Adiabatic Calorimeter. Energies 2020, 13, 2300. https://doi.org/10.3390/en13092300
González-Durán JEE, Rodríguez-Reséndiz J, Ramirez JMO, Zamora-Antuñano MA, Lira-Cortes L. Finite-Element Simulation for Thermal Modeling of a Cell in an Adiabatic Calorimeter. Energies. 2020; 13(9):2300. https://doi.org/10.3390/en13092300
Chicago/Turabian StyleGonzález-Durán, José Eli Eduardo, Juvenal Rodríguez-Reséndiz, Juan Manuel Olivares Ramirez, Marco Antonio Zamora-Antuñano, and Leonel Lira-Cortes. 2020. "Finite-Element Simulation for Thermal Modeling of a Cell in an Adiabatic Calorimeter" Energies 13, no. 9: 2300. https://doi.org/10.3390/en13092300
APA StyleGonzález-Durán, J. E. E., Rodríguez-Reséndiz, J., Ramirez, J. M. O., Zamora-Antuñano, M. A., & Lira-Cortes, L. (2020). Finite-Element Simulation for Thermal Modeling of a Cell in an Adiabatic Calorimeter. Energies, 13(9), 2300. https://doi.org/10.3390/en13092300






