A Novel Accurate and Fast Converging Deep Learning-Based Model for Electrical Energy Consumption Forecasting in a Smart Grid †
Abstract
1. Introduction
- A novel hybrid FS-FCRBM-GWDO forecast model is proposed that integrates the merits of individual techniques to enhance both metrics: (i) accuracy (MAPD, variance, and correlation), and (ii) convergence rate. The proposed model is capable of mapping the input space to the feature space to learn the stochastic and complex patterns of electrical energy consumption.
- The proposed FS-FCRBM-GWDO model considers both the exogenous influencing parameters and the historical electrical energy consumption pattern.
- A novel concept of feature interaction is developed in addition to relevancy and redundancy filters of feature selection techniques to make the feature selection process more effective.
- The ReLU and multivariate autoregressive algorithms are integrated with FCRBM to improve both accuracy and convergence rate, which are not present in the existing models.
- The GWDO algorithm is proposed for the optimization module to further reduce error in the forecasting results returned from the FCRBM based forecaster by fine-tuning the control parameters.
2. Related Work
3. The Proposed Deep Learning-Based Hybrid Model
3.1. Data Processing and Features Selection Module
3.1.1. Relevancy Filter Operation
3.1.2. Redundancy Filter Operation
3.1.3. Features Interaction Operation Session
3.1.4. The Modified Feature Selection Technique
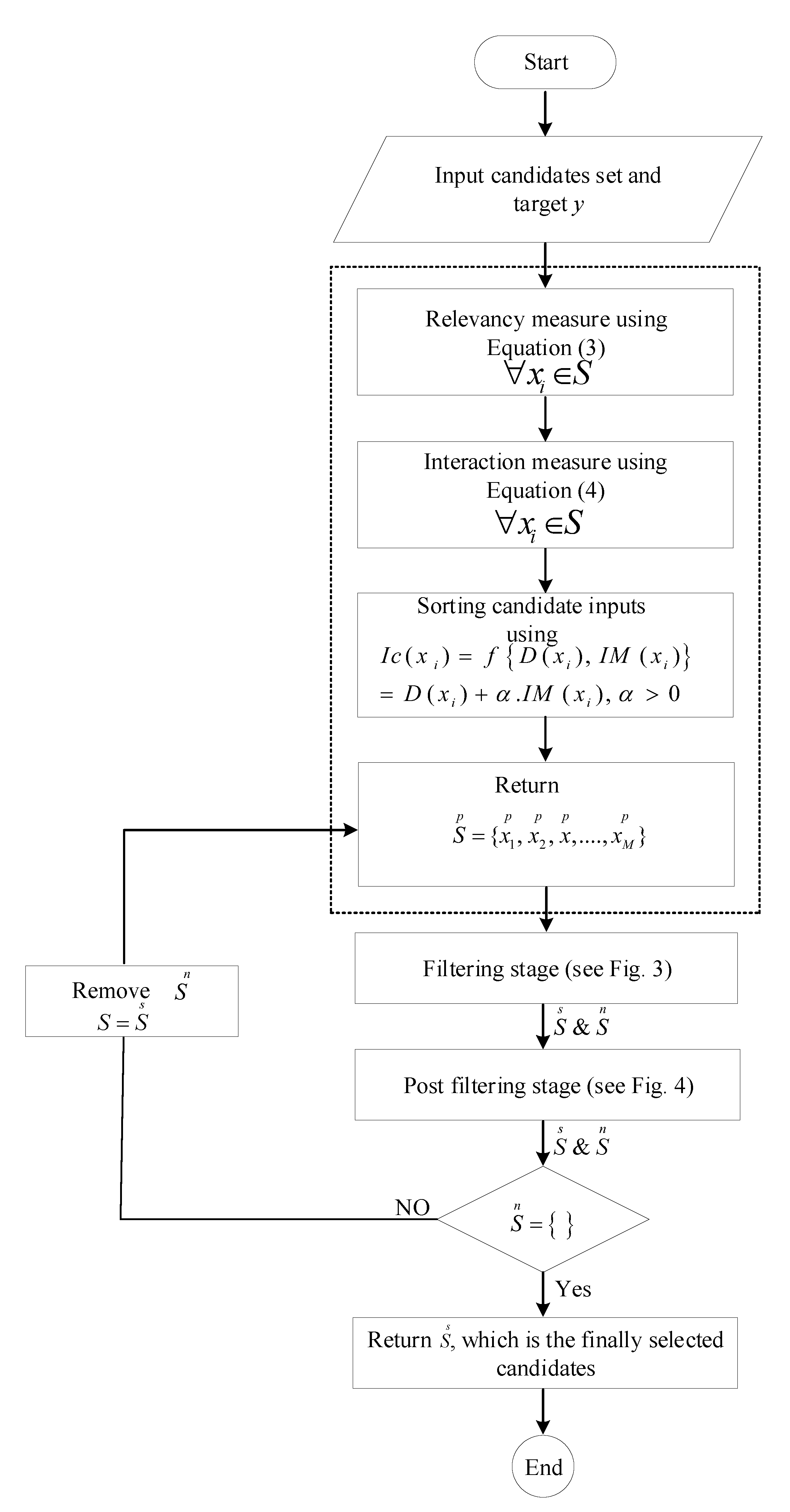
- The blocks enclosed in the dotted box in Figure 2 belong to the pre-filtering phase. In this phase, the relevancy and interaction measures are calculated, and candidate inputs are ranked based on the calculated measure.
- The information content can be measured from its individual information and the gained information using a modified version of Equation (4) mentioned in the flow chart in Figure 2. The function is a monotonically increasing function, and is a weight factor that weights the relevancy versus interaction measure. It can be adjusted and fine-tuned subject to the forecasting problem.
- The selected candidate inputs of the pre-filtering phase () are sorted in descending order based on the information content.
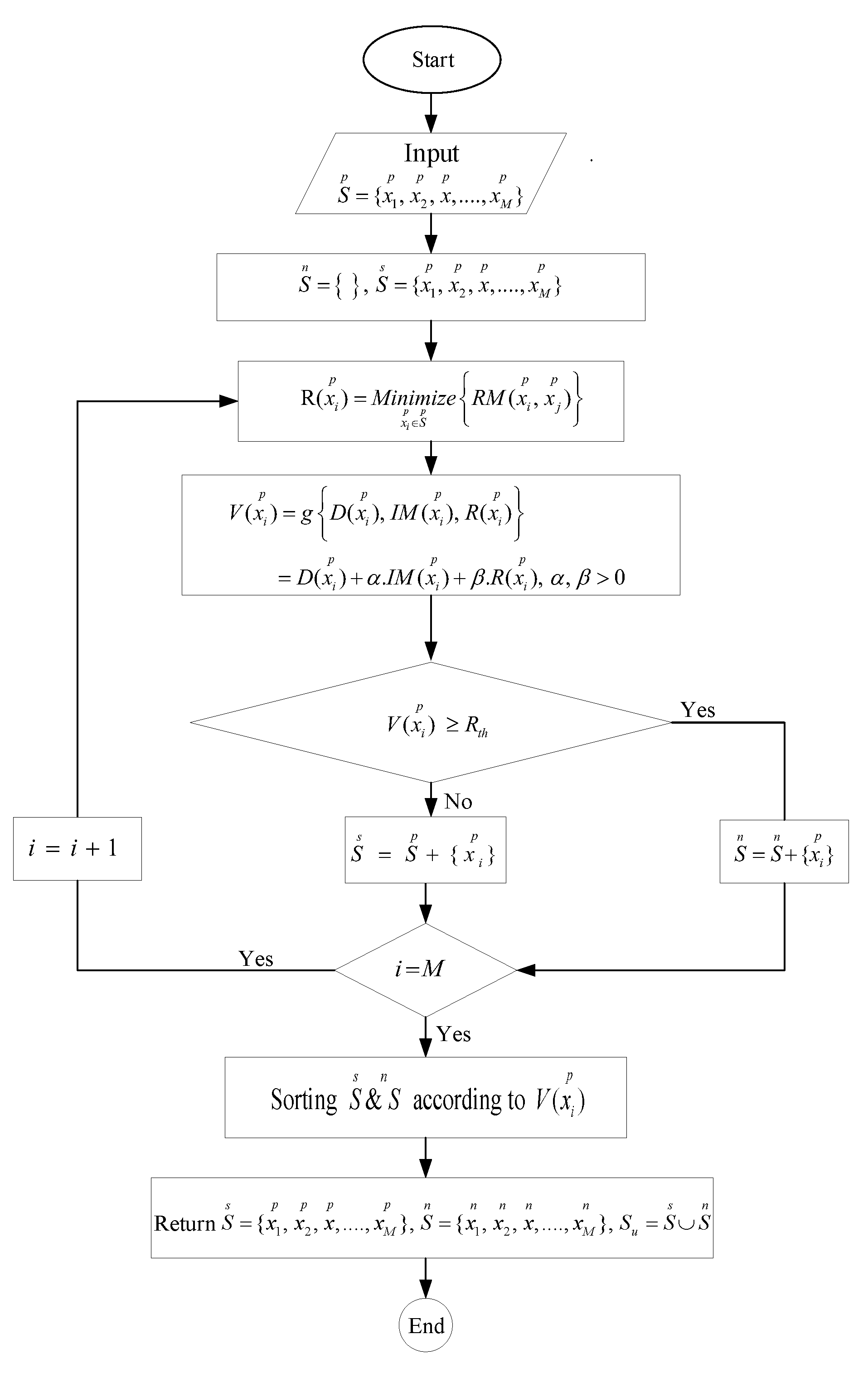
- The output of the pre-filtering phase is fed as an input to the filtering phase. In this step, the pre-selected features are partitioned into selected () and non-selected () features as shown in Figure 2. The redundancy measure is calculated by Equation (9) as:where indicates the redundancy measure for each candidate input .
- The information value of candidate features is evaluated based on three measures: redundancy, relevancy, and interaction, which is mathematically described as:where denotes information value, indicates a monotonically increasing linear function, and denotes adjustable parameter, respectively.
- Decision about the information value is taken as follows:where is the redundancy threshold. The information value is compared with the redundancy threshold; if it is greater than or equal to the redundancy threshold, then it will be put in the set of selected features list (), otherwise it will be added in the set of non-selected features ().
- The set of selected and non-selected features are sorted in descending order according to their information value and their union is also taken. The selected and non-selected feature sets and their union are given as input to the post-filtering stage, which is individually depicted in Figure 4.
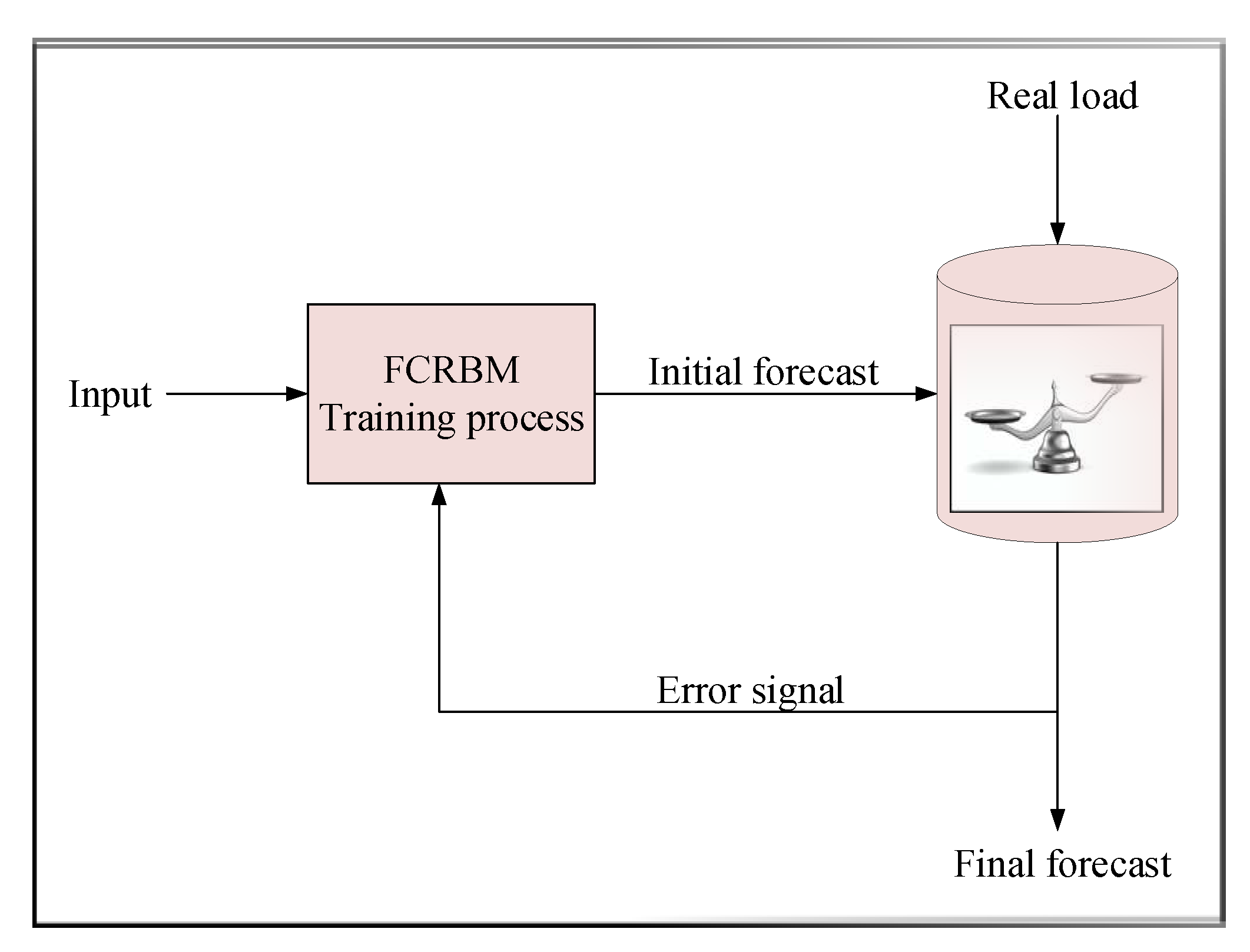
3.2. A Deep Learning FCRBM Model Based Forecasting Module
3.3. The Proposed GWDO Algorithm-Based Optimization Module
3.4. Utilization Module for Forecasting Results
4. Simulations Results, Performance Evaluation, and Discussion
- Accuracy = 100 − MAPD(x).
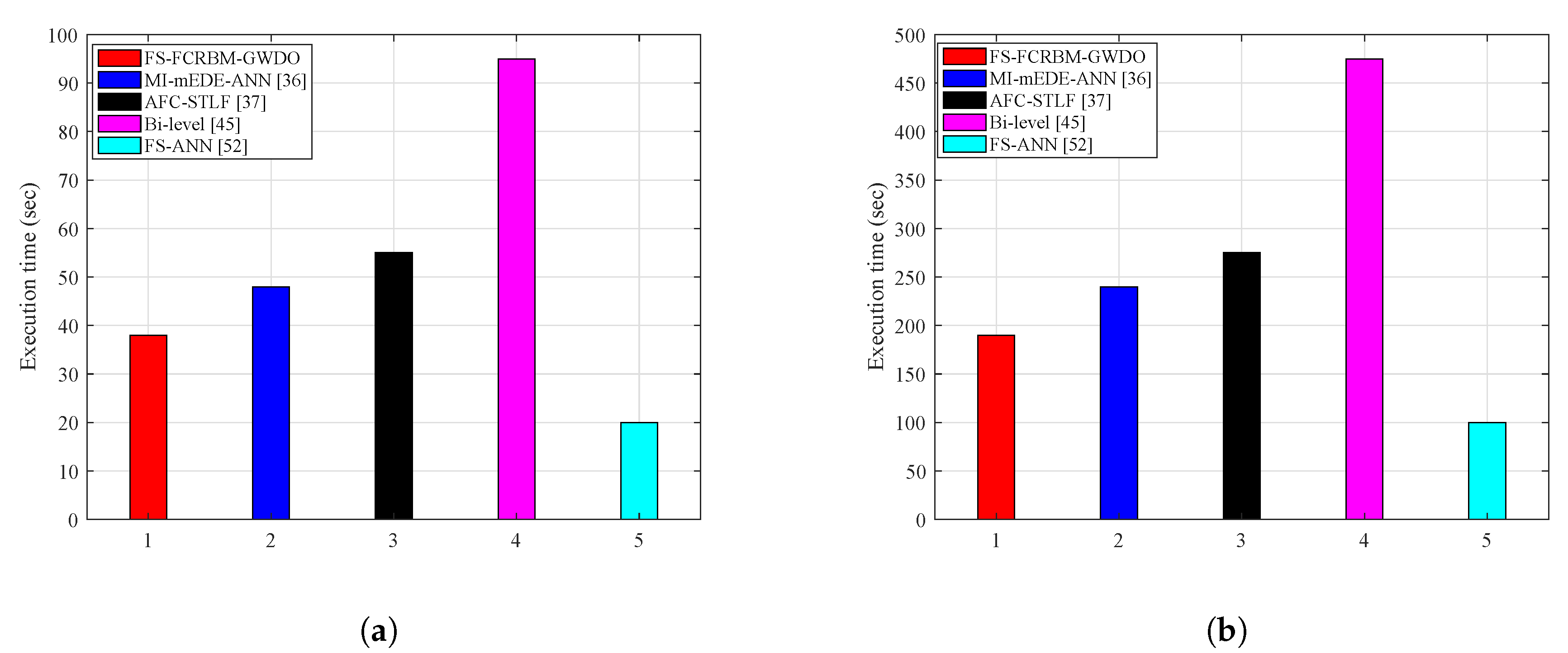
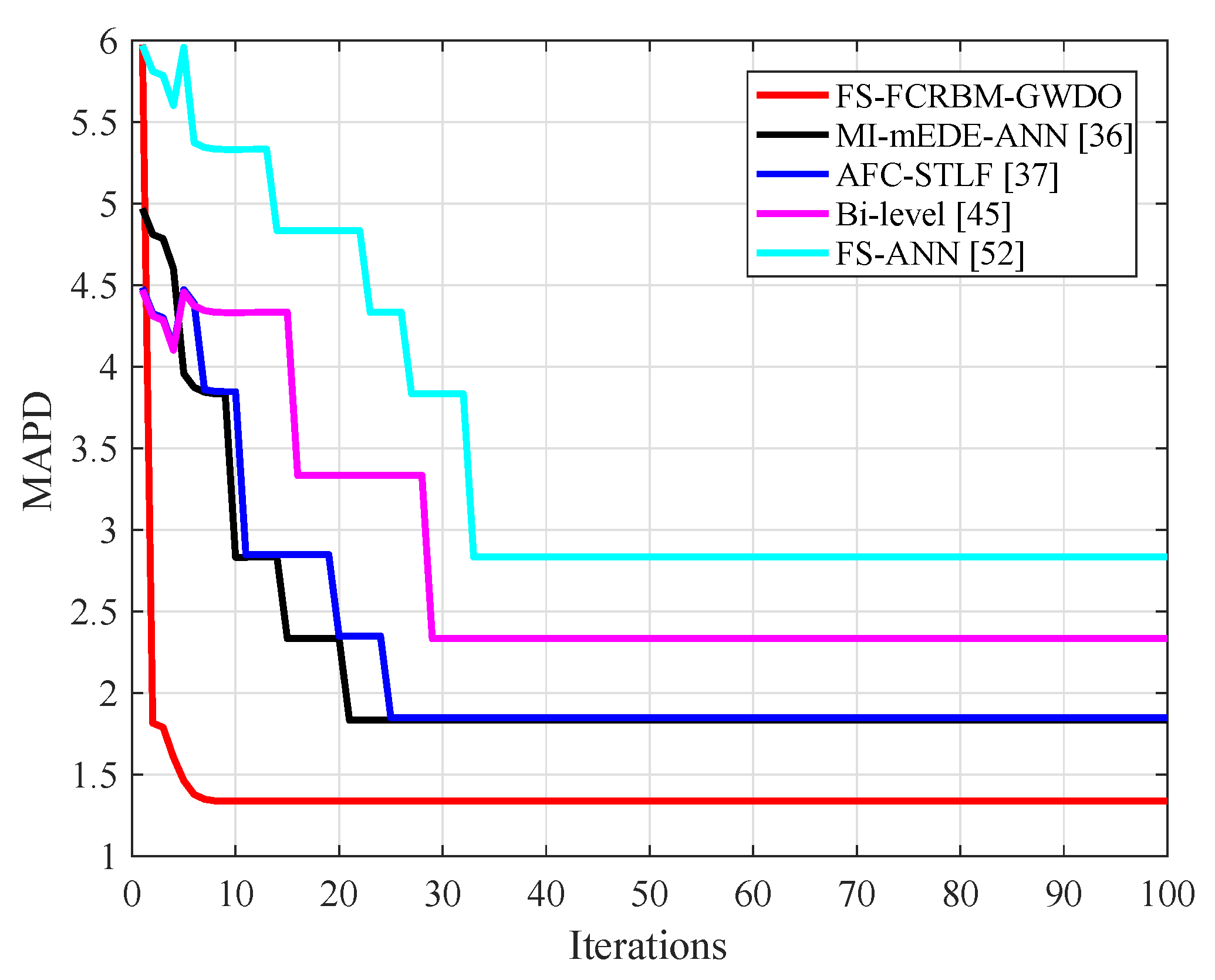
- Convergence speed corresponds to the execution time and the convergence rate: (i) execution time is the time taken by the forecasting model to return future electrical energy consumption pattern; and (ii) convergence rate is the rate at which the model converges to a particular epoch where its performance saturates and the error does not reduce any further with increase in the number of epochs. The forecasting models that have low execution time and converge at earlier epochs are considered fast. In this research, the execution time is measured in seconds, and the convergence rate is measured in terms of number of epochs.
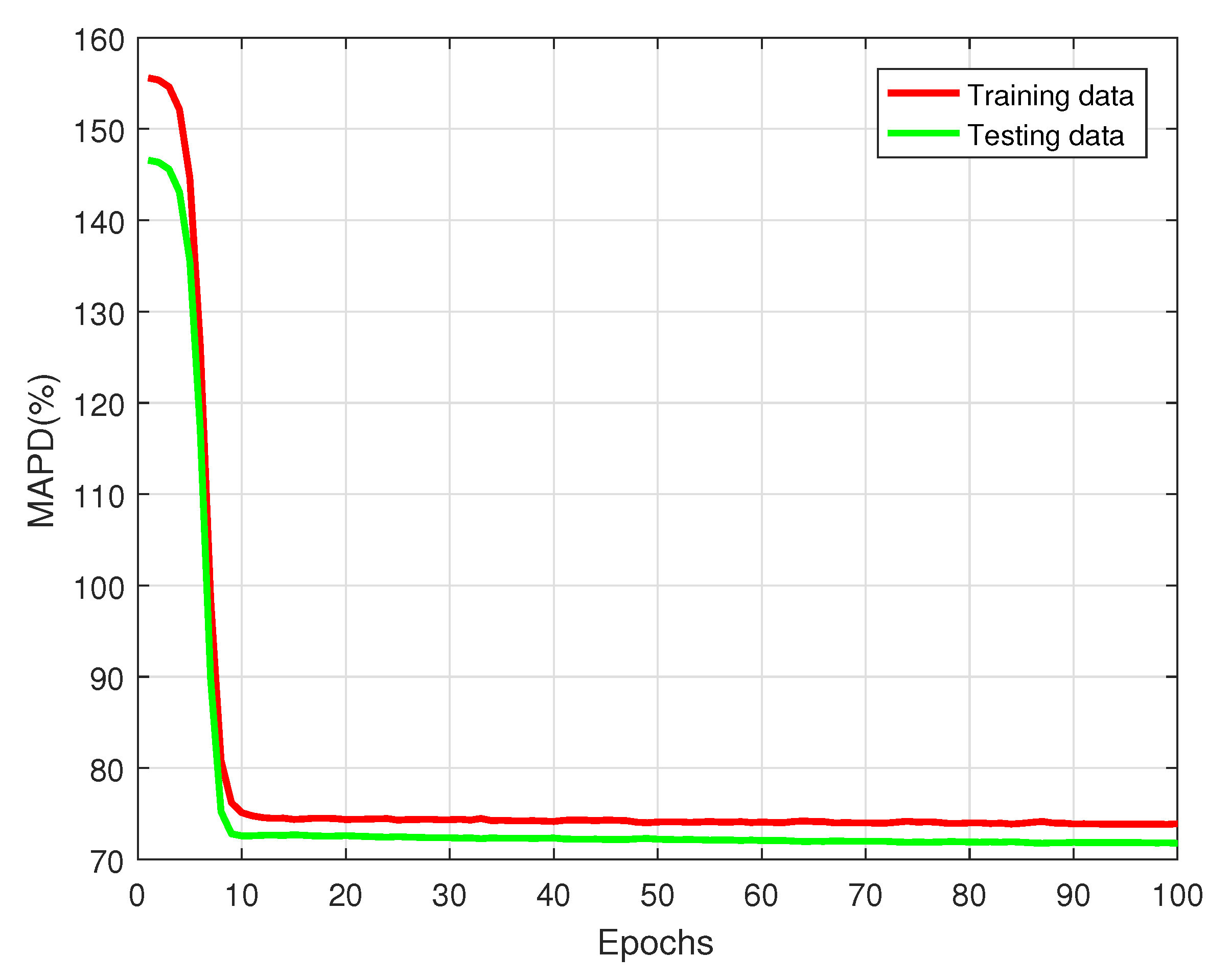
4.1. Proposed Model’s Learning Evaluation
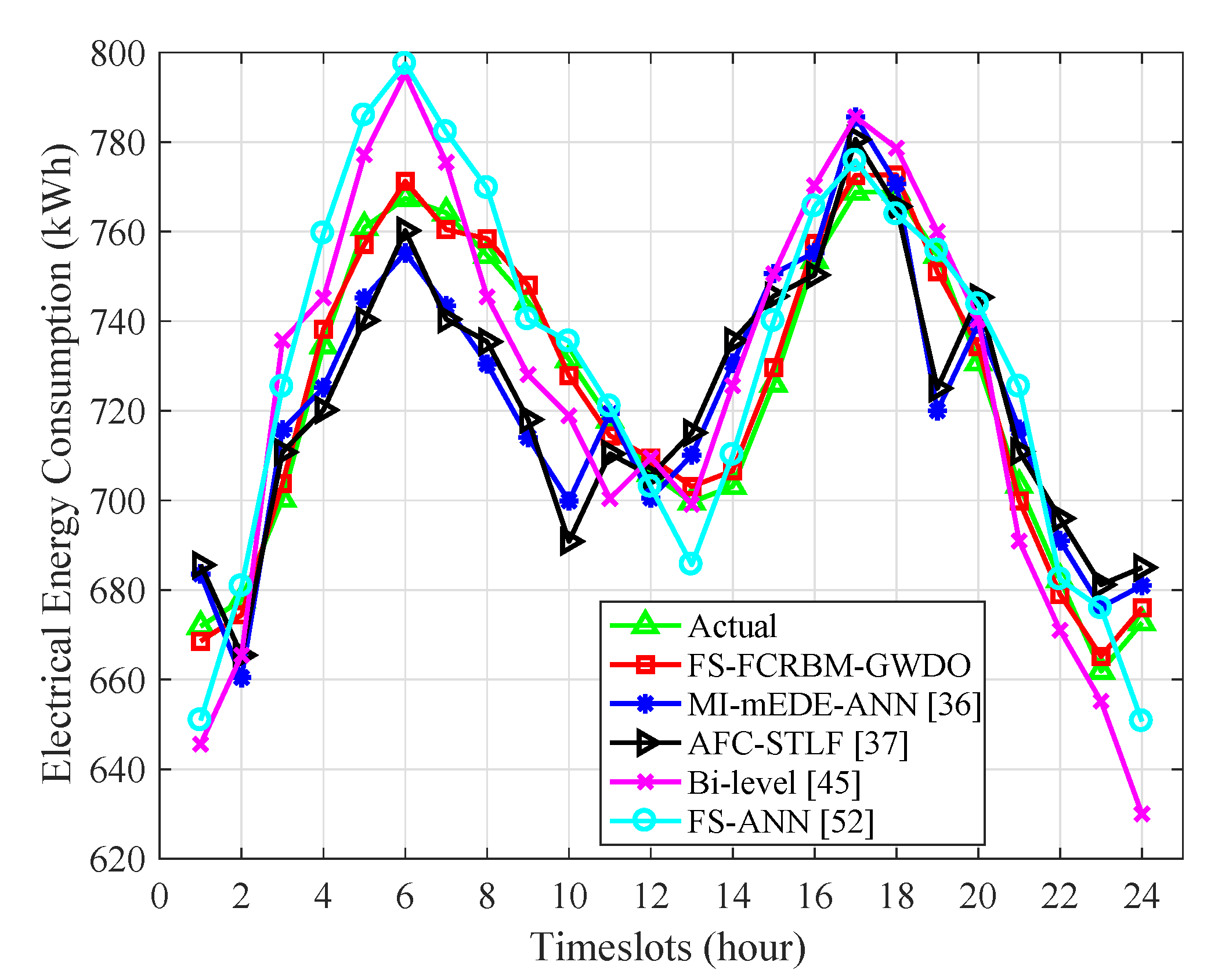
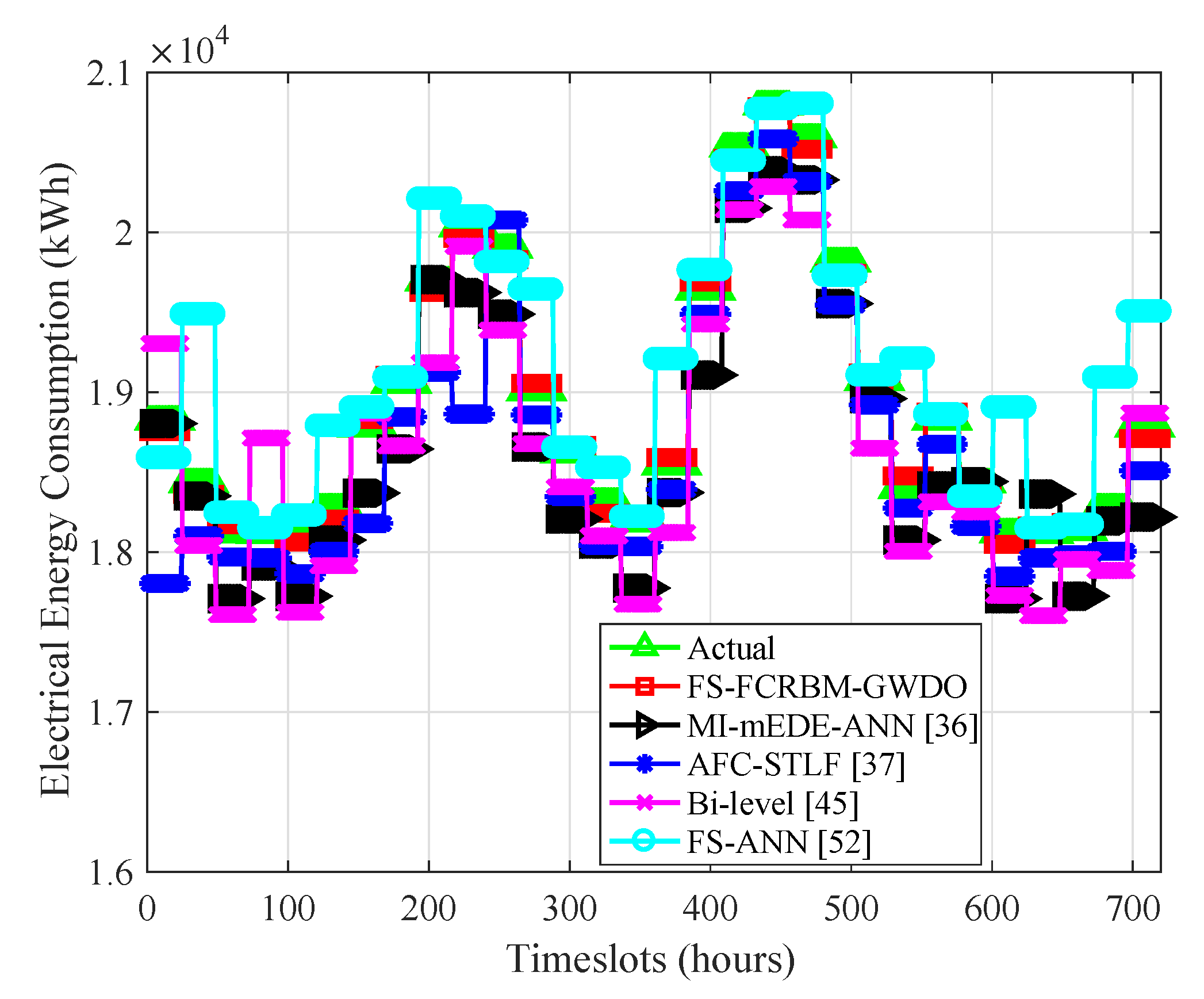
4.2. Day Ahead Electrical Energy Consumption Forecasting With Hour Resolution
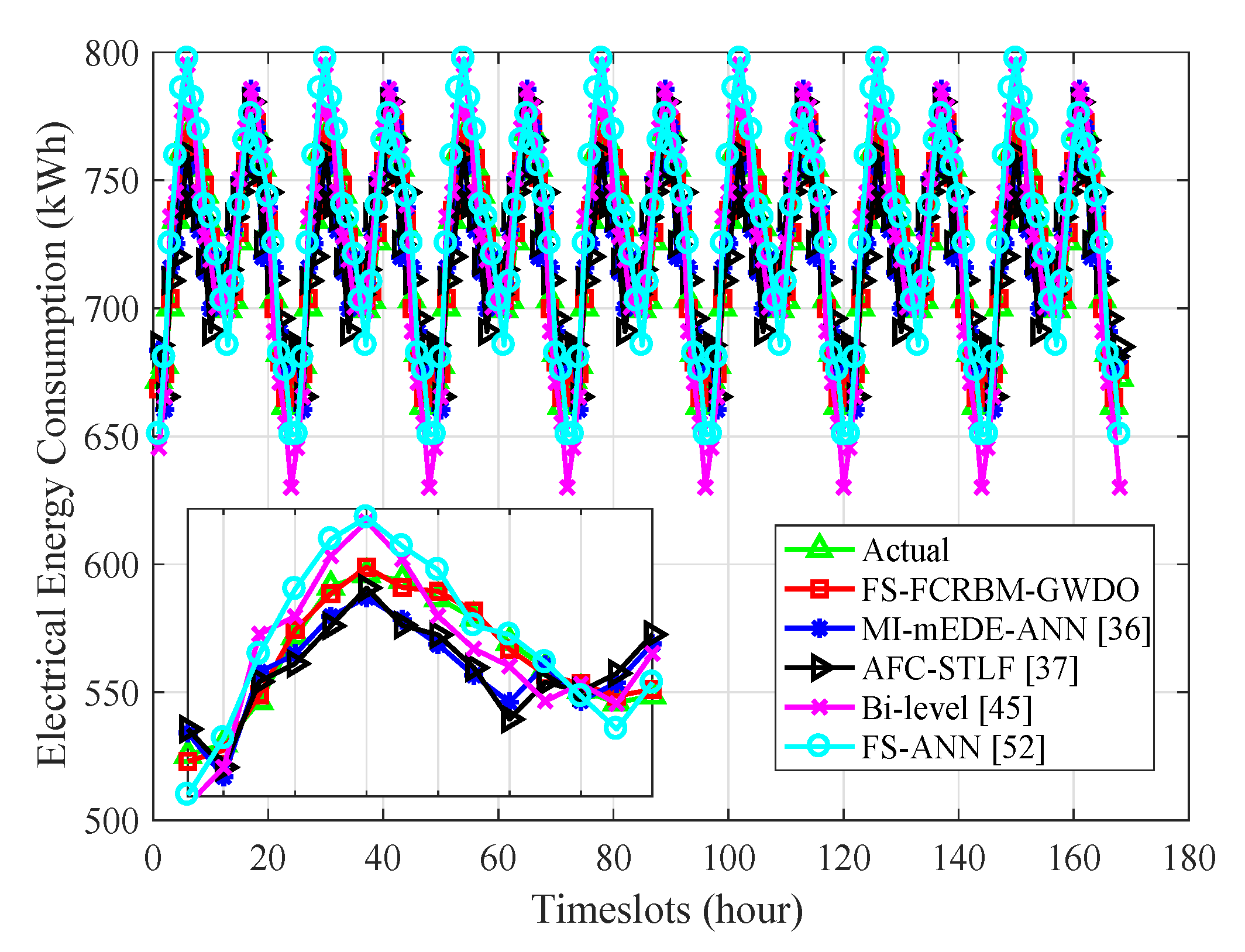
4.3. Electrical Energy Consumption Forecasting for Week and Month Ahead of Time Horizon with Hour Resolution
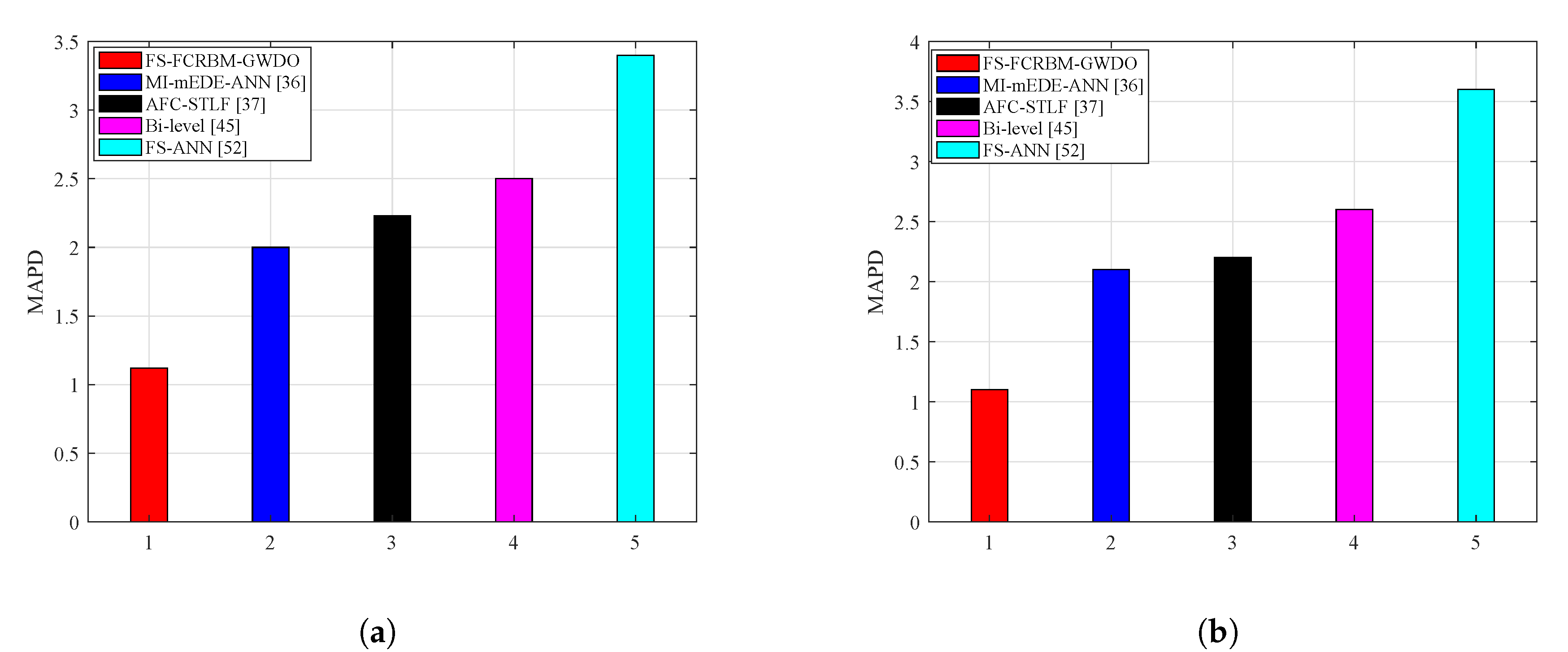
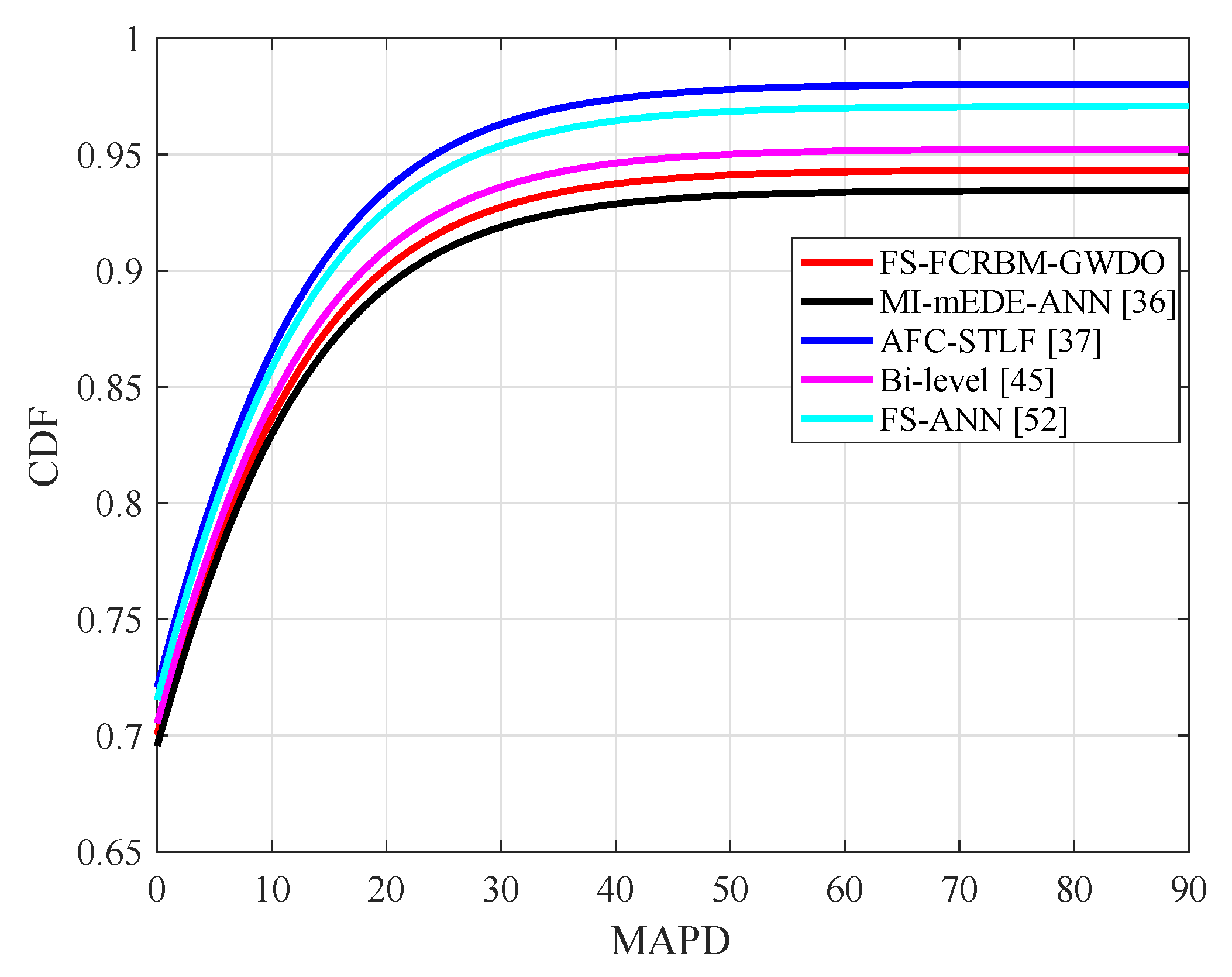
4.4. Performance Analysis of Proposed FS-FCRBM-GWDO Model in Terms of Convergence Speed and MAPD
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ARIMA | Autoregressive integrated moving average |
| AFC-STLF | Accurate fast converging short-term load forecasting |
| ANN | Artificial neural network |
| AI | Artificial intelligence |
| CPSO | Chaotic particle swarm optimization |
| CDF | Cumulative distribution function |
| DSM | Demand side management |
| DE | Differential evaluation |
| EDE | Enhanced differential evaluation |
| FCRBM | Factored conditional restricted Boltzmann machine |
| FFO | Fruit fly optimization |
| FS | Features selection |
| GWDO | Genetic wind driven optimization algorithm |
| GA | Genetic algorithm |
| GM | Grey forecasting model |
| GEFC | Global energy forecasting competition |
| ICER | Irish commission for energy regulation |
| mEDE | Modified enhanced differential evolution algorithm |
| MAPD | Mean absolute percentage deviation |
| MI | Mutual information |
| ReLU | Rectified linear unit |
| RGNN | Regression neural network |
| SVR | Support vector regression |
| SVM | Support vector machine |
| SG | Smart grid |
| Tanh | Tangent hyperbolic |
| WDO | Wind driven optimization |
| Notations | |
| Adjustable parameter | |
| R | Correlation |
| Normalized data | |
| Variance | |
| Candidates interaction | |
| Dew point | |
| d | Day |
| Electrical energy consumption data pattern | |
| Entropy | |
| Humidity | |
| h | Hour |
| X | Input data |
| Individual probability destribution | |
| Interaction gain based redundancy measure | |
| Interaction measure | |
| Information value | |
| Irrelevancy threshold | |
| Joint probability distribution | |
| Monotonically increasing function | |
| Mutual information | |
| Monotonically increasing linear function | |
| Non-selected features | |
| Relevance of input variable with the target variable | |
| Redundancy measure | |
| Redundancy measure | |
| Redundancy threshold | |
| Rectified linear unit | |
| Selected candidates in pre-filtering phase | |
| Selected features | |
| S | Set of input variables |
| Temperature | |
| y | Target variable |
| Weight factor | |
References
- Hafeez, G.; Alimgeer, K.S.; Wadud, Z.; Khan, I.; Usman, M.; Qazi, A.B.; Khan, F.A. An Innovative Optimization Strategy for Efficient Energy Management with Day-ahead Demand Response Signal and Energy Consumption Forecasting in Smart Grid using Artificial Neural Network. IEEE Access 2020. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Zhang, K. Short-term electric load forecasting based on singular spectrum analysis and support vector machine optimized by Cuckoo search algorithm. Electr. Power Syst. Res. 2017, 146, 270–285. [Google Scholar] [CrossRef]
- Lin, C.; Chou, L. A novel economy reflecting short-term load forecasting approach. Energy Convers. Manag. 2013, 65, 331–342. [Google Scholar] [CrossRef]
- Al-Hamadi, H.M.; Soliman, S.A. Short-term electric load forecasting based on Kalman filtering algorithm with moving window weather and load model. Electr. Power Syst. Res. 2004, 68, 47–59. [Google Scholar] [CrossRef]
- Sudheer, G.; Suseelatha, A. Short term load forecasting using wavelet transform combined with Holt–Winters and weighted nearest neighbor models. Int. J. Electr. Power Energy Syst. 2015, 64, 340–346. [Google Scholar] [CrossRef]
- Akay, D.; Atak, M. Grey prediction with rolling mechanism for electricity demand forecasting of Turkey. Energy 2007, 32, 1670–1675. [Google Scholar] [CrossRef]
- Song, K.; Baek, Y.; Hong, D.H.; Jang, G. Short-term load forecasting for the holidays using fuzzy linear regression method. IEEE Trans. Power Syst. 2005, 20, 96–101. [Google Scholar] [CrossRef]
- Guo, Y.; Nazarian, E.; Ko, J.; Rajurkar, K. Hourly cooling load forecasting using time-indexed ARX models with two-stage weighted least squares regression. Energy Convers. Manag. 2014, 80, 46–53. [Google Scholar] [CrossRef]
- Felice, M.D.; Alessandri, A.; Catalano, F. Seasonal climate forecasts for medium-term electricity demand forecasting. Appl. Energy 2015, 137, 435–444. [Google Scholar] [CrossRef]
- Sousa, J.C.; Neves, L.P.; Jorge, H.M. Assessing the relevance of load profiling information in electrical load forecasting based on neural network models. Int. J. Electr. Power Energy Syst. 2012, 40, 85–93. [Google Scholar] [CrossRef]
- Mori, H.; Yuihara, A. Deterministic annealing clustering for ANN-based short-term load forecasting. IEEE Trans. Power Syst. 2001, 16, 545–551. [Google Scholar] [CrossRef]
- Zeng, N.; Zhang, H.; Liu, W.; Liang, J.; Alsaadi, F.E. A switching delayed PSO optimized extreme learning machine for short-term load forecasting. Neurocomputing 2017, 240, 175–182. [Google Scholar] [CrossRef]
- Xia, C.; Wang, J.; McMenemy, K. Short, medium and long term load forecasting model and virtual load forecaster based on radial basis function neural networks. Int. J. Electr. Power Energy Syst. 2010, 32, 743–750. [Google Scholar] [CrossRef]
- Li, H.; Guo, S.; Li, C.; Sun, J. A hybrid annual power load forecasting model based on generalized regression neural network with fruit fly optimization algorithm. Knowl.-Based Syst. 2013, 37, 378–387. [Google Scholar] [CrossRef]
- Hafeez, G.; Alimgeer, K.S.; Qazi, A.B.; Khan, I.; Usman, M.; Khan, F.A.; Wadud, Z. A Hybrid Approach for Energy Consumption Forecasting with a New Feature Engineering and Optimization Framework in Smart Grid. IEEE Access 2020. [Google Scholar] [CrossRef]
- Liu, N.; Tang, Q.; Zhang, J.; Fan, W.; Liu, J. A hybrid forecasting model with parameter optimization for short-term load forecasting of micro-grids. Appl. Energy 2014, 129, 336–345. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, Y.; Liu, C.; Li, C.; Li, L. A hybrid application algorithm based on the support vector machine and artificial intelligence: An example of electric load forecasting. Appl. Math. Model. 2015, 39, 2617–2632. [Google Scholar] [CrossRef]
- Mocanu, E.; Nguyen, P.H.; Gibescu, M.; Kling, W.L. Deep learning for estimating building energy consumption. Sustain. Energy Grids Netw. 2016, 6, 91–99. [Google Scholar] [CrossRef]
- Javaid, N.; Hafeez, G.; Iqbal, S.; Alrajeh, N.; Alabed, M.S.; Guizani, M. Energy efficient integration of renewable energy sources in the smart grid for demand side management. IEEE Access 2018, 6, 77077–77096. [Google Scholar] [CrossRef]
- Hafeez, G.; Javaid, N.; Iqbal, S.; Khan, F. Optimal residential load scheduling under utility and rooftop photovoltaic units. Energies 2018, 11, 611. [Google Scholar] [CrossRef]
- Bayraktar, Z.; Komurcu, M.; Werner, D.H. Wind Driven Optimization (WDO): A novel nature-inspired optimization algorithm and its application to electromagnetics. In Proceedings of the 2010 IEEE Antennas and Propagation Society International Symposium, Toronto, ON, Canada, 11–17 July 2010; pp. 1–4. [Google Scholar]
- Hahn, H.; Meyer-Nieberg, S.; Pickl, S. Electric load forecasting methods: Tools for decision making. Eur. J. Oper. Res. 2009, 199, 902–907. [Google Scholar] [CrossRef]
- Taylor, J.W. An evaluation of methods for very short-term load forecasting using minute-by-minute British data. Int. J. Forecast. 2008, 24, 645–658. [Google Scholar] [CrossRef]
- De Felice, M.; Yao, X. Short-term load forecasting with neural network ensembles: A comparative study [application notes]. IEEE Comput. Intell. Mag. 2011, 6, 47–56. [Google Scholar] [CrossRef]
- Pedregal, D.J.; Trapero, J.R. Mid-term hourly electricity forecasting based on a multi-rate approach. Energy Convers. Manag. 2010, 51, 105–111. [Google Scholar] [CrossRef]
- Filik, Ü.B.; Gerek, Ö.N.; Kurban, M. A novel modeling approach for hourly forecasting of long-term electric energy demand. Energy Convers. Manag. 2011, 52, 199–211. [Google Scholar] [CrossRef]
- López, M.; Valero, S.; Senabre, C.; Aparicio, J.; Gabaldon, A. Application of SOM neural networks to short-term load forecasting: The Spanish electricity market case study. Electr. Power Syst. Res. 2012, 91, 18–27. [Google Scholar] [CrossRef]
- Zjavka, L.; Snášel, V. Short-term power load forecasting with ordinary differential equation substitutions of polynomial networks. Electr. Power Syst. Res. 2016, 137, 113–123. [Google Scholar] [CrossRef]
- Liu, D.; Zeng, L.; Li, C.; Ma, K.; Chen, Y.; Cao, Y. A distributed short-term load forecasting method based on local weather information. IEEE Syst. J. 2018, 12, 208–215. [Google Scholar] [CrossRef]
- Ghadimi, N.; Akbarimajd, A.; Shayeghi, H.; Abedinia, O. Two stage forecast engine with feature selection technique and improved meta-heuristic algorithm for electricity load forecasting. Energy 2018, 161, 130–142. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Hill, D.J.; Luo, F.; Xu, Y. Short-term residential load forecasting based on resident behaviour learning. IEEE Trans. Power Syst. 2018, 33, 1087–1088. [Google Scholar] [CrossRef]
- Hafeez, G.; Alimgeer, K.S.; Khan, I. Electric Load Forecasting based on Deep Learning and Optimized by Heuristic Algorithm in Smart Grid. Appl. Energy 2020, 306, 114915. [Google Scholar] [CrossRef]
- Vrablecova, P.; Ezzeddine, A.B.; Rozinajová, V.; Šárik, S.; Sangaiah, A.K. Smart grid load forecasting using online support vector regression. Comput. Electr. Eng. 2018, 65, 102–117. [Google Scholar] [CrossRef]
- González, J.P.; Roque, A.M.S.; Perez, E.A. Forecasting functional time series with a new Hilbertian ARMAX model: Application to electricity price forecasting. IEEE Trans. Power Syst. 2018, 33, 545–556. [Google Scholar] [CrossRef]
- Luo, J.; Hong, T.; Fang, S. Benchmarking robustness of load forecasting models under data integrity attacks. Int. J. Forecast. 2018, 34, 89–104. [Google Scholar] [CrossRef]
- Ahmad, A.; Javaid, N.; Mateen, A.; Awais, M.; Khan, Z. Short-Term Load Forecasting in Smart Grids: An Intelligent Modular Approach. Energies 2019, 12, 164. [Google Scholar] [CrossRef]
- Ahmad, A.; Javaid, N.; Guizani, M.; Alrajeh, N.; Khan, Z.A. An accurate and fast converging short-term load forecasting model for industrial applications in a smart grid. IEEE Trans. Ind. Inform. 2017, 13, 2587–2596. [Google Scholar] [CrossRef]
- Abedinia, O.; Amjady, N.; Zareipour, H. A new feature selection technique for load and price forecast of electrical power systems. IEEE Trans. Power Syst. 2017, 32, 62–74. [Google Scholar] [CrossRef]
- Amjady, N.; Keynia, F. A new prediction strategy for price spike forecasting of day-ahead electricity markets. Appl. Soft Comput. 2011, 11, 4246–4256. [Google Scholar] [CrossRef]
- Hafeez, G.; Javaid, N.; Riaz, M.; Umar, K.; Iqbal, Z.; Ali, A. An Innovative Model Based on FCRBM for Load Forecasting in the Smart Grid. In Proceedings of the International Conference on Innovative Mobile and Internet Services in Ubiquitous Computing, Sydney, NSW, Australia, 3–5 July 2019; Springer: Cham, Switzerland, 2019; pp. 49–62. [Google Scholar]
- Kwak, N.; Choi, C. Input feature selection for classification problems. IEEE Trans. Neural Netw. 2002, 13, 143–159. [Google Scholar] [CrossRef]
- Latham, P.E.; Nirenberg, S. Synergy, redundancy, and independence in population codes, revisited. J. Neurosci. 2005, 25, 5195–5206. [Google Scholar] [CrossRef]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef] [PubMed]
- Estévez, P.A.; Tesmer, M.; Perez, C.A.; Zurada, J.M. Normalized mutual information feature selection. IEEE Trans. Neural Netw. 2009, 20, 189–201. [Google Scholar] [CrossRef] [PubMed]
- Amjady, N.; Keynia, F.; Zareipour, H. Short-term load forecast of microgrids by a new bilevel prediction strategy. IEEE Trans. Smart Grid 2010, 1, 286–294. [Google Scholar] [CrossRef]
- Engelbrecht, A.P. Computational Intelligence: An Introduction, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]
- Anderson, C.W.; Stolz, E.A.; Shamsunder, S. Multivariate autoregressive models for classification of spontaneous electroencephalographic signals during mental tasks. IEEE Trans. Biomed. Eng. 1998, 45, 277–286. [Google Scholar] [CrossRef] [PubMed]
- Hafeez, G.; Islam, N.; Ali, A.; Ahmad, S.; Alimgeer, M.U.; Saleem, K. A Modular Framework for Optimal Load Scheduling under Price-Based Demand Response Scheme in Smart Grid. Processes 2019, 7, 499. [Google Scholar] [CrossRef]
- Bao, Z.; Zhou, Y.; Li, L.; Ma, M. A hybrid global optimization algorithm based on wind driven optimization and differential evolution. Math. Probl. Eng. 2015, 2015, 620–635. [Google Scholar] [CrossRef]
- Man, K.; Tang, K.; Kwong, S. Genetic algorithms: Concepts and applications [in engineering design]. IEEE Trans. Ind. Electron. 1996, 43, 519–534. [Google Scholar] [CrossRef]
- Wang, H.; Huang, J. Joint Investment and Operation of Microgrid. IEEE Trans. Smart Grid 2017, 8, 833–845. [Google Scholar] [CrossRef]
- Amjady, N.; Keynia, F. Day-ahead price forecasting of electricity markets by a new feature selection algorithm and cascaded neural network technique. Energy Convers. Manag. 2009, 50, 2976–2982. [Google Scholar] [CrossRef]
- PJM Energy Market. Available online: https://www.pjm.com/ (accessed on 8 March 2019).

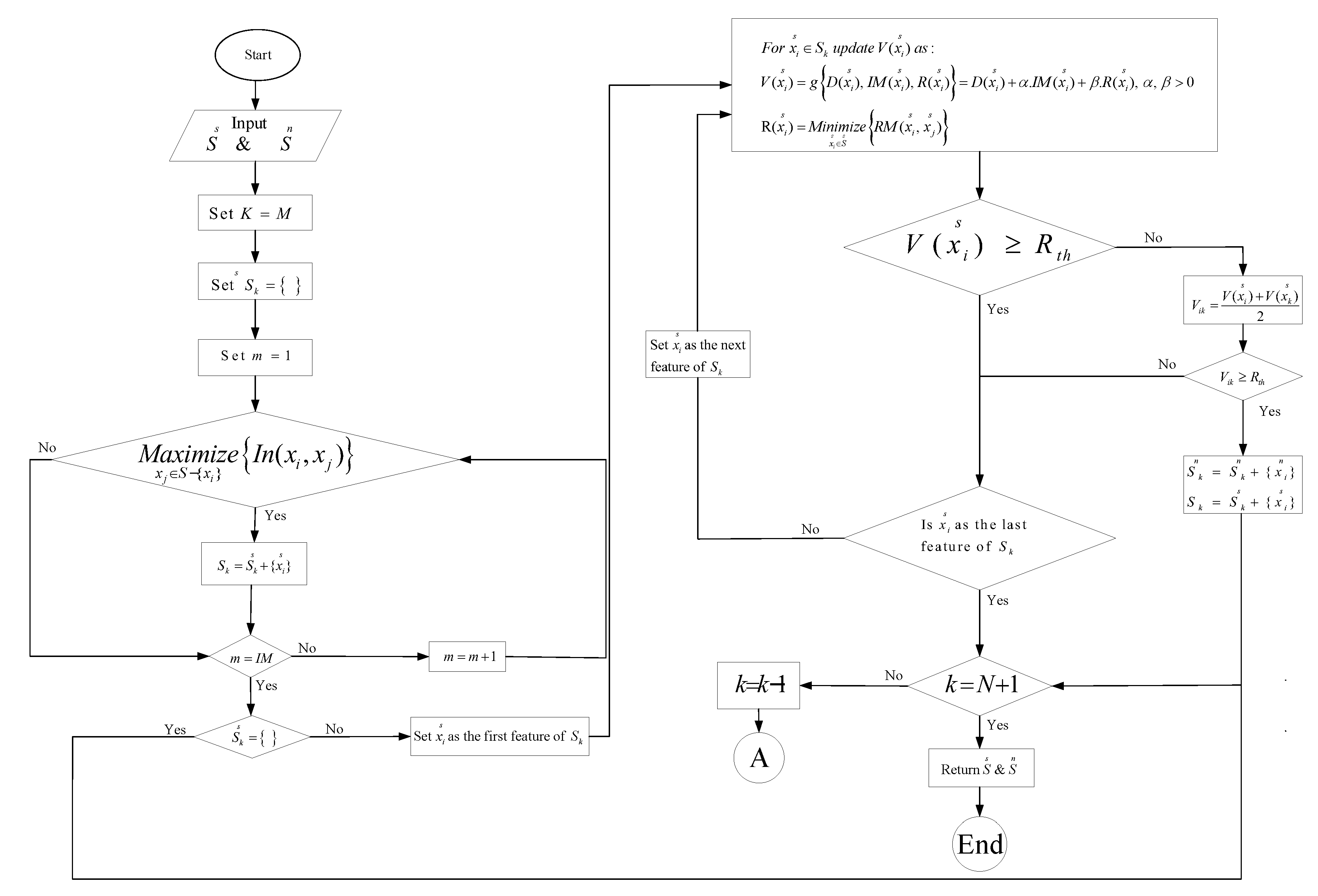
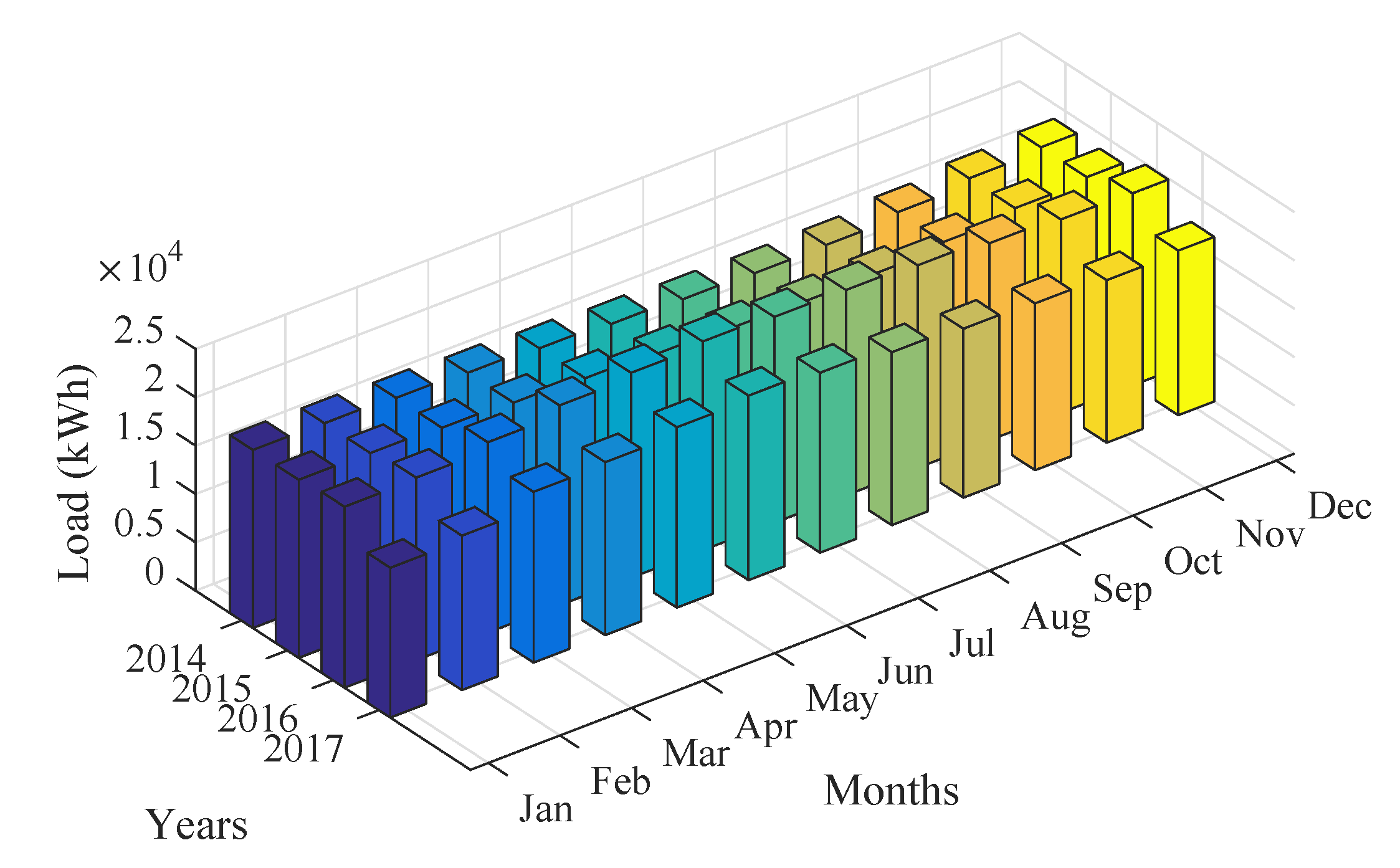
| Techniques | Objectives | Datasets | Limitations | Critical Remarks |
|---|---|---|---|---|
| ARIMA and exponential smoothing [23] | Forecast accuracy improvement for power generation scheduling in real-time. | National grid and Great Britain | This model is useful for only very short term load forecasting. | The prime focus of authors is on accuracy improvements for univariate methods while the accuracy improvement of univariate is not sufficient. |
| ANN and self-organizing map [27] | To build a decision support system for commercializing company bidding. | Spain power grid | This model achieves moderate accuracy at the cost of slow convergence rate (high execution time). | Meteorological and load data is used in this model and other exogenous parameters are ignored that significantly affect the forecast accuracy. |
| Differential polynomial neural network [28] | Reduction of generation cost and spinning reserve capacity. | Canada power grid | Unnecessary and overload prediction leads to large reserves and high cost. | Slow convergence and less accuracy is observed in this model, which have a direct impact on cost and spinning reserve. |
| ANN, ARIMA, and GM [29] | To improve the accuracy of bulk power system. | China Fujian Province power grid | The system becomes more complex by dividing the system into subnetworks. | Improvement in accuracy by using large exogenous parameters at the cost of high complexity and slow convergence rate. |
| Reglet and Elman neural network [30] | Accuracy and capability improvement for efficient operation of the power system. | Australian energy market commission | The model has large complexity. | This model has a large complexity that directly impacts the convergence rate. |
| Long term short term memory [31] | Forecast accuracy improvement for household scheduling. | Canadian household | The system model has slow convergence due to the incorporation of household appliances sequence. | The accuracy is notably improved using appliances consumption sequence, however, the convergence rate is compromised. |
| SVR [33] | Improvement of load forecasting accuracy for minimizing cost and energy imbalance. | Irish commission for energy regulation (ICER) | The model has a slow convergence speed. | The hyperparameters are tuned by the intelligent techniques which improved accuracy at the expense of increased execution time. |
| ARIMAX and quasi-newton algorithm [34] | Improvement of forecast accuracy for system operators and the market agent. | Spanish and German energy market | The convergence speed is compromised. | They improved accuracy is improved due to incorporating of sigmoid function. However, the computational time is increased. |
| ANN, SVR, and fuzzy interaction regression [35] | Improvement of resilience against attacks on data integrity. | Global energy forecasting competition (GEFC) 2012 | The resilience is improved at increased time complexity. | The power system resiliency is enhanced at the expense of higher complexity of modeling. |
| MI, ANN, and mEDE [36,37] | Improvement of convergence rate and accuracy for US EKPC and Dayton grid. | PJM market | The complexity of the model is increased. | The developed model outperforms for small datasize and worst perform for large datasize. |
| ANN-based hybrid models [38,39] | Microgrid accuracy improvement. | PJM market | The convergence rate is compromised while improving forecast accuracy. | The ANN forecaster improved the accuracy, which degrade the execution time. |
| Control Parameters | Value |
|---|---|
| Hidden layer | 1 |
| Neurons in hidden | 10 |
| Output layer | 1 |
| Number of output neurons | 1 |
| Number of epochs | 100 |
| Number of iterations | 100 |
| Learning rate | |
| Momentum | 0.6 |
| Initial weight | 0.1 |
| Initial bias | 0 |
| Max | 0.9 |
| Min | 0.1 |
| Decision variables | 2 |
| Population size | 24 |
| Delay of weight | 0.0002 |
| Historical load data | 4 years |
| Exogenous parameters | 4 years |
| Electrical Energy Consumption Forecasting Models | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Day | FS-FCRBM-GWDO | MI-mEDE-ANN | AFC-STLF | Bi-Level | FS-ANN | ||||||||||
| MAPD | R | MAPD | R | MAPD | R | MAPD | R | MAPD | R | ||||||
| 1 | 1.12 | 1.13 | 0.70 | 2.20 | 1.55 | 0.50 | 2.30 | 1.60 | 0.52 | 2.60 | 1.75 | 0.44 | 3.30 | 1.90 | 0.44 |
| 2 | 1.10 | 0.98 | 0.68 | 2.10 | 1.45 | 0.58 | 2.15 | 1.55 | 0.56 | 2.80 | 1.73 | 0.46 | 3.35 | 1.80 | 0.36 |
| 3 | 1.09 | 1.10 | 0.71 | 2.50 | 1.30 | 0.51 | 2.10 | 1.48 | 0.53 | 2.75 | 1.65 | 0.43 | 3.20 | 1.83 | 0.33 |
| 4 | 1.03 | 0.97 | 0.80 | 2.02 | 1.20 | 0.50 | 2.40 | 1.49 | 0.54 | 2.85 | 1.75 | 0.44 | 3.40 | 1.85 | 0.34 |
| 5 | 1.50 | 1.09 | 0.65 | 2.10 | 1.15 | 0.55 | 2.25 | 1.37 | 0.55 | 2.87 | 1.65 | 0.45 | 3.15 | 1.78 | 0.35 |
| 6 | 1.30 | 1.07 | 0.75 | 2.30 | 1.34 | 0.65 | 2.15 | 1.35 | 0.69 | 2.89 | 1.69 | 0.59 | 3.25 | 1.95 | 0.49 |
| 7 | 1.24 | 1.04 | 0.69 | 2.11 | 1.55 | 0.60 | 2.10 | 1.60 | 0.65 | 2.75 | 1.68 | 0.44 | 3.67 | 1.80 | 0.34 |
| 8 | 1.23 | 1.02 | 0.70 | 2.15 | 1.45 | 0.50 | 2.09 | 1.65 | 0.55 | 2.70 | 1.77 | 0.55 | 3.55 | 1.83 | 0.45 |
| 9 | 1.08 | 1.05 | 0.80 | 2.35 | 1.36 | 0.55 | 2.50 | 1.66 | 0.56 | 2.65 | 1.71 | 0.56 | 3.45 | 1.79 | 0.46 |
| 10 | 1.05 | 0.99 | 0.79 | 2.40 | 1.39 | 0.69 | 2.44 | 1.67 | 0.60 | 2.63 | 1.78 | 0.65 | 3.10 | 1.87 | 0.55 |
| 11 | 1.15 | 1.10 | 0.87 | 2.01 | 1.45 | 0.77 | 2.35 | 1.55 | 0.75 | 2.70 | 1.65 | 0.35 | 3.15 | 1.85 | 0.45 |
| 12 | 1.25 | 1.11 | 0.65 | 2.06 | 1.50 | 0.55 | 2.12 | 1.58 | 0.55 | 2.60 | 1.66 | 0.45 | 3.59 | 1.77 | 0.35 |
| 13 | 1.10 | 0.96 | 0.81 | 2.10 | 1.55 | 0.71 | 2.20 | 1.43 | 0.75 | 2.63 | 1.69 | 0.25 | 3.33 | 1.69 | 0.35 |
| 14 | 1.12 | 0.99 | 0.79 | 2.12 | 1.37 | 0.75 | 2.23 | 1.47 | 0.70 | 2.36 | 1.75 | 0.40 | 3.39 | 1.59 | 0.30 |
| 15 | 1.10 | 1.03 | 0.78 | 2.13 | 1.46 | 0.78 | 2.27 | 1.30 | 0.73 | 2.50 | 1.59 | 0.43 | 3.54 | 1.89 | 0.53 |
| 16 | 1.18 | 1.05 | 0.79 | 2.00 | 1.39 | 0.70 | 2.13 | 1.35 | 0.78 | 2.58 | 1.67 | 0.58 | 3.23 | 1.88 | 0.48 |
| 17 | 1.19 | 1.08 | 0.80 | 2.13 | 1.48 | 0.60 | 2.35 | 1.55 | 0.65 | 2.56 | 1.70 | 0.55 | 3.28 | 1.79 | 0.50 |
| 18 | 1.21 | 1.09 | 0.85 | 2.19 | 1.29 | 0.85 | 2.10 | 1.36 | 0.64 | 2.65 | 1.72 | 0.54 | 3.92 | 1.85 | 0.44 |
| 19 | 1.25 | 1.12 | 0.90 | 2.16 | 1.36 | 0.50 | 2.14 | 1.55 | 0.59 | 2.54 | 1.58 | 0.59 | 3.53 | 1.75 | 0.44 |
| 20 | 1.44 | 0.95 | 0.67 | 2.17 | 1.47 | 0.60 | 2.15 | 1.45 | 0.48 | 2.50 | 1.65 | 0.58 | 3.22 | 1.69 | 0.48 |
| 21 | 1.39 | 0.90 | 0.71 | 2.34 | 1.51 | 0.58 | 2.19 | 1.54 | 0.58 | 2.59 | 1.72 | 0.48 | 3.27 | 1.88 | 0.38 |
| 22 | 1.17 | 0.99 | 0.75 | 2.10 | 1.50 | 0.75 | 2.10 | 1.40 | 0.59 | 2.80 | 1.63 | 0.49 | 3.60 | 1.80 | 0.39 |
| 23 | 1.15 | 1.01 | 0.86 | 2.30 | 1.45 | 0.64 | 2.13 | 1.34 | 0.39 | 2.75 | 1.65 | 0.59 | 3.23 | 1.71 | 0.49 |
| 24 | 1.08 | 1.07 | 0.87 | 2.01 | 1.34 | 0.73 | 2.24 | 1.60 | 0.58 | 2.65 | 1.53 | 0.48 | 3.89 | 1.74 | 0.38 |
| 26 | 1.05 | 1.05 | 0.90 | 2.00 | 1.56 | 0.09 | 2.26 | 1.61 | 0.49 | 2.85 | 1.59 | 0.59 | 3.65 | 1.63 | 0.49 |
| 27 | 1.03 | 1.10 | 0.88 | 2.10 | 1.40 | 0.58 | 2.10 | 1.48 | 0.77 | 2.55 | 1.68 | 0.57 | 3.83 | 1.80 | 0.47 |
| 28 | 1.25 | 1.11 | 0.76 | 2.09 | 1.35 | 0.56 | 2.15 | 1.50 | 0.58 | 2.60 | 1.75 | 0.48 | 3.35 | 1.79 | 0.38 |
| 29 | 1.27 | 1.13 | 0.77 | 2.08 | 1.32 | 0.55 | 2.13 | 1.53 | 0.59 | 2.62 | 1.76 | 0.49 | 3.36 | 1.78 | 0.39 |
| Avg. | 1.10 | 1.03 | 0.79 | 2.20 | 1.25 | 0.65 | 2.10 | 1.35 | 0.60 | 2.60 | 1.72 | 0.55 | 3.60 | 1.80 | 0.45 |
| Electrical Energy Consumption Forecasting Models | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Month | FS-FCRBM-GWDO | MI-mEDE-ANN | AFC-STLF | Bi-Level | FS-ANN | ||||||||||
| MAPD | R | MAPD | R | MAPD | R | MAPD | R | MAPD | R | ||||||
| 1 | 1.10 | 1.03 | 0.78 | 2.13 | 1.46 | 0.78 | 2.27 | 1.30 | 0.73 | 2.50 | 1.59 | 0.43 | 3.54 | 1.89 | 0.53 |
| 2 | 1.44 | 0.95 | 0.67 | 2.17 | 1.47 | 0.60 | 2.15 | 1.45 | 0.48 | 2.50 | 1.65 | 0.58 | 3.22 | 1.69 | 0.48 |
| 3 | 1.25 | 1.11 | 0.65 | 2.06 | 1.50 | 0.55 | 2.12 | 1.58 | 0.55 | 2.60 | 1.66 | 0.45 | 3.59 | 1.77 | 0.35 |
| 4 | 1.03 | 0.97 | 0.80 | 2.02 | 1.20 | 0.50 | 2.40 | 1.49 | 0.54 | 2.85 | 1.75 | 0.44 | 3.40 | 1.85 | 0.34 |
| 5 | 1.19 | 1.08 | 0.80 | 2.13 | 1.48 | 0.60 | 2.35 | 1.55 | 0.65 | 2.56 | 1.70 | 0.55 | 3.28 | 1.79 | 0.50 |
| 6 | 1.15 | 1.01 | 0.86 | 2.30 | 1.45 | 0.64 | 2.13 | 1.34 | 0.39 | 2.75 | 1.65 | 0.59 | 3.23 | 1.71 | 0.49 |
| 7 | 1.24 | 1.04 | 0.69 | 2.11 | 1.55 | 0.60 | 2.10 | 1.60 | 0.65 | 2.75 | 1.68 | 0.44 | 3.67 | 1.80 | 0.34 |
| 8 | 1.23 | 1.02 | 0.70 | 2.15 | 1.45 | 0.50 | 2.09 | 1.65 | 0.55 | 2.70 | 1.77 | 0.55 | 3.55 | 1.83 | 0.45 |
| 9 | 1.25 | 1.11 | 0.65 | 2.06 | 1.50 | 0.55 | 2.12 | 1.58 | 0.55 | 2.60 | 1.66 | 0.45 | 3.59 | 1.77 | 0.35 |
| 10 | 1.18 | 1.05 | 0.79 | 2.00 | 1.39 | 0.70 | 2.13 | 1.35 | 0.78 | 2.58 | 1.67 | 0.58 | 3.23 | 1.88 | 0.48 |
| 11 | 1.15 | 1.10 | 0.87 | 2.01 | 1.45 | 0.77 | 2.35 | 1.55 | 0.75 | 2.70 | 1.65 | 0.35 | 3.15 | 1.85 | 0.45 |
| 12 | 1.21 | 1.09 | 0.85 | 2.19 | 1.29 | 0.85 | 2.10 | 1.36 | 0.64 | 2.65 | 1.72 | 0.54 | 3.92 | 1.85 | 0.44 |
| Avg. | 1.10 | 1.03 | 0.79 | 2.20 | 1.25 | 0.65 | 2.10 | 1.35 | 0.60 | 2.60 | 1.72 | 0.55 | 3.60 | 1.80 | 0.45 |
| Performance Parameters | Electrical Energy Consumption Forecasting Models | ||||
|---|---|---|---|---|---|
| FS-ANN | Bi-Level | AFC-STLF | MI-mEDE-ANN | FS-FCRBM-GWDO | |
| Computational complexity (level) | Low | High | Moderate | High | Moderate |
| Convergence rate (epochs) | 33th | 29th | 25th | 21th | 10th |
| Execution time (sec) | 20 | 95 | 56 | 48 | 38 |
| Accuracy (%) | 96.4 | 97.4 | 97.9 | 97.8 | 98.9 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hafeez, G.; Alimgeer, K.S.; Wadud, Z.; Shafiq, Z.; Ali Khan, M.U.; Khan, I.; Khan, F.A.; Derhab, A. A Novel Accurate and Fast Converging Deep Learning-Based Model for Electrical Energy Consumption Forecasting in a Smart Grid. Energies 2020, 13, 2244. https://doi.org/10.3390/en13092244
Hafeez G, Alimgeer KS, Wadud Z, Shafiq Z, Ali Khan MU, Khan I, Khan FA, Derhab A. A Novel Accurate and Fast Converging Deep Learning-Based Model for Electrical Energy Consumption Forecasting in a Smart Grid. Energies. 2020; 13(9):2244. https://doi.org/10.3390/en13092244
Chicago/Turabian StyleHafeez, Ghulam, Khurram Saleem Alimgeer, Zahid Wadud, Zeeshan Shafiq, Mohammad Usman Ali Khan, Imran Khan, Farrukh Aslam Khan, and Abdelouahid Derhab. 2020. "A Novel Accurate and Fast Converging Deep Learning-Based Model for Electrical Energy Consumption Forecasting in a Smart Grid" Energies 13, no. 9: 2244. https://doi.org/10.3390/en13092244
APA StyleHafeez, G., Alimgeer, K. S., Wadud, Z., Shafiq, Z., Ali Khan, M. U., Khan, I., Khan, F. A., & Derhab, A. (2020). A Novel Accurate and Fast Converging Deep Learning-Based Model for Electrical Energy Consumption Forecasting in a Smart Grid. Energies, 13(9), 2244. https://doi.org/10.3390/en13092244








