A Robust q-Rung Orthopair Fuzzy Information Aggregation Using Einstein Operations with Application to Sustainable Energy Planning Decision Management

Abstract

A q-rung orthopair fuzzy set (q-ROFS), an extension of the Pythagorean fuzzy set (PFS) and intuitionistic fuzzy set (IFS), is very helpful in representing vague information that occurs in real-world circumstances. The intention of this article is to introduce several aggregation operators in the framework of q-rung orthopair fuzzy numbers (q-ROFNs). The key feature of q-ROFNs is to deal with the situation when the sum of the q^th powers of membership and non-membership grades of each alternative in the universe is less than one. The Einstein operators with their operational laws have excellent flexibility. Due to the flexible nature of these Einstein operational laws, we introduce the q-rung orthopair fuzzy Einstein weighted averaging (q-ROFEWA) operator, q-rung orthopair fuzzy Einstein ordered weighted averaging (q-ROFEOWA) operator, q-rung orthopair fuzzy Einstein weighted geometric (q-ROFEWG) operator, and q-rung orthopair fuzzy Einstein ordered weighted geometric (q-ROFEOWG) operator. We discuss certain properties of these operators, inclusive of their ability that the aggregated value of a set of q-ROFNs is a unique q-ROFN. By utilizing the proposed Einstein operators, this article describes a robust multi-criteria decision making (MCDM) technique for solving real-world problems. Finally, a numerical example related to integrated energy modeling and sustainable energy planning is presented to justify the validity and feasibility of the proposed technique.

1. Introduction

Currently, creating a sustainable energy policy for countries poses a considerable challenge. It raises several issues such as energy policy definition and planning [1], the choice of energy sources [2], and the assessment of energy supply technologies [3]. Due to the critical, complex, subjective, and poorly structured nature of the issues themselves, many of the scientists’ contributions are directed to the area of building objective models of decision support. The reason for this phenomenon should be sought in the fact that modeling this class of problems requires correct mapping not only of the assessed alternatives/variants or scenarios. In such a case, experts must also consider the consequences of analyzing the decision problem from different perspectives and points of view taking into account several conflicting criteria [4]. For example, a sustainable energy planning process requires taking into account several environmental, social, and economic groups of factors in the decision making process [5]. Often, the shape of the final ranking is additionally influenced by the presence of interest groups [6], and this factor also requires objectification and correct mapping in the developed model [7]. The availability of measurement data of the model and their imprecision [8] (together with the preference of the decision makers uncertainty [9]) are not without significance. At the same time, it is a widely raised and still valid research challenge [10].

From the methodological point of view, current literature studies confirm that an extension of the decision support process beyond the classic optimization model of a single objective function is commonly accepted, described on a set of acceptable solutions [4]. This extension makes it possible to undertake multi-criteria problems, focusing on obtaining a solution that satisfies many, often conflicting goals. The existence of many criteria, conflicts between criteria, and the complex, subjective, and poorly structured nature of the decision problem constitute the paradigm of multi-criteria decision support [11]. It is on these foundations that many multi-criteria decision making (MCDM) [12] methods have been developed. The actual state-of-the-art in this area clearly confirms that MCDM methods handle the problem mentioned above practically and effectively. The analysis of the literature indicates the prevalence of the use of MCDM methods in energy decision making issues. MCDM methods are used as practical and useful tools to solve problems related to decision making on energy policy making [13] or RES technology selection and assessment [14]. This fact can be easily confirmed by review and meta-analysis papers like Løken [15], Martín-Gamboa et al. [16], Wang et al. [5], and Arce et al. [17]. These papers show the multitude of both practical problems in the field of energy policy and MCDM techniques used as a formal background for the models developed.

The literature studies also confirm the widespread use of fuzzy developments (based on the theory of fuzzy sets) of MCDM methods in energy issues [1,18]. The essence of this approach is based on the fact that fuzzy number theory models express the uncertainty in individual opinions to obtain more sensitive, concrete, and realistic modeling results [19]. This topic is widely discussed in the literature [20]. Many new extensions of MCDM methods are being developed with the use of successive tools of different generalizations of fuzzy sets that are being designed to handle the uncertain decision making environment [21]. It is worth noting that despite a large number of methodological and practical works in this area, the authors’ conclusions indicate the need to improve the workshop of existing models supporting this decision making process [18]. The reasons for this, apart from the obvious contradiction of the goals here, are a complex and multi-level set of criteria or natural uncertainty of measurement data and decision makers preferences, which address the numerous difficulties in accurately reflecting the MCDM model [19]. In response to the aforementioned shortcomings in the current paper, we developed a new robust MCDM technique based on Einstein operators with q-rung orthopair fuzzy numbers. We propose the score function, accuracy function, and certainty function for ranking q-rung orthopair fuzzy numbers (q-ROFNs). We present the mathematical procedure of our approach to solving sustainable energy planning problems in Pakistan.

The rest of this paper is organized as follows. Section 2 contains a literature review of the MCDM method’s usage in RES domain decision problems by using uncertain and imperfect information. In Section 3, we discuss the concept of q-rung orthopair fuzzy sets (q-ROFSs). We define some operational laws, basic aggregation operators, the score function, and the accuracy function for q-rung orthopair fuzzy numbers (q-ROFNs). In Section 4, we discuss the concept of the t-norm and t-conorm and Einstein operational laws for q-ROFSs. In Section 5, we introduce some new q-rung orthopair fuzzy Einstein aggregation operators. In Section 6, we develop q-ROFNs based multi-criteria decision making method and discuss integrated energy modeling and sustainable energy policy. In Section 7, we give the conclusion of the research work.

2. Literature Review

2.1. MCDM Background in the Sustainability Domain

The analysis of the genesis and primal areas of usage of multi-criteria decision support methods emphasizes their dynamic development, which began in the 1970s. In the 1980s, they were already amongst the primary management support tools. To confirm this fact, the work presented by Teckle [22] included the current state of the research, along with an extended analysis of the applications of MCDM methods in various management problems. Examples of areas of effective use of MCDM encompassed management of water resources [23,24], including waste (sewage) [25], management of forest resources [26] (more broadly environmental [27,28]), many decision problems in transport [29] and logistics [30], as well as model issues for the MCDM problems of land parcels [31] or human resource planning [32]. It is possible to point out many applications of multi-criteria decision support methods in the area of strategic problems, such as the evaluation of projects [33], plans and strategies [34], or the choice of a specific policy direction [35], selection and evaluation of public facilities (e.g., schools [36], hospitals [37]), regional development planning [38], capital investments [39] and budgeting [40], planning and implementation of the production process [41], economic policy [42], evaluation of information systems [43], or dedicated military objectives [44]. At the moment, the area of usage of MCDM methods has become extremely broad, and apart from the model above-mentioned classes of management problems, it covers the remaining spheres of economic practice, science, as well as everyday human decision problems.

In the last decade, the concept of sustainability has been one of the most important research topics. Generally, the term sustainability refers to social, economic, and environmental [45] aspects to ensure prosperity, environmental protection, and social unity [46]. According to the scientific literature, the sustainability concept has a multi-disciplinary form and a multi-faceted nature [47]. In recent years, the topics related to sustainability, sustainability development, and sustainability management have become the main factors determining the majority of business and organizational activities. To confirm this, many global, international, national, and regional strategies are based on sustainability aspects [48]. Sustainable decision making combines management theories and the principles of sustainability, considering environmental, social, and economic factors in the decision making process [5]. Therefore, making decisions in the area of sustainable development requires the reconciliation of contradictory goals. Frequently, decisions have a multi-level and multi-faceted nature, requiring the participation and involvement of many shareholders. Thus, the need for including conflicting goals, conflicting criteria, as well as many stakeholders in one decision making process causes the modeling of sustainability problems to be often carried out using MCDM methods. This fact is confirmed by many literature studies presenting various decision problems related to sustainability, yet successfully modeled using MCDM methods. For example, the problems include assessment of sustainability processes in a selected area [49], resource planning, corporate policy and strategy [50], public policy modeling [51], spatial planning, economic [52], or government policy planning [53], measuring of the sustainable information society [54], or modeling of sustainable population growth and urbanization problems [55,56].

Moreover, MCDM methods have also been applied in sustainable modeling of the consumer market [57], optimization of the sustainable portfolio [58], modeling of the sustainable use of resources [59], maximizing user conversion [60], or modeling of industrial development and the energy crisis [61]. Besides, in the area of sustainable company management, the applicability of the MCDM methods was confirmed in such management problems as: finance, information technology, logistics (including sustainable supply chain management [62] and the choice of a sustainable supplier) [4]. The ability to aggregate data and generate synthetic assessments of individual decision making variants allows MCDM methods to create sustainable development indicators for the energy industry [63], water areas [64], rural areas [52], the development of countries [65], agricultural development [66], or urban areas [55].

2.2. MCDM Methods in Energy Policy Modeling

In recent years, a growing interest in renewable energy sources (RES) has been observed. Determinants of such a situation can be found in, among others, the development of technologies and the search for the independence of national economies of many countries from conventional energy sources [67]. Furthermore, the progressive decline in the resources of natural energy forces changes in macro and micro energy strategies, while increasing their prices on the global market. It is worth mentioning that renewable energy sources can be used almost anywhere in the world. However, the main problem corresponds to the justification of the economic, technological, environmental, and social correctness of the location and construction of infrastructure using this type of resource. For instance, an improperly located farm can be a source of negative environmental and social impacts.

The inclusion of the aforementioned environmental imperatives in energy policy planning, as well as the addition of pro-social factors have resulted in the need to reconcile conflicting objectives and different stakeholders in the process of the planning and evaluation of energy policy in regions or countries. Some of the essential tools for model structuring and problem-solving are the MCDM methods [68]. Numerous literature review studies confirmed this fact [15,16,17,69]. What is important is that the American and European schools’ approaches to the multi-criteria decision support have become very popular in this area [70]. The popularity of “American school” methods, based on value/utility theory (usually single synthesizing criterion), has been confirmed, for example in [14,71]. Among them, the analytic hierarchy process (AHP) method is widely used. It is characterized by a relatively simple computational algorithm and, at the same time, the possibility of reflecting well the complex, hierarchical structure of this class of decision making problems. Numerous works in the field of energy policy using the AHP method can be pointed out, and examples of them concern in particular the selection of renewable energy sources for sustainable development [72], strategic renewable energy resources’ selection [73], energy source policy assessment [74], or sustainable energy planning [75]. The same group of methods (schools) includes TOPSIS and VIKOR. They are based on similar principles, and their application additionally allows for the construction of so-called “reference points” (ideal and anti-ideal solution). These methods have also proven effective in the assessment of economic and environmental energy performance [76], optimization of power generation systems [77], sustainable energy-storing optimization [78], or selecting sustainable energy conversion technologies [79]. It is worth noting that the methods of the “American school” are not entirely appropriate in modeling sustainable energy issues [80]. This is directly related to the fact that these methods are characterized by an undesirable effect of linear compensation (substitution) of criteria, which in practice significantly hinders and often makes it impossible to meet the paradigm of so-called “strong sustainability” [81]. The methods of the so-called “European school” are characterized by lower levels of criteria compensation (partial compensation/non-compensation), and thus stronger fulfillment of the strong sustainability paradigm. The most popular outranking methods include ELECTRE and PROMETHEE [82]. The techniques from the ELECTRE family show effectiveness in modeling problems, in which there is an under-specification of preferential information [83], and modeling this under-specification is done using pseudo-criteria (criteria with thresholds) and outranking relations [83], which constitute the foundation for building the final outranking graph. The methods of the PROMETHEE family are characterized by the same formal assumptions (outranking relation). However, the final ranking is in the form of alternative quantitative assessments [84]. Examples of the effective use of these methods in energy policy include the evaluation of power plants [85], the evaluation of sustainable energy sources [86], rank policies [87], or investment risk evaluation for new energy resources [88]. Regardless of the methods indicated, the need to objectify the models leads researchers towards building hybrid approaches. This means that several MCDM methods are used in one model or several models are constructed for benchmarking purposes. Such procedures in the area of energy policy can be found, for example, in the works [79,89,90,91].

A detailed analysis of the works indicates that apart from the proper selection of the appropriate MCDM method, the current challenge in this class of problems remains the accurate modeling of the data, the preferences of the interveners in the model, and more importantly, their imprecision [83]. It constitutes the correctness of the entire decision making process and the quality of the final recommendation [11].

2.3. MCDM Based Uncertain Data Modeling

For many years, the issue of vague and imperfect information has been at the forefront. Information aggregation is the key factor for decision management in the areas of business, management, engineering, psychology, social sciences, medical sciences, and artificial intelligence. Traditionally, the knowledge about an alternative has been believed to be considered as simple numbers. Nevertheless, knowledge cannot be accessed in a simple form at any time in the modern world. It is very important to address data inconsistencies in order to deal with these conditions. Zadeh [92] initiated the concept of the fuzzy set by means of the membership function. A fuzzy set is a significant mathematical model to define and assemble the objects whose boundaries are elusive by utilizing membership grades. Atanassov [93] introduced the intuitionistic fuzzy set (IFS) as an extension of the fuzzy set. Yager [94,95,96] introduced the Pythagorean fuzzy set (PFS) as an extension of Atanassov’s intuitionistic fuzzy set. Bashir et al. [97] discussed the convergences for intuitionistic fuzzy set theory as important fundaments to extend MCDM methods. A Pythagorean fuzzy number (PFN) is superior to an intuitionistic fuzzy number (IFN). Yager further introduced the idea of the q-rung orthopair fuzzy set (q-ROFS) as the extension of the Pythagorean fuzzy set (PFS) [98]. A q-rung orthopair fuzzy number (q-ROFN) is superior to both IFN and PFN because IFN and PFN both may be regarded as q-ROFN, but not conversely (see [96,98]). Yager [99] introduced the concept of ordered weighted averaging aggregation operators for MCDM. Akram et al. [100,101,102,103] proved the usefulness of m-polar fuzzy soft rough sets, neutrosophic incidence graphs, and m-polar fuzzy ELECTRE-Iin decision making problems. Ali et al. [104] presented new abilities of soft sets and rough sets with fuzzy soft sets. Garg and Arora [105,106,107,108] established certain concepts of IFsoft power and dual hesitant fuzzy soft aggregation operators. Hashmi et al. [109] introduced the notion of the m-polar neutrosophic set and m-polar neutrosophic topology and their applications to MCDM in medical diagnosis and clustering analysis. Hashmi and Riaz [110] introduced a new way to handle the censuses process by using the Pythagorean m-polar fuzzy Dombi aggregation operators. In Kumar and Garg [111], a new extension of the well-known TOPSIS method based on pair set analysis with the use of interval-valued intuitionistic fuzzy set theory was presented. Karaaslan [112] introduced neutrosophic soft sets with applications in decision making. Naeem et al. [113] introduced Pythagorean fuzzy soft MCGDM methods based on TOPSIS, VIKOR, and aggregation operators. The hybrid concept based on Pythagorean m-polar fuzzy sets and the TOPSIS method was presented in Naeem et al. [114]. Peng and Yang [115] discussed some new results of PFS and defined the Pythagorean fuzzy number (PFN). Fuzzy information measures and their applications were introduced in Peng et al. [116]. Peng and Selvachandran [117] developed state-of-the-art and future directions for PFS. The new concept of the Pythagorean fuzzy soft set (covering practical areas) was presented by [118]. Pend and Dau [119] investigated the use of single-valued neutrosophic MCDMto extend the MABACand TOPSIS methods. In their work, they used a new similarity coefficient using the score function. Riaz et al. [120,121,122] introduced the N-soft topology and soft rough topology with applications to group decision making. Riaz and Hashmi [123] presented the concept of the cubic m-polar fuzzy set application in multi-attribute group decision making (MAGDM) with application to the agribusiness domain.

MCDM problem solving based on the notion of linear Diophantine fuzzy set (LDFS) was presented in [124]. LDFS is superior ti IFS, PFS, and q-ROFS. Riaz and Hashmi [125] introduced novel concepts of MCDM based on soft rough Pythagorean m-polar fuzzy sets and Pythagorean m-polar fuzzy soft rough sets. New approaches based on the idea of bipolar fuzzy soft topology, cubic bipolar fuzzy sets, and cubic bipolar fuzzy ordered weighted geometric aggregation were also presented in [126,127,128]. Studies confirmed a broad spectrum of practical usage of the given extensions.

They presented various illustrations and decision making applications of these concepts by using different algorithms. In [129], the useful concept of bipolar fuzzy soft mappings was presented. The same idea was successfully applied in the new TOPSIS method extension and its applications to MCGDM [130].

Xu proposed the IF aggregation operators concept in [131]. In the book [132], Xu and Cai introduced the theory and applications of the intuitionistic aggregation of fuzzy information. Xu [133] investigated hesitant fuzzy sets theory and different ways of aggregation knowledge. The next stage of development was the research conducted by Ye [134], who showed an approach based on interval-valued hesitant fuzzy prioritized weighted aggregation (IVHFPWA) operators and their practical application to MCDM problems. The linguistic neutrosophic cubic numbers were first presented as an extended approach to solving MCDM problems in [135]. Two interesting approaches related to soft rough covering and rough soft hemirings were proposed by Zhan et al. [136,137]. Zhang et al. [138,139,140] proposed much work for using uncertain data to solve MCDM problems. As a result of their work, they presented fuzzy soft $\beta$-covering based fuzzy rough sets, covering on generalized intuitionistic fuzzy rough sets, and fuzzy soft coverings based fuzzy rough sets. Ali [141] presented two new approaches of q-rung orthopair fuzzy sets based on L-fuzzy sets and the notion of orbits. Liu and Wang [142] presented some q-rung orthopair fuzzy aggregation operators and their application to MCDM. Liu et al. [143] developed a ranking range based approach to MCDM under incomplete knowledge, and it was verified in the venture investment evaluation.

3. Preliminaries

In this section, the conceptual ideas related to q-ROFS are given that are used in the rest of the paper.

Definition 1

([98]). A q-rung orthopair fuzzy set (q-ROFS) in a finite universe ℧ is an object of the form:

$$\mathfrak{M}=\{<\aleph ,{\mathfrak{Y}}_{\mathfrak{M}}(\aleph ),{\mathcal{F}}_{\mathfrak{M}}(\aleph )>:\aleph \in \mho \}$$

where ${\mathfrak{Y}}_{\mathfrak{M}}(\aleph )$ and ${\mathcal{F}}_{\mathfrak{M}}(\aleph )$ represent the degree of membership and the degree of non-membership of the element $\aleph \in \mho$, respectively, to the set $\mathfrak{M}$ with the condition:

$$0\le {\mathfrak{Y}}_{\mathfrak{M}}{(\aleph )}^q+{\mathcal{F}}_{\mathfrak{M}}{(\aleph )}^q\le 1,(q\ge 1)$$

and the degree of indeterminacy is given as:

$${\pi }_{\mathfrak{M}}(\aleph )={({\mathfrak{Y}}_{\mathfrak{M}}{(\aleph )}^q+{\mathcal{F}}_{\mathfrak{M}}{(\aleph )}^q-{\mathfrak{Y}}_{\mathfrak{M}}{(\aleph )}^q{\mathcal{F}}_{\mathfrak{M}}{(\aleph )}^q)}^{1/q}$$

For each $\aleph \in \mho$, a basic element of the form $\langle {\mathfrak{Y}}_{\mathfrak{M}}(\aleph ),{\mathcal{F}}_{\mathfrak{M}}(\aleph )\rangle$ in a q-ROFS, denoted by $\mathfrak{M}$, is called the q-rung orthopair fuzzy number (q-ROFN). It can be written as $\mathcal{G}=\langle {\mathfrak{Y}}_{\mathfrak{M}},{\mathcal{F}}_{\mathfrak{M}}\rangle$.

Operational Laws on q-Rung Orthopair Fuzzy Numbers

Definition 2

([142]). Let ${\mathcal{G}}_1=\langle {\mathfrak{Y}}_1,{\mathcal{F}}_1\rangle$ and ${\mathcal{G}}_2=\langle {\mathfrak{Y}}_2,{\mathcal{F}}_2\rangle$ be q-ROFNs. Then:

(1) 

$\overline{{\mathcal{G}}_1}=\langle {\mathcal{F}}_1,{\mathfrak{Y}}_1\rangle$

(2) 

${\mathcal{G}}_1\vee {\mathcal{G}}_2=\langle max\{{\mathfrak{Y}}_1,{\mathcal{F}}_1\},min\{{\mathfrak{Y}}_2,{\mathcal{F}}_2\}\rangle$

(3) 

${\mathcal{G}}_1\wedge {\mathcal{G}}_2=\langle min\{{\mathfrak{Y}}_1,{\mathcal{F}}_1\},max\{{\mathfrak{Y}}_2,{\mathcal{F}}_2\}\rangle$

(4) 

${\mathcal{G}}_1\oplus {\mathcal{G}}_2=\langle {({\mathfrak{Y}}_1^q+{\mathfrak{Y}}_2^q-{\mathfrak{Y}}_1^q{\mathfrak{Y}}_2^q)}^{1/q},{\mathcal{F}}_1{\mathcal{F}}_2\rangle$

(5) 

${\mathcal{G}}_1\otimes {\mathcal{G}}_2=\langle {\mathfrak{Y}}_1{\mathfrak{Y}}_2,{({\mathcal{F}}_1^q+{\mathcal{F}}_2^q-{\mathcal{F}}_1^q{\mathcal{F}}_2^q)}^{1/q}\rangle$

(6) 

$\sigma {\mathcal{G}}_1=\langle {(1-{(1-{\mathfrak{Y}}_1^q)}^{\sigma })}^{1/q},{\mathcal{F}}_1^{\sigma }\rangle$

(7) 

${\mathcal{G}}_1^{\sigma }=\langle {\mathfrak{Y}}_1^{\sigma },{(1-{(1-{\mathcal{F}}_1^q)}^{\sigma })}^{1/q}\rangle$

Definition 3

([142]). Assume that ${\breve{\mathcal{G}}}_k=\langle {\mathfrak{Y}}_k,{\mathcal{F}}_k\rangle$ is a family of q-ROFNs, and $q-ROFWA:{\Lambda }^n\to \Lambda$, if:

$$\begin{array}{cc}\hfill q-ROFWA({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots {\breve{\mathcal{G}}}_n)& =\sum _{k=1}^n{\mathfrak{F}}_k{\breve{\mathcal{G}}}_k\hfill \\ \hfill & ={\mathfrak{F}}_1{\breve{\mathcal{G}}}_1\oplus {\mathfrak{F}}_2{\breve{\mathcal{G}}}_2\oplus \dots ,{\mathfrak{F}}_n{\breve{\mathcal{G}}}_n\hfill \end{array}$$

where Λ is the set of all q-ROFNs, $\mathfrak{F}={({\mathfrak{F}}_1,{\mathfrak{F}}_2,\dots ,{\mathfrak{F}}_n)}^T$ is the weight vector of $({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)$ such that $0\le {\mathfrak{F}}_k\le 1$, and the sum of the components of $\mathfrak{F}$ must be equal to one. Then, the q-ROFWA is called the q-rung orthopair fuzzy weighted average operator.

Based on q-ROFNs operational rules, we can also consider q-ROFWA with Theorem 1.

Theorem 1.

Let ${\breve{\mathcal{G}}}_k=\langle {\mathfrak{Y}}_k,{\mathcal{F}}_k\rangle$ be the family of q-ROFNs; we can find $q-ROFWG$ by:

$$q-ROFWA({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots {\breve{\mathcal{G}}}_n)=〈\sqrt[q]{(1-{\displaystyle \prod _{k=1}^n}{(1-{\mathfrak{Y}}_k^q)}^{{\mathfrak{F}}_k})},{\displaystyle \prod _{k=1}^n}{\mathcal{F}}_k^{{\mathfrak{F}}_k}〉$$

Definition 4.

Assume that ${\breve{\mathcal{G}}}_k=\langle {\mathfrak{Y}}_k,{\mathcal{F}}_k\rangle$ is the family of $q-ROFN$, and $q-ROFWG:{\Lambda }^n\to \Lambda$, if:

$$\begin{array}{cc}\hfill q-ROFWG({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots {\breve{\mathcal{G}}}_n)& ={\displaystyle \sum _{k=1}^n}{\breve{\mathcal{G}}}_k^{{\mathfrak{F}}_k}\hfill \\ \hfill & ={\breve{\mathcal{G}}}_1^{{\mathfrak{F}}_1}\otimes {\breve{\mathcal{G}}}_2^{{\mathfrak{F}}_2}\otimes \dots ,{\breve{\mathcal{G}}}_n^{{\mathfrak{F}}_n}\hfill \end{array}$$

where ${\Lambda }^n$ is the set of all $q-ROFNs,$$\mathfrak{F}={({\mathfrak{F}}_1,{\mathfrak{F}}_2,\dots ,{\mathfrak{F}}_n)}^T$ is the weight vector of $({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots ,{\breve{\mathcal{G}}}_n)$ such that $0\le {\mathfrak{F}}_k\le 1$, and the sum of the components of $\mathfrak{F}$ must be equal to one. Then, the $q-ROFWG$ is called the q-rung orthopair fuzzy weighted geometric operator. On the basis of the operational laws of q-ROFNs, we can also find $q-ROFWG$ by the theorem below.

Theorem 2.

Let ${\breve{\mathcal{G}}}_k=\langle {\mathfrak{Y}}_k,{\mathcal{F}}_k\rangle$ be the family of q-ROFNs; we can find $q-ROFWG$ by:

$$q-ROFWG({\breve{\mathcal{G}}}_1,{\breve{\mathcal{G}}}_2,\dots {\breve{\mathcal{G}}}_n)=〈{\displaystyle \prod _{k=1}^n}{\mathfrak{Y}}_k^{{\mathfrak{F}}_k},\sqrt[q]{(1-{\displaystyle \prod _{k=1}^n}{(1-{\mathcal{F}}_k^q)}^{{\mathfrak{F}}_k})}〉$$

Definition 5.

Suppose $\tilde{\Re }=\langle \mathfrak{Y},\mathcal{F}\rangle$ is a q-ROFN, then a score function $\mathfrak{E}$ of $\tilde{\Re }$ is defined as:

$$\mathfrak{E}\left(\tilde{\Re }\right)={\mathfrak{Y}}^q-{\mathcal{F}}^q$$

$\mathfrak{E}\left(\tilde{\Re }\right)\in [-1,1]$. The score of a q-ROFN defines its ranking, i.e., a high score defines a high preference of q-ROFN. However, the score function is not useful in many cases of q-ROFN. For example, let us consider ${\mathcal{G}}_1=\langle 0.6138,0.2534\rangle$ and ${\mathcal{G}}_2=\langle 0.7147,0.4453\rangle$ to be two q-ROFN. If we take the value of q to be two, then $\mathfrak{E}\left({\mathcal{G}}_1\right)=0.3125=\mathfrak{E}\left({\mathcal{G}}_2\right)$, i.e, the score functions of ${\mathcal{G}}_1$ and ${\mathcal{G}}_2$ are the same. Therefore, to compare the q-ROFNs, it is not necessary to rely on the score function.

We add a further method, the accuracy function, to solve this issue.

Definition 6.

Suppose $\tilde{\Re }=\langle \mathfrak{Y},\mathcal{F}\rangle$ is a q-ROFN, then an accuracy function $\mathfrak{R}$ of $\tilde{\Re }$ is defined as:

$$\mathfrak{R}\left(\tilde{\Re }\right)={\mathfrak{Y}}^q+{\mathcal{F}}^q$$

$\mathfrak{R}\left(\tilde{\Re }\right)\in [0,1]$. The high value of accuracy degree $\mathfrak{R}\left(\tilde{\Re }\right)$ defines the high preference of $\tilde{\Re }$.

Again, consider ${\mathcal{G}}_1=\langle 0.6138,0.2534\rangle$ and ${\mathcal{G}}_2=\langle 0.7147,0.4453\rangle$ to be two q-ROFNs. Then, their accuracy functions are $\mathfrak{R}\left({\mathcal{G}}_1\right)=0.4410$ and $\mathfrak{R}\left({\mathcal{G}}_2\right)=0.4410$,so by the accuracy function, we have ${\mathcal{G}}_1<{\mathcal{G}}_2$.

Definition 7.

Let $\tilde{\mathfrak{C}}=\langle {\mathfrak{Y}}_{\tilde{\mathfrak{C}}},{\mathcal{F}}_{\tilde{\mathfrak{C}}}\rangle$ and $\tilde{\mathfrak{B}}=\langle {\mathfrak{Y}}_{\tilde{\mathfrak{B}}},{\mathcal{F}}_{\tilde{\mathfrak{B}}}\rangle$ be any two q-ROFN and $\mathfrak{E}\left(\tilde{\mathfrak{C}}\right),\mathfrak{E}\left(\tilde{\mathfrak{B}}\right)$ be the score functions of $\tilde{\mathfrak{C}}$ and $\tilde{\mathfrak{B}}$, and $\mathfrak{R}\left(\tilde{\mathfrak{C}}\right),\mathfrak{R}\left(\tilde{\mathfrak{B}}\right)$ be the accuracy functions of $\tilde{\mathfrak{C}}$ and $\tilde{\mathfrak{B}}$, respectively, then:

(1) 

If $\mathfrak{E}\left(\tilde{\mathfrak{C}}\right)>\mathfrak{E}\left(\tilde{\mathfrak{B}}\right)$, then $\tilde{\mathfrak{C}}>\tilde{\mathfrak{B}}$

(2) 

If $\mathfrak{E}\left(\tilde{\mathfrak{C}}\right)=\mathfrak{E}\left(\tilde{\mathfrak{B}}\right)$, then:

• if $\mathfrak{R}\left(\tilde{\mathfrak{C}}\right)>\mathfrak{R}\left(\tilde{\mathfrak{B}}\right)$, then $\tilde{\mathfrak{C}}>\tilde{\mathfrak{B}}$,
• if $\mathfrak{R}\left(\tilde{\mathfrak{C}}\right)=\mathfrak{R}\left(\tilde{\mathfrak{B}}\right)$, then $\tilde{\mathfrak{C}}=\tilde{\mathfrak{B}}$.

4. Einstein Operational Laws of q-ROFNs

We will give an overview of the t-norm and t-conorm in this section and give examples relevant to these norms. Some of the properties of Einstein operations are given on q-ROFNs.

For the first time in the sense of probabilistic metric spaces, triangular norms have been adopted as we use them today. Throughout decision making, statistics, and theories on non-additive measures and cooperative games, they also play a significant role. Many parameterized t-norm families are renowned functional equation solutions. T-norms are used in fuzzy set theory at the intersection of two fuzzy sets. For modeling disjunction or union, t-conorms are used. These are a simple interpretation of the conjunction and disjunction in mathematical fuzzy logic semantics and are used in MCDM to combine criteria.

A triangular norm (t-norm) is a binary operation ✠ that satisfies the following conditions at the interval $[0,1]$:

(i)

$✠(\aleph ,\tilde{\partial })=✠(\tilde{\partial },\aleph )$

(ii)

$✠(\aleph ,✠(\tilde{\partial },\tilde{\mathfrak{Z}}))=✠(✠(\aleph ,\tilde{\partial }),\tilde{\mathfrak{Z}})$

(iii)

if $\tilde{\mathfrak{P}}\le \aleph$ and $\tilde{\partial }\le \tilde{\mathfrak{Z}}$, then $✠(\tilde{\mathfrak{P}},\tilde{\partial })\le ✠(\aleph ,\tilde{\mathfrak{Z}})$

(iv)

$✠(\aleph ,1)=1$ (neutral element one) and $✠(0,0)=0$

Here, some famous examples of the t-norm are given:

• ${✠}_M(\aleph ,\tilde{\partial })=min(\aleph ,\tilde{\partial })$ (minimum or G$\ddot{o}$del t-norm)
• ${✠}_P(\aleph ,\tilde{\partial })=\aleph .\tilde{\partial }$ (product t-norm)
• ${✠}_L(\aleph ,\tilde{\partial })=max(\aleph +\tilde{\partial }-1,0)$ (Lukasiewicz t-norm)

No t-norm can attain greater values than ${✠}_M$. The idempotents of a t-norm ✠ are those ℵ satisfying $✠(\aleph ,\aleph )=\aleph$. The bounds zero and one are trivial idempotents. A t-norm is called Archimedean if each sequence ${\aleph }_n,n\in N$, where ${\aleph }_1<1$ and ${\aleph }_n=✠({\aleph }_n,{\aleph }_n)$, converges to zero. A continuous t-norm is Archimedean iff it has no idempotents between zero and one. A continuous Archimedean t-norm is called strict if $✠(\aleph ,\aleph )>0$ for all $\aleph >0$. Continuous Archimedean t-norms that are not strict are called nilpotent. The product t-norm is strict, and the Lukasiewicz t-norm is nilpotent.

A triangular conorm (t-conorm) is a binary operation $\mathfrak{S}$ that satisfies the following conditions at the interval $[0,1]$:

(i)

$\mathfrak{S}(\aleph ,\tilde{\partial })=\mathfrak{S}(\tilde{\partial },\aleph )$

(ii)

$\mathfrak{S}(\aleph ,\mathfrak{S}(\tilde{\partial },\tilde{\mathfrak{Z}}))=\mathfrak{S}(\mathfrak{S}(\aleph ,\tilde{\partial }),\tilde{\mathfrak{Z}})$

(iii)

if $\tilde{\mathfrak{P}}\le \aleph$ and $\tilde{\partial }\le \tilde{\mathfrak{Z}}$, then $\mathfrak{S}(\tilde{\mathfrak{P}},\tilde{\partial })\le \mathfrak{S}(\aleph ,\tilde{\mathfrak{Z}})$

(iv)

$\mathfrak{S}(\aleph ,0)=1$ (neutral element zero) and $\mathfrak{S}(1,1)=1$

Here, some famous examples of t-conorm are given:

• ${\mathfrak{S}}_M(\aleph ,\tilde{\partial })=max(\aleph ,\tilde{\partial })$ (maximum or G$\ddot{o}$del t-conorm)
• ${\mathfrak{S}}_P(\aleph ,\tilde{\partial })=\aleph +\tilde{\partial }-\aleph .\tilde{\partial }$ (product t-conorm)
• ${\mathfrak{S}}_L(\aleph ,\tilde{\partial })=min(\aleph +\tilde{\partial },1)$ (Lukasiewicz t-conorm)

No t-conorm can attain smaller values than ${\mathfrak{S}}_M$. If ✠ is a t-norm, then $\mathfrak{S}(\aleph ,\tilde{\partial })=1-✠(1-\aleph ,1-\tilde{\partial })$ is a t-conorm, and vice versa. Thus, we obtain a dual pair of a t-norm and a t-conorm. There are several types of groups of t-norms and t-conorms that can be chosen to construct the intersections and unions. Einstein sums and Einstein products are good alternatives for algebraic sums and algebraic products because they provide a very smooth approximation. Einstein sums and products are examples of t-norms and t-conorms and are defined as follows in the q-ROF setting.

$${✠}_{ϵ}(\aleph ,\tilde{\partial })=\frac{\aleph {.}_{ϵ}\tilde{\partial }}{\sqrt[q]{1+(1-{\aleph }^q){.}_{ϵ}(1-{\tilde{\partial }}^q)}},{\mathfrak{S}}_{ϵ}(\aleph ,\tilde{\partial })=\sqrt[q]{\frac{{\aleph }^q+{\tilde{\partial }}^q}{1+{\aleph }^q{.}_{ϵ}{\tilde{\partial }}^q}}$$

Definition 8.

Let ${\mathcal{G}}_1=\langle {\mathfrak{Y}}_1,{\mathcal{F}}_1\rangle$ and ${\mathcal{G}}_2=\langle {\mathfrak{Y}}_2,{\mathcal{F}}_2\rangle$ be q-ROFNs and $\mathfrak{w}>0$ be any real number, then:

(i) 

$\overline{{\mathcal{G}}_1}=\langle {\mathcal{F}}_1,{\mathfrak{Y}}_1\rangle$

(ii) 

${\mathcal{G}}_1{\vee }_{ϵ}{\mathcal{G}}_2=\langle max\{{\mathfrak{Y}}_1,{\mathfrak{Y}}_2\},min\{{\mathcal{F}}_1,{\mathcal{F}}_2\}\rangle$

(iii) 

${\mathcal{G}}_1{\wedge }_{ϵ}{\mathcal{G}}_2=\langle min\{{\mathfrak{Y}}_1,{\mathfrak{Y}}_2\},max\{{\mathcal{F}}_1,{\mathcal{F}}_2\}\rangle$

(iv) 

${\mathcal{G}}_1{\otimes }_{ϵ}{\mathcal{G}}_2=〈\frac{{\mathfrak{Y}}_1{.}_{ϵ}{\mathfrak{Y}}_2}{\sqrt[q]{1+(1-{\mathfrak{Y}}_1^q){.}_{ϵ}(1-{\mathfrak{Y}}_2^q)}},\sqrt[q]{\frac{{\mathcal{F}}_1^q+{\mathcal{F}}_2^q}{1+{\mathcal{F}}_1^q{.}_{ϵ}{\mathcal{F}}_2^q}}〉$

(v) 

${\mathcal{G}}_1{\oplus }_{ϵ}{\mathcal{G}}_2=〈\sqrt[q]{\frac{{\mathfrak{Y}}_1^q+{\mathcal{F}}_2^q}{1+{\mathfrak{Y}}_1^q{.}_{ϵ}{\mathfrak{Y}}_2^q}},\frac{{\mathcal{F}}_1{.}_{ϵ}{\mathcal{F}}_2}{\sqrt[q]{1+(1-{\mathcal{F}}_1^q){.}_{ϵ}(1-{\mathcal{F}}_2^q)}}〉$

(vi) 

$\mathfrak{w}{.}_{ϵ}{\mathcal{G}}_1=〈\sqrt[q]{\frac{{(1+{\left({\mathfrak{Y}}_1\right)}^q)}^{\mathfrak{w}}-{(1-{\left({\mathfrak{Y}}_1\right)}^q)}^{\mathfrak{w}}}{{(1+{\left({\mathfrak{Y}}_1\right)}^q)}^{\mathfrak{w}}+{(1-{\left({\mathfrak{Y}}_1\right)}^q)}^{\mathfrak{w}}}},\frac{\sqrt[q]{2}{\left({\mathcal{F}}_1\right)}^{\mathfrak{w}}}{\sqrt[q]{{(2-{\left({\mathfrak{Y}}_1\right)}^q)}^{\mathfrak{w}}+{\left({\left({\mathcal{F}}_1\right)}^q\right)}^{\mathfrak{w}}}}〉$

(vii) 

${\mathcal{G}}_1^{\mathfrak{w}}=〈\frac{\sqrt[q]{2}{\left({\mathfrak{Y}}_1\right)}^{\mathfrak{w}}}{\sqrt[q]{{(2-{\left({\mathfrak{Y}}_1\right)}^q)}^{\mathfrak{w}}+{\left({\left({\mathfrak{Y}}_1\right)}^q\right)}^{\mathfrak{w}}}},\sqrt[q]{\frac{{(1+{\left({\mathcal{F}}_1\right)}^q)}^{\mathfrak{w}}-{(1-{\left({\mathcal{F}}_1\right)}^q)}^{\mathfrak{w}}}{{(1+{\left({\mathcal{F}}_1\right)}^q)}^{\mathfrak{w}}+{(1-{\left({\mathcal{F}}_1\right)}^q)}^{\mathfrak{w}}}}〉$

Theorem 3.

Let ${\mathcal{G}}_1$ and ${\mathcal{G}}_2$ be q-ROFNs and $\mathfrak{w},{\mathfrak{w}}_1,{\mathfrak{w}}_2\ge 0$ be any real number, then:

(i) 

${\mathcal{G}}_1{\otimes }_{ϵ}{\mathcal{G}}_2={\mathcal{G}}_2{\otimes }_{ϵ}{\mathcal{G}}_1$

(ii) 

${\mathcal{G}}_1{\oplus }_{ϵ}{\mathcal{G}}_2={\mathcal{G}}_2{\oplus }_{ϵ}{\mathcal{G}}_1$

(iii) 

${\left({\mathcal{G}}_1{\otimes }_{ϵ}{\mathcal{G}}_2\right)}^{\mathfrak{w}}={\mathcal{G}}_1^{\mathfrak{w}}{\otimes }_{ϵ}{\mathcal{G}}_2^{\mathfrak{w}}$

(iv) 

$\mathfrak{w}{.}_{ϵ}\left({\mathcal{G}}_1{\oplus }_{ϵ}{\mathcal{G}}_2\right)=\mathfrak{w}{.}_{ϵ}{\mathcal{G}}_1{\oplus }_{ϵ}\mathfrak{w}{.}_{ϵ}{\mathcal{G}}_2$

(v) 

${\mathcal{G}}_1^{{\mathfrak{w}}_1}{\otimes }_{ϵ}{\mathcal{G}}_1^{{\mathfrak{w}}_2}={\mathcal{G}}_1^{{\mathfrak{w}}_1+{\mathfrak{w}}_2}$

(vi) 

${\mathfrak{w}}_1{.}_{ϵ}\left({\mathfrak{w}}_2{.}_{ϵ}{\mathcal{G}}_1\right)=\left({\mathfrak{w}}_1{.}_{ϵ}{\mathfrak{w}}_2\right){.}_{ϵ}{\mathcal{G}}_1$

(vii) 

${\left({\mathcal{G}}_1^{{\mathfrak{w}}_1}\right)}^{{\mathfrak{w}}_2}={\left({\mathcal{G}}_1\right)}^{{\mathfrak{w}}_1{.}_{ϵ}{\mathfrak{w}}_2}$

(viii) 

${\mathfrak{w}}_1{.}_{ϵ}{\mathcal{G}}_1{\oplus }_{ϵ}{\mathfrak{w}}_2=({\mathfrak{w}}_1+{\mathfrak{w}}_2){.}_{ϵ}{\mathcal{G}}_1$

Proof. 

See Appendix A.1. □

Theorem 4.

Let ${\mathcal{G}}_1=\langle {\mathfrak{Y}}_1,{\mathcal{F}}_1\rangle$ and ${\mathcal{G}}_2=\langle {\mathfrak{Y}}_2,{\mathcal{F}}_2\rangle$ be q-ROFNs, then:

(i) 

${\mathcal{G}}_1^c{\vee }_{ϵ}{\mathcal{G}}_2^c={\left({\mathcal{G}}_1{\wedge }_{ϵ}{\mathcal{G}}_2\right)}^c$

(ii) 

${\mathcal{G}}_1^c{\wedge }_{ϵ}{\mathcal{G}}_2^c={\left({\mathcal{G}}_1{\vee }_{ϵ}{\mathcal{G}}_2\right)}^c$

(iii) 

${\mathcal{G}}_1^c{\otimes }_{ϵ}{\mathcal{G}}_2^c={\left({\mathcal{G}}_1{\oplus }_{ϵ}{\mathcal{G}}_2\right)}^c$

(iv) 

${\mathcal{G}}_1^c{\oplus }_{ϵ}{\mathcal{G}}_2^c={\left({\mathcal{G}}_1{\otimes }_{ϵ}{\mathcal{G}}_2\right)}^c$

(v) 

$\left({\mathcal{G}}_1{\vee }_{ϵ}{\mathcal{G}}_2\right){\oplus }_{ϵ}\left({\mathcal{G}}_1{\wedge }_{ϵ}{\mathcal{G}}_2\right)=\left({\mathcal{G}}_1{\oplus }_{ϵ}{\mathcal{G}}_2\right)$

(vi) 

$\left({\mathcal{G}}_1{\vee }_{ϵ}{\mathcal{G}}_2\right){\otimes }_{ϵ}\left({\mathcal{G}}_1{\wedge }_{ϵ}{\mathcal{G}}_2\right)=\left({\mathcal{G}}_1{\otimes }_{ϵ}{\mathcal{G}}_2\right)$

Proof. 

This is a trivial case. We omit it here. □

Theorem 5.

Let ${\mathcal{G}}_1=\langle {\mathfrak{Y}}_1,{\mathcal{F}}_1\rangle$, ${\mathcal{G}}_2=\langle {\mathfrak{Y}}_2,{\mathcal{F}}_2\rangle$ and ${\mathcal{G}}_3=\langle {\mathfrak{Y}}_3,{\mathcal{F}}_3\rangle$ be q-ROFNs, then:

(i) 

$\left({\mathcal{G}}_1{\vee }_{ϵ}{\mathcal{G}}_2\right){\otimes }_{ϵ}{\mathcal{G}}_3=\left({\mathcal{G}}_1{\otimes }_{ϵ}{\mathcal{G}}_3\right){\vee }_{ϵ}\left({\mathcal{G}}_2{\otimes }_{ϵ}{\mathcal{G}}_3\right)$

(ii) 

$\left({\mathcal{G}}_1{\wedge }_{ϵ}{\mathcal{G}}_2\right){\otimes }_{ϵ}{\mathcal{G}}_3=\left({\mathcal{G}}_1{\otimes }_{ϵ}{\mathcal{G}}_3\right){\wedge }_{ϵ}\left({\mathcal{G}}_2{\otimes }_{ϵ}{\mathcal{G}}_3\right)$

(iii) 

$\left({\mathcal{G}}_1{\vee }_{ϵ}{\mathcal{G}}_2\right){\oplus }_{ϵ}{\mathcal{G}}_3=\left({\mathcal{G}}_1{\oplus }_{ϵ}{\mathcal{G}}_3\right){\vee }_{ϵ}\left({\mathcal{G}}_2{\oplus }_{ϵ}{\mathcal{G}}_3\right)$

(iv) 

$\left({\mathcal{G}}_1{\wedge }_{ϵ}{\mathcal{G}}_2\right){\oplus }_{ϵ}{\mathcal{G}}_3=\left({\mathcal{G}}_1{\oplus }_{ϵ}{\mathcal{G}}_3\right){\wedge }_{ϵ}\left({\mathcal{G}}_2{\oplus }_{ϵ}{\mathcal{G}}_3\right)$

(v) 

$\left({\mathcal{G}}_1{\wedge }_{ϵ}{\mathcal{G}}_2\right){\vee }_{ϵ}{\mathcal{G}}_3=\left({\mathcal{G}}_1{\vee }_{ϵ}{\mathcal{G}}_3\right){\wedge }_{ϵ}\left({\mathcal{G}}_2{\vee }_{ϵ}{\mathcal{G}}_3\right)$

(vi) 

$\left({\mathcal{G}}_1{\vee }_{ϵ}{\mathcal{G}}_2\right){\wedge }_{ϵ}{\mathcal{G}}_3=\left({\mathcal{G}}_1{\wedge }_{ϵ}{\mathcal{G}}_3\right){\vee }_{ϵ}\left({\mathcal{G}}_2{\wedge }_{ϵ}{\mathcal{G}}_3\right)$

Proof. 

This is a trivial case. We omit it here. □

5. q-Rung Orthopair Fuzzy Einstein Aggregation Operators

In this section, we introduce several new Einstein operators for q-ROFNs, namely the q-rung orthopair fuzzy Einstein weighted averaging (q-ROFEWA) operator, the q-rung orthopair fuzzy Einstein ordered weighted averaging (q-ROFEOWA) operator, the q-rung orthopair fuzzy Einstein weighted geometric (q-ROFEWG) operator, and the q-rung orthopair fuzzy Einstein ordered weighted geometric (q-ROFEOWG) operator.

5.1. q-Rung Orthopair Fuzzy Einstein Weighted Averaging Operator

Definition 9.

Let ${\mathcal{G}}_p=\langle {\mathfrak{Y}}_p,{\mathcal{F}}_p\rangle$ be the family of q-ROFNs and (q-ROFEWA)$:{\Lambda }^n\to \Lambda$ if,

$$\begin{array}{cc}\hfill q-ROFEWA({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)& ={\displaystyle \sum _{s=1}^n}{\mathfrak{F}}_s{\mathcal{G}}_s\hfill \\ \hfill & ={\mathfrak{F}}_1{.}_{ϵ}{\mathcal{G}}_1{\oplus }_{ϵ}{\mathfrak{F}}_2{.}_{ϵ}{\mathcal{G}}_2{\oplus }_{ϵ}\dots {\oplus }_{ϵ}{\mathfrak{F}}_n{.}_{ϵ}{\mathcal{G}}_n\hfill \end{array}$$

where Λ is the set of all $q-ROFNs$, $\mathfrak{F}={({\mathfrak{F}}_1,{\mathfrak{F}}_2,\dots ,{\mathfrak{F}}_n)}^T$ is the weight vector of $({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)$ such that $0\le {\mathfrak{F}}_s\le 1$, and the sum of the components of $\mathfrak{F}$ must be equal to one. Then, the q-ROFEWA is called the q-rung orthopair fuzzy Einstein weighted averaging operator.

We can also consider q-ROFEWA by the following theorem on the basis of Einstein’s operational laws of q-ROFNs.

Theorem 6.

Let ${\mathcal{G}}_p=\langle {\mathfrak{Y}}_p,{\mathcal{F}}_p\rangle$ be the family of q-ROFNs; we can also find q-ROFEWA by:

$$\begin{array}{cc}\hfill q-ROFEWA({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)& =\langle \sqrt[q]{\frac{{\prod }_{s=1}^n{(1+{\left({\mathfrak{Y}}_s\right)}^q)}^{{\mathfrak{F}}_s}-{\prod }_{s=1}^n{(1-{\left({\mathfrak{Y}}_s\right)}^q)}^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^n{(1+{\left({\mathfrak{Y}}_s\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^n{(1-{\left({\mathfrak{Y}}_s\right)}^q)}^{{\mathfrak{F}}_s}}},\hfill \\ \hfill & \frac{\sqrt[q]{2}{\prod }_{s=1}^n{\mathcal{F}}_s^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^n{(2-{\left({\mathcal{F}}_s\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^n{\left({\left({\mathcal{F}}_s\right)}^q\right)}^{{\mathfrak{F}}_s}}\rangle \hfill \end{array}$$

where $\mathfrak{F}={({\mathfrak{F}}_1,{\mathfrak{F}}_2,\dots ,{\mathfrak{F}}_n)}^T$ is the weight vector of $({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)$ such that $0\le {\mathfrak{F}}_s\le 1$ and ${\sum }_{s=1}^n$ ${\mathfrak{F}}_s=1$ and the sum of the components of $\mathfrak{F}$ must be equal to one.

Proof. 

See Appendix A.2. □

Theorem 7.

The aggregated value using the q-ROFEWA operator is q-ROFN.

Proof. 

See Appendix A.3. □

Theorem 8.

Let ${\mathcal{G}}_p=\langle {\mathfrak{Y}}_p,{\mathcal{F}}_p\rangle$ be the family of q-ROFNs. Then, the q-ROFWA operator and the q-ROFEWA operator have the following relation:

$$q-ROFEWA({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)\le q-ROFWA({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)$$

Proof. 

See Appendix A.4. □

Example 1.

Let ${\mathcal{G}}_1=(0.64,0.90)$, ${\mathcal{G}}_2=(0.54,0.94)$, ${\mathcal{G}}_3=(0.45,0.63)$ and ${\mathcal{G}}_4=(0.59,0.26)$ be the family of q-ROFNs, and the weight vector for these numbers is $\mathfrak{F}=(0.3,0.2,0.4,0.1)$. $q=3$, then we have,

$$\begin{array}{cc}\hfill \sqrt[q]{\frac{{\prod }_{s=1}^4{(1+{\left({\mathfrak{Y}}_s\right)}^q)}^{{\mathfrak{F}}_s}-{\prod }_{s=1}^4{(1-{\left({\mathfrak{Y}}_s\right)}^q)}^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^4{(1+{\left({\mathfrak{Y}}_s\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^4{(1-{\left({\mathfrak{Y}}_s\right)}^q)}^{{\mathfrak{F}}_s}}}& =0.5519\hfill \\ \hfill \frac{\sqrt[q]{2}{\prod }_{s=1}^4{\mathcal{F}}_s^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^4{(2-{\left({\mathcal{F}}_s\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^4{\left({\left({\mathcal{F}}_s\right)}^q\right)}^{{\mathfrak{F}}_s}}& =0.7173\hfill \end{array}$$

and:

$$\begin{array}{cc}\hfill q-ROFEWA({\mathcal{G}}_1,{\mathcal{G}}_2,{\mathcal{G}}_3,{\mathcal{G}}_4)& =\langle \sqrt[q]{\frac{{\prod }_{s=1}^4{(1+{\left({\mathfrak{Y}}_s\right)}^q)}^{{\mathfrak{F}}_s}-{\prod }_{s=1}^4{(1-{\left({\mathfrak{Y}}_s\right)}^q)}^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^4{(1+{\left({\mathfrak{Y}}_s\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^4{(1-{\left({\mathfrak{Y}}_s\right)}^q)}^{{\mathfrak{F}}_s}}},\hfill \\ \hfill & \frac{\sqrt[q]{2}{\prod }_{s=1}^4{\mathcal{F}}_s^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^4{(2-{\left({\mathcal{F}}_s\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^4{\left({\left({\mathcal{F}}_s\right)}^q\right)}^{{\mathfrak{F}}_s}}\rangle \hfill \\ \hfill & =(0.5519,0.7173)\hfill \end{array}$$

Now, we use q-ROFWA operator on these q-ROFNs:

$$\begin{array}{cc}\hfill q-ROFWA({\mathcal{G}}_1,{\mathcal{G}}_2,{\mathcal{G}}_3,{\mathcal{G}}_4)& =〈\sqrt[q]{(1-{\displaystyle \prod _{k=1}^4}{(1-{\mathfrak{Y}}_k^q)}^{{\mathfrak{F}}_k})},{\displaystyle \prod _{k=1}^4}{\mathcal{F}}_k^{{\mathfrak{F}}_k}〉\hfill \\ \hfill & =(0.5543,0.6952).\hfill \end{array}$$

It can be easily seen that:

$$q-ROFEWA({\mathcal{G}}_1,{\mathcal{G}}_2,{\mathcal{G}}_3,{\mathcal{G}}_4)\le q-ROFWA({\mathcal{G}}_1,{\mathcal{G}}_2,{\mathcal{G}}_3,{\mathcal{G}}_4)$$

5.2. q-Rung Orthopair Fuzzy Einstein Ordered Weighted Averaging Operator

Definition 10.

Let ${\mathcal{G}}_p=\langle {\mathfrak{Y}}_p,{\mathcal{F}}_p\rangle$ be the family of q-ROFNs and (q-ROFEOWA)$:{\Lambda }^n\to \Lambda$ if,

$$\begin{array}{cc}\hfill q-ROFEOWA({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)& ={\displaystyle \sum _{s=1}^n}{\mathfrak{F}}_s{\mathcal{G}}_s\hfill \\ \hfill & ={\mathfrak{F}}_1{.}_{ϵ}{\mathcal{G}}_{\pounds \left(1\right)}{\oplus }_{ϵ}{\mathfrak{F}}_2{.}_{ϵ}{\mathcal{G}}_{\pounds \left(2\right)}{\oplus }_{ϵ}\dots {\oplus }_{ϵ}{\mathfrak{F}}_n{.}_{ϵ}{\mathcal{G}}_{\pounds \left(n\right)}\hfill \end{array}$$

where Λ is the set of all q-ROFNs, $\mathfrak{F}={({\mathfrak{F}}_1,{\mathfrak{F}}_2,\dots ,{\mathfrak{F}}_n)}^T$ is the weight vector of $({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)$ such that $0\le {\mathfrak{F}}_s\le 1$ and $\pounds \left(1\right),\pounds \left(2\right),\dots ,\pounds \left(n\right)$ is a permutation of $(1,2,\dots ,n)$ such that ${\mathcal{G}}_{\pounds (i-1)}\ge {\mathcal{G}}_{\pounds \left(i\right)}$. Then, the q-ROFEWA is called the q-rung orthopair fuzzy Einstein weighted averaging operator.

We can also consider q-ROFEOWA by the following theorem on the basis of Einstein’s operational laws of q-ROFNs.

Theorem 9.

Let ${\mathcal{G}}_p=\langle {\mathfrak{Y}}_p,{\mathcal{F}}_p\rangle$ be the family of q-ROFNs; we can also find q-ROFEWA by:

$$\begin{array}{cc}\hfill q-ROFEOWA({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)& =\langle \sqrt[q]{\frac{{\prod }_{s=1}^n{(1+{\left({\mathfrak{Y}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}-{\prod }_{s=1}^n{(1-{\left({\mathfrak{Y}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^n{(1+{\left({\mathfrak{Y}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^n{(1-{\left({\mathfrak{Y}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}}},\hfill \\ \hfill & \frac{\sqrt[q]{2}{\prod }_{s=1}^n{\mathcal{F}}_{\pounds \left(s\right)}^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^n{(2-{\left({\mathcal{F}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^n{\left({\left({\mathcal{F}}_{\pounds \left(s\right)}\right)}^q\right)}^{{\mathfrak{F}}_s}}\rangle \hfill \end{array}$$

where $\mathfrak{F}={({\mathfrak{F}}_1,{\mathfrak{F}}_2,\dots ,{\mathfrak{F}}_n)}^T$ is the weight vector of $({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)$ such that $0\le {\mathfrak{F}}_s\le 1$ and ${\sum }_{s=1}^n$ ${\mathfrak{F}}_s=1$. $\pounds \left(1\right),\pounds \left(2\right),\dots ,\pounds \left(n\right)$ is a permutation of $(1,2,\dots ,n)$ such that ${\mathcal{G}}_{\pounds (i-1)}\ge {\mathcal{G}}_{\pounds \left(i\right)}$.

Proof. 

The proof is the same as Theorem 3. □

Theorem 10.

Let ${\mathcal{G}}_p=\langle {\mathfrak{Y}}_p,{\mathcal{F}}_p\rangle$ be the family of q-ROFNs. Then, the q-ROFOWA operator and q-ROFEOWA operator have the following relation:

$$q-ROFEOWA({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)\le q-ROFOWA({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)$$

Proof. 

The proof is the same as Theorem 5. □

Example 2.

Let ${\mathcal{G}}_1=(0.64,0.90)$, ${\mathcal{G}}_2=(0.54,0.94)$, ${\mathcal{G}}_3=(0.45,0.63)$ and ${\mathcal{G}}_4=(0.59,0.26)$ be the family of q-ROFNs, and the weight vector for these numbers is $\mathfrak{F}=(0.3,0.2,0.4,0.1)$. Take $q=3$. First, we find score function of all q-ROFNs,

$$\mathfrak{E}\left({\mathcal{G}}_1\right)=-0.4669$$

$$\mathfrak{E}\left({\mathcal{G}}_2\right)=-0.6731$$

$$\mathfrak{E}\left({\mathcal{G}}_3\right)=-0.1589$$

$$\mathfrak{E}\left({\mathcal{G}}_4\right)=0.1878$$

Now, ${\mathcal{G}}_{\pounds \left(1\right)}={\mathcal{G}}_4$, ${\mathcal{G}}_{\pounds \left(2\right)}={\mathcal{G}}_3$, ${\mathcal{G}}_{\pounds \left(3\right)}={\mathcal{G}}_1$, and ${\mathcal{G}}_{\pounds \left(4\right)}={\mathcal{G}}_2$. Then, we have,

$$\begin{array}{cc}\hfill \sqrt[q]{\frac{{\prod }_{s=1}^4{(1+{\left({\mathfrak{Y}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}-{\prod }_{s=1}^4{(1-{\left({\mathfrak{Y}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^4{(1+{\left({\mathfrak{Y}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^4{(1-{\left({\mathfrak{Y}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}}}& =0.586006\hfill \\ \hfill \frac{\sqrt[q]{2}{\prod }_{s=1}^4{\mathcal{F}}_{\pounds \left(s\right)}^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^4{(2-{\left({\mathcal{F}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^4{\left({\left({\mathcal{F}}_{\pounds \left(s\right)}\right)}^q\right)}^{{\mathfrak{F}}_s}}& =0.608596\hfill \end{array}$$

and:

$$\begin{array}{cc}\hfill q-ROFEOWA({\mathcal{G}}_{\pounds \left(1\right)},{\mathcal{G}}_{\pounds \left(2\right)},{\mathcal{G}}_{\pounds \left(3\right)},{\mathcal{G}}_{\pounds \left(4\right)})& =\langle \sqrt[q]{\frac{{\prod }_{s=1}^4{(1+{\left({\mathfrak{Y}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}-{\prod }_{s=1}^4{(1-{\left({\mathfrak{Y}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^4{(1+{\left({\mathfrak{Y}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^4{(1-{\left({\mathfrak{Y}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}}},\hfill \\ \hfill & \frac{\sqrt[q]{2}{\prod }_{s=1}^4{\mathcal{F}}_{\pounds \left(s\right)}^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^4{(2-{\left({\mathcal{F}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^4{\left({\left({\mathcal{F}}_{\pounds \left(s\right)}\right)}^q\right)}^{{\mathfrak{F}}_s}}\rangle \hfill \\ \hfill & =(0.586006,0.608596)\hfill \end{array}$$

Now, we use the q-ROFOWA operator on these q-ROFNs:

$$\begin{array}{cc}\hfill q-ROFOWA({\mathcal{G}}_{\pounds \left(1\right)},{\mathcal{G}}_{\pounds \left(2\right)},{\mathcal{G}}_{\pounds \left(3\right)},{\mathcal{G}}_{\pounds \left(4\right)})& =〈\sqrt[q]{{(1-{\displaystyle \prod _{k=1}^4}{(1-{\mathfrak{Y}}_{\pounds \left(k\right)})}^q)}^{{\mathfrak{F}}_k})},{\displaystyle \prod _{k=1}^4}{\mathcal{F}}_{\pounds \left(k\right)}{)}^{{\mathfrak{F}}_k}〉\hfill \\ \hfill & =(0.587646,0.579922)\hfill \end{array}$$

It can be easily seen that:

$$q-ROFEOWA({\mathcal{G}}_{\pounds \left(1\right)},{\mathcal{G}}_{\pounds \left(2\right)},{\mathcal{G}}_{\pounds \left(3\right)},{\mathcal{G}}_{\pounds \left(4\right)})\le q-ROFOWA({\mathcal{G}}_{\pounds \left(1\right)},{\mathcal{G}}_{\pounds \left(2\right)},{\mathcal{G}}_{\pounds \left(3\right)},{\mathcal{G}}_{\pounds \left(4\right)})$$

5.3. q-Rung Orthopair Fuzzy Einstein Weighted Geometric Operator

Definition 11.

Let ${\mathcal{G}}_p=\langle {\mathfrak{Y}}_p,{\mathcal{F}}_p\rangle$ be the family of q-ROFNs and (q-ROFEWG)$:{\Lambda }^n\to \Lambda$ if,

$$\begin{array}{cc}\hfill q-ROFEWG({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)& ={\displaystyle \sum _{s=1}^n}{\mathcal{G}}_s^{{\mathfrak{F}}_s}\hfill \\ \hfill & ={\mathcal{G}}_1^{{\mathfrak{F}}_1}{\otimes }_{ϵ}{\mathcal{G}}_2^{{\mathfrak{F}}_2}{\otimes }_{ϵ}\dots {\otimes }_{ϵ}{\mathcal{G}}_n^{{\mathfrak{F}}_n}\hfill \end{array}$$

where Λ is the set of all q-ROFNs and $\mathfrak{F}={({\mathfrak{F}}_1,{\mathfrak{F}}_2,\dots ,{\mathfrak{F}}_n)}^T$ is the weight vector of $({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)$ such that $0\le {\mathfrak{F}}_s\le 1$. Then, the q-ROFEWG is called the q-rung orthopair fuzzy Einstein weighted geometric operator.

We can also consider q-ROFEWG by the following theorem on the basis of Einstein’s operational laws of q-ROFNs.

Theorem 11.

Let ${\mathcal{G}}_p=\langle {\mathfrak{Y}}_p,{\mathcal{F}}_p\rangle$$(p=1,2,\dots ,n)$ be the family of q-ROFNs. Then:

$$\begin{array}{cc}\hfill q-ROFEWG({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)& =\langle \frac{\sqrt[q]{2}{\prod }_{s=1}^n{\mathfrak{Y}}_s^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^n{(2-{\left({\mathfrak{Y}}_s\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^n{\left({\left({\mathfrak{Y}}_s\right)}^q\right)}^{{\mathfrak{F}}_s}},\hfill \\ \hfill & \sqrt[q]{\frac{{\prod }_{s=1}^n{(1+{\left({\mathcal{F}}_s\right)}^q)}^{{\mathfrak{F}}_s}-{\prod }_{s=1}^n{(1-{\left({\mathcal{F}}_s\right)}^q)}^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^n{(1+{\left({\mathcal{F}}_s\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^n{(1-{\left({\mathcal{F}}_s\right)}^q)}^{{\mathfrak{F}}_s}}}\rangle \hfill \end{array}$$

where $\mathfrak{F}={({\mathfrak{F}}_1,{\mathfrak{F}}_2,\dots ,{\mathfrak{F}}_n)}^T$ is the weight vector of $({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)$ such that $0\le {\mathfrak{F}}_s\le 1$ and ${\sum }_{s=1}^n$ ${\mathfrak{F}}_s=1$.

Proof. 

See Appendix A.5. □

Theorem 12.

The aggregated value using q-ROFEWG operator is q-ROFN.

Proof. 

See Appendix A.6. □

Theorem 13.

Let ${\mathcal{G}}_p=\langle {\mathfrak{Y}}_p,{\mathcal{F}}_p\rangle$ $(p=1,2,\dots ,n)$ be the family of q-ROFNs. Then, the q-ROFWG operator and q-ROFEWG operator have the following relation:

$$q-ROFEWG({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)\le q-ROFWG({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)$$

Proof. 

The proof is the same as Theorem 5. □

Example 3.

Let ${\mathcal{G}}_1=(0.54,0.83)$, ${\mathcal{G}}_2=(0.43,0.73)$, ${\mathcal{G}}_3=(0.26,0.67)$, and ${\mathcal{G}}_4=(0.63,0.91)$ be the family of q-ROFNs, and the weight vector for these numbers is $\mathfrak{F}=(0.4,0.2,0.1,0.3)$. If $q=3$, then we have,

$$\begin{array}{cc}\hfill \frac{\sqrt[q]{2}{\prod }_{s=1}^4{\mathfrak{Y}}_s^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^4{(2-{\left({\mathfrak{Y}}_s\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^4{\left({\left({\mathfrak{Y}}_s\right)}^q\right)}^{{\mathfrak{F}}_s}}& =0.504864\hfill \\ \hfill \sqrt[q]{\frac{{\prod }_{s=1}^4{(1+{\left({\mathcal{F}}_s\right)}^q)}^{{\mathfrak{F}}_s}-{\prod }_{s=1}^4{(1-{\left({\mathcal{F}}_s\right)}^q)}^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^4{(1+{\left({\mathcal{F}}_s\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^4{(1-{\left({\mathcal{F}}_s\right)}^q)}^{{\mathfrak{F}}_s}}}& =0.835576\hfill \end{array}$$

and:

$$\begin{array}{cc}\hfill q-ROFEWG({\mathcal{G}}_1,{\mathcal{G}}_2,{\mathcal{G}}_3,{\mathcal{G}}_4)& =\langle \frac{\sqrt[q]{2}{\prod }_{s=1}^4{\mathfrak{Y}}_s^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^4{(2-{\left({\mathfrak{Y}}_s\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^4{\left({\left({\mathfrak{Y}}_s\right)}^q\right)}^{{\mathfrak{F}}_s}},\hfill \\ \hfill & \sqrt[q]{\frac{{\prod }_{s=1}^4{(1+{\left({\mathcal{F}}_s\right)}^q)}^{{\mathfrak{F}}_s}-{\prod }_{s=1}^4{(1-{\left({\mathcal{F}}_s\right)}^q)}^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^4{(1+{\left({\mathcal{F}}_s\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^4{(1-{\left({\mathcal{F}}_s\right)}^q)}^{{\mathfrak{F}}_s}}}\rangle \hfill \\ \hfill & =(0.504864,0.835576)\hfill \end{array}$$

Now, we use q-ROFWG operator on these q-ROFNs:

$$\begin{array}{cc}\hfill q-ROFWG({\mathcal{G}}_1,{\mathcal{G}}_2,{\mathcal{G}}_3,{\mathcal{G}}_4)& =〈{\displaystyle \prod _{k=1}^4}{\mathfrak{Y}}_k^{{\mathfrak{F}}_k},\sqrt[q]{(1-{\displaystyle \prod _{k=1}^4}{(1-{\mathcal{F}}_k^q)}^{{\mathfrak{F}}_k})}〉\hfill \\ \hfill & =(0.502286,0.839142)\hfill \end{array}$$

It can be easily seen that:

$$q-ROFEWG({\mathcal{G}}_1,{\mathcal{G}}_2,{\mathcal{G}}_3,{\mathcal{G}}_4)\le q-ROFWG({\mathcal{G}}_1,{\mathcal{G}}_2,{\mathcal{G}}_3,{\mathcal{G}}_4)$$

5.4. q-Rung Orthopair Fuzzy Einstein Ordered Weighted Geometric Operator

Definition 12.

Let ${\mathcal{G}}_p=\langle {\mathfrak{Y}}_p,{\mathcal{F}}_p\rangle$ be the family of q-ROFNs and (q-ROFEOWG)$:{\Lambda }^n\to \Lambda$ if,

$$\begin{array}{cc}\hfill q-ROFEOWG({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)& ={\displaystyle \sum _{s=1}^n}{\mathcal{G}}_s^{{\mathfrak{F}}_s}\hfill \\ \hfill & ={\mathcal{G}}_{\pounds \left(1\right)}^{{\mathfrak{F}}_1}{\otimes }_{ϵ}{\mathcal{G}}_{\pounds \left(2\right)}^{{\mathfrak{F}}_2}{\otimes }_{ϵ}\dots {\otimes }_{ϵ}{\mathcal{G}}_{\pounds \left(n\right)}^{{\mathfrak{F}}_n}\hfill \end{array}$$

where Λ is the set of all $q-ROFNs$ and $\mathfrak{F}={({\mathfrak{F}}_1,{\mathfrak{F}}_2,\dots ,{\mathfrak{F}}_n)}^T$ is the weight vector of $({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)$ such that $0\le {\mathfrak{F}}_s\le 1$. $\pounds \left(1\right),\pounds \left(2\right),\dots ,\pounds \left(n\right)$ is a permutation of $(1,2,\dots ,n)$ such that ${\mathcal{G}}_{\pounds (i-1)}\ge {\mathcal{G}}_{\pounds \left(i\right)}$. Then, $q-ROFEWA$ is called the q-rung orthopair fuzzy Einstein weighted geometric operator.

On the basis of Einstein operational laws of q-ROFNs, we can also find q-ROFEOWG by the following theorem.

Theorem 14.

Let ${\mathcal{G}}_p=\langle {\mathfrak{Y}}_p,{\mathcal{F}}_p\rangle$ be the family of q-ROFNs; we can also find q-ROFEWA by:

$$\begin{array}{cc}\hfill q-ROFEOWG({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)& =\langle \frac{\sqrt[q]{2}{\prod }_{s=1}^n{\mathfrak{Y}}_{\pounds \left(s\right)}^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^n{(2-{\left({\mathfrak{Y}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^n{\left({\left({\mathfrak{Y}}_{\pounds \left(s\right)}\right)}^q\right)}^{{\mathfrak{F}}_s}},\hfill \\ \hfill & \sqrt[q]{\frac{{\prod }_{s=1}^n{(1+{\left({\mathcal{F}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}-{\prod }_{s=1}^n{(1-{\left({\mathcal{F}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^n{(1+{\left({\mathcal{F}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^n{(1-{\left({\mathcal{F}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}}}\rangle \hfill \end{array}$$

where $\mathfrak{F}={({\mathfrak{F}}_1,{\mathfrak{F}}_2,\dots ,{\mathfrak{F}}_n)}^T$ is the weight vector of $({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)$ such that $0\le {\mathfrak{F}}_s\le 1$. $\pounds \left(1\right),\pounds \left(2\right),\dots ,\pounds \left(n\right)$ is a permutation of $(1,2,\dots ,n)$ such that ${\mathcal{G}}_{\pounds (i-1)}\ge {\mathcal{G}}_{\pounds \left(i\right)}$.

Proof. 

The proof is the same as Theorem 11. □

Theorem 15.

Let ${\mathcal{G}}_p=\langle {\mathfrak{Y}}_p,{\mathcal{F}}_p\rangle$ be the family of q-ROFNs. Then, the q-ROFOWA operator and q-ROFEOWG operator have the following relation:

$$q-ROFEOWG({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)\le q-ROFOWG({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_n)$$

Proof. 

The proof is obvious. □

Example 4.

Let ${\mathcal{G}}_1=(0.54,0.83)$, ${\mathcal{G}}_2=(0.43,0.73)$, ${\mathcal{G}}_3=(0.26,0.67)$, and ${\mathcal{G}}_4=(0.63,0.91)$ be the family of q-ROFNs, and the weight vector for these numbers is $\mathfrak{F}=(0.4,0.2,0.1,0.3)$. If $q=3$, first we find the score function of all q-ROFNs,

$$\mathfrak{E}\left({\mathcal{G}}_1\right)=-0.4143$$

$$\mathfrak{E}\left({\mathcal{G}}_2\right)=-0.3095$$

$$\mathfrak{E}\left({\mathcal{G}}_3\right)=-0.2832$$

$$\mathfrak{E}\left({\mathcal{G}}_4\right)=-0.5035$$

Now, ${\mathcal{G}}_{\pounds \left(1\right)}={\mathcal{G}}_3$, ${\mathcal{G}}_{\pounds \left(2\right)}={\mathcal{G}}_2$, ${\mathcal{G}}_{\pounds \left(3\right)}={\mathcal{G}}_1$, and ${\mathcal{G}}_{\pounds \left(4\right)}={\mathcal{G}}_4$. Then we have,

$$\begin{array}{cc}\hfill \frac{\sqrt[q]{2}{\prod }_{s=1}^4{\mathfrak{Y}}_{\pounds \left(s\right)}^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^4{(2-{\left({\mathfrak{Y}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^4{\left({\left({\mathfrak{Y}}_{\pounds \left(s\right)}\right)}^q\right)}^{{\mathfrak{F}}_s}}& =0.406854\hfill \\ \hfill \sqrt[q]{\frac{{\prod }_{s=1}^4{(1+{\left({\mathcal{F}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}-{\prod }_{s=1}^4{(1-{\left({\mathcal{F}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^4{(1+{\left({\mathcal{F}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^4{(1-{\left({\mathcal{F}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}}}& =0.800078\hfill \end{array}$$

and:

$$\begin{array}{cc}\hfill q-ROFEOWG({\mathcal{G}}_{\pounds \left(1\right)},{\mathcal{G}}_{\pounds \left(2\right)},{\mathcal{G}}_{\pounds \left(3\right)},{\mathcal{G}}_{\pounds \left(4\right)})& =\langle \frac{\sqrt[q]{2}{\prod }_{s=1}^4{\mathfrak{Y}}_{\pounds \left(s\right)}^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^4{(2-{\left({\mathfrak{Y}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^4{\left({\left({\mathfrak{Y}}_{\pounds \left(s\right)}\right)}^q\right)}^{{\mathfrak{F}}_s}},\hfill \\ \hfill & \sqrt[q]{\frac{{\prod }_{s=1}^4{(1+{\left({\mathcal{F}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}-{\prod }_{s=1}^4{(1-{\left({\mathcal{F}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}}{{\prod }_{s=1}^4{(1+{\left({\mathcal{F}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}+{\prod }_{s=1}^4{(1-{\left({\mathcal{F}}_{\pounds \left(s\right)}\right)}^q)}^{{\mathfrak{F}}_s}}}\rangle \hfill \\ \hfill & =(0.406854,0.800078)\hfill \end{array}$$

Now, we use q-ROFOWG operator on these q-ROFNs:

$$\begin{array}{cc}\hfill q-ROFOWG({\mathcal{G}}_{\pounds \left(1\right)},{\mathcal{G}}_{\pounds \left(2\right)},{\mathcal{G}}_{\pounds \left(3\right)},{\mathcal{G}}_{\pounds \left(4\right)})& =〈{\displaystyle \prod _{k=1}^4}{({\mathfrak{Y}}_{\pounds \left(k\right)}}^{{\mathfrak{F}}_k},\sqrt[q]{{(1-{\displaystyle \prod _{k=1}^4}{(1-{\mathcal{F}}_{\pounds \left(k\right)})}^q)}^{{\mathfrak{F}}_k})}〉\hfill \\ \hfill & =(0.403389,0.807254)\hfill \end{array}$$

It can be easily seen that:

$$q-ROFEOWG({\mathcal{G}}_{\pounds \left(1\right)},{\mathcal{G}}_{\pounds \left(2\right)},{\mathcal{G}}_{\pounds \left(3\right)},{\mathcal{G}}_{\pounds \left(4\right)})\le q-ROFOWG({\mathcal{G}}_{\pounds \left(1\right)},{\mathcal{G}}_{\pounds \left(2\right)},{\mathcal{G}}_{\pounds \left(3\right)},{\mathcal{G}}_{\pounds \left(4\right)})$$

6. MCDM Problem for the Proposed Operators

We discuss the MCDM problem by using the proposed operators. Consider a set of alternatives $\widehat{\mathfrak{T}}=\{{\widehat{\mathfrak{T}}}_1,{\widehat{\mathfrak{T}}}_2,\dots ,{\widehat{\mathfrak{T}}}_m\}$ with m elements, and $\mathfrak{O}=\{{\mathfrak{O}}_1,{\mathfrak{O}}_2,\dots ,{\mathfrak{O}}_n\}$ is the finite set of criteria with n elements. The decision maker provides a matrix of his/her own opinion $D={\left({\zeta }_{ij}\right)}_{m\times n}$, where ${\zeta }_{ij}$ is given for the alternatives ${\widehat{\mathfrak{T}}}_i\in \widehat{\mathfrak{T}}$ with respect to the criteria ${\mathfrak{O}}_j\in \mathfrak{O}$ by the decision maker in the form of q-ROFNs. A MCDM problem can be expressed in the form of the decision matrix of $q-ROPFNs$ written by $D={\left({\zeta }_{ij}\right)}_{m\times n}={({\mathfrak{Y}}_{ij},{\mathcal{F}}_{ij})}_{m\times n}$:

$$\begin{array}{ccccc}& {\mathfrak{O}}_1& {\mathfrak{O}}_2\hfill & & {\mathfrak{O}}_n\\ \hfill \begin{array}{c}\hfill {\widehat{\mathfrak{T}}}_1\\ \hfill {\widehat{\mathfrak{T}}}_2\\ \\ \hfill {\widehat{\mathfrak{T}}}_m\end{array}& [\begin{array}{c}({\mathfrak{Y}}_{11},{\mathcal{F}}_{11})\\ ({\mathfrak{Y}}_{21},{\mathcal{F}}_{21})\\ ⋮\\ ({\mathfrak{Y}}_{m1},{\mathcal{F}}_{m1})\end{array}& \begin{array}{c}({\mathfrak{Y}}_{12},{\mathcal{F}}_{12})\\ ({\mathfrak{Y}}_{22},{\mathcal{F}}_{22})\\ ⋮\\ ({\mathfrak{Y}}_{m2},{\mathcal{F}}_{m2})\end{array}& \begin{array}{c}\cdots \cdots \\ \cdots \cdots \\ \ddots \ddots \\ \cdots \cdots \end{array}& \begin{array}{c}({\mathfrak{Y}}_{1n},{\mathcal{F}}_{1n})\\ ({\mathfrak{Y}}_{2n},{\mathcal{F}}_{2n})\\ ⋮\\ ({\mathfrak{Y}}_{mn},{\mathcal{F}}_{mn})\end{array}]\end{array}$$

The proposed operators will be applied to the MCDM, which involves Algortihm 1.

Algorithm 1. The decision-making algorithm based on q-ROFNs and Einstein Aggregation Operators

Step 1: Acquire a decision matrix $D={\left({\zeta }_{ij}\right)}_{m\times n}$ in the form of q-ROFNs from the decision maker. Step 2: The criteria involved in the decision matrix are defined by two types, namely cost-type criteria $\left({\tau }_c\right)$ and benefit-type criteria $\left({\tau }_b\right)$. If all criteria are the same types, there is no need for normalization, but there are two types of criteria in MCDM; in this case using the normalization formula the matrix D has been changed into normalizing matrix $Y\left(k_{ij}\right)=({\psi }_{ij},{\varphi }_{ij})$: $$k_{ij}=({\psi }_{ij},{\varphi }_{ij})=\left\{\begin{array}{cc}{\varsigma }_{ij}^c;\hfill & j\in {\tau }_c\hfill \\ {\varsigma }_{ij};\hfill & j\in {\tau }_b.\hfill \end{array}\right.$$ where ${\varsigma }_{ij}^c$ show the compliment of ${\varsigma }_{ij}$. Step 3: Use one of the suggested operators to determine cumulative assessments of the alternatives. $$k_i=q-ROFEWA(k_{i1},k_{i2},\dots ,k_{in}),(i=1,2,3,\dots ,m)$$ or: $$k_i=q-ROFEWG(k_{i1},k_{i2},\dots ,k_{in}),(i=1,2,3,\dots ,m)$$ Step 4: Calculate the score of all cumulative assessments of the alternatives. Step 5: Rank the alternatives by the score function and ultimately choose the most suitable alternative.

The flowchart of the proposed algorithm is presented in Figure 1.

6.1. Case Study

Electricity is a main energy resource among the different energy resources and has a high demand from the different economic sectors. Nevertheless, the production of electricity is followed by serious challenges of technology, climate, and sustainability. Fossil fuels such as coal, oil, and natural gas are the main primary energy resources used to generate electricity. It was recently reported that around 70% of electricity is produced worldwide from fossil fuels. Consequently, fossil fuel electricity generation also includes greenhouse gases (GHG), other emissions, and air pollutants. A comparison is made between coal, natural gas, nuclear, hydro, solar, wind, geothermal, and biomass generation. The parameters considered are system cost minimization, water footprint, and land intensity. The most popular energy modeling techniques include [144,145,146]:

• The energy and power evaluation program (ENPEP) is a nonlinear equilibrium model that balances the requirement for energy with available resources and technologies;
• Market allocation (MARKAL) is an integrated energy system that may be used to quantify the consequences of policy decisions on technology development and resource consumption;
• The model for the energy supply strategy alternatives and their general environmental impact (MESSAGE) combines technologies and fuels and constructs energy chains, which allows mapping energy flows from resource extraction to energy services; and
• The long-range energy alternatives planning system (LEAP) assists in energy policy analysis, especially tracking energy consumption, production, and resource extraction. These strategies are well designed for various levels of energy management. Energy models include a reliable framework to check predictions by organizing massive amounts of data in an open manner that reflects a stable system.

Across its background, Pakistan has suffered terrible energy challenges. The country’s energy crises, which extend mostly over a decade, have resulted in the collapse of thousands of factories, decreasing industrial production and influencing the lives of millions of families. For a developing country like Pakistan, choosing the best future direction of electricity generation is an inevitable challenge. In this context, energy modeling could be of great help if it takes into account the energy resource efficiency and the techno-economic and other relevant parameters to identify potential future energy pathways. Throughout the last quarter century, these crises have negatively affected the economy, with a loss of around 10% of the total gross domestic product(GDP). If not resolved at both the operational and strategic levels, Pakistan’s energy challenges could become a national interest threat [147].

In this analysis, electricity demand for the 2015–2050 time frame was calculated using the LEAP model. LEAP has become a consumer-friendly energy management tool that is used internationally for energy policy analysis. LEAP promotes a modeling approach based on scenarios by monitoring the growth, transition, and use of energy resources across the economy [148]. LEAP is a commonly used software tool developed at the Swedish Environment Institute for energy policy research and evaluation of climate change mitigation. LEAP has been implemented in far more than 190 countries around the world. The customers include state agencies, researchers, NGOs, consulting firms, and energy providers. It has been used from cities and countries to regional, national, and international applications in a wide range of dimensions. [149] When designing the modeling structure for Pakistan’s LEAP, 2015 was set as the reference year, as well 2050 as the final year. Reference (REF), which is an energy mechanism according to the latest plans and policies of the GOP, was the first supply side example. The paths of renewable energy technologies (RET) envisaged full penetration of renewable energy sources, and the scenario of clean coal maximum (CCM) foresees the use of reliable technologies for coal based power generation. The fourth scenario is called the energy efficiency and conservation (EEC) scenario. Pakistan’s total electricity requirement in 2050 is expected to be 1706.1 TWh, and in 2015, it was just 90.4 TWh. Because the REF, RET, and CCM scenarios were based on common demand-side assumptions, there was the same demand forecast for these three scenarios. For the EEC scenario, however, the projection of electricity demand for the same duration was calculated at 1373.2 TWh, which was 20 percent lower than the demand projected in the reference scenario.

Table 1. Concise overview of the main scenarios. CCM, clean coal maximum; EEC, energy efficiency and conservation; RET, renewable energy technologies.

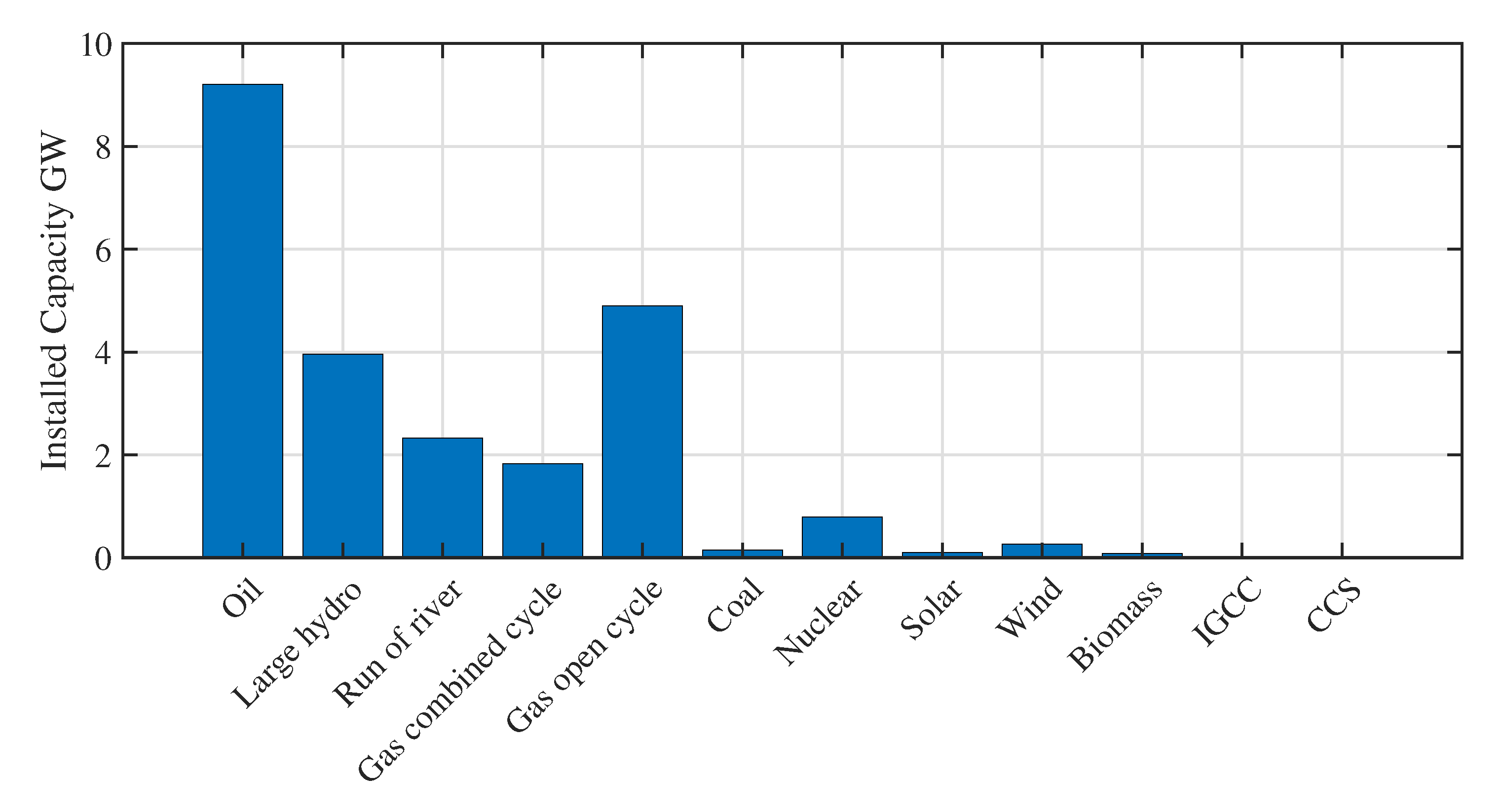
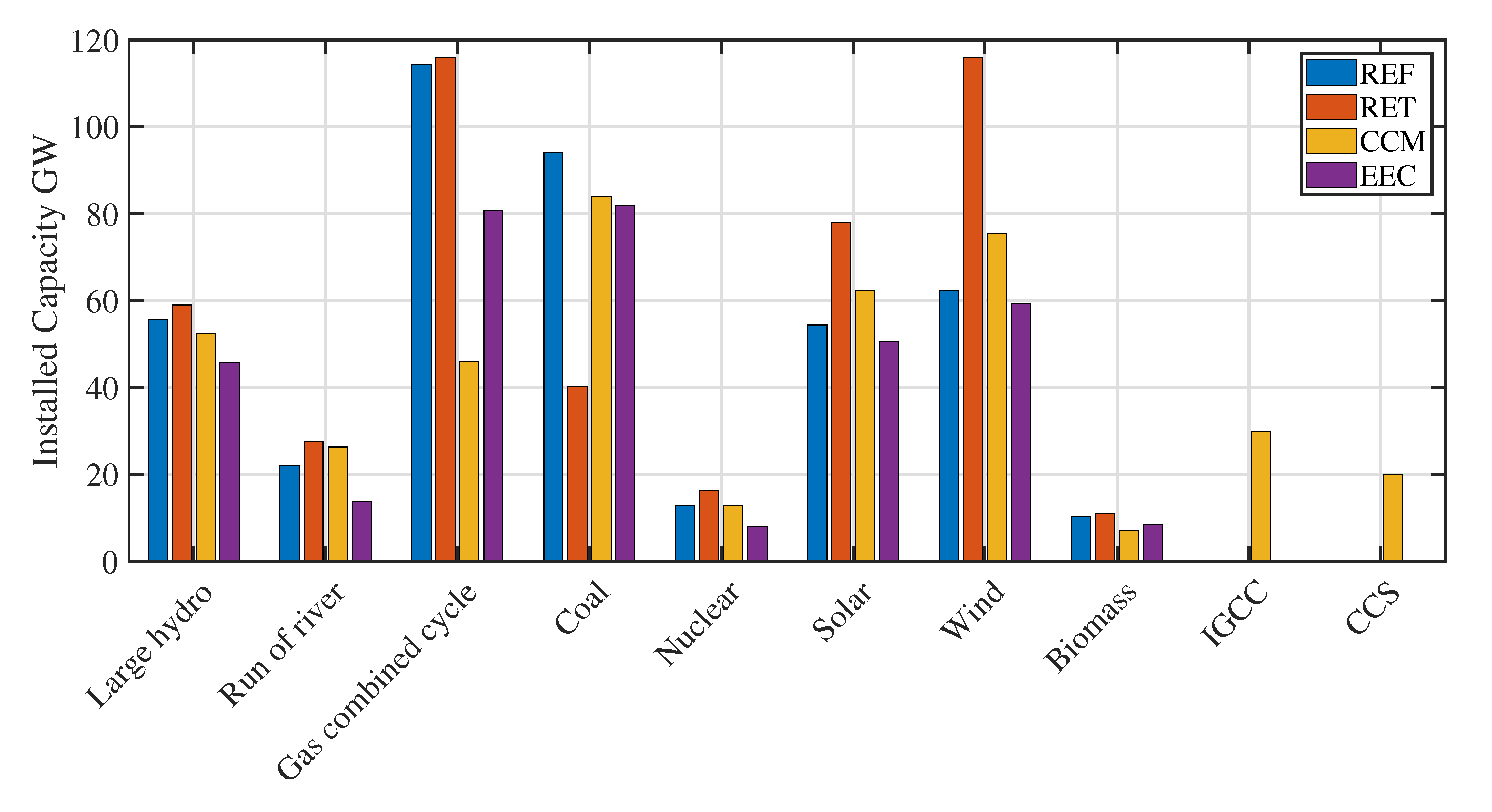
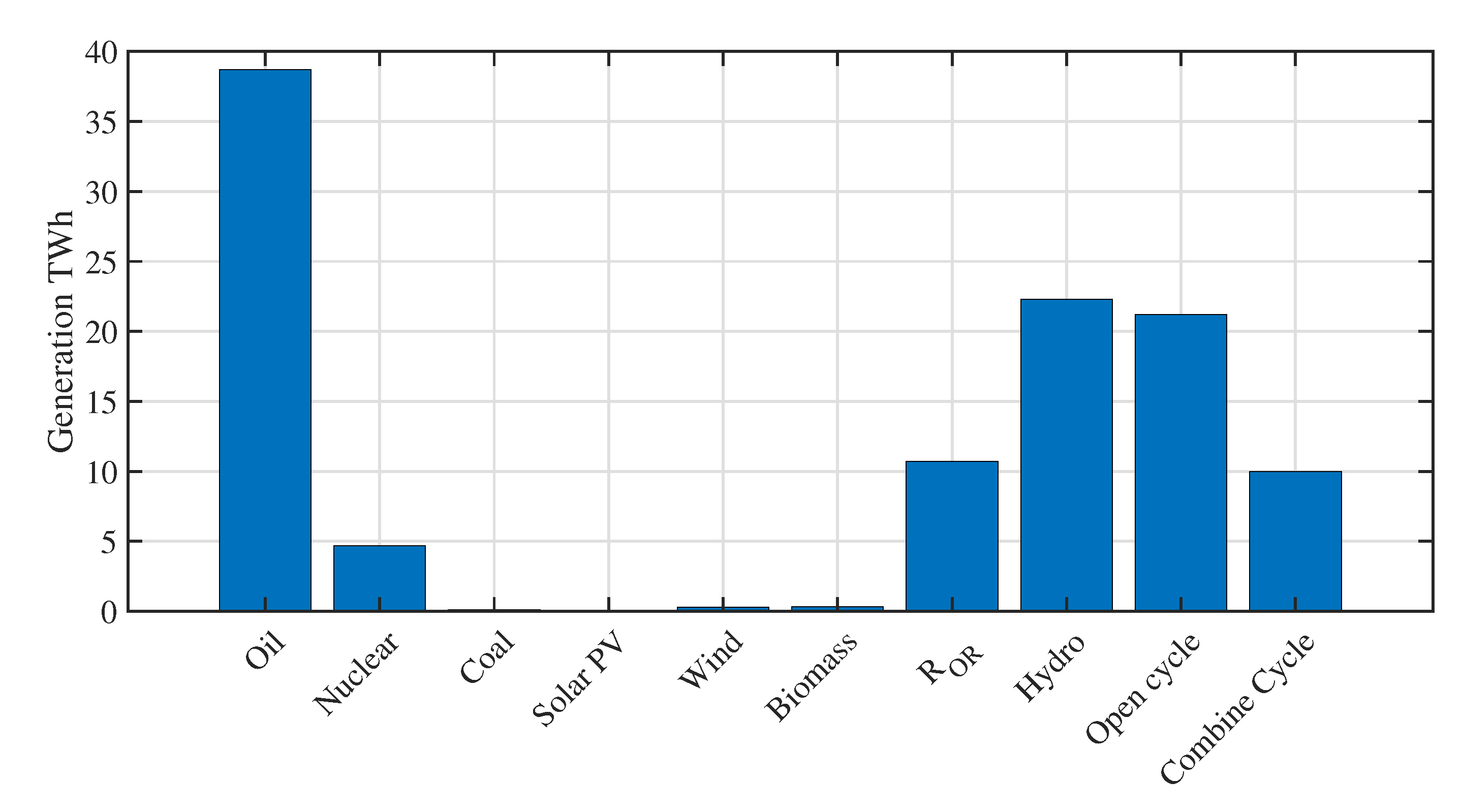
Scenario	Definition	Resources
CCM	The choice of clean coal is favorable under this scenario.	Indigenous coal, oil, gas, and nuclear.
EEC	The efficiency and conservation measures are considered under this scenario.	Strategies for productivity and capacity for recycling.
REF	The current proposal and policy of the state is being pursued in this situation.	As per the plans and policies of the state.
RET	Sustainable energy options and technology are favored under this situation.	Sources of renewable energy, hydro, solar, wind, and biomass.

shows a concise overview of the main scenarios (alternatives).

The supply side scenario alternatives were developed in the LEAP model in accordance with the different production technology’s resource potential and technical-economic parameters. The 2015/2050 generation (TWh) and installed power (GW) forecasts for various fuels and technologies are available. The total installed capacity in 2015 was 23.62 (GW). In 2015, the most widely used technology was oil and open cycle gas, which accounted for half of the installed capacity. Figure 2 presents installed capacity with respect to various fuels and technologies.

By the LEAP model, installed capacity by the different scenarios in 2050 was 425.94 (GW) by REF, 463.9 (GW) by RET, 416.21 (GW) by CCM, and 348.56 (GW) by EEC. Figure 3 shows installed capacity in different scenarios. The considered scenarios assumed a move away from oil processing and an increase in the share of renewable energy sources and increased use of coal.

Generation was 108.3 (TWh) from various fuels and innovations in 2015. Figure 4 presents the details, where most of the electricity was generated using oil and hydro technologies. In this area, technologies related to coal, solar PV, lifts, and biomass were marginal.

Through LEAP, model generation in 2050 will be 1373.2 (TWh) and through EEC, 1706.10 (TWh) by REF, RET, and CCM across different scenarios. Figure 5 presents the generation in various scenarios for Pakistan in 2050. Renewable energy, such as run of river, biomass, and wind, will have the largest share in electricity generation with varying degrees depending on the chosen scenario.

To determine the best alternative among the four scenarios given in Table 1, we have the following criteria given in

Table 2. Criteria for evaluating the best alternative.

	Criteria	Definition	Ref
$G_1$	Requirement for land	One of the key elements for an investment is land requirements. Furthermore, a good land call will assess monetary losses.	[150,151]
$G_2$	CO${}_2$ emissions	This selection criteria considers the emissions of CO${}_2$ and the costs related to waste treatment.	[152,153,154]
$G_3$	Waste disposal management	This alternative approach can be measured to reduce harm to life quality and improve sustainability by taking this criterion into account.	[153,154]
$G_4$	Risk	Measures the probability of failure.	[153,154,155]
$G_5$	Feasibility	Measures the energy scenario implementation probability.	[156,157]
$G_6$	Reliability	It is the capacity of a structure to operate according to the designed circumstances.	[83,84,158]
$G_7$	Job creation	Energy policies are measured by taking into consideration the labor effect measured by taking care of jobs directly and indirectly.	[47,49,158]
$G_8$	Investment cost	This consists of common expenditure throughout the establishment of a power plant, which covers the cost of machinery, manpower, construction, and infrastructure.	[63,91,159]
$G_9$	Political acceptance	This criterion examines that there may not be consensus among many of the views of the leaders on the planned energy policy.	[1,2,76,86]
$G_{10}$	Social acceptance	Social acceptance involves evaluating the company’s perceived understanding of ventures and measuring the customer’s opinions.	[1,2,15,69]

, which were selected on the basis of a literature review.

6.2. Illustrative Example

An illustrative example of the sustainable energy policy in Pakistan is given to illustrate the approach. Here, the set of alternatives is $\widehat{\widehat{\mathfrak{T}}}=\{{\widehat{\mathfrak{T}}}_1,{\widehat{\mathfrak{T}}}_2,{\widehat{\mathfrak{T}}}_3,{\widehat{\mathfrak{T}}}_4\}$ where ${\widehat{\mathfrak{T}}}_1$ = CCM, ${\widehat{\mathfrak{T}}}_2$ = EEC, ${\widehat{\mathfrak{T}}}_3$ = REF, and ${\widehat{\mathfrak{T}}}_4$ = RET. In evaluating these alternatives, we have the set of criteria $\mathfrak{O}=\{{\mathfrak{O}}_1,{\mathfrak{O}}_2,\dots ,{\mathfrak{O}}_{10}\}$ given in Table 2 and take $q=3$. Let $\mathfrak{F}=\{0.13,0.8,0.9,0.11,0.8,0.11,0.7,0.9,0.14,0.10\}$ be their corresponding weight vector, and assume that the expert provides his/her own point of view in the form of the decision matrix $D={\left({\zeta }_{ij}\right)}_{4\times 10}$ of the q-RONs as follows.

$$\begin{array}{cccccc}& {\mathfrak{O}}_1& {\mathfrak{O}}_2& {\mathfrak{O}}_3& {\mathfrak{O}}_4& {\mathfrak{O}}_5\\ \begin{array}{c}\hfill {\widehat{\mathfrak{T}}}_1\\ \hfill {\widehat{\mathfrak{T}}}_2\\ \hfill {\widehat{\mathfrak{T}}}_3\\ \hfill {\widehat{\mathfrak{T}}}_4\end{array}& (\begin{array}{c}(0.23,0.79)\\ (0.93,0.11)\hfill \\ (0.71,0.23)\\ (0.54,0.16)\end{array}& \begin{array}{c}(0.34,0.69)\\ (0.69,0.21)\hfill \\ (0.65,0.31)\\ (0.23,0.16)\end{array}& \begin{array}{c}(0.23,0.71)\\ (0.79,0.31)\hfill \\ (0.69,0.41)\\ (0.51,0.53)\end{array}& \begin{array}{c}(0.39,0.81)\\ (0.89,0.31)\hfill \\ (0.83,0.29)\\ (0.79,0.53)\end{array}& \begin{array}{c}(0.16,0.59)\\ (0.81,0.25)\hfill \\ (0.79,0.34)\\ (0.89,0.56)\end{array})\\ & {\mathfrak{O}}_6& {\mathfrak{O}}_7& {\mathfrak{O}}_8& {\mathfrak{O}}_9& {\mathfrak{O}}_{10}\\ \begin{array}{c}\hfill {\widehat{\mathfrak{T}}}_1\\ \hfill {\widehat{\mathfrak{T}}}_2\\ \hfill {\widehat{\mathfrak{T}}}_3\\ \hfill {\widehat{\mathfrak{T}}}_4\end{array}& (\begin{array}{c}(0.10,0.69)\\ (0.81,0.31)\hfill \\ (0.92,0.43)\\ (0.32,0.16)\end{array}& \begin{array}{c}(0.25,0.61)\\ (0.92,0.13)\hfill \\ (0.53,0.27)\\ (0.34,0.15)\end{array}& \begin{array}{c}(0.41,0.23)\\ (0.79,0.13)\hfill \\ (0.53,0.23)\\ (0.79,0.13)\end{array}& \begin{array}{c}(0.09,0.63)\\ (0.69,0.23)\hfill \\ (0.81,0.31)\\ (0.69,0.17)\end{array}& \begin{array}{c}(0.15,0.79)\\ (0.85,0.27)\hfill \\ (0.89,0.51)\\ (0.23,0.43)\end{array})\end{array}$$

First, we get the normalized decision matrix by taking the compliment of the cost-type criteria, in Table 2 ${\mathfrak{O}}_1$ = land requirement, ${\mathfrak{O}}_2=$ CO${}_2$ emission, ${\mathfrak{O}}_4$= risk, and ${\mathfrak{O}}_8$ = investment cost are the cost-type criteria. $Y\left(k_{ij}\right)=({\psi }_{ij},{\varphi }_{ij})$ is obtained by taking the compliment operation as follows.

$$\begin{array}{cccccc}& {\mathfrak{O}}_1& {\mathfrak{O}}_2& {\mathfrak{O}}_3& {\mathfrak{O}}_4& {\mathfrak{O}}_5\\ \begin{array}{c}\hfill {\widehat{\mathfrak{T}}}_1\\ \hfill {\widehat{\mathfrak{T}}}_2\\ \hfill {\widehat{\mathfrak{T}}}_3\\ \hfill {\widehat{\mathfrak{T}}}_4\end{array}& (\begin{array}{c}(0.79,0.23)\\ (0.11,0.93)\hfill \\ (0.23,0.71)\\ (0.16,0.54)\end{array}& \begin{array}{c}(0.69,0.34)\\ (0.21,0.69)\hfill \\ (0.31,0.65)\\ (0.16,0.23)\end{array}& \begin{array}{c}(0.23,0.71)\\ (0.79,0.31)\hfill \\ (0.69,0.41)\\ (0.51,0.53)\end{array}& \begin{array}{c}(0.81,0.39)\\ (0.31,0.89)\hfill \\ (0.29,0.83)\\ (0.53,0.79)\end{array}& \begin{array}{c}(0.16,0.59)\\ (0.81,0.25)\hfill \\ (0.79,0.34)\\ (0.89,0.56)\end{array})\\ & {\mathfrak{O}}_6& {\mathfrak{O}}_7& {\mathfrak{O}}_8& {\mathfrak{O}}_9& {\mathfrak{O}}_{10}\\ \begin{array}{c}\hfill {\widehat{\mathfrak{T}}}_1\\ \hfill {\widehat{\mathfrak{T}}}_2\\ \hfill {\widehat{\mathfrak{T}}}_3\\ \hfill {\widehat{\mathfrak{T}}}_4\end{array}& (\begin{array}{c}(0.10,0.69)\\ (0.81,0.31)\hfill \\ (0.92,0.43)\\ (0.32,0.16)\end{array}& \begin{array}{c}(0.25,0.61)\\ (0.92,0.13)\hfill \\ (0.53,0.27)\\ (0.34,0.15)\end{array}& \begin{array}{c}(0.23,0.41)\\ (0.13,0.79)\hfill \\ (0.23,0.53)\\ (0.13,0.79)\end{array}& \begin{array}{c}(0.09,0.63)\\ (0.69,0.23)\hfill \\ (0.81,0.31)\\ (0.69,0.17)\end{array}& \begin{array}{c}(0.15,0.79)\\ (0.85,0.27)\hfill \\ (0.89,0.51)\\ (0.23,0.43)\end{array})\end{array}$$

Determine the cumulative assessments of the alternatives by using the q-ROFEWA operator.

$$k_i=\mathrm{q}-\mathrm{ROFEWA}(k_{i1},k_{i2},\dots ,k_{in})$$

For $i=1$:

$$k_1=\mathrm{q}-\mathrm{ROFEWA}(k_{11},k_{12},\dots ,k_{1n})=(0.747534,0.0210146)$$

For $i=2$:

$$k_2=\mathrm{q}-\mathrm{ROFEWA}(k_{11},k_{12},\dots ,k_{1n})=(0.984792,0.00518705)$$

For $i=3$:

$$k_3=\mathrm{q}-\mathrm{ROFEWA}(k_{11},k_{12},\dots ,k_{1n})=(0.937416,0.0097189)$$

For $i=4$:

$$k_4=\mathrm{q}-\mathrm{ROFEWA}(k_{11},k_{12},\dots ,k_{1n})=(0.982514,0.00613556)$$

Now, the values of the score related to each scenario are:

$$\mathfrak{E}\left(k_1\right)=0.417719$$

$$\mathfrak{E}\left(k_2\right)=0.955066$$

$$\mathfrak{E}\left(k_3\right)=0.823751$$

$$\mathfrak{E}\left(k_4\right)=0.948453$$

Now, rate the aggregate collective preferred value of $k_i(i=1,2,3,4)$ using the score function in descending order. Figure 6 presents their comparison. $k_2$ corresponds to ${\widehat{\mathfrak{T}}}_2$. Therefore, ${\widehat{\mathfrak{T}}}_2$ is the desired scenario. Strategies for productivity and capacity for recycling were considered under this scenario. The second place was taken by the scenario assuming sources of renewable energy of hydro, solar, wind, and biomass. The last position was taken by a scenario related to indigenous coal, oil, gas, and nuclear.

$$k_2⪰k_4⪰k_3⪰k_1$$

7. Conclusions

Proper mapping of uncertainty data and decision makers’ preferences is one of the biggest challenges in interdisciplinary research. MCDM has been applied widely to solve a number of real-world problems that involve impreciseness, uncertainty, and vagueness in the data. We focused on information aggregation for MCDM based on Yager’s q-ROFS model as this model is more practical and useful than the existing Yager’s Pythagorean fuzzy model and Atanassov’s intuitionistic fuzzy model. The decision makers can easily choose membership and non-membership grades from the alternatives in a larger space with the q-rung orthopair fuzzy set model. Most arithmetic tools rely on the min-max value of the observation set, while aggregation operators are mathematical tools that play an important role in converting a set of observations into a unique aggregated value. Hence, using all of these concepts, we introduced several new aggregation operators, namely the q-rung orthopair fuzzy Einstein weighted averaging (q-ROFEWA) operator, the q-rung orthopair fuzzy Einstein ordered weighted averaging (q-ROFEOWA) operator, the q-rung orthopair fuzzy Einstein weighted geometric (q-ROFEWG) operator, and the q-rung orthopair fuzzy Einstein ordered weighted geometric (q-ROFEOWG) operator under the q-ROF information. Some interesting features of the proposed operators were discussed, and their illustration was also given. A brief introduction about the t-norm and t-conorm was described, and new the t-norm and t-conorm for q-ROFNs were established. Finally, a numerical example of the proposed approach was cited to demonstrate the practical application of integrated energy modeling and sustainable energy planning issues. This research lays the groundwork for comprehensive energy planning studies in Pakistan by combining energy modeling and decision support as a common sustainable energy planning policy formulation process. We hope our findings will be fruitful for the researchers working in the fields of information aggregation, decision support systems, engineering, image processing, artificial intelligence, and medical diagnosis. Long-term work will pay special attention to interval-valued q-ROF Einstein aggregation operators, hesitant q-ROF Einstein fuzzy aggregation operators, and q-ROF m-polar Einstein fuzzy aggregation operators.

During the research, some possible areas of improvement of the proposed approach and future work directions were identified. When analyzing the formal basis of Yager’s q-rung orthopair fuzzy sets, it would be interesting to take into account their consistency. Afterward, extensive comparative studies of the authors’ approach with other fuzzy MCDM methods are suggested, covering not only the order of result ranking variants, but also accuracy, uncertainty level, and so on. Another potential direction of the development of the proposed method is reusable reference model building, including a full and coherent set of assessment criteria in the problem of sustainable energy planning, which for other researchers would be an important element of the model objectification for this complex decision making problem, but also of the proposed method’s effectiveness studies.