A Computer Vision Line-Tracking Algorithm for Automatic UAV Photovoltaic Plants Monitoring Applications
Abstract
1. Introduction
2. Motivations
3. Proposed Solution
3.1. Edge Detection
3.2. Line Detection
4. Test Case
4.1. Simulation Environment Architecture
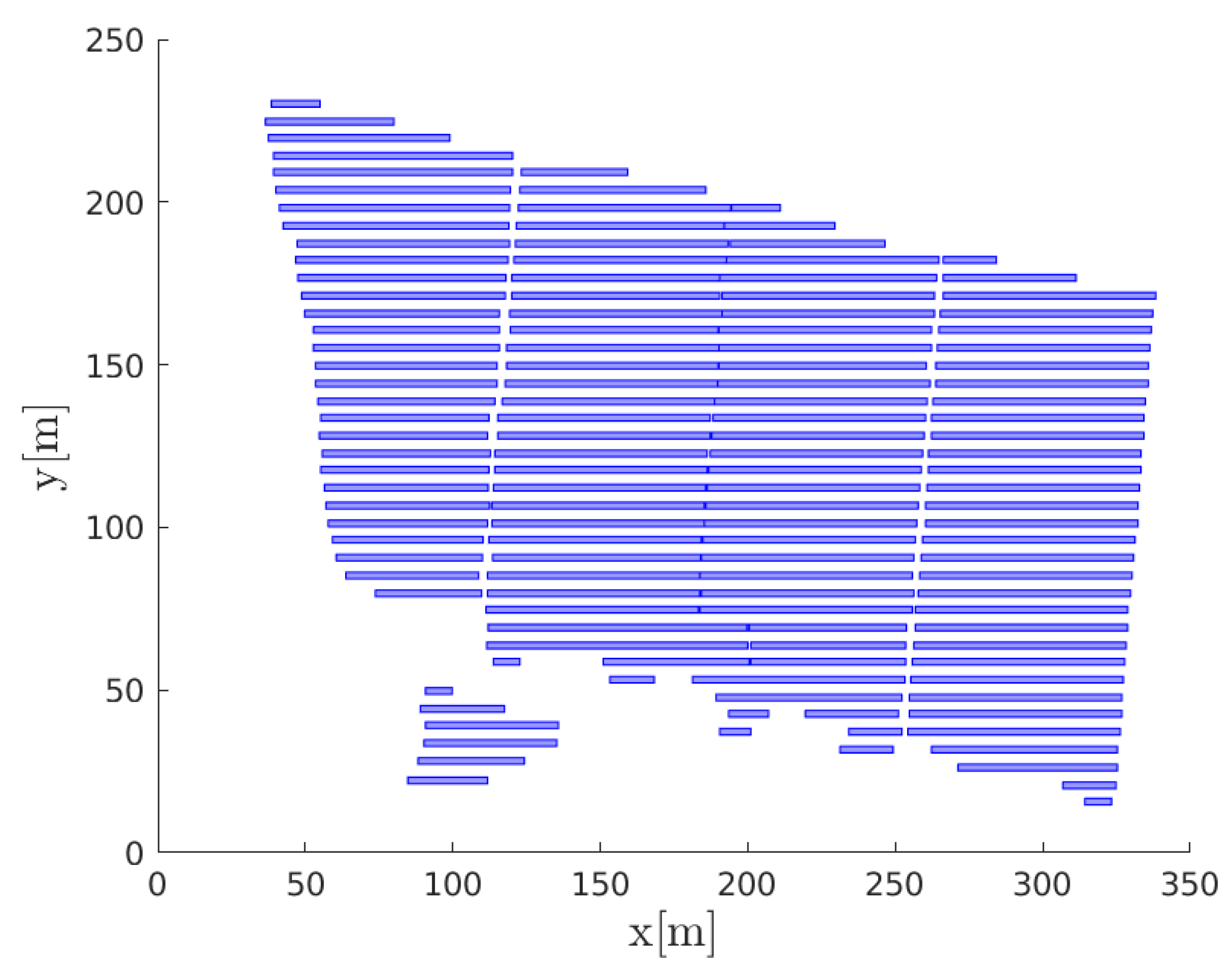
4.2. Field Case Study
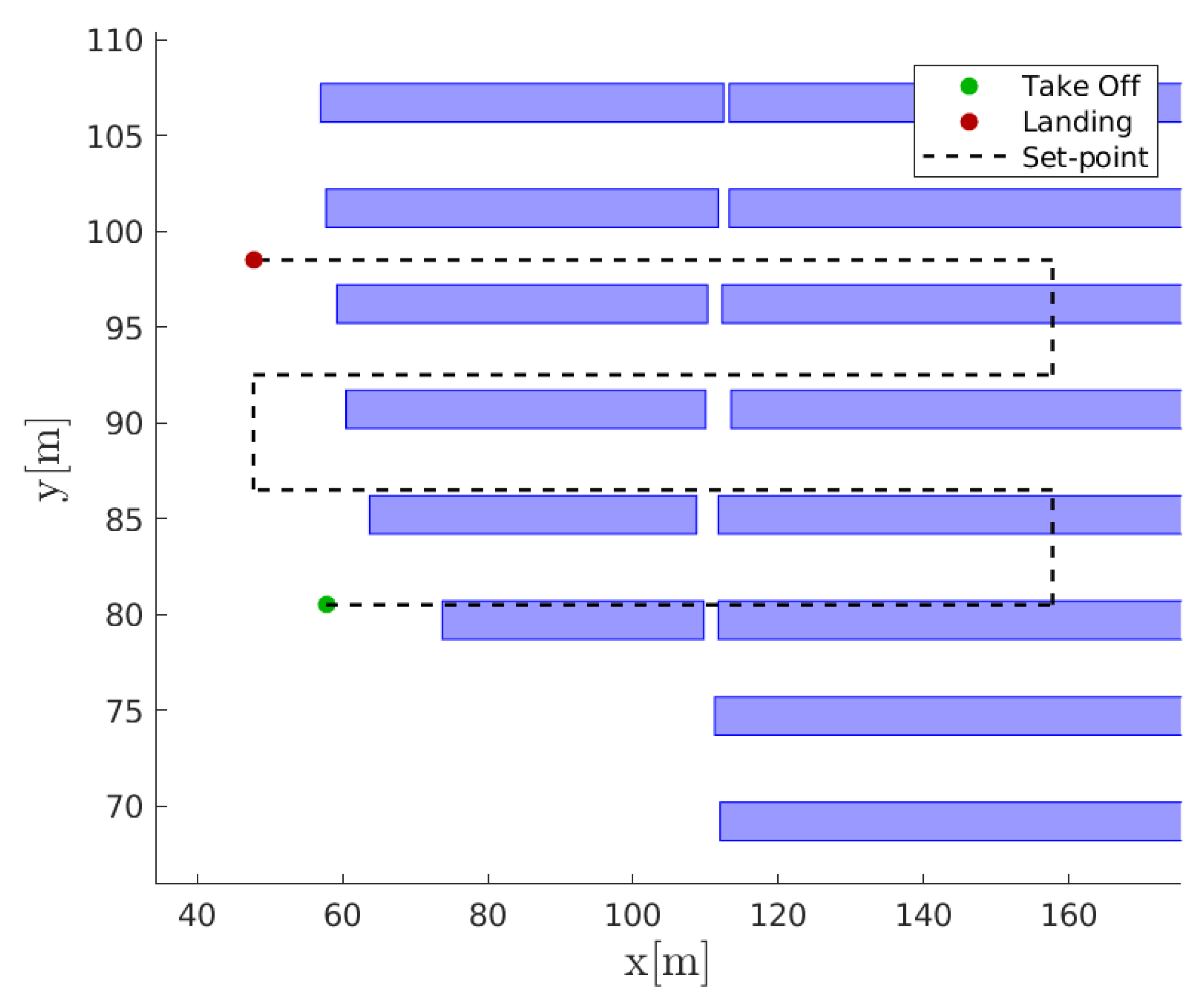
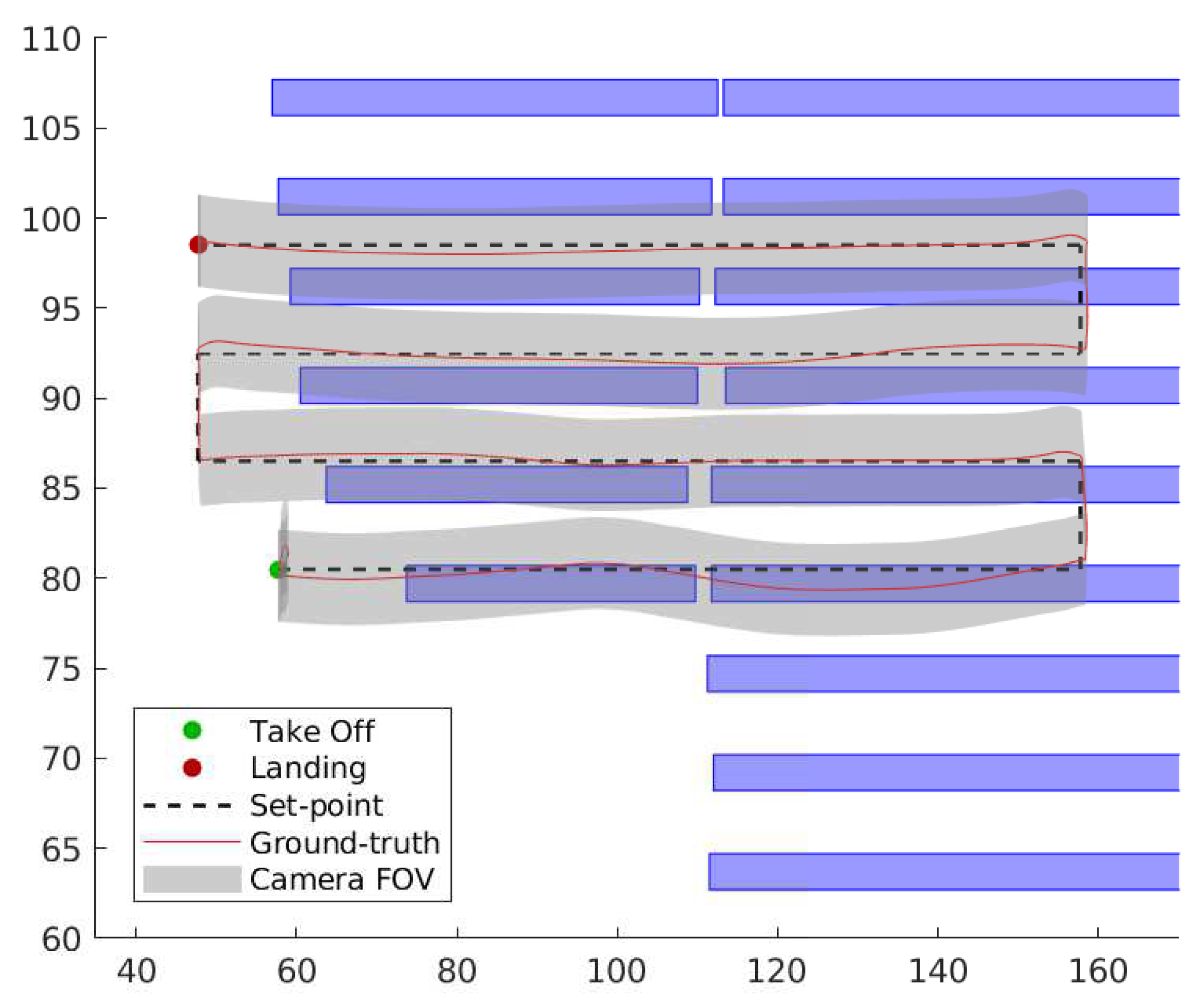
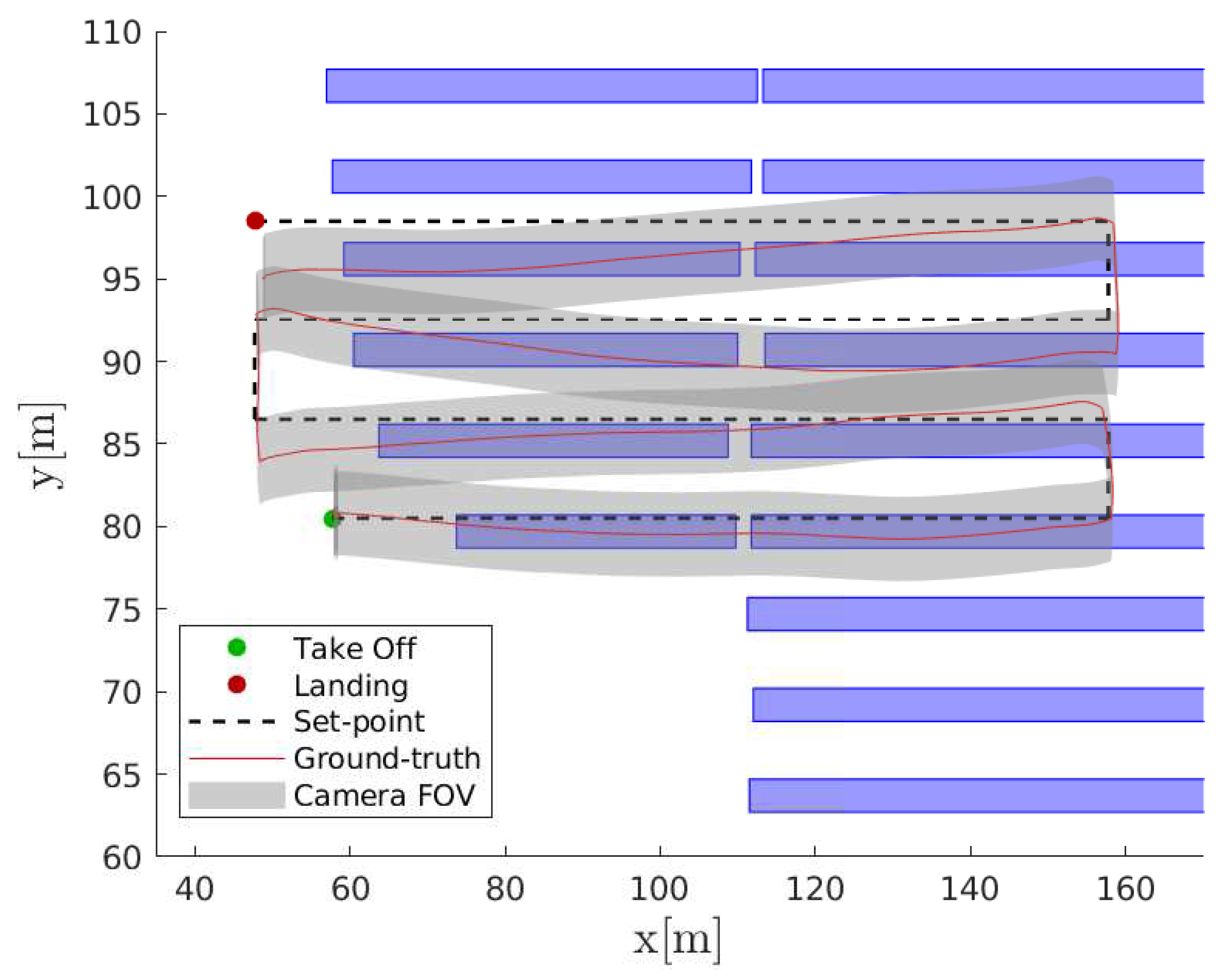
5. Flight Simulation Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
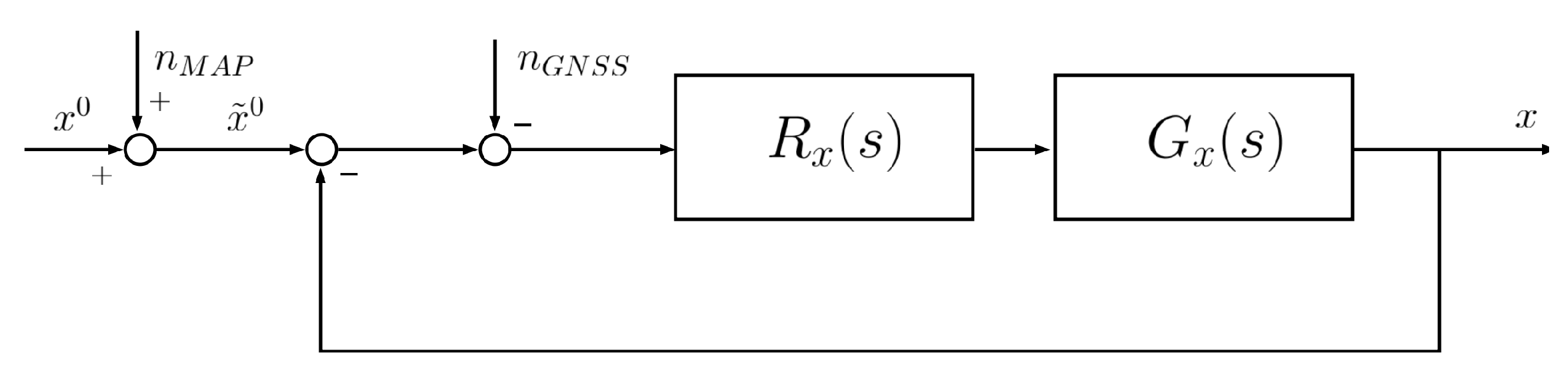
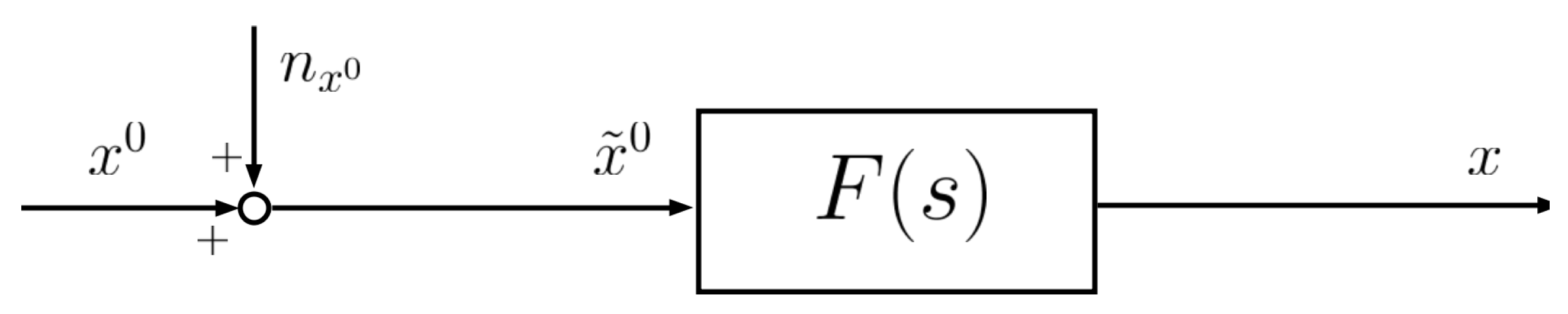
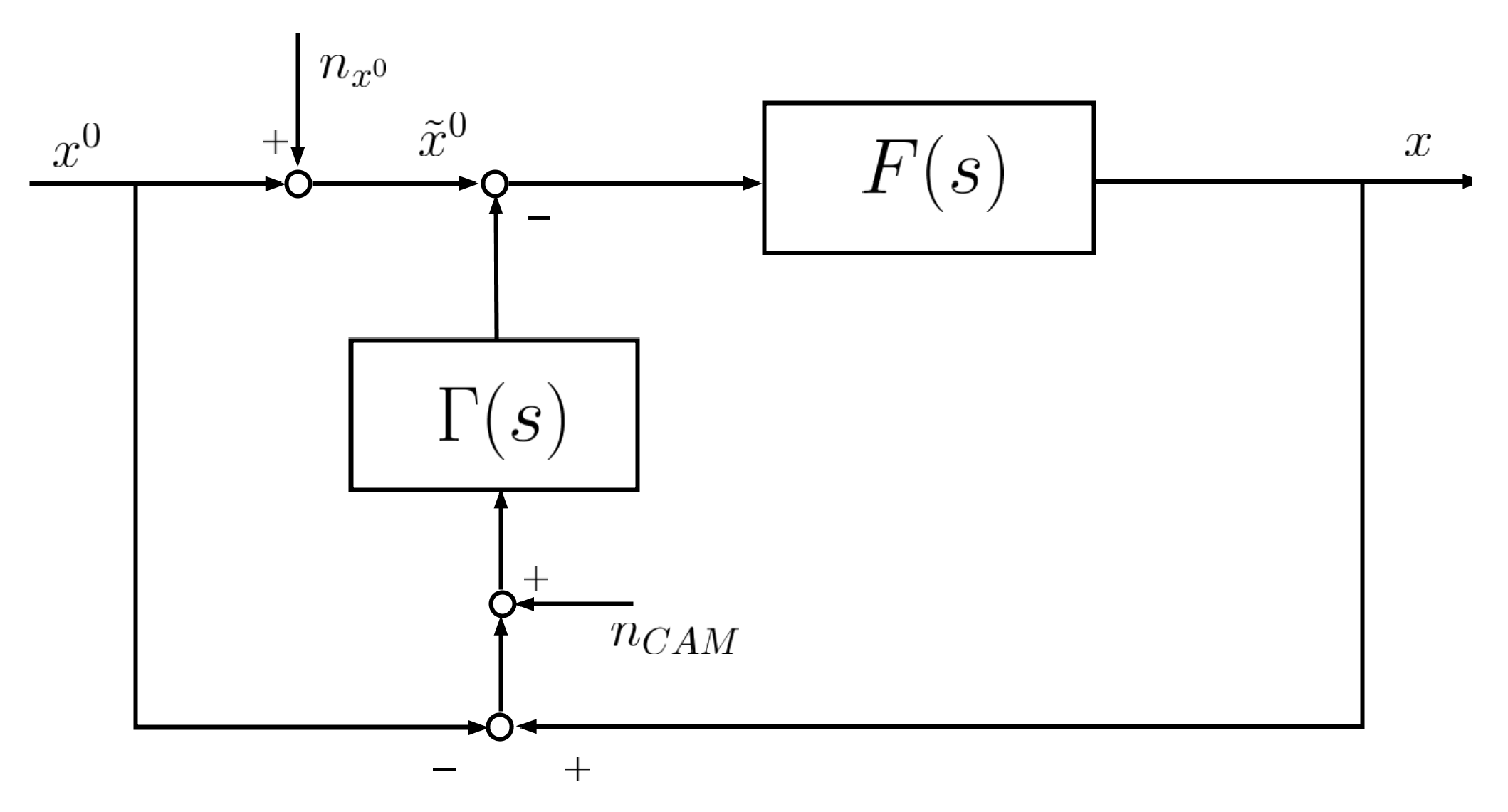
List of Symbols
| ground resolution. | |
| picture resolution. | |
| picture distance. | |
| H | cruise altitude. |
| f | focal length. |
| x | drone position. |
| drone position set-point. | |
| position dynamics transfer function. | |
| position controller transfer function. | |
| complementary sensitivity of position control system. | |
| GNSS measurement noise. | |
| map georeferencing error. | |
| position set-point received by the control system. | |
| simultaneous effect of noise and | |
| camera noise. | |
| compensator transfer function. | |
| compensator proportional gain. | |
| compensator integral gain. |
Acronyms
| UAV | Unmanned Aerial Vehicle. |
| PV | Photovoltaic. |
| GNSS | Global Navigation Satellite System. |
| SITL | Software in the loop. |
| GCS | Ground Control Station. |
| FOV | Field of View. |
| API | Application Programming Interface. |
References
- Grimaccia, F.; Leva, S.; Dolara, A.; Aghaei, M. Survey on PV Modules’ Common Faults After an O&M Flight Extensive Campaign Over Different Plants in Italy. IEEE J. Photovolt. 2017, 7, 810–816. [Google Scholar] [CrossRef]
- Packard, C.E.; Wohlgemuth, J.H.; Kurtz, S.R. Development of a Visual Inspection Data Collection Tool for Evaluation of Fielded PV Module Condition; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2012. [Google Scholar]
- Bradley, A.Z.; Meyer, A.A. Economic impact of module replacement. In Proceedings of the 2016 IEEE 43rd Photovoltaic Specialists Conference (PVSC), Portland, OR, USA, 5–10 June 2016; pp. 3492–3494. [Google Scholar]
- Peng, P.; Hu, A.; Zheng, W.; Su, P.; He, D.; Oakes, K.D.; Fu, A.; Han, R.; Lee, S.L.; Tang, J.; et al. Microscopy study of snail trail phenomenon on photovoltaic modules. RSC Adv. 2012, 2, 11359–11365. [Google Scholar] [CrossRef]
- Ebner, R.; Zamini, S.; Újvári, G. Defect analysis in different photovoltaic modules using electroluminescence (EL) and infrared (IR)-thermography. In Proceedings of the 25th European Photovoltaic Solar Energy Conference and Exhibition, Valencia, Spain, 6–10 September 2010; pp. 333–336. [Google Scholar]
- Cristaldi, L.; Faifer, M.; Lazzaroni, M.; Khalil, A.; Catelani, M.; Ciani, L. Failure modes analysis and diagnostic architecture for photovoltaic plants. In Proceedings of the 13th IMEKO TC10 Workshop on Technical Diagnostics, Advanced Measurement Tools in Technical Diagnostics for, Systems’ Reliability and Safety, Warsaw, Poland, 26–27 June 2014. [Google Scholar]
- Grimaccia, F.; Aghaei, M.; Mussetta, M.; Leva, S.; Quater, P.B. Planning for PV plant performance monitoring by means of unmanned aerial systems (UAS). Int. J. Energy Environ. Eng. 2015, 6, 47–54. [Google Scholar] [CrossRef]
- King, D.L.; Kratochvil, J.; Quintana, M.A.; McMahon, T. Applications for infrared imaging equipment in photovoltaic cell, module, and system testing. In Proceedings of the Conference Record of the Twenty-Eighth IEEE Photovoltaic Specialists Conference-2000 (Cat. No. 00CH37036), Anchorage, AK, USA, 15–22 September 2000; pp. 1487–1490. [Google Scholar]
- Vergura, S.; Marino, F.; Carpentieri, M. Processing infrared image of PV modules for defects classification. In Proceedings of the 2015 International Conference on Renewable Energy Research and Applications (ICRERA), Palermo, Itly, 22–25 November 2015; pp. 1337–1341. [Google Scholar]
- Grimaccia, F.; Leva, S.; Niccolai, A. PV plant digital mapping for modules’ defects detection by unmanned aerial vehicles. IET Renew. Power Gener. 2017, 11, 1221–1228. [Google Scholar] [CrossRef]
- Li, X.; Yang, Q.; Lou, Z.; Yan, W. Deep Learning Based Module Defect Analysis for Large-Scale Photovoltaic Farms. IEEE Trans. Energy Convers. 2018, 34, 520–529. [Google Scholar] [CrossRef]
- Niccolai, A.; Grimaccia, F.; Leva, S. Advanced Asset Management Tools in Photovoltaic Plant Monitoring: UAV-Based Digital Mapping. Energies 2019, 12, 4736. [Google Scholar]
- Gallardo-Saavedra, S.; Hernández-Callejo, L.; Duque-Perez, O. Image resolution influence in aerial thermographic inspections of photovoltaic plants. IEEE Trans. Ind. Inform. 2018, 14, 5678–5686. [Google Scholar] [CrossRef]
- Aghaei, M.; Dolara, A.; Leva, S.; Grimaccia, F. Image resolution and defects detection in PV inspection by unmanned technologies. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Roggi, G.; Giurato, M.; Lovera, M. A computer vision line-tracking algorithm for UAV GNSS-aided guidance. In Proceedings of the XXV International Congress of the Italian Association of Aeronautics and Astronautics, Rome, Italy, 9–12 September 2019. [Google Scholar]
- Hutchinson, S.; Hager, G.D.; Corke, P.I. A tutorial on visual servo control. IEEE Trans. Robot. Autom. 1996, 12, 651–670. [Google Scholar] [CrossRef]
- Sanderson, A.C.; Weiss, L.E. Image-based visual servo control of robots. In Robotics and industrial inspection; International Society for Optics and Photonics: Bellingham, WA, USA, 1983; Volume 360, pp. 164–169. [Google Scholar]
- Araar, O.; Aouf, N. Visual servoing of a Quadrotor UAV for autonomous power lines inspection. In Proceedings of the 22nd Mediterranean Conference on Control and Automation, Palermo, Italy, 16–19 June 2014; pp. 1418–1424. [Google Scholar]
- Mahony, R.; Hamel, T. Image-based visual servo control of aerial robotic systems using linear image features. IEEE Trans. Robot. 2005, 21, 227–239. [Google Scholar] [CrossRef]
- Azinheira, J.R.; Rives, P. Image-based visual servoing for vanishing features and ground lines tracking: Application to a uav automatic landing. Int. J. Optomech. 2008, 2, 275–295. [Google Scholar] [CrossRef]
- Frew, E.; McGee, T.; Kim, Z.; Xiao, X.; Jackson, S.; Morimoto, M.; Rathinam, S.; Padial, J.; Sengupta, R. Vision-based road-following using a small autonomous aircraft. In Proceedings of the 2004 IEEE Aerospace Conference Proceedings (IEEE Cat. No. 04TH8720), Big Sky, MT, USA, 6–13 March 2004; Volume 5, pp. 3006–3015. [Google Scholar]
- Paredes-Hernández, C.U.; Salinas-Castillo, W.E.; Guevara-Cortina, F.; Martínez-Becerra, X. Horizontal positional accuracy of Google Earth’s imagery over rural areas: A study case in Tamaulipas, Mexico. Boletim de Ciências Geodésicas 2013, 19, 588–601. [Google Scholar] [CrossRef]
- Ragheb, A.; Ragab, A.F. Enhancement of Google Earth Positional Accuracy. Int. J. Eng. Res. Technol. (IJERT) 2015, 4, 627–630. [Google Scholar]
- Jaafari, S.; Nazarisamani, A. Comparison between land use/land cover mapping through Landsat and Google Earth imagery. Am. J. Agric. Environ. Sci 2013, 13, 763–768. [Google Scholar]
- El-Hallaq, M. Positional Accuracy of the Google Earth Imagery in the Gaza Strip. J. Multidiscip. Eng. Sci. Technol. (JMEST) 2017, 4, 7249–7253. [Google Scholar]
- Khuwaja, Z.; Arain, J.; Ali, R.; Meghwar, S.; Ali Jatoi, M.; Shaikh, F. Accuracy Measurement of Google Earth Using GPS and Manual Calculations. In Proceedings of the International Conference on Sustainable Development in Civil Engineering (ICSDC 2017), Jamshoro, Pakistan, 5–7 December 2018. [Google Scholar]
- Kayton, M.; Fried, W.R. Avionics Navigation Systems; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Bačić, Ž.; Šugar, D.; Grzunov, R. Investigation of GNSS Receiver’s Accuracy Integrated on UAVs. In Proceedings of the Surveying the World of Tomorrow-From Digitalisation to Augmented Reality, Helsinki, Finland, 29 May–2 June 2017. [Google Scholar]
- Leva, S.; Aghaei, M.; Grimaccia, F. PV power plant inspection by UAS: Correlation between altitude and detection of defects on PV modules. In Proceedings of the 2015 IEEE 15th International Conference on Environment and Electrical Engineering (EEEIC), Rome, Italy, 10–13 June 2015; pp. 1921–1926. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Van Gool, L. Surf: Speeded up Robust Features; European Conference on Computer Vision; Springer: Berlin, Germany, 2006; pp. 404–417. [Google Scholar]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 886–893. [Google Scholar]
- Ahonen, T.; Hadid, A.; Pietikäinen, M. Face Recognition With Local Binary Patterns; European Conference on Computer Vision; Springer: Berlin, Germany, 2004; pp. 469–481. [Google Scholar]
- Zhang, Y.; Dai, S.; Song, W.; Zhang, L.; Li, D. Exposing Speech Resampling Manipulation by Local Texture Analysis on Spectrogram Images. Electronics 2019, 9, 23. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Moreno, A.; Puig, D. Breast Cancer Detection in Thermal Infrared Images Using Representation Learning and Texture Analysis Methods. Electronics 2019, 8, 100. [Google Scholar] [CrossRef]
- Roberts, L.G. Machine Perception of Three-Dimensional Solids. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1963. [Google Scholar]
- Prewitt, J.M. Object enhancement and extraction. Pict. Process. Psychopictorics 1970, 10, 15–19. [Google Scholar]
- Sobel, I.; Feldman, G. An 3x3 Isotropic Gradient Operator for Image Processing. In Pattern Classification and Scene Analysis; John Wiley & Sons: New York, NY, USA, 1973; pp. 271–272. [Google Scholar]
- Canny, J.F. A Computational Approach to Edge Detection. In Readings in Computer Vision; Fischler, M.A., Firschein, O., Eds.; Morgan Kaufmann: San Francisco, CA, USA, 1987; pp. 184–203. [Google Scholar] [CrossRef]
- Hough, P.V.C. Method and Means for Recognizing Complex Patterns. U.S. Patent 3,069,654, 18 December 1962. [Google Scholar]
- PX4. Available online: https://px4.io/ (accessed on 20 December 2019).
- MAVLink. Available online: https://mavlink.io/en/ (accessed on 20 December 2019).
- Gazebo. Available online: http://gazebosim.org/ (accessed on 20 December 2019).
- Open Source Robotic Foundation. ROS. Available online: https://www.ros.org/ (accessed on 20 December 2019).






| Defects | [pixel/cm] |
|---|---|
| Snail Trail | 8–10 |
| Dirty | 3–5 |
| White Spot | 2–3 |
| Encapsulant discoloration | 2–3 |
| Other | 6–8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roggi, G.; Niccolai, A.; Grimaccia, F.; Lovera, M. A Computer Vision Line-Tracking Algorithm for Automatic UAV Photovoltaic Plants Monitoring Applications. Energies 2020, 13, 838. https://doi.org/10.3390/en13040838
Roggi G, Niccolai A, Grimaccia F, Lovera M. A Computer Vision Line-Tracking Algorithm for Automatic UAV Photovoltaic Plants Monitoring Applications. Energies. 2020; 13(4):838. https://doi.org/10.3390/en13040838
Chicago/Turabian StyleRoggi, Gabriele, Alessandro Niccolai, Francesco Grimaccia, and Marco Lovera. 2020. "A Computer Vision Line-Tracking Algorithm for Automatic UAV Photovoltaic Plants Monitoring Applications" Energies 13, no. 4: 838. https://doi.org/10.3390/en13040838
APA StyleRoggi, G., Niccolai, A., Grimaccia, F., & Lovera, M. (2020). A Computer Vision Line-Tracking Algorithm for Automatic UAV Photovoltaic Plants Monitoring Applications. Energies, 13(4), 838. https://doi.org/10.3390/en13040838







