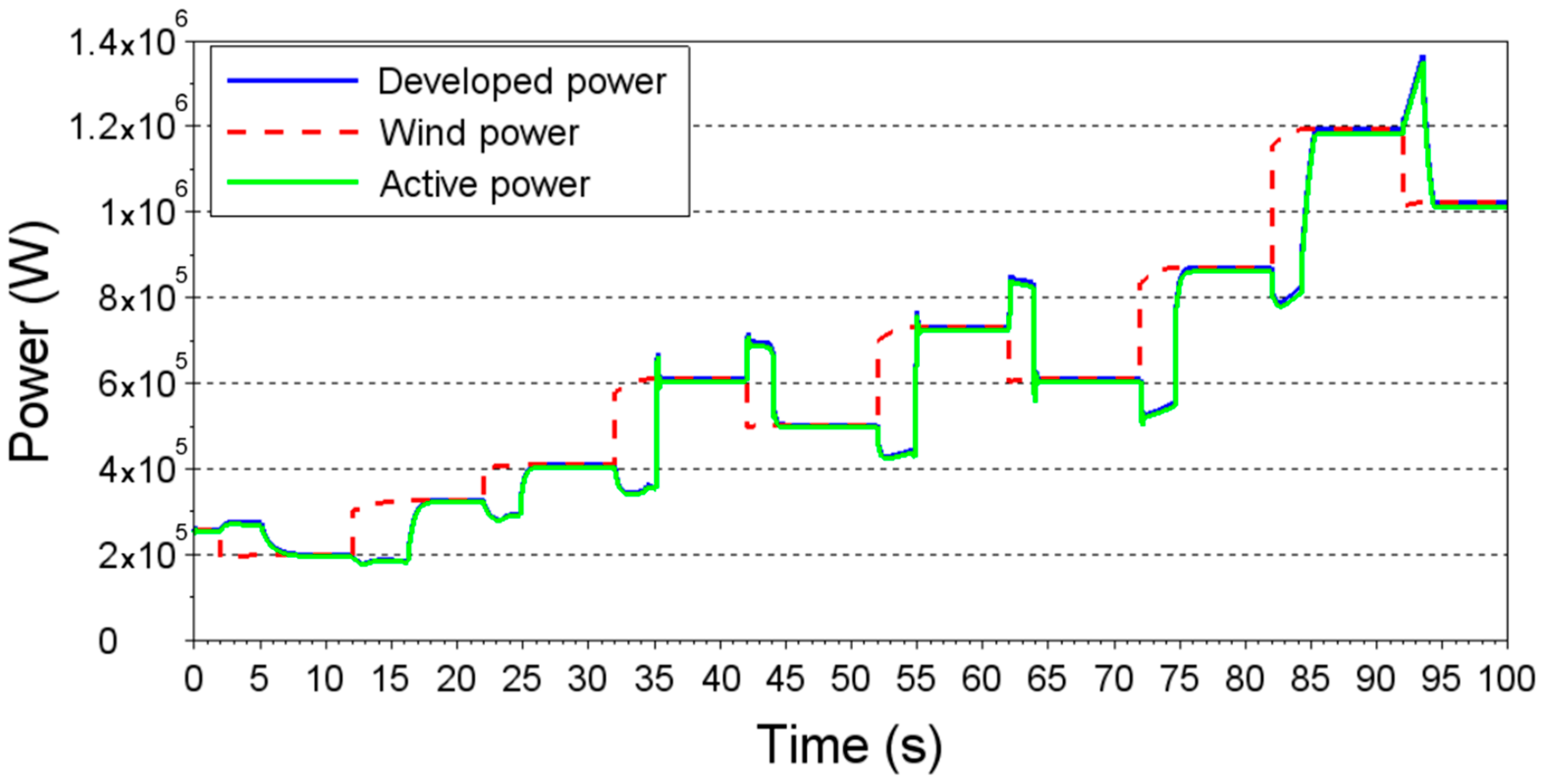
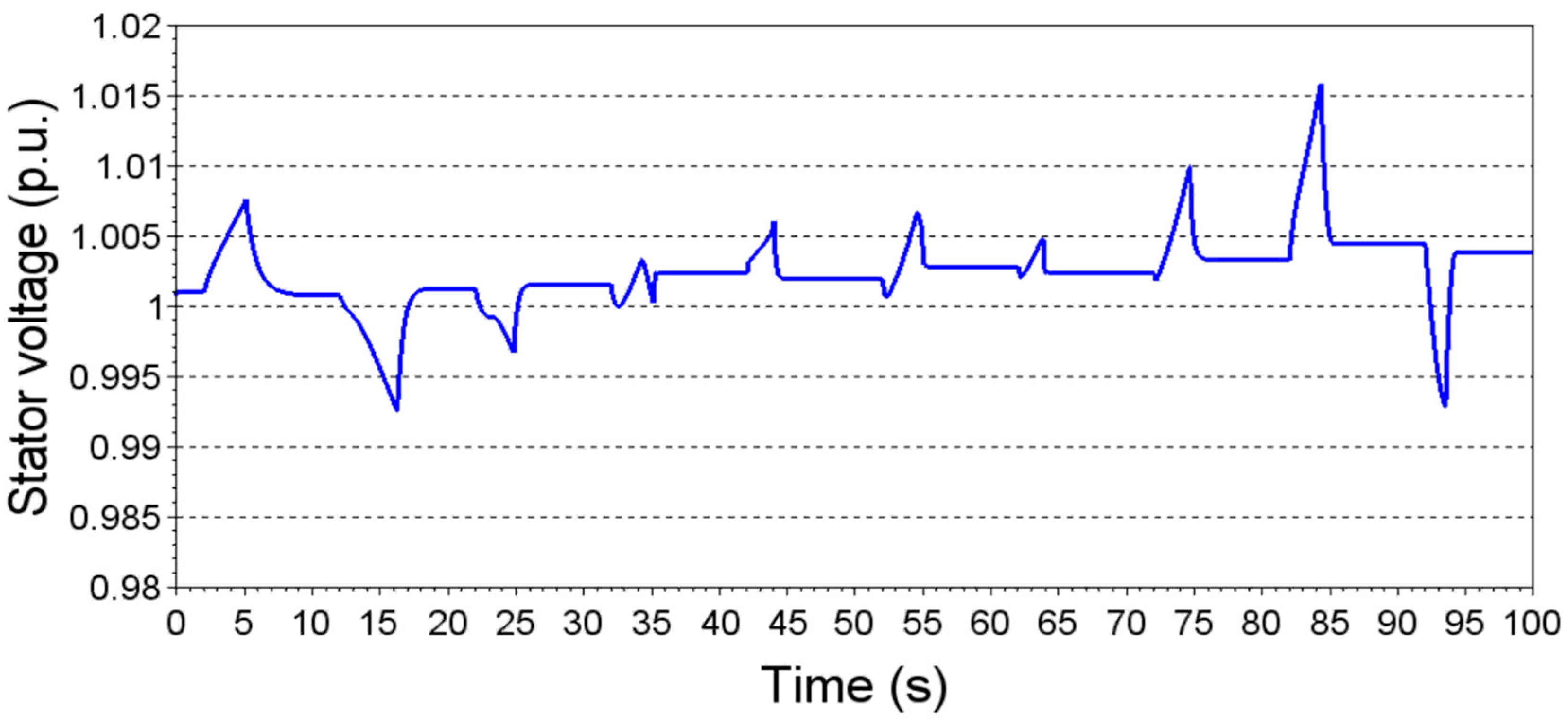
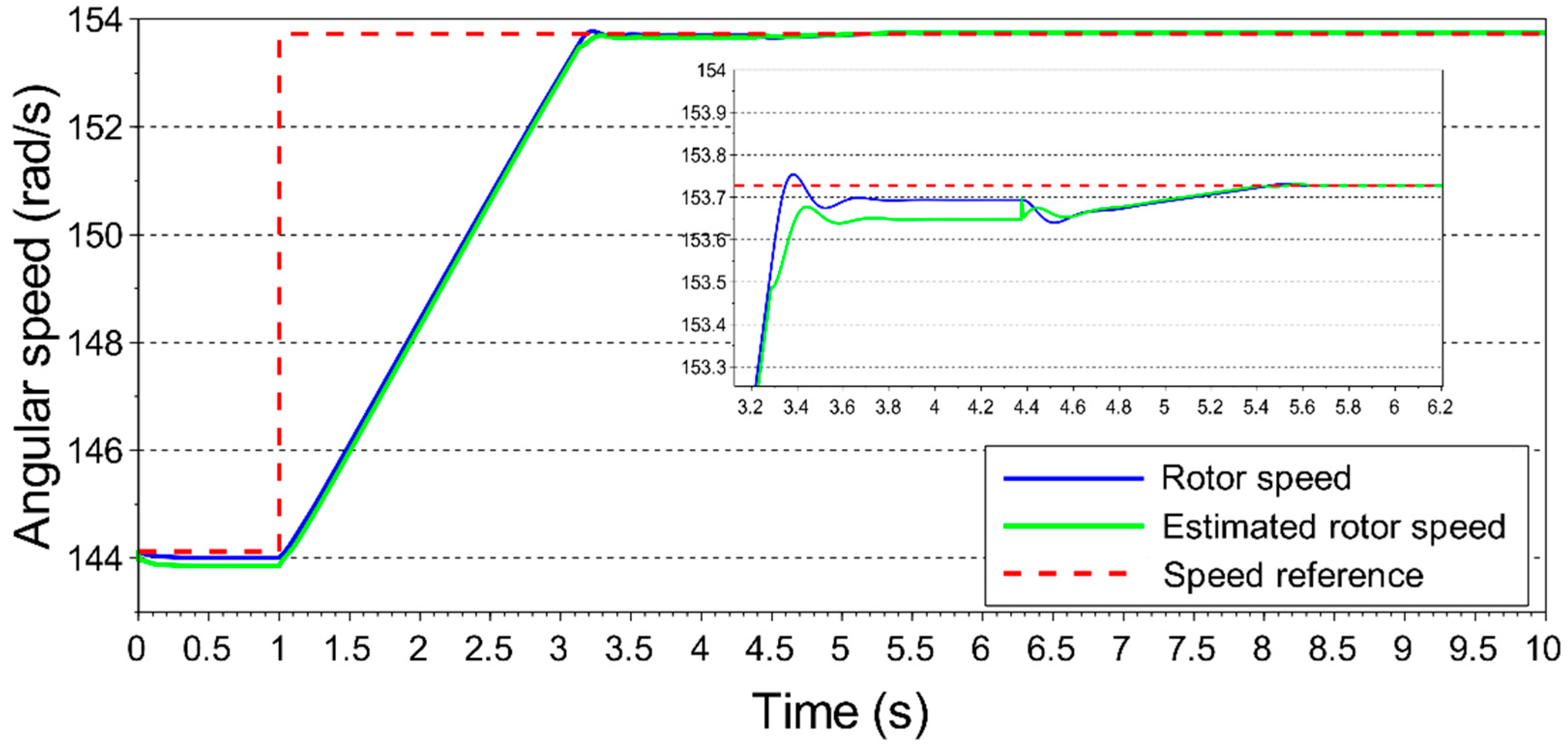
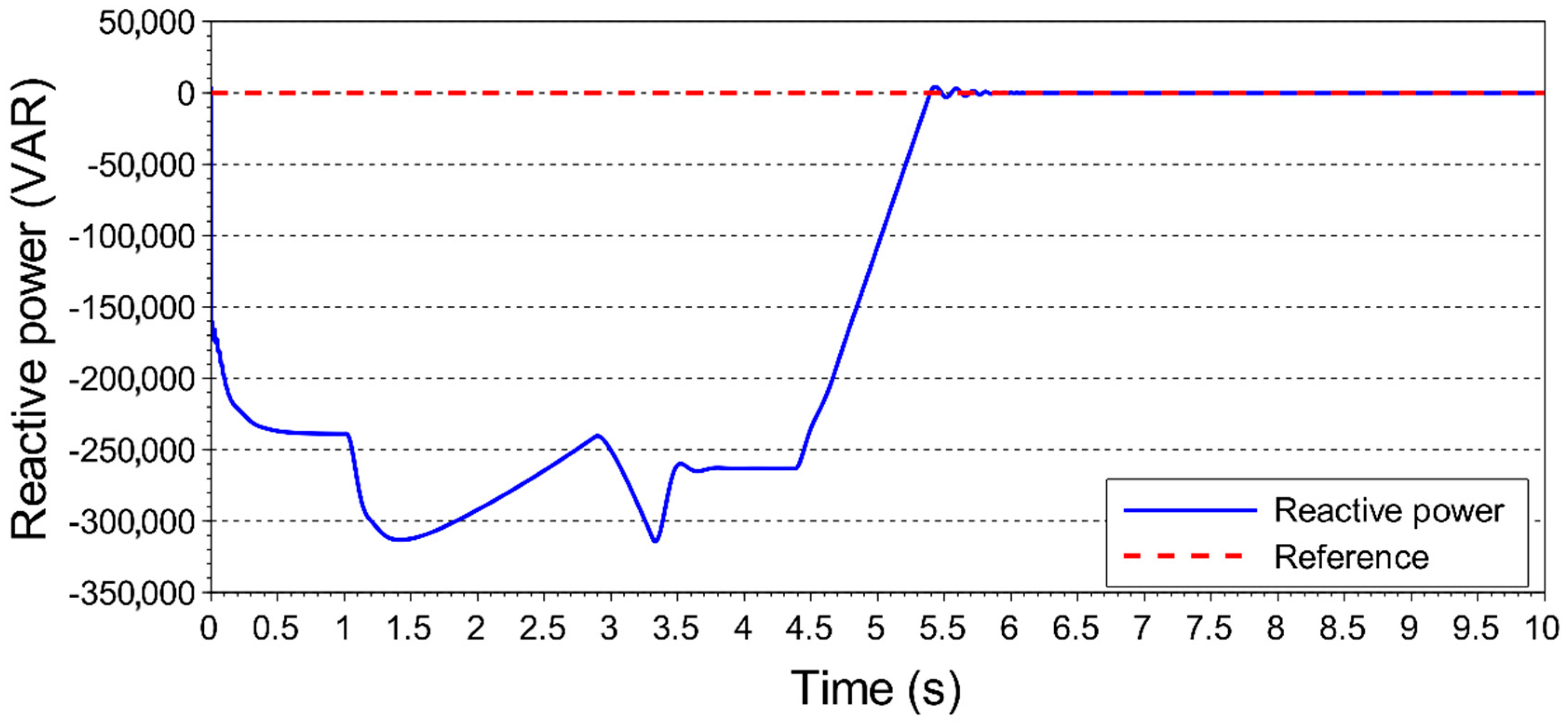
2.1. Wind Turbine
The mechanical power extracted from the wind by the turbine,
, is given in watts by
where
is the air density;
is the radius, in meters, of the circle described by the blades;
is the wind velocity, in m/s; and
is the power coefficient, which determines the capacity of the turbine by extracting power from the wind. It is a function of the pitch angle
and of the tip-speed ratio
[
28]. The tip-speed ratio
is calculated by
where
is the rotational velocity of the turbine. WECS using DFIG requires a mechanical velocity multiplier (gearbox-
) in order to convert the low rotational velocity of the turbine and the high mechanical torque into quantities compatible to the DFIG operation. Thus, the relationship between the turbine velocity and the DFIG rotor velocity is given by
where
is the mechanical speed of DFIG.
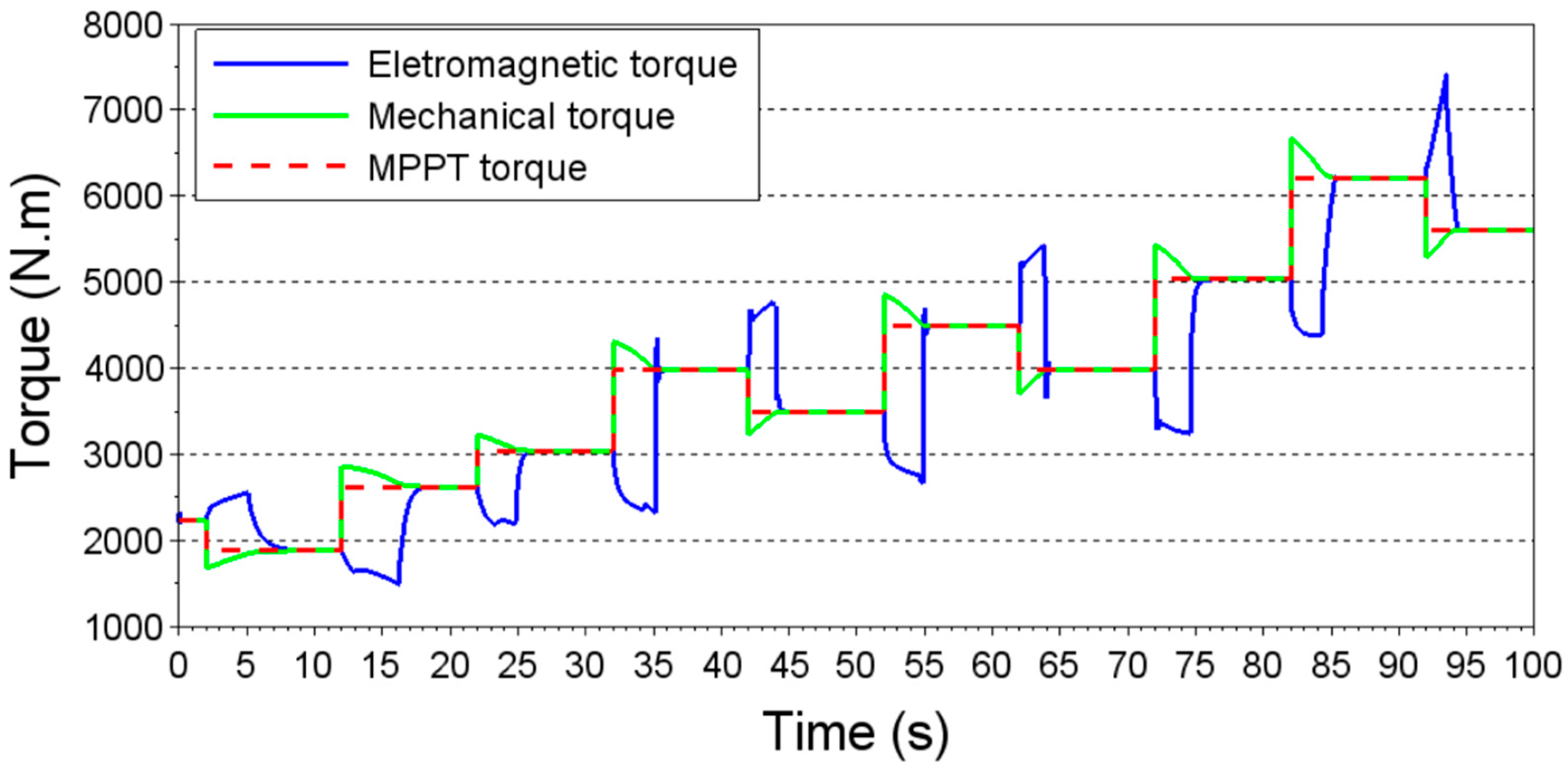
The mechanical torque,
, imposed by the turbine to the generator may be obtained from
The curve of the power coefficient
may assume different forms for different turbines. In this work, the adopted curve
is given in [
29].
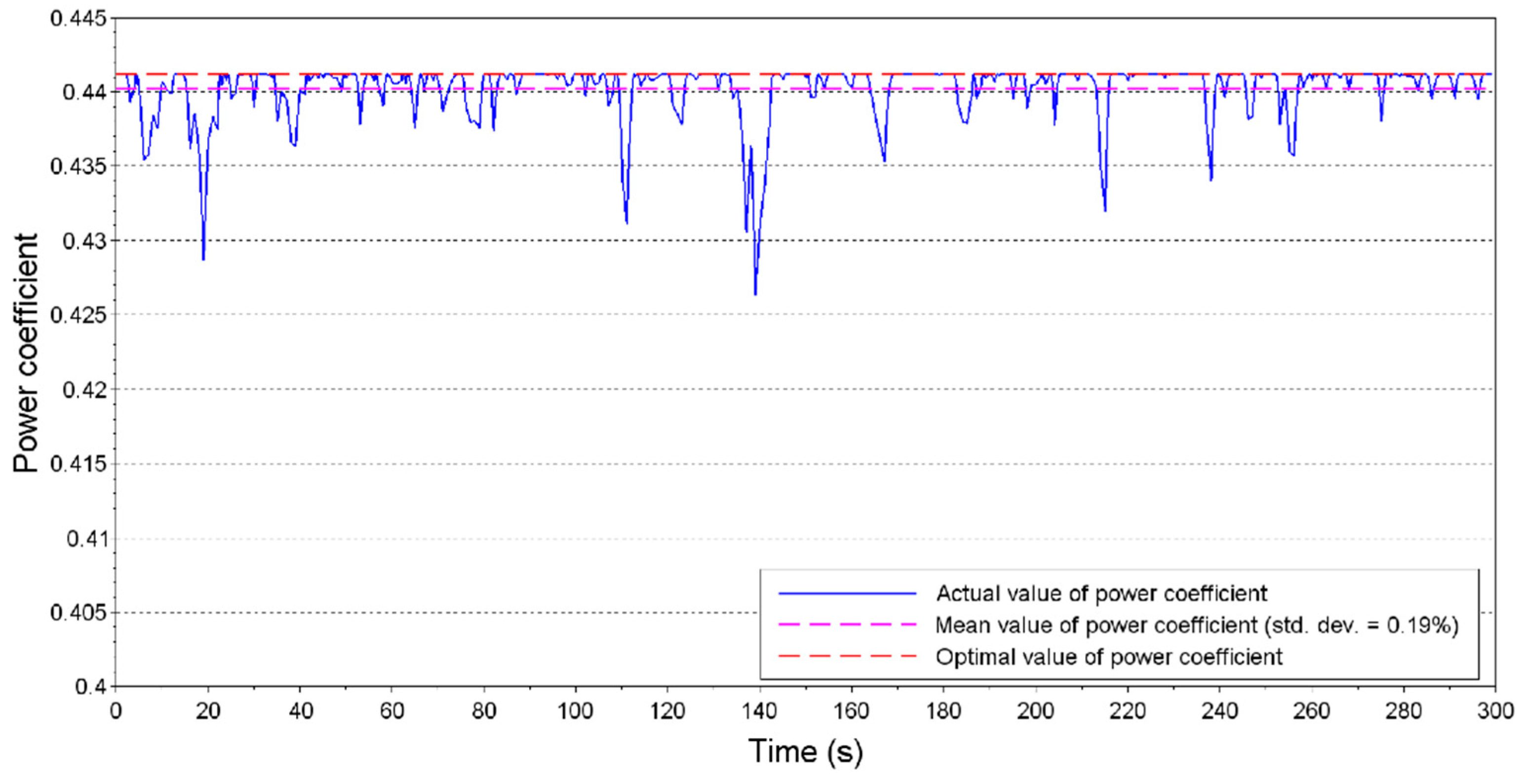
The maximum power extraction from wind occurs when the power coefficient assumes its maximal value, corresponding to
and
. To attend this condition, the reference velocity of the DFIG rotor, for different wind velocities, is given by
In order to maintain the turbine in Maximum Power Point Tracking (MPPT), the angular velocity must be controlled so that the power coefficient is continuously maximal, corresponding to an optimal tip-speed ratio. This must occur from the moment the generator begins to produce power, at a cut-in wind velocity, until the rotor reaches the maximal admitted velocity for the turbine. When this occurs, the control objective is no longer to maintain the optimal tip-speed ratio but to assure the turbine velocity is no higher than the maximal allowed value. This causes a reduction of the power coefficient, reducing the amount of power extracted from the wind. An increase in the wind velocity would lead the turbine to produce more power than the nominal power of DFIG. From this moment on, the pitch control acts on the pitch angle of the blades, so that the absorbed power by the turbine equals the nominal value of DFIG [
22,
29].
The turbine used in the present work was taken from [
29]. Its characteristics are shown in
Table 1.
2.3. Calculation of Reference Values for Control Variables
The operating point adopted as the basis for the control efficiency study proposed in this article corresponds to the maximum utilization of wind power and unit power factor in the stator. As explained in
Section 2.1, for the turbine to extract maximum wind power, the power coefficient must assume the value
. Therefore, Equation (4) calculates the reference speed and the corresponding reference slip in steady state.
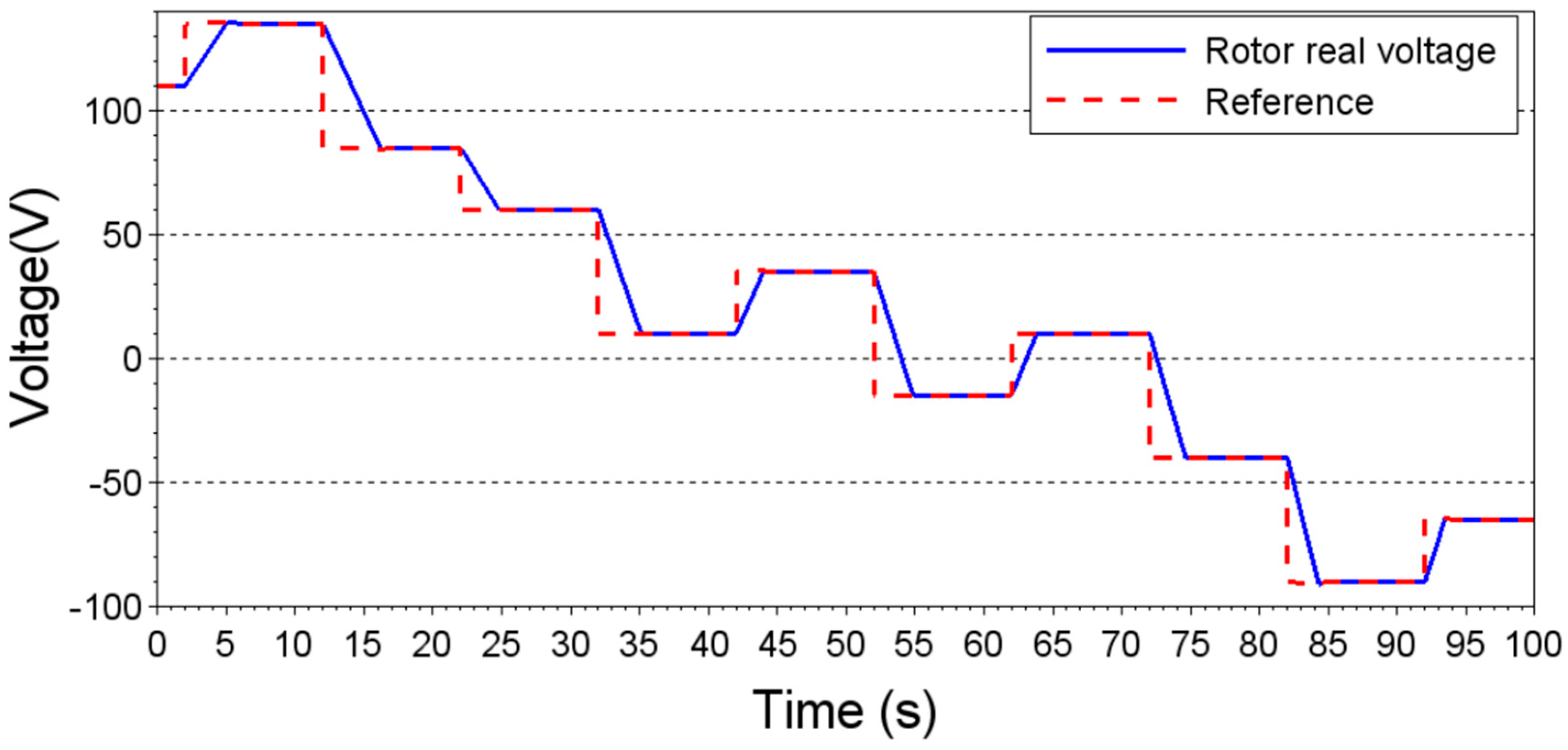
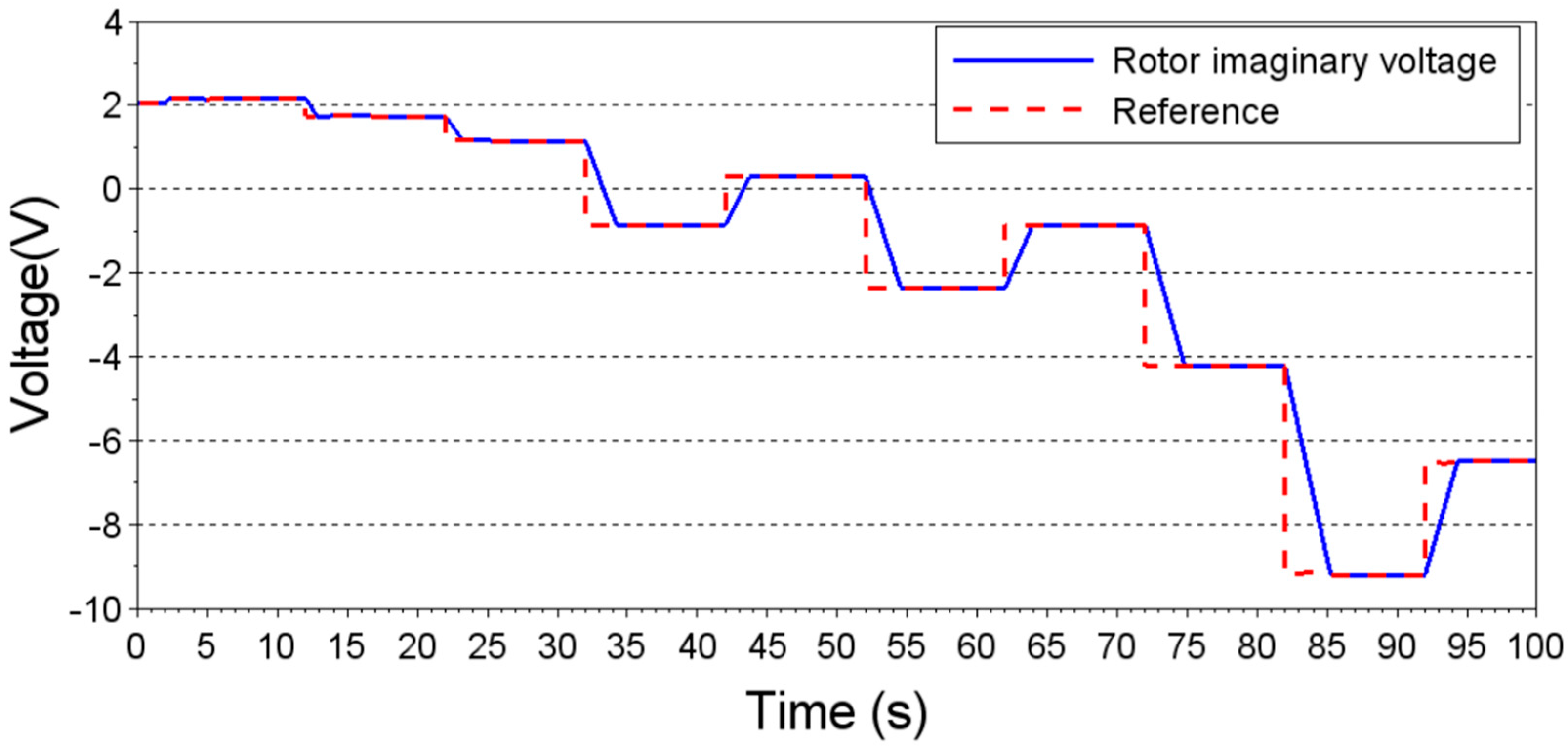
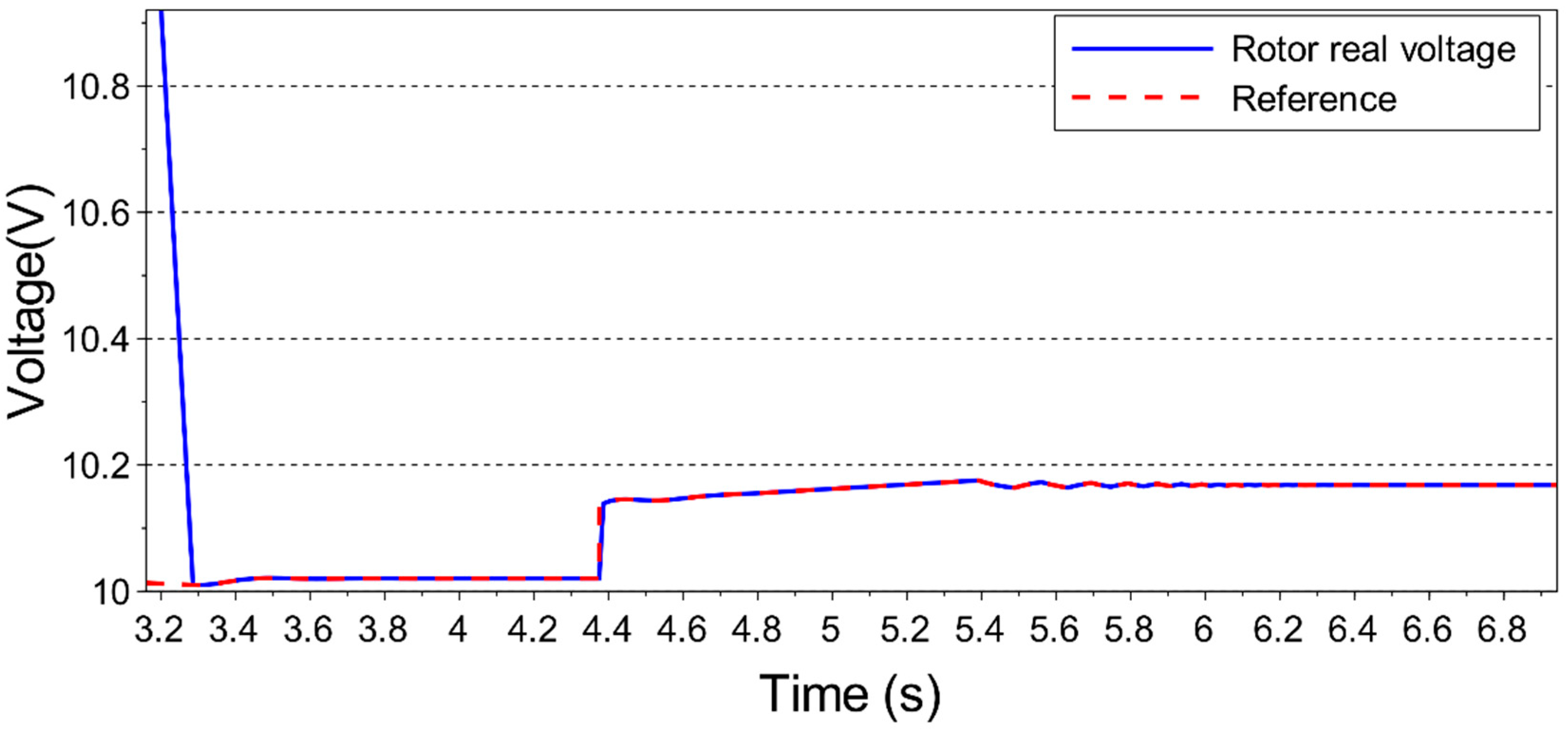
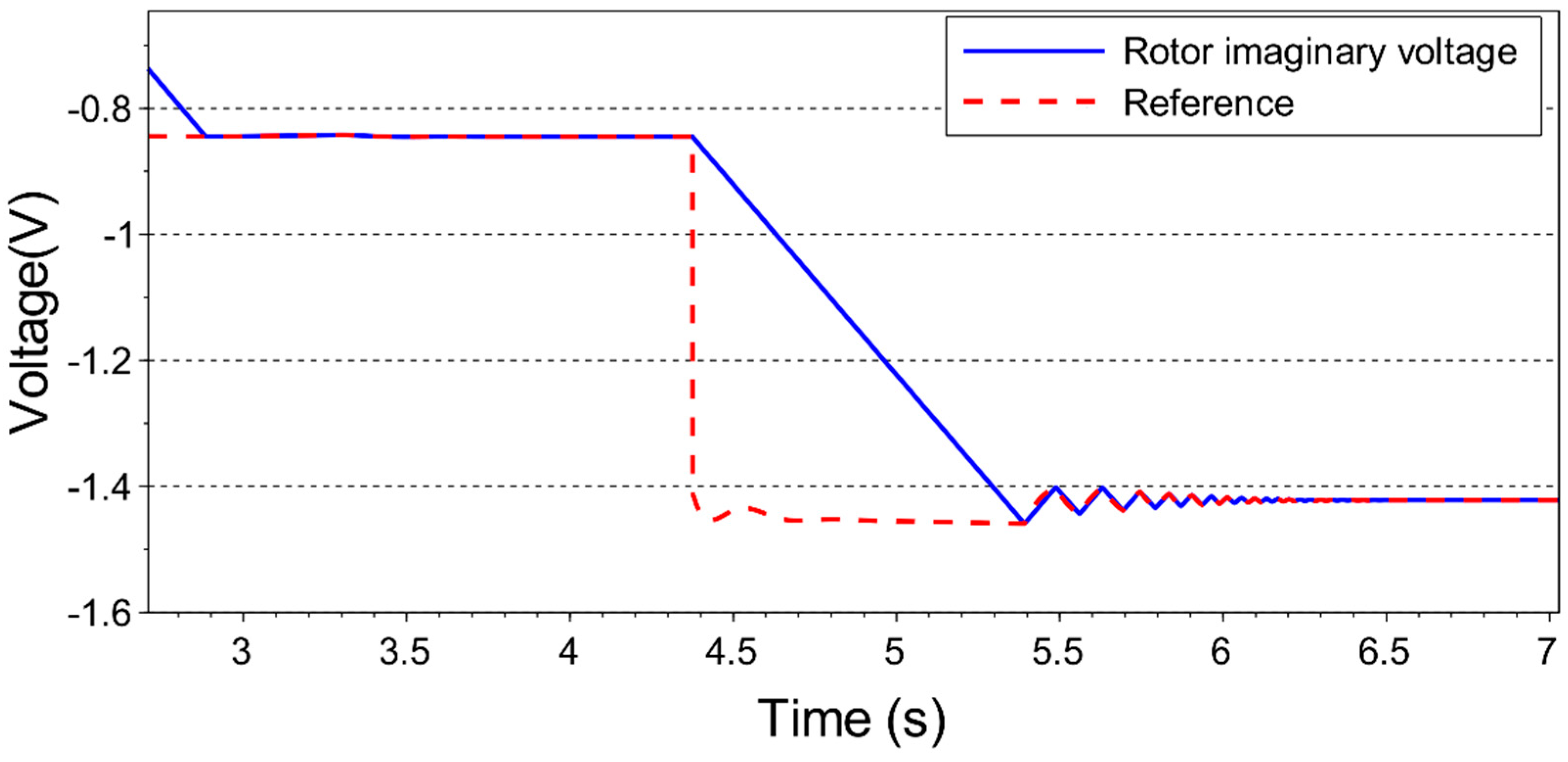
DFIG’s power generation and speed control are done by RSC, which is a voltage source PWM converter. Thus, it is necessary to define the voltage that the converter must supply to the DFIG rotor circuit to control it at the desired operating point. In most studies found in the literature, the rotor reference voltage is given in polar form; in the present work, the reference voltage will be calculated in its Cartesian form. Thus, the rotor reference voltage will have the following form:
This way, to keep DFIG operating at the desired operating point, the values of and must be known.
To extract maximum wind power, it is necessary that all mechanical energy absorbed by the turbine be transformed into electrical energy in the generator, disregarding the rotational losses, at the optimal power coefficient value. The second condition imposed on the control is that the stator reactive power is zero. Therefore, the equations system that defines the desired steady-state operating point for the wind turbine is
Equations (14) and (20) will form the system proposed in Equation (37) to find the values of
and
that ensures the DFIG will work at the desired operating point in steady state. Thus, the proposed equation system is
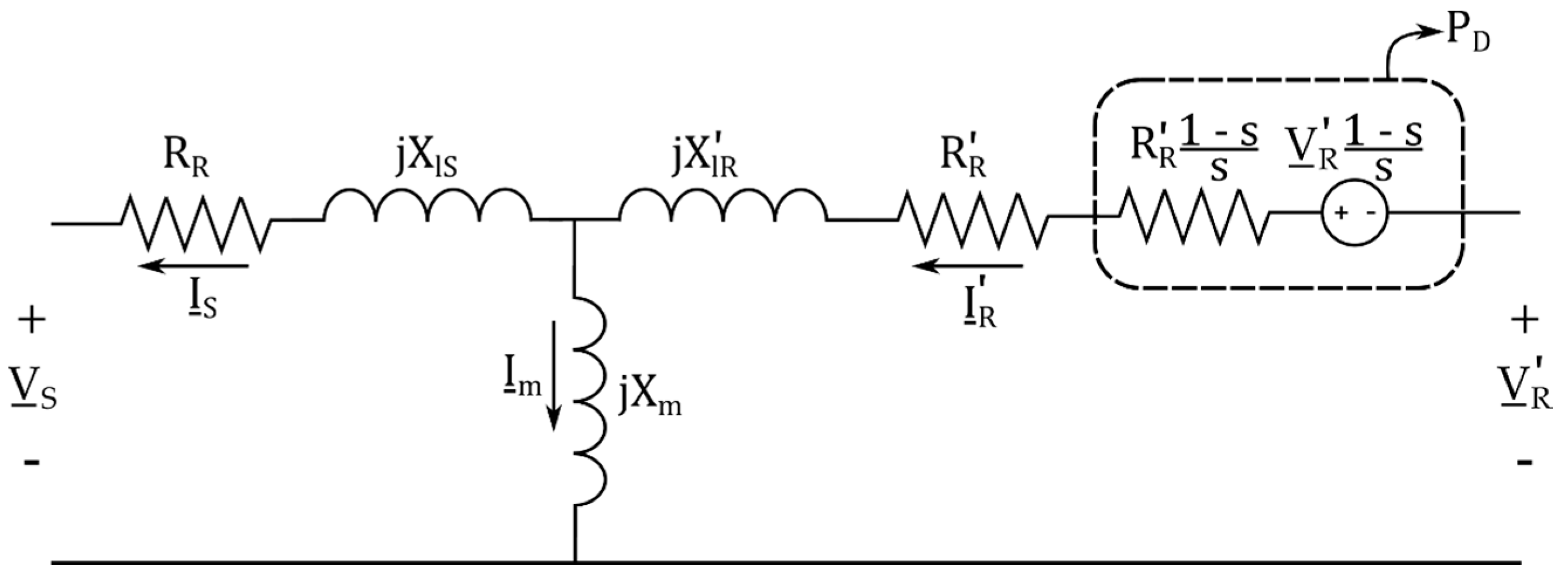
In addition to the DFIG equivalent circuit parameters, the variables that form the equation system above are the reference slip,
, which is known for the desired operating point; the stator voltage magnitude (
); and the control variables of RSC,
and
. As can be seen from
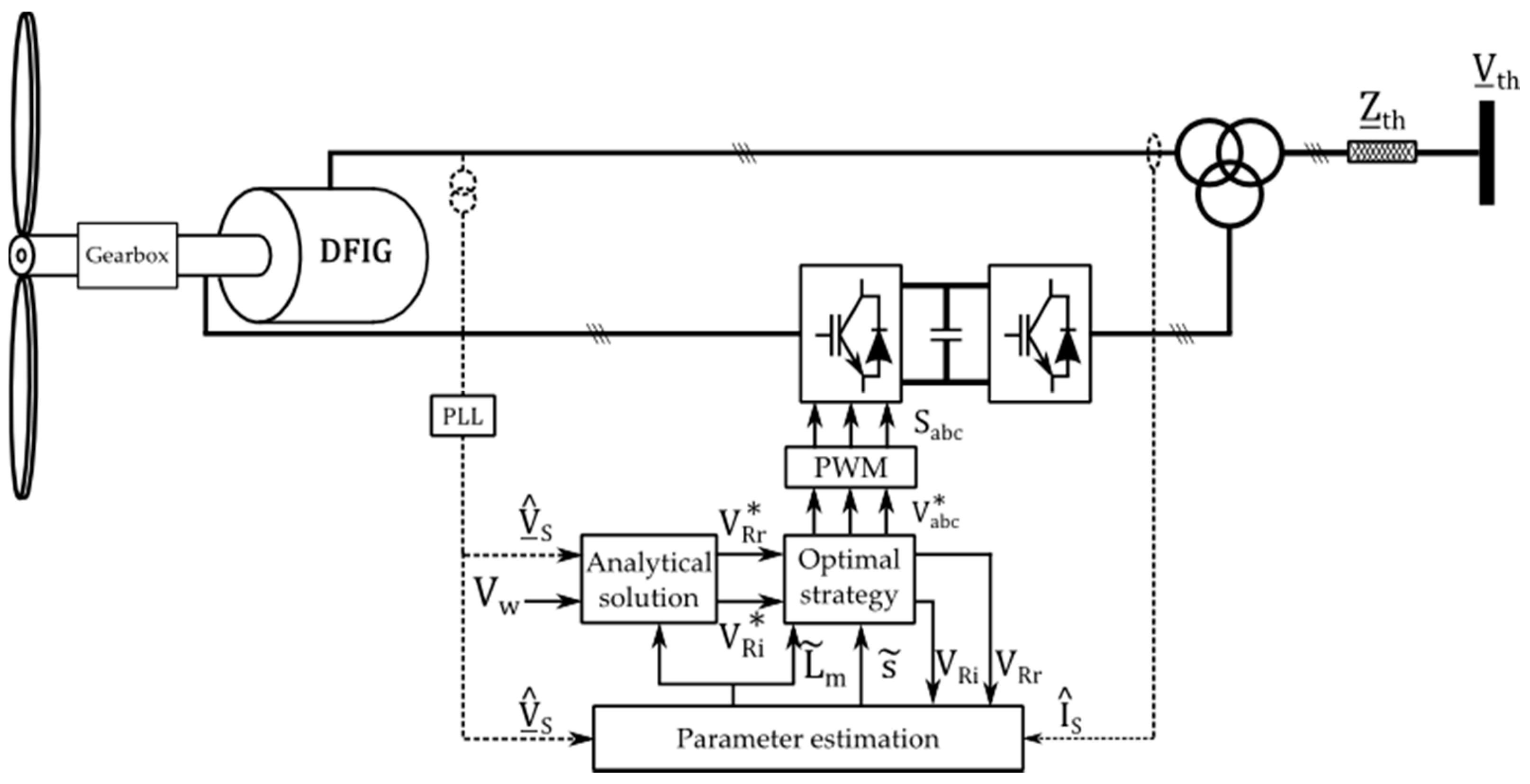
Figure 1, the stator voltage will vary transiently according to the net current generated by the DFIG. Thus, the use of voltage sensors to measure the amplitude and phase of the stator voltage is necessary for the solution of the equation system.
Having all the data, the system of equations has a simple solution obtained analytically by solving the system defined in Equation (38) (e.g., by variable elimination), thus finding the desired values. Observe that the
equation has a degree of 2, which results in two solutions. The choice of the appropriate solution is done by analyzing the magnitude of the current corresponding to each of these solutions. The value of the current is calculated by Equation (19), and the solution chosen will correspond to a current smaller than the magnitude of the DFIG rotor-rated current. The solution [
,
] is found considering
. As shown in the system proposed by
Figure 1, the voltage
has a nonzero phase angle, so it is necessary that the actual value of its angle be compensated at the end of the process of calculating the rotor voltage reference values. In the simulations, the stator voltage angle was obtained by the solution of the Thevenin equivalent circuit, but in practice, as it is not possible to know the equivalent of Thevenin at all times, it is necessary to use a Phase-Locked Loop (PLL) algorithm.
2.4. Velocity of the Control Variables Trajectory
The desired operating point is defined by the measured wind velocity, which determines the reference velocity
, according to Equation (4). A change in wind velocity requires new settings of the control variables. The new reference values for these variables,
and
, may be calculated directly by solving Equation (38). Thereafter, a strategy is required for defining the transition from initial steady-state values of these variables (
and
) until the corresponding final values (
and
), where
and
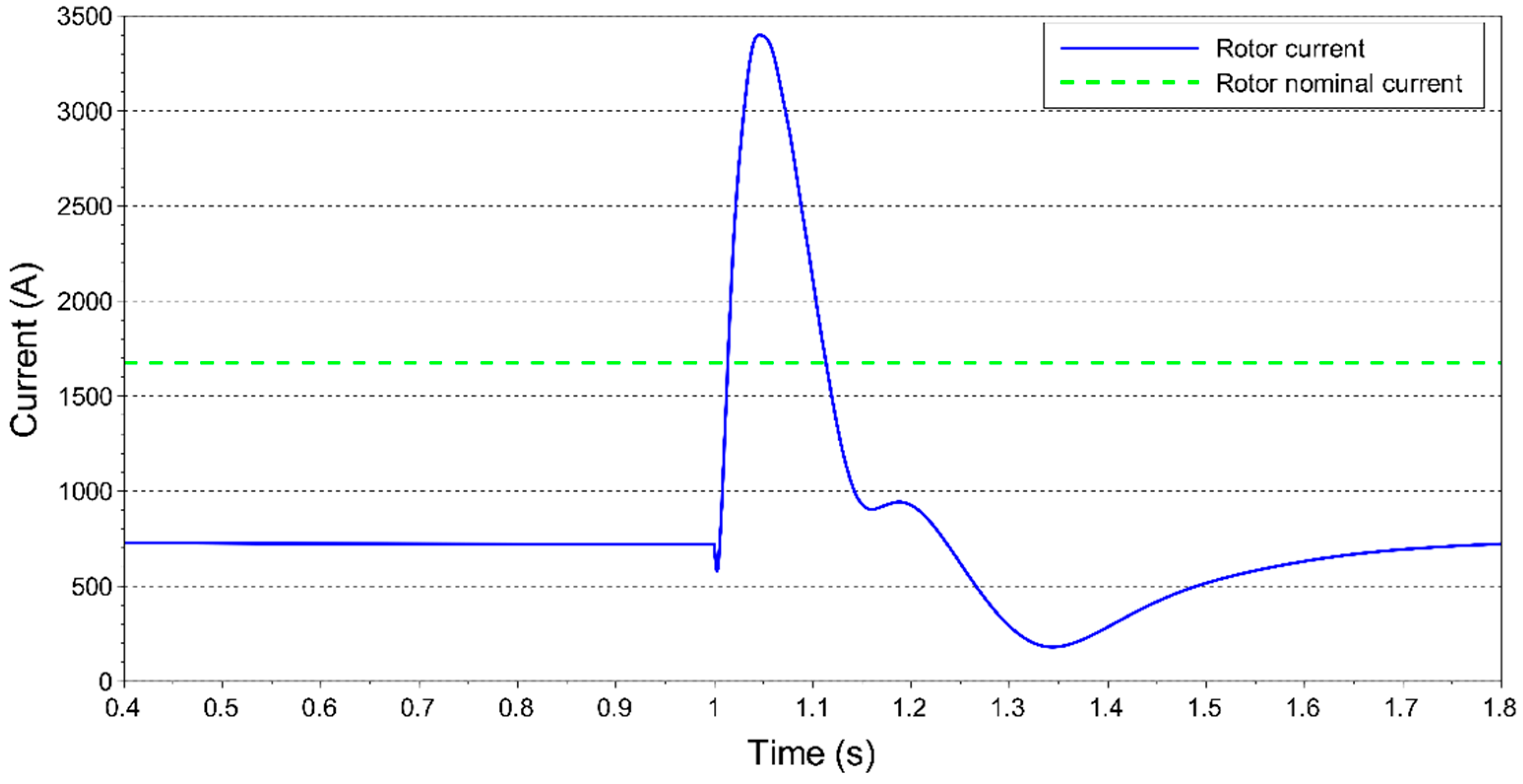
. A sudden change of the control variables to their new reference values may cause undesirable or even damaging transients to the network state. For exemplary purposes, a wind velocity step from 7 m/s to 7.5 m/s was simulated, with application of the corresponding rotor voltage step. The resulting rotor current is shown in
Figure 3, presenting a transient value high above the rated value.
The current transient caused by application of the rotor voltage step reaches, approximately, two times the rotor nominal current. A current of such magnitude could damage the circuits of the RSC converter. For this reason, the trajectory of control variables towards their reference value must be carefully designed, respecting physical limitations of generator components.
The basic idea of the strategy proposed here is to link the time variations of the control variables, ( and ), to the time variations of the machine speed () in order to define the evolution of the control variables, assuring their convergence compatible to the convergence of the rotor velocity, when steady state is reached. This way, major disturbances are avoided.
Firstly, it will be stated that no overshot in the time response of the rotor velocity is desirable. Thus, this velocity is assumed to change from a previous reference to the next one according to a time-varying exponential function:
where,
is the initial value of the velocity,
is its final value (
) and
is a frequency that defines the convergence of the rotor velocity. As the equations from the equivalent circuit presented in
Section 2.2.1 contain the variable slip, instead of velocity, a simple relationship between
and
can be obtained:
Combination of Equations (41) with (43) leads to
Evaluating Equation (44) in
gives
Equation (46) may be rearranged as
where
is the final slip, which must equal the new reference slip
; and
is the initial slip, which could equal the previous reference value, if the machine was previously in a steady state. In order to establish a relationship between the time variations of the control variables with the corresponding slip time variations, Equation (48) is proposed. The basic idea of these equations is to search the aims of maintaining both power conversion and reactive control dynamically.
Unlike the system of equations seen in Equation (38), where the reference slip is defined by wind speed, the system of equations proposed here takes into account slip variations that are proportional to the rotor speed variations. Adopting linearization at a time
:
thus, the equations system is defined by
where, the numerical values of the partial derivatives
,
,
and
as well
and
may be calculated at each time
using the expressions
where,
and
are, respectively, the numerator and denominator of the developed power from Equation (20). From Equation (54), the partial derivative of the developed power
is obtained as a function of slip, s. In this calculation,
and
are considered as defined in Equations (9) and (10). Thus, the solution of Equation (54) is
The partial derivative expressions of the stator reactive power are as follows:
where,
and
are, respectively, the numerator and denominator of the stator reactive power Equation (14).
and
are considered as shown in Equations (9) and (10). Thus, the solution of Equation (61) is
After evaluating all partial derivatives and knowing the variables
,
and
at each instant, the solution of the system of equations proposed in Equation (51) is simply given by
where
is calculated by Equation (47).
2.5. Optimizing Rotor Speed Convergence
Calculation of the convergence speeds of the control variables shown in Equation (66),
Section 2.4, depends on the calculation of
. In Equation (47) the variable
is responsible for defining the convergence speed of the rotor (mechanical) speed to its reference value, according to the exponential proposed in Equation (41). In order to maximize
to lead to a fast convergence of the rotor speed, as well as not violating DFIG limits, a nonlinear constrained optimization technique is proposed in this work. Nonlinear constrained programming problems propose the maximization or minimization and has the following generic form [
32]:
The problem consists of an objective function
, respecting limits imposed by constraint functions, which may be equality
or inequality
. Depending on the proposed problem and the nature of its component functions, different solution techniques may be applied. For the solution of the problem proposed in this work, the Lagrange multiplier method can be applied because it is a relatively simple problem, where the solution of the problem can be found analytically without the need for concern with numerical convergence, as in iterative methods. The first-order condition for the constrained problem using the Lagrange multiplier method is then given by [
32].
where
is the Lagrange Augmented Function (Lagrangian) and
is the Lagrange multiplier.
The optimization problem of variable
will be defined as follows for rising wind speed:
where
can be defined by Equations (34) and (41) for
as follows:
Torque
is calculated by Equation (3), and
is obtained from the developed power equation
, as shown below:
The net power is the difference between the stator and the rotor active power,
. Thus, from Equations (13) and (15),
is defined as
The limitation of the net power generated is justified by the fact that, to produce rotor acceleration, it is necessary that there is a difference between the mechanical torque and the electromagnetic torque, as can be observed by Equation (34). Thus, as the electromagnetic torque is directly proportional to the developed power, as shown in Equation (72), it is necessary to limit the distance of the electromagnetic torque, in order to respect an allowable limit of net power that already discounted the losses in the DFIG. This power limit will be proportional to the available wind power
the constant
is chosen by experimental simulations, and it is different for rising or falling wind speed, reflecting operational conditions of the site where the turbine will be installed.
The only constraint proposed in the problem is an inequality constraint, and for the solution of the first-order condition it must be considered active, that is
The first-order condition for the optimization problem proposed in Equation (70) is:
To find the stationary points of the function presented in Equation (77), it is necessary to assemble the system of equations that define the first-order condition for the Lagrange function and the problem constraint [
32], as shown below:
where:
Therefore, System (80) can be rewritten as
The solution of the system is obtained analytically by manipulating these equations. Dividing the first one by the second leads to
Thus, the Lagrange multiplier is eliminated, and an equation is obtained from which it is possible to explicit
as a function of
. Entering the following constants:
one obtains
Substitution of Equation (90) in constraint
leads to
This polynomial has two roots, which represent two possible solutions for . Replacing these solutions into Equation (90), yields two solution pairs [], known as stationary (or critical) points of the problem.
The first analysis of the critical points is done by observing the signal of the Lagrange multiplier
, calculated by the following equation, taken from the system presented in Equation (85):
When the constraint is of inequality type, the sign of the Lagrange multiplier expresses the need to use the imposed constraint to limit the objective function. If the problem is maximization and the inequality constraint is of type “greater or equal”, a positive sign of the multiplier indicates that the constraint is naturally limiting the objective function because its gradients are opposite to ensure the first-order condition seen in Equation (77). If the problem is minimization, with the inequality constraint of type “less than or equal”, a negative sign of the Lagrange multiplier leads to the same conclusion. When, in the cases presented, the signs are opposite, it means that the objective function is being forced to go to the constraint limit, in which case it would be unwanted.
After applying the first-order condition and calculating the critical points, it is necessary to analyze the second-order condition and the Hessian matrix of the problem. The second-order condition is applied as shown below:
and the Hessian matrix is presented below:
The analysis of the eigenvalues of the Hessian matrix is necessary to define the convexity of the region around each critical point and to verify if they are minimum or maximum points [
31]. The eigenvalues are obtained from the Hessian determinant as shown below:
If all the eigenvalues of the Hessian matrix, analyzed for a certain critical point, have a positive sign, then the region around the critical point is convex; therefore, this is a minimum. If negative, the critical point is a maximum of the objective function [
32].
The objective function and the constraint function of the problem proposed by Equation (70) are both second-order polynomials. Thus, it is expected that the critical points found are one maximum and one minimum. Therefore, the critical point that solves this problem will be one that maximizes the objective function. Similarly, when the wind is decreasing, the problem becomes minimization, as shown below:
All mathematical inferences presented throughout this section are valid for this formulation as well.
In the second-order condition, for the problem presented in Equation (70), we search for the critical point that generates the eigenvalue of the Hessian matrix, with negative sign, which maximizes the objective function. For the problem presented in Equation (96) the eigenvalue of the Hessian matrix should be positive.
At the end of the optimization process of
, we arrive at a pair
and
. Therefore,
and
The optimal values of the derivatives of the control variables
and
at
are determined from Equations (67) and (98).
As for the rotor speed, the exponential behavior for the convergence of control variables was also adopted. Therefore, generally,
where,
and
are the frequencies that define the convergence velocity, and
and
are the final values of the control variables (i.e., their reference values).
To find the optimal convergence frequencies
and
, a relationship to the optimal velocity convergence frequency is established. Deriving
and
:
Substituting Equations (102) and (103) into Equation (99) gives
Substituting Equation (98) into Equations (104) and (105) and analyzing them at
, one concludes
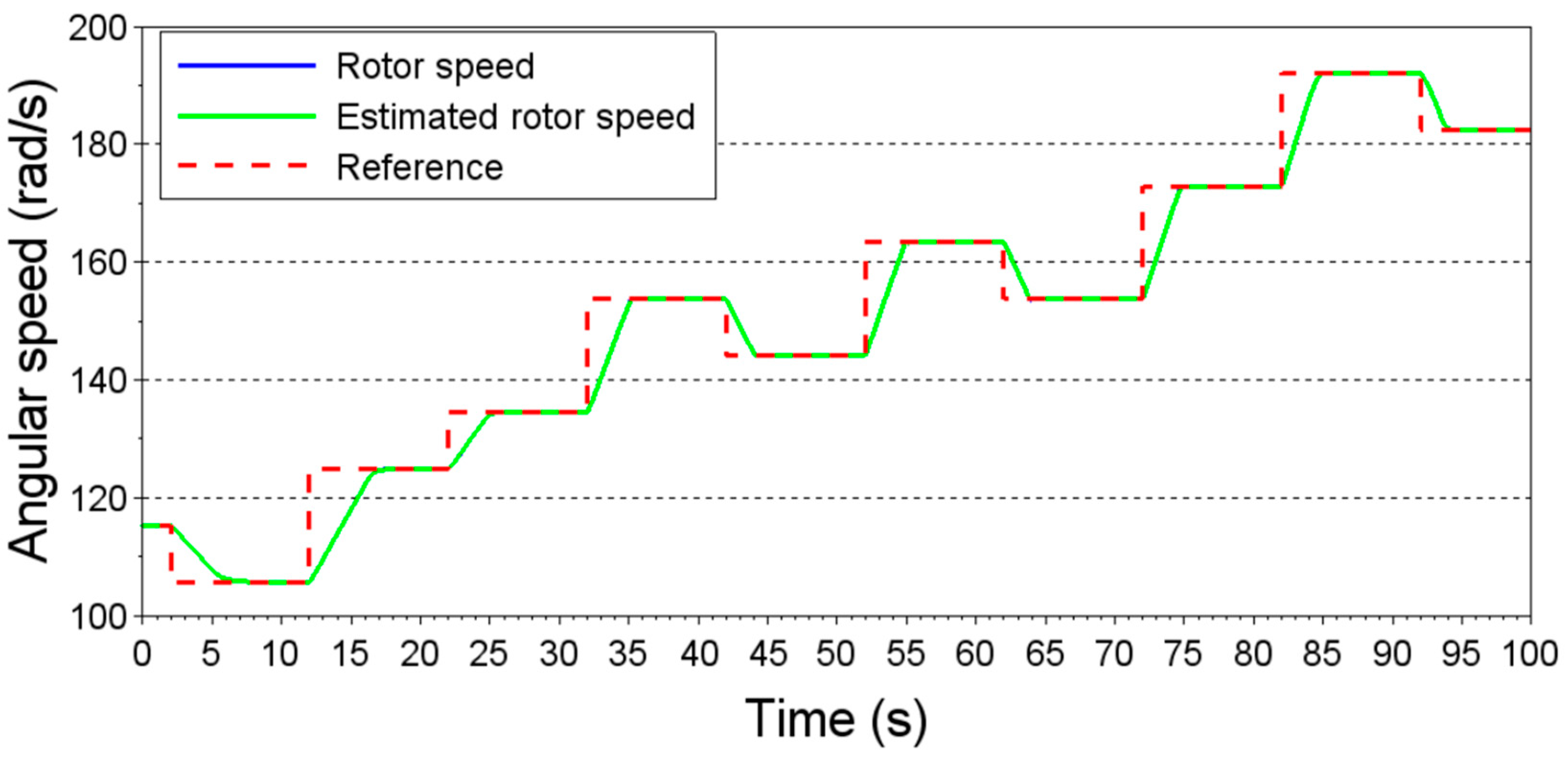
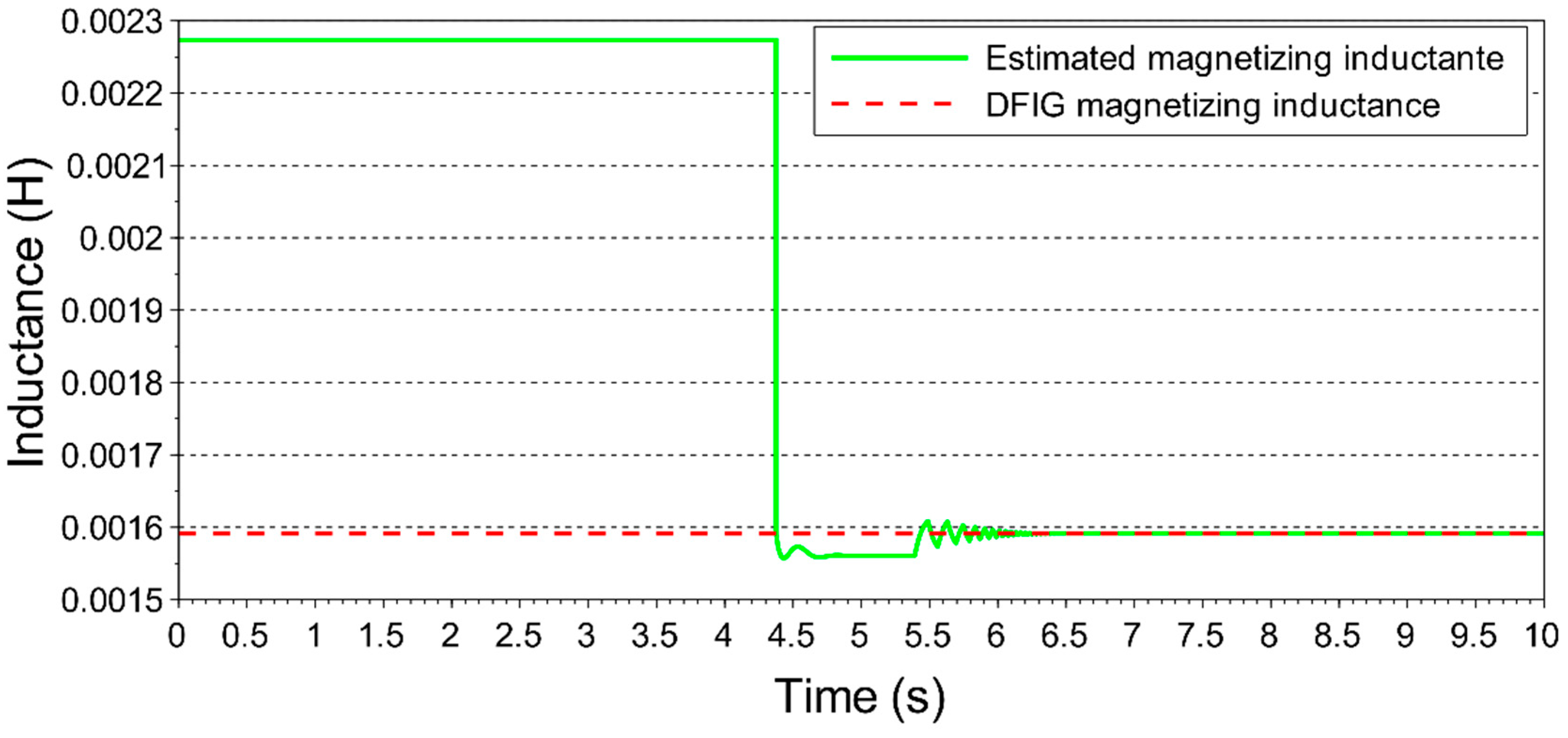
2.6. Speed Estimation and Magnetizing Inductance Correction
Magnetic saturation affects the inductance value of the DFIG, and consequently the control performance [
23]. However, the effect of this saturation mainly influences the magnetizing inductance since the path of the magnetic leakage flux is mainly air; thus, the variations of the leakage inductances are irrelevant to the control [
24]. Changes in inductance values may lead to a different operating point than expected. Still, considering that the magnetizing inductance is the parameter that has the highest value, compared to the other DFIG parameters, it is important to identify its value to ensure control efficiency. Because of these facts, a strategy is proposed here for estimating the value of the magnetizing inductance by means of measuring stator voltages and currents and estimating rotor slip and rotor currents. The proposed procedure considers that the identification of magnetizing inductance should not necessarily be performed at each step of the control. An error in its value would lead the DFIG to an erroneous steady-state operating point. This way, correction of the magnetizing inductance value should be performed when detecting the achievement of this condition, with differences in the expected values for variables such as, for example, reactive power. For this reason, the proposed strategy is based on the dynamic equations of DFIG, considering that, for steady state, one has
. It is assumed that the
d axis of the Park transform is aligned with the stator voltage, which means that
and
, where
and
are the stator voltages at the
d and
q coordinates. From these considerations and from Equations (27) to (34), the problem can be solved as follows:
It should be noted that Equations (27) to (34) assume that the directions of stator and rotor currents are entering the DFIG. The stator current direction assumed for the mathematical equation of the strategy proposed here, as shown in
Figure 2, comes out of the generator, so the stator current signals have been changed to suit the calculation.
From Equations (108) and (109), the value of the rotor currents can be estimated as follows:
The values of the variables represented with “~” are estimated, whereas the variables represented with “^” have their values measured. Therefore, and are the estimated values of rotor currents, and , , and are the measured values of stator voltages and currents, respectively. and are the estimated values of the magnetizing inductance and stator self-inductance, respectively. Initially, their nominal values are considered for the calculation.
As previously mentioned, variations in the dispersion inductances are irrelevant in the control, so it is possible to state that variations in the DFIG magnetizing inductance are reflected in equal proportions in the rotor and stator proper inductances, as follows:
where
and
are the nominal values provided by the manufacturer. Substituting Equation (31) into (114) results in
where,
Similarly to the rotor:
and, therefore, it is possible to modify Equations (112) and (113) to be exclusively dependent on
,
With the estimated values of rotor currents by Equations (120) and (121), it is possible to estimate the slip and magnetizing inductance by Equations (110) and (111), respectively, as shown below:
and the values of
and
are found by Equations (100) and (101).
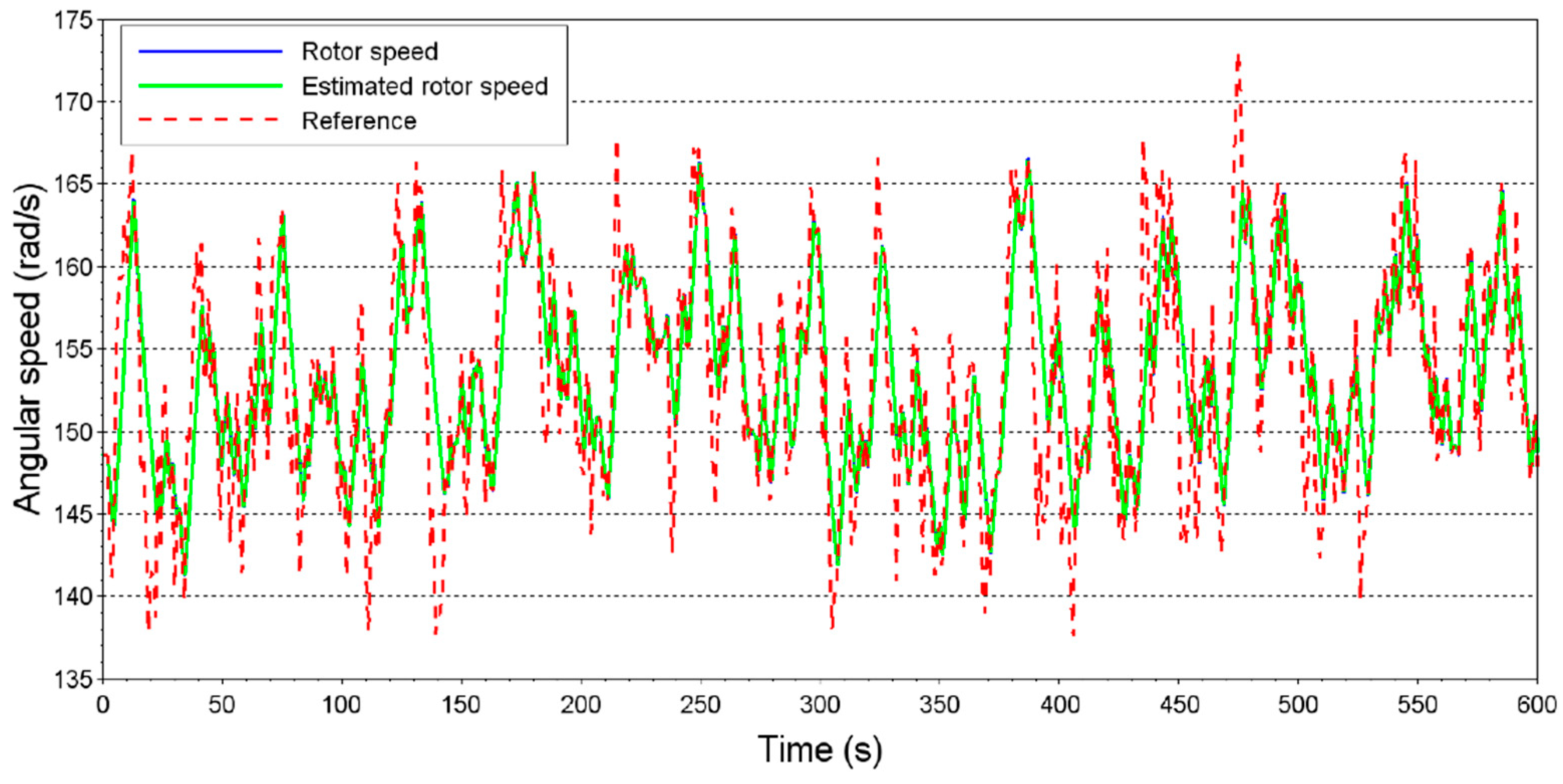
The slip estimation process is performed in real time, and its estimated value is used in the optimization process presented in
Section 2.4 and
Section 2.5. The estimation of magnetizing inductance is not performed in real time, as the current transient would generate unrealistic values for
. The strategy proposes that the magnetizing inductance value should be calculated when the machine is in a steady state and the stator reactive power is not close to zero, considering a tolerance. Failure to achieve this objective of steady-state control indicates that the value of the magnetizing inductance used in calculating the reference values of the control variables is different from the actual value. It is expected that, under this condition, the estimated rotor and slip current values are wrong. Upon detecting this condition, the value of
will be corrected using Equation (123), and the corrected value will be used for the calculation of the analytic solution and optimal strategy routines.
There are two values for possible for the solution of Equation (123). To achieve a less turbulent convergence toward the actual inductance value, the value closest to the value calculated in the previous step is always chosen.