Energy Footprint of Mechanized Agricultural Operations
Abstract
1. Introduction
2. Materials and Methods
2.1. Energy Cost of Agricultural Operations
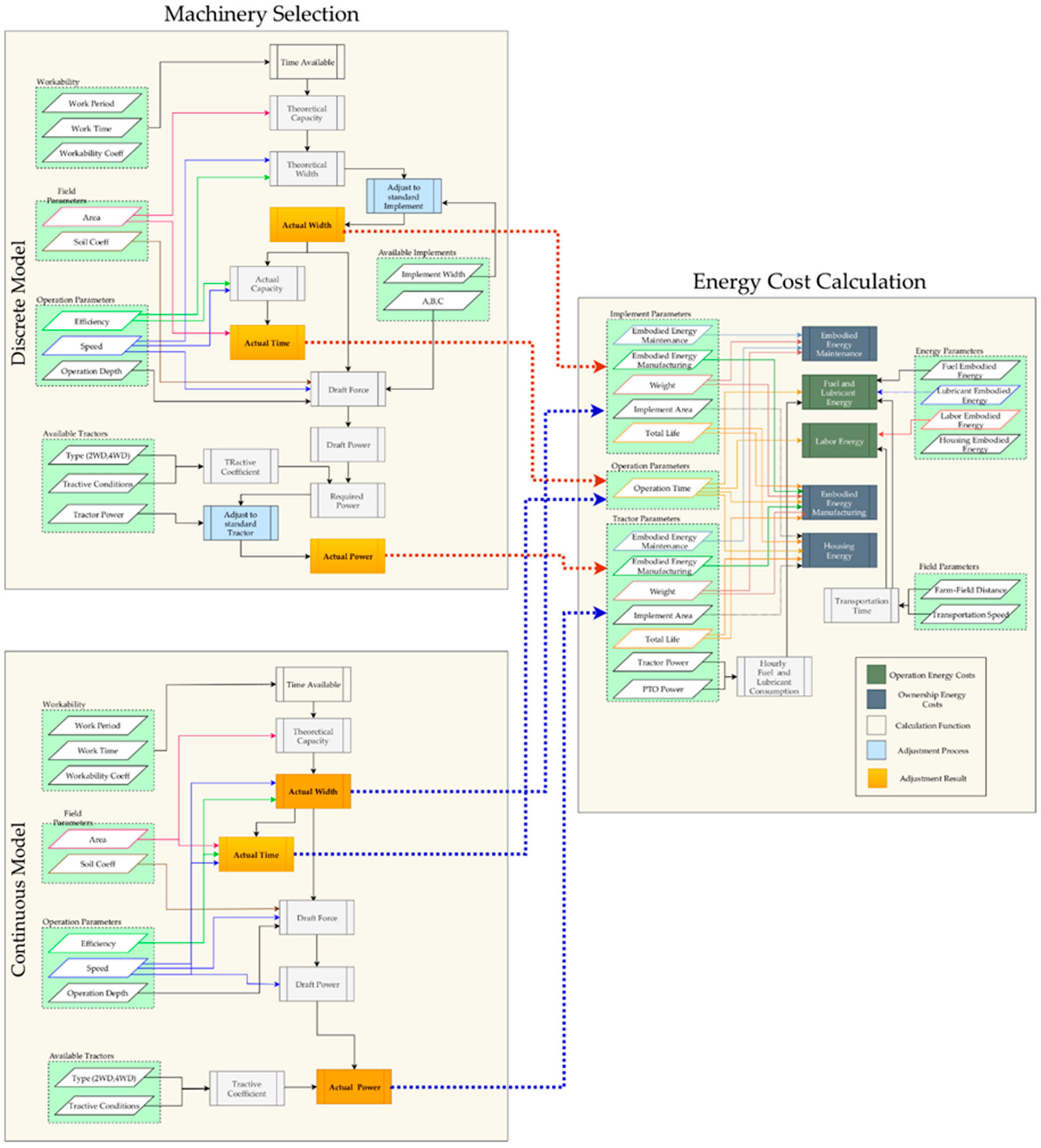
2.2. Energy Estimation Model
3. Case Study Description
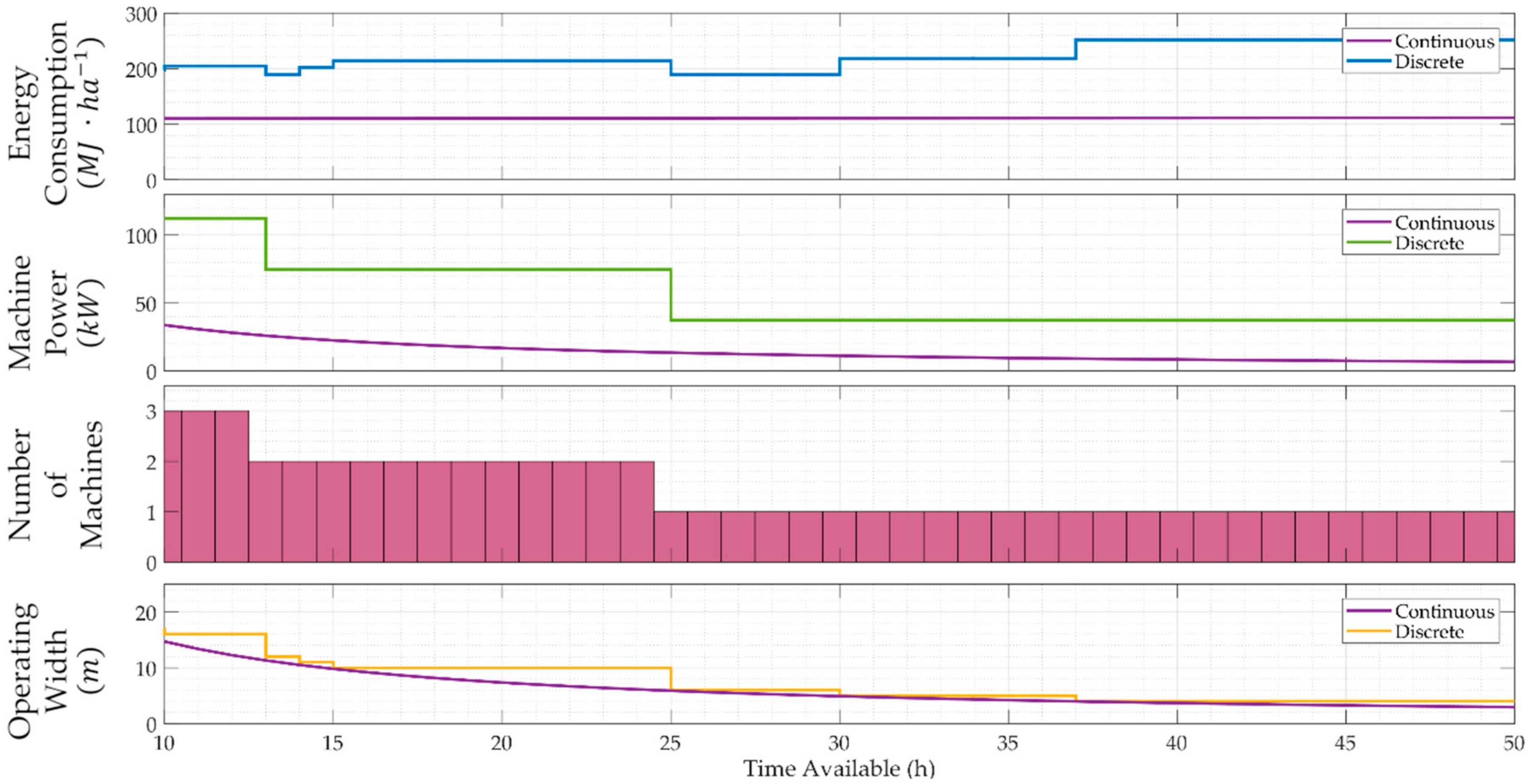
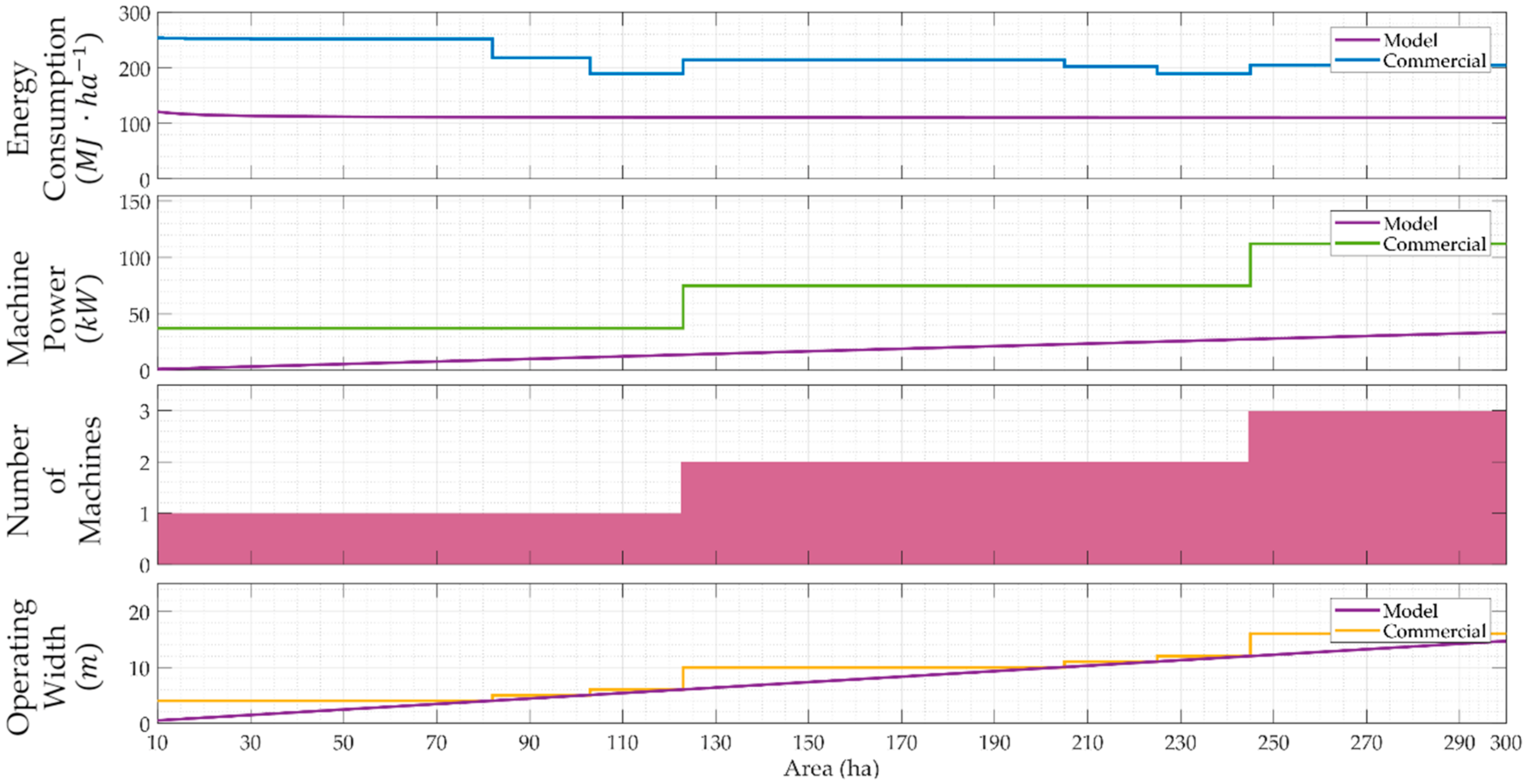
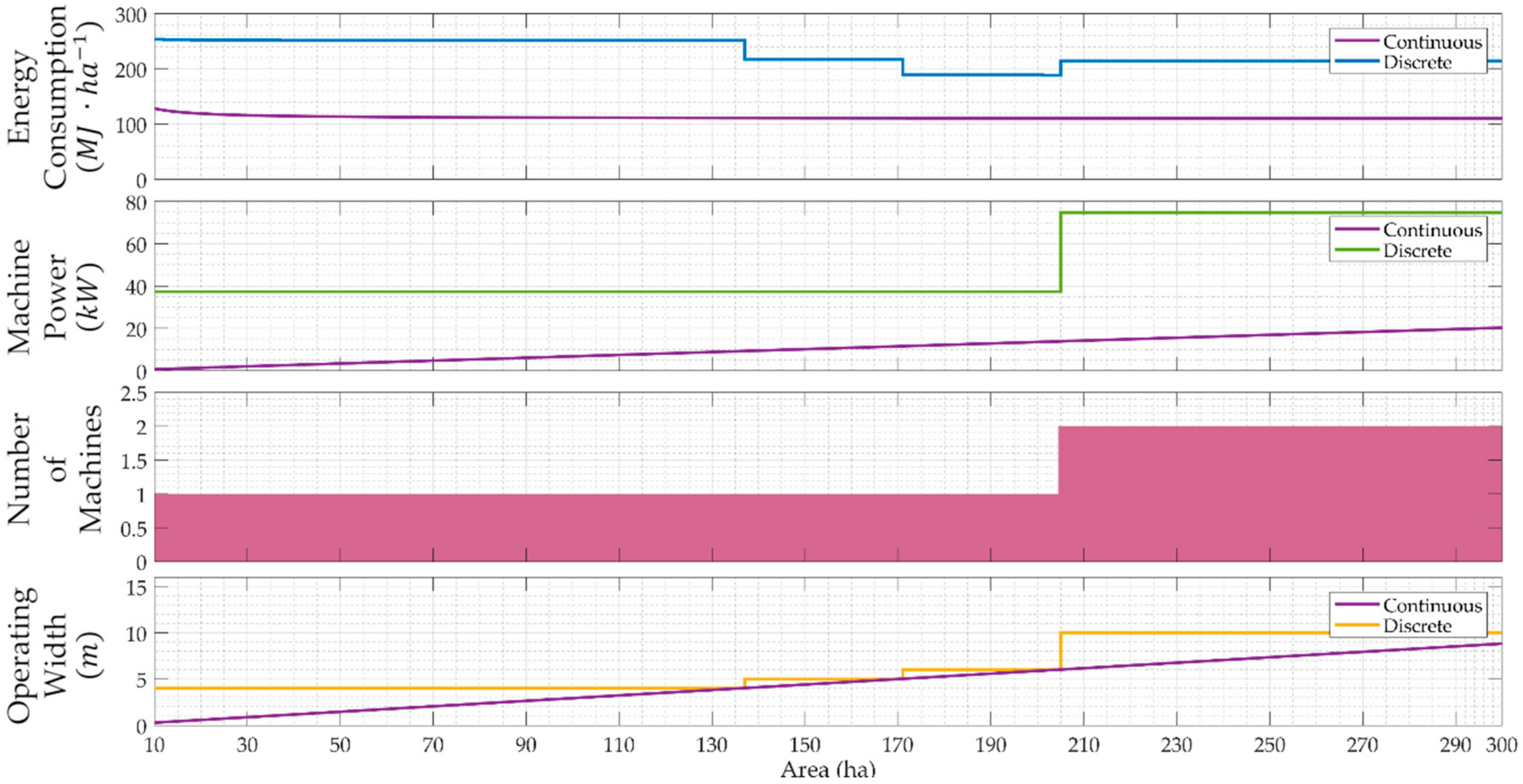
4. Results
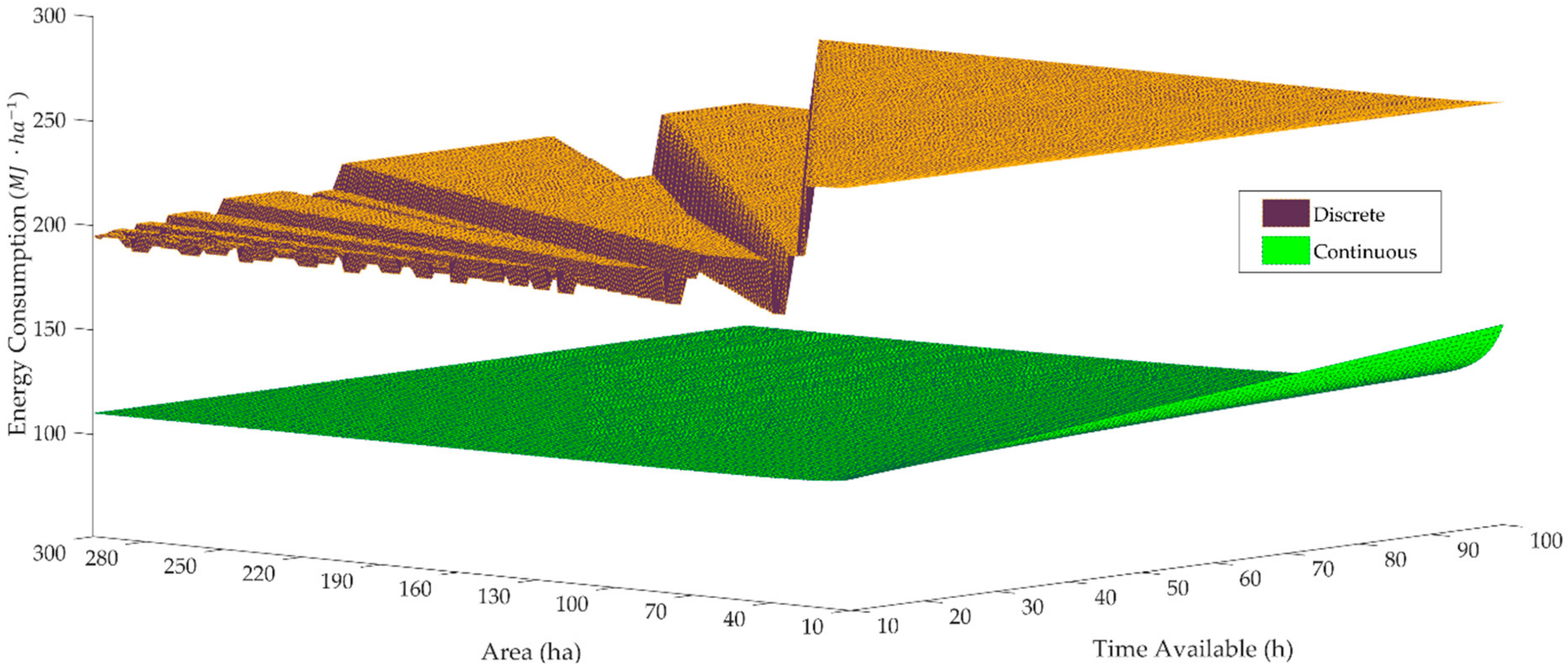
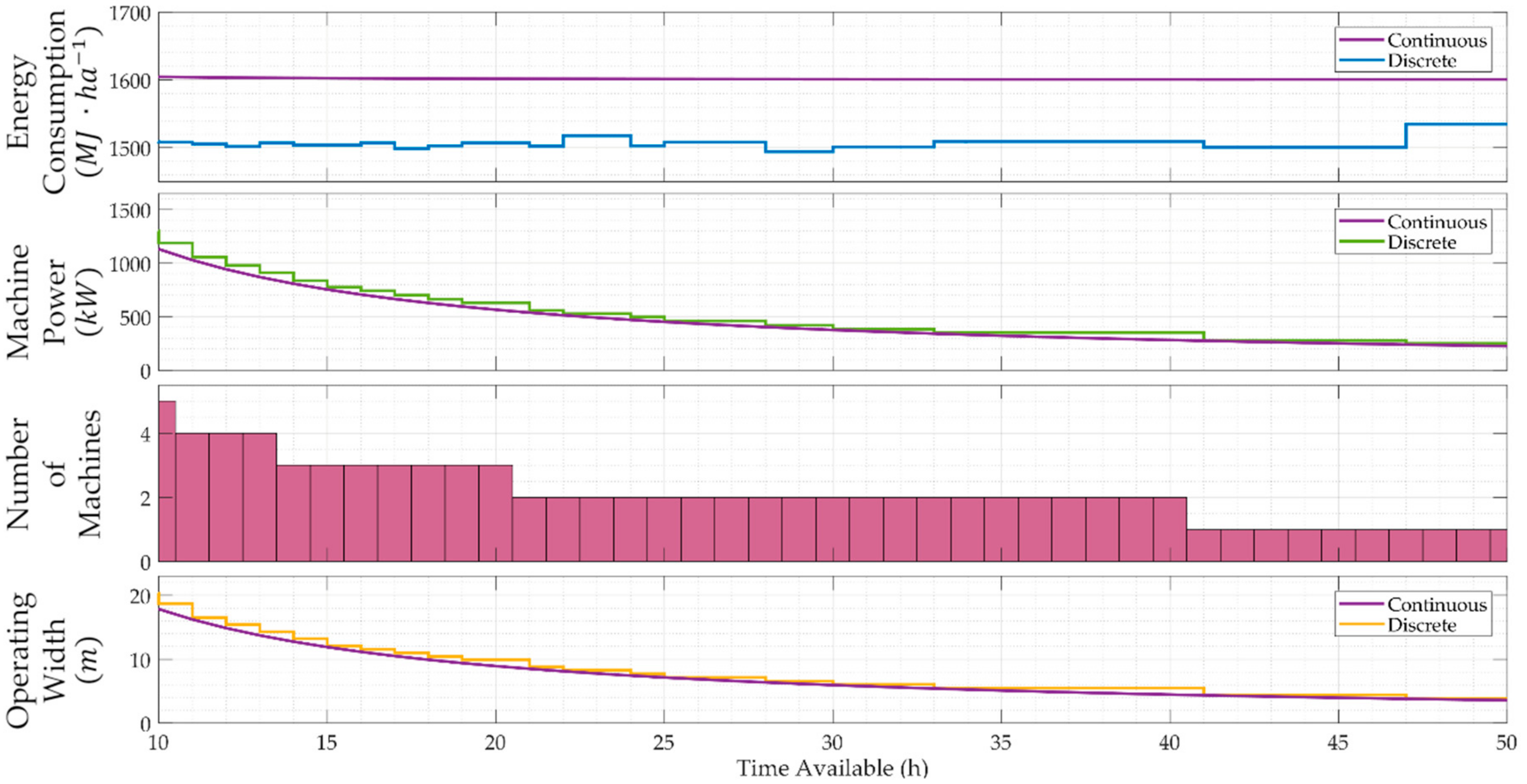
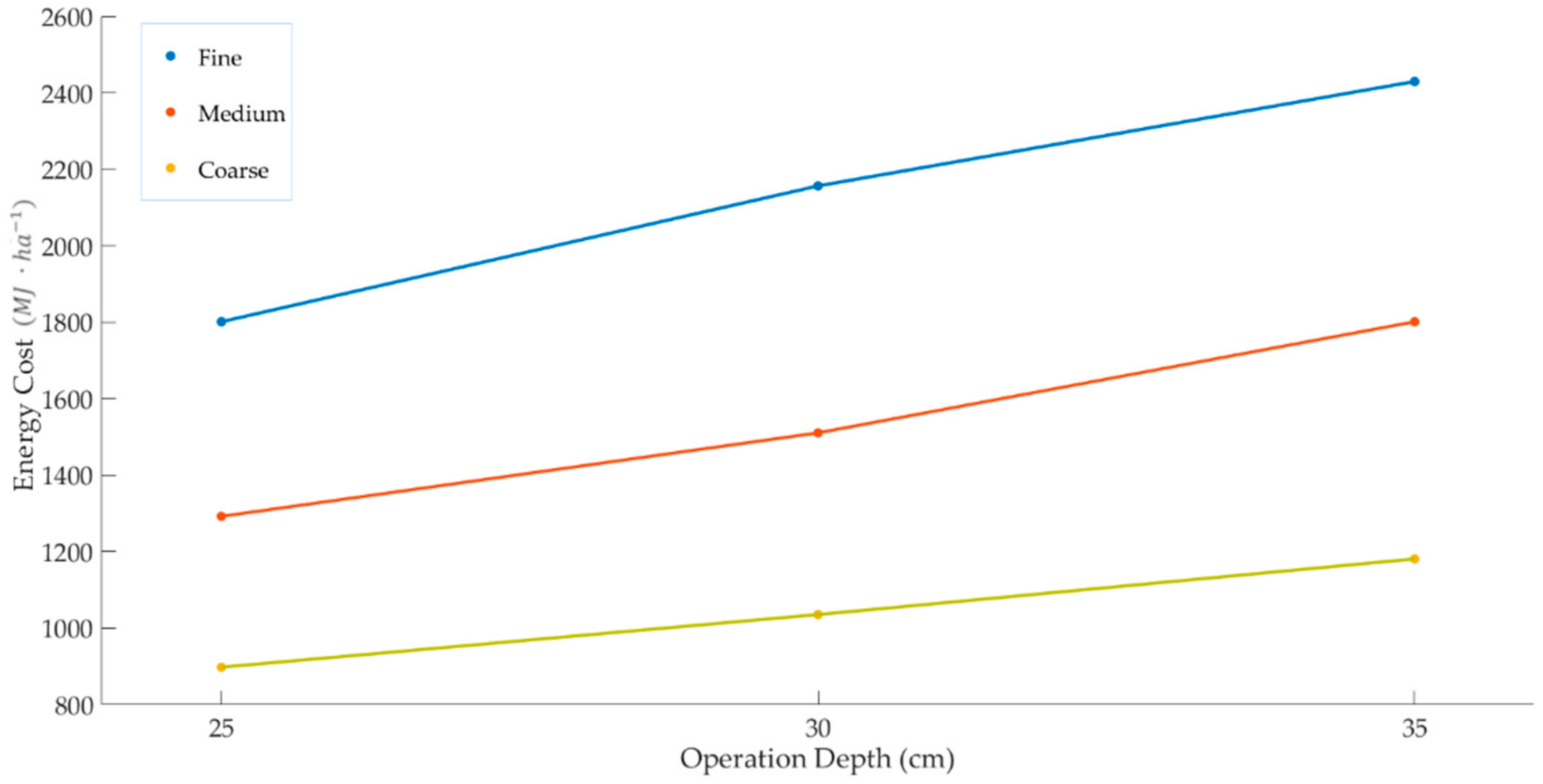
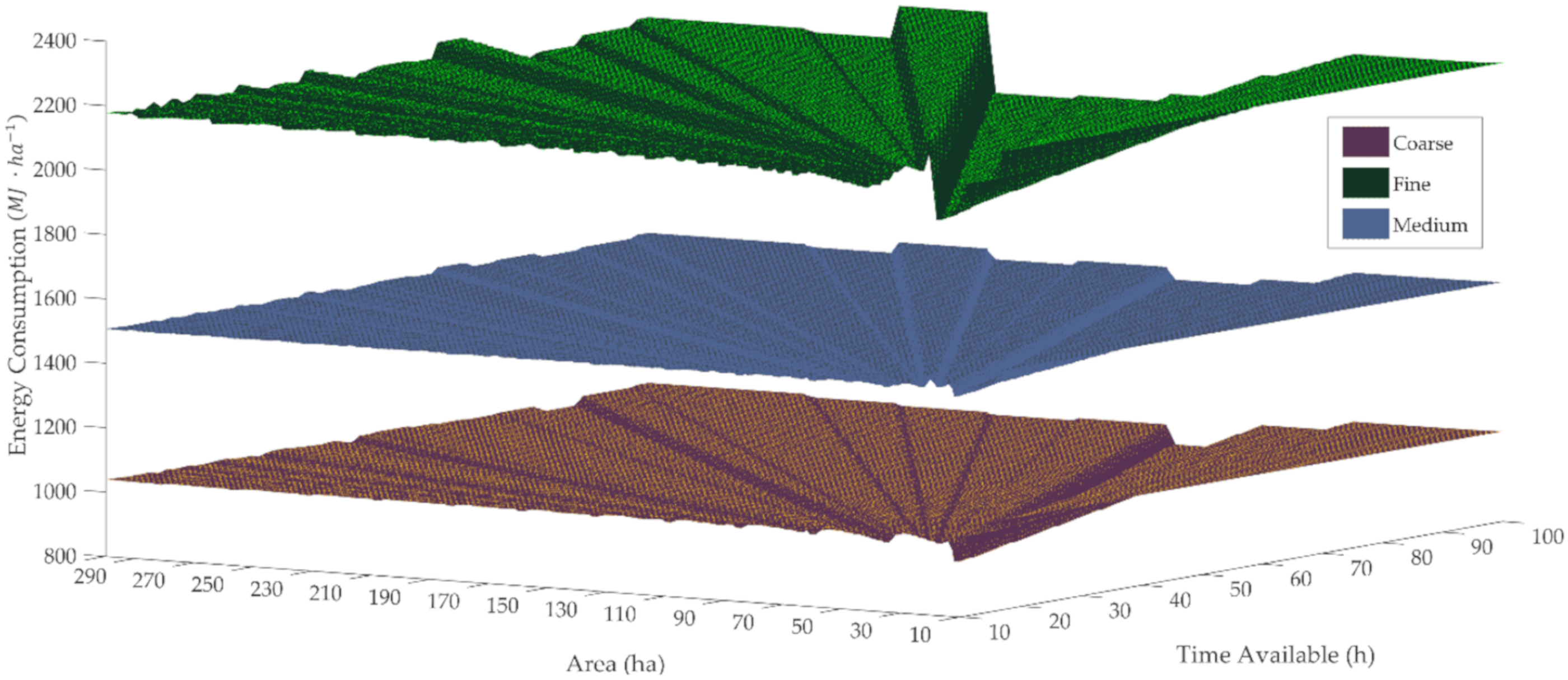
4.1. Field Cultivator
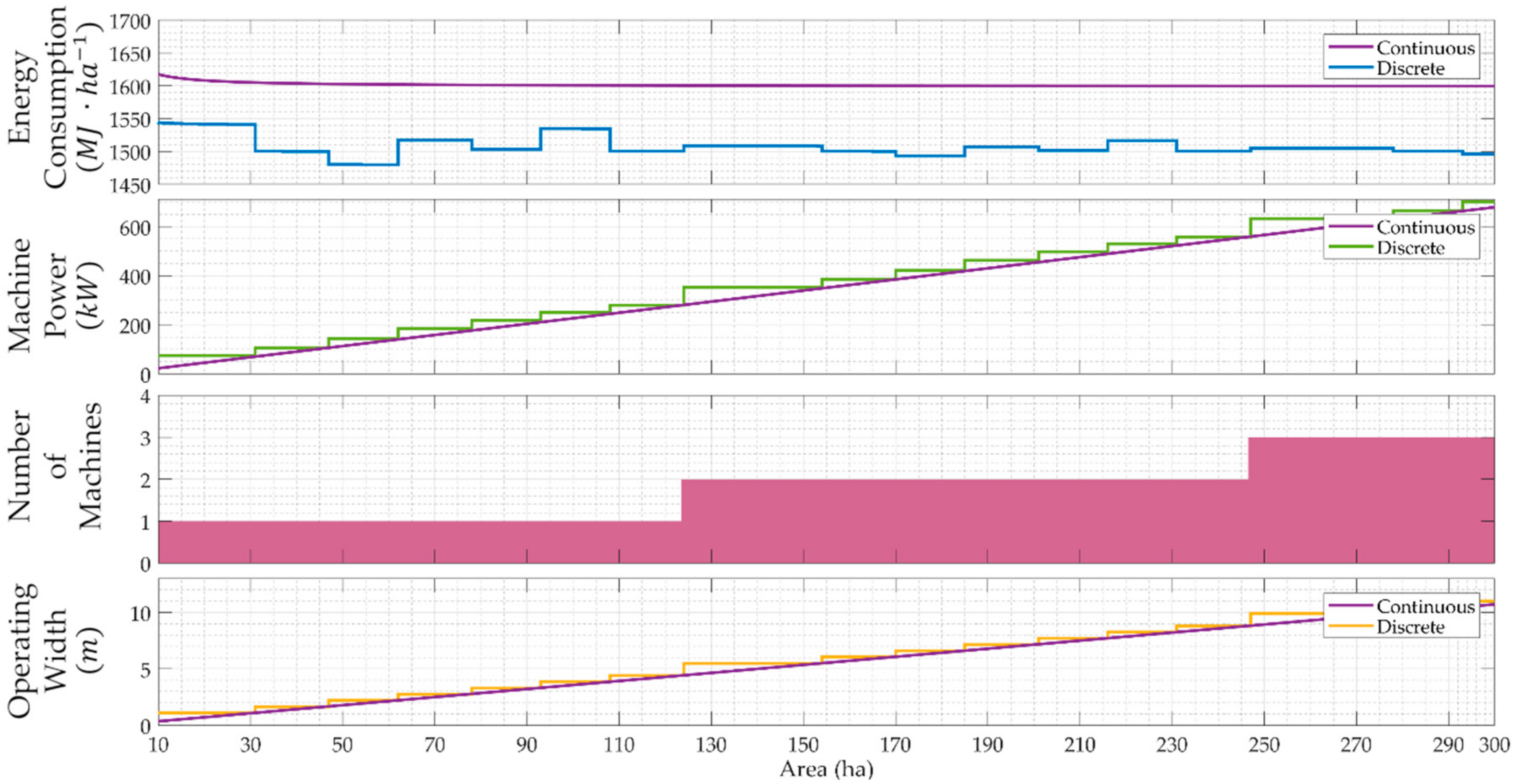
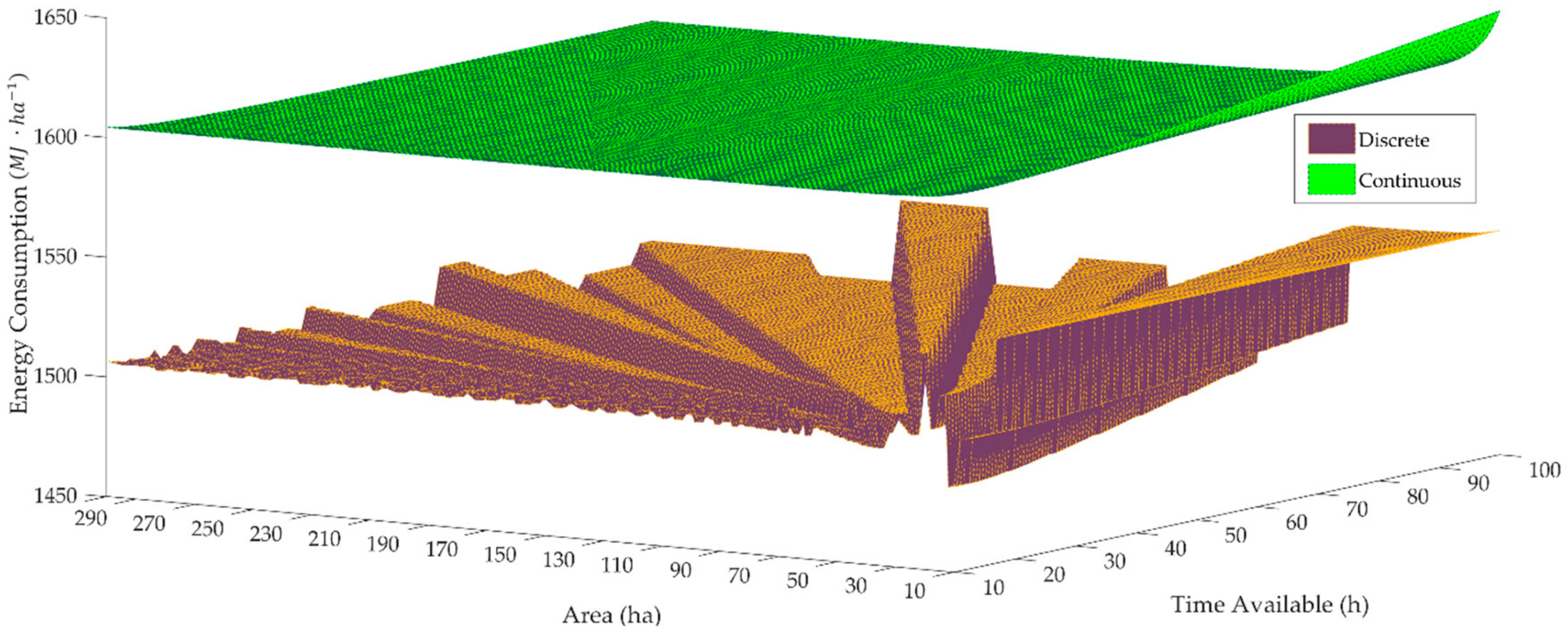
4.2. Moldboard Plow
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- De Olde, E.M.; Moller, H.; Marchand, F.; McDowell, R.W.; MacLeod, C.J.; Sautier, M.; Halloy, S.; Barber, A.; Benge, J.; Bockstaller, C.; et al. When experts disagree: The need to rethink indicator selection for assessing sustainability of agriculture. Environ. Dev. Sustain. 2017, 19, 1327–1342. [Google Scholar] [CrossRef]
- Bockstaller, C.; Beauchet, S.; Manneville, V.; Amiaud, B.; Botreau, R. A tool to design fuzzy decision trees for sustainability assessment. Environ. Model. Softw. 2017, 97, 130–144. [Google Scholar] [CrossRef]
- Rodias, E.C.; Lampridi, M.; Sopegno, A.; Berruto, R.; Banias, G.; Bochtis, D.D.; Busato, P. Optimal energy performance on allocating energy crops. Biosyst. Eng. 2019, 181, 11–27. [Google Scholar] [CrossRef]
- Lampridi, M.G.; Sørensen, C.G.; Bochtis, D.D. Agricultural Sustainability: A Review of Concepts and Methods. Sustainability 2019, 11, 5120. [Google Scholar] [CrossRef]
- Bockstaller, C.; Guichard, L.; Keichinger, O.; Girardin, P.; Galan, M.B.; Gaillard, G. Review article Comparison of methods to assess the sustainability of agricultural systems. A review. Agronomy 2009, 29, 223–235. [Google Scholar]
- Snapp, S.S.; Grabowski, P.; Chikowo, R.; Smith, A.; Anders, E.; Sirrine, D.; Chimonyo, V.; Bekunda, M. Maize yield and profitability tradeoffs with social, human and environmental performance: Is sustainable intensification feasible? Agric. Syst. 2018, 162, 77–88. [Google Scholar] [CrossRef]
- Allahyari, M.S.; Daghighi Masouleh, Z.; Koundinya, V. Implementing Minkowski fuzzy screening, entropy, and aggregation methods for selecting agricultural sustainability indicators. Agroecol. Sustain. Food Syst. 2016, 40, 277–294. [Google Scholar] [CrossRef]
- De Olde, E.M.; Oudshoorn, F.W.; Sørensen, C.A.G.; Bokkers, E.A.M.; De Boer, I.J.M. Assessing sustainability at farm-level: Lessons learned from a comparison of tools in practice. Ecol. Indic. 2016, 66, 391–404. [Google Scholar] [CrossRef]
- Sajjad, H.; Nasreen, I. Assessing farm-level agricultural sustainability using site-specific indicators and sustainable livelihood security index: Evidence from Vaishali district, India. Community Dev. 2016, 47, 602–619. [Google Scholar] [CrossRef]
- Gaviglio, A.; Bertocchi, M.; Demartini, E. A Tool for the Sustainability Assessment of Farms: Selection, Adaptation and Use of Indicators for an Italian Case Study. Resources 2017, 6, 60. [Google Scholar] [CrossRef]
- Peano, C.; Migliorini, P.; Sottile, F. A methodology for the sustainability assessment of agri-food systems. Ecol. Soc. 2014, 19, 19. [Google Scholar] [CrossRef]
- Chopin, P.; Tirolien, J.; Blazy, J.M. Ex-ante sustainability assessment of cleaner banana production systems. J. Clean. Prod. 2016, 139, 15–24. [Google Scholar] [CrossRef]
- De Luca, A.I.; Falcone, G.; Stillitano, T.; Iofrida, N.; Strano, A.; Gulisano, G. Evaluation of sustainable innovations in olive growing systems: A Life Cycle Sustainability Assessment case study in southern Italy. J. Clean. Prod. 2018, 171, 1187–1202. [Google Scholar] [CrossRef]
- Rodias, E.; Berruto, R.; Bochtis, D.; Busato, P.; Sopegno, A. A computational tool for comparative energy cost analysis of multiple-crop production systems. Energies 2017, 10, 831. [Google Scholar] [CrossRef]
- Bartzas, G.; Vamvuka, D.; Komnitsas, K. Comparative life cycle assessment of pistachio, almond and apple production. Inf. Process. Agric. 2017, 4, 188–198. [Google Scholar] [CrossRef]
- Strapatsa, A.V.; Nanos, G.D.; Tsatsarelis, C.A. Energy flow for integrated apple production in Greece. Agric. Ecosyst. Environ. 2006, 116, 176–180. [Google Scholar] [CrossRef]
- Rodias, E.; Berruto, R.; Bochtis, D.; Sopegno, A.; Busato, P. Green, yellow, and woody biomass supply-chain management: A review. Energies 2019, 12, 3020. [Google Scholar] [CrossRef]
- Viola, I.; Marinelli, A. Life Cycle Assessment and Environmental Sustainability in the Food System. Agric. Agric. Sci. Procedia 2016, 8, 317–323. [Google Scholar] [CrossRef][Green Version]
- Mantoam, E.J.; Romanelli, T.L.; Gimenez, L.M.; Milan, M. Energy demand and greenhouse gases emissions in the life cycle of coffee harvesters. Chem. Eng. Trans. 2017, 58, 175. [Google Scholar]
- Mantoam, E.J.; Romanelli, T.L.; Gimenez, L.M. Energy demand and greenhouse gases emissions in the life cycle of tractors. Biosyst. Eng. 2016, 151, 158–170. [Google Scholar] [CrossRef]
- Sørensen, C.G.; Halberg, N.; Oudshoorn, F.W.; Petersen, B.M.; Dalgaard, R. Energy inputs and GHG emissions of tillage systems. Biosyst. Eng. 2014, 120, 2–14. [Google Scholar] [CrossRef]
- Tassielli, G.; Renzulli, P.A.; Mousavi-Avval, S.H.; Notarnicola, B. Quantifying life cycle inventories of agricultural field operations by considering different operational parameters. Int. J. Life Cycle Assess. 2019, 24, 1075–1092. [Google Scholar] [CrossRef]
- Bochtis, D.; Sorensen, C.G.; Kateris, D. Operations Management in Agriculture, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2018; ISBN 9780128097168. [Google Scholar]
- Edwards, W. Farm Machinery Selection. Available online: https://www.extension.iastate.edu/agdm/crops/html/a3-28.html (accessed on 3 January 2020).
- Bochtis, D.D.; Sørensen, C.G.C.; Busato, P. Advances in agricultural machinery management: A review. Biosyst. Eng. 2014, 126, 69–81. [Google Scholar] [CrossRef]
- Marinoudi, V.; Sørensen, C.G.; Pearson, S.; Bochtis, D. Robotics and labour in agriculture. A context consideration. Biosyst. Eng. 2019, 184, 111–121. [Google Scholar] [CrossRef]
- Sørensen, C.G.; Nielsen, V. Operational analyses and model comparison of machinery systems for reduced tillage. Biosyst. Eng. 2005, 92, 143–155. [Google Scholar] [CrossRef]
- Lampridi, M.G.; Kateris, D.; Vasileiadis, G.; Marinoudi, V.; Pearson, S.; Sørensen, C.G.; Balafoutis, A.; Bochtis, D. A Case-Based Economic Assessment of Robotics Employment in Precision Arable Farming. Agronomy 2019, 9, 175. [Google Scholar] [CrossRef]
- Lee, J.; Cho, H.J.; Choi, B.; Sung, J.; Lee, S.; Shin, M. Life cycle assessment of tractors. Int. J. Life Cycle Assess. 2000, 5, 205–208. [Google Scholar] [CrossRef]
- Aguilera, E.; Guzmán, G.I.; Infante-amate, J.; García-ruiz, R.; Herrera, A.; Villa, I. Embodied energy in agricultural inputs. Incorporating a historical perspective. DT-SEHA 15. 2015, p. 119. Available online: http://hdl.handle.net/10234/141278 (accessed on 5 December 2019).
- Audsley, E.; Stacey, K.; Parsons, D.J.; Williams, A.G. Estimation of the greenhouse gas emissions from agricultural pesticide manufacture and use. Uma ética para quantos? 2014, p. 20. Available online: https://dspace.lib.cranfield.ac.uk/bitstream/handle/1826/3913/Estimation_of_the_greenhouse_gas_emissions_from_agricultural_pesticide_manufacture_and_use2009.pdf;jsessionid=DC4D51F03A8C73E065940B464D68BDBD?sequence=1 (accessed on 5 December 2019).
- Mantoam, E.J.; Mekonnen, M.M.; Romanelli, T.L. Energy demand and water footprint study of an agricultural machinery industry. Agric. Eng. Int. CIGR J. 2018, 20, 132. [Google Scholar]
- Kitani, O. CIGR Handbook of Agricultural Engineering, Volume 5: Energy and Biomass Engineering; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 1999. [Google Scholar]
- ASABE. ASAE D497.5 FEB 2006 Agricultural Machinery Management Data; ASABE: St. Joseph, MI, USA, 2006. [Google Scholar]
- Kitani, O.; Jungbluth, T.; Peart, R.; Ramdani, A. CIGR Handbook of Agricultural Engineering Volume V; CIGR: Liege, Belgium, 1999; ISBN 0929355970. [Google Scholar]
- Canakci, M.; Akinci, I. Energy use pattern analyses of greenhouse vegetable production. Energy 2006, 31, 1243–1256. [Google Scholar] [CrossRef]
- Kuswardhani, N.; Soni, P.; Shivakoti, G.P. Comparative energy input-output and financial analyses of greenhouse and open field vegetables production in West Java, Indonesia. Energy 2013, 53, 83–92. [Google Scholar] [CrossRef]
- Reineke, H.; Stockfisch, N.; Märländer, B. Analysing the energy balances of sugar beet cultivation in commercial farms in Germany. Eur. J. Agron. 2013, 45, 27–38. [Google Scholar] [CrossRef]
- Schramski, J.R.; Jacobsen, K.L.; Smith, T.W.; Williams, M.A.; Thompson, T.M. Energy as a potential systems-level indicator of sustainability in organic agriculture: Case study model of a diversified, organic vegetable production system. Ecol. Model. 2013, 267, 102–114. [Google Scholar] [CrossRef]
- Busato, P.; Berruto, R. Minimising manpower in rice harvesting and transportation operations. Biosyst. Eng. 2016, 151, 435–445. [Google Scholar] [CrossRef]
- ASABE. D497.7: Agricultural Machinery Management Proposed; ASABE: St. Joseph, MI, USA, 2015. [Google Scholar]
- ASAE. ASAE EP496.3—Agricultural Machinery Management; ASABE: St. Joseph, MI, USA, 2009. [Google Scholar]
- Tsatsarelis, C. Agricultural Machinery Management, 1st ed.; Giachoudi Publications: Thessaloniki, Greece, 2006; ISBN 960-7425-86-3. [Google Scholar]
- Saunders, C.; Barber, A.; Taylor, G. Food Miles-Comparative Energy/Emissions Performance of New Zealand’s Agriculture Industry; Agribusiness and Economics Research Unit, Lincoln University: Canterbury, New Zealand, 2006. [Google Scholar]

| Units | Moldboard Plow | Field Cultivator | |
|---|---|---|---|
| Implement Parameters A, B, and C 1 | - | 652-0-5.1 | 32-1.9-0 |
| Economic Life 1 | y | 15 | 15 |
| Total Life 1 | h | 2000 | 2000 |
| Efficiency 1 | % | 80 | 85 |
| Operating Speed 1 | 7 | 8 | |
| Operating Depth 2 | cm | 30 | 15 |
| Soil Coefficient (Medium Soil) 1 | - | 0.7 | 0.85 |
| Implement Width Range * | m | 1.1–4.4 | 4–6 |
| Energy Parameter | Units | Value |
|---|---|---|
| Tractor Embodied Energy (Manufacturing) 1 | 138 | |
| Implement Embodied Energy (Manufacturing) 1 | 180 | |
| Tractor Embodied Energy (Maintenance) 2 | % | 45 |
| Implement Embodied Energy (Maintenance) 2 | % | 30 |
| Labor Embodied Energy 3 | 2.2 | |
| Fuel Embodied Energy (Diesel) 1 | 47.8 | |
| Lubricant Embodied Energy 4 | 46 | |
| Housing Embodied Energy 2 | 21 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lampridi, M.; Kateris, D.; Sørensen, C.G.; Bochtis, D. Energy Footprint of Mechanized Agricultural Operations. Energies 2020, 13, 769. https://doi.org/10.3390/en13030769
Lampridi M, Kateris D, Sørensen CG, Bochtis D. Energy Footprint of Mechanized Agricultural Operations. Energies. 2020; 13(3):769. https://doi.org/10.3390/en13030769
Chicago/Turabian StyleLampridi, Maria, Dimitrios Kateris, Claus Grøn Sørensen, and Dionysis Bochtis. 2020. "Energy Footprint of Mechanized Agricultural Operations" Energies 13, no. 3: 769. https://doi.org/10.3390/en13030769
APA StyleLampridi, M., Kateris, D., Sørensen, C. G., & Bochtis, D. (2020). Energy Footprint of Mechanized Agricultural Operations. Energies, 13(3), 769. https://doi.org/10.3390/en13030769








